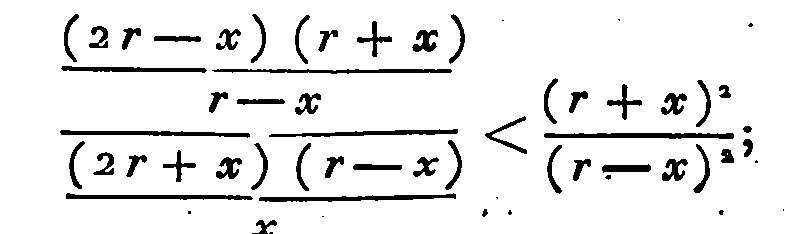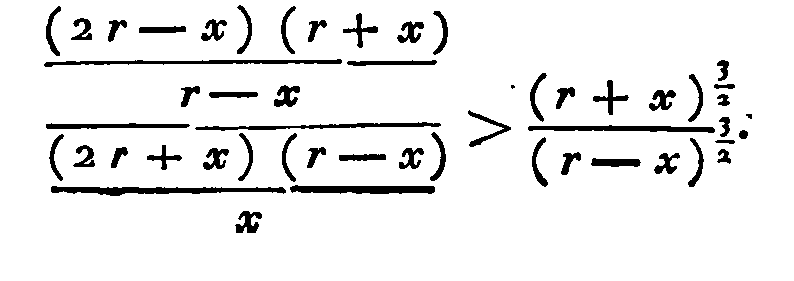DE
LA SPHÈRE ET DU CYLINDRE.
LIVRE SECOND.
livre 1
ARCHIMÈDE A DOSITHÉE, SALUT.
Tu m'avais engagé à écrire les
démonstrations des problèmes que j'avais envoyés à Conon; mais il est arrivé que
la plupart de ces problèmes découlent des théorèmes dont je t'ai déjà envoyé les
démonstrations ; tels sont, par exemple les théorèmes suivants :
La surface d'une sphère quelconque est
quadruple d'un de ses grands cercles.
La surface d'un segment sphérique
quelconque est égale à un cercle qui a un rayon égal à la droite menée du sommet
du segment à la circonférence de sa base.
Un cylindre qui a une base égale à un
grand cercle d'une sphère, et une hauteur égale au diamètre de cette sphère, est
égal à trois fois la moitié de cette sphère, et la surface de ce cylindre est
aussi égale à trois fois la moitié de la surface de cette même sphère.
Et enfin, tout secteur solide est égal
à un cône qui a une base égale à la partie de la surface de la sphère comprise
dans le secteur, et une hauteur égale au rayon de la sphère.
Tu trouveras dans le livre que je
t'envoie tous les théorèmes et tous les problèmes qui découlent des théorèmes
dont je viens de parler.
Quant aux choses que l’on trouve par d'autres considérations et qui regardent
les hélices et les conoïdes, je ferai en sorte de te les envoyer le plutôt
possible. Voici quel était le premier problème.
PROPOSITION I.
Une sphère étant donnée, trouver une
surface plane égale à la surface de cette sphère.
Cela est évident; car la démonstration
de ce problème est une suite du théorème dont nous venons de parler ; attendu
que le quadruple d'un grand cercle, qui est une surface plane, est égal à la
surface de la sphère.
PROPOSITION II.
Le problème suivant était le second.
Un cône ou un cylindre étant donné,
trouver une sphère égale à ce cône ou à ce cylindre.

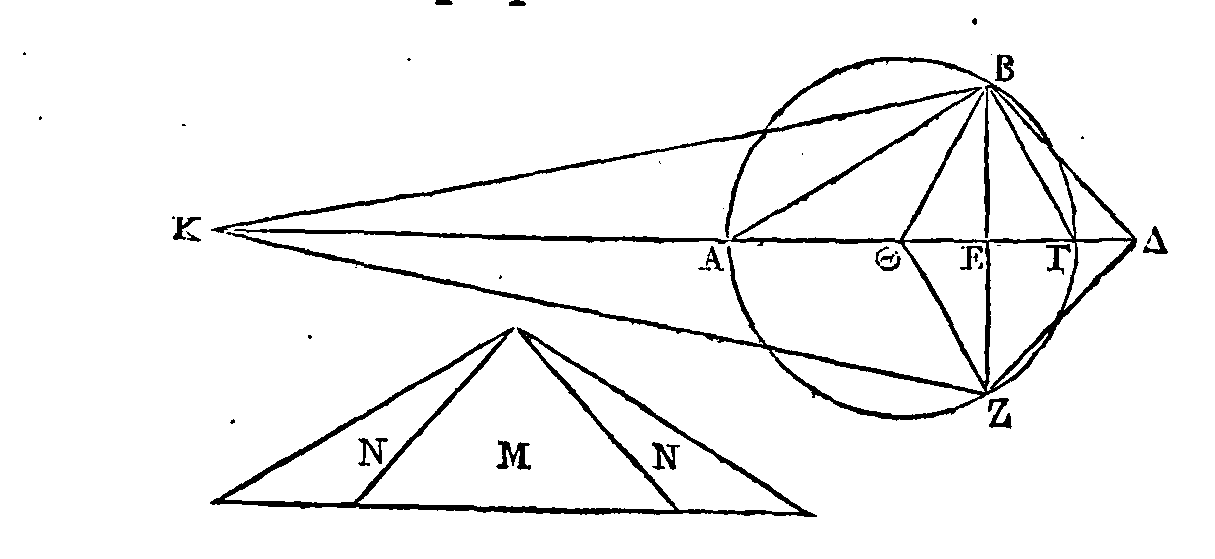
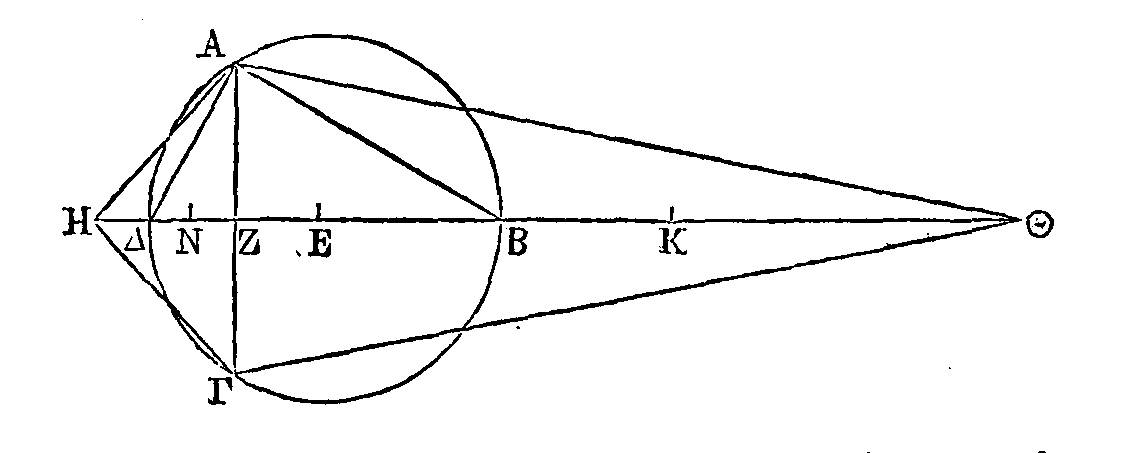
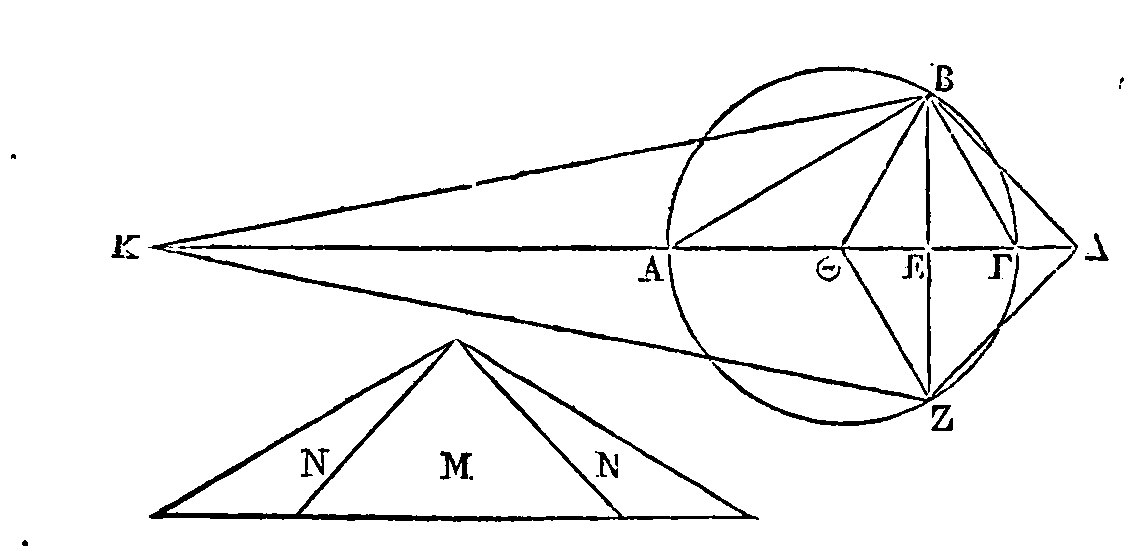
Soit
A
le cône ou le cylindre donné.
Que la sphère
B
soit égale à
A.
Supposons que le cylindre
ΓZΔ
soit
égal à trois fois la moitié du cône ou du cylindre A. Que le cylindre qui a pour
base le cercle décrit autour du diamètre
HΘ,
et pour axe la droite
KΛ
égale au diamètre de la sphère
B,
soit
égal à trois fois la moitié de la sphère
B
: le cylindre
E
sera
égal au cylindre
K.
Mais les bases des cylindres
égaux sont réciproquement proportionnelles à leurs hauteurs ; donc le cercle E
est au cercle
K,
c'est-à-dire le carré construit sur ΓΔ est au carré
construit sur
HΘ comme
KΛ
est à
EZ.
Mais
KΛ
est
égal à
HΘ ;
car
un cylindre qui est égal à trois fois la moitié de la sphère, et dont l’axe est
égal au diamètre de cette même sphère, a une base K égale à un grand cercle de
cette même sphère (I, 37). Donc le carré construit sur ΓΔ est au carré construit
sur
HΘ
comme
HΘ est à
EZ.
Que
la surface comprise sous ΓΔ,
MN
soit égale au carré
construit sur
HΘ
(α). Λa droite ΓΔ sera à la droite
MN
comme
le carré construit sur ΓΔ est au carré construit sur
HΘ,
c'est-à-dire comme
HΘ
est à EZ ; et par permutation,
la droite
ΓΔ
est à la droite HΘ comme HΘ est
à
MN,
et comme
MN
est à EZ. Mais les
deux droites
ΓΔ,
EZ
sont données (β); donc
les deux moyennes proportionnelles
HΘ, MN
entre les deux droites
ΓΔ,
EZ
sont aussi données. Donc
chacune des deux droites HΘ,
MN
est donnée.
On construira le problème de la
manière suivante. Soit a le cône
ou le cylindre donné. Il faut trouver une sphère égale au cône ou au cylindre A.
Que le cylindre dont la base est le
cercle décrit autour du diamètre
ΓΔ,
et dont l’axe est la droite
EZ, soit
égal à trois fois la moitié du cône ou du cylindre A. Prenons deux moyennes
proportionnelles HΘ,
MN entre ΓΔ,
EZ,
de manière que ΓΔ soit à HΘ comme HΘ est à
MN,
et comme
MN
est à
EZ
(γ) ; et concevons un
cylindre qui ait pour base le cercle décrit autour du diamètre HΘ,
et pour axe la droite
KΛ
égale au diamètre HΘ.
Je dis que le cylindre E
est égal au cylindre K.
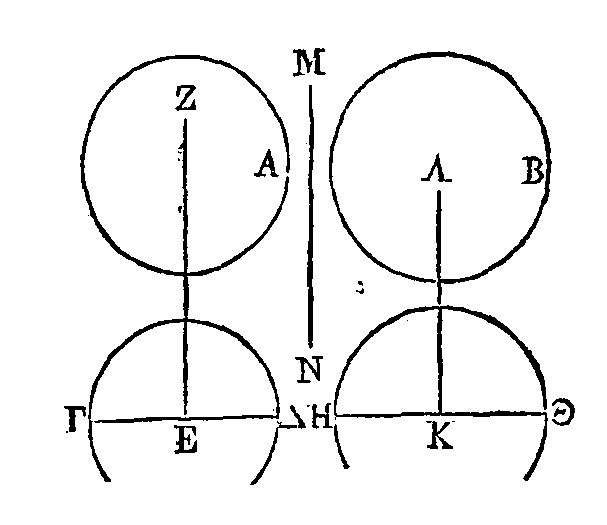
Puisque ΓΔ est à HΘ comme
MN
est à EZ; par
permutation, et à cause que HΘ est égal à
KΛ (δ),
la droite ΓΔ sera à la droite
MN,
c'est-à-dire, le carré
construit sur ΓΔ sera au carré construit sur HΘ comme le cercle E est au cercle
K. Mais le cercle E est au cercle
K
comme
KΛ
est à EZ; donc les bases
E, K
des cylindres sont
réciproquement proportionnelles à leurs hauteurs ; donc le cylindre
E
est égal au cylindre
K.
Mais
le cylindre K est égal à trois fois la moitié de la sphère qui a pour diamètre
la droite HΘ,
donc la sphère qui a un
diamètre égal à la droite HΘ,
c'est-à-dire, la sphère
B est égale au cône ou au cylindre A.
PROPOSITION III.
Un segment quelconque d'une sphère est
égal à un cône qui a la même base que ce segment, et pour hauteur une droite qui
est à la hauteur du segment comme une droite composée du rayon de la sphère et
de la hauteur de l'autre segment est à la hauteur de cet autre segment.
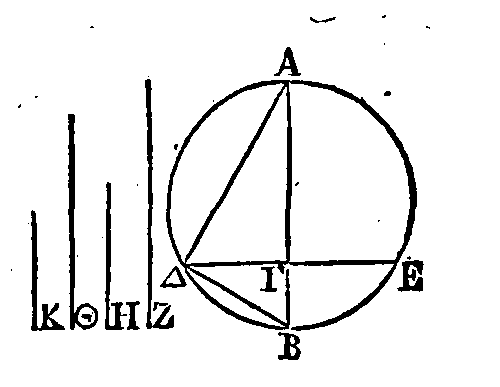
Soient une sphère et un de ses grands
cercles qui ait pour diamètre la droite AΓ. Coupons cette sphère par un plan
mené par la droite
BZ,
et perpendiculaire sur la droite AΓ. Que le
point
Θ soit le centre. Que la somme des
deux droites ΘA, AE soit à la droite
AE
comme
ΔE
est à
ΓE
; et de plus, que la somme des
deux droites ΘΓ,
ΓE
soit à la droite
ΓE
comme
KE
est à
EA.
Sur le cercle dont
BZ
est le diamètre, construisons
deux cônes qui aient pour sommets les points
K,
Δ. Je dis que le cône
BΔZ
est égal au segment de la
sphère qui est du côté Γ, et que le cône
BKZ
est égal au segment de la
sphère qui est du côté
A.
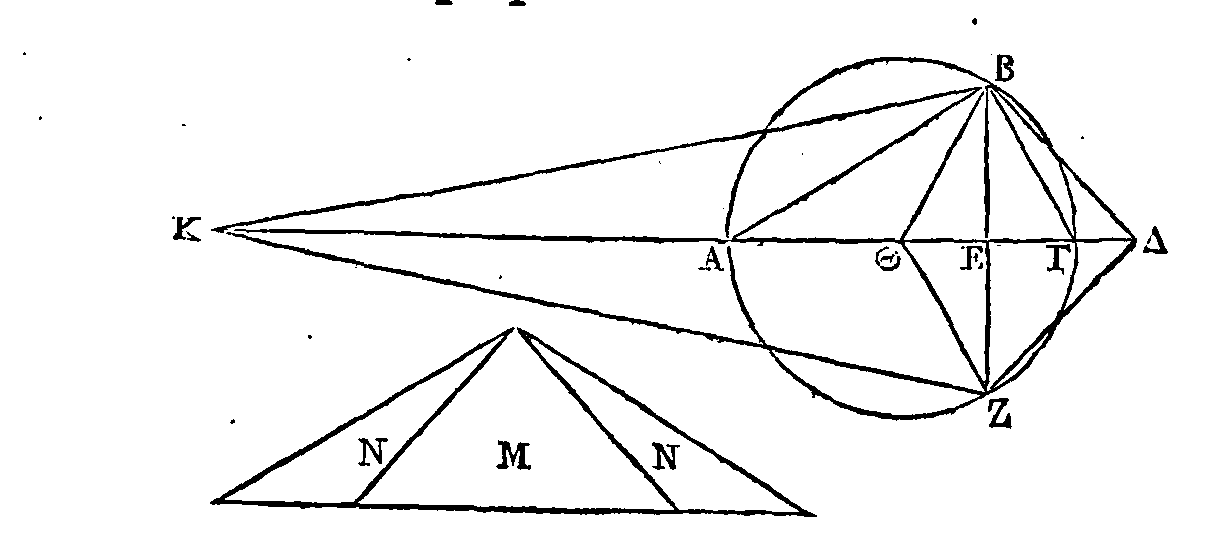
Menons les rayons
BΘ,
ΘZ : concevons un cône qui ait
pour base le cercle décrit autour du diamètre
BZ, et pour sommet le point
Θ.
Soit aussi un cône
M
qui ait une base égale à la
surface du segment sphérique BΓZ, c'est-à-dire à un cercle dont le rayon soit
égal à la droite BΓ ; et que la hauteur de ce cône soit égale au rayon de la
sphère. Le cône
M
sera égal au secteur solide BΓΘZ,
ainsi que cela a été démontré dans le premier livre (I, 50). Puisque
ΔE
est à
EΓ comme la somme des droites
ΘA,
AE est à la droite
ΔE
; par soustraction, la droite
ΓA
sera à
la droite
ΓE
comme
ΘA
est à
AE,
c'est-à-dire comme ΓΘ
est à
AE
; par
permutation, la droite ΔΓ sera à la droite ΓΘ
comme
ΓE
est à
EA ;
et enfin par addition, la
droite
ΘΔ sera à
la droite
ΘΓ comme
ΓA
est à
AE,
c'est-à-dire comme le carré construit sur
ΓB
est au carré construit sur
BE.
Donc
la droite
ΘΔ est à
la droite ΓΘ
comme le carré construit sur ΓB est au carré construit sur
BE.
Mais la droite ΓB est égale au
rayon du cercle M, et la droite
BE
est égale au rayon du cercle
décrit autour du diamètre
BZ ;
donc
ΔΘ
est à ΘΓ comme le cercle
M
est au cercle
décrit autour du diamètre
BZ. Mais la droite
ΘΓ
est égale à l'axe du cône
M ;
donc la droite
ΔΘ
est à l’axe du cône
M
comme le cercle
M
est au cercle décrit
autour du diamètre
BZ ;
donc le cône qui a pour base le
cercle
M, et
pour hauteur le rayon de la sphère est égal au rhombe solide
BΔZΘ,
ainsi que cela a été
démontré dans le quatrième lemme du premier livre (I, 17). Ou bien de la manière
suivante, puisque la droite AΘ est à la hauteur du cône
M
comme le cercle
M
est au cercle décrit autour du
diamètre
BZ, le
cône
M
sera
égal au cône qui a pour base le cercle décrit autour du diamètre
BZ
et pour hauteur la droite ΔΘ ;
caries bases de ces cônes sont réciproquement proportionnelles à leurs hauteurs.
Mais le cône qui a pour base le cercle décrit autour du diamètre
BZ,
et pour hauteur la droite ΔΘ,
est égal au rhombe solide
BΔZΘ
; donc le cône
M
est aussi égal au rhombe solide
BΔZΘ.
Mais le cône M est égal au secteur solide BΓZΘ
; donc le secteur solide
BΓZΘ
est égal au rhombe solide
BΔZΘ.
Donc si l'on retranche le cône commun qui a pour base le cercle décrit autour du
diamètre
BZ
et
pour hauteur la droite
BΘ,
le cône restant
BΔZ
sera égal au segment sphérique
BZΓ.

On démontrera semblablement que le
cône
BKZ
est
égal au segment sphérique
BAZ.
En effet, puisque la droite
KE
est à
la droite
EA
comme
la somme des droites
ΘΓ,
ΓE
est à la droite
ΓE;
par soustraction, la
droite
KA
est à
la droite AE comme
ΘΓ
est à
ΓE.
Mais
ΘΓ est
égal à
ΘA ;
donc, par permutation, la droite
KA
est à la droite AΘ
comme
AE
est à
EΓ.
Donc,
par addition, la droite KΘ
est à la droite
ΘA
comme AΓ est à
ΓE,
c'est-à-dire comme le carré
construit sur
BA
est au carré construit sur
BE.
Supposons de nouveau un cercle K, qui ait un rayon égal à la droite
AB.
Le cercle N sera égal à
la surface du segment sphérique
BAZ.
Concevons un cône N qui ait une
hauteur égale au rayon de la sphère ; ce cône sera égal au secteur solide
BΘZA,
ainsi que cela a été démontré dans
le livre premier (I, 50) (α). Mais nous avons démontré que la droite KΘ est à la
droite
ΘA
comme
le carré construit sur
AB
est au carré construit sur
BE,
c'est-à-dire comme le carré construit sur le rayon du cercle N est au carré du
rayon du cercle décrit autour du diamètre
BZ,
c'est-à-dire comme le cercle N est au cercle décrit autour du diamètre
BZ ;
et la droite AΘ
est égale à la hauteur du cône N ; donc la droite KΘ
est à la hauteur du cône N comme le cercle N est au cercle décrit autour du
diamètre
BZ.
Donc
le cône
N,
c'est-à-dire le secteur BΘZA est égal à la figure
BΘZK.
Donc si nous ajoutons à
chacun de ces deux solides le cône dont la base est le cercle décrit autour de
BZ, et dont la hauteur est la droite EΘ, le segment sphérique total
ABZ
sera égal au cône
BZK
(β). Ce qu'il fallait
démontrer.
Il est encore évident qu'en général un
segment sphérique est à un cône qui a la même base et la même hauteur que ce
segment, comme la somme du rayon de la sphère et de la hauteur de l'autre
segment est à la hauteur de cet autre segment; car la droite ΔE est à la droite
EΓ comme le cône
AZB,
c'est-à-dire le segment
BΓZ
est au cône BΓZ.
Les mêmes choses étant supposées, nous
démontrerons autrement que le cône
KBZ
est égal au segment sphérique
AZB. Soit un cône N qui ait une base égale à la surface de la sphère et une
hauteur égale au rayon. Ce cône sera égal à la sphère. En effet, nous avons
démontré que la sphère est quadruple du
cône qui a pour base un grand cercle de
cette sphère et pour hauteur un rayon de cette même sphère (I, 36); or le cône
N est aussi quadruple du
cône dont nous venons de parler, parce que la base du premier cône est quadruple
de la base du second, et que la surface de la sphère est quadruple d'un de ses
grands cercles. Puisque la somme des droites ΘA,
AE
est à la droite
AE
comme
ΔE
est à EΓ ; par soustraction et
par permutation, la droite ΘΓ sera à la droite
ΓΔ comme
AE
est à
EΓ.
De plus, puisque la droite
KE
est à
la droite
EA
comme
la somme des droites
ΘΓ,
ΓE sera à la droite
ΓE
; par soustraction et par
permutation, la droite
KA
sera à la droite ΓΘ ou à la
droite
ΘA
comme
AE
est à
EΓ, c'est-à-dire comme ΘΓ est à ΓΔ. Donc, par addition, et à cause que la droite
AΘ
est égale à la droite
ΘΓ,
la droite KΘ
sera à la droite
ΘΓ
comme
ΘΔ est à
ΔΓ ; et (γ) la droite totale
KΔ
est à la droite
ΔΘ
comme ΔΘ
est à ΔΓ, c'est-à-dire comme KΘ est à
ΘA.
Donc la surface comprise sous ΔΘ,
ΘK
est
égale à la surface comprise sous
ΔK,
ΘA. De plus, puisque KΘ
est à
ΘΓ comme
ΘΔ est à
ΓΔ ; par permutation, la droite KΘ
sera à la droite
ΘΔ
comme
ΘΓ est à
ΓΔ.
Mais nous avons démontré, que
ΘΓ est à
ΓΔ comme
AE
est à
EΓ ; donc KΘ est à
ΘΔ
comme
AE
est à
EΓ. Donc le carré construit sur KΔ est à la surface comprise sous KΘ, ΘA comme
le carré construit sur AΓ est à la surface
comprise sous
AE, EΓ
(δ). Mais on a démontré
que la surface comprise sous KΘ, ΘΔ est égale à la surface comprise sous KΔ, AΘ
donc le carré construit sur KΔ est à la surface comprise sous KΔ, AΘ,
c'est-à-dire que KΔ est à AΘ
comme le carré construit sur AΓ est à la surface comprise sous
AE,
EΓ c'est-à-dire au carré construit sur
EB.
Mais AΓ est égal au rayon du
cercle N ; donc le carré construit sur le rayon du cercle N est au carré
construit sur la droite
BE,
c'est-à-dire que le cercle N
est au cercle décrit autour du diamètre BZ comme KΔ est à AΘ,
c'est-à-dire comme la droite KA est à la hauteur du cône N. Donc le cône N,
c'est-à-dire la sphère, est égal au rhombe solide BΔZK (I, 17, lemme 4).
Ou bien de cette manière, donc le cercle N est au cercle décrit autour du
diamètre
BZ
comme
la droite KΔ est à la hauteur du cône N. Donc le cône N est égal au cône dont la
base est Je cercle décrit autour du diamètre
BZ
et dont la hauteur est ΔK ; car
les bases de ces cônes sont réciproquement proportionnelles, à leurs
hauteurs (I, 17, lemme 4). Mais le cône
N
est égal au rhombe solide
BKZΔ ;
donc le cône N, c'est-à-dire la sphère, est aussi égal au rhombe solide
BKZΔ, qui est
composé des cônes
BΔZ, BKZ.
Mais nous avons démontré
que le cône
BΔZ
est
égal au segment sphérique BΓZ ; donc le cône restant
BKZ
est égal au segment sphérique
BAZ
(γ).
PROPOSITION IV.
Le troisième problème était celui-ci :
couper une sphère donnée par un plan, de manière que les surfaces des segments
aient entre elles une raison égale à une raison donnée.
Supposons que cela soit fait. Que
AΔBE
soit
un grand cercle de la sphère, et que
AB
soit son diamètre ; que la
section du cercle
AΔBE
par ce plan soit la droite
ΔE,
et
menons.les droites AΔ, BΔ. Puisque la raison de la surface du segment
ΔAE
à la surface du segment
ΔBE
est
donnée; que la surface du segment
ΔAE
est égale à un cercle qui a un
rayon égal à la droite AΔ (I, 49) ; et que la surface du segment
ΔBE
est égale à un cercle qui a un
rayon égal à la droite ΔB: (I, 48) ; et à cause que les cercles dont nous venons
de parler sont entre eux comme les carrés construits sur les droites AΔ, AB,
c'est-à-dire comme les droites AΓ,
ΓB
; il est évident que la
raison de AΓ à
ΓB
est donnée, et par conséquent
le point Γ. Mais la droite
ΔE
est perpendiculaire sur AB ;
donc le plan qui passe par
ΔE
est donné de position.
On construira ce problème de la
manière suivante: soit la sphère dont
AΔBE
est un grand cercle et dont
AB
est le
diamètre. Que la raison donnée soit la même que celle de la droite Z à la droite
H.
Coupons la droite
AB
au point Γ, de manière que AΓ
soit à
ΓB
comme
Z est à H ; par le point Γ coupons la sphère par un plan perpendiculaire sur
AB
; et
que la commune section soit
ΔE.
Menons les droites AΔ,
ΔB.
Supposons enfin deux cercles Θ,
K
dont l'un ait un rayon
égal
à la droite
AΔ et l'autre un rayon égal à la droite ΔB. Le
cercle
Θ sera égal à la surface du segment
ΔAE, et
le cercle K
égal à la surface du segment
ΔBE,
ainsi
que cela a été démontré dans le premier
livre (I, 48 et 49). Puisque l'angle
AΔB
est
donné et que la droite
ΓA est perpendiculaire,
la droite
AΓ est à la droite
ΓB,
c'est-à-dire que
Z
est à
H
comme
le carré construit sur
AΔ
est au carré construit sur
ΔB, c'est-à-dire comme
le carré
construit sur le rayon du cercle
Θ est au carré construit sur
le rayon du cercle
K,
c'est-à-dire co.mme la surface du segment
sphérique
ΔBE
est à la surface du segment
sphérique
ABE.
PROPOSITION V.
Couper une sphère donnée de manière
que les segments aient entre eux une raison égale à une raison donnée.
Soit ABΓΔ la sphère donnée. Il faut la
couper par un plan de manière que les segments aient entre eux une raison égale
à une raison donnée.
Coupons cette sphère par un plan
conduit par AΓ. La raison dit segment sphérique AΔΓ au segment sphérique ABΓ
sera donnée. Coupons cette sphère par un plan qui passe par son
centre ; que cette section soit
le grand cercle
ABΓΔ;
que le point K
soit son centre, et ΔB
son diamètre. Que la
somme des droites KΔ, ΔΧ soit à la droite BΧ comme ΡΧ est à
ΧB
; et que la somme des droites
KB, BΧ
soit à la droite BΧ
comme
ΛΧ
est à
ΧΔ. Menons les droites
AΛ, ΛΓ,
AΡ, ΡΓ.

Le cône AΛΓ sera égal au segment
sphérique AΔΓ ; et le cône AΡΓ égal au segment
ABΓ
(II, 3). Donc la raison du cône
AΛΓ au cône AΡΓ sera donnée. Mais le premier cône est au second comme
ΛΧ
est à ΧΡ, puisque ces
deux cônes ont pour base le cercle décrit autour de la droite AΓ ; donc la
raison de
ΛΧ
est à
ΧΡ
est aussi donnée. Par la
même raison qu'auparavant, et par construction (II, 3), la droite ΛΔ est à la
droite KΔ comme
KB
est à
BΡ,
et comme
ΔΧ
est à
ΧB.
Mais
la droite ΡB est à la droite
BK
comme KΔ est à ΛΔ; donc par
addition la droite ΡK est à
KB,
c'est-à-dire à KΛ comme
KΛ
est à
ΛΔ.
Donc (α), la droite
totale
ΡΛ
est à
la droite totale KΛ comme
KΛ
est à ΛΔ. Donc la surface
comprise sous
ΡΛ,
ΛΔ est égale au carré construit
KΛ.
Donc
ΡΛ
est à
ΛΔ
comme le carré construit sur KΛ
est au carré construit sur ΛΔ (β). Mais ΛΔ est à ΔK comme ΔΧ est à
ΧB ;
donc par inversion et
par addition, la droite
KΛ
est à la droite ΛΔ comme BΔ est
à ΔΧ. Donc le carré construit sur
KΛ
est au carré construit sur
ΛΔ
comme
le carré construit sur BΔ est au carré construit sur ΔΧ. De plus, puisque
ΛΧ
est à ΔΧ comme la somme
des droites
KB,
BΧ
est à
BΧ
; par soustraction, la droite
ΛΔ
sera à
la droite ΔX comme
KB
est à
BΧ.
Faisons,
BZ
égal à
KB.
Il est évident que cette droite
tombera au-delà du point Ρ (γ). Mais la droite
ΛΔ
est à la droite ΔΧ comme
ZB
est à
BΧ;
donc
ΔΛ
sera à
ΛΧ
comme BZ est à ZΧ (δ). Puisque
non seulement la raison de
ΔΛ
à
ΛΧ
est donnée, mais encore celle
de
ΡΛ
à
ΛΧ, ainsi
que celle de
ΡΛ
à ΛΔ; et puisque la raison de
ΡΔ
à ΛΧ
est composée de la raison
ΡΛ
à
ΛΔ,
et de la raison de ΔΛ
à
ΛΧ
(ε) ; que
ΡΛ
est à
ΛΔ
comme le carré construit sur
ΔB
est au
carré construit sur
ΔΧ,
et que
ΔΛ
est à
ΛΧ
comme
BZ
est à
ZΧ, la raison de
ΡΛ
à
ΛΧ
est composée de la raison du
carré construit

sur
BΔ
au
carré construit sur
ΔΧ, et de la raison de BZ à ZΧ
(z). Faisons en sorte que
ΡΛ
soit à
ΛΧ
comme
BZ
est à ZΘ. Or la raison de ΡΛ
à ΛΧ
est donnée; donc la
raison de
ZB
à ZΘ
est aussi donnée. Mais la droite
BZ
est donnée, puisqu'elle est
égale au rayon; donc la droite ZΘ est aussi donnée. Donc la raison de
BZ
à ZΘ est composée de la
raison du carré construit sur BΔ au carré construit sur ΔΧ, et de la raison de
BZ
à ZΧ.
Mais la raison de
BZ
à ZΘ est composée de la raison
de
BZ
à ZΧ,
et de la raison de ZΧ à ZΘ ; donc si nous retranchons la raison commune de
BZ
à ZΧ,
la raison restante, c'est-à-dire la raison du carré construit sur la droite BΔ
qui est donné, au carré construit sur la droite ΔΧ, sera égale à la raison de ΧZ
à la droite ZΘ, qui est donnée ; mais la droite ZΔ est donnée. Il faut donc
couper la droite donnée
ΔZ
en un point Χ, de manière que
la droite ΧZ soit à la droite donnée ZΘ comme le carré construit sur BΔ est au
carré construit sur ΔΧ; et si cela est énoncé d'une manière générale, il y aura
une solution; si, au contraire, on ajoute les choses trouvées, c'est-à-dire que
ΔB est double de
BZ
et que
BZ
est plus grand que ZΘ,
il n'y aura aucune solution. Le problème doit donc être posé ainsi : étant
données deux droites ΔB, BZ dont ΔB soit double de BZ; étant
donné aussi le point
Θ
dans la droite
BZ,
couper la droite
ΔB
en un point Χ, de manière que
le carré construit sur BΔ soit un carré construit sur ΔΧ comme ΧZ est à ZΘ.
Χhacune de ces choses aura à la fin sa solution et sa construction (h).
On construira le problème de cette
manière : Que la raison donnée soit la même que celle de la droite Π à la droite
Σ, la droite Π étant plus grande que la droite Σ. Soit donnée aussi une
sphère quelconque ; que cette sphère soit coupée
par un plan conduit par le
centre. Que la section soit le cercle
ABΓΔ ; que
ΔB
soit le diamètre de ce cercle
et le point K son centre. Faisons
BZ
égal à
KB
; et coupons
BZ
en un point Θ de manière que ΘZ
soit à
ΘB comme
Π est à Σ. Coupons aussi BΔ en un point Χ, de manière que ΧZ soit à
ΘZ
comme le carré construit sur
BΔ
est au carré construit sur ΔΧ;
et faisons passer par le point Χ un plan perpendiculaire sur
BΔ.
Je dis que ce plan coupera la
sphère de manière que le plus grand segment sera au plus petit comme Π est à Σ.

Faisons en sorte que la somme des
droites
KB,
BΧ
soit à
la droite
BΧ
comme
ΛΧ
est à
ΔΧ ;
et
que la somme des droites
KΔ, ΔΧ
soit à la droite
ΔΧ
comme
ΡΧ
est à
ΧB.
Menons les droites
AΛ,
ΛΓ, AΡ, ΡΓ.
La surface comprise sous
ΡΛ,
ΛΔ,
sera par construction, ainsi que nous l'avons démontré plus haut, égale au carré
construit sur
ΛK
et la droite
KΛ
sera à la droite ΛΔ comme
BΔ
est à
ΔΧ.
Donc
le carré
construit sur
KΛ
est au carré construit sur
ΛΔ
comme
le carré construit sur BΔ est au carré construit sur ΔΧ. Mais la surface
comprise sous
ΡΛ,
ΛΔ
est égale au carré
construit sur
ΛK
; donc la droite
ΡΛ
est à la droite
ΛΔ
comme le
carré construit sur
ΛK
est au carré construit
sur
ΛΔ. Donc
aussi la droite
ΡΛ
est à la droite ΛΔ comme le
carré construit sur
BΔ
est au carré construit sur
ΔΧ,
c'est-à-dire, comme ΧZ est à ZΘ. Mais la somme des droites
KB,
BΧ
est à la droite
BΧ
comme
ΛΧ
est à
ΔΧ,
et la droite
KB
est égale à la droite BZ ; donc
la droite ZΧ sera à la droite
ΧB
comme
ΛΧ
est à
ΧΔ
; et par conversion, la droite
ΧZ sera à
ZB
comme
ΧΛ
est à
ΛΔ. Donc
aussi la droite
ΛΔ
sera à la droite
ΛΧ
comme BZ est à ZΧ. Mais
ΡΛ
est à
ΛΔ
comme ΧZ est à ZΘ ; et ΔΛ
est à
ΛΧ
comme BZ est à ZΧ ; donc, par
raison d'égalité dans la proportion troublée, la droite
ΡΛ
sera à la droite
ΛΧ
comme BZ est à ZΘ. Donc aussi
ΛΧ
est à
ΧΡ
comme
ZΘ est à ΘB. Mais ZΘ est à ΘB comme Π est à Σ ; donc aussi
ΛΧ
est à
ΧΡ,
c'est-à-dire que le cône
AΓΛ
est au cône AΡΓ, c'est-à-dire
que le segment sphérique AΔΓ est au segment ABΓ comme Π est à Σ (θ).
PROPOSITION VI.
Construire un segment sphérique
semblable à un segment sphérique donné, et égal à un autre segment sphérique
aussi donné.
Soient ABΓ,
EZH,
les deux segments
sphériques donnés. Que
la base du segment
ABΓ soit le cercle décrit autour du
diamètre
AB, et
que son sommet soit le point Γ ; que la base du segment
EZH
soit le cercle décrit autour du
diamètre
EZ, et
que son sommet soit le point
H.
Il faut construire un segment
qui soit égal au segment ABΓ et semblable au segment
EZH.
Supposons que ce segment soit trouvé,
et que ce soit le segment ΘKΛ qui a pour base le cercle décrit autour du
diamètre ΘK, et pour sommet le point
Λ.
Soient aussi dans ces sphères
les cercles ANBΓ, ΘXKΛ,
EOZH,
dont les diamètres soient perpendiculaires sur la base du segment, et dont les
centres soient les points Π, Ρ, Σ. Faisons en sorte que la somme des droites ΠN,
NT soit à la droite NT comme
ΧT
est à
TΓ ;
que la somme des droites ΡΞ, ΞΥ
soit à la droite ΞΥ comme
ΨΥ
est à
ΥΛ,
et qu'enfin la somme des droites ΣO, OΦ soit à OΦ comme ΩΦ est à ΦH. Concevons
des cônes qui aient pour bases les cercles décrits autour des diamètres
AB,
ΘK, EZ, et pour sommets
les points Ξ, Y, Ω.
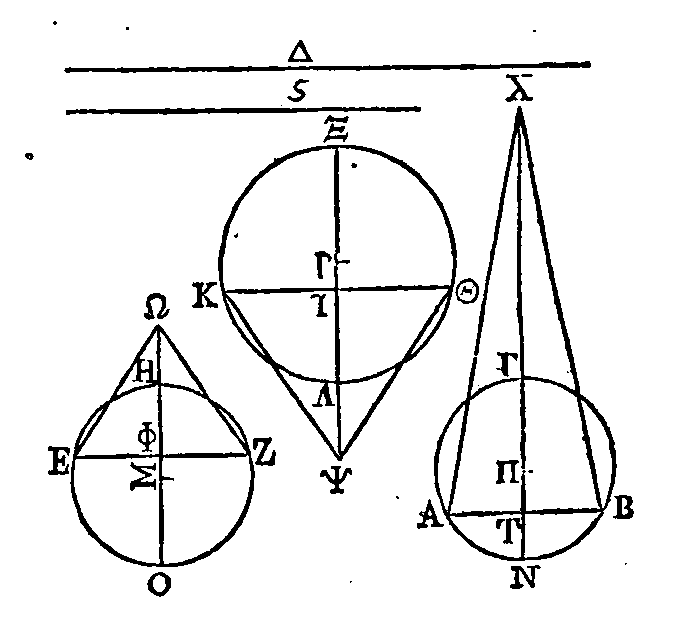
Le cône
ABΧ
sera égal au segment sphérique
ABΓ, le cône YΘK égal au segment sphérique
AKΛ,
et enfin le cône
EΩZ
égal au segment sphérique
EHZ, ce
qui a été démontré (2, 3). Puisque le segment sphérique ABΓ est égal au segment
ΘKΛ, le
cône
AΧB
sera
aussi égal au cône
ΨΘK.
Mais les bases des cônes égaux
sont réciproquement proportionnelles à leurs hauteurs ; donc le cercle décrit
autour du diamètre
AB
est au cercle décrit autour du
diamètre ΘK comme
ΨΥ
est à ΧT. Mais le premier
cercle est au second comme le carré construit sur
AB
est au carré construit sur
ΘK; donc
le carré construit sur
AB
est au carré construit
sur
ΘK
comme YΥ est à
ΧT.
Mais le segment
EZH
est semblable
au segment
ΘKΛ
; donc le cône EZH est aussi
semblable au cône
YΘK,
ce qui sera démontré (α) ; donc ΩΦ est à
EZ
comme ΨΥ est à
ΘK.
Mais la raison de ΩΦ à
EZ
est donnée; donc la
raison de
ΨΥ à
ΘK
est aussi donnée. Que
cette dernière raison soit la même
que celle de
ΧT
à Δ. Puisque la
droite
ΧT
est donnée, la droite Δ
est aussi donnée. Mais
ΨΥ est à
ΧT,
c'est-à-dire, le carré construit sur
AB
est au carré construit sur
ΘK comme
ΘK est à
Δ ; donc si nous supposons que la surface comprise sous
AB,
Ϛ soit égale au carré construit sur
ΘK,
le carré construit sur
AB
sera au carré construit sur
ΘK
comme
AB
est à
z. Mais on a démontré que le carré construit sur
AB
est au carré construit sur
ΘK
comme
ΘK
est à
Δ ; donc, par permutation, la droite
AB
est à la droite
ΘK
comme Ϛ est à Δ. Mais
AB
est à
ΘK
comme
ΘK
est à
Ϛ,
parce que la surface comprise sous
AB,
Ϛ est égale au carré construit sur
ΘK
; donc
AB
est à
ΘK
comme
ΘK
est
Ϛ,
et comme Ϛ
est à Δ. Donc les droites
ΘK, Ϛ
sont deux moyennes
proportionnelles entre
AB,
Δ.
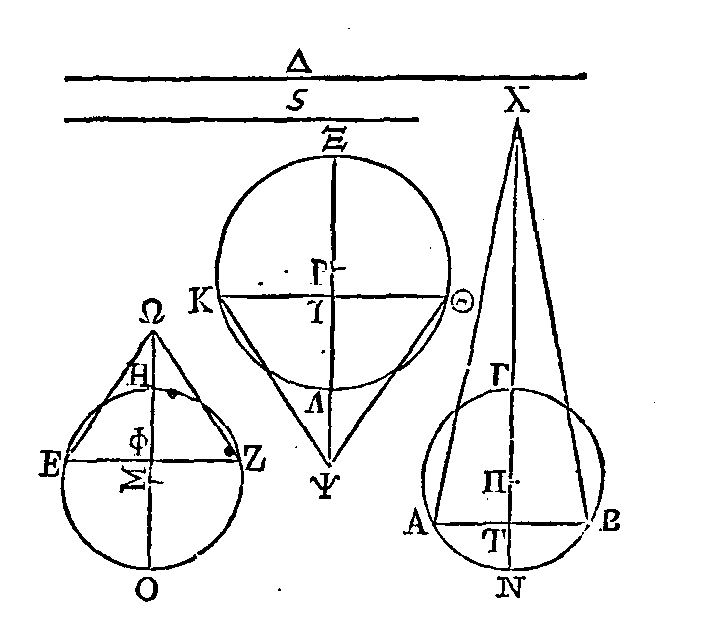
On construira ce problème de cette
manière. Soient deux segments sphériques ABΓ,
EZH
; que ABΓ soit celui
auquel il faut construire un segment égal, et
EZH
celui auquel il faut construire un segment semblable. Soient les grands cercles
AΓBN,
HEOΣ; que ΓN,
HO
soient leurs diamètres,
et Π, Σ leurs centres. Faisons en sorte que la somme des droites ΠN, NT soit à
la droite
NT
comme
ΧT
est à
TΓ ; et que la somme des droites ΣO, OΦ soit à OΦ comme ΩΦ est à ΦH. Le cône
ΧAB
sera
égal au segment sphérique ABΓ, et le cône ZΩE sera égal au segment sphérique
EHZ.
Faisons en sorte que ΩΦ soit à
EZ
comme
ΧT
est à
Δ
; entre les deux droites
AB,
Δ, prenons deux moyennes
proportionnelles ΘK, z,
de manière que
AB
soit à
ΘK
comme
ΘK
est à
Ϛ,
et comme Ϛ est à Δ. Sur
ΘK
construisons un segment
circulaire
ΘKΔ
semblable au segment circulaire
EZH
: achevons le cercle, et que
son diamètre soit
ΛΞ.
Concevons enfin une sphère dont
AΘΞK
soit
un grand cercle, et dont le centre soit le point Ρ ; et par la droite
ΘK,
faisons passer un plan perpendiculaire sur
ΛΞ.
Le segment sphérique construit
du côté où est la lettre
Λ
sera semblable au segment
sphérique
EZH,
puisque les segments circulaires sont semblables. Je dis aussi que ce segment
sphérique sera égal au segment ABΓ. Faisons en sorte que la somme des droites
ΠΞ, ΞΥ
soit à la droite ΞΥ comme YΥ est à
YΛ.
Le cône YΘK
sera égal au segment sphérique
ΘKΛ
(II, 3). Mais le cône YΘK est semblable au cône ZΩE; donc la droite ΩΦ est à la
droite
EZ,
c'est-à-dire, la droite ΧT est à Δ comme ΨΥ est à
ΘK.
Donc, par permutation, et par inversion, la droite ΨΥ est à
ΧT
comme
ΘK
est à
Δ.
Mais les droites
AB, KΘ,
Ϛ,
Δ sont tour à tour proportionnelles (β); donc le carré construit sur
AB
est au carré construit
sur
ΘK
comme
ΘK
est à
Δ.
Mais
la droite
ΘK
est à
la droite Δ comme ΨΥ est à
ΧT
; donc le carré construit sur
AB
est au
carré construit sur KΘ,
c'est-à-dire, le cercle décrit autour du diamètre
AB
est au cercle décrit autour du
diamètre
ΘK comme
ΨΥ est à ΧT ; donc le cône
ΧAB
est égal au cône ΨΘK. Donc le
segment sphérique ABΓ est aussi égal au segment-sphérique
ΘKΛ.
Donc on a construit un segment
sphérique
ΘKΛ
égal
au segment donné ABΓ, et semblable à l'autre segment sphérique donné
EZH
(γ).
PROPOSITION VII.
Étant donnés deux segments de la même
sphère, ou de différentes sphères, trouver un segment sphérique qui soit
semblable à l'un des deux et qui ait une surface égale à celle de l'autre.
Soient deux segments sphériques
construits dans les portions de circonférence ABΓ,
ΔEZ
; que le segment construit dans
la portion de circonférence ABΓ soit celui auquel le segment qu'il faut trouver
doit être semblable; et que le segment construit dans
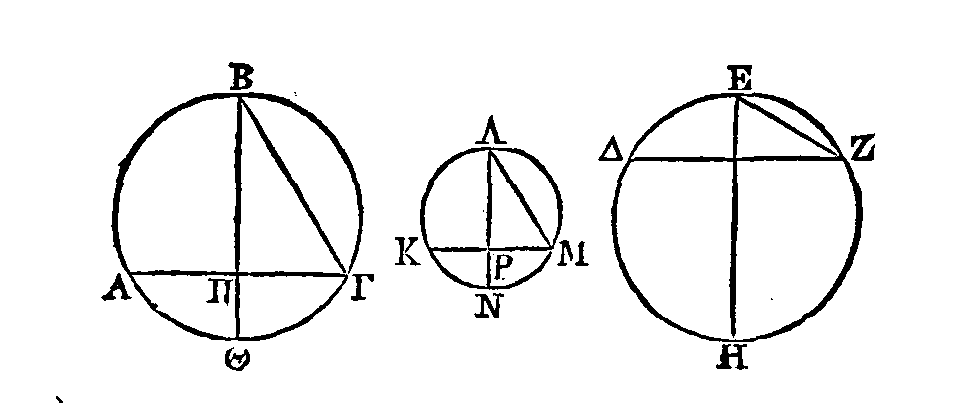
la portion de circonférence ΔEZ
soit celui à la surface
duquel la surface du segment qu'il faut trouver doit être égale. Supposons que
cela soit fait. Que le segment sphérique
KΛM
soit semblable au segment ABΓ
et que la surface de ce segment soit égale à la surface du segment ΔEZ.
Χoncevons les centres de ces sphères ; par leurs centres conduisons des plans
perpendiculaires sur les bases de ces segments; que les sections des sphères
soient les grands cercles
KΛMN,
BAΘΓ,
EZHΔ
; que
KM,
AΓ, ΔZ,
soient dans les bases des segments, et enfin que dans ces sphères les
diamètres perpendiculaires sur
KM,
AΓ, ΔZ soient les droites
ΛN,
BΘ,
EH.
Menons les droites
ΛM, BΓ,
EZ. Puisque la surface du segment sphérique
KΛM
est égale à la surface du
segment
ΔEZ, le
cercle qui a un rayon égal à la droite
MΛ
sera égal au cercle qui a un
rayon égal à la droite
EZ,
parce que nous avons démontré que les
surfaces des segments dont nous venons
de parler sont égales à des cercles qui ont des rayons égaux aux droites menées
des sommets des segments aux circonférences de leurs bases (I, 48). Donc la
droite
MΛ
est
aussi égale à la droite EZ. Mais puisque le segment
KΛM
est semblable au segment ABΓ,
la droite
ΡΛ
est à
la droite
ΡN
comme
BΠ est à ΠΘ ; et par inversion et par addition, la droite
NΛ
est à la droite
ΛΠ
comme
ΘB
est à BΠ. Mais
ΡΛ
est à
ΛM
comme BΠ est à
ΓB,
à cause des triangles semblables
ΛMΠ,
BΓΠ; donc
NΛ
est à
ΔM,
c'est-à-dire à
EZ
comme
ΘB
est à BΓ
et par permutation …. Mais la
raison de la droite
EZ
à
la droite
BΓ est donnée, puisque ces deux
droites sont données; donc la raison de
ΛN
à
BΘ
est aussi donnée. Mais la
droite BΘ est donnée ; donc la droite
ΛN
est aussi donnée. Donc la
sphère est donnée.
On construira le problème de cette,
manière. Soient ABΓ, ΔEZ les deux segments donnés; que ABΓ soit le segment
auquel celui qu'il faut trouver doit être semblable, et que ΔEZ soit le segment
à la surface duquel la surface de celui qu'il faut trouver doit être égale. Θue
la construction soit la même que dans la première partie ; et faisons en sorte
que BΓ soit à
EZ
comme BΘ
est à
NΛ
;
décrivons un cercle autour du diamètre an
; et enfin concevons une sphère dont AKNM
soit un grand cercle.
Coupons la droite
NΛ
au point Ρ, de manière que
ΘΠ soit à
ΘB comme
NΡ
est à
ΡΛ
; coupons le cercle AKNM
au point Ρ par un plan
perpendiculaire sur la droite
ΛN
; et menons la droite
ΛM.
Les segments circulaires
appuyés sur les droites KM, AΓ sont semblables. Donc les segments sphériques
sont aussi semblables. Mais
ΘB
est à BΠ comme
NΛ
est à
ΛΡ,
car cela s'ensuit de la construction, et
ΠB
est à BΓ comme
ΡΛ
est à ΛM; donc la droite
ΘB
est à
NΛ
comme BΓ est à
ΛM.
Mais
ΘB
est à
NΛ
comme
BΓ
est à
EZ
; donc EZ est égal à
ΛM.
Donc le cercle qui a
pour rayon la droite
EZ
est égal au cercle qui a
un rayon égal à la droite
ΛM.
Mais le cercle qui a pour rayon
la droite
EZ
est
égal à la surface du segment ΔEZ ; et le cercle qui a un rayon égal à la droite
ΛM
est égal à la surface du
segment KΛM,
ainsi que cela a été
démontré dans le premier livre (I, 48). Donc la surface du segment sphérique KΛM
est égale à la surface
du segment
ΔEZ
; et
ce même segment
KΛM
est semblable au segment
ABΓ.
PROPOSITION VIII.
Couper un segment d'une sphère par un
plan de manière que la raison de ce segment au cône qui a la même base et la
même hauteur que ce segment, soit égale à une raison donnée.
Que la sphère donnée soit celle dont
ABΓΔ
est
un grand cercle, et
BΔ
le diamètre. Il faut couper la
sphère par un plan conduit par AΓ de manière que la raison du segment ABΓ au
cône ABΓ soit égale à une raison donnée.
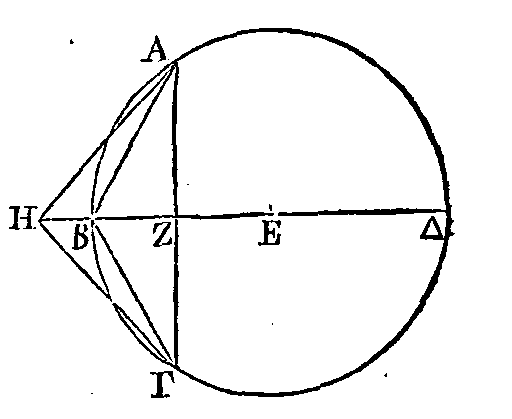
Supposons que cela soit fait. Que le
point
E
soit le
centre de la sphère. Que la somme des droites
EΔ, ΔZ
soit à
ΔZ
comme
HZ
est à
ZB
; le cône AΓH sera égal au
segment ABΓ (II, 3). Donc la raison du cône AHΓ au cône ABΓ est donnée.
Donc la raison de
HZ
à
ZB
est aussi donnée. Mais
HZ
est à
ZB
comme la somme des droites EΔ,
ΔZ est à la droite ΔZ ; donc la raison de la somme des droites EΔ, ΔZ à la
droite
ΔZ
est
donnée, et par conséquent la raison de EΔ à
ΔZ.
Donc la droite
ΔZ
est
donnée, et par conséquent la droite AΓ. Mais la raison de la somme des droites
EΔ, ΔZ
à la droite
ΔZ
est plus grande que la
raison de la somme des droites EΔ, ΔB à la droite ΔB; et la somme des droites
EΔ, ΔB est égale à la droite EΔ
prise trois fois, et enfin la droite
ΔB est égale à la droite
EΔ prise deux fois. Donc la raison de la somme des droites
EΔ, ΔZ
à
ΔZ
est plus grande que la raison
de trois à deux. Mais la raison de la somme des droites
EΔ,
ΔZ
à la
droite ΔZ est la même que la raison donnée. Il faut donc, pour que la
construction soit possible, que la raison donnée soit plus grande que la raison
de trois à deux.
On construira le problème de cette
manière. Que la sphère donnée soit celle dont
ABΓΔ
est un grand cercle, la droite
BΔ
le
diamètre, et le point E le centre; que la raison donnée soit la même que celle
de KΘ
à
KΛ,
et
que cette raison soit plus grande que celle de trois à deux. Mais trois sont à
deux comme la somme des droites EΔ, ΔB est à la droite ΔB ; donc la raison de ΘK
à
KΛ
est
plus grande que la raison de la somme des droites EΔ, ΔB à la droite
ΔB.
Donc, par soustraction,
la raison de
ΘΛ
à
ΛK
est plus grande que la raison
de EΔ à ΔB. Faisons en sorte que ΘΛ soit à
ΛK
comme EΔ est à
ΔZ
; par le point Z, menons la
droite AZΓ perpendiculaire sur
BΔ,
et par la droite AΓ, conduisons un plan perpendiculaire sur
BΔ.
Je dis que la raison du segment
sphérique ABΓ au cône ABΓ est la même que la raison de
ΘK
à
KΛ.
Car faisons en sorte que la
somme des droites EΔ, ΔZ soit à la droite ΔZ comme HZ est à
ZB
; le cône
ΓAH
sera égal au segment sphérique
ABΓ (II, 3). Mais ΘK est à
KΛ
comme la somme des droites,
EΔ,
ΔZ
est à la droite ΔZ,
c'est-à-dire comme HZ est à
ZB,
c'est-à-dire comme le cône
AHΓ
est au cône ABΓ (II, 3); et le
cône
AHΓ
est
égal au segment sphérique ABΓ. Donc le segment ABΓ est au cône
ABΓ
comme
ΘK
est à
KΛ.
PROPOSITION IX.
Si une sphère est coupée par un plan
qui ne passe pas par le centre ; la raison du grand segment au petit sera
moindre que la raison doublée de la surface du grand segment à la surface du
petit segment, et plus grande que la raison sesquialtère (α).
Soit une sphère ; que ABΓΔ soit un de
ses grands cercles, et BΔ le diamètre de ce cercle ; par la droite Ar,
conduisons un plan perpendiculaire sur le cercle ABΓΔ, et que ABΓ soit le plus
grand segment. Je dis que la
raison du segment
ABΓ au
segment AΔΓ est moindre que la raison doublée de la surface du grand segment à
la surface du petit, et plus grande que la raison sesquialtère.
Menons les droites
BA,
AΔ ; que le centre soit le point
E
; et faisons en sorte
que la somme des droites EΔ, ΔZ soit à la droite ΔZ comme
ΘZ
est à
ZB
; et
que la somme des droites
EB, EZ
soit à la droite
BZ
comme HZ est à ZΔ.
Concevons deux cônes qui aient pour base le cercle décrit autour du diamètre AΓ,
et leurs sommets aux points
Θ,
H. Λe cône AΘΓ sera égal au
segment ABΓ, et le cône AΓH égal au segment AΔΓ (II, 3). Mais le carré construit
sur
BA
sera
au carré construit sur AΔ comme la surface du segment ABΓ est à la surface du
segment
AΔΓ; ainsi que cela a été démontré plus haut (I, 48); il faut
donc démontrer que la raison du grand segment au petit segment est moindre que
la raison doublée de la surface du grand segment à la surface du petit segment :
ou ce qui est la même chose, il faut démontrer que la raison du cône AΘΓ
au cône AHΓ, c'est-à-dire que la raison de ZΘ
à
ZH
est
moindre que la raison doublée du carré construit sur
BA
au carré construit sur AΔ,
c'est-à-dire que la raison doublée de
BZ
à
ZΧ.
Puisque la somme des droites EΔ, ΔZ
est à la droite ΔZ comme ΘZ est à
ZB,
et que la somme des droites
EB,
BZ
est à la droite
BZ
comme
ZH
est à
ZΔ,
la droite
BZ
sera à
la droite
ZΔ
comme
ΘB
est à
BE
(β),
la droite
BE
étant égale à la droite
EΔ
; cela a été démontré
dans les théorèmes précédents. De plus, puisque la somme des droites
EB,
BZ est à la droite
BZ
comme
HZ est à
ZΔ,
si
nous faisons
BK
égal à
BE,
il est évident que
ΘB
sera plus grand que
BE,
à cause que
BZ
est
plus grand que ZΔ (γ) ; et la droite
KZ
sera à la droite
ZB
comme
HZ
est à
ZΔ (δ).
Mais nous avons démontré
que
ZB
est à
ZΔ
comme
ΘB
est à
BE, et la
droite
BE
est
égale à la droite
KB;
donc
ΘB
est à
BK
comme
KZ
est à
ZH.
Mais
la raison de
ΘZ
à
ZK
est
moindre que la raison de
ΘB
à
BK
(ε),
et nous avons démontré que
ΘB
est à
BK
comme
KZ
est à
ZH
; donc la raison de
ΘZ
à
ZK
est
moindre que la raison de KZ à
ZH.
Donc la surface comprise sous
ΘZ,
ZH
est plus petite que le
carré construit sur
ZK.
Donc la raison de la surface
comprise sous
ΘZ,
ZH
au
carré construit sur
ZH,
c'est-à-dire la raison de ZΘ
à ZH est moindre que la raison du carré construit sur
KZ
au carré construit sur
ZH.
Mais la raison du carré
construit sur
KZ
au carré construit sur
ZH
est doublée de la raison
de
KZ
à
ZH;
donc
la raison de
ΘZ
à
ZH
est
moindre que la raison doublée de
KZ
à
ZH.
Mais
KZ
est à
ZH
comme
BZ
est à ZΔ; donc la raison
de
ΘZ à
ZH
est
moindre que la raison doublée de
BZ
à
ZΔ,
et c'est là ce que nous cherchions.
Puisque
BE
est égal à
EΔ,
la surface comprise sous
BZ,
ZΔ
sera plus petite que la
surface comprise sous
BE, EΔ
(z). Donc la raison
de
BZ
à
BE
est moindre que la raison de EΔ
à ΔZ, c'est-à-dire que la raison de
ΘB
à
BZ.
Donc
le carré construit sur
ZB
est moindre que la surface
comprise sous
ΘB,
BE,
c'est-à-dire que la surface comprise sous
ΘB,
BK.
Que le carré construit
sur
BN
soit
égal à la surface comprise sous
ΘB,
BK
; la droite
ΘB
sera à la droite
BK
comme le carré construit
sur
ΘN est au
carré construit sur
NK
(θ). Mais la raison du carré
construit sur
ΘZ
au carré construit sur
ZK
est plus grande que la raison
du carré construit sur
ΘN
au carré construit sur
NK
; donc aussi la raison du carré
construit sur
ΘZ
au carré construit sur
ZK
est plus grande que la raison
de
ΘB à
BK,
c'est-à-dire que la raison de
ΘB
à
BE,
c'est-à-dire que la raison de
KZ
à
ZH.
Donc la raison de
ΘZ
à
ZH
est
plus grande que la raison sesquialtère de KZ à ZH, ce que nous démontrerons à la
fin (ι). Mais
ΘZ
est à
ZH
comme
le cône AΘΓ est au cône AHΓ,
c'est-à-dire comme le segment ABΓ est au segment AΔΓ. Mais
KZ
est à
KH
comme
BZ
est à
ZΔ
; c'est-à-dire comme le carré
construit sur
BΔ
est au carré construit sur AΔ ;
c'est-à-dire comme la surface du segment ABΓ est à la surface du segment AΔΓ;
donc la raison du grand segment au petit segment est moindre que la raison
doublée de la surface du grand segment à
la surface du petit segment, et plus grande que la
raison sesquialtère.
AUTREMENT (k).
Soit la sphère dont
ABΓΔ
est un grand cercle la droite
AΓ le diamètre, et le point E le centre; et que cette sphère soit coupée par un
plan conduit par
BΔ
et perpendiculaire sur AΓ. Je
dis que
la raison du grand segment
ΔAB
au petit BΓΔ est moindre que la
raison doublée de la surface du segment
ABΔ
à la surface du segment BΓΔ et
plus grande que la raison sesquialtère.
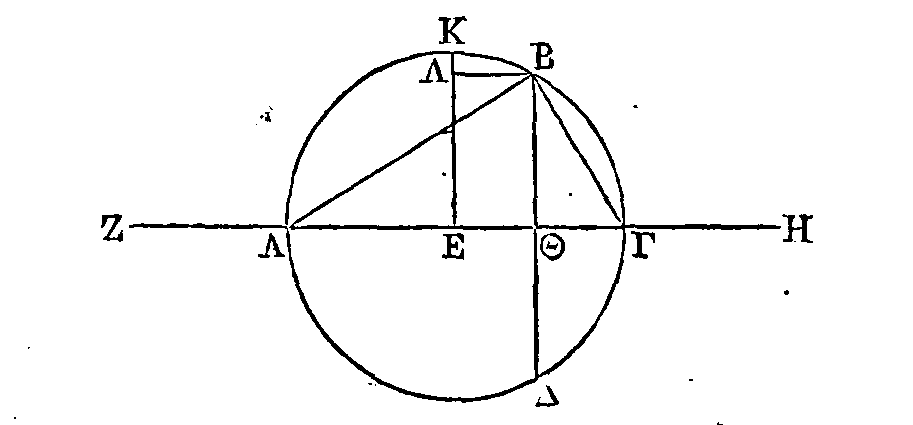
Menons les droites
AB, BΓ.
La raison de la surface
du segment
ABΔ
à la
surface du segment
BΓΔ
est égale à la raison du cercle
qui a pour rayon la droite
AB
au cercle qui a pour rayon la
droite BΓ, c'est-à-dire à la raison de AΘ à ΘΓ. Supposons que chacune des
droites AZ, ΓH soit égale au rayon du cercle. La raison du segment
BAΔ
au segment BΓΔ est
composée de la raison du segment
BAΔ
au cône qui a pour base le
cercle décrit autour du diamètre
BΔ
et pour sommet le point A,
de la raison du même cône au cône qui a la même base et qui a pour sommet le
point Γ, et enfin de la raison du cône dont nous venons de parler au segment BΓΔ
(λ). Mais la raison du segment
BAΔ
au cône
BAΔ
est la même que celle de HΘ à
ΘΓ, la raison du cône
BAΔ
au cône BΓΔ est la même que
celle de AΘ à ΘΓ, et enfin la raison du cône BΓΔ au segment
BΓΔ
est la même que la raison de AΘ
à ΘZ : et de plus la raison
qui est composée de la raison de
HΘ
à
ΘΓ et de
la raison de AΘ
à
ΘΓ est la
même que celle de la surface comprise sous AΘ,
ΘH
au carré construit sur
ΘΓ ; et
la raison qui est composée de la raison de la surface comprise sous
HΘ,
ΘA
au carré construit sur ΓΘ,
et de la raison de
AΘ
à
ΘZ
est la même que la
raison de la surface comprise sous
HΘ,
ΘA
et multipliée par
ΘA
au carré construit sur
ΘΓ
et multiplié par
ΘZ
(μ); et la raison de la surface comprise sous
HΘ,
ΘA et multipliée par
ΘA
au carré construit sur
ΘΓ
et multiplié par
ΘZ
est la même que la raison du carré construit sur AΘ
et multipliée par
ΘH
au carré construit sur
ΘΓ
et multiplié par
ΘZ
; et enfin la raison de la surface comprise sous HΘ,
ΘA et multipliée par
ΘA
au carré construit sur
ΘΓ
et multiplié par
ΘH
est la même que celle du carré construit sur
ΘA au carré construit sur
ΘΓ.
Donc, puisque la raison du carré construit sur
ΘA
et multiplié par
ΘH
au carré construit sur ΓΘ
et multiplié par ZΘ
est moindre que la raison doublée de AΘ
à
ΘΓ ; et
que la raison du carré construit sur
AΘ
au carré construit par
ΘΓ
est doublée de la raison de AΘ
à
ΘΓ ; la
raison du carré construit sur AΘ
et multiplié par
HΘ
au carré construit sur
ΘΓ
et multiplié par
ΘZ
sera moindre que la raison du carré construit sur AΘ
et multiplié par
HΘ
au carré construit sur ΓΘ
et multiplié par
ΘH.
Il faut donc démontrer que le carré construit par ΓΘ
et multiplié par ZΘ
est plus grand que le carré construit sur ΓΘ
et multiplié par
ΘH
; c'est pourquoi il faut démontrer que
ΘZ
est plus grand que
ΘH.
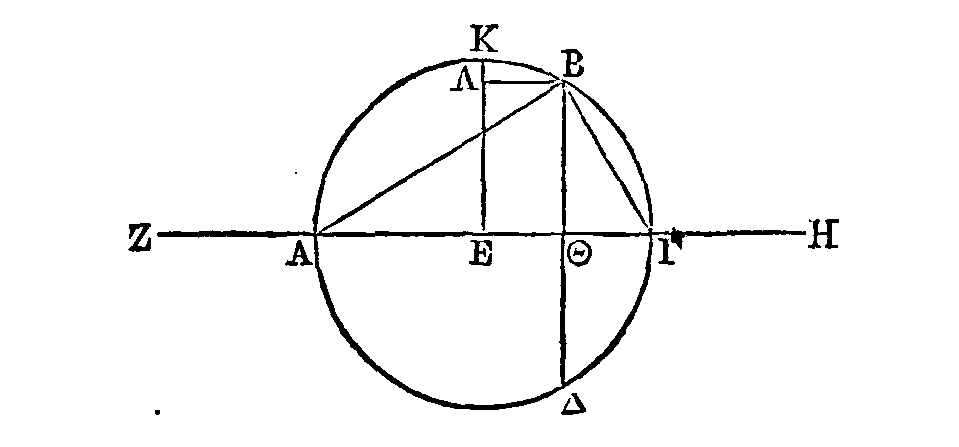
Je dis maintenant que la raison du
grand segment au plus petit est plus grande que la raison sesquialtère de la
surface du grand segment à la surface du petit segment. Mais on a démontré que
la raison des segments est la même que celle du carré construit sur AΘ
et multiplié par
ΘH
au carré construit sur ΓΘ
et multiplié par
ΘZ,
et la raison du cube construit sur
AB
au cube construit sur
BΓ
est sesquialtère de la
raison de la surface du grand segment à la surface du petit segment. Je dis donc
que la raison du carré construit sur AΘ
et multiplié par
ΘH
au carré construit sur ΓΘ
et multiplié par
ΘZ
est plus grande que la raison du cube construit sur AB au cube construit sur BΓ,
c'est-à-dire que la raison du cube construit sur
AΘ
au cube construit sur
ΘB
; c'est-à-dire que la raison du carré construit sur AΘ
au carré construit sur BΘ,
et que la raison de
AΘ
à
ΘB.
Mais la raison du carré construit sur AΘ
au carré construit sur
ΘB,
avec la raison de AΘ
à
ΘB
est la
même que celle du carré construit sur AΘ
à la surface comprise sous ΓΘ,
ΘB ; et la raison du carré
construit sur AΘ à la surface
comprise sous ΓΘ,
ΘB
est la même que celle du
carré construit sur AΘ
et multiplié par
ΘH
à la surface comprise sous ΓΘ,
ΘB et multipliée par
ΘH.
Je dis donc que la
raison du carré construit sur BΘ
et multiplié par
ΘH
au carré construit sur ΓΘ
et multiplié par
ΘZ
est plus grande que celle du carré construit sur AΘ
à la surface comprise sous
BΘ,
ΘΓ ; c'est-à-dire que celle du
carré construit sur AΘ
et multiplié par
ΘH
à la surface comprise sous BΘ,
ΘΓ et multipliée par
ΘH.
Il faut donc démontrer
que le carré construit sur ΓΘ
et multiplié par
ΘZ
est plus petit que la surface comprise sous BΘ,
ΘΓ et multipliée par
ΘH
; ce qui est la même
chose que de démontrer que la raison du carré construit
sur ΓΘ
à la surface comprise sous
BΘ,
ΘΓ est moindre que celle de
HΘ
à
ΘZ.
Il faut donc démontrer que la raison de HΘ
à
ΘZ est
plus grande que celle de ΓΘ
à
ΘB. Du
point E menons la droite
EK
perpendiculaire sur EΓ, et du
point
B
la
droite
BΛ
perpendiculaire sur la droite EK. Il reste à démontrer que la raison de
HΘ
à
ΘZ
est plus grande que la raison de ΓΘ
à
ΘB. Mais
la droite
ΘΓ est
égale à la somme des droites AΘ,
KE
; il faut donc démontrer
que la raison de HΘ
à la somme des droites ΘA,
KE,
est plus grande que la raison de ΓΘ
à
ΘB. C'est
pourquoi ayant retranché ΓΘ
de
ΘH et
EΛ
qui
est égale à
BΘ
de
KE, il
faudra démontrer que la raison de la droite restante ΓH à la somme des droites
restantes AΘ,
KΛ
est plus grande que
celle de ΓΘ
à
ΘB,
c'est-à-dire que celle de
ΘB
à
ΘA ;
c'est-à-dire que celle de ΛE à
ΘΛ
; et que, par permutation, la raison de
KE
à
EΛ
sera plus grande que la raison
de la somme des droites
KΛ,
ΘA à la droite
ΘA,
et qu'enfin, par soustraction, la raison de
KΛ
à ΛE sera plus grande que celle
de
KΛ
à
ΘA et que
par conséquent la droite
ΛE
sera plus petite que
ΘA
(ν).
PROPOSITION X.
Parmi les segments sphériques qui ont
des surfaces égales, celui qui comprend la moitié de la sphère est le plus
grand.
Soit une sphère dont ABΓΔ soit un de
ses grands cercles, et AΓ son diamètre, soit aussi une autre sphère dont
EZHΘ
soit un de ses grands
cercles, et
EH
son
diamètre. Que l'une soit coupée par un plan qui passe par son centre, et que
l'autre soit coupée par un plan qui ne passe pas par son centre. Que les plans
coupants soient perpendiculaires sur les diamètres AΓ,
EH
et que ces plans soient
conduits par les lignes ΔB, ZΘ. Le segment sphérique construit dans l'arc
ZEΘ
est la moitié de la
sphère ; et parmi les segments construits dans la circonférence BAΔ, un
des segments de la figure où se trouve la lettre Σ est plus grand que la
moitié de la sphère, tandis que l'autre est plus petit que la moitié de cette
même sphère. Que les surfaces des segments dont nous venons de parler soient
égales. Je
dis que la demi-sphère qui est construite dans l'arc
ZEΘ est plus grande que le
segment construit dans l'arc
BAΔ.
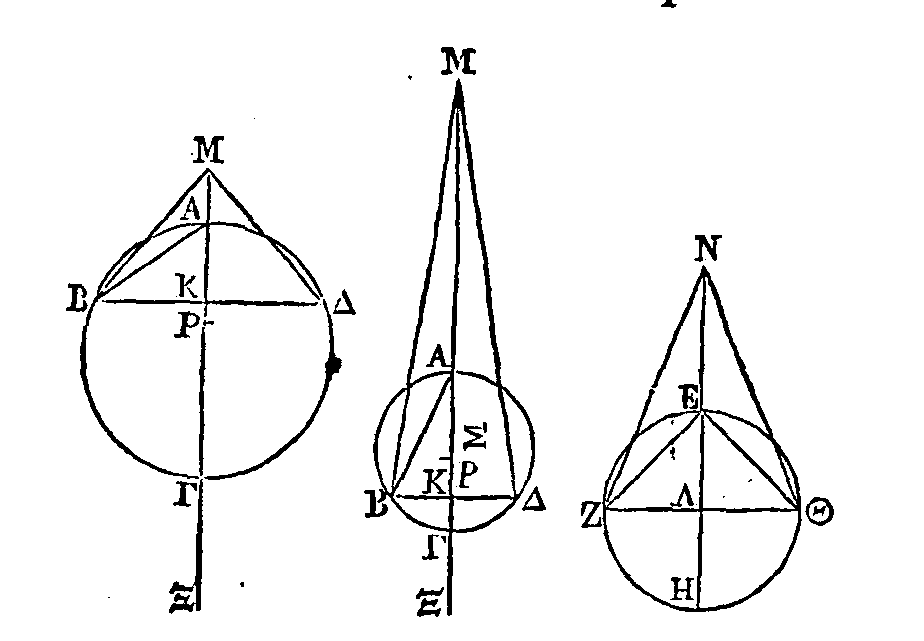
Car puisque les surfaces des segments
dont nous venons de parler sont égales, il est évident que la droite
BA
est égale à la droite
EZ.
Car
on a démontré que la surface d'un segment quelconque est égale à un cercle qui a
un rayon égal à la droite menée du sommet du segment à la circonférence de sa
base (I, 48). Mais dans la figure où se trouve la lettre Σ, l’arc
BAΔ
est plus grand que la
moitié de la circonférence; il est donc évident que le carré construit sur
AB
est
moindre que le double du carré construit sur
AK,
et plus grand que le double du carré construit sur le rayon. Que la droite ΓΞ
soit égale au rayon du cercle
ABΔ,
et faisons en sorte que ΓΞ soit à
ΓK
comme
MA
est à AK. Sur le cercle décrit
autour du diamètre
BΔ,
construisons un cône qui ait son sommet au point
M
; ce cône sera égal au segment
sphérique qui est construit dans l'arc
BAΔ
(II, 3). Faisons
EN
égal à
EΛ,
et sur le cercle décrit autour du diamètre ΘZ construisons un cône qui ait son
sommet au
point
N ;
ce cône sera égal à la demi-sphère construite dans l'arc
ΘEZ.
Mais la surface comprise sous
AΡ,
ΡΓ est plus grande que la surface comprise sous
AK,
KΓ, parce que le plus petit côté de l’une de ces surfaces est plus grand que le
plus petit
côté de l'autre (α);
et le carré construit sur
AΡ
est égal à la surface comprise
sous
AK,
ΓΞ, à
cause que ce carré est égal à la moitié du carré construit sur
AB
(β). Donc la somme de la
surface comprise sous AΡ, ΡΓ et du
carré construit sur
AΡ
est plus grande que la somme de
la surface comprise sous
AK,
KΓ et de la surface comprise sous AK, ΓΞ. Donc la surface comprise sous
ΓA,
AΡ est plus grande que
la surface comprise sous ΞK,
KA
(γ). Mais la
surface comprise sous
MK,
KΓ est égale à la surface comprise sous ΞK,
KA.
Donc la surface comprise
sous
ΓA, AΡ
est plus grande que la surface comprise sous
MK,
KΓ.
Donc
la raison de
ΓA
à
ΓK
est plus grande que la raison
de
MA à
AΡ.
Mais
la droite AΓ est à la droite ΓK comme le carré construit sur
AB
est au carré construit
sur
BK
; il
est donc évident que la raison de la moitié du carré construit sur
AB,
qui est égal au carré
construit sur
AΡ,
au carré construit sur
BK
est plus grande que la
raison de la droite
MK
au double de
AΡ,
laquelle est égale à
ΛN.
Donc la raison du
cercle décrit autour du diamètre
ΘZ au cercle décrit
autour du diamètre
BΔ
est plus grande que la raison
MK
à
NΛ.
Donc
le cône qui a pour base le cercle décrit autour du diamètre ZΘ
et pour sommet le point N est plus grand que le cône qui a pour base le cercle
décrit autour du diamètre
BΔ
et pour sommet le point M. Il
est donc encore évident que la demi-sphère construite dans l'arc EZΘ est plus
grande que le segment construit dans l'arc
BAΔ.
FIN DE LA SPHÈRE ET DU CYLINDRE.
COMMENTAIRE
LIVRE SECOND.
PROPOSITION II.
(α) Alors au lieu de
ΓΔ² : HΘ²
:: HΘ : EZ, on aura
ΓΔ
: ΓΔ²
x MN : EZ ; ou bien
ΓΔ
: MN :: HΘ : EZ, et par
permutation
ΓΔ
: HΘ
:: MN : EZ. Mais HΘ² =
ΓΔ
x
MN; donc
ΓΔ
: HΘ
:: HΘ : MN. Mais ΓΔ : HΘ :: MN : EZ ; donc ΓΔ: HΘ :: HΘ
: MN :: MN : EZ. Cette note se rapporte à la fin de la phrase précédente.
(β) Car le cylindre ΓZΔ étant
construit, il est évident que le diamètre de sa base et son axe sont
nécessairement donnés.
(γ) Archimède n'en donne pas le moyen.
Eutocius expose très au long les différentes manières de résoudre le problème
des deux moyennes proportionnelles. J'aurais fait avec plaisir un extrait de son
commentaire, si je n'avais pas craint de trop grossir le volume. Je me
contenterai de dire que ce problème a été résolu par Platon, Archytas, Héron,
Philon de Byzance, Apollonius, Dioclès, Pappus, Sporus, Menechime, Eratosthène
et Nicomède. On sait qu'avec la ligne droite et le cercle seulement le problème
n'a point de solution, c'est-à-dire qu'on ne saurait résoudre ce problème avec
la géométrie ordinaire,
(δ) Puisque ΓΔ : HΓ :: MN : EZ ; par
permutation et à cause que HΘ
= KΛ, on aura TA : MN :: KΛ : EZ. Mais
ΓΔ
: MN ::
ΓΔ : HΘ
; donc
ΓΔ
: HΘ
:: KΛ : EZ. Donc cer.
ΓΔ
:
cer. HΘ
:: KΛ : EZ. Donc les bases E, K
des cylindres sont réciproquement proportionnelles à leurs hauteurs.
PROPOSITION III.
(α) Il est entendu que la base de ce
cône doit être égale au cercle qui a pour rayon la droite BΓ.
(β) La démonstration du premier livre
ne regarde qu'un secteur sphérique dont la surface est plus petite que la moitié
de la surface de la sphère; mais il est facile d'en conclure que l'autre secteur
BΘZA est aussi égal à un cône qui a pour base le cercle décrit autour de BΓ
comme diamètre, et pour hauteur le rayon de la sphère.
(γ) Par permutation et
addition.
(δ) Dans toute proportion géométrique,
le carré de la somme des deux premiers termes est à leur produit comme le carré
de la somme des deux derniers est à leur produit. Soit la proportion géométrique
a : aq :: b : bq ; je dis qu'on aura :
(a + aq)² :
a²q :: (b + bq)² : b²q.
En effet, ces quatre quantités peuvent
être mises sous la forme suivante :
(1 +q)²a², a²q,
(1 +q)²b², b²q.
Divisant les deux premiers termes par
a² et les deux derniers par b², on aura les deux raisons
égales :
(1 + q)² : q,
et (1 + q)² : q.
(ε) On pourrait démontrer de la
manière suivante que AE : EΓ :: ΘA + AE : AE, lorsque le segment solide ABΓ est
égal au cône AΔΘ, ou ce qui est la même chose, lorsque le secteur solide BΓZΘ
est égal au rhombe solide
BΔZΘ.
Supposons donc que le secteur solide
BΓZΘ, ou le cône M soit
égal au rhombe solide
BΔZΘ. Nous
aurons,
ΘΔ
:
ΘΓ :: cer.
BΓ :
cer.
BE
:: BΓ² : BE² :: AΓ² :
AB² :: AΓ : AE. Donc
ΘA
: ΘΓ :: AΓ : AE. D'où l'on déduit,
par soustraction,
ΓΔ
:
ΘΓ :: EΓ : AE; par permutation,
ΓΔ
: EΓ ::
ΘΓ : AE; et enfin par addition,
ΔE : EΓ :: AΘ
+ AE : AE.
Ce qu'il
fallait démontrer.
Je démontrerais ensuite que
KE
:
EA ::
ΘΓ+ ΓE : ΓE, lorsque le segment
solide
BAZ
est
égal au cône BKZ, ou lorsque le secteur solide
BΘZA
est égal à la figure solide BΘZK,
en me conduisant de la même manière.
Supposons en effet que le secteur
solide BΘZA, ou que le cône N soit égal à la figure solide BΘZK;
nous aurons, KΘ :
AΘ :: cer.
BA
:
cer.
BE ::
BA²
: BE²
:: AΓ²
: BΓ²
:: AΓ : EΓ.
Donc KΘ : AΘ
:: AΓ : EΓ. D'où l'on déduit par soustraction, KA : AΘ
:: AE : EΓ; par permutation, KA : AE :: AΘ
: EΓ ; et enfin par addition, KE : AE ::
ΘΓ + EΓ : EΓ. Ce qu'il fallait démontrer.
PROPOSITION V.
(α) Par permutation et par addition.
(β) Parce que dans la
proportion continue, le premier terme est au troisième comme le carré du premier
est au carré du second.
(γ) En effet, puisque ΧΔ : ΧB
:: KB : BΡ, et que ΔΧ
est plus grand que BΧ,
la droite KB
sera plus grande que la
droite BΡ.
(δ) Parce que la somme des deux
premiers termes d'une proportion est au premier comme la somme des deux derniers
est au troisième.
(ε) Si l'on a trois quantités a,
b, c, la raison de la première à la seconde est la même que la raison
composée de la raison de la première à la troisième, et de la raison de la
troisième à la seconde; c'est-à-dire, que la raison de a : b est
composée de la raison de la raison a à b, et de la raison
de c : b; c'est à-dire, que la raison a à b
est égale à la raison de ac à bc.
(z) Cette solution et cette
construction ne se trouvent point dans Archimède. Voyez sur ce problème la note
suivante. Cette note, qui m'a paru très intéressante, m'a été communiquée par M.
Poinsot.
(θ) Il est bien aisé de voir que la
construction d'Archimède résoudrait le problème ; car il faut que le plus grand
segment soit au plus petit comme Π à Σ, ou le plus grand segment à la sphère
comme Π à Π + Σ ; or, en nommant r le rayon, et x l'apothème KΞ,
la première proportion d'Archimède,
ΘZ
: ΘB :: Π : Σ,
donne
ΘZ :
r
:: Π : Π
+Σ.
La
deuxième, (A)
ΧZ : ΘZ :: BΔ²
:
ΔΧ²,
devient 2r—
x
:
ΘZ ::
4r² : (r + x)². D'où, en multipliant par ordre, on tire :
2r —
x
:
r
::
4r²
Π : (r
+ x)² (Π +
Σ),
(B);
ou bien, en faisant passer le facteur
(r + x)² à l'autre extrême, et le facteur 4r²
à l'autre moyen, ce qui est permis :
(2r — x) (r +
x)²
:
4r3
:: Π : Π + Σ.
Mais le premier terme (2r —
x) (r+x)² étant multiplié par le tiers du rapport p de
la circonférence au diamètre, donne le volume du segment dont x est
l'apothème et r + x la flèche ; et le
deuxième 4r3 étant multiplié par le
même nombre donne la sphère. Donc, etc.
Réciproquement, si l'on voulait poser
immédiatement la proportion du problème, il faudrait faire : le segment, ou p/5
x (2r—x)
(r + x)², à la
sphère, ou
p/3 x 4r3
> comme Π à Π + Σ. D'où l'on
déduirait la proportion (B), qu'on pourrait regarder
comme le résultat des deux proportions (A)
qu'Archimède a su découvrir par son génie.

Archimède en promet pour la fin la
solution; mais cette solution ne se trouve pas; et s'il entend une solution
ordinaire, c'est-à-dire, par la règle et le compas, comment l'a-t-il pu trouver?
La proportion donne pour x l'équation du troisième degré :
x3—
3r²x + r². 2r
(Π-Σ)/(Π+Σ)
laquelle, comparée à la formule
générale x3 + px + q = 0, donne
p
essentiellement négatif, et p3/27 > q2/4,
et par conséquent tombe
dans le cas irréductible, et a ses
trois racines essentiellement réelles. Cette équation répond à la trisection
d'un arc
j
dont la corde
c
serait égale à 2r
(Π-Σ)/(Π+Σ)
dans
le cercle dont le rayon est r. Car
en nommant x la corde du tiers de cet arc, on a
par la géométrie x3— 3r²x + r².c = 0;
de sorte que l'une des racines de
l'équation est la corde de l'arc
j/3; et les deux autres sont les
cordes
respectives des arcs (u+j)/3,
(2u+j)/3 (en nommant u la circonférence
entière). Car on sait que la
même corde c répond, non seulement à l'arc
j,
mais encore aux arcs u+j,
2u+j ; et encore à une infinité d'autres 3u+j,
etc. u -
j,
2u -j,
etc., mais dont les tiers redonneraient les mêmes
cordes que les trois premiers.
Ainsi Archimède aurait, par sa
construction, exprimé des radicaux cubes par des radicaux carrés, et résolu le
problème de la trisection de l'angle, ce qui est impossible. Il faut donc penser
que s'il a donné la construction qu'il annonce, elle n'était pas géométrique,
c'est-à-dire qu'elle se faisait par le moyen du cercle et de quelque autre
section conique, telle que la parabole. Mais d'un autre côté, comme il n'emploie
jamais dans ses constructions que la règle et le compas, il est plus probable
qu'il n'avait pas encore de solution ; et que ne la jugeant pas d'abord
supérieure au cercle, il ne l'annonce pour la fin, que dans l'espérance où il
est de la trouver lorsqu'il viendra à s'en occuper d'une manière particulière.
Et cela devient plus probable encore, si l'on observe que l'inconnue de sa
proportion ayant nécessairement trois valeurs réelles différentes, il est
impossible que sa construction, quelle qu'elle fût, les ait distinguées pour lui
en donner une de préférence aux autres. Or, dans ce cas, il n'aurait pu
s'empêcher d'en faire la remarque, et de dire un mot sur ce singulier paradoxe,
d'avoir trois valeurs différentes, pour résoudre un problème qui n'a évidemment
qu'une seule solution ; car il est évident qu'il n'y a qu'une manière de couper
la sphère en deux segments qui soient dans une raison donnée. Il est donc peu
probable que la construction d'Archimède soit perdue, puisqu'il est
très-probable qu'elle n'a point existé.
Au reste, si l'on veut voir ce que
signifient les trois valeurs qu'on trouve pour l'apothème inconnue x,
on considérera que la
corde c de l'arc
j étant 2r
(Π-Σ)/(Π+Σ), et par conséquent
plus petite que le diamètre 2 r ;
j/3 est nécessairement moindre qu'un
sixième de la circonférence u. Par
conséquent la première racine
x
= cord. j/3 est nécessairement plus
petite que le rayon, et les
deux autres x' = cord. (u+j)/3,
x" = cord. (2u+j)/3, sont nécessairement plus grandes. De ces
trois valeurs, il n'y a donc que la première qui puisse résoudre le problème que
l'on a en vue, puisque l'apothème du segment est toujours plus petite que le
rayon de la sphère. Les deux autres racines résolvent donc quelque autre
problème analogue intimement lié à celui-là. Elles indiquent deux sections à
faire dans le solide décrit par la révolution de l'hyperbole équilatère de même
axe que le cercle générateur de la sphère ; et ces sections faites aux distances
x' et x" du centre, déterminent en effet deux segments
hyperboliques respectivement égaux à ceux de la sphère proposée. Car si l'on
nomme x la perpendiculaire abaissée du centre sur la base du segment
hyperbolique, de sorte que x — r en soit la flèche, on trouve,
pour le volume de ce segment,
(x3—
3r²x + x3) x
p/3
ce qui est aussi l'expression du
segment sphérique dont la flèche est r — x. Ainsi la liaison
intime de l'hyperbole équilatère au cercle, fait qu'on ne peut résoudre le
problème proposé dans la sphère, sans le résoudre en même temps dans
l'hyperboloïde de révolution.
La suite des signes dans l'équation,
x3—
3r²x + r². 2r (Π-Σ)/(Π+Σ)
= 0,
fait voir que des trois racines x, x', x",
deux sont nécessairement positives et la troisième négative ; et l'absence
du second terme montre que celle-ci est égale à la somme des deux autres. On
prendra donc les deux plus petites cordes, qui sont x et x',
en plus; et l'autre x' en moins. La première portée à droite à partir
du centre sur le diamètre répondra aux deux segments sphériques qui sont entre
eux comme
Π à Σ ; la
deuxième portée du même côté sur la même ligne répondra au segment hyperbolique
égal au segment sphérique adjacent; et la troisième portée à gauche répondra,
dans l'autre partie de l'hyperboloïde, à un segment égal au second segment
sphérique adjacent : de sorte que ces deux segments de l'hyperboloïde seront
aussi entre eux comme Π et Σ, et que leur somme sera aussi égale à la sphère
proposée.
Telle est l'analyse de ce problème
dont les divers exemples peuvent vérifier ce qu'on vient de dire. Θu'on suppose,
par exemple, Π = Σ, auquel cas on veut partager la sphère en deux parties
égales. On aura,
cord.
j
= 2r
(Π-Σ)/(Π+Σ) = 0;
par conséquent, x
= cord.
j/3
= 0.
Ce qui indique d'abord la section à
faire par le centre, comme cela doit être. Ensuite on aura :
x =
cord. u/3 = — r ΣΘΡ(3),
et x" = cord. 2u/3 = 2r ΣΘΡ(3);
ce qui répond à deux segments
hyperboliques égaux entre eux et à la demi sphère, comme on peut s'en assurer.
Si l'on suppose Σ = 0,
on a cord. j = 2r, et par conséquent
j = u/2.
On a donc x = cord. u/6 = r; ce qui indique un
segment nul et un autre égal à la sphère. Ensuite x" = cord. (5/6) u
= r, et x' = cord. u/2 = 2 r, ou plutôt — 2 r ; ce qui
indique deux segments dans l'hyperboloïde, l'un
nul et l'autre égal à la sphère. Au reste, dans ces deux cas, l'équation offre
d'elle-même ses racines; car dans le premier elle devient, x3
— 3 r ² x = 0, qui donne sur le champ x = 0, et x
= ± ΣΘΡ (3r²) = ± r ΣΘΡ (3); ce qui est le
côté du triangle équilatéral inscrit.
Dans le second cas, elle devient x3
— 3 r² x + 2r3 = 0, et se décompose en ces trois
facteurs, (x — r), (x — r), (x — 2 r).
Si l'on voulait construire l'équation
par le moyen du cercle et de la parabole, on pourrait employer le cercle dont
l'équation est : y2 + x2
— 4ry + 2rx
(Π-Σ)/(Π+Σ)
et la parabole dont l'équation est,
x²— ry = 0; car en éliminant y entre ces équations,
afin d'avoir les abscisses x qui répondent aux points d'intersection des
deux courbes, on trouve :
x4
— 3r²x² + r² 2r
x
(Π-Σ)/(Π+Σ) =
0 et
divisant par x,
x3
— 3r²x + r² 2r
(Π-Σ)/(Π+Σ) =
0;
ce qui est l'équation proposée.
Enfin, nous observerons que le
problème dont il s'agit étant proposé pour l'ellipsoïde de révolution, conduit
absolument à la même équation. Ainsi, en nommant a le demi-grand axe de
l'ellipse, on a, pour déterminer l'apothème x de deux segments qui sont
entre eux comme n et Σ, l'équation
x3
— 3a²x + a² 2a
(Π-Σ)/(Π+Σ) =
0;
et comme le second axe b
n'entre pas dans cette équation, on peut conclure qu'on aura toujours les mêmes
solutions pour tous les ellipsoïdes de révolution de même axe a;
et pour tous les hyper-boloïdes conjugués, puisque l'équation de l'ellipse ne
diffère de celle de l'hyperbole que par le signe du carré de ce second axe : et
c'est ce qui confirme encore ce que nous avons déjà dit, que la question ne peut
être proposée pour l'ellipsoïde, sans l'être en même temps pour l'hyperboloïde
conjugué.
PROPOSITION VI.
(α) Puisque les segments EZH, ΘKΛ sont
semblables, on aura
ΣO : ΦO :: ΡΞ : ΥΞ, et par addition,
ΣO + ΦO : Φ0 :: ΡΞ + ΥΞ : ΥΞ. Mais on a d'ailleurs,
ΣO + ΦO : ΦO :: ΩΦ : HΦ,
ΡΞ + ΥΞ : ΥΞ :: YΥ :: ΛΥ;
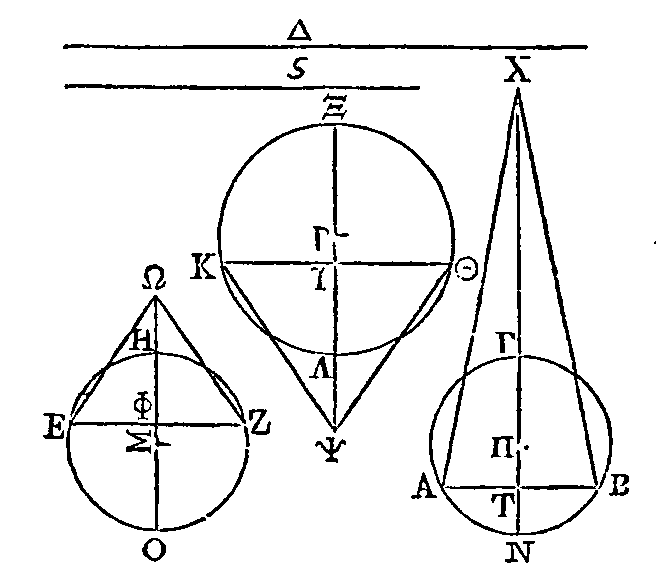
donc ΩΦ : HΦ :: YΥ : ΛY. Donc par
permutation ΩΦ : YΥ :: HΦ : ΛY. Mais HΦ : ΛY :: EZ :
KΘ,
à cause que les segments
sont semblables ; donc ΩΦ : YΥ :: EZ : KΘ. Donc les cônes
EZΩ,
YΘK sont semblables, puisque leurs
hauteurs sont proportionnelles aux diamètres de leurs bases.
(β) C'est-à-dire, qu'elles forment une
progression géométrique.
PROPOSITION IX.
(α) Une raison doublée d'une autre
raison est cette seconde raison multipliée par elle-même, et une raison
sesquialtère d'une autre raison est cette seconde raison multipliée par sa
racine carrée.
(β) Car la proportion EΔ +
ΔZ : ΔZ ::
ΘZ : ZB donne par soustraction la proportion suivante, EΔ : ΔZ
:: BΘ : ZB, qui devient, en
échangeant les extrêmes, BZ : ZΔ
:: BΘ : EΔ = BE.
(γ) En effet, dans la proportion BZ :
ZΔ :: ΘB : BE, la droite BZ étant
plus grande que la droite
ZΔ,
il est évident que
ΘB
sera plus grand que BE.
(δ) Et par permutation, KZ : HZ :: ZB
: ZΔ.
(ε) Car puisque BΘ
> BK, il est évident que
ΘB
: BZ > BK : BZ. Donc, par addition,
ΘZ
: BZ > KZ : BZ, et par conversion,
ΘZ
: ΘB < KZ : BK. Donc, par
permutation,
ΘZ
: KZ < ΘB : BK.
(z) La première surface étant égale.au
carré de l'ordonnée AZ, et la seconde étant égale au carré du rayon, la première
surface est plus petite que la seconde, parce que toute ordonnée qui ne passe
pas par le centre est plus petite que le rayon.
(θ) Puisque BN² =
ΘB
x BK, on aura,
ΘB
: BN :: BN : BK. Donc
ΘB
: BK :: BN² : BK².

Mais
ΘB
: BN :: BN : BK; donc, par addition,
ΘN
: BN :: KN : BK. Donc
ΘN²
: BN² ::
KN²
: BK² ; et par
permutation,
ΘN²:
KN² :: BN²: BK². Mais
ΘB
: BK :: BN² : BK² donc
ΘB
: BK ::
ΘN² :
KN².
(ι) Que les trois quantités a,
b, c soient telles que a² : b² > b :
c ; je
dis que a : c > b3/2 : c3/2.
Prenons une moyenne proportionnelle
d entre b et c, de manière qu'on ait b : d : :
d : c ; puisque a² : b2 > b
: c, et que b : c :: b² : d²,
nous aurons a² : b2 > b²
: d² ; ou bien a : b > b : d.
Faisons en sorte que c : d:
b : e forment une progression géométrique, on aura e : c
:: b3 : d3. Mais b : d
:: b1/2: c1/2,
parce que b : c :: b² : d²
; donc b3 : d3 :: b3/2
: c3/2. Donc e : c :: b3/2
: c3/2.
Mais a > e ; car si a
était égal à e, on aurait  a :
b : d : c, et par conséquent a2 : ba
:: b : c, et si a était plus petit que e, on aurait
a² : b² < b : c. Mais a² : b² > b
: c; donc a > e. Donc
a
: c > b2/3 : c2/3. Or,
Archimède a démontré que
ΘZ² : ZK² > ZK : ZH ; donc ΘZ : ZH > ZK3/2
: ZH3/2. a :
b : d : c, et par conséquent a2 : ba
:: b : c, et si a était plus petit que e, on aurait
a² : b² < b : c. Mais a² : b² > b
: c; donc a > e. Donc
a
: c > b2/3 : c2/3. Or,
Archimède a démontré que
ΘZ² : ZK² > ZK : ZH ; donc ΘZ : ZH > ZK3/2
: ZH3/2.
(λ)
En effet, puisque le
segment
BAΔ
:
cône
BAΔ
:: HΘ
: ΘΓ (2, 3); que le cône BAΔ : cône BΓΔ ::
AΘ :
ΘΓ, ces deux cônes ayant la
même base, et que le cône
BΓΔ : segment BΓΔ :: AΘ
: ΘZ (2, 3).
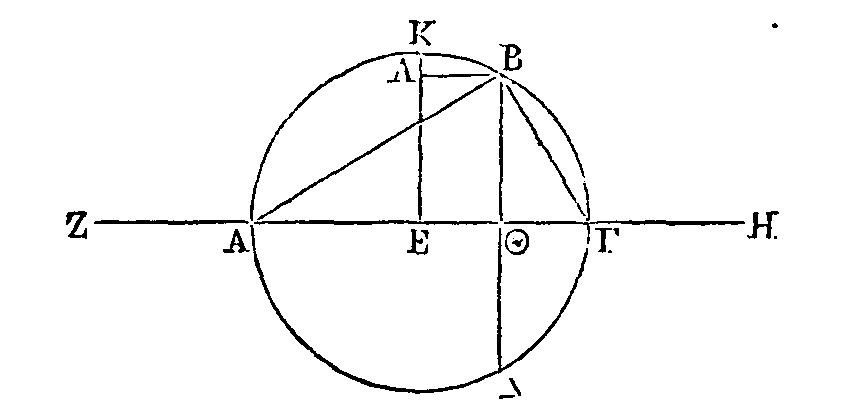
Multipliant ces trois proportions,
terme par terme, on aura : segment
BAΔ
x
cône
BAΔ
x
cône BΓΔ : cône
BAΔ x
cône BΓΔ
x segment
BΓΔ :: HΘ
x AΘ
x AΘ
:
ΘΓ x
ΘΓ x
ΘZ ; ou
bien,
segment
BAΔ
: segment BΓΔ :: segment
BAΔ
x cône
BAΔ
x cône BΓΔ : cône
BAΔ
x segment BΓΔ ::
HΘ
x
AΘ
x
AΘ : ΘΓ
x
ΘΓ x
ΘZ.
(μ) Soient quatre droites a,
c, d, b ; je dis que la raison composée de la raison de la
surface comprise sous a, b, au carré construit sur c,
et de la raison de b à d, est égale à la raison de la
surface comprise sous a, b, multipliée par b,
au carré de c, multiplié par d, ou ce qui est la même chose, je
dis que la raison composée de la raison de ab à ac² et de la
raison de b à d, est égale à la raison de ab
multiplié par b, au carré de c multiplié
par d; c'est-à-dire, que la raison
composée de la raison ab à c² et de la raison de b à d,
est égale à la raison de ab x b à c²d. Ce qui
est évident.
(ν) Cette proposition peut se
démontrer algébriquement avec la plus grande facilité.
Appelons r le rayon de la
sphère, et x la droite EZ. La droite ΔZ sera égale à r — x
; et le plus grand segment de la sphère, qui est
ABΓ, sera égal à ΘZ x (Π x AZ²)/3
c’est-a-dire à
((Π x AZ)/3) x
(2
r — x) (r + x)/(r — x)
et le plus petit segment, qui est AΔΓ,
sera égal à HZ x (Π x AZ²)/3,
c’est-à-dire à
((Π x AZ²)/3) x
(2 r + x) (r — x)/x
Il faut démontrer d'abord que la
raison de
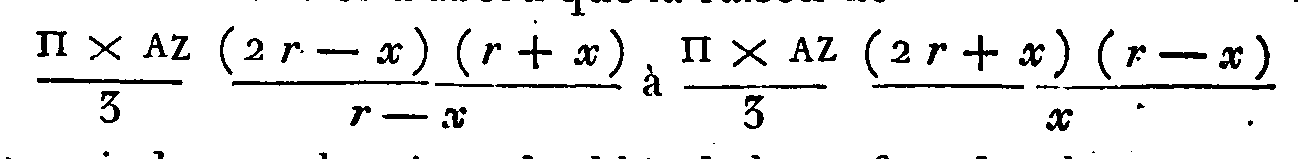 est moindre que la
raison doublée de la surface du plus grand segment à la surface du plus petit;
c'est-à-dire que est moindre que la
raison doublée de la surface du plus grand segment à la surface du plus petit;
c'est-à-dire que

Il faut démontrer ensuite que

Ou ce qui est la même chose, il faut
démontrer d'abord que (2 r — x) (r + x)
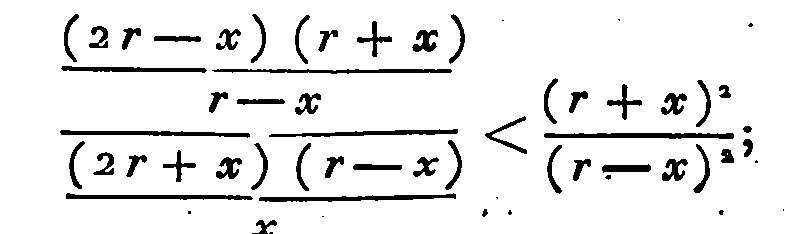
et il faut démontrer ensuite que
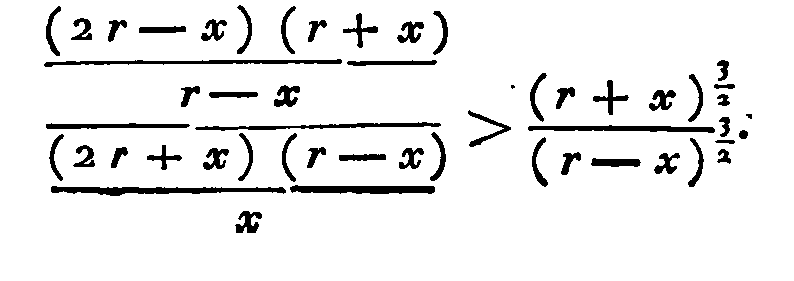
Ce qui sera évident, quand on aura
fait les opérations convenables.
PROPOSITION X.
(α) Si une droite est coupée en deux
parties inégales en un point et encore en deux autres parties inégales dans un
autre point, le rectangle compris sous les deux segments qui s'éloignent moins
du milieu de cette droite, est plus grand que le rectangle compris sous les deux
segments qui s'en éloignent davantage ; d'où il suit que si le plus petit côté
de l'un de ces rectangles est plus grand que le plus petit de l'autre rectangle,
le premier rectangle est plus grand que le second.
Cette proposition est démontrée
généralement dans Euclide, mais ici c'est un cas particulier facile à démontrer.
En effet, le rectangle AΡ x ΡΓ est
égal au carré de l'ordonnée qui passe par le point Ρ, et le rectangle AK x KΓ est égal au carré de l'ordonnée
KB. Mais l'ordonnée qui passe par le
point Ρ est plus grande que l'ordonnée
KB
y
donc le rectangle AΡ
x ΡΓ est plus grand que le rectangle AK
x KΓ.
(β) Le carré de AΡ est égal à AK x ΓΞ ; car puisque AΡ = EΛ, et que EΛ² =
EZ2/2,
il est évident que AΡ² = AB2/2,
puisque
AB
=
EZ.
(γ) En effet, puisque
AΡ
x ΡΓ +
AΡ²
>
AK
x
KΓ +
AK
x
ΓΞ,
on aura (ΡΓ + AΡ) AΡ < (KΓ + ΓΞ)
AK, ou
bien ΓA x AΡ > ΞK x
KA.
FIN DU COMMENTAIRE SUR LA SPHÈRE
ET LE CYLINDRE.
|

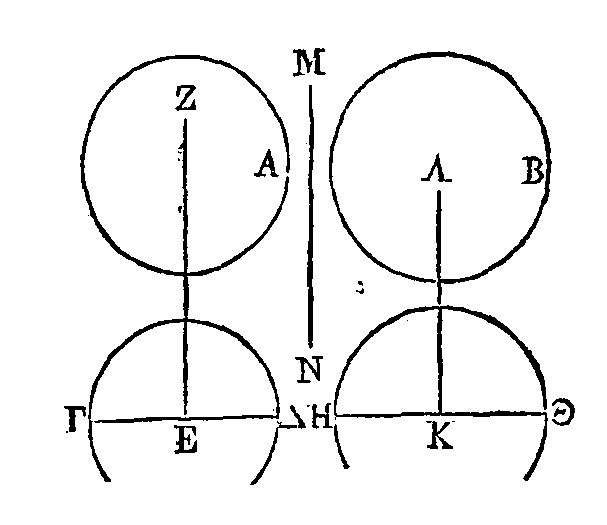







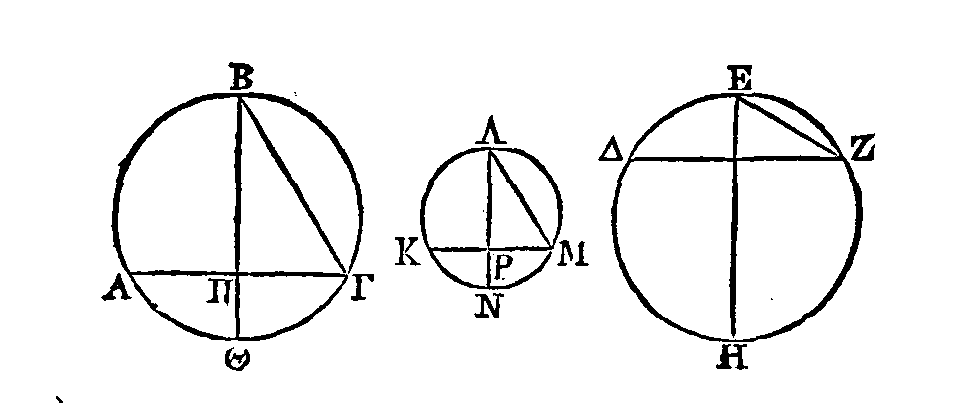
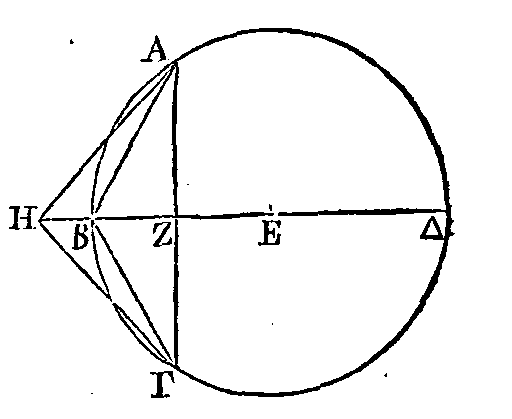



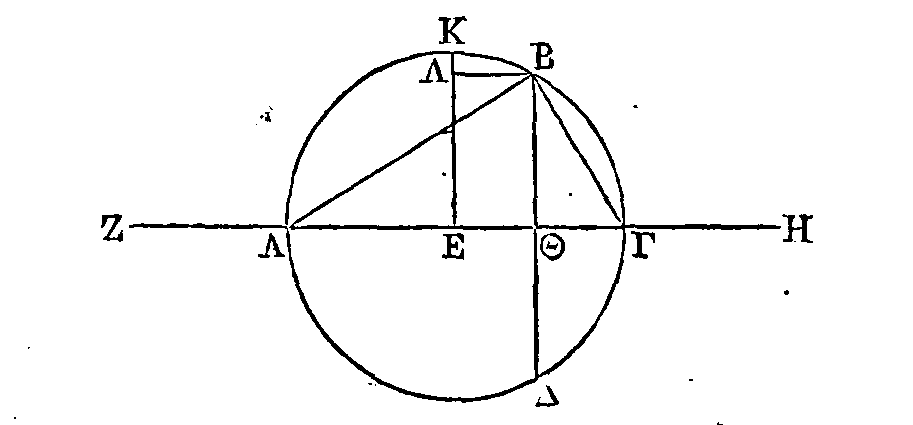
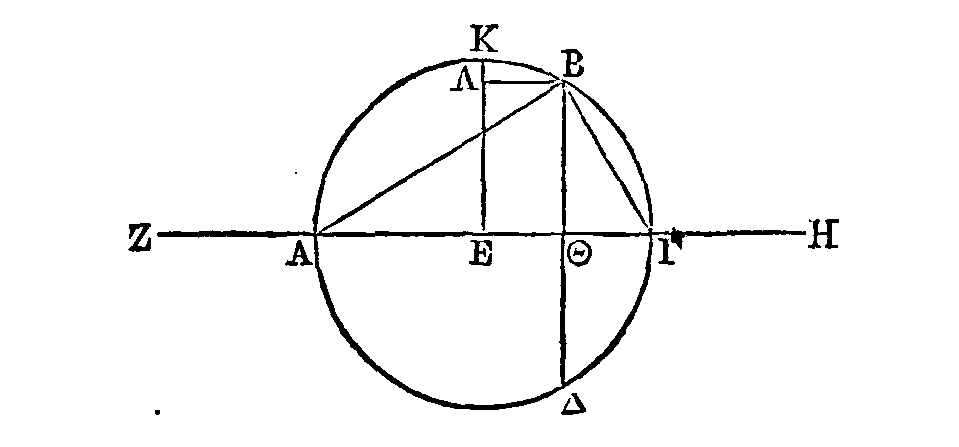
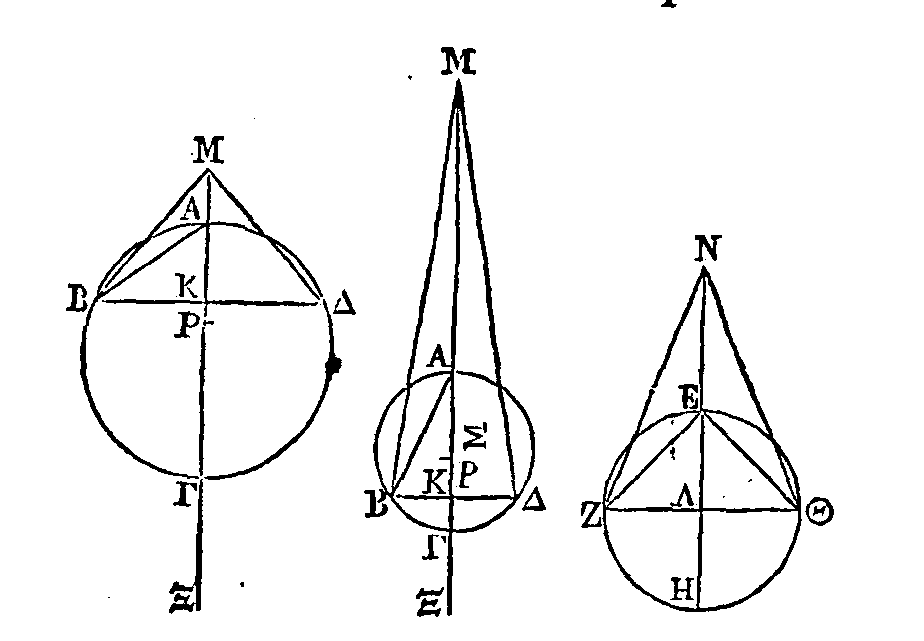


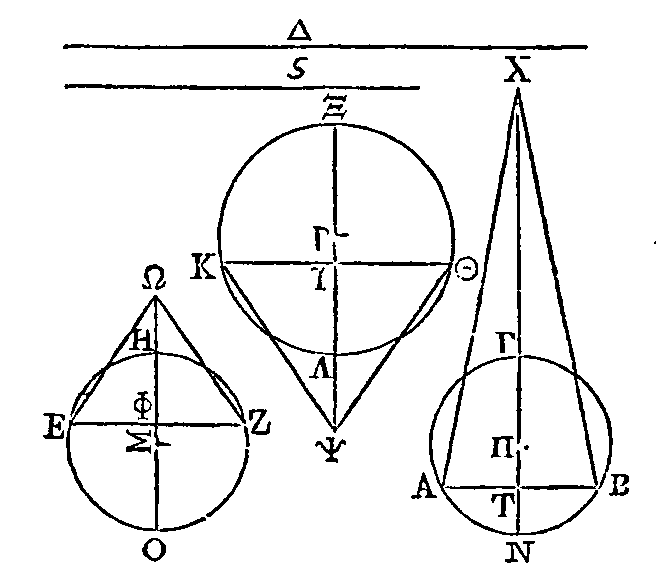

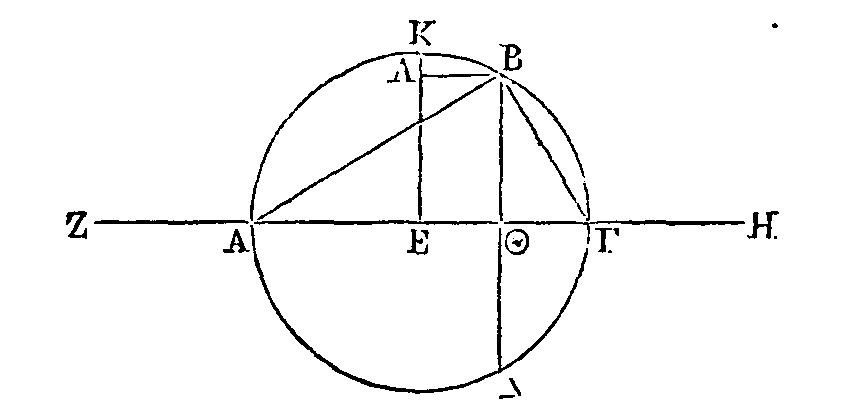
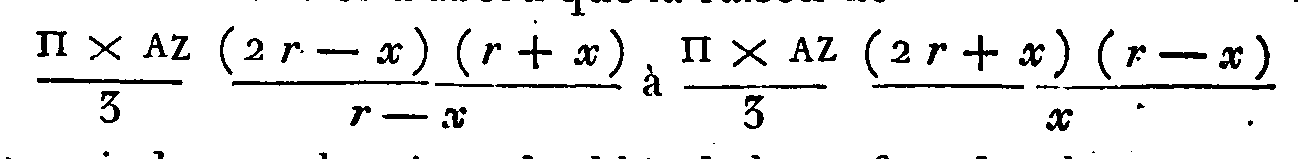 est moindre que la
raison doublée de la surface du plus grand segment à la surface du plus petit;
c'est-à-dire que
est moindre que la
raison doublée de la surface du plus grand segment à la surface du plus petit;
c'est-à-dire que