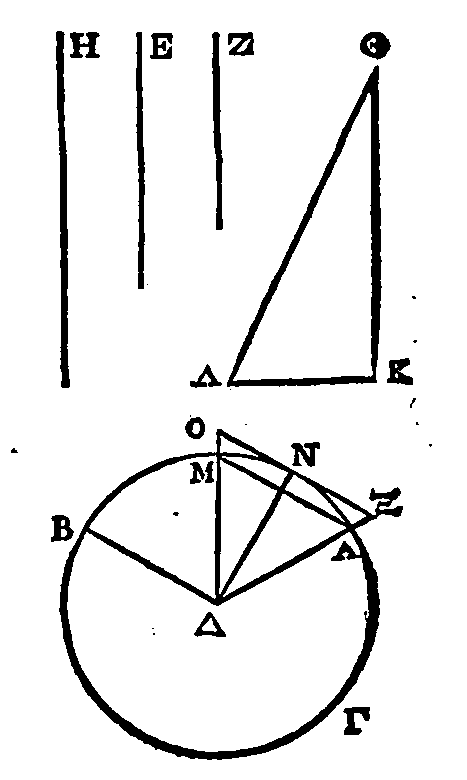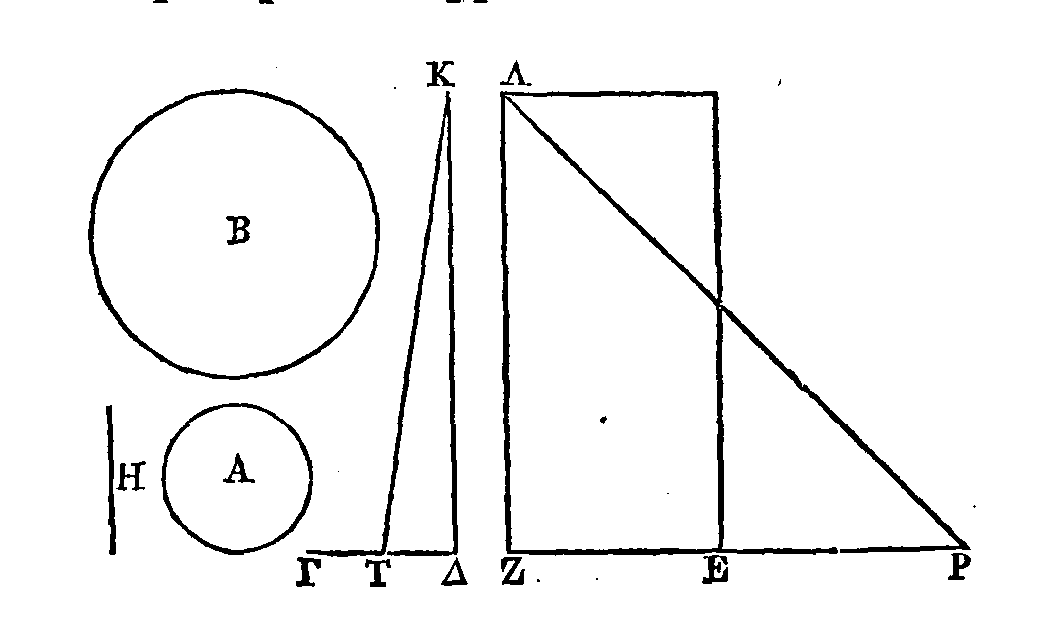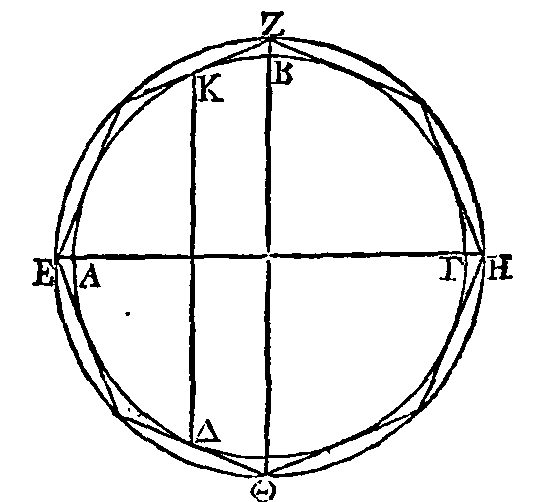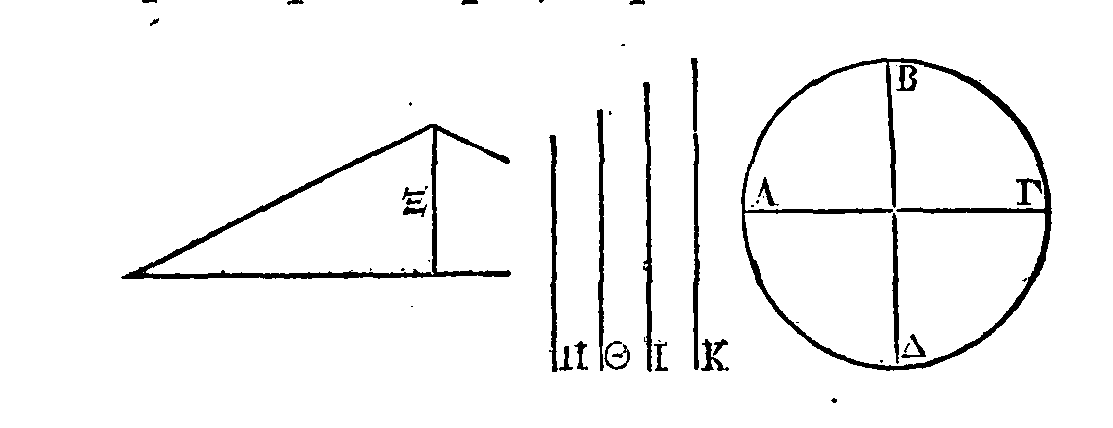OEUVRES
D'ARCHIMÈDΕ
DΕ LA SPHÈRE ET DU CYLINDRE.
LIVRE PREMIER.
ARCHIMÈDΕ A DOSITHEE, SALUT,
Je
t'avais déjà envoyé, avec leurs
démonstrations, les théorèmes que mes réflexions m'avaient fait découvrir ; le
suivant était au nombre de ces théorèmes :
Tout segment
compris entre une droite et la section du cône rectangle, est égal à quatre fois
le tiers d'un triangle qui a la même base et la même hauteur que le segment (α).
J'ai terminé
aujourd'hui les démonstrations de plusieurs théorèmes qui se sont présentés; et
parmi ces théorèmes, on distingue ceux qui suivent.
La surface de la sphère est quadruple d'un de ses grands cercles.
La surface d'un
segment sphérique est égale à un cercle ayant un rayon égal à la droite menée du
sommet du segment à la circonférence du cercle qui est la base du segment.
Un cylindre qui
a une base égale à un grand cercle de la sphère, et une hauteur égale au
diamètre de cette même sphère, est égal à trois fois la moitié de la sphère.
La surface du
cylindre est aussi égale à trois fois la moitié de la surface de la sphère.
Quoique ces
propriétés existassent essentiellement dans les figures dont nous venons de
parler, elles n'avoient point été remarquées par ceux qui ont cultivé la
géométrie avant nous; cependant il sera facile de connaître la vérité de nos
théorèmes, à ceux qui liront attentivement les démonstrations que nous en avons
données (β).
Il en a été de même de plusieurs choses qu'Eudoxe a considérées dans les
solides, et qui ont été admises, comme les théorèmes suivant:
Une pyramide est
le tiers d'un prisme qui a la même base et la même hauteur que la pyramide.
Un cône est le
tiers d'un cylindre qui a la même base et la même hauteur que le cône.
Ces propriétés
existaient essentiellement dans ces figures, et quoiqu'avant Eudoxe, il eût paru
plusieurs géomètres qui n'étaient point à mépriser, cependant ces propriétés
leur étaient inconnues, et ne furent découvertes par aucun d'eux.
Au reste, il
sera permis, à ceux qui le pourront, d'examiner ce que je viens de dire. Il eût
été à désirer que mes découvertes eussent été publiées du vivant de Conon ; car
je pense qu'il était très capable d'en prendre connaissance et d'en porter un
juste jugement. Quoi qu'il en soit, ayant pensé qu'il était bon de les faire
connaître à ceux qui cultivent les mathématiques, jeté les envoie appuyées de
leurs démonstrations: les personnes versées dans cette science pourront les
examiner à loisir. Porte-toi bien.
On expose
d'abord les propositions qui sont nécessaires pour démontrer les théorèmes dont
on vient de parler.
AXIOMES ET DÉFINITIONS.
1.
Il
peut y avoir dans un plan, certaines lignes courbes terminées qui soient
toutes du même côté des droites qui joignent leurs extrémités, ou qui du moins
n'aient aucune de leurs parties de l'autre côté de ces mêmes droites (α).
2. Une ligne
concave du même côté est celle dans laquelle, ayant pris deux points
quelconques, les droites qui joignent ces points tombent tout entières du même
côté de la ligne concave, ou bien quelques-unes tombent du même côté de la ligne
concave, et quelques autres sur cette ligne, tandis qu'aucune de ces droites ne
tombe de différents côtés (β).
3. Il
peut y avoir également des surfaces terminées qui, ayant leurs extrémités dans
un plan sans être dans ce plan, sont toutes placées du même côté du plan dans
lequel elles ont leurs extrémités, ou qui du moins n'ont aucune de leurs parties
de l'autre côté de ce même plan.
4. Une surface
concave du même côté est celle dans laquelle, ayant pris deux points
quelconques, les droites qui joignent ces points tombent du même côté de la
surface concave, ou bien quelques-unes de ces droites tombent du même côté de la
surface concave, et quelques autres dans cette surface, tandis qu'aucune de ces
droites ne tombe de différents côtés.
5. J'appelle secteur solide une figure terminée par la sur face
d'un cône qui coupe la sphère et qui a son sommet au centre, et par la surface
de la sphère qui est comprise dans le cône.
6. J'appelle rhombe solide, une figure solide composée de deux
cônes qui ont la même base, et dont les sommets sont de différents côtés du plan
dans lequel se trouve la base, de manière que les axes ne forment qu'une seule
et même droite. Je prends pour principes les propositions suivantes.
PRINCIPES.
1. La ligne droite est la plus courte de toutes celles qui
ont les mêmes extrémités (α).
2. Deux lignes qui sont dans un plan et qui ont les mêmes
extrémités sont inégales, lorsqu'elles sont l'une et l'autre concaves du même
côté et que l'une est comprise toute entière par l'autre, et par la droite qui a
les mêmes extrémités que cette autre, ou bien lorsque l'une n'est comprise qu'en
partie et que le reste est commun, la ligne comprise est la plus courte (β).
3. Pareillement lorsque des surfaces ont les mêmes limites dans un
plan, la surface plane est la plus petite.
4. Deux surfaces qui ont les mêmes limites dans un plan sont
inégales, lorsqu'elles sont l'une et l'autre concaves du même côté, et que l'une
est comprise toute entière par l'autre et par le plan qui a les mêmes limites
que cette autre ; ou bien lorsque l'une n'est comprise qu'en partie, et que le
reste est commun; la surface comprise est la plus petite.
5. Etant données deux lignes inégales, ou deux surfaces inégales,
ou bien deux solides inégaux, si l'excès de l'une de ces quantités sur l'autre
est ajouté à lui-même un certain nombre de fois, cet excès ainsi ajouté à
lui-même pourra sur passer l'une ou l'autre des quantités que l'on compare entre
elles (γ).
Ces choses étant
supposées, je procède ainsi qu'il suit.
PROPOSITION I.
Si un polygone
est inscrit dans un cercle, il est évident que le contour du polygone inscrit
est plus petit que la circonférence de ce cercle.
Car chaque côté
du polygone est plus petit que l'arc de la circonférence qu'il soutend (Princ.
1).
PROPOSITION II.
Si un polygone
est circonscrit à un cercle, le contour du polygone circonscrit est plus grand
que la circonférence de ce cercle.
Qu'un polygone
soit circonscrit à un cercle : je dis que le contour de ce polygone est plus
grand que la circonférence de ce cercle.
Car la somme des droites ΒΛ,
ΑΛ
est plus
grande que l'arc ΒΛ
; parce que ces droitescomprennent un arc
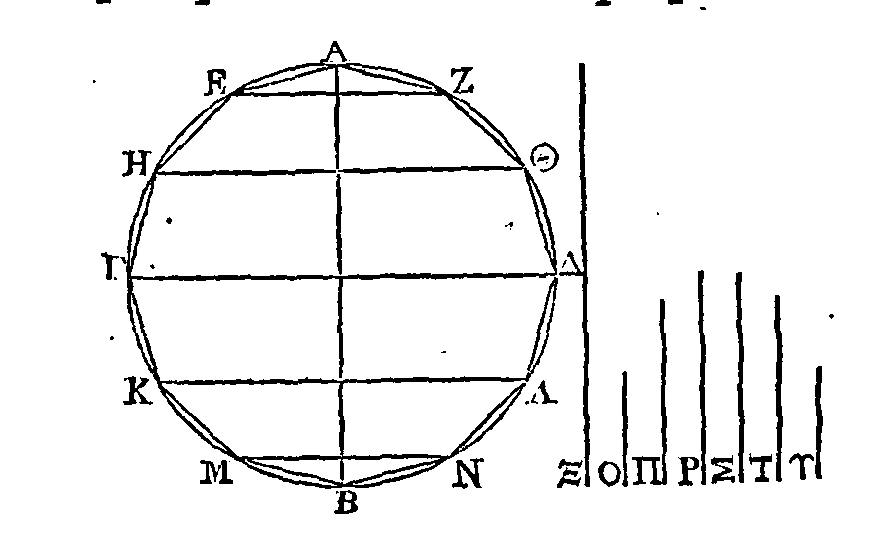
qui a les mêmes extrémités que
ces droites (Princ. 2). Semblablement la somme des droites ΔΓ, ΓΒ
est plus grande
que l'arc ΔΒ, la
somme des droites ΛΚ,
ΚΘ
plus grande que l'arc ΛΘ;
la .somme des droites ZH,
ΗΘ
plus
grande que l'arc ΖΘ, et enfin la somme des droites ΔΕ, EZ
plus
grande que l'arc ΔΖ. Donc le contour entier du polygone est plus grand que la
circonférence.
PROPOSITION III.
Deux quantités
inégales étant données, il est possible de trouver deux droites inégales dont la
raison de la plus grande à la plus petite soit moindre que la raison de la plus
grande quantité à la plus petite.
Soient deux
quantités inégales AB,
Δ;
que AB
soit la plus grande : je dis qu'il est possible de trouver deux droites inégales
qui remplissent les conditions de ce qui est proposé.
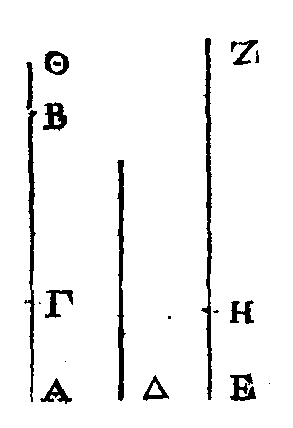
Que la droite ΒΓ soit égale à la droite
Δ; et prenons une certaine droite ZH.
Si la
droite ΓΑ
est
ajoutée à elle-même un certain nombre de fois, cette droite ainsi ajoutée à
elle-même surpassera la droite Δ (Princ. 5). Que cette droite soit ajoutée à
elle-même, et que le multiple de cette droite soit égal à la droite ΑΘ ; et enfin que la droite ZH
soit autant de
fois multiple de la droite
HE,
que la droite ΑΘ
l'est de la droite AΓ.
La droite ΘA sera à
la droite AΓ comme
ZH
est à
HE
;
et par inversion, la droite
EH
sera à
la droite
HZ
comme AΓ est à ΑΘ. Mais la droite ΑΘ
est plus grande que la droite Δ,
c'est-à-dire que la droite ΓΒ
; donc la raison de la droite
ΓΑ
à la droite ΑΘ
est moindre que la raison de la droite
ΓΑ
à la droite
ΓΒ
(α).
Donc, par addition, la raison de la droite EZ à la droite
ZH
est
moindre que la raison de
AB
à ΒΓ.
Mais la droite ΒΓ
est égale à la droite Δ
; donc la raison de
EZ
à
ZH
est
moindre que la raison de
AB
à Δ.
On a donc trouvé deux droites inégales qui remplissent les conditions de ce qui
est proposé ; c'est-à-dire, qu'on a trouvé deux droites inégales dont la raison
de la plus grande à la plus petite est moindre que la raison de la plus grande
quantité donnée à la plus petite.
PROPOSITION IV.
Deux quantités
inégales et un cercle étant donnés, il est possible d'inscrire un polygone dans
ce cercle, et de lui en circonscrire un autre, de manière que la raison du côté
du polygone circonscrit au côté du polygone inscrit soit moindre que la raison
de la plus grande quantité à la plus petite.
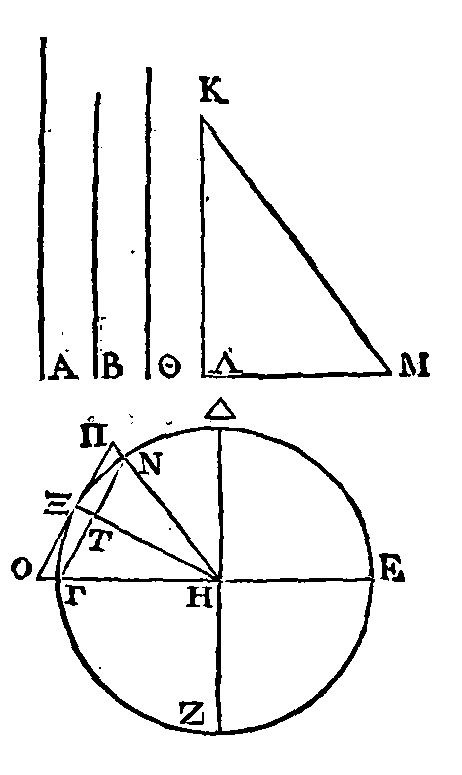
Soient donnés
les quantités A,
B,
et le cercle ΓΔΕΖ
: je dis qu'il est possible de faire ce qui est proposé.
Cherchons deux
droites Θ,
ΚΛ,
de manière que Θ
étant la plus grande, la raison de la droite Θ à la droite
ΚΛ soit moindre que la raison de la plus grande
quantité donnée à la plus petite (3). Du point Λ et sur la droite
ΚΛ,
élevons la perpendiculaire
ΛM;
et du point
K
menons la droite
KM
égale à
la droite Θ
; ce qui peut se faire. Conduisons les deux diamètres
ΓΕ,
ΔΖ
perpendiculaires l'un sur l'autre. Si l'angle ΔHΓ est partagé en deux parties égales, sa moitié en deux parties
égales, et ainsi de suite, il restera enfin un certain angle plus petit que le
double de l'angle
ΛΚM.
Qu'on ait cet
angle et que cet angle soit ΝΗΓ. Menons la corde ΝΓ. La droite ΝΓ sera le côté d'un polygone équilatère ; car puisque l'angle
ΝΗΓ
mesure l'angle droit ΔΗΓ,
et que l'arc ΝΓ mesure le quart de la circonférence, l'arc
ΝΓ
mesurera
la circonférence entière. Il est donc évident que la droite ΓΝ
est le côté d'un polygone équilatère. Partageons l’angle ΝΗΓ
en deux parties
égales par la droite HX, que la droite OΞP touche le cercle au point
Ξ
; et
menons les droites ΗΗΠ, HΓO, il est évident que la droite
ΠO sera le côté d'un polygone circonscrit au
cercle, équilatère et semblable au polygone inscrit dont le côté est ΝΓ.
Puisque l'angle ΝΗΓ
est moindre que le double de l’angle
ΛΚM,
et que l'angle ΝΗΓ
est double de l'angle
THΓ, l'angle THΓ
sera plus petit que l’angle
ΛΚM.
Mais les angles placés aux points
Λ,
T
sont droits; donc la raison de la droite
MK
à la
droite
ΛΚ
est plus grande que la raison de la
droite
ΓH
à la droite
HT (α).
Mais la droite
ΓH
est égale
à la droite HΞ ; donc la raison de
HΞ
à
HT,
c'est-à-dire la raison de ΠO à ΝΓ est moindre que la raison de
MK
à ΚΛ.
Mais la
raison de
KM
à
ΚΛ
est
moindre que la raison de A à
B,
et la droite ΠO
est le côté du polygone circonscrit, tandis que la droite
ΓΝ
est le
côté du polygone inscrit ....... (β). Ce qu'il fallait trouver.
PROPOSITION V.
Deux quantités
inégales et un secteur étant donnés, il est possible de circonscrire un polygone
à ce secteur, et de lui en, inscrire un autre, de manière que la raison du côté
du polygone circonscrit au côté du polygone inscrit soit moindre que la raison
de la plus grande quantité à la plus petite.
Soient E, Z
deux quantités inégales; que la quantité E soit la plus grande, que AΒΓ soit un cercle quelconque ayant pour centre
le point Δ
; au point Δ
construisons le secteur AΔΒ.
Il faut circonscrire un polygone au secteur
ABΔ,
et lui en
inscrire un autre, de manière que celui-ci ayant tous ses côtés,
excepté
BΔ, ΔA,
égaux, entre eux, les conditions de ce qui est proposé soient remplies.
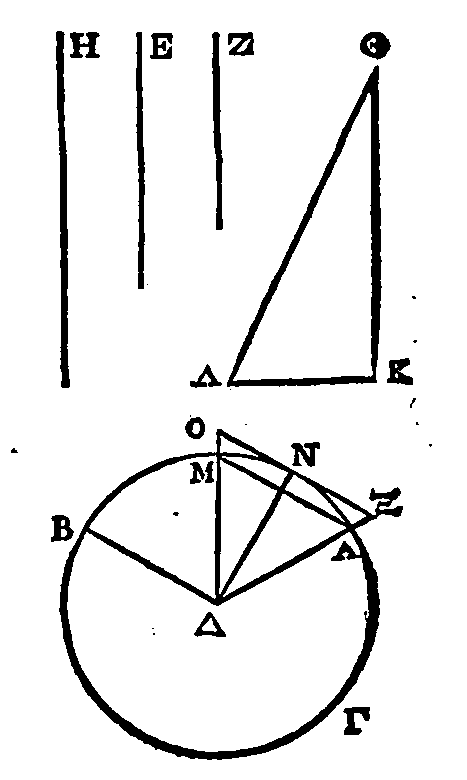
Cherchons deux
droites inégales H, ΘK, de manière que h
étant la plus grande, la raison de H à ΘK soit moindre que la raison de la plus grande quantité à la plus
petite; ce qui peut se faire (3). Ayant mené du point K
sur la
droite ΘK la perpendiculaire KA,
conduisons une
droite ΘA
égale à la droite H
; ce qui peut se faire, puisque la
droite H
est plus grande que la droite ΘK.
Si nous partageons l'angle AΔΒ
en deux parties égales, sa moitié en deux parties égales, et ainsi de suite, il
restera enfin un angle plus petit que le double de l'angle ΑΘK.
Que l'angle
restant soit AΔM
; la droite AM
sera le côté d'un polygone inscrit dans le secteur. Si l'angle AΔM est partagé en deux parties égales par la
droite ΔN,
et si par le point N
on conduit la droite ΞNO
tangente au secteur, cette droite sera le côté d'un polygone circonscrit au
secteur et semblable au polygone inscrit; et par la même raison que dans la
proposition précédente, la raison de ΞO
à
AM
sera
moindre que la raison de la quantité
E
à la
quantité Z.
PROPOSITION VI.
Un cercle et
deux quantités inégales étant donnés, circonscrire à ce cercle un polygone et
lui en inscrire un autre, de manière que la raison du polygone circonscrit au
polygone inscrit soit moindre que la raison de la plus grande quantité à la plus
petite.
Soient le cercle
A,
et les deux quantités inégales
E,
Z ; que
la plus grande soit E. Il faut circonscrire un polygone à ce cercle, et lui en inscrire
un autre, de manière que les conditions de ce qui est proposé soient remplies.
Je prends deux
droites inégales Γ, Δ, de manière que Γ étant la plus grande, la raison de Γ à Δ soit moindre que la raison de E
à Z
(5). Prenons une droite
H
moyenne proportionnelle entre Γ
et Δ ; la droite
Γ
sera plus grande que la droite H.
Circonscrivons un polygone au cercle A, et inscrivons-lui un autre polygone, ainsi que nous l'avons
enseigné (4), de manière que la raison du côté du polygone circonscrit au côté
du polygone inscrit soit moindre que la raison de Γ
à
H.
Il est
évident que la raison doublée du côté du polygone circonscrit au côté du
polygone inscrit sera moindre que la raison doublée de Γ
à H.
Mais la raison du polygone circonscrit au polygone inscrit est doublée de la
raison du côté du premier au côté du second, à cause que ces polygones sont
semblables; et la raison de la droite Γ à la droite Δ est doublée de la raison
de Γ
à
H
; donc la
raison du polygone circonscrit au polygone inscrit est moindre que la raison de
Γ
à Δ;
donc la raison du polygone circonscrit au polygone inscrit est encore moindre
que la raison de E
à Z.
Nous
démontrerons semblablement que deux quantités inégales et un secteur de cercle
étant donnés, on peut circonscrire au secteur et lui inscrire un polygone, de
manière que la raison du polygone circonscrit au polygone inscrit soit moindre
que la raison de la plus grande quantité à la plus petite.
Si un cercle ou
un secteur et une surface quelconque sont
donnés, il est évident que si
l'on inscrit à ce cercle ou à ce secteur et ensuite aux segments restants des
polygones équilatères, il restera enfin des segments de cercles ou de secteurs
qui seront moindres que la surface donnée. Ces choses sont démontrées dans les
Éléments (α).
PROPOSITION VII.
Il faut
démontrer qu'étant donnés un cercle, ou un secteur et une surface, on peut
circonscrire à ce cercle ou à ce secteur un polygone, de manière que la somme
des segments du polygone circonscrit soit moindre que la surface donnée. Il me
sera permis de transporter au secteur ce que j'aurai dit du cercle.
Soient donnés le
cercle A
et une surface quelconque B
: je dis qu'on peut circonscrire à ce cercle un polygone, de manière que
la somme des segments placés entre ce cercle et ce polygone soit moindre que la
surface B.
Puisqu'on a deux quantités inégales, dont la plus grande est
composée de la surface
B
et du cercle
A,
et dont la plus petite est ce même cercle, on pourra circonscrire au cercle
A
un polygone et lui en inscrire un autre, de manière que la raison du polygone
circonscrit au polygone inscrit soit moindre que la raison de la plus grande
des quantités dont nous venons de parler à la plus petite ; et le polygone
circonscrit sera tel que la somme des segments placés autour du cercle sera
moindre que la surface donnée B.
En effet,
puisque la raison du polygone circonscrit au polygone inscrit est moindre que la
raison de la somme de la surface B et du cercle A à ce même cercle, et que le cercle est
plus grand que le polygone inscrit, la raison du
polygone circonscrit au cercle A
sera encore moindre que la raison de la somme de la surface B et du cercle A à ce même cercle. Donc, par soustraction, la
raison de la somme des segments restants du polygone circonscrit au cercle
A
est moindre que la raison de la surface
B
au cercle
A.
Donc la
somme des segments du polygone circonscrit est moindre que la surface
B
(α).
Cela peut se démontrer encore de la manière suivante.
Puisque la
raison du polygone circonscrit au cercle
A
est moindre que
la raison de la somme de la surface B et du cercle A à ce même cercle, il s'ensuit que le polygone
circonscrit, est moindre que la somme de la surface
B
et du
cercle A.
Donc la somme des segments placés autour du cercle est moindre que la surface
B.
Nous
ferons les mêmes raisonnements par rapport au secteur.
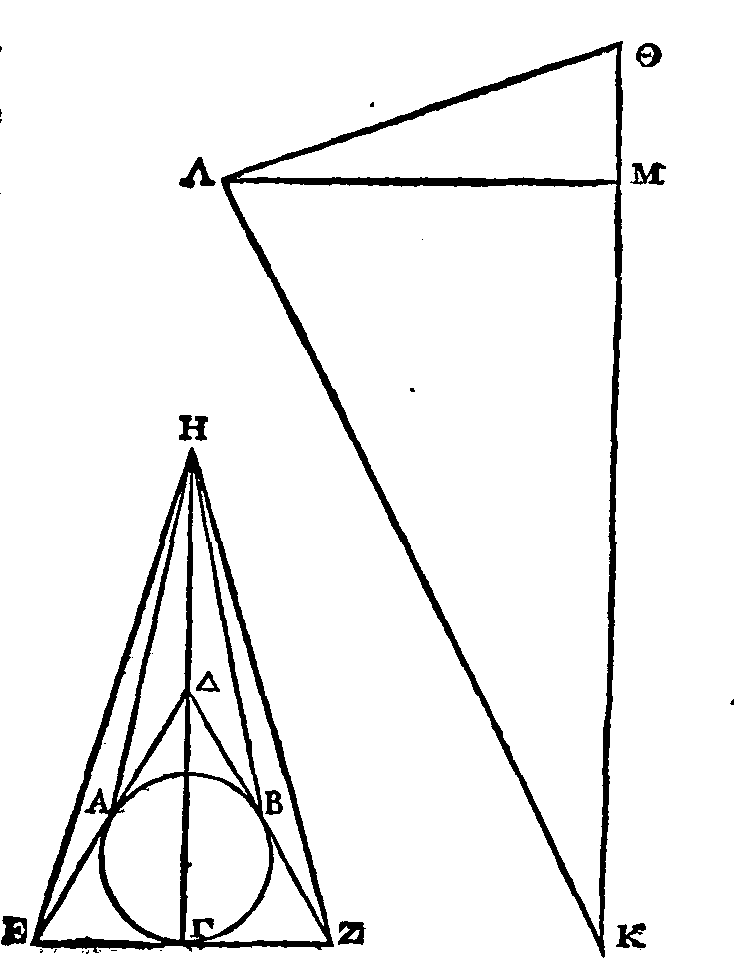
PROPOSITION VIII.
Si dans un cône
droit on inscrit une pyramide ayant une base équilatère, la surface de cette
pyramide, la base exceptée, est égale à un triangle ayant une base égale au
contour de la base de la pyramide, et une hauteur égale à la perpendiculaire
menée du sommet sur un des côtés de la base.
Soit le cône
droit dont la base est le cercle AΒΓ. Inscrivons-lui une pyramide ayant pour base le triangle
équilatéral AΒΓ.
Je dis que la surface de cette pyramide, la base exceptée, est égale au triangle
dont nous avons parlé.
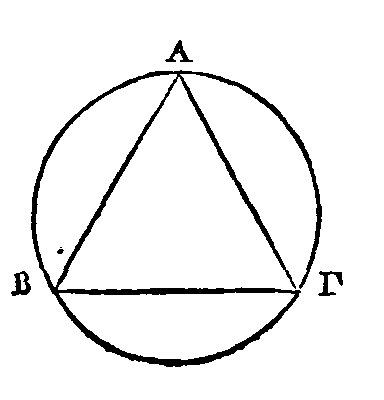
Car puisque le
cône est droit, et que la base
de la pyramide est équilatère, les hauteurs des
triangles qui comprennent la pyramide sont égales entre elles. Mais ces
triangles ont pour base les droites
AB,
ΒΓ,
ΓΑ,
et pour hauteur
la droite dont nous venons de parler ; donc la somme de ces triangles,
c'est-à-dire la surface de la pyramide, le triangle. AΒΓ
excepté, est égale à un triangle ayant pour base une droite égale à la somme des
droites
AB,
ΒΓ,
ΓΑ,
et pour hauteur, une droite égale à celle dont nous venons de parler.
AUTRE DΕMONSTRATION PLUS
CLAIRE.
Soit le cône
droit dont la base est le cercle AΒΓ, et dont le sommet est le point Δ. Inscrivons dans ce cône une pyramide ayant
pour base le triangle équilatéral
AΒΓ;
et menons
les droites
ΔA,
ΔΓ,
ΔΒ.

Je dis que la
somme des triangles AΔΒ, AΔΓ, BΔΓ est égale à un triangle dont la base est égale au contour
du triangle
AΒΓ,
et dont la perpendiculaire menée du sommet sur la base est égale à la
perpendiculaire menée du point A
sur la droite ΒΓ.
Menons les
perpendiculaires
ΔK,
ΔΛ, ΔM;
ces
droites seront égales entre elles. Supposons un triangle
EZH
ayant une
base égale au contour du triangle AΒΓ, et une hauteur ΗΘ
égale à la droite ΔΛ.
Puisque la surface comprise sous les droites ΒΓ,
ΔK
est
double du triangle AΒΓ (α); que la surface comprise sous les droites
AB, ΔΛ
est double du triangle ABΔ,
et que la surface comprise sous les droites AΓ, AM est
double du triangle AΔΓ,
la surface comprise sous le contour du triangle AΒΓ, c'est-à-dire sous la droite
EZ,
et sous
la droite
ΔΛ, c'est-à-dire sous la droite
ΗΘ,
est double de la somme des triangles
AΔΒ,
ΒΔΓ, AΔΓ. Mais la surface comprise sous les droites
EZ,
ΗΘ
est double du triangle
EZH;
donc le triangle
EZH
est égal
de la somme des triangles
AΔΒ,
ΒΔΓ, AΔΓ.
PROPOSITION IX.
Si une pyramide
est circonscrite à un cône droit, la surface de cette pyramide, la base
exceptée, sera égale à un triangle ayant une base égale au contour de la base de
la pyramide et une hauteur égale au côté du cône.
Soit un cône
ayant pour base le cercle AΒΓ. Circonscrivons à ce cône une pyramide, de manière que sa base,
c'est-à-dire le polygone ΔΕZ soit circonscrit au cercle AΒΓ. Je dis que la surface de la pyramide, la
base exceptée, est égale au triangle dont nous venons de parler.
En effet,
puisque l'axe du cône est perpendiculaire sur la base, c'est-à-dire sur le
cercle AΒΓ,
et que les droites menées du centre aux points de contact sont perpendiculaires
sur les tangentes, les droites menées du sommet du
cône aux points de contact, seront
perpendiculaires sur les droites
ΔΕ,
ZE,
ZΔ.
Donc les
perpendiculaires
HA, HΒ, HΓ dont nous venons de parler, sont égales entre
elles; car ces perpendiculaires sont les côtés du cône. Supposons un triangle
ΘΚΛ, ayant une base
ΘK
égale au contour du triangle
ΔΕZ, et une hauteur
ΛM
égale à
HA.
Puisque
la surface comprise sous les droites
ΔΕ,
AH
est double du
triangle
EΔH
; que la surface comprise sous les
droites
ΔΖ,
HB est double du triangle ΔΖH,
et qu'enfin la surface comprise sous les droites
EZ, ΓH
est
double du triangle
EHZ;
la surface
comprise sous les droites ΘΘ,
AH,
c'est-à-dire MΛ,
est double de la somme des triangles
EΔH, ZΔH,
EHZ.
Mais la
surface comprise sous ΘK, ΛM
est
double du triangle ΛΚΘ;
donc la surface de la pyramide, la base exceptée, est égale à un triangle ayant
une base égale au contour du triangle ΔΕZ, et une hauteur égale au côté du cône.
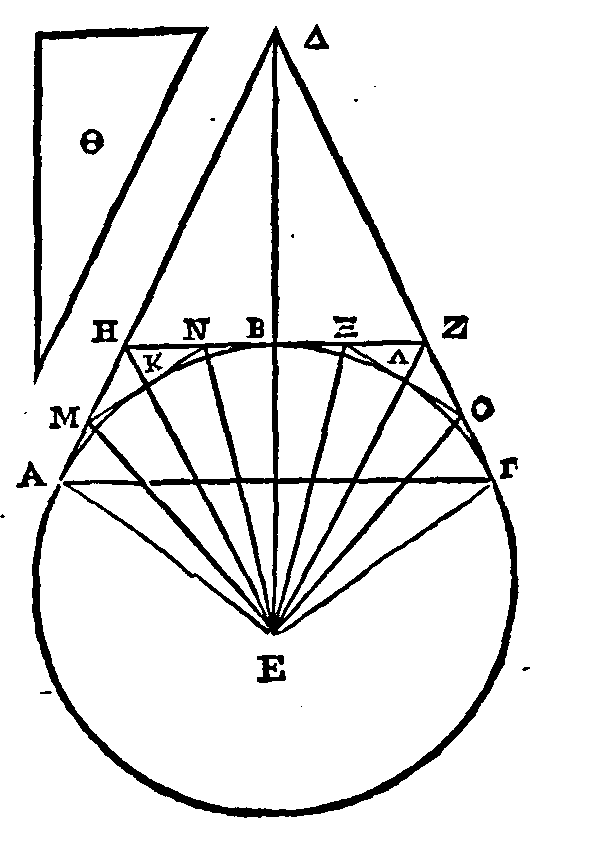
PROPOSITION X.
Si l’on mène une
corde dans le cercle qui est la base d'un cône droit, et si l'on joint, par des
droites, les extrémités de cette corde et le sommet du cône, le triangle terminé
par cette corde et les droites qui joignent les extrémités de cette corde et le
sommet du cône, sera plus petit que la surface du cône comprise entre les
droites qui joignent les extrémités de cette corde et le sommet du cône.
Que le cercle
AΒΓ
soit la
base d'un cône droit, dont le point Δ est le sommet Menons la corde
AΓ,
et joignons les points A, Γ
avec le point Δ
par les droites
AΔ, ΔΓ.
Je dis que le triangle AΔΓ
est plus petit que la surface du cône comprise entre les droites
AΔ,
ΔΓ.
Partageons l'arc
AΒΓ
en deux parties égales au point B,
et menons les droites
AB,
ΓΒ,
ΔΒ.
La somme des
triangles
ABΔ, ΒΓΔ
sera
certainement plus grande que le triangle AΔΓ. Que la surface Θ soit l'excès de la somme des deux premiers triangles sur le
triangle AΔΓ. La
surface Θ
sera ou plus petite que la somme des segments
AB,
ΒΓ, ou elle n'est pas plus petite. Supposons
d'abord qu'elle ne soit pas plus petite. Puisque l'on a deux surfaces, dont
l'une est celle du cône comprise entre AΔ, ΔΒ, avec le segment AEB,
et dont l'autre est le triangle
AΔΒ, et que ces deux surfaces ont pour
limite le contour du triangle
AΔΒ,
la première qui comprend la seconde sera plus grande que la seconde qui est
comprise par la première. (Princ. 4.) Donc la surface du cône
comprise entre
AΔ, ΔΒ,
avec le segment
AEB,
est plus grande que le triangle ABΔ.
Semblablement la surface du cône comprise entre
BΔ,
ΔΓ, avec le segment ΓZB,
est plus grande que le triangle BΔΓ.
Donc la surface totale du cône comprise entre
AΔ, ΔΓ, avec la surface
Θ est plus grande que la
somme des triangles dont nous venons de parler, Mais la somme des triangles dont
nous venons de parler, est égale au triangle AΔΓ
réuni à la surface Θ
; donc si l'on retranche la surface commune Θ, la surface restante du cône qui est comprise entre
AΔ,
ΔΓ,
sera plus grande que le triangle AΔΓ.
Que la surface
Θ
soit moindre que la somme des segments AB, ΒΓ. Si l'on partage les arcs
AB,
ΒΓ
en deux parties égales, et leurs moitiés en deux parties égales, et ainsi de
suite, il restera enfin des segments dont la somme sera moindre que la surface
Θ.
Que les segments restants soient ceux qui sont appuyés sur les droites
AE, EB, BZ, ZΓ ;
et menons les droites
ΔΕ, ΔΖ.
Par la même raison, la surface du cône comprise entre
AΔ,
ΔΕ,
avec le segment
appuyé sur
ΔΕ,
sera plus grande que le triangle
AΔΕ ;
et la surface comprise entre EΔ,
ΔΒ, avec le segment appuyé
sur
EB,
est aussi plus grande que le triangle
EΔΒ.
Donc la surface
du cône comprise entre AΔ,
ΔΒ,
avec les
segments
AE, EB,
est plus grande
que la somme des triangles AΔΕ, EBΔ ; et puisque la somme des triangles AEΔ, ΔΕB
est plus grande que le triangle ABΔ,
ce qui est démontré, la surface du cône comprise entre
AΔ,
ΔΒ,
avec les segments appuyés sur
AE, EB
sera encore plus
grande que le triangle
AΔΒ.
Par la même
raison, la surface comprise entre
BΔ,
ΔΓ, avec les segments appuyés sur
BZ,
ZΓ,
sera plus grande que le triangle
BΔΓ.
Donc la surface
totale comprise entre AΔ, ΔΓ, avec les segments dont nous venons de parler, est plus grande que
la somme des triangles
ABΔ,
ΔΒΓ.
Mais la
somme de ces triangles est égale au triangle AΔΓ réuni à la surface Θ,
et les segments dont nous venons de parler sont moindres que la surface Θ
; donc la surface restante comprise entre AΔ, ΔΓ est plus grande que le triangle AΔΓ.
PROPOSITION XI.
Si l'on mène des
tangentes au cercle qui est la base d'un cône droit; si ces tangentes sont dans
le même plan que ce cercle et se rencontrent mutuellement; et si, des points de
contact et du point où ces droites se rencontrent, on mène des droites au '
sommet du cône, la somme des triangles terminé par ces tangentes et par les
droites qui joignent leurs extrémités et le sommet du cône, sera plus grande que
la surface du cône comprise entre les droites qui joignent les points de contact
et le sommet du cône.
Soit un cône
ayant pour base le cercle
AΒΓ,
et pour sommet
le point E:
menons les droites AΔ, ΔΓ,
tangentes au cercle AΒΓ;
que ces tangentes soient dans le même plan que ce cercle,
et du point
E,
qui est
le sommet du cône, menons aux points
A,
Δ, Γ
les droites
EA, EΔ,
EΓ.
Je dis que la somme des triangles
AΔΕ, ΔΕΓ
est plus
grande que la surface du cône comprise entre les droites
AE, ΓΕ
et l'arc AΒΓ.
Menons une
droite
HBZ
tangente
au cercle et parallèle à la droite AΓ. L'arc AΒΓ sera certainement partagé en deux parties
égales au point
B.
Des points
H, Z,
menons au point E
les droites HE,
ZE.
Puisque la somme
des droites
HΔ, ΔΖ
est plus grande
que la droite HZ,
si l'on ajoute de part ou d'autre les droites
HA,
ZΓ,
la somme des droites AΔ, ΔΓ
sera plus grande que la somme des droites
AH, HZ,
ZΓ.
Mais les droites AE,
EB, EΓ, qui sont les côtés d'un cône droit,
sont égales entre elles et ces droites sont perpendiculaires sur les tangentes
du cercle
AΒΓ,
ainsi que cela est démontré dans un lemme; donc la somme des surfaces comprises
sous ces perpendiculaires et sous les bases des triangles
AEΔ,
ΔΕΓ, est
plus grande que la somme des surfaces comprises sous ces mêmes perpendiculaires
et sous les bases des triangles AHE,
HEZ, ZEΓ;
parce que
la somme des bases
AH, HZ,
ZΓ est plus petite que la somme des bases
ΓΔ, ΔA,
tandis que les hauteurs sont égales, puisqu'il est évident que la droite menée
du sommet du cône droit au point de contact de la base est perpendiculaire sur
la tangente. Que la surface Θ soit l'excès de la somme des triangles
AEΔ,
ΔΓΕ
sur la somme des triangles AHE,
HEZ, ZEΓ.
La surface Θ sera ou
plus petite que la somme des segments
AHB,
BZΓ
placés autour de l'arc AΒΓ,
ou cette surface ne sera pas plus petite.
Supposons
d'abord que la surface Θ
ne soit pas plus petite. Puisque l'on a deux surfaces composées, dont l'une est
la surface de la pyramide, qui a pour base le trapèze HAΓZ et pour sommet le point E,
et dont l'autre est la surface du cône comprise entre AE, EΓ avec le segment
AΒΓ,
et que ces deux surfaces ont pour limite le contour du triangle AEΓ ; il est évident que la surface de la
pyramide, le triangle AEΓ excepté, est plus grande que la surface du cône comprise entre
AE,
EΓ,
réunie au segment, AΒΓ.
(Princ. 4). Donc si l’on retranche le segment commun AΒΓ, la somme des triangles
AHE, HEZ, ZEΓ
restants,
avec la somme des- segments
AHB, BZΓ placés autour du cercle, sera plus glande que
la surface du cône comprise entre les droites
AE,
EΓ.
Mais la surface Θ
n'est pas plus petite que la somme des segments
AHB,
BZΓ
placés autour du cercle; donc la somme des triangles
AHE,
HEZ,
ZEΓ,
avec la surface Θ,
est plus grande que la surface du cône comprise entre
AE,
EΓ.
Mais la somme des triangles
AHE, HEZ,
ZEΓ,
avec la surface Θ,
est égale à la somme des triangles
AEΔ,
ΔΕΓ ; donc la somme des triangles
AEΔ,
ΔΕΓ
est plus grande que la surface du cône dont nous venons de parler.
Supposons en
second lieu que la surface Θ soit plus petite que la somme des segments placés autour du
cercle. Si l'on circonscrit continuellement des polygones aux segments, en
partageant les arcs en deux parties égales, et en menant des tangentes, il
restera enfin certains segments dont la somme sera plus petite que la surface
Θ.
Que les segments restants soient
AMK, KNB, BΞΛ,
AOΓ,
et que la somme de ces segments soit plus petite que la surface Θ. Menons des droites au point E.
Il est encore évident que la somme des triangles
AHE,
HEZ,
ZEΓ
sera plus grande que la somme des triangles
AEM,
MEN,
NEΞ, ΞEO,
OEΓ; car la somme des bases des premiers
triangles est plus
grande que la somme des bases des seconds, et que les
hauteurs sont égales de part et d'autre. Mais la surface de la pyramide qui a
pour base le polygone AMNΞOΓ, et pour sommet le point E, le triangle
AEΓ excepté, est plus grande que la surface du
cône comprise entre AE, EΓ, réunie au segment AΒΓ; donc si on retranche de part et d'autre le
segment AΒΓ,
la somme des triangles restants
AEM,
MEN,
NEΞ, ΞEO,
OEΓ, avec
les segments restants
AMK, KNB, BΞΛ,
AOΓ,
placés autour du cercle, sera plus grande que la surface du cône comprise entre
ae, Er. Mais la surface &
est plus grande que la somme des segments restants dont nous venons de parler et
qui sont placés autour du cercle : et l'on a démontré que la somme des triangles
AHE, HEZ,
ZEΓ est plus grande que la somme des triangles
AEM,
MEN, NEΞ, ΞEO,
OEΓ
; donc à plus forte raison la somme des triangles
AHE,
HEZ, ZEΓ avec la surface Θ,
c'est-à-dire, la somme des triangles
AΔΕ,
ΔΕΓ est plus grande que la surface du cône
comprise entre
AE,
EΓ.
PROPOSITION XII.
La surface d'un
cylindre droit, comprise entre deux droites placées dans sa surface, est plus
grande que le parallélogramme terminé par ces deux droites et par celles qui
joignent leurs extrémités.
Soit le cylindre
droit dont une des bases est le cercle
AB,
et dont la base opposée est le cercle ΓΔ. Menons les droites AΓ,
BΔ.
Je dis que la
surface du cylindre comprise entre les droites AΓ,
BΔ
est plus
grande que le parallélogramme
AΓΔΒ.
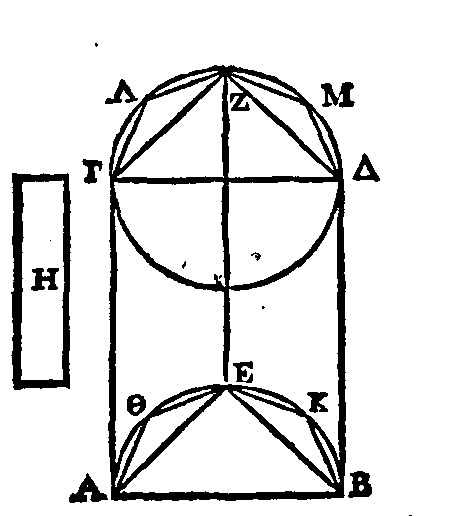
Partageons les
arcs
AB, ΓΔ en deux
parties égales aux points
E, Z ; et menons les droites AE,
EB, ΓZ, ZΔ.
Puisque la somme des droites AE,
EB
est plus grande
que la droite
AB, et que les parallélogrammes construits
sur ces droites ont la même hauteur, la somme des parallélogrammes dont les
bases sont les droites AE,
EB
sera plus
grande que le parallélogramme
ABΔΓ
; car
leur hauteur est la même que celle du cylindre. Que l’excès de la somme des
parallélogrammes dont les bases sont AE, EB
sur le parallélogramme
ABΔΓ
soit la surface H.
La surface
H
sera ou
plus petite que la somme des segments plans AE,
EB,
ΓZ,
ZΔ,
ou elle ne sera pas plus petite. Supposons d'abord qu'elle ne soit pas plus
petite. Puisque la surface du cylindre qui est comprise entre les droites AΓ, BΔ,
avec les segments
AEB,
ΓZΔ,
a pour limite le plan du parallélogramme
ABΔΓ ;
que la surface
qui est composée des parallélogrammes dont les bases sont AE,
EB et dont la hauteur est la même que celle du
cylindre, avec les triangles
AEB,
ΓZΔ,
a aussi pour limite le plan du parallélogramme
ABΔΓ; que l'une de ces surfaces comprend
l'autre, et que ces deux surfaces sont concaves du. même côté, la surface
cylindrique comprise entre les droites AΓ,
BΔ,
avec les
segments plans
AEB,
ΓZΔ, sera plus grande que la surface qui est
composée non seulement des parallélogrammes dont les bases sont AE,
EB,
et dont la hauteur est la même que celle du cylindre, mais encore des triangles
AEB,
ΓZΔ.
(Princ.
4.) Donc si l'on retranche les triangles
AEB,
ΓZΔ,
la surface cylindrique restante qui est comprise entre les droites
AΓ, BΔ,
avec les segments plans AE,
EB,
ΓZ,
ZΔ,
sera plus
grande que la surface composée des parallélogrammes
dont les bases sont les droites AE,
EB,
et dont la
hauteur est la même que celle du cylindre. Mais la somme des parallélogrammes
dont les bases sont AE,
EB,
et dont la hauteur est la même que celle du cylindre, est égale au
parallélogramme
AΓΔΒ
réuni à
la surface
H ; donc
la surface cylindrique restante qui est comprise entre les droites AΓ, BΔ est plus grande que le parallélogramme
AΓΔΒ.

Supposons en
second lieu que la surface H soit plus petite que la somme des segments plans AE,
EB,
ΓZ,
ZΔ.
Si l’on partage
en deux parties égales chacun des arcs AE,
EB,
ΓZ,
ZΔ,
aux points
Θ, K,
Λ, M
; si l’on
mène les droites ΑΘ, ΘE,
EK, KB, ΓΑ,
ΛZ, ZM, MΔ ;
si l’on retranche les triangles
ΑΘE, EKB, ΓΔΖ, ZMΔ,
dont la somme
n'est pas plus petite que la moitié de la somme des segments plans
AE,
EB,
ΓZ,
ZΔ, et si l’on continue de faire la même chose,
il restera enfin certains segments dont la somme sera moindre que la surface
H.
Que les
segments restants soient ΑΘ, ΘE, EK, KB,
ΓΑ, ΛZ, ZM, MΔ. Nous démontrerons de la même manière que la sommé des
parallélogrammes dont les bases sont ΑΘ, ΘE,
EK,
KB,
et dont la hauteur est la même que celle du cylindre, sera plus grande que fa
somme des parallélogrammes dont les bases sont les droites AE,
EB,
et dont
la hauteur est la même que celle du cylindre. Mais la surface du cylindre
comprise entre les droites AΓ,
BΔ,
avec les segments plans
AEB,
ΓZΔ, et la surface qui est composée des
parallélogrammes dont les bases sont ΑΘ, ΘE,
EK, KB,
et dont
la hauteur est la même que celle du cylindre, avec les figures rectilignes
ΑΘEKB,
ΓΛZMΔ,
ont pour limite le plan du parallélogramme
AΓΔΒ
; donc si
l'on retranche les figures rectilignes
ΑΘEKB,
ΓΛZMΔ,
la surface cylindrique
restante qui est comprise entre les droites
AΓ, ΔΒ, avec les segments plans
ΑΘ, ΘE,
EK, KB, ΓΑ, ΛZ, ZM, MΔ,
sera plus grande
que la surface composée des parallélogrammes dont les bases sont les droites ΑΘ,
ΘE,
EK, KB,
et dont la hauteur est la même que celle du cylindre. Mais la somme des
parallélogrammes dont les bases sont ΑΘ, ΘE,
EK, KB,
et dont la hauteur est la même que celle du cylindre, est plus grande que la
somme des parallélogrammes dont les bases sont
AE, EB
et dont
la hauteur est la même que celle du cylindre ; donc la surface cylindrique
comprise entre les droites AΓ, b
A, avec les segments plans ΑΘ, ΘE,
EK, KB, ΓΑ, ΛZ, ZM, MΔ, est plus grande que la somme des
parallélogrammes dont les bases sont les droites AE,
EB,
et dont la hauteur est la même que celle du cylindre. Mais la somme des
parallélogrammes dont les bases sont les droites AE, EB
et dont la hauteur est la même que celle du cylindre, est égale au
parallélogramme
AΓΔΒ
réuni à
la surface
H; donc
la surface cylindrique comprise entre les droites AΓ,
BΔ,
avec les segments plans ΑΘ, ΘE,
EK, KB, ΓΑ, ΛZ, ZM, MΔ,
est plus grande que le parallélogramme
AΓΔΒ
réuni à la
surface H.
Mais la somme des segments ΑΘ, ΘE,
EK, KB, ΓΑ, ΛZ, ZM,
MΔ,
est plus
petite que la surface H ; donc la surface cylindrique restante comprise entre les droites
AΓ,
BΔ
est plus
grande que le parallélogramme
AΓΔΒ.
PROPOSITION XIII.
Si par les
extrémités de deux droites qui sont dans la surface d'un cylindre droit
quelconque, on mène des tangentes aux cercles qui sont les bases du cylindre, si
ces droites sont dans le plan de ces cercles et si elles se rencontrent, la
somme des parallélogrammes compris ' sous les tangentes et sous les côtés du
cylindre, sera plus grande que la surface cylindrique comprise entre les droites
qui sont dans sa surface.
Que le cercle AΒΓ
soit la base d'un cylindre droit quelconque, et que dans la surface de ce
cylindre soient deux droites ayant pour extrémités les points A, Γ ; par les points
A, Γ
menons au cercle AΒΓ
des tangentes qui soient dans le même plan que lui et qui se coupent
mutuellement au point
H.
Imaginons que dans l'autre base du cylindre,
et par les extrémités des droites qui sont dans sa surface on ait mené des
droites tangentes au cercle. Il faut démontrer que la somme des parallélogrammes
compris sous les tangentes et sous les côtés du cylindre est plus grande
que la surface du cylindre construite sur l'arc AΒΓ.
Menons au cercle
AΒΓ
la tangente
EZ ;
et des points E, Z, menons au plan de la base supérieure des
droites parallèles à l'axe du cylindre. La somme des parallélogrammes compris
sous les droites
AH, HΓ
et sous les
côtés du cylindre est plus grande que la somme des parallélogrammes compris sous
les droites
AE, EZ,
ZΓ, et sous les côtés du cylindre. Car puisque
la somme des droites
EH, HZ est plus grande que la droite
EZ,
si on ajoute de part et d'autre les droites
AE,
ZΓ, la somme des droites
HA, HΓ
sera plus grande que la somme des droites
AE, EZ,
ZΓ. Que l'excès de la somme des parallélogrammes
compris sous les droites
HA,
HΓ,
et sous les côtés du cylindre sur la somme des parallélogrammes compris sous les
droites
AE, EZ, ZΓ
et sous les côtés du cylindre, soit la surface
K.
La moitié de la
surface
K
sera ou plus grande que la somme des
figures comprises entre les droites
AE,
EZ, ZΓ,
et les arcs AB, ΒΓ
; ou elle ne sera pas plus
grande. Supposons d'abord qu'elle soit plus grande.
Puisque le contour du parallélogramme construit sur la droite AΓ
est la limite de la surface qui est composée des parallélogrammes construits sur
les droites
AE, EZ, ZΓ
du trapèze AEZΓ et
de celui qui lui est opposé dans l'autre base du cylindre, et que le contour du
parallélogramme construit sur AΓ est aussi la limite de la surface qui est composée de la surface
du cylindre construite sur l'arc AΒΓ, du segment AΒΓ, et de celui qui lui est opposé, les surfaces
dont nous venons de parler ont la même limite dans un même plan. Mais l'une et
l'autre de ces surfaces sont concaves du même côté, et l'une de ces surfaces est
comprise par l'autre, le reste étant commun ; donc la surface qui est comprise
est la plus petite. (Princ. 4.) Donc si on retranche les
parties communes, c'est-à-dire, le segment AΒΓ
et celui qui lui est opposé, la surface du cylindre construite sur l'arc
AΒΓ sera plus petite que la surface composée non-seulement des
parallélogrammes construits sur les droites
AE,
EZ, ZΓ,
mais encore des segments
AEB,
BZΓ et de ceux qui leur sont opposés. Mais la surface composée des
parallélogrammes dont nous venons de parler, avec les segments dont nous venons
aussi de parler, est plus petite que la surface composée des parallélogrammes
construits sur les droites
AH,
HΓ ; car la somme des parallélogrammes
construits sur les-droites
AE, EZ,
ZΓ, avec la surface K,
qui est plus grande que la somme des segments
AEB,
BZΓ,
est égale à la somme des parallélogrammes construits sur
AH,
HΓ;
donc la somme des parallélogrammes compris sous la droite AH, ΓH et sous les côtés du cylindre, est plus
grande que la surface du cylindre construite sur l'arc AΒΓ.
Si la surface
K
n'était pas plus grande que la somme des segments
AEB,
BZΓ,
on mènerait des tangentes au cercle, de manière, que la somme des segments
restants placés autour du cercle fût
moindre que la moitié de la surface
K
(7) ; et
l'on démontrerait le reste comme on l’a fait plus haut.
Ces choses étant
démontrées, les propositions suivantes découlent nécessairement de ce qui a été
dit plus haut.
La surface d'une
pyramide inscrite dans un cône droit, la base exceptée, est plus petite
que la surface du cône.
Car chacun des
triangles qui renferment la pyramide est moindre que la surface du cône comprise
entre les côtés du triangle. Donc la surface totale de la pyramide, la base
exceptée, est moindre que la surface du cône.
La surface de la
pyramide circonscrite à un cône droit, la base exceptée, est plus grande que la
surface du cône.
Si un prisme est
inscrit dans un cylindre droit, la surface du prisme, qui est composée de
parallélogrammes, est plus petite que la surface du cylindre, la base exceptée.
Car chaque
parallélogramme du prisme est moindre que la surface du cylindre construite sur
ce parallélogramme.
Si un prisme est
circonscrit à un cylindre droit, la surface du prisme composée de
parallélogrammes est plus grande que la surface du cylindre, la base exceptée.
PROPOSITION XIV.
La surface d'un
cylindre droit quelconque, la base exceptée, est égale à un cercle dont le rayon
est moyen proportionnel entre le côté du cylindre et le diamètre de sa base.
Que le cercle
A
soit la base d'un cylindre droit quelconque; que la droite ΓΔ
soit égale au
diamètre du cercle A, et la droite
EZ
égale au côté du
cylindre; que la droite H soit moyenne proportionnelle entre ΔΓ,
EZ
; et
supposons un cercle B dont le
rayon soit égal à la droite H.
Il faut démontrer que le cercle B est égal à la surface du cylindre, la base exceptée.
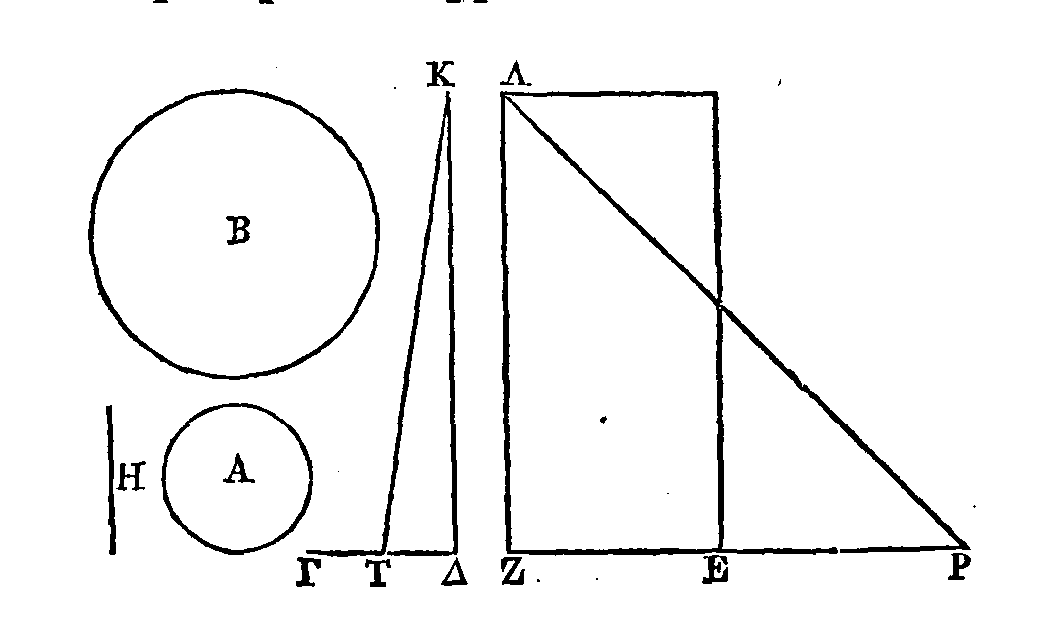
Car si ce cercle
n'est pas égal à la surface du cylindre, il est plus grand ou plus petit.
Supposons, si cela est possible, qu'il
soit plus petit. Puisque l'on a
deux quantités inégales, la surface du cylindre et le cercle B,
on pourra inscrire dans le cercle
B
un polygone
équilatère et lui en circonscrire un autre, de manière que la raison du polygone
circonscrit au polygone inscrit soit moindre que la raison de la surface du
cylindre au cercle B (6). Supposons que l'on ait circonscrit au cercle A
un polygone semblable à celui qui est circonscrit au cercle
B
; et
imaginons que le polygone circonscrit au cercle A soit la base d'un prisme circonscrit à ce
cylindre; que la droite KΔ soit égale au contour du polygone circonscrit au cercle A
; que la droite
ΛZ
soit
égale à cette même droite KΔ, et que la droite ΓT soit la moitié de la droite ΓΔ.
Le triangle
KΔT
sera égal
au polygone circonscrit au cercle A ; parce que la base de ce triangle est égale
au contour de ce polygone, et que sa hauteur est égale au rayon du cercle A
et le parallélogramme
EA
sera égal à la
surface du prisme circonscrit au cylindre, parce que ce parallélogramme est
compris sous le côté du cylindre et sous une droite égale au contour de la base
du prisme. Faisons
la droite EΡ
égale à la
droite EZ.
Le triangle
ZΡΛ
sera égal
au parallélogramme
EΛ,
et par
conséquent à la surface du prisme. Mais les polygones circonscrits aux cercles
A, B
sont semblables; donc ces polygones sont entre eux comme les carrés des
rayons des cercles
A, B.
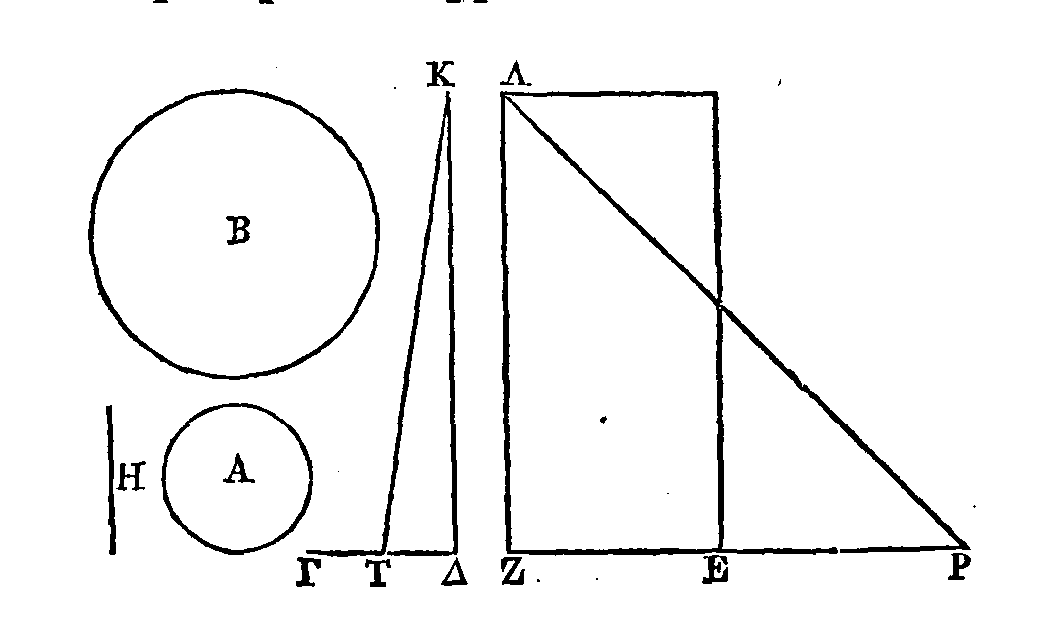
Donc le triangle
KTΔ
est au
polygone circonscrit au cercle
B
comme le carré
de TΔ
est au carré de H
; car les droites TΔ,
H
sont égales aux
rayons des cercles A, B. Mais le carré de TΔ est au carré de H
comme la droite TΔ
est à la droite
ΡZ
; car la
droite H
est moyenne proportionnelle entre TΔ, ΡZ, attendu qu'elle est moyenne proportionnelle entre
ΓΔ,
EZ.
Mais pourquoi la
droite
H
est-elle moyenne proportionnelle entre
TΔ,
ΡZ (α)? Le voici: Puisque la droite ΔT
est égale à la droite TΓ,
et que la droite
ΡE
est aussi
égale à la droite EZ, la droite ΓΔ est double de la droite
TΔ,
et la
droite ΡZ
double de
ΡE. Δonc
la droite ΔΓ est à
la droite ΔT comme
la droite
ΡZ est à
la droite
ZE.
Donc la
surface comprise sous les droites
ΓΔ,
EZ
est égale à la surface comprise sous les droites TΔ, ΡZ. Mais le carré construit sur la droite H
est égal à la surface comprise sous
ΓΔ,
EZ
; donc le carré construit à la droite H est aussi égal à la surface comprise sous
ΓΔ,
EZ.
Donc TΔ
est à H
comme H
est à ΡZ.
Donc le carré construit sur la droite
TΔ
est au carré
construit sur la droite
H
comme la droite
TΔ
est à la
droite
ΡZ ;
car
lorsque trois droites sont proportionnelles entre
elles, la première est à la troisième comme la figure construite sur la première
droite est à la figure semblable construite de la même manière sur la seconde.
Mais le triangle KTΔ
est au triangle ΡΛZ
comme la droite
TΔ
est à la
droite ΡZ,
parce que les droites
KΔ, ΛZ
sont égales
entre elles; donc le triangle
KTΔ
est au polygone
circonscrit au cercle B comme le triangle
KTΔ
est au
triangle
ΡZΛ.
Donc le triangle
ZΛΡ
est égal
au polygone circonscrit au cercle B. Donc la surface du prisme qui est
circonscrit au cylindre est aussi égale au polygone qui est circonscrit au
cercle
B.
Mais la raison du polygone qui est
circonscrit au cercle B au polygone qui est inscrit dans ce même cercle, est moindre que
la raison de la surface du cylindre A au cercle B ; donc la raison de la surface du prisme qui
est circonscrit à ce cylindre au polygone qui est inscrit dans le cercle B,
est encore moindre que la raison de la surface du cylindre au cercle B,
et par
permutation ……. (β),
ce qui est impossible; car la surface du
prisme circonscrit au cylindre est plus
grande que la surface du cylindre, ainsi que cela a été démontré (13); et le
polygone inscrit dans le cercle
B
est
moindre que le cercle
B
(1). Donc le
cercle
B
n'est pas
plus petit que la surface du cylindre.
Supposons en
second lieu, si cela est possible, que le cercle B soit plus grand que la surface du cylindre.
Imaginons qu'on ait inscrit dans le cercle B un polygone, et qu'on lui en ait circonscrit
un autre, de manière que la raison du polygone circonscrit au polygone inscrit
soit moindre que la raison du cercle
B
à la
surface du cylindre (6). Inscrivons dans le cercle A
un polygone semblable à celui qui est inscrit dans le cercle
B
; que le
polygone inscrit dans le cercle A soit la base d'un prisme; que la droite
KΔ
soit égale au contour du polygone inscrit dans ce cercle, et que la droite
ZΛ
soit
égale à cette
droite. Le triangle KTΔ sera plus grand que le polygone inscrit dans
le cercle A
; parce
que ce triangle a une base égale au contour de ce polygone, et une hauteur plus
grande que la perpendiculaire menée du centre sur un des côtés du
polygone;
et le parallélogramme
EΛ
sera égal
à la surface du prisme inscrit, qui est composée de parallélogrammes; parce que
cette surface est comprise sous le côté du cylindre, et sous une droite
égale au contour du polygone qui est la base du prisme ; donc le triangle
ΡAZ
est aussi
égal à la surface de ce prisme. Mais les polygones inscrits dans les cercles
A, B
sont semblables; donc ces polygones sont entre eux comme les carrés des rayons
de ces cercles. Mais les triangles
KTΔ,
ZΡΛ
sont
aussi entre eux comme les carrés des rayons des cercles A, B (γ);
donc le polygone inscrit, dans le cercle A est au polygone inscrit dans le cercle
B comme le triangle
KTΔ
est au
triangle
ΛZΡ.
Mais le polygone inscrit dans le cercle
A
est plus petit que le triangle KTΔ
; donc le polygone inscrit dans le cercle B est plus petit que le triangle
ZΡΛ.
Donc le
polygone inscrit dans le cercle
B
est aussi
plus petit que la surface du prisme inscrit dans le cylindre, ce qui est
impossible; car la raison du polygone qui est circonscrit au cercle
B
au
polygone qui lui est inscrit, est moindre que la raison du cercle B
à la surface du cylindre; donc
par permutation …… (d). Mais le polygone circonscrit au cercle
B
est plus
grand que ce même cercle B
(2); donc le polygone inscrit dans le cercle
B
est plus grand que la surface du cylindre, et par conséquent plus grand que la
surface du prisme. Donc le cercle
B
n'est pas plus
grand que la surface du cylindre. Mais on a démontré qu'il n'est pas plus petit;
donc il lui est égal.
PROPOSITION XV.
La surface d'un
cône droit quelconque, la base exceptée, est égale à un cercle dont le rayon est
moyen proportionnel entre le côté du cône et le rayon du cercle qui est la base
du cône.
Soit le cône
droit dont le cercle A est la base; que la droite Γ soit le rayon de la base ; que la droite
Δ
soit égale au côté du cône; que la droite E soit moyenne proportionnelle entre Γ,
Δ, et enfin que le cercle B
ait pour rayon une droite égale à la droite E. Je dis que le cercle
B
est égal
à la surface du cône, la base exceptée.
Car si le cercle
B
n'est pas égal à la surface du cône, la base exceptée, il est ou plus grand ou
plus petite Supposons d'abord qu'il soit plus petit Puisqu'on a deux
quantités inégales, la surface du cône et le cercle
B,
et que la surface du cône est la plus grande, on peut inscrire dans le cercle
B
un
polygone équilatère, et lui circonscrire un polygone semblable au premier, de
manière que la raison du polygone circonscrit au polygone inscrit soit moindre
que la raison de la surface du cône au cercle
B
(6).
Imaginons que l'on ait circonscrit au cercle A un polygone semblable au polygone circonscrit
au cercle
B
; et supposons
que le polygone circonscrit au cercle A soit la base d'une pyramide qui ait le même sommet que le cône.
Puisque les polygones circonscrits aux cercles A,
B
sont
semblables, ils sont entre eux comme les carrés des rayons de ces cercles ;
c'est-à-dire, comme les carrés des droites Γ, E, ou comme les droites Γ, Δ.
Mais le polygone circonscrit au cercle A est à la surface de la pyramide circonscrite au cône, comme la
droite Γ
est à la droite Δ.
En effet, la droite Γ
est égale à la perpendiculaire menée du centre du cercle sur un des côtés du
polygone; la droite A
est égale au côté du cône; et le contour du polygone est la hauteur commune de
deux rectangles dont les moitiés sont le polygone circonscrit au cercle A,
et la surface de la pyramide circonscrite au cône. Donc le polygone circonscrit
au cercle A
est au polygone circonscrit au cercle B,
comme le polygone circonscrit au cercle A est à la surface de la pyramide circonscrite au cône. Donc la
surface de la pyramide est égale au polygone circonscrit au cercle
B.
Donc
puisque la raison du polygone qui est circonscrit au cercle
B
au
polygone inscrit est moindre que la raison de la surface du cône au cercle
B,
la raison de la surface de la pyramide qui est circonscrite au cône au polygone
inscrit dans le cercle
B, sera moindre que la raison de la
surface du cône au cercle
B
(α).
Ce qui est impossible; car la surface de la pyramide est plus grande que la
surface du cône, ainsi que nous l'avons démontré (13); et le polygone inscrit
dans le cercle B
est au contraire plus petit que le cercle B. Donc le cercle B n'est pas plus petit que la surface du cône.

Je dis à présent
que le cercle
B
n'est pas plus grand que la surface du
cône. Car supposons, si cela est possible, que ce
cercle soit plus grand. Supposons de nouveau qu'on ait
inscrit dans le cercle B
un polygone, et qu'on lui en ait circonscrit un autre; de manière que la raison
du polygone circonscrit au polygone inscrit soit moindre que la raison du cercle
B
à la surface du cône (6). Inscrivons dans le cercle A un polygone semblable à celui qui est inscrit dans le cercle
B
; et
concevons que ce polygone soit la base d'une pyramide, qui ait le même sommet
que le cône. Puisque les polygones inscrits dans les cercles A,
B
sont semblables,
ces polygones sont entre eux comme les carrés des rayons de ces cercles. Donc la
raison du polygone inscrit dans le cercle A au polygone inscrit dans le cercle
B
est égale
à la raison de Γ à Δ. Mais la raison de Γ à Δ est plus grande que la raison du polygone
inscrit dans le cercle A à la surface de la pyramide inscrite dans le cône; car la raison
du rayon du cercle A au côté du cône est plus grande que la raison de la
perpendiculaire menée du centre sur le côté du polygone à la perpendiculaire
menée du sommet du cône sur le côté du même polygone (β).
Donc la raison du polygone inscrit dans le cercle A au polygone inscrit dans le cercle
B
est plus
grande que la raison du premier polygone à la surface de la pyramide. Donc la
surface de la pyramide est plus grande que le polygone inscrit dans le cercle
B.
Mais la
raison du polygone qui est circonscrit au cercle
B
au
polygone qui lui est inscrit, est moindre que la raison du cercle B
à la surface du cône; donc la raison du polygone qui est circonscrit au cercle
B
à la surface de la pyramide inscrite dans le cône, est encore moindre que la
raison du cercle
B
à la
surface du cône ….. (γ). Ce qui est impossible ; car le polygone circonscrit est
plus grand que le cercle
B
(2), tandis que
la surface de la pyramide inscrite dans le cône est plus petite que la surface
du cône (13). Donc le cercle
B
n'est pas plus
grand
que la surface du cône. Mais ou a démontré qu'il n'est
pas plus petit : donc il lui est égal.
PROPOSITION XVI.
La surface d'un
cône droit quelconque est à sa base comme le côté du cône est au rayon de sa
base.
Soit un cône
droit qui ait pour base le cercle A. Que la droite B soit égale au rayon du cercle A, et la droite
Γ égale au côté de ce cône. Il faut démontrer
que la surface du cône est au cercle A comme Γ est à
B.
Prenons une
droite E
moyenne proportionnelle entre
B,
Γ ; et supposons un cercle Δ
qui ait un rayon égal à la droite E. Le cercle Δ sera égal à la surface du cône, ainsi que cela a été démontré dans
le théorème précédent. Mais on a démontré aussi que le cercle Δ
est au cercle A
comme la droite Γ
est à la droite
B,
car ces deux raisons sont égales chacune à la raison du carré de la droite
E
au carré
de la droite B; parce que les cercles sont entre eux comme les carrés décrits sur
leurs diamètres, et par conséquent comme les carrés décrits sur leurs rayons, à
cause que ce qui convient aux diamètres convient aussi à leurs moitiés; or, les
rayons des cercles A, Δ sont égaux aux droites B,
E ……
(α).
Il est donc évident que la surface du cône est à la
surface du cercle A
comme la droite Γ
est à la droite
B.
LEMME.
Soit le
parallélogramme
BAH
et que
BH
soit sa
diagonale. Que le côté
BA
soit coupé en
deux parties d'une manière quelconque au point Λ. Par le point Λ menons la droite
ΛΘ
parallèle au côté
AH,
et par le
point Z
la droite
KA,
parallèle
au côté
BA.
Je dis que la surface comprise sous
BA,
AH
est égale à la
surface comprise sous
BΔ,
ΔΖ, et à
la surface comprise sous
ΔA
et sous une
droite composée de ΔΖ,
AH
(α).
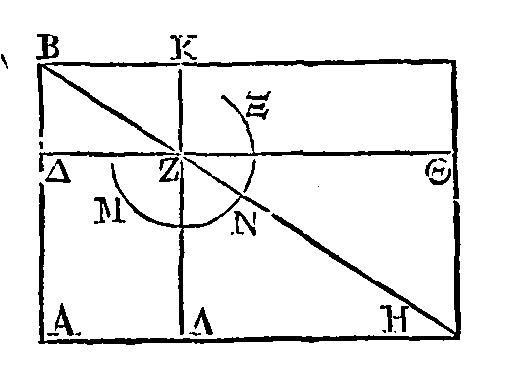
En effet, la
surface comprise sous
BA, AH
est la surface totale
BH.
Mais la surface comprise sous les
droites
BΔ,
ΔΖ est la surface BZ ; la surface comprise sous
ΔA,
et sous une droite composée de ΔΖ,
AH,
est le gnomon
MNΞ,
parce que
la surface comprise sous les droites
ΔA, AH
est égale
à la surface
KH,
le complément
ΚΘ
étant
égal au complément
ΔΛ,
et enfin la surface comprise sous ΔA, ΔΖ est égale à la surface
ΔΛ.
Donc la
surface totale
BH,
c'est-à-dire
celle qui est comprise sous les droites
BA,
AH
est égale à la
surface comprise sous les droites
BΔ,
ΔΖ, et au
gnomon
MNΘ,
qui est égal à la surface comprise sous
ΔA
et sous une
droite composée de
AH,
ΔΖ.
PROPOSITION XVII.
Si un cône droit
est coupé par un plan parallèle à la base, la surface comprise entre les plans
parallèles est égale à un cercle dont le rayon est moyen proportionnel entre la
partie du côté du cône comprise entre les plans parallèles et entre une droite
égale à la somme des rayons des cercles qui sont dans les plans parallèles.
Soit un cône
dont le triangle qui passe par l'axe soit égal au triangle
AΒΓ.
Coupons
ce cône par un plan parallèle à la base ; que ce plan produise la section
ΔΕ, et que la droite BH
soit l'axe de ce cône. Supposons un cercle dont le rayon soit moyen
proportionnel entre la droite AΔ
et entre la somme des droites ΔΖ,
HA
; et que ce
cercle soit Θ.
Je dis que ce cercle est égal à la surface du cône comprise entre
ΔΕ,
AΓ.
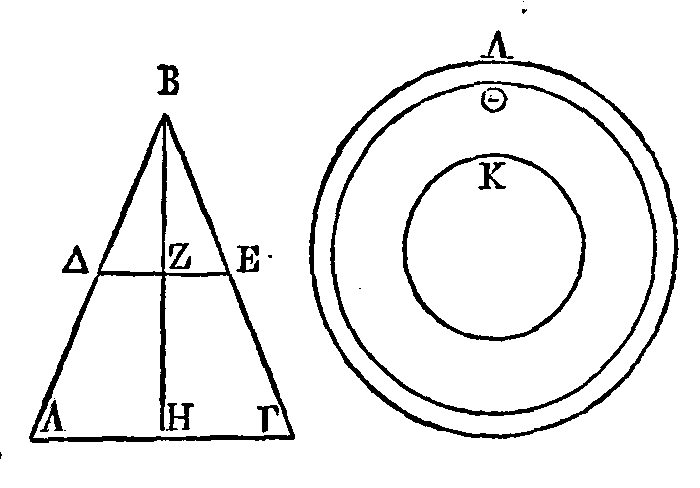
Supposons les
deux cercles Λ,
K ;
que le carré
construit sur le rayon du cercle K soit égal à la surface comprise sous les
droites
BΔ, ΔΖ,
et que le carré construit sur le rayon du cercle Λ,
soit égal à la surface comprise sous les droites
BA, AH.
Λe cercle
Λ
sera égal à la surface du cône
AΒΓ,
et le cercle
K égal à
la surface du cône
ΔΕB (15).
En effet, la
surface comprise sous
BA, AH est égale à la surface comprise sous
BΔ, ΔΖ,
et à la surface comprise sous AΔ et sous une droite composée ΔΖ,
AH,
à cause que la droite ΔΖ
est parallèle à la droite
AH
(16, lemme). Mais la
surface comprise sous
AB,
AH
est égale
au carré construit sur le rayon du cercle
Λ
; la
surface comprise sous
BΔ, ΔΖ
est égale au carré construit sur le rayon du cercle K,
et la surface comprise sous ΔA et une droite composée de
ΔΖ, AH,
est égale
au carré construit sur le rayon du cercle Θ. Donc le carré construit sur le rayon du
cercle A est égal à la somme des
carrés construits sur les rayons des cercles K, Θ. Donc le cercle
A
est égal
aux cercles
K,
Θ. Mais le cercle A est égal à la surface du cône
BAΓ,
et le cercle K
égal à la surface du cône ΔΒE;
donc la surface restante comprise entre les plans parallèles AE, AΓ est égale à la surface du cercle
Θ.
LEMMES.
1. Les cônes qui
ont des hauteurs égales sont entre eux comme leurs bases, et ceux qui ont des
bases égales sont entre eux comme leurs hauteurs.
2. Si un
cylindre est coupé par un plan parallèle à sa base, les deux cylindres seront
entre eux comme leurs axes.
3. Lorsque des cônes et des cylindres
ont les mêmes bases, les cônes sont eux comme les cylindres (α).
4. Les bases des cônes égaux sont réciproquement proportionnelles
aux hauteurs de ces cônes; et les cônes dont les bases sont réciproquement
proportionnelles à leurs hauteurs sont égaux entre eux.
5. Les cônes dont les diamètres des bases et dont les hauteurs,
c'est-à-dire les axes sont proportionnels, sont entre eux en raison triplée des
diamètres de leurs bases.
Toutes ces choses ont été démontrées
par ceux qui ont existé avant nous (β).
PROPOSITION XVIII.
Si l’on a deux
cônes droits, si la surface de l'un est égale à la base de l'autre, et si la
perpendiculaire menée du centre de la base du premier sur son côté, est égale à
la hauteur du second, ces deux cônes sont égaux.
Soient les deux
cônes droits
AΒΓ,
ΔΕZ
; que la
base du cône AΒΓ soit égale à la surface du cône
ΔΕZ
; que la
hauteur
AH
soit égale à la perpendiculaire ΚΘ,
menée du centre Θ
sur un côté du cône, savoir sur
ΔΕ.
Je dis que ces deux cônes sont égaux.
Puisque la base
du cône AΒΓ
est égale à la surface du cône
ΔΕZ,
et que les
choses qui sont égales entre elles, ont la même raison avec une troisième, la
base du cône BAΓ
est à la base du cône
ΔΕZ
comme la surface du cône
ΔΕZ
est à la
base du cône
ΔΕZ.
Mais la surface
du cône
ΔΕZ
est à sa base comme ΔΘ
est à ΘK;
car on a démontré que la surface d'un cône droit quelconque est à sa base comme
le côté du cône est au rayon de la base, c'est-à-dire comme
ΔΕ
est à
EΘ
(16); et la droite
EΔ
est à la
droite
EΘ
comme la
droite ΑΘ
est à la droite ΘK,
parce que les triangles ΔΕΘ,
ΔΚΘ
sont équiangles;
et de plus
la droite
ΘK
est égale
à la droite
AH.
Donc la base du
cône
BAΓ
est à la base du cône
ΔΕZ
comme la
hauteur du cône
ΔΕZ
est à la hauteur
du cône AΒΓ.
Donc les bases des cônes AΒΓ,
ΔΕZ
sont
réciproquement proportionnelles à leurs hauteurs. Donc le cône BAΓ est égal au cône
ΔΕZ
(17,
lemme 4 ).
PROPOSITION XIX.
Un rhombe
quelconque composé de deux cônes droits est égal à un cône qui a une base égale
à la surface de l'un des cônes qui composent le rhombe, et une hauteur égale à
la perpendiculaire menée du sommet de l'autre cône sur le côté du premier cône.
Soit un rhombe
AΒΓΔ
composé de deux cônes droits, dont la base est le cercle décrit autour du
diamètre ΒΓ,
et dont la hauteur est la droite
AΔ.
Supposons un
autre cône
ΗΘK, qui ait une base égale à la surface du
cône AΒΓ,
et une hauteur égale à la perpendiculaire menée du point Δ sur le côté
AB
ou
sur ce côté prolongé. Que cette perpendiculaire soit
ΔΖ,
et que la hauteur du cône ΘHK
soit la droite
ΘΛ
égale à
la droite ΔΖ. Je
dis que le rhombe
AΒΓΔ
est égal au cône
ΗΘK.
Supposons un
autre cône
MNΞ,
dont
la base soit égale à celle du cône AΒΓ et dont la hauteur soit égale à
AΔ.
Que la
hauteur de ce cône soit NO. Puisque NO est égal à AΔ, la droite
NO
est à la droite
ΔΕ
comme AΔ
est à ΔΕ.
Mais AΔ
est à ΔΕ
comme le rhombe AΒΓΔ
est au cône ΒΓΔ (α)
; et NO
est à ΔΕ
comme le cône
MNΞ
est au
cône ΒΓΔ
; parce que ces deux cônes ont des bases égales. Donc le cône
MNΞ
est au
cône ΒΓΔ
comme le rhombe AΒΓΔ
est au cône ΒΓΔ.
Donc le cône MNΞ
est égal au rhombe AΒΓΔ.
Mais la surface du cône AΒΓ
est égale à la base du cône ΗΘK
; donc la
surface du cône AΒΓ est à sa base comme la base du cône ΗΘK
est à la
base du cône parce que la base du cône AΒΓ est égale à la base du cône MNΞ.
Mais la surface du cône AΒΓ
est à sa base comme
AB
est à
BE
(16), c'est-à-dire comme
AΔ
est à ΔΖ ; car les triangles ABE,
AΔΖ
sont semblables.
Donc la base du cône
ΗΘK
est à la base du
cône
MNΞ
comme
AΔ
est à
ΔΖ.
Mais la
droite AΔ
est égale à la droite
NO,
par supposition, et la droite
ΔΖ
est aussi
égale à la droite
ΘΛ ;
donc la base du
cône
ΗΘK
est à la
base du cône
MNΞ
comme la hauteur
NO
est à la hauteur
ΘΛ.
Donc les
bases des cônes ΗΘK, MNΞ sont réciproquement proportionnelles à leurs hauteurs. Donc ces
cônes sont égaux (17, lemme 4). Mais on a démontré que le cône
MNΞ
est égal
au rhombe
AΒΓΔ.
Donc le cône
ΗΘK
est aussi
égal au rhombe
AΒΓΔ.
PROPOSITION XX.
Si un cône droit
est coupé par un plan parallèle à la base, et si sur le cercle qui est produit
par cette section, on conçoit un cône ayant son sommet au centre de la base ; si
l’on retranche du cône total le rhombe produit par cette construction, le reste
sera égal à un cône ayant une base égale à la surface du cône comprise entre les
plans parallèles, et une hauteur égale à la perpendiculaire menée du centre de
la base sur un côté du cône.
Soit le cône
droit AΒΓ
; coupons ce cône par un plan parallèle à la base; que ce plan produise la
section
ΔΕ
; que le
centre de la base soit le point Z, et que le cercle décrit autour du diamètre
ΔΕ
soit la
base d'un cône ayant son sommet au point Z. Le rhombe
BΔΖE
sera
composé de deux cônes droits. Supposons un cône
ΚΘΛ
dont la
base soit égale à la surface comprise entre les plans ΔΕ, AΓ,
et dont la hauteur soit égale à la perpendiculaire ZH menée du point Z
sur le côté AB.
Je dis que si l'on retranche le rhombe
BΔΖE
du cône AΒΓ,
le reste sera égal au cône ΘΚΛ.
Soient les deux
cônes
MNΞ, OPΡ
; que la base du cône MNΞ
soit égale à la surface du cône AΒΓ, et que sa hauteur soit égale à la droite
ZH.
Le cône
MNΞ
sera égal
au cône AΒΓ ; car lorsque l'on a deux cônes droits, si la surface de l'un est
égale à la base de l'autre, et si la perpendiculaire menée du centre de la base
du premier sur son côté, est égale à la hauteur du second, ces
deux cônes sont égaux (18). Que la base du cône
ΟΠΡ
soit égale à la surface du cône
ΔΒE,
et sa hauteur
égale à la droite
ZH
; le cône ΟΠΡ
sera égal au rhombe
BΔΖE,
ainsi que cela a été démontré plus haut (19). Puisque la surface du cône AΒΓ
est composée de la surface du cône
BΔΕ,
et de la surface
comprise entre ΔΕ, AΓ ; que la surface du cône AΒΓ est égale à la base du cône
MNΞ
; que la
surface du cône
ΔΒE
est égale à la
base du cône OΠΡ,
et qu'enfin la surface comprise entre ΔΕ, AΓ est égale à la base du cône
ΘKA,
la base du cône
MNΞ
sera
égale aux bases des cônes ΘΚΛ, ΟΠΡ. Mais ces cônes ont la même hauteur ; donc le cône
MNΞ
est égal
aux cônes
ΘΚΛ,
ΟΠΡ. Mais le cône
MNΞ
est égal au cône
AΒΓ,
et le cône ΠΟΡ est
égal au rhombe
BΔΕZ;
donc ce
qui reste du cône AΒΓ, après en avoir ôté le rhombe
ΔΒEZ,
est égal
au cône
ΘΚΛ.
PROPOSITION XXI.
Si un des cônes
d'un rhombe composé de cônes droits est coupé par un plan parallèle à la base;
si le cercle produit par cette section est la base d'un cône qui a le même
sommet que l'autre cône du rhombe ; et si du rhombe total, on retranche le
rhombe produit par cette construction, ce qui restera du rhombe total sera égal
à un cône qui aura une base égale à la surface comprise entre les plans
parallèles, et une hauteur égale à la perpendiculaire menée du sommet du second
cône sur le côté du premier.
Que AΒΓΔ
soit un rhombe composé de deux cônes droits ; coupons un de ces cônes par un
plan parallèle à la base, et que ce plan produise la section EZ ; que le cercle produit par cette section
soit la base d'un cône qui ait son sommet au point Δ,
cette construction produira le rhombe
EBZΔ.
Retranchons ce
rhombe du rhombe total; et supposons un cône
ΘΚΛ,
qui ait
une base égale à la surface comprise entre AΓ,
EZ,
et une hauteur égale à la perpendiculaire menée du point Δ sur la droite
BA,
ou sur
son prolongement. Je dis que le reste dont nous avons parlé est égal au cône
ΘΚΛ.
Soient les deux
cônes
MNΞ, ΟΠΡ. Que la base du cône
MNΞ
soit égale à la surface du cône AΒΓ, et que sa hauteur soit égale à la droite
ΔH
: d'après
ce que nous avons démontré (19), le cône
MNΞ
est égal au rhombe AΒΓΔ.
Que la base du cône ΟΠΡ soit égale à la surface du cône
EBZ,
et sa hauteur égale à la droite
ΔH ;
le cône
ΟΠΡ sera
aussi égal au rhombe
EBZΔ
(19). Mais puisque la surface du cône
AΒΓ
est composée de la surface du cône
EBZ,
et de la surface comprise entre
EZ,
AΓ
; que la surface du cône AΒΓ
est égale à la base du cône
MNΞ ;
que la surface du cône EBZ
sera égale à la base du cône ΟΠΡ, et qu'enfin la surface comprise entre
EZ,
AΓ
est égale à la base du cône
ΘΚΛ,
la
base du cône
MNΞ est
égale à la somme des bases des cônes ΟΠΡ,
ΘΚΛ.
Mais ces
cônes ont la même hauteur ; donc le cône
MNΞ
est égal à la somme des cônes
ΘΚΛ,
ΟΠΡ.
Mais le cône
MNΞ est
égal au rhombe AΒΓΔ,
et le cône ΟΠΡ égal
au rhombe
EBZΔ;
donc le
cône restant
ΘΚΛ est égal à ce qui reste du rhombe AΒΓΔ.
PROPOSITION XXII.
Si l'on inscrit
dans un cercle un polygone équilatère et d'un nombre pair de côtés ; et si l'on
joint les côtés de ce polygone par des droites parallèles à une
des droites qui sous-tendent deux côtés de ce même polygone, la somme des
droites qui joignent les côtés du polygone est au diamètre du cercle, comme la
droite qui soutend la moitié des côtés du polygone inscrit moins un est à un
côté de ce polygone.
Soit le cercle
AΒΓΔ;
inscrivons-lui le polygone AEZBΗΘΓMNΔΛΚ
et menons les droites EK, ZΛ, BΔ, HN, ΘM.
Il est évident que ces droites seront
parallèles à une de celles qui sous-tendent deux côtés de ce polygone. Je dis
que la somme des droites dont nous avons parlé est au diamètre du cercle comme
la droite
ΓΕ
est à la droite EA.
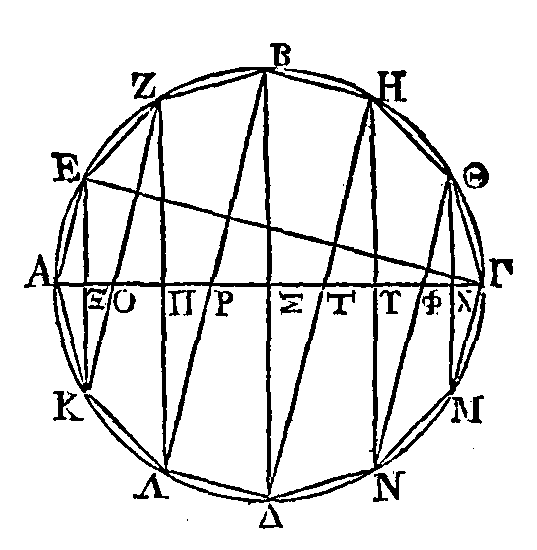
Menons les
droites
ZK,
ΛΒ,
HΔ, ΘN.
La droite
ZK
sera parallèle à la droite EA ; la droite
ΒΛ
parallèle
à la droite
ZK
; la droite
ΔH
parallèle
à la droite
ΒΛ ;
la droite ΘN
parallèle à
ΔH
; et
enfin la droite
TM
parallèle à ΘN.
Puisque les deux droites
EA, KZ
sont parallèles,
et que l'on a mené les deux droites
EK,
AO,
la droite EΞ est à
la droite
ΞA
comme la
droite KΞ
est à la droite ΞΘ.
Par la même raison, la droite
KΞ
est à la droite
ΞO
comme la droite ΖΠ
est à la droite ΠΟ
; la droite ZΠ
est à la droite ΠO
comme la droite AP
est à la droite ΠΡ
; la droite ΑΠ
est à la droite ΠΡ
comme la droite ΒΣ
est à la droite ΣΠ
; la
droite ΒΣ
est à la droite
ΣΠ
comme la
droite ΔS
est à la droite ΣΤ;
la droite
ΔS
est à la droite ΣΤ
comme la droite ΗΥ
est à la
droite ΥΤ ;
la droite
ΗΥ
est à la
droite
UT
comme la droite ΝΥ
est à la droite ΥΧ
; la droite ΝΥ
est à la droite ΥΦ
comme la
droite ΘΧ
est à la droite ΧΦ
; et enfin la droite ΘΧ
est à la droite ΧΦ
comme la droite ΜΧ
est à la droite CΓ.
Δonc la somme de toutes les droites
EΞ,
ΞK,
ΖΠ, ΠΛ, ΒΣ,
ΣΔ,
ΗΥ,
ΥΝ,
ΘΧ,
ΧΜ, est à la somme de toutes les droites
AΞ, ΞO,
ΟΠ,
ΠΡ, ΡΣ, ΣΤ,
ΤΥ, ΥΦ, ΦΧ, ΧΓ,
comme une de ces premières droites est à une des
secondes. Δonc la somme des droites
EK,
ZΛ,
BΔ, HN,
ΘM
est au
diamètre AΓ
comme la droite
EΞ
est à la
droite
ΞA.
Mais la droite EΞ
est à la droite
ΞA
comme la
droite
ΓΕ
est à la droite
EA
; donc la
somme des droites
EK, ZΛ,
BΔ, HN,
ΘM est au diamètre AΓ comme la droite
ΓΕ
est à la droite
EA.
PROPOSITION XXIII.
Si l'on inscrit
dans un segment de cercle un polygone d'un nombre pair de côtés, dont
tous les côtés, excepté la base, soient égaux entre eux; si l'on joint les côtés
du polygone par des parallèles à la base du segment, la somme de ces parallèles,
avec la moitié de la base du segment, est à la hauteur du segment, comme la
droite menée de l'extrémité du diamètre à l'extrémité d'un des côtés du polygone
est à un côté du polygone.
Conduisons dans
le cercle AΒΓ une
droite quelconque AΓ.
Dans le segment AΒΓ,
et au-dessus de AΓ,
inscrivons un polygone d'un nombre pair de côtés, dont tous les côtés, excepté
la base AΓ,
soient égaux ; et menons les droites
ZH, EΘ
parallèles à la
base du segment. Je dis que la somme des droites
ZH, EΘ,
AΞ est à
la droite
BΞ
comme la
droite
ΔΖ
est au côté
ZB.
Menons les
droites
HE, ΑΘ
; ces droites seront parallèles à la droite
ZB.
Par la même
raison que dans le théorème précédent, la droite KZ est à la droite
KB
comme la
droite
HK
est à la droite
ΚΛ,
comme
EM
est à
MΛ,
comme
MΘ
est à
MN
et comme
ΞA
est à
ΞN.
Donc la
somme des droites
ZK, KH,
EM,
MΘ,
AΞ
est à la
somme des droites
BK,
ΚΛ,
ΛΜ,
MN, NΞ, comme une des premières droites est à une des secondes. Donc la
somme des droites
ZH, EΘ,
AΞ
est à la
droite
BΞ
comme la droite
ZK
est à la
droite
KB.
Mais la droite
ZK
est à la
droite
KB
comme la droite
ΔΖ
est à la
droite
ZB.
Donc la somme des droites
ZH, EΘ, AΞ
est à la droite
BΞ
comme la
droite
ΔΖ
est à la droite
ZB.
PROPOSITION XXIV.
Que
AΒΓΔ
soit un grand
cercle d'une sphère ; inscrivons dans ce cercle un polygone équilatère dont le
nombre des côtés soit divisible par quatre (α). Soient AΓ,
BΔ
deux diamètres (β).
Si le diamètre AΓ
restant immobile, le cercle dans lequel le polygone est inscrit fait une
.révolution, il est évident que sa circonférence se mouvra selon la surface de
la sphère, et que les sommets des angles, excepté ceux qui sont placés aux
points A, Γ,
décriront dans la surface de la sphère des circonférences de cercles dont les
plans seront perpendiculaires sur le
cercle AΒΓΔ. Les diamètres de ces cercles seront des
droites qui étant parallèles à la droite BΔ, joignent les angles du polygone.
Les côtés du polygone décriront les surfaces de certains cônes,
savoir : les côtés
AZ,
AN
décriront
la surface d'un cône dont la base est le cercle qui a pour diamètre la droite
ZN
et dont
le sommet est le point A ; les côtés
ZH, MN
décriront
la surface d'un cône dont la base est le cercle qui a pour diamètre la droite
MH,
et dont le sommet est le point où les droites
ZH,
MN
prolongées se
rencontrent avec la droite AΓ ; et enfin les côtés
BH,
MΔ
décriront la
surface du cône dont la base est le cercle qui a pour diamètre la droite
BΔ,
et dont
le sommet est le point où les droites
BH, ΔM
prolongées se rencontrent avec la droite AΓ. Pareillement dans l'autre demi-cercle, les côtés décriront aussi
des surfaces de cônes semblables à celles dont nous venons de parler. De cette
manière il sera inscrit dans la sphère une certaine figure qui sera comprise par
les surfaces dont nous venons de parler, et dont la surface sera plus petite que
la surface de la sphère. En effet, la sphère étant partagée en deux parties par
un plan qui est mené par un droite
BΔ,
et perpendiculaire sur le cercle AΒΓΔ, la surface de l'un des hémisphères et la surface de la figure
inscrite ont les mêmes limites dans un seul plan, puisque ces deux surfaces ont
pour limites la circonférence du cercle qui est décrite autour du diamètre
BΔ,
et qui est pendiculaire sur le cercle AΒΓΔ ; ces deux surfaces sont concaves du même côté, et l’une de ces
surfaces est comprise par l'autre et par un plan qui a les mêmes limites que
cette autre (Princ. 4). Pareillement la surface de la figure qui
est inscrite dans l'autre hémisphère, est aussi plus petite que la surface de
cet hémisphère. Donc la surface totale de la figure inscrite dans la sphère est
plus petite que la surface de la sphère.
PROPOSITION XXV.
La surface de la
figure inscrite dans une sphère est égale à un cercle dont le carré du rayon est
égal à la surface comprise, sous un des côtés du polygone, et sous une droite
égale à, la somme des droites qui joignent les côtés du polygone, en formant des
quadrilatères, et qui sont parallèles à une droite qui sous-tend deux côtés du
polygone.
Que
AΓΒΔ
soit un
grand cercle de la sphère. Inscrivons dans ce cercle un polygone équilatère dont
le nombre des côtés soit divisible par quatre. Concevons qu'une figure ait été
engendrée
dans la sphère par le polygone inscrit. Menons les
droites
EZ, ΗΘ, ΓΔ,
ΚΛ,
MN,
et que ces droites soient parallèles à la droite qui soutend deux côtés du
polygone. Supposons un cercle Ξ
dont le carré du rayon soit égal à la surface comprise sous la droite AE, et sous une droite égale à la somme des
droites
EZ, ΗΘ,
ΓΔ, ΚΛ,
MN.
Je dis que ce
cercle est égal à la surface de la figure inscrite dans la sphère.

Supposons les
cercles O,
Π, Ρ, Σ, T, Υ.
Que le
carré du rayon du cercle O soit égal à la surface comprise sous
EA
et sous
la moitié de EZ ; que le carré du rayon du cercle P soit égal à la surface comprise sous la
droite
EA,
et sous la moitié de la
somme des droites
EZ, ΗΘ
; que le carré
du rayon du cercle Ρ soit égal à la surface comprise sous la droite
EA,
et sous
la moitié de la somme des droites ΗΘ,
ΓΔ
;
que le carré du rayon du cercle Σ soit égal à la surface comprise sous la droite AE,
et sous la moitié de la somme des droites
ΓΔ, ΚΛ,
que le
carré du rayon du cercle T soit égal à la surface comprise sous la droite AE,
et sous la moitié de la somme des droites
ΚΛ,
MN,
et qu'enfin le carré du rayon du cercle
Υ
soit égal à la
surface comprise sous la droite
AE,
et sous la moitié de la droite
MN.
Mais le cercle O
est égal à la surface du cône
AEZ
(15); le cercle
Π
égal à la surface comprise entre
EZ,
ΗΘ (17); le cercle Ρ
égal à la surface comprise entre ΗΘ, ΓΔ ; le cercle S égal à la surface comprise entre
ΔΓ,
ΚΛ
; le
cercle
T
égal à la surface comprise entre
ΚΛ, MN,
et enfin le cercle Υ
égal à la surface du cône
MBN.
Donc la somme de ces cercles est égale
à la surface inscrite dans la sphère. Mais il est évident que la somme des
carrés des rayons des cercles O, Π, Ρ, Σ, T,
Υ
est égale à la surface comprise sous
AE,
et sous la somme
des demi-droites
EZ, ΗΘ,
ΓΔ,
ΚΛ,
MN,
prises deux
fois, c'est-à-dire la somme des droites totales
EZ, ΗΘ,
ΓΔ, ΚΛ,
MN.
Donc la
somme des carrés des rayons des cercles O, Π, Ρ, Σ, T,
Υ
est égale à la surface comprise sous
AE,
et sous
la somme des droites
EZ, ΗΘ,
ΓΔ,
ΚΛ,
MN.
Mais le carré du
rayon du cercle Ξ est égal à la surface comprise sous la droite
AE,
et sous
une droite composée de toutes les droites
EZ, ΗΘ,
ΓΔ, ΚΛ,
MN.
Donc le
carré du rayon du cercle Ξ est égal à la somme des carrés des rayons de tous les cercles
Ο, Π, Ρ, Σ,
T, Υ. Donc le cercle S
est égal à la somme des cercles O, Π, Ρ, Σ, T,
Υ
(α).
Mais l'on
a démontré que la somme des cercles Ο, Π, Ρ, Σ, T,
Υ est égale à la surface de la figure dont nous avons parlé. Donc le
cercle Ξ
est aussi égal à la surface de cette figure.
PROPOSITION XXVI.
La surface d'une figure inscrite dans une sphère et terminée par
des surfaces coniques, est plus petite que quatre grands cercles de la sphère.
Soit AΒΓΔ
un grand cercle d'une sphère. Inscrivons dans ce cercle un polygone équiangle et
équilatère, dont le nombre des côtés soit divisible par quatre. Concevons que
sur ce polygone on ait construit une figure terminée par des surfaces coniques.
Je dis que la surface de la figure inscrite est plus petite que quatre grands
cercles de cette sphère.
Menons les deux
droites
EI,
ΘM,
sous-tendant chacune deux côtés du polygone, et les droites
ZK,
ΔΒ,
HΛ
parallèles aux droites
EI,
ΘM. Supposons un cercle Ρ
dont
le carré du rayon soit égal à la surface comprise sous la droite
EA,
et sous
une droite égale à la somme des droites
EI, ZK, BΔ, HΛ,
ΘM.
D'après ce qui a
été démontré (25), ce cercle est égal à la surface de la figure dont nous
venons de parler. Mais l'on a démontré qu'une droite
égale à la somme des droites
EI, ZK, BΔ, HΛ, ΘM,
est au diamètre ΛΓ
du cercle
AΒΓΔ
comme
ΓΕ
est à
EA
(22).
Donc la surface comprise sous une droite égale à la somme des droites dont
nous venons de parler, et sous la droite
EA,
c'est-à-dire le carré du rayon du cercle Ρ, est égal à la surface comprise sous les droites
AΓ, ΓΕ.
Mais la surface comprise sous AΓ,
ΓΕ est plus petite que le carré de
AΓ
; donc le carré du rayon du cercle Ρ est plus petit que le carré de
AΓ.
Donc le
rayon du cercle Π est plus petit que AΓ. Donc le diamètre du cercle Ρ
est plus petit que le double du diamètre du cercle AΒΓΔ.
Donc deux
diamètres du cercle AΒΓΔ
sont plus grands que le diamètre du cercle Π. Donc le quadruple du carré construit sur le diamètre du cercle
AΒΓΔ,
c'est-à-dire sur AΓ,
est plus grand que le carré construit sur le rayon du cercle Π. Mais le quadruple du carré construit sur
AΓ
est au carré construit sur le diamètre du cercle Π, comme le quadruple du cercle AΒΓΔ
est au cercle Π.
Donc le quadruple du cercle AΒΓΔ
est plus grand que le cercle Π.
Donc le cercle Π
est plus petit que le quadruple d'un grand cercle. Mais on a démontré que le
cercle Π
est égal à la surface de la figure dont nous venons de parler (25); donc la
surface de la figure dont nous venons de parler est plus petite que le quadruple
d'un grand cercle de la sphère.
PROPOSITION XXVII.
Une figure
inscrite dans la sphère et terminée par des surfaces coniques, est égale à un
cône qui a une base égale à la surface de la figure inscrite dans la sphère, et
une hauteur égale à la perpendiculaire menée du centre de la sphère sur un côté
du polygone.
Soit une sphère
; que AΒΓΔ
soit un grand cercle de cette sphère, et que le reste soit comme dans le
théorème précédent. Que Ρ
soit un cône droit, qui ait une base égale à la surface de la figure inscrite
dans cette sphère, et une hauteur égale à la
perpendiculaire menée du centre de cette sphère sur un
côté du polygone. Il faut démontrer que la figure inscrite dans cette sphère est
égale, au cône Ρ.
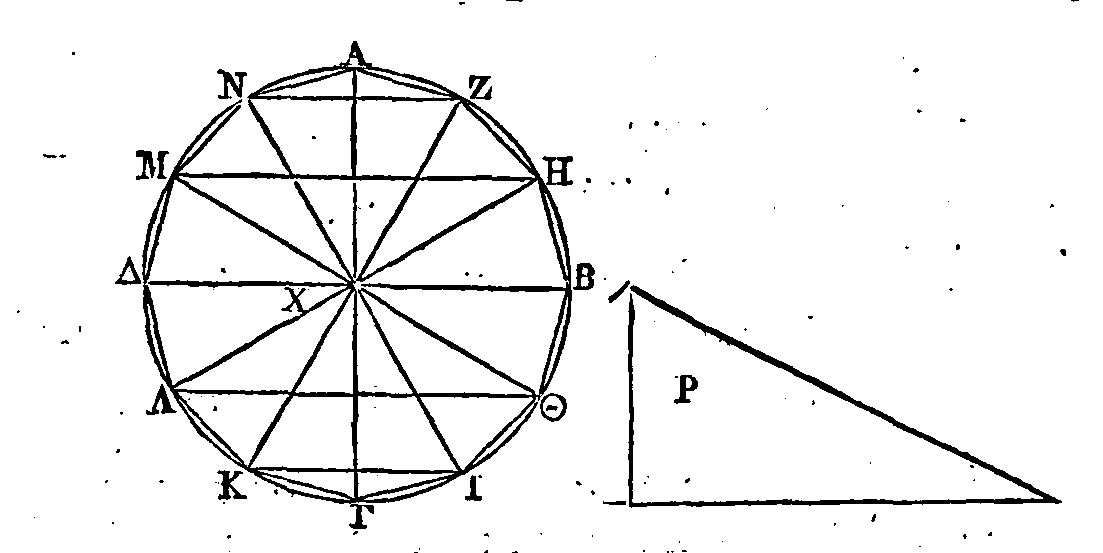
Sur les cercles
décrits autour des diamètres
ZN,
HM, ΘΛ,
IK,
construisons des cônes qui .aient leur sommet au centre de
la sphère. On aura un rhombe solide composé dû cône dont la base est le cercle
décrit autour du diamètre
ZN,
et dont le sommet est le point A ; et du cône dont la base est le même cercle et dont le sommet est
le point Χ. Ce rhombe est égal: à un cône qui a une base égale à la surface
du cône NAZ,
et une hauteur égale à la perpendiculaire menée du point Χ sur la
droite AZ
(19). Le reste du rhombe terminé par la surface conique placée entre les
plans parallèles conduits par les droites ZN,
HM,
et entre
les surfaces des cônes
ZNΧ, HMΧ,
est égal à un cône qui a une base égale à la surface conique comprise entre
les plans parallèles conduits par les droites
ZN, HM, et pour hauteur une droite égale à la
perpendiculaire menée du point Χ sur la droite
ZH,
ainsi que cela a été démontré (21). De plus le reste de cône terminé par la
surface conique comprise entre les plans parallèles menés par les droites
HM,
BΔ,
entre la surface du cône HMΧ
et entre
le cercle décrit autour du diamètre BΔ, est égal à un cône qui a une base égale à la
surface conique comprise entre les plans parallèles menés par les droites
HM,
BΔ, et une hauteur égale à la perpendiculaire
menée du point C sur la droite
BH
(20). Dans
l'autre hémisphère, on aura pareillement un rhombe ΧKΓI, et autant de restes de cônes que dans le
premier hémisphère, et ce rhombe et ces restes de cônes seront égaux, chacun à
chacun, aux cônes dont nous venons de parler. Il est donc évident que la figure
totale inscrite dans la sphère est égale à la somme de tous les cônes dont nous
venons de parler. Mais la somme de ces cônes est égale au cône Ρ,
parce que le cône Ρ
a une
hauteur égale à la hauteur de chacun des cônes dont nous venons de parler; et
une base égale â la somme de leurs bases. Il est donc
évident que la figure inscrite
dans la sphère est égale au cône Ρ.
PROPOSITION XXVIII.
Une figure
inscrite dans une sphère et terminée par des surfaces coniques, est plus petite
quelle quadruple d'un cône qui a une base égale à un grand cercle de cette
sphère, et une hauteur égale à un rayon de cette même sphère.
En effet, que
Ρ
soit un cône égal à la figure inscrite ; c'est-à-dire que ce cône ait une base
égale à la surface de la figure inscrite et une hauteur égale à la droite menée
du centre du cercle sur un des côtés du polygone inscrit. Soit aussi un cône
Ξ,
qui ait une base égale au cercle AΒΓΔ et une hauteur égale au rayon du cercle AΒΓΔ.
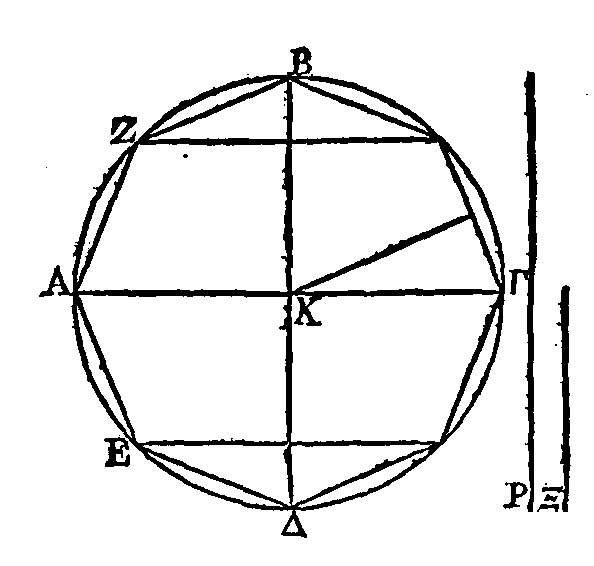
Puisque le cône Ρ a une base égale à la surface de la figure inscrite dans la sphère
et une hauteur égale à la perpendiculaire menée du point Υ
sur le côté
AZ,
et
puisqu'il a été démontré que la surface de la figure inscrite est plus petite
que le quadruple d'un grand cercle d'une sphère (26), la base du cône Ρ
est plus petite que le quadruple de la base du cône Ξ. Mais la hauteur du cône Ρ
est plus petite que la hauteur du cône Ξ ; donc, puisque le cône Ρ a une base plus petite que le quadruple de la
base du cône Ξ, et une hauteur plus petite que celle du cône Ξ,
il est évident que le cône Ρ
est plus petit que le quadruple du cône Ξ. Mais le cône
Ρ
est égal à la
figure inscrite (27) ; donc la figure inscrite est plus petite que le quadruple
du cône Ξ.
PROPOSITION XXIX,
Que AΒΓΔ
soit un grand cercle d'une sphère. Circonscrivons à ce cercle un polygone
équiangle et équilatère ; que le nombre des côtés de ce polygone soit divisible
par quatre. Circonscrivons un cercle au polygone circonscrit Le centre du cercle
circonscrit sera le même que le centre du cercle AΒΓΔ. Si le diamètre EH
restant
immobile, le plan du polygone EZΗΘ et le cercle AΒΓΔ font une révolution, il est évident que la circonférence du cercle
AΒΓΔ
se mouvra selon la surface de la sphère, et que la circonférence du cercle
EZΗΘ
décrira la surface d'une autre sphère qui aura le même centre que la plus
petite. Les points de contact des côtés du polygone décriront dans la surface de
la plus petite sphère des cercles perpendiculaires sur le cercle AΒΓΔ
; les angles du polygone, excepté les angles placés aux points
E,
H,
décriront des circonférences de cercle dans la surface de la plus grande sphère,
dont les plans seront perpendiculaires sur le cercle EZΗΘ ; et les côtés du polygone décriront des
surfaces coniques comme dans le théorème précédent.
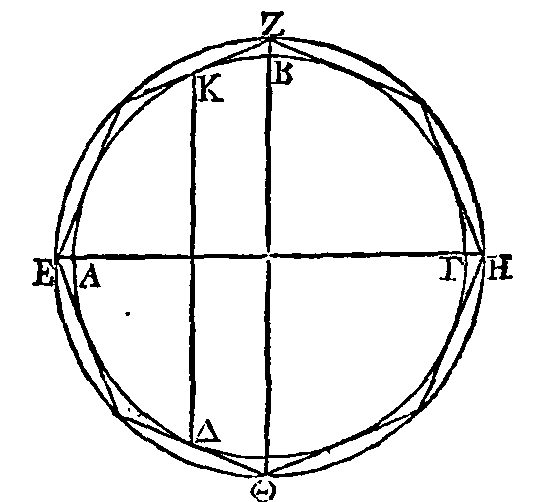
Il est donc
évident qu'une figure terminée par des surfaces coniques sera circonscrite à la
petite sphère et inscrite dans la grande. Nous démontrerons de la manière
suivante, que la surface de la figure circonscrite est plus grande que la
surface de la sphère. Que KΔ
soit le diamètre d'un des cercles de la petite sphère, et K, Δ les points où deux côtés du polygone
circonscrit touchent le cercle AΒΓΔ.
La sphère étant partagée en deux parties par
un plan conduit par la droite KΔ et perpendiculaire sur le
cercle AΒΓΔ,
la surface de la figure circonscrite à la sphère sera aussi partagée en deux
parties par le même plan. Or il est évident que les surfaces obtenues de cette
manière ont les mêmes limites dans un même plan, car la limite de l'une et de
l'autre est la circonférence du cercle qui est décrit autour du diamètre KΔ
et qui est perpendiculaire sur le cercle AΒΓΔ ; et de plus l'une et l'autre de ces surfaces sont concaves du
même côté, et l'une est comprise par l'autre et par un plan qui a les mêmes
limites que cette autre (Princ. 4). Donc la surface du segment
sphérique qui est comprise est plus petite que la surface de la figure
circonscrite à ce même segment. Semblablement, la surface de l'autre segment
sphérique est aussi plus petite que la surface de la figure circonscrite à ce
même segment. Il est donc évident que la surface totale d'une sphère est plus
petite que la surface de la figure circonscrite à cette sphère.
PROPOSITION XXX.
La surface d'une figure circonscrite à une sphère est égale à un
cercle dont le carré du rayon est égal à la surface comprise sous un des côtés
.du polygone, et sous une droite égale à la somme des droites qui joignent les
angles du polygone et qui sont parallèles à une de celles qui sous-tendent deux
côtés du polygone.
En effet, la
figure circonscrite à la petite sphère est inscrite dans la grande. Mais on a
démontré que la surface de la figure inscrite dans la sphère et terminée par des
surfaces coniques est égale à un cercle dont le carré du rayon est égal à la
surface comprise sous un des côtés du polygone et sous une droite égale à la
somme des droites qui joignent les angles du polygone et qui sont parallèles à
une des droites qui sous-tendent deux côtés du polygone (25), Donc ce qui
a été proposé plus haut est évident,
PROPOSITION XXXI.
La surface de la
figure circonscrite à une sphère est plus grande que le quadruple d'un grand
cercle de cette sphère.
Soient une
sphère et un grand cercle, et que le reste soit comme dans les théorèmes
précédents. Que le cercle a soit
égal à la surface de la figure proposée qui est circonscrite à la petite sphère.
Puisqu'on a
inscrit dans le cercle
EZΗΘ
un polygone
équilatère dont le nombre des angles est pair, la somme des parallèles au
diamètre ΘZ,
qui joignent les angles du polygone est à ΘZ comme
ΚΘ
est à
KZ.
Donc la
surface comprise sous un côté du polygone et sous une droite égale à la somme
des droites qui joignent les angles du polygone, est égale à la surface comprise
sous ΖΘ, ΘK. Donc le carré du rayon du cercle Λ
est égal à la surface comprise sous ΖΘ,
ΘK (25). Donc le rayon du cercle Λ
est plus grand
que ΘK.
Mais la droite ΘK
est égale au diamètre du cercle AΒΓΔ (α) puisque ΘK est double de ΧΣ qui est le rayon du cercle AΒΓΔ.
Il est donc évident que le cercle Λ,
c'est-à-dire la surface de la figure circonscrite à une sphère, est plus grand
que le quadruple d'un grand cercle de cette sphère.
PROPOSITION XXXII.
La figure
circonscrite à la petite sphère est égale à un cône qui a pour base un cercle
égal à la surface de cette figure, et pour hauteur une droite égale au rayon de
cette sphère.
En effet, la
figure circonscrite à la petite sphère est inscrite dans la plus grande. Or on a
démontré qu'une figure inscrite et terminée par des surfaces coniques est égale
à un cône' qui a pour base un cercle égal à la surface de cette figure, et pour
hauteur une droite égale à la perpendiculaire menée du centre de la sphère sur
le côté du polygone; et cette perpendiculaire est égale au rayon de la
petite sphère (27). Donc ce qui a été posé plus haut est évident,
PROPOSITION XXXIII.
Il suit de-là
que la figure circonscrite à la petite sphère est plus grande que le quadruple
d'un cône qui a pour base un cercle égal à un grand cercle de cette sphère,
et pour hauteur une droite égale au rayon de cette même sphère.
En effet,
puisque cette figure est égale à un cône qui a une base égale à la surface de
cette même figure, et une hauteur égale à la perpendiculaire menée du centre sur
le côté du polygone, c'est-à-dire au rayon de la petite sphère (32), et que la
surface de la figure circonscrite à une sphère est plus grande que quatre grands
cercles (3&), la figure circonscrite à la petite sphère est plus grande que le
quadruple d'un cône qui a pour base un grand cercle de cette sphère, et pour
hauteur un rayon de cette même sphère; car cette figure est égale
à un cône plus grand que le quadruple du cône dont
nous venons de parler, puisque le premier a une base plus grande que le
quadruple de la base du second et une hauteur égale.
PROPOSITION XXXIV.
Si l'on inscrit
une figure dans une sphère, et si on lui en circonscrit une autre; et si l’on
fait faire une révolution aux polygones semblables qui ont été construits plus
haut, la raison de la surface de la figure circonscrite à la surface de la
figure inscrite, sera doublée de la raison du côté du polygone qui est
circonscrit à un grand cercle à un des côtés du polygone qui est inscrit
dans ce même cercle ; et la raison de la figure circonscrite à la figure
inscrite sera triplée de la raison du côté du polygone circonscrit au côté du
polygone inscrit.
Que AΒΓΔ
soit un grand cercle d'une sphère; inscrivons dans ce cercle un polygone
équilatère dont le nombre des côtés soit divisible par quatre. Circonscrivons à
ce même cercle un autre polygone semblable au premier; que les côtés du
polygone circonscrit soient tangents aux milieux des arcs sous-tendus par les
côtés du polygone inscrit; que les droites EH, ΘZ soient deux diamètres du cercle qui comprend le polygone
circonscrit ; que ces diamètres se coupent à angles droits et soient placés de
la même manière que les diamètres AΓ,
BΔ
; et
concevons qu'on ait joint les angles opposés du polygone par des droites ; ces
droites seront parallèles entre elles et aux droites
BZ, ΘΔ.
Cela posé, le
diamètre
EH
restant immobile, si l'on fait faire
une révolution aux polygones, les côtés de ces polygones circonscriront une
figure à la sphère et lui en inscriront une autre. Il faut démontrer que la
raison de la surface de la figure circonscrite à la surface de la figure
inscrite est doublée de la raison de
EA
à
AK
; et que
la raison de la figure circonscrite à la figure inscrite est triplée de la,
raison de
EA
à
AK.
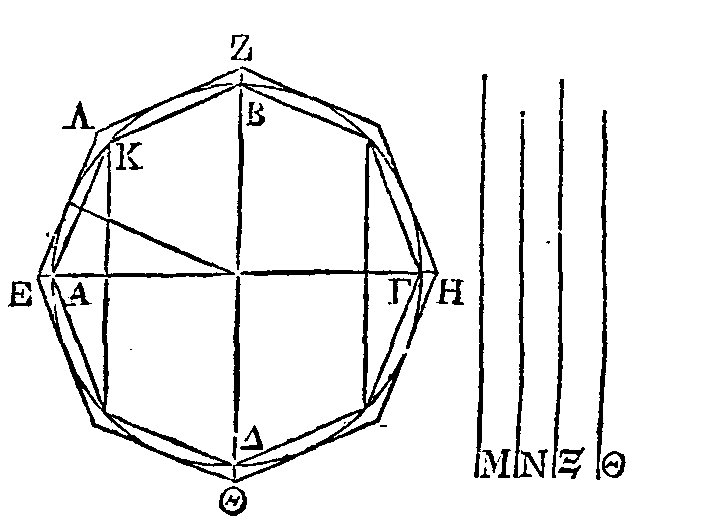
Que
M
soit un
cercle égal à la surface de la figure circonscrite à la sphère, et N
un cercle égal à la surface de la figure inscrite. Le carré du rayon du cercle
M
est égal
à la surface comprise sous la droite ΕΛ
et sous
une droite égale à la somme des droites qui joignent les angles du polygone
circonscrit (36) ; et le carré du rayon du cercle N
est égal à la surface comprise sous la droite
AK
et sous
une droite égale à la somme des droites qui joignent les angles du polygone
inscrit (25). Mais les polygones circonscrits et inscrits sont semblables
; il est donc évident que les surfaces comprises sous les droites dont nous
venons de parler, c'est-à-dire les surfaces comprises sous les sommes des
droites qui joignent les angles des polygones et sous les côtés de ces
mêmes polygones, sont des figures semblables entre elles (α).
Donc ces figures sont entre elles comme les carrés des côtés des polygones.
Mais les surfaces qui sont comprises sous les droites dont nous venons de
parler, sont entre elles comme les carrés des rayons des cercles
M, N.
Donc les diamètres des cercles M, N
sont entre eux comme les côtés des polygones. Mais les cercles
M, N
sont
entre eux en raison doublée de leurs diamètres; et ces cercles sont égaux aux
surfaces des figures Circonscrites et inscrites. Il est donc évident que la
raison de la surface de la figure qui est circonscrite à la sphère à la
surface de la figure inscrite est doublée de la raison
du côté ΕΛ
au côté
AK.
Soient
maintenant deux cônes O, Ξ.
Que le cône Ξ
ait une base égale au cercle
M, et le cône O
une base égale au cercle M
; que le cône Ξ
ait une hauteur égale au rayon de la sphère, et que le cône O ait une hauteur égale à la perpendiculaire
menée du centre de la sphère sur le côté
AK.
D'après
ce qui a été démontré, le cône Ξ est égal à la figure circonscrite(32), et le cône O
égal à la figure inscrite (27). Mais les polygones
sont semblables ; donc le côté
ΕΛ
est au côté AK
comme le
rayon de la sphère est à la perpendiculaire menée du
centre de la sphère sur le côté
AK.
Donc la
hauteur du cône Ξ
est
à la hauteur du cône O comme
ΕΛ
est à
AK.
Mais le
diamètre du
cercle
M
est au
diamètre du cercle N comme ΕΛ
est à AK
; donc
les diamètres des bases des cônes
Ξ, O sont proportionnels à leurs
hauteurs ; donc ces cônes sont
semblables. Donc les cônes, Ξ, O sont
entre eux en raison triplée des
diamètres des cercles
M, N.
Il est
donc évident que la raison de
la figure circonscrite à la figure
inscrite est triplée de la raison du côté
ΕΛ
au côté
AK.
PROPOSITION XXXV.
La surface d'une
sphère quelconque est quadruple d'un de ses grands cercles.
Soit une sphère
quelconque; que A soit un cercle quadruple d'un des grands cercles de cette sphère.
Je dis que le cercle A est égal à la surface de cette sphère.
Car, si le cercle A n'est pas égal à
la surface de la sphère, il est ou plus grand ou plus petit. Supposons d'abord
que la surface de la sphère soit plus grande que le cercle A. Puisqu'on a deux
quantités inégales, la surface de la sphère et le cercle A, on peut prendre deux droites inégales de
manière que la raison de la plus grande à la plus petite soit moindre que la
raison de la surface de la sphère au cercle
A
(3).
Prenons les droites B, Γ, et que la droite A soit moyenne proportionnelle entre les droites
B,
Γ.
Concevons que la sphère soit coupée par un plan conduit par son centre, selon le
cercle EZΗΘ.
Inscrivons un polygone dans ce cercle, et circonscrivons-lui en un autre de
manière que le polygone circonscrit soit semblable au polygone inscrit; et que
la raison du côté du polygone circonscrit au côté du polygone inscrit soit
moindre que la raison de la droite
B
à la droite
A (4). Il est
évident que la raison doublée du côté du premier polygone au côté du second
polygone sera encore moindre que la raison doublée de la droite B à la droite
A.
Mais la raison de B à Γ
est doublée de la raison de
B
à A, et la raison de la surface du solide
circonscrit à la sphère à la surface du solide inscrit est doublée de la raison
du côté du polygone circonscrit au côté du polygone inscrit (34). Donc la raison
de la surface de la figure qui est circonscrite à la sphère à la surface de la
figure inscrite est moindre que la raison de la surface de la sphère au cercle A
(α),
ce qui est absurde. En effet, la surface de la figure circonscrite est plus
grande que la surface de la sphère, et la surface de la figure inscrite est au
contraire plus petite que celle du cercle A ; car on a démontré que la surface de la
figure inscrite est plus petite que quatre grands
cercles d'une sphère (26), et par conséquent plus petite que le cercle
A qui est égal à quatre grands cercles. Donc la
surface d'une sphère n'est pas plus grande que le cercle A.
Je dis maintenant que la surface de la sphère n'est pas plus petite
que le cercle A. Supposons, si cela est possible, qu'elle soit plus petite.
Cherchons pareillement deux droites B, Γ, de manière que la raison de B
à Γ
soit moindre que la raison du cercle
A
à la surface de
la sphère (5), et que la droite A soit moyenne proportionnelle entre
B, Γ.
Inscrivons dans le cercle EΘHZ
un polygone et circonscrivons-lui un autre poly gone, de manière que la raison
du côté du polygone circonscrit au côté du polygone inscrit soit moindre que la
raison de B
à A
(4). La raison doublée du côté du polygone circonscrit à un côté du polygone
inscrit sera encore moindre que la raison doublée de B à A. Donc la raison de la surface de la figure
circonscrite à la surface de la figure inscrite est moindre que la raison da
cercle A
à la surface de la sphère ce qui est absurde. En effet, la surface de la figure
circonscrite est plus grande que le cercle A (31), tandis que la
surface de la figure inscrite
est plus petite que la surface de la sphère. Donc la surface d'une sphère n'est
pas plus petite que le cercle A. Mais nous avons démontré qu'elle n'est pas
plus grande. Donc la surface d'une sphère est égale au cercle A
c'est-à-dire à quatre grands cercles.
PROPOSITION XXXVI.
Une sphère
quelconque est quadruple d'un cône qui a une base égale à un grand cercle de
cette sphère et une hauteur égale au rayon de cette même sphère.
Soit une sphère
quelconque; et que AΒΓΔ soit un de ses grands cercles. Que cette sphère ne
soit pas le quadruple du cône dont nous venons de parler ; et supposons, si cela
est possible, qu'elle soit plus grande que le quadruple de ce cône. Soit
Ξ
un
cône qui ait une base quadruple du cercle AΒΓΔ, et une hauteur égale au rayon de la sphère ;
la sphère sera plus grande que le cône Ξ. Nous aurons donc deux quantités inégales, la
sphère et ce cône. Nous pourrons donc prendre deux droites telles que la raison
de la plus grande à la plus petite soit moindre que la raison de la sphère au
cône Ξ (3). Que ces droites soient K, H. Prenons deux autres droites, de manière que
K
surpasse I
de la même quantité, que I
surpasse Θ,
et que Θ
surpasse
H.
Concevons
que l'on ait inscrit dans le cercle AΒΓΔ un polygone dont le nombre des côtés soit
divisible par quatre, et qu'on ait circonscrit à ce même cercle un polygone
semblable au polygone inscrit, comme dans les théorèmes précédents. Que la
raison du côté du polygone circonscrit au côté du polygone inscrit soit moindre
que la raison de
K
à I
(4) ; et que les diamètres AI, BΔ se coupent entre eux à angles
droits. Si le diamètre AΓ
restant immobile, on fait faire une révolution au plan des polygones, on
inscrira une figure dans la sphère et on lui en circonscrira une autre ; et la
raison de la figure circonscrite à la figure inscrite sera triplée de la raison
du côté du polygone qui est circonscrit au cercle
AΒΓΔ
au côté du polygone qui lui est inscrit. Mais la raison du côté du polygone
circonscrit au côté du polygone inscrit est moindre que la raison de K à I ; donc la raison de la figure circonscrite à
la figure inscrite est moindre que la raison triplée de K
à I.
Mais la raison de K
à H
est plus
grande que la raison triplée de K à I ; car cela suit évidemment des lemmes (α).
Donc la raison de la figure circonscrite à la figure inscrite est encore moindre
que la raison de K
à H.
Mais la
raison de K
à H
est
moindre que la raison de la sphère au cône Ξ et par permutation ….. (β)
ce qui ne peut être. En effet, la figure circonscrite est plus grande que la
sphère, et la figure inscrite est plus petite que le cône Ξ, à cause que le cône
Ξ
est quadruple d'un cône qui a une base égale au cercle AΒΓΔ, et une hauteur égale au rayon de la sphère.
Mais la figure inscrite est moindre que le quadruple du cône dont nous venons de
parler (28). Donc la sphère n'est pas plus grande que le quadruple du cône dont
nous venons de parler.

Supposons, si
cela est possible, que la sphère soit plus petite que le quadruple du cône dont
nous avons parlé. Prenons les droites K, H, de manière que la droite K étant plus grande
que
la droite H, la raison de
K
à H
soit moindre que la raison du cône Ξ à la sphère. Soient encore les deux droites
Θ, I,
comme dans la première partie du théorème. Concevons que l’on ait inscrit un
polygone dans le cercle AΒΓΔ
et qu'on lui en ait circonscrit un autre, de manière que la raison du côté du
polygone circonscrit au côté du polygone inscrit soit moindre que la raison de
K
à
I
(4). Que
le reste soit construit de la même manière qu'on l'a fait plus haut. La raison
de la figure solide circonscrite à la figure inscrite sera triplée de la raison
du côté du polygone circonscrit au cercle AΒΓΔ au côté du polygone inscrit dans ce même
cercle. Mais la raison du côté du premier polygone au côté du second polygone
est moindre que la raison de
K
à
I
; donc
la raison de la figure circonscrite à la figure inscrite est moindre que la
raison triplée de
K
à
I
; Mais la raison
de
K
à
H
est plus
grande que la raison triplée de
K
à
I
; donc la
raison de la figure circonscrite à la figure inscrite est moindre que la raison
de
K
à
H.
Mais la raison de
K
à
H
est
moindre que la raison du cône Ξ à la sphère (α), ce qui est impossible. Car la figure inscrite est plus petite
que la sphère, tandis que la figure circonscrite est plus grande que le cône Ξ
(33).
Donc la sphère n'est pas plus petite que le quadruple du cône qui a une base
égale au cercle
AΒΓΔ,
et une hauteur égale au rayon de la sphère. Mais on a démontré que la sphère
n'est pas plus grande ; donc la sphère est quadruple de ce cône.
PROPOSITION XXXVII.
Ces choses étant
démontrées, il est évident que tout cylindre qui a une base égale à un grand
cercle d'une sphère et une hauteur égale au diamètre de cette sphère, est égal à
trois fois
la moitié de cette sphère, et que la surface de ce
cylindre, les bases étant comprises, est aussi égale à trois fois la moitié de
la surface de cette même sphère.
Car le cylindre
dont nous venons de parler est le sextuple d'un cône qui a la même base que ce
cylindre et une hauteur égale au rayon de la sphère. Mais la sphère est le
quadruple de ce cône; il est donc évident que le cylindre est égal à trois fois
la moitié de la sphère.
De plus, puisque
l’on a démontré que la surface d'un cylindre, les bases exceptées, est égale à
un cercle dont le rayon est moyen proportionnel entre le côté du cylindre et le
diamètre de sa base (14), et que le côté du cylindre dont nous venons de parler
est égal au diamètre de sa base, à cause que ce cylindre est circonscrit à une
sphère ; il est évident que cette moyenne proportionnelle est égale au diamètre
de la base. Mais le cercle qui a un rayon égal au diamètre de la base du
cylindre est le quadruple de la base du cylindre, c'est-à-dire le quadruple d'un
grand cercle de la sphère ; donc la surface du cylindre, ses bases exceptées,
est le quadruple d'un grand cercle de la sphère. Donc la surface totale du
cylindre, avec les bases, est le sextuple d'un grand cercle. Mais la surface de
la sphère est le quadruple d'un grand cercle ; donc la surface totale du
cylindre est égale à trois fois la moitié de la surface de la Sphère.
PROPOSITION XXXVIII.
La surface d'une
figure inscrite dans un segment sphérique est égale à un cercle dont le carré du
rayon est égal à la surface comprise sous le côté du polygone inscrit dans le
segment d'un grand cercle, et sous la somme des droites parallèles à
la base du segment, réunie avec la moitié de la base
du segment.
Soit une sphère,
et dans cette sphère un segment qui ait pour base le cercle décrit autour du
diamètre ah. Inscrivons dans ce
segment une figure terminée par des surfaces coniques ainsi que nous l'avons
dit. Que AΗΘ soit
un grand cercle, et AΓΕΘZΔH
un polygone dont les côtés, excepté le côté AH,
soient pairs en nombre. Prenons un cercle
Λ
dont le
carré du rayon soit égal à la surface comprise sous le côté
AΓ
et sous
la somme des droites
EZ,
ΓΔ, réunie avec la moitié de la base,
c'est-à-dire
AK.
Il faut
démontrer que le cercle
Λ
est égal à la surface de la figure
inscrite.
Prenons un
cercle
M
dont le
carré du rayon soit égal à la surface comprise sous le côté EΘ
et sous la moitié de
EZ
; ce cercle sera égal à la surface du cône,
dont la base est le cercle décrit autour du diamètre EZ,
et dont le Sommet est le point Θ (15). Prenons un autre cercle N dont le carré du rayon soit égal à la surface
comprise sous EΓ, et sous la moitié de la somme des droites
EZ,
ΓΔ
(17); ce
cercle sera égal à la surface du cône comprise entre les plans parallèles
conduits par les droites
EZ, ΓΔ.
Prenons
semblablement un autre cercle Ξ dont le carré du rayon soit égal à la surface comprise sous
AΓ
et sous la moitié de la somme des droites
ΓΔ,
AH.
Ce cercle
sera aussi égal à la surface du cône comprise entre les plans parallèles
conduits par les droites AH, ΓΔ.
La somme de ces cercles sera donc égale à la
surface totale de la figure inscrite dans le segment ; et la somme des carrés de
leurs rayons sera égale à la
surface comprise sous un côté AΓ
et sous la somme des droites
EZ,
ΓΔ,
réunie
avec la moitié de la base
AK.
Mais le carré du
rayon Λ
était aussi égal à cette surface ; donc le cercle
Λ
est égal à la
somme des cercles
M, N,
Ξ. Donc le cercle
Λ
est égal à la
surface de la figure inscrite dans le segment.
PROPOSITION XXXIX.
Qu'une sphère
soit coupée par un plan qui ne passe pas par son centre; et que
AEZ
soit un
grand cercle de cette sphère, perpendiculaire sur le plan qui le coupe.
Inscrivons dans le segment AΒΓ un polygone dont les côtés, excepté la base
AB,
soient égaux et pairs en nombre. Si, comme dans les théorèmes
précédents, le diamètre ΓZ
restant immobile, on fait faire une révolution au polygone, les angles
Δ,
E,
A,
B
décriront les
circonférences des cercles, dont les diamètres sont
ΔΕ,
AB
; et les côtés
du polygone décriront des surfaces coniques. De cette manière il sera produit
une figuré solide terminée par des surfaces coniques, ayant pour base le cercle
décrit autour du diamètre AB et
pour sommet le point Γ. Cette figure, ainsi que dans les théorèmes précédents, aura une
surface plus petite que la surface du segment dans lequel cette figure est
comprise, parce que la circonférence du cercle décrit autour du diamètre
AB
est la limite du segment et de la figure
inscrite; que chacune de ces deux surfaces est concave
du même côté, et que l'une est comprise par l'autre (Princ.
4).
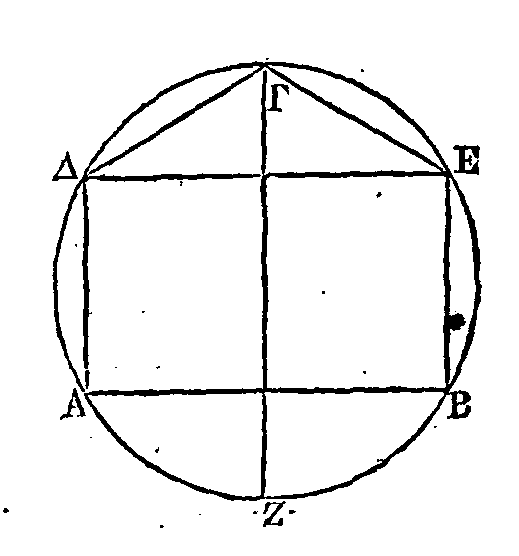
PROPOSITION XL.
La surface de la
figure inscrite dans un segment de sphère est plus petite qu'un cercle dont le
rayon est égal à la droite menée du sommet du segment à la circonférence du
cercle qui est la base du segment.
Soit une sphère
; et que
ABZE
soit un de ses grands cercles. Soit
dans cette sphère un segment qui ait pour -base le cercle décrit autour du
diamètre
AB.
Inscrivons dans ce segment la figure
dont nous venons de parler. Dans le segment du cercle décrivons un polygone, et
faisons le reste comme nous l'avons fait plus haut Menons le diamètre de la
sphère
ΑΘ,
et les droites
ΛE, ΘA.
Soit M un cercle qui ait un rayon égal à la droite
ΑΘ.
Il faut démontrer que le cercle M est plus grand que la surface de la figure inscrite.
En effet, nous
avons démontré que la surface de la figure inscrite est .égale à un cercle dont
le carré du rayon est égal à la surface comprise sous EΘ,
et sous la somme des droites
EZ, ΓΔ, KA
(38). Nous avons
encore démontré que la surface comprise sous EΘ et sous la somme des droites
EZ, ΓΔ, KA
est égale à la surface comprise sous les droites
EA, ΚΘ
(23). Mais la surface comprise sous
EA, ΚΘ,
est plus petite que le carré construit sur
ΑΘ,
parce que la surface comprise sous
ΛΘ,
ΘK
est égale
au carré construit sur ΑΘ. Il est donc évident que le rayon du cercle qui est égal à
la surface de la figure inscrite est plus petit que le rayon du
cercle
M
; d'où il suit que le cercle M
est plus grand que la surface de la figure inscrite.
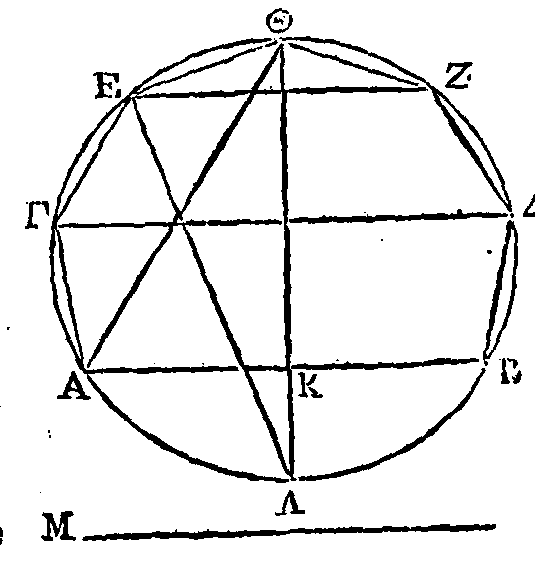
PROPOSITION XLI.
La figure
inscrite dans un segment et terminée par des surfaces coniques, avec le cône qui
a la même base que la figure inscrite, et qui a son sommet au centre de la
sphère, est égale à un cône qui a une base égale à la surface de la figure
inscrite, et une hauteur égale à la perpendiculaire menée du centre de la sphère
sur le côté du polygone.
Soient une
sphère et un grand cercle de cette sphère. Que AΒΓ soit un segment plus petit que le
demi-cercle. Que le point E
soit le centre. Dans le segment AΒΓ
inscrivons, comme dans les théorèmes précédents, un polygone dont les côtés,
excepté le côté AΓ,
soient égaux entre eux. Si
BE
restant immobile, on fait faire une
révolution à la sphère, elle engendrera une figure terminée par des surfaces
coniques. Que le cercle décrit autour des diamètres AΓ
soit la base d'un cône qui ait son sommet au centre de la sphère. Prenons un
cône K,
qui ait une base égale à la surface de la figure inscrite et une hauteur égale
à la perpendiculaire menée du centre
E sur un des côtés du polygone. Il faut
démontrer que le cône K est égal à la figure dont nous venons de parler, réunie au cône
AEΓ.

Sur les cercles
qui ont pour diamètres les droites ΗΘ,
ZA
t
construisons
deux cônes qui aient leurs sommets au point E. Le rhombe solide HBΘE
est égal
à un cône qui a une base égale à la surface du cône HBΘ,
et une hauteur égale à la perpendiculaire menée du point E sur
HB
(19). Le
reste qui est terminé par la surface comprise entre les plans parallèles
conduits par les droites ΗΘ,
ZΛ,
et par les surfaces coniques
ZEΛ,
HEΘ, est égal à un cône qui a une base égale à la surface comprise
entre les plans parallèles conduits par les droites
ΗΘ, ZΛ,
et une hauteur égale à la perpendiculaire menée du point E sur
ZH
(20); et
enfin le reste qui est terminé par la surface comprise entre les plans
parallèles conduits par les droites
ZΛ,
AΓ, et
par les surfaces coniques AEΓ,
ZEΛ
est égal à un
cône qui a une base égale à la surface comprise entre les plans parallèles
conduits par les droites ZΛ,
AΓ
; et une hauteur
égale à la perpendiculaire menée du point E sur
ZA.
Donc la
somme des cônes dont nous venons de parler est égale à la figure inscrite,
réunie au cône
AEΓ.
Mais tous ces
cônes ont une hauteur égale à la perpendiculaire menée du point E
sur un des côtés du polygone, et la somme de leurs bases est égale à la surface
de la figure
AZHBΘΛΓ;
et de
plus le cône
K
a la même
hauteur, et sa base est égale à la surface de la figure inscrite. Donc le cône
K
est égal à la somme des cônes dont nous venons de parler. Mais nous avons
démontré que la somme des cônes dont nous venons de parler est égale à la figure
inscrite, réunie au cône AEΓ.
Donc le cône K
est égal à la figure inscrite, réunie au cône EAΓ.
Il suit
manifestement de là que le cône qui a pour base un cercle dont le rayon est égal
à la droite menée du sommet
du segment à la circonférence du cercle qui est la
base du segment, et une hauteur égale au rayon de la sphère, est plus grand que
la figure inscrite, réunie au cône AEΓ. En effet, le cône dont nous venons de parler
est plus grand qu'un cône égal à la figure inscrite, réunie au cône qui a la
même base
que le segment et dont le sommet est le centre de la
sphère, c'est-à-dire plus grand qu'un cône qui a une base égale à la surface de
la figure inscrite et une hauteur égale à la perpendiculaire menée du centre sur
le côté du polygone; car nous avons démontré que la base du premier est plus
grande que la base du second (50); et la hauteur du premier est plus grande que
la hauteur du second.
PROPOSITION XLII.
Soit une sphère;
que AΒΓ
soit un de ses grands cercles; que la droite AB coupe un segment plus petit que la moitié de ce cercle; que le
point Δ
soit le centre du cercle AΒΓ ; et du centre Δ aux points
A, B
menons les
droites AΔ,
ΔΒ.
Circonscrivons
un polygone au secteur produit par cette construction, et circonscrivons aussi
un cercle à ce polygone. Ce cercle aura
certainement le même centre que
le cercle
AΒΓ.
Si le diamètre
EK
restant immobile, nous faisons faire une révolution au polygone, le cercle
circonscrit décrira la surface d'une sphère ; les angles du polygone décriront
des cercles dont les diamètres sont des droites qui étant parallèles à
AB,
joignent les angles du polygone; les points où les côtés du polygone touchent le
plus petit cercle, décriront dans la petite sphère des cercles dont les
diamètres sont des droites qui étant parallèles à
AB,
joignent les
points de contact ; et les côtés du polygone décriront des surfaces coniques. De
cette manière on circonscrira une figure terminée par des surfaces coniques dont
la base sera le cercle décrit autour du diamètre
ZH.
La
surface de la figure dont nous venons de parler est plus grande que la surface
du petit segment sphérique dont la base est le cercle décrit autour du diamètre
AB.
En effet, menons
les tangentes
AM,
BN
; ces
tangentes décriront une surface conique, et la figure produite par la révolution
du polygone
AMΘEΛNB
aura une surface
plus grande que la surface du segment sphérique dont la base est le cercle
décrit autour du diamètre AB, parce que ces deux surfaces ont pour limite, dans un seul et même
plan, le cercle décrit autour du diamètre
AB,
et que le segment est compris par la figure. Or la surface conique engendrée par
les droites
ZM, HN
est plus grande que la surface conique engendrée par
MA,
NB
; parce
que la droite
ZM
est plus grande
que la droite
MA
comme étant opposée à un angle droit,
et que la droite NH est aussi plus grande que la droite
NB
: mais
lorsque cela arrive, une des surfaces engendrées est plus grande que
l'autre (α),
ainsi que cela a été démontré dans les lemmes. Il est donc évident que la
surface circonscrite est plus grande que la surface du segment de la petite
sphère.
PROPOSITION XLIII.
Il suit
manifestement du théorème qui précède, que la surface de la figure circonscrite
à un secteur sphérique est égale à un cercle dont le carré du rayon est égal à
la surface comprise sous un côté du polygone et sous la somme des droites qui
joignent les angles du polygone, réunie avec la moitié de la base du polygone
dont nous venons de parler.
Car la figure
qui est circonscrite au secteur est inscrite dans le segment de la plus grande
sphère. Cela est évident d'après ce que nous avons dit plus haut (38).
PROPOSITION XLIV.
La surface d'une
figure circonscrite à un segment sphérique est plus grande que le cercle dont le
rayon est égal à la droite menée du sommet du segment à la circonférence du
cercle qui est la base du segment.
Soit une sphère;
que AΔΒΓ
soit
un de ses grands cercles, et le point
E
son
centre. Circonscrivons au secteur
AΔΒ
un
polygone
ΛZK,
et à ce polygone un cercle. Que cette
construction engendre une figure, comme plus haut. Soit aussi un cercle N
dont le carré du rayon soit égal à la surface comprise sous un des côtés du
polygone, et sous la somme des droites qui
joignent les angles, réunie à la moitié de la droite
ΚΛ.
Or, la
surface dont nous venons de parler est égale à la surface comprise sous la
droite MΘ,
et sous la droite
ZH,
qui est la hauteur du segment de la plus grande sphère, ainsi que cela a été
démontré plus haut (23). Donc le carré du rayon du cercle N est égal à la surface comprise sous
MΘ,
HZ.
Mais la droite
HZ
est plus grande que la droite ΔΞ,
qui est la hauteur du petit segment; car si l'on mène la droite KZ,
cette droite sera parallèle à la droite ΔA.
Mais la droite
AB
est aussi
parallèle à la droite
ΚΛ,
et la droite
ZE,
est
commune ; donc le triangle
ZKH
est semblable au
triangle
ΔAΞ.
Mais la droite
ZK
est plus
grande que la droite AΔ; donc la droite ZH
est plus grande que la droite ΔΞ.
De plus,
la droite MΘ est
égale au diamètre ΓΔ.
En effet, joignons les points
E, O
; puisque
la droite
MO est
égale à la droite OZ,
et la droite ΘE
égale à la droite
EZ,
la
droite
EO
est certainement parallèle à la droite
MΘ,
Donc la
droite MΘ
est double de la droite
EO.
Mais la droite ΓΔ
est aussi double de la droite EΘ
; donc la droite MΘ
est égale à la droite ΓΔ.
Mais la surface comprise sous les droites ΓΔ,
ΔΞ
est égale
au carré construit sur la droite
AΔ.
Donc la
surface de la figure
KZΛ
est plus grande
que le cercle dont le rayon est égal à la droite menée du sommet du segment à la
circonférence du cercle qui est la base du segment, c'est-à-dire à la
circonférence du cercle décrit autour du diamètre
AB
; car le
cercle N est égal à la surface de la figure circonscrite au secteur (α).

PROPOSITION XLV.
La figure
circonscrite à un secteur, avec le cône qui a pour base le cercle décrit autour
du diamètre ΚΛ, et pour sommet le centre de la sphère, est égale à un cône qui a
une
base égale à la surface de la figure circonscrite, et
une hauteur égale à la perpendiculaire menée du centre sur un des côtés du
polygone. Il est évident que cette perpendiculaire est égale au rayon de la
sphère.
Car la figure
circonscrite au secteur est en même temps inscrite dans le segment de la grande
sphère, qui a le même centre que la petite. Donc cela est évident d'après ce qui
a été dit plus haut (41).
PROPOSITION XLVI.
Il suit du
théorème précédent, que la figure circonscrite, avec le cône, est plus grande
qu'un cône qui a une base égale à un cercle ayant un rayon égal à la droite
menée du sommet du segment de la petite sphère à la circonférence du cercle qui
est la base de ce segment, et une hauteur égale au rayon de la sphère.
Car le cône qui
sera égal à la figure circonscrite, réunie au cône, aura certainement une base
plus grande que le cercle dont nous venons de parler, tandis qu'il aura une
hauteur égale au rayon de la petite sphère.
PROPOSITION XLVII.
Soient une
sphère et un grand cercle de cette sphère; que le segment AΒΓ soit plus petit que la moitié de ce grand
cercle, et que le point Δ soit le centre de ce cercle. Inscrivons dans le secteur
AΒΓ
un polygone équiangle; circonscrivons à ce même secteur un polygone semblable au
premier, et que les côtés de ces deux polygones soient parallèles.
Circonscrivons un cercle au polygone circonscrit. Si, comme dans les
théorèmes précédents, la droite
ΔΒ
restant
immobile, nous faisons faire une révolution à ces cercles, les côtés des
polygones engendreront deux figures terminées par des surfaces coniques. Il faut
démontrer que la raison de la surface de la figure circonscrite à la surface de
la figure inscrite est doublée de la raison du côté du polygone circonscrit au
côté du polygone inscrit; et que la raison de ces figures réunies au cône est
triplée de la raison de ces mêmes côtés.
Soit
M
un cercle
dont le carré du rayon soit égal à la surface comprise sous le côté du polygone
circonscrit, et sous la somme des droites qui joignent les angles, avec la
moitié de la droite
EZ.
Le cercle
M
sera égal
à la surface de la figure circonscrite. Soit
N
un autre
cercle dont le carré du rayon soit égal à la surface comprise sous le côté du
polygone inscrit, et sous la somme des droites qui joignent les angles, avec la
moitié de la droite AΓ. Ce cercle sera égal à la surface de la figure inscrite. Mais les
surfaces dont nous venons de parler sont
entre elles comme le carré
décrit sur
EK
et le carré
décrit sur ΑΛ
(α). Donc le polygone circonscrit est au
polygone inscrit comme le cercle
M
est au cercle
N.
Il est donc évident que la raison de la surface de la figure circonscrite à la
surface de la figure inscrite est doublée de la raison de EK à
ΑΛ,
c'est-à-dire qu'elle est égale à la raison du polygone circonscrit au polygone
inscrit.
A présent, soit
Ξ
un cône qui ait une base égale au cercle
M,
et une hauteur égale au rayon de la petite sphère; ce cône sera égal à la figure
circonscrite, réunie au cône qui a pour base le
cercle décrit autour du
diamètre EZ
et pour sommet le point Δ
(45). Soit
O un
autre cône qui ait une base égale au cercle N et une hauteur égale à la perpendiculaire menée du point
Δ
sur ΑΛ.
Ce cône
sera égal à la figure inscrite, réunie au cône qui a pour base le cercle décrit
autour du diamètre AΓ, et pour sommet le point Δ, ainsi que cela a été démontré (41). Mais la
droite
EK
est au rayon de la petite sphère comme
la droite ΑΛ
est à la perpendiculaire menée du
centre Δ
sur ΑΛ
; et il
est démontré que
EK
est à
ΑΛ
comme le
rayon du cercle
M
est au rayon du
cercle N (β), et comme le diamètre du premier cercle est au diamètre du second. Donc le
diamètre du cercle qui est la base du cône Ξ est au diamètre du cercle qui est la base du cône O,
comme la hauteur du cône Ξ
est à la hauteur du cône O.
Donc ces cônes sont semblables; donc la raison du cône Ξ
au cône O est triplée de la raison du diamètre de la
base du premier au diamètre de la base du second. Il est donc évident que la
raison de la figure circonscrite, réunie au cône, à la figure inscrite, réunie
au cône, est triplée de la raison
EK
à
ΑΛ.
PROPOSITION XLVIII.
La surface d'un
segment sphérique quelconque plus petit que la moitié de la sphère, est égale à
un cercle qui a pour rayon une droite menée du sommet du segment à la
circonférence du cercle qui est la base du segment.
Soit une sphère
; que AΒΓ
soit un de ses grands cercles. Soit un segment plus petit que la moitié de cette
sphère, qui ait pour
base le cercle décrit autour du diamètre
AΓ,
et perpendiculaire sur le cercle AΒΓ. Prenons un cercle Z dont le rayon soit égal à la droite AB.
Il faut démontrer que la surface du segment AΒΓ est égale à la surface du cercle Z.
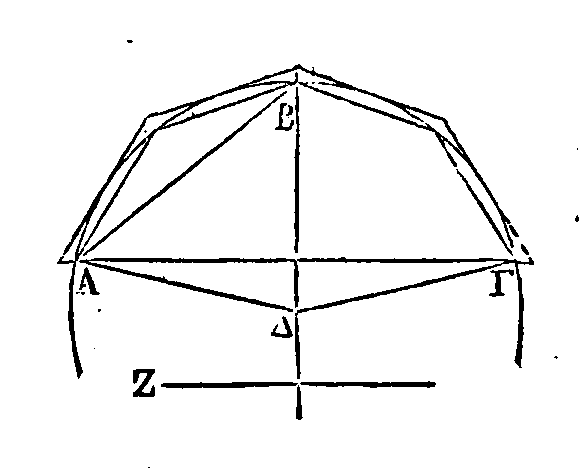
Que la surface
de ce segment ne soit point égale au cercle Z ; et supposons d'abord qu'elle soit plus
grande. Prenons le centre Δ ; du centre Δ menons des droites aux points A, Γ, et prolongeons ces droites. Puisque l'on a
deux quantités
inégales, savoir la surface du segment et le cercle
Z,
inscrivons dans le secteur AΒΓ
un polygone équilatère et équiangle; et circonscrivons-lui un polygone
semblable, de manière que, la raison du polygone circonscrit au polygone inscrit
soit moindre que la raison de la surface du segment au cercle Z (6). Ayant fait faire, comme auparavant, une
révolution au cercle AΒΓ, on aura deux figures terminées par des surfaces coniques, l'une
circonscrite et l'autre inscrite ; et la surface de la figure circonscrite sera
à la surface de la figure inscrite comme le polygone circonscrit est au polygone
inscrit; car chacune de ces raisons est doublée de la raison du côté du polygone
circonscrit au polygone inscrit (47). Mais la raison du polygone circonscrit au
polygone inscrit est moindre que la raison de la surface du segment dont nous
venons de parler au cercle Z (α); et la surface de la figure circonscrite est
plus grande que la surface du segment; donc la surface de la figure inscrite est
plus grande que le cercle Z. Ce qui ne peut être; car on a démontré que
la surface de la figure dont nous venons de parler est moindre que le cercle
Z (40).
Supposons à
présent que le cercle Z soit plus grand que la surface du segment.
Circonscrivons et inscrivons des polygones semblables, de manière que la raison
du polygone circonscrit au polygone inscrit soit moindre que la raison du cercle
z à la surface du
segment …… (β).
Donc la surface du
segment n'est pas plus petite que le
cercle z. Mais on a démontré qu'elle n'est pas plus
grande ; donc elle lui est égale.
PROPOSITION XLIX.
Si le segment
est plus grand que la moitié de la sphère, sa surface sera encore égale à un
cercle dont le rayon est égal à la droite menée du sommet du segment à la
circonférence du cercle qui est la base du segment.

Soient une
sphère et un de ses grands cercles; supposons que le cercle ait été coupé par un
plan perpendiculaire conduit par la droite
AΔ.
Que le segment
BΔ
soit plus
petit que la moitié de la sphère ; que le diamètre
ΒΓ
soit
perpendiculaire sur AΔ;
et des points B, Γ
menons au point A
les droites
BA,
AΓ.
Soit
un cercle E
qui ait
un rayon égal à
AB
; soit aussi un
cercle
Z qui ait
un rayon égal à AΓ;
et soit enfin un cercle H
qui ait un rayon égal à ΓΒ.
Le cercle H
est égal à la somme des deux cercles E, Γ. Mais le cercle
H
est égal à la
surface totale de la sphère, parce que chacune de ces surfaces est quadruple du
cercle décrit autour du diamètre ΒΓ ; et le cercle
E
est égal à la
surface du segment
ABΔ, ainsi que
cela a été démontré pour un segment moindre que la
moitié de la sphère (48); donc le cercle restant Z est égal à la surface du segment AΓΔ ; et ce segment est plus grand que la moitié
de la sphère.
PROPOSITION L.
Un secteur
quelconque d'une sphère est égal à un cône qui a une base égale à la surface du
segment sphérique qui est dans le secteur, et une hauteur égale au rayon de
cette sphère.
Soit une sphère
; que
ABΔ
soit un de ses grands cercles. Que le point
Γ
soit le centre de ce cercle. Soit un cône qui ait pour base un cercle égal à la
surface décrite par l'arc ABΔ
et pour hauteur une droite égale à ΒΓ. Il faut démontrer que le secteur
AΒΓΔ
est égal
au cône dont nous venons de parler.
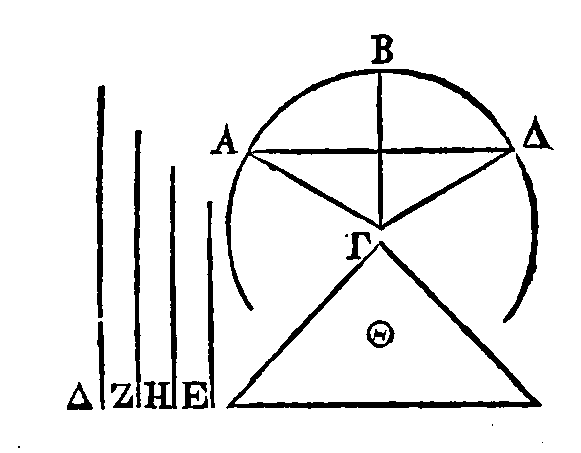
Car si ce
secteur n'est pas égal à ce cône, supposons que ce secteur soit plus grand. Que
le cône dont nous venons de parler soit Θ. Puisque nous avons deux quantités inégales,
le secteur et le cône Θ, cherchons deux droites Δ,
E,
dont la plus grande soit Δ
; que la raison de Δ
à E
soit moindre que la raison du secteur à ce cône (5). Prenons ensuite deux
droites Z,
H,
de manière que
l'excès de Δ sur
Z
soit égal à l'excès de Z
sur H,
et à l'excès de H
sur E.
Dans le plan du cercle, circonscrivons au secteur un polygone équilatère dont le
nombre des angles soit pair, et inscrivons dans ce même secteur un polygone
semblable au premier, de manière que la raison du côté du polygone circonscrit
au côté du polygone inscrit soit moindre que la raison de
Δ
à Z
(6). Ayant fait faire une révolution au cercle ABΔ, comme dans les théorèmes précédents, on aura deux figures
terminées par des surfaces coniques. La raison de la figure circonscrite, avec
le cône qui a son sommet au point Γ, à la figure inscrite, avec ce même cône,
sera triplée de la raison du côté du polygone circonscrit au côté du polygone
inscrit (47). Mais la raison du côté du polygone circonscrit au côté du polygone
inscrit est moindre que la raison de Δ à Z ; donc la raison de la figure solide
circonscrite dont nous venons de parler à la figure inscrite est moindre que la
raison triplée de Δ à Z. Mais la raison de Δ à E est plus grande que la raison triplée de
Δ à Z (α);
donc la raison de la figure solide circonscrite au secteur à la figure inscrite
est moindre que la raison de Δ à
E.
Mais la raison
de Δ
à
E
est
moindre que la raison du secteur solide au cône Θ ; donc la raison de la figure solide qui est
circonscrite au secteur à la figure inscrite est moindre que la raison du
secteur solide au cône Θ, et par permutation …… (β). Mais la figure solide circonscrite est plus
grande que le secteur; donc la figure inscrite au
secteur est plus grande que le cône Θ. Ce qui ne peut être; car on a démontré, dans
les théorèmes précédents, que cette figure est plus grande que ce cône,
c'est-à-dire qu'un cône qui a pour base un cercle dont le rayon est égal à la
droite menée du sommet du segment à la circonférence du cercle qui est la base
du segment, et pour hauteur une droite égale au rayon de la sphère (41). Mais le
cône dont nous venons de parler est le même que le cône Θ,
puisque ce cône a une base égale à la surface du segment, c'est-à-dire au cercle
dont nous avons parlé, et pour hauteur une droite égale au rayon
de la sphère. Donc le
secteur solide n'est pas plus grand que le cône Θ.
Supposons à
présent que le cône Θ
soit plus grand que le secteur solide. Que la raison de la droite Δ à la droite E, dont la droite
Δ
est plus grande, soit moindre que la raison du cône au secteur. Prenons
également deux droites Z,
H,
de manière que
la raison du côté du polygone qui est circonscrit dans le secteur plan et dont
le nombre des angles est pair, au côté du polygone inscrit soit moindre que la
raison de Δ
à Z
; et circonscrivons au secteur solide une figure solide, et inscrivons-lui une
autre figure solide. Nous démontrerons de la même manière que la raison de la
figure qui est circonscrite au secteur solide à la figure inscrite est moindre
que la raison de Δ
à E,
et que la raison du cône Θ
au secteur. Donc la raison du secteur au cône Θ est moindre que la raison de la figure solide inscrite dans le
segment à la figure circonscrite. Mais le secteur est plus grand que la figure
qui lui est inscrite ; donc le cône Θ est plus grand que la figure circonscrite, ce
qui ne peut être. Car on a démontré qu'un tel cône est plus petit que la figure
circonscrite au secteur (44). Donc le secteur est égal au cône Θ.
COMMENTAIRE
SUR LES DΕUX LIVRES DΕ LA SPHÈRE ET DU CYLINDRE.
LIVRE PREMIER.
ARCHIMÈDΕ A DOSITHEE.
(α)
La
section du cône rectangle est une parabole.
Un cône
rectangle est un cône droit dont les côtés, c'est-à-dire les intersections.de sa
surface convexe et du plan conduit par l'axe, forment un angle droit. Si ces
côtés forment un angle aigu, le cône s'appelle cône acutangle, et il s'appelle
cône obtusangle, si ces côtés forment un angle obtus.
Il suit
évidemment de là que, si l'on coupe perpendiculairement un des côtés d'un cône
rectangle par un plan, la section du cône rectangle sera une parabole; puisque
le plan coupant sera parallèle à l'autre côté du cône. La section du cône
acutangle, serait une ellipse, et la section du cône obtusangle, une hyperbole.
C'est ainsi que les anciens Γéomètres, avant Apollonius, considéraient les
sections du cône qui donnent la parabole, l'ellipse et l'hyperbole. Voyez
la note (α)
de la lettre d'Archimède à Dosithée, qui est à la tête du Traité des Conoïdes et
des Sphéroïdes.
Dans Archimède,
la parabole est toujours nommée section du cône rectangle; l'ellipse, section du
cône acutangle, et l'hyperbole, section du cône obtusangle. Pour éviter ces
circonlocutions, et à l'exemple d'Apollonius, j'emploierai désormais les mots
parabole, ellipse et hyperbole.
(β)
Ce passage d'Archimède est très obscur ; j'ai suivi la leçon de
M. Delambre. Voici la lettre qu'il me fit l'honneur de
m'écrire au sujet de ce passage :
Paris, ce 14
décembre 1806.
« A peine
étiez-vous sorti, Monsieur, qu'il m'est venu un doute sur le sens que nous
donnons au passage obscur de la lettre à Dosithée. Voici comme on pourrait
l'entendre : « Ces propositions étaient renfermées dans la nature de ces
figures, quoiqu'aucun géomètre avant nous ne les eût aperçues ; mais pour se
convaincre de leur vérité, il suffira de comparer mes théorèmes aux
démonstrations que j'ai données sur ces figures. La même chose est arrivée à
Eudoxe. Ses théorèmes sur la pyramide et le cône étaient aussi dans la nature,
et n'avoient été reconnus par aucun géomètre avant lui. Je laisse le jugement
sur mes découvertes à ceux qui seront en état de les examiner. Plût à Dieu que
Conoix vécût encore, il aurait été bien en état d'en dire son avis ».
» Ainsi il ne
s'agit pas dans la comparaison des figures aux théorèmes, de juger si ces
théorèmes sont nouveaux, mais s'ils sont vrais. De ce qu'ils n'ont été vus par
personne, il ne s'ensuit pas qu'on doive les regarder comme douteux ; la même
chose est arrivée à Eudoxe, qui a trouve sur la pyramide et le cône des
théorèmes nouveaux et qui pourtant ont été admis; que les géomètres examinent
donc mes propositions et les jugent. Voilà je pense le vrai sens de la lettre.
Les mots
ut quivis facile intelliget
ne sont pas exactement dans le grec ;
ut y manque, et cet ut change le sens. Au lieu de ut le
grec porte et. Ces propositions sont dans la nature, et pour
les comprendre il suffit de comparer les théorèmes aux figures et aux
démonstrations. J'avoue pourtant que l'expression grecque me paraît
trop peu développée, καὶ νοήσειν ὅς,
et comprendra celui qui. Remarquons que ce mot νοήσειν,
comprendra, se mettra dans la tête, ne serait pas le
mot propre s'il s'agissait de reconnaître seulement la nouveauté du théorème.
Pour décider si un théorème est nouveau, l’intelligence ne fait rien ; il
suffit d'avoir des yeux et de savoir lire ; mais pour s'assurer de la vérité
d'un théorème, il faut être en, état de suivre une démonstration,
et souvent celles d'Archimède ont besoin qu'on ait
quelque intelligence et quelque force de tête.
Je serais tenté
de croire le passage altéré, et qu'il a dû être originairement à peu près ainsi
: Καὶ νοήσειν ὃς ἂν τούτων τῶν θεωρηάτων ταῖς ἀκοδείξεσι ἀντιπαραβάλῃ αὐτὰ τὰ σχήματα. Je
mets θεθεωρημένων,
au lien de σχημάτων,
et σχήματα
au lieu de θεθεωρημένα.
C'est une simple transposition, alors le sens est clair, et alors Archimède dira
: Pour comprendre mes propositions, en sentir l'exactitude, il suffit
de comparer la figure à la démonstration des théorèmes, c'est-à-dire
de suivre sur la figure la démonstration des théorèmes. Cependant on peut
soutenir la leçon de Torelli, en entendant littéralement le mot démonstration.
Aujourd'hui par ce mot nous entendons une preuve claire et irrésistible;
mais dans le fait il ne signifie que l'action d'exposer, de montrer.
Pour sentir la vérité de ces propositions, il suffit de les comparer à ce
que montrent ces figures; ou l'inspection seule de la figure
mettra dans tout son jour la vérité des théorèmes.
» Au reste, ce
passage est tellement tronqué dans un manuscrit n° 2360, qu'il est impossible
d'en rien tirer ; heureusement il est en lui-même très peu important. Voyez
les variantes édit. de Torelli.
» J'ai l'honneur
d’être, etc. »
AXIOMES.
(α)
Archimède appelle lignes courbes, non seulement les lignes qui ne sont ni
droites, ni composées de lignes droites, mais encore les lignes brisées et les
lignes mixtilignes.
D'après le
premier axiome, un arc de cercle est une courbe, qui est toute entière du même
côté de la droite qui joint ses extrémités. Si une courbe était composée d'une
demi-circonférence de cercle et d'un rayon qui joindrait une de ses extrémités,
cette courbe n'aurait aucune de ses parties de l'autre côté de la droite qui
joindrait ses extrémités, quand même cette droite serait prolongée: alors
seulement une partie de la courbe serait sur le prolongement de la droite qui
joindrait ses extrémités. Ce qui n'arriverait point, si l'arc était plus grand
que la demi-circonférence.
(β)
Cet axiome, qui a beaucoup embarrassé les commentateurs, est cependant de la
plus grande clarté. Il suffit pour le comprendre de faire attention qu'une ligne
courbe, quelle qu'elle soit, a deux côtés aussi bien qu'une ligne droite.
Soit la courbe
AΡIΣK.
Les lettres ΒΓΔΕΗΘ
sont placées d'un des côtés de cette courbe, et les lettres AMNΞOΠ
sont placées de
l'autre
côté; Si l'on s'imaginait que le point
A
se mût dans la courbe AΡIΣK
jusqu'à ce qu'il fût arrivé au point K, on pourrait dire que les lettres
ΒΓΔΕΗΘ sont à la droite de la courbe, et que
les lettres AMNΞOΠ
sont à sa
gauche.
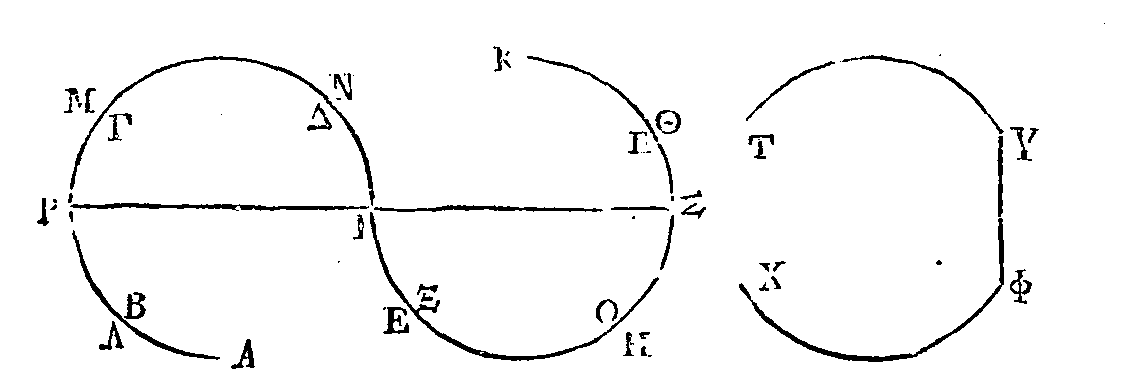
Cela posé,
joignons les deux points ΡΣ de cette courbe par la droite ΡΖ. Il est évident que la droite
ΡΣ
sera de différents côtés de cette courbe; la portion ΡΙ sera d'un côté, et la portion
ΙΣ
sera de l'autre; ou si l'on veut, la première portion sera à la droite de la
courbe, et la seconde à sa gauche. Donc cette courbe n'est pas concave du même
côté, puisque la droite ΡΣ,
qui joint deux de ses points, est de différents côtés de cette courbe.
Une
circonférence de cercle, une portion de sa circonférence, une ellipse, une
portion de l'ellipse, une parabole et une hyperbole, sont au contraire des
courbes concaves du même côté, parce que les droites qui joindraient deux points
quelconques de ces courbes, seraient nécessairement des mêmes côtés de ces
courbes.
Soit la ligne
courbe TΥΦΧ, qui est composée de deux arcs ΤΥ, ΧΦ appartenant à un même cercle, et d'une droite
ΥΦ
menée du point Υ
au point Φ
; cette courbe sera encore concave du même côté,
parce que les droites qui joignent deux
points quelconques de cette courbe tombent toutes du même côté, excepté la
droite menée du point Υ au point
Φ, qui tombe sur cette ligne courbe.
Il sera facile
d'appliquer au quatrième axiome ce que je viens de dire du second.
PRINCIPES.
(α)
Ce principe n'est point, comme beaucoup de Γéomètres l'ont cru, une définition
de la ligne droite : c'est simplement l'énoncé d'une de ses propriétés.
(β)
Il est des personnes qui pensent que l'injure des temps a fait périr une partie
des Éléments d'Euclide, qui regardent le cylindre, le cône et la sphère : ces
personnes sont dans l'erreur. Tous les théorèmes qu'on regrette de ne pas
trouver dans Euclide, ne peuvent être démontrés qu'à l'aide des principes 2 et
4 : or Euclide n'a jamais fait usage de ces deux principes ; on ne doit donc pas
être surpris de ne pas trouver dans ses Éléments les théorèmes, dont nous venons
de parler, et qu'Archimède démontre dans ce traité.
Plusieurs
Γéomètres ont tenté, mais en vain, de démontrer ces deux principes, lorsque les
lignes courbes et les surfaces courbes ne sont point des assemblages de lignes
droites et de surfaces planes. Si ces deux principes pouvaient être démontrés,
ils l'auraient été par Archimède. Je dis dans la Préface la raison pourquoi il
est impossible de démontrer ces deux principes.
(γ)
Ce principe est une conséquence de la première proposition du
dixième livre d'Euclide.
PROPOSITION III.
(α)
Mais ΓΑ
est à
ΑΘ
comme HE
est à
ZH
; donc la raison de EH
à ZH
est moindre que la raison de ΓΑ
à ΓΒ.
PROPOSITION IV.
(α)
Si l'angle THΓ était
égal à l'angle
ΛΚM, il est évident que la raison de MK à
ΛΚ serait la même que la raison de ΓH
à HT.
Si nous supposons ensuite que l'angle THΓ diminue, la droite ΓH diminuera aussi, et la raison de
ΓH
à HT
deviendra plus petite; donc alors la raison de MK à ΛΚ sera plus grande que la raison de
ΓH
à HT.
(β)
Donc la raison du côté du polygone circonscrit au côté du polygone
inscrit est moindre que la raison de A à B.
PROPOSITION VI.
(α)
Cette proposition est démontrée dans les Éléments d'Euclide. Voyez la
proposition ii, livre
xii.
PROPOSITION VIL
(α)
Appelons P le polygone circonscrit, et p le polygone inscrit. Puisque P :
p <A + B : A, et que P < A, on aura à plus forte raison P : A < A + B :
A. Donc par soustraction P — A : A < B : A. Donc P — A, c'est-à-dire la somme
des segments placés autour du cercle est plus petite que la surface B.
PROPOSITION VIII.
(α) Lorsqu'Archimède parle d'une surface comprise sous deux droites, il entend
toujours parler d'un rectangle, dont une de ces droites est la base et dont
l'autre est la hauteur.
PROPOSITION XIV.
(α)
La raison en est simple; car puisque ΓΔ : H :: H : EZ, il est
évident qu’on aura ΓΔ/2
— : H
:: H
: 2 x EZ,
ou bien
TΔ
: H
:: H
: PZ.
(β)
La raison de la surface du prisme à la surface du cylindre est
moindre que la raison du polygone inscrit dans le cercle
B
au cercle
B.
Voilà ce qui est sous-entendu, et ce qu'Archimède sous-entend toujours dans la
suite, lorsqu'il a un raisonnement semblable à faire. Pour que le lecteur
puisse, dans ce cas, suppléer ce qui manque, il faut qu'il se souvienne que,
lorsqu'on a quatre quantités, et que la raison de la première à la seconde est
moindre que la raison de la troisième à la quatrième, la raison de la première à
la troisième est encore moindre que la raison de la seconde à la quatrième.
(γ)
Parce que ces triangles sont entre eux comme les droites TΔ, ΡΖ, et que nous avons vu dans la première partie
de la démonstration que
TΔ
est à ΡΖ
comme TΔ²
est à
H².
(d)
La raison du polygone qui est circonscrit au cercle B à ce même cercle, est moindre que la raison
du polygone inscrit dans le cercle B à la surface du cylindre.
PROPOSITION XV.
(α)
Donc, par permutation, la raison de la surface de la pyramide qui est
circonscrite au cône à la surface du cône est moindre que la raison du polygone
inscrit dans le cercle B
au cercle B.
(β)
En effet, la raison du rayon du cercle A
au côté du cône est la même que la raison de la perpendiculaire menée du centre
du
cercle A
sur le côté du polygone à la parallèle au côté du cône menée du milieu du côté
du polygone et terminée à l'axe du cône. Mais la perpendiculaire menée du sommet
du cône sur le côté du polygone est plus longue que la parallèle dont nous
venons de parler; donc la raison du rayon du cercle A au côté du polygone est
plus grande que la raison de la perpendiculaire menée du centre sur le côté du
polygone à la perpendiculaire menée du sommet du cône sur le côté de ce même
polygone.
(γ)
Donc, par permutation, la raison du polygone circonscrit au cercle
B
est
moindre que la raison de la surface de la pyramide inscrite à la surface du
cône.
PROPOSITION XVI.
(α)
Donc le cercle Δ
est au cercle A
comme le carré de E
est au carré de B.
Mais à cause que E
est moyen proportionnel entre Γ et B, la droite Γ est à la droite
B
comme le carré
de E
est au carré de B ; donc le cercle
Δ
est au cercle A
comme Γ
est à
B
; mais le
cercle
Δ
est égal à la surface du cône.
LEMME.
(α)
Le parallélogramme BH pourrait n'être pas un rectangle, mais alors
par les surfaces comprises sous BA, AH; sous BΔ, ΔΖ,
etc.
il faudrait entendre des rectangles dont les droites AH, ΔΖ seraient les bases et les droites BA,
BΔ
les hauteurs.
LEMMES.
(α)
Les cylindres qui ont la même base sont entre eux comme leurs hauteurs ; donc
les cônes qui ont la même base sont aussi entre eux comme leurs hauteurs : ce
qui est l'inverse du premier lemme. Je pense qu'il y a une omission, et que le
lemme doit
être posé ainsi : Lorsque des cônes et des cylindres
ont les mêmes bases et les mêmes hauteurs, les cônes sont entre eux comme les
cylindres.
(β)
Voyez le douzième livre d'Euclide.
PROPOSITION XIX.
(α)
Car puisque les cônes BAΓ, BΔΓ
ont la même base, la droite AE est à la droite
ΔΕ
comme le cône
BAΓ
est au cône BΔΓ
(17, lemm. 1). Donc, par addition, la droite
AΔ
est à la droite ΔΕ
comme le rhombe AΒΓΔ
est au cône BΔΓ.
PROPOSITION XXIV.
(α)
Archimède veut que le nombre des côtés soit divisible par quatre, afin que deux
diamètres perpendiculaires l'un sur l'autre aient leurs extrémités aux angles du
polygone inscrit.
(β)
Perpendiculaires l'un sur l'autre.
PROPOSITION XXV.
(α)
En effet, puisque les cercles sont proportionnels aux carrés

de leurs rayons,
le carré du rayon du cercle Ξ est au cercle Ξ,
comme le carré du rayon du cercle
O
est au cercle O,
comme le carré du rayon du cercle Π est au cercle Π, comme le carré du rayon du cercle
Ρ est au cercle Ρ, comme le carré du rayon du cercle Σ
est au cercle Σ,
comme le carré du rayon du cercle T est au cercle T, comme le carré du rayon du cercle
Υ est au cercle Υ. Donc le carré du rayon du cercle
Ξ
est au cercle Ξ
comme la somme des carrés des rayons des cercles O, Π, Ρ, Σ , T, Υ est à la somme des cercles O,
Π, Ρ, Σ , T, Υ.
Mais le carré du rayon des cercles Ξ
est égal à la somme des carrés des rayons des cercles O,
Π, Ρ, Σ , T, Υ
; donc le cercle Ξ
est égal à la somme des cercles O, Π, Ρ, Σ , T, Υ.
PROPOSITION XXXI.
(α)
Car les deux triangles ΚΘZ, ΣΧΖ étant semblables, la droite ΘZ
est à ΧΖ
comme ΘK
est à ΧΣ.
Mais ΘZ
est double de ΧΖ
; donc ΘK
est double du rayon ΧΣ
; donc ΘK
est égal au diamètre du cercle
AΒΓΔ.
PROPOSITION XXXIV.
(β)
Car puisque les droites qui joignent les angles du polygone circonscrit, et les
droites qui joignent les angles du polygone inscrit sont entre elles comme les
côtés des polygones, la somme des premières droites est à la somme des secondes
droites comme ΕΛ
est à AK.
Donc les surfaces comprises sous les sommes des droites qui joignent les angles
des polygones et les côtés des polygones sont des figures semblables.
PROPOSITION XXXV.
(α)
Donc, par permutation, la raison de la surface de la figure circonscrite à la
surface de la sphère est moindre que la raison de surface de la figure inscrite
au cercle A.
PROPOSITION XXXVI.
(α)
Soient a, a — d, a — 2d, a — 5d,
quatre termes d'une progression arithmétique décroissante, et que ces quatre
termes soient ou tous positifs ou tous négatifs. Je dis que la raison du premier
terme au quatrième est plus grande que la raison triplée du premier au second,
c'est-à-dire, que
a /(a-3d) > a3/(a-d)3
J'élève a
— d au cube; je fais disparaître les dénominateurs. La réduction étant
faite, la première quantité devient 3 ad2, et la
seconde d 3. Mais 3 ad2 est plus
grand que d 3, puisque a est plus grand que d,
donc
a /(a-3d) > a3/(a-d)3
Donc la raison
du premier terme d'une progression arithmétique décroissante au quatrième terme
est plus grande que la raison triplée du premier terme au second.
(β)
Mais la raison de K à H est moindre que la raison de la sphère au cône Ξ
; donc la raison de la figure circonscrite à la figure inscrite est encore
moindre que la raison de la sphère au cône. Donc, par permutation, la raison de
la figure circonscrite à la sphère est encore moindre que la raison de la figure
inscrite au cône.
(γ)
Donc la raison de la figure circonscrite à la figure inscrite est
encore moindre que la raison du cône Ξ à la sphère. Donc, par permutation, la raison
de la figure circonscrite au cône Ξ est moindre que la raison de la figure
inscrite à la sphère.
PROPOSITION XLII.
(α)
En effet, la surface engendrée par la droite MZ est égale à un cercle dont le rayon est moyen proportionnel entre
la droite
ZM et la
moitié de la somme des droites ZH, MN (17), et la surface décrite par la droite MA
est égale à un cercle dont le rayon est moyen proportionnel entre la droite
MA
et la
moitié de la somme des droites
ΔΒ,
MN. Mais ZM est plus grand que
MA, et
ZH
plus grand que AB
; donc la première moyenne proportionnelle est plus grande que la seconde. Donc
la surface décrite par ZM
est plus grande que la surface décrite par
MA.
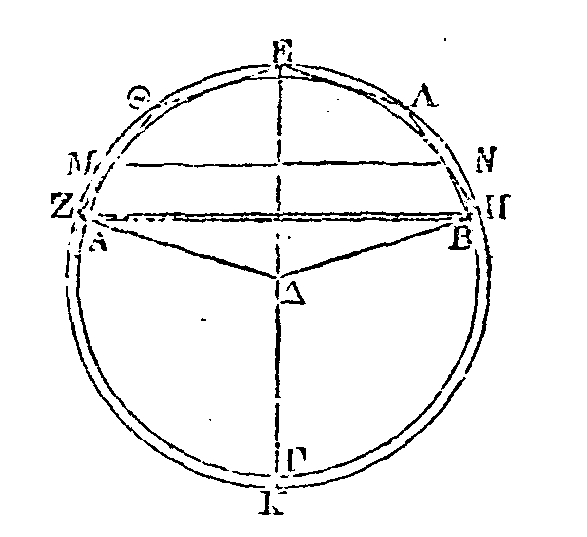
PROPOSITION XLIV.
(α)
Ce qui précède, à partir de ces mots mais la surface, etc. est un peu
obscur, voici ce qu'on pourrait mettre à sa place. Donc le carré du rayon du
cercle N,
qui est égal à la surface comprise sous MΘ, HZ est encore égal à la surface comprise sous
ΓΔ,
HZ. Mais
le carré de la droite
ΔA
est égal à la surface comprise sous
ΓΔ,
ΔΞ,
et nous venons de démontrer que HZ
est plus grand que ΔΞ
; donc la surface comprise sous ΓΔ,
HZ est plus grande que la surface comprise sous
ΓΔ, ΔΞ.
Donc
le carré du rayon du cercle N, qui est égal à la première surface, est plus grand que le carré
de la droite
ΔA, qui est égal à la seconde surface. Donc le rayon du
cercle N
est plus grand que la droite
ΔA.
Donc le cercle N,
et par conséquent la surface de la figure circonscrite au segment sphérique
KZΛ,
est plus grande que le cercle décrit autour du diamètre ΔA.

PROPOSITION XLVII.
(α)
En
effet, les droites qui joignent les angles du polygone circonscrit, et les
droites qui joignent les angles du polygone inscrit sont proportionnelles aux
côtés des polygones ; donc la somme des droites qui joignent les angles du
polygone circonscrit est à la somme des droites qui joignent les angles du
polygone inscrit, comme EK
est à ΑΛ.
Donc la surface comprise sous
EK
et sous la somme des droites qui
joignent les angles du polygone circonscrit, conjointement avec la moitié de
EZ,
est semblable à la surface comprise sous ΑΛ et sous la somme des droites qui joignent les angles du polygone
inscrit, conjointement avec la moitié de AΓ. Donc la première figure est à la seconde
comme le carré de EK est au carré de ΑΛ. Mais le carré du rayon du cercle M est égal à la première figure, et le carré du
rayon du cercle N est égal à la seconde ; donc le premier carré est au second
comme le carré de EK est au carré de ΑΛ. Donc le cercle M, c'est-à-dire la surface de la figure circonscrite est au cercle
N,
c'est-à-dire à la surface de la figure inscrite comme le carré de EK est au carré de
ΑΛ.
(β)
Puisque dans la première partie de cette démonstration, l'on a vu
que le carré de EK est au carré de AΛ comme le cercle M est au cercle N, il est évident que EK est à AΛ comme le rayon du cercle M
est au rayon du cercle N.
PROPOSITION XLVIII.
(α)
Donc la raison de la surface de la figure circonscrite à la surface
de la figure inscrite est moindre que la raison de la
surface du segment au cercle Z. Donc, par permutation, la raison de la surface de la figure
circonscrite à la surface du segment est moindre que la raison de la surface de
la figure inscrite au cercle Z.
(β)
Puisque le polygone circonscrit est au polygone inscrit comme la surface de la
figure circonscrite est à la surface de la figure inscrite, la raison de la
surface de la figure circonscrite à la surface de la figure inscrite est moindre
que la raison du cercle Z
à la surface du segment. Donc, par permutation, la surface de la figure
circonscrite au cercle Z
est moindre que la raison de la surface de la figure inscrite à la surface du
segment. Mais la surface de la figure circonscrite est plus grande que le cercle
Z
(44) ; donc la surface de la figure inscrite est plus grande que la surface du
segment; ce qui ne peut être.
PROPOSITION L.
(α)
Voyez la note (α)
de la proposition xxxvi.
(β)
Donc la raison de la figure solide circonscrite au secteur est
moindre que la raison de la figure inscrite au cône Θ.
|