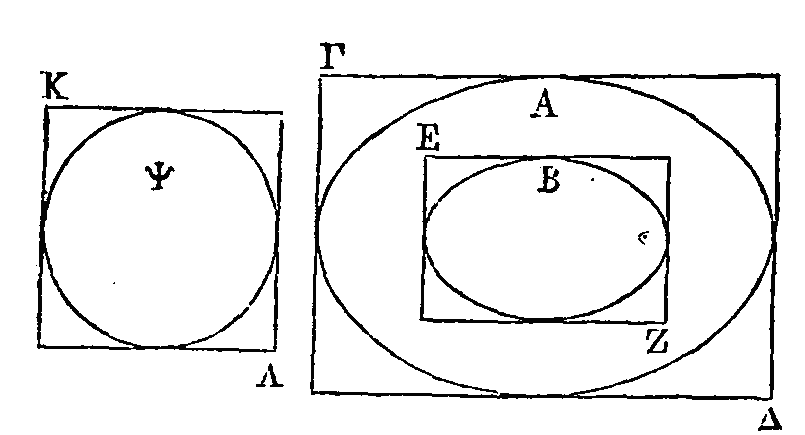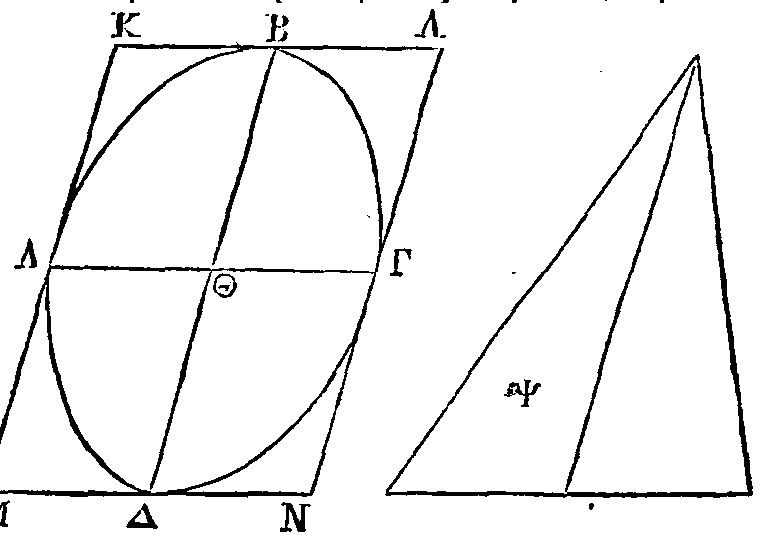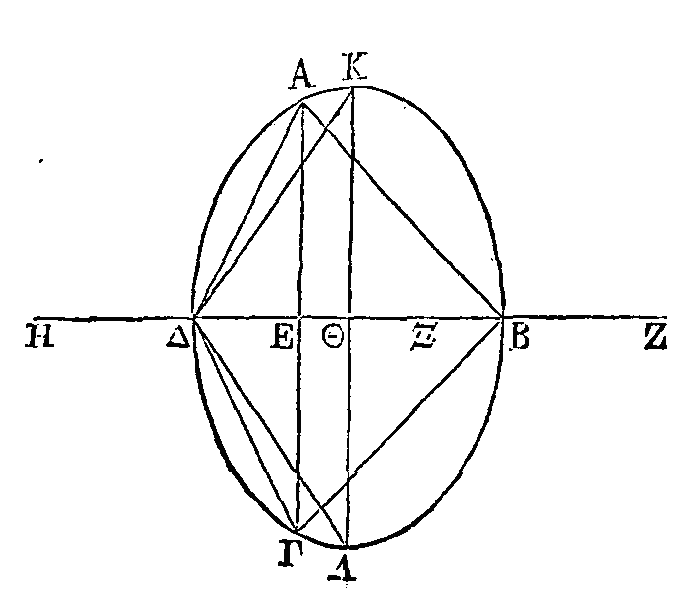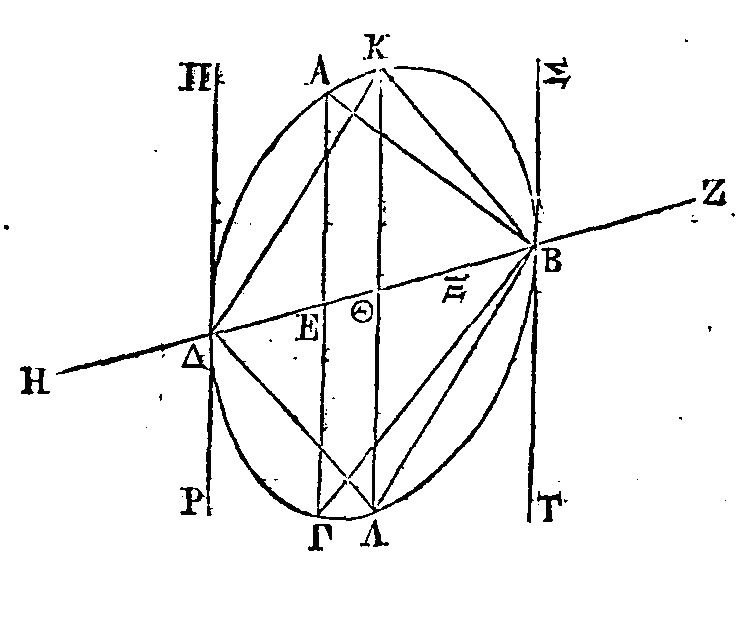ARCHIMEDE

DES CONOÏDES ET DES SPHÉROÏDES.

ARCHIMÈDE A DOSITHEE, SALUT.

Je t'envoie dans ce livre, non seulement les démonstrations du reste des théorèmes qui ne se trouvaient pas parmi celles qui t'ont déjà été adressées, mais encore les démonstrations d'autres théorèmes que j'ai découverts dans la suite et qui ont tenu longtemps mon esprit incertain, parce que après les avoir examinés à plusieurs reprises, ils me paraissaient présenter beaucoup de difficultés. Voilà pourquoi ces théorèmes n'avaient pas été donnés avec les autres. Mais les ayant de nouveau considérés avec plus de soin, j’ai trouvé les solutions qui m'avaient échappé.

Ce qui restait des premiers théorèmes regardait le conoïde parabolique. Quant à ceux qui ont été découverts en dernier lieu, ils regardent le conoïde hyperbolique et les sphéroïdes.

Parmi les sphéroïdes, j'appelle les uns allongés et les autres aplatis.

Relativement au conoïde parabolique, on posait ce qui suit:

Si une parabole tourne autour de son diamètre immobile jusqu'à ce qu'elle soit revenue au même endroit d'où elle avait commencé à se mouvoir, la figure comprise par la parabole s'appelle conoïde parabolique ; le diamètre immobile s'appelle l'axe du conoïde; et le point où l'axe rencontre la surface du conoïde s'appelle le sommet du conoïde.

Si un plan touche un conoïde parabolique, et si l'on conduit un autre plan qui soit parallèle au plan tangent et qui retranche un certain segment du conoïde, la partie du plan coupant comprise par la section du conoïde, s'appelle la base du segment qui est coupé; le point où l'autre plan touche le conoïde s'appelle le sommet, et la partie de la droite qui est menée du sommet du segment parallèlement à l'axe du conoïde et qui est comprise dans le conoïde, s'appelle l'axe du segment.

On proposait d'examiner ce qui suit :

Pourquoi lorsque des segments d'un conoïde parabolique sont coupés par un plan perpendiculaire sur l'axe, le segment retranché est-il égal à trois fois la moitié d'un cône qui a la même base et le même axe que ce segment?

Pourquoi lorsqu'un conoïde parabolique est coupé par deux plans conduits d'une manière quelconque, les segments retranchés sont-ils entre eux en raison doublée de leurs axes?

Relativement au conoïde hyperbolique, on posait ce qui suit :

Une hyperbole, son diamètre et ses asymptotes étant placés dans un même plan, si le plan dans lequel sont placées les lignes dont nous venons de parler tourne autour du diamètre immobile, jusqu'à ce qu'il soit revenu au même endroit d'où il avait commencé à se mouvoir, il est évident que les asymptotes comprendront un cône droit dont le sommet sera le point où les asymptotes se rencontrent, et dont l'axe sera le diamètre immobile. La figure comprise par l'hyperbole s'appelle conoïde hyperbolique; le diamètre immobile s'appelle l'axe du conoïde ; et le point de la surface du conoïde rencontré par l'axe s'appelle le sommet ; le cône compris par les asymptotes s'appelle le cône contenant le conoïde; la droite comprise entre le sommet du conoïde et le sommet du cône s'appelle l'ajoutée à l'axe (α).

Si un plan touche un conoïde hyperbolique, et si l'on conduit un autre plan qui soit parallèle au premier et qui retranche un certain segment du conoïde, la partie du plan coupant comprise par la section du conoïde s'appelle la basé du segment ; le point où un des plans touche le conoïde s'appelle le sommet du segment ; et la droite qui est comprise dans le segment et qui fait partie de celle qui est menée par le sommet du conoïde et par le sommet du cône qui contient le conoïde s'appelle l'axe du segment ; et la droite qui est comprise entre les sommets dont nous venons de parler s'appelle l'ajoutée à l'axe.

Tous les conoïdes paraboliques sont semblables ; et parmi les conoïdes hyperboliques, ceux dont les cônes contenants sont semblables s'appellent semblables (β).

On propose d'examiner ce qui suit :

Pourquoi lorsqu'un conoïde hyperbolique est coupé par un plan perpendiculaire sur l'axe, le segment retranché est-il au cône qui a la même base et le même axe que le segment comme une droite composée de l'axe du segment et du triple de la droite ajoutée à l'axe est à une droite composée de l'axe du segment et du double de la droite ajoutée à l'axe?

Pourquoi lorsqu'un conoïde hyperbolique est coupé par un plan non perpendiculaire sur l'axe, le segment retranché est-il à la figure qui a la même base et le même axe que le segment, et qui est un segment de cône comme une droite composée de l'axe du segment et du triple de la droite ajoutée à l'axe est à une droite composée de l'axe du segment et du double de la droite ajoutée à l'axe?

Relativement aux sphéroïdes, nous posons ce qui suit:

Si une ellipse tourne autour de son grand diamètre immobile jusqu'à ce qu'elle soit revenue dans le même endroit d'où elle avait commencé à se mouvoir, la figure produite par l'ellipse s'appelle sphéroïde allongé. Si l'ellipse tourne autour du petit diamètre immobile jusqu'à ce qu'elle soit revenue au même endroit d'où elle avait commencé à se mouvoir, la figure qui est décrite par l'ellipse s'appelle sphéroïde aplati ; et le diamètre immobile s'appelle l'axe de ces deux sphéroïdes ; le point de la surface du sphéroïde rencontré par l'axe s'appelle le sommet ; le milieu de l'axe s'appelle le centre ; et la droite perpendiculaire sur le milieu de l'axe s'appelle le diamètre.

Si des plans parallèles touchent un de ces sphéroïdes sans le couper, et si un autre plan parallèle aux plans tangents coupe le sphéroïde, la partie du plan coupant comprise dans les sphéroïdes s'appelle la base des segments; les points où les plans parallèles touchent le sphéroïde s'appellent les sommets; et enfin les droites qui sont comprises dans les segments et qui font partie de la droite qui joint leurs sommets s'appellent les axes des segments.

On démontrera que les plans qui touchent un sphéroïde ne touchent sa surface qu'en un seul point, et que la droite qui joint les points de contacts passe par le centre du sphéroïde.

On appelle sphéroïdes semblables ceux dont les axes sont proportionnels aux diamètres.

Parmi les segments de sphéroïdes et de conoïdes, on appelle semblables ceux qui, étant retranchés de figures semblables, ont des bases semblables, et dont les axes soit qu'ils soient perpendiculaires sur les plans des bases, soit qu'ils fassent des angles égaux avec les diamètres homologues des bases ont entre eux la même raison que les diamètres homologues de leurs bases.

On propose d'examiner ce qui suit, relativement aux sphéroïdes :

Pourquoi lorsqu'un de ces sphéroïdes est coupé par un plan conduit par son centre et perpendiculaire sur l'axe, chacun des segments produits par cette section est-il double du cône qui a la même base et le même axe que le segment?

Pourquoi lorsqu'un de ces sphéroïdes est coupé par un plan perpendiculaire sur l'axe, mais non mené par le centre, le, plus grand des segments produits par cette section est-il au cône qui a la même base et le même axe que ce segment comme une droite composée de la moitié de l'axe du sphéroïde et de l'axe du petit segment est à l'axe du petit segment?

Pourquoi le petit segment est-il au cône qui a la même base et le même axe que ce segment comme une droite composée du demi-axe du sphéroïde et de l'axe du grand segment est à l'axe du grand segment?

Pourquoi lorsqu'un de ces sphéroïdes est coupé par un plan mené par son centre et non perpendiculaire sur l'axe, chacun des segments produits par cette section est-il double de la figure qui a la même base et le même axe que le segment? Cette figure est un segment de cône.

Pourquoi lorsqu'un de ces sphéroïdes est coupé par un plan qui n'est point mené par le centre, ni perpendiculaire sur l'axe, le plus grand des segments produits par cette section est-il à la figure qui a la même base et le même axe que le segment comme une droite composée de la moitié de celle qui joint les sommets des segments et de l’axe du petit segment est à l'axe du petit segment?

Pourquoi enfin le petit segment est-il à la figure qui a la même base et le même axe que le segment comme une droite composée de la moitié de celle qui joint les sommets des segments et de la moitié de l’axe du grand segment est à l'axe du grand segment? Cette figure est aussi un segment de cône.

Les théorèmes dont nous venons de parler étant démontrés, à l'aide de ces théorèmes on trouve non-seulement plusieurs théorèmes, mais plusieurs problèmes. Tels sont, par exemple, les théorèmes suivants :

Les sphéroïdes semblables, et les segments semblables des sphéroïdes et des conoïdes sont entre eux en raison triplée de leurs axes.

Les carrés construits sur les diamètres des sphéroïdes égaux sont réciproquement proportionnels à leurs axes, et les sphéroïdes sont égaux entre eux lorsque les carrés construits sur leurs diamètres sont réciproquement proportionnels aux axes.

Tel est aussi le problème suivant :

Un segment de sphéroïde ou de conoïde étant donné, en retrancher un segment par un plan parallèle à un autre plan donné de manière que le segment produit par cette section soit égal à un cône, ou à un cylindre, ou à une sphère donnée.

Je vais d'abord exposer les théorèmes et tout ce qui est nécessaire pour démontrer les propositions dont je viens de parler, et j'écrirai ensuite les démonstrations de ces propositions. Sois heureux.

*********************

Si un cône est coupé par un plan qui rencontre tous ses côtés, la section sera ou un cercle ou une ellipse. Si la section est un cercle, il est évident; que le segment retranché du côté du sommet sera un cône. Si la section est une ellipse, la figure retranchée du côté du sommet sera appelée un segment de cône. La base du segment sera le plan compris par l'ellipse. Son sommet sera le point qui est le sommet du cône, et son axe sera la ligne droite menée du sommet du cône au centre de l'ellipse.

Si un cylindre est coupé par deux plans parallèles qui rencontrent tous les côtés du cylindre, les sections seront ou des cercles ou des ellipses égales et semblables entre elles. Si les sections sont des cercles, il est évident que la figure comprise entre les plans parallèles est un cylindre. Si les sections sont des ellipses, la figure comprise entre les plans parallèles sera appelée un segment de cylindre. La base du segment sera l'un ou l'autre des plans compris dans les ellipses, son axe sera la droite qui joint les centres des ellipses, et qui fait partie de l'axe du cône.

PROPOSITION I.

Si l'on a un certain nombre de quantités inégales qui se surpassent également et dont l'excès soit égal a la plus petite, et si l'on a d'autres quantités en nombre égal dont chacune soit égale à la plus grande des premières, la somme des quantités égales sera plus petite que le double de la somme des quantités qui se surpassent également ; et si l'on retranche la plus grande des quantités inégales, la somme des quantités égales sera plus grande que le double de la somme des quantités inégales restantes.

Cela est évident (α).

PROPOSITION II.

Si un certain nombre de quantités sont proportionnelles deux à deux à d'autres quantités semblablement arrangées et en nombre égal; si les premières, ou seulement quelques-unes d'entre elles sont comparées avec certaines autres quantités sous des raisons quelconques ; et si les secondes quantités sont aussi comparées avec certaines autres quantités correspondantes sous les mêmes raisons, la somme des premières quantités sera à la somme des quantités avec lesquelles elles sont comparées comme la somme des dernières est à la somme des quantités avec lesquelles elles sont aussi comparées (α).

Soient certaines quantités A, B, Γ, Δ, E, Z. Que ces quantités soient proportionnelles deux à deux à d'autres quantités H, Θ, I, K, Λ, M, en nombre égal ; de manière que A soit à B comme H est à Θ, que B soit à Γ comme Θ est à I, et ainsi de suite. Que les quantités A, B, Γ, Δ, E, Z, soient comparées avec certaines autres quantités N, Ξ, O, Π, Ρ, Σ correspondantes sous certaines raisons ; et que les quantités H, Θ, I, K, Λ, M soient comparées avec certaines autres quantités correspondantes T, Υ, Φ, Χ, Ψ, Ω sous les mêmes raisons, de manière que A soit à N comme H est à T, et que B soit à Ξ comme Θ est à Υ, et ainsi de suite. Il faut démontrer que la somme des quantités A, B, Γ, Δ, E, Z est à la somme des quantités N, Ξ, O, Π, Ρ, Σ comme la somme des quantités H, Θ, I, K, Λ, M est à la somme des quantités T, Υ, Φ, Χ, Ψ, Ω.

Car puisque N est à A comme T est à H ; que A est à B comme H est à Θ ; et qu'enfin B est à Ξ comme Θ est à Υ, il s'ensuit que N est à Ξ comme T est à Υ. Pareillement Ξ sera à O comme Υ est à Φ, et ainsi de suite. Puisque la somme des quantités A, B, Γ, Δ, E, Z est à A comme la somme des quantités H, Θ, I, K, Λ, M est à H ; que A est à N comme H est à T, et qu'enfin la quantité N est à la somme des quantités N, Ξ, O, Π, Ρ, Σ comme la quantité T à la somme des quantités T, Υ, Φ, C, Ψ, Ω ; il est évident que la somme des quantités A, B, Γ, Δ, E, Z est à la somme des quantités N, Ξ, O, Π, Ρ, Σ comme la somme des quantités H, Θ, I, K, Λ, M est à la somme des quantités T, Υ, Φ, C, Ψ, Ω. Si parmi les quantités A, B, Γ, Δ, E, Z, les quantités A, B, Γ, Δ, E, seulement sont comparées avec les quantités N, Ξ, O, Π, Ρ, la quantité Z n'étant point comparée avec une autre quantité, et si parmi les quantités H, Θ, I, K, Λ, M les quantités H, Θ, I, K, Λ sont comparées avec les quantités correspondantes T, Υ, Φ, Χ, Ψ, la quantité M n'étant point comparée avec une autre quantité, il est encore évident que la somme des quantités A, B, Γ, Δ, E, Z est à la somme des quantités N, Ξ, O, Π, Ρ comme la somme des quantités H, Θ, I, K, Λ, M est à la somme des quantités T, Υ, Φ, Χ, Ψ. (β)

PROPOSITION III.

Si l'on a un certain nombre de lignes égales entre elles ; si l'on applique à chacune d'elles une surface dont la partie excédente soit un carré. Si les côtés des carrés se surpassent également et si leur excès est égal au côté du plus petit côté carré; si de plus, on a d'autres surfaces en même nombre que les premières et égales chacune à la plus grande de celles-ci, la raison de la somme des surfaces égales à la somme des surfaces inégales sera moindre que la raison d'une droite composée du côté du plus grand carré et d'une des lignes égales à une droite composée du tiers du côté du plus grand carré et de la moitié d'une des lignes égales : et la raison de la somme des surfaces égales à la somme des surfaces inégales, la plus grande exceptée, sera plus grande que cette même raison (α).

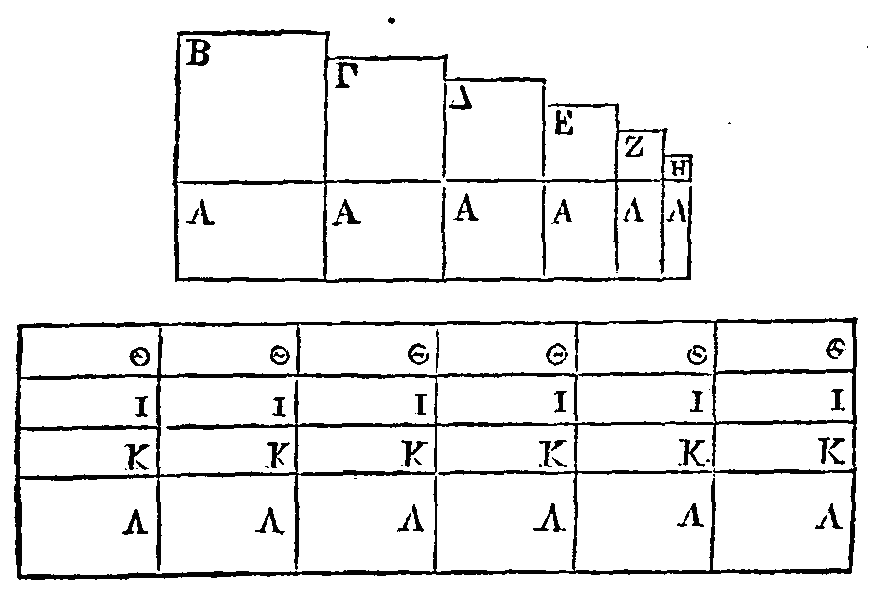
Soit un certain nombre de lignes égales désignées par A ; qu'à chacune d'elles soit appliquée une surface dont la partie excédente soit un carré. Que les côtés B, Γ, Δ, E, Z, H de ces carrés se surpassent également entre eux ; que leur excès soit égal au côté du plus petit carré; que B soit le plus grand côté et H le plus petit. Soient de plus d'autres surfaces dans chacune desquelles se trouvent les lettres ΘIKΛ ; que ces surfaces soient en même nombre que les premières, que chacune d'elles soit égale à la plus grande, c'est-à-dire à celle qui est appliquée sur AB. Que la ligne ΘI soit égale à A et la ligne KΛ égale à B ; que chacune des lignes ΘI soit double de I et que chacune des lignes KΛ soit triple de K. Il faut démontrer que la raison de la somme des surfaces dans lesquelles se trouvent les lettres ΘIKΛ à la somme des surfaces AB, AΓ, AΔ, AE, AZ, AH est moindre que la raison de la ligne ΘIKΛ à la ligne IK ; et que la raison de la somme des surfaces égales à la somme des surfaces inégales, la plus grande exceptée, est plus grande que cette même raison.

En effet, les surfaces où se trouve la lettre A se surpassent également entre elles, et leur excès est égal à la plus petite; car les surfaces appliquées sur les droites A et les largeurs de ces surfaces se surpassent également; de plus les surfaces où se trouvent les lettres ΘI sont en même nombre que ces surfaces inégales, et chacune d'elles est égale à la plus grande de celles-ci. Donc la somme des surfaces où se trouvent les lettres ΘI sera plus petite que le double de la somme des surfaces où se trouve la lettre A ; et si l'on retranche la plus grande des surfaces où se trouve la lettre A, la somme des surfaces où se trouvent les lettres ΘI sera plus grande que la somme, des surfaces restantes où se trouve la lettre A (1). Donc la somme des surfaces où se trouve la lettre I est plus petite que la somme des surfaces où se trouve la lettre A, et plus grande que la somme de ces surfaces, si l'on en retranche la plus grande. On a de plus certaines lignes B, Γ, Δ, E, Z, H qui se surpassent également et dont l'excès est égal à la plus petite, et l'on a aussi d'autres lignes où se trouvent les lettres KΛ qui sont en même nombre que les premières, et dont chacune est égale à la plus grande de celles-ci. Donc la somme des carrés décrits sur les droites qui sont chacune égales à la plus grande, est plus petite que le triple de la somme des carrés décrits sur les droites qui se surpassent également, et si l'on retranche le carré décrit sur la plus grande ligne des droites inégales, la somme des carrés décrits sur les droites qui sont égales chacune à la plus grande des droites inégales, sera plus grande que le triple des carrés restants, ainsi que cela est démontré dans le livre des Hélices (prop. 10, cor.) (β). Donc la somme des surfaces où se trouve la lettre K est plus petite que la somme des surfaces où se trouvent les lettres B, Γ, Δ, E, Z, H et plus grande que la somme des surfaces où se trouvent les lettres Γ, Δ, E, Z, H. Donc la somme des surfaces où se trouvent les lettres IK est plus petite que la somme des surfaces où se trouvent les lettres AB, AΓ, AΔ, AE, AZ, AH et plus grande que la somme des surfaces où se trouvent les lettres AΓ, AΔ, AE, AZ, AH. Il est donc évident que la raison de la somme des surfaces dans lesquelles sont les lettres ΘI, KΛ à la somme des surfaces dans lesquelles sont les lettres AB, AΓ, AΔ, AE, AZ, AH est moindre que la raison de la ligne ΘΛ à la ligne IK; et que si l’on retranche la surface où se trouvent les lettres AB, la première raison sera plus grande que la seconde (γ).

Si des droites menées du même point sont tangentes à une section quelconque d'un cône, et si d'autres droites parallèles à ces tangentes se coupent mutuellement dans la section du cône, les surfaces comprises sous les segments de ces droites seront entre elles comme les carrés des tangentes. La surface comprise sous les segments de l'une des droites correspond au quarré de la tangente parallèle à cette droite. Cela est démontré dans les Eléments (δ).

PROPOSITION IV.

Si d'une même parabole, on retranche deux segments quelconques qui aient des diamètres égaux, ces segments seront égaux entre eux, ainsi que les triangles qui leur sont inscrits et qui ont la même base et la même hauteur que les segments. J'appelle diamètre d'un segment quelconque une droite qui coupe en deux parties égales toutes les parallèles à la base.

Que ABΓ soit une parabole ; qu'on retranche de cette parabole les deux segments AΔE, ΘBΓ. Que ΔZ soit le diamètre du segment AΔE et BH celui du segment ΘBΓ ; que les diamètres AZ, BH soient égaux entre eux. Il faut démontrer que les segments AΔE, ΘBΓ sont égaux entre eux, ainsi que les triangles qui leur sont inscrits de la manière que nous l'avons dit.

D'abord, que la droite ΘΓ qui retranche un des segments soit perpendiculaire sur le diamètre de la parabole. Que la droite M soit le paramètre (α), et du point A conduisons la droite AK perpendiculaire sur ΔZ. Puisque la droite ΔZ est le diamètre du segment, la droite AE est coupée en deux parties égales au point Z, et cette même droite ΔZ est parallèle au diamètre de la parabole. La droite ΔZ coupe donc en deux parties égales toutes les parallèles à la droite AE (β). Que le carré de AZ soit au carré de AK comme N est à M. Les carrés des ordonnées parallèles à AE seront égaux aux surfaces comprises sous la droite N et sous les abscisses ; ce qui est démontré dans les éléments des sections coniques (γ). Le carré de AZ est donc égal à la surface comprise sous N et ΔZ. Mais le carré de ΘH est égal à la surface comprise sous la droite M et sous la droite BH, parce que ΘH est perpendiculaire sur l'axe (δ), donc le carré de AZ est au carré de ΘH comme N est à M ; parce que les droites ΔZ, BH sont supposées égales. Mais le carré de AZ est au carré de AK comme N est à M ; donc les droites ΘH, AK sont égales. Mais les droites BH, ΔZ sont aussi égales entre elles ; donc la surface comprise sous ΘH, BH est égale à la surface comprise sous AK, ΔZ ; donc le triangle ΘHB est égal au triangle ΔAZ; donc leurs doubles sont aussi égaux. Mais le segment AΔE est égal à quatre fois le tiers du triangle AΔE et le segment ΘBΓ égal à quatre fois le tiers du triangle ΘBΓ (Quadr. de la Parabole, prop. 24); il est donc évident que non seulement les segments, mais encore les triangles inscrits dans les segments sont égaux entre eux. Si aucune des droites qui retranchent les segments n'est perpendiculaire sur le diamètre, on prendra sur le diamètre de la parabole une droite égale au diamètre d'un des segments, et l’on mènera par l'extrémité de cette droite une perpendiculaire sur le diamètre de la parabole. Ce nouveau segment sera égal à chacun des deux autres segments. Donc ce qui avait été proposé est évident.

PROPOSITION V.

La surface comprise dans l'ellipse est au cercle décrit autour du grand diamètre de l'ellipse comme le petit diamètre est au grand, c'est-à-dire, au diamètre du cercle.

Soit l'ellipse ABΓΔ dont le grand diamètre est la droite AΓ et le petit la droite BΔ. Décrivons un cercle autour de AΓ comme diamètre. Il faut démontrer que la surface comprise dans l'ellipse est à ce cercle comme BΔ est à ΓA, c'est-à-dire à EZ.

Que le cercle Ψ soit au cercle AEΓZ comme BΔ est à EZ. Je dis que le cercle Ψ est égal à la surface comprise dans l'ellipse. Car si le cercle Ψ n'est pas égal à la surface comprise dans l'ellipse, supposons d'abord qu'il soit plus grand, si cela est possible. On peut inscrire dans le cercle Ψ un polygone dont le nombre des angles soit pair et qui soit plus grand que la surface comprise dans l'ellipse ABΓΔ. Supposons qu'il soit inscrit. Inscrivons dans le cercle AEΓZ un polygone semblable à celui qui est inscrit dans le cercle Ψ. Menons des angles de ce polygone des perpendiculaires sur le diamètre AΓ, et joignons par des droites les points où ces perpendiculaires rencontrent l'ellipse ; nous aurons un certain polygone inscrit dans l'ellipse qui sera au polygone inscrit dans le cercle AEΓZ comme BΔ est à EZ. Car les perpendiculaires EΘ, KΛ étant coupées proportionnellement aux points M, B, il est évident que le trapèze ΛE sera au trapèze ΘM comme ΘE est à BΘ (α). Par la même raison, les autres trapèzes placés dans le cercle sont aux autres trapèzes placés dans l'ellipse chacun à chacun comme EΘ est à BΘ. Mais les triangles placés dans le cercle vers les points A, Γ sont aussi aux triangles placés dans l'ellipse vers ces mêmes points chacun à chacun comme EΘ sera à BΘ. Donc le polygone entier inscrit dans le cercle sera au polygone entier inscrit dans l'ellipse comme EZ est à BΔ. Mais le polygone inscrit dans le cercle AEΓZ est au polygone inscrit dans le cercle Ψ comme EZ est à BΔ, parce que ces cercles sont entre eux comme ces polygones. Donc le polygone inscrit dans le cercle Ψ est égal au polygone inscrit dans l'ellipse : ce qui ne peut être, car on avait supposé le polygone inscrit dans le cercle Ψ plus grand que la surface comprise dans l'ellipse.

Supposons enfin que le cercle Ψ soit plus petit. On peut inscrire dans l'ellipse un polygone dont le nombre des côtés soit pair et qui soit plus grand que le cercle Ψ (β). Que ce polygone soit inscrit. Prolongeons jusqu'à la circonférence du cercle les perpendiculaires menées des angles du polygone sur le diamètre AΓ. On aura encore un certain polygone inscrit dans le cercle AEΓZ qui sera au polygone inscrit dans l'ellipse comme EZ est à BΔ. Inscrivons dans le cercle Ψ un polygone semblable à celui qui est inscrit dans le cercle AEΓZ. Nous démontrerons que le polygone inscrit dans le cercle Ψ est égal au polygone inscrit dans l'ellipse. Ce qui est impossible. Donc le cercle Ψ n'est pas plus petit que l'ellipse. Il est donc évident que la surface comprise dans l'ellipse est au cercle AEΓZ comme BΔ est à EZ.

PROPOSITION VI.

La surface comprise dans l'ellipse est à un cercle quelconque comme la surface comprise sous les deux diamètres de l'ellipse est au carré du diamètre du cercle.

Que la surface comprise dans l'ellipse soit celle où se trouve la lettre Χ. Que les diamètres de l'ellipse soient les droites AΓ, BΔ et que AΓ soit le plus grand. Que le cercle soit celui où se trouve la lettre Ψ, et que son diamètre soit la droite EZ. Il faut démontrer que la surface Χ est au cercle Ψ comme la surface comprise sous AΓ, BΔ est au carré de EZ.

Décrivons un cercle autour de AΓ comme diamètre. La surface Χ sera au cercle dont le diamètre est la droite Ar comme la surface comprise sous AΓ, BΔ est au carré de AΓ ; car on a démontré que l'ellipse est au cercle comme BΔ est à AΓ (5). Mais le cercle qui a pour diamètre AΓ est au cercle qui a pour diamètre EZ comme le carré de AΓ est au carré de EZ (α); il est donc évident que la surface Χ est au cercle Ψ comme la surface comprise sous AΓ, BΔ est au carré de EZ.

PROPOSITION VII.

Les surfaces comprises dans les ellipses sont entre elles comme les surfaces comprises sous leurs diamètres.

Que les surfaces comprises dans les ellipses soient celles où se trouvent les lettres A, B. Que la surface ΓΔ soit celle qui est comprise sous les diamètres de l'ellipse qui comprend la surface A et que la surface EZ soit celle qui est comprise sous les diamètres de l'autre ellipse. Il faut démontrer que la surface A est à la surface B comme ΓΔ est à EZ.

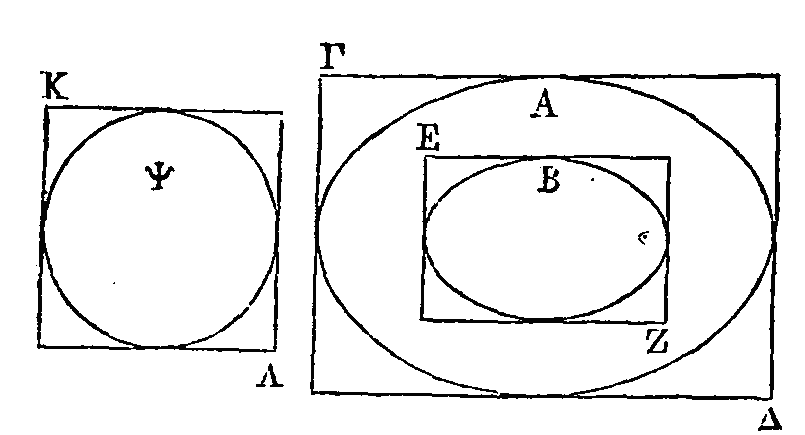
Prenons le cercle où se trouve la lettre Ψ. Que le carré construit sur son diamètre soit KΛ. La surface A sera au cercle Ψ comme ΓΔ est à KΛ, et le cercle Ψ sera à la surface B comme KΛ est à EZ (α). Il est donc évident que la surface A est à la surface B comme ΓΔ est à EZ.

Il suit évidemment de là que les surfaces contenues dans des ellipses semblables sont entre elles comme les carrés des diamètres homologues.

PROPOSITION VIII.

Etant données une ellipse et une ligne élevée du centre de cette ellipse perpendiculairement sur son plan, il est possible de trouver un cône qui ait pour sommet l'extrémité de cette perpendiculaire et dans la surface duquel se trouve l'ellipse donnée.

Soient données une ellipse et une ligne élevée du centre de l’ellipse perpendiculairement sur son plan. Faisons passer un plan par cette perpendiculaire et par le petit diamètre. Que le petit diamètre soit la droite AB. Que le centre de l'ellipse soit le point Δ ; que la perpendiculaire élevée du centre de l'ellipse soit la droite ΓΔ et que son extrémité soit le point Γ. Supposons que l'ellipse donnée ait été décrite autour de AB comme diamètre dans un plan perpendiculaire sur ΓΔ. Il faut trouver un cône qui ait pour sommet le point Γ et dans la surface duquel se trouve l'ellipse donnée.

Du point Γ aux points A, B, conduisons deux droites et que ces droites soient prolongées. Du point A, conduisons la droite AZ, de manière que la surface comprise sous AE, EZ soit au carré de EΓ comme le carré de la moitié du grand diamètre est au carré de ΔΓ ; ce qui peut se faire, parce que la raison de la surface comprise sous AE, EZ au carré de EΓ est plus grande que la raison de la surface comprise sous AΔ, ΔB au carré de ΔΓ (α). Par la droite AZ faisons passer un plan perpendiculaire sur le plan dans lequel se trouvent les droites ΓA, AZ. Décrivons dans ce plan un cercle autour de AZ comme diamètre, et que ce cercle soit la base d'un cône qui ait pour sommet le point Γ. On démontrera que l'ellipse donnée se trouve dans la surface de ce cône.

Car si l'ellipse ne se trouve pas dans la surface de ce cône, il faut qu'il y ait quelque point dans l'ellipse qui ne soit pas dans la surface de ce cône. Supposons qu'on ait pris dans l'ellipse un point quelconque Θ qui ne soit pas dans la surface du cône; et du point Θ, conduisons ΘK perpendiculaire sur AB. Cette droite sera perpendiculaire sur le plan ΓAZ. Du point Γ au point K conduisons une droite et prolongeons-la jusqu'à ce qu'elle rencontre AZ en un point Λ, et ensuite du point Λ et dans le cercle décrit autour de AZ élevons sur AZ la perpendiculaire ΛM. Supposons que le point M soit dans la circonférence de ce même cercle ; et par le point Λ et le point E, conduisons les droites ΞO, ΠΡ parallèles à AB.

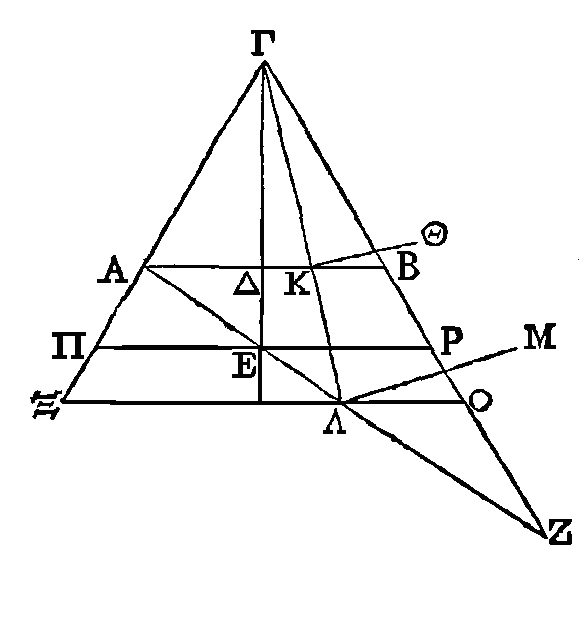
Puisque la surface comprise sous AE, EZ est au quarré de EΓ comme le carré de la moitié du grand diamètre est au carré de ΔΓ, et que le carré de EΓ est à la surface comprise sous EΠ, EΡ comme le carré de ΔΓ est à la surface comprise sous AΔ, ΔB, la surface comprise sous AE, EZ sera à la surface comprise sous ΠE, EΡ comme le carré de la moitié du grand diamètre est à la surface comprise sous AΔ, BΔ (β). Mais la surface comprise sous AE, EZ est à la surface comprise sous EΠ, EΡ comme la surface comprise sous AΛ, ΛZ est à la surface comprise sous ΛΞ, ΛO (γ) ; et le carré de la moitié du grand diamètre est à la surface comprise sous AΔ, ΔB comme le carré de ΘK est à la surface comprise sous AK, KB (δ). Donc la surface comprise sous AΛ, ΛZ est à la surface comprise sous ΞΛ, ΛO comme le carré de ΘK est à la surface comprise sous AK, KB.

Mais la surface comprise sous ΞΛ, ΛO est au carré de ΓΔ comme la surface comprise sous AK, KB est au carré de ΓK (ε). Donc la surface comprise sous AΛ, ΛZ est au carré de ΓΛ comme le carré de ΘK est au carré de KΓ. Mais le carré de ΛM est égal à la surface comprise sous AΛ, ΛZ, car on a mené la droite ΛM perpendiculaire dans le demi-cercle décrit autour de AZ. Donc le carré de ΛM est au carré de ΛΓ comme le carré de ΘK est au carré de KΓ. Donc les points Γ, Θ, M sont dans une même droite. Mais la droite ΓM est dans la surface du cône ; il est donc évident que le point Θ est dans la surface du cône. Mais on avait supposé qu'il n'y était pas. Il n'est donc aucun point de l'ellipse qui ne soit dans la surface du cône dont nous avons parlé. Donc l'ellipse est toute entière dans la surface de ce cône.

PROPOSITION IX.

Etant données une ellipse et une oblique élevée de son centre dans le plan qui passe par un de ses diamètres et qui est perpendiculaire sur le plan de l'ellipse, il est possible de trouver un cône qui ait pour sommet l'extrémité de cette oblique et dans la surface duquel se trouve l'ellipse donnée.

Que la droite BA soit un des diamètres de l'ellipse ; que le centre soit le point Δ, et que l'oblique élevée du centre, ainsi qu'il a été dit, soit ΔΓ. Supposons que l'on ait décrit l'ellipse donnée autour de AB comme centre, dans un plan perpendiculaire sur celui où se trouvent les droites AB, ΓΔ. Il faut trouver un cône qui ait son sommet au point Γ, et dans la surface duquel se trouve l'ellipse donnée.

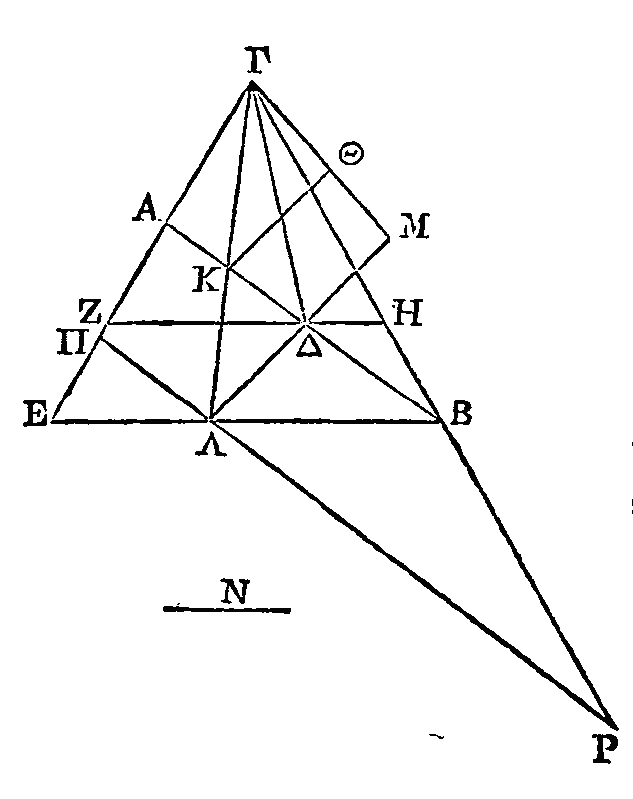
Les droites AΓ, ΓB ne sont pas égales, car la droite ΓΔ n'est pas perpendiculaire sur le plan dans lequel se trouve l'ellipse. Que la droite EΓ soit égale à la droite ΓB, et que la droite N soit égale à la moitié de l'autre diamètre qui est le diamètre conjugué de AB et par le point Δ menons la droite ZH parallèle à EB. Par la droite EB faisons passer un plan perpendiculaire sur celui où se trouvent les droites AΓ, ΓB ; et autour de EB comme diamètre décrivons un cercle ou une ellipse (α). Décrivons un cercle, si le carré de N est égal à la surface comprise sous ZΔ, ΔH (β). Si le contraire arrive, décrivons une ellipse de manière que le carré de son autre diamètre soit au carré de EB comme le carré de N est à la surface comprise sous ZΔ, ΔH (γ). Prenons ensuite un cône dont le sommet soit le point Γ et dans la surface duquel se trouvent le cercle ou l'ellipse décrits autour de EB comme diamètre; ce qui est possible, parce que la droite menée du point Γ sur le milieu de EB est perpendiculaire sur le plan conduit par la droite EB. L'ellipse décrite autour du diamètre AB se trouvera aussi dans la surface de ce cône ; car si cela n'est point, il y aura quelque point dans l'ellipse qui ne sera pas dans la surface du cône. Supposons donc qu'on ait pris un point quelconque Θ dans l'ellipse qui ne soit pas dans la surface du cône; et par ce point Θ conduisons la droite KΘ perpendiculaire sur AB ; menons la droite ΓK, et prolongeons-la de manière qu'elle rencontre EB au point Λ. Par le point Λ et dans le plan perpendiculaire qui passe par EB, menons une droite ΛM perpendiculaire sur EB ; supposons que le point M soit dans la surface du cône et par le point Λ menons ΠΡ parallèle à AB. Le carré de N sera à la surface comprise sous ZΔ, ΔH comme le carré de ΛM est à la surface comprise sous EΛ, ΛB (δ). Mais la surface comprise sous ZΔ, ΔH est à la surface comprise sous AΔ, ΔB comme la surface comprise sous EΛ, ΛB est à la surface comprise sous ΠΛ, ΛΠ (ε). Donc le carré de N est à la surface comprise sous AΔ, ΔB comme le carré de ΛM est à la surface comprise sous HΛ, ΛΠ. Mais le carré de N est à la surface comprise sous AΔ, ΔB comme le carré de ΘK est à la surface comprise sous AK, KB ; parce que dans une même ellipse on a mené des perpendiculaires sur le diamètre AB. Donc la raison du carré ΛM à la surface comprise sous ΠΛ, ΛΠ est la même que la raison du carré de ΘK à la surface comprise sous AK, KB. Mais la raison de la surface comprise sous ΠΛ, ΛΠ au carré de ΛΓ est la même que la raison de la surface comprise sous AK, KB au carré de KΓ ; donc la raison du carré de ΛM au carré de ΛΓ est la même que la raison du carré de ΘK au carré de KΓ. Donc les points Γ, Θ, M sont en ligne droite. Mais la droite ΓM est dans la surface du cône, donc le point Θ est aussi dans la surface, du cône. Mais on avait supposé qu'il n'y était pas ; donc ce qu'il fallait démontrer est évident.

PROPOSITION X.

Étant données une ellipse et une oblique élevées de son centre dans un plan qui passe par un de ses diamètres et qui est perpendiculaire sur le plan de l'ellipse, on peut trouver un cylindre dont l'axe soit sur cette oblique et dans la surface duquel se trouve l'ellipse donnée.

Que BΔ soit le diamètre conjugué de l'ellipse ; que le point Δ en soit le centre et que ΓΔ soit la droite élevée du centre ainsi qu'il a été dit. Supposons qu'on ait décrit l'ellipse donnée autour de AB comme diamètre, dans un plan perpendiculaire sur le plan dans lequel sont les droites AB, ΓΔ. Il faut trouver un cylindre dont l'axe soit sur la droite ΓΔ et dans la surface duquel se trouve l'ellipse donnée.

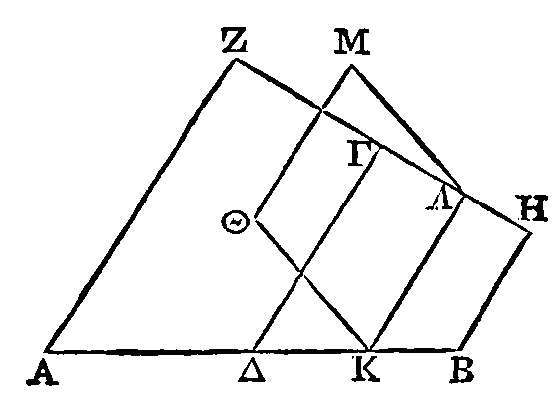
Des points A, B, menons les droites AZ, BH parallèles à ΓΔ. L'autre diamètre de l'ellipse sera ou égal à l'intervalle des droites AZ, BH, ou plus grand, ou plus petit. Qu'il soit d'abord égal à la droite ZH menée perpendiculairement sur ΓΔ. Par la droite ZH, conduisons un plan perpendiculaire sur ΓΔ, et dans ce plan décrivons un cercle autour de ZH comme diamètre, et que ce cercle soit la base d'un cylindre qui ait pour axe la droite ΓΔ. L'ellipse donnée sera dans la surface de ce cylindre. Car si elle n'y est pas, il y aura quelque point dans cette ellipse qui ne sera point dans la surface du cylindre. Supposons qu'on ait pris un point quelconque Θ dans l'ellipse qui ne soit pas dans la surface du cylindre. Du point Θ, menons la droite ΘK perpendiculaire sur AB. Cette droite sera perpendiculaire sur le plan dans lequel se trouvent les droites AB, ΓΔ. Du point K menons la droite KΛ parallèle à ΓΔ, et du point Λ et dans le plan du cercle décrit autour de ZH comme diamètre, élevons la droite ΛM perpendiculaire sur ZH. Supposons que le point M est dans la demi-circonférence décrite autour de ZH comme diamètre. La raison du carré de la perpendiculaire ΘK à la surface comprise sous AK, KB sera la même que la raison du carré de ZΓ à la surface comprise sous AΔ, ΔB ; parce que ZH est égal à l'autre diamètre de l'ellipse (α). Mais la raison de la surface comprise sous ZL, LH à la surface comprise sous AK, KB est aussi la même que la raison du carré de ZΓ au carré du demi-diamètre AΔ de l'ellipse (β). Donc la surface comprise sous ZL, LH est égale au carré de ΘK. Mais le carré de LM est aussi égal à cette surface ; donc les perpendiculaires ΘK, ML sont égales. Donc les droites LK, MΘ sont parallèles. Donc les droites ΔΓ, MΘ sont aussi parallèles. Donc ΘM est dans la surface du cylindre ; parce que cette droite est menée parallèlement à l'axe du point M qui est dans la surface du cylindre. Il est donc évident que le point Θ est aussi dans la surface du cylindre. Mais on avait supposé qu'il n'y était pas. Donc ce qu'il fallait démontrer est évident.

Il est encore évident que le cylindre qui comprend l'ellipse sera droit, si l'autre diamètre est égal à la distance des droites qui sont menées des extrémités du diamètre AB parallèlement à l'oblique élevée menée du centre.

Que l'autre diamètre soit plus grand que ZH ; et supposons qu'il soit égal à ΠZ. Par la droite ΠZ, conduisons un plan perpendiculaire sur celui où se trouvent les droites AB, ΓΔ ; et dans ce plan et autour de ΠZ comme diamètre décrivons un cercle et que ce cercle soit la base d'un cylindre qui ait pour axe la droite ΔΡ.

On démontrera de la même manière que l'ellipse est dans la surface de ce cylindre.

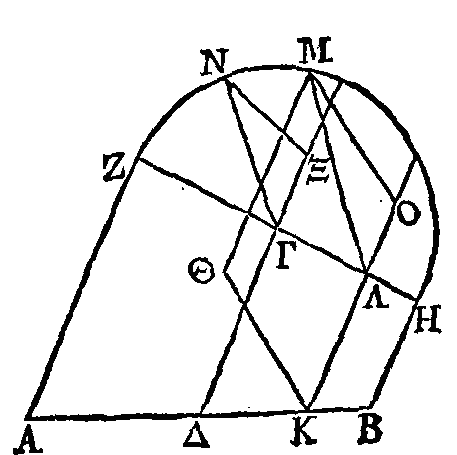
Que l'autre diamètre soit plus petit que ZH et que l'excès du carré de ZΓ sur le carré de la moitié de l'autre diamètre soit le carré de ΓΞ. Du point Ξ menons la droite ΞN égale à la moitié de l'autre diamètre, et que cette droite soit perpendiculaire sur le plan où se trouvent les droites AB, ΓΔ, et supposons que le point N soit au-dessus de ce plan. La droite ΓN sera égale à ΓZ (δ). Décrivons ensuite un cercle dans le plan où se trouvent les droites ZH, ΓN, autour de ZH comme diamètre; ce cercle passera par le point N. Que ce cercle soit la base d'un cylindre qui ait pour axe la droite ΓΔ. Je dis que l'ellipse sera dans la surface de ce cylindre.

Car si l'ellipse n'est pas dans la surface de ce cylindre, il y aura quelque point dans l'ellipse qui ne sera pas dans cette surface. Prenons un point quelconque Θ dans cette ellipse ; de ce point menons la droite ΘK perpendiculaire sur AB ; du point K menons la droite KΛ parallèle à ΓΔ, et du point Λ et dans le demi-cercle décrit autour de ZH comme diamètre, menons la droite ΛM perpendiculaire sur ZH. Supposons que le point M soit dans la demi circonférence décrite autour de ZH ; et de ce point conduisons la perpendiculaire MO sur la droite KΛ prolongée.

Cette droite sera perpendiculaire sur le plan où se trouvent les droites AB, ΓΔ ; parce que KΛ est perpendiculaire sur ZH. Donc le carré de MO est au carré de MΛ comme le carré de ΞN est au carré de NΓ. (ε) Mais le carré de MΛ est à la surface comprise sous AK, KB comme le carré de ΓN est au carré de AΔ ; car le carré de MΛ est égal à la surface comprise sous ΛZ, ΛH ; et le carré de ΓN est égal au carré de ΓZ. Donc le carré de MO est à la surface comprise sous AK, KB comme le carré de NΞ est au carré de AΔ. Mais le carré de KΘ est à la surface comprise sous AK, KB comme le carré de ΞN est au carré de AΔ, parce que ΞN est égal à la moitié de l'autre diamètre. Il est donc évident que les perpendiculaires MO, OK sont égales et par conséquent les droites KO, ΘM (ζ). Mais la droite MΘ est parallèle à l'axe du cylindre, et le point M est dans la surface de ce même cylindre; donc le point O est aussi dans cette surface, mais on avait supposé qu'il n'y était pas ; il est donc évident que l'ellipse est nécessairement dans la surface du cylindre.

PROPOSITION XI.

Il a été démontré par ceux qui ont vécu avant nous que deux cônes sont entre eux en raison composée des bases et des hauteurs On démontrera de la même manière que deux segments quelconques de cône sont entre eux en raison composée des bases et des hauteurs. On démontrera aussi qu'un segment quelconque de cylindre est triple du segment de cône qui a la même base et la même hauteur que le premier segment, de la même manière que l'on démontre qu'un cylindre est le triple d'un cône qui a la même base et la même hauteur (α).

PROPOSITION XII.

Si un conoïde parabolique est coupé par un plan conduit par l'axe ou parallèlement à l’axe, la section sera une parabole, et cette parabole sera la même que celle qui comprend le conoïde. Son diamètre sera la commune section du plan coupant et de celui qui lui étant perpendiculaire passe par l'axe. Si ce conoïde est coupé par un plan perpendiculaire sur l'axe, la section sera un cercle ayant son centre dans l'axe.

Si un conoïde hyperbolique est coupé par un plan conduit par l'axe ou parallèlement à l'axe, ou enfin par le sommet du cône qui comprend le conoïde, la section sera une hyperbole. Si le plan coupant passe par l'axe, l'hyperbole sera la même que celle qui comprend le conoïde, et si le plan coupant est parallèle à l'axe, l'hyperbole sera semblable à celle qui comprend le conoïde; et enfin si le plan coupant passe par le sommet du cône qui comprend le conoïde, l'hyperbole ne sera pas semblable à l'hyperbole qui comprend le conoïde. Le diamètre de l'hyperbole sera la commune section du plan coupant et de celui qui lui étant perpendiculaire passe par l'axe. Si le plan coupant est perpendiculaire sur l’axe, la section sera un cercle ayant son centre dans l’axe du conoïde.

Si un sphéroïde allongé ou aplati est coupé par un plan conduit par l'axe ou parallèlement à l’axe la section sera une ellipse. Si le plan coupant passe par l'axe, l'ellipse sera la même que celle qui comprend le sphéroïde; et si le plan coupant est parallèle à l’axe, elle sera semblable à celle qui comprend le sphéroïde. Le diamètre sera la commune section du plan coupant et de celui qui lui étant perpendiculaire passe par l'axe. Si le plan coupant est perpendiculaire sur l'axe, la section sera un cercle ayant son centre dans l'axe.

Si chacune des figures dont nous venons de parler est coupée par un plan mené par l'axe, les perpendiculaires menées sur le plan coupant des points qui sont dans la surface de ces figures et non dans la section tombent en dedans de la section de la figure.

Les démonstrations de toutes ces propositions sont connues (α).

PROPOSITION XIII.

Si un conoïde parabolique est coupé par un plan qui ne soit pas conduit par l'axe, ni parallèle à l’axe, ni perpendiculaire sur l'axe, la section sera une ellipse dont le grand diamètre sera la section du plan coupant par celui qui lui étant perpendiculaire passe par l'axe du conoïde; et le petit diamètre sera égal à l'intervalle des droites menées parallèlement à l'axe par les extrémités du grand diamètre.

Coupons un conoïde parabolique par un plan, comme nous l'avons dit ; coupons ensuite le conoïde par l'axe par un autre plan perpendiculaire sur le plan coupant ; que la section du conoïde soit la ligne ABΓ ; que la section du plan coupant par le second plan soit la droite AΓ ; et que BΔ soit l'axe du conoïde et le diamètre de la section par l'axe. Il faut démontrer que la section du conoïde par un plan conduit par la droite AΓ est une ellipse ; que son grand diamètre est la droite AΓ, et que son petit diamètre est égal à la droite AΛ : la droite ΓΛ étant parallèle à BΔ et la droite AΛ perpendiculaire sur ΓΛ.

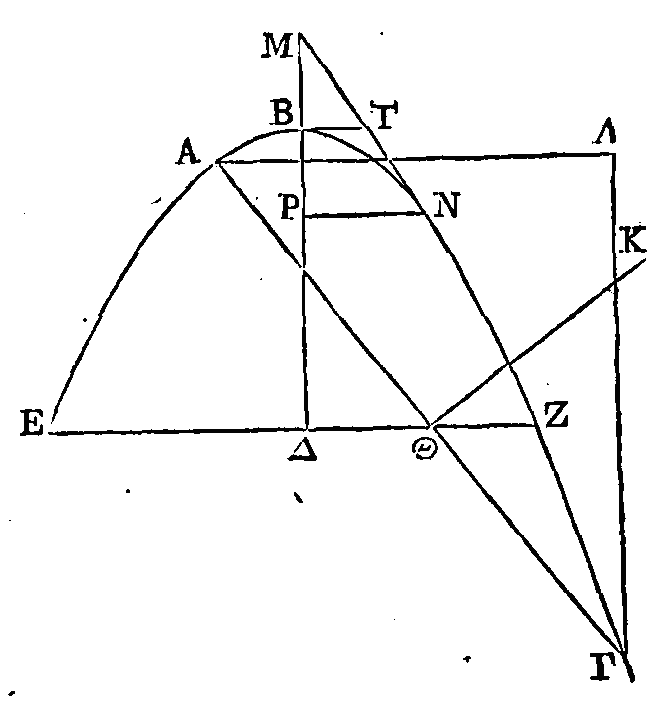
Supposons qu'on ait pris dans la section un point quelconque K. Du point K conduisons la droite KΘ perpendiculaire sur ΓA. La droite KΘ sera perpendiculaire sur le plan dans lequel se trouve la parabole AΓB ; parce que le plan coupant est aussi perpendiculaire sur ce même plan. Par le point Θ menons la droite ΘZ faisant des angles droits avec BΔ, et conduisons un plan par les droites EZ, KΘ. Ce plan sera perpendiculaire sur BΔ ; et le conoïde sera coupé par un plan perpendiculaire sur l'axe. La section sera donc un cercle ayant pour centre le point Δ. Donc le carré de KΘ sera égal à la surface comprise sous ZΘ, ΘE ; car un demi-cercle ayant été construit sur EZ et la droite KΘ étant perpendiculaire, la droite KΘ sera une moyenne proportionnelle (α), et son carré sera par conséquent égal à la surface comprise sous EΘ, ΘZ. Menons la droite MN tangente à la parabole et parallèle à AΓ ; et que cette droite soit tangente au point N. Conduisons aussi la droite BΓ tangente à la parabole et parallèle à EZ. La surface comprise sous AΘ, ΘΓ sera à la surface comprise sous EΘ, ΘZ comme le carré de NT est au carré de BT ; ce qui est démontré (β). Mais TM est égal à NT ; parce que BΡ est égal à BM ; donc la surface comprise sous AΘ, ΘΓ est au carré de KΘ comme le carré de TM est au carré de TN. Donc, par conversion, le carré de la perpendiculaire ΘK est à la surface comprise sous AΘ, ΘΓ comme le carré de BΓ est au carré de TM. Mais les triangles ΓAΛ, TMB sont semblables (γ); donc le carré de la perpendiculaire ΘK est au rectangle compris sous AΘ, ΘΓ comme le carré de AΛ est au carré de AΓ. Nous démontrerons semblablement que les carrés des autres perpendiculaires menées de la section sur AΓ sont entre eux comme le carré de AΛ au carré de AΓ. Il est donc évident que la section AΓ est une ellipse (ε) ; que le grand diamètre est la droite AΓ et que le petit diamètre est égal à AΛ.

PROPOSITION XIV.

Si un conoïde hyperbolique est coupé par un plan qui rencontre tous les côtés du cône comprenant le conoïde, et qui ne soit pas perpendiculaire sur l'axe, la section sera une ellipse ; son grand diamètre sera la section du plan coupant par celui qui lui étant perpendiculaire passe par l'axe.

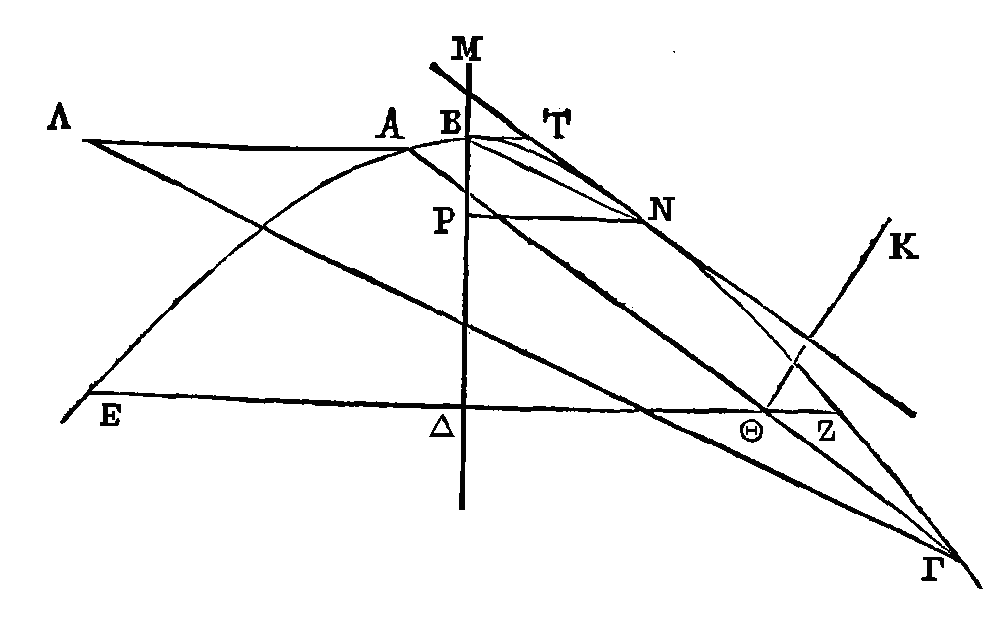
Coupons un conoïde parabolique par un plan, ainsi qu'il a été dit ; que ce même conoïde soit coupé par l’axe par un plan perpendiculaire sur le plan coupant; que la section du conoïde soit l'hyperbole ABΓ ; que AΓ soit la section du plan qui coupe le conoïde; que BΔ soit l'axe du conoïde, et le diamètre de la section. Supposons que dans la section l'on ait pris un point quelconque K. Du point K conduisons la droite KΘ perpendiculaire sur AΓ. Cette droite sera perpendiculaire sur le plan de l'hyperbole ABΓ. Du point Θ menons la droite EZ perpendiculaire sur BΔ, et par les droites EZ, KΘ conduisons un plan qui coupe le conoïde; le conoïde sera coupé par un plan perpendiculaire sur l’axe. La section sera donc un cercle qui aura pour centre le point Δ. Le carré de la perpendiculaire KΘ sera donc égal à la surface comprise sous EΘ, ΘZ. Menons une droite MN qui étant parallèle à AΓ touche l'hyperbole au point N, et menons aussi la droite BT tangente à l'hyperbole et parallèle à EZ. La surface comprise sous EΘ, HZ sera à la surface comprise sous AΘ, ΘΓ comme le carré de BT est au carré de TN (α): Donc le carré de ΘK est à la surface comprise sous AΘ, ΘΓ comme le carré de BT est au carré de TN. On dénombrera semblablement que les autres carrés des perpendiculaires menées de la section sur AΓ sont aux surfaces comprises sous les segments de AΓ formés par ces perpendiculaires comme le carré de BΓ est au carré de TN. Mais la droite BT est plus petite que la droite TN, à cause que la droite MT est plus petite que la droite TN, la droite MB étant plus petite que la droite BΡ, ce qui est une propriété de l’hyperbole (β). Il est donc évident que cette section est une ellipse. Semblablement si la droite ΓΛ est parallèle à BN, et la droite AΛ perpendiculaire sur BΔ, le grand diamètre sera la droite AΓ et le petit diamètre la droite AΛ (γ).

PROPOSITION XV.

Si un sphéroïde allongé est coupé par un plan qui ne soit pas perpendiculaire sur l'axe, la section sera une ellipse. Le grand diamètre sera la section du plan coupant par un plan qui lui étant perpendiculaire passe par l'axe.

Si le plan coupant passe par l'axe, ou s'il est parallèle à l'axe, la chose est évidente. Que le conoïde soit coupé différemment. Coupons le même Conoïde par un autre plan conduit par l'axe et perpendiculaire sur le plan coupant; que cette section soit l'ellipse ABΓΔ ; que ΓA soit la section du plan coupant;  que BΔ soit l'axe du sphéroïde et le diamètre de l'ellipse ; que le point Χ soit le centre, et que ΠΡ soit le petit diamètre. Menons la droite BT perpendiculaire sur BΔ, et la droite HN parallèle à AΓ et tangente à l'ellipse au point N ; et par le point Χ menons la droite MΛ parallèle à AΓ. Nous démontrerons, comme nous l'avons fait plus haut, que les carrés des perpendiculaires menées de la section sur AΓ sont aux surfaces comprises sous les segments de AΓ comme le carré de BT est au carré de TN.

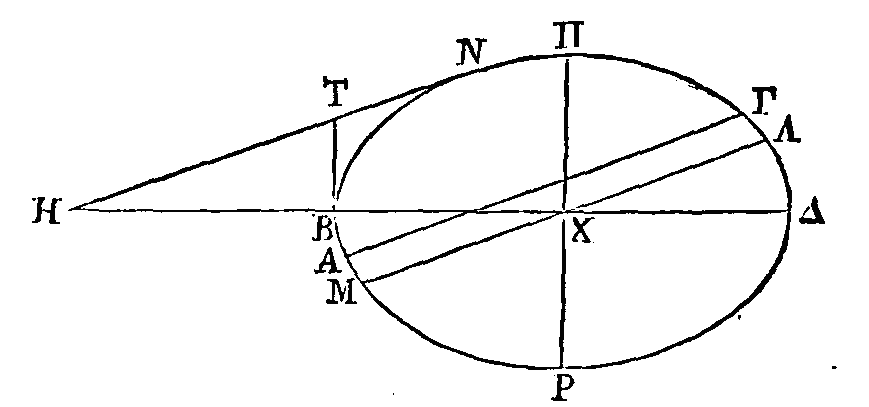
Il est donc évident que la section est une ellipse et que AΓ est un diamètre. Mais il faut démontrer que AΓ est son grand diamètre. En effet, la surface comprise sous ΠΧ, ΧΡ est à la surface comprise sous MΧ, ΧΛ comme le carré de BT est au carré de NT, parce que les droites ΠΡ, MN sont parallèles au carré de NT, parce que les droites ΠΡ, MN sont parallèles aux tangentes (α). Mais la surface comprise sous ΠΧ, ΧΡ est plus petite que la surface comprise sous MΧ, ΧΛ, parce que ΧΠ est plus petit que ΧΛ. Donc le carré de BT est plus petit que le carré de TN. Donc les carrés des perpendiculaires menées de la section sur AΓ sont moindres que les surfaces comprises sous les segments de AΓ. Il est donc évident que ΓA est le plus grand diamètre.

Si un sphéroïde aplati est coupé par un plan, la démonstration sera la même; et le petit diamètre sera celui qui est compris dans le sphéroïde.

Il suit de ce que nous venons de dire, que si toutes ces figures sont coupées par des plans parallèles, leurs sections seront semblables ; car la raison des carrés des perpendiculaires aux surfaces comprises sous les segments est toujours la même.

PROPOSITION XVI.

Dans un conoïde parabolique, parmi les droites qui sont menées par un point quelconque de sa surface parallèlement à l'axe, celles qui son menées vers le côté où le conoïde est convexe tombent hors du conoïde, et celles qui sont menées vers le côté opposé tombent en dedans.

Car ayant conduit un plan par l'axe et par le point par lequel l'on a mené une parallèle à l'axe, la section sera une parabole dont le diamètre sera l'axe du conoïde. Mais dans la parabole, parmi les droites qui sont conduites parallèlement au diamètre, celles qui sont menées vers le côté où la parabole est convexe sont hors de la parabole, et celles qui sont menées vers le côté opposé sont dans la parabole. Donc la proposition est évidente.

Dans un conoïde hyperbolique, parmi les droites qui sont menées par un point quelconque de sa surface parallèlement à une droite menée du sommet du cône qui comprend le conoïde dans le conoïde même, celles qui sont menées vers le côté où le conoïde est convexe tombent hors du conoïde, et celles qui sont menées vers le côté opposé tombent en dedans.

Car ayant conduit un plan par la droite qui est menée dans le conoïde par le sommet du cône qui comprend le conoïde, et par le point par lequel on a mené une parallèle à cette droite, la section sera une hyperbole, et son diamètre sera la droite menée du sommet du cône dans le conoïde (12). Mais dans une hyperbole, parmi les droites qui sont menées par un de ses points parallèlement à une droite, comme nous l'avons dit, celles qui sont menées vers le côté où l'hyperbole est convexe, tombent hors de l'hyperbole, et celles qui sont menées vers le côté opposé tombent en dedans.

Si un plan touche des conoïdes sans les couper, il ne les touchera qu'en un seul point; et le plan conduit par le point de contact et par l'axe sera perpendiculaire sur le plan tangent. Car qu'un plan touche un conoïde en plusieurs points, si cela est possible. Prenons deux points où ce plan touche le conoïde. Menons par ces points des parallèles à l'axe. Si par ces droites on fait passer un plan, ce plan passera par l'axe ou sera parallèle à l'axe. La section du conoïde sera donc une section conique (12), et ces deux points seront dans cette section. Donc, puisque ces points sont dans une surface, ils sont aussi dans un plan. Donc la droite qui joint ces points sera en dedans de la section conique, et par conséquent en dedans de la surface du conoïde. Mais cette même droite est dans le plan tangent, puisque ces points sont dans ce plan; donc une certaine partie du plan tangent est en dedans du conoïde. Ce qui est impossible ; car on avait supposé qu'il ne le coupait point. Donc ce plan ne touchera le conoïde qu'en un seul point.

Il est évident que le plan conduit par le point de contact et par l’axe est perpendiculaire sur le plan tangent, si ce plan est tangent au sommet du conoïde ; car ayant conduit par l'axe deux plans, les sections du conoïde seront des sections coniques ayant pour diamètre l'axe même. Mais les droites qui sont les sections du plan tangent et qui sont tangentes à l'extrémité du diamètre forment des angles droits avec le même diamètre. Il y aura donc deux droites dans le plan tangent qui seront perpendiculaires sur l'axe. Donc le plan tangent sera perpendiculaire sur l'axe et par conséquent sur le plan conduit par l'axe.

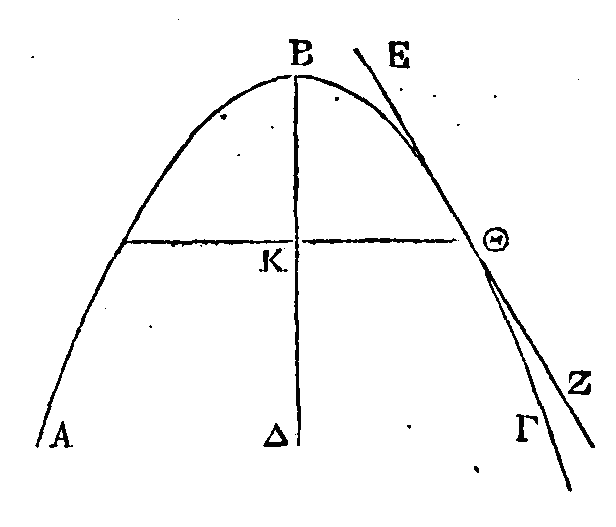
Que le plan ne soit pas tangent au sommet du conoïde. Conduisons un plan par le point de contact et par l'axe ; que la section du conoïde soit la section conique ABΓ ; que BΔ soit l'axe du conoïde et le diamètre de cette section, et que la section du plan tangent soit la droite EΘZ qui touche la section conique au point Θ. Par le point Θ conduisons la droite ΘK perpendiculaire sur le diamètre BΔ, et par cette droite menons un plan perpendiculaire sur l'axe. Ce plan engendrera un cercle dont le centre sera le point K. La section de ce plan par le premier sera une droite tangente au cercle et faisant des angles droits avec la droite ΘK. Cette droite sera donc perpendiculaire sur le plan où se trouvent les droites KΘ, BΔ. Il est donc évident que le plan tangent est perpendiculaire sur ce plan, puisque les droites qui sont dans ce plan lui sont perpendiculaires.

PROPOSITION XVII

Si un plan touche un sphéroïde allongé ou aplati sans le couper, il ne le touchera qu'en un seul point, et le plan qui passe par le point de contact et par l’axe sera perpendiculaire sur le plan tangent.

Que ce plan touche un sphéroïde en plusieurs points. Prenons deux points où ce plan touche le sphéroïde; par chacun de ces points, menons des droites parallèles à l’axe ; si par ces droites nous menons un plan, la section du sphéroïde sera une ellipse et ces points seront dans cette section. Donc la droite placée entre ces deux points sera en dedans de la section conique, et par conséquent en dedans de la surface du sphéroïde. Mais cette même droite est aussi dans le plan tangent, parce que les deux points s'y trouvent placés. Donc une certaine partie du plan tangent sera en dedans du sphéroïde. Mais cela n'est point, car on avait supposé qu'il ne le coupait point. Il est donc évident que ce plan ne touche le sphéroïde qu'en un seul point.

Nous démontrerons de la même manière que nous l'avons fait dans les conoïdes, que le plan conduit par le point de contact et par l'axe sera perpendiculaire sur le plan tangent.

Si un conoïde ou un sphéroïde allongé ou aplati est coupé par un plan conduit par l'axe; si l'on mène une droite tangente à la section qui est engendrée, et si par la tangente on conduit un plan perpendiculaire sur le plan coupant, ce plan touchera 3a figure au même point où cette droite touche la section conique.

Car ce plan ne touchera pas en un autre point la surface de cette figure; s'il en était autrement, la perpendiculaire menée de ce point sur le plan coupant tomberait hors de la section conique, puisqu'elle tomberait sur la tangente, à cause que ces plans sont perpendiculaires entre eux; ce qui ne peut être, car il est démontré qu'elle tombé en dedans (12).

PROPOSITION XVIII.

Si deux plans parallèles touchent un sphéroïde allongé ou aplati, la droite qui joindra les points de contact passera par le centre du sphéroïde.

Si les plans font des angles droits avec l'axe, la chose est évidente. Supposons que les angles ne soient pas droits. Le plan conduit par l'axe et par un des points de contact sera perpendiculaire sur le plan qu'il coupe et par conséquent sur le plan parallèle à celui-ci. Il faut donc qu'un même plan passe par l'axe et par les deux points de contact, sans quoi il y aurait deux plans perpendiculaires sur un même plan qui seraient conduits par une même droite non perpendiculaire sur ce plan; car on a supposé que l'axe n'était pas perpendiculaire sur les plans parallèles. Donc les points de contact et l'axe seront dans le même plan ; et le sphéroïde sera coupé par un plan conduit par l'axe. Donc la section sera une ellipse et les sections des plans tangents qui touchent l'ellipse aux points de contact des plans seront parallèles. Or si des droites parallèles sont tangentes à une ellipse, le centre de l'ellipse et les points de contact sont dans une même droite.

PROPOSITION XIX.

Si deux plans parallèles touchent un sphéroïde allongé ou aplati, et si par le centre du sphéroïde on conduit un plan parallèle aux plans tangents, les droites menées de la section qui est engendrée parallèlement à la droite qui joint les points de contact tombent hors du sphéroïde.

Que ce que nous avons dit soit fait; prenons un point quelconque dans la section qui est engendrée, et par ce point-et par la droite qui joint les points de contact conduisons un plan, ce plan coupera le sphéroïde et les plans parallèles. Que la section du sphéroïde soit l'ellipse ABΓΔ ; que les sections des plans tangents soient les droites EZ, HΘ ; que le point pris à volonté soit A, et que la droite qui joint les points de contact soit BΔ. Cette droite passera par le centre (18). Que la section du plan parallèle aux plans tangents soit ΓA. Cette droite passera aussi par le centre, parce que le plan où elle est passe par le centre. Donc, puisque la section ABΓΔ est ou un cercle ou une ellipse; que les deux droites EZ, HΘ sont tangentes à cette section et que par le centre on leur a conduit une parallèle AΓ, il est évident que les droites menées des points A, Γ parallèlement à BΔ sont tangentes à la section et tombent en dehors du sphéroïde (α).

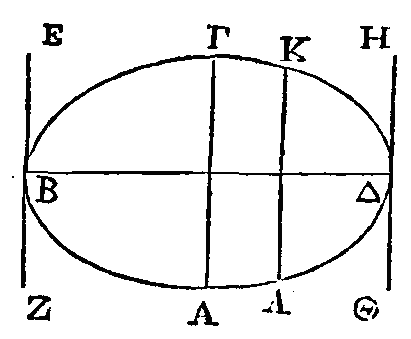
Si le plan parallèle aux tangentes n'est pas conduit par le centre, comme KΛ, il est évident que parmi les droites menées de la section, celles qui sont menées vers le côté où est le petit segment tombent hors du sphéroïde, et que celles qui sont menées vers le côté opposé tombent en dedans (β).

PROPOSITION XX.

Si un sphéroïde quelconque est coupé par un plan conduit par le centre, ce sphéroïde ainsi que sa surface, est coupé en deux parties égales par ce plan.

Coupons un sphéroïde par un plan conduit par son centre ; ou ce plan coupera le sphéroïde par l'axe, ou bien il le coupera à angles droits ou obliques. Si ce plan coupe le sphéroïde par l'axe ou s'il est perpendiculaire sur l'axe, non seulement le sphéroïde, mais encore sa surface sera coupée en deux parties égales; car il est évident qu'une partie du sphéroïde convient avec l'autre partie, et qu'une partie de sa surface convient aussi avec l'autre partie.

Mais supposons que le plan coupant ne passe pas par l'axe, et qu'il ne soit pas perpendiculaire sur l'axe. Coupons le sphéroïde par un plan qui passe par l'axe et qui soit perpendiculaire sur le plan coupant ; que la section du sphéroïde soit l'ellipse ABΓΔ ; que la droite BΔ soit le diamètre de l'ellipse et l'axe du sphéroïde ; que le point Θ soit le centre, et que la section du plan que coupe le sphéroïde par le centre soit la droite AΓ. Prenons un autre sphéroïde égal et semblable au premier ; coupons-le par un plan conduit par l'axe ; que sa section soit, l'ellipse EZHN ; que eh soit le diamètre de l'ellipse et l'axe du sphéroïde, et le point K le centre. Par le centre K, menons la droite ZN, faisant l'angle K égal à l'angle Θ ; et par la droite ZN conduisons un plan perpendiculaire sur le plan où se trouve la section EZHN.

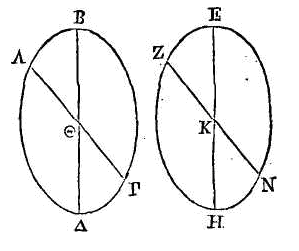
On aura deux ellipses ABΓΔ, EZHN égales et semblables. C'est pourquoi ayant posé EH sur BΔ et ZN sur AΓ, ces deux ellipses conviendront parfaitement. Mais le plan conduit par NZ et le plan conduit par AΓ conviennent encore parfaitement, puisqu'ils sont conduits l'un et l'autre par une même droite dans un même plan ; donc le segment qui est retranché du sphéroïde, du côté où se trouve le point E, par le plan conduit par NZ, et l'autre segment qui est retranché de l'autre sphéroïde, du côté où se trouve le point B, par le plan conduit par la droite AΓ, conviennent parfaitement. Donc les segments restants, et les surfaces de ces segments conviennent encore parfaitement.

Si l'on pose la droite EH sur BΔ, de manière que le point E soit posé sur le point Δ, le point H sur le point B, et enfin si l'on pose la droite qui est entre les points N, Z sur la droite qui est entre les points A, Γ, il est évident que les ellipses conviendront parfaitement, que le point Z tombera sur le point Γ et le point N sur le point Γ. Semblablement, le plan conduit par NZ, et le plan conduit par AΓ conviennent parfaitement, et le segment qui est retranché, du côté où se trouve le point H, par le plan conduit par NZ, et le segment qui est retranché, du côté où se trouve le point B, par le plan conduit par AΓ, conviennent encore parfaitement.

Mais celui qui est du côté où se trouve le point E, et celui qui est du côté où se trouve le point A conviennent encore parfaitement; donc, puisque le même segment convient parfaitement avec l'un et avec l'autre segment, il est évident que ces segments sont égaux, et que leurs surfaces sont aussi égales.

PROPOSITION XXI.

Etant donné un segment d'un conoïde parabolique ou hyperbolique retranché par un plan perpendiculaire sur l'axe, ou bien un segment d'un sphéroïde allongé ou aplati retranché semblablement, de manière cependant que celui-ci ne soit pas plus grand que la moitié du sphéroïde, on peut inscrire dans chaque segment une figure solide composée de cylindres ayant tous la même hauteur, et lui en inscrire une autre de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que toute quantité solide proposée.

Soit donné un segment tel que ABΓ. Coupons ce segment par un plan conduit par l’axe; que la section de ce segment soit la section conique ABΓ, et que celle du plan qui coupe le segment soit la droite AΓ. Que la droite BΔ soit l'axe du segment, et le diamètre de la section conique. Puisque l'on a supposé que le plan coupant est perpendiculaire sur l'axe, la section sera un cercle ayant pour diamètre la droite ΓA. Que ce cercle soit la base d'un cylindre qui ait pour axe la droite BΔ. La surface de ce cylindre tombera hors du segment, parce que c'est un segment de conoïde, ou bien un segment de sphéroïde qui n'est pas plus grand que la moitié du sphéroïde (16 et 19).

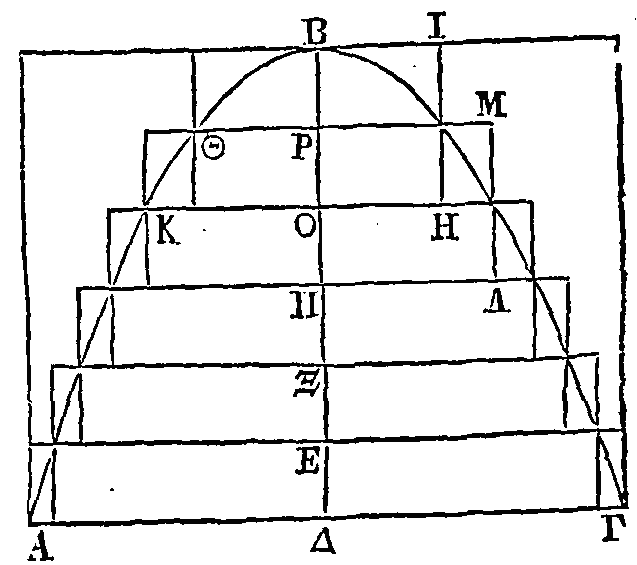
C'est pourquoi, si le cylindre est coupé continuellement en deux parties par un plan perpendiculaire sur l'axe, ce qui restera sera à la fin moindre que la quantité solide proposée. Que le reste qui est moindre que la quantité solide proposée soit le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite EΔ. Partageons, aux points Ρ, O, Π, Ξ, la droite BΔ en parties égales chacune à EΔ ; par les points de division conduisons à AΓ des parallèles terminées à la section conique, et par ces parallèles faisons passer des plans perpendiculaires sur BΔ. Les sections seront des cercles qui auront leurs centres dans BΔ. Sur chacun de ces cercles construisons deux cylindres dont chacun ait un axe égal à EΔ ; que l'un d'eux soit du côté du cylindre où est le point Δ, et l'autre du côté du cylindre où est le point B. Il est évident que l'on aura inscrit dans le segment une certaine figure solide composée des cylindres qui sont construits qu'on lui en aura aussi circonscrit une autre composée des cylindres qui sont construits du côté du côté où est le point Δ, et qu’on lui aura aussi circonscrit une autre composée des cylindres qui sont construits du côté où est le point B. Il reste à démontrer que l'excès de la figure circonscrite sur la figure inscrite est moindre que la quantité solide proposée. Or, chacun des cylindres qui sont dans la figure inscrite est égal au cylindre qui est construit sur le même cercle du côté où est le point B, c'est-à-dire que le cylindre ΘH sera égal au cylindre ΘI, le cylindre KΛ au cylindre KM, et ainsi de suite. Donc la somme des uns de ces cylindres est égale à celle des autres. Il est donc évident que l'excès de la figure circonscrite sur la figure inscrite est le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre et pour axe la droite EΔ. Or, ce cylindre est moindre que la quantité solide proposée.

PROPOSITION XXII.

Etant donné un segment d'un conoïde parabolique ou hyperbolique retranché par un plan non perpendiculaire sur l'axe, ou un segment de sphéroïde allongé ou aplati retranché semblablement de manière cependant que celui-ci ne soit pas plus grand que la moitié du sphéroïde, on peut inscrire dans chaque segment une figure solide composée de segments de cylindre ayant tous une hauteur égale, et lui en circonscrire une autre de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre qu'une quantité solide donnée.

Soit donné un segment tel que nous l'avons dit. Coupons ce segment par un autre plan conduit par l'axe et perpendiculaire sur le plan qui retranche le segment donné. Que la section du segment soit la section conique ABΓH, et la section du plan qui retranche le segment, la droite ΓA. Puisqu'on suppose que le plan qui retranche le segment n'est point perpendiculaire sur l'axe, la section sera une ellipse, ayant pour diamètre la droite AΓ (15). Que la droite OΥ parallèle à ΓA soit tangente à la section conique au point B ; et par la droite ΦΥ faisons passer un plan parallèle au plan conduit par AΓ. Ce plan touchera le conoïde au point B (17). Si le segment appartient à un conoïde parabolique, du point B menons la droite BΔ parallèle à l'axe ; si le segment appartient à un conoïde hyperbolique, du sommet du cône contenant le conoïde conduisons une droite au point B ; prolongeons cette droite, et que son prolongement soit BΔ ; si enfin le segment appartient à un sphéroïde, de son centre conduisons une droite au point B, et que la partie de cette droite comprise dans le segment soit BΔ.

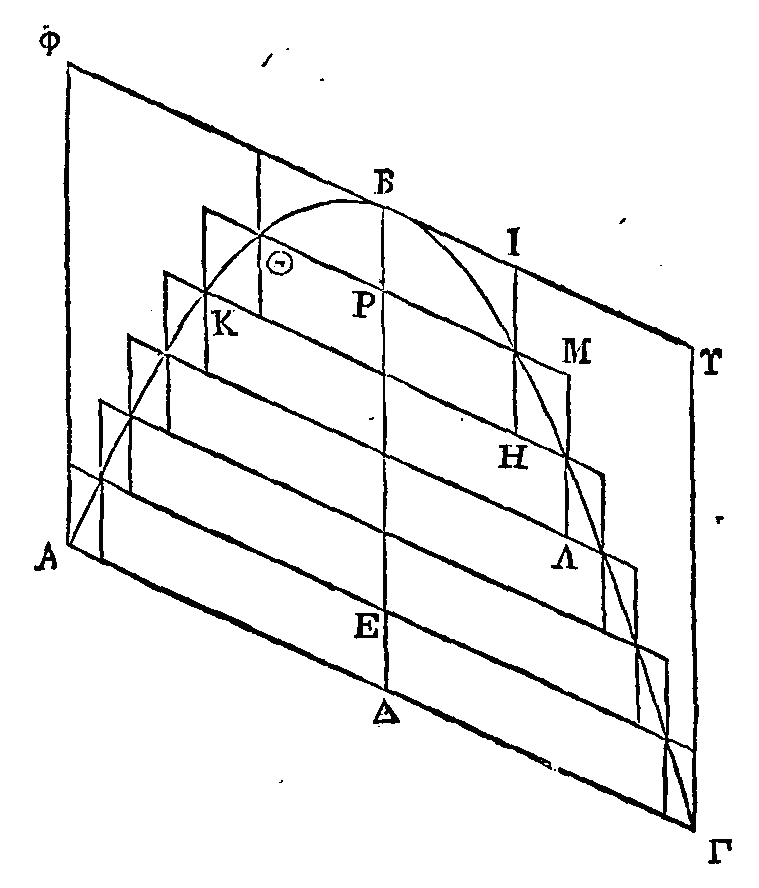
Il est d'abord évident que la droite BΔ partagera en deux parties égales la droite AΓ. Donc le point B sera le sommet du segment, et la droite BΔ son axe. On a donc une ellipse décrite autour de AΓ comme diamètre, et une oblique BΔ menée de son centre dans un plan qui passe par un de ses diamètres et qui est perpendiculaire sur le plan de l'ellipse. On peut donc trouver un cylindre qui ait son axe sur la droite BΔ, et dans la surface duquel se trouve l'ellipse qui est décrite autour de AΓ comme diamètre (10). La surface de ce cylindre tombera hors du segment; car c'est un segment de conoïde, ou bien un segment de sphéroïde qui n'est pas plus grand que la moitié du sphéroïde (16 et 19). L'on aura donc un certain segment de cylindre ayant pour base une ellipse décrite autour de AΓ comme diamètre, et pour axe la droite BΔ. C'est pourquoi si l’on coupe continuellement ce segment en deux parties égales par des plans parallèles au plan conduit par AΓ, ce qui restera sera moindre que la quantité solide proposée. Que le segment qui a pour base l'ellipse décrite autour de AΓ comme diamètre, et pour axe la droite EΔ soit moindre que la quantité solide proposée. Partageons ΔB en parties égales chacune à ΔE ; par les points de division menons à AΓ des droites parallèles et terminées à l'ellipse; et par ces droites faisons passer des plans parallèles au plan conduit par AΓ. Ces plans couperont la surface du segment, et les sections seront des ellipses semblables à celle qui est décrite autour de AΓ comme diamètre, parce que ces plans sont parallèles entre eux (15. Cor.) Construisons sur chaque ellipse deux segments de cylindre; que l'un soit du côté de l'ellipse où est le point Δ et l'autre du côté où est le point B. Que ces segments de cylindres aient pour axe une droite égale à ΔE. On aura donc certaines figures solides composées de segments de cylindre ayant la même hauteur, dont l'une sera inscrite et l'autre circonscrite. Il reste à démontrer que l'excès de la figure circonscrite sur la figure inscrite est moindre que la quantité solide proposée. On démontrera comme dans la proposition précédente que l'excès de la figure circonscrite sur la figure inscrite est un segment qui a pour base l'ellipse décrite autour de AΓ comme diamètre et pour axe la droite EΔ. Or, ce segment est moindre que la grandeur solide proposée.

Ces choses étant établies, nous allons démontrer celles qui ont été proposées relativement à ces figures.

PROPOSITION XXIII.

Un segment quelconque d'un conoïde parabolique retranché par un plan perpendiculaire sur l'axe est égal à trois fois la moitié du cône qui a la même base et le même axe que ce segment.

Soit un segment d'un conoïde parabolique retranché par un plan perpendiculaire sur l'axe. Coupons ce segment par un autre plan conduit par l'axe; que la section de sa surface soit la parabole ABΓ ; que la section du plan qui retranche le segment soit la droite ΓA, et que l'axe du segment soit la droite BΔ. Soit aussi un cône qui ait la même base et le même axe que le segment, ayant pour sommet le point B. Il faut démontrer que le segment du conoïde est égal à trois fois la moitié de ce cône.

Supposons que le cône Ψ soit égal à trois fois la moitié du cône dont la base est le cercle décrit autour de AΓ comme diamètre et dont l’axe est BΔ. Soit aussi un cylindre qui ait pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite BΔ. Le cône Ψ sera égal à la moitié du cylindre total; parce que le cône Ψ est égal à trois fois la moitié de l'autre cône. Je dis que le segment du conoïde est égal au cône Ψ.

Car si le segment du conoïde n'est pas égal au cône Ψ, il est plus grand ou plus petit. Qu'il soit d'abord plus grand, si cela est possible. Inscrirons dans le segment une figure solide composée de cylindres qui aient la même hauteur; circonscrivons-lui en un autre de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du segment sur le cône Ψ. Que parmi les cylindres dont la figure circonscrite est composée, le plus grand soit celui qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite EΔ ; et que le plus petit soit celui qui a pour base le cercle décrit autour de ΣT comme diamètre et pour axe la droite BΘ. Que parmi les cylindres dont la figure inscrite est composée, le plus grand soit celui qui a pour base le cercle décrit autour de KΛ comme diamètre et pour axe la droite ΔE ; et que le plus petit soit celui qui a pour base le cercle décrit autour de ΣΓ comme diamètre et pour axe la droite ΘI. Que les plans de tous ces cylindres soient prolongés jusqu'à la surface du cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre et pour axe la droite BΔ, Le cylindre total sera partagé en autant de cylindres qu'il y en a dans la figure circonscrite, et chacun de ces cylindres sera égal au plus grand des cylindres circonscrits. Mais l'excès de la figure circonscrite au segment sur la figure inscrite est moindre que l'excès du segment sur le cône Ψ ; il est donc évident que la figure inscrite dans le segment est plus grande que le cône Ψ (α).

Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΔE est au premier des cylindres placés dans la figure inscrite, qui a pour axe la droite ΔE comme le carré de la droite ΔA est au carré de la-droite KE ; et le carré de la droite ΔE est au carré de la droite KE comme BΔ est à BE, et comme ΔA est à EΞ (β). On démontrera semblablement que le second des cylindres placés dans le cylindre total, qui a pour axe la droite EZ est au second des cylindres placés dans, la figure inscrite comme ΠE, c'est-à-dire ΔA, est à ZΩ. De plus, chacun des autres cylindres placés dans le cylindre total sera à chacun des cylindres qui sont placés dans la figure inscrite, et qui ont le même axe comme le rayon de la base est à la partie de ce rayon placée entre les droites AB, BΔ. Donc la somme de tous les cylindres placés dans le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre et pour axe la droite BΔ, est à la somme de tous les cylindres placés dans la figure inscrite comme la somme des rayons des cercles qui sont dans les bases des cylindres dont nous venons de parler est à la somme des droites qui sont placées entre les droites AB, BΔ (2) (γ). Mais si des secondes droites dont nous venons de parler, on retranche les droites AΔ, la somme des premières droites dont nous venons de parler est plus grande que le double de la somme des secondes droites restantes (1) (δ). Donc la somme des cylindres placés dans le cylindre total qui a pour axe la droite ΔB est plus grande que le double de la figure inscrite. Donc le cylindre total qui a pour axe BΔ est plus grand que le double de la figure inscrite. Mais ce cylindre est double du cône Ψ ; donc la figure inscrite est plus petite que le cône Ψ. Ce qui ne peut être ; car on a démontré qu'elle est plus grande. Donc le segment du conoïde n'est pas plus grand que le cône Ψ.

Je dis à présent que ce segment n'est pas plus petit. Inscrivons dans le segment une figure, et circonscrivons-lui en une autre, de manière que l'excès de l'une sur l'autre soit moindre que l'excès du cône Ψ sur le segment Faisons le reste comme auparavant. Puisque la figure inscrite est plus petite que le segment, et que la figure inscrite diffère moins de la figure circonscrite que le segment ne diffère du cône, il est évident que la figure circonscrite est plus petite que le cône Ψ.

Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΔE est au premier des cylindres placés dans la figure circonscrite, qui a pour axe la même droite EΔ comme le carré de AΔ est à ce même carré (ε); le second des cylindres placés dans le cylindre total, qui a pour axe la droite EZ est au second des cylindres placés dans la figure circonscrite, qui a pour axe la droite EZ comme le carré de ΔA au carré de KE ; et le carré de ΔA est au carré de KE comme BΔ est à BE et comme ΔA est à EΞ. De plus, chacun des autres cylindres placés dans le cylindre total, qui a pour axe une droite égale à ΔE est à chacun des cylindres qui sont placés dans la figure circonscrite, et qui ont le même axe comme le rayon de la base, est à la partie de ce rayon placée entre les droites AB, BΔ. Donc la somme des cylindres placés dans le cylindre total qui a pour axe la droite BΔ est à la somme des cylindres placés dans la figure circonscrite comme la somme des premières droites est à la somme des secondes (2). Mais la somme des premières droites, c'est-à-dire la somme des rayons des cercles qui sont les bases des cylindres est moindre que le double de la somme des droites qui sont retranchées de ces rayons, réunie à la droite AΔ (1); il est donc évident que la somme des cylindres placés dans le cylindre total est moindre que le double de la somme des cylindres placés dans la figure circonscrite. Donc le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre et pour axe la droite BΔ est plus petit que le double de la figure circonscrite. Mais ce cylindre n'est pas plus petit que le double de la figure circonscrite, puisqu'il est au contraire plus grand que le double de cette figure; car ce cylindre est double du cône Ψ, et l'on a démontré que la figure circonscrite est plus petite que le cône Ψ. Donc le segment du conoïde n'est pas plus petit que le cône Ψ. Mais on a démontré qu'il n'est pas plus grand ; donc le segment du conoïde est égal à trois fois la moitié du cône qui a la même base et le même axe que ce segment.

PROPOSITION XXIV.

Si un segment d'un conoïde parabolique est retranché par un plan non perpendiculaire sur l'axe, ce segment sera parallèlement égal à trois fois la moitié du segment de cône qui a la même base et le même axe que ce segment.

Qu'un segment d'un conoïde parabolique soit retranché comme nous l'avons dit. Coupons ce même segment par un autre plan conduit par l'axe et perpendiculaire sur celui qui coupe la figure; que la section de la figure soit la parabole ABΓ, et que la section du plan coupant soit la droite AΓ. Menons à la droite AΓ une parallèle AΓ qui soit tangente à la parabole au point B ; et menons la droite BΔ parallèle à l'axe. Cette droite coupera en deux parties égales la droite AΓ (α).

Faisons passer par la droite ΦΥ un plan parallèle à celui qui est conduit par AΔ. Ce plan sera tangent au conoïde au point B ; le point B sera le sommet du segment et la droite BΔ son axe. Puisque le plan conduit par Ai n'est point perpendiculaire sur l’axe et que ce plan coupe le conoïde, la section sera une ellipse ayant pour grand diamètre la droite AΓ (13). Puisque l'on a une ellipse décrite autour de AΓ comme diamètre et une oblique menée de son centre dans un plan qui est conduit par le diamètre de l'ellipse et qui est perpendiculaire sur son plan, on peut trouver un cylindre qui ait son axe sur la droite BΔ et dans la surface duquel se trouve l'ellipse (10). On peut de même trouver un cône qui ait pour sommet le point B et dans la surface duquel se trouve l'ellipse (9). On aura donc un certain segment de cylindre ayant pour base l'ellipse décrite autour de AΓ comme diamètre et pour axe la droite BΔ ; on aura de plus un segment de cône ayant la même base et le même axe que le segment de cylindre et le segment du conoïde. Il faut démontrer que le segment du conoïde est égal à trois fois la moitié du segment de cône.

Que le cône Ψ soit égal à trois fois la moitié du segment de cône. Le segment de cylindre qui a la même base et le même axe que le segment du conoïde sera double du cône Ψ ; parce que ce cône est égal à trois fois la moitié du segment de cône qui a la même base et le même axe que le segment du conoïde; et que le segment de cône dont nous venons de parler est le tiers du segment de cylindre qui a la même base et le même axe que le segment du conoïde (11). Il est donc nécessaire que le segment du conoïde soit égal au cône Ψ.

Car si ce segment ne lui est pas égal, il sera plus grand ou plus petit. Supposons d'abord qu'il soit plus grand, si cela est possible. Inscrivons dans le segment une figure solide composée de segments de cylindre qui aient la même hauteur, et circonscrivons-lui ensuite une autre figure solide, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès du segment du conoïde sur le cône Ψ. Prolongeons les plans des segments de cylindre jusqu'à la surface du segment de cylindre qui a la même base et le même axe que le segment du conoïde. Le premier des segments placés dans le segment de cylindre total, qui a pour axe la droite ΔE, est au premier des segments placés dans la figure inscrite, qui a pour axe la droite ΔE comme le carré de AΔ est au carré de KE ; car ces segments qui ont une hauteur égale sont entre eux comme leurs bases. Mais les bases de ces segments qui sont des ellipses semblables, sont entre elles comme les carrés de leurs  diamètres correspondants (β) ; et les moitiés de ces diamètres sont les droites AΔ, KE; et de plus, le carré de AΔ est au carré de KE comme BΔ est à BE ; parce que la droite BA est parallèle au diamètre, que les droites AΔ, KE sont parallèles à la droite qui touche la parabole au point B, et que BΔ est à BE comme AΔ est à EΞ. Donc, le premier des segments placés dans le segment de cylindre total est au premier des segments placés dans la figure inscrite comme AΔ est à EΞ. De même, chacun des autres segments placés dans le segment de cylindre total, qui a pour axe une droite, égale à EΔ, est à chacun des segments correspondants qui sont placés dans la figure inscrite, et qui ont le même axe comme le demi-diamètre des bases est à la partie de ce demi-diamètre placée entre les droites AB, BΔ. Nous démontrerons, comme nous l'avons fait plus haut, que la figure inscrite est plus grande que le cône Ψ, et que le segment de cylindre qui a la même base et le même axe que le segment du conoïde, est plus grand que le double de la figure inscrite. Donc, le segment de cylindre sera aussi plus grand que le double du cône Ψ. Mais il n'est pas plus grand que le double de ce cône, puisqu'il est seulement le double de ce cône. Donc le segment du conoïde n'est pas plus grand que le cône Ψ. On démontrera de la même manière qu'il n'est pas plus petit. Il est donc évident qu'il lui est égal. Donc, le segment du conoïde est égal à trois fois la moitié du segment de cône qui a la même base et le même axe que ce segment.

PROPOSITION XXV.

Si deux segments d'un conoïde parabolique sont retranchés par deux plans dont l'un soit perpendiculaire sur l'axe et dont l'autre ne lui soit pas perpendiculaire ; et si les axes des segments sont égaux, ces segments seront égaux entre eux.

Retranchons deux segments d'un conoïde parabolique, ainsi que nous l'avons dit. Coupons ensuite le conoïde par un plan conduit par l'axe et par un plan perpendiculaire sur l'axe. Que la section du conoïde soit la parabole ABΓ, ayant pour diamètre la droite BΔ. Que les sections des plans soient les droites AZ, et, dont l’une EΓ est perpendiculaire sur l'axe, et dont l'autre ZA ne lui est pas perpendiculaire. Que les droites BΘ, KΛ qui sont les axes des segments soient égales entre elles et que les sommets des segments soient les points B, Λ. Il faut démontrer que le segment du conoïde dont le sommet est le point b, est égal au segment du conoïde dont le sommet est le point A.

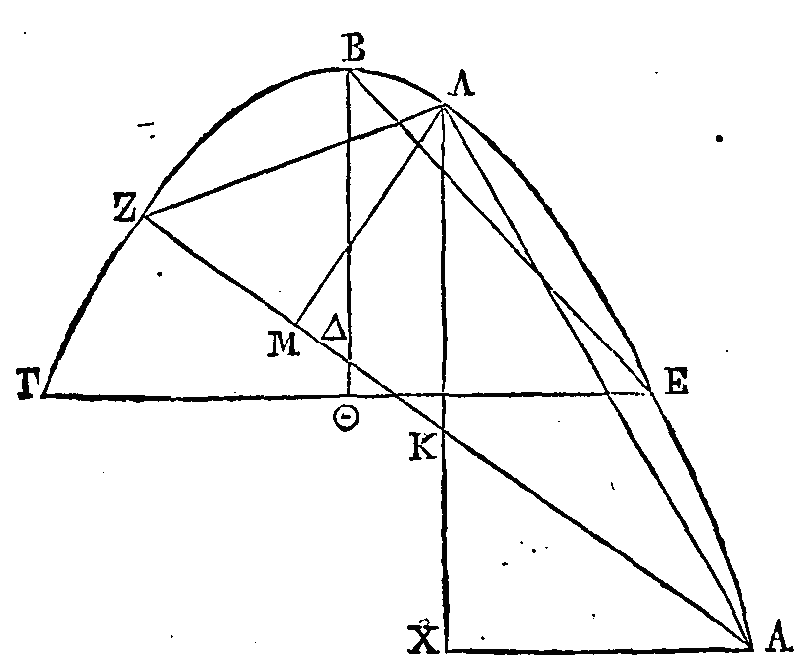
Puisque d'une même parabole, on a retranché deux segments, dont l'un est AΛZ et l'autre EBΓ, et que leurs diamètres KΛ, ΘB sont égaux entre eux, le triangle AΛK sera égal au triangle EΘB ; car on a démontré que le triangle AΛZ est égal au triangle EBΓ (4). Menons la droite AΧ perpendiculaire sur la droite KΛ prolongée. Puisque les droites BΘ, KΛ sont égales entre elles, les droites EΘ, AΧ seront aussi égales entre elles (4). Dans le segment dont le sommet est le point B, inscrivons un cône qui ait la même base et le même axe que ce segment; et dans le segment dont le sommet est le point Λ, inscrivons un segment de cône qui ait la même base et le même axe que ce segment Du point Λ, conduisons sur ΔZ la perpendiculaire ΛM. Cette perpendiculaire sera la hauteur du segment de cône dont le sommet est le point Λ. Mais le segment de cône dont le sommet est le point Λ et le cône dont le sommet est le point B sont entre eux en raison composée des bases et des hauteurs (α). Donc, ce segment de cône et ce cône sont entre eux en raison composée de la raison de la surface comprise dans l'ellipse décrite autour de AZ comme diamètre au cercle décrit autour de EΓ comme diamètre, et de la raison de ΛM à BΘ.

Mais la raison de la surface comprise dans l'ellipse à ce même cercle est la même que la raison de la surface comprise sous les diamètres de l'ellipse au carré du diamètre EΓ (6) ; donc le segment de cône dont le sommet est le point Λ, et le cône dont le sommet est le point B sont entre eux en raison composée de la raison de KA à EΘ, et de la raison de ΛM à BΘ ; car la droite KA est la moitié du diamètre de la base du segment de cône qui a pour sommet le point Λ ; la droite EΘ est la moitié du diamètre de la base du cône, et les droites AM, BΘ sont les hauteurs du segment de cône et du cône (γ). Mais ΛM est à BΘ comme ΛM est à KΛ, parce que BΘ est égal à KΛ ; et ΛM est à KΔ, comme ΧA est à AK (δ) ; de plus la raison du segment de cône au cône est composée de la raison de KA à AΧ, car AΧ est égal à EΘ, et de la raison de ΛM à BΘ ; et parmi les raisons dont nous venons de parler, la raison de AK à AΧ est la même que la raison de ΛK à ΛM. Donc le segment de cône est au cône comme ΛK est à ΛM et comme ΛM est à BΘ. Mais BΘ est égal à KΛ (ε) ; il est donc évident que le segment de cône qui a pour sommet le point Λ est égal au cône qui a pour sommet le point B. Il suit évidemment de là que les segments du conoïde sont égaux, puisque l'un d'eux est égal à trois fois la moitié d'un cône (23), et que l'autre est égal à trois fois la moitié d'un segment de cône qui est égal à ce même cône (24)

PROPOSITION XXVI.

Si deux segments d'un conoïde parabolique sont retranchés par un plan conduit d'une manière quelconque, ces segments sont entre eux comme les carrés de leurs axes.

Que deux segments d'un conoïde parabolique soient retranchés comme on voudra ; que K soit égal à l’axe de l'un et Λ égal à l'axe de l'autre. Il faut démontrer que ces segments sont entre eux comme les carrés des droites K, Λ.

Coupons le conoïde par un plan conduit par l'axe du segment, et que sa section soit la parabole ABΓ, ayant pour axe la droite BΔ Prenons BΔ égal à K ; et par le point Δ conduisons un plan perpendiculaire sur l'axe. Le segment du conoïde qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite BΔ, est égal à un segment qui a un axe égal à K. Si K est aussi égal à Λ, il est évident que les segments seront égaux entre eux ; car ils seront égaux chacun à une même quantité solide; mais les carrés des droites K, Λ seront égaux entre eux ; donc les segments seront entre eux comme les carrés de leurs axes.

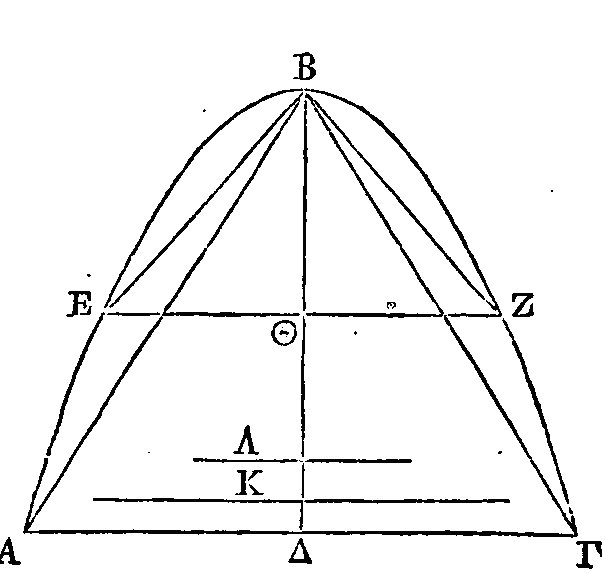
Si Λ n'est pas égal à K, que Λ soit égal à BΘ. Par le point Θ conduisons un plan perpendiculaire sur l'axe. Le segment qui a pour base le cercle décrit autour de EZ comme diamètre, et pour axe la droite BΘ est égal à un segment qui a un axe égal à Λ. Construisons deux cônes qui aient pour base les cercles décrits autour de AΓ, EZ comme diamètres, et pour sommet le point B. Le cône qui a pour axe la droite BΔ, et le cône qui a pour axe la droite BΘ sont entre eux en raison composée de la raison du carré de AΔ au carré de ΘE, et de la raison de BΔ à BΘ (α). Mais le carré de AΔ est au carré de ΘE comme BΔ est à BΘ (β); donc, le cône qui a pour axe BΔ, et le cône qui a pour axe BΘ sont entre eux en raison composée de la raison de BΔ à ΘB et de la raison de BΔ à BΘ. Mais cette raison est la même que celle du carré de ΔB au carré de ΘB ; et le cône qui a pour axe la droite BΔ est au cône qui a pour axe la droite ΘB comme le segment du conoïde qui a pour axe la droite ΔB au segment qui a pour axe la droite ΘB ; car chacun de ces segments est égal à trois fois la moitié de chacun de ces cônes (23); de plus, le segment du conoïde qui a un axe égal à K est égal au segment qui a pour axe la droite BΔ ; le segment du conoïde qui a pour, axe une droite égale à Λ est égal au segment qui a pour axe la droite ΘB (25), et la droite K est égale à la droite BΔ, et la droite Λ est égale à la droite ΘB. Il est donc évident que le segment du conoïde qui a un axe égal à K est au segment du conoïde qui a un axe égal à Λ comme le carré de K est au carré de Λ.

PROPOSITION XXVII.

Un segment d'un conoïde hyperbolique retranché par un plan perpendiculaire sur l'axe est à un cône qui a la même base et le même axe que ce segment comme une droite composée de l'axe du segment et du triple de la droite ajoutée à l'axe est à une droite composée de l'axe du segment et du double de la droite ajoutée à l'axe.

Retranchons un segment d'un conoïde hyperbolique par un plan perpendiculaire sur l'axe. Coupons ce même segment par un autre plan conduit par l'axe. Que la section du conoïde soit l'hyperbole ABΓ ; et que la section du plan qui retranche le segment soit la droite AΓ ; que l’axe du segment soit BΔ, et que la droite ajoutée à l'axe soit la droite BΘ, et que les droites ZΘ, ZH soient égales chacune à BΘ. Il faut démontrer le segment est au cône qui a la même base et le même axe que le segment comme HΔ est à ZΔ.

Soit un cylindre qui ait la même base et le même axe que le segment, et dont les côtés soient ΦA, ΓΥ. Soit de plus un cône Ψ ; et que ce cône soit à celui qui a la même base et le même axe BΔ que le segment comme HΔ est à ΔZ. Je dis que le segment du conoïde est égal au cône Ψ.

Car si le segment du conoïde n'est pas égal au cône Ψ, il est plus grand ou plus petit. Qu'il soit d'abord plus grand, si cela est possible. Inscrivons dans le segment une figure solide composée de cylindre ayant une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du segment du conoïde sur le cône Ψ. Prolongeons les plans de tous ces cylindres jusqu'à la surface du cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre et pour axe la droite BΔ. Le cylindre total sera partagé en autant de cylindres qu'il y en a dans la figure circonscrite, et chacun de ces cylindres sera égal au plus grand de ceux-ci. Puisque l'excès de la figure circonscrite sur la figure inscrite est moindre que l'excès du segment sur le cône Ψ, et que la figure circonscrite est plus grande que le segment, il est évident que la figure inscrite est plus grande que le cône Ψ.

Que BΡ soit le tiers de BΔ ; la droite HΔ sera triple de ΘΡ. Puisque le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite BΔ est au cône qui a la même base et le même axe comme HΔ est à ΘΡ, et que le cône dont nous venons de parler est au cône Ψ comme ZΔ est à HΔ ; par raison d'égalité dans la proportion troublée, le cylindre dont nous venons de parler sera au cône Ψ comme ZΔ est à ΘΡ. Soient les droites où se trouve la lettre Ξ ; que leur nombre soit le même que celui des segments de la droite BΔ, que chacune d'elles soit égale à la droite ZB, et qu'à chacune d'elles on applique une surface dont la partie excédante soit un carré, que la plus grande de ces surfaces soit égale à la surface comprise sous ZΔ, ΔB, et que la plus petite soit égale à la surface comprise sous ZO, OB (α). Les côtés des carrés se surpasseront également, parce que les segments de BΔ qui leur sont égaux se surpassent également. Que le côté du plus grand carré où se trouve la lettre M soit égal à BΔ, et le côté du plus petit carré égal à BO. Soient ensuite d'autres surfaces dans, lesquelles se trouvé la lettre Ω : qu'elles soient en même nombre que les premières, et que chacune de ces surfaces, soit égale à la plus grande des premières qui est comprise sous ZB, ΔB (β).

Le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite ΔE est au cylindre qui a pour base le cercle décrit autour de KΛ comme diamètre, et pour axe la droite ΔE comme le carré de ΔA est au carré de KE. Mais cette dernière raison est la même que la raison de la surface comprise sous ZΔ, ΔB à la surface comprise sous ZE, BE. Ce qui est une propriété de l'hyperbole; car la droite qui est double de l'ajoutée à l'axe, c'est-à-dire de celle qui est menée du centre est le côté transverse de l'hyperbole (γ). Mais la surface ΞM est égale à la surface comprise sous ZΔ, BΔ, et la surface ΞN est égale à la surface comprise sous ZE, BE ; car la droite Ξ est égale à ZB, la droite N à BE, et la droite M à BΔ. Donc, le cylindre qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite ΔE est au cylindre qui a pour base le cercle décrit autour de KΛ comme diamètre, et pour axe la droite ΔE comme la surface Ω est à la surface ΞN. Nous démontrerons semblablement que chacun, des autres cylindres qui sont placés dans le cylindre total, et qui ont pour axe une droite égale à ΔE est au cylindre qui est dans la figure inscrite et qui a le même axe comme la surface Ω est à la surface qui lui est correspondante parmi celles qui sont appliquées à la ligne Ξ, et dont les parties excédantes sont des carrés (δ). On a donc certaines quantités, savoir les cylindres qui sont placés dans le cylindre total, et dont chacun a un axe égal à la droite ΔE, et certaines autres quantités, savoir les surfaces où se trouve la lettre Ω, qui sont en même nombre que les premières; et ces quantités sont proportionnelles deux à deux, parce que ces cylindres sont égaux entre eux ainsi que les surfaces Ω. Or, quelques-uns de ces cylindres sont comparés avec d'autres cylindres qui sont dans la figure inscrite, le dernier n'étant point comparé avec un autre; et de plus, parmi les surfaces dans lesquelles se trouve la lettre Ω, quelques-unes sont comparées avec d'autres surfaces correspondantes qui sont appliquées à la ligne Ξ, et dont les parties excédantes sont des carrés, sous les mêmes raisons, la dernière n'étant point comparée avec une autre. Il est donc évident que la somme des cylindres qui sont placés dans le cylindre total est à la somme des cylindres qui sont placés dans la figure inscrite comme la somme des surfaces Ω est à la somme de toutes celles qui sont appliquées, la plus grande étant exceptée (2). Mais on a démontré que la raison de la somme de toutes les surfaces a à la somme de toutes les surfaces qui sont appliquées, la plus grande étant exceptée, est plus grande que la raison de la droite MΞ à une droite composée de la moitié de Ξ et de la troisième partie de M (3). Donc la raison du cylindre total à la figure inscrite est plus grande que la raison de ZΔ à ΘΡ, et cette dernière raison est la même que celle du cylindre total au cône Ψ, ainsi que cela a été démontré. Donc la raison du cylindre total à la figure inscrite est plus grande que la raison du cylindre au cône Ψ. Donc le cône Ψ est plus grand que la figure inscrite. Ce qui ne peut être; car on a démontré que la figure inscrite est plus grande que le cône Ψ. Donc le segment du conoïde n'est pas plus grand que le cône Ψ.

Mais il n'est pas plus petit. Car qu'il soit plus petit, si cela est possible. Inscrivons dans le segment une figure solide composée de cylindres ayant une hauteur égale et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du côté sur le segment; et faisons le reste comme auparavant. Puisque la figure inscrite est plus petite que le segment, et que l'excès de la figure circonscrite sur la figure inscrite est plus petit que l'excès du cône sur le segment, il est évident que la figure circonscrite sera plus petite que le cône Ψ.

Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΔE est au premier des cylindres placés dans la figure circonscrite, qui a pour axe la droite ΔE comme la surface Ω est à la surface ΞM ; car ces cylindres sont égaux entre eux, ainsi que ces surfaces. De plus, chacun des autres cylindres qui sont placés dans le cylindre total, et qui ont pour axe une droite égale à ΔE est au cylindre qui lui est correspondant dans la figure inscrite, et qui a le même axe, comme la surface Ω est à la surface correspondante parmi celles qui sont appliquées à la droite Ξ, et dont les parties excédantes sont des carrés ; parce que chacun des cylindres circonscrits, le plus grand étant excepté, est égal à chacun des cylindres inscrits, le plus grand n'étant pas excepté. Donc le cylindre total est à la figure inscrite comme la somme des surfaces Ω est à la somme des surfaces qui sont appliquées, et dont les parties excédantes sont des carrés. Mais on a démontré que la raison de la somme des surfaces Ω à la somme de toutes les autres surfaces est moindre que la raison de la droite ΞM à une droite composée de la moitié de Ξ et du tiers de M. Donc la raison du cylindre total à la figure circonscrite sera moindre que la raison de ZΔ à ΘΡ. Mais ZΔ est à ΘΡ comme le cylindre total est au cône Ψ. Donc la raison de ce même cylindre à la figure circonscrite est moindre que la raison de ce cylindre au cône Ψ. Donc la figure circonscrite est plus grande que le cône Ψ. Ce qui est impossible ; car on a démontré que la figure circonscrite est plus petite que le cône Ψ. Donc le segment du conoïde n'est pas plus petit que le cône Ψ. Donc, puisqu'il n'est ni plus grand ni plus petit, la proposition est démontrée.

PROPOSITION XXVIII.

Si un segment d'un conoïde hyperbolique est retranché par un plan non perpendiculaire sur l'axe, le segment du conoïde sera au segment de cône qui a la même base et le même axe que le segment comme une droite composée de l'axe du segment, et du triple de la droite ajoutée à l'axe est à une droite composée de l'axe du segment, et du double de la droite ajoutée à l'axe.

Qu'un segment d'un conoïde hyperbolique soit retranché par un plan, comme nous l'avons dit. Coupons le segment par un autre plan conduit par l'axe, et perpendiculaire sur le premier. Que cette section soit l'hyperbole ABΓ ; que la section du plan qui retranche le segment soit la droite ΓA ; et enfin que le sommet du cône qui contient le conoïde soit le point Θ. Par le point B, conduisons la droite ΦΨ parallèle à AΓ ; cette droite sera tangente à l'hyperbole au point B. Prolongeons la droite qui joint le point Θ et le point B ; cette droite partagera AΓ en deux parties égales (α) ; le point B sera le sommet du segment ; la droite BΔ, son axe, et enfin la droite BΘ, l'ajoutée à l'axe. Que les droites ΘZ et ZH soient égales chacune à BΘ, et par la droite ΦΨ faisons passer un plan parallèle au plan conduit par AΓ ; ce plan touchera le conoïde au point B. Puisque le plan conduit par AΓ coupe le conoïde sans être perpendiculaire sur l'axe, la section sera une ellipse qui aura pour grand diamètre la droite ΓA (14). Puisque l'on a une ellipse décrite autour de AΓ comme diamètre, et que la droite BΔ est menée de son centre dans le plan qui passe par le diamètre, et qui est perpendiculaire sur le plan de l'ellipse, on peut trouver un cylindre qui ait son axe sur la droite BΔ, et dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (10). Ce cylindre étant trouvé, on aura un certain segment de cylindre ayant la même base et le même axe que le segment du conoïde et dont l'autre base sera le plan conduit par ΦΨ. De plus, on pourra trouver un cône qui ait pour sommet le point B, et dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (9). Ce cône étant trouvé, on aura un segment de cône ayant la même base et le même axe que le segment du cylindre et le segment du conoïde. Il faut démontrer que le segment du conoïde est au segment de cône dont nous venons de parler comme HΔ est à ΔZ.

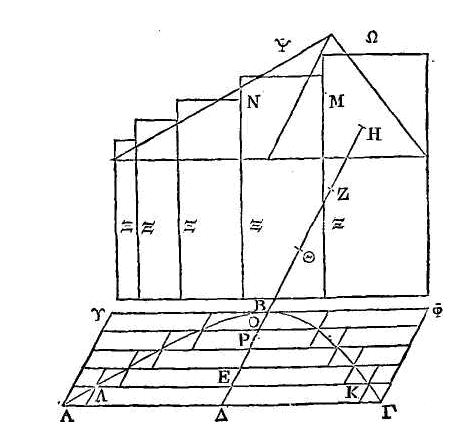
Que HΔ soit à ΔZ comme le cône Ψ est au segment de cône. Je dis que le segment du conoïde sera égal au cône Ψ ; car si le segment du conoïde n'est pas égal au cône Ψ, qu'il soit plus grand, si cela est possible. Inscrivons dans le segment du conoïde une figure solide composée de segments de cylindre qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du segment du conoïde sur le cône Ψ. Puisque l'excès de la figure circonscrite qui est plus grande que le segment sur la figure inscrite est plus petit que l'excès du segment sur le cône Ψ, il est évident que la figure inscrite sera plus grande que le cône Ψ.

Prolongeons les plans de tous les segments qui sont dans la figure inscrite jusqu'à la surface du segment de cylindre qui a la même base et le même axe que le segment du conoïde. Que BΡ soit la troisième partie de BΔ ; et faisons le reste comme auparavant. Le premier des segments placés dans le segment total de cylindre, qui a pour axe la droite ΔE est au premier des segments placés dans la figure inscrite, qui a pour axe ΔE comme le carré de AΔ est au carré de KE ; car les segments qui ont la même hauteur sont entré eux comme leurs bases. Mais les bases sont des ellipses semblables; donc ces bases sont entre elles comme les carrés des diamètres correspondants (7).

Mais le carré de AΔ est au carré de KE comme la surface comprise sous ZΔ, ΔB est a la surface comprise sous ZE, EB; parce que l'on a mené la droite ZΔ du point Θ où les asymptotes se rencontrent, et que les droites AΔ, KE sont parallèles à la tangente menée par le point B (β) : de plus, la surface comprise sous ZΔ, ΔB est égale à la surface Ω, et la surface comprise sous ZE, EB est égale à la surface ΞN. Donc le premier des segments placés dans le segment total, qui a pour axe la droite ΔE est au premier segment qui est placé dans la figure inscrite, et qui a pour axe la droite ΔE comme la surface Ω est à la surface ΞN. De même chacun des autres segments qui sont placés dans le segment total, et qui ont pour axe une droite égale à ΔE est au segment correspondant qui est placé dans la figure inscrite, et qui a pour axe une droite égale à ΔE, comme la surface Ω est à la surface correspondante parmi les surfaces qui sont appliquées à la droite ΞΧ, et dont les parties excédantes sont des carrés. On a donc certaines quantités, savoir les segments qui sont placés dans le cylindre total, et certaines autres quantités, savoir les surfaces où se trouve la lettre Ω, qui sont en même nombre que les segments, et qui sont proportionnelles deux à deux. Mais ces segments sont comparés avec d'autres segments qui sont dans la figure inscrite ; et le dernier n'est point comparé avec un autre; et de plus, les surfaces Ω sont comparées, sous les mêmes raisons, avec d'autres surfaces correspondantes qui sont appliquées à la ligne Ξ, et dont les parties excédantes sont des carrés; et la dernière n'est point comparée avec une autre. Il est donc évident que la somme des premiers segments est à la somme des seconds comme la somme de toutes les surfaces Ω est à la somme de toutes celles qui sont appliquées, la plus grande étant exceptée (2). Mais la raison de la somme des surfaces Ω à la somme de toutes surfaces appliquées, la plus grande étant exceptée, est plus grande que la raison de la droite MΞ à une droite composée de la moitié de Ξ et du tiers de M (2). Donc, la raison du segment total à la figure inscrite est plus grande que la raison de la droite ΞM à une droite composée de la moitié de Ξ et du tiers de M ; et par conséquent plus grande que la raison de ZΔ à ΘΡ. Donc, la raison du segment total à la figure inscrite est plus grande que la raison du segment total au cône Ψ. Ce qui est impossible ; car on a démontré que la figure inscrite est plus grande que le cône Ψ. Donc le segment du conoïde n'est pas plus grand que le cône Ψ.

Si l’on suppose que le segment du conoïde est plus petit que le cône Ψ, nous inscrirons dans ce segment une figure solide composée de segments de cylindre qui aient la même hauteur, et nous lui en circonscrirons une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du cône Ψ sur le segment. Nous démontrerons de la même manière que la figure circonscrite est plus petite que le cône Ψ ; et que la raison du segment de cylindre qui a la même base et le même axe que le segment du conoïde à la figure circonscrite est moindre que la raison de ce segment de cylindre au cône Ψ. Ce qui ne peut être. Donc le segment du conoïde n'est pas plus petit que le cône Ψ ; donc la proposition est évidente.

PROPOSITION XXIX.

La moitié d'un sphéroïde quelconque coupé par un plan conduit par le centre, et perpendiculaire sur l’axe est double du cône qui a la même base et le même axe que le segment.

Qu'un sphéroïde soit coupé par un plan conduit par le centre et perpendiculaire sur l'axe; qu'il soit encore coupé par un autre plan conduit par l'axe ; que la section du sphéroïde soit l'ellipse ABΓΔ, ayant pour diamètre l'axe du sphéroïde BΔ, et pour centre le point Θ : il est indifférent que BΔ soit le grand ou le petit diamètre de l'ellipse. Que la section du plan qui coupe le segment soit la droite ΓA. Cette droite passera par le centre, et fera des angles droits avec BΔ ; parce que l'on suppose que ce plan passe par le centre, et qu'il est perpendiculaire sur l'axe. Il faut démontrer que le segment qui est la moitié du sphéroïde, et qui a pour base le cercle décrit autour de AΓ comme diamètre, et pour sommet le point B, est double du cône qui a la même base et le même axe que ce segment.

Que le cône Ψ soit double de celui qui a la même base et le même axe ΘB que le segment. Je dis que la moitié du sphéroïde est égale au cône Ψ. Car si la moitié du sphéroïde n'est pas égale au cône Ψ, supposons d'abord qu'elle soit plus grande, si cela est possible. Dans le segment qui est la moitié du sphéroïde, inscrivons une figure solide composée de cylindres, ayant une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du demi-sphéroïde sur le cône Ψ. Puisque la figure circonscrite est plus grande que le demi-sphéroïde, l'excès du demi-sphéroïde sur la figure inscrite sera plus petit que l'excès du demi-sphéroïde sur le cône Ψ, il est évident que la figure inscrite dans le demi-segment sera plus grande que le cône Ψ.

Soit un cylindre qui ait pour base le cercle décrit autour de AΓ comme diamètre, et pour axe la droite BΘ. Puisque ce cylindre est triple du cône qui a la même base et le même axe que le segment, et que le cône Ψ est double de ce cône, il est évident que ce cylindre sera égal à trois fois la moitié du cône Ψ. Prolongeons les plans de tous les cylindres dont la figure inscrite est composée jusqu'à la surface du cylindre qui a la même base et le même axe que le segment. Le cylindre total sera partagé en autant de cylindres qu'il y en a dans la figure circonscrite, et chacun de ces cylindres sera égal au plus grand de ceux-ci. Prenons des droites où se trouve la lettre Ξ ; que ces droites soient en même nombre que les segments de la droite BΘ, et que chacune d'elles soit égale à la droite BΘ : sur chacune d'elles décrivons un carré. Du dernier de ces carrés retranchons un gnomon qui ait pour largeur la droite BI, ce gnomon sera égal à la surface comprise sous BI, IΔ (β). Du carré suivant retranchons un gnomon qui ait une largeur double de BI ; ce gnomon sera égal à la surface comprise sous BΧ, ΧΔ. Continuons de retrancher de chaque carré qui suit un gnomon qui ait une largeur plus grande d'un segment que la largeur du gnomon qui précède; chacun de ces gnomons sera égal à une surface comprise sous deux segments de BΔ, un de ces segments étant égal à la largeur du gnomon. Mais le carré qui reste du second carré a un côté égal à la droite ΘE (γ) ; donc le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΘE est au premier des cylindres placés dans la figure inscrite, qui a pour axe la même droite ΘE comme le carré de ΔΘ est au carré de KE, et par conséquent comme la surface comprise sous BΘ, ΘΔ est à la surface comprise sous BE, EΔ (δ). Donc le premier cylindre est au second cylindre comme le premier carré est au gnomon qui a été retranché du second carré. Semblablement, chacun des autres cylindres qui ont pour axe une droite égale à ΘE sera au cylindre qui est dans la figure inscrite, et qui a le même axe comme le carré qui lui correspond est au gnomon qui a été retranché du carré suivant. On a donc certaines quantités, savoir les cylindres qui sont placés dans le cylindre total, et certaines autres quantités, savoir les carrés des droites Ξ, Ξ qui sont en même nombre que les cylindres ; et ces quantités sont proportionnelles deux à deux. Mais ces cylindres sont comparés à d'autres quantités, savoir aux cylindres placés dans la figure inscrite, et le dernier n'est point comparé à un autre ; et les carrés sont comparés à d'autres quantités dans les mêmes raisons, savoir aux gnomons correspondants qui sont retranchés des carrés, et le dernier carré n'est point comparé à un autre. Donc la somme de tous les cylindres placés dans le cylindre total est à la somme de tous les autres cylindres comme la somme de tous les carrés est à la somme de tous les gnomons qui en sont retranchés (3). Donc le cylindre qui a la même base et le même Axe que le segment est à la figure inscrite comme la somme de tous les carrés est à la somme de tous les gnomons qui en sont retranchés. Mais la somme de ces carrés est plus grande que trois fois la moitié de la somme des gnomons qui en sont retranchés.

En effet, on a pris certaines lignes ΞΡ, ΞΣ, ΞT, ΞΥ, ΞΦ, qui se surpassent également, et dont la plus petite est égale à leur excès ; l'on a pris de plus d'autres lignes désignées par les lettres Ξ Ξ qui sont en même nombre que les premières, et dont chacune est égale à la plus grande des dernières. Donc la somme des carrés construits sur les lignes dont chacune est égale à la plus grande est plus petite que le triple de la somme des carrés construits sur les droites qui se surpassent également ; et si l'on retranche le carré construit sur la plus grande droite, cette somme sera plus grande que le triple de la somme des carrés restants ; ce qui a été démontré dans les choses que nous avons publiées sur les hélices (10, cor.). Mais puisque la somme de tous ces carrés est plus petite que le triple de la somme des autres carrés qui ont été retranchés de ceux-ci ; il est évident que cette somme est plus grande que trois fois la moitié de la somme des surfaces restantes (α). Donc cette somme est plus grande que trois fois la moitié de la somme des gnomons. Donc aussi le cylindre qui a la même base et le même axe que le segment est plus grand que trois fois la moitié de la figure inscrite (β). Ce qui est impossible ; car ce cylindre est égal à trois fois la moitié du cône Ψ, et l'on a démontré que la figure inscrite est plus grande que le cône Ψ. Donc la moitié du sphéroïde n'est pas plus grande que le cône Ψ.

La moitié du sphéroïde n'est pas plus petite que le cône Ψ. Qu'elle soit plus petite, si cela est possible. Inscrivons de nouveau dans la moitié du sphéroïde une figure solide composée de cylindres qui aient la même hauteur ; et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès du cône Ψ sur la moitié du sphéroïde ; et faisons le reste comme auparavant, Puisque la figure inscrite est plus petite que le segment, il est évident que la figure circonscrite sera plus petite que le cône Ψ.

Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΘE est au premier des cylindres placés dans la figure circonscrite, qui a pour axe la droite ΘE, comme le premier carré est à ce même carré. Le second des cylindres placés dans le cylindre total, qui a pour axe la droite EΠ est au second des cylindres placés dans la figure, circonscrite, qui a pour axe la droite EΠ, comme le, second carré est au gnomon qui en est retranché. De même, chacun des autres cylindres qui sont placés dans le cylindre total, et qui ont pour axe une droite égale à ΘE est au cylindre correspondant qui est placé dans la figure circonscrite, et qui a le même axe, comme le carré correspondant est au gnomon qui en est retranché. Donc la somme de tous les cylindres qui sont placés dans le cylindre total est à la somme de tous les cylindres qui sont placés dans la figure circonscrite comme la somme de tous les carrés est à une surface égale à la somme du premier carré, et des gnomons qui sont retranchés des autres carrés (2). Mais la somme de tous les carrés est plus petite trois fois la moitié d'une surface égale à la somme du premier carré, et des gnomons qui sont retranchés des autres carrés ; parce que cette somme est plus grande que le triple de la somme des carrés construits sur les droites inégales, le carré construit sur la plus grande droite étant excepté (Hélices, pro. 10. cor.). Donc, le cylindre qui a la même base et le même axe que le segment est plus petit que trois fois la moitié de la figurée circonscrite. Ce qui ne peut être; car ce cylindre est égal à trois fois la moitié du cône Ψ; et l'on a démontré que la figure circonscrite est plus petite que le cône Ψ. Donc la moitié du sphéroïde n'est pas plus petite que le cône Ψ. Donc elle lui est égale, puisqu'elle n'est ni plus grande ni plus petite.

PROPOSITION XXX.

Si un sphéroïde quelconque est coupé par un plan conduit par le centre et non perpendiculaire sur l'axe, la moitié du sphéroïde sera encore double d'un segment de cône qui aura la même base et le même axe que le segment.

Coupons le sphéroïde. Coupons-le ensuite par un autre plan conduit par l'axe et perpendiculaire sur le plan coupant; que la section du sphéroïde soit l'ellipse ABΓΔ, dont le centre est le point Θ ; et que la section du plan coupant soit la droite AΓ. Cette droite passera par le point Θ ; parce qu'on a supposé que le plan était conduit par le centre. On aura donc une certaine ellipse décrite autour de AΓ comme diamètre AΓ, parce qu'on a supposé que le plan coupant n'était pas perpendiculaire sur l’axe. Menons les droites KΛ, MN parallèles à AΓ ; et que ces droites soient tangentes à l'ellipse aux points B, Δ ; et par ces droites faisons passer des plans parallèles à celui qui a été conduit par la droite AΓ. Ces plans toucheront le sphéroïde aux points B, Δ, la droite qui joint les points B, Δ passera par le point Θ (18); les sommets des segments seront les points B, Δ, et les axes les droites BΘ, ΘΔ. On peut donc trouver un cylindre dont l'axe soit la droite BΘ, dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (10). Ce cylindre étant trouvé, on aura un segment de cylindre qui aura la même base et le même axe que la moitié du sphéroïde. On peut de plus trouver un cône qui ait son sommet au point B, et dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (9). Ce cône étant trouvé, on aura un certain segment de cône qui aura la même base et le même axe que le segment du sphéroïde; Je dis que la moitié du sphéroïde est double de ce cône.

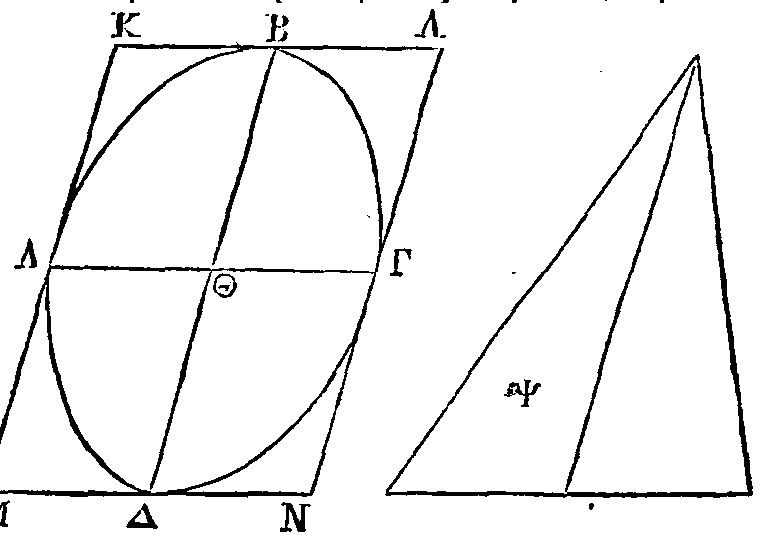
Que le cône Ψ soit double de ce segment de cône. Si la moitié du sphéroïde n'est pas égale au cône Ψ, qu'il soit plus grand, si cela est possible. Inscrivons dans la moitié du sphéroïde une figure composée de segments de cylindre qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès de la moitié du sphéroïde sur le cône Ψ. Nous démontrerons de la même manière que nous l'avons fait plus haut, que la figure inscrite est plus grande que le cône Ψ ; que le segment de cylindre qui a la même base et le même axe que ce segment est égal à trois fois la moitié du cône Ψ ; et que ce segment est plus grand que trois fois la moitié de la figure inscrite dans la moitié du sphéroïde. Ce qui ne peut être. Donc la moitié du sphéroïde n'est pas plus grande que le cône Ψ.

Que la moitié du sphéroïde soit plus petite que le cône Ψ.

Inscrivons dans la moitié du sphéroïde une figure solide composée de segments de cylindres qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès du cône Ψ sur la moitié du sphéroïde. Nous démontrerons encore, comme nous l'avons fait plus haut, que la figure circonscrite est plus petite que le cône Ψ ; que le segment de cylindre qui a la même base et le même axe que le segment du sphéroïde est égal à trois fois la moitié du cône Ψ ; et que ce segment est plus petit que trois fois la moitié de la figure circonscrite. Ce qui ne peut être. Donc la moitié du sphéroïde n'est pas plus petite que le cône Ψ. Mais si la moitié du sphéroïde n'est ni plus grande ni plus petite que ce cône, elle lui est égale. Donc la proposition est évidente.

PROPOSITION XXXI.

Qu'un segment quelconque d’un sphéroïde soit retranché par un plan perpendiculaire sur l'axe, sans passer par le centre; que ce même segment soit coupé par un autre plan conduit par l'axe ; que la section du sphéroïde soit l'ellipse ABΓ, dont le diamètre BZ est l’axe du sphéroïde, et dont le centre est le point Θ ; et que la section du plan qui retranche le segment soit la droite AΓ. Cette droite sera perpendiculaire sur BZ ; parce que l'on a supposé que le plan coupant était perpendiculaire sur l'axe. Que le segment qui est produit par cette section, et qui a son sommet au point B soit plus petit que la moitié du sphéroïde; et que ZH soit égal à BΘ. Il faut démontrer que le segment qui a pour sommet le point B est au cône qui a la même base et le même axe que ce segment comme ΔH est à ΔZ.

Le segment d'un sphéroïde quelconque coupé par un plan perpendiculaire sur l'axe qui ne passe pas par le centre est au cône qui a la même base et le même axe que ce segment, comme une droite composée de la moitié de l'axe du sphéroïde, et de l'axe du plus grand segment est à l'axe du plus grand segment.

Soit un cylindre qui ait la même base et le même axe que le plus petit segment. Prenons de plus un cône Ψ qui soit au cône qui a la même base et le même axe comme ΔH est à ΔZ. Je dis que le cône Ψ est égal au segment qui a son sommet au point B. Car si ce cône ne lui est pas égal, qu'il soit d'abord plus petit, si cela est possible. Inscrivons dans le segment une figure solide composée de cylindres qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du segment du sphéroïde sur le cône Ψ (21). Puisque l'excès de la figure circonscrite sur la figure inscrite est plus petit que l'excès du segment sur ce cône, il est évident que la figure inscrite est plus grande que le cône Ψ.

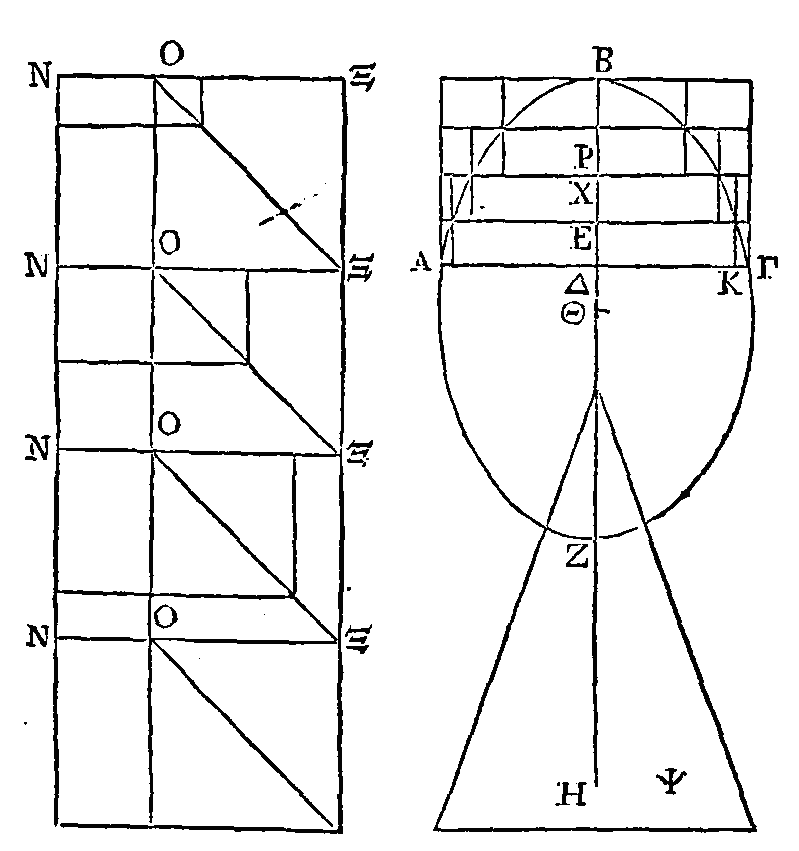
Que BΡ soit la troisième partie de BΔ. Puisque BH est triple de BΘ, et BΔ triple de BΡ, la droite ΔH sera triple de ΘΡ. (α) Donc le cylindre qui a la même base que le segment, et pour axe la droite BΔ est au cône qui a la même base et le même axe comme ΔH est à ΘΡ. Mais le cône dont nous venons de parler est au cône Ψ comme ΔZ est à ΔH. Donc, par raison d'égalité dans la proportion troublée, le cylindre qui a la même base et le même axe que le segment est au cône Ψ comme ΔZ est à ΘΡ. Prenons à présent les lignes dans lesquelles sont les lettres Ξ N ; supposons que ces droites soient en même nombre que les segments qui sont dans la droite BΔ, et qu'elles soient égales chacune à la droite ZΔ. Que chacune des droites ΞO soit égale à la droite BΔ. Chacune des droites restantes NO sera double de la droite ΘΔ. (β) Appliquons à chacune des droites NΞ une surface qui ait une largeur égale à BΔ ; dans chacune de ces surfaces construisons un carré, et menons sa diagonale. Retranchons de la première de ces surfaces un gnomon qui ait une largeur égale à BE ; retranchons de la seconde un gnomon qui ait une largeur égale à BΧ ; retranchons de la même manière de chaque surface qui suit immédiatement un gnomon qui ait une largeur plus petite d'un segment de BΔ que le gnomon précédent. Il est évident que le gnomon qui a été retranché de la première surface sera égal à la surface comprise sous BE, EZ, et le reste sera une surface appliquée sur NO, dont la partie excédante sera un carré qui a pour côté une droite égale à ΔE (γ). Le gnomon qui est retranché de la seconde surface sera égal à la surface comprise sous ZΧ, ΧB, et le reste sera une surface appliquée sur NO dont la partie excédante sera un carré, et ainsi de suite. Cela étant ainsi, prolongeons les plans de tous les cylindres dont la figure inscrite dans le segment est composée jusqu'à la surface du cylindre qui a la même base et le même axe que le segment. Le cylindre total sera partagé en autant de cylindres qu'il y en a dans la figure circonscrite, et chacun de ces cylindres sera égal au plus grand de ces derniers. Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΔE, est au premier des cylindres placés dans la figure inscrite, qui a pour axe la droite ΔE comme le carré de AΓ est au carré de KE. Mais cette dernière raison est la même que celle de la surface comprise sous BΔ, ΔZ à la surface comprise sous BE, EZ.

Donc le premier des cylindres placés dans le cylindre total est au premier des cylindres placés dans la figure inscrite comme la première surface est ail gnomon qui en a été retranché. Semblablement, chacun des autres cylindres qui sont placés dans le cylindre total, et ^:qui ont pour axe une droite égale à ΔE sera au cylindre correspondant qui est placé dans la figure inscrite et qui a le même axe, comme la surface qui lui correspond est au gnomon qui en a été retranché. On a donc certaines quantités, savoir les cylindres qui sont placés dans le cylindre total; on a de plus certaines autres quantités, savoir les surfaces qui sont appliquées sur ΞN, et qui ont pour largeur une droite égale à BΔ ; et ces dernières quantités sont en même nombre que les cylindres, et leur sont proportionnels deux à deux. Mais ces cylindres sont comparés à d'autres cylindres qui sont dans la figure inscrite, le dernier n'étant point comparé à un autre; et ces surfaces sont comparées à d'autres semblablement placées, dans des raisons égales, c'est-à-dire aux gnomons qui sont retranchés de ces premières surfaces, et la dernière surface n'est point comparée avec une autre. Il est donc évident que la somme de tous les premiers cylindres est à la somme de tous les autres cylindres tomme la somme de toutes ces surfaces est à la surface de tous les gnomons (2). Donc le cylindre qui a la même base et le même axe que le segment est à la figure inscrite comme la somme de toutes ces surfaces est à la somme de tous les gnomons. Mais l'on a certaines lignes égales dans lesquelles sont les lettres N O, et à chacune desquelles on a appliqué une surface dont la partie excédante est un carré ; les côtés des carrés se surpassent également, et cet excès est égal au côté du plus petit carré : on a de plus d'autres surfaces appliquées à NΞ, qui ont pour largeur une droite égale à BΔ, qui sont en même nombre que les premières, et dont chacune est égale à la plus grande de celles-ci. Il est donc évident que la raison de la somme de toutes les surfaces dont chacune est égale à la plus grande, à la somme de toutes les autres est moindre que la raison de ΞN à une droite composée de la moitié de NO et du tiers de ΞO (3). Il est donc évident que la raison de la somme de ces surfaces à la somme des gnomons est plus grande que la raison de la droite ΞN à une droite composée de la moitié de NO et des deux tiers de ΞO (α). Donc la raison du cylindre qui a la même base et le même axe que le segment à la figure inscrite dans le segment est plus grande que la raison de ΞN à une droite composée de la moitié de NO et des deux tiers de OΞ. Mais la droite ΔZ est égale à ΞN ; la droite ΔΘ est égale à la moitié de NO, et la droite ΔΡ égale aux deux tiers de ΞO ; donc la raison du cylindre total à la figure inscrite dans le segment est plus grande que la raison de ΔZ à ΘΡ. Mais l'on a démontré que le cylindre est au cône Ψ comme ΔZ est à ΘΡ ; donc la raison du cylindre à la figure inscrite est plus grande que la raison de ce même cylindre au cône Ψ. Ce qui ne peut être ; car on a démontré que la figure inscrite est plus grande que le cône Ψ. Donc le segment du sphéroïde n'est pas plus grand que le cône Ψ.

Que ce segment soit plus petit que le cône Ψ, si cela est possible. Inscrivons de nouveau dans le segment une figure solide composée de cylindres qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès du cône Ψ sur le segment, et faisons le reste comme auparavant. Puisque la figure inscrite est plus petite que le segment, et que l'excès de la figure circonscrite sur la figure inscrite est plus petit que l'excès du cône Ψ sur le segment, il est évident que la figure circonscrite est plus petite que le cône Ψ.

Le premier des cylindres placés dans le cylindre total, qui a pour axe la droite ΔE est au premier des cylindres placés dans la figure circonscrite, qui a le même axe, comme la dernière des surfaces qui sont appliquées à ΞN, et qui ont une largeur égale à la droite BΔ est à cette même surface; car ces cylindres sont égaux, ainsi que ces surfaces ; le second des cylindres placés dans le cylindre total, qui a pour axe une droite égale à ΔE est au cylindre correspondant dans la figure circonscrite comme la première des surfaces qui sont appliquées à ΞΛ, et qui ont une largeur égale à BΔ est au gnomon qui en est retranché ; et chacun des autres cylindres qui sont placés dans le cylindre total et qui ont un axe égal à la droite ΔE est au cylindre qui lui est correspondant dans la figure circonscrite comme la surface qui lui est correspondante parmi celles qui sont appliquées à ΞN est au gnomon qui en a été retranché avant celui qu'on nomme le dernier. Donc, par la même raison qu'auparavant, la somme de tous les cylindres placés dans le cylindre total est à la somme de tous les cylindres placés dans la figure circonscrite comme la somme de toutes les surfaces qui sont appliquées à ΞN est à une surface composée de la dernière surface et de tous les gnomons qui sont retranchés des autres surfaces. Puisque l'on a démontré que la raison de la somme de toutes les surfaces appliquées à ΞN à la somme de. toutes les surfaces qui sont appliquées à NO, et dont les parties excédantes sont des carrés, la plus grande étant exceptée, est plus grande que la raison de ΞN à une droite égale composée de la moitié de NO et du tiers de ΞO, il est évident que la raison de la somme de ces mêmes surfaces à la somme des surfaces restantes, savoir la dernière surface et les gnomons qui sont retranchés des surfaces restantes est moindre que la raison de la droite de ΞN à une droite composée de la moitié de NO et des deux tiers de ΞO. Il est donc évident que la raison du cylindre qui a la même base et le même axe que le segment à la figure circonscrite est moindre que la raison de ZΔ à ΘΡ. Mais la raison du cylindre dont nous venons de parler au cône Ψ est la même que celle de ΔZ à ΘΡ, donc la raison du cylindre à la figure circonscrite est moindre que la raison de ce même cylindre au cône Ψ. Ce qui ne peut être; car on a démontré que la figure circonscrite est plus petite que le cône Ψ. Donc le segment du sphéroïde n'est pas plus petit que le cône Ψ. Donc il lui est égal, puisqu'il n'est ni plus grand ni plus petit.

PROPOSITION XXXII.

Si un sphéroïde est coupé par un plan qui ne passe pas par le centre, et qui ne soit pas perpendiculaire sur l'axe, le plus petit segment sera au segment de cône qui a la même base et le même axe que le segment comme une droite composée de la moitié de la droite qui joint les sommets des segments qui sont produits par le plan coupant et de l'axe du petit segment est à l'axe du grand segment.

Coupons un sphéroïde quelconque, comme nous venons de le dire. Coupons ensuite le sphéroïde par un plan conduit par l’axe et perpendiculaire sur le premier ; que cette section du sphéroïde soit l'ellipse ABΓΔ, et que la section du plan qui retranche le segment soit la droite ΓA. Menons à la droite AΓ les parallèles ΠΡ, ΣT qui touchent l'ellipse aux points B, Z ; et par ces parallèles faisons passer des plans parallèles au plan conduit par AΓ. Ces plans toucheront le sphéroïde aux points B, Z, et la droite BZ qui joindra les sommets des segments passera par le centre (18). Que le point Θ soit le centre du sphéroïde et de l'ellipse. Puisque le sphéroïde est coupé par un plan non perpendiculaire sur l'axe, la section est une ellipse qui a pour diamètre la droite AΓ (15). Prenons un cylindre dont l’axe soit la droite BΔ, et dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (10). Prenons aussi un cône qui ait son sommet au point B, et dans la surface duquel se trouve l'ellipse décrite autour de AΓ comme diamètre (9). On aura un certain segment de cylindre ayant la même base et le même axe que le segment du sphéroïde ; on aura aussi un certain segment de cône ayant la même base et le même axe que le segment du sphéroïde. Il faut démontrer que le segment du sphéroïde dont le sommet est le point B est au segment de cône qui a la même base et le même axe que ce segment, comme ΔH est à ΔZ.

Que la droite ZH soit égale à la droite ΘZ. Prenons un cône Ψ qui soit au segment de cône qui a la même base et le même axe que le segment du sphéroïde, comme ΔH est à ΔZ. Si le segment du sphéroïde n'est pas égal au cône Ψ, qu'il soit d'abord plus grand, si cela est possible. Inscrivons dans le segment du sphéroïde une figure solide composée de segments de cylindre qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit plus petit que l'excès du segment du sphéroïde sur le cône Ψ. On démontrera, comme nous l'avons fait plus haut, que la figure inscrite est plus grande que le cône Ψ, et que la raison du segment de cylindre qui a la même base et le même axe que le segment à la figure inscrite est plus grande que la raison de ce segment de cylindre au cône Ψ. Ce qui ne peut être. Donc le segment du sphéroïde n'est pas plus grand que le cône Ψ.

Qu'il soit plus petit, si cela est possible. Inscrivons de nouveau dans le segment du sphéroïde une figure solide composée de segments de cylindre qui aient une hauteur égale, et circonscrivons-lui en une autre, de manière que l'excès de la figure circonscrite sur la figure inscrite soit moindre que l'excès du cône Ψ sur le segment du sphéroïde. On démontrera de la même manière que nous l'avons fait plus haut, que la figure circonscrite est plus petite que le cône Ψ, et que la raison du segment de cylindre qui a la même base et le même axe que le segment du sphéroïde à la figure circonscrite est moindre que la raison du segment de cylindre au cône Ψ. Ce qui ne peut être. Donc le segment du sphéroïde n'est pas plus petit que le cône Ψ. Donc ce qu'il fallait démontrer est évident.

PROPOSITION XXXIII.

Le grand segment d'un sphéroïde quelconque coupé non par son centre par un plan perpendiculaire sur l'axe est au cône qui a la même base et le même axe que ce segment, comme une droite composée de la moitié de l'axe du sphéroïde et de l'axe du petit segment est à l'axe du petit segment.

Coupons un sphéroïde quelconque comme on vient de le dire ; que ce même sphéroïde soit coupé par un autre plan conduit par l'axe et perpendiculaire sur le premier ; que cette section soit l'ellipse ABΓ ayant pour diamètre la droite BΔ qui est l'axe du sphéroïde, et que la section du plan qui retranche le segment soit la droite ΓA. Cette droite sera perpendiculaire sur EΔ. Que le grand segment soit celui qui a son sommet au point B, et que le centre du sphéroïde soit le point Θ. Faisons les droites ΔH, BZ chacune égale à ΔΘ. Il faut démontrer que le segment du sphéroïde dont le sommet est le point B est au cône qui a la même base et le même axe que ce segment comme EH est à EΔ.

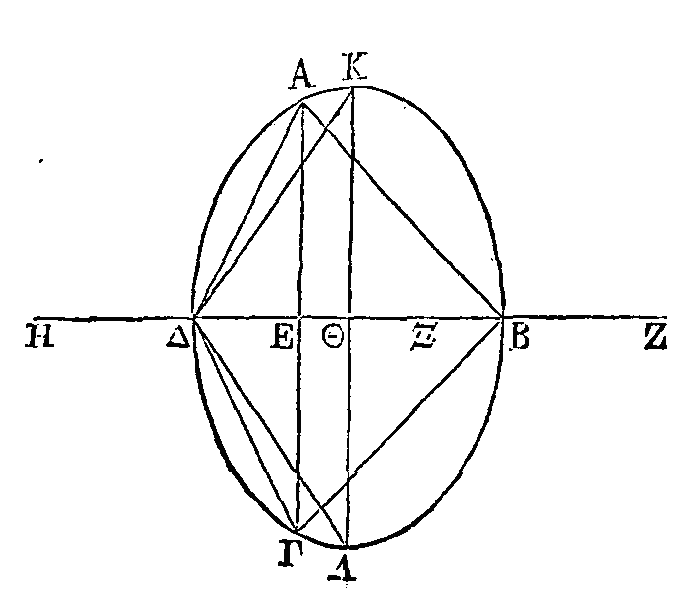
Coupons le sphéroïde par un plan conduit par le centre et perpendiculaire sur l'axe, et que le cercle qui est produit par cette section soit la base d'un cône qui ait son sommet sur Δ. Le sphéroïde total sera double du segment qui a pour base le cercle décrit sur KΛ comme diamètre et qui a pour sommet le point Δ. Mais le segment dont nous venons de parler est double du cône qui a la même base et le même axe que le segment. Ce qui a été démontré (29). Donc le sphéroïde total est quadruple du cône dont nous venons de parler. Mais ce cône et celui qui a pour base le cercle décrit autour de AΓ comme diamètre et pour sommet le point Δ sont en raison composée de la raison de ΘΔ à EΔ, et de la raison du carré de KΘ au carré de EA ; et la raison du carré de KΘ au carré de EA est la même que celle de la surface comprise sous BΘ, ΘΔ à la surface comprise sous BE, EΔ ; et de plus, la raison de ΘΔ à EΔ est la même que la raison de ΞΔ à ΘΔ. Donc la surface comprime sous ΞΔ, BΘ est à la surface comprise sous BΘ, ΘΔ comme ΔΘ est à ΔE. Mais la raison composée de la raison de la surface comprise sous ΞΔ, ΘB à la surface comprise sous BΘ, ΘΔ, et la raison de la surface comprise sous BΘ, ΘΔ à la surface comprise sous BE, EΔ sont les mêmes que la raison de la surface comprise sous ΞΔ, BΘ à la surface comprise sous BE, EΔ. Donc le cône qui a pour base le cercle décrit autour de KΛ comme diamètre, et qui a pour sommet le point Δ est au cône qui a pour base le cercle décrit autour de AΓ comme diamètre et pour sommet le point Δ, comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous BE, EΔ.

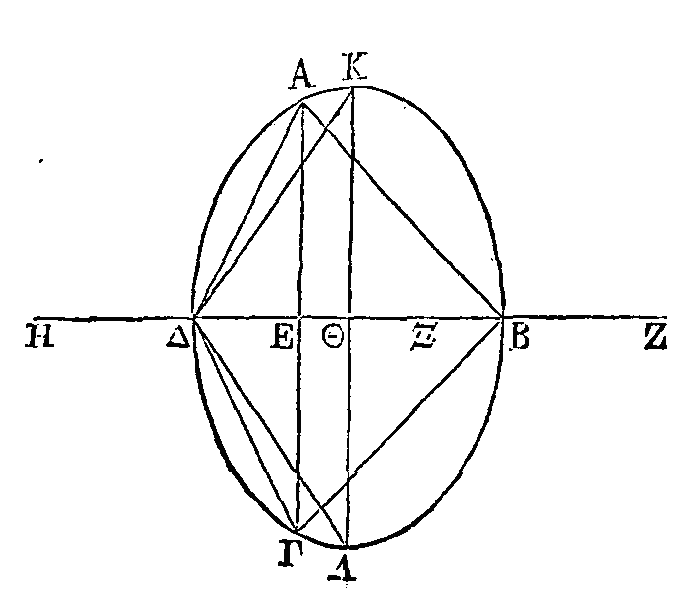
Mais le cône qui a pour base le cercle décrit autour de AΓ comme diamètre et pour sommet le point Δ est au segment du sphéroïde qui a la même base et le même axe, comme la surface comprise sous BE, EΔ est à la surface comprise sous ZE, EΔ, c'est-à-dire comme BE est à EZ ; car on a démontré qu'un segment plus petit que la moitié du sphéroïde est au cône qui a la même base et le même axe que ce segment, comme une droite composée de la moitié de l'axe du sphéroïde et de l'axe du grand segment est à l'axe du grand segment, c'est-à-dire comme ZE est à BE (32). Donc le cône qui est dans la moitié du sphéroïde est au segment qui est plus petit que la moitié du sphéroïde comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous ZE, ΔE. Mais le sphéroïde total est au cône qui est dans la moitié du sphéroïde comme la surface comprise sous ZH, ΞΔ est à la surface comprise sous BΘ, ΞΔ ; car le sphéroïde total et la première surface sont quadruples du cône et de la seconde surface; et le cône qui est dans la moitié du sphéroïde est au segment qui est plus petit que la moitié du sphéroïde comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous ZE, EΔ ; et de plus, le sphéroïde total est au plus petit segment comme la surface comprise sous ZH, ΞΔ est à la surface comprise sous ZE, EΔ ; donc le plus grand segment du sphéroïde est au plus petit comme l'excès de la surface comprise sous ZH, ΞΔ sur la surface comprise sous ZE, ΔE est à la surface comprise sous ZE, EΔ. Mais l'excès de la surface comprise sous ZH, ΞΔ sur la surface comprise sous ZE, EΔ est égal à la surface comprise sous ΞΔ, EH, conjointement avec la surface comprise sous ZE, ΞE ; donc le plus grand segment du sphéroïde est au plus petit comme la surface comprise sous ΞΔ, EH, conjointement avec la surface comprise sous ZE, ΞE est à la surface comprise sous ZE, EΔ.

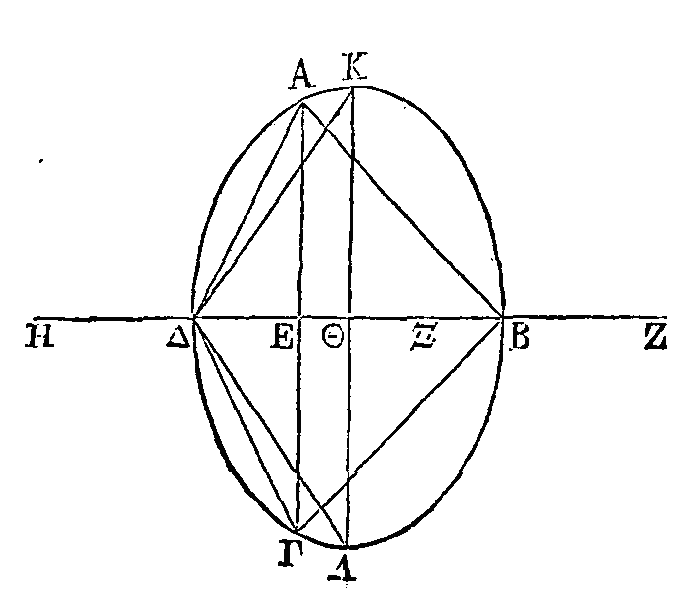
Mais le plus petit segment du sphéroïde est au cône qui a la même base et le même axe que lui, comme la surface comprise sous ZE, EΔ est à la surface comprise sous BE, EΔ ; car la première raison est la même que celle de ZE à BE ; et le cône qui est dans le plus petit segment est au  cône qui est dans le plus grand segment comme la surface comprise sous BE, EΔ est au carré de BE ; car ces cônes qui ont la même base sont entre eux comme leurs hauteurs. Donc le plus grand segment du sphéroïde est au cône qui est dans ce segment comme la surface comprise sous ΞΔ, EH, conjointement avec la surface comprise sous ZE, ΞE est au carré de BE. Mais cette raison est la même que celle de EH à EΔ ; parce que la surface comprise sous ΞΔ, EH est à la surface comprise sous ΞΔ, EΔ comme EH est à EΔ ; et que la surface comprise sous ZE, ΞE est à la surface comprise sous ZE, ΘE comme la surface EH est à EΔ ; car ΞE est à ΘE comme EH est à EΔ, les droites ΞΔ, ΘΔ, ΔE étant successivement proportionnelles, et ΘΔ étant égal à HΔ. Donc la surface comprise sous ΞΔ, EH, conjointement avec la surface comprise sous ZE, ΞE, est à la surface comprise sous ΞΔ, EΔ, conjointement avec la surface comprise sous ZE, ΘE comme EH est à EΔ. Mais le carré de BE est égal à la surface comprise sous ΞΔ, EΔ, conjointement avec la surface comprise sous ZE, ΘE; parce que le carré de BE est égal à la surface comprise sous ΞΔ, EΔ, et que l'excès du carré de BE sur le carré de BΘ est égal à la surface comprise sous ZE, ΘE, les droites BΘ, BZ étant égales entre elles. Il est donc évident que le grand segment du sphéroïde est au cône qui a la même base et le même axe que ce segment, comme EH est à EΔ.

PROPOSITION XXXIV.

Si un sphéroïde est coupé par un plan qui ne passe pas par le centre, et qui ne soit pas perpendiculaire sur l'axe, le plus grand segment du sphéroïde sera au segment de cône qui a la même base et le même axe que lui, comme une droite composée de la moitié de la droite qui joint les sommets des segments qui ont été produits par cette section, et de l'axe du petit segment est à l'axe du petit segment:

Coupons un sphéroïde par un plan, comme nous venons de le dire. Coupons ensuite le sphéroïde par un autre plan qui passe par l'axe et qui soit perpendiculaire sur le plan coupant.

Que la section du sphéroïde soit l'ellipse ABΓΔ, et la section du plan coupant, la droite ΓA. Menons à la droite AΓ les parallèles ΠΡ, ΣT qui touchent l'ellipse aux points Δ, B ; et par ces parallèles conduisons des plans parallèles au plan conduit par AΓ. Ces plans toucheront le sphéroïde aux points B, Δ, et les points B, Δ seront les sommets des segments. Menons la droite BΔ qui joigne les sommets des segments qui ont été engendrés ; cette droite passera par le centre (18). Que le centre soit le point Θ. Que le plus grand segment du sphéroïde soit celui dont le sommet est le point B. Faisons la droite ΔH égale à ΔΘ, et la droite BZ égale aussi à ΔΘ. Il faut démontrer que le plus grand segment est à un segment de cône qui a la même base et le même axe que ce segment, comme EH est à EΔ.

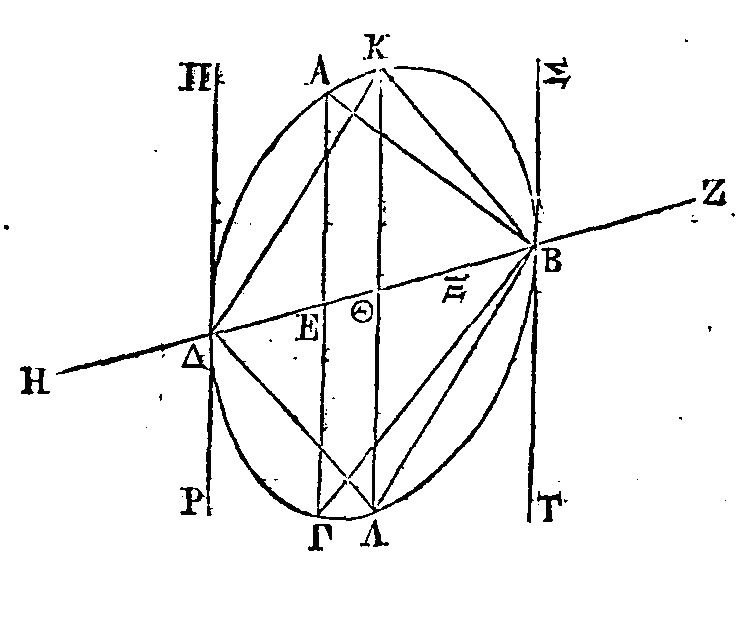
Coupons le sphéroïde par un plan conduit par le centre et parallèle au plan conduit par AΓ ; et inscrivons dans la moitié du sphéroïde un segment de cône qui ait son sommet au point Δ. Que la droite ΞΔ soit à la droite ΘΔ, comme ΔΘ est à EΔ. On démontrera de la même manière que nous l'avons fait plus haut, que le segment de cône inscrit dans la moitié du sphéroïde est au segment de cône inscrit dans le plus petit segment, comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous BE, EΔ ; et que le segment de cône inscrit dans le plus petit segment est au segment dans lequel il est inscrit, comme la surface comprise sous BE, EΔ est à la surface comprise sous ZE, EΔ. Donc le segment de cône inscrit dans la moitié du sphéroïde est au plus petit segment de ce sphéroïde, comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous ZE, EΔ. Donc le sphéroïde total sera au segment de cône inscrit dans la moitié du sphéroïde, comme la surface comprise sous ZH, ΞΔ est à la surface comprise sous BΘ, ΞΔ ; car le sphéroïde total et la première surface sont quadruples du cône et de la surface comprise sous BΘ, ΞΔ. Mais le segment de cône dont nous venons de parler est au plus petit segment du sphéroïde, comme la surface comprise sous ΞΔ, BΘ est à la surface comprise sous ZE, EΔ ; donc le sphéroïde total est au plus petit segment du sphéroïde comme la surface comprise sous ZH, ΞΔ est à la surface comprise sous EZ, EΔ.

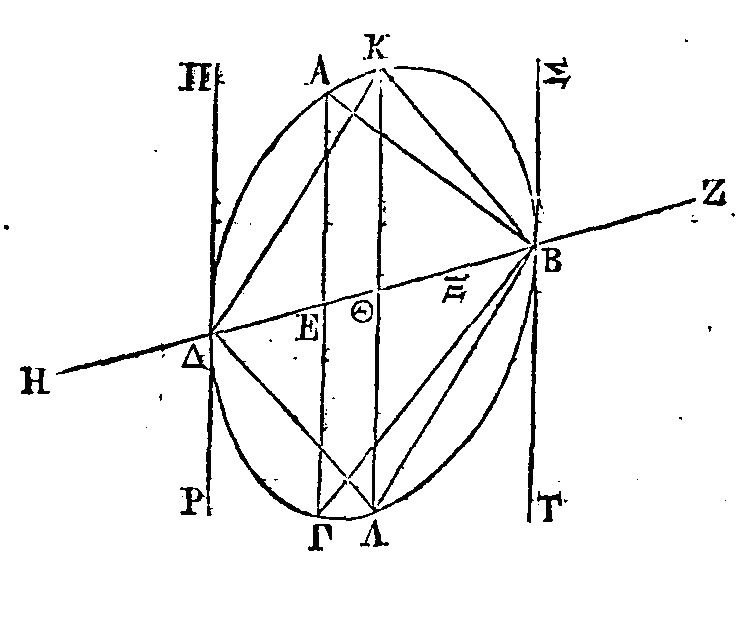
Mais le plus grand segment du sphéroïde est au plus petit comme l'excès de la surface comprise sous ZH, ΞΔ sur la surface comprise sous ZE, EΔ est à la surface comprise sous ZE, EΔ; et le plus petit segment du sphéroïde est au segment de cône qui lui est inscrit comme la surface comprise sous ZE, EΔ est à la surface comprise sous BE, EΔ ; car on a démontré que cette raison est la même que celle de ZE à BE ; et enfin le segment de cône inscrit dans le plus petit segment est au segment de cône inscrit dans le plus grand segment comme la surface comprise sous BE, EΔ est au carré de BE ; car les segments de cône dont nous venons de parler ayant la même base, sont entre eux comme leurs hauteurs, et ces hauteurs sont entre elles comme les droites ΔE, EB. Donc le plus grand segment du sphéroïde est au segment de cône qui lui est inscrit comme l'excès de la surface comprise sous HZ, ΞΔ sur la surface comprise sous ZE, EΔ est au carré de BE. On démontrera de la même manière que nous l'avons fait plus haut, que cette raison est la même que celle de EH à EΔ.

FIN DES CONOÏDES ET DES SPHEROIDES

COMMENTAIRE SUR LES CONOÏDES ET LES SPHÉROÏDES.

ARCHIMÈDE A DOSITHÉE.

(α) Dans Archimède l'ellipse, la parabole et l'hyperbole sont toujours nommées section du cône acutangle, section du cône rectangle et section du cône obtusangle.

Par cône acutangle, il entend un cône droit dont les côtés qui sont les intersections de sa surface et du plan conduit par l'axe, forment un angle aigu. Si ces intersections forment un angle droit, le cône s'appelle rectangle, et si elles forment un angle obtus, le cône s'appelle obtusangle.

En effet, que chacun de ces cônes soit coupé par un plan perpendiculaire sur un des côtés de l'angle formé par le plan qui passe par l'axe, il est évident que la section du cône acutangle sera une ellipse, puisque le plan coupant rencontrera l'autre côté du cône ; que la section du cône rectangle sera une parabole, puisque le plan coupant sera parallèle à l'autre côté, et que la section du cône obtusangle sera une hyperbole , puisque le plan coupant rencontrera le prolongement de l'autre côté.

Archimède ayant nommé section du cône rectangle, ce que nous appelons parabole, et section du cône obtusangle, ce que nous appelons hyperbole, il nomme conoïde rectangle, le solide de révolution engendré par une parabole, et conoïde obtusangle, le solide de révolution engendré par une hyperbole. Pour éviter les circonlocutions, et à l'exemple d'Apollonius, j'emploierai les mots ellipse, parabole et hyperbole, et par conséquent les mots conoïde parabolique et conoïde hyperbolique.

(β) Toutes les paraboles sont semblables; donc tous les conoïdes paraboliques sont encore semblables. Les hyperboles semblables sont celles dont les axes sont proportionnels. Donc les conoïdes hyperboliques semblables sont ceux qui sont engendrés par des hyperboles semblables.

PROPOSITION I.

(α) Soit a la plus petite des quantités inégales, et n le nombre de ces quantités ; la plus grande égalera an ; leur somme égalera n(an + a)/ 2, et le double de leur somme égalera (an + a)n, c'est-à-dire an² + an ; mais la somme des quantités égales est égale à an² ; donc la somme des quantités égales est plus petite que le double de la somme de celles qui se surpassent également de la quantité an, c'est-à-dire de la plus grande des quantités inégales. Mais la somme des quantités inégales, la plus grande étant exceptée, est égale à a(n — 1)(n — 1)/2, et le double de cette somme est égale à a(n — 1) (n — 1) , c'est-à-dire à an² — 2an + a; donc la somme des quantités égales surpasse le double de la somme des quantités inégales, la plus grande étant exceptée, de 2an — a, c'est-à-dire du double de la plus grande des quantités inégales, moins la plus petite de ces quantités. Donc la somme des quantités égales est plus grande que la somme des quantités inégales, la plus grande étant exceptée.

PROPOSITION II.

 (α) Soient les quantités a, ab, abc, etc.     ae, abf, abcg, etc.          d, db, dbc, etc.              de, dbf, dbcg, etc.

l'on aura a : ab :: d : db ; ab : abc :: db : dbc ; a : ae :: d : de ; ab : abf :: db : dbf ; abc : abcg :: dbc : dbcg, etc. Je dis que a + ab + abc : ae + abf + abcg :: d + db + dbc : de + dbf + dbcg. Ce qui est évident ; car en échangeant les moyens et en décomposant, on a

a(1 + b + bc) : d(1 + b+ bc) : : a (e + bf + bcg) : d (e + bf+ bcg), c'est-à dire a : d :: a : d.

(β) Cela est évident, car dans ce cas au lieu de la proportion a(1 + b + bc) : d(1 + b + bc) :: a (e + bf+ bcg) : d(e + If + bcg), on aurait a(1 + b) : d( 1 + b) :: a (e + bf) : d (e + bf).

PROPOSITION III.

(α) Appliquer à une ligne une surface dont la partie excédante soit un carré, c'est appliquer à cette ligne un rectangle tel que l'excès de sa hauteur sur cette même ligne soit égal à sa base:

(β) Voyez cette proposition et la note (α) qui l'accompagne.

(γ) Cette proposition d'Archimède pourrait se démontrer algébriquement de la manière suivante.

Que le côté du plus petit carré soit 1, et le nombre des carrés n. Que a soit une des lignes qu'Archimède appelle A. La somme des carrés sera égale à (2n³ + 3n²+n)/6, et la somme des rectangles où est la lettre A sera égale à (a+an)n/2, c'est-à-dire (an+ an²)/2. Donc la somme des carrés, conjointement avec la somme des rectangles , sera égale à ((2n³ + 3n²+n)/6) + (an+ an²)/2

La somme de tous les rectangles où sont les lettres Θ, I, K, Λ est égale à (a + n)n².

Il faut démontrer que la raison de (a + n)n² à ((2n³ + 3n²+n)/6) + (an+ an²)/2 est moindre que la raison de n+a à (n/3 + a/2), et que la raison de (n + a)n² à ((2n³ + 3n²+n)/6) + (an+ an²)/2 — (a+n)/n est plus grande que la raison de n+a  à  (n/3 + a/2), c'est-à-dire qu'il faut démontrer que

(n + a) n² / [((2n³ + 3n²+n)/6) + (an+ an²)/2] est plus petit que (n+a) / (n/3 + a/2), et que

(n + a) n² / [((2n³ + 3n²+n)/6) + ((an+ an²)/2) — (a+n)/n] est plus grand que (n+a) / (n/3 + a/2).

Dans le premier cas, je fais disparaître les dénominateurs, je supprime les facteurs communs, et la première quantité devient 2 n² + 3 an, et la seconde devient 2n² + 3an + 3a + 3n + 1. Or, la première quantité est plus petite que la seconde; donc le premier cas est démontré. Pour le second cas, je me conduis d'une manière semblable. La première quantité devient 2n² + 3an + 3a + 6n, et la seconde devient 2n² + 3an + 1. Or, la première quantité est plus grande que la seconde ; donc le second cas est aussi démontré.

(δ) Apollonius, liv. III, prop. 17 et 18.

PROPOSITION IV.

(β) Apollonius, liv. I, prop. 46.

(γ) Conduisons la droite ΔN tangente à la parabole au point Δ ; prolongeons HB, et du point Δ menons la perpendiculaire ΔM sur BH. Nommons ΔM, y, et BM, x ; que Λ soit le paramètre. On aura

ΔM = Racine carrée (Λx), MN = 2x, ΔN = Racine carrée (4x² + Λx), AZ= Racine carrée [(4x + Λ) ΔZ].

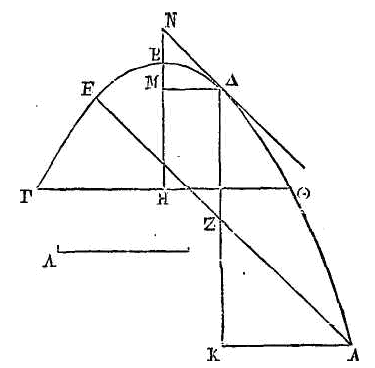
Les deux triangles AKZ, ΔMN étant semblables, on aura

AZ : AK :: Racine carrée (4x² + Λx): Racine carrée (Λx); ou bien

AZ² : AK² :: 4x² + Λx : Λx; c'est-à-dire AZ² : AK² :: 4x + Λ : Λ. Donc N = 4x + Λ. Mais 4x + Λ est égal au paramètre du diamètre ΔK ; donc AZ² = N x ΔZ

(δ) Apollonius, liv. I, prop. 11.

PROPOSITION V.

(α) En effet, puisque MΛ : KΛ :: BΘ : EΘ, on aura MA + BΘ : KΛ + EΘ :: BΘ : EΘ. Multipliant la première raison par AΘ, on aura, (MΛ + BΘ ) AΘ : ( KΛ + EΘ ) AΘ :: BΘ : EΘ.

Mais le premier produit est égal au trapèze compris entre les ordonnées du cercle, et le second produit est égal au trapèze compris entre les ordonnées de l'ellipse ; donc trapèze EΛ : trapèze ΘM :: ΘE : BΘ.

(β) Euclide, liv. ΞII, prop. 2, démontre qu'on peut inscrire dans un cercle un polygone de manière que la somme des segments placés entre la circonférence et les côtés du polygone soit plus petite qu'une surface donnée. On démontrerait absolument de la même manière qu'on peut inscrire dans une ellipse un polygone dont la somme des segments compris entre l'ellipse et les côtés du polygone inscrit serait plus petite qu'une surface donnée. Cela posé, si l'on inscrit dans l'ellipse un polygone dont la somme des segments soit plus petite que l'excès de la surface comprise dans l'ellipse sur le cercle Ψ, il est évident que le polygone inscrit sera plus grand que le cercle Ψ.

PROPOSITION VI.

(α) Donc si l'on multiplie ces deux proportions termes par termes, et si l'on supprime les facteurs communs des deux termes de chaque raison, la surface Χ sera au cercle Ψ comme la surface comprise sous AΓ, BΔ est au carré de EZ.

PROPOSITION VII.

(α) Donc par raison d'égalité, la surface A sera à la surface B comme ΓΔ est à EZ.

PROPOSITION VIII.

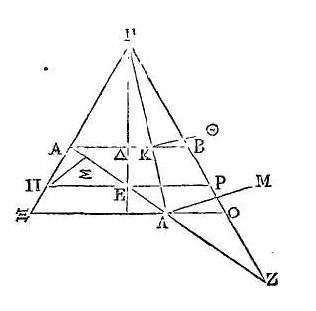
(α) Par le point E menons la droite ΠE parallèle à AB, on aura les deux proportions suivantes,

AΔ : ΠE :: ΔΓ : ΓE; ΔB : EΡ :: ΔΓ : EΓ. Ces deux proportions donnent AΔ x ΔB : ΠE x EΡ :: ΔΓ² : EΓ² ; ou bien AΔ x ΔB : ΔΓ² :: ΠE x EΡ : EΓ². Mais l'angle Z est plus petit que l'angle ΡΠΓ, qui est égal à l'angle ΠΡΓ. Donc l'angle Z est plus petit, que l'angle ΡΠΓ. Faisons l'angle EΠΣ égal à l'angle Z. Les deux triangles ZEΡ, EΠΣ seront semblables. Donc ΠE : EZ :: ΣE : EΡ ; donc ΠE x EΡ = ΣE x EZ.

Mais ΠE x EΡ : EΓ² :: AΔ x ΔB : ΔΓ² ; donc ΣE x EZ : EΓ² :: AΔ x ΔB : ΔΓ². Donc la raison de AE x EZ à EΓ² est plus grande que la raison de AΔ x ΔB à ΔΓ².

(β) Par raison d'égalité.

(γ) En effet, AE : EΠ :: AΛ : ΛΣ , et EZ : EΡ :: ΛZ : ΛO. Donc AE x EZ : EΠ x EΡ :: AΛ x ΛZ : ΛΞ x ΛO.

(δ) Parce que dans l'ellipse le carré de la moitié du grand diamètre est au carré de la moitié du petit diamètre comme le carré d'une ordonnée est au produit des abscisses correspondantes.

(ε) Par raison d'égalité.

PROPOSITION IX.

(α) Dans cet endroit, Archimède se sert pour la première fois du mot elleiyis, ellipsis.

(β) Dans ce cas, le problème serait résolu.

(γ) Dans l'ellipse le carré d'une ordonnée est au produit des abscisses correspondantes comme le carré du diamètre conjugué est au carré du diamètre. Donc N² est à ZΔ x ΔH comme le carré du diamètre conjugué de l'ellipse décrite autour du diamètre ZH est au carré de ZH. Mais le carré du diamètre conjugué de l'ellipse décrite autour du diamètre E est au carré de EB comme N² est à ZΔ x ΔO. Donc le carré du diamètre conjugué de l'ellipse décrite autour du diamètre EB est au carré de son autre diamètre EB comme le carré du diamètre conjugué de l'ellipse décrite autour de ZH est au carré de son autre diamètre ZH. Donc ces ellipses sont semblables.

 (δ) En effet, on a supposé que le carré de N est à ZΔ x ΔH comme le carré du diamètre conjugué de l'ellipse décrite autour de EB est au carré du diamètre EB, c'est-à-dire comme le carré du demi-diamètre conjugué est au carré de la moitié de EB. Mais le carré du demi-diamètre conjugué est au carré du demi-diamètre EB, comme le carré de l'ordonnée ΛM est à EΛ x ΛB (Apoll. liv. I, prop. 21). Donc le carré de N est à ZΔ x ΔH comme ΛM est à EΛ x ΛB.

 (ε) Car les triangles semblables ZΔA, EΔΠ, et les triangles semblables ΔBH, ΛΡB donnent ZΔ : AΔ :: EΛ : ΠΛ ; ΔH : ΔB :: ΛB : ΛΠ.

D'où l'on déduit ZΔ x ΔH : AΔ x ΔB :: EΛ x ΛB ou ΛM² : ΠΛ x ΛΡ.

PROPOSITION X.

(α) C'est-à-dire que la raison du carré de l'ordonnée ΘK au produit des abscisses correspondantes AK, KΛ, est la même que la raison du carré du demi-diamètre ZΓ au carré du demi-diamètre AΔ (Apoll., liv. I, prop. 21).

(β) Car les droites ZA, ΓΔ, HB étant parallèles, on aura ZΛ : AK :: ZΓ : AΔ ; ΛH : KB :: ZΓ : AΔ ; ce qui donne ZΛ x ΛH : AK x KB :: ZΓ² : AΔ².

(δ) En effet, puisque ΓΞ² = ZΓ² — NΞ², nous aurons ZΓ² = ΓΞ² + NΞ². Mais ΓN² = ΓΞ² + NΞ² ; donc ΓN²= ZΓ².

(γ) A cause que les deux triangles AMO, ΓNΞ sont semblables.

(ζ) Car lorsque l'on a deux proportions, et que ces deux proportions ne diffèrent que par les deux premiers termes, les deux premiers termes sont égaux entre eux.

PROPOSITION XI.

(α) Ces propositions se démontrent comme Euclide a démontré celles qui leur sont analogues.

PROPOSITION XII.

(α) Ces propositions sont démontrées par Fr. Commandin et par Torelli.

PROPOSITION XIII.

(α) Entre EΘ, ΘZ.

(β) Apollonius, liv. III, prop. 17.

(γ) Donc TB est à TM comme AΛ est à AΓ, et par conséquent TB² est à TM² comme AΛ² est à AΓ².

(ε) Apollonius, liv. I, prop, 21.

PROPOSITION XIV.

(α) Apollonius, liv. III, prop. 17.

(β) La droite BT est plus petite que la droite TN ; car la droite BT est plus petite que la droite MT, qui est plus petite que la droite TN, à cause que la droite MB est plus petite que BΡ, ce qui arrive dans l'hyperbole ;  

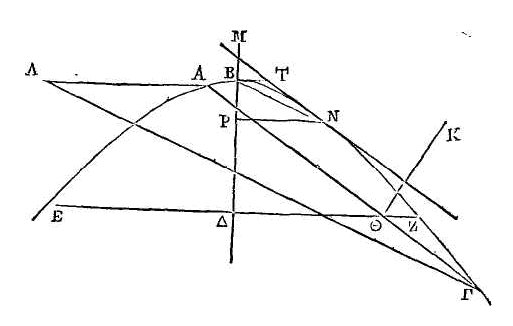
et c'est ce qu'il est facile de démontrer. En effet, soit y une ordonnée de l'hyperbole; x l'abscisse, et a le grand diamètre. La droite MΡ égalera (ax + xx)/(x+a/2), et MB égalera (ax/2)/(x+a/2). Or, (ax/2)/(x+a/2) est plus petit que ((ax/2) + x/2)/(x+a/2) ; donc MB est plus petit que ½ Mr. Donc MB est plus petit que BΡ.

(γ) Archimède ne démontre point que AΓ est le grand diamètre de l'ellipse, et que AΛ en est le petit, parce que cela peut se démontrer, à peu de chose près, de la même manière que dans la proposition précédente. Si l'on voulait compléter la démonstration précédente, après ces mots il est donc évident que cette section est une ellipse, il faudrait ajouter ce qui suit: Joignons les points B, N par la droite BN; menons la droite ΓΛ parallèle à NB, et la droite ΛA perpendiculaire sur BΔ. Les deux triangles BTN, ΛAΓ seront semblables. Donc BΓ : TN :: ΛA : AΓ ; ou bien BΓ² : TN² :: ΛA² : AΓ².

Mais KΘ² : AΘ x ΘΓ :: BΓ² : TN² ; donc KΘ² : AΘ x ΘΓ :: ΛA² ; AΓ². Il est donc encore évident que le grand diamètre est la droite AΓ, et que le petit diamètre est la droite AΛ.

La dernière phrase de cette démonstration est tout à-fait altérée dans le texte grec. Dans les manuscrits et dans toutes les éditions, les lignes Ar, aa, BN manquent dans la figure. Voici le texte grec de cette dernière phrase : Δῆλον ἔστι ὅτι ἁ τόμα ἐστιν ὀξυγωνία κώνου τομά· καὶ διάμετρος αὐτᾶς ἁ μείζων ΑΓ. Ὁμοίως καθετᾶ ὅσης τᾶς ΝΡ ἐν τᾷ τοῦ ἀμβλογωνέα κώνου τομᾶ, διάμετρος ταύτας μείζων ἐστὶν ἁ ΓΛ.  Ce qui étant traduit mot à mot veut dire : « Il est donc encore certain que c'est une section du triangle acutangle, et que son grand diamètre est la droite AΓ. La droite NΡ étant semblablement perpendiculaire dans la section du cône obtusangle, son grand diamètre est la droite ΓΛ ».

Ce qui ne présente aucun sens. En effet, si le grand diamètre de l'ellipse est la droite AΓ, ce même diamètre ne pourrait pas être une droite différente désignée par ΓΛ qui n'existe pas dans la figure. Heureusement la proposition précédente nous offre le moyen de rétablir la figure, ainsi que le texte grec dans toute son intégrité. J'ai rétabli la figure, et voici le texte grec tel qu'il doit être : Δῆλον ἔστι ὅτι ἁ τόμα ἐστιν ὀξυγωνία κώνου τομά· καὶ διάμετρος αὐτᾶς ἁ μείζων ΑΓ. ἁ δὲ ἐλλάσσων διάμετρος ἴασα ἐστὶ τᾷ ΛΑ, τᾶς μέν ΓΛ παρὰ τὰν ΒΝ ἐούσας, τᾶς δὲ ΑΛ καθετᾶ ἐπὶ τὰν ΒΔ.

PROPOSITION XV.

(α) Apollonius, liv. III, prop. 17.

PROPOSITION XIX.

(α) Apollonius, liv. II, prop. 6.

(β) D'après la proposition 47 du premier livre d'Apollonius,

PROPOSITION XXIII.

(α) Car puisque fig. cir. — fig. ins. < seg. — Ψ, à plus forte raison seg. — fig. ins. < seg. — Ψ. Donc fig. ins. > Ψ.

(β) Apollonius, liv. I, prop. 20.

(γ) En effet, on a six cylindres égaux et six droites égales, qui sont les rayons de ces cylindres, et ces cylindres sont proportionnels deux à deux à ces droites; de plus cinq de ces cylindres sont comparés aux cylindres inscrits, et les droites égales sont comparées aux droites placées entre les droites BΔ , BA, sous les mêmes raisons (2).

(δ) C'est-à-dire la somme des rayons des bases des cylindres compris dans le cylindre total.

(ε) Parce que le premier cylindre, placé dans le cylindre total, est égal au premier des cylindres circonscrits.

PROPOSITION XXIV.

(α) Apollonius, liv. II, prop. 46.

(β) Idem, liv. I, prop. 20.

PROPOSITION XXV.

(α) Pour rendre cette conclusion évidente, je vais faire voir que la raison de KA à EΘ est la même que la raison de la surface comprise sous les diamètres de l'ellipse au carré du diamètre EΓ. Pour cela je suppose une parallèle à BΔ menée par le point A, et une parallèle à ΓE menée par le point Z. La parallèle menée par le point Z et prolongée jusqu'à l'autre parallèle, sera égale au petit diamètre de l'ellipse (13). En effet, la portion de la parallèle à ΓE menée par le point Z , et qui est placée entre le point Z et la droite BΔ , est à la portion de cette même parallèle qui est placée entre la droite BΔ et la parallèle à BΔ menée par le point A, comme ZK est à KA Mais ZK est égal à KA ; donc la parallèle à ΓE placée entre le point Z et la parallèle à BΔ menée par le point A, est partagée en deux parties égales par la droite BΔ. Mais une des parties de cette parallèle est égale à ΧA, et ΧA est égal à EΘ (4) ; donc la parallèle à ΓE, menée du point Z et prolongée jusqu'à la parallèle à BΔ menée par le point A, est égale à ΓE. Mais cette parallèle est égale au petit diamètre de l'ellipse décrite autour de AZ comme diamètre (13); donc la droite ΓE est aussi égale au petit diamètre de cette ellipse.

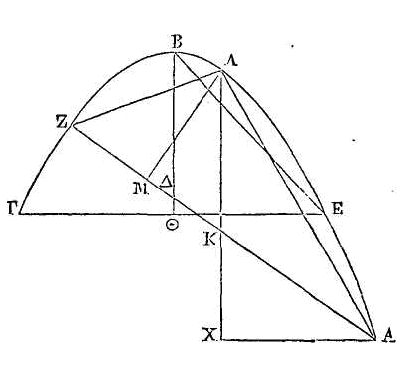
Cela posé, il est évident que KA : EΘ :: AZ x ΓE : ΓE x ΓE ; car supprimant le facteur commun, et divisant la dernière raison par deux, on a KA : EΘ :: KA : EΘ.

(β) A cause des triangles semblables KAM, KAΧ.

(γ) C'est-à-dire que le segment de cône est au cône comme la surface comprise sous ΛK, ΛM est à la surface comprise sous ΛK, ΛM.

PROPOSITION XXVI.

(α) Car ces deux cônes sont entre eux en raison composée de la raison du cercle décrit autour du diamètre AΓ, au cercle décrit autour du diamètre EZ, et de la raison BΔ à BΘ. Mais la raison dû cercle décrit autour de AΓ comme diamètre, au cercle décrit autour du diamètre EZ est égale à la raison du carré de AΔ au carré de EΘ. Donc ces deux cônes sont entre eux en raison composée de la raison du carré de AΔ au carré de EΘ, et de la raison de BΔ à BΘ.

(β) Apollonius, liv. I, prop. 21.

PROPOSITION XXVII

(α) Voyez la note (γ) de la proposition 5.

(γ) Apollonius, liv. I, prop. 21.

PROPOSITION XXVIII.

(α) Apollonius, liv. I, prop. 46.

(β) Idem, liv. I, prop. 21.

PROPOSITION XXIX.

(α) Dans le carré AΓ, menons la diagonale BΔ ; et par le point Z de cette diagonale menons les droites ΘK, HE parallèles aux côtés AB, AΔ. La réunion des deux rectangles AZ, ZΓ et le carré ΘH , forment le gnomon du carré AΓ.

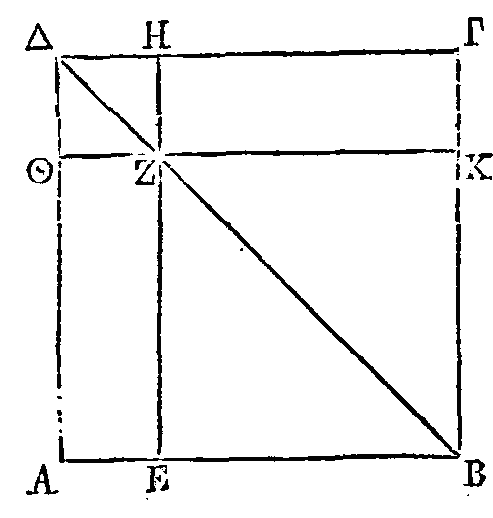
La largeur du gnomon étant AE, qui est égal à BI dans la figure d'Archimède, et le côté du carré étant égal au demi-diamètre de l’ellipse, le rectangle AH sera égal à la surface comprise sous ΘΔ, BI, et la droite HΓ étant égale à BI, le rectangle ZΓ sera égal à la surface comprise sous IΘ, BI. Donc le gnomon sera égal à la surface comprise sous BI, IΔ.

(β) Le second carré est le premier de la rangée à droite, le premier étant celui qui est seul.

PROPOSITION XXXI.

(α) Que BH = 3 BΘ ; que BΔ = 3 BΡ. Il est évident que BH — BΔ = 3 BΘ — 3 BΡ = 3 (BΘ — BΡ), c'est-à-dire que ΔH = 3 ΘΡ.

(β) Puisque NΞ = ZΔ, que OΞ = BΔ, il est évident que NΞ — ΘΞ = ZΔ — BΔ , c'est-à-dire que NO = 2 ΔΘ.

(γ) C'est-à-dire, retranchons du rectangle NΞ un gnomon dont l'a largeur ΦΞ, qui est égale à TO, soit égale à BΔ. Ce gnomon renfermera le rectangle NΞ, moins le rectangle NΩ. Or, ce gnomon égale le rectangle OΥ + le rectangle ΦΥ, c'est-à-dire NΞ x TO + ΦΩ x ΩΥ = (NΞ + ΦΩ) x ΩΥ = BE x EZ.

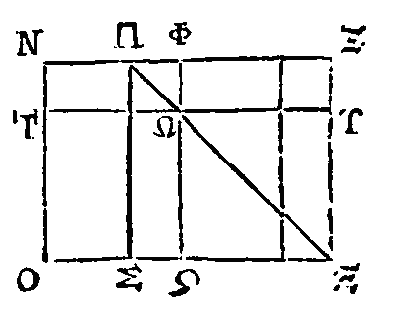
FIN DU COMMENTAIRE SUR LES CONOÏDES ET LES SPHEROÏDES.