ARCHIMÈDE

DE LA QUADRATURE DE LA PARABOLE.

ARCHIMEDE A DOSITHEE, SALUT

Lorsque j'eus appris que Conon, le seul de mes amis qui me restait encore, était mort; que tu étais étroitement lié d'amitié avec lui, et très versé dans la géométrie; je fus grandement affligé de la mort d'un homme qui était mon ami et qui avait dans les sciences mathématiques une sagacité tout à fait admirable ; et je pris la résolution de t'envoyer, comme je l'aurais fait à lui-même, un théorème de géométrie, dont personne ne s'était encore occupé et qu'enfin j'ai voulu examiner. J'ai découvert ce théorème, d'abord par des considérations de mécanique, et ensuite par des raisonnements géométriques. Parmi ceux qui ont cultivé la géométrie avant nous, quelques-uns ont entrepris de faire voir comment il serait possible de trouver une surface rectiligne égale à un cercle ou à un segment de cercle. Ils ont ensuite essayé de carrer la surface comprise par la section d'un cône entier et par une droite ; mais en admettant des lemmes difficiles à accorder (α). Aussi ont-ils été repris par plusieurs personnes comme n'ayant point atteint leur but. Mais je ne sache pas qu'il se soit encore trouvé une seule personne qui ait cherché à carrer la surface comprise sous une droite et une parabole. Ce que nous avons certainement fait aujourd'hui ; car nous démontrons qu'un segment quelconque compris par une droite et par une parabole est égal à quatre fois le tiers du triangle qui a la même base et la même hauteur que le segment (β). Pour démontrer ce théorème, nous nous sommes servis du lemme suivant : Si deux surfaces sont inégales, ce dont la plus grande surpasse la plus petite étant ajouté à lui-même un certain nombre de fois, il peut arriver que ce reste ainsi ajouté à lui-même surpasse une surface proposée et limitée. Les géomètres qui ont vécu avant nous, ont aussi fait usage de ce lemme pour démontrer que les cercles sont entre eux en raison doublée de leurs diamètres, et les sphères en raison triplée ; qu'une pyramide est le tiers d'un prisme qui a la même base et la même hauteur que cette pyramide, et qu'un cône est le tiers d'un cylindre qui a la même base et la même hauteur que ce cône. Or, les théorèmes démontrés de cette manière n'ont pas paru moins évidents que ceux qui ont été démontrés autrement; Ceux que je viens de publier ont donc le même degré d'évidence. Comme j'ai écrit les démonstrations de ce théorème, je te les envoie. Tu verras comment il a été résolu d'abord par des considérations de mécanique, et ensuite par des raisonnements géométriques. Nous mettrons en tête de ce traité les éléments des sections coniques qui sont nécessaires pour démontrer ce théorème. Porte-toi bien.

PROPOSITION I.

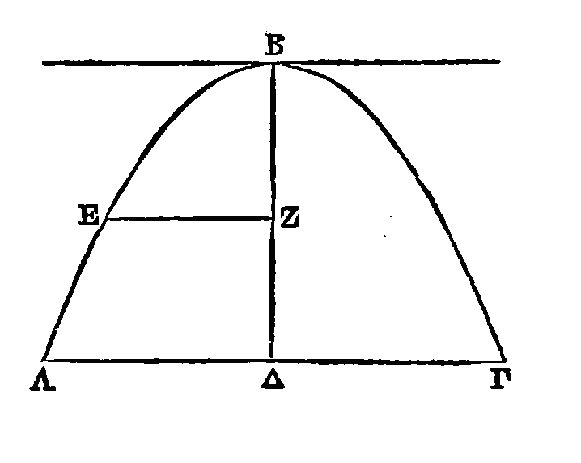
Soit ABΓ une parabole; que BΔ soit une droite parallèle au diamètre, ou le diamètre lui-même ; que la droite AΔΓ soit parallèle à la tangente au point B. Les droites AΔ, ΔΓ seront égales entre elles ; et si la droite AΔ est égale à la droite AΓ, la droite AΓ sera parallèle à la tangente au point B (α).

PROPOSITION II.

Si ABΓ est une parabole ; si la droite BΔ est une droite parallèle au diamètre, ou le diamètre lui-même; si la droite AΔΓ est parallèle à la droite qui touche la parabole au point B, et si la droite ΓE touche la parabole au point Γ, les droites ΔB, BE seront égales entre elles (α).

PROPOSITION III.

Si ABΓ est une parabole ; et si BΔ est une parallèle au diamètre ou le diamètre lui-même, et si l’on conduit certaines droites AΔ, EZ parallèles à la tangente au point B, les carrés des droites AΔ, EZ seront entre eux comme les droites AΔ, BZ.

Cela est démontré dans les éléments des sections coniques (α).

PROPOSITION IV.

Soit ABΓ un segment compris par une droite et par une parabole. Du milieu de AΓ conduisons une droite BΔ qui soit une parallèle au diamètre, ou le diamètre lui-même, menons la droite BΓ et prolongeons-la. Si nous conduisons une autre droite ZΘ qui soit parallèle à BΔ, et qui coupe les deux droites AΓ et ΓB, la droite ZΘ sera à la droite ΘH comme ΔA est à ΔZ.

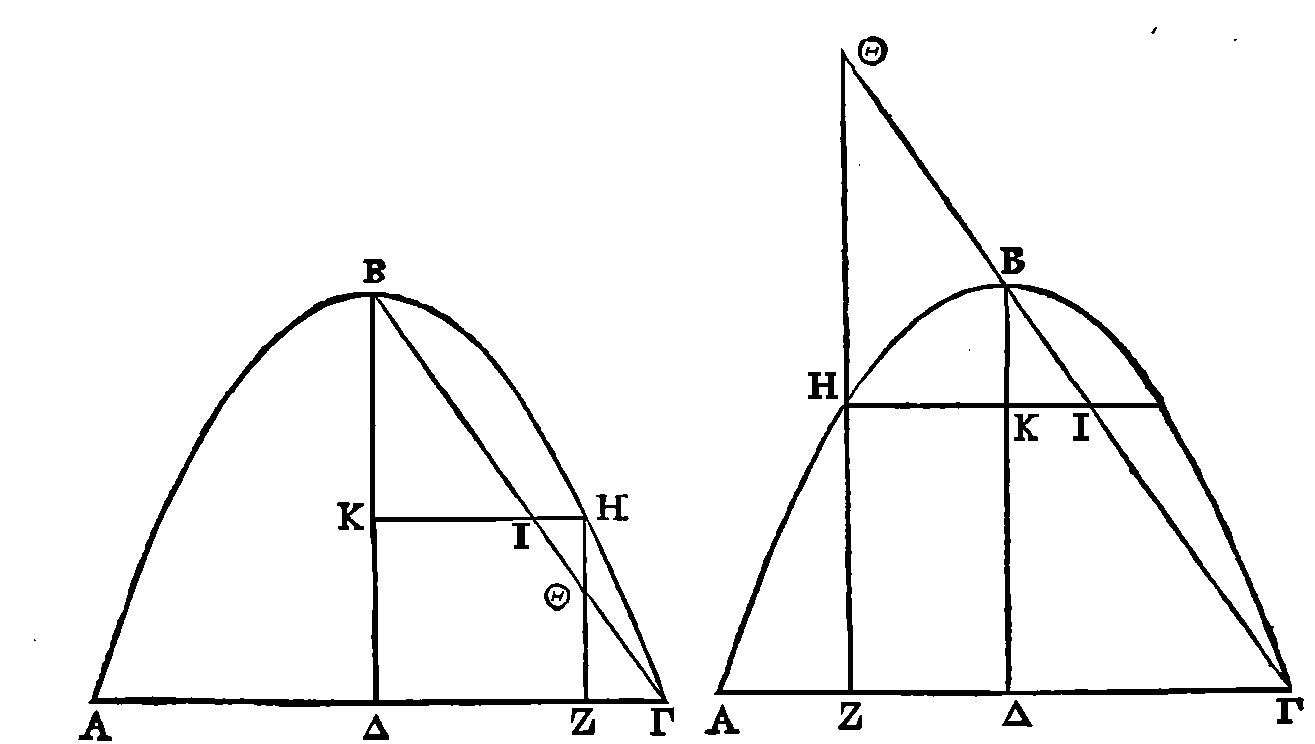
Par le point H conduisons KH parallèle à AΓ. Le carré de AΓ sera au carré de KH comme BΔ est à BK. Ce qui est démontré. Δonc le carré de ΔΓ est au carré de ΔZ comme BΓ est à BI ; car les droites ΔZ, KH sont égales. Donc le carré de BΓ est au carré de BΘ comme BΓ est à BI. Donc les droites BΓ, BΘ, BI sont proportionnelles (α). Donc BΓ est à BΘ comme ΓΘ est à ΘI (β). Donc ΘZ est à ΘH comme ΓΔ est à ΔZ. Mais ΔA est égal à ΔΓ ; il est donc évident que ΔA est à ΔZ comme ZΘ est à ΘH.

PROPOSITION V.

Soit ABΓ un segment compris par une droite et par une parabole. Du point A conduisons la droite ZA parallèle au diamètre, et du point Γ la droite ΓZ qui touche la parabole au point Γ. Si dans le triangle ZAΓ, on conduit une droite parallèle à AZ, la droite KL qui coupe la parabole et la droite AΓ qui va d'un point de la parabole à un autre, seront coupées dans la même raison, et la partie de la droite AΓ qui est du côté du point A, et la partie de droite KL qui est du côté du même point seront des termes correspondants de la proportion.

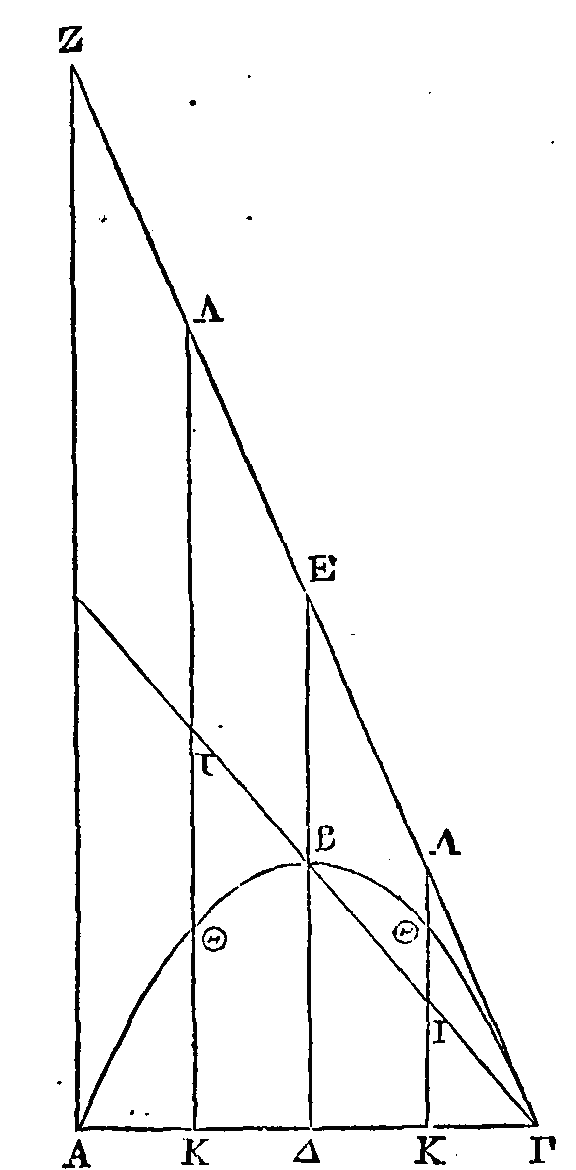
Conduisons une droite quelconque ΔE parallèle à AZ. Θue d'abord cette droite coupe en deux parties égales la droite AΓ. Puisque ABΓ est une parabole, qu'on a conduit la droite BΔ parallèle au diamètre, et que AΔ est égal à AΓ, la droite AΓ sera parallèle à la droite qui touche la parabole au point B. De plus, puisque ΔE est parallèle à l’axe, que du point Γ on a mené la droite, ΓE tangente à la parabole au point Γ, et que ΔΓ est parallèle à la tangente au point B, la droite EB sera égale à BΔ (2). Donc AΔ est à ΔΓ comme ΔB est à BE. On a donc démontré ce qui était proposé, lorsque la droite qui a été menée partage AΓ en deux parties égales.

Supposons que cette droite ne partage pas la droite AΓ en deux parties égales. Conduisons une droite KΛ parallèle à AZ. Il faut démontrer que AK est à KΓ comme KΘ est à ΘΛ. Car puisque la droite BE est égale à BΔ, et que la droite IΛ est aussi égale à la droite KI, la droite KΛ sera à la droite KI comme AΓ est à ΔA. Mais KI est à ΘK comme ΔA est à AK. Ce qui est démontré dans la proposition précédente ; donc KΘ est à KΛ comme AK est à AΓ (α). Donc KΘ est à ΘΛ comme AK est à KΓ. Donc la proposition est démontrée.

PROPOSITION VI.

Supposons que les choses que nous nous proposons d'examiner soient placées devant les yeux dans un plan perpendiculaire sur l'horizon et passant par la droite AB ; que ce qui est du côté du point Δ soit au bas, et que ce qui est placé de l'autre côté soit en haut. Que le triangle BΔΓ soit rectangle, ayant l'angle droit en B, et que le côté BΓ soit égal à la moitié du fléau de la balance, c'est-à-dire que ΔB soit égal à BΓ. Que ce triangle soit suspendu aux points B, Γ. Que la surface Z soit suspendue à l'autre extrémité de la balance, c'est-à-dire au point A, de manière que la surface Z suspendue au point A soit en équilibre avec le triangle BΔΓ ainsi placé. Je dis que la surface Z est la troisième partie du triangle ΔBΓ.

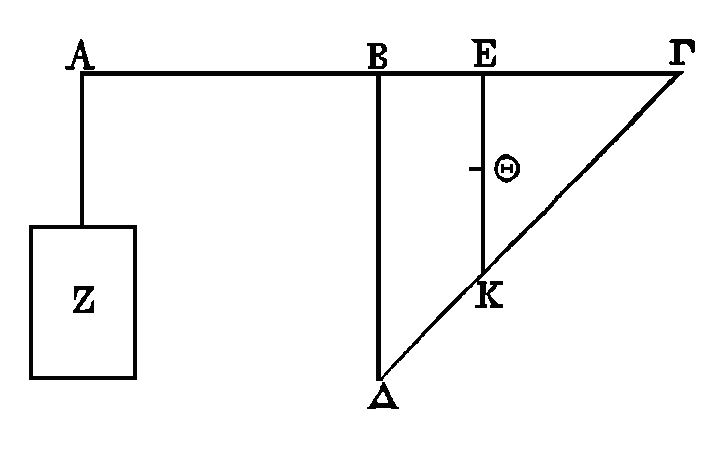
Car puisqu'on suppose que la balance est en équilibre, la droite AΓ sera parallèle à l'horizon, et les droites qui sont perpendiculaires sur AΓ, dans le plan perpendiculaire sur l'horizon, seront elles-mêmes perpendiculaires sur l'horizon. Coupons la droite BΓ au point E, de manière que ΓE soit double de la droite EB; conduisons KE parallèle à BΔ, et partageons cette droite en deux parties égales au point Θ. Le point Θ sera le centre de gravité du triangle BΔΓ ; ce qui est démontré dans les mécaniques. Donc si le triangle qui est suspendu aux points b., r en est détaché, et si son centre de gravité est suspendu au point E, il restera dans sa position actuelle, car une chose qui est suspendue demeure en repos lorsque le point de suspension et le centre de gravité sont dans la même verticale. Ce qui est aussi démontré. Donc, puisque la position du triangle BΓΔ, par rapport à la balance, est la même qu'auparavant, la surface Z lui fera pareillement équilibre ; et puisque la surface Z et le triangle BΔΓ sont en équilibre, l'un étant suspendu au point A et l'autre étant suspendu au point E, il est constant que les longueurs sont réciproquement proportionnelles à ces surfaces, c'est-à-dire que la longueur AB est à la longueur BE comme le triangle BΔΓ est à la surface Z. Mais la longueur AB est triple de la longueur BE ; donc le triangle BΔΓ est aussi triple de la surface Z.

Il est encore évident que si le triangle était triple de la surface Z, ces deux surfaces seraient pareillement en équilibre.

PROPOSITION VII.

Que la droite AΓ soit une balance, dont le milieu soit le point B. Que le triangle ΓΔH soit suspendu- par rapport au point B.

Que le triangle ΓΔH soit obtusangle, ayant pour base la droite ΔH, et pour hauteur une droite égale à la moitié de la balance. Suspendons le triangle AΓH aux points B, Γ. Que la surface Z suspendue au point A soit en équilibre avec le triangle ΓΔH ainsi placé. On démontrera pareillement que la surface Z est la troisième partie du triangle ΓΔH.

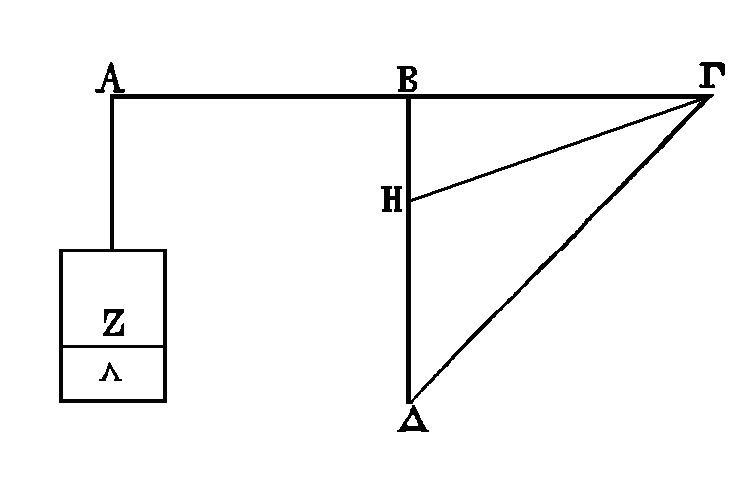
Suspendons au point A une autre surface qui soit la troisième partie du triangle BΓH. Le triangle BΓΔ sera certainement en équilibre avec la surface ZΛ. Donc puisque le triangle BΓH est en équilibre avec la surface Λ, que le triangle BΓΔ est en équilibre avec la surface ZΛ, et que la surface ZΛ est le tiers du triangle BΓΔ, il est constant que le triangle ΓΔH est triple de la surface Z.

PROPOSITION VIII.

Que la droite AΓ soit une balance, dont le milieu soit le point B. Suspendons, par rapport au point B, un triangle rectangle ΓΔE, ayant l'angle droit en E ; suspendons ce triangle aux points Γ, E. Suspendons au point A une surface Z, de manière qu'elle soit un équilibre avec le triangle ΓΔE ainsi placé. Que le triangle ΓΔE soit à la surface K comme AB est à BE : je dis que la surface Z est moindre que le triangle ΓΔE et plus grande que la surface K.

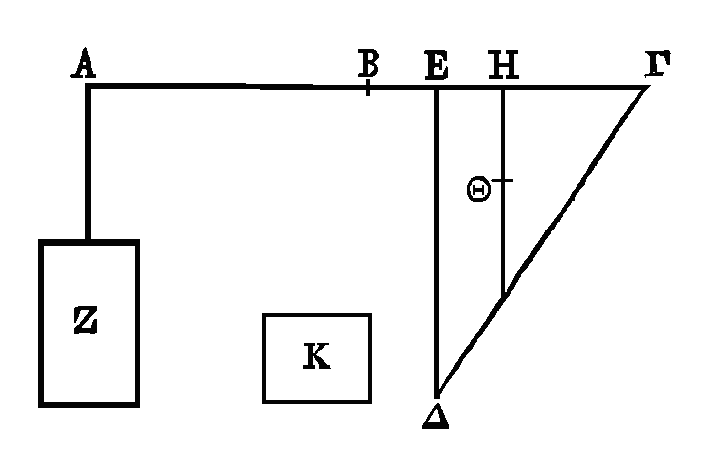
Car prenons le centre de gravité du triangle ΔEΓ ; que son centre de gravité soit le point Θ. Conduisons ΘH parallèle à ΔE. Puisque le triangle ΓΔE est en équilibre avec la surface Z, le triangle ΓΔE sera à la surface Z comme AB est à BH. Donc la surface Z est plus petite que le triangle ΓΔE ; mais le triangle ΓΔE est à la surface Z comme BA est à BH, et ce même triangle est à la surface K comme BA est à BE ; il est donc évident que la raison du triangle ΓΔE à la surface K est plus grande que la raison de ce même triangle à la surface Z. Donc la surface Z est plus grande que la surface K.

PROPOSITION IX.

Soit AΓ une balance dont le milieu soit le point B. Que ΓΔK soit un triangle obtusangle ayant pour base la droite ΔK et pour hauteur la droite EΓ. Que ce triangle soit suspendu aux points Γ, E de la balance ; et que la surface Z soit suspendue au point A, de manière qu'elle soit en équilibre avec le triangle ΔΓK ainsi placé. Que le triangle ΓΔK soit à la surface Λ comme AB est à BE : je dis que la surface Z est plus grande que la surface Λ et plus petite que le triangle ΔΓK.

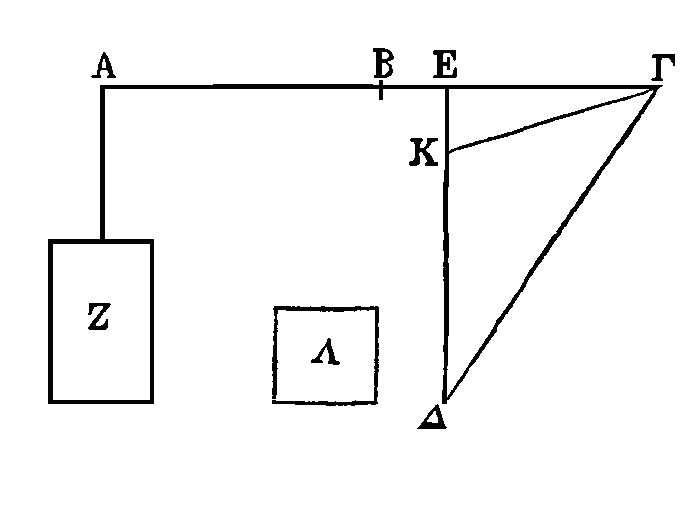
On démontrera cette proposition de la même manière que la précédente.

PROPOSITION X.

Soit la balance ABΓ dont le milieu soit le point B ; soit aussi le trapèze BΔHK, ayant des angles droits en B, H et le côté KΔ dirigé vers le point Γ. Que BA soit à BH comme le trapèze BΔHK est à la surface Λ. Que le trapèze BΔHK soit suspendu aux points B, H de la balance. Qu'une surface Z soit suspendue au point A, de manière qu'elle soit en équilibre avec le trapèze ABKH ainsi placé. Je dis que la surface Z est moindre que la surface Λ.

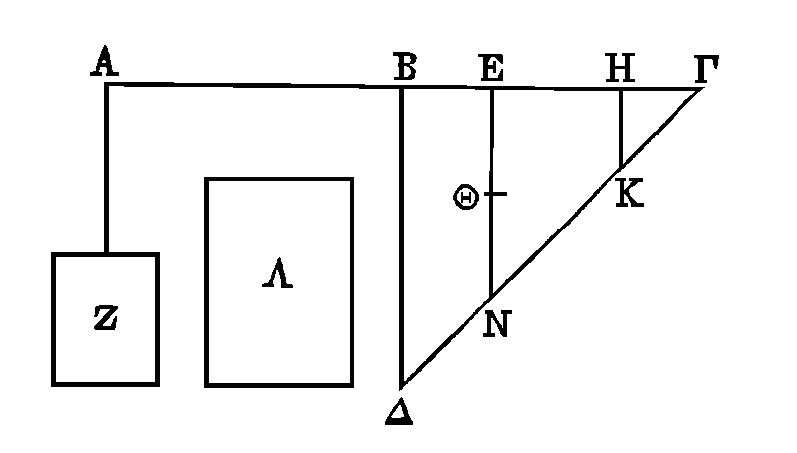
Coupons AΓ au point E, de manière que EH soit à BE comme le double de ΔB, conjointement avec KH est au double de KH, conjointement avec BΔ. Conduisons par le point E la droite EN parallèle à BΔ, et partageons cette droite en deux parties égales au point Θ. Le centre de gravité du trapèze BΔHK sera le point Θ. Car cela a été dans les mécaniques (α). Que le trapèze BΔHK soit suspendu au point E, et qu'il soit détaché des points B, H, par la même raison que nous avons dit plus haut, le trapèze ainsi placé restera en repos et sera en équilibre avec la surface Z. Donc puisque le trapèze BΔHK suspendu au point E est en équilibre avec la surface Z suspendue au point A, le trapèze BΔHK sera à la surface Z comme la droite BA est à la droite BE. Donc la raison du trapèze BΔAK à la surface Z est plus grande que la raison de ce trapèze à la surface Λ, puisque la raison de AB à BE est plus grande que la raison de AB à BH. Donc la surface Z sera plus petite que la surface Λ.

PROPOSITION XI.

Soit AΓ une balance, dont le milieu soit le point B. Soit le trapèze KΔTΡ, ayant ses côtés KΔ, TΡ dirigés vers le point Γ, et les côtés AΡ, KT perpendiculaires sur BΓ. Que ΔΡ tombe sur le point B. Que le trapèze ΔKTΡ soit à la surface Λ comme AB est à BH. Que le trapèze ΔKTΡ soit suspendu aux points B, H de la balance, et la surface Z au point A, de manière que la surface Z soit en équilibre avec le trapèze ΔKTΡ ainsi placé. On démontrera, comme on l'a fait plus haut, que la surface Z est moindre que la surface Λ.

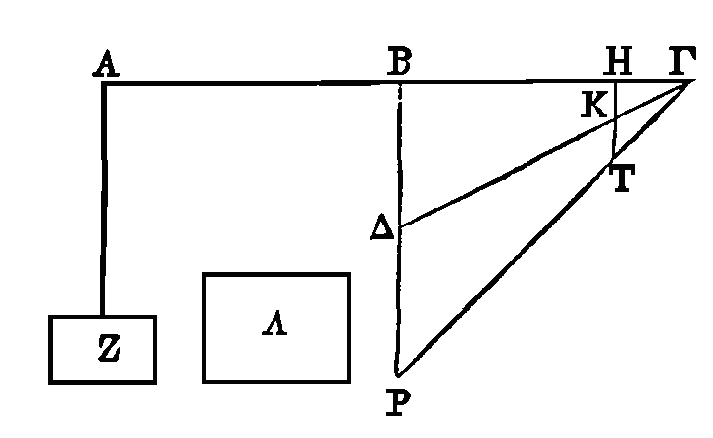
PROPOSITION XII.

Soit une balance AΓ, dont le milieu soit le point B. Soit le trapèze ΔEKH ayant des angles droits en E, H et les côtés KA, EH dirigés vers le point Γ. Que le trapèze ΔEKH soit à la surface M comme AB est à BH, et que le trapèze ΔKEH soit à la surface Λ comme AB est à BE. Que le trapèze ΔKEH soit suspendu aux points E, H de la balance; et que la surface Z soit suspendue au point A, de manière qu'elle soit en équilibre avec le trapèze ainsi placé. Je dis que la surface Z est plus grande que la surface Λ, et plus petite que la surface M.

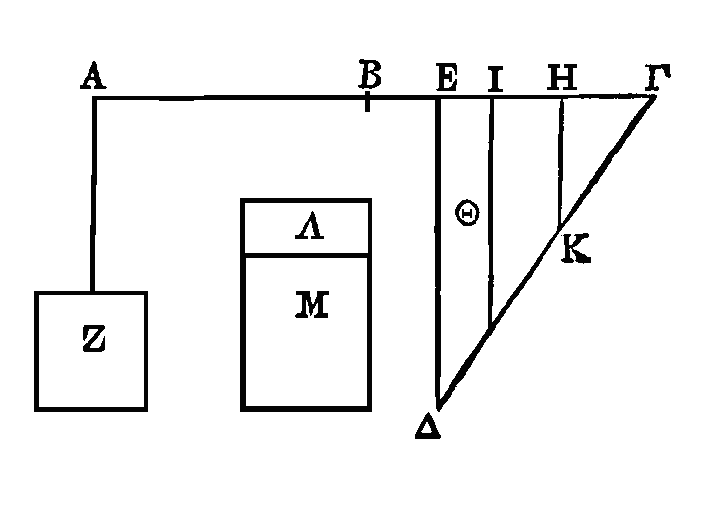
Prenons le centre de gravité du trapèze ΔEKH, et que son centre de gravité soit le point Θ. Nous prendrons son centre de gravité comme nous l'avons fait plus haut (10). Conduisons ΘI parallèle à ΔE. Que le trapèze ΔEKH soit suspendu au point I de la balance, et qu'il soit détaché dés points E, H. Par la même raison que nous avons dit plus haut, le trapèze étant ainsi placé restera en repos et sera en équilibre avec la surface Z (6). Donc puisque le trapèze ΔEKH suspendu au point I est en équilibre avec la surface Z suspendue au point A, le trapèze sera à la surface Z comme AB est à BI. Il est donc évident que la raison du trapèze à la surface Λ sera plus grande que la raison du trapèze à la surface Z. Mais la raison du trapèze à la surface M est moindre que la raison du trapèze à la surface Z ; donc la surface Z est plus grande que la surface Λ, et plus petite que la surface M.

PROPOSITION XIII.

Soit AΓ une balance, dont le milieu soit le point B. Soit le trapèze KΔTΡ, ayant ses côtés KΔ, TΡ dirigés vers le point Γ, et ses côtés ΔT, KΡ perpendiculaires sur BΓ. Que le trapèze ΔKTΡ soit suspendu aux points E, H de la balance, et que la surface Z soit suspendue au point A, de manière qu'elle soit en équilibre avec le trapèze ΔKTΡ ainsi placé. Que le trapèze ΔKTΡ soit à la surface Λ comme AB est à BE ; et que ce même trapèze soit à la surface M comme AB est à BH. On démontrera de la même manière que nous l'avons fait plus haut, que la surface Z est plus grande que la surface Λ, et plus petite que la surface M.

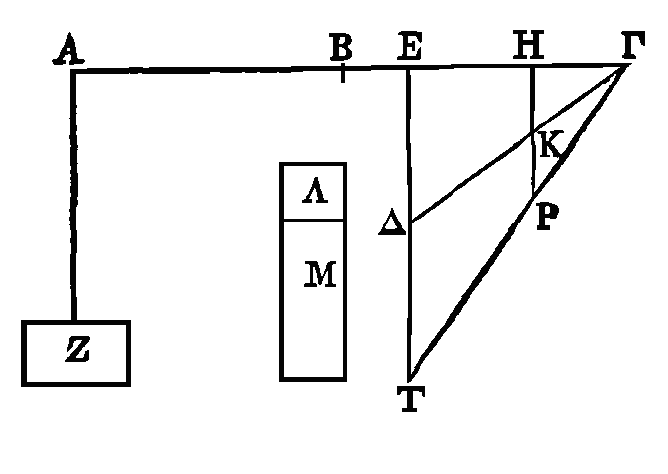
PROPOSITION XIV.

Soit un segment BΘΓ compris par une ligne droite et par une parabole. Que la droite BΓ soit d'abord perpendiculaire sur le diamètre. Du point B conduisons la droite BΔ parallèle au diamètre ; et du point Γ conduisons la droite ΓΔ tangente à la parabole au point Γ. Λe triangle BΓΔ sera rectangle. Partageons la droite BΓ en un certain nombre de parties BE, EZ, ZH, HI ; par les points de division conduisons les droites EΣ, ZT, HΥ, IX parallèles au diamètre. Joignons avec le point Γ les points où ces droites coupent la parabole, et prolongeons les droites qui joignent ces points. Je dis que le triangle BΔΓ est plus petit que le triple de la somme des trapèzes KE, ΛZ, MH, NI et du triangle XIΓ, et plus grand que le triple de la somme des trapèzes ZΦ, ΠΘ, HΠ et du triangle IOΓ.

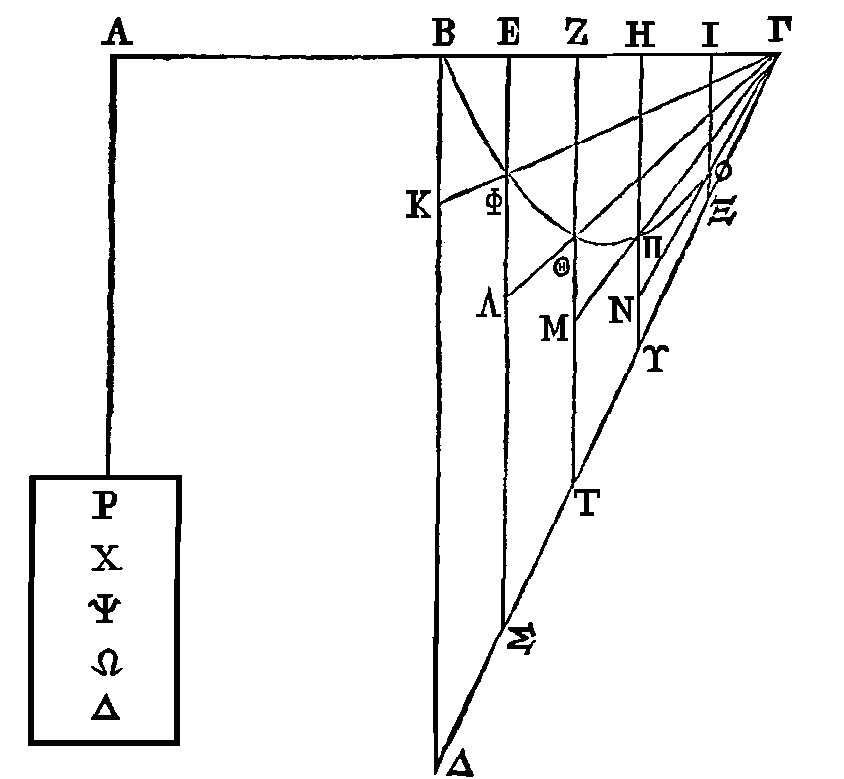
Prolongeons la droite ΓB, et faisons AB égale à BΓ. Supposons une balance AΓ dont le milieu soit le point B ; et qui soit suspendue par le point B. Suspendons le triangle BΔΓ aux points B, Γ de la balance ; de l'autre côté de la balance suspendons au point A les surfaces Ρ, Χ, Ψ, Ω, Δ. Que la surface Ρ soit en équilibre avec le trapèze ΔE ainsi placé, la surface Χ avec le trapèze ZΣ, la surface Ψ avec le trapèze ΥH, la surface Ω avec le trapèze ΥI, et enfin la surface Δ avec le triangle XIΓ. La somme des premières surfaces sera en équilibre avec la somme des secondes. Donc le triangle BΔΓ sera triple de la surface ΡΧΨΩΔ (6). Puisqu'on à un segment BΓΘ compris par une droite et par une parabole, que du point B on a conduit la droite BΔ parallèle au diamètre, et du point Γ la droite ΓΔ tangente à la parabole au point Γ et que de plus l'on a conduit une autre droite ΣE parallèle aussi au diamètre, la droite BΓ sera à la droite BE comme ΣE est à EΘ (α). Donc aussi BA est à BE comme le trapèze ΔE est au trapèze KE (β). On démontrera semblablement que AB est à BZ comme le trapèze ΣZ est au trapèze ΛZ ; que AB est à BH comme le trapèze ΓH est au trapèze MH, et enfin que AB est à BI comme le trapèze ΥI est au trapèze NI. Donc puisque le trapèze ΔE a des angles droits en B, E, et deux côtés dirigés vers le point Γ, que la surface Ρ, suspendue au point A de la balance, est en équilibre avec le trapèze ainsi placé, et que BA est à BE comme le trapèze ΔE est au trapèze KE, le trapèze KE sera plus grand que la surface Ρ car cela a été démontré (10). Puisque le trapèze ZΣ a des angles droits en Z, E, et le côté ΣT dirigé vers le point Γ, que la surface Χ, suspendue au point A de la balance, est en équilibre avec le trapèze ainsi placé ; que la droite BA est à la droite BE comme le trapèze ZΣ est au trapèze ZΘ ; et que la droite AB est à la droite BZ comme le trapèze ZΣ est au trapèze ΛZ, la surface Χ sera plus petite que le trapèze ΛZ, et plus grande que le trapèze ZΦ ; car cela a été démontré (12). Par la même raison, la surface Ψ est plus petite que le trapèze MH, et plus grande que le trapèze ΓH ; la surface Ω plus petite que le trapèze NOIH, et plus grande que le trapèze ΠI, et enfin la surface Δ plus petite que le triangle XIΓ, et plus grande que le triangle ΓIO (8). Donc puisque le trapèze KE est plus grand que la surface Ρ, le trapèze ΛZ plus grand que la surface Χ, le trapèze MH plus grand que la surface Ψ, le trapèze NI plus grand que la surface Ω, et enfin le triangle XIΓ plus grand que la surface Δ, il est évident que la somme des surfaces dont nous venons de parler est plus grande que la surface ΡΧΨΩΔ. Mais la surface ΡΧΨΩΔ est la troisième partie du triangle AΓΔ ; donc le triangle BΓΔ est plus petit que le triple de la somme des trapèzes KE, ΛZ, MH, NI et du triangle XIΓ. De plus, puisque le trapèze ZΦ est plus petit que la surface Χ (12), le trapèze ΘH plus petit que la surface Ψ, le trapèze IΠ plus petit que le trapèze Ω, et enfin le triangle IOΓ plus petit que la surface Δ (8), il est encore évident que la somme des trapèzes dont nous venons de parler est plus petite que la surface ΔΩΨΧ. Donc le triangle BΔΓ est plus grand que le triple de la somme des trapèzes ΦZ, ΘH, IΠ et du triangle IΓO, et plus petit que le triple de la somme de ceux dont nous avons parlé auparavant.

PROPOSITION XV.

Soit un segment BΘΓ compris par une droite et par une parabole. Que la droite BΓ ne soit pas perpendiculaire sur le diamètre. Il faut nécessairement que l'une ou l'autre des droites, ou celle qui est menée par le point B du même côté du segment parallèlement au diamètre, ou celle qui est menée du point Γ, fasse un angle obtus avec la droite BΓ. Que la droite menée par le point B fasse un angle obtus. Par le point B menons la droite BΔ parallèle au diamètre, et du point Γ, la droite ΓΔ tangente à la parabole au point Γ. Partageons la droite BΓ en un certain nombre de segments BE, EZ, ZH, HI, IX, et des points de division E, Z, H, I, conduisons les droites EΣ, ZT, HΥ, IX parallèles au diamètre, et joignons avec le point Γ les points où la parabole est coupée par ces droites, et prolongeons les droites qui joignent ces points. Je dis que le triangle BΔΓ est plus petit que le triple de la somme des trapèzes BΦ, AZ, ΛH, NI et du triangle ΓIX, et plus grand que le triple de la somme des trapèzes ZΦ, HΘ, IΠ et du triangle ΓOI.

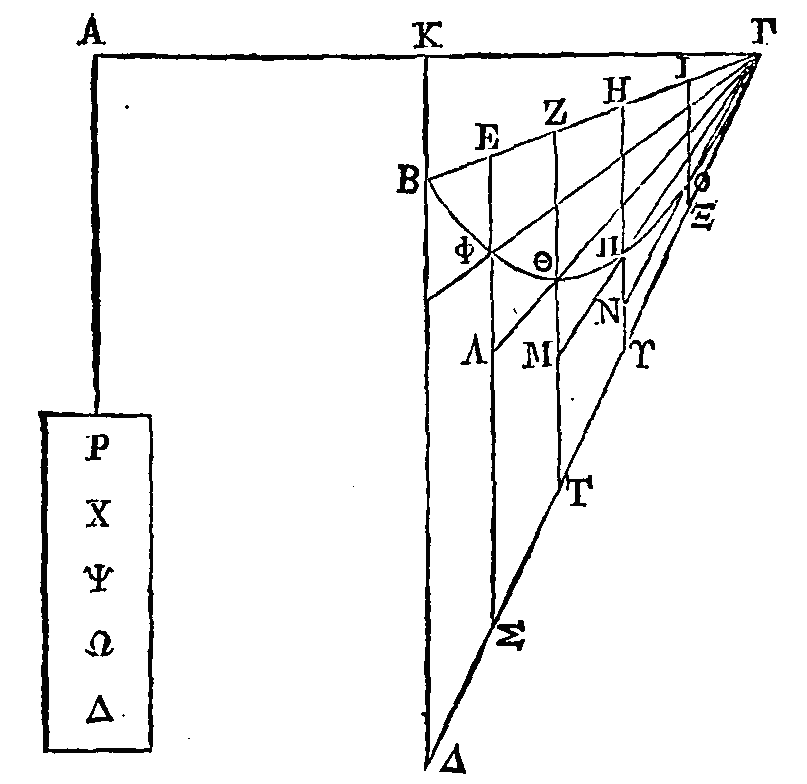
Prolongeons ΔB vers le côté opposé; menons la perpendiculaire ΓK, et faisons AK égal à ΓK. Supposons une balance AΓ dont le milieu soit le point K, et suspendons cette balance par le point K. Suspendons par rapport à la moitié de la balance le triangle ΓKΔ, c'est-à-dire aux points Γ, K. Ce triangle étant placé comme il l'est actuellement, suspendons de l'autre côté de la balance au point A, les surfaces Ρ, Χ, Ψ, Ω, Δ ; que la surface Ρ soit en équilibre avec le trapèze ΔE ainsi placé. Que la surface Χ soit en équilibre avec le trapèze ZΣ ; la surface Ψ avec le trapèze TH ; la surface Ω avec le trapèze ΨI, et enfin la surface Δ avec le triangle ΓIX. Il est évident que la somme des premières surfaces sera en équilibre avec la somme des secondes surfaces. Donc le triangle ΔBΓ sera triple de la surface ΡΧΨΩΔ. On démontrera, comme nous l'avons fait plus haut, que le trapèze BΦ est plus grand que la surface Ρ ; que le trapèze ΘE est plus grand que la surface Χ, et que le trapèze ZΦ est plus petit; que le trapèze MH est plus grand que la surface Ψ, et que le trapèze HΘ est plus petit; que le trapèze NI est plus grand que la surface Ω, et que le trapèze NI est plus petit, et enfin que le triangle XIΓ est plus grand que la surface Λ, et que le triangle ΓIO est plus petit. Donc la proposition est évidente.

PROPOSITION XVI.

Soit BΘΓ un segment compris par une droite et par une parabole. Du point B conduisons une parallèle au diamètre, et du point Γ une tangente à la parabole au point Γ. Que la surface Z soit la troisième partie du triangle BΔΓ. Je dis que le segment BΘΓ est égal à la surface Z.

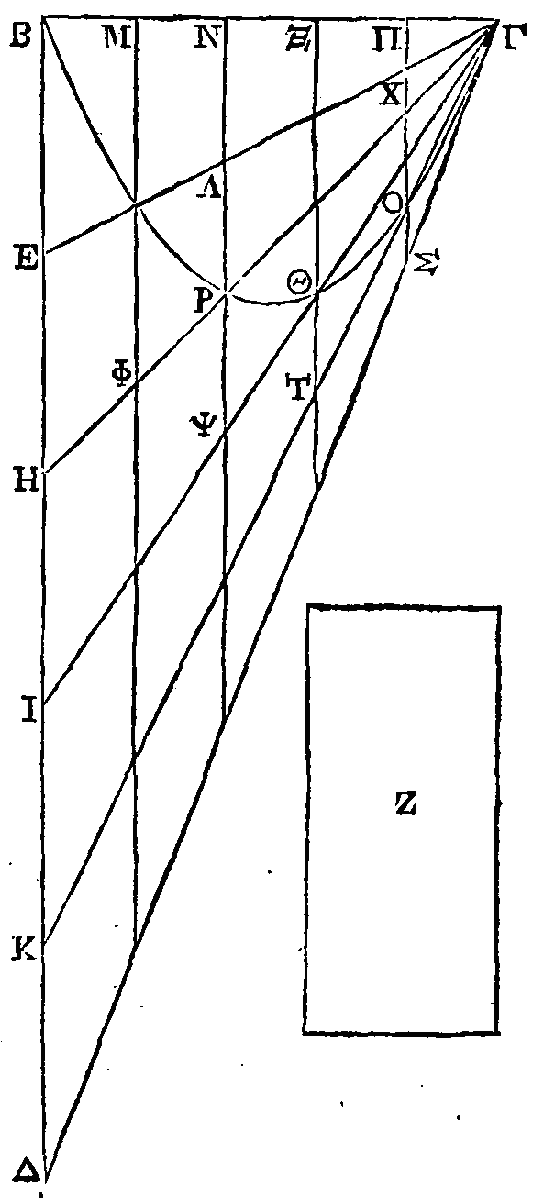
Car si le segment BΘΓ n'est pas égal à la surface Z, il est plus grand ou plus petit. Qu'il soit plus grand, si cela est possible. L'excès du segment BΘΓ sur la surface Z, ajouté un certain nombre de fois à lui-même, sera plus grand que le triangle BΓΔ. Or, il est possible de prendre une surface qui soit plus petite que cet-excès, et qui soit une partie du triangle BΔΓ. Que le triangle BΓE soit plus petit que l'excès dont nous venons de parler, et qu'il soit une partie du triangle BΔΓ. Il est évident que la droite BE sera une même partie de BΔ. C'est pourquoi, partageons BΔ en autant de parties égales que l'excès du segment sur la surface Z a été ajouté de fois à lui-même, et que les points de division soient les points E, H, I, K. Joignons par des droites les points H, I, K avec le point Γ. Ces droites couperont la parabole, puisque la droite ΓΔ touche la parabole au point Γ. Par les points où ces droites coupent la parabole, menons les droites MΦ, NΠ, ΧΘ, ΠO parallèles au diamètre; ces droites seront aussi parallèles à BΔ. Donc puisque le triangle BΓE est plus petit que l'excès du segment BΘΓ sur la surface Z, il est évident que la surface Z et le triangle BΓE, pris ensemble, sont plus petits que le segment BΘΓ. Mais la somme des trapèzes ME, ΦΛ, ΘΡ, ΘO et du triangle ΓOΣ que la parabole traverse, est égale au triangle BΓE ; parce que le trapèze ME est commun; que le trapèze MΛ est égal au trapèze ΦΛ ; que le trapèze ΛX égal au trapèze ΘΠ ; que le trapèze ΧX égal au trapèze OΘ et que le triangle ΓΧΠ égal au triangle ΓOΣ. Donc la surface Z est plus petite que la somme des trapèzes MΛ, ΧΠ, ΠΘ et du triangle ΠOΓ (α). Mais le triangle BΔΓ est triple de la surface Z ; donc le triangle BΔΓ est plus petit que le triple de la somme des trapèzes MΛ, ΡX, ΘΠ et du triangle ΠOΓ. Ce qui ne peut être ; car on a démontré qu'il est plus grand que le triple de cette somme (14). Donc le segment BΘΓ n'est pas plus grand que la surface Z.

Je dis actuellement que le segment BΘΓ n'est pas plus petit que la surface Z. Supposons, s'il est possible, qu'il soit plus petit. L'excès de la surface Z sur le segment BΘΓ ajouté un certain nombre de fois à lui-même, sera plus grand que le triangle BΔΓ. Or, on peut prendre une surface qui soit plus petite que cet excès, et qui soit une partie du triangle BΔΓ. Θue le triangle BΓE soit plus petit que ces excès ; que ce triangle soit une partie du triangle BΔΓ et que le reste soit comme auparavant. Puisque le triangle BΓE est plus petit que l'excès de la surface Z sur le segment BΘΓ, le triangle BΓE et le segment BΘΓ pris ensemble seront plus petits que la surface Z. Mais la surface Z est plus petite que la somme des trapèzes EM, ΦN, ΨX, ΠT et du triangle ΓΠΣ ; car le triangle BΔΓ est triple de la surface Z, et plus petit que le triple de la somme des trapèzes dont nous venons de parler ; ainsi qu'on l'a démontré dans la proposition précédente. Donc le triangle BΓE, conjointement avec le segment BΘΓ est plus petit que la somme des trapèzes EM, ΦN, ΨX, ΠT et du triangle ΓHΣ. Donc si l'on retranche le segment commun, le triangle ΓBE sera plus petit que la somme des surfaces restantes. Ce qui est impossible; car on a démontré que le triangle BEΓ est égal à la somme des trapèzes EM, ΦΛ, ΘΡ, ΘO et du triangle ΓOΣ, laquelle somme est plus grande que la somme des surfaces restantes (β). Donc le segment BΘΓ n'est pas plus petit que la surface Z. Mais on a démontré qu'il n'est pas plus grand; donc le segment BΘΓ est égal à la surface Z.

PROPOSITION XVII.

Cela étant démontré, il est évident qu'un segment quelconque compris par une droite et par une parabole est égal à quatre fois le tiers d'un triangle qui a la même base et la même hauteur que le segment.

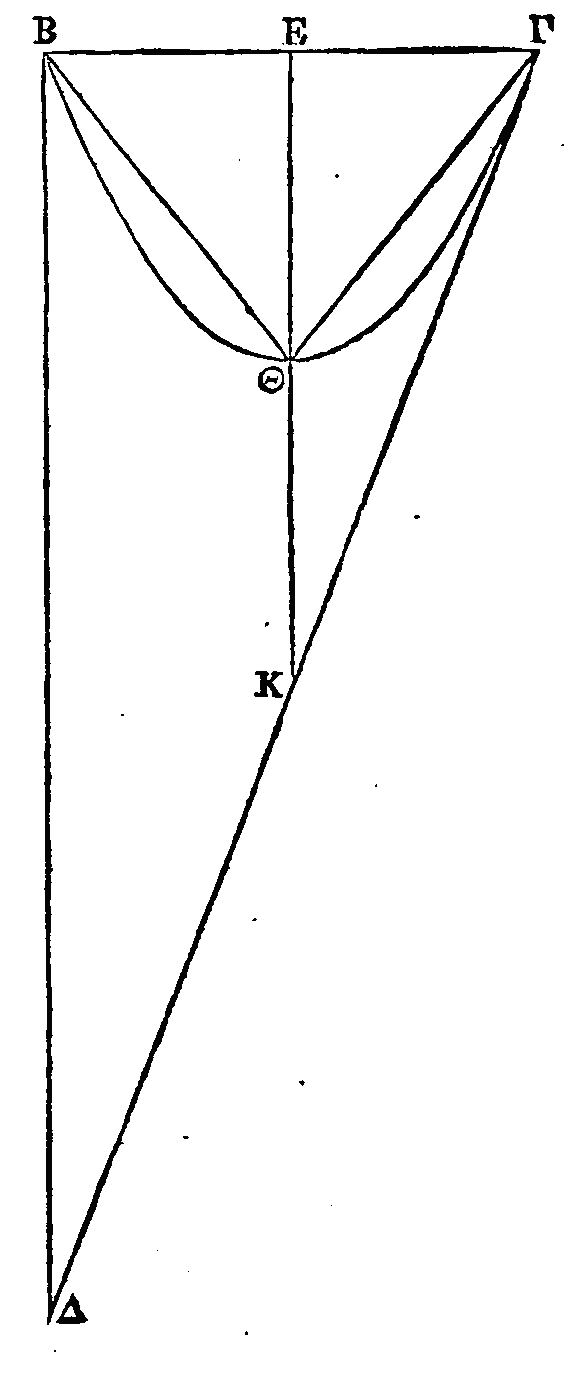
En effet, soit un segment compris par une droite et par une parabole dont le sommet soit, le point Θ. Inscrivons-lui un triangle BΘΓ qui ait la même base et la même hauteur que le segment. Puisque le point Θ est le sommet du segment, la droite menée du point Θ, parallèlement au diamètre, coupe en deux parties égales la droite BΓ ; parce que BΓ est parallèle à la tangente au point Θ (2). Conduisons la droite EΘ parallèle au diamètre; du point B conduisons aussi la droite BA parallèle au diamètre, et du point Γ la droite ΓΔ tangente à la parabole au point Γ. Puisque KΘ est parallèle au diamètre, que ΓΔ touche la parabole au point Γ, et que EΓ est parallèle à la tangente au point Θ, le triangle BΔΓ sera quadruple du triangle BΘΓ (α). Puisque le triangle BΔΓ est quadruple du triangle Ber, et qu'il est triple du segment BΘΓ,  il est évident que le segment BΘΓ est égal à quatre fois le tiers du triangle BΘΓ.

Lorsque des segments sont compris par une droite et par une courbe, la droite s'appelle la base du segment; la plus grande des perpendiculaires menées de la courbe à la base du segment, s'appelle la hauteur du segment, et enfin le point de la courbe d'où la plus grande perpendiculaire est abaissée, sur la base, s'appelle le sommet.

PROPOSITION XVIII.

Si dans un segment compris par une droite et par une parabole, on conduit du milieu de la base une droite parallèle au diamètre, le sommet du segment est le point de la parabole rencontré par la droite parallèle au diamètre.

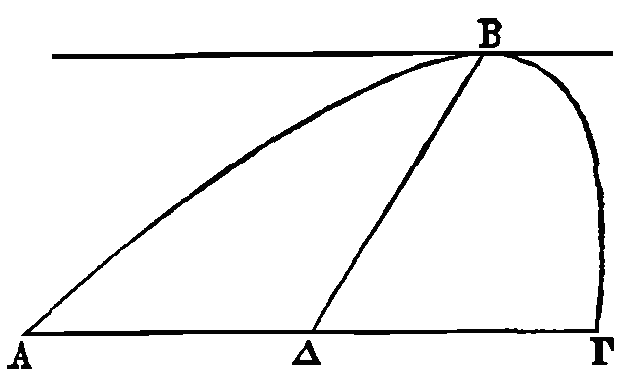
Soit ABΓ un segment compris par une droite et par une parabole. Du milieu de AΓ conduisons la droite ΔB parallèle à un diamètre. Puisque dans une parabole nous avons mené BΔ parallèle au diamètre, et que les droites AΔ, ΔΓ sont égales, la droite AΓ et la droite qui touche la parabole au point B seront parallèles (1). Il est donc évident que de toutes les perpendiculaires menées de la parabole sur la droite ΔΓ, celle qui est menée du point b sera la plus grande. Donc le point B est le sommet du segment.

PROPOSITION XIX.

Si dans un segment compris par une droite et par une parabole, on conduit deux droites parallèles au diamètre, l'une du milieu de la base et l'autre du milieu de la moitié de la base; celle qui est conduite du milieu de la base est égale à quatre fois le tiers de celle qui est conduite du milieu de la moitié de la base.

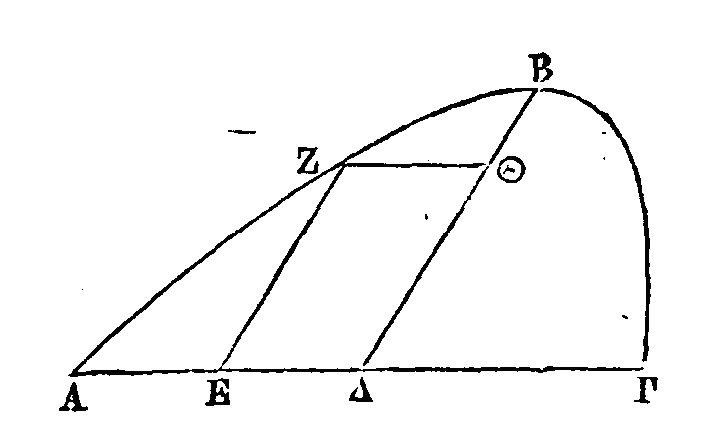
Soit ABΓ un segment compris par une droite et par une parabole. Du milieu de AΓ et du milieu AΔ, conduisons les droites BΔ, EZ, parallèles au diamètre de BΔ. Conduisons aussi ZΘ parallèle à AΓ. Puisque dans une parabole nous avons conduit la droite BΔ parallèle au diamètre, et les droites AΔ, ZΘ parallèles à la droite qui touche la parabole au point B, la droite BΔ sera à la droite BΘ comme le carré construit sur AΔ est au carré construit sur ZΘ (3). Donc BΔ est quadruple de BΘ. Il est donc évident que la droite BΔ est égale à quatre fois le tiers de la droite EZ.

PROPOSITION XX.

Si dans un segment compris par une droite et par une parabole, on inscrit un triangle qui ait la même base et la même hauteur que le segment, le triangle inscrit sera plus grand que la moitié du segment.

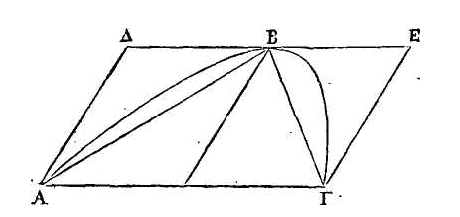
Que le segment ABΓ soit tel que celui dont nous venons de parler. Inscrivons-lui un triangle qui ait la même hauteur que ce segment (18). Puisque le triangle a la même base et la même hauteur que le segment, le point B sera le sommet du segment. Donc AΓ est parallèle à la droite qui touche la parabole au point B. Par le point B conduisons la droite ΔE parallèle à la droite AΓ, et des points A, Γ les droites AΔ, ΓE parallèles au diamètre. Ces droites tomberont hors de la parabole. Donc puisque le triangle ABΓ est la moitié du parallélogramme AΔEΓ, il est évident qu'il est plus grand que la moitié du segment.

Cela étant démontré, il est évident qu'on peut inscrire dans; ce segment un polygone de manière que la somme des segments; restants soit plus petite que toute surface donnée. Car en retranchant continuellement une surface plus grande que la moitié, nous diminuerons continuellement la somme des segments restants, et nous la rendrons par conséquent plus petite que toute surface proposée.

PROPOSITION XXI.

Si dans un segment compris par une droite et par une parabole, on inscrit un triangle qui ait la même base et la même-hauteur que le segment; et si dans les segments restants l'on inscrit d'autres triangles qui aient la même base et la même hauteur que ces segments, le triangle inscrit dans le segment entier est égal à huit fois chacun des autres triangles qui sont inscrits dans les segments restants.

Soit le segment ABΓ tel que celui dont nous venons de parler. Partageons AΓ en deux parties égales au point Δ ; conduisons BΔ parallèle au diamètre. Le point B sera le sommet du segment (18), Donc le triangle ABΓ aura la même base et la même hauteur que le segment. Partageons ensuite AΔ en deux parties égales au point E, et conduisons la droite EZ parallèle au diamètre. La droite AB sera partagée en deux parties égales au point Θ. Donc le point Z sera le sommet du segment AZB. Donc le triangle AZB a la même base et la même hauteur que le segment AZB. Il faut démontrer que le triangle ABΓ est égal à huit fois le triangle ABZ.

En effet, la droite BΔ est égale à quatre fois le tiers de la droite EZ (19) et au double de la droite EΘ. Donc EΘ est double de ΘZ. Donc aussi le triangle AEB est double du triangle ZBA ; car le triangle AEΘ est double du triangle AΘZ, et le triangle ΘBE double du triangle ZΘB. Donc le triangle ABΓ est égal à huit fois le triangle AZB. Nous démontrerons de la même manière qu'il est aussi égal à huit fois le triangle qui est inscrit dans le segment BHΓ.

PROPOSITION XXII.

Si l'on a un segment compris par une droite et par une parabole ; si des surfaces en aussi grand nombre que l'on voudra, sont placées à la suite les unes dés autres; si chacune d'elles contient quatre fois celle qui la suit immédiatement ; et si la plus grande de ces surfaces est égale à un triangle qui ait la même base et la même hauteur que le segment, la somme de toutes ces surfaces sera plus petite que le segment.

Soit un segment AΔBEΓ compris par une droite et par une parabole. Soient aussi autant de surfaces Z, H, Θ, I que l'on voudra, placées les unes à la suite des autres; que Z soit le quadruple de H, et égal à un triangle qui ait la même base et la même hauteur que le segment. Je dis que le segment est plus grand que la somme des surfaces Z, H, Θ, I.

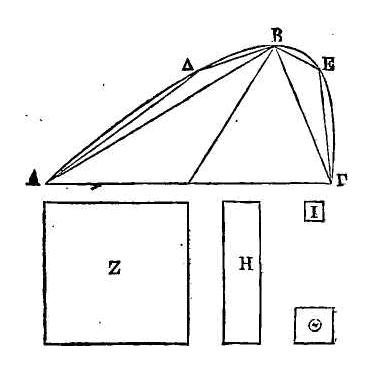
Que le sommet du segment entier soit le point B, et les sommets des segments restants les points Δ, E. Puisque le triangle ABΓ est égal à huit fois chacun des triangles ABΔ, BEΓ, il est évident qu'il est le quadruple de ces deux triangles pris ensemble. Mais le triangle ABΓ est égal à la surface Z ; donc par la même raison la somme des triangles AΔB, BEΓ est égale à la surface H. On démontrera pareillement que la somme des triangles qui sont inscrits dans les segments restant, et qui ont la même base et la même hauteur que ces segments est égale à la surface Θ. Mais la somme des triangles qui sont inscrits, dans les segments suivants est égale à la surface I. Donc la somme de toutes les surfaces proposées est égale à un certain polygone inscrit dans le segment. Il est donc évident que la somme de-toutes ces surfaces est plus petite que le segment.

PROPOSITION XXIII.

Si tant de grandeurs que l’on voudra, sont placées à la suite les unes des autres, et si chacune d'elles contient quatre fois celle qui suit immédiatement, la somme de ces grandeurs, conjointement avec le tiers de la plus petite est égale à quatre fois le tiers de la plus grande.

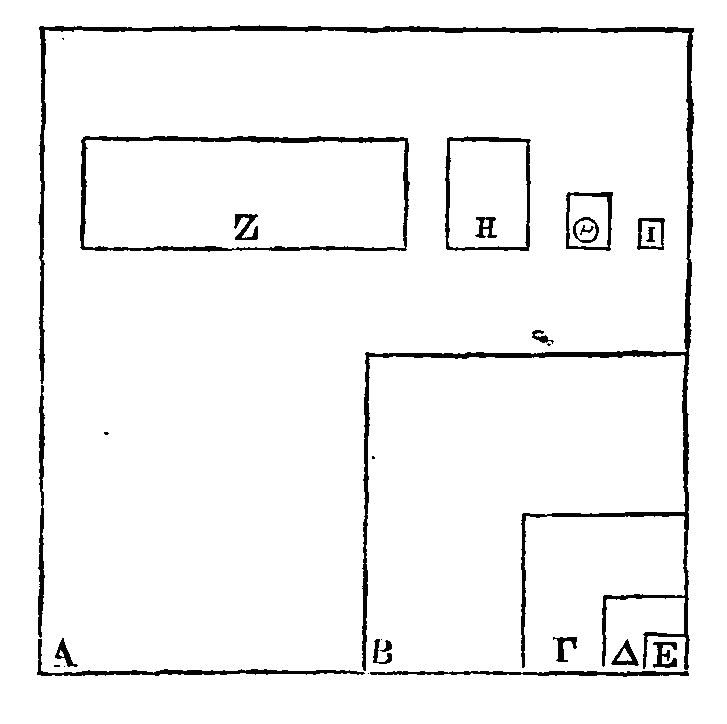
Soient tant de grandeurs que l’on voudra A, B, Γ, Δ, E, placées à la suite les unes des autres, dont chacune contienne quatre fois celle qui suit immédiatement. Que la plus grande soit A ; que Z soit le tiers de B; que H soit le tiers de Γ ; que Θ soit le tiers de Δ, et I le tiers de E. Puisque Z est le tiers de B, et que B est le quart de A, les grandeurs B, Z prises ensemble seront le tiers de A. Par la même raison, les grandeurs H, Γ prises ensemble, sont le tiers de B ; les grandeurs Θ, A prises ensemble, le tiers de Γ, et les grandeurs I, E prises ensemble, le tiers de A. Donc la somme des grandeurs B, Γ, D, E, Z, H, Θ, I est le tiers de la somme des grandeurs A, B, Γ, D. Mais la somme des grandeurs Z, H, Θ est le tiers de la somme des grandeurs B, Γ, D; donc la somme des grandeurs restantes B, Γ, D, E, I est le tiers de la grandeur restante A. Donc la somme des grandeurs A, B, Γ, Δ, E, conjointement avec la grandeur I, c'est-à-dire avec le tiers de la grandeur E, est égal à quatre fois le tiers de la grandeur A (α).

PROPOSITION XXIV.

Un segment quelconque compris par une droite et par une parabole est égal à quatre fois le tiers d'un triangle qui a la même base et la même hauteur que ce segment.

Soit AΔBEΓ un segment compris par «ne droite et par une parabole. Soit aussi tin triangle ABΓ qui ait la même base et la même hauteur que le segment. Que la surface K soit égale à quatre fois le tiers du triangle ABΓ. Il faut démontrer que la surface K est égale au segment AΔBEΓ.

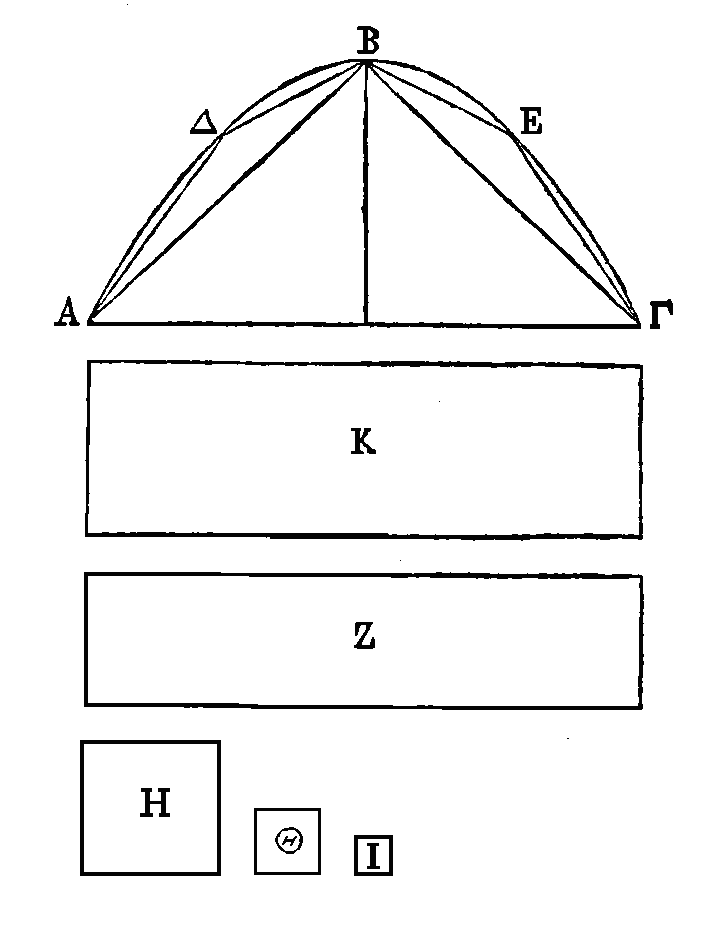
Car si la surface K n'est pas égale au segment AΔBEΓ, elle est ou plus grande ou plus petite. Supposons d'abord, si cela est possible, que le segment AΔBEΓ soit plus grand que la surface K. Inscrivons les triangles AΔB, BEΓ, ainsi que cela a été dit (21). Inscrivons dans les segments restants d'autres triangles qui aient la même base et la même hauteur que ces segments; et continuons d'inscrire dans les segments restants deux triangles qui aient la même base et la même hauteur que ces segments. La somme des segments restants sera certainement plus petite que l'excès du segment AΔBEΓ sur la surface K. Donc le polygone inscrit sera plus grand que la surface K. Ce qui ne peut être. En effet, le triangle ABΓ étant quadruple de la somme des triangles AΔB, BEΓ, la somme de ceux-ci quadruple la somme de ceux qui sont inscrits dans les segments suivants, et ainsi de suite, des surfaces sont placées les unes à la suite des autres, et chacune d'elles contient quatre fois celle qui suit immédiatement (21). D'où il suit que la somme de toutes ces surfaces est plus petite que quatre fois le tiers de la plus grande de ces surfaces (23). Mais la surface K est égale à quatre fois le tiers de cette surface ; donc le segment ADBEΓ n'est pas plus grand que la surface K.

Supposons à présent, si cela est possible, que le segment ADBEΓ soit plus petit que la surface K. Que le triangle ABΓ soit égale à la surface Z ; que la surface H soit le quart de la surface Z ; que la surface Θ soit le quart de la surface H et ainsi de suite, jusqu'à ce que la dernière surface soit plus petite que l'excès de la surface K sur le segment. Que cette dernière surface soit I. La somme des surfaces Z, H, Θ, I, conjointement avec le tiers de la surface I, est égale à quatre fois le tiers de la surface Z (23). Mais la surface K est égale à quatre fois le tiers de la surface Z ; donc la surface K est égale à la somme des surfaces Z, H, Θ, I, conjointement avec le tiers de la surface I. Mais l'excès de la surface K sur la somme des surfaces Z, H, Θ, I est plus petite que la surface I, et l'excès de la surface K sur le segment est plus grand que la surface I ; il est donc évident que la somme des surfaces Z, H, Θ, I est plus grande que le segment. Ce qui ne peut être; car on a démontré que si des surfaces en aussi grand nombre qu'on voudra, sont placées

les unes à la suite des autres, si chacune d'elles contient quatre fois celle qui suit immédiatement, et si la plus grande de toutes est égale au triangle inscrit dans le segment, la somme de ces surfaces est plus petite que le segment (22). Donc le segment AΔBEΓ n'est pas plus petit que la surface K. Mais nous avons démontré qu'il n'est pas plus grand; donc il est égal à la surface K. Mais la surface K est égale à quatre fois le tiers du triangle ABΓ ; donc le segment AΔBEΓ est égal à quatre fois lie tiers du triangle ABΓ.

FIN DE LA QUADRATURE DE LA PARABOLE.

COMMENTAIRE SUR LA QUADRATURE DE LA PARABOLE.

ARCHIMÈDE A DOSITHEE.

(α) Archimède veut parler sans doute de l'ellipse.

(β) Le lemme dont Archimède fait usage est fondé sur le corollaire de la première proposition du dixième livre des Eléments d'Euclide.

PROPOSITION I.

(α) Apollonius, liv. I, prop. 46, et liv. II, prop. 5. Archimède appelle diamètre ce que nous appelons axe, et ce que nous appelons diamètre, il l'appelle parallèle au diamètre.

PROPOSITION II.

(α) Apollonius, liv. I, prop. 35.

PROPOSITION IIΙ

(α) Apollonius, liv. I, prop. 20.

PROPOSITION IV.

(α) En effet, puisque BΓ : BI :: BΓ² : BΘ², on aura BΘ² x BΓ = BI x BΓ² ou bien BΘ² = BI x BΓ². D'où l'on tire BΓ : BΘ :: BΘ : BI.

 (β) Parce que la proposition BΓ : BΘ :: BΘ : BI donne BΓ + BΘ : BΘ + BI :: BΓ : BΘ, c'est-à-dire ΓΘ : IΘ :: BΓ : BΘ, ou bien BΓ : BΘ :: ΓΘ : IΘ.

PROPOSITION V.

(α) Car comparant les deux proportions KΛ : KI :: AΓ : ΛA ; KI : ΘK :: ΔA : AK, on a par raison d'égalité KΛ : ΘK :: AΓ : AK, ou bien KΘ : KΛ :: AK : AΓ ; ce qui donne KΘ : KΛ — ΘK :: AK : AΓ — AK, ou bien KΘ : ΘΛ :: AK : KΓ.

PROPOSITION X.

(α) Livre I, prop. 15 de l'Equilibre des plans.

PROPOSITION XIV.

(α) En effet, on a démontré dans la proposition 5 que BE : EΓ :: EΦ : ΦΣ. Ce qui donne BE + EΓ : BE :: EΦ + ΦΣ : EΦ ; c'est-à-dire que BΓ : BE :: ΣE : EΦ.

(β) Parce que le trapèze ΔE est: au trapèze KE comme la droite menée du milieu de BE parallèlement à BΔ, et terminée à la droite ΔΣ, est à la droite menée du milieu de BE parallèlement à la droite BK et terminée à la droite KΦ. Mais cette première droite est à la seconde comme ΣE : ΦE, et ΣE : ΦΣ :: BΓ ou BA : EE; donc BA : BE :: trapèze ΔE : trapèze KE.

PROPOSITION XVI.

(α) Car puisque le triangle BΓE et la surface Z pris ensemble sont plus petits que le segment BΘΓ, si nous retranchons de part et d'autre BΓE, nous aurons Z < BΘΓ — BΓE, ou bien Z < BΘΓ — ME — ΛΘ — ΘΠ— ΘO — ΓOΣ, c'est-a-dire Z < MΛ + XΠ + ΠΘ + ΠOΓ.

PROPOSITION XVII.

(α) Car si l'on prolonge la droite ΓΘ jusqu'à la droite BΔ, cette droite partagera BΔ en deux parties égales, parce que EΘ = ΘK. Donc la droite ΓΘ prolongée partagera le triangle BΓΔ en deux triangles égaux. Mais le triangle formé par BΓ, par ΓΘ prolongé et par la moitié de B est double du triangle BΓΘ; donc le triangle BΓΔ est quadruple du triangle BΓΘ.

PROPOSITION XXIII.

(α) Cette proposition peut se démontrer algébriquement d'une manière très simple. Soit a la plus petite de ces grandeurs et u la plus grande. La somme de ces grandeurs égalera (4u — a)/3, et si l'on ajoute a/3, l'on aura 4u.

FIN DU COMMENTAIRE SUR LA QUADRATURE DE LA PARABOLE.