LIVRE SECOND.
PROPOSITION PREMIÈRE.
Si deux surfaces qui sont comprises
par une droite et par une parabole, et qui peuvent par conséquent s'appliquer
sur une droite donnée, n'ont pas le même centré de gravité, le centre de gravité
de la grandeur composée des deux premières sera dans la droite qui joint les
centres de gravité, la droite dont nous venons de parler étant partagée de
manière que ses segments soient réciproquement proportionnés aux surfaces
paraboliques. Soient deux surfaces
AB, ΓΔ,
telles que celles
dont nous
venons de parler. Que leurs centres de gravité soient les points
E, Z, et
que la surface
AB
soit à la surface ΓΔ comme ZΘ
est à
ΘE. Il faut démontrer que le
point Θ est le centre de gravité de la grandeur composée des deux grandeurs
AB, ΓΔ.
Que chacune des droites
ZH,
ZK
soit égale à EΘ, et la
droite
EΛ
égale
à la droite ZΘ, c'est-à-dire à la droite
HE.
La droite ΛΘ sera aussi égale à
la droite
KΘ
; et
la surface
AB
sera à
la surface
ΓΔ
comme
ΛH
est à
HK ;
car
chacune des droites
ΛH, HK
est double de chacune
des droites ZΘ, ΘE. Appliquons sur la droite
ΛH
de l'un et de l'autre côté, la
surface
AB
; de
manière que la surface
MN
soit égale à la surface
AB
(α). Le centre de
gravité de la surface
MN
sera le point
E (i,
9). Achevons le
rectangle NΞ. La surface
MN
sera à la surface
NΞ
comme
ΛH
est à
NK.
Mais la surface
AB
est-à la surface
ΓΔ
comme
ΛH
est à
HK ;
donc la surface
AB
est à la surface
ΓΔ
comme la surface
MN
est à
la surface
NΞ,
et par permutation ……………… Mais la surface
AB
est égale à la surface
MN
; donc la surface ΓΔ est
égale à la surface
NH.
Puisque le centre de gravité de
NΞ
est le
point Z, que la droite
AΘ
est égale à la droite ΘK,
et que la droite entière
ΛK
partage les côtés opposés en
deux parties égales, le point Θ sera le centre de gravité de la surface entière
ΠM (i, 9). Mais la surface MΠ est
égale à une surface composée de
MN, NΞ;
donc le point Θ est le
centre de gravité de la surface composée des surfaces
AB, ΓΔ.
Si dans le segment qui est compris par
une droite et par
une parabole, on inscrit un triangle qui ait la même base et la
même hauteur que le segment; si dans les segments restants ont inscrit des
triangles qui aient la même base et la même hauteur que ces segments, et si l'on
continue d'inscrire de la même manière des triangles dans les segments restants,
la figure produite est dite inscrite régulièrement dans le segment (β).
Il est évident que les droites qui joignent les angles de la figure inscrite de
cette manière, non seulement ceux qui sont les plus près du sommet, mais encore
ceux qui viennent ensuite, seront parallèles à la base du segment. Ces droites
seront coupées en deux parties égales par le diamètre du segment; et ces mêmes
droites couperont le diamètre de manière que ses segments, en comptant pour un
celui qui est vers le sommet, seront entre eux comme les nombres successivement
impairs. Ce qu'il faut démontrer (γ).
PROPOSITION II.
Si dans un segment compris par une
droite et par une parabole, on inscrit régulièrement une figure rectiligne, le
centre de gravité de la figure rectiligne sera dans le diamètre du segment.
Que le segment ABΓ soit tel que celui
dont nous venons de
parler. Inscrivons-lui régulièrement la figure rectiligne
AEZHBΘΛIKΓ. Que BΔ soit le diamètre du
segment. Il faut démontrer que le centre de gravité de cette figure rectiligne
est dans
BΔ.

Car puisque le centre de gravité du
trapèze AEKΓ est dans la droite
ΛΔ
(i, 15), le centre de gravité du
trapèze
EZIH
dans
MΛ,
le
centre de gravité du trapèze ZHΘI dans
MN,
et enfin le centre de gravité
du triangle HBΘ dans
BN,
il est évident que le centre de
gravité de la figure rectiligne entière sera dans BΛ.
PROPOSITION III.
Si dans deux segments semblables
compris par une droite et par une parabole, on inscrit régulièrement des figures
rectilignes qui aient le même nombre de côtés, les centres de gravité des
figures rectilignes seront semblablement placés dans les diamètres des segments
(α).
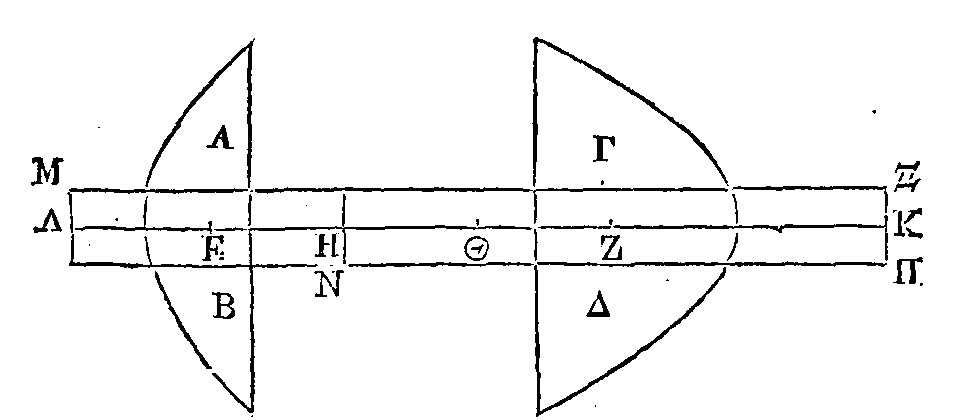
Soient les deux segments
ABΓ,
ΞOΠ. Inscrivons-leur régulièrement des figures rectilignes qui aient chacune le
même nombre de côtés. Que BΔ,
OΡ
soient les diamètres des
segments. Menons les droites
EK, ZI,
HΘ ; et les droites ΣT,
ΥΦ, ΧΨ. Puisque les diamètres BΔ,
ΡO
sont partagés
semblablement par les parallèles ; que leurs segments sont comme les nombres
successivement impairs, et que ces segments sont égaux en nombre, il est évident
que non seulement les segments des diamètres, mais encore les parallèles, seront
dans les mêmes raisons (β). Mais les centres de gravité des trapèzes AEKΓ, ΞΣTΠ
seront semblablement placés dans les droites
ΛΔ,
ΩΠ, parce que la raison
de
AΓ à
EK
est la même que la raison de ΞΠ
à ΣT (i, 15 ) ; les centres de
gravité des trapèzes
ezik,
ΣΥΦT
seront semblablement
placés dans les droites
ΛM,
ΩϚ;
les centres de gravité des trapèzes
ZΘ, ΥΨ seront semblablement placés dans les droites
MN,
ϚϞ,
et les centres de gravité des triangles
HBΘ,
ΧOΨ
seront encore
semblablement placés dans les droites
BN,
OϞ
; et de plus les trapèzes et les triangles sont proportionnels. Il est donc
évident que le centre de gravité de la figure rectiligne entière inscrite dans
le segment
ABΓ, et le
centre de gravité de la figure rectiligne entière inscrite dans le segment ΞΘΠ
sont semblablement placés dans les diamètres
BΔ,
OΡ. Ce qu'il fallait démontrer.
PROPOSITION IV.
Le centre de gravité d'un segment
quelconque compris par une droite et par une parabole est dans le diamètre du
segment.
Soit
ABΓ
un segment tel que celui
dont nous venons de
parler. Que son diamètre soit
BΔ. Il faut démontrer que le
centre de gravité du segment dont nous venons de parler est dans la droite BΔ.
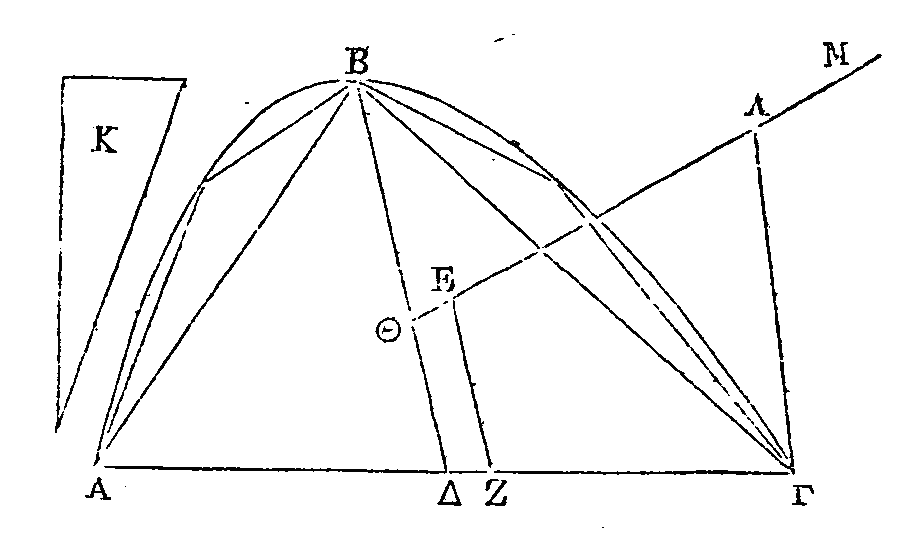
Que cela ne soit point; et que le
point E soit son centre de gravité. Par ce point conduisons
EZ
parallèle à BΔ. Inscrivons dans
le segment un triangle ABΓ, ayant la même base et la même hauteur que ce
segment; et que ΓZ soit à ΔZ comme le triangle ABΓ est à la surface
K.
Inscrivons régulièrement
dans le segment une figure rectiligne, de manière que la somme des segments
restants soit moindre que la surface K (α). Le centre de gravité de la figure
rectiligne inscrite est dans la droite BΔ (ii,
2); que son centre de gravité soit le point Θ Menons la droite
ΘE;
et ayant prolongé cette droite,
conduisons ΓΛ parallèle à
BΔ.
Il est évident que la raison de
la figure rectiligne inscrite dans le segment à la somme des segments restants
est plus grande que la raison du triangle ABΓ à la surface
K.
Mais le triangle ABΓ est à la
surface
K comme ΓZ est à ZΔ; donc la raison de la figure inscrite dans le
segment à la somme des segments restants est plus grande que la raison de ΓZ à
ZΔ,
c'est-à-dire de
ΛE
à EΘ. Que
ME
soit à
EΘ
comme la figure rectiligne
inscrite est à la somme des segments. Donc puisque le centre de gravité du
segment entier est le point
E,
et que le centre de gravité de la figure inscrite est le point Θ, il est évident
que le centre de gravité de la grandeur restante qui est composée de tous les
segments restants sera dans la droite ΘE prolongée, de manière que son
prolongement soit à ΘE comme la figure rectiligne inscrite est à la somme des
segments restants (i, 8). Donc le
centre de gravité de la grandeur composée des segments restants sera le point M.
Ce qui est absurde; car tous les segments restants sont du même côté de la
droite menée par le point
M
parallèle à
BΔ.
Il est donc évident que le
centre de gravité est dans BΔ.
PROPOSITION V.
Si dans un segment compris par une
droite et par une parabole, on inscrit régulièrement une figure rectiligne, le
centre de gravité du segment est plus près du sommet que le centre de gravité de
la figure rectiligne.
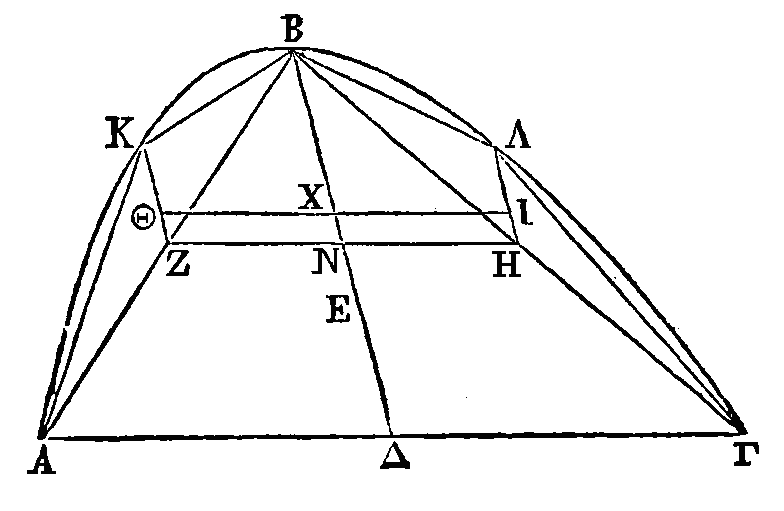
Soit ABΓ un segment tel que celui dont
nous venons de parler;
que
BΔ
soit son diamètre.
Inscrivons-lui d'abord régulièrement
le triangle
ABΓ. Partageons BΔ au point
E,
de manière que BE soit double de EΔ. Le point E sera le centre de gravité du
triangle ABΓ. Partageons les droites AB, BΓ en deux parties égales aux points Z,
H, et par les points Z,
H
conduisons les droites
ZK, ΛH
parallèles à BΔ; le centre de gravité du segment
AKB
sera dans la droite
ZK, et le
centre de gravité du segment BΓΛ dans la droite
HΛ
(ii,
4). Que ces centres de gravité soient les points Θ, I. Menons ΘI. Puisque la
figure ΘZHI est un parallélogramme (α), et que
ZN
est égal à
NH,
la droite ΧΘ sera égale à la droite ΧI. Donc le centre de gravité de la grandeur
composée des deux segments
AKB,
BΛΓ sera dans le milieu de ΘI, c'est-à-dire en Χ ; car ces segments sont égaux
(β). Puisque le centre de gravité du triangle ABΓ est le point E, et que le
centre de gravité de la grandeur composée des deux segments
AKB,
EΛΓ est le point Χ, il est évident que le centre de gravité du segment total ABΓ
sera dans
ΧE,
c'est-à-dire entre les points Χ et E (ii,
8). Donc le centre de gravité du segment entier sera plus près du sommet que le
centre de gravité du triangle régulièrement inscrit.
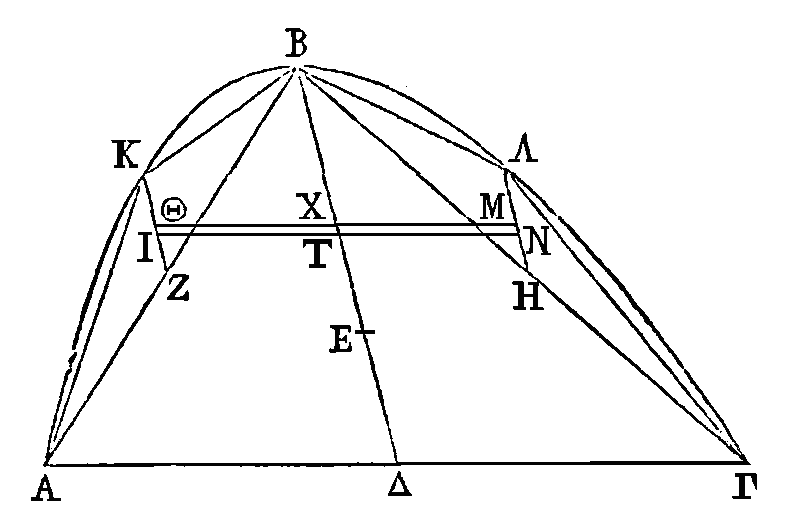
Inscrivons ensuite régulièrement dans
le segment ABΓ le pentagone AKBΛΓ. Que la droite BΔ soit le diamètre du segment
entier, et les droites
KZ, ΛH
les diamètres des
segments
AKB, BΛΓ.
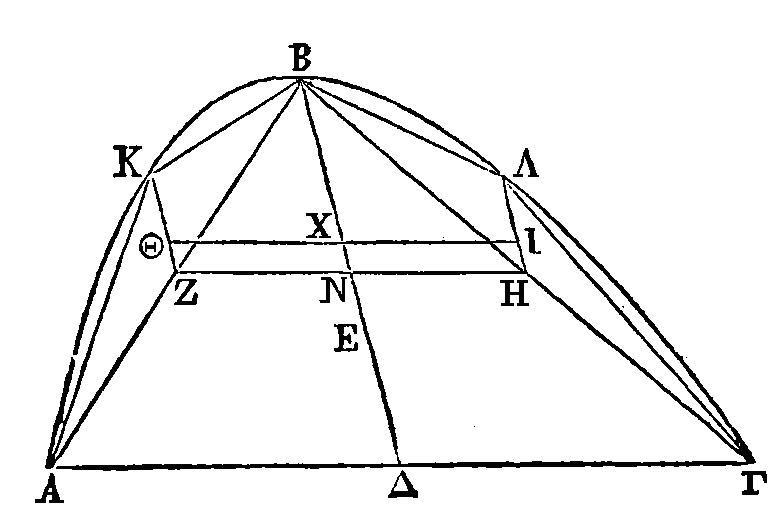
Puisque dans le segment
AKB
on a inscrit régulièrement un
triangle, le centre de gravité du segment entier est plus près du sommet que le
centre de gravité du triangle. Que le point Θ soit le centre de gravité du
segment AKB et le point I celui
du triangle; que le point
M
soit le centre de
gravité du segment BΛΓ, et le point
N
celui du triangle. Joignons les
points Θ,
M
et les points I,
N.
La droite ΘΧ sera égale
à la droite
ΧM,
et la
droite IT à la droite
TN.
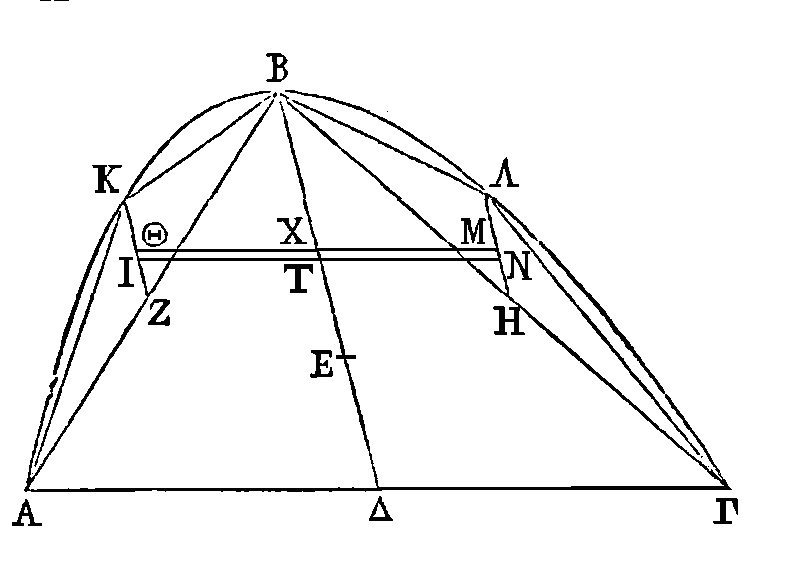
Mais le triangle BΛΓ est égal au
triangle
AKB,
et
le segment BΛΓ au segment
AKB,
car on a démontré dans d'autres
livres que ces segments sont égaux à quatre fois le tiers des triangles (γ) ;
donc, le point Χ sera le centre de gravité de la grandeur composée des segments
AKB, BΛΓ,
et le point T le centre de gravité de la grandeur composée des triangles
AKB,
BΛΓ.
Donc puisque le point
E
est le
centre de gravité du triangle ABΓ, et le point Χ le centre de gravité de la
grandeur composée des segments
AKB,
BΛΓ,
il est évident que le
centre de gravité du segment entier ABΓ est dans la droite ΧE,
partagée de manière que
la partie dont l'extrémité est le point Χ soit à la plus petite partie comme le
triangle ABΓ est à la somme des segments
AKB,
BΛΓ (i, 8). Mais le centre de
gravité du pentagone AKBΛΓ est dans la droite ET, partagée de manière que la
partie dont l'extrémité est le point T, soit à l'autre partie comme le triangle
ABΓ est à la somme des triangles
AKB,
BΛΓ.
Donc puisque la raison
du triangle
ABΓ à la somme des triangles
KAB,
ABΓ est plus grande que la raison du triangle ABΓ à la somme des segments AKB, BΛΓ
(d), il est évident que le centre de gravité du segment ABΓ est plus près du
sommet
B
que le
centre de gravité de la figure rectiligne inscrite. On pourra faire le même
raisonnement pour toutes les figures rectilignes régulièrement inscrites.
PROPOSITION VI.
Un segment compris par une droite et
par une parabole étant donné, on peut lui inscrire régulièrement une figure
rectiligne, de manière que la droite qui est entre le centre de gravité du
segment et celui de la figure rectiligne soit plus petite que toute droite
proposée.
Soit donné le segment ABΓ tel que
celui dont nous venons de parler ; que son centre de gravité soit le
point Θ. Inscrivons-lui régulièrement le triangle ABΓ, et que Z soit la droite
proposée. Que le triangle ABΓ soit à la surface
K
comme
BΘ
est à Z. Inscrivons
régulièrement dans le segment ABΓ la figure rectiligne
AKBΛΓ,
de manière que la somme
des segments restants soit plus petite que la surface
K.
Que le point E soit le centre
d« gravité de la figure rectiligne inscrite. Je dis que la droite ΘE est plus
petite que la droite Z.
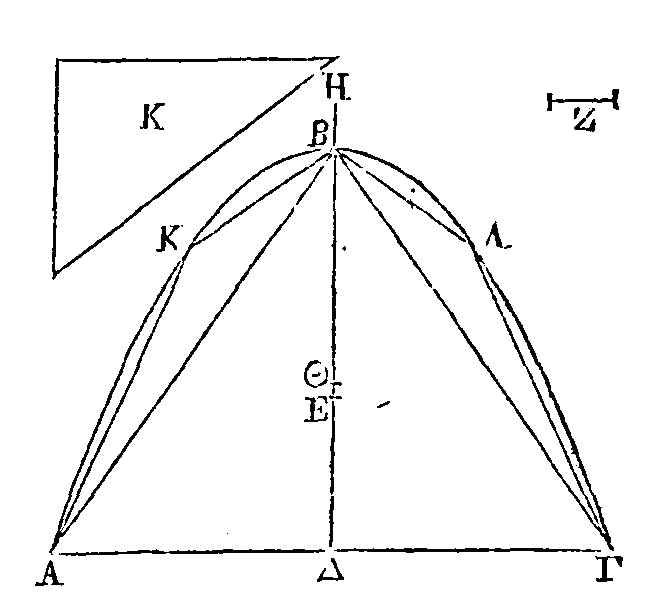
Car si la droite ΘE n'est pas plus
petite que la droite Z, elle lui est égale ou plus grande. Mais puisque la
raison de la figure rectiligne AKBΛΓ à la somme des segments restants est plus
grande que la raison du triangle ABΓ à la surface
K
(α), c'est-à-dire que la
raison de la droite
ΘB à la droite
Z,
et que la raison ΘB à
Z
n'est pas moindre que la raison de ΘB à ΘE ; parce que ΘE n'est pas plus petit
que
Z, la
raison de la figure rectiligne AKBΛΓ à la somme des segments restants sera
encore plus grande que la raison des BΘ à ΘE. C'est pourquoi, si nous faisons en
sorte que la figure rectiligne AKBΛΓ soit à la somme des segments restants comme
une autre droite est à la droite ΘE, cette autre droite sera plus grande que la
droite
BΘ.
Que
cette autre droite soit
ΘN.
Puisque le point Θ est le
centre de gravité du segment ABΓ, et le point E le centre de gravité de la
figure rectiligne AKBΛΓ, si l’on prolonge la droite EΘ et si l'on prend une
certaine partie de son prolongement qui soit à
ΘE
comme la figure rectiligne AKBΛΓ
est à la somme des segments restants, cette partie du prolongement sera plus
grande que
ΘB.
Que
HΘ soit donc à ΘE comme la figure rectiligne AKBΛΓ est aux segments restants; le
point H sera le centre de gravité de la grandeur composée de tous les segments
restants. Ce qui ne peut être; car si l’on conduit par le point
N
une droite parallèle à BΓ, les
segments restants seront du même côté que le segment entier. Il est donc évident
que la droite ΘE est moindre que la droite
Z
; ce qu'il fallait démontrer (β).
PROPOSITION VII.
Les centres de gravité de deux
segments semblables compris par une droite et par une parabole, coupent leurs
diamètres dans la même raison.
Soient les deux segments ABΓ,
EZN
tels que ceux dont nous
venons de parler. Que BΔ, ZΘ soient leurs diamètres ; que le point K soit le
centre de gravité du segment ABΓ, et le point
Λ
le centre de gravité du segment
EZN.
Il
faut démontrer que les points
K, Λ
coupent les diamètres en
parties proportionnelles.
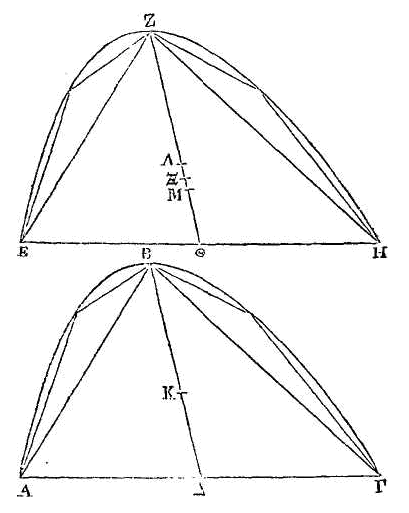
Car si cela n'est point, que
ZM
soit à ΘM comme KB
est à KΔ. Inscrivons
régulièrement dans le segment
EZN
une figure rectiligne, de
manière que la droite qui est entre le centre de gravité du segment et le centre
de gravité de la figure rectiligne soit
plus petite que
ΛM.
Que le point
Ξ
soit le centre de
gravité de la figure inscrite. Inscrivons dans le segment
ABΓ
une figure rectiligne semblable à celle qui est inscrite dans le segment
EZN
c'est-à-dire
régulièrement (α). Le centre de gravité de cette dernière figure sera plus près
du sommet que le centre de gravité du segment (ii,
5). Ce qui ne peut être. Il est donc évident que BK est à KΛ comme
ZΛ
est à
ΛΘ.
PROPOSITION VIII.
Le centre de gravité d'un segment
compris par une droite et par une parabole partage le diamètre, de manière que
la partie qui est vers le sommet est égale à trois fois la moitié de la partie
qui est vers la base.
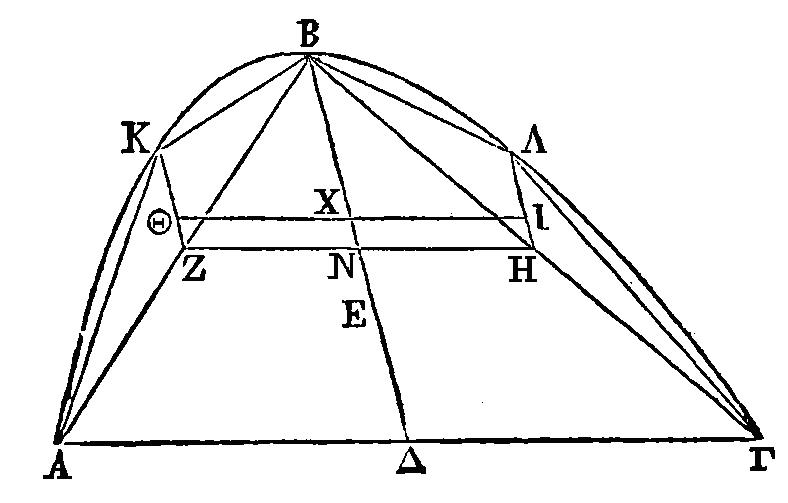
Soit un segment ABΓ tel que celui dont
nous venons de parler. Que
BΔ
soit son diamètre, et le point e son centre de gravité. Il faut démontrer que la
droite BΘ est égale aux trois moitiés de la droite ΘΔ.
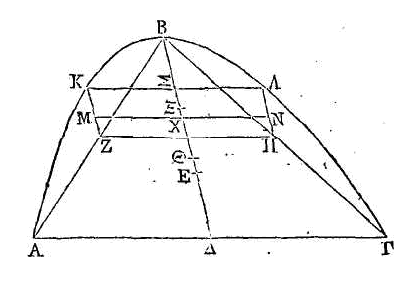
Inscrivons régulièrement dans le
segment ABΓ le triangle dont le centre de gravité soit le point
E.
Partageons chacune des droites
AB, BΓ en
deux parties égales aux points Z, H, et conduisons les droites
KZ, NΛ
parallèles à BΔ : ces
droites seront les diamètres des segments
AKB, BΛΓ.
Que le point
M
soit le centre de gravité du
segment AKB, et le point N le centre de gravité du segment
BΛΓ.
Menons les droites
ZN,
MN, KΛ. Le point Χ sera
le centre de gravité de la grandeur composée de ces deux segments. Puisque
BΘ
est à
ΘΔ comme
KM
est à
MZ (α), par addition et par permutation, la droite BΔ sera à la droite
KZ
comme ΘΔ est à
MZ.
Mais la droite
BΔ
est quadruple de
KZ,
ainsi qu'on le démontrera à la fin,
à l'endroit où est la lettre
Θ (β). Donc la droite ΔΘ est
quadruple de la droite
MZ.
Donc la droite restante BΘ est
aussi quadruple de la droite restante
KM
c'est-à-dire de la droite ΣΧ.
Donc la somme des droites restantes
BΣ; ΞO
est triple de la
droite
ΣΧ (γ).
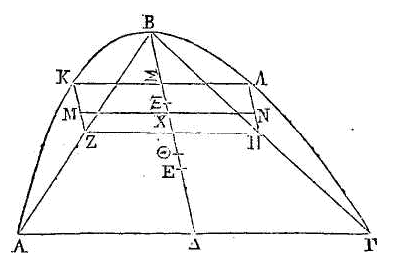
Que
BΣ
soit triple de ΣΞ; la
droite ΧΘ sera triple de ΞΧ. Puisque
BΔ
est quadruple de
BΣ,
car cela se démontre, et que BΣ
est triple de ΣΞ, la droite ΞB sera le tiers de
BΣ.
Mais EΔ est le tiers de
ΔB,
parce que le point E est le centre de gravité du triangle
ABΓ.
Donc la droite restante ΞE est
le tiers de la droite
BΔ.
Puisque le point Θ est le centre de gravité du segment entier, que le point Χ
est le centre de gravité de la grandeur composée des deux segments
AKB,
BΛΓ, et qu'enfin le
point
E
est le
centre de gravité du triangle ABΓ, le triangle ABΓ sera à la somme des segments
restants comme
ΧΘ
est à
ΘE (i,
8). Mais le triangle ABΓ est triple de la somme des segments ; parce que le
segment entier est égal à quatre fois le tiers du triangle ABΓ (d) ; donc
ΧΘ
est triple de ΘE. Mais on a démontré que
ΧΘ
est triple de ΧΞ; donc
ΞE,
c'est-à-dire ΔE est
quintuple de EΘ, car les droites ΞE, ΔE sont égales. Donc ΔΘ est sextuple de ΘE.
Mais BΔ est triple de
ΔE (e);
donc
BΘ
est égal aux trois moitiés de ΘΔ.
Ce qu'il fallait démontrer.
PROPOSITION IX.
Si quatre lignes droites sont
continuellement proportionnel les, si l’on prend une droite qui soit aux trois
cinquièmes de l'excès de la plus grande sur la troisième, comme la plus petite
est à l'excès de la plus grande sur la plus petite, et si l'on prend une autre
droite qui soit à l'excès de la plus grande sur la troisième, comme une droite
composée du double de la plus grande, du quadruple de la seconde, du sextuple de
la troisième, du triple de la quatrième, est à une droite composée du quintuple
de la plus grande, du décuple de la seconde, du décuple de la troisième
et du quintuple de la quatrième; ces deux droites prises ensemble seront les
deux cinquièmes de la plus grande (α).
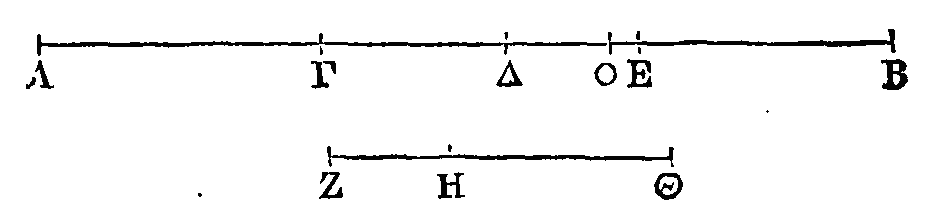
Soient
AB, BΓ, BΔ,
BE quatre droites
proportionnelles. Que la droite
ZN
soit aux trois cinquièmes de la
droite AΔ comme
BE
est à
EA,
et que HΘ soit à AΔ comme une droite composée du double de
AB,
du quadruple de BΓ, du sextuple de BΔ et
du triple de
BE,
est à une droite composée du
quintuple de
AB,
du décuple de
ΓB,
du décuple de
BΔ
et du quintuple de
BE.
Il faut démontrer que ZΘ
est égal aux deux cinquièmes de
AB.

Puisque les droites
AB, BΓ, BΔ,
BE sont
proportionnelles, les droites
AΓ,
ΓΔ,
ΔE
seront dans la même
raison (β). Donc la somme des droites
AB,
BΓ est à
BΔ,
et la
somme des
droites
BΔ,
BΓ, est à
EB
comme
AΔ est à
ΔE,
et
comme la somme de tous les antécédents est à la somme de tous les conséquents.
Donc AΔ est à ΔE comme une droite composée du double de
AB,
du triple de ΓB et de
ΔB
est à une droite
composée du double de
BΔ
et de
BE.
Mais une droite composée du
double de AB, du quadruple de BΓ, du quadruple de
BΔ,
du double de
BE,
est à une droite composée du
double de
BΔ
et de
BE
comme
la droite ΔA sera à une droite plus petite que ΔE; que ce soit à
ΔO.
La dernière raison sera égale à
la première. Donc
OA
sera à AΔ comme une droite
composée du double de AB, du quadruple de ΓB, du sextuple de
BΔ,
du triple de
BE
est à une droite composée du
double de chacune des droites
AB, EB,
et du quadruple de chacune des droites ΓB, BΔ.
Mais
AΔ
est à
HΘ
comme
une droite composée du quintuple de chacune des droites
AB, BE,
et du décuple de chacune
des droites
ΓB,
BΔ,
est à la droite composée du double de
AB,
du quadruple de ΓB, du triple
de
EB
et du
sextuple de
BΔ.
Donc
les raisons étant disposées différemment, c'est-à-dire la proportion étant
troublée, par raison d'égalité, la droite OA sera à HΘ comme une droite composée
du quintuple de chacune des droites
AB, BE
et du décuple de chacune
des droites ΓB, BΔ,
est à une droite
composée du double de chacune des droites
AB, BE
et du quadruple de
chacune des droites ΓB, BΔ.
Mais une droite composée
du quintuple de chacune des droites,
AB, BE,
et du décuple de chacune
des droites ΓB, BΔ, est à une droite composée du double de chacune
des droites
AB, BE
et
du quadruple de chacune des droites
ΓB, BΔ, comme cinq est à deux; donc
AO
est à HΘ comme cinq est à deux.
De plus, puisque OΔ est à
ΔA
comme
EB,
conjointement avec le double de
BΔ
est à
une droite composée du double de chacune des droites
AB, BE
et du quadruple de chacune des droites ΓB, BΔ,
et que
AΔ
est à
ΔE comme une droite composée du double de AB,
du triple de ΓB
et de BΔ,
est à une droite
composée de
EB
et du
double de BΔ. Donc les raisons étant autrement disposées, c'est-à-dire la
proportion étant troublée, par raison d'égalité, la droite OΔ sera à la droite
ΔE
comme
une droite composée du double de
AB,
du triple de BΓ et de BΔ, est à une droite composée du double de chacune des
droites
AB, BE
et
du quadruple de chacune des droites ΓB, BΔ.
Donc
EO
est à
EΔ
comme une droite composée de
ΓB, du
triple de BΔ et du double de
EB,
est à une droite composée du double de chacune des droites
AB, BE
et du quadruple de
chacune des droites ΓB, BΔ.
Mais
ΔE
est à
EB
comme AΓ est à
ΓB,
et comme ΓΔ est à ΔB, et par
addition, comme le triple de ΓΔ est au triple de
ΔB,
et comme le double de
ΔE
est au double de
EB
; donc aussi une droite
composée de AΓ, du triple de
ΓΔ
et du double de
ΔE
est à une droite composée de
ΓB, du triple de ΔB et du double de
EB.
Donc les raisons étant
autrement disposées, c'est-à-dire la proportion étant troublée, par raison
d'égalité la droite EO
sera à
la droite
EB
comme une droite composée de
AΓ, du triple de
ΓΔ
et du double de ΔE est à une
droite composée du double de chacune des droites
AB, BE
et du quadruple de chacune des droites ΓB, BΔ.
Donc la droite entière
OB
est à
EB
comme
une droite composée du triple de
AB,
du sextuple de
ΓB
et du triple de BΔ est à une
droite composée du double de chacune des droites
AB, BE,
et du quadruple de chacune des droites ΓB, BΔ. Puisque non seulement les droites
EΔ, ΔΓ,
ΓA
ont la même raison, mais
encore les sommes des droites
EB, BA,
des
droites
ΔB,
ΓB
et des droites
ΓB,
ΓA; donc une droite composée des droites
EB, BΔ
sera à une droite
composée des droites AB, BΓ et des droites
ΓB,
BA
comme
EΔ
est à
ΔA.
Donc, par addition, la droite
AE
est à
AΔ comme une droite composée des droites
EB,
BΔ, et des droites
AB, BΓ,
et des droites ΓB,
BΔ,
c'est-à-dire des droites
EB, BA
et du double de chacune
des droites
ΔB, BΓ
est à une droite composée de chacune des droites

BΔ, BA et du double de BΓ. Donc la
raison du double au double sera la même, c'est-à-dire qu'une droite composée du
double de chacune des droites
EB, BA,
et du quadruple de chacune des droites ΓB,
BΔ
est à une droite
composée du double de chacune des droites
AB,
BΔ et du quadruple de ΓB, comme
EA
est à AΔ. Donc EA est aux trois
cinquièmes de AΔ comme une droite composée du double de chacune des droites
AB, BE,
du quadruple de chacune des droites ΓB, BΔ
aux trois cinquièmes de
la droite composée du double de chacune des droites AB, BΔ, et du quadruple de
ΓB.
Mais
EA
est
aux trois cinquièmes de
AΔ
comme
EB
est à
ZH
; donc
EB
est à
ZH
comme une droite composée du
double de chacune des droites
AB, BE
et du quadruple de
chacune des droites ΔB, BΓ est aux trois cinquièmes de la droite composée du
double de chacune des droites
AB,
BΔ et du quadruple de ΓB. Mais
on a démontré qu'une droite composée du triple de chacune des droites AB, BΔ et
du sextuple de
ΓB,
est à une droite composée du double de chacune des droites
AB, BE
et du quadruple de
chacune des droites ΓB, BΔ,
comme OB est à
EB
; donc, par raison d'égalité,
une droite composée du triple de chacune des droites AB, BΔ et du sextuple de
ΓB,
est aux trois cinquièmes d'une droite
composée du double de chacune des droites AB, BΔ, du quadruple de ΓB, comme
OB
est à
ZH.
Mais
la droite composée du triple de chacune des droites AB, BΔ et du sextuple de ΓB,
est à une
droite composée du double de chacune des droites
AB, BΔ
et du
quadruple de
ΓB
comme trois est à deux. Mais la
première droite est aux trois cinquièmes de cette droite comme
cinq est à deux, et l'on a
démontré que
AO est à HΘ
comme cinq est à deux. Donc la droite entière
BA
est à la droite entière ZΘ
comme cinq est à deux. Cela étant ainsi, il faut que ce soit les deux cinquièmes
de
AB
Ce
qu'il fallait démontrer.
PROPOSITION X.
Le centre de gravité d'un segment
retranché d'une surface parabolique est dans la ligne droite qui est le diamètre
du segment partagée en cinq parties égales ; et il est placé dans la
partie du milieu, coupée de manière que la portion qui est plus près de la plus
petite base du segment, soit à l'autre portion comme un solide ayant pour base
le carré construit sur la moitié de la grande base du segment, et pour hauteur
le double de la plus petite base, conjointement avec la plus grande, est à un
solide ayant pour base le carré construit sur la moitié de la plus petite base
du segment et pour hauteur le double de la plus grande base du segment,
conjointement avec la plus petite base du segment.
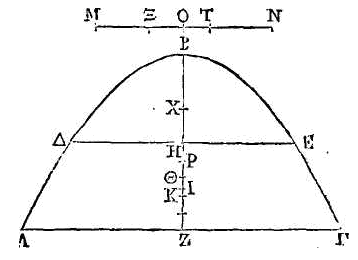
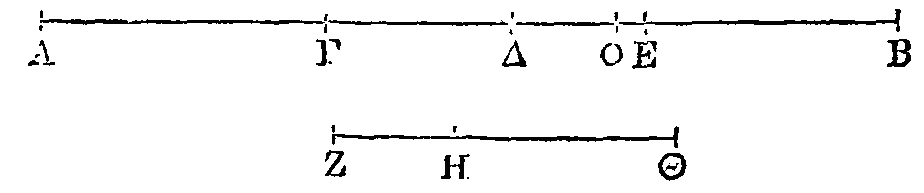
Soient dans une parabole les deux
droites AΓ,
ΔE;
que
BZ
soit le diamètre du
segment
ABΓ.
Il
est évident que
HZ
sera aussi le diamètre du
segment AΔEΓ, et que les droites AΓ,
ΔE
sont parallèles à la
tangente au point
B
(α). Partageons la
droite
HZ en cinq parties égales, et que
ΘK
soit
la partie du milieu. Que
ΘI
soit à
IK
comme
un solide ayant pour base le carré construit sur
AZ
et pour hauteur le double de la
droite ΔH,
conjointement avec la droite
AZ,
est à un solide ayant pour base le carré construit sur
ΔH
et pour hauteur le double de la
droite
AZ,
conjointement avec la droite
ΔH.
Il faut démontrer que le point
I est le centre de gravité du segment AΔEΓ.

Que
MN
soit égal à ZB, et
NO
égal à
HB.
Prenons une droite
NΞ
moyenne proportionnelle
entre
MN,
NO, et la
droite
TN
quatrième proportionnelle à ces trois droites. Faisons en sorte que
TM
soit à
TN
comme ZΘ
est à une droite
IΠ
menée
du point I ; son autre extrémité tombera où l’on voudra, car il est indifférent
que son autre extrémité tombe entre Z,
H
ou entre
H, B.
Puisque
ZB
est un diamètre de la parabole,
c'est-à-dire, ou le premier ou un diamètre parallèle au premier (β), et que les
droites
AZ, ΔH
sont des ordonnées, parce qu'elles sont parallèles à la tangente au point B,
le carré construit sur
AZ
sera au carré construit sur
ΔH
comme
ZB
est à
BH,
c'est-à-dire comme
MN
est à
NO.
Mais
MN
est à
NO
comme le carré construit sur
MN
est au
carré construit sur
NΞ,
donc le carré construit sur
AZ
est au carré construit
sur
ΔH
comme le carré construit sur
MN
est au
carré construit sur
NΞ.
Donc
AZ
est à
ΔH
comme
MN
est à
NΞ.
Donc le cube construit sur
AZ
est au
cube construit sur
ΔH
comme le cube construit sur
MN
est au
cube construit sur NΞ. Mais le cube construit sur
AZ
est au cube construit sur
ΔH
comme
le segment BAΓ est au segment
ΔBE;
et le cube construit sur
MN
est au cube construit
sur
NΞ
comme
MN
est à
NT.
Donc,
par soustraction, le segment AΔΓE est au segment
ABE
comme
MT
est à
TN,
c'est-à-dire comme les trois cinquièmes de
HZ
est à
IΠ.
Puisqu'un solide qui a pour
base le carré construit sur
AZ
et pour hauteur le double de
AH,
conjointement avec la droite
AZ,
est au cube construit sur
AZ
comme le double de la droite
ΔH,
conjointement avec la droite
AZ
est à ZA, et par conséquent
comme le double de
NΞ,
conjointement avec
MN
est à
NM.
Donc le cube construit sur
AZ
est au
cube construit sur
ΔH
comme
MN
est à
NT.
Mais le cube construit sur
ΔH
est à
un solide ayant pour base le carré construit sur ΔH et pour hauteur le double de
la droite
AZ,
conjointement avec la droite
ΔH
comme
ΔH
est au double de la droite
ΔZ,
conjointement avec la droite
ΔH,
et comme la droite
TN
est au double de la droite
ON,
conjointement avec la droite
TN.
On a donc quatre
quantités, savoir : le solide qui a pour base le carré .construit sur
AZ
et pour hauteur le
double de la droite ΔH, conjointement avec la droite
AZ;
le cube construit sur
AZ;
le cube construit sur
ΔH,
et le
solide qui a pour base le carré de
ΔH
et pour hauteur le double de la
droite
AZ,
conjointement avec la droite
ΔH;
et ces quatre quantités sont
proportionnelles deux à deux à quatre quantités, savoir : au double de la droite
NΞ, conjointement avec la droite
NM,
à la droite
MN,
à la droite
NT,
et enfin au double de la droite
NO,
conjointement avec la droite
NT.
Donc par raison d'égalité, le
solide qui a
pour base le carré construit sur
AZ
et pour hauteur le double de la
droite
ΔH,
conjointement avec la droite
AZ
est au solide qui a pour base
le carré construit sur
ΔH
et pour hauteur le double de la
droite
AZ,
conjointement avec la droite
ΔH,
comme le double de la droite
NΞ,
conjointement avec la droite
NM
est le double de la droite
NO,
conjointement avec
la droite
NT.
Mais
le premier solide dont nous venons de parler est au second solide dont nous
venons aussi de parler, comme ΘI est à
IK;
donc ΘI est à
IK
comme la première droite
composée est à la seconde droite composée. Donc, par addition et en quintuplant
les antécédents, la droite
ZH
sera à la droite
IK
comme une droite
composée du quintuple de chacune des droites
MN,
NT,
et la décuple de chacune des droites
NΞ, NO
est au double de la
droite
ON,
conjointement avec la droite
NT.
Mais
ZH
est aux deux cinquièmes
de
ZK
comme une droite composée du quintuple
de chacune des droites
MN,
NT,
du décuple de chacune
des droites
ΞN, NO
est aune droite composée du double de chacune des droites
MN,
NT
et du quadruple de chacune des droites ΞN,
NO.
Donc une droite composée
du quintuple de chacune des droites
MN,
NT
et du décuple de chacune des droites ΞN,
NO
sera à
une droite composée du double de
MN,
du quadruple de
NΞ,
du sextuple de
ON
et du triple de
NT,
comme
ZH
est à ZI. Donc puisque les quatre droites
MN,
NΞ, ON, NT
sont
continuellement proportionnelles, la droite
NT
est à
TM
comme la droite ΡI qui a
été prise est aux trois cinquièmes de
ZH,
c'est-à-dire à
MO.
Mais une droite composée
du double de
NM,
du quadruple de NΞ, du sextuple de
NO
et du triple de
NT
est à une droite composée dû
quintuple de chacune des droites
MN,
NT,
du décuple de chacune,
des droites ΞN,
NO,
comme l'autre droite
IZ qui a été prise est à
ZH,
c'est-à-dire à
MO.
Donc la droite
ΡZ,
d'après ce que nous avons démontré plus haut, sera les deux cinquièmes de
MN,
c'est-à-dire de ZB. Donc le point Ρ est le, centre de
gravité du segment
ABΓ.
Que le point Χ soit le
centre de gravité du segment
ΔBE
; le centre de gravité
du segment AΔEΓ sera dans une droite
placée dans la direction de
ΧΡ,
qui sera à la droite
ΧΡ
comme le segment AΔEΓ est au segment restant (i,
8). Mais le point I est ce centre de gravité, car
BΡ
est égal aux trois
cinquièmes de
ZB
et
BΧ
aux trois cinquièmes de
HB;
donc la droite
ΧΡ
est égale aux trois
cinquièmes de la droite restante
HZ.
Mais le segment AΔEΓ est au segment
ΔBE
comme
MT
est à
NT,
et
MT
est à
NT
comme les trois cinquièmes de
HZ, qui
est
ΧΡ, est à
ΡI.
Donc
le segment
AΔEΓ
est au segment
ΔBE
comme
ΧΡ
est à
ΡI.
Mais le point Ρ est le centre
de gravité du segment total, et le point Χ le centre de gravité du segment
ΔBE.
Il est donc évident que le point I est
le centre de gravité du segment AΔEΓ.
FIN DE L'ÉQUILIBRE DES PLANS.
COMMENTAIRE
LIVRE
SECOND.
PROPOSITION I.
(α) Puisque le segment
AB
est égal à quatre fois le tiers
du triangle qui a la même base et la même hauteur que le segment (voyez
le Traité de la Quadrature de la
Parabole), il sera facile de transformer ce triangle en un rectangle dont la
base soit égale à la droite
ΛH.
(β) Le grec dit γνωρίμος comme
on sait; en sorte que cette phrase
signifie, nommons cette figure inscrite dans le
segment, suivant l’acception ordinaire. Je ne blâme pourtant
pas le mot régulièrement, il vaut peut-être mieux que tout ce
qu'on pourrait mettre en place. Je dis seulement que la traduction n'est pas
littérale, non plus que dans le latin. (Delambre)
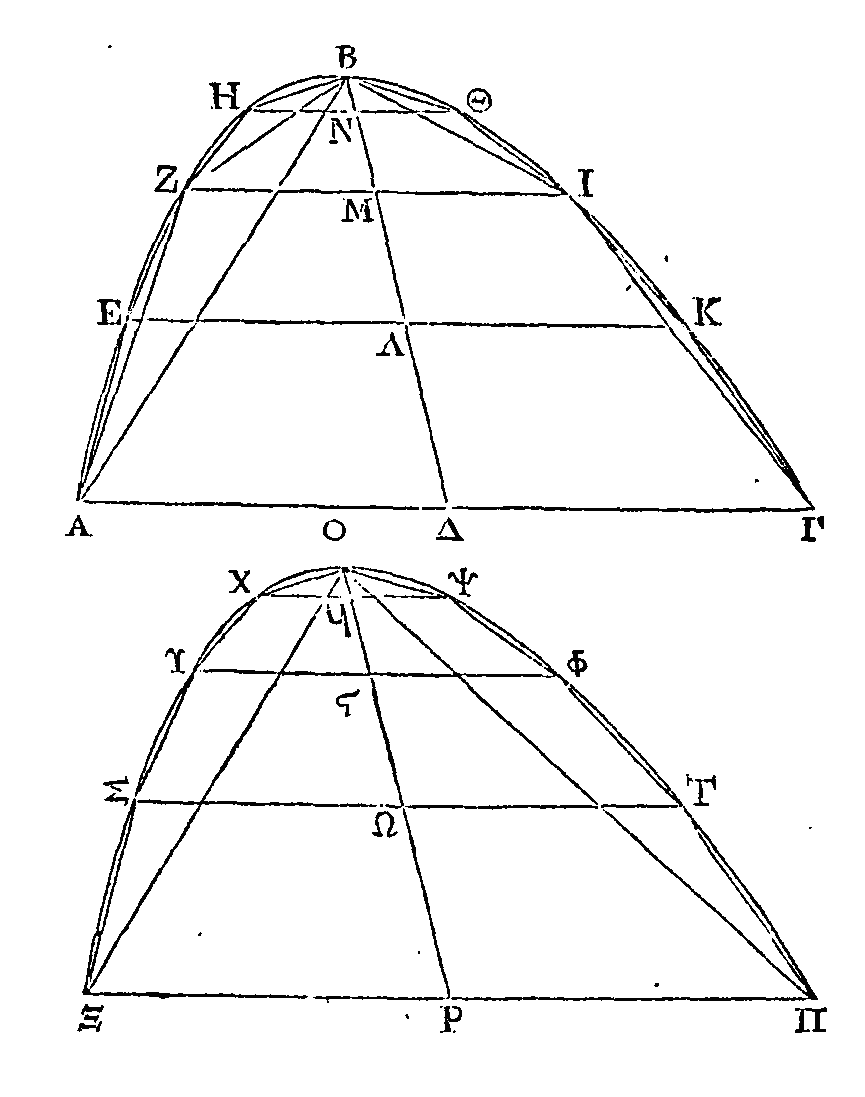
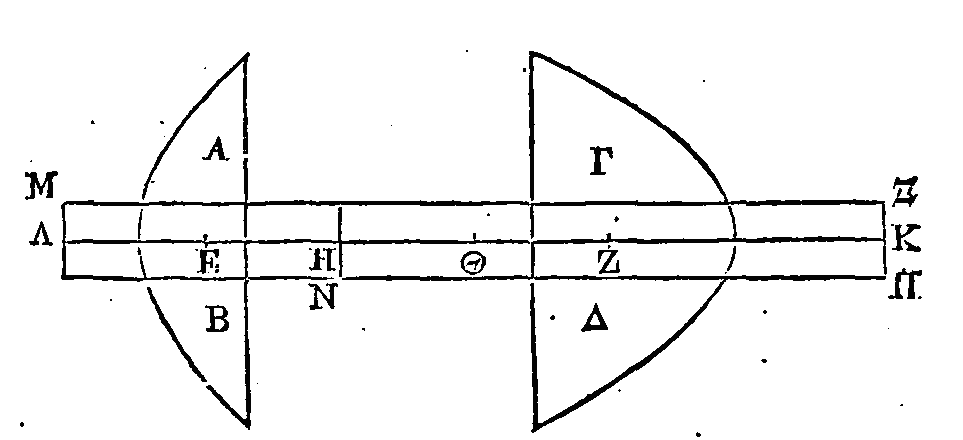
(γ) Dans le segment parabolique
ABΓ, dont
BΔ
est le diamètre, ou une
parallèle au diamètre, inscrivons régulièrement la figure rectiligne ABΓ. Menons
les droites EΛ, ZM, HN, ΘΞ,
IO, KΠ parallèles au diamètre, et menons ensuite les droites EK, ZI, HΘ. Il
faut démontrer que les droites
EK, ZI, HΘ sont
parallèles à la base AΓ du segment ; que ces droites sont coupées en deux
parties égales par le diamètre BΔ,
et que les droites
BΧ,
ΧΨ, ΨΩ, ΩΔ, sont entre elles comme les nombres 1, 3, 5, 7.

Puisque ZM est parallèle au diamètre
BΔ, la
droite AT sera égale à TB (Quadr. de la Parab.
prop. 1). Donc AM est égal à
MΔ.
Par la même raison, la droite AϚ
étant égale à ϚZ,
et la droite ZϞ
étant égale à la droite BϞ,
la droite AΛ sera égale à ΛM, et la droite MN égale à la droite NΔ. Mais la
droite AM est égale à MΔ ; donc les droites AΛ, ΛM, MN,
NΔ
sont égales entre elles. On démontrera semblablement que les
droites
ΔΞ, ΞO,
OΠ,
ΠΓ sont égales entre elles. Mais
AΔ
est égal à ΔΓ; donc les droites
AΛ, ΛM, MN,
NΔ,
ΔΞ, ΞO,
OΠ,
ΠΓ sont toutes égales entre elles. Mais AΛ : ΛΠ ::
AΔ
:
BΔ,
et ΠΓ : ΠΣ :: ΓΔ : BΔ ::
AΔ : BΔ ; donc AΛ :
ΛR :: ΠΓ : ΠΣ. Mais AΛ = ΠΓ ; donc
ΛR = ΠΣ. Mais ΛΠ : RE :: AΔ : ΛΔ (Quadr. de la Parabole, prop.
iv), et ΠΣ : ΣK :: ΔΓ : ΔΠ :: AΔ :
ΛΔ ; donc ΛΡ : ΡE :: ΠΣ : ΣK. Mais ΛΡ = ΠΣ ; donc ΡE = ΣK. Donc ΛE = KΠ. Donc EK
est parallèle à AΓ. On démontrerait de la même manière que les droites ZI, HΘ
sont parallèles à AΓ.
Puisque les droites EK, AΠ sont
parallèles entre elles, ainsi que les droites
EΛ, BΔ,
KΠ, et que ΛΔ est égal à
ΔΠ, la droite EΩ sera égale à ΩK. Par la même raison, la droite ZΨ
est égale à ΨI, et
la droite HΧ
égale à ΧΘ. Donc le
diamètre
BΔ
partage les droites EK, ZI, HΘ en deux parties égales.
Puisque BΔ : BΨ :: 4 : 1 (Quadr.
de la Parab. prop.
xix), et que BΨ :
EΧ
:: 4 : 1, il est évident
que si la droite
BΧ
vaut 1, la droite EΨ vaudra 4;
la droite
ΧΨ,
3 ;
et la droite BΔ, 16. D'où il suit que ZT vaudra 4, et que ΨΔ ou ZM vaudra
12. Menons la droite EΦ parallèle
à AB, on aura ZT : ZΦ :: 4 : 1 (Quadr. de la Parabole, prop.
xix). Donc ΦT, c'est-à-dire EΡ,
vaudra 3, et ΛΡ, qui est égal à la moitié de MT, vaudra 4. Donc ME, c'est-à-dire
ΩΔ, vaudra 7, et par conséquent ΨΩ, qui est égal à ΨΔ —
ΩA, vaudra 5.
Donc
BΧ
étant
1, ΧΨ vaudra 3, ΨΩ vaudra 5, et ΩΔ vaudra 7. Donc les droites
BΧ,
ΧΨ, ΨΩ,
ΩΔ
sont entre elles comme
les nombres 1, 3, 5, 7.
PROPOSITION III.
(a) Voyez la note (a) de la
lettre à Dosithée qui est en tête du Traité des Conoïdes.
(b) Puisque les segments des diamètres
BΔ.,
OΡ
sont entre eux comme les
nombres 1, 3, 5, 7, 9, etc. il est évident que les segments homologues seront
proportionnels.il n'est pas moins évident que les parallèles homologues seront
encore proportionnelles. En
effet, puisque
HN2
: ZM2
:: BN : BM :: 1 : 4, et que ΧϞ
2
: ΥϚ
2
:: OϞ
: ΘϚ
:: 1 : 4; nous aurons HN
: ZM :: ΧϞ
: ΨϚ,
et par conséquent HΘ : ZI : ΧΨ : ΥΦ et ainsi de suite.
(α) Cela est évident d'après ce qui
est dit dans le dixième livre des Eléments d'Euclide, et dans le premier livre
de la Sphère et du Cylindre.
PROPOSITION V.
(α) Car puisque la droite menée du
point K au point Λ, et la droite ZH sont parallèles à AΓ (2, 1), et que la
droite KZ est parallèle à ΛH, il est évident que KZ = ΛH. Mais les droites ZΘ,
HI
sont les mêmes parties de droites égales ; donc
ΘZ = IH. Donc cette figure ΘZHI est un
parallélogramme.
(b) Les deux segments AKB, BΛΓ sont
égaux. En effet, KZ = ΛΠ, et les perpendiculaires menées du point B sur les
droites prolongées ZK, HΛ sont égales, parce que les droites KZ, ΛH sont
également éloignées de la droite
BΔ.
Donc le triangle
BKZ
est égal au triangle
BΛH.
Le triangle
KZΛ
est égal au triangle AHΓ,
par la même raison. Donc le triangle
BKA
est égal au triangle BΛΓ. Mais
le segment
BKA
est
égal à quatre fois le tiers du triangle BKA, et le segment BΛΓ est aussi égal à
quatre fois le tiers du triangle BΛΓ (Quadr. de la Parabole,
prop. xxiv). Donc le segment
BKA est égal au segment BΛΓ.
(γ) Quadr. de la Parabole,
prop. xxiv.
(δ) Puisque le centre de
gravité du triangle ABΓ est le point E, et que le centre de gravité de la somme
des triangles AKB, BΛΓ est le point T, il est évident que le centre de gravité
de la figure rectiligne
AKBΛΓ
sera placé dans un point
Ρ de la droite TE, les segments ΡE, TΠ,
ΡE
de cette droite étant
proportionnels au triangle ABΓ, et à la somme des triangles
AKB,
BΛΓ (1, 8). Mais la raison du
triangle ABΓ à la somme des triangles
KAB,
ABΓ est plus grande que
la raison
ABΓ à la somme des segments ; car la
somme des segments est plus grande que la somme des triangles. Donc si la droite
ET est partagée en deux segments, de manière que celui qui est du côté du point
T soit au segment qui est du côté du point E, comme le triangle ABΓ est à la
somme des segments, il est évident que le point de division tombera au-dessus du
point Ρ.
PROPOSITION VI.
(α) Cela est évident, puisque la
figure rectiligne AKBΛΓ est plus grande que le triangle, et qu'au contraire la
somme des segments restants est plus petite que la surface K.
PROPOSITION VII.
(α) La figure inscrite régulièrement
dans le segment ABΓ sera semblable à la figure inscrite dans le segment
EZH,
si la figure inscrite
dans le segment ABΓ a le même nombre de côtés que la figure inscrite dans le
segment EZH. Car puisque les points B, Z
sont les sommets de segments semblables, les figures
rectilignes seront semblables.
PROPOSITION VIII.
(α) En effet, puisque les segments
sont semblables, leurs centres de gravité sont semblablement placés dans leurs
diamètres.
(β) Eutocius démontre celte
proposition, qui ne l'est point par Archimède.
Soit la parabole ABΓ, ayant pour
diamètre la droite
BΔ.
Menons l'ordonnée
AΔ,
et la droite AB ; coupons AB en deux parties égales au point Z, et par ce point
menons la droite ZK parallèle à BΔ.
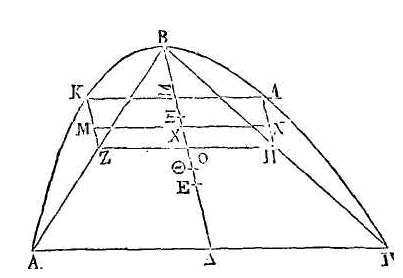
Cette droite sera le diamètre du
segment AKB. Par les points
K,
Z, menons les droites KΣ, ZO
parallèles à
AΔ.
Puisque AZ est égale à BZ, la
droite AB sera double de ZB, la droite AB double de BO et AΔ double de ZO,
c'est-à-dire de KZ. Donc le carré de
AΔ
est quadruple du quarré de KΣ,
et par conséquent la droite BΔ
quadruple de BΣ. Donc
puisque
BΔ
est
double de BO, la droite BO
sera double de BΣ ;.
Mais ZO est égal à KZ, puisque
KZΣO
est un parallélogramme ; donc
BΔ
est
quadruple de KZ.
(γ) Puisque BΘ = 4 ΣΧ, il est évident
que BΘ — ΣΧ, c'est-à-dire BΣ + ΧΘ sera égal à 3 ΣΧ.
(δ) Voyez la Quadrature de la
Parabole, prop. 24.
(ε) Puisque ΔE = 5 EΘ, la droite AΓ
égalera 6 EΘ. Mais BΔ = 3 ΔE ; donc
BΔ
=
15
EΘ ;
donc BΘ = 9 EΘ; donc BΘ : AΘ ::
9 EΘ :
6
EΘ
:: 9 :
6 :: 3 : 2. Donc BΘ = 3/2
ΘΔ.
PROPOSITION IX.
(α) La démonstration de cette
proposition est courte et facile, lorsqu'on emploie l'algèbre.
Soit la progression suivante  a
: b : c : d, et que d : a — d
:: x :
(3a — 3c)/5 a
: b : c : d, et que d : a — d
:: x :
(3a — 3c)/5
l’on aura x = (3ad
– 3cd)/(5a – 5d).
Que 2a
+ 4b+ 6c
+ 3d : 5a + 10b + 10c +
5d :: y : a — c, on aura
y = (2a
2 + 4ab + 6ac + 3ad — 2ac — 4bc
— bc 2 — 3cd) / (5a+10b
+ 10c + 5d)
ou bien en faisant la réduction
y = (2a
2 + 4ab + 4ac + 3ad + 4bc — 6c
2 — 3cd) / (5a+10b
+ 10c + 5d)
réunissant ces deux équations, les
réduisant au même dénominateur, et faisant attention que bc = ad,
on aura x + y = 2a/5. Ce qu'il fallait démontrer.
« Quelquefois Eutocius, en suivant de
trop près la marche d'Archimède, n'est guère moins obscur que lui; et c'est ce
qu'on remarque principalement à la prop. 9 du livre II de l'Équilibre des Plans.
La démonstration d'Archimède a trois énormes colonnes in-folio, et n'est
rien moins que lumineuse. Eutocius commence sa note en disant, que le théorème
est fort peu clair, et il omet de l'expliquer de son mieux. Il y emploie quatre
colonnes du même format et d'un caractère plus serré, sans réussir davantage; au
lieu que quatre lignes d'algèbre suffisent à M. Peyrard pour mettre la vérité du
théorème dans le plus grand jour. Il est peu croyable qu'Archimède ait pu
arriver par une voie si longue à la proposition qu'il voulait établir ; et il
est beaucoup plus probable qu'il en
aura reconnu la vérité par quelque autre moyen, et
que, bien sûr de celte vérité, il aura pris ce détour pour la démontrer, en ne
supposant que des propositions avouées et reçues des Géomètres de son temps ». (Rapport
fait à l'Institut par MM. La Grange et Delambre.)
(β) Que
BE
soit représenté par a,
et que la raison soit q. Il est évident que
BΔ
= aq ;
BΓ = aq 2 ;
ab = aq 3.
Mais AΓ =
AB
— BΓ ; ΓΔ
=
BΓ —
BΔ, et AE =
ΔB
— BE.
Donc AΓ = aq 3 — aq 2 ; ΓΔ
= aq 2 — aq;
BE = aq — a. Mais les trois quantités aq
3 — aq 2, aq 2
— aq, aq — a forment une progression dont la raison est
q. Donc les trois quantités AΓ,
ΓΔ, ΔE
forment une progression.
PROPOSITION X.
(α) Archimède suppose que les bases
des segments sont parallèles.
(β) Le premier diamètre de la parabole
est celui sur lequel les ordonnées sont perpendiculaires.
FIN DU COMMENTAIRE SUR L'ÉQUILIBRE
DES PLANS
|