ARCHIMEDE
DE LA MESURE DU CERCLE.
PROPOSITION PREMIÈRE.
Un
cercle quelconque est égal à un
triangle rectangle dont un des côtés de l'angle droit est égal au rayon de ce
cercle, et dont l'autre côté de l'angle droit est égal à la circonférence de ce
même cercle.
Que ABΓΔ soit le cercle proposé. Je
dis que ce cercle est égal au triangle E.
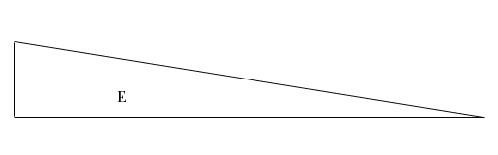

Que le cercle soit plus grand, si cela
est possible. Inscrivons dans ce cercle le carré AΓ, et partageons les arcs en
deux
parties égales jusqu'à ce que la somme des segments restants soit
plus petite que l'excès du cercle sur le triangle (1, 6); on aura une figure
rectiligne qui sera encore plus grande que le triangle (α).
Prenons le centre N, et menons la perpendiculaire NΞ ; la perpendiculaire NΞ
sera plus petite qu'un des côtés de l'angle droit du triangle E. Mais le contour
de la figure rectiligne est encore plus petit que l'autre côté de l'angle droit
de ce même triangle, puisque
le contour de cette figure est plus
petit que la circonférence du cercle (1, 1). Donc la figure rectiligne est plus
petite que le triangle, ce qui est absurde (β).
Que le cercle soit plus petit que le
triangle E, si cela est possible. Circonscrivons un carré à ce cercle, et
partageons les arcs en deux parties égales, et par les points de division,
menons des tangentes. Puisque l'angle
OAΡ
est droit, la droite
OΡ
est plus grande que la
droite
MΡ, à
cause que
MΡ
est
égal à
ΡA.
Donc
le triangle ΡOΠ est plus grand que la moitié de la figuré
OZAM
(γ). Que les segments
restants soient tels que ΡZA et que la somme de ces segments soit moindre que
l'excès du triangle E sur le cercle
ABΓΔ.
La figure rectiligne sera encore plus petite que le triangle
E.
Ce qui est absurde, puisque
cette figure est plus grande, à cause que
NA
est égale à la hauteur du
triangle, et que le contour de cette figure est plus grand que la base de ce
même triangle.
Donc le cercle est égal au triangle
E.
PROPOSITION II.
Un cercle est au carré construit sur
son diamètre, à très peu de chose près, comme 11 est à 14.
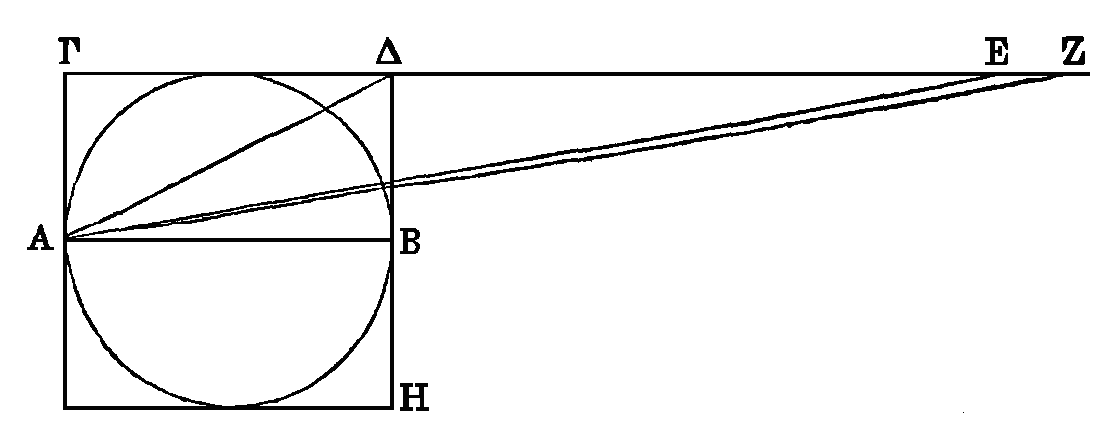
Soit le cercle dont le diamètre est a
AB.
Circonscrivons à ce cercle le carré
ΓHΔ;
que la droite ΔE soit double du
coté ΓΔ, et que
EZ
en soit la septième partie,
Puisque le triangle
AΓE
est
au triangle
AΓΔ comme 21 est à 7, et que le
triangle AΓΔ est au triangle
AEZ
comme 7 est à 1, le triangle
AΓZ
sera
au triangle AΓΔ comme 22 est à 7. Mais le carré
ΓH
est quadruple du triangle AΓΔ;
donc le triangle AΓZ est au carré de
ΓH
comme 22 est à 28; ou comme 11
est à 14. Mais le triangle AΓZ est égal au cercle
AB,
puisque la hauteur AΓ est égale au rayon du cercle, et que sa base est égale à
la circonférence du même cercle, cette circonférence étant, à peu de chose près,
égale au triple du diamètre réuni au septième de ce diamètre, ainsi que cela
sera démontré; donc le cercle est au carré ΓH, à très peu de chose près,
comme 11 est à 14.
PROPOSITION III.
La circonférence d'un cercle
quelconque est égale au triple du diamètre réuni à une certaine portion du
diamètre, qui est plus petite que le septième de ce diamètre, et plus grande que
les 10/71e de ce même diamètre.
Soit le cercle dont AΓ est le diamètre
et dont le point E est le centre ; que la droite
ΓΛZ
soit une tangente, et que
l'angle
ZEΓ soit la troisième partie d'un angle droit La droite EZ sera à
la droite ZΓ comme 306 est à 153; et la raison de EΓ à ΓZ sera plus grande que
la raison de 265 à 153(α).
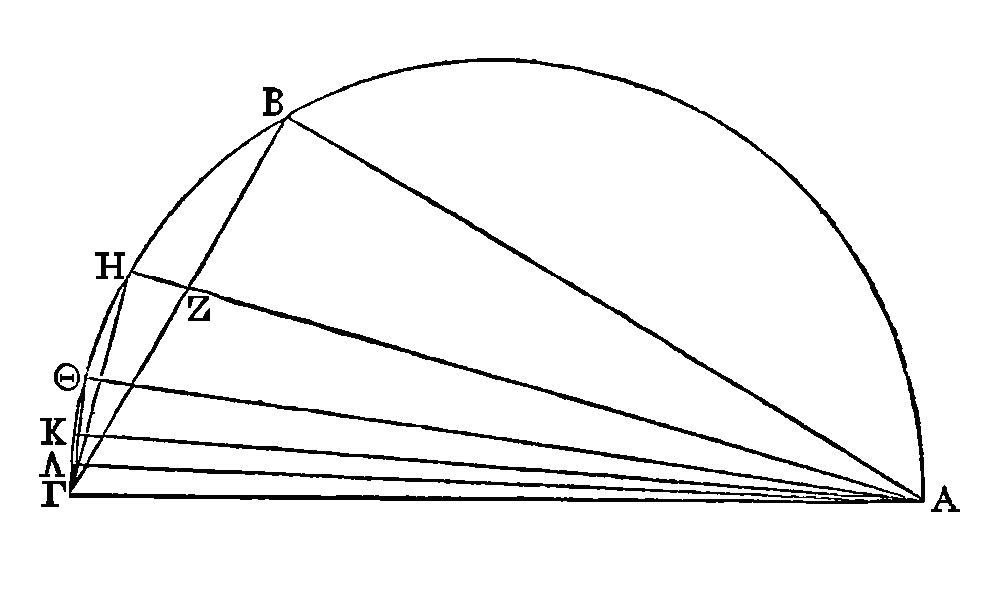
Partageons l'angle ZEΓ en deux parties
égales par la droite
EH
; la droite
ZE
sera à la droite EΓ comme
ZH
est à
HΓ.
Donc,
par permutation et par addition, la somme des droites
ZE,
EΓ est à la droite ZΓ comme EΓ est à
ΓH.
Donc la raison de la droite
ΓE
à la
droite
ΓH
est
plus grande que la raison de 571 à 153. Donc la raison du carré de
EH
au carré de HΓ est plus
grande que la raison de 349450 à 23409, et la raison de
EH
à HΓ plus grande que la raison
de 591 1/8 à 153 (β).
Partageons l'angle HEΓ en deux parties
égales par la droite EH ; la raison de EΓ à ΓΘ sera plus grande que la raison de
1162 à 153. Donc la raison de ΘE à ΘΓ est plus grande que la raison de 1162 1/8
à 153.
Partageons encore l'angle ΘEΓ en deux
parties égales par la droite
EK
; la raison de EΓ à ΓK sera,
plus grande que la raison de 2334 ¼ à 153. Donc la raison de
EK
à ne est plus grande que la
raison de 2339 ¼ à 153.
Partageons enfin l'angle KEΓ en deux
parties égales par la droite
ΛE ;
la raison de
EΓ
à ΛΓ sera plus grande que la
raison de 4673 ½ à 153.
Donc, puisque l'angle ZEΓ qui est la
troisième partie d'un angle droit, a été partagé quatre fois en deux parties
égales, l'angle ΛEΓ sera la quarante-huitième partie d'un angle droit.
Construisons au point E un angle
ΓEM
égal à l'angle ΛEΓ et
prolongeons ZΓ vers le point M ; l'angle
ΛEM
sera la vingt-quatrième partie
d'un angle droit. Donc la droite
ΛM
est le côté d'un polygone de 96
côtés, circonscrit au cercle.
Donc, puisque nous avons démontré que
la raison de
EΓ
à
ΓΛ
est plus grande que la raison
de 4673 ½ à 153, et à cause que AΓ est double de EΓ, et
ΛM
double de
ΓΛ,
la raison de AΓ à
ΛM
sera encore plus grande que la
raison de 4673 ½ à 153. Donc
la raison de la droite
AΓ au contour d'un polygone de 96
côtés est plus grande que la raison de 4673 ½ à 14688.
Donc la raison du contour de ce
polygone à son diamètre est moindre que la raison de 14688 à 4673 ½. Mais
parmi ces deux nombres, le premier contient trois fois le second avec un reste
qui est de 667 ½, et ce reste est plus petit que la y partie du nombre 4673 ½ ;
donc le contour du polygone circonscrit contient le diamètre trois fois, plus
une partie de ce diamètre qui est moindre que sa septième partie et demie. Donc,
à plus forte raison, la circonférence du cercle est moindre que le triple du
diamètre augmenté d'un septième et demi de ce même diamètre.
Soit le cercle dont AΓ est le
diamètre. Que l'angle BAΓ soit la troisième partie d'un angle droit; la raison
de
AB
à BΓ
sera moindre que la raison de 1351 à 780 ; et la raison de AΓ à
ΓB
sera la même que celle de 1560
à 780.
Partageons l'angle
BAΓ
en deux parties égales par la
droite
AH.
Puisque l'angle BAH est non seulement égal à l'angle HΓB, mais encore à l'angle
HAΓ,
l'angle
HΓB
sera
égal à l'angle HAΓ. Mais l'angle droit AHΓ est commun; donc le troisième angle
HZΓ sera égal au troisième angle AΓH. Donc les triangles AHΓ,
ΓHZ
sont équiangles; donc
AH
est à
HΓ comme ΓH à HZ, et comme AΓ
est à
ΓZ. Mais AΓ est à ΓZ comme la somme
des droites
ΓA,
AB
est à
la droite BΓ ; donc la somme des droites BA, AΓ est à la droite BΓ comme
AH
est à
HΓ. Donc la raison de
AH
à HΓ est moindre que la raison
de 2911 à 780, et la raison de AΓ à ΓH moindre que la raison de 3013 ¾ à 780.
Partageons l'angle
ΓAH
en deux parties égales par la
droite AΘ ; la raison de AΘ à ΘΓ sera pareillement moindre que la raison de 5924
¾ à 780, ou bien que la raison de 1823 à 240 ; car ces deux derniers nombres
sont chacun les 4/13 des deux premiers. Donc la raison de AΓ à ΓK est moindre
que la raison de 1838 9/11e à 240.
Partageons encore l'angle ΘAΓ en deux
parties égales par la droite
KA
; la raison de
KA
à KΓ sera moindre que la raison
de 3661 9/11e à 240, ou bien que la raison de 1007 à 66; car ces deux
derniers nombres sont chacun les 11/40e des deux premiers. Donc la
raison de AΓ à ΓΛ est moindre que la raison de 1009 1/6 à 66.
Partageons enfin l'angle KAΓ en deux
parties égales par la droite
ΛA
; la raison de
AΛ
à ΛΓ sera moindre que la raison
de 2016 1/6 à
66, et la raison de
AΓ à
ΓΛ
moindre que la raison de 2017 ¼
à 66.
Donc la raison de AΓ à ΓA est plus
grande que la raison de 66 à 2017 ¼. Donc, la raison du contour du polygone au
diamètre est plus grande que la raison de 6336 à 2017 ¼. Mais parmi ces nombres,
le premier contient le second trois fois avec un reste qui est plus grand que
les 10/71e du second. Donc le contour d'un polygone de 96 côtés
inscrit dans un cercle est plus grand que le triple de son diamètre augmenté des
10/71e de ce diamètre. Donc, à plus forte raison, la circonférence du
cercle est plus grande que le triple du diamètre augmenté
des 10/71e de ce diamètre.
Donc, la circonférence d'un cercle est
égale au triple de son diamètre augmenté d'une portion de son diamètre qui est
plus petite que le septième de ce diamètre et plus grande que les 10/71e
de ce même diamètre.
FIN DE LA MESURE DU CERCLE.
COMMENTAIRE
SUR LA MESURE DU CERCLE.
PROPOSITION PREMIÈRE.
(α)
En effet, puisque la somme des
segments restants est égale au cercle moins la figure rectiligne inscrite, le
cercle moins cette figure rectiligne sera plus petit que le cercle moins le
triangle. Donc la figure rectiligne est plus grande que le triangle.
(β) Car nous venons de démontrer que
la figure rectiligne est plus grande que ce triangle.
(γ) En effet, puisque OΡ > ΡM, le
triangle OAΡ est plus grand que le triangle ΡAM ; par la même raison le triangle
OAΠ est plus grand que le triangle ΠAZ.
PROPOSITION III
(α) Car le sinus du tiers d'un angle
droit étant égal à la moitié du rayon, et le rayon étant au sinus comme la
sécante est à la tangente, il est évident que EZ sera double de ZΓ, c'est-à-dire
que EZ : ZΓ :: 306 : 153. Mais ZE = 306, et ZΓ = i53 ; donc la
droite
ΓE égalera ΣΘΡ (3o6²— 153²)
c'est-à-dire 265 et une fraction. Donc TE : ZΓ > 265 : 153.
(β) Puisque la raison de ΓE :
ΓH > 571 : 153, il est évident que si
ΓH vaut 153, la droite ΓE surpassera
571. Donc ΓE² +
ΓH²
: ΓH²
> 571² +
153² : 153. Mais
ΓE² + ΓH² = EH² ; donc EH² : ΓH² >
571²
+ 153² : 153² ; c'est-à-dire,
EH²
: ΓH² > 349450 : 23409; et si
l’on
extrait les racines carrées, on aura
EH :
ΓH > 591 1/8 : 153.
FIN DU COMMENTAIRE SUR LA MESURE
BU CERCLE.
|