ARCHIMÈDE

DE L'EQUILIBRE DES PLANS

OU

DE LEURS CENTRES DE GRAVITÉ.

LIVRE PREMIER.

DEMANDES

1°. Des graves égaux suspendus à des longueurs égales sont en équilibre (α).

2°. Des graves égaux suspendus à des longueurs inégales ne sont point en équilibre ; et celui qui est suspendu à la plus grande longueur est porté en bas.

3°. Si des graves suspendus à de certaines longueurs sont en équilibre, et si l'on ajoute quelque chose à un de ces graves, ils ne sont plus en équilibre ; et celui auquel on ajoute quelque chose est porté en bas.

4°. Semblablement, si l'on retranche quelque chose d'un de ces graves, ils ne sont plus en équilibre ; et celui dont on n'a rien retranché est porté en bas.

5°. Si deux figures planes semblables sont appliquées exactement l'une sur l'autre, leurs centres de gravité seront placés l'un sur l'autre.

6. Les centres de gravité des figures inégales et semblables sont semblablement placés.

Nous disons que des points sont semblablement placés dans des figures semblables, lorsque les droites menées de ces points à des angles égaux forment des angles égaux avec les côtés homologues.

7°. Si des grandeurs suspendues à de certaines longueurs sont en équilibre, des grandeurs égales aux premières suspendues aux mêmes longueurs seront encore en équilibre.

8°. Le centre de gravité d'une figure quelconque dont le contour est concave du même côté, se trouve nécessairement en dedans de la figure.

Cela posé, je procède ainsi qu'il suit:

PROPOSITION I.

Lorsque des graves suspendus à des longueurs égales sont en équilibre, ces graves sont égaux entre eux.

Car s'ils étaient inégaux, après avoir ôté du plus grand son excès, les graves restants ne seraient pas en équilibre, puisque l'on aurait ôté quelque chose d'un des graves qui sont en équilibre (Dem. 5). Donc lorsque des graves suspendus à des longueurs égales sont en équilibre, ces graves sont égaux entre eux.

PROPOSITION II.

Des graves inégaux suspendus à des longueurs égales ne sont pas en équilibre ; et le grave qui est le plus grand est porté en bas.

Car ayant ôté l'excès, ces graves seront en équilibre, parce que des graves égaux suspendus à des longueurs égales sont en équilibre (Dem. 1). Donc, si l’on ajoute ensuite ce qui a été ôté, le plus grand des deux graves sera porté en bas, car on aura ajouté quelque chose à un des graves qui sont en équilibre (Dem. 3).

PROPOSITION III.

Des graves inégaux suspendus à des longueurs inégales peuvent être en équilibre, et alors le plus grand sera suspendu à la plus petite longueur.

Que A, B soient des graves inégaux, et que A soit le plus grand. Que ces graves suspendus aux longueurs AΓ, ΓB soient en équilibre. Il faut démontrer que la longueur AΓ est plus petite que la longueur ΓB.

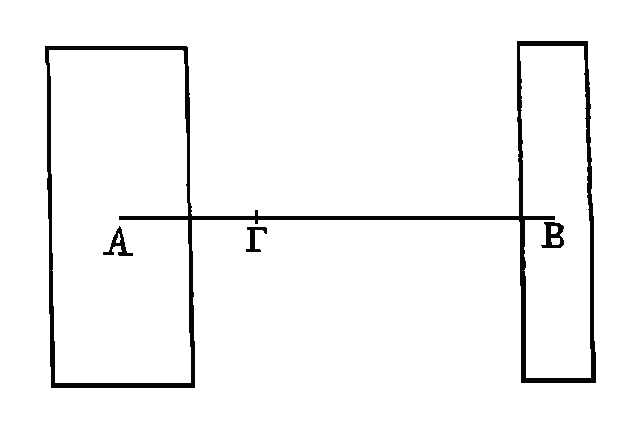
Que la longueur AΓ ne soit pas la plus petite. Retranchons l'excès de A sur B. Puisque l'on a ôté quelque chose d'un des graves qui sont en équilibre ; le grave B sera porté en bas (Dem. 4). Mais ce grave ne sera point porté en bas; car si ΓA est égal à ΓB il y aura équilibre (Dem. 1); et si ΓA est plus grand que ΓB, ce sera au contraire le grave A qui sera porté en bas; puisque des graves égaux suspendus à des longueurs inégales ne restent point en équilibre, et que le grave suspendu à la plus grande longueur est porté en bas (Dem. 2). Donc ΓA est plus petit que ΓB. Donc, si des graves suspendus à des longueurs inégales sont en équilibre, il est évident que ces graves seront inégaux, et que le plus grand sera suspendu à la plus petite longueur.

PROPOSITION IV.

Si deux grandeurs égales n'ont pas le même centre de gravité, le centre de gravité de la grandeur composée de ces deux grandeurs est le point placé au milieu de la droite qui joint les centres de gravité de ces deux grandeurs (α).

Que le point A soit le centre de gravité de la grandeur A, et le point B le centre de gravité de la grandeur B. Ayant mené la droite AB, partageons cette droite en deux parties égales au point Γ. Je dis que le centre de gravité de la grandeur composée des deux grandeurs A, B est le point Γ.

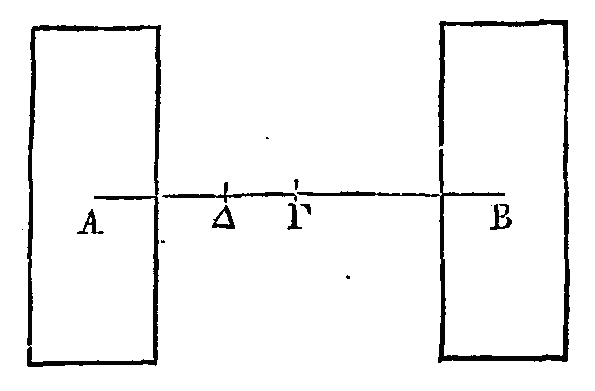
Car, si le point Γ n'est pas le centre de gravité de la grandeur qui est composée des deux grandeurs A, B, supposons, si cela est possible, que ce soit le point Δ. Il est démontré que le centre de gravité est dans la droite AB (β). Puisque le point Δ est le centre de gravité de la grandeur composée des deux grandeurs A, B, le point Δ étant soutenu, les grandeurs A, B seront en équilibre. Donc les grandeurs A, B suspendues aux longueurs AΔ, ΔB sont en équilibre. Ce qui ne peut être ; car des grandeurs égales suspendues à des longueurs inégales ne sont point en équilibre (Dem. 2). Il est donc évident que le point Γ est le centre de gravité de la grandeur qui est composée des grandeurs A, B.

PROPOSITION V.

Si les centres de gravité de trois grandeurs sont placés dans une même droite ; si ces grandeurs ont la même pesanteur, et si les droites placées entre les centres de gravité sont égales, le centre de gravité de la grandeur composée de toutes ces grandeurs sera le point qui est le centre de gravité de la grandeur du milieu.

Soient les trois grandeurs A, B, Γ; que leurs centres de gravités soient les points A, B, Γ placés dans une même droite; et que les grandeurs A, B, Γ soient égales entre elles, ainsi que les droites AΓ, ΓB. Je dis que le centre de gravité de la grandeur composée de toutes ces grandeurs est le point Γ.

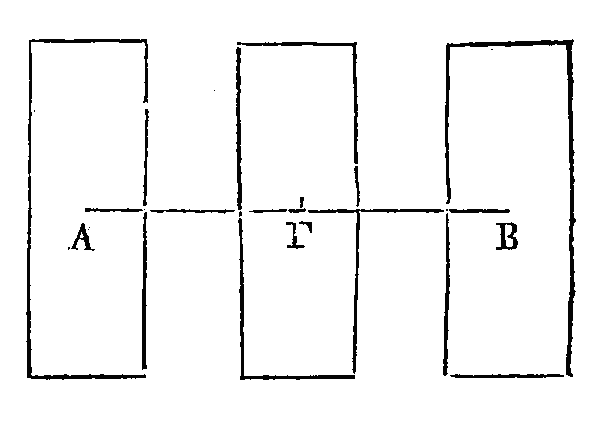
Car, puisque les grandeurs A, B ont là même pesanteur,-leur centre de gravité sera le point Γ (4); car les droites AΓ, ΓB sont égales. Mais le point Γ est aussi le centre de gravité de la grandeur Γ ; il est donc évident que le centre de gravité de la grandeur composée de toutes ces grandeurs sera le point qui est le centre de gravité de la grandeur du milieu.

Il suit évidemment de là que, si les centres de gravité de tant de grandeurs que l'on voudra et d'un nombre impair, sont dans la même droite, si celles qui sont également éloignées de celle qui est au milieu ont la même pesanteur, et si les droites comprises entre les centres de gravité sont égales, le centre de gravité de la grandeur composée de toutes les grandeurs sera le point qui est le centre de gravité de la grandeur du milieu.

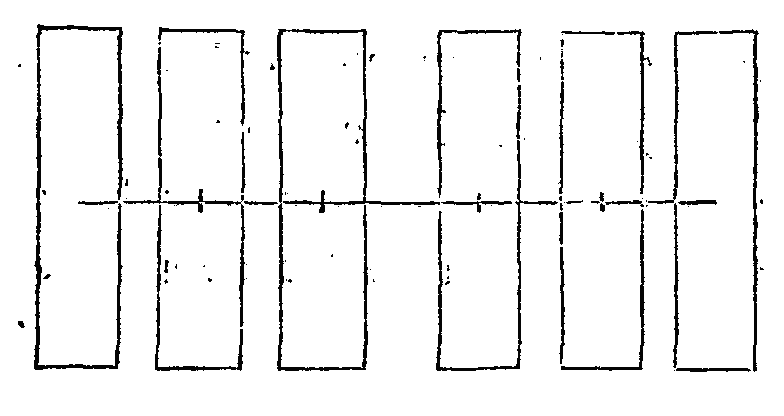
Si ces grandeurs sont d'un nombre pair, si leurs centres de gravité sont dans la même droite, si celles du milieu et celles qui sont également éloignées de part et d'autre des grandeurs du milieu ont la même pesanteur, et si les droites placées entre les centres de gravité sont égales, le centre de gravité de la grandeur composée de toutes ces grandeurs sera le point placé au milieu de la droite qui joint les centres de gravité, ainsi que, cela est représenté dans la figure (α).

PROPOSITION VI.

Des grandeurs commensurables sont en équilibre, lorsqu'elles sont réciproquement proportionnelles aux longueurs, auxquelles ces grandeurs sont suspendues.

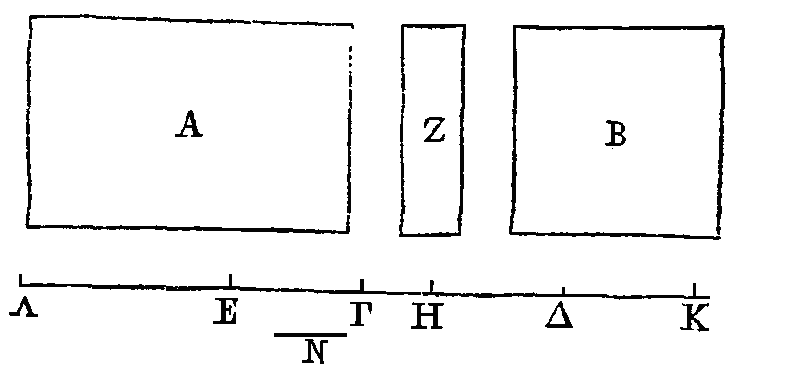
Soient les grandeurs commensurables A, B ; que leurs centres de gravité soient les points A, B ; soit une certaine longueur EΔ ; et que la grandeur A soit à la grandeur B comme la longueur ΔΓ est à la longueur ΓE. Il faut démontrer que le centre de gravité de la grandeur composée des deux grandeurs A, B, est le point Γ.

Puisque A est à B comme ΔΓ est à ΓE, et que les grandeurs A, B sont commensurables, les droites ΓΔ, ΓE seront aussi commensurables, c'est-à-dire qu'elles seront entre elles comme une droite est à une droite. Donc les droites EΓ, ΓΔ ont une commune mesure. Que cette commune mesure soit N. Supposons que chacune des droites ΔH, ΔK soit égale à la droite EΓ et que la droite EΔ soit égale à la droite AΓ. Puisque la droite ΔH est égale à la droite ΓE, la droite AΓ sera égale à la droite EH, et la droite ΛE égale à la droite EH. Donc la droite ΛH est double de la droite AΓ, et la droite HK double de la droite ΓE. Donc la droite N mesure chacune des droites ΛH, HK, puisqu'elle mesure leurs moitiés. Mais A est à B comme la droite AΓ est à la droite EΓ, et la droite AΓ est à la droite ΓE comme la droite ΛH est à la droite HK, puisque les droites ΛH, HK sont doubles des droites ΔΓ, ΓE ; donc A est à B comme ΛH est à HK. Que A soit autant de fois multiple de Z que ΛH l'est de N. La droite ΛH sera à la droite N comme A est à Z. Mais KH est à ΛH comme B est à A : donc, par raison d'égalité, la droite KH est à la droite N comme B est à Z. Donc autant de fois KH est multiple de N, autant de fois B l'est de Z. Mais on a démontré que A est aussi un multiple de Z. Donc Z est la commune mesure de A et de B. Donc si ΛH est partagé dans des segments égaux chacun à N, et A dans des segments égaux chacun à Z, les segments égaux chacun à N, qui sont dans ΛH, seront en même nombre que les segments égaux chacun à Z qui sont dans A. Donc si à chacun des segments de ΛH, on applique une grandeur égale à Z, qui ait son centre de gravité dans le milieu de chacun des segments, toutes ces grandeurs seront égales à A, et le centre de gravité de la grandeur composée de toutes ces grandeurs sera le point E ; car elles sont en nombre pair, attendu que ΛE est égal à HE (5). On démontrera semblablement que si à chacun des segments de KH, on applique une grandeur égale à Z, qui ait son centre de gravité au milieu de chacun de ces segments, toutes ces grandeurs seront égales à B, et que le centre de gravité de la grandeur composée de toutes ces grandeurs sera le point Δ. Mais la grandeur A est appliquée au point E et La grandeur B au point A; donc certaines grandeurs égales entre elles sont placées sur une droite, leurs centres de gravité ont entre eux le même intervalle, et ces grandeurs sont en nombre pair. Il est donc évident que le centre de gravité de la grandeur composée de toutes ces grandeurs est le point placé au milieu de la droite, sur laquelle sont les centres de gravité des grandeurs moyennes (5). Mais la droite ΛE est égale à la droite ΓΔ et la droite EΓ égale à la droite ΛK ; donc la droite entière ΛΓ est égale à la droite entière ΓK. Donc le centre de gravité de la grandeur composée de toutes ces grandeurs est le point Γ. Donc la grandeur A étant appliquée au point E, et la grandeur B au point Δ, ces grandeurs seront en équilibre autour du point Γ (α).

PROPOSITION VII.

Des grandeurs incommensurables sont en équilibre, lorsque ces grandeurs sont réciproquement proportionnelles aux longueurs auxquelles ces grandeurs sont suspendues.

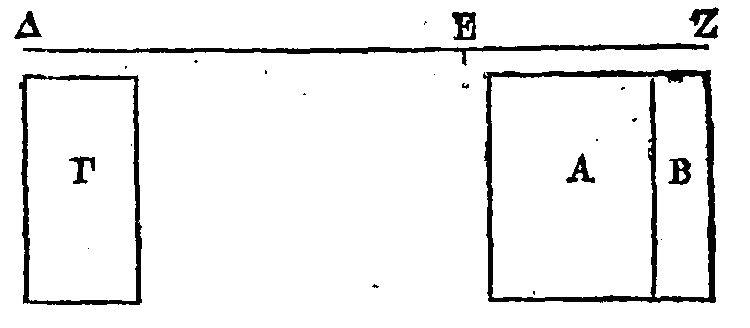
Que les grandeurs AB, Γ soient incommensurables, et que ΔE, EZ soient les longueurs auxquelles ces grandeurs sont suspendues. Que la grandeur AB soit à la grandeur Γ comme la longueur EΔ est à la longueur EZ. Je dis que le centre de gravité de la grandeur composée des deux grandeurs AB, Γ est le point E.

Car si les grandeurs AB, Γ ne sont pas en équilibre, lorsque l'une est appliquée au point Z et l'autre au point A, la grandeur AB est trop grande, par rapport à la grandeur Γ, pour qu'elle soit eh équilibre avec elle, ou elle n'est pas assez grande ; que la grandeur AB soit trop grande. Retranchons de AB moins qu'il ne faudrait pour rétablir l'équilibre, mais juste ce qu'il faut pour ôter l'incommensurabilité. Les grandeurs A, Γ seront commensurables. Mais la raison de A à Γ sera moindre que la raison de ΔE à EZ ; donc les grandeurs A, Γ suspendues aux longueurs ΔE, EZ ne seront point en équilibre, lorsque l'une sera appliquée au point Z et l'autre au point A (6). Par la même raison, elles ne seront point en équilibre, si on suppose que la grandeur Γ est trop grande, par rapport à la grandeur AB, pour qu'elle puisse être en équilibre avec elle (α).

PROPOSITION VIII.

Si d'une grandeur quelconque, ou retranche une certaine grandeur qui n'ait pas le même centre de gravité que la grandeur entière, pour avoir le centre de gravité de la grandeur restante, il faut prolonger, vers le côté où est le centre de gravité de la grandeur entière, la droite qui joint les centres de gravité de la grandeur totale et de la grandeur retranchée ; prendre ensuite sur le prolongement de la droite qui joint les centres de gravité dont nous venons de parler, une droite qui soit à la droite qui joint les centres de gravité comme la pesanteur de la grandeur retranchée est à la pesanteur de la grandeur restante, le centre de gravité de la grandeur restante sera l'extrémité de la droite prise sur le prolongement (α).

Que le point Γ soit le centre de gravité dune grandeur AB. De AB retranchons une grandeur AΔ, dont le centre de gravité soit le point E. Ayant mené la droite EΓ et l'ayant prolongée, retranchons de son prolongement une partie ΓZ qui soit à la droite ΓE comme la grandeur AΔ est à la grandeur ΔH. Il faut démontrer que le point Z est le centre de gravité de la grandeur ΔH.

Que le point Z ne soit pas le centre de gravité de ΔH, mais bien un autre point Θ, si cela est possible. Puisque le point E est le centre de gravité de la grandeur AΔ, et le point Θ le centre de gravité de la grandeur ΔH, le centre de gravité de la grandeur composée des deux grandeurs AΔ, ΔH sera dans la droite EΘ partagée de manière que ses segments soient réciproquement proportionnels à ces deux grandeurs (6 et 7) (β). Donc le point Γ ne coïncidera pas avec la section dont nous venons de parler. Donc le point Γ n'est pas le centre de gravité de la grandeur composée des deux grandeurs AΔ, ΔH, c'est-à-dire de AB. Mais il l'est par supposition ; donc le point Θ n'est pas le centre de gravité de la grandeur ΔH.

PROPOSITION IX.

Le centre de gravité d'un parallélogramme quelconque est dans la droite qui joint les milieux de deux côtés opposés. Soit le parallélogramme ABΓΔ, dont les milieux des côtés AB, ΓΔ sont joints par la droite EZ. Je dis que le centre de gravité du parallélogramme ABΓΔ est dans la droite EZ.

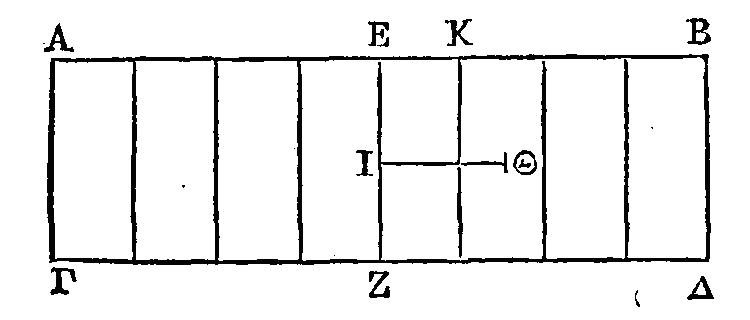
Que cela ne soit point ainsi ; et supposons, si cela est possible, que le point Θ soit le centre de gravité. Menons la droite ΘI parallèle à AB. Si la droite EB est continuellement partagée en deux parties, il restera enfin un segment plus petit que ΘI. Partageons donc chacune des droites AE, EB dans des segments égaux chacun à EK, et par les points de division conduisons des droites parallèles à EZ. Le parallélogramme entier sera divisé dans des parallélogrammes égaux et semblables chacun à KZ. Donc ces parallélogrammes égaux et semblables chacun au parallélogramme KZ, étant appliqués exactement les uns sur les autres, leurs centres de gravité s'appliqueront aussi exactement les uns sur les autres (Dem. 4). Donc ces parallélogrammes seront certaines grandeurs égales chacune à KZ, et en nombre pair, ayant leurs centres de gravité placés dans la même droite (α). Mais les grandeurs moyennes sont égales, et ainsi que toutes celles qui sont également distantes de part et d'autre des moyennes, et les droites placées entre le centre de gravité sont aussi égales entre elles; donc le centre de gravité de la grandeur qui est composée de toutes ces grandeurs, est dans la droite qui joint les centres de gravité des grandeurs moyennes (5). Mais cela n'est point, puisque le point Θ tombe au-delà de la moitié des parallélogrammes. Il est donc évident que le centre de gravité du parallélogramme est dans la droite EZ.

PROPOSITION X.

Le centre de gravité d'un parallélogramme est le point où les deux diagonales se rencontrent.

Soit le parallélogramme ABΓΔ; que EZ coupe les côtés AB, ΓΔ, en deux parties égales, et que KΛ coupe aussi les côtés AΓ, BΔ en deux parties égales. Le centre de gravité du parallélogramme ABΓΔ sera dans la droite EZ ; ce qui a été démontré (9). Par la même raison, il sera aussi dans la droite KΛ. Donc le point Θ est le centre de gravité. Mais les diagonales se rencontrent au point Θ ; donc la proposition est démontrée.

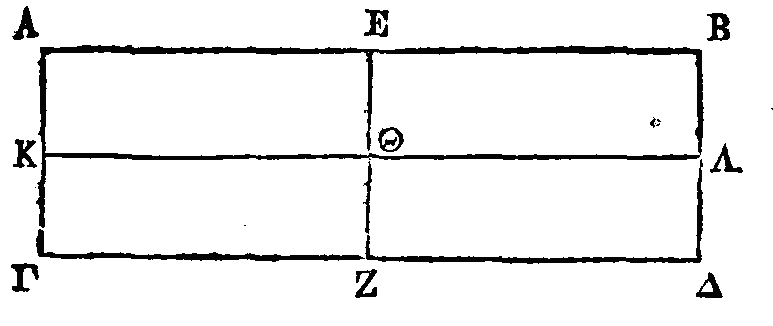
On peut encore démontrer autrement cette proposition. Soit le parallélogramme ABΓΔ, dont ΔB est la diagonale. Les triangles ABΔ, BΓΔ sont égaux et semblables. Donc ces triangles étant placés exactement l'un sur l'autre, leurs centres de gravité seront appliqués l'un sur l'autre (Dem. 5). Que le point E soit le centre de gravité du triangle ABΔ. Partageons la droite ΔB en deux parties égales au point Θ. Ayant conduit la droite EΘ et l'ayant prolongée, prenons ZΘ égal à EΘ. Le triangle ABΔ étant appliqué exactement sur le triangle BΔΓ, le côté AΔ sur le côté ΔΓ et le côté AΔ sur le côté BΓ, la droite ΘE s'appliquera exactement sur la droite ZΘ et le point E sur le point Z. Mais le centre de gravité du triangle ABΔ s'applique exactement sur le centre de gravité du triangle BΓΔ (Dem. 5); donc puisque le centre de gravité du triangle ABΔ est le point E, et que le centre de gravité du triangle ABΓ est le point Z, il est évident que le centre de gravité de la grandeur composée de ces deux triangles, est le point placé au milieu de la droite EZ, qui est certainement le point Θ.

PROPOSITION XI.

Si deux triangles sont semblables, si des points sont semblablement placés dans ces triangles, et si l'un de ces points est le centre de gravité du triangle dans lequel il est placé, l'autre point sera aussi le centre de gravité du triangle- dans lequel il est placé. Nous disons que des points sont semblablement placés dans des figures semblables, lorsque les droites menées de ces points à des angles égaux font des angles égaux avec les côtés homologues.

Soient les deux triangles ABΓ, ΔEZ ; et que AΓ soit à ΔZ comme AB est à AE, et comme BΓ est à EZ. Que dans les triangles dont nous venons de parler, les points Θ, N soient semblablement placés, et que le point Θ soit le centre de gravité du triangle ABΓ. Je dis que le point N est aussi le centre de gravité du triangle ΔEZ.

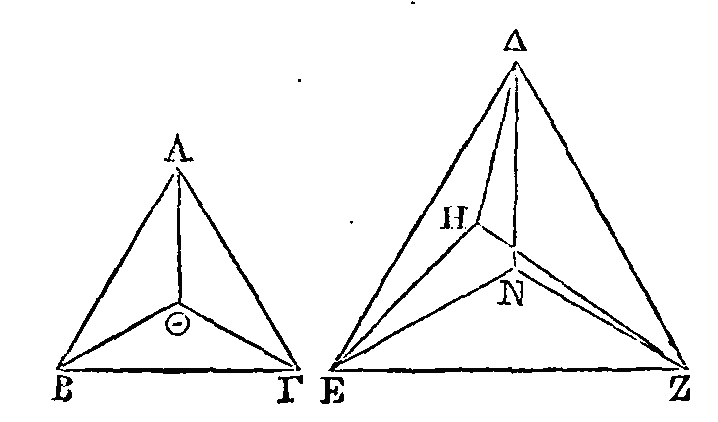
Que le point N ne soit pas le centre de gravité du triangle ΔEZ, et que ce soit un autre point H, si cela est possible. Menons les droites ΘA, ΘB, ΘΓ, ΔN, EN, ZN, ΔH, EH, ZH. Puisque les triangles ABΓ, ΔEZ sont semblables, que leurs centrés de gravité sont les points Θ, H, et que les centres de gravité des figures semblables sont semblablement placés, c'est-à-dire que les droites menées des centres de gravité aux angles égaux et correspondants, forment des angles égaux avec les côtés homologues, l'angle HΔE sera égal à l'angle ΘAB. Mais l'angle ΘAB est égal à l'angle EΔN, puisque les points Θ, N sont semblablement placés. Donc l'angle EΔH est égal à l'angle EΔN, c'est-à-dire que le plus grand est égal au plus petit; ce qui ne peut être. Donc le point N n'est pas le centre de gravité du triangle ΔEZ. Donc le point N dont nous avons parlé est son centre de gravité.

PROPOSITION XII.

Si deux triangles sont semblables, et si le centre de gravité de l'un est dans la droite menée d'un des angles au milieu de la base, le centre de gravité de l'autre sera aussi dans une droite semblablement menée.

Soient les deux triangles ABΓ, ΔEZ. Que AΓ soit à ΔZ comme AB est à ΔE, et comme BΓ est à ZE. Ayant partagé la droite AΓ en deux parties égales au point H, menons la droite BH. Que le point Θ, pris dans la droite BH, soit le centre de gravité du triangle ABΓ. Je dis que le centre de gravité du triangle EΔZ sera aussi dans une droite semblablement menée.

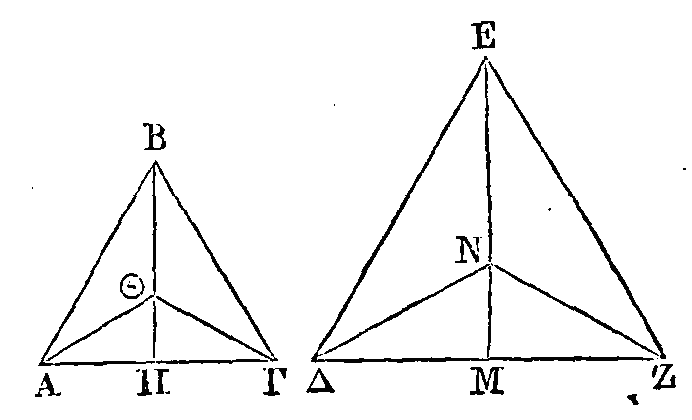
Partageons ΔZ en deux parties égales au point M, et menons la droite EM. Faisons en sorte que BH soit à BΘ comme ME est à EN, et menons les droites AΘ, ΘΓ, ΔN, NZ. Puisque AH est la moitié de ΓA, et ΔM la moitié de ΔZ, la droite BA sera à la droite EΔ comme AH est à ΔM. Mais ces côtés qui sont proportionnels sont placés autour d'angles égaux; donc l'angle AHB est égal à l'angle ΔME. Donc AH est à ΔM comme BH est à EM. Mais BH est à BΘ comme ME est à EN (α), donc, par raison d'égalité, la droite AB est à la droite ΔE comme BΘ est à EN. Mais ces côtés qui sont proportionnels sont placés autour d'angles égaux ; donc l'angle BAΘ est égal à l'angle EΔN. Donc l'angle restant ΘAΓ est aussi égal à l'angle NΔZ. Par la même raison, l'angle BΓΘ est égal à l'angle EZN, et l'angle ΘΓH égal à l'angle NZM. Mais on a démontré que l'angle ABΘ est égal à l'angle ΔEM ; donc l'angle restant ΘBΓ est aussi égal à l'angle NEZ. D'où il suit que les points Θ, N sont semblablement placés sur des côtés homologues, et qu'ils forment des angles égaux. Donc les points Θ, N sont semblablement placés. Mais le point Θ est le centre de gravité du triangle ABΓ ; donc le point N est aussi le centre de gravité du triangle ΔEZ (Dem. 6).

PROPOSITION XIII.

Le centre de gravité d'un triangle quelconque est dans la droite qui est menée d'un des angles au milieu de la base.

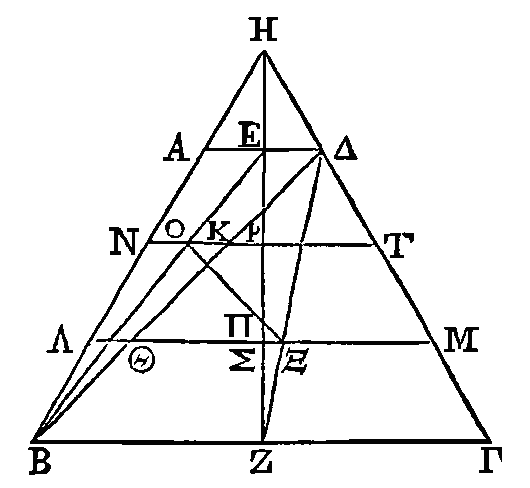
Soit le triangle ABΓ, et que dans ce triangle la droite AΔ soit menée au milieu de la base. Il faut démontrer que le centre de gravité du triangle ABΓ est dans la droite AΔ.

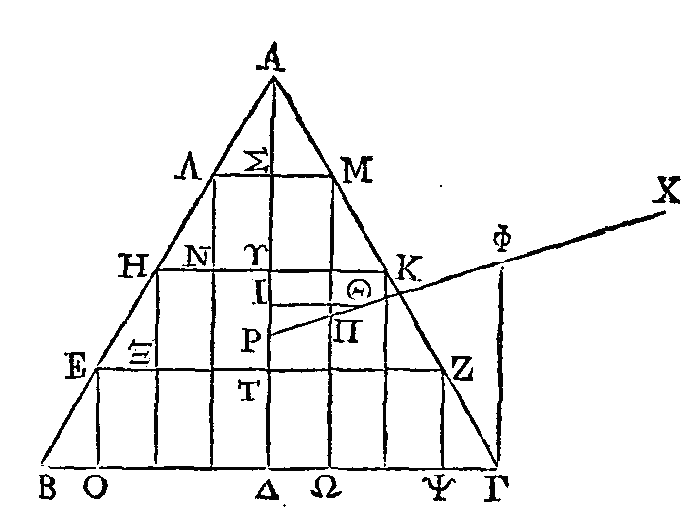
Que cela ne soit point ainsi; et que le point Θ soit son centre de gravité, si cela est possible. Par ce point conduisons la droite ΘI parallèle à BΓ. Si la droite ΔΓ est continuellement partagée en deux parties égales, il restera enfin un segment moindre que ΘI. Partageons chacune des droites BΔ, Δ en segments égaux ; par les points de division conduisons des parallèles à AΔ, et menons les droites EZ, HK, ΛM; ces droites seront parallèles à BΓ (α). Or, le centre de gravité du parallélogramme MN est dans la droite ΥΣ, celui du parallélogramme KΞ, dans la droite TΥ, et enfin celui du parallélogramme ZO, dans la droite ΥΔ. Donc le centre de gravité de la grandeur composée de toutes ces grandeurs est dans la droite ΣΔ (5). Que son centre de gravité soit le point Ρ. Menons la droite ΡΘ, et ayant prolongé cette droite, conduisons la droite ΓΦ parallèle à AΔ. Le triangle AΔΓ est à la somme de tous les triangles qui sont semblables au triangle AΔΓ et qui sont construits sur les droites AM, MK, KZ, ZΥ, comme ΓA est à AM; parce que les droites AM, MK, KZ, ZΓ sont égales entre elles (β). Mais le triangle AΔB est aussi à la somme de tous les triangles construits sur les droites AΛ, ΛH, HE, EB comme BA est à AΛ; donc le triangle ABΓ est à la somme de tous les triangles dont nous venons de parler comme ΓA est à AM. Mais la raison de ΓA à AM est plus grande que la raison de ΦΡ à ΡΘ; car ΓA est à AM comme ΦΡ est à ΡΠ, parce que les triangles sont semblables (g) ; donc la raison du triangle ABΓ à la somme des triangles dont nous avons parlé est plus grande que la raison de ΦΡ à ΡΘ. Donc par soustraction, la raison de la somme des parallélogrammes MN, KΞ, ZO à la somme des triangles restants est plus grande que la raison de ΦΘ à ΘΡ. Que la droite ΞΘ soit à la droite ΘΡ comme la somme des parallélogrammes est à la somme des triangles. Puisque l’on a une certaine grandeur ABΓ dont le centre de gravité est le point Θ, que de cette grandeur on a ôté une grandeur composée des parallélogrammes MN, KΞ, ZΘ, et que le centre de gravité de la grandeur retranchée est le point Ρ, le centre de gravité de la grandeur restante qui est composée des triangles restants sera dans la droite ΡΘ prolongée, et le prolongement de cette droite sera à la droite ΘΡ comme la grandeur retranchée est à la grandeur restante (8). Donc le point x est le centre de gravité de la grandeur composée des triangles restants. Ce qui ne peut être ; car ayant conduit par le point x, et dans le plan du triangle ABΓ une droite parallèle à AΔ, tous les triangles seraient du même côté de cette droite, c'est-à-dire de l'un ou de l'autre côté. Donc la proposition est évidente.

AUTREMENT.

Soit le triangle ABΓ ; menons la droite AΔ au milieu de BΓ. Je dis que le centre de gravité du triangle ABΓ est dans la droite AΔ.

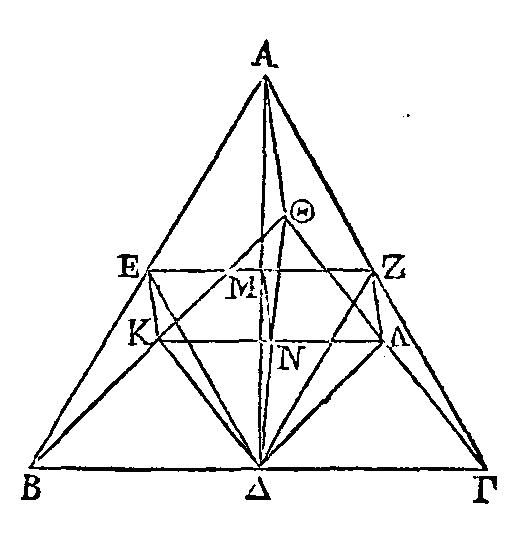
Que cela ne soit pas ainsi, et que le centre de gravité soit le point Θ, si cela est possible. Menons les droites AΘ, ΘB, ΘΓ, et les droites EΔ, ZE aux milieux de BA, AΓ. Conduisons ensuite les droites EK, ZΛ parallèles à la droite AΘ, et menons enfin les droites KΔ, ΛΔ, ΔK, ΔΘ, MN. Puisque le triangle ABΓ est semblable au triangle ΔZΓ, à cause que BA est parallèle à ZΔ, et puisque le centre de gravité du triangle ABΓ est le point Θ, le centre de gravité du triangle ZΔΓ sera le point Λ ; car il est évident que les points Θ, Λ sont semblablement placés dans chaque triangle (α) (11). Par la même raison, le centre de gravité du triangle EBΔ est le point K. Donc le centre de gravité de la grandeur composée des triangles EBΔ, ZΔΓ est au milieu de la droite KΛ, parce que les triangles EBΔ, ZΔΓ sont égaux. Mais le point N est le milieu de KΛ, parce que BE est à EA comme BK est à ΘK, et que ΓZ est à ZA comme ΓΛ est à ΛΘ. Donc, puisque cela est ainsi, la droite KΛ est parallèle à la droite BΓ. Mais on a mené la droite ΔΘ ; donc BΔ est à ΔΓ comme KN est à NΛ. Donc le centre de gravité de la grandeur composée des deux triangles, dont nous venons de parler, est le point N. Mais le centre de gravité du parallélogramme AEΔZ est le point M ; donc le centre de gravité de la grandeur composée de toutes ces grandeurs est dans la droite MN. Mais le centre de gravité du triangle ABΓ est le point Θ ; donc la droite MN prolongée passera par le point Θ. Ce qui est impossible. Donc le centre du triangle ABΓ n'est point hors de la droite AΔ. Il est donc dans cette droite.

PROPOSITION XIV.

Le centre de gravité d'un triangle quelconque est le point où se coupent mutuellement des droites menées des angles du triangle aux milieux des côtés.

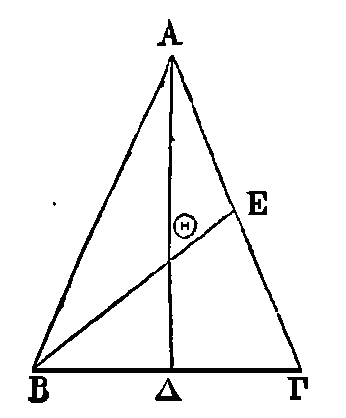
Soit le triangle ABΓ. Conduisons la droite AΔ au milieu du côté BΓ, et la droite BE au milieu du côté AΓ. Le centre de gravité du triangle ABΓ est dans les deux droites AΔ, BE, ce qui a été démontré (13). Donc le point Θ est le centre de gravité du triangle ABΓ.

PROPOSITION XV.

Le centre de gravité d'un trapèze quelconque ayant deux côtés parallèles, est dans la droite qui joint les milieux des deux côtés parallèles, partagée de manière que la partie placée vers le point où le plus petit des côtés parallèles est partagé en deux parties égales, soit à l'autre partie comme le double du plus grand des côtés parallèles, conjointement avec le plus petit est au double du plus petit, conjointement avec le plus grand.

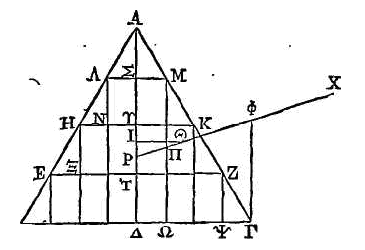
Soit le trapèze ABΓΔ, ayant les côtés AΔ, BΓ parallèles. Que la droite EZ joigne les milieux des côtés AΔ, BΓ. Il est évident que le centre de gravité du trapèze est dans la droite EZ : car si nous prolongeons les droites ΓΔH, ZEH, BAH, ces droites se rencontreront en un même point (α). Donc le centre de gravité du triangle HBΓ est dans la droite HZ. Mais le centre de gravité du triangle AHΔ est aussi dans la droite EH; donc le centre de gravité du trapèze restant ABΓΔ est aussi dans la droite EZ (8). Menons la droite BΔ, et partageons cette droite en trois parties égales aux points K, Θ; par ces points conduisons les droites ΛΘM, NKT parallèles à BΓ, et menons ΔZ, BE, OΞ. Le centre de gravité du triangle ABΓ sera dans ΘM, parce que ΘB est le tiers de BΔ (β), et que la droite MΘ a été conduite par le point Θ parallèlement à la base MΘ. Mais le centre du triangle ABΓ est dans la droite ΔZ; donc le point Ξ est le centre de gravité du triangle dont nous venons de parler. Mais, par la même raison, le point O est le centre de gravité du triangle ABΔ ; donc le centre de

gravité de la grandeur composée des triangles ABΔ, BΔΓ, c'est-à-dire du trapèze, est dans la droite OΞ. Mais le centre de gravité du trapèze dont nous venons de parler est aussi dans la droite EZ; donc le point Π est le centre de gravité du trapèze ABΓΔ. Donc le triangle BΓΔ est au triangle ABΔ comme OΠ est à ΠΞ (6 et 7). Mais le triangle BΔΓ est au triangle ABΔ comme BΓ est à AΔ, et on est à ΠΞ comme ΠΡ est à ΠΣ; donc BΓ est à AΔ comme ΡΠ est à ΠΣ. Donc aussi le double de BΓ, conjointement avec AΔ est au double de AΔ, conjointement avec BΓ comme le double de ΡΠ, conjointement avec ΠΣ est au double de ΠΣ, conjointement avec ΠΡ. Mais le double de ΡΠ, conjointement avec ΠΣ est égal à ΣΡ, conjointement avec ΡΠ, c'est-à-dire à ΡΞ; et le double de ΠΣ, conjointement avec ΠΡ est égal à ΡΠ, conjointement avec ΠΣ, c'est-à-dire à ΠZ. Donc la proposition est démontrée.

COMMENTAIRE SUR LES DEUX LIVRES DE L'ÉQUILIBRE DES PLANS.

LIVRE PREMIER.

DEMANDES.

(α) Ces graves sont ou des surfaces, ou des solides : on considère ces surfaces et ces solides comme homogènes et comme ayant des pesanteurs proportionnelles à leurs grandeurs.