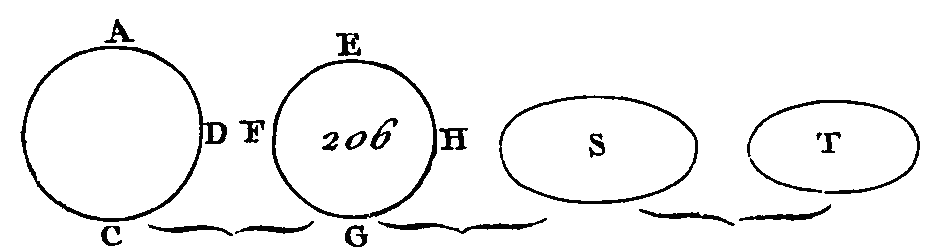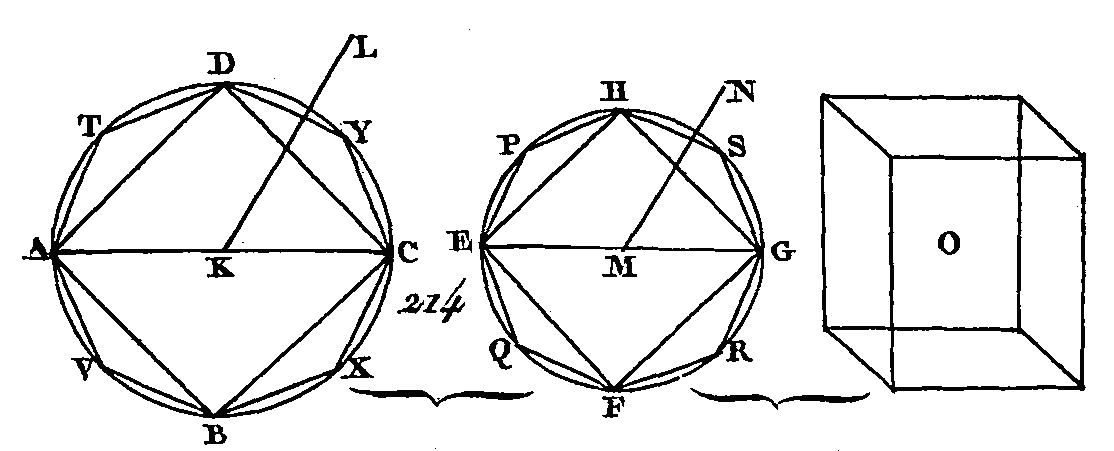INTRODUCTION - GEOMETRIE LIVRE I - LIVRE II - LIVRE III - LIVRE IV- LIVRE VI - LIVRE XI

Éléments de Géométrie : livre XII

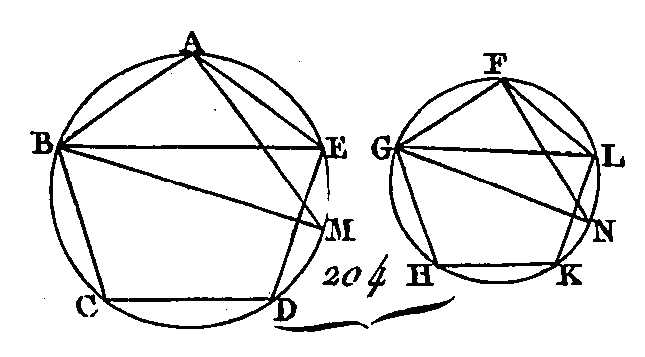
EUCLIDE

ÉLÉMENTS DE GÉOMÉTRIE

ELEMENTS

LIVRE XII.

PROPOSITION PREMIÈRE.

THÉORÈME.

Les polygones semblables inscrits dans des cercles sont entre eux comme les carrés des diamètres.

Soient les cercles ABCDE, FGHKL (fig. 204) dans  lesquels sont décrits les polygones semblables ABC DE, FGHKL ; que les diamètres de ces cercles soient BM, GN : je dis que le polygone ABCDE est au polygone FGHKL comme le carré de BM est au carré de GN.

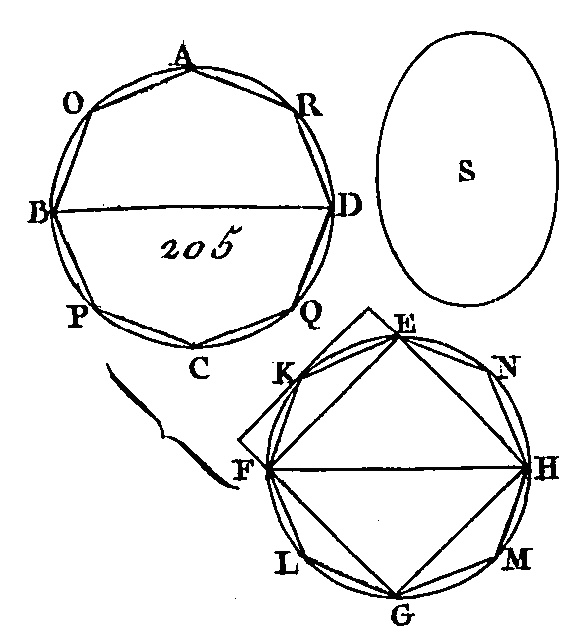
Menez BE, AM, GL, FN. Puisque le polygone ABCDE est semblable au polygone FGHKL, que l'angle BAE est égal à l'angle GFL (déf. 1. 6) et que BA est à AE comme GF est à FL, les deux triangles BAE, GFL ont un angle égal à un angle, savoir, l'angle BAE égal à l'angle GFL et les côtés placés autour de ces angles sont proportionnels entre eux : donc les deux triangles ABE, FGL sont équiangles (prop. 6. 6) : donc l'angle AEB est égal à l'angle FLG, mais l'angle AEB est égal à l'angle AMB (prop. 21. 3), car ils sont appuyés sur le même arc et l'angle FLG est aussi égal à l'angle FNG : donc l'angle AMB est égal à l'angle FNG; mais l'angle droit BAM est égal à l'angle droit GFN : donc l'angle restant est égal à l'angle restant : donc les deux triangles ABM, FGN sont équiangles : donc BM est à GN comme BA est à GF (prop. 4. 6). Mais les carrés des droites BM, GN sont en raison doublée des droites BM, GN (prop. 20. 6), et les polygones ABCDE, FGHKL sont en raison doublée des côtés BA, GF : donc le polygone ABCDE est au polygone FGHKL comme le carré de BM est au carré de GN. Donc les polygones semblables inscrits dans des cercles sont entre eux comme les carrés des diamètres ; ce qu'il fallait démontrer.

PROPOSITION II.

THÉORÈME.

Les cercles sont entre eux comme les carrés de leurs diamètres.

Soient les cercles ABCD, EFGH (fig. 205) et que leurs diamètres soient BD, FH : je dis que le cercle ABCD est au cercle EFGH comme le carré de BD est au carré de FH.

Si cela n'est point, le carré du diamètre BD sera au carré du diamètre FH comme le cercle ABCD est à une surface plus grande ou à une surface plus petite que le cercle EFGH. Supposons d'abord que cette surface soit plus petite et qu'elle soit S. Dans le cercle EFGH décrivez le carré EFGH; le carré décrit dans ce cercle est plus grand que la moitié du cercle EFGH, parce que si par les points E, F, G, H nous menons des tangentes à ce cercle, le carré EFGH sera la moitié du carré circonscrit (prop. 47. 11, prop. 1.3): mais un cercle est plus petit que le carré circonscrit : donc le carré EFGH est plus grand que la moitié du cercle EFGH. Partagez les arcs EF, FG, GH, HE en deux parties égales aux points K, L, M, N, et menez les droites EK, KF, FL, LG, GM, MH, HN, NF. Chacun des triangles EKF, FLG, GMH, HNE est plus grand que la moitié du segment dans lequel il est placé ; parce que si par les points K, L, M, N nous menons des tangentes au cercle, et si sur les droites EF, FG, GH, HE et entre ces tangentes nous construisons des parallélogrammes, chacun des triangles EKF, FLG, GMH, HNE sera la moitié du parallélogramme dans lequel il est placé (pr. 37. 1). Mais chaque segment est plus petit qu'un parallélogramme : donc chacun des triangles EKF, FLG, GMH, HNE est plus grand que la moitié du segment dans lequel il est placé. Si nous partageons ensuite les arcs restants en deux parties égales, et si nous joignons leurs extrémités par des droites, et si nous continuons toujours de faire la même chose, il nous restera certains segments de cercles dont la somme sera moindre que l'excès du cercle EFGH sur l'espace S ; car nous avons démontré dans le premier théorème du dixième Livre que deux quantités inégales étant données, si l'on retranche de la plus grande quantité une partie plus grande que la moitié de cette quantité, si on retranche ensuite de ce qui reste une partie plus grande que la moitié de ce reste, et si l'on continue toujours de faire la même chose, il reste enfin une certaine quantité qui est moindre que la plus petite des quantités données. Supposons qu'on ait pour reste les segments du cercle EFGH placés sur les cordes EK, KF, FL, LG, GM, MH, HN, NE, et que ces segments soient moindres que l'excès du cercle EFGH sur l'espace S, il est évident que le polygone EKFLGMHN sera plus grand que l'espace S. Décrivez dans le cercle ABCD un polygone AOBPCQDR semblable au polygone EKFLGMHN ; le carré de BD sera au carré de F H comme le polygone AOBPCQDR est au polygone EKFLGMHN (prop. 1. 12) ; mais par supposition le carré de BD est au carré de FH comme le cercle ABCD est à l'espace S : donc le cercle ABCD est à l'espace S comme le polygone AOBPCQDR est au polygone EKFLGMHN, et en échangeant les plans des moyens, le cercle ABCD est au polygone qui lui est inscrit comme l'espace S est au polygone EKFLGMHN; mais le cercle ABCD est plus grand que le polygone qui lui est inscrit : donc l'espace S est plus grand que le polygone EKFLGMHN; mais, par supposition, il est au contraire plus petit, ce qui est impossible : donc le carré de BD n'est point au carré de FH comme le cercle ABCD est à un espace quelconque plus petit que le cercle EFGH. Nous démontrerons semblablement que le carré de FH n'est point au carré de BD comme le cercle EFGH est à un espace quelconque plus petit que le cercle ABCD. Je dis ensuite que le carré de BD n'est point au carré de FH comme le cercle ABCD est à un espace quelconque plus grand que le cercle EFGH ; car si cela est possible, supposons que le carré de BD soit au carré de FH comme le cercle ABCD est à un espace plus grand, et supposons que S soit cet espace. En mettant les antécédents à la place des conséquents et les conséquents à la place des antécédents, le carré de FH sera au carré de BD comme l'espace S est. au cercle ABCD ; mais on démontrera plus bas que l'espace S est au cercle ABCD comme le cercle EFGH est à un espace quelconque plus petit que le cercle ABCD : donc le carré de FH est au carré de BD comme le cercle EFGH est à un espace plus petit que le cercle ABCD, ce qui a été démontré impossible ; donc le carré de BD n'est pas au carré de FH comme le cercle ABCD est à un espace quelconque plus grand que le cercle EFGH. Mais on a démontré que le carré de BD n'est point au carré de FH comme le cercle ABCD est à un espace quelconque plus petit que le cercle EFGH : donc le carré de BD est au carré de FH comme le cercle ABCD est au cercle EFGH.

Donc les cercles sont entre eux comme les carrés des diamètres ; ce qu'il fallait démontrer.

LEMME.

Si l'espace S est plus grand que le cercle EFGH (fig. 206) : je dis que l'espace S est au cercle ABCD comme le cercle EFGH est à un espace quelconque plus petit que le cercle ABCD.

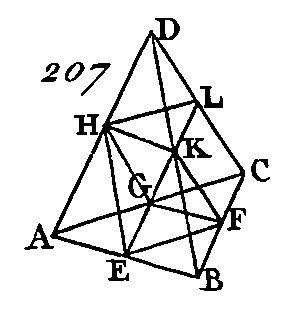
Car supposons que l'espace S soit au cercle ABCD comme le cercle EFGH est à un espace T : je dis que l'espace T est plus petit que le cercle ABCD; car puisque l'espace S est au cercle ABCD comme le cercle EFGH est à l'espace T, en échangeant les plans des moyens, l'espace S sera au cercle EFGH comme le cercle ABCD est à l'espace T (prop. 16. 6). Mais par supposition l'espace S est plus grand que le cercle EFGH : donc le cercle ABCD est plus grand que l'espace T ; et par conséquent l'espace S est au cercle ABCD comme le cercle EFGH est à un espace quelconque plus petit que le cercle ABCD.

PROPOSITION III.

THÉORÈME.

Toute pyramide triangulaire[1] peut se diviser en deux pyramides triangulaires égales et semblables entre elles et semblables à la pyramide totale, et en deux prismes égaux qui sont plus grands que la moitié de la pyramide entière.

Soit une pyramide dont la base soit le triangle ABC (fig. 207) et dont le sommet soit le point D : je dis que la pyramide ABCD peut se diviser en deux pyramides triangulaires égales et semblables entre elles et semblables à la pyramide totale, et en deux prismes égaux qui sont plus grands que la moitié de la pyramide totale.

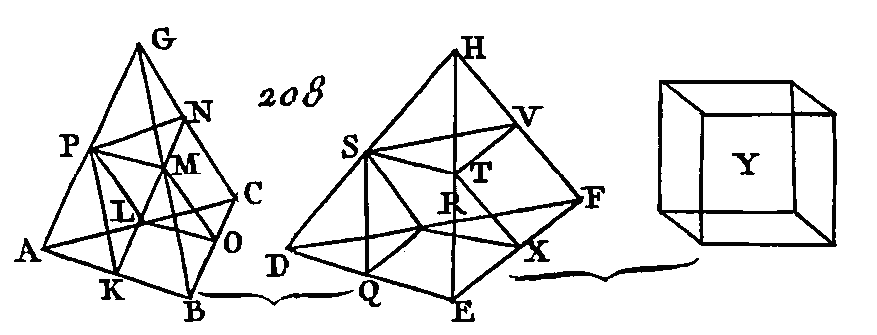
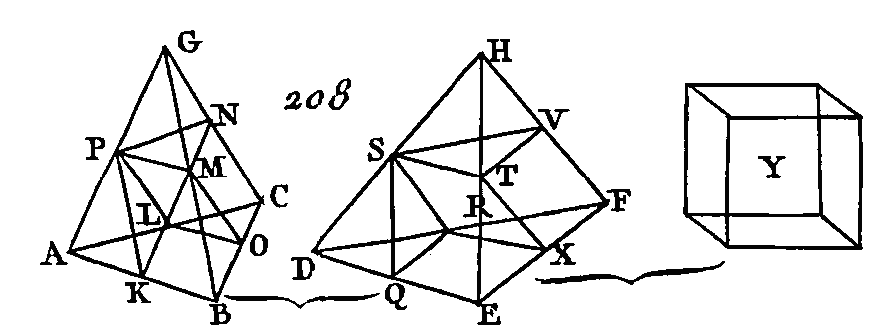
Partagez les côtés AB, BC, CA, AD, DB, DC en deux parties égales aux points E, F, G, H, K, L, et menez les droites EH, EG, GH, HK, KL, LH, EK, KF, FG. Puisque AE est égal à EB et AH égal à HD, la droite EH sera parallèle à la droite DB (prop. 2. 6). La droite HK est parallèle à la droite AB, par la même raison : donc la figure HEBK est un parallélogramme : donc HK est égal à EB (prop. 34. 1). Mais EB est égal à AE : donc AE sera égal à HK. Mais AH est égal à HD: donc les deux droites AE, AH sont égales aux deux droites KH, HD, chacune à chacune ; mais l'angle EAH est égal à l'angle KHD (prop. 29. 1) : donc la base EH est égale à la base KD (prop. 4. 1) donc le triangle AEH est égal et semblable au triangle HKD. Par la même raison, le triangle AHG est égal et semblable au triangle HLD. Puisque les deux droites EH, HG qui se touchent sont parallèles aux deux droites KD, DL qui se touchent et qui ne sont pas dans le même plan, ces droites comprendront des angles égaux (prop. 10. 11): donc l'angle EHG est égal à l'angle KDL. De plus, puisque les deux droites EH, HG sont égales aux deux droites KD, DL, chacune à chacune, et que l'angle EHG est égal à l'angle KDL, la base EG sera égale à la base KL : donc le triangle EHG est égal et semblable au triangle KDL. Par la même raison, le triangle AEG est égal et semblable au triangle HKL: donc la pyramide dont la base est le triangle AEG et dont le sommet est le point H est égale et semblable à la pyramide dont la base est le triangle HKL et dont le sommet est le point D. Puisque la droite HK est parallèle à un des côtés du triangle ADB, savoir, au côté AB, le triangle ADB sera équiangle avec le triangle DHK (prop. 29. 1) : donc ces deux triangles auront leurs côtés proportionnels (prop. 4. 6), et seront par conséquent semblables. Par la même raison, le triangle DBC est semblable au triangle DKL et le triangle ADC est semblable aussi au triangle DHL. Mais puisque les deux droites BA, AC qui se touchent sont parallèles aux deux droites KH, HL qui se touchent et qui ne sont pas dans le même plan, ces droites comprendront des angles égaux (prop. 10. 11): donc l'angle BAC est égal à l'angle KHL. Mais BA est à AC comme KH est à HL : donc le triangle ABC est semblable au triangle HKL (prop. 6. 6), et par conséquent la pyramide dont la base est le triangle ABC et dont le sommet est le point D est semblable à la pyramide dont la base est le triangle HKL et dont le sommet est le point D. Mais nous avons démontré que la pyramide dont la base est le triangle HKL et dont le sommet est le point D est semblable à la pyramide dont la base est le triangle AEG et dont le sommet est le point H : donc la pyramide dont la base est le triangle ABC et dont le sommet est le point D est semblable à la pyramide dont la base est le triangle AEG et dont le sommet est le point H : donc l'une et l'autre des pyramides AEGH, HKLD sont semblables à la pyramide totale ABCD. Puisque BF est égal à FC, le parallélogramme EBFG sera double du triangle GFC (pr. 41. 1) ^: mais deux prismes de même hauteur dont l'un a pour base un parallélogramme et dont l'autre a pour base un triangle sont égaux entre eux lorsque le parallélogramme est double du triangle (prop. 40. 11) : donc le prisme compris sous les deux triangles BKF, EHG et sous les trois parallélogrammes EBFG, EBKH, KHGF est égal au prisme qui est compris sous les deux triangles GFC, HKL et les trois parallélogrammes KFCL, LCGH, HKFG. Mais il est évident que chacun de ces prismes et celui dont la base est le parallélogramme EBFG opposé à la droite HK et celui dont la base est le triangle GFC opposé au triangle KLH est plus grand que chacune des pyramides dont les bases sont AEG, HKL et les sommets les points H, D; puisque si nous menons les droites EF, EK, le prisme dont la base est le parallélogramme EBFG opposé à la droite HK est plus grand que la pyramide qui a pour base le triangle. EBF et pour sommet le point K. Mais la pyramide qui a pour base le triangle EBF et pour sommet le point K est égale à la pyramide qui a pour base le triangle AEG et pour sommet le point H (déf. 10. 11), car elles sont comprises sous des plans égaux et semblables : donc le prisme qui a pour base le parallélogramme EBFG opposé à la droite HK est plus grand que la pyramide qui a pour base le triangle AEG et pour sommet le point H. Mais le prisme qui a pour base le parallélogramme EBFG opposé à la droite HK est égal au prisme qui a pour base le triangle GFC opposé au triangle HKL ; et la pyramide qui a pour base le triangle AEG et pour sommet le point H est égale à la pyramide qui a pour base le triangle HKL et pour sommet le point D : donc les deux prismes dont nous venons de parler sont plus grands que les deux pyramides qui ont pour bases les triangles AEG, HKL et pour sommets les points H, D : donc la pyramide totale qui a pour base le triangle ABC et pour sommet le point D a été divisée en deux pyramides triangulaires égales et semblables entre elles et semblables à la pyramide totale et en deux prismes égaux qui sont plus grands que la moitié de la pyramide totale ; ce qu'il fallait démontrer.

PROPOSITION IV.

THÉORÈME.

Si deux pyramides triangulaires de même hauteur sont divisées l'une et l'autre en deux pyramides égales entre elles et semblables à la pyramide totale et en deux prismes égaux, si ces nouvelles pyramides sont divisées de la même manière et ainsi de suite, la base de l'une de ces pyramides sera à la base de l'autre pyramide comme tous les prismes de l'une de ces pyramides sont à un même nombre de prismes contenus dans l'autre pyramide.

Soient deux pyramides triangulaires de même hauteur qui aient pour bases les triangles ABC, DEF (fig. 208) et pour sommets les points G, H ; que chacune de ces pyramides soit divisée en deux pyramides égales entre elles et semblables aux pyramides totales et en deux prismes égaux, que ces nouvelles pyramides soient divisées de la même manière et ainsi de suite : je dis que la base ABC sera à la base DEF comme tous les prismes contenus dans la pyramide ABCG sont au même nombre de prismes contenus dans la pyramide DEFH.

Puisque BO est égal à OC et AL égal à LC, la droite AB sera parallèle à la droite OL (prop. 2. 6), et le triangle ABC sera semblable au triangle LOC (prop. 4. 6). Le triangle DEF sera semblable au triangle RXF, par la même raison ; et puisque la droite BC est double de la droite CO et la droite EF double aussi de la droite FX, la droite BC sera à la droite CO comme la droite EF est à la droite FX. Mais les figures rectilignes semblables et semblablement posées ABC, LOC ont été décrites sur les droites BC, CO, et les figures rectilignes semblables et semblablement posées DEF, RXF ont été décrites sur les droites EF, FX : donc le triangle ABC est au triangle LOC comme le triangle DEF est au triangle RXF (prop. 22. 6), et en échangeant les plans des moyens, le triangle ABC est au triangle DEF comme le triangle LOC est au triangle RXF. Mais on démontrera plus bas que le triangle LOC est au triangle RXF comme le prisme qui a pour base le triangle LOC opposé à PMN est au prisme qui a pour base le triangle RXF opposé à STV : donc le triangle ABC est au triangle DEF comme le prisme qui a pour base le triangle LOC opposé à PMN est au prisme qui a pour base le triangle RXF opposé à STV; et puisque les deux prismes qui sont dans la pyramide ABCG sont égaux entre eux et que les deux prismes qui sont dans la pyramide DEFH sont aussi égaux entre eux, le prisme qui a pour base le parallélogramme KLOB opposé à la droite MP sera au prisme qui a pour base le triangle LOC opposé à PMN comme le prisme qui a pour base le parallélogramme EQRX opposé à la droite ST est au prisme qui a pour base le triangle RXF opposé à STV : donc, en ajoutant les conséquents aux antécédents (prop. 15. 5), les prismes KBOLMP, LOCMNP sont au prisme LOCMNP comme les prismes QEXRST, RXFSTV sont au prisme RXFSTV, et enfin en échangeant les places des moyens, les prismes KBOLPM, LOCPMN sont aux prismes QEXRST, RXFSTV comme le prisme LOCMNP est au prisme RXFSTV. Mais on a démontré que le prisme LOCMNP est au prisme RXFSTV comme la base LOC est à la base RXF et comme la base ABC est à la base DEF : donc le triangle ABC est au triangle DEF comme les deux prismes qui sont dans la pyramide ABCG sont aux deux prismes qui sont dans la pyramide DEFH. Si nous partageons de la même manière les nouvelles pyramides, savoir les pyramides PMNG, STVH, la base PMN sera à la base STV comme les deux prismes de la pyramide PMNG sont aux deux prismes de la pyramide STVH. Mais la base PMN est à la base STV comme la base ABC est à la base DEF : donc la base ABC est à la base DEF comme les deux prismes de la pyramide ABCG sont aux deux prismes de la pyramide DEFH, comme les deux prismes de la pyramide PMNG sont aux deux prismes de la pyramide STVH et comme les quatre prismes sont aux quatre prismes. On démontrera la même chose pour tous les autres prismes qu'on obtiendra par la division des pyramides AKLP et DQRS, et en général de toutes les pyramides égales en nombre ; ce qu'il fallait démontrer.

LEMME.

Nous démontrerons de la manière suivante que le triangle LOC est au triangle BXF comme le prisme qui a pour base le triangle LOC opposé à PMN, est le prisme qui a pour base le triangle RXF opposé à STV.

Dans les mêmes figures imaginez des perpendiculaires menées des points G, H sur les plans des triangles ABC, DEF. Ces perpendiculaires seront égales entre elles, parce qu'on a supposé ces pyramides égales en hauteur. Puisque la droite GC et la perpendiculaire menée du point G sont coupées par les plans parallèles ABC, PMN, ces deux droites seront coupées proportionnellement (prop. 11. 11). Or la droite GC est coupée en deux parties égales au point N par le plan PMN : donc la perpendiculaire menée du point G sur le plan ABC est coupée en deux parties égales par le plan PMN par la même raison, la perpendiculaire menée du point H sur le plan DEF est coupée en deux parties égales par le plan STV. Mais les perpendiculaires menées des points G, H sur les plans ABC, DEF sont égales entre elles: donc les perpendiculaires menées des triangles PMN, STV sur les triangles ABC, DEF sont égales entre elles : donc les prismes qui ont pour bases les triangles LOC, RXF opposés à PMN, STV sont égaux en hauteur : donc les parallélépipèdes qui sont décrits sur les prismes égaux en hauteur dont nous venons de parler sont entre eux comme leurs bases, et il en sera de même de leurs moitiés, c'est-à-dire que les bases LOC, RXF seront entre elles comme les prismes dont nous avons parlé ; ce qu'il fallait démontrer.

PROPOSITION V.

THÉORÈME.

Les pyramides triangulaires qui ont la même hauteur sont entre elles comme leurs bases.

Que les pyramides dont les bases sont les triangles ABC, DEF (fig. 208) et dont les sommets sont les points G, H aient la même hauteur : je dis que la base ABC est à la base DEF comme la pyramide ABCG est à la pyramide DEFH.

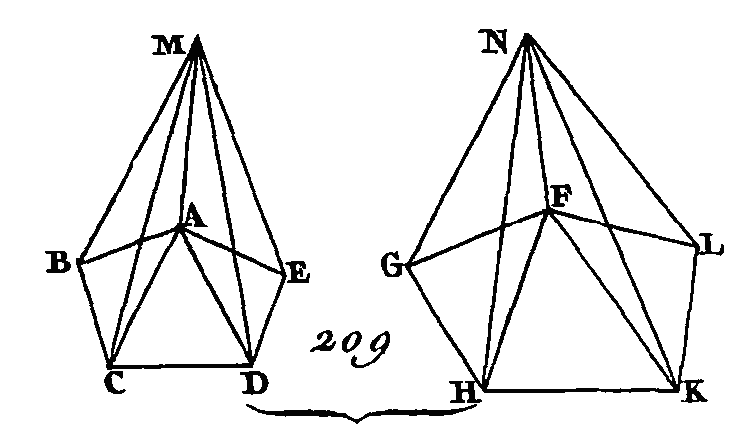
Car si cela n'est point, la base ABC sera à la base DEF comme la pyramide ABCG est à un solide plus petit que la pyramide DEFH ou a un solide plus grand. Supposons d'abord que la base ABC soit à la base DEF comme la pyramide ABCDH est à un solide plus petit et que ce solide soit Y. Divisez la pyramide DEFH en deux pyramides égales entre elles et semblables à la pyramide totale, et en deux prismes égaux ; les deux prismes seront plus grands que la moitié de la pyramide totale (prop. 3. 12). Que les nouvelles pyramides obtenues par cette division soient partagées de la même manière jusqu'à ce qu'on ait obtenu de la pyramide DEFH certaines pyramides qui soient plus petites que l'excès de la pyramide DEFH sur le solide Y. Qu'on cherche ces pyramides, et qu'elles soient par exemple DQRS, STVH, les prismes restants de la pyramide DEFH seront plus grands que le solide Y. Partagez semblablement la pyramide ABCG en autant de parties que la pyramide DEFH. La base ABC sera à la base DEF comme les prismes de la pyramide ABCG sont aux prismes de la pyramide DEFH (prop. 4. 12); mais par supposition la base ABC est à la base DEF comme la pyramide ABCG est au solide Y : donc la pyramide ABCG est au solide Y comme les prismes de la pyramide ABCG sont aux prismes de la pyramide DEFH, et en échangeant les places des moyens, la pyramide ABCG est aux prismes qu'elle renferme comme le solide Y est aux prismes de la pyramide DEFH. Mais la pyramide ABCG est plus grande que les prismes qu'elle renferme : donc le solide Y est plus grand que les prismes que renferme la pyramide DEFH; mais, au contraire, il est plus petit; ce qui ne peut être : donc la base ABC n'est point à la base DEF comme la pyramide ABCG est à un solide quelconque plus petit que la pyramide DEFH. Nous démontrerons semblablement que la base DEF n'est point à la base ABC comme la pyramide DEFH est- à un solide quelconque plus petit que la pyramide ABCG. Je dis enfin que la base ABC n'est point à la base DEF comme la pyramide ABCH est à un solide plus grand que la pyramide DEFH; car supposons, si cela est possible, que la base ABC soit à la base DEF comme la pyramide ABCG est à un solide quelconque plus grand que la pyramide DEFH et que ce solide soit Y. En mettant les antécédents à la place des conséquents et les conséquents à la place des antécédents, la base DEF sera à la base ABC comme le solide Y est à la pyramide ABCG. Mais le solide Y est à la pyramide ABCG comme la pyramide DEFH est à un solide quelconque plus petit que la pyramide ABCG, ainsi que cela a été démontré : donc la base DEF est à la base ABC comme la pyramide DEFG est à un solide quelconque plus petit que la pyramide ABCG, ce qui est absurde : donc la base ABC n'est point à la base DEF comme la pyramide ABCG est à un solide quelconque plus grand que la pyramide DEFH. Mais on a démontré que la base ABC n'est point à la base DEF comme la pyramide ABCG est à un solide quelconque plus petit que la pyramide DEFH : donc la base ABC est à la base DEF comme la pyramide ABCG est à la pyramide DEFH.

Donc les pyramides triangulaires qui ont la même hauteur sont entre elles comme leurs bases ; ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Les pyramides qui ont la même hauteur et qui ont des polygones pour bases sont entre elles comme leurs bases.

Que les pyramides dont les bases sont les polygones ABCDE, FGHKL (fig. 209) et dont les sommets sont les points M, N aient la même hauteur : je dis que la base ABCDE est à la base FGHKL comme la pyramide ABCDEM est à la pyramide FGHKLN.

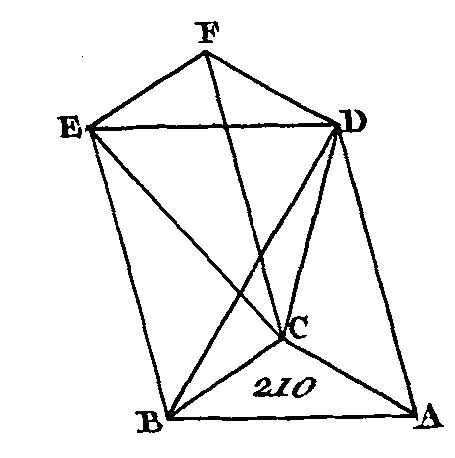
Partagez la base ABCDE en triangles et que ces triangles soient ABC, ACD, ADE ; partagez aussi la base FGHKL en triangles et que ces triangles soient FGH, FHK, FKL, et supposons que chacun de ces triangles soit la base d'une pyramide qui ait la même hauteur que les deux pyramides qu'on avait d'abord. Puisque le triangle ABC est au triangle ACD comme la pyramide ABCM est à la pyramide ACDM  (prop. 5. 12), si l'on ajoute les conséquents aux antécédents, le quadrilatère ABCD sera au triangle ACD comme la pyramide ABC DM est à la pyramide ABCM (prop. 18. 5); mais le triangle ACD est au triangle ADE comme la pyramide ACDM est à la pyramide ADEM: donc la base ABCD sera à la base ADE comme la pyramide ABCDM est à la pyramide ADEM (prop. 22. 5) : donc en ajoutant les conséquents aux antécédents, la base ABCDE sera à la base ADE comme la pyramide ABCDEM est à la pyramide ADEM. Par la même raison, la base FGHKL est à la base FKL comme la pyramide FGHKLN est à la pyramide FKLN ; et puisque ces deux pyramides triangulaires ont la même hauteur, la base ADE sera à la base FKL comme la pyramide ADEM est à la pyramide FKLN : donc puisque la base ABCDE est à la base ADE comme la pyramide ABCDEM est à la pyramide ADEM, et que la base ADE est à la base FKL comme la pyramide ADEM est à la pyramide FKLN, la base ABCDE sera à la base FKL comme la pyramide ABCDEM est à la pyramide FKLN (prop. 22. 5) ; mais la base FKL est à la base FGHKL comme la pyramide FKLN est à la pyramide FGHKLN : donc la base ABCDE est à la base FGHKL comme la pyramide ABCDEM est à la pyramide FGHKLM.

Donc les pyramides qui ont la même hauteur et dont les bases sont des polygones sont entre elles comme leurs, bases; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Tout prisme triangulaire peut se diviser en trois pyramides triangulaires égales entre elles.

Soit un prisme dont la base soit le triangle ABC opposé au triangle DEF (fig. 210) : je dis que le prisme ABCDEF peut être partagé en trois pyramides triangulaires égales entre elles.

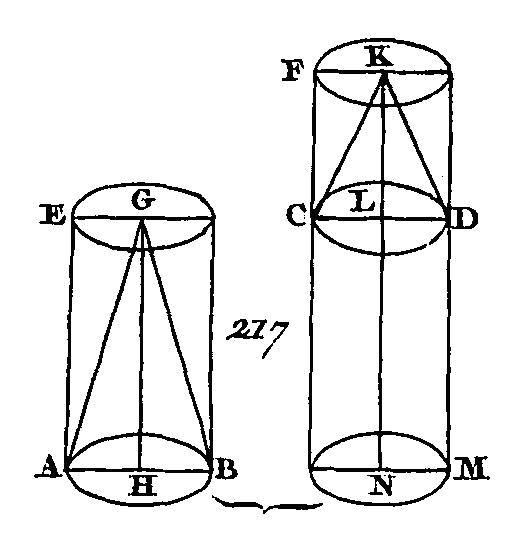
Menez les droites BD, EC, CD. Puisque la figure ABED est un parallélogramme dont BD est la diagonale, le triangle ABD sera égal au triangle EDB (prop. 34. 1) : donc la pyramide qui a pour base le triangle ABD et pour sommet le point C est égale à la pyramide qui a pour base le triangle EDB et pour sommet le point C (prop. 5. 12) ; mais la pyramide qui a pour base le triangle EDB et pour sommet le point C est égale à la pyramide qui a pour base le triangle EBC et pour sommet le point D, car elles sont comprises dans les mêmes plans : donc la pyramide qui a pour base le triangle ABD et pour sommet le point C est égale à la pyramide qui a pour base le triangle EBC et pour sommet, le point D. De plus, puisque la figure FCBE est un parallélogramme qui a pour diagonale la droite CE, le triangle ECF est égal au triangle CBE (prop. 34. 1) : donc la pyramide qui a pour base le triangle BEC et pour sommet le point D est égale à la pyramide qui a pour base le triangle ECF et pour sommet le point D (prop. 5. 11). Mais on a démontré que la pyramide qui a pour base le triangle BCE et pour sommet le point D est égale à la pyramide qui a pour base le triangle ABD et pour sommet le point C : donc la pyramide qui a pour base le triangle C EF et pour sommet le point D est égale à la pyramide qui a pour base le triangle ABD et pour sommet le point C : donc le prisme ABCDEF a été partagé en trois pyramides triangulaires égales entre elles, mais la pyramide qui a pour base le triangle ABD et pour sommet le point C est égale à la pyramide qui a pour base le triangle CAB et pour sommet le point D, car ces pyramides sont comprises sous les mêmes plans ; mais on a démontré que la pyramide qui a pour base le triangle ABD et pour sommet le point C est la troisième partie du prisme qui a pour base le triangle ABC opposé au triangle DEF : donc la pyramide qui a pour base le triangle ABC et pour sommet le point D est la troisième partie d'un prisme qui a la même base, savoir, le triangle ABC opposé au triangle DEF; ce qu'il fallait démontrer.

COROLLAIRE.

Il suit manifestement de là que toute pyramide est la troisième partie d'un prisme qui a la même base et la même hauteur ; car une des bases du prisme étant une figure rectiligne quelconque, la base opposée sera une figure égale et semblable, et ce prisme pourra être divisé en prismes qui auront des bases triangulaires et dont les bases opposées seront des triangles.

PROPOSITION VIII.

THÉORÈME.

Les pyramides semblables qui ont des bases triangulaires sont entre elles en raison triplée de leurs côtés homologues.

Soient deux pyramides semblables et semblablement placées qui aient pour bases les triangles ABC, DEF (fig. 211) et pour sommets les points G, H : je dis que les pyramides ABCG, DEFH sont entre elles en raison triplée des côtés BC, EF.

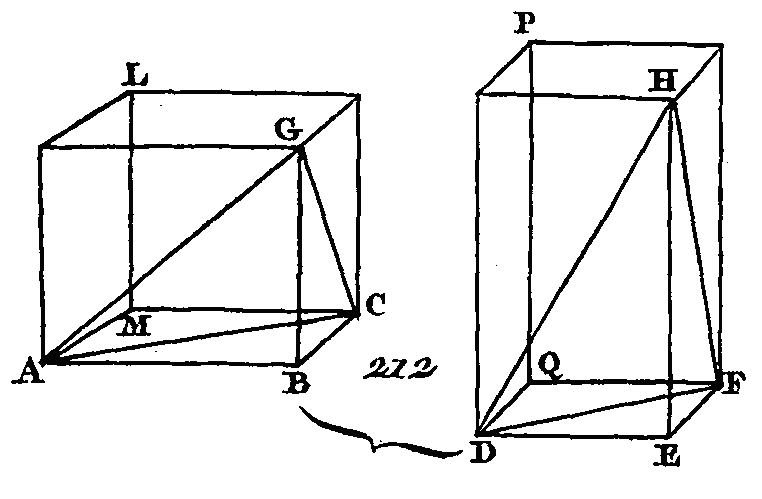
Achevez les parallélépipèdes BGML, EHQP. Puisque la pyramide ABCG est semblable à la pyramide DEFH, l'angle ABC sera égal à l'angle DEF (déf. 9. 11), l'angle GBC égal à l'angle HEF, l'angle ABG égal à l'angle DEH et AB sera à DE comme BC est à EF et comme BG est à EH : donc, puisque AB est à DE comme BC est à EF et que les côtés placés autour d'angles égaux sont proportionnels, le parallélogramme BM sera semblable au parallélogramme EQ. Par la même raison, le parallélogramme BN sera semblable au parallélogramme ER et le parallélogramme BK semblable au parallélogramme EO : donc les trois parallélogrammes BM, KB, BN sont semblables aux trois parallélogrammes EQ, EO, ER ; mais les trois parallélogrammes MB, BK, BN sont égaux et semblables aux trois parallélogrammes opposés et les trois parallélogrammes EQ, EO, ER sont aussi égaux et semblables aux trois parallélogrammes opposés (prop. 24. 11): donc les parallélépipèdes BGML, EHQP sont compris dans des plans semblables et égaux en nombre : donc le parallélépipède BGML est semblable au parallélépipède EHQP (déf. 9. 11). Mais les parallélépipèdes semblables sont entre eux en raison triplée de leurs côtés homologues (pr. 33. 11) : donc les parallélépipèdes BGMH, EHQP sont entre eux en raison triplée des côtés homologues BC, EF; mais le parallélépipède BGML est au parallélépipède EHQP comme la pyramide ABCG est à la pyramide DEFH (prop. 15. 5), car une pyramide est la sixième partie d'un parallélépipède, puisqu'un prisme triangulaire qui est la moitié d'un parallélépipède est triple d'une pyramide : donc les pyramides ABCG, DEFH sont entre elles en raison triplée des côtés BC, EF ; ce qu'il fallait démontrer.

COROLLAIRE.

De là il suit évidemment que les pyramides semblables qui ont des polygones pour bases sont entre elles en raison triplée de leurs côtés homologues ; car ces pyramides peuvent être divisées en pyramides triangulaires, puisque les polygones semblables qui sont les bases de ces pyramides peuvent être divisés en un même nombre de triangles semblables entre eux et proportionnels à ces polygones : donc une des pyramides triangulaires contenue dans la première pyramide est à une autre des pyramides triangulaires contenue dans la seconde pyramide comme la somme de toutes les .pyramides triangulaires contenues dans la première pyramide est à la somme de toutes les pyramides triangulaires contenues dans l'autre pyramide, c'est-à-dire comme une des pyramides qui a pour base un polygone est à l'autre pyramide qui a aussi pour base un polygone. Mais les pyramides triangulaires semblables sont entre elles en raison triplée de leurs côtés homologues : donc les pyramides semblables qui ont pour bases des polygones sont entre elles en raison triplée de leurs côtés homologues.

PROPOSITION IX.

Les bases des pyramides égales, qui ont des bases triangulaires sont réciproquement proportionnelles aux hauteurs de ces pyramides, et les pyramides triangulaires qui ont des bases réciproquement proportionnelles à leurs hauteurs sont égales entre elles.

Soient deux pyramides égales qui aient les bases triangulaires ABC, DEF (fig. 212) dont les sommets soient les points G, H : je dis que les bases des pyramides ABCG, DEFH sont réciproquement proportionnelles aux hauteurs de ces pyramides, c'est-à-dire que la base ABC est à la base DEF comme la hauteur de la pyramide DEFH est à la hauteur de la pyramide ABCG.

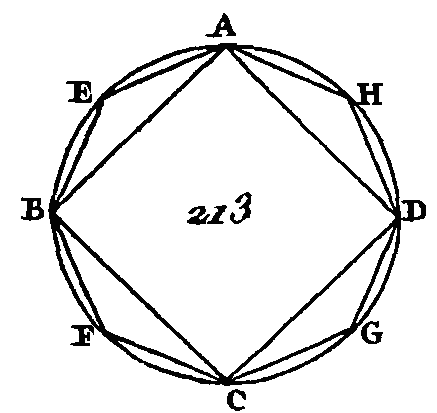
Achevez les parallélépipèdes BGML, EHQP. Puisque la pyramide ABCG est égale à la pyramide DEFH, que le parallélépipède BGML est sextuple de la pyramide ABCG et que le parallélépipède EHQP est aussi sextuple de la pyramide DEFH, le parallélépipède BGML sera égal au parallélépipède EHQP (pr. 15. 5). Mais les bases des parallélépipèdes égaux sont réciproquement proportionnelles aux hauteurs de ces parallélépipèdes (prop. 34. 11) : donc la base BM est à la base EQ comme la hauteur du parallélépipède EHQP est à la hauteur du parallélépipède BGML. Mais la base BM est à la base EQ comme le triangle ABC est au triangle DEF : donc le triangle ABC est au triangle DEF comme la hauteur du parallélépipède EHQP est à la hauteur dû parallélépipède BGML. Mais la hauteur du parallélépipède EHQP est la même que la hauteur de la pyramide DEFH et la hauteur du parallélépipède BGML est la même que la hauteur de la pyramide ABCG : la base ABC est à la base DEF comme la hauteur de la pyramide DEFH est à la hauteur de la pyramide ABCG : donc les bases des pyramides ABCG, DEFH sont réciproquement, proportionnelles à leurs hauteurs.

Si les bases des pyramides ABCG, DEFH sont réciproquement proportionnelles à leurs hauteurs, c'est-à-dire que si la base ABC est à la base DEF. Comme la hauteur de la pyramide DEFH est à la hauteur de la pyramide ABCG, je dis que la pyramide ABCG sera égale à la pyramide DEFH.

Faites la même construction. Puisque la base ABC est à la base DEF comme la hauteur de la pyramide DEFH est à la hauteur de la pyramide ABCG et que la base ABC est à la base DEF comme le parallélogramme BM est au parallélogramme EQ, le parallélogramme BM sera au parallélogramme EQ comme la hauteur de la pyramide DEFH est à la hauteur de la pyramide ABCG. Mais la hauteur de la pyramide DEFH est la même que la hauteur du parallélépipède EHQP, et la hauteur de la pyramide ABCG est la même que la hauteur du parallélépipède BGML : donc la base BM est à la base EQ comme la hauteur du parallélépipède EHQP est à la hauteur du parallélépipède BGML ; mais les parallélépipèdes qui ont leurs bases, réciproquement proportionnelles à leurs hauteurs s.pnt égaux; entre eux (pr. 34. 11) ; donc le parallélépipède BGML est égal au parallélépipède EHQP. Mais la pyramide ABCG est la dixième partie du parallélépipède BGML et la  pyramide DEFH est aussi la sixième partie du parallélépipède EHQP ; donc la pyramide ABCG est égale à la pyramide DEFH.

Donc les bases des pyramides égales qui ont des bases triangulaires sont réciproquement proportionnelles aux hauteurs de ces pyramides, et les pyramides triangulaires qui ont des bases, réciproquement proportionnelles à leurs hauteurs sont égales entre elles; ce qu'il fallait démontrer.

 PROPOSITION X.

THÉORÈME.

Un cône est la troisième partie d'un cylindre qui a la même base et une hauteur égale.

Qu'un cône ait la même base qu’un cylindre, savoir le cercle ABCD (fig. 213) et une hauteur égale ; je dis que ce cône est la troisième partie de ce cylindre.

Car si le cylindre n’est pas le triple du cône, il sera plus grand que le triple ou plus petit ; supposons d'abord qu'il soit plus grand que le triple. Décrivez dans le cercle ABCD le carré, ABCD ; le carré ABCD sera plus grand que la moite du cercle ABCD. Sur le carré ABCD élevez un prisme qui ait la même hauteur que le cylindre ; ce prisme sera plus grand que la moitié du cylindre ; parce que si l'on circonscrit un carré au cercle ABCD, le carré inscrit sera la moitié du carré circonscrit, mais les parallélépipèdes, c'est-à-dire les prismes élevés sur ces bases ont la même hauteur : donc ces prismes sont, entre eux comme leurs bases : donc le prisme élevé sur le carré ABCD est la moitié du prisme élevé sur le carré circonscrit au cercle ABCD; mais le cylindre est plus petit que le prisme élevé sur le carré circonscrit au cercle ABCD : donc le prisme élevé sur le carré ABCD, qui a une hauteur égale à celle du cylindre, est plus grand que la moitié du cylindre. Partagez les arcs AB, BC, CD, DA en deux parties égales aux points E, F, G, H, et menez les droites AE, EB, BF, FC, CG, GD, DH, HA; chacun des triangles AEB, BFG, CGD, DHA sera plus grand que le demi-segment du cercle où il est placé, comme nous l'avons démontré plus haut (prop. 2. 12); sur chacun de ces triangles élevons des prismes qui aient une hauteur égale à celle du cylindre ; chacun de ces prismes sera plus grand que la moitié du segment respectif du cylindre, parce que si par les points E, F, G, H on mène des parallèles aux droites AB, BC, CD, DA, et si sur les droites AB, BC, CD, DA et si entre ces parallèles on construit des parallélogrammes sur lesquels on élève des parallélépipèdes qui aient la même hauteur que le cylindre, les prismes qui auront pour bases les triangles AEB, BFC, CGP, DHA seront les moitiés de chacun de ces parallélépipèdes. Mais les segments du cylindre sont plus petits que ces parallélépipèdes : donc les prismes qui ont pour bases les triangles AEB, BFC, CGD, DHA sont plus grands que les moitiés des segments respectifs du cylindre. Partageons les arcs restants en deux parties égales, joignons leurs extrémités par des droites, sur chacun de ces triangles élevons des prismes qui aient la même hauteur que le cylindre, et continuons de faire la même chose jusqu'à ce qu'il reste certains segments du cylindre qui soient plus petits que l'excès du cylindre sur le triple du cône (prop. 1. 10). Supposons que les segments restants du cylindre soient AE, EB, BF, FC, CG, GD, DH, HA; il est évident que le prisme restant qui a pour base le polygone AEBFCGDH et qui a la même hauteur que le cylindre sera plus grand que le triple du cône ; mais le prisme qui a pour base le polygone AEBFCGDH et qui a la même hauteur que le cylindre, est triple de la pyramide qui a pour base le polygone AEBFCGDH et qui a le même sommet que le cône (prop. 7. 12): donc la pyramide qui a pour base le polygone AEBFCGDH et qui a le même sommet que le cône est plus grande que le cône qui a pour base le cercle ABCD ; mais au contraire la pyramide est plus petite, car le cône comprend la pyramide ; ce qui est impossible : donc le cylindre n'est pas plus grand que le triple du cône.

Je dis à présent que le cylindre n'est pas plus petit que le triple du cône ; car s'il pouvait arriver que le cylindre fût moindre que le triple du cône, le cône serait plus grand que la troisième partie du cylindre. Dans le cercle ABCD décrivons le carré ABCD; le carré ABCD sera plus grand que la moitié du cercle ABCD. Sur le carré ABCD élevez une pyramide qui ait le même sommet que le cône, cette pyramide sera plus grande que la moitié du cône ; parce que si nous circonscrivons un carré au cercle ABCD, le carré ABCD sera la moitié du carré circonscrit à ce cercle, ainsi que nous l'avons démontré ; et si sur ces carrés nous élevons des parallélépipèdes, c'est-à-dire des prismes, celui qui sera élevé sur le carré inscrit dans le cercle sera la moitié du prisme élevé sur le carré circonscrit, car ces parallélépipèdes sont entre eux comme leurs bases (prop. 32. 11); mais leurs troisièmes parties sont aussi entre elles comme leurs bases : donc la pyramide qui a pour base le carré ABCD est la moitié de la pyramide qui a pour base le carré circonscrit au cercle. Mais la pyramide élevée sur le carré circonscrit au cercle est plus grande que le cône, car elle le comprend : donc la pyramide qui a pour base le carré ABCD et qui a le même sommet que le cône est plus grand que la moitié du cône. Partagez les arcs AB, BG, CD, DA eu deux parties égales aux points E, F, G, H, et menez les droites AE, EB, BF, FC, CG, GD, DH, HA. Chacun des triangles AEB, BFC, CGD, DHA sera plus grand que la moitié dû segment respectif du cercle ABCD; sur chacun des triangles AEB, BFC, CGD, DHA élevez des pyramides qui aient le même sommet que le cône; chacune de ces pyramides sera plus grande que la moitié du segment respectif du cône. Partageons les arcs restants en deux_; parties égales, et joignons leurs extrémités par des droites; sur chacun dé: ces triangles élevons, une pyramide qui ait le: même sommet que le cône et continuons de faire la même chose; il restera enfin certaines portions: de cône qui, seront moindres que l'excès du cône sur la troisième partie du cylindre (prop. 1. 10). Qu'on ait ces portions restantes du cône, et qu'elles soient celles qui ont pour bases les segments AE, EB, BF, FC, CG, GD, DH, HA. La pyramide restante qui a pour base le polygone AEBFCGDH et qui a le même sommet que le cône est plus grande que la troisième partie du cylindre. Mais la pyramide qui a pour base le polygone AEBFCGDH et qui a le même sommet que le cône, est la troisième partie du prisme qui a pour base le polygone AEBFCGDH et qui a la même hauteur que le cylindre (pr. 7. 12) : donc le prisme qui a pour base le polygone AEBFCGDH et qui a la même hauteur que le cylindre est plus grand que le cylindre qui a pour base le cercle ABCD; mais le prisme est au contraire plus petit que le cylindre, car le cylindre comprend ce prisme ; ce qui est impossible : donc le cylindre n'est pas plus petit que le triple du cône; mais on a démontré qu'il n'est pas plus grand que le triple : donc le cylindre est le triple du cône et par conséquent le cône est la troisième partie du cylindre.

Donc un cône est la troisième partie d'un cylindre qui a la même base et une hauteur égale, ce qu'il fallait démontrer.

PROPOSITION XI.

THÉORÈME.

Les cônes et les cylindres qui ont la même hauteur sont entre eux comme leurs bases.

Que les cônes et les cylindres dont les bases sont les cercles ABCD, EFGH (fig. 214), dont les axes sont les droites KL, MN, et dont les diamètres des bases sont les droites AC, EG aient la même hauteur : je dis que le cercle ABCD sera au cercle EFGH comme le cône AL est au cône EN.

Car si cela n'est point, le cercle ABCD est au cercle EFGH comme le cône AL sera à un solide quelconque plus petit ou plus grand que le cône EN. Que le cercle ABCD soit d'abord au cercle EFGH comme le cône AL est au solide plus petit que le cône EN ; que ce solide soit O, et que l'excès du cône EN sur le solide O soit égal au solide Z, le cône EN sera égal aux solides O, Z. Dans le cercle EFGH décrivons le carré EFGH ; ce carré sera plus grand que la moitié de ce cercle. Sur le carré EFGH élevons une pyramide qui ait la même hauteur que le cône. Cette pyramide sera plus grande que la moitié du cône ; car si nous décrivons un carré autour du cercle EFGH, et si sur ce carré nous élevons une pyramide qui ait la même hauteur que le cône, la pyramide inscrite, sera la moitié de la pyramide circonscrite, parce que ces pyramides sont comme leurs hases (prop. 6. 13); mais le cône est plus petit que la pyramide circonscrite : donc la pyramide qui a pour hase le carré EFGH et qui a le même sommet que le cône est plus grande que la moitié du cône. Partageons les arcs EF, FG, GH, HE en deux parties égales aux points P, Q, R, S, et menons les droites HP, PE, EQ, QF, FR, RG, GS, SH; chacun des triangles HPE, EQF, FRG, GSH sera plus grand que la moitié du segment respectif du cercle. Sur chacun des triangles HPE, EQF, FRG, GSH élevons une pyramide qui ait la même hauteur que le cône ; chacune de ces pyramides sera plus grande que la moitié du segment respectif du cône. Si donc nous, partageons en deux parties égalas les arcs, restant et si nous joignons les extrémités de ces arcs par des droites, et si sur chacun des triangles nous élevons des pyramides qui aient la même hauteur que le cône, et si nous continuons de faire la même chose, il restera enfin certains segments du cône qui seront plus petits que le solide Z (pr. 1. 10). Supposons que l'on ait ces segments et que ces segments soient ceux qui ont pour bases les segments circulaires HP, PE, EQ, QF, FR, RG, GS, SH. La pyramide restante qui a pour base le polygone HPEQFRGS et qui a la même hauteur que le cône sera plus grande que le solide O. Dans le cercle ABCD décrivons un polygone DTAVBXCY qui soit semblable au polygone HPEQFRGS et semblablement placé, et sur le polygone DTAVBXCY élevons une pyramide qui ait la même hauteur que le cône AL. Puisque le carré de AC est au carré de EG comme le polygone DTAVBXCY est au polygone HPEQFRGS (pr. 20. 6, pr. 1. 12), et que le carré de AC est au carré de EG comme le corde ABGD est au cercle EFGH (pr. 2. 12), le cercle ABCD sera au cercle EFGH comme le polygone DTAVBXCY est au polygone HPEQFRGS (prop. 11. 5). Mais par supposition le cercle ABCD est au cercle EFGH comme le cône AL est au solide O, et le polygone DTAVBXCY est au polygone HPEQFRGS comme la pyramide qui a pour base 'le polygone DTAVBXGY et pour sommet le point L est à la pyramide qui a pour base le polygone HPEQFRGS et pour sommet le point N (prop. 6. 12) : donc le cône AL est au solide O comme la pyramide qui a pour basé le polygone DTAVBXCY et pour sommet le point L est à la pyramide qui a pour base le polygone HPEQFRGS et pour sommet le point N : donc en échangeant les plans des moyens, le cône AL est à la pyramide qui lui est inscrite comme le solide O est à la pyramide inscrite dans le^; cône EN. Mais le cône AL est plus grand que la pyramide qui lui est inscrite : donc le solide O est plus grand que la pyramide qui est inscrite dans le cône EN ; mais le solide O est ad contraire plus petit que la pyramide inscrite dans le cône EN, ce qui est une absurdité : donc le cercle ABCD n'est point au cercle EFGH comme le cône AL est à un solide quelconque plus petit que le cône EN. On démontrera semblablement que le cercle EFGH n'est point au cercle ABCD comme le cône EN est à un solide quelconque plus petit que le cône AL.

Je dis à présent que le cercle ABCD n'est point au cercle EFGH comme le cône AL est à un solide quelconque plus grand que le cône EN.

Supposons que cela soit possible et que le cercle ABCD soit au cercle EFGH comme le cône AL est à un solide plus grand que le cône EN et que ce solide soit O. Mettons les conséquents à la place des antécédents et les antécédents à la place des conséquents, le cercle EFGH sera au cercle ABCD comme le solide O est au cône AL. Mais le solide O est au cône AL comme le cône EN est à un solide quelconque plus petit que le cône AL ; donc le cercle EFGH est au cercle ABCD comme le cône EN est à un solide plus petit que le cône AL ; ce que nous avons démontré impossible : donc le cercle ABCD n'est point au cercle EFGH comme le cône AL est à un solide quelconque plus grand que le cône EN. Mais on a démontré que le cercle ABCD n'est point au cercle EFGH comme le cône AL est à un solide plus petit que le cône EN : donc le cercle ABCD est au cercle EFGH comme le cône AL est au cône EN. Mais un cône est à un cône comme un cylindre est à un cylindre, car un cylindre est le triple d'un cône (prop. 10. 12) : donc les cercles ABCD, EFGH sont entre eux comme les cylindres qui ont ces cercles pour bases et qui ont des hauteurs égales à celles des cônes.

Donc les cônes et les cylindres qui ont la mettre hauteur sont entre eux comme leurs bases, ce qu'il fallait démontrer.

PROPOSITION XII.

THÉORÈME.

Les cônes et cylindres semblables sont entre eux en raison triplée des diamètres de leurs bases.

Que les cônes et les cylindres qui ont pour bases les cercles ABCD, EFGH (fig. 215), pour diamètres de leurs bases les droites BD, FH et pour axes les droites KL, MN soient semblables entre eux : je dis que le cône qui a pour base le cercle ABCD et pour sommet le point L, est au cône qui a pour base le cercle EFGH et pour sommet le point N en raison triplée de BE à FH.

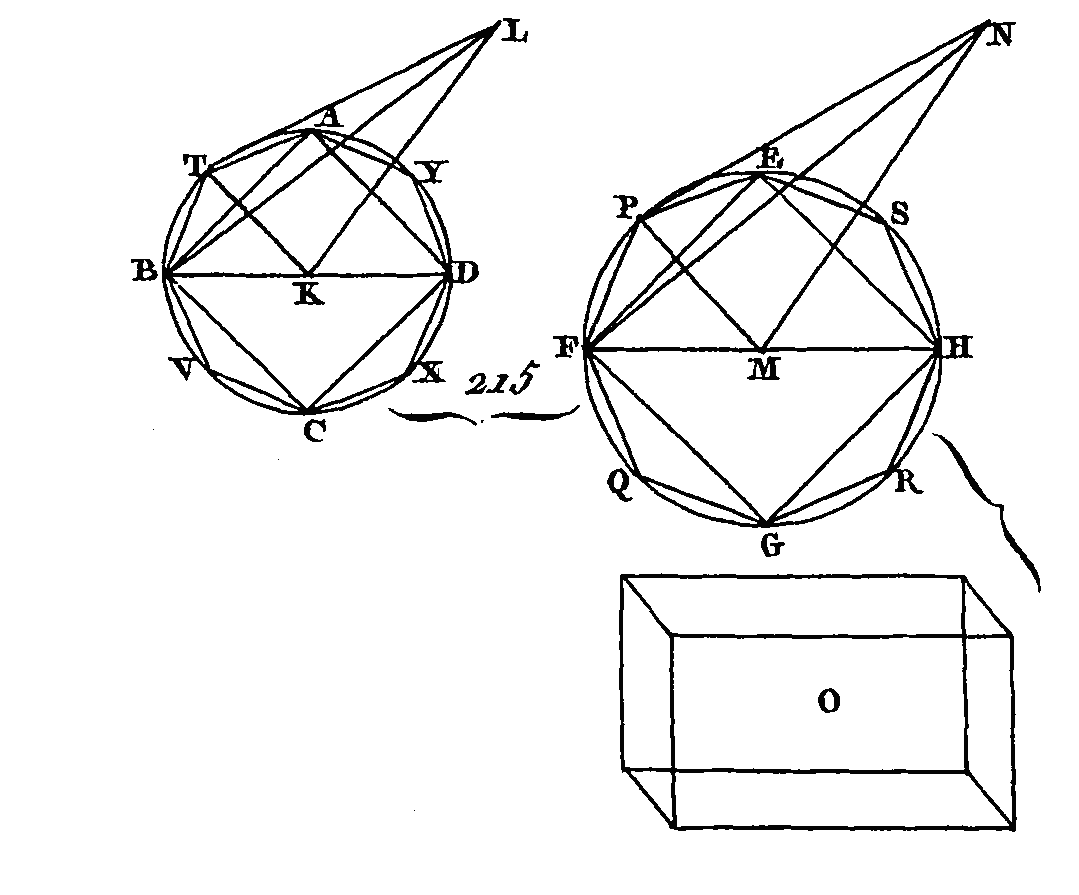
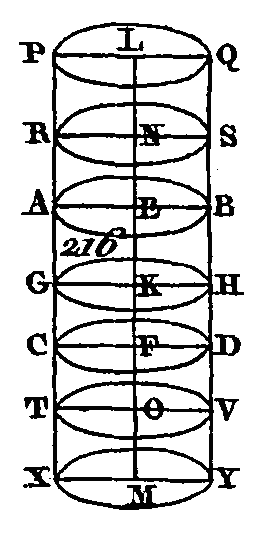
Car si le cône ABCDL n'est point au cône EFGHN eu raison triplée du diamètre BD au diamètre FH, le cône ABCDL sera à un solide quelconque plus grand ou plus petit que le cône EFGHN en raison triplée du diamètre BD au diamètre FH. Supposons d'abord que le cône ABCDL soit à un solide O plus petit, que le cône EFGHN en raison triplée du diamètre AD au diamètre FH; dans le cercle EFGH décrivons le carré EFGH; le carré EFGH sera plus petit que la moitié du cercle EFGH. Ensuite sur le carré EFGH élevez une pyramide qui ait la même hauteur que le cône ; cette pyramide sera plus grande que la moitié du cône. Partager les arcs EF, FG, GH, HE en deux parties égales aux points P, Q, R, S, et menez les droites EP, PF, FQ, QG, GR, RH, HS, SE ; chacun des triangles EPF, FQG, GRH, HSE sera plus grand que la moitié du segment respectif du cercle EFGH. Sur chacun de ces triangles, élevez des pyramides qui aient le même sommet que le cône; chacun de ces pyramides sera plus grande que la moitié du segment respectif du cône. Si nous partageons les arcs restants en deux parties égales, si nous joignons les extrémités de ces arcs par des droites et si nous élevons sur chacun de ces triangles des pyramides qui aient le même sommet que le cône et si nous continuons de faire la même chose,  il restera enfin certains segments de cône qui seront plus petits que l'excès du cône EFGHN sur le solide O (prop. 1. 10). Supposons que l'on ait ces segments, que ces segments soient ceux qui sont élevés sur les segments circulaires EP, PF, FQ, QG, GR, RH, HS, SE, la pyramide restante qui a pour base le polygone EPFQGRHS et pour sommet le point N sera plus grande que le solide O ; dans le cercle ABCD décrivez un polygone ATBVCXDY qui soit semblable au polygone EPFQGRHS et semblablement placé. Sur le polygone ATBVCXDY élevez une pyramide qui ait le même sommet que le cône; que LBT soit un des triangles qui comprennent la pyramide dont la base est le polygone ATBVCXDY et dont le sommet est le point L, que NFP soit un des triangles qui comprennent la pyramide dont la base est le polygone EPFQGRHS et dont le sommet est le point N, et enfin menez les droites KT, MP. Puisque le cône ABCDL est semblable au cône EFGHN, la droite BD sera à la droite FH comme l'axe KL est à l'axe MN (déf. 24. 11) ; mais BD est à FH comme BK est à FM: donc BK est à FM comme KL est à MN : donc en échangeant les plans des moyens, B K sera à KL comme FM est à MN. Mais les angles BKL, FMN sont égaux parce qu'ils sont droits, et ces angles égaux sont compris par des côtés proportionnels : donc le triangle BKL est semblable au triangle FMN (prop. 6. 6). De plus, puisque la droite BK est à la droite KT comme la droite FM est à la droite MP et que ces droites comprennent les angles égaux BKT, FMP, car la portion des quatre angles droits placés au centre H que comprend l’angle BKT est la même portion des quatre angles droits placés au centre M que comprend l'angle FMP : donc puisque les côtés qui comprennent les angles égaux BKC, FMP sont proportionnels, le triangle BKT est semblable au triangle FMP (prop. 6. 6). De plus, puisqu'on a démontré que BK est à KL comme FM est à MN, et à cause que BK est égal à KT et FM égal à MP, la droite KT sera à la droite KL comme PM est à MN. Mais les côtés qui comprennent les angles droits TKL, PMN sont proportionnels : donc le triangle LKT est semblable au triangle JNMP. Mais à cause de la similitude des triangles BKL, FMN la droite LB est à la droite BK comme la droite NF est à la droite FM, et à cause de la similitude des triangles BKT, FMP la droite KB est à la droite BT comme la droite MF est à la droite FP: donc la droite LB est à la droite BT comme la droite NF est à la droite FP (prop. 22. 5). De plus, à cause de la similitude des triangles LTK, NPM la droite LT est à la droite TK comme la droite NP est à la droite PM, et à cause de la similitude des triangles KBT, PMF la droite KT est à la droite TB comme la droite MP est à la droite PF : donc la droite LT sera à la droite TB comme la droite NP est à la droite PF. Mais on a démontré que TB est à BL comme PF est à FN : donc TL est à LB comme PN est à NF: donc les côtés des triangles LTB, NPF sont proportionnels : donc les triangles LTB, NPF sont équiangles et par conséquent semblables entre eux (prop. 5. 6) : donc la pyramide qui a pour base le triangle BKT et pour sommet le point L est semblable à la pyramide qui a pour case le triangle FMP et pour sommet le point N (déf. 9. 11); car ces deux pyramides sont comprises sous des plans semblables et égaux .en nombre ; mais les pyramides semblables qui ont des bases triangulaires sont entre elles eu raison -triplée de leurs côtés homologues (prop. 8. 12): donc les pyramides BKTL, FMPN sont entre elles en raison triplée des droites BK, FM. Si, nous menons des droites des points A, Y, D, X, C, V au point K et des points E, S, H, R, G, Q au point M, et si sur les triangles que ces droites forment avec les côtés des polygones inscrits nous élevons des pyramides qui aient les mêmes sommets que le cône, nous démontrerons semblablement que chaque pyramide du polygone ATBVCXDY est à chaque pyramide <lu polygone EPFQGRHS en raison triplée du côté BK au côté homologue F M, c'est-à-dire du diamètre BD au diamètre F H. Mais un seul des antécédents est à un seul des conséquents comme tous les antécédents sont à tous les conséquents (prop. 12. 5): donc la pyramide BKÏL est à la pyramide FMPN comme la pyramide totale qui a pour base le polygone ATBVCXDY et pour sommet le point L est à la pyramide totale qui a pour base le polygone EPFQGRHS et pour sommet le point N : donc la pyramide qui a pour base le polygone ATBVXDY et pour sommet le point L est à la pyramide qui a pour base le polygone EPFQGRHS en raison triplée du diamètre BD au diamètre FH. Mais on a supposé que le cône qui a pour base le cercle ABCD et pour sommet le point L est au solide O en raison triplée de BD à FH : donc le cône qui a pour base le cercle ABCD et pour sommet le point L est au solide O comme la pyramide qui a pour base le polygone ATBVCXDY et pour sommet le point L est à la pyramide qui a pour base le polygone EPFQGRHS et pour sommet le point N : donc, en échangeant les places des moyens (prop. 16. 5), le cône qui a pour base le cercle ABCD et pour sommet le point L est à la pyramide qui a pour base le polygone ATBVCXDY et pour sommet le point N comme le solide O est à la pyramide qui a pour base le polygone EPFQGRHS et pour sommet le point N. Mais le cône qui a pour base le cercle ABCD et pour sommet le point L est plus grand que la pyramide inscrite; car le cône la comprend : donc le solide Q est plus grand que la pyramide qui a pour base le polygone EPFQGRHS et pour sommet le point N ; mais au contraire ce solide est plus petit que cette pyramide ; ce qui est impossible :, donc le cône qui a pour base le cercle ABCD et pour sommet le point L n'est point à un solide quelconque plus petit que le cône qui a pour base le cercle EFGH et pour sommet le point N en raison triplée de BD à FH. Nous démontrerons semblablement que le cône EFGHN n'est point à un solide quelconque plus petit que le cône ABCDL en raison triplée de FH à BD. Je dis enfin que le cône ABCDH n'est point à un solide quelconque plus grand que le cône EFGHN en raison triplée de BD à FH ; car s’il peut arriver que le cône ABCDL, soit à un solide O plus grand que le cône EFGHN en raison triplée de BD à FH, en mettant les conséquents à la place des antécédents et les antécédents à la place ses conséquents, le solide O sera au cône ABCDL en raison triplée de FH à BD. Mais le solide O est au cône ABCDL comme le cône EFGHN est à un solide plus petit que le cône ABCDL: donc le cône EFGHN est à un solide quelconque plus petit que le cône ABCDL en raison triplée de FH à BD, ce qui a été démontré impossible : donc le cône ABCDL n'est point à on solide quelconque plus grand que le cône EFGHN en raison triplée de BD à FH. Mais on a démontré que le cône ABCDL n'est point à un solide quelconque plus petit que le cône EFGHN en raison triplée de BD à FH : donc le cône ABCDL est au cône EFGHN en raison triplée de BD à FH ; mais un cône est à un autre cône comme un cylindre est à un autre cylindre ; car un cylindre qui a la même base qu'un cône et une hauteur égale est triple de ce cône, puisqu'on a démontré qu'un cône est la troisième partie du cylindre qui a la même base et une hauteur égale (prop. 11. 12): donc ces cylindres semblables sont entre eux en raison triplée des droites BD, F H.

Donc les cônes et les cylindres semblables sont entre eux en raison triplée des diamètres des bases, ce qu'il fallait démontrer.

PROPOSITION XIII.

THÉORÈME.

Si un cylindre est coupé par un plan parallèle aux plans opposés, l'un de ces cylindres sera à l’autre cylindre comme l'axe du premier est à l'axe du second.

Que le cylindre AD (fig. 216) soit coupé par un plan GH parallèle aux plans opposés AB, CD, et que ce plan rencontre l'axe EF, au point K : je dis que le cylindre BG est au cylindre GD comme l'axe EK est à l'axe KF.

Prolongez de part et d'autre l'axe EF vers les points L, M, et prenez autant de droites que vous voudrez EN, NL égales chacune à l'axe EK ; prenez aussi autant de droites, que vous voudrez FO, OM égales chacune à l'axe FK ; par les points L, N, O, M conduisez des plans parallèles aux plans AB, CD, et dans les plans qui passent par les points L, N, O, M et autour des centres L, N, O, M imaginez des cercles PQ, RS, TV, XY égaux aux cerclés AB, CD; imaginez ensuite les cylindres QR, RB, DT, TY. Puisque les axes LN, NE, EK sont égaux entre eux, les cylindres QR, RB, BG seront entre eux comme leurs bases  (prop. 11. 12) ; mais les bases sont égales : donc les cylindres QR, RB, BG sont égaux entre eux. Puisque les axes LN, NE, EK sont égaux entre eux, que les cylindres QR, RB, BG sont aussi égaux entre eux et que le nombre des axes LN, NF, EK est égal au nombre des cylindres QR, RB, BG, l'axe KL sera multiple de l'axe EK autant de fois que le cylindre QG est multiple du cylindre GB ; par la même raison, l'axe MK est multiple de l’axe KF autant de fois que le cylindre YG est multiple du cylindre GD. Si l'axe KL est égal à l'axe KM, le cylindre QG sera égal au cylindre GY ; si l'axe KL est plus grand que l'axe KM, le cylindre QG sera plus grand que le cylindre GY, et si l'axe KL est plus petit que l'axe KM, le cylindre QG sera plus petit que le^; cylindre GY. On a donc quatre quantités, savoir les axes EK, KF et les cylindres BG, GD et l’on a pris des équimultiples de l'axe EK et du cylindre BG savoir, l'axe KM et le cylindre QG; on a pris aussi des équimultiples de l’axe KF et du cylindre GD, savoir, l'axe KM et le cylindre GY; on a démontré aussi que si l'axe KL surpasse l'axe KM, le cylindre QG surpassera le cylindre GY, que si l'axe KL est égal à l'axe KM, le cylindre QG sera égal au cylindre GY, et que si l'axe KL est plus petit que l'axe KM, le cylindre KM sera plus petit que le cylindre GY : donc l'axe EK est à l'axe KF comme le cylindre BG est au cylindre GD (déf. 4. 5), ce qu’il fallait démontrer.

PROPOSITION XIV.

THÉORÈME.

Les cônes et les cylindres qui ont des bases égales sont entre eux comme leurs hauteurs.

Que les cylindres FD, EB (fig. 217) aient des bases égales AB, CD : je dis que le cylindre EB est au cylindre FD comme l'axe GH est à l’axe KL.

Prolongez l'axe KL vers le point N, faites LN égal à l'axe GH et autour de l'axe LN imaginez le cylindre CM. Puisque les cylindres EB, CM ont la même hauteur, ces cylindres sont entre eux comme leurs bases (prop. 11. 12) ; mais leurs bases sont égales : donc les cylindres EB, CM seront égaux entre eux. Mais puisque le cylindre FM est coupé par le plan CD parallèle aux plans opposés, le cylindre CM sera au cylindre FD comme l'axe LN est à l'axe KL. Mais le cylindre CM est égal au cylindre EB et l'axe LN égal à l'axe GH : donc le cylindre EB est au cylindre FD comme l’axe G H est à l'axe KL (prop. 13. 12); mais le cylindre EB est au cylindre FD comme le cône ABG est au cône CDK, car les cylindres sont triples des cônes (prop. 10.12) : donc l’axe GH est à l'axe KL comme le cône ABG est au cône CDK et comme le cylindre EB est au cylindre FD ; ce qu'il fallait démontrer.

PROPOSITION XV.

THÉORÈME.

Les bases des cônes ou des cylindres égaux sont réciproquement proportionnelles aux hauteurs de cônes de ces cylindres ; et lorsque les bases des cônes ou des cylindres sont réciproquement proportionnelles aux hauteurs, les cônes ou les cylindres sont égaux entre eux.

Que les cônes et les cylindres dont les bases sont les cercles ABCD, EFGH (fig. 218), dont les diamètres des bases sont les droites AC, EG et dont les axes sont les droites KL, MN qui sont en même tems les hauteurs des cônes et des cylindres soient égaux entre eux ; achevez les cylindres AO, EP : je dis que les bases de ces cylindres AO, EP sont réciproquement proportionnelles aux hauteurs; c'est-à-dire que la base ABCD est à la base EFGH comme la hauteur MN est à la hauteur KL.

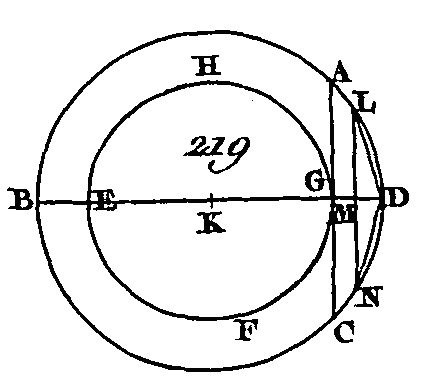
La hauteur KL est égale à la hauteur MN où elle lui est inégale ; qu'elle lui soit d'abord égale. Puisque le cylindre AO est égal au cylindre EP et que les cônes ou les cylindres qui ont la même hauteur sont entre eux comme leurs bases (prop. 11. 12), la base ABGD sera égale à la base EFGH : donc les bases sont réciproquement proportionnelles aux hauteurs, c'est-à-dire que ABCD est à EFGH comme la hauteur MN est à la hauteur KL. Supposons à présent que la hauteur KL ne soit point égale à la hauteur MN et que la hauteur MN soit la plus grande. De la hauteur MN retranchez la droite QM égale à la droite KL et par le point Q coupez le cylindre EP par le plan STV parallèle aux cercles opposés EFGH, RPX, et imaginez un cylindre ES dont la base soit le cercle EFGH et la hauteur l'axe QM. Puisque par supposition le cylindre AO est égal au cylindre EP et que ES est un autre cylindre, le cylindre AO sera au cylindre ES comme le cylindre EP est au cylindre ES (prop. 7. 5). Mais le cylindre AO est au cylindre ES comme la base ABCD est à la base EFGH (prop. 11. 12), car les cylindres AO, ES ont la même hauteur; mais le cylindre EP est au cylindre ES comme la hauteur MN est à la hauteur MQ (prop. 13. 12), car le cylindre EP est coupé par le plan TVS parallèle aux plans opposés ; mais la base ABCD est à la base EFGH comme la hauteur MN est à la hauteur MQ, et la hauteur MQ est égale à la hauteur KL : donc la base ABCD est à la base EFGH comme la hauteur MN est à la hauteur KL : donc les bases des cylindres AO, EP sont réciproquement proportionnelles aux hauteurs de ces cylindres.

A présent que les bases des cylindres AO, EP soient réciproquement proportionnelles aux hauteurs de ces cylindres, c'est-à-dire que la base ABCD soit à la base EFGH comme la hauteur MN est à la hauteur KL : je dis que le cylindre AO est égal au cylindre EP.

Faites la même construction. Puisque la base ABCD est à la base EFGH comme la hauteur MN: est à la hauteur KL et puisque la hauteur KL est égale à la hauteur MQ, la base ABCD sera à la base EFGH comme la hauteur MN est à la hauteur MQ; mais la base ABCD est à la base EFGH comme le cylindre AO est au cylindre ES (prop. 11. 12), car ils ont la même hauteur, et la hauteur MN est à la hauteur MQ comme le cylindre EP est au cylindre ES  (prop. 13. 12) : donc le cylindre AO est au cylindre ES comme le cylindre EP est au cylindre ES : donc le cylindre AO est égal au cylindre EP (prop. 9. 5) : la démonstration sera la même pour les cônes;, ce qu'il fallait démontrer.

PROPOSITION XVI.

PROBLÈME.

Deux cercles concentriques étant donnés, décrire dans le plus grand un polygone dont les côtés soient égaux et pairs en nombre et qui ne touche point le plus petit cercle.

Soient les deux cercles ABCD, EFGH (fig. 219) ayant le même centre K : il faut dans le plus grand cercle ABCD décrire un polygone dont les côtés soient égaux et pairs en nombre et qui ne touche point le plus petit cercle EFGH.

Par le centre K menez la droite BD ; par le point G menez la droite AG perpendiculaire sur BD et prolongez cette droite vers le point C. La droite AC touchera le cercle EFGH (prop. 16. 3). Partagez la demi-circonférence BAD en deux parties égales et sa moitié en deux parties égales, et ainsi de suite jusqu'à ce qu'il reste un arc plus petit que l'arc AD (prop. 1. 10). Qu'on ait cet arc et que cet arc soit LD ; par le point L conduisez sur BD la perpendiculaire LM ; prolongez celte perpendiculaire vers le point N et menez les droites LD, DN ; la droite LD sera égale à la droite DN; et puisque la droite LN est parallèle à la droite AC et que la droite AC touche le cercle EFGH, la droite LN ne touchera point le cercle EFGH, à plus forte raison les droites LD, DN ne toucheront point ce même cercle : donc si l'on applique à la circonférence ABCD, à la suite les unes des autres, des droites égales à la droite LD (prop. 1. 4), on décrira un polygone dont les côtés seront égaux et pairs en nombre et qui ne touchera point le cercle EFGH ; ce qu'il fallait faire.

PROPOSITION XVII.

PROBLÈME.

Deux sphères concentriques étant données, décrire dans la plus grande un polyèdre dont les faces ne touchent point la surface de la plus petite.

Imaginez deux sphères qui aient le même centre A (fig. 220) : il faut dans la plus grande sphère décrire un polyèdre dont les faces ne touchent point la surface de la plus petite.

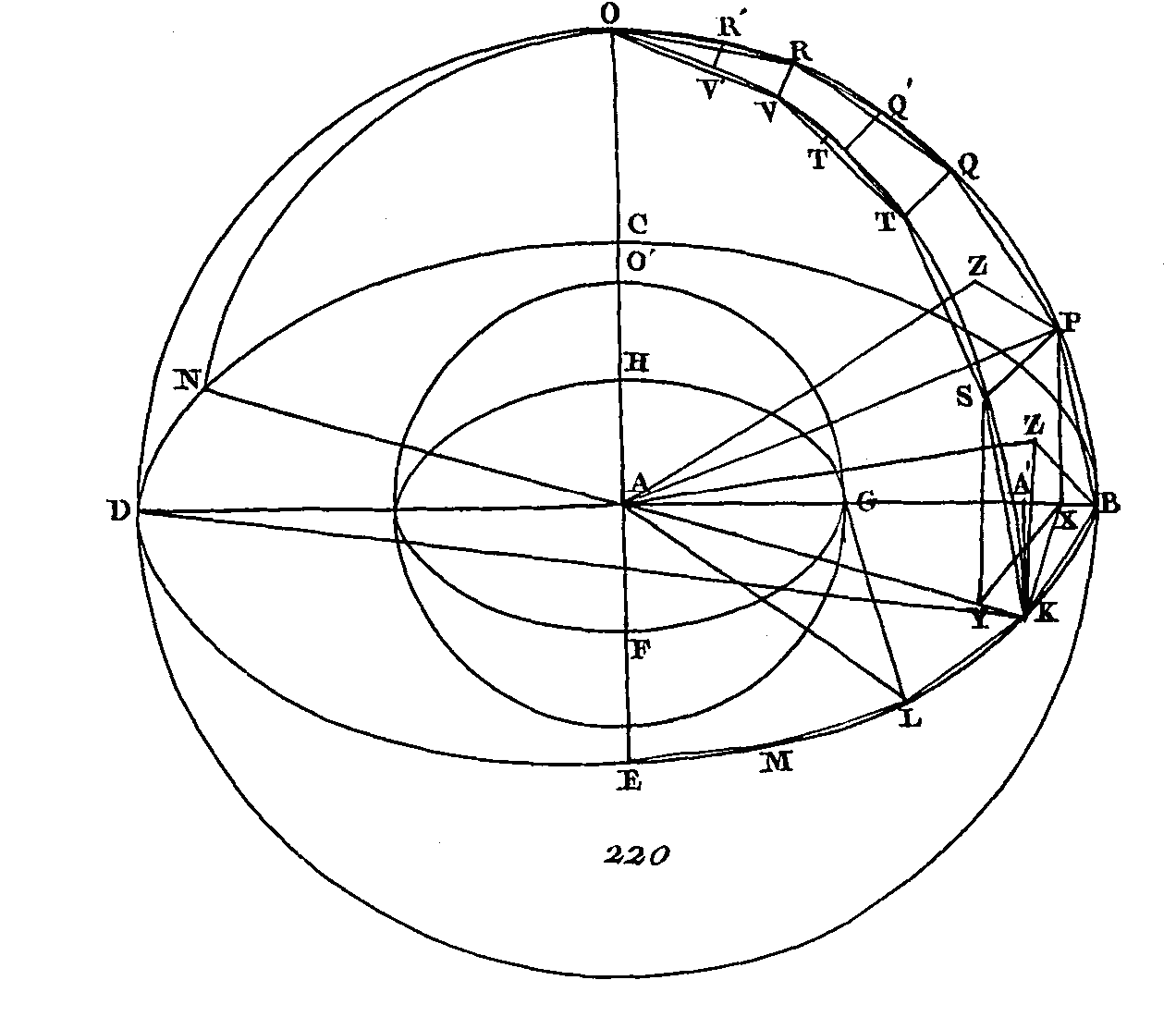
Faites passer un plan quelconque par le centre de ces sphères, les sections seront des cercles, parce qu'une sphère étant engendrée par tin demi-cercle qui tourne autour de son diamètre immobile (déf. 14. 11)_} dans quelque position que nous concevions ce demi-cercle, le plan prolongé de ce demi-cercle produira nécessairement une circonférence de cercle sur la surface de la sphère ; et il est évident que cette circonférence sera celle, d'un grand cercle, parce que le diamètre de la sphère, qui est aussi celui du demi-cercle, est la plus grande de toutes les droites menées dans le cercle ou dans la sphère (prop. 15. 5). Supposons en conséquence que BCDE soit un cercle de la plus grande sphère et que FGH soit un cercle de la plus petite ; menez leurs diamètres BD, CE de manière qu'ils soient perpendiculaires l'un sur l'autre. Les deux cercles BCDE, FGH ayant le même centre décrivez dans le plus grand BCDE un polygone dont les côtés soient égaux et pairs en nombre et qui rie touche point le plus petit cercle FGH (prop. 16. 12); que les côtés de ce polygone qui sont dans le quart de cercle BE soient BK, KL, LM, ME ; menez la droite KA que vous prolongerez vers N ; au point A et sur le plan du cercle BCDE élevez la perpendiculaire A 0 qui rencontre la surface de la sphère au point O, et par la droite AO et par chacune des droites BD, KN conduisez deux plans qui, d'après ce que nous avons dit, produiront deux grands cercles dans la surface de la sphère. Supposons qu'on ait ces deux grands cercles et que BOD, KON en soient les moitiés, et que BD, KN en soient les diamètres. Puisque la droite OA est perpendiculaire sur le plan du cercle BCDE, tous les plans qui passeront par cette droite AO seront perpendiculaires sur le plan du cercle BCDE (prop. 18. 11) : donc les demi-cercles BOD, KON sont perpendiculaires sur ce même plan ; et puisque les demi-cercles BED, BOD, KON sont égaux, car leurs diamètres EC, BD, KN sont égaux entre eux, les quarts de leurs circonférences BE, BO, KO seront égaux entre eux : donc les quarts de cercle BO, KO contiendront chacun autant de côtés du polygone inscrit que le quart de cercle BE, et les côtés contenus dans les quarts de cercles BO, KO seront égaux aux côtés BK, KL, LM, ME, chacun à chacun. Menez les côtés BP, PQ, QR, RO, KS, ST, TV, VO et conduisez les droites SP, TQ, VR, et des points P, S abaissez des perpendiculaires sur le plan du cercle BCDE; ces perpendiculaires tomberont sur les communes sections BD, KN des plans des demi-cercles BOD, KON (prop. 38, 11), puisque ces plans sont perpendiculaires sur le plan du cercle BCDE, par construction; que ces perpendiculaires tombent donc sur ces communes sections et que ces perpendiculaires soient PX, SY ; menez la droite XY. Puisqu'on a pris les arcs égaux BP, KS dans les demi-circonférences égales BOD, KON et qu'on a mené les perpendiculaires PX, SY, la droite PX sera égale à la droite SY et la droite BX égale à la droite KY. Mais la droite totale BA est égale à la droite totale KA : donc la droite restante XA est égale à la droite restante YA : donc BX est à XA comme KY est à YA : donc la droite XY est parallèle à la droite KB (prop. 2. 6); et puisque chacune des droites PX, SY est perpendiculaire sur le plan du cercle BCDE, la droite PX sera parallèle à la droite SY (prop. 6. 11); mais on a démontré que ces droites sont égales : donc les droites YX, SP sont égales et parallèles (pr. 33. 11) ; et puisque la droite YX est parallèle à la droite SP et à la droite KB, la droite SP sera parallèle à la droite KB (prop. 9. 11); mais ces droites sont jointes par les droites BP, KS : donc le quadrilatère KBPS est dans un seul plan, car si deux droites sont parallèles et si dans chacune de ces droites on prend des points quelconques, les droites qui joignent ces points sont dans le même plan que ces parallèles (prop. 7. 11). Par la même raison l'un et l'autre des quadrilatères SPQT, TQRV sont dans un seul plan; mais le triangle VRO est aussi dans un seul plan (prop. 2. 11) : donc si des points P, S, Q, T, R, V on conçoit des droites menées au point A, on aura construit entre les arcs BO, KO un certain polyèdre composé des pyramides dont les hases seront les quadrilatères KBPS, SPQT, TQRV, et le triangle VRO et dont le sommet commun sera le point A. Si sur chacun des côtés KL, LM, ME nous faisons la même construction que nous avons faites sur le côté KB, si nous faisons ensuite la même chose dans les autres quarts de cercle et dans l'autre hémisphère, nous aurons inscrit dans la sphère un certain polyèdre qui sera composé des pyramides dont les hases sont les quadrilatères KBPS, SPQT, TQRV et le triangle VRO, elles quadrilatères et les triangles correspondais à ces quadrilatères et à ce triangle et dont le sommet commun sera le point A.

Je dis à présent que ce polyèdre ne touche point la surface de la petite sphère dans laquelle est le cercle FGH. Du point A menez la droite AZ perpendiculaire sur le plan du quadrilatère KBPS (prop. 11. 11), que cette perpendiculaire rencontre ce plan au point Z et menez les droites BZ, ZK. Puisque AZ est perpendiculaire sur le plan du quadrilatère KBPS, elle sera perpendiculaire sur toutes les droites, qui la rencontrent et qui sont dans ce plan (déf. 3. 11) : donc AZ est perpendiculaire sur l'une et l'autre des droites BZ, ZK; mais puisque AB est égal à AK, le carré de AB sera égal au carré de AK; mais les carrés des droites AZ, ZB sont égaux au carré de AB (prop. 47. 1), car l'angle en Z est droit par construction, et les carrés de AZ, ZK sont égaux au carré de AK : donc les carrés des droites AZ, ZB sont égaux aux carrés des droites AZ, ZK. Retranchant le carré de AZ qui est commun, le carré de BZ sera égal au carré de ZK : donc la droite BZ est égale à la droite ZK. On démontrera semblablement que les droites menées du point Z aux points P, S sont égales chacune à l'une et à l'autre clés droites BZ, ZK : donc le cercle décrit du centre Z et avec un intervalle égal à une des droites ZB, ZK passera aussi par les points P, S : donc le quadrilatère KB PS sera inscrit dans un cercle ; et puisque la droite KB est plus grande que la droite YX et que la droite YX est égale à la droite SP, la droite KB sera plus grande que la droite SP. Mais la droite KB est égale à l'une et à l'autre des droites KS, BP : donc l'une et l'autre des droites KS, BP sont plus grandes que la droite SP. Puisque le quadrilatère KBPS est décrit dans un cercle et que les droites KB, BP, KS sont égales, que la droite PS est plus petite et que la droite BZ est menée; du centre du cercle, le carré de KB sera, plus grand que le double du carré de BZ. Du point K menez la droite KA' perpendiculaire sur BD. Puisque la droite BD est plus petite que le double de DA' et que DB est à DA' comme le rectangle compris sous DB, BA' est au rectangle compris sous DA', A'B (prop. 1. 6), si l'on décrit un carré sur BA' et si sur A'D on complète le parallélogramme compris sous A'D, A'B, le rectangle compris sous DB, BA' sera plus petit que le double de celui qui est compris sous DA', A'B. Menez la droite KD. Le parallélogramme compris sous DB, BA' égal au carré de KB (prop. 8. 6), et le parallélogramme compris sous DA', A'B égal au carré de KA' : donc le carré de KB est plus petit que le double du carré de KA' ; mais le carré de KB est plus grand que le double du carré de BZ : donc le carré de KA' est plus grand que le carré de BZ ; et puisque BA est égal à KA, le carré de BA sera égal au carré de KA. Mais les carrés des droites BZ, ZA sont égaux au carré de la droite BA (prop. 47. 1), et les carrés des droites KA', A'A égaux au carré de la droite KA : donc les carrés des droites BZ, ZA sont égaux aux carrés des droites KA', A'A ; mais le carré de KA' est plus grand que le carré de BZ : donc le carré de A'A est plus petit que le carré de ZA: donc la droite AZ est plus grande que la droite AA' : donc la droite AZ est à plus forte raison plus grande que la droite A G ; mais la droite AZ est une perpendiculaire sur une des faces du polyèdre et la droite AG est un rayon de la plus petite sphère : donc les faces de ce polyèdre ne touchent point la surface de la plus petite sphère.

AUTREMENT.

Nous allons démontrer autrement et d'une manière plus prompte que la droite AZ est plu» grande que la droite AG. Du point G conduisez une perpendiculaire GL sur AG et menez AL. Puisque si l'on partage en deux parties égales l'arc EB et la moitié de cet arc en deux parties égales et ainsi de suite, il restera enfin un certain arc plus petit que celui de la circonférence du cercle BCD qui est sous-tendu par une droite égale à la droite GL (prop. 1. 10). Qu'on ait cet arc et que cet arc soit KB, la droite KB est plus petite que la droite GL ; mais puisque le quadrilatère BKSP est inscrit dans un cercle et que les droites PB, BK, KS sont égales et que la droite PS est plus petite que chacune de ces droites, l'angle BZK sera obtus : donc la droite BK sera plus grande que la droite BZ; mais la droite GL est plus grande que BK par construction : donc à plus forte raison la droite GL sera plus grande que la droite BZ et par conséquent le carré de GL sera plus grand que le carré de BZ ; mais puisque la droite AL est égale à la droite AB, le carré de AL sera égal au carré de AB ; mais les carrés des droites AG, GL sont égaux au carré de la droite AL et les carrés des droites BZ, ZA sont égaux aux carrés de la droite AB : donc les carrés des droites AG, GL sont égaux aux carrés des droites BZ, ZA ; mais le carré de BZ est plus petit que le carré de GL: donc le carré de ZA est plus grand que le carré de AG : donc la droite AZ est plus grande que la droite AG.

Donc, deux sphères concentriques ayant été données, on a décrit dans la plus grande un polyèdre dont les faces ne touchent pas la surface de la plus petite ; ce qu'il fallait faire.

COROLLAIRE.

Si l'on décrit dans une autre sphère un polyèdre semblable à celui qui est décrit dans la sphère BCDE, le polyèdre décrit dans la sphère BCDE sera au polyèdre qui est décrit dans une autre sphère en raison triplée du diamètre de la sphère BCDE au diamètre de l'autre sphère; car ayant divisé ces polyèdres en pyramides égales en nombre et dans le même ordre, on aura des pyramides semblables. Mais les pyramides semblables sont en raison triplée des côtés homologues (cor. 8. 12) : donc la pyramide qui a pour base le quadrilatère KBPS et pour sommet le point A sera à la pyramide correspondante de l'autre sphère en raison triplée d'un côté de la première au côté homologue de la seconde, c'est-à-dire en raison triplée du rayon AB de la sphère qui a pour centre le point A au rayon de l'autre sphère. Semblablement chacune des pyramides comprises dans la sphère qui a pour centre le point A sera à chacune des pyramides du même ordre comprise dans l'autre sphère en raison triplée du rayon AB au rayon de l'autre sphère. Mais un des antécédents est à un des conséquents comme tous les antécédents sont à tous les conséquents (prop. 12. 5) : donc le polyèdre total compris dans la sphère qui a pour centre le point A est au polyèdre total compris dans l'autre sphère en raison triplée du rayon AB au rayon de l'autre sphère, c'est-à-dire en raison triplée du diamètre AB au diamètre de l'autre sphère ; ce qu'il fallait démontrer.

PROPOSITION XVIII.

THÉORÈME.

Les sphères sont entre elles en raisons triplées de leurs diamètres.

Imaginez les sphères ABC, DEF (fig. 221) dont les diamètres sont les droites BC, EF : je dis que la sphère ABC est à la sphère DEF en raison triplée du diamètre BC au diamètre EF.

Car si cela n'est point, la sphère ABC sera à une sphère plus petite ou à une sphère plus grande que la sphère DEF en raison triplée de BC à EF. Supposons d'abord que la sphère ABC soit à une sphère plus petite, savoir à la sphère GHK en raison triplée de BC à EF. Imaginez la sphère DEF placée autour du même centre que la sphère GHK; décrivez dans la plus grande sphère DEF un polyèdre dont les faces ne touchent point la surface de la plus petite sphère GHK (prop. 17. 12), et dans la sphère ABC décrivez un polyèdre semblable à celui qui est décrit, dans la sphère DEF; le polyèdre inscrit dans la sphère ABC sera au polyèdre inscrit dans la sphère DEF en raison triplée de BC à EF (cor. 17. 12); mais, par supposition, la sphère ABC est à la sphère GHK en raison triplée de BC à EF : donc la sphère ABC est à la sphère GHK comme le polyèdre inscrit dans la sphère ABC est au polyèdre inscrit dans la sphère DEF (prop. 11. 5) : donc en échangeant les places des moyens la sphère ABC sera au polyèdre inscrit dans cette sphère comme la sphère GHK est au polyèdre inscrit dans la sphère DEF; mais la sphère ABC est plus grande que le polyèdre qui lui est inscrit : donc la sphère GHK est plus grande que le polyèdre inscrit dans la sphère DEF ; mais au contraire il est plus petit, car il est inscrit dans cette sphère, ce qui est impossible : donc la sphère ABC n'est point à une sphère plus petite que la sphère DEF en raison triplée de BC à EF. Nous démontrerons semblablement que la sphère DEF n'est point à une sphère plus petite que la sphère ABC en raison triplée de EF à BC. Je dis de plus que la sphère ABC n'est point à une sphère plus grande que la sphère DEF en raison triplée de BC à EF; car si cela peut se faire, supposons que la sphère ABC soit à une sphère plus grande que la sphère DEF, savoir à la sphère LMN en raison triplée de BC à EF; en mettant les conséquents à la placé des antécédents et les antécédents à la place des conséquents, la sphère LMN sera à la sphère ABC en raison triplée du diamètre EF au diamètre BC. Mais la sphère LMN est à la sphère ABC comme la sphère DEF est à une sphère plus petite que la sphère ABC, ainsi que cela a été démontré, puisque la sphère LMN est plus grande que la sphère DEF : donc la sphère DEF est à une sphère plus petite que la sphère ABC en raison triplée de EF à BC; ce qui a été démontré impossible : donc la sphère ABC n'est point à une sphère plus grande que la sphère DEF en raison triplée de BC à EF ; mais nous avons démontré que la sphère ABC n'est point à une sphère plus petite que la sphère DEF en raison triplée de AB à EF : donc la sphère ABC est à la sphère DEF en raison triplée de AB à EF ; ce qu'il fallait démontrer.

FIN DU DOUZIÈME ET DERNIER LIVRE.

NOTES.

LIVRE I. — DEFINITION IV.

CETTE définition d’Euclide a paru insignifiante à plusieurs géomètres; pour en comprendre le sens, comparons une ligne droite avec une autre ligne qui ait les mêmes extrémités. Soit pour cet effet la droite AFGE (fig. 240) et la ligne ABCDE.

La ligne AB est également placée entré ses points A et B, c’est-à-dire qu’elle ne s’avance ni vers la droite ni vers la gauche, qu’elle ne va ni en haut ni en bas; il en est de même de la ligne BC ; mais il n’en est pas de même de la ligne ABC, car cette ligne s’avance vers B. La ligne CDE n’est pas également placée entre ses points C et E, car elle s’avance vers D: donc la ligne ABCDE n’est pas également placée entre ses points A, B, C, E, car elle 8’avance tantôt vers un endroit, tantôt vers un autre. La ligne AFGE est au contraire également placée entre ses points A et F, F et G, G et E, A et G, F et E, A et E, car elle ne s’avance jamais vers aucun côté.

Selon Archimède, la ligne droite est la plus courte des lignes qui ont les mêmes extrémités.

Selon Platon, la ligne droite est celle dont les extrémités sont ombragées par les points intermédiaires. Ne pourrait-on pas dire que la ligne droite est celle qui peut tourner sur extrémités immobiles sans changer de place?

Cette définition est analogue à celle de la ligne droite et peut par conséquent être expliquée d’une manière analogue.

Selon Héron, la superficie plane est celle sur toutes les parties de laquelle on peut appliquer une ligne droite.

LIVRE I. — DÉFINITION XXXIII.

Cette définition renferme une condition superflue car si les côtés opposés d’un quadrilatère sont égaux, les angles opposés sont nécessairement égaux. (Robert Simson.) 

LIVRE I. — AXIOME VIII.

Cet axiome veut dire que les lignes, que les surfaces qui s’appliquent exactement les unes sur les autres sont égales que les angles dont les côtés s’appliquent exactement les uns sur les autres sont égaux, et que deux solides sont égaux lorsque les faces de l’un s’appliquent exactement sur les faces de l’autre. Si l’on disait que les choses qui s’appliquent exactement les unes sur les autres sont égales, on ne pourrait point se servir de cet axiome, lorsque l’on voudrait conclure que deux solides dont les faces s’appliquent exactement les unes sur les autres, sont égaux entre eux.

LIVRE I. — PROPOSITION VII.

Cette proposition a deux cas, car il peut arriver que le point D tombe dans le triangle ABC. Robert Simson démontre Le second cas; mais cela était inutile, car le second cas est compris implicitement dans la proposition XXI du même livre, où Euclide démontre que les deux droites BD, DC sont plus courtes que les droites BA, AC; car il est évident que si les deux droites BD, D sont plus courtes que les deux droites BA, AC, les deux droites BD ,C ne seront point égales aux deux droites BA, AC, chacune à chacune.

LIVRE I. — PROPOSITION XXIV.

Car puisque, &c. lisez que parmi les droites DE, DF la droite DE soit celle qui n’est pas plus grande que la droite DF. Puisque, &c (Robert Simson).

LIVRE I. — PROPOSITION XXXV.

Robert Simson remarque que cette proposition a trois cas, et qu’Euclide ne démontre que le cas où le point E tombe entre le point D et le point F.

Les deux autres cas ont lieu lorsque le point E (fig. 241) tombe sur le point D et lorsque le point E tombe entre le point A et le point D (fig. 242). Voici comment on peut démontrer ces deux autres cas:

Après avoir démontré, pour le second cas, que le triangle ABD (fig. 241) et égal au triangle DCF, et après avoir ajouté chacun de ces deux triangles égaux le triangle BCD, on conclura que le parallélogramme ABCD sera égal au parallélogramme BCFD.

Après avoir démontré, pour le troisième cas, que le triangle ABE (fig. 242) est égal au triangle DC, et après avoir ajouté à chacun de ces deux triangles égaux le quadrilatère BCDE, on conclura que le parallélogramme ABCD sera égal au parallélogramme BCF

LIVRE IV — COROLLAIRE DE LA PROPOSITION XXV.

Hexagone, lisez hexagone équilatéral et équiangle. (Robert Simson).

 LIVRE VI. —DEFINITION II.

Rober Simson trouve cette définition obscure et la remplace par la suivante:

«  Les figures, les triangles et les parallélogrammes, par exemple, sont réciproques lorsque les côtés qui comprennent deux angles sont proportionnels, de manière qu’un côté de la première figure est à un côté de la seconde comme un autre côté de la seconde est à un autre côté de la première. Je donne la préférence à la définition d’Euclide, mais j’approuve la définition de Robert Simson comme explication.

LIVRE VI. — DEFINITION V.

Euclide entend par la quantité d’une raison le quotient qui résulte la division de l’antécédent par son conséquent: D’où il suit que la quantité d’une raison peut toujours être représentée par une fraction dont le numérateur est l’antécédent de la raison et dont le dénominateur est le conséquent.

Soient les raisons suivantes : a : b, c : d, e : f

Les quantités de ces raisons sont les fractions a/b, c/d, e/f dont le produit est la fraction ace/bdf, ou la raison ace : bdf qui est une raison composée des raisons a : b, c : d, e : f.

Il est évident que l’antécédent ace de la raison composée est égal au produit de tous les antécédents des raisons composantes, et que le conséquent bdf de la raison composée est égal au produit de tous les conséquents des raisons composantes; d’où il suit qu’on pourrait énoncer la définition V de la manière suivante:

Une raison composée de raisons est celle dont l’antécédent est égal au produit de tous les antécédents de raisons composantes et dont le conséquent est égal au produit de tous les conséquents des raisons composantes.

LIVRE XI. — DEFINITION X.

Cette définition n’est pas proprement une définition, mais bien un théorème qu’il faut démontrer. Je donnerai la démonstration de cette définition dans le cas où les angles solides ne sont pas compris par plus de trois angles plans; je ne démontrerai que ce cas, parce que dans toutes les démonstrations qui sont appuyées sur cette définition, il n’est pas question d’un seul solide dont les angles solides soient compris par plus de trois angles plans.

Robert Simson soutient que la définition X n’est pas vraie dans tous les cas, et que par conséquent un grand nombre de démonstrations du XI^e Livre et plusieurs démonstrations du Livre XII ont un fondement ruineux; en conséquence il supprime cette définition et la remplace par trois théorèmes, qu’il met à la suite de la proposition XXII.

Pour démontrer que la définition X est fausse dans certains cas, Robert Simson suppose deux solides qui ont le même nombre, de faces semblables et égales mais dont l’un a un angle solide rentrant, tandis que tous les angles solides de l’autre sont saillants. Mais n’est-il pas évident qu’Euclide n’avait en vue que les solides qui n’ont point d’angles rentrants? Etait-il nécessaire de l’énoncer d’une manière expresse? Cette définition est vraie dans tous les cas, lorsque les angles solides sont saillants. Voyez les notes qui sont à la suite des Eléments de Géométrie de A. M. Legendre.

Le théorème que Robert Simson met à la place de cette définition est exprimé ainsi: « Les solides qui sont contenus dans des plans semblables, égaux en nombre et en grandeur et semblablement posés, et dont les angles solides ne sont pas contenus par plus de trois angles plans, sont égaux et semblables entre eux ».

Ce théorème renferme une condition superflue; de cela seul que deux solides sont terminés par le même nombre de faces égales et semblables, les faces de ces solides sont également posées dans chaque solide. C’est comme si l’on disait que les triangles qui sont terminés par des droites égales et semblablement posées sont égaux et semblables.

Le théorème de Robert Simson a deux cas; car une face du premier solide étant appliquée exactement sur la face homologue du second, il peut arriver que les autres faces du premier solide s’appliquent exactement sur les autres faces du second solide, et il peut arriver aussi que le premier solide soit placé hors du second. Robert Simson ne démontre que le premier cas, et il ne parle pas du second, qui sert de base aux démonstrations XXVIII et XL du XI^e Livre et aux démonstrations III et IV du XII^e Livre: donc toutes ces démonstrations ont véritablement un fondement ruineux par le moyen des corrections de Robert Simson.[2]

LIVRE XI. — PROPOSITION XV.

Après cette phrase, « et puisque BA est parallèle à la droite OH », Robert Simson veut qu’on ajouter « car chacune de ces deux droites est parallèle à la droite ED qui n’est pas dans le même plan que ces droites. »

N.B. Les propositions suivantes, qui sont la démonstration de la définition X, doivent être mises après la proposition XXII.

PROPOSITION A.

Si deux angles solides sont compris chacun par trois angles plans, et si les angles plans du premier sont égaux aux angles plans du second, chacun à chacun, les plans des angles égaux seront également inclinés les uns sur les autres dans les deux solides.

Soient les deux angles solides A et A’ (fig. 243); que l’angle solide A soit compris par les trois angles plans BAC, CAD, DAB; que l’angle solide A’ soit compris par les trois angles plans B’A’C’, C’A’D’, D’A’B’; que l’angle BAC soit, égal à l’angle B’A’C’, l’angle CAD égal à l’angle C’AD’ et l’angle DAB égal à l’angle D’A’B’ : je dis que les plans des angles égaux sont également inclinés les uns sur les autres dans les deux angles solides.

D’un point quelconque B de la droite AB menez dans le plan BAD la droite BD perpendiculaire sur la droite AB; du même point B menez dans le plan BAC la droite EC perpendiculaire sur la droite AB; joignez les points C, D faites la droite A’B’ égale à la droite AB, et du point B’ menez dans le plan A’B’D’ la droite B’D’ perpendiculaire sur la droite A’B’, et dans le plan B’A’C’ la droite BC’ perpendiculaire sur la droite A’B’; joignez les points C’, D’. La droite Ail étant égale à la droite A’B’, l’angle BAD égal à l’angle B’A’D’, et l’angle ABD étant droit ainsi que l’angle A’B’D’, les triangles ABD, A’B’D’ seront égaux donc la droite BD est égale à la droite B’D’ et la droite AD égale à la droite A’D’. La droite BC est égale à la droite B’C’ et la droite AC égale à la droite A’C’, par la même raison. Mais l’angle CAD est égal à l’angle C’A’D’, la droite AC égale à la droite A’C’ et la droite AD égale à la droite A’D’ donc le triangle CAD est égal au triangle C’A’D’: donc les deux triangles BCD, B’C’D’ ont leurs côtés égaux chacun à chacun : donc ces deux triangles ont aussi leurs angles égaux chacun à chacun donc l’angle CBD est égal â l’angle C’B’D’ : donc l’inclinaison du plan CBA sur le plan DBA est égale à l’inclinaison du plan C’B’A’ sur le plan D’B’A’. On démontrera de la même manière que les plans des autres angles égaux sont également inclinés les uns sur les autres dans ces deux angles solides.

Donc si deux angles solides sont compris chacun par trois angles plans, et si les angles plans du premier sont égaux aux angles plans du second, chacun à chacun, les plans des angles égaux seront également inclinés les uns sur les autres dans les deux solides; ce qu’il fallait démontrer.

PROPOSITION B.

Si deux angles solides sont compris chacun par trois angles plans, et si les angles plans du premier sont égaux aux angles plans du second, chacun à chacun, angles solides seront égaux entre eux.

Soient les angles solides A, A’; que les angles plans BAC, CAD, DAB de l’angle solide A soient égaux aux angles plans B’A’C’, C’A’D’, D’A’B’ de l’angle solide A, chacun à chacun : je dis que l’angle solide A sera égal à l’angle solide A’.

Appliquons exactement l’angle BAD sur son égal B’A’D’, il peut arriver que les autres angles plans qui sont égaux dans les deux angles solides A, A’ soient placés des mêmes côtés ou ne soient pas placés des mêmes côtés. Supposons d’abord que l’angle BAD étant appliqué exactement sur son égal B’A’D’, les autres angles plans qui sont égaux dans les deux angles solides A, A’ soient placés des mêmes côtés. Puisque l’inclinaison du plan de l’angle BAC sur le plan de l’angle BAD est égale à l’inclinaison du plan de l’angle B’A’C’ sur le plan de l’angle B’A’D’ (pr. 4), le plan de l’angle BAC s’appliquera exactement sur le plan de l’angle B’A’C’; mais l’angle BAC est égal à l’angle B’A’C’ donc la droite AC s’applique exactement sur la droite A’C’; mais la droite AD est appliquée sur la droite A’D’ et la droite AC sur la droite A’C’ donc l’angle plan DAC s’applique exactement sur l’angle plan D’A’C’ donc les trois angles plans de l’angle solide A s’appliquent exactement sur les trois angles plans de l’angle solide A’ donc les angles solides A et A’ sont égaux.

Supposons en second lieu que les angles plans BAD, dab, qui sont égaux entre eux, soient appliqués exactement l’un sur l’autre, la droite AB sur la droite ad et la droite AD sur la droite ab, et que les autres angles plans qui sont égaux entre eux ne soient pas placés des mêmes côtés; il est évident, dans cette supposition, que le plan BAC ne s’appliquera point sur le plan dac, parce que l’inclinaison du plan BAC sur le plan BAD n’est pas égale à l’inclinaison du plan dac sur le plan dab. Le plan DAC ne s’appliquera point sur le plan bac, par la même raison : donc les angles plans BAD, dab étant appliqués exactement l’un sur l’autre, la droite AB sur la droite ad et la droite An sur la droite ab, les autres angles plans qui sont égaux dans ces deux angles solides ne s’appliqueront pas les nus sur les autres.

Si l’on plaçait l’angle plan BAD sur l’angle plan bad, de manière que le point A tombât sur le point a, que la droite AB s’appliquât sur la droite ab, il est évident que la droite AD s’appliquerait sur la droite ad ; mais alors le plan de l’angle BAC aurait la position bac’, et le plan de l’angle CAD aurait la position C’ad, de sorte que l’angle solide A serait placé au-dessous du plan abd. D’où je conclus que le principe de superposition ne peut pas être employé pour démontrer l’égalité de deux angles solides qui sont compris chacun par trois angles plans et dont les angles plans du premier sont égaux aux angles plans du second, chacun à chacun, lorsqu’ayant appliqué l’un sur l’autre deux angles plans qui sont égaux, les autres angles égaux de ces angles solides ne sont pas placés des mêmes côtés:[3] donc, dans ce cas, l’on doit se contenter de dire que deux angles solides qui sont compris chacun par trois angles plans et dont les angles plans du premier sont égaux aux angles plans du second sont égaux entre eux, parce que leurs parties constituantes, leurs angles plans et leurs inclinaisons sont égaies de part et d’autre.

Donc si deux angles solides sont compris chacun par trois angles plans, et si les angles plans du premier sont égaux aux angles plans du second, chacun à chacun, ces angles solides sont égaux entre eux; ce qu’il fallait démontrer.

PROPOSITION C.

Les solides qui sont contenus dans le même nombre de faces égales et semblables entre elles et dont les angles solides ne sont pas compris par plus de trois angles plans sont égaux et semblables entre eux.

Soient les solides ABCDEF, A’B’C’D’E’F’ (fig. 244) dont les angles solides ne sont pas compris par plus de trois angles plans et que ces solides soient contenus sous le même nombre de faces égales et semblables, c’est-à-dire que les faces ABC, DEF, BD, BE, EC soient semblables et égales aux faces A’B’C’, D’E’F’, B’D’, B’E’, E’C’ je dis que ces solides sont égaux et semblables.

Si l’on pose une face quelconque ABC du premier solide sur la face homologue A’B’C’ du second, de manière que les côtés de ces faces, qui sont des côtés homologues des faces égales et semblables BD, BE, EC, B’D’, B’E’, E’C’ soient appliqués exactement les uns sur les autres, ces deux solides seront placés du même côté sur le plan A’B’C’, où ils seront placés l’un au-dessus et l’autre au-dessous du plan A’B’C’.[4]

Supposons d’abord que les deux solides ABCDEF, A’B’C’D’E’F’ soient placés du même côté sur le plan A’B’C’. Puisque l’inclinaison du plan AF sur le plan ABC est égale l’inclinaison du plan A’.F’ sur le plan A’]3’C’ (pr.A), la face AF s’appliquera exactement sur la face A’F’ qui lui est semblable et égale. Les autres faces du solide ABCDEF s’appliqueront exactement sur les autres faces des solides A’B’C’D’E’F’, par la même raison: donc ces deux solides seront égaux. Mais les faces homologues sont également inclinées les unes sur les autres dans ces deux solides (pr. A): donc les deux solides ABCDEF, A’B’C’D’E’F’, qui sont contenus dans le même nombre de faces égales et semblables, sont égaux et semblables entre eux

Supposons en second lieu que les solides ABCDEF, abcdef soient placés l’un au-dessus et l’autre au-dessous du plan abc ; il est évident que dans ce cas le principe de superposition ne peut pas être employé pour démontrer l’égalité de deux solides qui sont contenus dans le même nombre de faces égales et semblables entre elles, et dont les angles solides ne sont pas compris par plus de trois angles plans: donc l’on doit se contenter de dire que ces deux solides sont égaux et semblables, parce que leurs parties constituantes, savoir, leurs faces, les inclinaisons de ces faces (pr. A), leurs angles solides (pr. B), sont parfaitement égales de part et d’autre.

Donc les solides qui sont contenus dans le même nombre de faces égales et semblables entre elles, et dont les angles solides ne sont pas compris par plus de trois angles plans, sont égaux et semblables entre eux; ce qu’il fallait démontrer.

LIVRE XI. — PROPOSITION XXVIII.

Selon Robert Simson et Clavius, Euclide aurait dû démontrer que les diagonales CF, DE sont parallèles; ce que Robert Simson démontre de la manière suivante:

« Soit le parallélépipède AB (fig. 188) et que les diagonales DE, CF joignent les extrémités des mêmes arêtes; puisque chacune des arêtes CD, FE est parallèle à l’arête GA qui n’est pas dans le même plan, les arêtes CD, FE seront parallèles: donc les diagonales CF, DE sont dans le même plan que les arêtes CD, FE, et sont parallèles entre elles: je dis, &c. »

LIVRE XI. — PROPOSITION XXIX.

Cette proposition a trois cas, et Euclide n’en démontre qu’un seul. En effet, il peut arriver que la droite MH tombe sur la droite GE ou bien entre la droite GE et la droite FD. Pour démontrer ces deux derniers cas, on fera des raisonnements analogues à ceux qu’on a faits pour démontrer les deux derniers cas de la proposition XXXV du I^er Livre. Voyez la note sur cette proposition.

LIVRE XII. — PROPOSITION XVII.

Cette démonstration est incomplète selon Robert Simson et selon moi. Après avoir démontré que le quadrilatère BKSP ne touchera point la surface de la plus petite sphère, Euclide conclue que les faces du polyèdre inscrit ne toucheront point la surface de la plus petite sphère. J’ai complété cette démonstration d’Euclide.

FIN.

DE L’IMPRIMERIE DE CRAPELET.