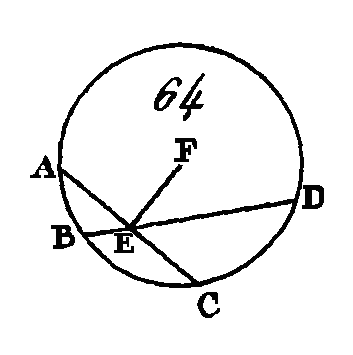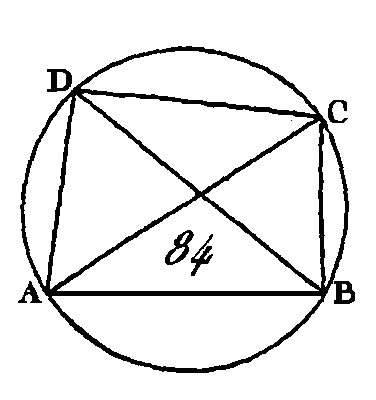INTRODUCTION -GEOMETRIE LIVRE I - LIVRE II - LIVRE IV - LIVRE VI

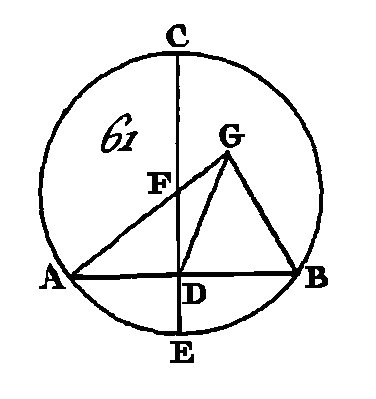
EUCLIDE

ELEMENTS DE GEOMETRIE

LIVRE III.

DÉFINITIONS.

1. Les cercles égaux sont ceux dont les diamètres sont égaux, ou ceux dont les droites menées des centres aux circonférences sont égales.

2. Une droite qui touchant le cercle et qui étant prolongée ne le coupe point, est appelée tangente du cercle.

3. Les cercles qui se touchant ne se coupent point, sont appelés cercles tangents.

4. Dans le cercle on dit que les droites sont également éloignées du centre, lorsque les perpendiculaires menées du centre sur ces droites sont égales.

5. On dit qu'une droite est plus éloignée du centre lorsque la perpendiculaire qui tombe sur elle est plus grande.

6. Un segment de cercle est une figure qui est comprise entre une droite et la circonférence du cercle.

7. L'angle du segment est celui qui est compris par une droite et la circonférence du cercle.

8. Un angle est dans le segment lorsque l'on prend un point quelconque dans la circonférence du segment, et que l'on conduit de ce point deux lignes droites aux extrémités de la droite qui est la base du segment ; l'angle est compris par les deux lignes droites qui ont été menées d'un point de la circonférence.

9. Mais lorsque les droites qui comprennent l'angle embrassent une portion de la circonférence, cet angle est dit appuyé sur la circonférence.

10. Un secteur de cercle est une figure comprise entre deux rayons qui font un angle au centre et la portion de la circonférence qu'embrassent ces deux rayons.

11. Les segments des cercles sont semblables lorsqu'ils reçoivent des angles égaux ou lorsque les angles qu'ils contiennent sont égaux entre eux.[1]

PROPOSITION PREMIÈRE.

PROBLÈME.

Trouver le centre d'un cercle donné.

Soit ABC (fig. 61) le cercle donné : il faut trouver le centre du cercle ABC.

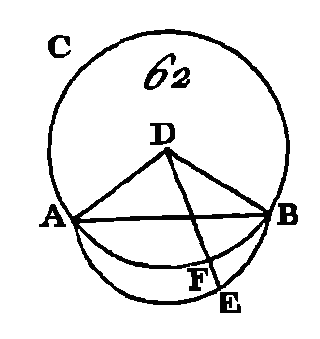
Conduisez dans le cercle une droite quelconque AB, partagez-la en deux parties égales au point D (prop. 10. I) ; du point D élevez une perpendiculaire DC sur AB (prop. 11. I), prolongez la droite DC jusqu'en E, et partagez CE en deux parties égales au point F : je dis que le point F est le centre du cercle ABC.

Car supposons que le point F ne le soit pas, et que ce soit le point G, si cela est possible. Conduisez les droites GA, GD, GB. Puisque la droite AD est égale à la droite DB et que la droite DG est commune, les deux droites AD, DG seront égales aux deux droites DB, DG, chacune à chacune ; mais la base GA est égale à la base GB, puisque ce sont deux droites menées du centre à la circonférence (déf. 15. I) : donc l'angle ADG est égal à l'angle GDB (prop. 8. I); mais lorsqu'une droite tombant sur une autre droite fait avec elle les angles de suite égaux, chacun de ces angles égaux est droit (déf.10. I) : donc l'angle GDB est droit; mais l'angle FDB est droit aussi : donc l'angle FDB est égal à l'angle GDB; c'est-à-dire que le plus grand est égal au plus petit, ce qui est impossible : donc le point G n'est pas le centre du cercle ABC. On démontrera de la même manière que tout autre point, excepté le point F, n'est pas le centre du cercle.

Donc le point F est le centre du cercle.

COROLLAIRE.

De là il suit évidemment que si dans un cercle une droite en coupe une autre en deux parties égales en faisant avec elle deux angles droits, le centre du cercle est placé dans la droite sécante.

PROPOSITION II.

THÉORÈME.

Si l'on prend deux points quelconques dans la circonférence d'un cercle, la droite qui joint ces deux points tombera dans le cercle.

Soit le cercle ABC (fig. 62) ; qu'on prenne deux points quelconques A, B, dans la circonférence de ce cercle : je dis que la droite qui est menée du point A au point B, tombe dans le cercle.

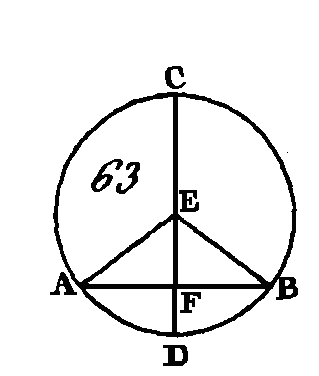
Si cette droite ne tombe pas dans le cercle, supposons, s'il est possible, qu'elle tombe en dehors, en AEB par exemple ; cherchez le centre du cercle ABC (prop. 1. III), supposons que D soit ce centre ; menez les rayons AD, DB, et prolongez DF jusqu'en E.

Puisque la droite DA est égale à la droite DB, l'angle DAE sera égal à l'angle DBE (prop. 5. I) ; et puisque l'on a prolongé un côté AEB du triangle DAE, l'angle DEB sera plus grand que l'angle DAE (prop. 16. I) ; mais l'angle DAE est égal à l'angle DBE : donc l'angle DEB est plus grand que l'angle DBE ; mais le plus grand côté est opposé à un plus grand angle (prop. 18. I) : donc la droite DB est plus grande que la droite DE ; mais la droite DF est égale à la droite DB : donc la droite DF est plus grande que la droite DE ; c'est-à-dire que la plus petite surpasse la plus grande, ce qui est impossible : donc la droite menée du point A au point B ne tombe pas hors du cercle. Nous démontrerons de la même manière qu'elle ne tombe pas dans la circonférence : donc elle tombe en-dedans du cercle. Donc si l'on prend deux points quelconques de la circonférence, la droite qui joint ces deux points tombe en-dedans du cercle; ce qu'il fallait démontrer.

PROPOSITION III.

THÉORÈME.

Si dans un cercle une droite qui passe par le centre coupe en deux parties égales une droite qui ne passe pas par le centre, la première droite coupera la seconde à angles droits ; et si la première coupe la seconde à angles droits, elle la coupera en deux parties égales.

Soit le cercle ABC (fig. 63) ; supposons que la droite CD menée dans le cercle par le centre coupe la droite AB, qui ne passe pas par le centre, en deux parties égales au point F : je dis que la première droite coupe la seconde à angles droits.

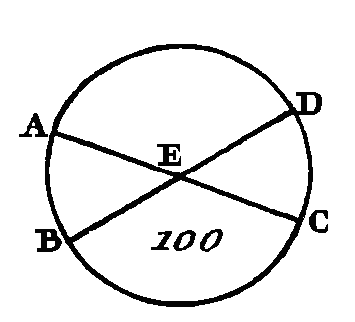
Cherchez le centre du cercle ABC (prop. 1. III); supposons que son centre soit le point E, conduisez les droites EA, EB.

Puisque la droite AF est égale à la droite FB et que la droite FE est commune, les deux droites AF, FE sont égales aux deux droites FB, FE ; mais la hase EA est égale à la hase EB : donc l'angle AFE sera égal à l'angle BFE (prop. 8. I); mais lorsqu'une droite tombant sur une autre droite, fait les angles de suite égaux entre eux, chacun de ces angles est droit : donc chacun des angles AFE, BFE est droit: donc la droite CD, menée par le centre et coupant en deux parties égales la droite AB qui ne passe pas par le centre, coupe la droite AB à angles droits.

Si la droite CD coupe la droite AB à angles droits, je dis qu'elle la coupe aussi en deux parties égales, c'est-à-dire que la droite AF est égale à la droite FB.

Faites la même construction ; puisque la droite EA est égale à la droite EB, l'angle EAF sera égal à l'angle EBF (prop. 5. I) ; mais l'angle droit AFE est égal à l'angle droit BFE : donc les deux triangles EAF, EBF auront deux angles égaux à deux angles, chacun à chacun, et un coté égal à un côté, c'est-à-dire un côté commun qui est opposé à des angles égaux : donc ces deux triangles auront les autres côtés égaux aux autres côtés (prop. 26. I) : donc la droite AF est égale à la droite BF.

Donc si dans un cercle une droite qui passe par le centre coupe en deux parties égales une autre droite qui ne passe pas par le centre, la première coupera la seconde à angles droits ; et si la première coupe la seconde à angles droits, elle la coupera en deux parties égales ; ce qu'il fallait démontrer.

PROPOSITION IV.

THÉORÈME.

Si dans un cercle deux droites qui ne passent point par le centre se coupent, elles ne se couperont point en deux parties égales.

Soit le cercle ABCD (fig. 64), et supposons que les deux droites AC, BD, qui ne sont point conduites par le centre, se coupent mutuellement au point E : je dis qu'elles ne se coupent point en deux parties égales.

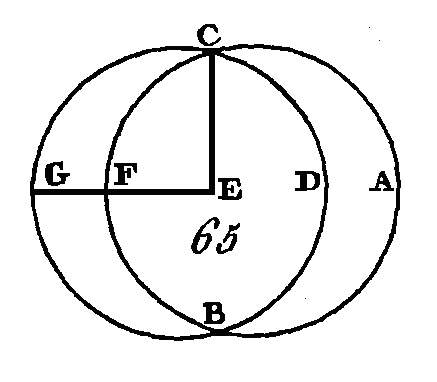
Supposons, s'il est possible, qu'elles se coupent en deux parties égales, de manière que AE soit égal à EC et BE égal à ED : prenez le centre du cercle ABCD, et supposons que son centre soit le point F ; menez FE.

Puisque la droite FE conduite par le centre, coupe en deux parties égales la droite AC qui n'est point conduite par le centre, la première coupera la seconde à angles droits (prop. 3. III): donc l'angle FEA est droit. De plus, puisque la droite FE coupe en deux parties égales la droite BD qui n'est pas conduite par le centre, la première coupera la seconde à angles droits, donc l'angle FEB est droit. Mais on a démontré que l'angle FEA est droit aussi : donc l'angle FEA est égal à l'angle FEB; c'est-à-dire que le plus petit est égal au plus grand, ce qui est impossible: donc les droites AC, BD ne se coupent point en deux parties égales.

Donc si dans un cercle deux droites qui ne sont point conduites par le centre se coupent mutuellement, elles ne se couperont point en deux parties égales ; ce qu'il fallait démontrer.

PROPOSITION V.

THÉORÈME.

Si deux cercles se coupent mutuellement, ils n’auront pas le même centre.

Que les deux cercles ABC, CDG (fig. 65) se coupent mutuellement aux deux points B, G : je dis qu'ils n'auront pas le même centre.

Supposons, s'il est possible, qu'ils aient le même centre et que ce centre soit le point E ; après avoir conduit la droite E C, conduisez la droite EFG d'une manière quelconque.

Puisque le point E est le centre du cercle ABC, la droite EC sera égale à la droite EF (déf. 15. I). De plus, puisque le point E est le centre du cercle CDG, la droite EC sera égale à la droite EG. Mais on a démontré que la droite EC est égale à la droite EF : donc la droite EF est égale à la droite EG, c'est-à-dire que la plus petite est égale à la plus grande, ce qui est impossible. Donc le point E n'est pas le centre des cercles ABC, CDG.

Donc si deux cercles se coupent mutuellement, ils n'auront pas le même centre ; ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Si deux cercles se touchent intérieurement, ils n'auront pas le même centre.

Que les deux cercles ABC, CDE (fig. 66) se touchent intérieurement au point C : je dis qu'ils n'auront pas le même centre.

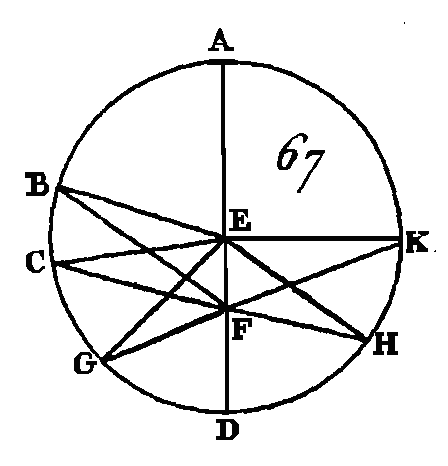
Supposons que cela se puisse et que leur centre soit le point F ; après avoir conduit la droite FC, conduisez d'une manière quelconque la droite FEB.

Puisque le point F est le centre du cercle ABC, la droite FC est égale à la droite FB. De plus, puisque le point F est le centre du cercle CDE, la droite FC est égale à la droite FE. Mais on a démontré que la droite FC est égale à la droite FB : donc la droite FE est égale à la droite FB; c'est-à-dire que la plus petite est égale à la plus grande, ce qui est impossible : donc le point F n'est point le centre des cercles ABC, CDE. Donc si deux cercles se touchent intérieurement, ils n'auront pas le même centre ; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Si dans le diamètre d'un cercle on prend un point quelconque qui ne soit pas. le centre de ce cercle, et si de ce point on conduit des droites à la circonférence, la plus grande sera celle qui passera par le centre, et la plus petite sera le reste du diamètre; quant aux autres droites, celle qui sera plus proche de celle qui passe par le centre sera plus grande que celle qui en est plus éloignée; et enfin du même point on ne peut conduire de part et d'autre de la plus petite que deux droites qui soient égales.

Soit le cercle ABCD (fig. 67), que AD soit son diamètre, prenez un point quelconque F qui ne soit pas le centre de ce cercle, que. le centre du cercle soit le point E ; du point F conduisez à la circonférence ABCD les droites FB, FC, FG : je dis que la droite FA est la plus grande, que la droite FD est la plus petite, et que parmi les autres la droite FB est plus grande que la droite FC, et que la droite FC est plus grande que la droite FG.

Conduisez les droites BE, CE, GE.

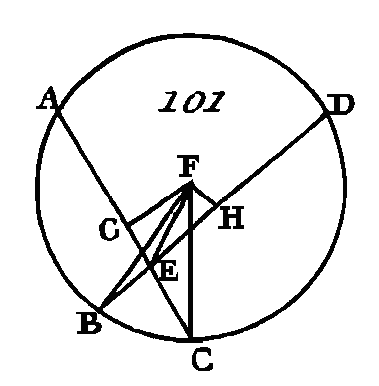
Puisque deux côtés d'un triangle sont plus grands que le côté restant (prop. 21. I), les droites EB, EF seront plus grandes que la droite BF; mais la droite AE est égale à la droite BE : donc les droites BE, EF sont égales à la droite AF : donc la droite AF est plus grande que la droite BF. De plus, puisque la droite BE est égale à la droite CE et que la droite EF est commune, les deux droites BE, EF sont égales aux deux droites CE, EF; mais l’angle BEF est plus grand que l'angle CEF : donc la base BF est plus grande que la base CF (prop. 24. I) ; par la même raison la base CF plus grande que la base FG.

De plus, puisque les droites GF, FE sont plus grandes que la droite EG et que la droite EG est égale à la droite ED, les droites GF, FE seront plus grandes que la droite ED : donc si on retranche la droite commune EF, la droite restante GF sera plus grande que la droite restante FD : donc la droite FA est la plus grande, et la droite FD la plus petite : donc la droite FB est plus grande que la droite FC, et la droite FG plus grande que la droite FG.

Je dis aussi que du point F, on ne peut conduire à la circonférence ABCD, de part et d'autre de la pins petite FD, que deux droites égales ; car sur la droite EF et au; point donné E pris; sur cette droite construisez l’angle FEH égal à l'angle GEF (prop. 23. I), et conduisez la droite FH. Puisque la droite GE est égale à la droite EH et que la droite EF est commune y. les deux droites GE, EF sont égales aux deux, droites HE, EF; mais l'angle GEF est égal à l'angle HEF par construction : donc la base FG sera égale à la base FH (prop. 4. I) : je dis que du point F on ne peut conduire une autre droite égale à FG. (Dar supposons que cela se, puisse, et que ce soit la droite FK ; puisque la droite FK est égale à FG, et que FH est aussi égale à FG, la droite FH sera égale à la droite FK, c'est-à-dire que la droite qui est plus près de celle qui passe par le centre est égale à celle qui en est plus éloignée ; ce qui ne peut être.

AUTREMENT.

Conduisez la droite EK; puisque la droite GE est égale à la droite EK, que la droite FE est commune, et que la base GF est égale à la Base FK, l'angle GEF sera égal à l'angle KEF (prop. 8. I) ; mais l'angle GEF est aussi égal à l'angle HEF : donc l'angle HEF sera égal à l'angle KEF, c'est-à-dire que le plus petit est égal au plus grand ; ce qui est impossible : donc par le point F on ne peut pas conduire à la circonférence une autre droite qui soit égale à GF : donc on n'en peut conduire qu'une seule.

Donc si dans le diamètre d'un cercle on prend un point quelconque qui ne soit pas le centre de ce cercle, et si de ce point on conduit des droites à la circonférence, la plus grande sera celle qui passe par le centre, et la plus petite sera le reste du diamètre ; quant aux autres droites, celle qui sera plus proche de celle qui passe par le centre sera plus grande que celle qui en est plus éloignée ; et enfin du même point on ne peut conduire de part et d'autre de la plus petite que deux droites qui soient égales ; ce qu'il fallait démontrer.

PROPOSITION VIII.

THÉORÈME.

Si l'on prend un point quelconque hors d'un cercle, et si de ce point on conduit à ce cercle plusieurs droites dont l'une passe par le centre et dont les autres passent partout où l'on voudra; parmi tes droites qui vont à la circonférence concave y la plus grande est celle qui passe par le centre; celle qui est plus près de celle qui passe par le centre est plus grande que celle qui s'en éloigne davantage; mais parmi les droites qui vont à la circonférence convexe, la plus petite est celle qui est comprise entre le point pris hors du cercle et le diamètre ; et celle qui est plus près de la plus petite est plus courte que celle qui s'en éloigne davantage; enfin de ce point on ne peut, mener à la circonférence et de part et d'autre de la plus petite que deux droites qui soient égales.

Soit le cercle ABC (fig. 68), et hors de ce cercle soit pris un point quelconque D ; de ce point menez à ce cercle les droites DA, DE, DF, DC, et supposons que DA passe par le centre: je dis que de toutes les droites qui vont à la circonférence concave AEFC, la droite DA, qui passe par le centre, est la plus grande, et que celle qui est plus près de celle qui passe par le centre est plus grande que celle qui s'en éloigne davantage, c'est-à-dire que la droite DE est plus grande que la droite DF, et la droite DF plus grande que la droite DC ; mais parmi les droites qui vont à la circonférence convexe HLKG, celle qui est comprise entre le point D et le diamètre AG est la plus petite, et celle qui est plus près de la plus petite est toujours plus courte que celle qui s'en éloigné davantage ; c'est-à-dire que la droite DK est plus courte que la droite DL, et la droite DL plus courte que la droite DH.

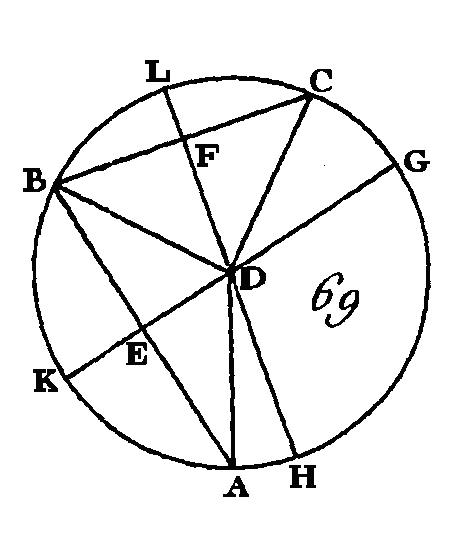
Cherchez le centre du cercle ABC (prop. 1. III), supposons que M soit ce centre; conduisez les droites ME, MF, MC, MR, ML; MH.

Puisque la droite A M est égale à la droite EM, si nous leur ajoutons une droite commune MD, la droite AD sera égale aux droites EM, MD; mais les droites EM; MD sont plus grandes que la droite ED (prop. 20. I) : donc la droite AD est plus, grande que la droite ED. De plus, puisque la droite ME est égale à la droite MF, et que la droite MD est commune, les droites EM, MD seront égales aux droites MF, MD; mais l'angle EMD est plus grand que l'angle FMD : donc la base ED sera plus grande que la base FD (prop. 24 I.) Nous démontrerons de la même manière que la droite FD est plus grande que la droite CD : donc la droite DA est la plus grande, la droite DE est plus grande que la droite DF, et la droite DF plus grande que la droite CD.

De plus, puisque les droites MK, KD sont plus grandes que la droite MD (prop. 20. I), et que la droite M G est égale à la droite MK, la droite restante KD sera plus grande que la droite restante GD : donc la droite GD est plus petite que la droite KD : donc elle est la plus petite. Si des extrémités du côté MD du triangle MLD on conduit intérieurement les droites MK, KD, les droites MK, KD seront plus petites que les droites ML, LD (prop. 21. I) ; mais la droite MK est égale à la droite ML : donc la droite restante DK est plus petite que la droite restante DL. Nous démontrerons de la même manière que la droite DL est plus petite que la droite DH : donc la droite DG est la plus petite, et la droite DK est plus petite que la droite DL, et la droite DL plus petite que la droite DH.

Je dis encore que du point D on ne peut conduire au cercle, de part et d'autre de la plus petite, que deux droites égales. Construisez sur la droite MD, et au point donné M, un angle DMB égal à l'angle KMD, et conduisez DB, Puisque la droite MK est égale à la droite MB et que la droite MD est commune, les deux droites KM, MD sont égales aux deux droites BM, MD, chacune à chacune; mais l'angle KMD est égal à l'angle BMD : donc la base DK est égale à la base DB (prop. 4. I) : je dis qu'il est impossible de conduire du point D au cercle ABC une autre droite qui soit égale à la droite DK. Supposons que cela se puisse et que cette droite soit DN ; puisque la droite DK est égale à la droite DN et la droite DB égale aussi à la droite D K, la droite DB sera égale à la droite DN, c'est-à-dire que la droite qui est plus près de la plus petite est égale à la droite qui s'en éloigne davantage; ce qui a été démontré impossible.

AUTREMENT.

Conduisez la droite MN; puisque la droite KM est égale à la droite MN, que la droite MD est commune et que la base DK est égale à la base DN, l'angle KMD sera égal à l'angle DMN (prop. 8. I); mais l'angle KMD est égal à l'angle BMD : donc l'angle BMD est égal à l'angle NMD, c'est-à-dire que le plus petit est égal au plus grand, ce qui est impossible : donc il est impossible de conduire du point D au cercle ABC, et de part et d'autre de la plus petite droite GD, plus de deux droites égales.

Donc si l'on prend un point quelconque hors d'un cercle, et si de ce point on conduit à ce cercle plusieurs droites dont l'une passe par le centre et dont les autres passent partout où l'on voudra ; parmi les droites qui vont à la circonférence concave, la plus grande est celle qui passe par le centre ; celle qui est plus près de celle qui passe par le centre est plus grande que celle qui s'en éloigne davantage ; mais parmi les droites qui vont à la circonférence convexe, la plus petite est celle qui est comprise entre le point pris hors du cercle et le diamètre ; et celle qui est plus près de la plus petite est plus courte que celle qui s'en éloigne davantage ; enfin de ce point on ne peut mener à la circonférence, et de part et d'autre de la plus petite, que deux droites qui soient égales ; ce qu'il fallait démontrer.

PROPOSITION IX.

THÉORÈME.

Si dans un cercle l'on prend un point quelconque, et si parmi les droites menées de ce point à la circonférence il y en a plus de deux qui soient égales entre elles, ce point sera le centre du cercle.

Soit le cercle ABC (fig. 69), que dans ce cercle l'on prenne le point D et qu'il y ait plus de deux droites égales entre elles qui aillent, de ce point à la circonférence, c'est-à-dire les droites DA, DB, DC: je dis que le point D est le centre du cercle ABC.

Conduisez les droites AB, BC, et partagez-les en deux parties égales aux points E, F (prop. 10. I), conduisez les droites ED, DF, que vous prolongerez vers les points G, K, H, L.

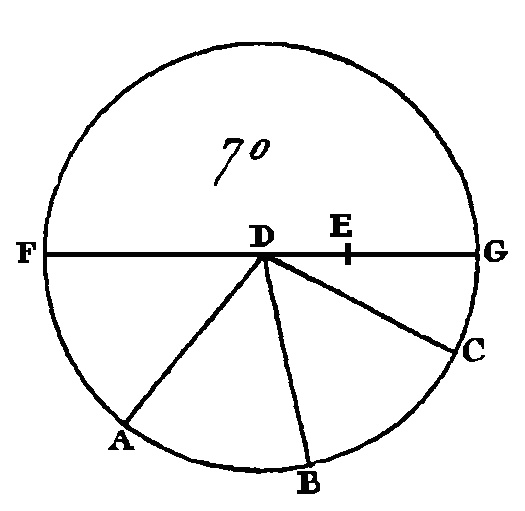
Puisque la droite AE est égale à la droite EB, et que la droite ED est commune, les deux droites AE, ED seront égales aux deux droites BE, ED ; mais la base DA est égale à la base DB : donc l'angle AED est égal à l’angle BED (prop. 8. I), et par conséquent chacun des angles AED, BED est droit : donc la droite GR, qui coupe la droite AB en deux parties égales, la coupe aussi à angles droits ; mais lorsque dans un cercle une droite coupe une autre droite en deux parties égales et à angles droits, le centre du cercle est placé dans la droite sécante (cor. 1. III) : donc le centre du cercle ABC sera dans la droite GK ; par la même raison le centre du cercle ABC sera placé dans la droite HL ; mais les droites GK, HL n'ont qu'un seul point commun qui est le point D : donc le point D est le centre du cercle ABC.

Donc si dans un cercle on prend un point quelconque, et si parmi les droites menées de ce point à la circonférence il y en a plus de deux qui soient égales entre elles, ce point sera le centre du cercle.

AUTREMENT.

Dans le cercle ABC (fig. 70) soit pris un point quelconque D, et que parmi les droites menées du point D à la circonférence ABC il y en ait plus de deux qui soient égales entre elles, c'est-à-dire les droites DA, DB, DC : je dis que le point D est le centre du cercle ABC.

Supposons, s'il est possible, que le point D ne soit pas le centre du cercle ABC, et supposons que le centre de ce cercle soit le point E, conduisez la-droite DE et prolongez-la vers F, G.

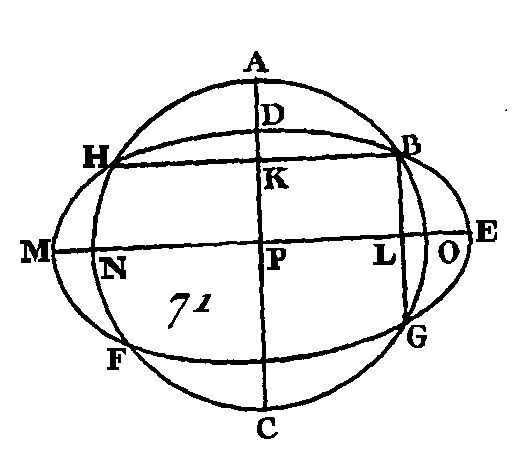
La droite FG sera un diamètre du cercle ABC. Si l'on prend dans le diamètre FG du cercle ABC un point D qui ne soit pas le centre de ce cercle, la droite DG sera la plus grande de toutes, et la droite DC sera plus grande que la droite DB, et la droite DB plus grande que la droite DA (prop. 7. III) ; mais ces droites sont égales, ce qui ne peut être : donc le point E n'est pas le centre du cercle ABC. Nous démontrerons de la même manière qu'il n'y a pas d'autre point, excepté le point D, qui soit le centre du cercle ADC : donc le point D est le centre du cercle ABC.

PROPOSITION X.

THÉORÈME.

Une circonférence de cercle ne peut couper la circonférence d'un autre cercle qu'en deux points.

Supposons que cela puisse arriver, et que la circonférence du cercle ABC (fig. 71) coupe la circonférence du cercle DEF en plus de deux points : savoir, aux points B, G, H; conduisez les droites BG, BH, et partagez-les en deux parties égales aux points K, L; par les points K, L, conduisez les droites KC, LM perpendiculaires sur BG, BH, et prolongez-les vers les points A, E.

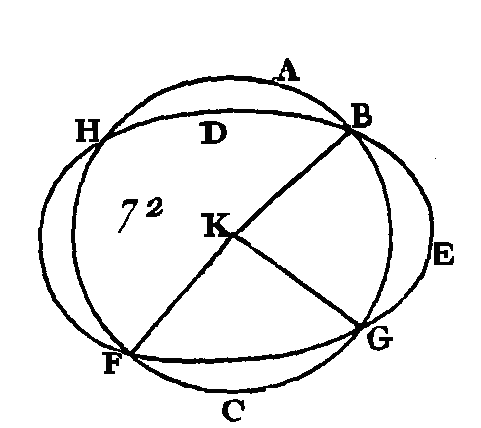
Puisque dans le cercle ABC, la droite AC coupe la droite BH en deux parties égales et à angles droits, le centre du cercle ABC sera placé dans la droite AC (corol. 1. III). De plus, puisque dans le même cercle ABC la-droite NO coupe la droite BG en deux parties égales et à angles droits le centre du cercle ABC sera placé dans la droite NO. On à démontré que le centre est placé dans la droite AC, et les deux droites AC, MO ne se rencontrent qu'au seul point O : donc le point O est le centre du cercle ABC. Nous démontrerons de la même manière que le point O est le centre du cercle DEF : donc les deux cercles ABC, DEF, qui se coupent mutuellement, auront le même centre O; ce qui est impossible (prop. 5. III).

Donc la circonférence d'un cercle ne peut pas couper la circonférence d'un autre cercle en plus de deux points ; ce qu'il fallait démontrer.

AUTREMENT.

Car que la circonférence du cercle ABC (fig. 72) coupe la circonférence du cercle DEF en plus de deux points, savoir, aux points B, G, F ; prenez le centre du cercle ABC, et que son centre soit le point K; menez les droites KF, KG, KB.

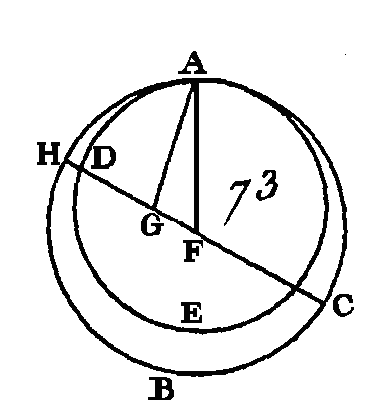
Puisque dans le cercle DEF on a pris un point K, et que parmi les droites qui vont de ce point à la circonférence DEF il y en a plus de deux qui sont égales entre elles, savoir, les droites KB, KF, KG, le point K sera le centre du cercle DEF (prop. 9. III); mais le point K est le centre du cercle ABC : donc ces deux circonférences, qui se coupent, auront le même centre ; ce qui est impossible (prop. 5. III).

Donc une circonférence de cercle ne peut pas couper la circonférence d'un autre cercle en plus de deux points ; ce qu'il fallait démontrer.

PROPOSITION XI.

THÉORÈME.

Si deux circonférences de cercle se touchent intérieurement, et si on prend leurs centres, la droite qui joindra leurs centres ira au point de contact si elle est prolongée.

Que les deux cercles ABC, ADE (fig. 73) se touchent intérieurement au point A ; qu'on prenne leurs centres, que le point F soit le centre du cercle ABC, et que le point G soit le centre du cercle ADE : je dis que la droite menée du point G au point F ira au point de contact A, si elle est prolongée.

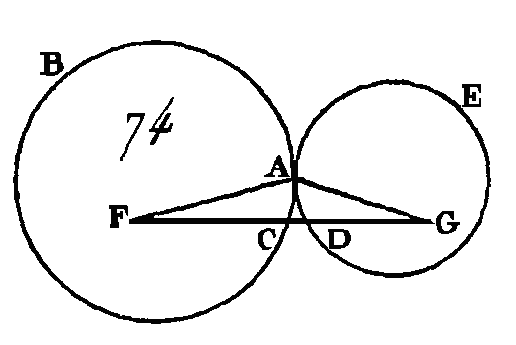
Supposons, s'il est possible, que cette droite étant prolongée n'aille pas au point de contact et qu'elle ait la position FGDH; menez les droites AF, AG.

Puisque les droites AG, GF sont plus grandes que la droite FA (prop. 20. I), c'est-à-dire que la droite FH, car la droite FA est égale à la droite FB, puisqu'elles partent du même centré: donc si on ôte la droite commune FG, la droite AG sera plus grande que la droite GH ; mais la droite AG est égale à la droite GD : donc la droite GD est plus grande que la droite GH ; c'est-à-dire que la plus petite surpasse la plus grande ; ce qui est impossible : donc la droite menée du point F au point G ne peut pas passer autre part qu'au point de contact A : donc elle passe au point de contact.

Donc si deux cercles se touchent intérieurement, la droite qui joint leurs centres passera par le point de contact, si elle est prolongée ; ce qu'il fallait démontrer.

AUTREMENT.

Supposons que la droite menée du point G au point F ait la position GFC et qu'elle soit prolongée directement vers le point H, menez les droites AG, AF.

Puisque les droites AG, GF sont plus grandes que la droite AF, et que la droite AF est égale à la droite CF, ou bien à la droite FH, si l'on retranche la droite commune FG, la droite restante AG sera plus grande que la droite restante GH, mais AG est égal à GD : donc la droite GD est plus grande que la droite GH, c'est-à-dire que la plus petite surpasse la plus grande; ce qui est impossible. Si le centre du grand cercle est hors du petit cercle, nous démontrerons de même qu'il s'en suit une absurdité.

PROPOSITION XII.

THÉORÈME.

Si deux circonférences de cercle se touchent extérieurement, la droite qui joindra les deux centres passera par le point de contact.

Que les circonférences des deux cercles ABC, ADE (fig. 74) se touchent extérieurement au point A ; qu'on prenne leurs centres, que le centre du cercle ABC soit le point F, et que le centre du cercle ADE soit le point G : je dis que la droite qui est conduite du point F au point G passe par le point de contact.

Supposons, s'il est possible, que le contraire arrive, et que cette droite ait la position FCDG ; conduisez les droites AF, AG.

Puisque le point F est le centre du cercle ABC, la droite FA sera égale à la droite FC. De plus, puisque le point G est le centre du cercle ADE, la droite AG sera égale à la droite GD ; mais on a démontré que la droite FA est égale à la droite FC : donc les droites FA, AG sont égales aux droites FC, DG : donc la droite totale FG est plus grande que les droites FA, AG; mais, au contraire, elle est plus petite (prop. 20. I), ce qui est impossible : donc la droite menée du point F au point G ne peut pas passer autre part qu'au point de contact : donc il faut nécessairement qu'elle passe au point de contact.

Donc si deux circonférences de cercles se touchent extérieurement, la droite qui joindra leurs centres passera par le point de contact, ce qu'il fallait démontrer.

PROPOSITION XIII.

THÉORÈME.

Une circonférence de cercle ne peut pas toucher une autre circonférence de cercle en plus d'un point, soit qu'elle la touche intérieurement, soit qu'elle la touche extérieurement.

Car si cela est possible, supposons d'abord que la circonférence du cercle ABDC (fig. 75) touche intérieurement la circonférence du cercle EBFD en plusieurs points, savoir aux points B, D.

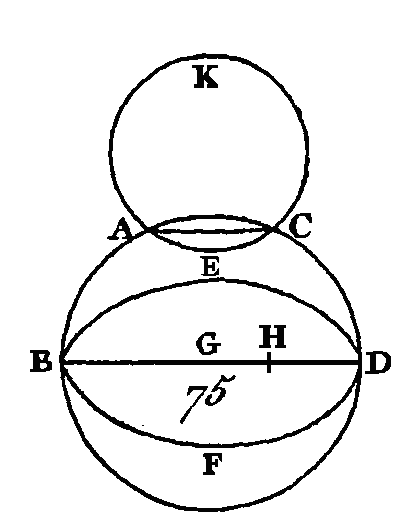
Cherchez les centres des cercles ABDC, EBFD ; que le point G soit le centre du premier et le point H le centre du second.

La droite qui est conduite du point G au point H passera par les points B, D (prop. 11. III). Qu'elle ait la position BGHD ; puisque le point G est le centre du cercle ABDC, la droite BG est égale à la droite GD : donc la droite BG est plus grande que la droite HD, et la droite BH beaucoup plus grande que la droite HD. De plus, puisque le point H est le centre du cercle EBFD, la droite BH est égale à la droite HD; mais on a démontré qu'elle est beaucoup plus grande, ce qui est impossible : donc une circonférence de cercle ne touche point intérieurement une autre circonférence de cercle en plus d'un point.

Je dis encore qu'il est impossible qu'une circonférence de cercle touche extérieurement une autre circonférence de cercle en plus d'un point ; car si cela était possible, il faudrait que la circonférence du cercle ACK touchât extérieurement la circonférence du cercle ABDC en plus d'un point, aux points A, C, par exemple ; conduisez la droite AG.

Puisque dans la circonférence des cercles ABDC, ACK on a pris deux points quelconques A, C, la droite qui joint ces deux points tombera intérieurement dans l'une et l'autre des deux circonférences (prop. 2. III); mais la droite qui tombe dans le cercle ABDC tombera hors du cercle ACK (déf. 3. III), ce qui est absurde : donc une circonférence de cercle ne touche point extérieurement une autre circonférence de cercle en plus d'un point. On a démontré qu'une circonférence ne touche point intérieurement une autre circonférence en plus de deux points.

Donc une circonférence de cercle ne touche point une autre circonférence de cercle en plus d'un point, soit qu'elle la touche intérieurement, soit qu'elle la touche extérieurement; ce qu'il fallait démontrer.

PROPOSITION XIV.

THÉORÈME.

Dans un cercle les droites égales sont également éloignées du centre, et celles qui sont également éloignées du centre sont égales.

Soit le cercle ABDC (fig. 76) et que les droites AB, CD, prises dans sa circonférence, soient égales : je dis que ces deux droites sont également éloignées du centre.

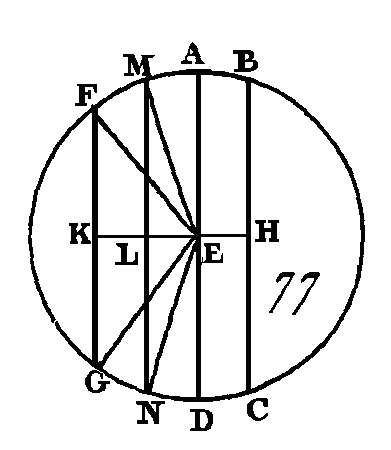
Cherchez le centre du cercle ABDC, et que ce centre soit le point E ; de ce point conduisez les droites EF, E G perpendiculaires sur les droites AB, CD, et menez les droites AE, EC.

Puisque la droite EF, menée par le centre, coupe à angles droits la droite AB, qui n'est pas menée par le centre, elle la coupe en deux parties égales (prop. 3. III) : donc la droite AF est égale à la droite FB, et par conséquent la droite AB est double de la droite AF. Par la même raison la droite CD est double de la droite CG; mais la droite AB est égale à la droite CD : donc la droite AF est égale à la droite CG : et puisque la droite AE est égale à la droite EC, le carré de la droite AE est égal au carré de la droite EC ; mais les carrés des droites AF, FE sont égaux au carré de la droite AE (prop. 47. I) car l'angle AFE est droit; et les carrés des droites EG, GC sont égaux au carré de la droite EC, puisque l'angle CGE est droit : donc les carrés des droites AF, FE sont égaux aux carrés des droites CG, GE; mais le carré de la droite AF est égal au carré de la droite CG, puisque la droite AF est égale à la droite CG : donc le carré restant de la droite FE est égal au carré restant de la droite EG : donc la droite FE est égale à la droite EG ; mais dans un cercle les droites sont dites également éloignées du centre lorsque les perpendiculaires menées du centre sur ces lignes sont égales (déf. 4. III) : donc les droites AB, CD sont également éloignées du centre.

Supposons actuellement que les droites AB, CD soient également éloignées du centre ; c'est-à-dire, supposons que la droite FE soit égale à la droite EG : je dis que la droite AB est égale à la droite CD.

Avec les mêmes constructions nous démontrerons également que la droite AB est double de la droite AF, et que la droite CD est double aussi de la droite CG. Puisque la droite AE est égale à la droite EC, le carré de la droite AE sera égal au carré de la droite EC ; mais les carrés des droites EF, FA sont égaux au carré de la droite de AE (prop. 47. I), et les carrés des droites EG, GC égaux au carré de la droite EC : donc les carrés des droites EF, FA sont égaux aux carrés des droites EG, GC ; mais le carré de la droite EG est égal au carré de la droite EF, car la droite EG est égale à la droite EF : donc le carré restant de la droite AF est égal au carré restant de la droite CG : donc la droite AF est égale à la droite CG ; mais la droite AB est double de la droite AF, et la droite CD double de la droite CG : donc la droite AB sera égale à la droite CD.

Donc dans une circonférence de cercle les droites égales sont également distantes du centre, et les droites également distantes du centre sont égales ; ce qu'il fallait démontrer.

PROPOSITION XV.

THÉORÈME.

Dans une circonférence de cercle le diamètre est la plus grande de toutes les droites, et la droite qui est plus près du centre est plus grande que celle qui en est plus éloignée.

Soit le cercle ABCD (fig. 77) dont le diamètre est la droite AD et dont le centre est le point E ; que la droite BC soit plus près du centre E que la droite FG : je dis que la droite AD est la plus grande de toutes, et que la droite BC est plus grande que la droite FG.

Conduisez du centre les droites EH, EK perpendiculaires sur BC, FG. Puisque la droite BC est plus près du centre que la droite FG, la droite EK sera plus grande que la droite EH (déf. 5. III); faites la droite EL égale à la droite EH, et par le point L conduisez la droite LM perpendiculaire sur EK, prolongez la droite LM vers le point N, et menez les droites EM, EN, EF, EG.

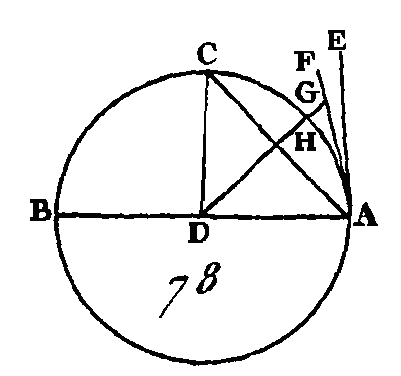
Puisque la droite EL est égale à la droite EH, la droite MN sera égale à la droite BC (prop. 14. III). De plus, puisque la droite AE est égale à la droite EM et la droite ED égale à la droite EN, la droite AD sera égale aux droites ME, EN; mais les droites ME, EN sont plus grandes que la droite MN : donc la droite AD est plus grande que la droite MN ; mais la droite MN est égale à la droite BC: donc la droite AD est plus grande que la droite BC; et puisque les deux droites ME, EN sont égales aux deux droites FE, EG, et que l'angle MEN est plus grand que l'angle FEG, la base MN sera plus grande que la base FG (prop. 24. I) Mais on a démontré que la droite MN est égale à la droite BC : donc la droite BC est plus grande que la droite FG : donc le diamètre AD est la plus grande de toutes les droites, et la droite BC est plus grande que la droite FG.

Donc dans une circonférence de cercle le diamètre est la plus grande de toutes les droites, et la droite qui est plus près du centre est plus grande que celle qui en est plus éloignée ; ce qu'il fallait démontrer.

PROPOSITION XVI.

THÉORÈME.

Une droite perpendiculaire sur le diamètre d'un cercle et menée par une de ses extrémités, tombe hors de ce cercle; il est impossible qu'il y ait une droite dans l'espace qui est compris entre cette perpendiculaire et la circonférence ; l'angle du demi-cercle est plus grand qu'aucun angle rectiligne aigu, et l'autre angle est plus petit qu'aucun angle rectiligne aigu.

Soit le cercle ABC (fig. 78) dont le point D est le centre et la droite AB le diamètre : je dis que la perpendiculaire sur la droite AB, menée par le point A, tombe hors du cercle.

Car si cela n'est point, supposons s'il est possible, qu'elle tombe en-dedans et qu'elle ait la position AC ; conduisez la droite DC.

Puisque la droite DA est égale à la droite DC, l'angle DAC sera égal à l'angle ACD (prop. 5. I) ; mais l'angle DAC est droit : donc l'angle ACD est droit aussi : donc les angles DAC, ACD sont égaux à deux angles droits, ce qui est impossible (prop. 17. I) : donc la perpendiculaire au diamètre AB, menée par le point A ne tombe point dans le cercle. Nous démontrerons de la même manière qu'elle ne tombe point sur la circonférence : donc il est nécessaire qu'elle tombe en dehors, et qu'elle ait la même position que la droite AE.

Je dis qu'il est impossible qu'il y ait une droite dans l'espace qui est compris entre la droite AE et la circonférence CHA.

Car si cela est possible, supposons qu'il y ait une droite qui ait la position FA ; du point D menez une droite DG perpendiculaire à FA.

Puisque l'angle AGD est droit et que l'angle DAG est plus petit qu'un angle droit, la droite AI sera plus grande que la droite DG; mais la droite DA est égale à la droite DH : donc la droite DH est plus grande que la droite AG, c'est-à-dire que la plus petite surpasse la plus grande, ce qui est impossible : donc il est impossible qu'il y ait une droite dans l'espace qui est compris entre cette perpendiculaire et la circonférence.

Je dis de plus, que l'angle du demi-cercle qui est compris par la droite BA et la circonférence CHA est plus grand qu'aucun angle rectiligne aigu, et que l’angle restant compris par la circonférence CHA et la droite AE est plus petit qu'aucun angle rectiligne aigu.

Car s'il y a un angle rectiligne plus grand que l'angle compris par la droite BA et par la circonférence CHA, pu s'il y a un angle rectiligne plus petit que l'angle compris par la circonférence CHA et par la droite AE, supposons que dans l'espace compris entre la circonférence CHA et la droite AE, il y ait une droite quelconque qui fasse un angle plus grand que celui qui est compris par la droite BA et la circonférence CHA, savoir, un angle compris par deux droites, et qu'il y ait un angle plus petit que celui qui est compris par la circonférence CHA et la droite AE ; mais il n'y en a point : donc il n'y a point d'angle aigu qui, étant compris par des droites, soit plus grand que l'angle compris par la droite BA et la circonférence CHA, ni d'angle plus petit que celui qui est compris par la circonférence CHA et la droite AE ; ce qu'il fallait démontrer.

COROLLAIRE.

Il suit manifestement de là que la droite perpendiculaire au diamètre, et menée d'une de ses extrémités, touche la circonférence, et que cette droite ne la touche qu'en un seul point, parce que nous avons démontré que les droites que rencontre le cercle en deux points, entrent dans le cercle (prop. 2. III).

PROPOSITION XVII.

PROBLEME.

D'un point donné, conduire une droite qui touche la circonférence d'un cercle donné.

Soit A (fig. 79) un point donné quelconque et BCD le cercle donné, il faut conduire, du point À une droite qui touche la circonférence du cercle BCD.

Prenez le centre de ce cercle, conduisez la droite AE; du centre E et avec un intervalle EA, décrivez la circonférence AFG (dem. 3) ; par le point D conduisez une perpendiculaire DP sur la droite EA et menez les droites EBF, AB : je dis que la droite AB menée du point A, touche la circonférence du cercle BCD.

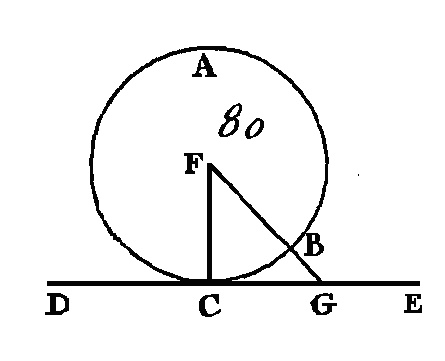
Puisque le point E est le centre des cercles BCD, AFG, la droite EA sera égale à la droite EF, et la droite ED égale à la droite EB : donc les deux droites AE, EB sont égales aux deux droites FE, ED; mais ces droites comprennent un angle commun qui est en E : donc la base DF est égale à la base AB, le triangle DEF au triangle EBA, et les autres angles de l'un de ces triangles sont égaux aux autres angles de l'autre triangle (prop. 4. I) donc l'angle EBA est égal à l'angle EDF ; mais l'angle EDF est droit : donc l'angle EBA est droit aussi. Mais la droite EB est un rayon et la perpendiculaire à une des extrémités d'un diamètre touche le cercle (prop. 16. III) : donc la droite AB touche le cercle.

Donc la droite AB, qui a été menée par le point A, touche le cercle BCD ; ce qu'il fallait faire.

PROPOSITION XVIII.

THÉORÈME.

Si une droite touche la circonférence d'un cercle i et si du centre on mène une droite au point de contact, cette dernière droite sera perpendiculaire sur la première.

Que la droite DE (fig. 80) touche au point C la circonférence du cercle ABC; prenez le centre F de ce cercle, et de ce centre conduisez la droite FG au point C : je dis que la droite FC est perpendiculaire sur la droite DE.

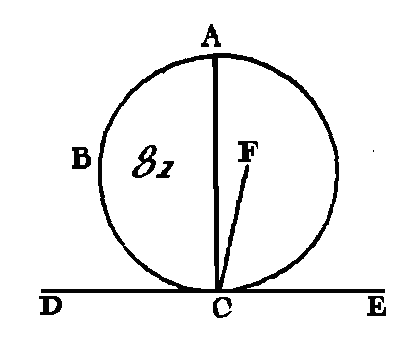
Car si elle ne l'est, pas, du point F conduisez la droite FC perpendiculaire sur la droite DE (prop. 12. I).

Puisque l'angle FGC est droit, l'angle GCF sera aigu (prop. 17. I); mais un plus grand angle est opposé à un plus grand côté (prop. 19. I): donc la droite FG est plus grande que la droite FG; or la droite FG est égale à la droite FB : donc la droite FB est plus grande que la droite FG ; c'est-à-dire que la plus petite surpasse la plus grande ; ce qui est impossible : donc la droite FG n'est pas perpendiculaire sur la droite DE. Nous démontrerons d'une manière semblable qu'il n'y a point d'autre droite, excepté FC, qui soit perpendiculaire sur la droite DE: donc la droite FC est perpendiculaire sur la droite DE.

Donc si une droite touche une circonférence de cercle, et si du centre on mène une droite au point de contact, cette dernière droite sera perpendiculaire sur la première; ce qu'il fallait démontrer.

PROPOSITION XIX.

Si une droite touche le cercle, et si par le point de contact on lui mène une perpendiculaire, cette perpendiculaire passera par le centre.

Qu'une droite DE (fig. 81) touche le cercle ABC au point C ; par le point C conduisez une perpendiculaire sur la droite DE : je dis que la perpendiculaire AG passera par le centre. Car si cela n'est point, supposons, s'il est possible, que le centre soit le point F, et menons la droite CF.

Puisque la droite DE touche le cercle ABC et que la droite FC a été menée du centre au point de contact, la droite FC sera perpendiculaire sur la droite DE, (prop. 18. III) : donc l'angle FCE, est droit, mais l'angle ACE est droit aussi : donc l'angle FCE est égal à l'angle; ACE, c'est-à-dire que le plus petit est égal au plus grand, ce qui est impossible : donc le point F n'est pas le centre du cercle ABC. Nous de montrerons d'une manière semblable qu'il n'y a aucun autre point qui puisse être le centre du cercle, à moins qu'il ne soit placé dans la droite AC.

Donc si une droite touche un cercle, et si par le point de contact on lui mène une perpendiculaire, cette perpendiculaire passera par le centre ; ce qu'il fallait démontrer.

PROPOSITION XX.

THÉORÈME.

Dans le cercle, l'angle au centre est double de l’angle à la circonférence, quand ils ont pour base la même portion de la circonférence.

 Soit le cercle ABC (fig. 82), que l'angle BEC soit au centre de ce cercle, que l'angle BAC soit à la circonférence, et que ces deux angles aient pour, basé la même portion de la circonférence BC : je dis que l'angle BEC est double de l'angle BAC.

Conduisez la droite AE et prolongez-la jusqu'en F.

Puisque la droite EA est égale à la droite EB, l’angle EAB sera égal à l’angle EBA (prop. 5. I) ; donc les angles EAB, EBA sont doubles de l'angle EAB ; mais l'angle BEF est égal aux angles EAB, EBA (prop. 32. I); donc l'angle BEF est double de l'angle EAB. L'angle FEC est double de l'angle FAC par la même raison; donc l'angle total BEC est double de l'angle total BAC.

Que l'angle BAC change de position et qu'il devienne BDC ; conduisez la droite DE et prolongez-la jusqu'en G. Nous démontrerons semblablement que l'angle GEC est double de l'angle GDG ; mais l'angle GEB est double de l'angle GDB : donc l'angle restant BEC est double de l'angle restant BDC.

Donc dans le cercle, l'angle au centre est double de l'angle à la circonférence, quand ils ont pour base la même portion de la circonférence ; ce qu'il fallait démontrer.

PROPOSITION XXI.

THÉORÈME.

Les angles placés dans un même segment de cercle sont égaux entre eux.

Soit le cercle ABCD (fig. 83) et que les angles BAD, BED soient placés dans le même segment BAED : je dis que ces angles sont égaux entre eux.

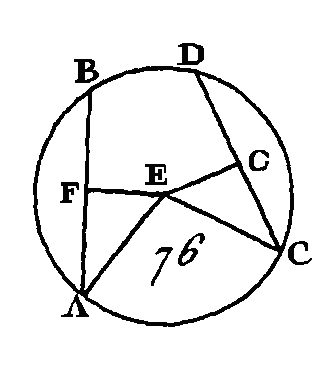
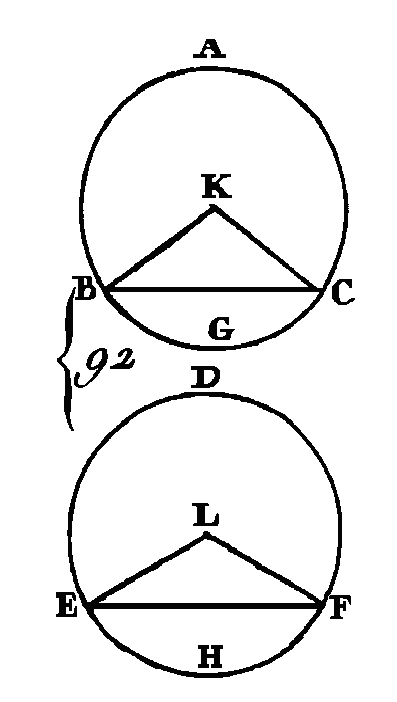
Prenons le centre du cercle ABCD (prop. 1. III), et que ce centre soit le point F ; menez les droites BF, FD.

Puisque l'angle BFD est au centre, que l'angle BAD est à la circonférence, et que ces deux angles ont pour base la même portion de la circonférence, l'angle BFD sera double de l’angle BAD (prop. 20. III) ; l'angle BFD est double aussi de l'angle BED, par la même raison : donc l'angle BAD est égal à l’angle BED (ax. 7). Donc les angles, placés dans le même segment de cercle, sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXII.

THÉORÈME.

Les angles opposés des quadrilatères inscrits dans des cercles sont égaux à deux droits.

Soit le cercle ABCD (fig. 84) et que le quadrilatère ABCD soit inscrit dans ce cercle : je dis que les angles opposés de ce quadrilatère sont égaux à deux droits.

Conduisez les droites AC, BD.

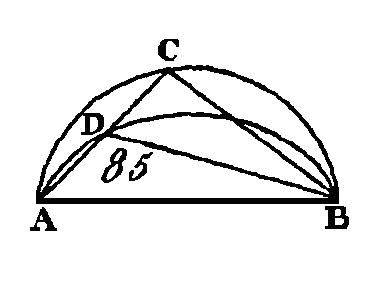
Puisque les trois angles de tout triangle sont égaux à deux droits (prop. 32. I), les trois angles CAB, ABC, BCA du triangle ABC seront égaux à deux angles droits; mais l'angle CAB est égal à l'angle BDC (prop. 21. III), car ces deux angles sont placés dans le même segment BADC ; l’angle ACB est égal à l'angle ADB, parce que ces deux angles sont placés dans le même segment ; donc l'angle total ADC est égal aux angles BAC, ACB ; donc si nous ajoutons un angle commun ABC, les angles ABC, BAC, ACB seront égaux aux angles ABC, ADC; mais les angles ABC, BAC, ACB sont égaux à deux droits : donc les angles ABC, ADC sont égaux à deux angles droits. Nous démontrerons semblablement que les angles BAD, DCB sont aussi égaux à deux droits.

Donc les angles opposés des quadrilatères inscrits dans des cercles sont égaux à deux droits ; ce qu'il fallait démontrer.

PROPOSITION XXIII.

THÉORÈME.

Sur une même droite, on ne peut pas décrire du même côté deux segments de cercles semblables et inégaux.

Supposons que cela soit possible ; décrivez du même côté et sur la même droite AB (fig. 85) deux segments de cercle ACB, ADB semblables et inégaux, et conduisez la droite ADC et les droites CB, DB.

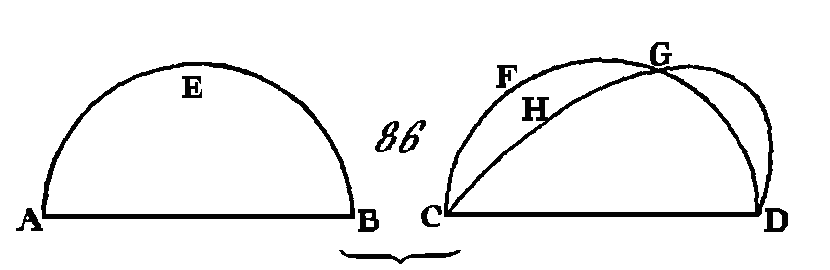
Puisque le segment ACB est semblable au segment ADB, et que les segments de cercles semblables sont ceux qui reçoivent des angles égaux (déf. 11. III), l'angle ACB sera égal à l'angle ADB, c'est-à-dire qu'un angle intérieur est égal à un angle extérieur ; ce qui est impossible (prop. 16. I).

Donc sur une même droite on ne peut pas décrire du même côté deux segments de cercles semblables et inégaux ; ce qu'il fallait démontrer.

PROPOSITION XXIV.

THÉORÈME.

Sur des droites égales, les segments de cercles semblables sont égaux entre eux.

Que sur les droites égales AB, CD (fig. 86) soient décrits les segments de cercles semblables AEB, CFD : je dis que le segment AEB est égal au segment CFD.

Car le segment AEB étant appliqué sur le segment CFD, le point A sur le point C et la droite AB sur la droite CD, le point B s'appliquera sur le point D, puisque la droite AB est égale à la droite CD ; mais la droite AB s'appliquant exactement sur la droite CD, le segment AEB s'appliquera exactement sur le segment CFD ; car si la droite AB s'appliquant exactement sur la droite CD, le segment AEB ne s'applique pas exactement sur le segment CFD, le segment AEB changera de position et prendra par exemple la position CHGD; mais une circonférence de cercle ne peut couper une autre circonférence de cercle en plus de deux points (prop. 10. III), et la circonférence CHGD coupe la circonférence GFD en plus de deux points, savoir, aux points G, G, D, ce qui est impossible; donc la droite AB s'appliquant exactement sur la droite CD, il est impossible que le segment AED ne s'applique pas exactement sur le segment CFD : donc le premier segment s'appliquera exactement sur le second : donc il lui sera égal.

Donc, sur des droites égales, les segments de cercles semblables sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXV.

PROBLEME.

Un segment de cercle étant donné, décrire le cercle dont il est segment.

Soit ABC (fig. 87, 88, 89) le segment de cercle donné : il faut décrire le cercle dont ABC est le segment.

Coupez la droite AC en deux parties égales au point D (prop. 10. I), du point D conduisez la perpendiculaire DB sur AC (prop. 11. I), et menez la droite AB ; l'angle ABD est ou plus grand que l'angle BAD, ou il lui est égal, ou il est plus petit.

Supposons d'abord qu’il soit plus grand; sur la droite donnée BA; (fig. 87) et au, point donné A faites l'angle BAE égal à l'angle ABD (prop. 23. I), prolongez la droite, DB jusqu'en. E, et conduisez la droite EC. Puisque l'angle ABE est égal à l'angle BAE, la droite BE sera égale à la droite EA (prop. 6. I), et puisque la droite AD est égale à la droite DC et que la droite DE est commune, les deux droites AD, DE sont égales aux deux droites CD, DE, chacune à chacune ; mais l'angle ADE est égal à l'angle CDE, car ils sont droits l'un et l'autre ; donc la base AE est égale à la base EC (prop. 4. I) a s’il a été démontré que la droite AE est égale à la droite EB : donc la droite BE est égale à la droite EC : donc les trois droites AE, EB, EC sont égales entre elles : donc la circonférence de cercle décrite du point E comme, centre, et avec un intervalle égal à l'une des droites AE, EB, EC, passera par les autres points, et le cercle sera décrit : donc un segment de cercle ayant été donné, on a décrit le cercle dont il est segment (prop. 9. III). Il est évident que le segment ABC est plus petit qu'un demi-cercle, puisque le centre E est placé en-dehors de ce segment.

Si l'angle ABD (fig. 88) est égal à l'angle BAD, la droite AD étant égale à chacune des droites BD, DC, les trois droites DA, DB, DC seront égales entre elles ; le point. D sera le centre du cercle entier (prop. 9. III), et le segment ABC sera un demi-cercle.

Mais si l'angle ABD (fig. 89) est moindre que l'angle BAD, et si sur la droite BA et au point A donné dans cette droite, on fait l'angle BAE égal à l'angle ABD, le centre E sera en-dedans du segment ABC et sur la droite DB, et le segment sera plus grand qu'un demi-cercle. Donc étant donné un segment de cercle, on a décrit le cercle dont il est segment ; ce qu'il fallait faire.

PROPOSITION XXVI.

THÉORÈME.

Dans des cercles égaux des angles égaux s'appuient sur des arcs égaux, soit qu'ils soient placés tous deux au centre ou tous deux à la circonférence.

Soient ABC, DEF (fig. 90) des cercles égaux, qu'aux centres de ces cercles soient les angles égaux BGC, EHF, et qu'à leurs circonférences soient les angles égaux BAC, EDF je dis que l'arc BKC est égal à l'arc ELF.

Conduisez les droites BC, EF.

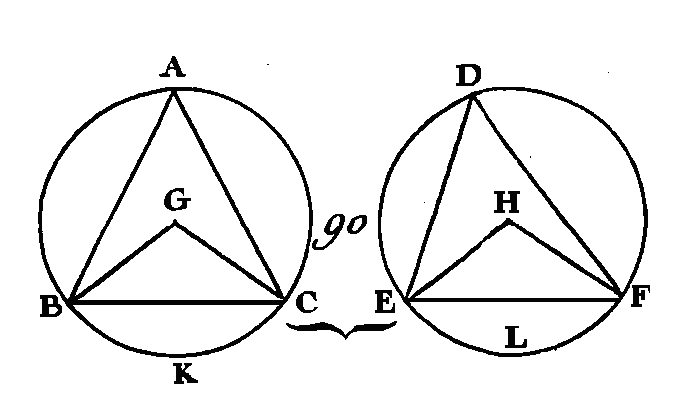
Puisque les cercles ABC, DEF sont égaux, leurs rayons seront égaux : donc les deux droites BG, GC sont égales aux deux droites EH, HF ; mais les angles G, H sont égaux : donc la base BC est égale à la base EF (prop. 4. I). Puisque l'angle A est égal à l'angle D, le segment BAC sera semblable au segment EDF (déf. 11. III) ; mais ces segments sont placés sur les droites égales BC, EF, et les segments semblables, qui sont placés sur des droites égales, sont égaux entre eux (prop. 24. III) : donc le segment BAC est égal au segment EDF ; mais le cercle entier ABC est égal au cercle entier DEF : donc le segment restant BKC est égal au segment restant ELF : donc l'arc BKC sera égal à l'arc ELF.

Donc, dans les cercles égaux, des angles égaux s'appuient sur des arcs égaux, soit qu'ils soient placés tous deux au centre ou tous deux à la circonférence ; ce qu'il fallait démontrer.

PROPOSITION XXVII.

THÉORÈME.

Dans les cercles égaux, les angles qui s'appuient sur des arcs égaux sont égaux entre eux, soit qu'ils soient placés tous deux au centre ou tous deux à la circonférence.

Que dans les cercles égaux ABC, DEF (fig. 91) les angles au centre BGC, EHF, et les angles à la circonférence BAC, EDF s'appuient sur les arcs égaux BC, EF : je dis que l'angle BGG est égal à l'angle EHF, et l'angle BAC égal à l'angle EDF.

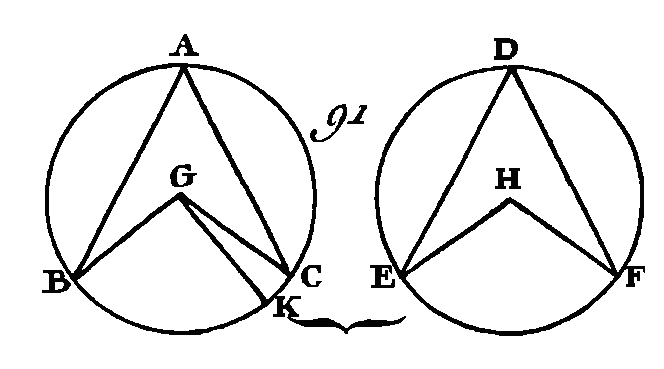
Car si l'angle BGG est égal à l'angle EHF, il est évident que l'angle BAC est égal à l'angle EDF (prop. 20. III) ; car si cela n'est pas, l'un de ces angles est nécessairement plus grand que l'autre. Supposons que l'angle BGC soit le plus grand. Sur la droite BG et au point G faisons l'angle BGK égal à l'angle EHF (prop. 23. I); or les angles égaux s'appuient sur des arcs égaux lorsqu'ils sont placés au centre (prop. 26. III) : donc l'arc BK est égal à l'arc EF, mais, l'arc EF est égal à l'arc BC : donc l'arc BK est égal à l'arc BC, c'est-à-dire que le plus petit est égal au plus grand ; ce qui est impossible donc les angles BGC, EHF ne sont pas inégaux : donc ils sont égaux ; mais l'angle en A est la moitié de l'angle BGC et l'angle en D la moitié de l'angle EHF (prop. 20. III) : donc l'angle en À est égal à l'angle en D.

Donc, dans les cercles égaux, les angles qui s'appuient sur des arcs égaux sont égaux entre eux, soit qu'ils soient placés tous deux au centre ou tous deux à la circonférence ; ce qu'il fallait démontrer.

PROPOSITION XXVIII.

THÉORÈME.

Dans les cercles égaux, des cordes égales, sous-tendent des arcs égaux, le plus grand arc étant égal au plus grand, et le plus petit égal au plus petit.

Soient ABC, DEF (fig. 92) deux cercles égaux, et BC, EF deux cordes égalés qui sous-tendent les deux grands arcs BAC ; EDF, et les deux petits arcs BGC, EHF : je dis que le grand arc BAC est égal au grand arc EDF, et que le petit arc BGC est égal au petit arc EHF.

Prenez les centres E, L de ces cercles (prop. 1. III), et menez les droites BK, KC, EL, LF.

Puisque ces cercles sont égaux leurs rayons seront égaux : donc les deux droites BK, KC sont égales aux deux droites EL, LF ; mais la base BC est égale à la base EF : donc l'angle BKC est égal à l'angle ELF (prop. 8. I) ; or les angles égaux s'appuient sur des arcs égaux quand ils sont placés aux centres (prop. 26. III) ; donc l'arc BGC est égal à l'arc EHF ; mais la circonférence entière ABC est égale à la circonférence entière DEF : donc l'arc restant ABC est égal à l'arc restant EDF.

Donc, dans des cercles égaux, des cordes égales sous-tendent des arcs égaux, le plus grand arc étant égal au plus grand, et le plus petit égal au plus petit ; ce qu'il fallait démontrer.

PROPOSITION XXIX.

THÉORÈME.

Dans des cercles, égaux des cordes égales sous-tendent des, arcs égaux.

Soient, les cercles égaux ABC, DEF (fig. 92) ; que dans ces cercles soient pris les arcs égaux BGC, EHF, et menez les cordes BG, EF : je dis que la corde BC est égale à la corde EF.

Prenez les centres K, L de ces cercles, et menez les droites BK KC, EL, LF. Puisque l'arc BGC est égal à l'arc EHF, l'angle BKC est égal à l'angle ELF (prop. 27. III); et puisque les cercles ABC, DEF sont égaux, leurs rayons seront égaux : donc les deux droites BK, KC sont égales aux deux droites EL, LF ; mais ces droites comprennent des angles égaux : donc la base BC est égale à la base EF (prop. 4. I)

Donc, dans des cercles égaux, des cordes égales sous-tendent des arcs égaux ; ce qu'il fallait démontrer.

PROPOSITION XXX.

PROBLÈME.

Partager un arc donné en deux parties, égales.

Soit ADB (fig. 93) un arc donné : il faut partager l'arc ADB en deux parties.

Menez la corde AB, et partagez-la en deux parties égales en C (prop. 10. I) ; du point C élevez une perpendiculaire CD sur la corde AB (prop. 11. I), et menez les droites AD, DB.

Puisque la droite AC est égale à la droite CB et que la droite CD est commune, les deux droites AC, CD sont égales aux deux droites BC, CD ; mais l'angle ACD est égal à l'angle BCD; car ils sont droits l’un et l'autre ; donc la base AD est égale à la base DB (prop. 4. I), or les cordes égales sous-tendent des arcs égaux, le plus grand arc étant égal au plus grand, et le plus petit égal au plus petit (prop. 28. III) ; mais l'un et l'autre des arcs AD, DB est moindre qu'une demi-circonférence : donc l'arc AD est égal à l'arc DB.

Donc l'arc donné a été partagé en deux parties égales ; ce qu'il fallait faire.

PROPOSITION XXXI.

THÉORÈME.

Dans un cercle, l'angle qui est compris dans le demi-cercle est droit; celui qui est compris dans un segment plus grand est plus petit qu'un angle droit, et celui qui est compris dans un segment moindre est plus grand qu'un angle droit. L'angle d'un plus grand segment est plus grand qu'un angle droit, et celui d'un segment moindre est plus petit qu'un angle droit.

Soit un cercle ABCD (fig. 94) dont le diamètre est BC et le centre le point E ; menez les droites BA, AC, AD, DG : je dis que l'angle qui est compris dans le demi-cercle BAC est droit ; que l'angle compris dans le segment ABC plus grand qu'un demi-cercle, savoir, l'angle ABC est plus petit qu'un angle droit, et que l'angle compris dans le segment ADC plus petit qu'un demi-cercle, savoir, l'angle ADC est plus grand qu'un angle droit.

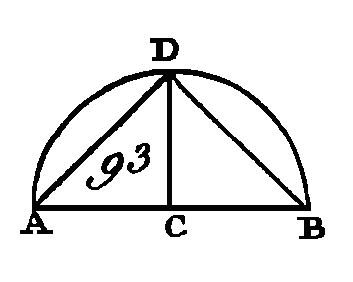
Conduisez la droite AE, et prolongez BA vers F. Puisque la droite BE est égale à la droite E A, l'angle EAB sera égal à l'angle EBA (prop. 5. I). De plus, puisque la droite EA est égale à la droite EC, l'angle ACE sera égal à l'angle CAE : donc l'angle total BAC est égal aux deux angles ABC, ACB; mais l'angle extérieur FAC du triangle ABC est égal aux deux angles ABC, ACB (prop. 32. I) : donc l'angle BAC est égal à l'angle FAC : donc chacun de ces angles est droit (prop. 10. I) : donc l'angle BAC, compris dans le demi-cercle BAC, est droit.

Puisque les deux angles AB C, B AC du triangle ÀBC sont plus petits que deux droits (prop. 17. I), et que l'angle BAC est droit, l'angle ABC sera plus petit qu'un angle droit, et cet angle est compris dans le segment ABC plus grand qu'un demi-cercle.

Puisque le quadrilatère ABCD est placé dans un cercle et que les angles opposés des quadrilatères décrits dans des cercles sont égaux à deux angles droits (prop. 22. III), les angles ABC, ADC sont égaux à deux angles droits ; mais l'angle ABC est plus petit qu'un angle droit : donc l'angle restant ADC est plus grand qu'un angle droit, et cet angle est compris dans le segment ADC plus petit qu'un demi-cercle.

Je dis en outre que l'angle d'un plus grand segment, compris par l'arc ABC et la droite AC, est plus grand qu'un angle droit, et que l'angle d'un segment moindre, compris, par l'arc ADC et la droite AC, est moindre qu'un angle droit, et cela est certainement évident ; car puisque l'angle compris par les droites BA, AC est droit, l'angle compris par l'arc ABC et la droite AC sera plus grand qu'un angle droit. De plus, puisque l'angle compris par les droites CA, AF est droit, l'angle compris par la droite CA et l'arc ADC sera plus petit qu'un angle droit.

Donc, dans un cercle, l'angle compris dans un demi-cercle est droit ; celui qui est compris dans un plus grand segment est plus petit qu'un angle droit, et celui qui est compris dans un segment plus petit est plus grand qu'un angle droit. De plus, l'angle d'un plus grand segment est plus grand qu'un angle droit, et l'angle d'un segment moindre est plus petit ; ce qu'il fallait démontrer.

AUTREMENT.

L'angle BAC est droit, puisque l'angle AEC est double de l'angle BAE, car il est égal aux deux angles intérieurs et opposés (prop. 32. I) ; mais l'angle AEB est double de l'angle EAC : donc les angles AEB, AEC seront doubles de l'angle BAC ; mais les angles AEB, AEC sont égaux à deux angles droits (prop. 13. I) : donc l'angle ABC est droit ; ce qu'il fallait démontrer.

COROLLAIRE.

De là il suit manifestement que si l'un des angles d'un triangle est égal aux deux autres, cet angle sera droit, parce que son angle de suite est égal aux deux autres ; or quand deux angles de suite sont égaux, ces deux angles sont droits l'un et l'autre (déf. 10. I).

PROPOSITION XXXII.

THÉORÈME.

Si une droite touche la circonférence d'un cercle, et si du point de contact on conduit une corde, les angles que cette corde fait avec la tangente seront égaux aux angles qui sont placés dans les segments alternes du cercle.

Que la droite EF (fig. 95) touche la circonférence du cercle ABCD au point B, et que du point B soit conduite la corde BD d'une manière quelconque : je dis que les angles que la corde BD fait avec la tangente EF sont égaux à ceux qui sont compris dans les segments alternes du cercle ; c'est-à-dire que l'angle FBD est égal à l'angle compris dans le segment DAB, et que l'angle EBD est égal à l'angle qui est compris dans le segment DCB.

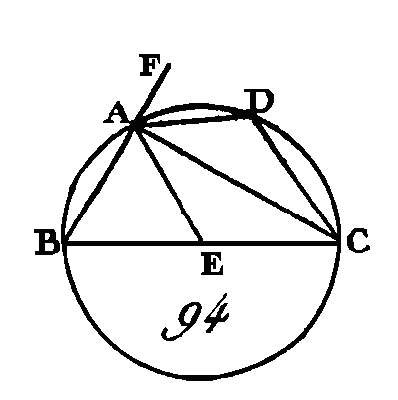
D'un point B conduisez la droite BA perpendiculaire sur EF (prop. 11. I), et dans l'arc BD prenez un point quelconque C et menez les cordes AD, DC, CB.

Puisque la droite EF touche la circonférence du cercle AB CD au point B, et que la droite BA a été menée du point de contact B perpendiculaire sur la tangente EF, le centre du cercle AB CD sera placé sur la droite B A (prop. 19. III) : donc l'angle ADB, compris dans le demi-cercle, est droit (prop. 31. III) : donc les angles restants BAD, ABD sont égaux à un angle droit; mais l'angle ABF est droit par construction : donc l'angle ABF est égal aux angles BAD, ABD (ax. 10) : donc si on retranche l'angle commun ABD, l'angle restant DBF est égal à celui qui est compris dans le segment alterne du cercle, c'est-à-dire à l'angle BAD. Actuellement, puisque le quadrilatère ABCD est inscrit dans le cercle, ses angles opposés sont égaux à deux droits (prop. 22. III) : donc les angles DBF, DBE seront égaux aux angles BAD, BCD (prop. 13. I); mais on a démontré que l'angle BAD est égal à l'angle DBF : donc l'angle restant DBE sera égal à celui qui est compris dans le segment alterne du cercle DCB, c'est-à-dire à l'angle DCB.

Donc si une droite touche la circonférence d'un cercle, et si du point de contact on conduit une corde, les angles que cette corde fera avec la tangente seront égaux à ceux qui sont compris dans les segments alternes ; ce qu'il fallait démontrer.

PROPOSITION XXXIII.

THÉORÈME.

Sur une droite donnée, décrire un segment de cercle qui reçoive un angle égal à un angle donné.

Soit AB (fig. 96, 97, 98) la droite donnée et C l’angle donné : il faut sur la droite donnée AB décrire un segment de cercle qui reçoive un angle égal à l'angle donné C. L'angle C est aigu ou droit ou obtus.

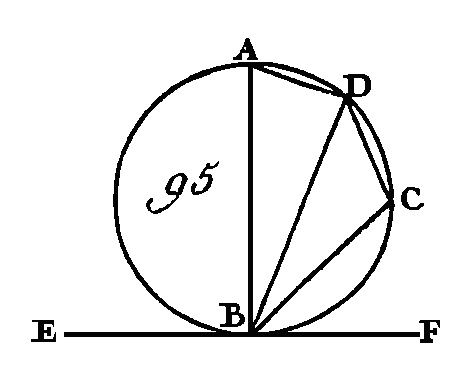
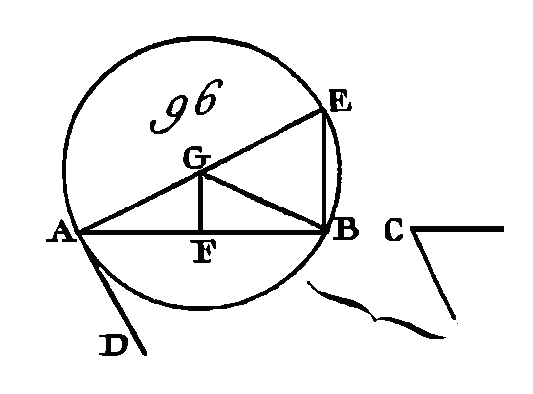
Supposons d'abord que cet angle soit aigu, comme dans la figure 96; sur la droite AB et au point A construisez un angle BAD égal à l'angle C (prop. 23. I) ; l'angle BAD sera aigu. Du point A conduisez la droite AE perpendiculaire sur la droite AD (prop. 11. I) ; partagez AB en deux parties égales au point F (prop. 10. I) y et du point F conduisez la droite FG perpendiculaire sur la droite AB, et menez la droite GB. Puisque la droite AF est égale à la droite FB et que la droite FG est commune, les deux droites AF, FG sont égales aux deux droites FB, FG ; mais l'angle AFG est égal à l'angle GFB : donc la base AG est égale à la base GB (prop. 4. I) : donc la circonférence décrite du centre G et avec l'intervalle AG passera par le point B. Décrivez cette circonférence et qu'elle soit ABE, et menez la droite EB. Puisque du point A, extrémité du diamètre AE, on à conduit sur la droite AE une perpendiculaire AD, cette perpendiculaire AD touchera la circonférence (prop. 16. III) ; et puisque la droite AD touche la circonférence du cercle ABE, et que du point de contact qui est en A on a conduit une corde AB, l'angle DAB sera égal à l'angle qui est dans, le segment alterne du cercle (prop. 32. III); c'est-à-dire à l'angle AEB ; mais l'angle DAB est égal à l'angle C : donc l'angle C sera égal à l'angle AEB : donc sur la droite donnée AB, on décrit un segment de cercle AEB qui reçoit un angle AEB égal à l'angle donné C.

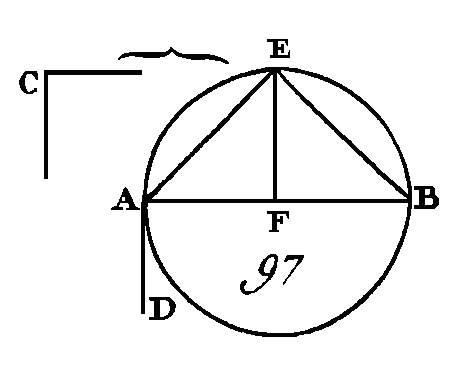
Supposons ensuite que l'angle C soit droit, et qu'il faille décrire sur la droite AB un segment de cercle qui reçoive un angle égal à l'angle droit C. Construisez un angle BAD égal à l'angle droit C (prop. 23. I), comme dans la figure 97 ; partagez la droite AB en deux parties égales au point F (prop. 10. I), et du centre F et avec un intervalle égal à l'une ou à l'autre des droites AF, FB, décrivez la circonférence de cercle AEB. La droite AD est tangente à la circonférence ABE (prop. 16. III), parce que l'angle BAD est droit, et l'angle BAD est égal à l'angle qui est compris dans le segment AEB, cap cet angle est droit, puisqu'il est compris dans un demi-cercle (prop. 31. III) ; mais l'angle BAD est égal à l'angle C : donc on a décrit sur la droite AB un segment de cercle AEB qui reçoit un angle égal à l'angle droit C.

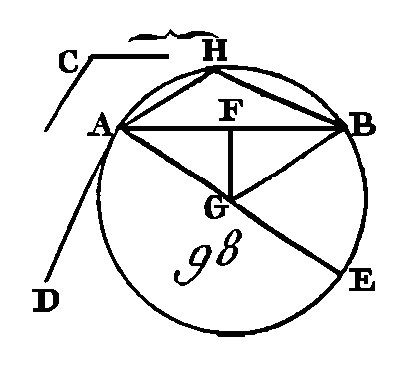
Enfin que l'angle C soit obtus ; sur la droite AB et au point A construisez un angle BAD égal à l'angle C, comme dans la figure 98 (prop. 25. I) et conduisez la droite AE perpendiculaire à la droite AD (prop. 11. I) ; partagez la droite AB en deux parties égales au point F (prop. 10. I) ; du point F conduisez sur AB la perpendiculaire FG, et menez la droite GB. Puisque la droite AF est égale à la droite FB et que la droite FA est commune, les deux droites FA, FG sont égales aux deux droites BF, FG ; mais l'angle AFG est égal à l'angle GFB : donc la base AG est égale à la base GB (prop. 4. I) : donc la circonférence de cercle décrite du point G avec l'intervalle AG passera par le point B. Que cette circonférence ait la position AEB ; puisqu'on a mené la droite AD perpendiculaire à l'extrémité du diamètre AE, la droite AD touchera la circonférence (prop. 16. III), et parce que la droite AB a été menée du point de contact qui est en A, l'angle BAD est égal à celui qui est compris dans le segment alterne du cercle. Mais l'angle BAD est égal à l'angle C : donc l'angle qui est dans le segment AHB sera égal à l'angle C : donc on a décrit sur la droite AB un segment de cercle AHB qui reçoit un angle égal à l'angle C ; ce qu'il fallait faire.

PROPOSITION XXXIV.

PROBLÈME.

D'un cercle donné, retrancher un segment qui reçoive un angle égal à un angle donné.

Soit ABC (fig. 99) le cercle donné, et D l'angle donné : il faut du cercle ABC retrancher un segment qui reçoive un angle égal à l'angle donné D.

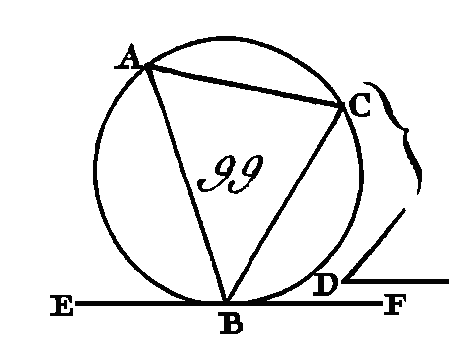
Menez une droite EF qui touche le cercle ABC au point B (prop. 17. III), et sur la droite FE et au point B, pris dans cette droite, faites l'angle FBC égal à l'angle D (prop. 23. I).

Puisque la droite EF touche le cercle ABC et que la droite BC a été menée du point de contact B, l'angle FBC sera égal à celui qui est compris dans le segment alterne du cercle BAC (prop. 32. III) ; mais l'angle FBC est égal à l'angle D : donc l'angle qui est compris dans le segment BAC sera égal à l'angle D.

Donc d'un cercle donné ABC on a retranché le segment BAC qui reçoit un angle égal à l'angle donné D ; ce qu'il fallait faire.

PROPOSITION XXXV.

THÉORÈME.

Si dans un cercle, deux cordes se coupent mutuellement, le rectangle compris sous les segments de l'une de ces cardes est égal au rectangle compris sous les segments de l'autre.

Que dans le cercle ABCD (fig. 100) les deux cordes, AC, BD se coupent mutuellement au point E : je dis que le rectangle compris sous les droites. AE, EG est égal à celui qui est compris sous les droites DE, EB.

Si les droites AG, BD passent par le centre, de manière que le point E soit le centre du cercle ABCD, il est évident que les droites AE, EC, DE, EB étant égales, le rectangle compris sous les droites AE, EC est égal à celui qui est compris sous les droites DE, EB.

Si les droites AC, DB (fig. 101) ne passent pas par le centre, prenez le centre du cercle ABCD (prop. 1. III), que ce centre soit le point F ; du centre F conduisez les droites FG, FH perpendiculaires sur les droites AC, DB (prop. 12. I), et menez les droites FB, FC, FE.

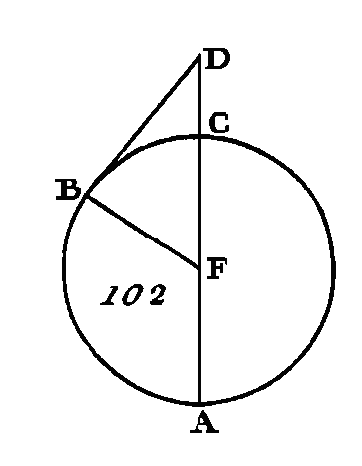
Puisque la droite GF menée par le centre est perpendiculaire sur la droite AG qui n'est pas menée par le centre, la droite GF coupe la droite AC à angle droit, et la partage en deux parties égales (prop. 3. III) : donc la droite AG est égale à la droite GC. Puisque la droite AC est coupée en deux parties égales au point G et en deux parties inégales au point E, le rectangle compris sous les droites AE, EC avec le carré de GE, est égal au carré de GC (prop. 5. II) : donc si nous ajoutons à ces quantités le carré de GF, le rectangle compris sous les droites AE, EC, avec les carrés de GE, GF, est égal aux carrés de CG, GF. Mais le carré de FE est égal aux carrés de EG, GF (prop. 47. I), et le carré de FC égal aux carrés de CG, GF : donc le rectangle compris sous tes droites AE, EC, avec le carré de FE, est égal au carré de FC. Or la droite FC est égale à la droite FB : donc le rectangle compris sous les droites AE, EC, avec le carré de EF, est égal au carré de FB. Par la même raison le rectangle compris sous les droites DE, EB, avec le carré de FE, est égal au carré de FB. Mais on a démontré que le rectangle compris sous les droites AE, EC, avec le carré de FE, est égal au carré de FB : donc le rectangle compris sous les droites AE, EC, avec le carré de FE, est égal au rectangle compris sous les droites DE, EB, avec le carré de FE: donc si on retranche le carré de FE, qui est commun, le rectangle restant compris sous AE, EC sera égal au rectangle restant compris sous DE, EB.

Donc si dans un cercle deux cordes se coupent mutuellement, le rectangle compris sous les segments de Tune sera égal au rectangle compris sous les segments de l'autre ; ce qu'il fallait démontrer.

PROPOSITION XXXVI.

THÉORÈME.

Si l’on prend un point quelconque hors d'un cercle, et si de ce point on mène deux droites dont l'une coupe le cercle et dont l'autre lui soit tangente, le rectangle compris sous la sécante entière et le segment extérieur qui est intercepté par ce point et l'arc convexe sera égal au quatre de la tangente.

Que hors du cercle ABC (fig. 102) soit pris un point quelconque D, et que de ce point soient menées deux droites DCA, DB; que la droite DCA coupe le cercle ABC, et que la droite AB lui soit tangente : je dis que le rectangle compris sous AD, DC est égal au carré de DB, soit que la droite DCA passe par le centre ou non.

Supposons d'abord qu'elle passe par le centre du cercle AB C, et que ce centre soit le point F ; menez la droite FB. L'angle FBD sera droit (prop. 18. III). Puisque la droite AC est coupée en deux parties égales au point F et que la droite CD lui est ajoutée) le rectangle compris sous les droites AD, DC, avec le carré de FC, sera égal au carré de FD (prop. 6. II) ; mais la droite FC est égale à la droite FB : donc le rectangle compris sous AD, DC, avec le carré de F B, est égal au carré de FD ; mais le carré de FD est égal aux carrés des droites FB, BD (prop. 47. I) car l'angle FBD est droit : donc le rectangle compris sous AD, DC, avec le carré de FB, est égal aux carrés des droites FB, BD. Donc si on retranche le carré de FB, qui est commun, le rectangle compris sous les droites AD, DC sera égal au carré de la tangente DB.

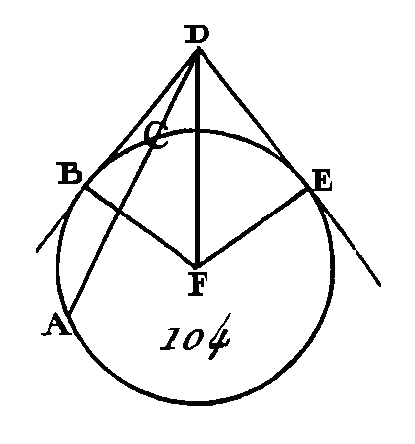
Supposons à présent que la droite DCA (fig. 103) ne passe pas par le centre du cercle ABC ; prenons le centre E, et du point E conduisons sur la droite AC la perpendiculaire EF (prop. 12. I), et menons les droites EB, EC, ED. Puisque l'angle EFD est droit, et que la droite EF menée par le centre coupe à angles droits la droite AC qui n'est pas menée par le centre, la droite EF coupera la droite AC en deux parties égales (prop. 3. III) : donc la droite AF est égale à la droite FC. De plus, puisque, la droite AC est coupée en deux parties égales au point F et que la droite. CD lui est ajoutée, le rectangle compris sous les droites AD, DC, avec le carré de FC, sera égal au carré de FD (prop. 6. II) : donc si on ajoute à ces deux quantités le carré de FE, le rectangle compris sous les droites AD, DC, avec les carrés des droites CF, FE, est égal aux carrés de DF, FE. Mais le carré de DE est égal aux carrés de DF, FE (prop. 47. I) car l'angle EFD est droit, et le carré de CE est égal aux carrés de CF, FE : donc le rectangle compris sous les droites ÀD, DC, avec le carré de CE, est égal au carré de ED ; mais la droite CE est égale à la droite EB : donc le rectangle compris sous les droites AD, DC, avec le carré de EB, est égal au carré de ED; mais les carrés de EB, BD sont égaux au carré de ED (prop. 47. I) puisque l'angle EBD est droit : donc le rectangle compris sous les droites AD, DC, avec le carré de EB, est égal aux carrés de EB, BD : donc si on retranche le carré de EB, qui est commun, le rectangle restant compris sous les droites AD, DC sera égal au carré de DB.

Donc si hors du cercle on prend un point quelconque, et si de ce point on mène deux droites dont l'une coupe le cercle et dont l'autre lui soit tangente, le rectangle compris sous la sécante entière et le segment extérieur qui est intercepté par ce point et l'arc convexe sera égal au carré de la tangente ; ce qu'il fallait démontrer.

PROPOSITION XXXVII.

THÉORÈME.

Si l'on prend un point quelconque hors d'un cercle, et si de ce point on mène deux droites dont l'une coupe le cercle et dont l'autre tombe sur sa circonférence, et si le rectangle compris sous la sécante totale et le segment extérieur intercepté entre ce point et tare convexe est égal au carré de la droite qui tombe sur la circonférence, cette dernière droite sera tangente à la circonférence.

Que hors du cercle ABC (fig. 104) soit pris un point quelconque D, et que de ce point on mène les deux droites DCA, DB dont la droite DCA coupe le cercle et dont la droite DB tombe sur sa circonférence ; si le rectangle compris sous les droites AD, DC est égal au carré de DB : je dis que la droite DB est tangente au cercle ABC.

Conduisez la droite DE de manière qu'elle soit tangente au cercle ABC (prop. 17. III), et prenez le centre du cercle ABC (prop. 1. III), que le point F soit ce centre ; menez les droites FE, FB, FD; l'angle FED sera droit (prop. 18. III).

Puisque la droite DE touche le cercle ABC et que la droite DCA le coupe, le rectangle compris sous AD, DG sera égal au carré de DE (prop. 36. III) ; mais le rectangle compris sous AD, DC est supposé égal au carré de DB : donc le carré de DE sera égal au carré de DB, et par conséquent la droite DE sera égale à la droite DB. Mais la droite FE est égale à la droite FB : donc les deux droites DE, EF sont égales aux deux droites DB, BF, mais la base FD est commune : donc l'angle DEF est égal à l'angle DBF (prop. 8. I) ; mais l'angle DEF est droit : donc l'angle DBF est droit aussi ; mais la droite FB prolongée est un diamètre, et la droite qui est perpendiculaire à l'extrémité d'un diamètre est tangente au cercle (prop. 16. III). On démontrerait la même chose si le centre était placé sur la droite AC.

Donc si l'on prend un point quelconque hors d'un cercle, et si de ce point on mène deux droites dont l'une coupe le cercle et dont l'autre tombe sur la circonférence, et si le rectangle compris sous la sécante totale et le segment extérieur intercepté par ce point et l'arc convexe est égal au carré de la droite qui tombe sur la circonférence, cette dernière droite sera tangente à la circonférence ; ce qu'il fallait démontrer.

FIN DU TROISIÈME LIVRE.