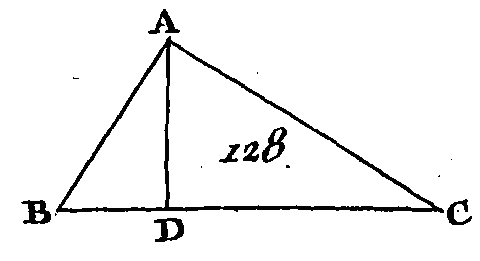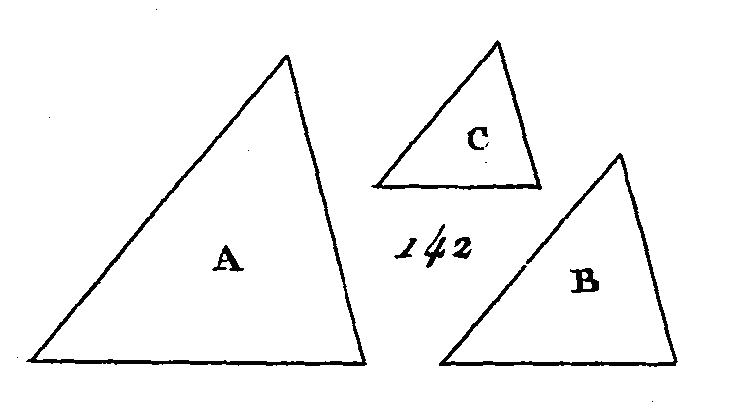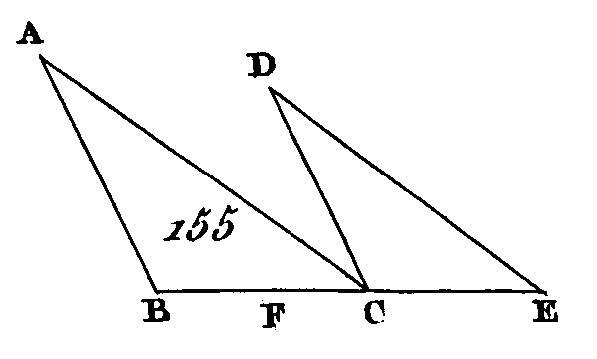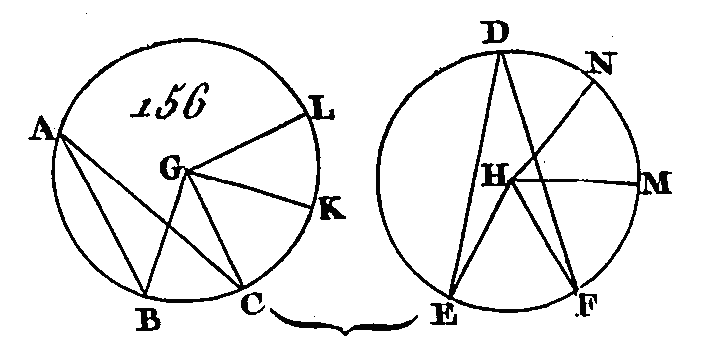INTRODUCTION -GEOMETRIE LIVRE I - LIVRE II - LIVRE III - LIVRE IV

EUCLIDE

ELEMENTS

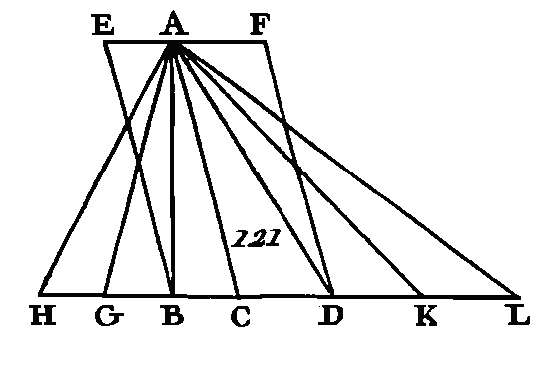
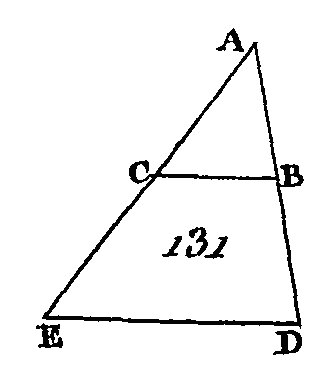
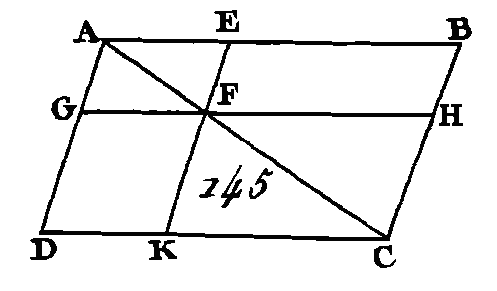
LIVRE VI.

DÉFINITIONS.

1. Les figures rectilignes semblables sont celles dont les angles sont égaux chacun à chacun et dont les côtés placés autour des angles égaux sont proportionnels.

2. Les figures sont réciproques lorsque les antécédents et les conséquents des raisons se trouvent dans l'une et l'autre figure.

3. Une droite est dite coupée en extrême et moyenne raison lorsque la droite totale est au plus grand segment comme le plus grand segment est au plus petit.

4. La hauteur d'une figure est une perpendiculaire menée de son sommet sur sa base.

5. On dit qu'une raison est composée de raisons lorsque les quantités des raisons multipliées entre elles produisent la quantité de cette raison.

PROPOSITION PREMIÈRE.

THÉORÈME.

Les triangles et les parallélogrammes qui ont la même hauteur sont entre eux comme leurs bases.

Soient les triangles ABC, ACD (fig. 121) et les parallélogrammes EC, CF qui ont la même hauteur, savoir, la perpendiculaire menée du point A sur la droite BD : je dis que le triangle ABC est au triangle ACD et que le parallélogramme EC est au parallélogramme CF comme la base BC est à la base CD.

Prolongez la droite BD de part et d'autre vers les points H, L, et faites les droites BG, GH égales chacune à la base B C ; faites aussi les droites DK, KL égales chacune à la base CD, et menez les droites AG, AH, AK, AL.

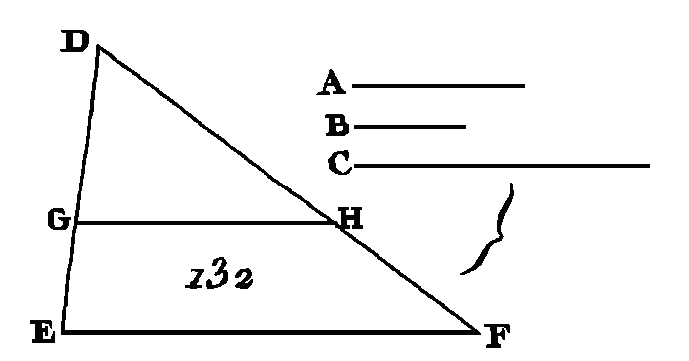
Puisque les droites CB, BG, GH sont égales entre elles, les triangles AGH, AGB, ABC seront égaux entre eux (prop. 38. I) : donc le triangle AHC contient le triangle ABC autant de fois que la base HC contient la base BC. Par la même raison le triangle ALC contient le triangle ACD autant de fois que la base LC contient la base CD. Si la base HC est égale à la base CL, le triangle AHC sera égal au triangle ABC (prop. 38. I) ; si la base HC surpasse la base CL, le triangle AHC surpassera le triangle ALC, et si cette base est plus petite le triangle sera plus petit. Ayant donc quatre quantités, savoir, les deux bases BC, CD et, les deux triangles ABC, ACD, on a pris des équimultiples de la base BC et du triangle ABC, savoir, la base HC et le triangle AHC ; on a pris aussi d'autres équimultiples de la base CD et du triangle ACD, savoir, la base CL et le triangle ALC ; et l'on a démontré que si la base HC surpasse la base CL, le triangle AHC surpassera le triangle ALC; que si la base HC est égale à la base CL, le triangle AHC sera égal au triangle ALC, et que si la base HC est plus petite que la base GL, le triangle AHC sera plus petit que le triangle ALC : donc le triangle ABC est au triangle ACD comme la base BC et la base CD (déf. 5. 5).

Puisque le parallélogramme EC est double du triangle ABC, que le parallélogramme FC est double aussi du triangle ACD (prop. 41. I), et à cause que les parties ont entre elles la même raison que leurs équimultiples (prop. 15. V), le parallélogramme EC sera un parallélogramme FC comme le triangle ABC est un triangle ACD : donc puisqu'on a démontré que le triangle ABC est au triangle ACD comme la base BC est à la base CD; et à cause que le parallélogramme EC est au parallélogramme FC comme le triangle ABC est au triangle ACD, le parallélogramme EC sera au parallélogramme FC comme la base BC est à la base CD (prop. 11. V).

Donc les triangles et les parallélogrammes qui ont la même hauteur sont entre eux comme leurs bases ; ce qu'il fallait démontrer.

PROPOSITION II.

THÉORÈME.

Si l’on conduit une droite qui soit parallèle à un des côtés d'un triangle, cette droite coupera proportionnellement les côtés de ce triangle; et si deux côtés d'un triangle sont coupés proportionnellement, la droite qui joindra les sections sera parallèle au côté restant du triangle.

Que l'on mène la droite DE (fig. 122) de manière qu'elle soit parallèle à un des côtés du triangle ABC : je dis que CE est à EA comme BD est à DA. Menez les droites BE, CD.

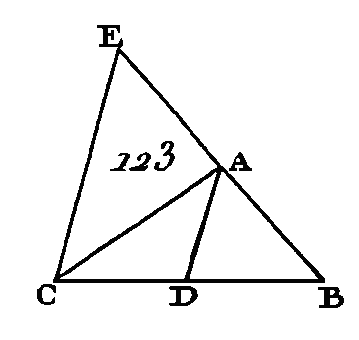
Le triangle BDE est égal au triangle CDE (prop. 37. I), parce qu'ils ont la même base et qu'ils sont compris entre les mêmes parallèles.

Mais deux quantités égales ont la même raison avec une même quantité (prop. 7. V) : donc le triangle CDE est au triangle ADE comme le triangle BDE est au triangle ADE. Mais le triangle BDE est au triangle ADE comme BD est à DA : car ces deux triangles, qui ont la même hauteur, savoir, la perpendiculaire menée du point E sur la base AB, sont entre eux comme leurs bases (prop. 1. VI). Par la même raison le triangle CDE est au triangle ADE comme CE est à EA : donc BD est à DA comme CE est à EA (prop. 11. V).

Si les côtés AB, AC du triangle ABC sont coupés proportionnellement aux points D, E de manière que BD soit à DA comme CE est à EA, et si l'on mène la droite DE : je dis que la droite DE est parallèle à la droite BC.

Faites la même construction. Puisque BD est à DA comme CE est à EA, que BD est à DA comme le triangle BDE est au. triangle ADE (prop. 1. VI), et que CE est à EA comme le triangle CDE est au triangle ADE; le triangle BDE sera au triangle ADE comme le triangle CDE est au triangle ADE (prop. 11. V) : donc chacun des triangles BDE, CDE a la même raison avec le triangle ADE : donc le triangle BDE est égal au triangle CDE (prop. 9, V), et ils ont la même base. Mais des triangles égaux et construits sur la même base sont compris entre les mêmes parallèles (prop. 39. I) : donc la droite DE est parallèle à la droite BC.

Donc si l'on conduit une droite qui soit parallèle à un des côtés d'un triangle, cette droite coupera proportionnellement les côtés de ce triangle ; et si les côtés d'un triangle sont coupés proportionnellement, la droite qui joindra les sections sera parallèle au côté restant de ce triangle ; ce qu'il fallait démontrer.

PROPOSITION III.

THÉORÈME.

Si un angle d’un triangle est partagé en deux parties égales, et si la droite qui partage cet angle coupe la base, les segments de la base auront la même raison que les autres côtés de ce triangle ; et si les segments de la hase ont la même raison que les autres côtés du triangle, la droite qui est menée du sommet à la section partagera l'angle de ce triangle en deux parties égales.

Soit le triangle ABC (fig. 123), que l'angle BAC soit partagé en deux parties égales par la droite AD : je dis que BD est à DC comme BA est à AC.

Par le point C menez la droite CE parallèle à la droite DA (prop. 31. I) ; prolongez la droite BA jusqu'à ce qu'elle rencontrera la droite CE au point E.

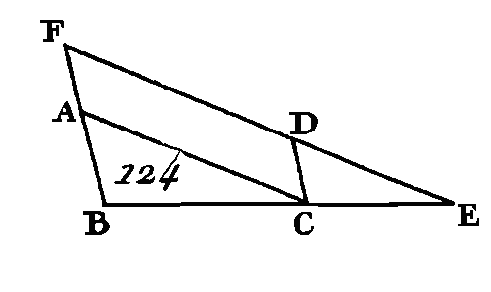
Puisque la droite AC tombe sur les parallèles AD, EC, l'angle ACE sera égal à l'angle CAD (prop. 29. I) ; mais l'angle CAD est supposé égal à l'angle BAD : donc l'angle BAD sera égal à l'angle ACE. De plus, puisque la droite BAE tombe sur les parallèles AD, EC, l'angle extérieur BAD est égal à l'angle intérieur AEC (prop. 29. I). Mais on a démontré que l'angle ACE est égal à l'angle BAD : donc l'angle ACE sera égal à l'angle AEC : donc le côté AE sera égal au côté AC (prop. 6. I). Puisque la droite AD est parallèle à un des côtés du triangle BCE, savoir, au côté EC, la droite BD sera à la droite DC comme la droite BA est à la droite AE (prop. 2. VI). Mais la droite AE est égale à la droite AC : donc la droite BD est à la droite DC comme la droite BA est à la droite AC (prop. 7. V).

Supposons à présent que la droite BD soit à la droite DC comme la droite BA est à la droite AC ; menez la droite AD : je dis que l'angle BAC est partagé en deux parties égales par la droite AD.

Faites la même construction. Puisque BD est à DC comme BA est à AC, et que BD est à DC comme BA. est à AE (prop. 2. VI), car la droite AD est parallèle à un des côtés du triangle BCE, savoir au côté EC, il est évident que BA sera à AC comme BA est à AE : donc la droite AC est égale à la droite AE (prop. 9. V) : donc l'angle AEC est égal à l'angle ACE (prop. 5, I); mais l'angle AEC est égal à l’angle extérieur BAD (prop. 29. I), et l'angle ACE égal à l'angle alterne CAD : donc l'angle BAD sera égal à l'angle CAD : donc l'angle BAC est partagé en deux parties égales par la droite AD.

Donc si un angle d'un triangle est partagé en deux parties égales, et si la droite qui partage cet angle coupe la base, les segments de la base auront la même raison que les autres côtés de ce triangle ; et si les segments de la base ont la même raison que les autres côtés du triangle, la droite qui est menée du sommet à la section de la base partage l’angle de ce triangle en deux parties égales ; ce qu'il fallait démontrer.

PROPOSITION IV.

THÉORÈME.

Dans les triangles équiangles, les côtés qui sont autour des angles égaux sont proportionnels ; et on appelle côtés homologues ceux qui sous-tendent des angles égaux.

Soient les triangles équiangles ABC, DCE (fig. 124) dont l'angle ABC soit égal à l'angle DCE, l'angle ACB égal à l'angle DEC, et l'angle BAC égal à l'angle CDE : je dis que dans les deux triangles ABC, DCE, les côtés qui sont autour des angles égaux sont proportionnels, et que les côtés qui sous-tendent des angles égaux sont homologues.

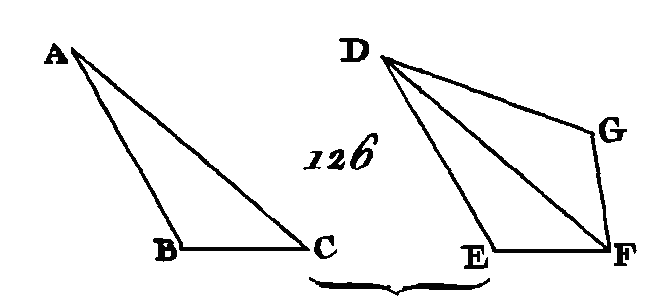
Placez le côté BC dans la direction de CE; puisque les angles ABC, ACB sont moindres que deux angles droits (prop. 17. I), et que l'angle ACB est égal à l'angle DEC, les angles ABC, DEC seront plus petits que deux angles droits : donc les deux droites BA, ED étant prolongées se rencontreront entre elles (ax. 11) et supposons qu'elles se rencontrent au point F.

Puisque l'angle DCE est égal à l'angle ABC, la droite DC sera parallèle à la droite BF (prop. 28. I). De plus, puisque l'angle ACB est égal à l'angle DEC, la droite AC sera parallèle à la droite FE. Donc la figure FACD est un parallélogramme : donc la droite FA est égale à la droite FD et la droite AC égale à la droite FD (prop. 34. I) et puisqu'un des côtés du triangle FBE, savoir, le côté AC est parallèle au côté FE, le côté BA sera au côté AF comme le côté BC est au côté CE (prop. 2. VI). Mais la droite AF est égale à la droite CD ; donc BA est à CD comme BC est à CE (prop. 7. V), et, en alternant, AB est à BC comme CD est à CE (prop. 16. V). De plus, puisque la droite CD est parallèle à la droite BF, la droite BC sera à la droite CE comme la droite FD est à la droite DE. Mais la droite DF est égale à la droite AC : donc BC est à CE comme AC est à ED, et en alternant, BC est à CA comme CE est à ED; mais puisqu'on a démontré que AB, est à BC comme DC est à CE, et que BC est à CA comme CE est à ED, la droite BA sera à la droite AC comme CD est à DE (prop. 23. V). Donc dans les triangles équiangles les côtes qui sont autour des angles égaux sont proportionnels, et les côtés qui sous-tendent des angles égaux sont homologues ; ce qu'il fallait dé montrer.

PROPOSITION V.

THÉORÈME.

Si deux triangles ont leurs côtés proportionnels, ces deux triangles seront équiangles et les angles sous-tendus par les côtés homologues seront égaux.

Soient deux triangles ABC, DEF (fig. 125) dont les côtés soient proportionnels, de manière que AB soit à BC comme DE est à EF, que BC soit à CA comme EF est à FD et que BA soit à AC comme ED est à DF : je dis que les triangles ABC, DEF sont équiangles et que les angles sous-tendus par les côtés homologues sont égaux, savoir, l'angle ABC égal à l'angle DEF, l'angle BCA égal à l'angle EFD, et enfin l'angle BAC égal à l'angle EDF.

Construisez sur la droite EF et aux points E, F l'angle FEG égal à l'angle ABC et l'angle EFG égal à l'angle BCA (prop. 25. I) ; le troisième angle BAC sera égal au troisième angle ÉGF (prop. 32. I) : donc les triangles ABC, EGF sont équiangles : donc dans les deux triangles ABC, EGF, les côtés qui sont autour des angles égaux sont proportionnels et les côtés qui sous-tendent les angles égaux sont homologues (prop. 4. VI) : donc AB est à BC comme GE est à EF, mais AB est à BC comme DE est à EF : donc DE est à EF comme GE est à EF (prop. 11. V) : donc l'une et l'autre des droites DE, GE ont la même raison avec la droite EF : donc la droite DE est égale à la droite GE (prop. 9. V). La droite DF sera égale à la droite GF, par la même raison. Donc, puisque la droite EG est égale à la droite DE, et que la droite EF est commune, les deux droites DE, EF sont égales aux deux droites GE, EF ; mais la base DF est égale à la base GF : donc l'angle DEF est égal à l'angle GEF (prop. 8. I); donc le triangle DEF est égal au triangle GEF et les autres angles qui sont sous-tendus par les côtés égaux sont encore égaux : donc l'angle DFE est égal à l'angle GFE et l'angle EDF égal à l'angle EGF. Puisque DEF est égal à l'angle GEF et que l'angle GEF est égal à l'angle ABC, par construction, l'angle ABC sera égal à l'angle DEF. Par la même raison l'angle ACB sera égal à l'angle DFE et l'angle A égal à l'angle D : donc les triangles ABC, DEF sont équiangles.

Donc si deux triangles ont leurs côtés proportionnels, ces deux triangles seront équiangles, et les angles sous-tendus par les côtés homologues seront égaux ; ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Si deux triangles ont un angle égal à un angle, et si les côtés qui sont autour des angles égaux sont proportionnels, ces deux triangles seront équiangles et les angles sous-tendus par les côtés homologues seront égaux.

Soient les deux triangles ABC, DEF (fig. 126), ayant un angle BAC égal à un angle EDF, et ayant de plus les côtés qui sont autour des angles égaux proportionnels entre eux, de manière que BA soit à AC comme ED est à DF : je dis que les triangles ABC, DEF sont équiangles et que l'angle ABC est égal à l'angle DEF et l'angle ACB égal à l'angle DFE.

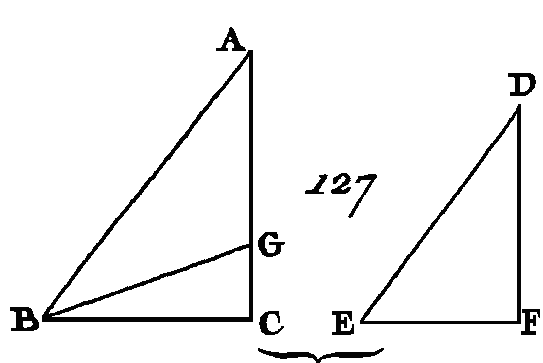
Sur la droite DF et aux points D, F construisez l'angle FDG égal à l'un ou à l'autre des angles BAC, EDF et l'angle DFG égal à l'angle ACB (prop. 23. I). L'angle restant B sera égal à l'angle restant G (prop. 32. I) : donc les triangles ABC, DGF sont équiangles : donc B A est à AC comme GD est à DF (prop. 4. VI) ; mais on suppose que BA est à AC comme ED est à DF : donc ED est à DF comme GD est à DF (prop. 11. V) : donc le côté ED est égal au côté DG (prop. 9. V); mais le côté DF est commun : donc les deux droites ED, DF sont égales aux deux droites GD, DF; mais l'angle EDF est égal à l'angle GDF : donc la base EF est égale à la base FG (prop. 4. I) donc le triangle DEF égal au triangle GDF et les autres angles qui sont sous-tendus par les côtés égaux sont encore égaux : donc l'angle DFG est égal à l'angle DFE et l'angle G égal à l'angle E. Mais l'angle DFG est égal à l'angle ACB, par construction : donc l'angle ACB est égal à DFE; mais l'angle BAC est supposé égal à l'angle EDF : donc l'angle restant B est égal à l'angle restant E (prop. 32. I) : donc les deux triangles ABC, DEF sont équiangles.

Donc si deux triangles ont un angle égal à un angle, et si les côtés qui sont autour des angles égaux sont proportionnels, ces deux triangles seront équiangles, et les angles sous-tendus par les côtés homologues seront égaux ; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Si deux triangles ont un angle égal à un angle, si les côtés placés autour de deux autres angles sont proportionnels entre eux, et si chacun des angles restons est en même temps ou plus petit ou n'est pas plus petit qu'un angle droit, les triangles seront équiangles et les angles adja-cens aux côtés proportionnels seront égaux.

Soient les deux triangles ABC, DEF (fig. 127) ayant un angle égal à un angle, savoir, l'angle BAC égal à l'angle EDF et les côtés qui sont autour de deux autres angles ABC, DEF proportionnels entre eux, de manière que DE soit à EF comme AB est à BC, et que chacun des deux autres angles ACB, DFE soit plus petit qu'un angle droit : je dis que les triangles ABC, DEF sont équiangles, que l'angle ABC est égal à l'angle DEF, et l'angle ACB égal à l'angle DFE.

Car si l'angle ABC n'est pas égal à l'angle DEF, l'un d'eux sera plus grand. Que l'angle ABC soit le plus grand. Construisez sur la droite AB et au point B un angle ABG égal à l'angle DEF (prop. 23. I).

Puisque l'angle A est égal à l'angle D et l’angle ABG égal à l'angle DEF, l'angle AGB sera égal à l'angle DFE (prop. 32. I) : donc les triangles ABG, DEF sont équiangles : donc AB est à BG comme DE est à EF (prop. 4. VI) ; mais par supposition DE est à EF comme AB est à BC : donc AB est à BC comme AB est à BG (prop. 11. V) : donc la droite AB a la même raison avec chacune des droites BC, BG : donc la droite BC sera égale à la droite BG et par conséquent l'angle BGC est égal à l'angle BCG (prop. 5. I) ; mais on a supposé que l'angle G est plus petit qu'un angle droit : donc l'angle BGC est plus petit qu'un angle droit et par conséquent l'angle de suite AGB est plus grand, qu'un angle droit (prop. 13. I) ; mais on a démontré que l'angle AGB est égal à l'angle F : donc l'angle F est plus grand qu'un angle droit ; mais on a supposé qu'il était plus petit qu'un, angle droit, ce qui est absurde : donc les angles, ABG, DEF ne sont pas inégaux : donc ils sont égaux ; mais l'angle A est égal à l'angle D : donc l'angle C est égal à l'angle F : donc les triangles ABC, DEF sont égaux.

Supposons à présent que l'un et l'autre des angles C, F n'est pas plus petit qu'un angle droit : je dis encore que les triangles ABC, DEF sont équiangles.

Ayant fait la même construction, nous démontrerons semblablement que le côté BC est égal au côté BG et l'angle C égal à l'angle BGC ; mais l'angle C n'est pas plus petit qu'un angle droit : donc l'angle BGC n'est pas plus petit qu'un angle droit : donc deux angles du triangle BGC ne sont pas plus petits que deux angles droits, ce qui est impossible (prop. 17. I) : donc les angles ABC, DEF ne sont pas inégaux : donc ils sont égaux ; mais l'angle A est égal à l'angle D : donc l'angle C est égal à l'angle F (prop. 32. I) : donc les triangles ABC, DEF sont équiangles.

Donc si deux triangles ont un angle égal à un angle, si les côtés placés autour de deux autres angles sont proportionnels entre eux, et si chacun-des angles restants est en même tems plus petit ou n'est pas plus petit qu'un angle droit, les triangles seront équiangles et les angles adja-cens aux côtés proportionnels seront égaux ; ce qu'il fallait démontrer.

PROPOSITION VIII.

THÉORÈME;

Si dans un triangle rectangle on conduit une perpendiculaire de l'angle droit sur la base, les triangles placés autour de la perpendiculaire sont semblables au triangle total et semblables entre eux.

Soit le triangle rectangle ABC (fig. 128) dont l'angle BAC est droit; du point A conduisez la perpendiculaire AD sur la base BC : je dis que les triangles ABD, ADC sont semblables au triangle total ABC et semblables entre eux.

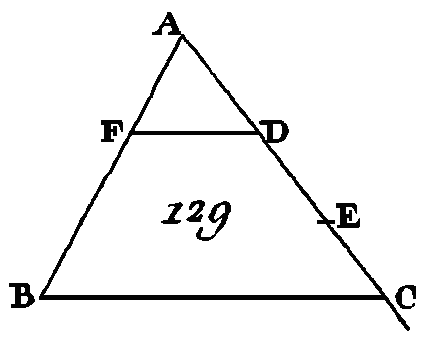
Car puisque l'angle BAC est égal à l'angle ADB, étant droits l'un et l'autre, et que l'angle B est commun aux deux triangles ABC, ABD, l'angle restant ACB sera égal à l'angle restant BAD (prop. 32. I) : donc les deux triangles ABC, ABD sont équiangles : donc le côté BC qui sous-tend l'angle droit du triangle ABC, est au côté BA qui sous-tend l'angle droit du triangle ABD comme le côté AB qui sous-tend l'angle C du triangle ABC, est au côté BD qui sous-tend un angle égal à l'angle C, c'est-à-dire l'angle BAD du triangle ABD, et enfin comme le côté AC est au côté AD qui soutend un angle B commun à ces deux triangles : donc les triangles ABC, ABD sont équiangles, et les côtés placés autour à des angles égaux sont proportionnels entre eux (prop. 4. VI) : donc le triangle ABC est semblable au triangle ABD (déf. 1. VI). Nous démontrerons que de même le triangle ADC est semblable au triangle ABC : donc chacun des triangles ABD, ADC est semblable au triangle total ABC.

Je dis de plus que les triangles ABD, ADC sont semblables entre eux.

Car puisque l'angle droit BDA est égal à l'angle droit ADC, et à cause qu'il a été dé montré que l'angle BAD est égal à l'angle C, l'angle restant B sera égal à l'angle restant DAC (prop. 32. I) : donc les deux triangles ABD, ADC sont équiangles : donc le côté BD du triangle ABD, qui sous-tend l'angle BAD est au côté DA du triangle ADC, qui sous-tend l'angle C égal à l'angle BAD, comme le côté AD du triangle ABD qui sous-tend l'angle B est au côté DC du triangle ADC qui sous-tend l'angle DAC égal à l'angle B, et comme le côté BA qui soutend l'angle droit ADB est au côté AC qui soutend l’angle droit ADC (prop. 4. VI) : donc le triangle ABD est semblable au triangle ADC (déf. 1. VI).

Donc si dans un triangle rectangle, on conduit une perpendiculaire de l'angle droit sur la base, les triangles placés autour de la perpendiculaire sont semblables au triangle total et semblables entre eux ; ce qu'il fallait démontrer.

COROLLAIRE.

Il suit de là que, dans un triangle rectangle la perpendiculaire conduite de l'angle droit, sur la base, est moyenne proportionnelle entre les segments de la base, et que chaque côté de l'angle droit est moyen proportionnel entre la base et le segment qui lui est contigu.

PROPOSITION IX.

PROBLÈME.

D'une droite donnée retrancher une partie demandée.

Soit AB (fig. 129) la droite donnée : il faut de la droite AB retrancher une partie demandée.

Que la partie demandée soit le tiers de cette droite du point A conduisez une droite quelconque AC qui fasse avec la droite AB un angle quelconque ; prenez sur la droite À C un point quelconque D et faites les droites DE, EC égales chacune à la droite AD (prop. 3. I); conduisez ensuite la droite BC et par le point D conduisez la droite DF parallèle à la droite BC (prop. 31. I).

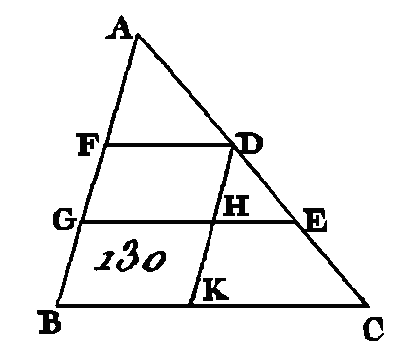
Puisqu'on a conduit la droite FD parallèle à un des côtés du triangle ABC, savoir, au côté BC, la droite CD sera à la droite DA comme la droite BF est à la droite FA (prop. 2. VI); mais la droite CD est double de la droite DA : donc la droite BF est double de la droite FA : donc la droite BA est double de la droite AF.

Donc on a retranché de la droite donnée AB sa troisième partie demandée ; ce qu'il fallait faire.

PROPOSITION X.

PROBLÈME.

Partager une droite donnée qui n'est point partagée de la même manière qu'une autre droite donnée est partagée.

Soit AB (fig. 130) la droite donnée qui n'est point partagée et AC la droite donnée qui est partagée: il faut partager la droite AB qui n'est pas partagée de la même manière que la droite AC est partagée.

Que la droite AC soit partagée aux points D, E, et que les droites AC, AB soient placées de manière qu'elles comprennent un angle quelconque. Conduisez la droite BC, et par les points D, E, conduisez les droites DF, EG parallèles à la droite BC (prop. 31. I), et par le point D conduisez la droite DHK parallèle à la droite AB.

Les figures FH, HB sont des parallélogrammes, et par conséquent la droite DH est égale à la droite FG et la droite HK égale à la droite GB (prop. 34. I) et puisqu'on a conduit la droite HE parallèle à un des côtés du triangle DKC, savoir, au côté KC, la droite CE sera à la droite ED comme la droite KH est à la droite HD (prop. 2. VI); mais puisque la droite KH est égale à la droite BG et que la droite HD est égale à la droite GF, la droite CE est à la droite ED comme la droite BG est à la droite GF. De plus, puisqu'on a conduit la droite F D parallèle à un des côtés du triangle AGE, savoir au côte EG, la droite ED sera à la droite DA comme ]a droite G F est à la droite FA. Mais on a démontré que la droite CE est à la droite ED comme la droite BG est à la droite GF : donc la droite CE est à la droite ED comme la droite BG est à la droite GF, et la droite ED est à la droite DA comme la droite GF est à la droite FA.

Donc la droite donnée AB, qui n'est partagée, a été partagée de la même manière que la droite donnée AC; ce qu'il fallait faire.

PROPOSITION XI.

PROBLÈME.

Deux droites étant données, trouver une troisième proportionnelle.

Soient AB, AC (fig. 131) les deux droites données; placez-les de manière qu'elles comprennent un angle quelconque : il faut trouver une troisième proportionnelle aux droites AB, AC.

Prolongez les droites AB, AC vers les points D, E; faites la droite BD égale à la droite AC; menez la droite BC, et, par le point D, menez la droite DE parallèle à la droite BC (prop. 31. I).

Puisque la droite BC est parallèle à un des côtés du triangle ADE, savoir au côté DE, la droite AB sera à la droite BD comme la droite AC est à la droite CE (prop. 2. VI); mais la droite BD est égale à la droite AC : donc la droite AB est à la, droite AC comme la droite AC est à la droite CE.

Donc les deux droites AB, AC ayant été, données, on a trouvé une troisième proportionnelle CE; ce qu'il fallait faire.

PROPOSITION XII.

PROBLÈME.

Trois droites étant données, trouver une quatrième proportionnelle.

Soient A, B, C (fig. 132), les trois droites données, il faut trouver une quatrième proportionnelle aux trois droites A, B, C.

Menez les deux droites DE, DF, comprenant un angle quelconque EDF ; faites la droite DG égale à la droite A, la droite GE égale à la droite B et la droite DH égale à la droite C. Menez la droite GH, et par le point E menez la droite EF parallèle à la droite GH.

Puisque la droite GH est parallèle à un des côtés du triangle DEF, savoir au côté EF, la droite DG sera à la droite GE comme la droite DH est à la droite HF (prop. 2. VI). Mais la droite DG est égale à la droite A, la droite GE égale à la droite B, et la droite DH égale à la droite C : donc la droite A est à la droite B comme la droite C est à la droite HF.

Donc trois droites A, B, C étant données, on a trouvé, une quatrième proportionnelle HF ; ce qu'il fallait faire.

PROPOSITION XIII.

PROBLÈME.

Deux droites étant données, trouver une moyenne proportionnelle.

Soient AB, BC (fig. 133) les deux droites données ; il faut trouver une moyenne proportionnelle entre ces deux droites.

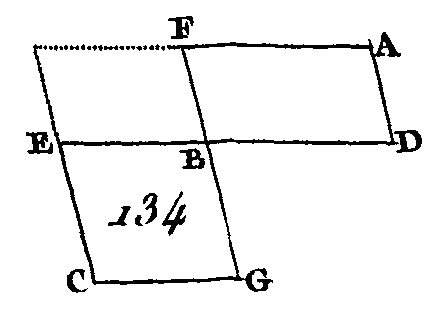
Placez ces deux droites dans la même direction, et sur la droite AC décrivez le demi-cercle ADC, du point B élevez la perpendiculaire AC et menez les droites AD, DC (prop. 11. I).

Puisque l'angle ADC est dans un demi-cercle, cet angle est droit (prop. 31. III); et puisque dans le triangle rectangle ADC on a conduit de l’angle droit la droite DB perpendiculaire sur la base, la droite DB sera moyenne proportionnelle entre les segments de la base AB, BC (corrol. 8. VI).

Donc les deux droites AB, BC ayant été données, on a trouvé une moyenne proportionnelle DB; ce qu'il fallait faire.

PROPOSITION XIV.

PROBLÈME.

Si deux parallélogrammes égaux ont un angle égal à un angle, les côtés qui sont placés autour des angles égaux sont réciproquement proportionnels ; et si deux parallélogrammes ont un angle égal à un angle, et si les cotés qui sont placés autour des angles égaux sont réciproquement proportionnels, ces deux parallélogrammes sont égaux entre eux.

Soient AB, BC (fig. 134) deux parallélogrammes égaux, ayant deux angles égaux en B. Placez la droite BE dans la direction de DB; la droite BC sera dans la direction de FB (prop. 14. I) : je dis que les côtés des parallélogrammes AB, BC qui sont placés autour des angles égaux sont réciproquement proportionnels, c'est-à-dire que DB est à BE comme GB est à BF.

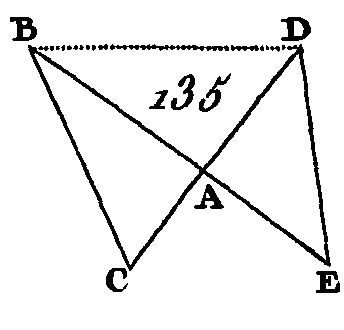
Achevez le parallélogramme FE.

Puisque le parallélogramme AB est égal au parallélogramme BC et que EF est un troisième parallélogramme, AB sera à FE comme BC est à FE (prop. 7. V); mais AB est à FE comme DB est à BE (prop. 1. VI); et BC est à FE comme GB est à BF : donc DB est à BE comme GB est à BF (prop. 11. V) : donc les côtés des parallélogrammes AB, BC qui sont autour des angles égaux sont réciproquement proportionnels.

Supposons à présent que les côtés qui sont autour des angles égaux soient réciproquement proportionnels, c'est-à-dire que DB soit à BE comme GB est à BF : je dis que le parallélogramme AB est égal au parallélogramme BC.

Puisque DB est à BE comme GB est à BF que DB est à BE comme le parallélogramme AB est au parallélogramme FE (prop. 1. VI), et que GB est à BF comme le parallélogramme BC est au parallélogramme FE, AB sera à FE comme BG est à FE (prop. 11. V) : donc le parallélogramme AB est égal au parallélogramme BC. (prop. 9. V).

Donc si deux parallélogrammes égaux ont un angle égal à un angle, les côtés qui sont autour des angles égaux sont réciproquement proportionnels ; et si deux parallélogrammes ont un angle égal à un angle, et si les côtés qui sont autour des angles égaux sont réciproquement proportionnels, ces deux parallélogrammes sont égaux; ce qu'il fallait démontrer.

PROPOSITION XV.

THÉORÈME.

Si deux triangles égaux ont un angle égal à un angle, les côtés placés autour des angles égaux sont réciproquement proportionnels ; et si deux triangles ont un angle égal à un angle, et si les côtés placés autour de ces angles égaux sont réciproquement proportionnels, ces deux triangles sont égaux entre eux.

Soient ABC, ADE (fig. 135) des triangles égaux, ayant un angle égal à un angle, savoir, l'angle BAC égal à l'angle DAE : je dis que les côtés des triangles ABC, ADE placés autour des angles égaux sont réciproquement proportionnels entre eux, c'est-à-dire que CA est à AD comme EA est à AB.

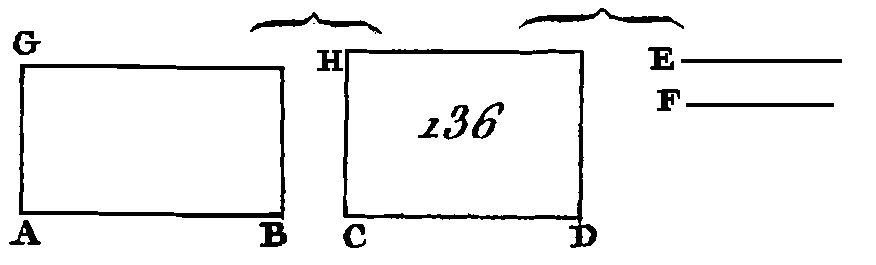
Placez ces triangles de manière que la droite CA soit dans la direction de la droite AD; la droite EA sera dans la direction de la droite AB (prop. 14. I). Menez la droite BD.

Puisque le triangle ABC est égal au triangle ADE et que ABD est un autre triangle, le-triangle CAB sera au triangle BAD comme le triangle ADE est au triangle BAD (prop. 7. V) ; mais le triangle CAB est au triangle BAD comme CA est à AD (prop. 1. VI), et le triangle EAD est au triangle BAD comme EA est à AB : donc CA est à AD comme EA est à AB (prop. 11. V) : donc les côtés des triangles ABC, ADE, qui sont autour des angles égaux, sont réciproquement proportionnels.

Supposons à présent que les côtés des triangles ABC, ADE soient réciproquement proportionnels, c'est-à-dire que CA soit à AD comme EA est à AB : je dis que le triangle ABC l’est égal au triangle ADE. Menez BD.

Puisque CA est à AD comme EA est à AB, que CA est à AD comme le triangle ABC est au triangle BAD (prop. 1. VI), et que EA est à AB comme le triangle EAD est au triangle BAD, le triangle ABC sera au triangle BAD comme le triangle EAD est au triangle BAD (prop. 11. V) : donc l'un et l'autre des triangles ABC, ADE ont la même raison avec le triangle BAD : donc le triangle ABC est égal au triangle EAD (prop. 9. V).

Donc si deux triangles égaux ont un angle égal a un angle, les côtés placés autour de ces angles égaux sont réciproquement proportionnels ; et si deux triangles ont un angle égal à un angle, et si les côtés placés autour des angles égaux sont réciproquement proportionnels, ces deux triangles seront égaux ; ce qu'il fallait démontrer.

PROPOSITION XVI.

THÉORÈME.

Si quatre droites sont proportionnelles, le rectangle compris sous les deux droites extrêmes est égal au rectangle qui est compris sous les deux droites moyennes ; et si le rectangle compris sous deux droites extrêmes est égal à celui qui est compris sous deux droites moyennes, ces quatre droites sont proportionnelles.

Soient AB, CD, E, F (fig. 136) quatre droites proportionnelles de manière qu'on ait AB est à CD comme E est à F : je dis que le rectangle compris sous les droites AB, F est égal au rectangle compris sous les droites CD, E.

Des points A, C et sur les droites AB, CD élevez les perpendiculaires AG, CH (prop. 11. I), faites la droite AG égale à la droite F et la droite CH égale à la droite E, et terminez les parallélogrammes BG, DH.

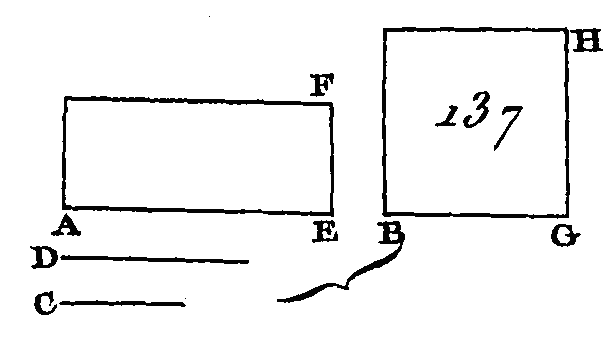
Puisque AB est à CD comme E est à F et que E est égal à CH et F égal à AG, AB sera à CD comme CH est à AG (prop. 7. V) : donc les côtés des parallélogrammes BG, DH placés autour des angles égaux sont, réciproquement, proportionnels ; mais lorsque les côtés des parallélogrammes équiangles qui sont autour des angles égaux sont réciproquement proportionnels, ces parallélogrammes sont égaux entre eux (prop. 14. VI) : donc le parallélogramme BG est égal au parallélogramme DH, mais le parallélogramme BG est compris sous les droites AB, F ; car AG est égal à F, et le parallélogramme DH est compris sous les droites CD, E ; puisque CH est égal à E : donc le rectangle compris sous les droites AB, F est égal à celui qui est compris sous les droites CD, E.

Si le rectangle compris sous les droites AB, F est égal à celui qui est compris sous les droites CD, E : je dis que ces quatre droites sont proportionnelles, c'est-à-dire que AB est à CD comme E est à F.

Faites la même construction ; le rectangle compris sous les droites AB, F est égal à celui qui est compris sous les droites CD, E ; mais le, rectangle BG est compris sous les droites AB, F ; car AG est égal à F et le rectangle DH est compris sous les droites CD, E, car CH est égal à E : donc le parallélogramme BG est égal au parallélogramme DH et ces deux parallélogrammes sont équiangles. Mais les côtés des parallélogrammes égaux et équiangles placés autour des angles égaux sont réciproquement proportionnels (prop. 14. VI) : donc AB est à CD comme CH est à AG; mais CH est égal à E et AG égal à F : donc AB est à CD comme E est à F.

Donc si quatre droites sont proportionnelles, le rectangle compris sous les droites extrêmes est égal au rectangle compris sous les droites moyennes ; et si un rectangle compris sous deux droites extrêmes est égal à un rectangle compris sous deux droites moyennes, ces quatre droites sont, proportionnelles ; ce qu'il fallait démontrer.

PROPOSITION XVII.

THÉORÈME.

Si trois droites sont proportionnelles, le rectangle compris sous les droites extrêmes est égal au carré de la droite moyenne; et si un rectangle compris sous deux droites extrêmes est égal au carré d'une droite moyenne, ces trois droites sont proportionnelles.

Soient AE, BG, C (fig. 137) trois droites proportionnelles, de manière que l'on ait AE est à BG comme BG est à C : je dis que le rectangle compris sous les droites AE, C est égal au carré de BG.

Faites la droite D égale à la droite BG.

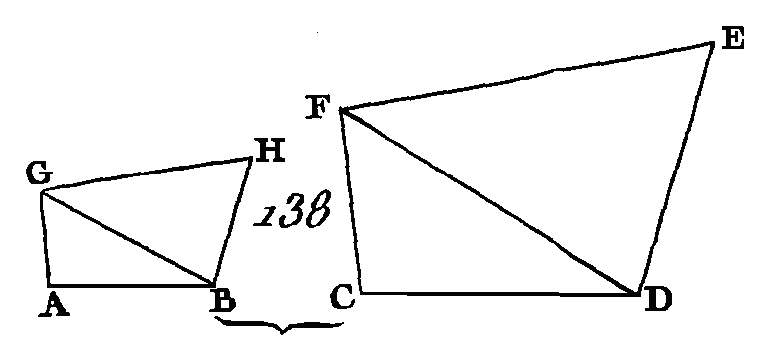
Puisque AE est à BG comme BG est à C et que BG est égal à D, la droite AE sera à la droite BG comme la droite D est à la droite C ; mais si quatre droites sont proportionnelles, le rectangle compris sous les droites extrêmes est égal à celui qui est compris sous les droites moyennes (prop. 16. VI) : donc le rectangle compris sous les droites AE, C est égal à celui qui est compris sous les droites BG, D. Mais le rectangle compris sous les droites BG, D est égal au carré de BG, car la droite BG est égale à la droite D : donc le rectangle compris sous les droites AE, C est égal au carré de BG.

Si le rectangle compris sous les droites AE, C est égal au carré de BG : je dis que AE est à BG comme BG est à C.

Faites la même construction. Puisque le rectangle compris sous les droites AE, C est égal au carré de BG et que le carré de BG est un rectangle compris sous les droites BG, D, car BG est égal à D, le rectangle compris sous les droites AE, C. est égal au rectangle compris sous les droites BG, D. Mais si un rectangle compris sous deux droites extrêmes est égal à un rectangle compris sous deux droites moyennes, les quatre droites seront proportionnelles (prop 16. VI) : donc AE est à BG comme D est à C; mais BG est égal à D : donc AE est à BG comme BG est à C. Donc si trois droites sont proportionnelles, le rectangle compris sous les droites extrêmes sera égal au carré de la droite moyenne ; et si un rectangle compris sous deux droites extrêmes est égal au carré de la droite moyenne, ces trois droites seront proportionnelles, ce qu'il fallait démontrer.

PROPOSITION XVIII.

PROBLEME.

Sur une droite donnée, décrire une figure rectiligne semblable à une autre et semblablement placée.

Soit AB (fig. 138) la droite donnée et CE la figure donnée : il faut sur la droite AB décrire une figure semblable à la figure CE et semblablement placée.

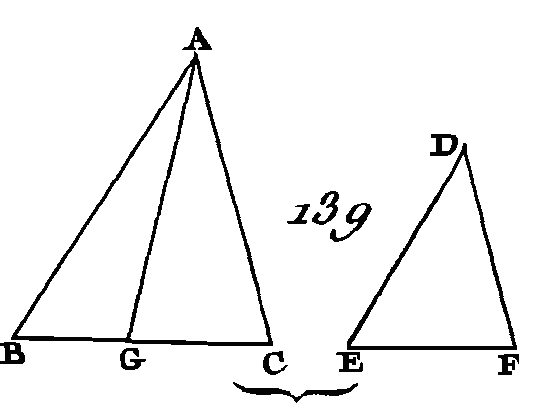
Menez la droite DF, et sur la droite AB et aux points A, B faites l'angle GAB égal à l'angle C, et l’angle ABG égal à l'angle CDF (prop. 23. I); l'angle restant CFD sera égal à l'angle restant AGB (prop. 32. I) : donc les triangles FCD, GAB sont équiangles : donc F D est à GB comme FC est à GA, et comme CD est à AB (prop. 4. VI). Construisez ensuite sur la droite BG et aux points B, G l'angle BGH égal à l'angle DFE et l'angle GBH égal à l'angle FDE ; l'angle E restant sera égal à l'angle H restant : donc les triangles FDE, GBH sont équiangles : donc FD est à GB comme FE est à GH, et comme ED est à HB (prop. 4. VI). Mais on a démontré que FD est à GB comme FC est à GA, et comme CD est à AB : donc FC est à G A comme CD est à AB, comme FE est à GH, et comme ED est à HB (prop. 11. V). Mais l'angle CFD est égal à l'angle AGB par construction, et l'angle DFE égal à l'angle BGH : donc l'angle total CFE est égal à l'angle total AGH. Par la même raison, l'angle CDE est égal à l'angle ABH, l'angle C égal à l'angle A et l'angle E égal à l'angle H : donc les figures AH, CE sont équiangles, et elles ont les côtés opposés aux angles égaux proportionnels entre eux : donc les deux figures AH, CE sont semblables (déf. 1. VI).

Donc, sur la droite AB on a décrit la figure AH semblable à la figure CE et semblablement placée ; ce qu'il fallait faire.

PROPOSITION XIX.

THÉORÈME.

Les triangles semblables sont entre eux en raison doublée des côtés homologues.

Soient ABC, DEF (fig. 139) deux triangles semblables, ayant l'angle B égal à l'angle E. Supposons que AB soit à BC comme DE est à EF, de manière que le côté BC soit l'homologue du côté EF (déf. 12. V) : je dis que les triangles ABC, DEF sont entre eux en raison doublée des côtés BC, EF.

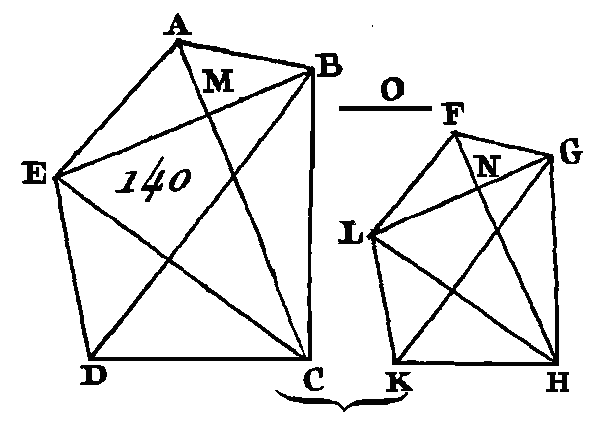
Prenez une troisième proportionnelle BG (fig. 138) aux droites BC, EF, de manière que BC soit à EF comme EF est à BG, et menez la droite GA (prop. 11. VI).

Puisque AB est à BC comme DE est à EF, si l'on rechange les places des moyens, on aura AB est à DE comme BC est à EF (prop. 16. V) ; mais BC est à EF comme EF est à BG : donc AB est à DE comme EF est à BG (prop. 11. 5) : donc les côtés des triangles ABG, DEF placés autour des angles égaux sont réciproquement proportionnels. Mais deux triangles sont égaux entre eux lorsqu'ils ont un angle égal à un angle et lorsque les côtés placés autour des angles égaux sont réciproquement proportionnels (prop. 15. VI) : donc le triangle ABG est égal au triangle DEF. Mais puisque BC est à EF comme EF est à BG, et que lorsque trois droites sont proportionnelles, la première et la troisième sont entre elles en raison doublée de la première et de la seconde (déf. 10. V), les droites BC et BG seront entre elles en raison doublée de BC et de EF ; mais BC est à BG comme le triangle ABC est au triangle ABG (prop. 1. VI) : donc le triangle ABC et le triangle ABG sont entre eux en raison doublée de BC et de EF ; mais le triangle ABG est égal au triangle DEF : donc le triangle ABC et le triangle DEF sont entre eux en raison doublée de BC et de EF (prop. 7. V).

Donc les triangles semblables sont entre eux en raison doublée des côtés homologues ; ce qu'il fallait démontrer.

COROLLAIRE.

Il suit manifestement de là que si trois droites sont proportionnelles, la première sera à la troisième comme triangle décrit sur la première est triangle semblable qui est décrit semblablement sur la seconde, puisqu'il a été démontré que CB est à BG comme le triangle ABC est au triangle ABG, c'est-à-dire au triangle DEF.

PROPOSITION XX.

THÉORÈME.

Les polygones semblables peuvent se diviser en triangles semblables, égaux en nombre et proportionnels aux polygones ; et ces polygones sont entre eux en raison doublée de leurs côtés homologues.

Soient ABCDE, FGHKL (fig. 140) deux polygones semblables et que le côté AB soit l'homologue du côté FG : je dis que les polygones ABCDE, FGHKL peuvent se diviser en triangles semblables, égaux en nombre et proportionnels aux polygones, et que les polygones ABCDE, FGHKL sont entre eux en raison doublée des côtés AB, FG.

Menez les droites BE, EC, GL, LH.

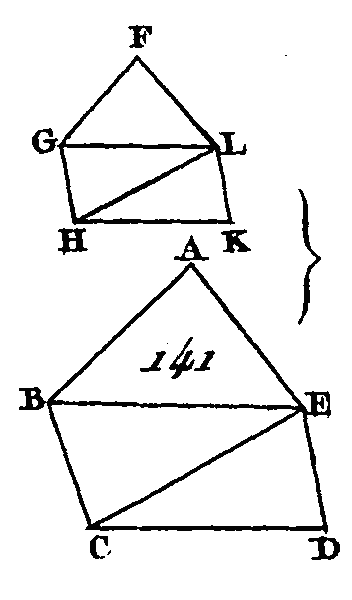
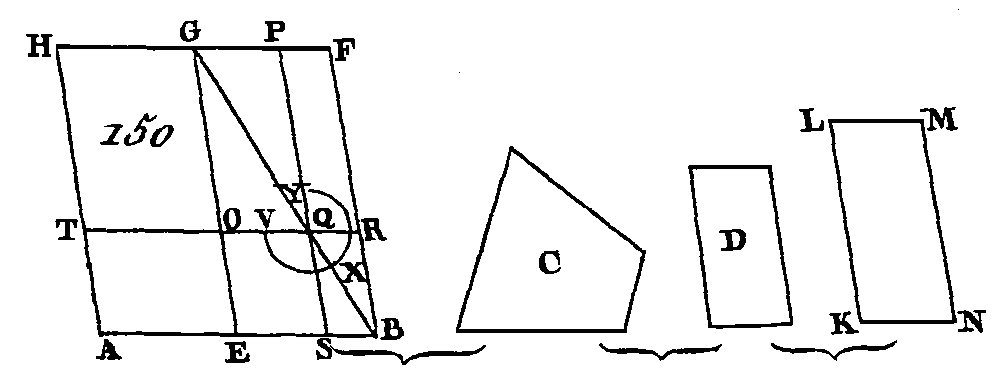
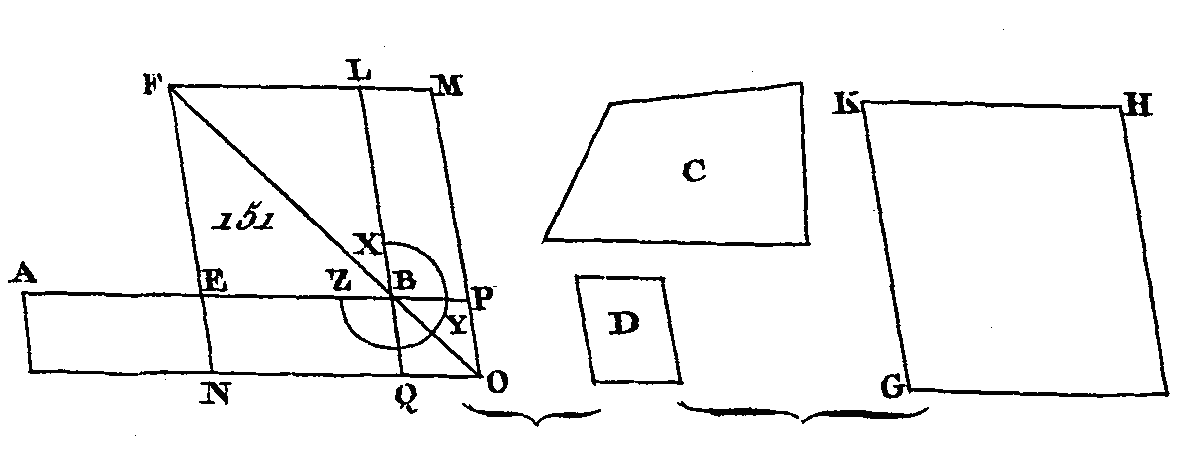
Puisque le polygone ABCDE est semblable au polygone FGHKL, l'angle BAE est égal à l'angle GFL ; mais BA est à AE comme GF est à FL : donc, puisque ces deux triangles ont un angle égal à un angle et que les côtés placés autour des angles égaux sont proportionnels, les triangles ABE, FGL seront équiangles (prop. 6. VI), et par conséquent semblables (prop. 4. VI) : donc l'angle ABE est égal à l'angle FGL; mais l'angle total ABC est égal à l'angle total FGH, à cause de la similitude des polygones : donc l'angle restant EBC est égal à l'angle restant LGH ; mais à cause de la similitude des triangles ABE, FGL, EB est à BA comme LG est à GF, et à cause de la similitude des polygones, AB est à BC comme FG est à GH, EB sera à BC comme LG est à GH (prop. 22. V), c'est-à-dire que les côtés placés autour des angles égaux EBC, LGH seront proportionnels : donc les triangles EBC, LGH sont équiangles (prop. 6. VI), et par conséquent semblables (prop. 4. VI). Par la même raison, les triangles ECD, LHK sont encore semblables : donc les polygones ABCDE, FGHKL sont divisés en triangles semblables et égaux en nombre.

Je dis de plus que ces triangles sont proportionnels aux polygones, c'est-à-dire que ces triangles sont entre eux comme les antécédents ABE, EBC, ECD sont aux conséquents FGL, LGH, LHK; je dis encore que les polygones ABCDE, FGHKL sont en raison doublée des côtés homologues, c'est-à-dire en raison doublée des côtés AB, FG.

Menez les droites AC, FH.

Puisqu'à cause de la similitude des polygones l'angle ABC est égal à l'angle FGH, et que AB est à BC comme F G est à GH, les triangles ABC, FGH seront équiangles (prop. 6. VI) : donc l'angle BAC est égal à l'angle GFH et l'angle BCA égal à l'angle GHF. De plus, puisque l'angle BAM est égal à l'angle GFN et qu'il a été démontré que l'angle ABM est égal à l'angle FGN, l'angle restant AMB sera égal à l'angle restant FNG (prop. 32. I) : donc les deux triangles ABM, FGN sont équiangles. Nous démontrerons semblablement que les deux triangles BMC, GNH sont équiangles : donc AM est à MB comme FN est à NG, et BM est à MC comme GN est à NH (prop. 4. VI) : donc AM est à MC comme FN est à NG (prop. 23. 5); mais A M est à MC comme le triangle ABM est au triangle MBC, comme le triangle AME est au triangle EMC, car ils sont entre eux comme leurs bases (prop. 1. VI), mais un seul des antécédents est à un seul des conséquents comme tous les antécédents sont à tous les conséquents (prop. 12. V) : donc le triangle AMB est au triangle BMC comme le triangle ABE est au triangle CBE; mais AMB est à BMC comme AM est à MC : donc AM est à MC comme le triangle ABE est au triangle EBC (prop. 11. V). Par la même raison FN est à NH comme le triangle FGL est au triangle GLH ; mais AM est à MC comme FN est à NH : donc le triangle ABE est au triangle BEC comme le triangle FGL est au triangle GLH (prop. 11. V) : ou bien en échangeant les places des moyens, le triangle ABE est au triangle FGL comme le triangle BEC est au triangle GLH (prop. 16. V). Nous démontrerons semblablement, après avoir mené BD, GH, que le triangle BEC est au triangle GLH comme le triangle ECD est au triangle LHK; mais puisque le triangle ABE est au triangle FGL comme le triangle EBC est au triangle LGH et comme le triangle ECD est au triangle LHK, un des antécédents sera à un des conséquents comme tous les antécédents seront à tous les conséquents (prop. 12. V) : donc le triangle ABE est au triangle FGL comme le polygone ABCDE est au polygone FGHKL; mais les triangles ABE, FGL sont entre eux en raison doublée des côtés AB, FH ; car les triangles semblables sont en raison doublée des côtés homologues (prop. 19. 6): donc les polygones ABCDE, FGHKL sont en raison doublée des côtés homologues AB, FG.

Donc les polygones semblables peuvent être divisés en un même nombre de triangles semblables et proportionnels aux polygones ; et les polygones semblables sont entre eux en raison doublée des côtés homologues ; ce qu'il fallait démontrer.

COROLLAIRE I.

On démontrera de la même manière que les quadrilatères semblables sont en raison doublée des côtés homologues ; mais cela a été démontré pour les triangles semblables (corol. 19. VI) : donc généralement les figures rectilignes semblables sont entre elles en raison doublée des côtés homologues.

COROLLAIRE II.

Si nous prenons une troisième proportionnelle O aux deux droites AB, FG, les droites AB, O seront en raison doublée des droites AB, FG (déf. 10. V) ; mais les polygones et les quadrilatères sont entre eux en raison doublée des côtés homologues, c'est-à-dire en raison doublée des côtés AB, FG ; l'on démontre cela pour les triangles ; il est donc généralement évident que si trois droites sont proportionnelles, la première et la troisième sont entre elles en raison doublée de la figure décrite sur la première, et de la figure semblable décrite semblablement sur la seconde.

AUTREMENT.

Nous démontrerons autrement et plus brièvement que les triangles sont proportionnels aux polygones de la manière suivante :

Soient les polygones ABCDE, FGHKL (fig. 141). Menez BE, EC, GL, LH : je dis que le triangle ABE est au triangle FGL comme le triangle EBC est au triangle LGH et comme le triangle CDE est au triangle H KL.

Puisque les triangles ABE, FGL sont semblables, les triangles ABE, FGL sont en raison doublée des côtés BE, GL (prop. 19. VI). Par la même raison les triangles BEC, GLH sont en raison doublée des côtés BE, GL : donc le triangle ABE est au triangle FGL comme le triangle EBC est au triangle LGH (prop. 11. V). De plus, puisque le triangle EBC est semblable au triangle LGH, les triangles EBC, LGH sont en raison doublée des droites CE,-HL (prop. 19. VI). Par la même raison les triangles ECD, LHK sont en raison doublée des droites CE, HL : donc le triangle EBC est au triangle LGH comme le triangle ECD est au triangle LHK (prop. 11. V) ; mais on a démontré que le triangle EBC est au triangle LGH comme le triangle ABE est au triangle FGL : donc le triangle ABE est au triangle FGL comme le triangle BEC est au triangle GLH et comme le triangle ECD est au triangle LHK : donc un des antécédents est à un des conséquents comme tous les antécédents sont à tous les conséquents (prop. 12. V) ; et le reste comme dans la première démonstration ; ce qu'il fallait démontrer.

PROPOSITION XXI.

THÉORÈME.

Les figures rectilignes qui sont semblables à une même figure rectiligne sont semblables entre elles.

Que chacune des figures rectilignes A, B (fig. 142) soit semblable à la figure rectiligne C : je dis que la figure rectiligne A est semblable à la figure rectiligne B.

Car puisque les figures rectilignes A et B sont semblables, ces deux figures sont équiangles et les côtés placés autour des angles égaux sont proportionnels (déf. 1. VI). De plus, puisque les figures rectilignes B, C sont semblables, ces deux figures sont équiangles et les côtés placés autour des angles égaux sont proportionnels : donc l'une et l'autre des figures rectilignes A, B sont équiangles avec la figure rectiligne C, et les côtés placés autour des angles égaux sont proportionnels : donc les figures rectilignes A, B sont équiangles (ax. 1), et les côtés placés autour des angles égaux sont proportionnels (prop. 11. V) : donc les figures rectilignes A, B sont semblables (déf. 1. VI); ce qu'il fallait démontrer.

PROPOSITION XXII.

THÉORÈME.

Si quatre droites sont proportionnelles, les figures rectilignes semblables, construites semblablement sur ces droites, seront proportionnelles ; et si les figures rectilignes semblables et construites semblablement sur ces droites sont proportionnelles, ces droites seront proportionnelles.

Soient AB, CD, EF, GH (fig. 143) quatre droites proportionnelles, de manière que AB soit à CD comme EF est à GH. Soient décrites sur les droites AB, CD les figures rectilignes semblables et semblablement placées KAB, LCD, et sur les droites EF, GH soient décrites les figures semblables et semblablement placées MF, NH : je dis que la figure rectiligne KAB est à la figure rectiligne LCD comme la figure rectiligne MF est à la figure rectiligne NH.

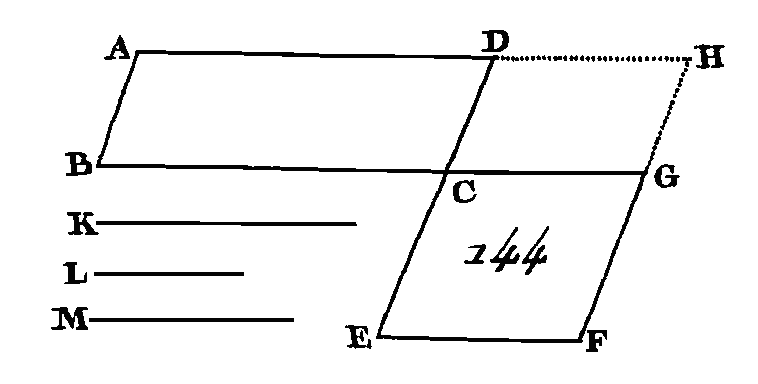
Prenez une troisième proportionnelle O aux droites AB, CD, et une troisième proportionnelle P aux droites EF, GH (prop. 11. VI). Puisque AB est à CD comme EF est à GH et que CD est à O comme GH est à P, AB sera à O comme EF est à P (prop. 22. V) ; mais AB est à O comme la figure rectiligne KAB est à la figure rectiligne LCD (cor. 2. prop. 20. VI), et EF est à P comme la figure rectiligne MF est à la figure rectiligne NG : donc KAB est à LCD comme MF est à NH (prop. 11. V).

Si la figure rectiligne KAB est à la figure rectiligne LCD comme la figure rectiligne MF est à la figure rectiligne NH : je dis que AB est à CD comme EF est à GH.

Prenons une quatrième proportionnelle aux trois droites AB, CD, EF de manière que l’on ait AB est à CD comme EF est à QR (prop. 12.6), et sur QR décrivez la figure rectiligne SR de manière qu'elle soit semblable à l'une et à l'autre des figures MF, NH, et semblablement placée (prop. 18. VI).

Puisque AB est à CD comme EF est à QR, que les figures rectilignes KAB, LCD décrites sur les droites AB, CD sont semblables et semblablement placées, et que les figures rectilignes MF, SR décrites sur les droites EF, QR sont semblables et semblablement placées, la figure rectiligne KAB est à la figure rectiligne LCD comme MF est à SR, ainsi que dans la première partie de cette proposition ; mais on suppose que la figure rectiligne KAB est à la figure rectiligne LCD comme la figure rectiligne MF est à la figure rectiligne NH : donc la figure rectiligne MF a la même raison avec l'une et l'autre des figures rectilignes NH, SR (prop. 11. V) : donc la figure rectiligne NH est égale à la figure rectiligne SR (prop. 9. V) ; mais la figure rectiligne NH est semblable à la figure SR et semblablement placée : donc GH est égal à QR (lem. suiv.), et puisque AB est à CD comme EF est à QR et que QR est égal à GH, AB sera à CD comme EF est à GH (prop. 7. V). Donc si quatre droites sont proportionnelles, les figures rectilignes semblables, construites semblablement sur ces droites, seront proportionnelles ; et si les figures rectilignes semblables et semblablement construites sur ces droites sont proportionnelles, ces droites seront proportionnelles ; ce qu'il fallait démontrer.

LEMME.

Si des figures rectilignes sont égales et semblables ; nous démontrerons de cette manière que leurs côtés homologues sont égaux entre eux.

Supposons que les figures rectilignes NH, SR soient égales et semblables, et que HG soit à GN comme QR est à QS : je dis que QR est égal à GH.

Car si ces droites sont inégales, une d'elles sera plus grande ; supposons que la droite QR soit plus grande que la droite HG. Puisque QR est à QS comme HG est à GN, si on échange les places des moyens, QR sera à HG comme QS est à GN (prop. 16. V) ; mais QR est plus grand que HG : donc QS sera plus grand que GN : donc la figure rectiligne RS est plus grande que la figure rectiligne HN (prop. 20. VI) ; mais elle lui est égale, ce qui est impossible : donc les droites QR, GH ne sont pas inégales : donc elles sont égales ; ce qu'il fallait démontrer.

PROPOSITION XX 111.

THÉORÈME.

Les parallélogrammes équiangles sont entre eux en raison composée des côtés.

Soient les parallélogrammes équiangles AC, CF (fig. 144), ayant l'angle BCD égal à l'angle ECG : je dis que les parallélogrammes AC, CF sont entre eux en raison composée des côtés, c'est-à-dire, en raison composée de la raison de BC à CG et de la raison DC à CE.

Placez la droite B C dans la direction de la droite CG; la droite DC sera placée dans la direction de CE (prop. 14. I). Achevez le parallélogramme DG; prenez une droite quelconque R, de manière que BC soit à CG comme, R est à L et que DC soit à CE comme L est à M (prop. 12. VI).

Les raisons de R à L et de L à M sont les mêmes que les raisons des côtés, c'est-à-dire de BC à CG et de DC à CE; mais la raison de R à M est composée de la raison de R à L et de la raison de L à M (déf. 5. VI) : donc les droites R et L sont entre elles en raison composée des côtés ; et puisque BC est à CG comme le parallélogramme AC est au parallélogramme CH (prop. 1. VI), et que BC est à CG comme R est à L, R sera à L comme le parallélogramme AC est au parallélogramme CH (prop. 11. V). De plus, puisque DC est à CE comme le parallélogramme CH est au parallélogramme CF, et que DC est à CE comme L est à M (prop. 1. VI), L sera à M comme le parallélogramme CH est au parallélogramme CF (prop. 11. V) : donc puisqu'il a été démontré que R est à L comme le parallélogramme AC est au parallélogramme CH, et que L est à M comme le parallélogramme CH est au parallélogramme GF, K sera à M comme le parallélogramme AC est au parallélogramme C F (prop. 22. V). Mais les droites K et M sont en raison composée des côtés : donc les parallélogrammes AC, CF sont entre eux en raison composée des côtés.

Donc les parallélogrammes équiangles sont entre eux en raison composée des côtés ; ce qu'il fallait démontrer.

PROPOSITION XXIV.

THÉORÈME.

Dans tout parallélogramme, les parallélogrammes placés autour du diamètre sont semblables au parallélogramme total et semblables entre eux.

Soit le parallélogramme ABCD (fig. 145) dont AC est le diamètre ; qu'autour du diamètre AC soient les parallélogrammes EG, HK : je dis que les parallélogrammes EG, HK, sont semblables au parallélogramme total ABCD et semblables entre eux.

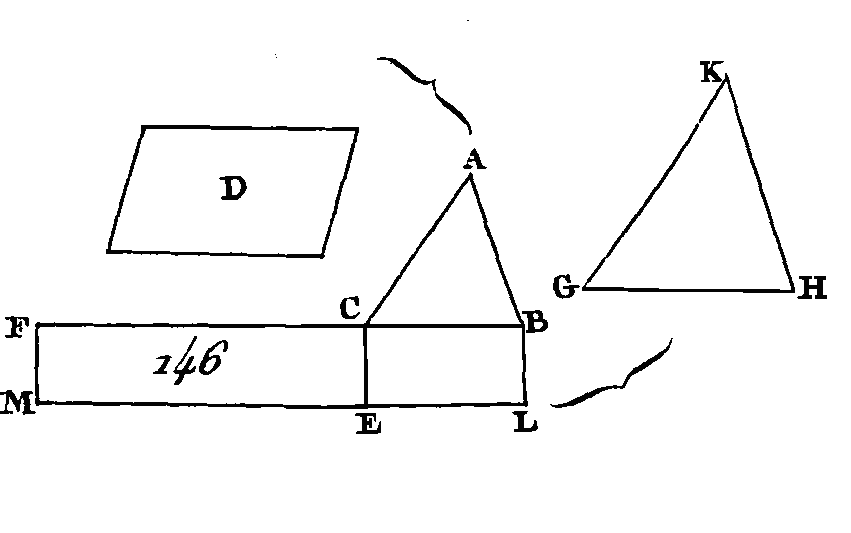
Car puisque la droite EF est parallèle à un des côtés du triangle ABC, savoir au côté BC, la droite BE sera à la droite EA comme la droite GF est à la droite FA (prop. 2. VI). De plus, puisque la droite FG est parallèle à un des côtés du triangle ACD, savoir au côté CD, la droite CF sera à la droite FA comme la droite DG est à la droite GA ; mais on a démontré que CF est à FA comme BE est à EA : donc BE est à EA comme DG est à GA (prop. 11. V) ; ajoutant les conséquents aux antécédents (prop. 18. V), BA sera à AE comme DA est à AG, et enfin en échangeant les places des moyens (prop. 16. V), BA sera à AD comme AE est à AG : donc les côtés des parallélogrammes ABCD, EG qui comprennent un angle commun BAD sont proportionnels. Puisque GF est parallèle à DC, l'angle AGF est égal à l'angle ADC (prop. 29. I), et l'angle GFA égal à l'angle DCA; mais l'angle DAC est commun aux deux triangles ADC, AGF : donc les triangles ADC, AGF sont équiangles. Les triangles ABC, AFE sont équiangles, par la même raison : donc le parallélogramme total ABCD et le parallélogramme EG sont équiangles : donc AD est à DC comme AG est à GF (prop. 4. VI) ; et AC est à CB comme AF est à FE, et de plus CB est à BA comme FE est à EA : donc puisqu'on a démontré que DC est à GA comme GF est à FA et que AC est à CB comme AF est à FE, DC sera à CB comme GF est à FE (prop. 23. V); donc les côtés dès parallélogrammes ABCD, EG qui sont autour des angles égaux sont proportionnels : donc le parallélogramme ABCD est semblable au parallélogramme EG (déf. 1. VI). Le parallélogramme ABCD est semblable au parallélogramme KH, par la même raison : donc chacun des parallélogrammes EG, HK est semblable au parallélogramme ABCD; mais les figures qui sont semblables chacune à une autre figure, sont semblables entre elles (prop. 21. VI) : donc le parallélogramme EG est semblable au parallélogramme HK.

Donc, dans tout parallélogramme, les parallélogrammes placés autour du diamètre sont semblables au parallélogramme total et semblables entre eux; ce qu'il fallait démontrer.

PROPOSITION XXV.

PROBLÈME.

Construire une figure semblable à une figure donnée et égale à une autre figure aussi donnée.

Soit ABC (fig. 146) la figure donnée, à laquelle il faut construire une figure semblable, et D la figure à laquelle il faut la faire égale : il faut construire une figure qui soit semblable à la figure ABC et égale à la figure D.

Construisez sur la droite BC un parallélogramme BE qui soit égal au triangle ABC, (prop. 44 et 45. I) et sur la droite CE et dans l'angle FCE qui est égal à l'angle CBL, construisez un parallélogramme CM égal à la figure D ; la droite BC sera dans la direction de CF, et la droite LE dans la direction de EM (prop. 14. I). Prenez une moyenne proportionnelle GH entre les droites BC, CF (prop. 13. VI), et sur cette moyenne proportionnelle G H, construisez une figure KGH semblable à la figure ABC et semblablement placée (prop. 18. VI).

Puisque BC est à GH comme GH est à CF, et puisque, lorsque trois droites sont proportionnelles, la première est à la troisième comme la figure qui est construite sur la première est à la figure semblable construite sur la seconde et semblablement placée (cor. 2, prop. 20. VI), la droite BC sera à la droite CF comme le triangle ABC est au triangle KGH; mais BC est à CF comme le parallélogramme BE est au parallélogramme EF (prop. 1. VI), et le triangle ABC est au triangle KGH comme le parallélogramme BE est au parallélogramme EF : donc en changeant les places des moyens (prop. 16. V), le triangle ABC sera au parallélogramme BE comme le triangle KGH est au parallélogramme EF; mais le triangle ABC est égal au parallélogramme BE, par construction : donc le triangle KGH est égal au parallélogramme EF ; mais le parallélogramme EF est égal à la figure D : donc le triangle KGH est aussi égal à la figure D; mais le triangle KGH est semblable au triangle ABC, par construction.

Donc on a construit une figure KGH semblable à la figure ABC et égale à une autre figure donnée; ce qu'il fallait faire.

PROPOSITION XXVI.

THÉORÈME.

Si d'un parallélogramme on retranche un parallélogramme qui soit semblable au parallélogramme entier et semblablement placé, et qui ait avec lui un angle commun, ces deux parallélogrammes seront placés autour du même diamètre.

Que du parallélogramme ABCD (fig. 147) on retranche le parallélogramme AEFG semblable au parallélogramme ABCD et semblablement placé et ayant avec lui un angle commun DAB : je dis que les parallélogrammes ABCD, AEFG sont placés autour du même diamètre.

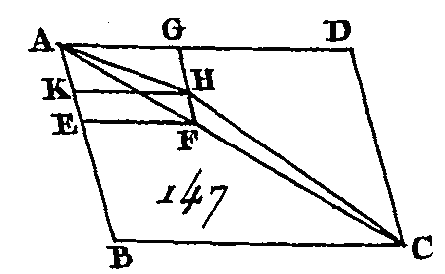
Car si cela n'est point, supposons, si cela est possible, que la droite AHC soit leur diamètre, et par le point H conduisons la droite HK parallèle à l'une et à l'autre des droites AD, BC. Puisque les parallélogrammes ABCD, KG sont placés autour du même diamètre, le parallélogramme ABCD sera semblable au parallélogramme KG (prop. 24. VI) : donc DA est à AB comme G A est à AK (déf. 1. VI), mais à cause de la similitude des parallélogrammes ABCD, EG, la droite DA est à la droite AB comme la droite GA est à la droite AE : donc G A est à AE comme GA est à AK (prop. 11. V) : donc la droite GA a la même raison avec chacune des droites AK, AE : donc la droite AK sera égale à la droite AE (prop. 9. V), c'est-à-dire que la plus petite sera égale à la plus grande, ce qui est impossible : donc les parallélogrammes ABCD, KG ne sont point placés autour du même diamètre : donc les parallélogrammes ABCD, AEFG sont placés autour du même diamètre. Donc si d'un parallélogramme on retranche un parallélogramme qui soit semblable au parallélogramme total et semblablement placé, et qui ait avec lui un angle commun, ces deux parallélogrammes seront placés autour du même diamètre ; ce qu'il fallait démontrer.

PROPOSITION XXVII.

THÉORÈME.

De tous les parallélogrammes qui sont appliqués sur la même droite et qui sont défaillants de parallélogrammes semblables au parallélogramme décrit sur la moitié de cette droite et semblablement placés que lui, le plus grand est celui qui est appliqué sur la moitié de cette droite et qui est semblable à son défaut.[1]

Soit la droite AB (fig. 148), que cette droite soit coupée en deux parties égales au point C, et que sur cette droite AB soit appliqué le parallélogramme AD qui est défaillant du parallélogramme CE semblable à celui qui est décrit sur la moitié de AB, c'est-à-dire sur AC : je dis que de tous les parallélogrammes qui sont appliqués sur la droite AB et qui sont défaillants de parallélogrammes semblables au parallélogramme CE et semblablement placés que lui, le plus grand est le parallélogramme AD. En effet, appliquez sur la droite AB le parallélogramme AF défaillant du parallélogramme RH semblable au parallélogramme CE et semblablement placé que lui : je dis que le parallélogramme AD est plus grand que le parallélogramme AF.

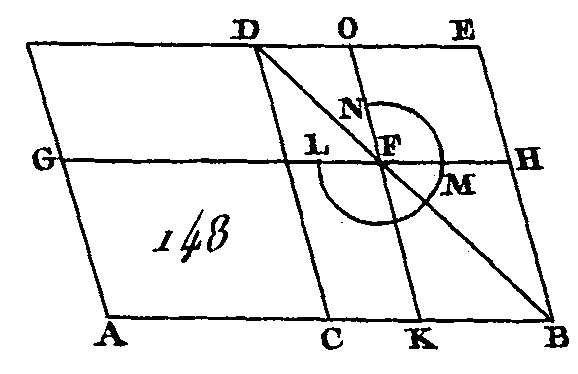
Puis le parallélogramme CE est semblable au parallélogramme KH, ces deux parallélogrammes seront placés autour du même diamètre (prop. 26. VI). Menez leur diamètre DB et décrivez la figure.

Puisque le parallélogramme CF est égal au parallélogramme FE (prop. 43. I), si l'on ajoute à chacun le parallélogramme KH, le parallélogramme total CH sera égal au parallélogramme total KE. Mais CH est égal à CG (prop. 36. I), parce que la droite AC est égale à la droite CB. Donc GC est égal à EK : donc si nous ajoutons à chacune de ces quantités le parallélogramme CF, le parallélogramme total AF sera égal au gnomon LMN : donc le parallélogramme CE, c'est-à-dire le parallélogramme AD, est plus grand que le parallélogramme AF (prop. 36. I).

Partageons de nouveau la droite AB (fig. 149) en deux parties égales au point C, et appliquons sur cette droite le parallélogramme AL défaillant du parallélogramme CM, et de plus appliquons sur la droite AB le parallélogramme AE défaillant du parallélogramme DF, semblablement posé et semblable au parallélogramme qui est décrit sur la moitié de AB, c'est-à-dire au parallélogramme CM. Je dis que le parallélogramme AL qui est appliqué sur la moitié de la droite AB est plus grand que le parallélogramme AE.

Car puisque les parallélogrammes DF et CM sont semblables, ces deux parallélogrammes sont autour du même diamètre (prop. 26. VI). Soit EB leur diamètre et décrivez la figure.

Attendu que LF est égal à LH (prop. 36. I), car FG est égal à GH, LF sera plus grand que EK. Mais LF est égal à LD (prop. 43. I) : donc DL est plus grand que EK : donc si nous ajoutons à chacun de ces deux parallélogrammes le parallélogramme KD; le parallélogramme total AL sera plus grand que le parallélogramme total AE.

Donc de tous les parallélogrammes qui sont appliqués sur la même droite et qui sont défaillants de parallélogrammes semblables au parallélogramme décrit sur la moitié de cette droite et semblablement placés que lui, le plus grand est celui qui est appliqué sur la moitié de cette droite et qui est semblable à son défaut ; ce qu'il fallait démontrer.

PROPOSITION XXVIII.

PROBLÈME.

Sur une droite donnée appliquer un parallélogramme qui soit égal à une figure rectiligne donnée et qui soit défaillant d'un parallélogramme semblable à un autre parallélogramme donné; il faut que la figure rectiligne donnée, à laquelle on doit substituer une figure qui lui soit égale, ne soit pas plus grande que le parallélogramme qui est appliqué sur la moitié de la droite donnée; les défauts du parallélogramme appliqué sur la moitié de cette droite et de celui qui doit être défaillant d'un parallélogramme semblable étant semblables entre eux.

Soit AB (fig. 150) la droite donnée à laquelle il faut appliquer un parallélogramme égal à la figure rectiligne donnée C, que cette figure soit plus petite que le parallélogramme appliqué sur la moitié de la droite AB, les défauts étant semblables, et que le parallélogramme auquel le défaut doit être semblable soit D. Il faut sur la droite AB appliquer un parallélogramme qui soit égal à la figure rectiligne donnée C et qui soit défaillant d'un parallélogramme semblable au parallélogramme D.

Coupez la droite AB en deux parties égales au point E (prop. 10. I), et sur EB décrivez le parallélogramme EBFG semblable au parallélogramme D et semblablement placé que lui (prop. 18. VI), et terminez le parallélogramme AG. Le parallélogramme AG est égal à la figure C, ou il est plus grand que cette figure. Si le parallélogramme AG est égal à la figure C, on a fait ce qui était proposé ; car on a appliqué sur la droite AB un parallélogramme AG égal à la figure rectiligne donné C et défaillant d'un parallélogramme EF semblable au parallélogramme D. Au contraire, si le parallélogramme HE n'est pas égal à la figure rectiligne C, ce parallélogramme sera plus grand que cette figure. Mais HE est égal à EF : donc EF est plus grand que C. Construisez le parallélogramme KLMN de manière que ce parallélogramme soit égal à l'excès du parallélogramme EF sur la figure C, et semblable au parallélogramme D et semblablement placé que lui (prop. 25. VI) ; mais EF est semblable à D : donc le parallélogramme KM sera semblable au parallélogramme EF. Que la droite LK soit l'homologue de la droite GE et la droite LM l'homologue de la droite G F. Puisque le parallélogramme EF est égal aux deux figures C, KM, le parallélogramme EF sera plus grand que le parallélogramme KM : donc la droite GE est plus grande que la droite KL, et la droite GF plus grande que la droite LM (prop. 20. VI). Faites la droite GO égale à la droite LK, et la droite GP égale à la droite LM (prop. 3. I), et terminez le parallélogramme OGPQ (prop. 31. I). Le parallélogramme OP sera égal et semblable au parallélogramme KM (prop. 26. VI) ; mais le parallélogramme KM est semblable au parallélogramme EF : donc le parallélogramme OP est semblable au parallélogramme EF (prop. 21. VI): donc ces deux parallélogrammes sont autour du même diamètre (prop. 26. VI). Soit GQB leur diamètre et décrivez la figure.

Puisque le parallélogramme EF est égal aux deux figures C, KM, et que OP est égal à KM, le gnomon restant VXY sera égal à la figure restante C; et à cause que PR est égal à OS (prop. 43. I), si l'on ajoute à chacun de ces deux parallélogrammes le parallélogramme RS, le parallélogramme total P B sera égal au parallélogramme total OB. Mais OB est égal à TE (prop. 36. I), parce que le côté AE est égal au côté EB : donc TE est égal à PB : donc si on ajoute à chacun de ces deux parallélogrammes TE, PB le parallélogramme OS, le parallélogramme total TS sera égal au gnomon total VXY. Or on a démontré que le gnomon VXY est égal à C : donc le parallélogramme TS est égal à la figure rectiligne C.

Donc on a appliqué sur la droite AB un parallélogramme TS qui est égal à la figure rectiligne donnée C et qui est défaillant d'un parallélogramme BS semblable à un parallélogramme D, puisque BS est semblable à PO ; ce qu'il fallait faire.

PROPOSITION XXIX.

PROBLÈME.

Appliquer sur une droite donnée un parallélogramme qui soit égal à une figure rectiligne donnée et qui soit excédent d'un parallélogramme semblable à un autre parallélogramme donné.

Soit AB (fig. 151) la droite donnée à laquelle il faut appliquer un parallélogramme qui soit égal à une figure rectiligne donnée C et qui soit excédent d'un parallélogramme semblable au parallélogramme D : il faut sur la droite AB appliquer un parallélogramme qui soit égal à la figure rectiligne C, et qui soit excédent d'un parallélogramme semblable au parallélogramme D.

Partagez la droite AB en deux parties égales au point E (prop. 9. I), sur la droite EB décrivez le parallélogramme EL semblable au parallélogramme D et semblablement placé que lui, et construisez le parallélogramme GH égal aux deux figures EL, C, et semblable au parallélogramme D et semblablement posé que lui (prop. 25. VI); le parallélogramme GH sera semblable au parallélogramme EL. Que le côté KH soit l'homologue du côté FL et le côté KG l'homologue du côté FE. Puisque le parallélogramme GH est plus grand que le parallélogramme EL, la droite KH sera plus grande que la droite EL et la droite KG plus grande que la droite FE. Prolongez FL et FE jusqu'à ce que la droite FLM soit égale à la droite KH et jusqu'à ce que la droite FEN soit égale à la droite KG (prop. 3. I), et terminez le parallélogramme MN. Le parallélogramme MN sera égal et semblable au parallélogramme GH ; mais le parallélogramme EL est semblable au parallélogramme GH : donc le parallélogramme MN sera semblable au parallélogramme EL (prop. 21. VI) : donc les deux parallélogrammes FL, MN seront autour du même diamètre (prop. 26. VI). Conduisez leur diagonale FO et terminez la figure.

Puisque le parallélogramme GH est égal aux deux figures EL, G et que MN est égal à GH, le parallélogramme MN sera égal aux deux figures EL, C : donc, si l'on retranche le parallélogramme commun EL, le gnomon restant ZYX sera égal à la figure rectiligne C ; et puisque EA est égal à EB, le parallélogramme AN sera égal au parallélogramme NB (prop. 36. I), c'est-à-dire au parallélogramme LP (prop. 43. I): donc si nous ajoutons à chacun de ces deux parallélogrammes le parallélogramme EO, le parallélogramme total AO sera égal au gnomon total ZYX; mais le gnomon ZYX est égal à la figure rectiligne C : donc le parallélogramme AO est égal à la figure rectiligne C.

Donc on a appliqué sur la droite donnée AB un parallélogramme AO qui est égal à la figure rectiligne C et qui est excédent d'un parallélogramme QP semblable au parallélogramme D, parce que le parallélogramme QP est semblable au parallélogramme LE ; ce qu'il fallait faire.

PROPOSITION XXX.

PROBLÈME.

Couper une droite finie et donnée en moyenne et extrême raison.

Soit la droite AB (fig. 152) finie et donnée: il faut couper cette droite AB en moyenne et extrême raison.

Sur la droite AB construisez le carré BG (prop. 46. I) et sur la droite AC appliquez un parallélogramme CD qui soit égal au carré BG et dont le parallélogramme excédent AD soit semblable au carré BC (prop. 29. VI).

La figure BC est un carré : donc la figure AD sera aussi un carré; et puisque BC est égal à CD, si l'on retranche la partie commune CE, la figure restante BF sera égale à la figure restante AD ; mais ces deux figures sont équiangles : donc les côtés des figures BF, AD qui sont autour des angles égaux sont réciproquement proportionnels (prop. 14. VI) : donc FE est à ED comme AE est à EB; mais FE est égal à AC (fig. 34. I), c'est-à-dire à AB et ED est égal à AE : donc AB est à AE comme AE est à EB ; mais AB est plus grand que AE : donc ÀE est plus grand que EB.

Donc la droite AE a été coupée au point E en moyenne et extrême raison, et sa partie AE est son plus grand segment ; ce qu'il fallait faire.

AUTREMENT.

Soit AB (fig. 153) la droite donnée : il faut couper cette droite en moyenne et extrême raison.

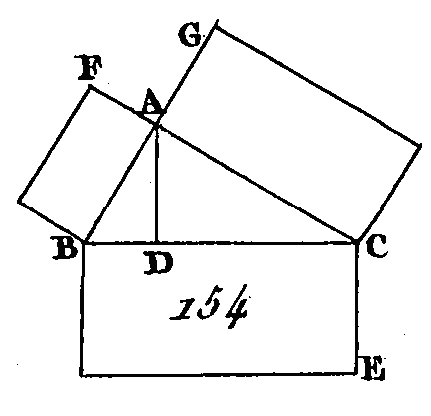
Partagez la droite AB au point C de manière que le rectangle compris sous les droites AB, BC soit égal au carré de AC (prop. 11. II).

Puisque le rectangle compris sous les droites AB, BC est égal au carré de AC, AB sera à AC comme AC est à CB (prop. 17. VI) : donc la droite AB a été coupée en moyenne et extrême raison (déf. 3. VI) ; ce qu'il fallait faire.

PROPOSITION XXXI.

THÉORÈME.

Dans les triangles rectangles, la figure construite sur le côté qui sous-tend l'angle droit est égale aux figures semblables qui sont décrites semblablement sur les côtés qui comprennent l'angle droit.

Soit le triangle rectangle ABC (fig. 154) dont l'angle BAC est droit : je dis que la figure construite sur BC est égale aux ligures semblables décrites semblablement sur les côtés BA, AC.

Conduisez sur BC la perpendiculaire AD.

Puisque dans le triangle ABC on a conduit de l'angle A sur la base BC la perpendiculaire AD, les triangles ABD, ADC placés autour de la perpendiculaire sont semblables au triangle total ABC et semblables entre eux (prop. 8. VI). Puisque le triangle ABC est semblable au triangle ABD, CB sera à BA comme AB est à BD; mais lorsque trois droites sont proportionnelles, la première droite est à la troisième comme, la figure construite sur la première droite est à la figure semblable construite semblablement sur la seconde (prop. 2. cor. 20. VI) : donc CB est à BD comme la figure construite sur CB est à la figure semblable construite semblablement sur BA. Par la même raison, BC est à CD comme la figure construite sur BC est à la figure décrite sur CA : donc BC est à BD plus DC comme la figure construite sur BC est aux figures semblables qui sont décrites semblablement sur BA, AC ; mais BC est égal à BD plus DC[2] : donc la figure construite sur BC est égale aux figures semblables qui sont décrites semblablement sur BA, AC.

Donc dans les triangles rectangles, la figure qui est construite sur le côté qui sous-tend l'angle droit est égale aux figures semblables qui sont semblablement décrites sur les côtés qui comprennent l'angle droit ; ce qu'il fallait démontrer.

AUTREMENT.

Puisque les figures semblables sont entre elles en raison doublée des côtés homologues (prop. 25. VI), la figure construite sur BC et celle qui est construite sur BA seront entre elles en raison doublée des côtés BC, BA ; mais le carré construit sur BC et le carré construit sur BA sont en raison doublée de BC, BA (prop. 1. cor. 20. VI) : donc la figure construite sur BC est à celle qui est construite sur BA comme le carré de BC est au carré de BA (prop. 11. V). Par la même raison la figure construite sur BC est à celle qui est construite sur CA comme le carré de BC est au carré de CA : donc la figure construite sur BC est aux figures construites sur BA, AC comme le carré de B C est aux carrés de BA et de AC. Mais le carré de BC est égal aux carrés de BA et de AC (prop. 47. I) : donc la figure construite sur BC est égale aux figures semblables qui sont semblablement décrites sur BA et sur AG; ce qu'il fallait démontrer.

PROPOSITION XXXII.

THÉORÈME.

Si deux triangles qui ont deux cotés proportionnels à deux côtés sont disposés selon un angle de manière que leurs côtés homologues soient parallèles, les autres côtés formeront une seule droite.

Soient les deux triangles ABC, DCE (fig. 155) qui aient les deux côtés BA, AC proportionnels aux deux côtés CD, DE de manière que B A soit à AC comme CD est à DE, et que AB soit parallèle à DC et AG parallèle aussi à DE : je dis que BC et CE ne formeront qu'une seule droite.

Puisque AB est parallèle à DC et que AC tombe sur ces deux droites, les angles alternes BAC, ACD sont égaux entre eux (prop. 29. I). Par la même raison, l'angle CDE est égal à l'angle ACD : donc l'angle BAC est égal à l'angle CDE ; et puisque les deux triangles ABC, ACE ont deux angles égaux en A et en D, et que les côtés qui comprennent ces deux angles égaux sont proportionnels, c'est-à-dire que BA est à AC comme CD est à DE, les triangles ABC, DCE seront équiangles (prop. 6. VI) : donc l'angle ABC est égal à l'angle DCE. Mais on a démontré que l'angle ACD est égal à l'angle BAC : donc l'angle total ACE est égal aux deux angles ABC, BAC : donc, si nous ajoutons à chacune de ces deux quantités l'angle ACB, les angles ACE, ACB seront aux angles BAC, ACB, ABC ; mais les angles BAC, ACB, ABC sont égaux à deux angles droits (prop. 32. I) : donc les angles ACE, ACB sont égaux à deux angles droits : donc avec une droite quelconque AC et au point C les deux droites BC, CE placées de différents côtés font les angles de suite ACE, ACB égaux à deux angles droits : donc les deux droites BC, CE ne forment qu'une seule droite (prop. 14. I).

Donc si deux triangles qui ont deux côtés proportionnels à deux côtés sont disposés selon un angle de manière que leurs côtés homologues soient parallèles, les autres côtés formeront une seule droite ; ce qu'il fallait démontrer.

PROPOSITION XXXIII.

THÉORÈME.

Dans les cercles égaux, les angles sont proportionnels aux arcs qu'ils comprennent, soit que ces angles soient placés aux centres ou bien aux circonférences. Il en est de même des secteurs qui sont placés aux centres.

Soient les cercles égaux ABC, DEF (fig. 156), que les angles BGC, EHF soient placés à leurs centres G, H, et que les angles BAC, EDF soient placés à leurs circonférences : je dis que l'arc BC est à l'arc EF comme l'angle BGC est à l'angle EHF, comme l'angle BAC est à l'angle EDF et comme le secteur GBC est au sec-leur HEF.

Faites les arcs de suite CK, KL, etc. égaux chacun à l'arc BC ; faites aussi les arcs de suite FM, MN, etc. égaux chacun à l'arc EF, et menez les rayons GK, GL, HM, UN.

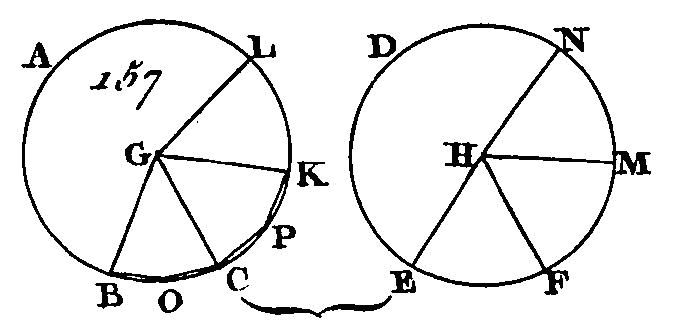
Puisque les arcs BC, CK, KL sont égaux entre eux, les angles BGC, CGH, KGL sont aussi égaux entre eux (prop. 27. III) : donc l'arc BL est multiple de Tare BC autant de fois que l'angle BGL est multiple de l'angle BGC. Par la même raison, l'arc EN est multiple de l'arc EF autant de fois que l'angle EHN est multiple de l'angle EHF. Donc si l'arc BL est égal à l'arc EN, l'angle BGL sera égal à l'angle EHN (prop. 27. III), si l'arc BL est plus grand que l'arc EN, l'angle BGL sera plus grand que l'angle EHN, et si l'arc BL est plus petit que l'arc EN, l'angle BGL sera plus petit que l'angle EHN. Ayant donc quatre quantités, savoir les arcs BC, EF et deux angles AGC, BHF, on a pris des équimultiples de l'arc BC et de l'angle BGL, savoir, l'arc BL et l'angle BGL; on a pris aussi des équimultiples de l'arc EF et de l'angle EHF, savoir, l'arc EN et l'angle EHN ; mais on a démontré que si l'arc BL surpasse l'arc EN, l'angle BGL surpassera l'angle EHN; que si l'arc BL est égal à l'arc EN, l'angle BGL sera égal à l'angle EHN, et que si Parc BL est plus petit que l'arc EN, l'angle BGL sera plus petit que l’angle EHN : donc l'arc BC est à l'arc EF comme l'angle BGC est à l'angle EHF (déf. 5. V); mais l'angle BGC est à l'angle EHF comme l'angle BAC est à l'angle EDF (prop. 15. V), car ils sont doubles les uns des autres (prop. 20. III) : donc l'arc BC est à l'arc EF comme l'angle BGC est à l'angle EHF, et comme l'angle BAC est à l'angle EDF. Donc dans des cercles égaux, les angles sont proportionnels aux arcs, soit que ces angles soient placés aux centres ou bien aux circonférences ; ce qu'il fallait démontrer.

Je dis de plus que l'arc BC est à l'arc EF comme le secteur GBC est au secteur HEF.

Menez les droites BC, CK (fig. 157), et ayant pris sur les arcs BC, CK, les points O, P, conduisez les droites BO, OC, CP, PK.

Puisque les deux droites BG, GC sont égales aux deux droites CG, GK, et qu'elles comprennent des angles égaux, la base BC sera égale à la base CK : donc le triangle GBC est égal au triangle GCK (prop. 4. I) ; et à cause que l'arc BC est égal à l'arc CK, et que le reste CAB de la circonférence qui complète le cercle entier ABC est égal au reste KAC de la circonférence qui complète le même cercle (ax. 5), l'angle BOC sera égal à l’angle CPK (prop. 27. III) : donc le segment BOC est semblable au segment CPK (déf. 11. III), et ces deux segments sont placés sur des droites égales ; mais les segments semblables qui sont placés sur des droites égales sont égaux (prop. 24. III) : donc le segment BOC est égal an segment CPK ; mais le triangle BGC est égal au triangle CGK : donc le secteur total GBC sera égal au secteur total GCK (ax. 2). Par la même raison, le secteur GKL sera égal à l’un ou à l'autre des secteurs GKG, GCB : donc les trois secteurs GBC, GCK, GK.L sont égaux entre eux. Les secteurs HEF, HFM, HMN sont pareillement égaux entre eux : donc l'arc BL est multiple de l'arc B C autant de fois que le secteur GBL est multiple du secteur GBC. Par la même raison, l'arc EN est multiple de l'arc EF autant de fois que le secteur HEN est multiple du secteur HEF : donc d'après ce que l'on vient de voir, si l'arc BL est égal à l'arc EN, le secteur GBL sera égal au secteur HEN ; si l'arc BL surpasse l'arc EN, le secteur GBL surpassera le secteur HEN, et si l'arc BL est plus petit que l'arc EN, le secteur GBL sera plus petit que le secteur HEN. Ayant donc quatre quantités, savoir les deux arcs BC, EF et les deux secteurs GBC, HEF, on a pris des équimultiples de l'arc BC et du secteur GBC, savoir, l'arc BL et le secteur GBL; on a pris aussi des équimultiples de l'arc EF et du secteur HEF, savoir, l'arc EN et le secteur HEN ; mais on a démontré que si l'arc BL surpasse l'arc EN, le secteur GBL surpassera le secteur HEN, que si l’arc BL est égal à l'arc EN, le secteur GBL sera égal au secteur HEN, et que si l'arc BL est plus petit que l'arc EN, le secteur GBL sera plus petit.que le secteur GEN : donc l’arc BC est à l'arc EF comme le secteur GBC est au secteur HEF (déf. 5. V).

COROLLAIRE.

Il est évident qu'un secteur est à un autre secteur comme l'angle du premier secteur est à l'angle du second secteur (prop. 11. V).

FIN DU SIXIÈME LIVRE.