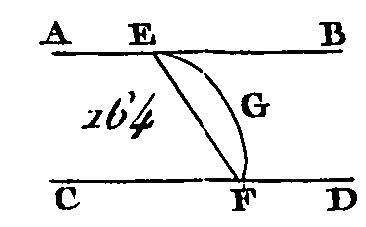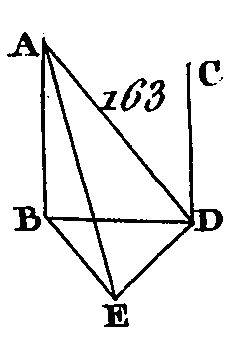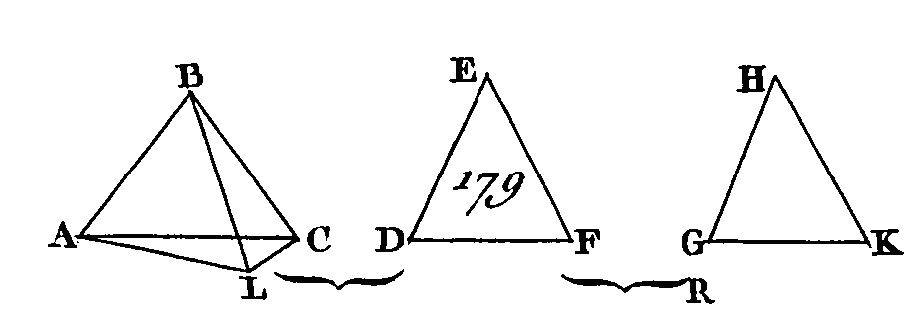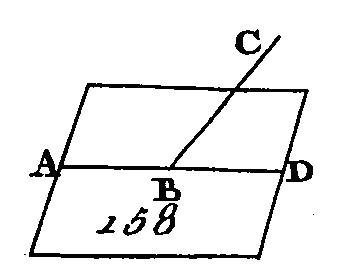
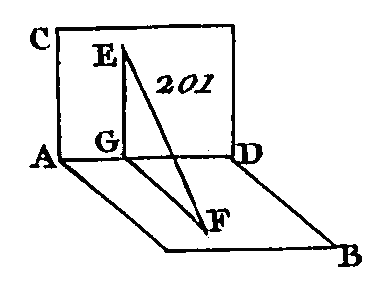
EUCLIDE

ÉLÉMENTS DE GÉOMÉTRIE

EUCLIDE

LIVRE XI.

DEFINITIONS.

1. Un solide est ce qui a longueur, largeur et épaisseur.

2. Un solide est terminé par des surfaces.

3. Une droite est perpendiculaire sur un plan lorsqu'elle fait des angles droits avec toutes les droites qui la rencontrent et qui sont dans ce plan.

4. Un plan est perpendiculaire sur un plan, lorsque les perpendiculaires menées dans un seul plan sur la commune section des plans sont perpendiculaires sur l'autre plan.

5. L'inclinaison d'une droite sur un plan est l'angle aigu compris par cette même droite et par la droite qui joint le point du plan que la première droite rencontre et le point de ce plan que rencontre la perpendiculaire menée sur ce plan de l'extrémité supérieure de la première droite.

6. L'inclinaison d'un plan sur un plan est l'angle aigu compris entre les perpendiculaires sur leur commune section, menées d'un point de cette commune section dans l'un et dans l'autre plan.

7. L'inclinaison d'un plan sur un plan est égale à l'inclinaison d'un autre plan sur un autre plan, lorsque les angles de leurs inclinaisons sont égaux entre eux.

8. Les plans parallèles sont ceux qui, étant prolongés, ne se rencontrent point.

9. Les solides semblables sont ceux qui sont contenus dans le même nombre des plans semblables.

10. Les solides semblables et égaux sont ceux qui sont contenus dans le même nombre de plans semblables et égaux.

11. Un angle solide est l'inclinaison de plus de deux droites les unes vers les autres, qui se rencontrent et qui ne sont pas dans le même plan.

AUTREMENT.

Un angle plan est celui qui est compris par plus de deux angles plans qui ne sont pas dans le même plan et qui sont construits dans le même point.

12. Une pyramide est un solide compris sous des plans qui, étant construits sur un seul plan, se réunissent dans un même point.

13. Un prisme est un solide compris sous des plans, dont deux plans opposés sont égaux, semblables et parallèles, et dont les autres plans sont des parallélogrammes.

14. Une sphère est un solide compris sous la surface décrite par l'arc d'un demi-cercle qui tourne autour du diamètre immobile jusqu'à ce qu'il soit revenu au même endroit d'où il était parti.

15. L'axe de la sphère est cette droite immobile autour de laquelle tourne le demi-cercle.

16. Le centre de la sphère est le même que celui du demi-cercle.

17. Un diamètre de la sphère est une droite menée par le centre et terminée de l'un et de l'autre côté par la surface de la sphère.

18. Un cône est un solide compris sous la superficie décrite par deux côtés d'un triangle rectangle tournant autour d'un des côtés de l'angle droit qui reste immobile, jusqu'à ce qu'il soit revenu au même endroit d'où il était parti. Si le côté immobile est égal à l'autre côté de l'angle droit, le cône est rectangle; s'il est plus petit, il est obtus-angle, et s'il est plus grand le cône est acutangle.

19. L'axe, du cône est la droite immobile autour de laquelle tourne le triangle rectangle.

20. La base du cône est le cercle décrit par un des côtés qui tournent.

21. Un cylindre est un solide compris sous la surface décrite par trois côtés d'un parallélogramme rectangle tournant autour du quatrième côté qui reste immobile jusqu'à ce que ce rectangle soit revenu au même endroit d'où il était parti.

22. L'axe du cylindre est la droite immobile autour de laquelle tourne le parallélogramme.

23. Les bases du cylindre sont les cercles décrits par les deux côtés opposés du parallélogramme qui se meuvent.

24. Les cônes et les cylindres semblables sont ceux dont les axes et dont les diamètres des bases sont proportionnels.

25. Un cube est un solide compris sous six carrés égaux.

26. Un tétraèdre est un solide compris sous quatre triangles égaux et équilatéraux.

27. Un octaèdre est un solide compris sous huit triangles égaux et équilatéraux.

28. Un dodécaèdre est un solide compris sous douze pentagones égaux, équilatéraux et équiangles.

29. Un icosaèdre est un solide compris sous vingt triangles égaux et équilatéraux.

PROPOSITION PREMIÈRE.

THÉORÈME.

Une partie d'une droite ne peut être dans un plan et une autre partie de cette droite hors de ce plan.

Supposons, si cela peut se faire, qu'une partie AB (fig. 158) de la droite ABC soit dans un plan et une autre partie BC hors de ce plan.

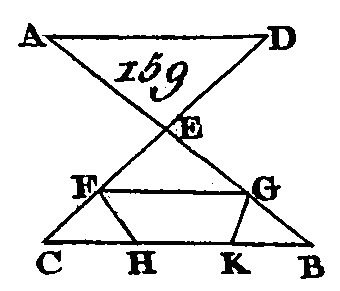
Prolongez la droite AB dans le plan sur lequel elle est placée ; soit BD le prolongement de cette droite; les deux droites ABC, ABD auront une partie commune AB, ce qui est impossible, car deux droites ne peuvent se rencontrer qu'en un seul point, autrement elles se confondraient.

Donc une partie d'une droite n'est point dans un plan et une autre partie de cette droite hors de ce plan ; ce qu'il fallait démontrer.

PROPOSITION II.

THÉORÈME.

Si deux droites se coupent, elles sont dans un seul plan ; tout triangle est aussi placé dans un seul plan.

Que les deux droites AB, CD (fig. 159) se coupent mutuellement au point E : je dis que les droites AB, CD sont dans un seul plan ; je dis aussi que tout triangle est placé dans un seul plan.

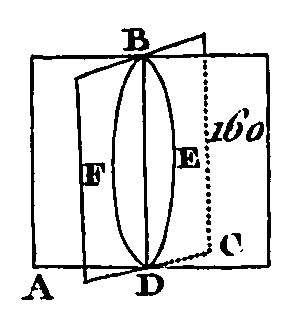
Prenez sur les droites EB, EC deux points quelconques F, G ; menez CB, FG et FH, GK: je dis d'abord que le triangle EBC est placé dans un seul plan, car si la partie FHC ou la partie GBK du triangle EBC est dans un plan et l'autre partie dans un autre plan, une partie de l'une des droites EG, EB sera dans un plan et l'autre partie dans un autre plan; mais si une partie FCBG du triangle ECB est dans un plan et l'autre partie dans un autre plan, une certaine partie de l'une et de l'autre des droites EC, EB sera dans un plan et certaine autre partie dans un autre plan; ce qui a été démontré absurde : donc le triangle EBC est dans un seul plan; mais l'un et l'autre des droites EC, EB sont, dans le même plan que le triangle BCE, et les droites AB, CD sont dans le même plan que l'une et que l'autre des droites EC, EB (prop. 1. 11) : donc les droites AB, CD sont dans un seul plan, et tout triangle est aussi placé dans un seul plan ; ce qu'il fallait démontrer.

PROPOSITION III.

THÉORÈME.

Si deux plans se coupent mutuellement, leur commune section est une ligne droite.

Que les deux plans AB, BC (fig. 160) se coupent mutuellement et que leur commune section soit DB : je dis que la ligne DB est une ligne droite.

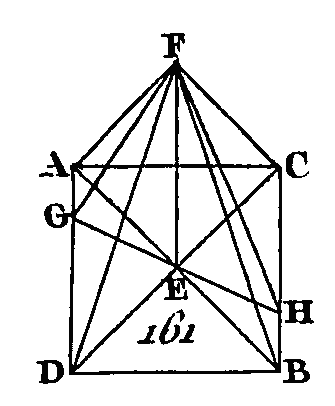
Car si cela n'est point, du point D au point B et sur le plan AB conduisez la droite DEB, et sur le plan BC conduisez la droite DFB ; les extrémités des deux droites DEB, DFB seront les mêmes, et ces deux droites renfermeront un espace, ce qui est absurde (ax. 12) : donc les lignes DEB, DFB ne sont pas des lignes droites. Nous démontrerons semblablement que toute autre ligne menée du point D au point B n’est point une ligne droite, excepté la ligne DB, c'est-à-dire la commune section des plans AB, BC.

Donc si deux plans se coupent mutuellement, leur commune section sera une ligne droite ; ce qu'il fallait démontrer.

PROPOSITION IV.

THÉORÈME.

Si deux droites se coupent mutuellement, la droite qui sera perpendiculaire sur ces deux droites, à leur section commune, le sera aussi sur le plan qui passera par ces deux droites.

Que les deux droites AB, CD (fig. 161) se coupent mutuellement au point E et que la droite EF leur soit perpendiculaire au point E : je dis que la droite EF est aussi perpendiculaire sur le plan qui passé par les droites AB, CD.

Prenez les droites AE, EB, CE, ED égales entre elles. Par le point E et sur le plan AB conduisez d'une manière quelconque une droite GEH, menez AD, CB, et ensuite d'un point quelconque F conduisez les droites FA, FG, FD, FC, FH, FB. Puisque les deux, droites AE, ED sont égales aux deux droites CE, EB, et que ces droites comprennent des angles égaux (prop. 15. 1), la base AD sera égale à la base CB (prop. 4. 1) le triangle AED égal au triangle CEB, et l'angle DAE égal à l'angle EBG ; mais l'angle AEG est égal à l'angle BEH (prop. 15. 1) : donc les deux triangles AGE, BEH ont deux angles égaux à deux angles, chacun à chacun; mais les côtés AE, EB adjacents à des angles égaux sont égaux entre eux : donc les autres côtés de ces triangles seront aussi égaux entre eux (prop. 26. 1) : donc GE est égal à EH et AG égal à BH ; et puisque AE est égal à EB et que la perpendiculaire FE est commune, la base FA sera égale à la base FB (prop. 4. 1) Par la même raison, FC sera aussi égal à FD. De plus, puisque la droite AD est égale à la droite CB et la droite FA égale à la droite FB, les deux droites FA, AD seront égales aux deux droites FB, BC, chacune à chacune; mais on a démontré que la base FD est égale à la base FC : donc l'angle FAD est égal à l'angle FBC (prop. 8. 1) ; mais on a démontré de plus que AG est égal à BH et FA est égal à FB : donc les deux droites FA, AG sont égales aux deux droites FB, BH ; mais on a démontré que l'angle FAG est égal à l'angle FBH; donc la base FG est égale à la base FH (prop. 4. 1) ; et, puisqu'on a démontré encore que GE est égal à EH, et à cause que la droite EF est commune, les deux droites GE, EF seront égales aux deux droites HE, EF ; mais la base FH est égale à la base FG : donc l'angle GEF est égal à l'angle HEF (prop. 8. 1) : donc l'un et l'autre des angles GEF, HEF sont droits : donc la droite FE fait des angles droits avec la droite GH, de quelque manière que la droite GH soit menée dans le plan AB par le point E. Nous démontrerons semblablement que la droite FE fait des angles droits avec toutes les droites qui la rencontrent et qui sont, dans le plan AB ; mais une droite est perpendiculaire sur un plan lorsqu'elle fait des angles droits avec toutes les droites qui la rencontrent et qui, sont placées dans ce plan (déf. 3. 11) : donc la droite EF est perpendiculaire sur le plan AB ; mais le plan AB est celui qui passe par les deux droites AB, CD: donc la droite FE est perpendiculaire sur le plan qui passe par les droites AB, CD.

Donc si deux droites se coupent mutuellement, et si une droite est perpendiculaire sur ces deux droites à leur commune section, cette droite sera aussi perpendiculaire sur le plan qui passe par ces deux droites ; ce qu'il fallait démontrer.

PROPOSITION V.

THÉORÈME.

Si trois droites, se rencontrent et si une droite leur est perpendiculaire à leur commune section, ces_: trois droites seront dans un seul plan.

Si une droite AB (fig. 162) est perpendiculaire, sur trois droites BC, BD, BE au point de contact B : je dis que les trois droites BC, BD, BE sont dans, un seul plan.

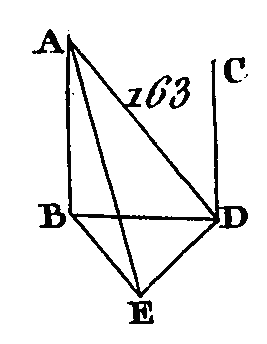
Car, supposons, si cela est possible, que BD, BE soient dans un plan et BC dans un autre, plan élevé au-dessous du premier ; faites passer un plan par les droites AB, BC ; la commune, section de ce plan avec le plan inférieur sera mie ligne droite (prop. 3. 11); que cette droite soit BF. Il est évident que les trois droites AB, BC, BF sont dans le plan qui passe par les droites AB, BC : donc puisque la droite AB est perpendiculaire sur l'une et l'autre des droites BD, BE, cette droite sera perpendiculaire sur le plan qui passe par DB, BE (prop. 4. 11) mais le plan qui passe par DB, BE est le plan intérieur : donc la droite AB est perpendiculaire sur le plan inférieur : donc cette droite sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce plan (déf. 3. 11); mais cette perpendiculaire est rencontrée dans le plan inférieur par la droite BF : donc l'angle ABF est droit; mais on a supposé que l'angle ABG est droit : donc les deux angles ABF, ABC, placés dans le même-plan, sont égaux entre eux, ce qui est impossible (ax. 9) : donc la droite BC n'est pas dans un plan élevé au-dessus de celui qui passe par les droites BD, BE : donc les trois droites BC, BD, BE sont dans un seul plan.

Donc si trois droites se rencontrent, et si une droite leur est perpendiculaire à leur commune section, ces trois droites seront dans un seul plan, ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Si deux droites sont perpendiculaires sur le même plan, ces deux droites seront parallèles.

Que les deux droites AB, CD (fig. 163)^:soient perpendiculaires sur un même plan, je dis que AB est parallèle à. CD.

Supposons que ces perpendiculaires rencontrent ce plan aux points B, D ; menez la droite BD; conduisez dans ce plan la droite DE perpendiculaire sur BD, et après avoir fait DE égal à AB menez les droites BE, AE, AD.

Puisque la droite AB est perpendiculaire sur le plan BDE, elle est perpendiculaire sur toutes les droites, qui la rencontrent et qui sont dans ce plan (déf. 3. 11) ; mais cette droite est rencontrée par l'une et l'autre des droites BD, BE; qui sont dans ce plan : donc les angles ABD, ABE sont droits l’un et l'autre. Par la même raison, les angles CDB, CDE sont aussi droits l'un et l'autre. Mais puisque la droite AB est égale à la droite DE et que la droite BD est commune, les deux droites AB, BD sont égales aux deux droites ED, DB; mais ces droites comprennent des angles droits : donc la base AD, est égale à la base BE (prop. 4. 1), et puisque la droite AB est égale à la droite DE et la droite AD égale à la droite DE; les deux droites AB, BE sont égales aux deux droites ED, DB ; mais la base AE est commune ; donc l'angle ABE est égal à l’angle EDA (prop. 8. 1); mais l'angle ABE est droit: donc l'angle EDA est droit aussi; donc la droite ED est perpendiculaire sur la droite DA; mais, la droite ED, est perpendiculaire sur l'une et l'autre des droites BD, DC: donc ED est perpendiculaire sur les trois droites BD, DA, DC à leur point de contact : donc les trois droites BD, DA, DC sont dans un seul plan (prop. 5. 11) ; mais la droite AB est dans le même plan que les droites BD, DA, car tout triangle est dans un seul plan (prop. 2. 11) : donc les trois droites AB, BD, DC sont dans un seul plan ; mais les angles ABD, BDC sont droits l'un et l'autre : donc la droite AB est parallèle à la droite CD (prop. 28. 1).

Donc si deux droites sont perpendiculaires sur le même plan, ces deux droites seront parallèles entre elles ; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Si deux droites sont parallèles, et si l’on prend sur chacune de ces droites des points quelconques, la droite qui joindra ces points sera dans le même plan que les parallèles.

Soient AB, CD (fig. 164) deux droites parallèles, et soient pris dans ces droites des points quelconques E, F : je dis que la droite qui joint les points E, F est dans le même plan que les deux parallèles.

Supposons que cela ne soit point, et supposons, si cela est possible, que cette droite soit dans un plan élevé au-dessus du premier et qu'elle ait par exemple, la position EGF ; par la ligne EGF conduisez un plan qui fasse avec le plan inférieur une section qui sera une ligne-droite (prop. 3. 11); que cette section soit EF : il est évident que les deux droites EGF, EF renfermeront un espace, ce qui est impossible (ax. 12) : donc la droite conduite du point E au point F n'est point dans un plan élevé au-dessus du premier : donc elle est dans celui qui, passe par les parallèles AB, CD.

Donc si deux droites sont parallèles, et si l'on prend dans l'une et l'autre de ces parallèles des points quelconques, la droite qui joindra ces points sera dans le même plan que les parallèles ; ce qu'il fallait démontrer.

PROPOSITION VIII.

THÉORÈME.

Si deux, droites sont parallèles et si l'une d'elles est perpendiculaire sur un plan, l’autre sera aussi perpendiculaire sur ce plan.

Soient AB, CD (fig. 163) deux droites parallèles, et que l'une de ces droites AB soit perpendiculaire sur le plan BED : je dis que l'autre droite CD sera aussi perpendiculaire sur ce plan.

Que les droites AB, CD rencontrent le plan BED aux points B, D, Menez BD. Les droites AB, DC, BD seront dans le même plan (prop. 7.11). Conduisez dans le plan BED la droite DE perpendiculaire sur BD; faites ensuite DE égal à AB, et menez BE, AE, AD. Puisque AB est perpendiculaire sur le plan AED, elle sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce plan (déf. 3. 11) ; donc les angles ABD, ABE sont droits l'un et l'autre ; et puisque la droite BD tombe sur les, droites AB, CD, les angles ABD, CDB seront égaux à deux angles droits (prop. 29. 1). Mais l'angle ABD est droit : donc l'angle CDB est droit aussi : donc CD est perpendiculaire sur BD ; et puisque la droite AB est égale à la droite DE, et que la droite BD est commune, les deux droites AB, DB sont égales aux deux droites. ED, DB; mais l'angle ABD est égal à l'angle EDB, car ils sont droits l'un et l'autre : donc la base AD est égale à la base BE (prop. 4. 1) et puisque AB est égal à DE et BE égal à AD, les deux droites AB, BE seront égales aux deux droites ED, DA, chacune à chacune ; mais la base AB est commune : donc l'angle ABE est égal à l'angle EDA (prop. 8. 1) ; mais l'angle ABE est droit : donc l'angle EDA est droit aussi: donc ED est perpendiculaire sur DA, mais ED est aussi perpendiculaire sur BD : donc la droite ED sera perpendiculaire sur le plan qui passe par les droites BD, DA (prop. 4. 11) : donc la droite ED est perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce plan. Mais la droite DC est dans le plan qui passe par les droites BA, AD, parce que les droites AB, BD sont dans, le plan qui passe par les droites BD, DA (prop. 2. 11) ; et la droite DC est dans le même plan que les droites AB, BD (prop. 7. 11): donc la droite ED est perpendiculaire sur DC ; donc la droite CD est perpendiculaire sur DE ; mais la droite CD est perpendiculaire sur la droite BD : donc la droite CD est perpendiculaire sur les deux droites DE, DB à leur point de rencontre D : donc la droite CD est perpendiculaire sur le plan qui passe par les droites DE, DB (prop. 4. 11) ; mais le plan qui passe par les droites DE, DB est le plan BED : donc CD est perpendiculaire sur le plan BED ; ce qu'il fallait démontrer.

PROPOSITION IX.

THÉORÈME.

Les droites qui sont parallèles à une même droite, sans être dans le même plan que cette autre droite, sont cependant parallèles entre elles.

Que l'une et l'autre des droites AB, CD (fig. 165) soient parallèles à la droite EF, et que les droites AB, CD né soient pas dans le même plan que la droite EF : je dis que la droite AB est parallèle à la droite CD.

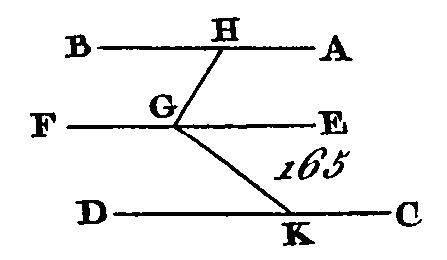
Prenez sur EF un point quelconque G, et de ce point menez dans le plan qui passe par EF, AB la droite GH perpendiculaire sur EF, et dans le plan qui passe par FE, CD, menez la droite GK perpendiculaire aussi sur FE : puisque la droite EF est perpendiculaire sur l'une et l'autre des droites GH, GK, la droite EF sera aussi perpendiculaire sur le plan qui passe par les droites GH, GK (prop. 4. 11) ; mais AB est parallèle à EF : donc AB est perpendiculaire sur le plan qui passe par les points H, G, K (prop. 8. 11) ; par la même raison CD est perpendiculaire sur le plan qui passe par les points H, G, K : donc les droites AB, CD sont perpendiculaires l'une et l'autre sur le plan qui passe par les points H, G, K ; mais si deux droites sont perpendiculaires sur un seul plan, ces deux droites sont parallèles entre elles (prop. 6. 11) : donc la droite AB est parallèle à la droite CD, ce qu'il fallait démontrer.

PROPOSITION X.

THÉORÈME.

Si deux droites qui se touchent sont parallèles à deux droites qui se touchent et qui ne sont pas dans le même plan, ces droites comprendront des angles égaux.

Que les deux droites AB, BC (fig. 166) qui se touchent soient parallèles aux deux droites DE, EF qui se touchent et qui ne sont pas dans le même plan : je dis que l'angle ABC est égal à l'angle DEF.

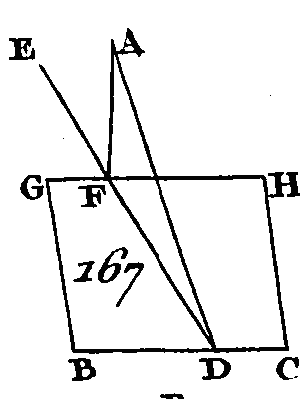
Prenez les droites BA, BC, ED, EF égales entre elles, et menez les droites AD, CF, BE, AC, DF. Puisque BA est égal et parallèle à ED, AD sera égal et parallèle à BE (prop. 35. 1). Par la même raison CF sera égal et parallèle à BE : donc les deux droites AD, CF sont égales et parallèles chacune à la droite BE ; mais les droites qui sont parallèles à une même droite sont parallèles entre elles (prop. 9. 11) : donc la droite AD est parallèle et égale à la droite CF ; mais ces parallèles sont jointes par les droites AC, DF : donc la droite AC est parallèle et égale à la droite DF ; et puisque les droites AB, BC sont égales aux deux droites DE, EF, et que la base AC est égale à la base DF, l’angle ABC sera égal à l'angle DEF (prop. 8. 1).

Donc si deux droites qui se touchent sont parallèles à deux droites qui se touchent et qui ne sont pas dans le même plan, ces deux droites comprendront des angles égaux ; ce qu'il fallait démontrer.

PROPOSITION XI.

PROBLÈME.

D'un point donné hors d'un plan, mener une perpendiculaire sur ce plan.

Soit A (fig. 167) le point donné hors d'un plan, soit BH le plan donné : il faut du point A mener une perpendiculaire sur ce plan.

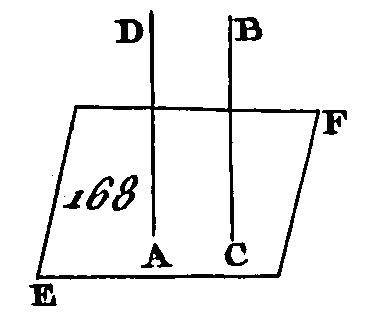
Dans le plan donné, conduisez une droite BC d'une manière quelconque, et du point A menez la droite AD perpendiculaire sur BC (prop. 12. 1). Si la droite AD est aussi perpendiculaire sur ce plan, on aura fait ce qui était proposé ; si cela n'est pas, du point D et dans le plan donne menez sur BC la perpendiculaire DE (prop. 11. 1), et du point A menez sur DE la perpendiculaire AF (prop. 12. 1), et enfin par le point F conduisez la droite GH parallèle à BC.

Puisque BC est perpendiculaire sur l'une et sur l’autre des droites DA, DE, la droite BC sera perpendiculaire sur le plan qui passe par les droites ED, DA, et parallèle à la droite GH (prop. 4. 11) ; mais si deux droites sont parallèles et si l'une d'elles est perpendiculaire sur un plan, l'autre droite est aussi perpendiculaire sur ce même plan (prop. 8. 11): donc GH est perpendiculaire sur le plan qui passe par ED, DA, et par conséquent perpendiculaire sur toutes les droites qui se rencontrent dans ce plan (déf. 3. 11) ; mais la droite AF rencontre la droite GH dans le plan qui passe par ED, DA : donc la droite GH est perpendiculaire sur AF : donc AF est perpendiculaire sur GH ; mais AF est perpendiculaire sur DF, par construction : donc la droite AF est perpendiculaire sur l’une et sur l'autre des droites GH, DE ; mais si une droite est perpendiculaire au point de contact sur deux droites qui se rencontrent, elle sera aussi perpendiculaire sur le plan qui passe par ces deux droites (prop. 4. 11) : donc FA est perpendiculaire sur le plan qui passe par ED, GH; mais le plan qui passe par ED, GH est le plan BH : donc la droite AF est perpendiculaire sur le plan BH.

Donc du point donné A, pris au-dessus d'un plan, on a mené une perpendiculaire AF sur ce plan; ce qu'il fallait faire.

PROPOSITION XII.

PROBLÈME.

D'un point donné dans un plan donné, élever une perpendiculaire sur ce plan.

Soit EF (fig. 168) le plan donné, et soit A le point donné dans ce plan : il faut du point A élever une perpendiculaire sur ce plan.

D'un point quelconque B, pris au-dessus du plan donné, menez une perpendiculaire BC sur ce plan (prop. 31. 11), et par le point A menez AD parallèle à BC (prop. 31. 1).

Puisque les deux droites AD, CB sont parallèles et que BC, l'une de ces droites, est perpendiculaire sur le plan donné, l'autre droite AD sera aussi perpendiculaire sur ce plan (prop. 8. 11).

Donc, d'un point donné dans un plan donné; on a élevé une perpendiculaire sur ce plan ; ce qu'il fallait faire.

PROPOSITION XIII.

THÉORÈME.

D'un point donné dans un plan donné, on ne peut élever du même côté deux perpendiculaires sur ce plan.

Supposons que cela soit possible; du point donné A (fig. 169) pris dans le plan donné, élevez du même côté les deux perpendiculaires AB, AC sur ce plan ; conduisez un plan par les deux droites BA, AC; ce plan fera au point A avec le plan donné une section qui sera une ligne, droite (prop. 3. 11); que cette section soit DAE; les droites AB, AC, DAE seront dans le même plan; mais puisque CA est perpendiculaire sur le plan donné _t elle sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans le plan donné (déf. 3. 11) ; mais la droite DAE, qui est dans le plan donné, rencontre la droite CA : donc l'angle CAE est droit. L'angle BAE est droit, par la même raison ; donc l’angle CAE et l'angle BAE qui sont dans le même plan sont égaux entre eux, ce qui est impossible (ax. 9)

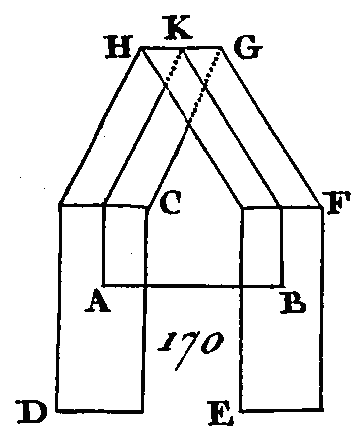
Donc, d'un point donné dans un plan donné, on ne peut élever deux perpendiculaires sur ce plan; ce qu'il fallait démontrer.

PROPOSITION XIV.

THÉORÈME.

Les plans sur lesquels une même droite est perpendiculaire sont parallèles entre eux.

Que la droite AB (fig. 170) soit perpendiculaire sur l'un et l'autre plan CD, EF : je dis que ces plans sont parallèles.

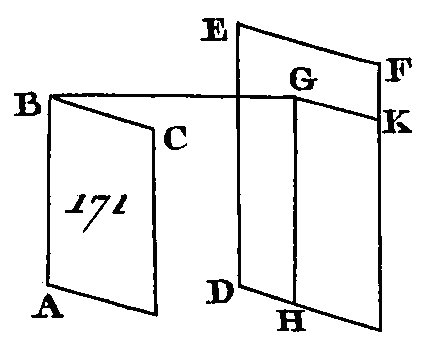
Car si cela n'est point, ces plans étant prolongés se rencontreront et leur section sera une ligne droite (prop. 3. 11). Que cette section soit GH; ayant pris dans cette section un point quelconque K, menez AK, BK. Puisque la droite AB est perpendiculaire sur le plan EF, cette droite sera perpendiculaire sur la droite BK, qui est placée dans le prolongement du plan EF (déf. 3. 11) : donc l'angle ABK est droit. L'angle BAK est droit, par la même raison : donc les deux angles ABK, BAK du triangle ABK sont égaux à deux angles droits; ce qui est impossible (prop. 17. 1) : donc les plans CD, EF étant prolongés, ne se rencontreront point entre eux : donc les plans CD, EF sont parallèles.

Donc les plans sur lesquels une même droite est perpendiculaire sont parallèles entre eux ; ce qu'il fallait démontrer.

PROPOSITION XV.

THÉORÈME.

Si deux droites qui se rencontrent sont parallèles à deux droites qui se rencontrent et qui ne sont pas dans le même plan, les plans qui passeront par ces droites seront parallèles.

Que les droites AB, BC (fig. 171) qui se rencontrent soient parallèles à deux droites DE, EF qui se rencontrent et qui ne sont pas dans le même plan : je dis que les plans qui passent par les droites AB, BC et par les droites DE, EF ne se rencontreront point s'ils sont prolongés.

Du point B menez sur le plan qui passe par les droites DE, EF la perpendiculaire BG qui rencontre ce plan au point G (prop. 11. 11); par le point G menez la droite GH parallèle a la droite ED et la droite GK parallèle à la droite EF (prop. 31. 1). Puisque la droite BG est perpendiculaire sur le plan qui passe par les droites DE, EF, elle sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce même plan (déf. 3. 11) ; mais cette droite est rencontrée par l'une et l'autre des droites GH, GK qui sont dans le plan qui passe par les droites DE, EF : donc les angles BGH, BGK sont droits l'un et l'autre; et puisque BA est parallèle à la droite GH, les angles GBA, BGH seront égaux à deux angles droits (prop. 29. 1) ; mais l'angle BGH est droit : donc l'angle GBA sera droit : donc GB est perpendiculaire sur BA. Par la même raison, BG est perpendiculaire sur BC : donc puisque la droite BG est perpendiculaire sur les deux droites BA, BC qui se coupent mutuellement, la droite BG sera perpendiculaire sur le plan qui passe par les deux droites AB, BC (prop. 4. 11). Par la même raison, la droite BG est perpendiculaire sur le plan qui passe par les droites GH, GK. Mais le plan qui passe par les droites GH, GR est le même que celui qui passe par les droites DE, EF : donc la droite BG est perpendiculaire sur le plan qui passe par les droites DE, EF. Mais on a démontré que la droite BG est perpendiculaire sur le plan qui passe par les droites AB, BC, et cette droite est encore perpendiculaire sur le plan qui passe par les droites DE, EF : donc la droite BG est perpendiculaire sur l'un et l'autre des plans qui passent par les droites AB, BC et par les droites DE, EF ; mais les plans sur lesquels une même droite est perpendiculaire sont parallèles entre eux (prop. 14. 11) : donc le plan qui passe par les droites AB, BC est parallèle à celui qui passe par les droites DE, EF.

Donc si deux droites qui se rencontrent sont parallèles à deux droites qui se rencontrent et qui ne sont pas dans le même plan, les plans qui passeront par ces droites seront parallèles entre eux ; ce qu'il fallait démontrer.

PROPOSITION XVI.

THÉORÈME.

Si deux plans parallèles sont coupés par un plan quelconque, leurs communes sections seront parallèles.

Que les deux plans parallèles AB, CD (fig. 172) Soient coupés par un plan quelconque EFGH, et que leurs communes sections soient EF, GH : je dis que EF est parallèle à GH.

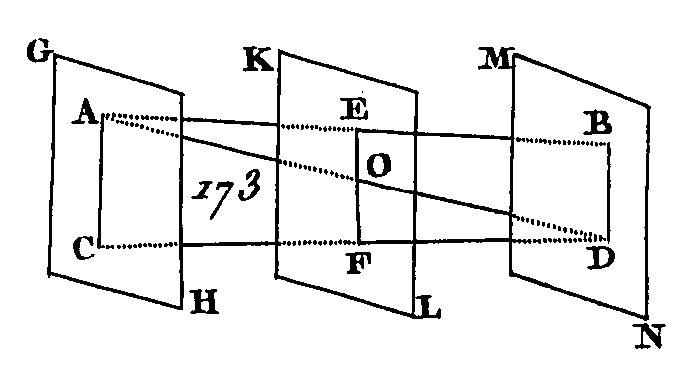
Supposons que cela ne soit point ; prolongez les droites EF, GH, ces droites se rencontreront ou du côté des points F, H, ou du côté des points E, G. Prolongez ces droites du côté des points F, H, et supposons qu'elles se rencontrent au point K ; puisque EFK est dans le plan AB, tous les points pris dans EFK seront dans le même plan ; mais le point K est un des points pris sur EFK : donc le point K est dans le plan AB. Par la même raison, le point K est dans le plan CD : donc les plans AB, CD prolongés, se rencontreront entre eux; mais ces deux plans ne se rencontreront point puisqu'ils sont parallèles : donc les droites EF, GH prolongées ne se rencontreront point du côté des points; F, H. Nous démontrerons semblablement que les droites EF, GH prolongées ne se rencontreront point du côté des points E, G. Mais les droites qui ne se rencontrent d'aucun côté sont parallèles (déf. 35. 1) : donc les droites EF, GH sont parallèles.

Donc si deux plans parallèles sont coupés par un plan quelconque, leurs communes sections, seront parallèles entre elles ; ce qu'il fallait démontrer.

PROPOSITION XVII.

THÉORÈME.

Si deux droites sont coupées par des plans parallèles_} elles seront coupées proportionnellement.

Que les deux droites AB, CD (fig. 173) soient coupées par les plans parallèles GH, KL, MN aux points A, E, B, C, F, D: je dis que AE est à EB comme CF est à FD.

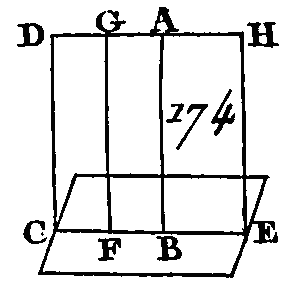
Menez les droites AC, BD, AD; supposons que lai droite AD rencontre le plan KL au point O ; et conduisez les droites EO, OF. Puisque les deux plans parallèles KL, MN sont coupés par le plan EBDG, leurs sections EO, BD sont parallèles (prop. 16. 11) ; puisque les deux plans parallèles GH, KL sont coupés par le plan AOFC, leurs sections communes AC, FO sont parallèles, par la même raison. Mais puisque EO est parallèle à un des côtés du triangle ABD, savoir au côté BD, le côté AE sera au côté EB comme le côté AO est au côté OD (prop. 2. 6). De plus, puisque le côté OF est parallèle à un des côtés du triangle ADC, savoir au côté AC, le côté AO est au côté OD comme le côté CF est au côté FD. Mais on a démontré que le côté AO est au côté OD comme le côté AE est au côté EB : donc le côté AE est au côté EB comme le côté CF est au côté FD (prop. 11. 5).

Donc si deux droites sont coupées par des plans parallèles, ces droites seront coupées proportionnellement ; ce qu'il fallait démontrer.

PROPOSITION XVIII.

THÉORÈME.

Si une droite est perpendiculaire sur un plan, tous les plans qui passant par cette droite sont perpendiculaires sur ce même plan.

Qu'une droite quelconque AB (fig. 174) soit perpendiculaire sur un plan : je dis que tous les plans qui passent par cette droite sont perpendiculaires sur ce même plan.

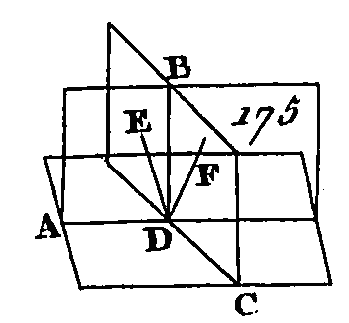
Par la droite AB conduisez le plan DE, et que la droite CE soit la commune section du plan DE et du plan donné; sur la droite CE prenez un point quelconque F ; de ce point et dans le plan DE conduisez la droite FG perpendiculaire sur la droite CE. Puisque la droite AB est perpendiculaire sur le plan donné, cette droite sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce plan (déf. 3. 11): donc la droite AB est perpendiculaire sur la droite CE : donc l'angle ABF est droit ; mais l'angle GFB est droit aussi : donc AB est parallèle à FG (prop. 28. 1) ; mais AB est perpendiculaire sur le plan donné : donc FG sera perpendiculaire sur ce même plan (prop. 8. 11) ; mais un plan est perpendiculaire sur un plan, lorsque les droites menées dans l'un de ces plans sont perpendiculaires sur leur commune section et sur l'autre plan (déf. 4. 11) : donc la droite FG menée dans le plan DE et perpendiculaire sur la droite CE, commune section des plans, est aussi perpendiculaire sur le plan donné : donc le plan DE est perpendiculaire sur le plan donné. Nous démontrerons semblablement que tous les autres plans qui passent par la droite AB sont aussi perpendiculaires sur le plan donné.

Donc si une droite est perpendiculaire sur un plan, tous les plans qui passeront par cette droite seront perpendiculaires sur ce même plan ; ce qu'il fallait démontrer.

PROPOSITION XIX.

THÉORÈME.

Si deux plans qui se coupent mutuellement sont perpendiculaires sur un plan, leur commune section sera aussi perpendiculaire sur ce plan.

Que deux plans AB, BC (fig. 175) qui se coupent mutuellement soient perpendiculaires sur un plan donné, et que leur commune section soit BD : je dis que la droite BD est perpendiculaire sur le plan donné.

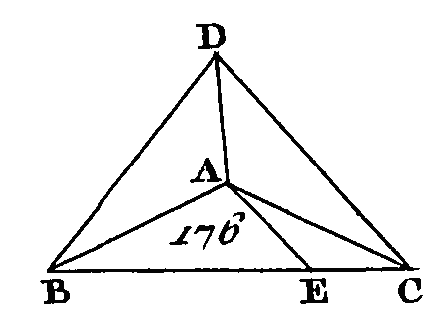
Supposons que cela ne soit point ; du point D menez dans le plan AB la droite DE perpendiculaire sur la droite AD (prop. 11. 1), et du point D et dans le plan BC menez la droite DF perpendiculaire sur la droite CD. Puisque le plan AB est perpendiculaire sur le plan donné et que la droite DE a été menée dans le plan AB perpendiculaire à la commune section AD de ces plans, la droite DE sera perpendiculaire sur le plan donné. Nous démontrerons semblablement que DF est perpendiculaire sur le plan donné : donc du point D on a mené du même côté deux perpendiculaires sur le plan donné ; ce qui est impossible (prop. 13. 11) : donc du point D ou ne peut pas mener d'autres droites qui soient perpendiculaires sur le plan donné, si ce n'est la commune section DB des plans AB, BC.

Donc si deux plans qui se coupent mutuellement sont perpendiculaires sur un plan donné, leur commune section sera perpendiculaire sur ce plan ; ce qu'il fallait démontrer.

PROPOSITION XX.

THÉORÈME.

Si un angle solide est compris sous trois angles plans, deux de ces angles, de quelque manière qu'on les prenne, sont plus grands que le troisième.

Que l'angle solide A (fig. 176) soit compris, sous les trois angles plans BAC, CAD, DAB : je dis que deux quelconques des trois angles plans BAC, CAD, DAB, de quelque manière qu'on les prenne, sont plus grands que l'angle restant.

Car si les angles BAC, CAD, DAB sont égaux entre eux, il est évident que deux quelconques de ces angles, de quelque manière qu'on les prenne, sont plus grands que l'angle restant. Supposons que ces trois angles ne sont point égaux entre eux, et que l'angle BAC est le plus grand. Sur la droite AB et au point A faisons dans le plan qui passe par BAC l'angle BAE égal à l'angle DAB (prop. 23. 11). Faisons AE égal à AD (prop. 3. 1), menons ensuite par le point E la droite BEC qui coupe les droites AB, AC aux points B, C, menons aussi les droites DB, DC. Puisque la droite DA est égale à la droite AE et que la droite AB est commune, les deux droites DA, AB sont égales aux deux droites AE, AB ; mais l'angle DAB est égal à l'angle BAE : donc la base DB est égale à la base BE (prop. 4. 1) ; et puisque les deux droites DB, DC sont plus grandes que la droite BC et que la droite DB est égale à la droite BE, la droite restante DC sera plus grande que la droite restante EC ; mais puisque la droite DA est égale à la droite AE, que la droite AC est commune et que la base DC est plus grande que la base EC, l'angle DAC sera plus grand que l'angle EAC, (prop. 25. 1). Mais l'angle DAB est égal à l'angle BAE, par construction : donc les angles DAB, DAC sont plus grands que l'angle BAC. Si l'on prend deux autres angles quelconques, nous démontrerons semblablement qu'ils sont plus grands que l'angle restant.

Donc si un angle solide est compris sous trois angles plans, deux quelconques de ces angles, de quelque manière qu'on les prenne, sont plus grands que le troisième; ce qu'il fallait démontrer.

PROPOSITION XXI.

THÉORÈME.

Tout angle solide est compris sous des angles plans qui sont moindres que quatre angles droits.

Soit l'angle solide A (fig. 177) compris sous les angles plans BAC, CAD, DAB : je dis que les angles BAC, CAD, DAB sont moindres que quatre angles droits.

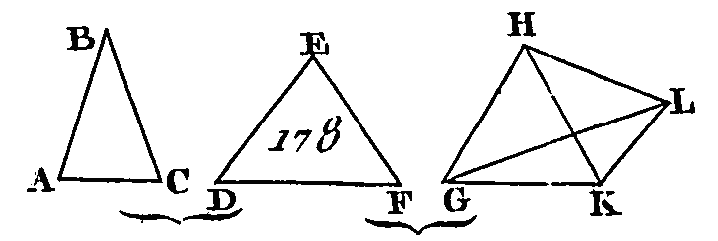
Dans chacune des droites AB, AC, AD, prenez des points quelconques B, C, D, et menez BC, CD, DB. Puisque l'angle solide B est compris sous les trois angles plans CBA, ABD, CBD, deux quelconques de ces triangles sont plus grands que l'angle restant (prop. 20. 11) : donc les angles CBA, ABD sont plus grands que l'angle CBD. Par la même raison, les angles BCA, ACD sont plus grands que l'angle BCD, et les angles CDA, ADB plus grands que l'angle CDB : donc les six angles CBA, ABD, BCA, ACD, ADC, ADB sont plus grands que les trois angles CBD, BCD, CDB. Mais les trois angles CBD, BCD, CDB sont égaux à deux angles droits (prop. 32. 1): donc les six angles CBA, ABD, BCA, ACD, ADC, ADB sont plus grands que deux angles droits ; mais puisque les trois angles de chacun des triangles ABC, ACD, ADB sont égaux à deux angles droits, les neuf angles CBA, ACB, BAC, ACD, DAC, CDA, ADB, DBA, BAD de ces trois triangles sont égaux à six angles droits ; mais les six angles ABC, BCA, ACD, CDA, ADB, DBA sont plus grands que deux angles droits : donc les angles restants BAC, CAD, DAB qui contiennent l'angle solide sont plus petits que quatre angles droits.

Donc tout angle solide est compris sous des angles plans plus petits que quatre angles droits ; ce qu'il fallait démontrer.

PROPOSITION XXII.

THÉORÈME.

Si l'on a trois angles plans, dont deux de ces angles, de quelque manière qu'on les prenne, sont plus grands que l'angle restant, et si ces angles sont compris par des côtés égaux, on pourra construire un triangle avec les droites qui joignent ces côtés égaux.

Soient les trois angles plans ABC, DEF, GHK (fig. 178) dont deux de ces angles, de quelque manière qu'on les prenne, sont plus grands que l'angle restant, c'est-à-dire que les deux angles ABC, DEF sont plus grands que l'angle GHK, que les deux angles DEF, GHK sont plus grands que l'angle ABC, et enfin que les deux angles GHK, ABC sont plus grands que l'angle DEF ; que les droites AB, BC, DE, EF, GH, HK soient égales ; menez AC, DF, GK : je dis qu'on peut construire un triangle avec des droites égales aux droites AC, DF, GK ; c'est-à-dire que deux quelconques des droites AC, DF, GK, de quelque manière qu'on les prenne, sont plus grandes que la droite restante.

Si les angles ABC, DEF, GHK sont égaux entre eux, il est évident qu'on pourra construire un triangle avec des droites égales aux droites AC, DF, GK qui sont alors égales entre elles. Au contraire, si ces angles ne sont point égaux, sur la droite HK et au point H, faites l'angle KHL égal à l'angle ABC (prop. 23. 1) ; faites aussi la droite HL égale à une des droites AB, BC, DE, EF, GH, HK, et menez les droites GL, KL. Puisque les deux droites AB, BC sont égales aux deux droites KH, HL, et que l'angle B est égal à l'angle KHL, la base AC sera égale à la base KL (prop. 4. 1) et puisque les angles ABC, GHK sont plus grands que l'angle DEF et que l'angle ABC est égal à l'angle KHL, l'angle GHL sera plus grand que l'angle DEF. De plus, puisque les deux droites GH, HL sont égales aux deux droites DE, EF et que F angle GHL est plus grand que l'angle E, la base GL sera plus grande que la base DF (prop. 24. 1) ; mais les droites GK, KL sont plus grandes que la droite GL (prop. 20. 1) : donc, à plus forte raison, les droites GK, KL sont plus grandes que la droite DF ; mais KL est égal à AC : donc les droites AC, GK sont plus grandes que la droite restante DF. Nous démontrerons semblablement que les droites AC, DF sont plus grandes que la droite GK; et que les droites GK, DF sont aussi plus grandes que la droite AC : donc on peut construire un triangle avec des droites égales aux droites AC, DF, GK (prop. 22. 1).

AUTREMENT.

Soient donnés les trois angles plans ABC, DEF, GHK (fig. 179) dont deux de ces angles, de quelque manière qu'on les prenne, sont plus grands que l'angle restant ; que ces angles soient compris par des droites égales AB, BC, DE, EF, GH, HK.

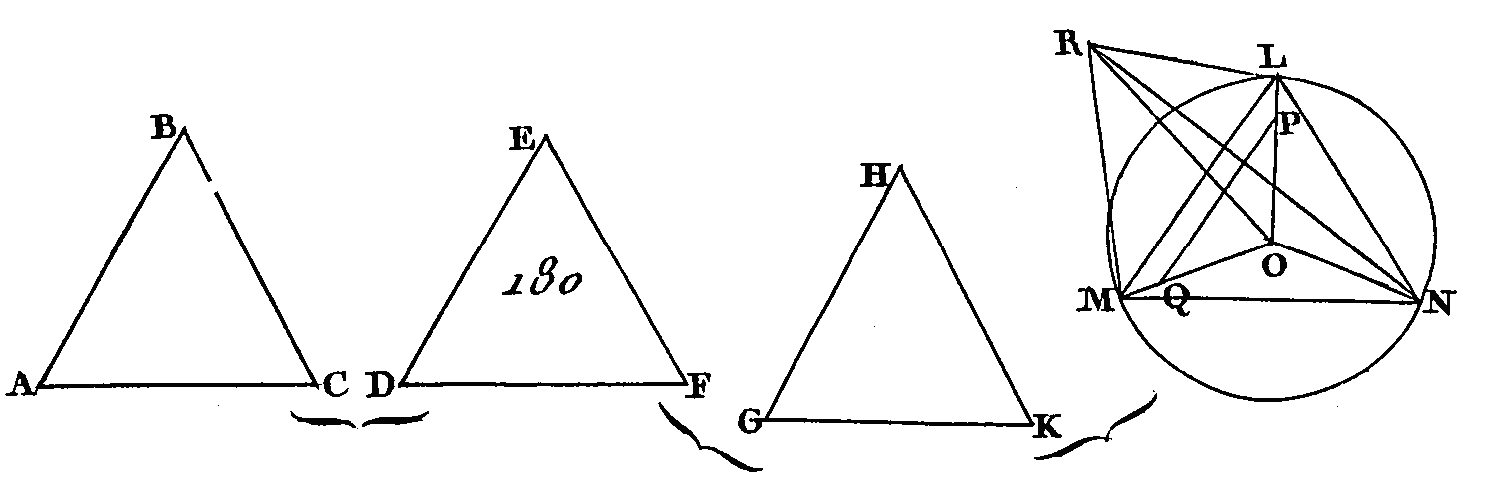
Menez les droites AC, DF, GK : je dis qu'on peut construire un triangle avec des droites égales aux droites AC, DF, GK; c'est-à-dire que deux de ces droites, de quelque manière qu'on les prenne, sont plus grandes que la droite restante. Si les angles ABC, GHK sont égaux, les droites AC, DF, GK seront égales entre elles (prop. 4. 1) et deux de ces droites seront plus grandes que la droite restante. Au contraire, si ces angles ABC, DEF, GHK sont inégaux, et si l'angle ABC est plus grand que l’un et que l'autre des angles E, H, la droite AC sera plus grande que l'une et que l'autre des droites DF, GK (prop. 24. 1); et il est évident que la droite AC avec l'une ou avec l'autre des droites DF, GK sera plus grande que la droite restante. Je dis aussi que les droites DF, GK sont plus grandes que la droite AC. Sur la droite AB et au point B construisez l'angle ABL égal à l'angle GHK (prop. 23. 1) ; faites la droite BL égale à une des droites AB, BC, DE, EF, GH, HK, et menez AL, LC. Puisque les deux droites AB, BL sont égales aux deux droites GH, HK, chacune à chacune, et qu'elles comprennent des angles égaux, la base AL sera égale à la base GK (prop. 4. 1) ; et puisque les angles E, H sont plus grands que l'angle ABC et que l'angle GHK est égal à l'angle ABL, l'angle restant E sera plus grand que l'angle LBC. De plus, puisque les deux droites LB, BC sont égales aux deux droites DE, EF, chacune à chacune, et que l'angle DEF est plus grand que l'angle LBC, la base DF sera plus grande que la base LC (prop. 24. 1). Mais on a démontré que la droite GK est égale à la droite AL : donc les droites DF, GK sont plus grandes que les droites AL, LC, mais les droites AL, LG sont plus grandes que la droite AC (prop. 20. 1) : donc à plus forte raison les droites DF, GK sont plus grandes que la droite AC : donc deux des droites AC, DF, GK, de quelque manière qu'on les prenne, sont plus grandes que la droite restante.

Donc on peut construire un triangle avec trois droites égales aux droites AC, DF, GK (prop. 22. 1) ; ce qu'il fallait démontrer.

PROPOSITION XXIII.

PROBLÈME.

Construire un angle solide avec trois angles plans dont deux de ces angles, de quelque manière qu'on tes prenne, sont plus grands que l’angle restant; il faut que ces trois angles soient plus petits que quatre angles droits.

Soient donnés les trois angles plans ABC, DEF, GHK (fig. 180) dont deux de ces angles, de quelque manière qu'on les prenne, sont plus grands que l'angle restant; que ces trois angles soient plus petits que quatre angles droits : il faut avec des angles égaux aux angles ABC, DEF, GHK construire un angle solide.

Faites les droites AB, BC, DE, EF, GH, HK égales entre elles et menez AC, DF, GK. On peut avec des droites égales à AC, DF, GK construire mi triangle (prop. 22. 11). Construisez le triangle LMN (prop. 22. 1) de manière que LM soit égal à AC, MN égal à DF et LN égal à GK. Décrivez ensuite une circonférence de cercle LMN autour du triangle LMN (prop. 5. 4); prenez le centre de ce cercle qui sera ou dans le triangle LMN ou sur un de ses côtés, ou hors de ce triangle.

Que le centre du cercle soit d'abord dans le triangle, et que ce centre soit O ; menez LO, MO, NO : je dis que AB est plus grand que LO ; car si cela n'est point, la droite AB sera égale à la droite LO ou plus petite que cette droite. Supposons d'abord qu'elle lui soit égale. Puisque AB est égal à LO et que AB est égal à BC, LO sera égal à BC ; mais LO est égal à OM : donc les deux droites AB, BC sont égales aux deux droites LO, OM, chacune à chacune; mais la base AC est supposée égale à la base LM : donc l'angle ABC est égal à l'angle LOM (prop. 8. 1). Par la même raison, l'angle DEF est égal à l'angle MON et l'angle GHK égal à l'angle NOL:_: donc les trois angles ABC, DEF, GHK sont égaux aux trois angles LOM, MON, NOL; mais les trois angles LOM, MON, NOL sont égaux à quatre angles droits : donc les trois angles ABC, DEF, GHK sont égaux à quatre angles; mais on les a supposés plus petits, que quatre angles droits, ce qui est absurde : donc la droite AB n'est pas égale à la droite LO : je dis de plus que la droite AB n'est pas plus petite que la droite LO. Car supposons, si cela est possible, qu'elle soit plus petite, et que la droite AB soit égale à la, droite OP et la droite BC égale à la droite OQ; menez PQ. Puisque la droite AB est égale à la droite BC, la droite OP sera égale à la droite OQ ; donc la droite restante PL sera égale à la droite restante QM : donc la droite LM est-parallèle à la droite PQ (prop. 2. 6): donc les triangles LMO, PQO sont équiangles : donc OL est à LM comme OP est à PQ (prop. 4. 6) et en échangeant les places des moyens, LO est à OP comme LM est à PQ (prop. 16. 5) ; mais LO est plus grand que OP : donc LM est plus grand que PQ ; mais LM est égal à AC, par construction : donc AC sera plus grand que PQ ; et puisque les deux droites AB, BC sont égales aux deux droites PO, OQ et.que la base AC est plus grande que la base PQ, l'angle ABC sera plus grand que l'angle POQ (prop. 24. 1) Nous démontrerons semblablement que l'angle DEF est plus grand que l'angle MON et l'angle GHK plus grand que l'angle NOL : donc les trois angles ABC, DEF, GHK sont plus grands que les angles LOM, MON, NOL ; mais les angles ABC, DEF, GHK sont supposés plus petits que quatre angles droits : donc à plus forte raison les trois angles LOM, MON, NOL sont plus petits que quatre angles droits:; mais ces trois angles sont égaux à quatre angles droits, ce qui est absurde : donc la droite AB n'est pas plus petite que la droite LO. On a démontré qu'elle ne lui est point égale : donc la droite AB est plus grande que la droite LO. Du point O élevez une perpendiculaire OR sur le plan du cercle LMN (prop. 12. 11). Supposons que le carré de OR soit égal à l'excès du carré de AB sur le carré de LO (lem. suiv.), et menons les droites RL, RM, RN. Puisque la droite OR est perpendiculaire sur le plan du cercle LMN, cette, droite sera perpendiculaire sur chacune des droites LO, MO, NO (déf. 3. 11); et puisque LO est égal à QM et que la droite OR est commune et qu’elle est perpendiculaire sur ces deux droites, la base LR sera égale à la base RM (prop. 4. 1). Par la même raison, la droite RN est égale à l'une et à l'autre des droites RL, RM : donc les trois droites RL, RM, RN sont égales entre elles. Puisque le carré fait sur OR est égal à l'excès du carré de AB sur le carré LO, le carré de AB sera égal aux carrés des droites LO, OR; mais le carré de RL est égal aux carrés des droites LO, OR (prop. 47. 1), car l'angle LOR est droit : donc le carré de la droite AB est égal au carré de la droite RL : donc la droite AB est égale à la droite RL ; mais chacune des droites BC, DE, EF, GH, HK est égale à la droite AB, et chacune des droites RM, RN est égale à la droite RL : donc chacune des droites AB, BC, DE, EF, GH, HKL est égale à chacune des droites RL, RM, RN ; mais puisque les deux droites LR, RM sont égales aux deux droites AB, BC et que la base LM est égale à la base AC, l'angle LRM sera égal à l'angle ABC (prop. 8. 1). L'angle MRN sera égal à l'angle DEF et l'angle LRN égal à l'angle GHK, par la même raison : donc avec les trois angles plans LRM, MRN, LRN, qui sont égaux aux trois angles donnés, on a construit un angle solide R qui est compris sous les angles LRM, MRN, LRN.

Que le centre du cercle sort présentement sur un des côtés, savoir, sur le côté MN (fig. 181), et que le centre de ce cercle soit le point O, menez OL : je dis de nouveau que AB est plus grand que LO ; car si cela n'est point, la droite AB sera égale à la droite LO ou bien elle sera plus petite que cette droite. Supposons d'abord qu'elle lui soit égale ; les deux droites AB, BC, c'est-à-dire les deux droites DE, EF, sont égales aux deux droites MO, OL, c'est-à-dire à la droite MN ; mais la droite MN est supposée égale à la droite DP : donc les droites DE, EF sont égales à la droite DF, ce qui ne peut être (prop. 20. 1) : donc la droite AB n'est point égale à la droite LO. On démontrerait semblablement qu'elle n'est pas plus petite, car de cette supposition il s'ensuivrait une plus grande absurdité : donc la droite AB est plus grande que la droite LO. Si l'on mène la droite RO perpendiculaire sur le plan du cercle, et si l'on suppose que le carré de OR soit égal à l'excès du carré de AB sur le carré LO (lem. suiv.), le problème sera résolu.

Que le centre du cercle soit enfin hors du triangle LMN (fig. 182), et que le centre de ce cercle soit O ; menez LO, MO, NO : je dis que la droite AB est plus grande que la droite LO ; car si cela n'est point, elle lui sera égale pu plus petite. Supposons d'abord qu'elle lui soit égale ; dans cette supposition les deux droites AB, BC sont égales aux deux droites MO, OL, chacune à chacune ; mais la base AC est aussi égale à la base ML : donc l'angle ABC est égal à l'angle MOL (prop. 8. 1). L'angle GHK est égal à l'angle LON, par la même raison : donc l'angle total MON est égal aux deux angles ABC, GHK; mais les angles ABC, GHK sont plus grands que l'angle DEF : donc l'angle MON est plus grand que l'angle DEF; et puisque les deux droites DE, EF sont égales aux deux droites MO, ON, et que la base DF est égale à la base MN, l'angle MON sera égal à l'angle DEF (prop. 8. 1) ; mais on a démontré qu'il est plus grand, ce qui est absurde : donc la droite AB n'est pas égale à la droite LO. Nous démontrerons de suite qu'elle n'est pas plus petite, donc elle est nécessairement plus grande. Si nous menons de nouveau la droite OR perpendiculaire sur le plan du cercle, et si nous supposons cette perpendiculaire égale à une droite dont le carré soit égal à l'excès du carré de la droite AB sur le carré de la droite LO (lem. suiv.), le problème sera résolu. Je dis, à présent que la droite AB n'est, pas plus petite que la droite LO. Supposons, si cela est possible, qu'elle soit plus petite ; faites OP égal à AB et OQ égal à BC et menez PQ. Puisque AB est égal à BC, la droite OP sera égale à la droite OQ : donc la droite restante PL sera égale à la droite restante QM : donc la droite LM est parallèle à la droite QP (prop. 2. 6) : donc les deux triangles LMO, QOP sont équiangles r. donc LO est à LM comme OP est à PQ (prop. 4. 6), et en échangeant les plans des moyens, LO est à OP comme LM est à PQ; mais LO est plus grand que OP : donc LM est plus grand que PQ ; mais LM est égal à AC par construction: donc AC sera plus grand que PQ ; mais puisque les deux droites AB, BC sont égales aux deux droites PO, OQ, chacune à chacune, et que la base AC est plus grande que la base PQ, l'angle ABC sera plus grand que l'angle POQ (prop. 25. 1). Si l'on prend la droite OV égale à chacune des droites OP, OQ, et si l'on mène PV, nous démontrerons semblablement que l'angle GHK est plus grand que l’angle POV. Sur la droite LO et au point O, pris sur celle droite, construisez l'angle LOS égal à l'angle ABC et l'angle LOT égal à l'angle GHK; faites chacune des droites OS, OT égale à l'a droite PO, et menez PS, PT, ST. Puisque les deux droites AB, BC sont égales aux deux droites PO, OS, et que l'angle ABC est égal à l'angle POS, la base AC, c'est-à-dire la droite LM, sera égale à la base PS (prop. 4. 1). La droite LN sera égale à la droite PT, par la même raison; et puisque les deux droites ML, LN sont égales aux deux droites PS, PT et que l'angle MLN est plus grand que l'angle SPT, la base MN sera plus grande que la base ST (prop. 24. 1) ; mais MN est égal à DF : donc DF sera plus grand que ST : donc puisque les deux droites DE, EF sont égales aux deux droites SO, OT et que la base DF est plus grande que la base ST, l'angle DEF sera plus grand que SOT (prop. 25. 1) ; mais l'angle SOT est égal aux angles ABC, GHK : donc l'angle DEF est plus grand que les angles ABC, GHK : mais il est au contraire plus petit ; ce qui est impossible.

LEMME.

Nous allons faire voir de quelle manière on fait sur RO un carré qui soit égal à l'excès du carré de la droite AB sur le carré de la droite LO.

Soient les droites AB, LO (fig. 183); que AB soit la plus grande, et sur cette droite décrivez la demi-circonférence ABC, et appliquez dans la demi-circonférence ABC une droite AC égale à la droite LO et menez la droite BC.

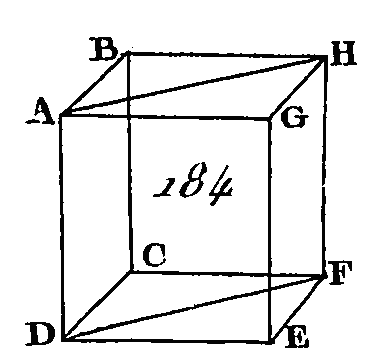
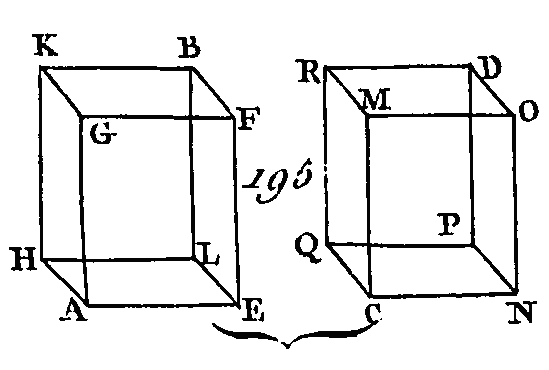
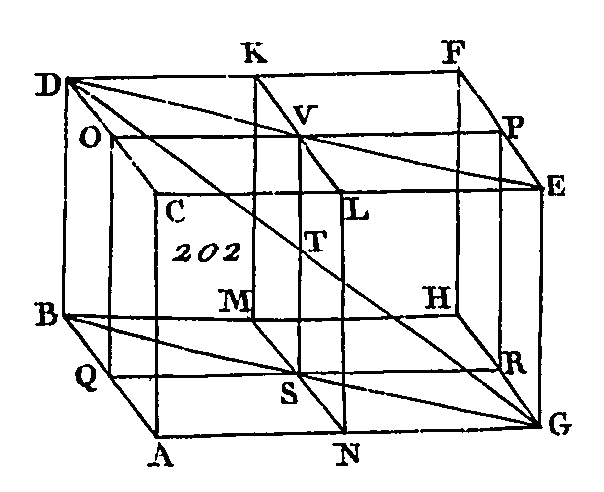
Puisque l'angle ACB est compris dans le demi-cercle ABC, l'angle ACB sera droit (prop. 31. 3) : donc le carré de la droite AB est égal aux carrés des droites AC, CB (prop. 47. 1)^: donc le carré de AB surpasse le carré de AC du carré de CB ; mais AC est égal à LO ; donc le carré de AB surpasse le carré de LO du carré de CB : donc si nous faisons, la droite OR égale à la droite CB, le carré de la droite AB surpassera le carré de la droite LO du carré de la droite OR; ce que nous voulions faire.

PROPOSITION XXIV.

THÉORÈME.

Si un solide est compris sous des plans parallèles, les plans opposés sont des parallélogrammes a égaux.

Que le solide CDHG (fig. 184) soit compris, sous les plans parallèles AC, GF, AH, DF, FB, AE : je dis que les plans opposés sont des parallélogrammes égaux.

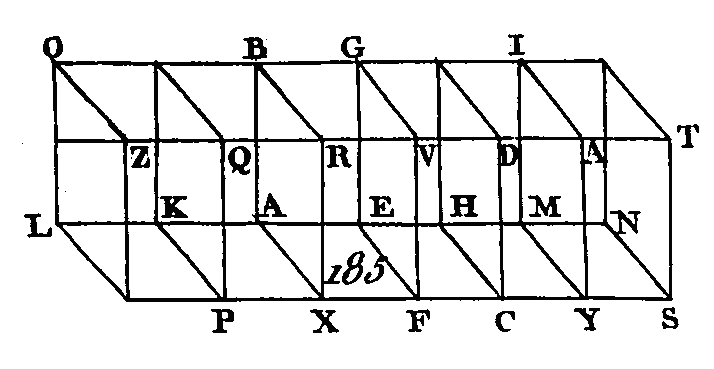
Puisque les deux plans parallèles BG, CE sont coupés, par le plan AC, leurs communes, sections sont parallèles. (prop. 16. 11) : donc la droite AB est parallèle à la droite DC. De plus, puisque les deux plans parallèles BF, AE sont coupés sur le plan AC, leurs communes sections sont parallèles : donc la droite AD est parallèle à la droite BC ; mais on a démontré que la droite AB est parallèle à la droite DC : donc le plan AC est un parallélogramme. Nous démontrerons semblablement que chacun des plans DF, FG, GB, BF, AE est un parallélogramme.

Menez les droites AH, DF. Puisque AB est parallèle à DC et BH parallèle à CF, les deux droites AB, BH qui se rencontrent seront parallèles aux deux droites DC, CF qui se rencontrent et qui ne sont pas dans le même plan : donc ces droites comprendront des angles égaux (prop. 10. 11) : donc l'angle ABH est égal à l'angle DCF ; et puisque les deux droites AB, BH sont égales aux deux droites DC, CF (prop. 34. 1), et que l'angle ABH est égal à l'angle DCF, la base AH sera égale à la base DF (prop. 4. 1) et le triangle ABH égal au triangle DCF ; mais le parallélogramme BG est double du triangle ABH et le parallélogramme CE double aussi du triangle DCF (prop. 34.1) : donc le parallélogramme BG sera égal au parallélogramme CE. Nous démontrerons semblablement que le parallélogramme AC est égal au parallélogramme GF et le parallélogramme AE égal au parallélogramme BF.

Donc si un solide est compris sous des plans parallèles, les plans opposés sont des parallélogrammes égaux; ce qu'il fallait démontrer.

PROPOSITION XXV.

THÉORÈME.

Si un parallélépipède est coupé par un plan parallèle à des plans opposés, les solides obtenus par cette section seront entre eux comme leurs hases.

Que le parallélépipède ABCD (fig. 185) soit coupé par un plan VE parallèle aux plans opposés RA, DH : je dis que le solide ABFV est au solide EGCD comme la base AEFX est à la base EHCF.

Prolongez de part et d'autre la droite AH et prenez autant de droites égales que vous voudrez HM, MN égales chacune à la droite EH; prenez aussi autant de droites que vous voudrez AK, KL égales chacune à la droite AE et achevez les parallélogrammes LP, KX, HY, MS, et les parallélépipèdes AQ, KZ, DM, MT. Puisque les droites LK, KA, AE sont égales entre elles, les parallélogrammes LP, KX, AF seront égaux entre eux. (prop. 38. 1). Les parallélogrammes KO, KB, AG sont aussi égaux entre eux, ainsi que les parallélogrammes LZ, KQ, AR (pro. 24. 11) car ces parallélogrammes sont opposés. Par la même raison, les parallélogrammes EC, HY, MS sont encore égaux entre eux, ainsi que les parallélogrammes HG, HI, IN et les parallélogrammes DH, MA, NT : donc trois plans des solides LQ, KR, AV sont égaux à trois plans; mais trois plans de ces solides sont égaux à trois plans opposés : donc les trois parallélépipèdes LQ, KR, AV seront égaux entre eux (déf. 10. 11). Les trois parallélépipèdes ED, DM, MT sont égaux entre eux, par la même raison : donc la base LF est multiple de la base AF autant de fois que le parallélépipède LV est multiple du parallélépipède AV. Par la même raison la base NF est multiple de la base HF autant de fois que le parallélépipède NV est multiple du parallélépipède HV. Enfin si la base LF est égale à la base NF, le parallélépipède LV sera égal au parallélépipède NV ; si la base LF surpasse la base NF, le parallélépipède LV surpassera le parallélépipède NV, et si la base LF est plus petite que la base NF, le parallélépipède, LV sera plus petit que le parallélépipède MV. On a donc quatre quantités, savoir, les deux bases AF, FH et les deux parallélépipèdes AV, VH, et l'on a pris des équimultiples de la base AF et du parallélépipède AV, savoir, la base LF et le parallélépipède LV ; on a pris aussi des équimultiples de la base HF et du parallélépipède HV, savoir, la base NF et le parallélépipède NV. Mais on a démontré que si la base LF surpasse la base NF, le parallélépipède LV surpassera le parallélépipède NV ; que si la base LV est égale à la base NV, le parallélépipède LV sera égal au parallélépipède NV, et que si la base LV est plus petite que la base NV, le parallélépipède LV sera plus petit que le parallélépipède NV : donc le parallélépipède AV est au parallélépipède VH comme la base AF est à la base FH (déf. 5. 5) ; ce qu'il fallait démontrer.

PROPOSITION XXVI.

ProblÈme.

Sur une droite donnée et à un point donné dans cette droite, construire un angle solide égal à un angle solide donné.

Soit AB (fig. 186) la droite donnée, A le point donné dans cette droite, et D l'angle solide donne et compris sous les plans EDC, EDF, FDC: il faut sur la droite donnée AB et au point A donné dans cette droite construire un angle solide égal à l'angle solide donné D.

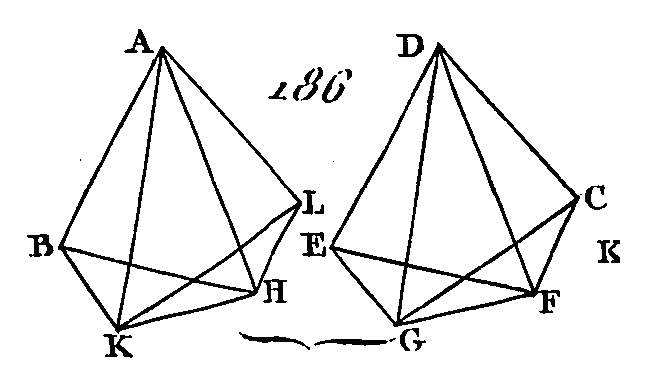
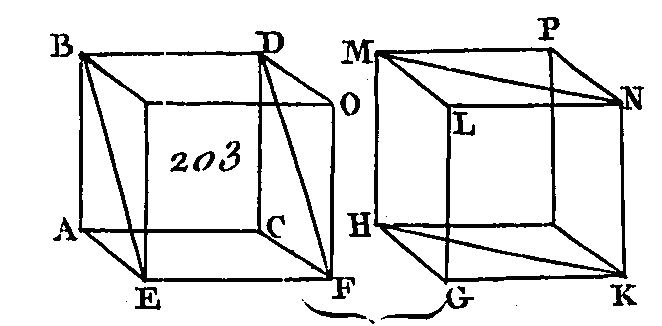
Prenez dans la droite DF un point quelconque F, et de ce point menez une perpendiculaire FG sur le plan qui passe par les droites ED, DC (prop. 11. 11) ; que la perpendiculaire FG rencontre le plan DEC au point G ; menez la droite DG. Ensuite sur la droite AB et au point donné A pris dans cette droite construisez l'angle BAL égal à l'angle EDC (prop. 23. 1), et l'angle BAK égal à l'angle EDG ; faites ensuite AK égal à DG (prop. 3. 1) ; du point K menez KH perpendiculaire sur le plan qui passe par BAL (prop. 12. 11), faites enfin la droite KH égale à la droite GF et menez la droite HA : je dis que l'angle solide A, compris sous les angles BAL, BAH, HAL, est égal à l'angle solide D, compris sous les angles EDC, EDF, FDC.

Faites AB égal à DE et menez les droites HB, KB, FE, GE. Puisque la droite FG est perpendiculaire sur le plan EDC, cette droite sera perpendiculaire sur toutes les droites qui la rencontrent et qui sont dans ce plan (déf. 3. 11) : donc chacun des angles FGD, FGE est droit; chacun des angles HKA, HKB est droit, par la même raison; et puisque les deux droites KA, AB sont égales aux deux droites GD, DE, chacune à chacune, et que ces droites comprennent des angles égaux, la base B K sera égale à la base EG (prop. 4. i) ; mais la droite KH est égale à la droite GF, et les angles HKB, FGE sont droits l'un et l'autre : donc la droite HB est égale à la droite FE. De plus, puisque les deux droites AK, KH sont égales aux deux droites DG, GF, et que ces droites comprennent des angles droits, la base AH sera égale à la base DF ; mais la droite AB est égale à la droite DE : donc les deux droites HA, AB sont égales aux deux droites FD, DE; mais la base HB est égale à la base FE : donc l'angle BAH sera égal à l'angle EDF. L'angle HAL est égal à l'angle FDC, par la même raison ; en effet, faites la droite AL égale à la droite DC, et menez les droites KL, HL, GC, FC. Puisque l'angle total BAL est égal à l'angle total EDG et que l'angle BAK est égal à l'angle EDG, l'angle restant KAL sera égal à l'angle restant GDC ; et puisque les deux droites KA, AL sont égales aux deux droites GD, DC, et qu'elles renferment des angles égaux, la base KL sera égale à la base GC (prop. 4. 1) ; mais la droite KH est égale à la droite GF : donc les deux droites LK, KH sont égales aux deux droites CG, GF ; mais ces deux droites renferment des angles droits : donc la base HL est égalé à la base FC. De plus, puisque les deux droites HA, AL sont égalés aux deux droites FD, DC et que la base HL est égale à la base FC, l'angle H AL sera égal à l'angle FDC (prop. 8. 1); mais l'angle BAL est égal à l'angle EDC : donc, sur une droite donnée et à un point pris dans cette droite, on a construit un angle solide égal à un angle solide donné; ce qu'il fallait faire.

PROPOSITION XXVII.

PROBLÈME.

Sur une droite donnée décrire un parallélépipède qui soit semblable à un parallélépipède donné et semblablement placé que lui.

Soit AB (fig. 187) la droite donnée et DC le parallélépipède donné : il faut décrire sur la droite AB un parallélépipède qui soit semblable au parallélépipède donné DC et semblablement placé que lui.

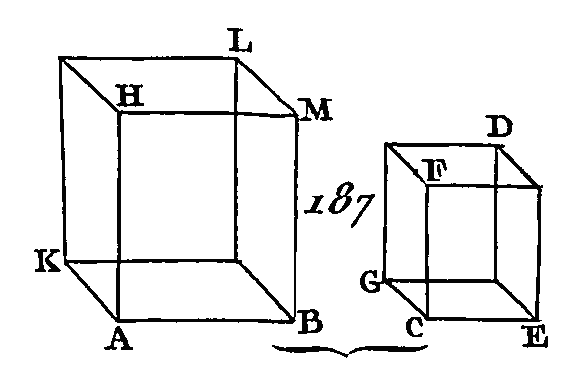
Sur la droite AB et au point A donné dans cette droite construisez un angle solide qui soit compris sous les angles plans BAH, HAK, KAB et qui soit égal à l'angle solide C, de manière que l'angle BAH soit égal à l'angle ECF, l'angle BAK égal à l'angle ECG et l'angle KAH égal à l'angle GCF, et ensuite faites en sorte que EC soit à CG comme BA est à AK, et que GC soit à CF comme KA est à AH (prop. 12. 6) : EC sera à CF comme BA est à AH (prop. 22. 5) ; terminez le parallélogramme BH et le parallélépipède AL.

Puisque EC est à CG comme BA est à AK, les côtés qui sont autour des angles égaux ECG, BAK seront proportionnels : donc le parallélogramme GE sera semblable au parallélogramme KB (prop. 4. 6). Par la même raison, le parallélogramme GF sera semblable au parallélogramme KH, et le parallélogramme FE semblable au parallélogramme HB : donc trois parallélogrammes du parallélépipède CD sont semblables à trois parallélogrammes du parallélépipède AL ; mais trois parallélogrammes de ces parllélépipèdes sont égaux et semblables à trois parallélogrammes opposés (prop. 24. 1) donc le parallélépipède total CD sera semblable au parallélépipède total AL.

Donc, sur la droite AB, on a construit un parallélépipède AL qui est semblable à un parallélépipède donné CD et semblablement placé ; ce qu'il fallait faire.

PROPOSITION XXVIII.

THÉORÈME.

Si un parallélépipède est coupé par un plan selon les diagonales de deux plans opposés, le parallélépipède sera coupé en deux parties égales par ce plan.

Que le parallélépipède AB (fig. 188) soit coupé par le plan CDEF selon les diagonales des deux plans opposés CF, DE : je dis que le parallélépipède AB sera coupé en deux parties égales par le plan CDEF.

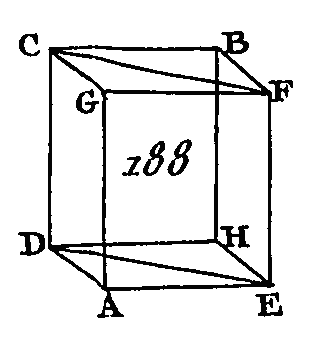
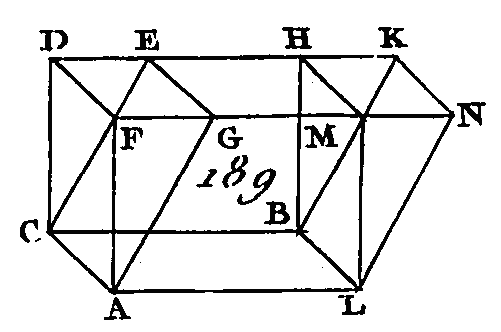
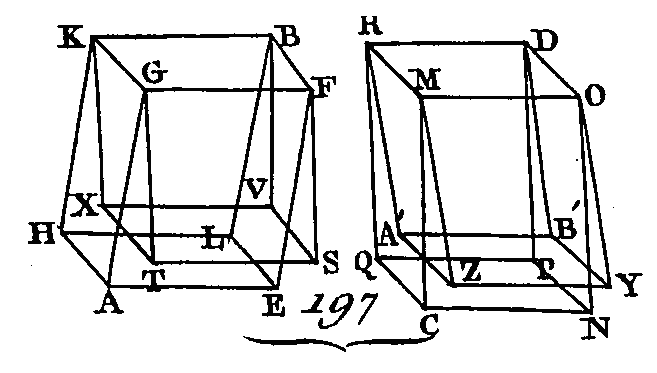
Puisque le triangle CGF est égal au triangle CBF (prop. 34. 1) et le triangle ADE égal au triangle DEH, de plus, puisque le parallélogramme CA est égal au parallélogramme BE (prop. 24. 11), car ces deux parallélogrammes sont opposés, et puisque le parallélogramme GE est aussi égal au parallélogramme CH, le prisme compris sous les deux triangles CGF, ADE et sous les trois parallélogrammes GE, AC, CE, sera égal au prisme compris sous les deux triangles CFB, DEH, et les trois parallélogrammes CH, BE, CE, car ils sont compris sous des plans égaux en nombre et en grandeur (déf. 10. 11) : donc le parallélépipède total AB est coupé en deux parties égales par le plan CDEF ; ce qu'il fallait démontrer.

PROPOSITION XXIX.

THÉORÈME.

Les parallélépipèdes qui ont la même base et la même hauteur, et dont les arêtes sont placées dans les mêmes droites, sont égaux entre eux.

Que les parallélépipèdes CM, CN (fig. 189) aient la même base AB et la même hauteur, et que les arêtes AF, AG, LM, LN, CD, GE, BH, B K soient dans les mêmes droites FN, DK : je dis que le parallélépipède CM est égal au parallélépipède CN.

Car puisque chacune des figures CH, CK est un parallélogramme, la droite CB sera égale à chacune des droites DH, EK (prop. 34. 1) : donc la droite DH sera égale à la droite EK. Retranchez la partie commune EH, la droite restante DE sera égale à la droite restante HK : donc le triangle DEC est égal au triangle HKB (prop. 8. 1), et le parallélogramme DG égal au parallélogramme HN (prop. 56. 1). Par la même raison le triangle AFG est égal au triangle LMN. Mais le parallélogramme CF est égal au parallélogramme BM et le parallélogramme CG égal au parallélogramme BN (prop. 24. n), car ces parallélogrammes sont opposés : donc le prisme contenu sous les deux triangles AFG, DEC et sous les trois parallélogrammes AD, DG, GC est égal au prisme contenu sous les deux triangles LMN, HBK et sous les trois parallélogrammes BM, NH, BN (déf. 10. 11) : donc si nous ajoutons à chacun de ces prismes le solide dont une des bases est le parallélogramme AB et dont l'autre base est le parallélogramme GEHM, le parallélépipède total CM sera égal au parallélépipède total CN.

Donc les parallélépipèdes qui ont la même base et la même hauteur, et dont les arêtes sont placées dans les mêmes droites sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXX.

THÉORÈME.

Des parallélépipèdes qui ont la même base et la même hauteur, et dont les droites insistantes ne sont point placées dans les mêmes droites, sont égaux entre eux.

Soient CM, CN (fig. 190) des parallélépipèdes qui ont la même base AB et la même hauteur, et dont .les droites insistantes AF, AG, LM, LN, CD, CE, BH, BK ne sont point placées dans les mêmes droites : je dis que le parallélépipède CM est égal au parallélépipède CN.

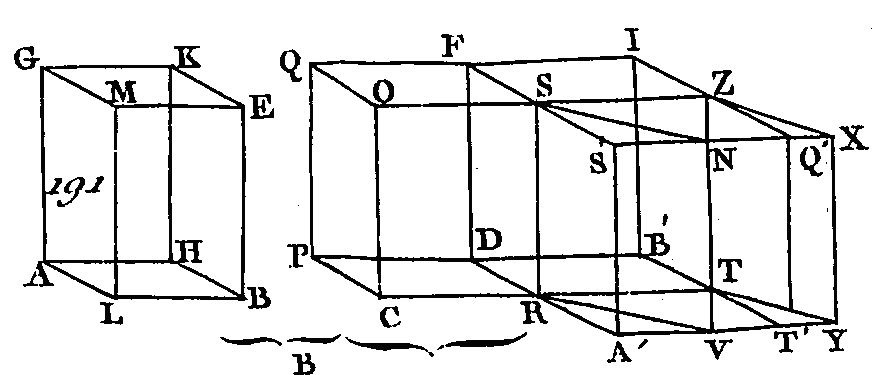
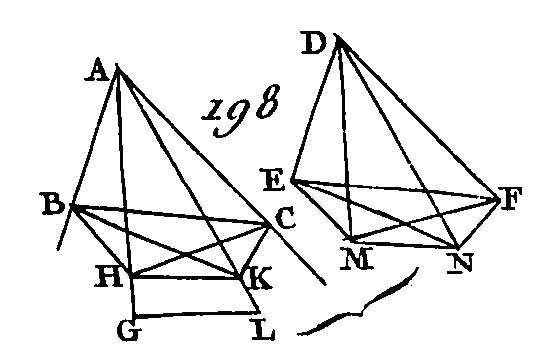
Prolongez les droites NK, DH et les droites GE, FM, et que ces droites se rencontrent aux points P, R, Q, O. Menez AO, LP, CQ, BR. Le parallélépipède CM, dont la base est le parallélogramme ACBL opposé au parallélogramme FDHM sera égal au parallélépipède CP dont la base est le parallélogramme ACBL opposé au parallélogramme OQRP (pr. 29. 11), car ces deux parallélogrammes ont la même base et la même hauteur, et leurs droites insistantes AF, AO, LM, LP, CD, CQ, BH, BR sont dans les mêmes droites FP, DR; mais le parallélépipède CP dont la base est le parallélogramme ACBL opposé au parallélogramme OQRP est égal au parallélépipède CN dont la base est le parallélogramme ACBL opposé au parallélogramme GEKN (prop. 29. 11); car ces deux parallélépipèdes ont la même base et la même hauteur, et leurs arêtes AG, AO, CE, CQ, LN, LP, BK, BR sont dans les mêmes droites GQ, NR : donc le parallélépipède CM est égal au parallélépipède CN.

Donc les parallélépipèdes qui ont la même base et la même hauteur, et dont les arêtes ne sont point placées dans les mêmes droites, sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXXI.

THÉORÈME.

Les parallélépipèdes qui ont des bases égales et la même hauteur, sont égaux entre eux.

Que les parallélépipèdes AE, CF (fig. 191) aient des bases égales AB, CD et la même hauteur : je dis que le parallélépipède AE est égal au parallélépipède CF.

Supposons d'abord que les arêtes HK, BE, AG, LM, PQ, DF, CO, RS soient perpendiculaires sur les bases AB, CD, et que l'angle ALB ne soit pas égal à l'angle CRD. Conduisez la droite RT dans la direction de la droite CR, et faites sur la droite RT et au point R pris dans cette droite l'angle TRV égal à l'angle ALB (prop. 23. 1), faites la droite RT égale à la droite AL et la droite RV égale à la droite LB; par le point V conduisez la droite YV parallèle à la droite RT, achevez la base RY et le parallélépipède ZV. Puisque les deux droites TR, RV sont égales aux deux droites AL, LB et qu'elles comprennent des angles égaux, le parallélogramme RY sera égal et semblable au parallélogramme HL. De plus, puisque RT est égal à AL et RS égal à LM et que ces droites comprennent des angles égaux, le parallélogramme RZ sera égal et semblable au parallélogramme AM. Le parallélogramme SV sera égal et semblable au parallélogramme LE, par la même raison : donc trois parallélogrammes du parallélépipède AE seront égaux et semblables à trois parallélogrammes du parallélépipède ZV: donc puisque trois parallélogrammes sont égaux et semblables à trois parallélogrammes opposés (prop. 24. 11), le parallélépipède total AE sera égal au parallélépipède total ZV. Prolongez DR, YV, et que ces droites se rencontrent au point A’ ; par le point T conduisez la droite TT’ parallèle à la droite DA’, et prolongez TT’, PD jusqu'à ce qu'elles se rencontrent au point B’, et complétez les parallélépipèdes A’Z, RI. Le parallélépipède ZA’ qui a pour base le parallélogramme RZ opposé au parallélogramme A’Q’ est égal au parallélépipède ZV qui a pour base le parallélogramme RZ opposé au parallélogramme VX, attendu que ces deux parallélépipèdes ont la même base RZ et la même hauteur, et que les droites insistantes RA’, RV, TT ’, TY, SS’, SN, ZQ’, ZX sont placées dans les mêmes droites A’Y, S’X ; mais le parallélépipède ZV est égal au parallélépipède AE : donc le parallélépipède AE est égal au parallélépipède ZA’. Mais le parallélogramme RVYT est égal au parallélogramme A’T (prop. 35. 1), car ces deux parallélogrammes ont la même base RT et sont compris entre les mêmes parallèles RT, A’Y, et le parallélogramme RVYT est égal au parallélogramme C D parce que le parallélogramme CD est égal au parallélogramme AB : donc le parallélogramme A’T sera égal au parallélogramme CD, mais DT est un autre parallélogramme : donc la base CD est à la base DT comme la base A’T est à la base DT (prop. 7. 5); et puisque le parallélépipède CI est coupé par le plan RF parallèle aux plans opposés, la base CD sera à la base DT comme le parallélépipède CF est au parallélépipède RI (prop. 25. 11). Par la même raison, puisque le parallélépipède A’I est coupé par le plan RZ parallèle aux plans opposés, la base A’T sera à la base DT comme le parallélépipède AZ est au parallélépipède RI; mais la base CD est à la base DT comme la base A’T est à la base TD : donc le parallélépipède CF est au parallélépipède RI comme le parallélépipède AZ est au parallélépipède RI (prop. 15. 5) : donc puisque chacun des parallélépipèdes CF, A’Z a la même raison avec le parallélépipède RI, le parallélépipède CF sera égal au parallélépipède A’Z (prop. 9. 5) ; mais on a démontré que le parallélépipède A’Z est égal au parallélépipède AE : donc le parallélépipède AE est égal au parallélépipède CF.

Supposons à présent que les droites insistantes AG, HK, BE, LM, CO, PQ, DF, RS (fig. 192) ne soient point perpendiculaires sur les bases AB, CD : je dis encore que le parallélépipède AE sera égal au parallélépipède CF.

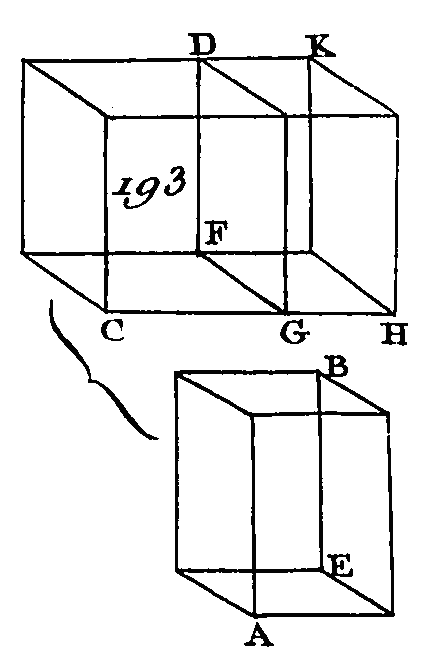
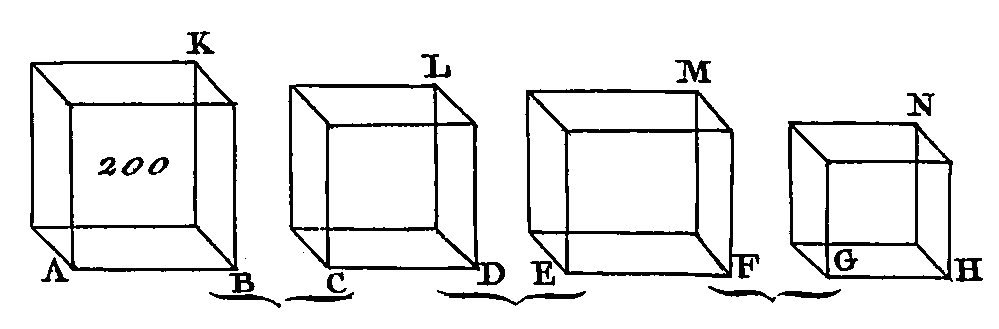
Des points K, E, G, M, Q, F, O, S conduisez sur les plans LN, A’D les perpendiculaires KN, ET, GV, MX, QY, FZ, OA’, SI qui rencontrent ces plans aux points N T, V, X, Y, Z, A’, I (prop. 11. 11), et menez les droites NT, VX, NV, TX, YZ, YA’, A’I, ZI. Le parallélépipède KX sera égal au parallélépipède QI (prop. 31. 11), parce que les parallélépipèdes KX, QI ont des bases égales KM, QS, et la même hauteur, et que leurs arêtes sont perpendiculaires sur leurs bases. Mais le parallélépipède KX est égal au parallélépipède AE (prop. 30. 11), et le parallélépipède QI égal au parallélépipède CF, puisqu'ils ont la même base et la même hauteur, et que leurs arêtes ne sont pas dans les mêmes droites : donc le parallélépipède AE est égal au parallélépipède CF.

Donc les parallélépipèdes qui ont des bases égales et la même hauteur, sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXXII.

THÉORÈME.

Les parallélépipèdes qui ont la même hauteur sont entre eux comme leurs bases.

Soient AB, CD (fig. 193) deux parallélépipèdes qui aient la même hauteur : je dis que ces parallélépipèdes sont entre eux comme leurs bases, c'est-à-dire que le parallélépipède AB est au parallélépipède CD comme la base AE est à la base CF.

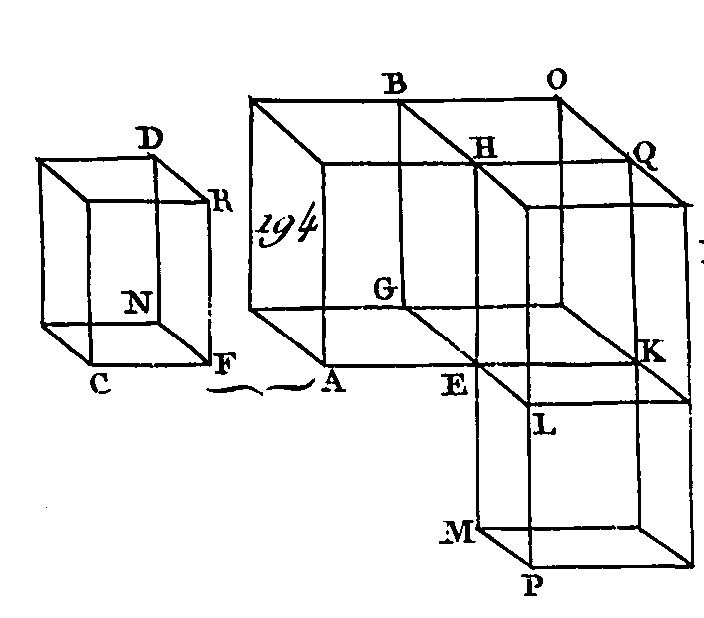
Appliquez sur FG un parallélogramme FH qui soit égal au parallélogramme AE (prop. 45. 1), et sur la base FH construisez le parallélépipède GK dont la hauteur soit la même que celle du parallélépipède CD. Le parallélépipède AB sera égal au parallélépipède GK (prop. 31. 11), car ces parallélépipèdes ont des bases égales AE, FH et la même hauteur. Puisque le parallélépipède CK est coupé par un plan DG parallèle aux plans opposés, le parallélépipède HD sera au parallélépipède DC comme la base HF est à la base CF (prop. 25. 11) ; mais la base FH est égale à la base, AE et le parallélépipède GK égal au parallélépipède AB : donc le parallélépipède AB est au parallélépipède CD comme la base AE est à la base CF.

Donc les parallélépipèdes qui ont la même hauteur sont entre eux comme leurs bases ; ce qu'il fallait démontrer.

PROPOSITION XXXIII.

THÉORÈME.

Les parallélépipèdes semblables sont entre eux en raison triplée de leurs côtés homologues.

Soient AB, CD (fig. 194) deux parallélépipèdes semblables et que le côté AE soit l'homologue du côté CF : je dis que les parallélépipèdes AB, CD sont entre eux en raison triplée des côtés AE, CF.

Menez les droites EK, EL, EM dans la direction des droites AE, GE, HE ; faites EK égal à CF, EL égal à FN et EM égal à FR; achevez le parallélogramme KL et le parallélépipède KP. Les deux droites EK, EL sont égales aux deux droites CF, FN ; l'angle REL est égal à l'angle CFN, parce que l'angle AEG est égal à CFN, à cause de la similitude des parallélépipèdes AB, CD : donc le parallélogramme KL sera égal et semblable au parallélogramme CN. Par la même raison, le parallélogramme KM est égal et semblable au parallélogramme CR, et le parallélogramme PE égal et semblable au parallélogramme DF : donc trois parallélogrammes du parallélépipède KP sont égaux et semblables à trois parallélogrammes du parallélépipède CD : donc puisque trois parallélogrammes sont égaux et semblables à trois parallélogrammes opposés (prop. 24. 11), le parallélépipède total KP sera égal et semblable au parallélépipède total CD (déf. 10. 11). Achevez le parallélogramme GK, et sur les bases GK, KL construisez deux parallélépipèdes EO, LQ qui aient la même hauteur que le parallélépipède AB. Puisqu'à cause de la similitude des parallélépipèdes AB, CD le côté AE est au côté CF comme le côté EG est au côté FN comme le côté EH est au côté FR, et puisque FC est égal à EK, le côté FN est égal à EL, et que FR est égal au côté EM, AE sera au côté EK comme le côté GE est au côté EL et comme le côté HE est au côté EM. Mais AE est à EK comme le parallélogramme AG est au parallélogramme GK (prop. 1. 6), et GE est à EL comme le parallélogramme GK est au parallélogramme KL, et, de plus, HE est à EM comme le parallélogramme QE est au parallélogramme RM : donc le parallélogramme AG est au parallélogramme GK comme le parallélogramme GK est au parallélogramme KL et comme le parallélogramme QE est au parallélogramme KM. Mais AG est à GK comme le parallélépipède AB est au parallélépipède EO (prop. 32. 11), et GK est à KL comme le parallélépipède OE est au parallélépipède QL, et de plus QE est à KM comme le parallélépipède QL est au parallélépipède KP : donc le parallélépipède AB est au parallélépipède EO comme le parallélépipède EO est au parallélépipède QL et comme le parallélépipède QL est au parallélépipède KP ; mais si l'on a quatre quantités de suite qui soient proportionnelles, la première et la quatrième seront entre elles en raison triplée de la première et de la seconde (déf. 11. 5) : donc les parallélépipèdes AB, KP sont entre eux en raison triplée des parallélépipèdes AB, EO ; mais AB est à EO comme le parallélogramme AG est au parallélogramme GK et comme la droite AE est à la droite EK (prop. 1. 6) : donc les parallélépipèdes AB, KP sont en raison triplée des droites AE, EK. Mais le parallélépipède RP est égal au parallélépipède CD et la droite EK égale à la droite CF : donc les parallélépipèdes AB, CD sont en raison triplée des côtés homologues AE, CF ; ce qui fallait démontrer.

COROLLAIRE.

Il suit manifestement de là, que si quatre droites sont proportionnelles, la première sera à la quatrième comme le parallélépipède construit sur la première est au parallélépipède semblable et semblablement construit sur la seconde, puisque la première et la quatrième droite sont en raison triplée de la première et de la seconde.

PROPOSITION XXXIV.

THÉORÈME.

Les bases des parallélépipèdes égaux sont réciproquement proportionnelles aux hauteurs ; et les parallélépipèdes dont les bases sont réciproquement proportionnelles aux hauteurs sont égaux entre eux.

Que les parallélépipèdes AB, CD (fig. 195) soient égaux : je dis que leurs bas.es sont réciproquement proportionnelles à leurs hauteurs; c'est-à-dire que la base EH est à la base NQ comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB.

Supposons d'abord que les droites insistantes AG, EF, LB, HK, CM, NO, PD, QR soient perpendiculaires sur les bases : je dis que la base EH est à la base NQ comme CM est à AG. Si la base EH est égale à la base NQ et le parallélépipède AB égal au parallélépipède CD, la hauteur CM sera égale à la hauteur AG ; car si les bases EH, NQ étant égales, les hauteurs AG, C M n'étaient pas égales, le parallélépipède AB ne serait point égal au parallélépipède CD (prop. 31. 11) ; mais ces deux parallélépipèdes sont supposés égaux : donc les hauteurs CM, AG ne sont pas inégales : donc elles sont égales : donc la base EH est à la base NQ comme CM est à AG, d'où il suit évidemment que les bases des parallélépipèdes AB, CD sont réciproquement proportionnelles à leurs hauteurs.

Supposons à présent que la base EH ne soit pas égale à la base NQ et que la base EH soit la plus grande ; puisque le parallélépipède AB est égal au parallélépipède CD la hauteur CM sera plus grande que la hauteur AG ; car si cela n'était point, les parallélépipèdes AB, CD ne seraient pas égaux (prop. 31. 11) ; mais ils sont supposés égaux. Faites CT (fig. 196) égal à AG et sur la base NQ construisez un parallélépipède XC dont la hauteur soit CT. Puisque le parallélépipède AB est égal au parallélépipède CD et que XC est un autre parallélépipède avec lequel les deux parallélépipèdes égaux AB, CD ont la même raison (prop. 7. 5), le parallélépipède AB sera au parallélépipède CX comme le parallélépipède CD est au parallélépipède CX; mais le parallélépipède AB est au parallélépipède CX comme la base EH est à la base NQ (prop. 32. 11), car les parallélépipèdes AB, CX sont égaux en hauteur, et le parallélépipède CD est au parallélépipède CX comme la base MQ est à la base QT (prop. 25. 11), et comme le côté MC est au côté CT (prop. 1. 6): donc la base EH est à la base NQ comme le côté MC est au côté CT ; mais CT est égal à AG : donc la base EH est à la base NQ comme le côté MC est au côté AG : donc les bases des parallélépipèdes AB, CD sont réciproquement proportionnelles aux hauteurs.

Supposons ensuite que les bases des parallélépipèdes AB, CD soient réciproquement proportionnelles aux hauteurs, c'est-à-dire que la base EH soit à la base NQ comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB : je dis que les parallélépipèdes AB, CD sont égaux entre eux.

Que les arêtes soient encore perpendiculaires sur les bases. Si la base EH est égale à la base NQ et si la base EH est à la base NQ comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB, la hauteur du parallélépipède CD sera égale à la hauteur du parallélépipède AB. Mais les parallélépipèdes qui ont des bases égales et la même hauteur sont égaux entre eux (prop. 31. 11): donc le parallélépipède AB sera égal au parallélépipède CD.

Mais supposons que la base EH ne soit point égale à la base NQ et que EH soit la plus grande base ; la hauteur du parallélépipède CD sera plus grande que la hauteur du parallélépipède AB, c'est-à-dire que CM sera plus grand que AG; faites CT égal à AG, achevez également le parallélépipède CX. Puisque la base EH est à la base NQ comme le côté CM est au coté AG et que AG est égal à CT, la base EH sera à la base NQ comme le côté MC est au côté CT. Mais la base EH est à la base NQ comme le parallélépipède AB est au parallélépipède CX (prop. 32. 11), car les parallélépipèdes AB, CX sont égaux en hauteur; mais le côté MC est au côté CT (prop. 1. 6), comme la base MQ est à la base QT et comme le parallélépipède CD est au parallélépipède CX (prop. 25. 11); donc le parallélépipède AB est au parallélépipède CX comme le parallélépipède CD est au parallélépipède CX : donc l'un et l'autre des parallélépipèdes AB, CD ont la même raison avec le parallélépipède CX : donc le parallélépipède AB sera égal au parallélépipède CD (prop. 9. 5) ; ce qu'il fallait démontrer.

Supposons maintenant que les arêtes FE, BL, GA, KH, ON, DP, MC, RQ (fig. 197) ne soient point perpendiculaires sur les bases des parallélépipèdes. Des points F, G, B, K, O, M, D, R conduisez sur les plans des bases EH, NQ des perpendiculaires qui rencontrent ces plans aux points S, T, V, X, Y, Z, B’, A’, et achevez les parallélépipèdes FX, OA (prop. 11. 11) : je dis que les bases des parallélépipèdes égaux AB, CD sont réciproquement proportionnelles aux hauteurs, c'est-à-dire que la base EH est à la base NQ comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB. Mais le parallélépipède AB est égal au parallélépipède CD ; le parallélépipède BT est égal au parallélépipède AB (prop. 30. 11) car ils ont la même base FK et la même hauteur, et leurs droites insistantes ne sont point placées dans les mêmes droites ; et le parallélépipède DC est égal aussi au parallélépipède DZ, car ces deux parallélépipèdes ont la même base OR et la même hauteur, et leurs droites insistantes ne sont point dans les mêmes droites : donc le parallélépipède BT est égal au parallélépipède DZ. Mais nous venons de voir que les bases des parallélépipèdes égaux dont les hauteurs sont perpendiculaires sur les bases sont réciproquement proportionnelles aux hauteurs : donc la base FK est à la base OR comme la hauteur du parallélépipède DZ est à la hauteur du parallélépipède BT. Mais la base FK est égale à la base EH (prop. 24. 11), et la base OR égale à la base NQ : donc la base EH est à la base NQ comme la hauteur du parallélépipède DZ est à la hauteur du parallélépipède BT. Mais les hauteurs des parallélépipèdes DZ, BT sont les mêmes que celles des parallélépipèdes DC, BA : donc la base EH est à la base WQ comme la hauteur du parallélépipède DC est à la hauteur du parallélépipède BA : donc les bases des parallélépipèdes AB, CD sont réciproquement proportionnelles à leurs hauteurs.

Supposons enfin que les bases des parallélépipèdes AB, CD soient réciproquement proportionnelles aux hauteurs, c'est-à-dire que la base EH soit à la base NQ comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB : je dis que le parallélépipède AB est égal au parallélépipède CD.

Faites la même construction. Puisque la base EH est à la base NQ comme la hauteur du parallélépipède C D est à la hauteur du parallélépipède AB, que la base EH est égale à la base FK et la base NQ égale à la base OR, la base FK sera à la base OR comme la hauteur du parallélépipède CD est à la hauteur du parallélépipède AB. Mais les hauteurs des parallélépipèdes AB, CD sont les mêmes que celles des parallélépipèdes BT, DZ : donc la base FK est à la base OR comme la hauteur du parallélépipède DZ est à la hauteur du parallélépipède BT: donc les bases des parallélépipèdes BT, DZ sont réciproquement proportionnelles aux hauteurs. Mais nous avons démontré que les parallélépipèdes qui ont leurs hauteurs perpendiculaires sur les bases et qui ont leurs bases réciproquement proportionnelles aux hauteurs sont égaux entre eux : donc le parallélépipède BT est égal au parallélépipède DZ. Mais le parallélépipède BA est égal au parallélépipède BT (prop. 30. 11), car ces deux parallélépipèdes ont la même base FK et la même hauteur, et leurs arêtes ne sont point dans les mêmes droites ; et outre cela le parallélépipède DZ est égal au parallélépipède DC, puisque ces deux parallélépipèdes ont la même base OR et la même hauteur, et que leurs droites insistantes ne sont pas dans les mêmes droites : donc le parallélépipède AB est égal au parallélépipède CD ; ce qu'il fallait démontrer.

PROPOSITION XXXV.

THÉORÈME.

Si des sommets de deux angles égaux on mène au-dessus de leurs plans des droites qui fassent avec leurs côtés des angles égaux chacun à chacun ; si dans ces droites on prend des points quelconques, si de ces points on mène des perpendiculaires sur les plans des angles donnés, et si des points où ces perpendiculaires rencontrent ces plans on mène des droites aux sommets des angles donnés, les angles compris par ces droites et par celles qu'on a d'abord menées des sommets des angles au-dessus de leurs plans, seront égaux entre eux.

Soient les deux angles égaux BAC, EDF (fig. 198) ; des points A, D menez au-dessus des plans de ces angles les droites AG, DM qui fassent avec les côtés de ces mêmes angles des angles égaux chacun à chacun, savoir, l'angle GAB égal à l'angle MDE et l'angle GAC égal à l'angle MDF ; prenez sur les droites AG, DM des points quelconques G, M ; des points G, M menez sur les plans BAC, EDF les perpendiculaires GL, MN qui rencontrent ces plans aux points L,N, et menez les droites LA, ND : je dis que l'angle GAL est égal à l'angle MDN.

Faites la droite AH égale à la droite DM, et par le point H menez la droite HK parallèle à la droite GL. Puisque la droite GL est perpendiculaire sur le plan BAC, la droite HK sera aussi perpendiculaire sur le plan BAC (prop. 8. 11) ; des points K, N conduisez sur AB, AC, DF, DE les perpendiculaires KB, KC, NF, NE et menez HC, CB, MF, FE. Puisque le carré de la droite HA est égal aux carrés des droites HK, KA et que les carrés des droites KC, CA sont égaux au carré de la droite KA (prop. 47. 1) ; le carré de la droite HA sera égal aux carrés des droites HK, KC, CA. Mais le carré de la droite HC est égal aux carrés des droites HK, KC : donc le carré de la droite HA sera égal aux carrés des droites HC, CA : donc l'angle HCA est droit. L'angle DFM est droit, par la même raison : donc l'angle ACH est égal à l'angle DFM. Mais l'angle HAC est égal à l’angle MDF: donc les deux triangles MDF, HAC ont deux angles égaux à deux angles, chacun à chacun, et un coté égal à un coté, c'est-à-dire les côtés adjacents à des angles égaux, savoir, le côté AH qui est égal au côté DM par construction : donc ces deux triangles ont les autres-côtés égaux aux autres côtés, chacun à chacun (prop. 26. 1) : donc AC est égal à DF. Nous démontrerons semblablement que AB est égal à DE. Menez les droites HB, ME. Puisque le carré de la droite AH est égal aux carrés des droites AK, KH et que les carrés des droites AB, BK sont égaux au carré de la droite AK, les carrés des droites AB, BK, KH seront égaux au carré de la droite AH. Mais le carré de la droite BH est égal aux carrés des droites BK, KH, car l'angle HKB est droit à cause que la droite HK est perpendiculaire sur le plan BAC : donc le carré de la droite AH est égal aux carrés des droites AB, BH : donc l'angle ABH est droit. L'angle DEM est droit, par la même raison ; mais l'angle BAH est égal à l'angle EDM, par supposition, et la droite AH est égale à la droite DM : donc la droite AB est égale à la droite DE ; donc puisque AG est égal à DF et AB égal à DE, les deux droites CA, AB sont égales aux deux droites FD, DE; mais l'angle CAB est égal à l'angle FDE : donc la base BC est égale à la base EF (prop. 4. 1), le triangle égal au triangle et les autres angles égaux aux autres angles : donc l'angle ACB est égal à l'angle DFE; mais l'angle droit ACK est égal à l'angle droit DFN, par construction : donc l'angle restant BCK est égal à l'angle restant EFN. Par la même raison l'angle GBK est égal à l'angle FEN : donc les deux triangles CBK, FEN ont deux angles égaux à deux angles, chacun à chacun, et un côté égal à un côté, c'est-à-dire les côtés qui sont adjacents à des angles égaux, savoir, le côté BC qui est égal au côté EF : donc ces deux triangles auront les autres côtés égaux aux autres côtés (prop. 26. 1) : donc le côté CK est égal au côté FN ; mais AC est égal à DF : donc les deux droites AC, CK sont égales aux deux droites DF, FN et ces droites comprennent des angles droits : donc la base AK est égale à la base DN (prop. 4. 1) ; et puisque la droite AH est égale à la droite DM, le carré de AH sera égal au carré de DM ; mais les carrés des droites AK, KH sont égaux au carré de la droite AH (prop. 47. 1), car l'angle AKH est droit et les carrés des droites DN, NM sont égaux au carré de la droite. DM, parce que l'angle DNM est droit : donc les carrés des droites AK, KH sont égaux aux carrés des droites DN, NM; mais le carré de AK est égal au carré de DN : donc le carré de KH est égal au carré de NM : donc la droite HK est égal à la droite MN : donc puisque les deux droites HA, AK sont égales aux deux droites. MD, DN, chacune à chacune, et qu'on a démontré que la base H K est égale à la base NM, l'angle HAK sera égal à l'angle MDN (prop. 8. 1), ce qu'il fallait démontrer.

COROLLAIRE.

Il suit manifestement de là que si deux angles sont égaux à deux angles et que si des sommets de ces angles et au-dessus de leurs plans on mène des droites qui fassent avec les côtés des angles donnés des angles égaux chacun à chacun, les perpendiculaires menées de ces droites sur les plans des premiers angles, sont égales entre elles, si les points d'où elles, partent sont également éloignés des sommets de ces angles.

PROPOSITION XXXVI.

THÉORÈME.

Si trois droites sont proportionnelles, le parallélépipède construit avec ces trois droites est égal au parallélépipède construit avec la droite moyenne ; il faut que ce dernier parallélépipède, qui sera équilatéral, soit équiangle avec le premier parallélépipède.

Soient trois droites proportionnelles A, B, C (fig. 199), de manière que A soit à B comme B est à C : je dis que le parallélépipède construit avec les trois droites A, B, C est égal au parallélépipède construit avec la droite B ; il faut que ce dernier parallélépipède, qui sera équilatéral, soit équiangle avec le premier parallélépipède.

Soit l'angle solide E compris sous les trois angles plans DEG, GEF, FED ; faites chacune des droites DE, GE, EF égales à la droite B, et achevez le parallélépipède EK. Faites ensuite LM égal à A, sur la droite LM et au point L construisez un angle solide qui étant compris sous les plans NLO, OLM, MLN soit égal à l'angle solide E (prop. 26. 11) ; faites LO égal à B, et LN égal à C. Puisque A est à B comme B est à C, que A est égal à LM, que B est égal à chacune des droites LO, EF, EG, ED et que C est égal à LN, la droite LM sera à la droite EF comme la droite DE est à la droite LN : donc les côtés placés autour des angles égaux MLN, DEF sont réciproquement proportionnels : donc le parallélogramme MN est égal au parallélogramme DF (prop. 14. 6) ; et puisque les deux angles DEF, NLM sont égaux, que les droites LO, EG qui sont égales entre elles et qui sont menées au-dessus des plans des angles égaux DEF, NLM font avec leurs côtés des angles égaux, chacun à chacun, les perpendiculaires menées des points G, O sur les plans DEF, NLM seront égales entre elles (corol. 35. 11); donc les parallélépipèdes LH, EK ont la même hauteur. Mais les parallélépipèdes qui ont des bases égales et la même hauteur sont égaux entre eux (prop. 31.11) : donc le parallélépipède HL est égal au parallélépipède EK. Mais le parallélépipède HL a été construit avec les trois droites A, B, C, et le parallélépipède EK a été construit avec la droite B : donc le parallélépipède construit avec les trois droites A, B, C est égal au parallélépipède construit avec la droite B, lequel est équilatéral et équiangle avec le premier parallélépipède.

Donc si trois droites sont proportionnelles, le parallélépipède construit avec ces trois droites est égal au parallélépipède construit avec la droite moyenne, et ce dernier parallélépipède est équilatéral et équiangle avec le premier parallélépipède ; ce qu'il fallait démontrer.

PROPOSITION XXXVII.

THÉORÈME.

Si quatre droites sont proportionnelles, les parallélépipèdes semblables et semblablement construits sur ces droites sont proportionnels, et si des parallélépipèdes semblables et semblablement construits sur quatre droites sont proportionnels, ces droites seront aussi proportionnelles entre elles.

Soient quatre droites proportionnelles AB, CD, EF, GH (fig. 200), de manière que AB soit à CD comme EF est à GH; construise» sur les quatre droites AB, CD, EF, GH les parallélépipèdes semblables et semblablement posés KA, LC, ME, NG : je dis que KA est à LC comme ME est à NG.

Puisque le parallélépipède KA est semblable au parallélépipède LC, les parallélépipèdes KA, LC seront entre eux en raison triplée des côtés AB, CD (prop. 35. 11). Par la même raison, les parallélépipèdes ME, NG, seront entre eux en raison triplée des côtés EF, G H. Mais, par hypothèse, AB est a C D comme EF est à GH: donc AK est à LC comme ME est à NG.

Si le parallélépipède AK est au parallélépipède LC comme le parallélépipède ME est au parallélépipède NG: je dis que la droite AB est à la droite CD comme la droite EF est à la droite GH.

Puisque les parallélépipèdes AK, LC sont entre eux en raison triplée des côtés AB, CD, et que les parallélépipèdes ME, NG sont aussi en raison triplée des côtés EF, GH, et à cause que AK est à LC comme ME est à NG, la droite AB sera à la droite CD comme la droite EF est à la droite GH.

Donc si quatre droites sont proportionnelles, les parallélépipèdes semblables et semblablement construits sur ces quatre droites seront proportionnels ; et si quatre parallélépipèdes construits sur quatre droites sont proportionnels, ces quatre droites seront aussi proportionnelles ; ce qu'il fallait démontrer.

PROPOSITION XXXVIII.

THÉORÈME.

Si un plan est perpendiculaire sur un autre plan, et si d'un point pris dans un de ces plans on conduit une perpendiculaire sur l'autre plan, cette perpendiculaire tombera sur la section commune des plans.

Que le plan CD (fig. 201) soit perpendiculaire sur le plan AB, que leur commune section soit AD, et que dans le plan CD soit pris un point, quelconque E : je dis que la perpendiculaire menée du point E sur le plan AB tombe sur la droite AD.

Que cette perpendiculaire tombe, si cela est possible, hors de la commune section des plans ; qu'elle ait, par exemple, la position E F et qu'elle rencontre le plan AB au point F ; du point F et dans le plan AB conduisez la droite FG perpendiculaire sur DA (prop. 10. 1), cette droite sera certainement perpendiculaire sur le plan CD (déf. 4. 11). Menez EG.

Puisque la droite FG est perpendiculaire sur le plan CD et qu'elle rencontre la droite EG qui est dans le plan CD, l'angle FGE sera droit (clef. 5. 11). Mais la droite EF est perpendiculaire sur le plan AB : donc, l'angle EFG est droit : donc le triangle EFG a deux angles droits, ce qui est absurde (prop. 17. 1): donc la perpendiculaire menée du point E sur le plan AB ne tombe pas hors de la droite DA : donc elle tombe sur la droite DA.

Donc si un plan est perpendiculaire sur un autre plan, et si d'un point pris dans un de ces plans on mène une droite perpendiculaire sur l'autre plan, cette droite sera perpendiculaire sur la commune section des plans; ce qu'il fallait démontrer.

PROPOSITION XXXIX.

THÉORÈME.

Si dans un parallélépipède on coupe en deux parties égales les côtés des plans opposés, et si par leurs sections on mène des plans, la commune section de ces plans et le diamètre du parallélépipède se couperont mutuellement en deux parties égales.

Que dans le parallélépipède AF (fig. 202) les côtés des plans opposés CF, AH soient coupés en deux parties égales aux points K, L, M, N, O, Q, P, R, et par les sections de ces côtés soient conduits les plans KN, OR; que la commune section de ces plans soit VS, et que le diamètre du parallélépipède soit DG : je dis que les droites VS, DG se coupent en deux parties égales, c'est-à-dire que VT est égal à TS et DT égal à TG.

Menez DV, VE, BS, SG. Puisque DO est parallèle à PE, les angles alternés DOV, VPE sont égaux entre eux (prop. 29. 1) ; et puisque DO est égal à PE, OV égal à VP et que ces droites comprennent des angles égaux, la base DV sera égale à la base VE, le triangle DOV égal au triangle VPE, et les autres angles égaux aux autres angles : donc l'angle OVD est égal à l'angle PVE : donc la ligne DVE est une ligne droite (prop. 14. 1). Par la même raison, la ligne BSG est aussi une ligne droite, et la droite BS est égale à la droite SG. Puisque la droite CA est égale et parallèle à DB et que la droite CA est aussi égale et parallèle à la droite EG, la droite DB sera égale et parallèle à la droite EG (pr. 30. 1) ; mais ces droites sont jointes par les, droites DE, BG : donc la droite DE est parallèle à la droite BG (prop. 33. 1); mais on a pris dans chacune de ces droites des points quelconques D, V, G, S et on a mené les droites DG, VS : donc ces droites sont dans un seul plan (prop. 7. 11) : donc puisque la droite DE est parallèle à la droite BG, les angles EDT, BGT sont égaux, car ils sont alternes (prop. 29. 1); mais l'angle DTV est égal à l'angle GTS (prop. 15. 1) : donc les deux triangles DTV, GTS ont deux angles égaux à deux angles, un côté égal à un côté, ces côtés sous-tendant des angles égaux, c'est-à-dire que le côté DV est égal au côté GS, car ces côtés sont les moitiés des droites DE, BG : donc ces deux triangles auront les autres côtés égaux aux autres côtés (prop. 26. 1) : donc DT est égal à TG et VT égal à TS.

Donc si dans un parallélépipède on coupe en deux parties égales les côtés des plans opposés, et si par leurs sections on mène des plans, la commune section de ces plans et le diamètre du parallélépipède se couperont mutuellement en deux parties égales ; ce qu'il fallait démontrer.

PROPOSITION XL.

THÉORÈME.

Si deux prismes sont égaux en hauteur, si l'un d'eux a pour base un parallélogramme et l’autre un triangle, et si le parallélogramme est double du triangle, ces prismes seront égaux.

Soient ABCDEF, GHKLMN (fig. 203) des prismes égaux en hauteur, que l'un d'eux ait pour base le parallélogramme AF et l'autre le triangle GHK, et que le parallélogramme AF soit double du triangle GHK : je dis que le prisme ABCDEF est égal au prisme GHKLMN.

Achevez les parallélépipèdes AO, GP. Puisque le parallélogramme AF est-double du triangle GHK et le parallélogramme HK double aussi du triangle GHK, le parallélogramme AF sera égal au parallélogramme HK. Mais les parallélépipèdes qui ont des bases égales et la même hauteur sont égaux entre eux (prop. 31. 11): donc les parallélépipèdes AO, GP sont égaux; mais le prisme ABCDEF est la moitié du parallélépipède AO et le prisme GHKLMN la moitié du parallélépipède GP : donc le prisme ABCDEF est égal au prisme GHKLMN.

Donc si deux prismes ont la même hauteur, si l'un d'eux a pour base un parallélogramme et l'autre un triangle, et si le parallélogramme est double du triangle, ces deux prismes sont égaux ; ce qu'il fallait démontrer.

FIN DU ONZIEME LIVRE.