INTRODUCTION -GÉOMÉTRIE LIVRE I - LIVRE III - LIVRE IV - LIVRE VI

LIVRE II.

DÉFINITIONS.

1. Tout parallélogramme rectangle est dit contenu sous les deux droites qui comprennent un angle droit.

2. Dans tout parallélogramme, on appelle gnomon la réunion de l'un quelconque des parallélogrammes décrits autour de la diagonale avec les deux compléments.

PROPOSITION PREMIÈRE.

THÉORÈME.

Si l'on a deux droites, et si l'une d'elles est partagée en un certain nombre de parties, le rectangle compris sous ces deux droites est égal aux rectangles compris sous la droite qui n'a point été partagée, et sous chacun des segments de l'autre.

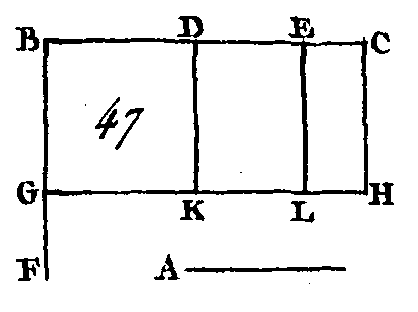
Soient deux droites A, BC (fig. 47), et que la droite BC soit partagée d'une manière quelconque aux points D, E : je dis que le rectangle compris sous les droites A, BC est égal au rectangle compris sous les droites A, BD, au rectangle compris sous les droites A, DE, et au rectangle compris sous les droites A, EC.

Conduisez par le point B la droite BF perpendiculaire sur la droite BC (prop. 11. I)[1]; faites la droite BG égale à la droite A, et par le point G conduisez la droite GH parallèle à la droite BC (prop. 31. I); par les points D, E, C, conduisez ensuite les droites DK, EL, CH, parallèles à la droite BG.

Le rectangle BH est égal aux rectangles BK, DL, EH; mais le rectangle BH est compris sous les droites A, BC, car il est compris sous les droites GB, BC, dont la droite BG est égale à la droite A ; le rectangle BK est compris sous les droites A, BD, car il est compris sous les droites GB, BD, dont la droite GB est égale à la droite A; le rectangle DL est compris sous les droites A, DE, puisque DK, c'est-à-dire BG, est égale à la droite A; et enfin, le rectangle EH est compris sous les droites A, EC : donc le rectangle compris sous les droites A, BC est égal, au rectangle compris sous les droites A, BD, au rectangle compris sous les droites A, DE ; et enfin au rectangle compris sous les droites A, EC.

Donc si l'on a deux droites, et si l'une d'elles est partagée en un certain nombre de parties, le rectangle compris sous ces deux droites est égal aux rectangles compris sous la droite qui n'a point été partagée et sous chacun des segments de l'autre ; ce qu'il fallait démontrer.

PROPOSITION II.

THÉORÈME.

Si une droite est partagée d'une manière quelconque en deux parties, le rectangle compris sous la droite totale et sous l’un et l'autre segment, est égal au carré de la droite entière.

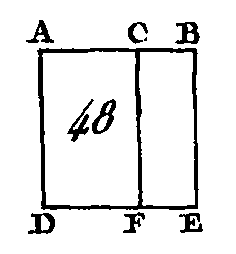
Que la droite AB (fig. 48) soit partagée d'une manière quelconque au point C : je dis que le rectangle-compris sous les droites AB, BÇ, avec le rectangle compris sous les droites BA, AC, est égal au carré de la droite AB.

Sur la droite. AB construisez le carré ADEB (prop. 46. I), et par le point C conduisez la droite CF parallèle à l'une et à l'autre des droites AD, BE (prop. 31. I).

Le carré AE est égal aux rectangles: AF, CE ; mais le carré AE est construit sur la droite AB ; le rectangle AF est compris sous les droites BA, AC, car il est compris sous les droites DA, AC, dont la droite AD est égale à AB; et enfin le rectangle CE est compris sous les droites AB, BC, puisque la droite BE est égale à la droite AB ; donc le rectangle compris sous les droites BA, AC, avec le rectangle compris sous les droites AB, BC, est égal au carré de la droite AB.

Donc si une droite est partagée d'une manière quelconque en deux parties, les rectangles compris sous la droite totale et sous chacun des segments sont égaux au quatre construit sur la droite totale ; ce qu'il fallait démontrer.

PROPOSITION III.

THÉORÈME.

Si une droite est partagée d'une manière quelconque en deux parties, le rectangle compris sous la droite totale et l'un des segments, est égal au rectangle compris sous les segments et au carré formé sur le segment premièrement pris.

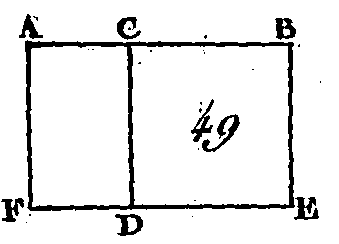
Que la droite AB (fig. 49) soit partagée en un point quelconque C : je dis que le rectangle compris sous les droites AB, BC est égal rectangle compris sous les droites AC, CB, et au carré de la droite BC.

Sur la droite BC construisez le carré CDEB (prop. 46. I), prolongez en F la droite ED, et par le point A conduisez la droite AF parallèle à l'une ou à l'autre des droites CD, BE (prop. 31. I).

Le rectangle AE est certainement égal aux rectangles AD, CE; mais le rectangle AE est compris sous les droites AB, BC, car il est compris sous les droites AB, BE, dont la droite BE est égale à la droite BC ; le rectangle AD est compris sous les droites AC , CB, puisque la droite DE est égale à la droite CB; et enfin le carré DB est construit sur la droite BC : donc le rectangle compris sous les droites AB, BC est égal au rectangle compris sous les droites AC, CB et au carré de la droite BC.

Donc si une droite est partagée d'une manière quelconque en deux parties, le rectangle compris sous la droite totale et sous un des segments, est égal au rectangle compris sous les segments et au carré construit sur le segment premièrement pris ; ce qu'il fallait démontrer.

PROPOSITION IV.

THÉORÈME.

Si une droite est partagée d'une manière quelconque en deux parties, le carré construit sur la droite entière est égal aux carrés formés sur les deux segments et au double du rectangle compris sous ces deux segments.

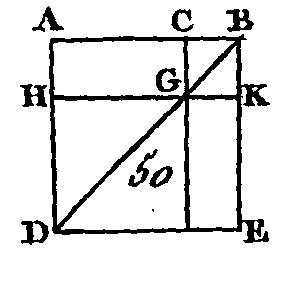
Que la droite AB (fig. 50) soit partagée d'une manière quelconque au point C : je dis que le carré construit sur AB est égal aux carrés construits sur AC, CB, et au double du rectangle compris sous les segments AC, CB.

Construisez le carré ADEB sur la droite AB (prop. 46. I), conduisez la droite BD; par le point C conduisez la droite CGF parallèle à l'une ou à l'autre des droites AD, BE (prop. 31. I), et par le point G conduisez la droite HK parallèle à l'une ou à l'autre des droites AB, DE.

Puisque la droite CF est parallèle à la droite AD, et que la droite BD tombe sur ces deux droites, l'angle extérieur BGC sera égal à l'angle intérieur et opposé ADB (prop. 29. I) ; mais l'angle ADB est égal à l'angle ABD (prop. 5. I), parce que le côté BA est égal au côté AD ; donc l'angle CGB est égal à l'angle GBC : donc le côté BC est égal au côté CG (prop. 6. I) ; mais le côté CB est égal au côté GK (prop. 34. I), et le côté CG égal au côté BK : donc le côté GK est égal au côté GG : donc le quadrilatère CGKB est équilatère. Je dis dé plus qu'il est rectangle; car puisque la droite CF est parallèle à la droite BK, et que la droite CB tombe sur ces deux droites, les angles KBC, GCB sont égaux à deux droites (prop. 29. I); mais l'angle KBC est droit (déf. 50. I) : donc l'angle GCB est droit aussi : donc les angles opposés CGK, GKB seront encore droits (prop. 34. I) : donc le quadrilatère CGKB est rectangle. Mais on a démontré qu'il était équilatère; donc ce quadrilatère est un carré, et ce carré est construit sur la droite BC. Par la même raison le quadrilatère HF est encore un carré qui est construit sur HG, c'est-à-dire sur AC. Donc HF, CK sont deux carrés construits sur AC, CB; et puisque le rectangle AG est égal au rectangle GE (prop. 43. I), et que ce rectangle AG est compris sous les droites AC, CB, la droite GC étant égale à CB, le rectangle GE sera égal à un rectangle qui est compris sous les droites AC, GB : donc les rectangles AG, GE sont égaux au double du rectangle qui est compris sous les droites CB ; mais les carrés HF, CK sont construits sur les droites AC, CB: donc les quatre figures HF, CK, AG, GE sont égales aux carrés construits sur AC, CB et au double du rectangle compris sous les droites AC, CB; mais les quatre figures HF, CK, AG, GE composent toute la figure ADEB qui est le carré construit sur AB ; donc le carré construit sur AB est égal aux carrés construits sur AC, CB, et au double du rectangle compris sous les droites AC, CB.

Donc si une droite est partagée d'une manière quelconque, le carré de la droite entière est égal au carré des segments et au double du rectangle compris sous ces segments; ce qu'il fallait démontrer.

AUTREMENT.

Je dis que le carré construit sur la droite AB est égal aux carrés construits sur AC, CB et au double du rectangle compris sous AC, CB.

En effet, puisque dans la même figure le côté BA est égal au côté AD, l'angle ABD sera égal à l'angle ADB (prop. 5. I); et comme les trois angles d'un triangle quelconque sont égaux à deux droites (prop. 32. I), les trois angles ABD, ADB, BAD du triangle ABD seront égaux à deux droits. Mais l'angle BAD est droit : donc les deux autres angles ABD, ADB sont égaux à un angle droit ; or ces deux angles sont égaux entre eux : donc chacun des angles ABD, ADB est égal à la moitié d'un angle droit. Mais l'angle BCG est droit, car il est égal à l'angle intérieur et opposé BAD : donc l'angle restant CGB est la moitié d'un angle droit; donc l'angle CGB est égal à l'angle CBG : donc le côté BC est égal au côté CG (prop. 34. I) ; mais CB est égal à KG, et CG égal aussi à BK (prop. 34. I) : donc le quadrilatère CK est équilatère ; mais il a un angle droit : donc ce quadrilatère est un carré, et ce carré est construit sur le segment CB. Le quadrilatère HF est un carré, par la même raison, et ce carré est construit sur le segment AC : donc les quadrilatères CK, HF sont deux carrés, et ces deux carrés sont construits sur les segments AC, CB. De plus, puisque le rectangle AG est égal au rectangle EG (prop. 31. I), et que le rectangle AG est compris sous les droites AC, CB, car la droite CG est égale à la droite CB, le rectangle EG est égal au rectangle compris sous les droites AC, CB : donc les rectangles AG, GE sont égaux au double du rectangle qui serait compris sous les droites AC, CB, mais les carrés CK, HF sont égaux à ceux qui seraient construits sur les segments AC, CB : donc les quatre figures CK, HF, AG, GE sont égales aux carrés construits sur les segments AC, CB, et au double du rectangle compris sous ces mêmes segments. Mais les figures CK, HF, AG, GE composent toute la figure AE qui est le carré construit sur AB.

Donc le carré formé sur la droite AB est égal aux carrés formés sur les droites AC, CB, et au double du rectangle compris sous les mêmes droites AC, CB; ce qu'il fallait démontrer,

COROLLAIRE.

Il suit de là que, dans les carrés, les parallélogrammes qui sont autour de la diagonale sont toujours des carrés.

PROPOSITION V.

Si une droite est coupée en deux parties égales et en deux parties inégales, le rectangle compris sous les deux segments inégaux de la droite entière avec le quatre de la droite qui est placée entre les points de section, est égal au carré de la moitié de cette droite.

Qu'une droite quelconque AB (fig. 51) soit coupée en deux parties égales au point C et en deux parties inégales au point D : je dis que le rectangle compris sous les droites AD, DB, avec le carré construit sur CD, est égal au carré construit sur CB.

Sur la droite BC construisez le carré CEFB (prop. 46. I), et conduisez la droite BE ; par le point D conduisez la droite DHG parallèle à l'une ou à l'autre des droites CE, BF (prop. 31. I) ; par le point H conduisez la droite KLM parallèle à l'une ou à l'autre des droites CB, EF, et enfin par le point A conduisez la droite AK parallèle à l'une ou l'autre des droites CL, BM.

Puisque le complément CH est égal au complément HF (prop. 43. ï), si nous ajoutons à chacun de ces compléments le quatre DM, le rectangle total CM sera égal au rectangle total DF ; mais le rectangle CM est égal au rectangle AL (prop. 56. I), puisque la droite AC est égale à la droite CB : donc le rectangle AL est égal au rectangle DF; donc si nous ajoutons le rectangle CH à chacun de ces deux rectangles, le rectangle total AH sera égal aux rectangles DF, DL; mais le rectangle AH est compris sous les droites AD, DB, puisque la droite DH est égale à la droite DB; or les rectangles FD, DL forment le gnomon NOP : donc le gnomon NOP est égal au rectangle compris sous les droites AD, DB ; donc si nous ajoutons à chacune de ces deux quantités le carré LG qui est égal au carré de CD (corol. 4. II), le gnomon NOP et le carré LG seront égaux au rectangle compris sous les droites AD, DB, et au carré construit sur CD; mais le gnomon NOP et le carré LG forment tout le carré CEFB qui est construit sur CB : donc le rectangle compris sous AD, DB, avec le carré construit sur CD, est égal au carré construit sur CB.

Donc si une droite est coupée en deux parties égales et en deux parties inégales, le rectangle compris sous les deux segments inégaux de la droite totale avec le carré de la droite qui est placée entre les deux points de section, est égal au carré de la moitié de cette droite ; ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Si une ligne droite est coupée en deux parties égales, et si on lui ajoute, directement une droite qui ait la même direction, le rectangle compris sous une droite composée de la première droite et de la droite ajoutée, et sous la droite ajoutée avec le carré de la moitié de la première ligne droite, est égal au carré d'une droite composée de la moitié de la première ligne droite et de la droite ajoutée.

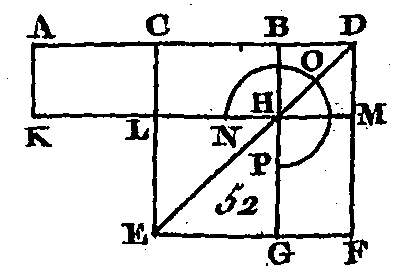
Qu'une ligne droite quelconque AB (fig. 52) soit coupée en deux parties égales au point C ; qu'on lui ajoute directement une droite quelconque BD : je dis que le rectangle compris sous AD, DB, avec le carré de la droite CB, est égal au carré de CD.

Sur la droite CD décrivez le carré CEFD (prop. 46. I); conduisez la droite DE; par le point B conduisez la droite BHG parallèle à l'une ou à l'autre des droites CE, DF (prop. 31. I); par le point H conduisez la droite KLM parallèle à l'une ou à l'autre des droites ÀD, EF, et enfin par le point A conduisez la droite AK parallèle à l'une ou à l'autre des droites CL, DM. Puisque la droite AC est égale à la droite CB, le rectangle AL sera égal au rectangle CH (prop. 36. I) ; mais le rectangle CH est égal au rectangle HF (prop. 43. I) : donc le rectangle AL sera égal au rectangle HF; donc si nous ajoutons à chacun de ces rectangles le rectangle CM, le rectangle total AM sera égal au gnomon NOP ; mais le rectangle A M est compris sous les droites AD, DB, car DM est égal à DB (corrol. 4. II) ; donc le gnomon NOP est égal à un rectangle qui est compris sous les droites AD, DB ; donc si nous ajoutons à chacune de ces deux quantités le carré LG qui est égal au carré construit sur CB, le rectangle compris sous les droites AD, DB avec le carré construit sur BC sera égal au gnomon NPO et au carré LG. Mais le gnomon NPO et le carré LG composent le carré total CEFD qui est construit sur CD : donc le rectangle compris sous AD, DB avec le carré construit sur BC est égal au carré construit sur CD.

Donc si une ligne droite est coupée en deux parties égales et si on lui ajoute directement une droite qui ait la même direction, le rectangle compris sous une droite composée de la première ligne droite et de la droite ajoutée, et sous la droite ajoutée, avec le carré de la moitié de la première ligne droite, est égal au carré d'une droite composée de la moitié de la première ligne droite et de la droite ajoutée ; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Si une droite est partagée en deux parties d'une manière quelconque, le carré de la droite entière et le carré de l'un de ses segments égalent le double du rectangle compris sous la droite entière et ce segment et le carré de l'autre segment.

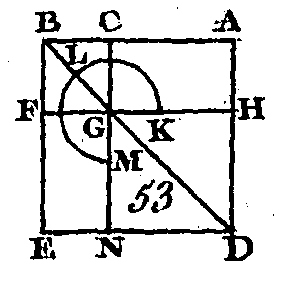
Qu'une droite quelconque AB (fig. 53) soit partagée d'une manière quelconque au point C : je dis que le carré de AB et le carré de BC sont égaux au double du rectangle compris sous AB, BC, et au carré de AC,

Sur AB décrivez le carré ADEB (prop. 46. I) et construisez la figure.

Puisque le rectangle AG est égal au rectangle GE (prop. 43. I), si nous ajoutons à l'un et à l'autre le carré CF, le rectangle AF sera égal au rectangle CE : donc les rectangles AF, CE sont doubles du rectangle AF; mais les rectangles AF, CE composent le gnomon KLM et le carré CF : donc le gnomon KLM et le carré CF sont doubles du rectangle AF; mais le double du rectangle compris sous les droites AB, BC est double du rectangle AF, car la droite BF est égale à la droite BC (cor. 4. II) : donc le gnomon KLM et le carré CF sont égaux au double du rectangle compris sous les droites AB, BC; donc si nous ajoutons à ces quantités le carré HN, qui est construit sur la droite AC, le gnomon KLM et les carrés CF, HN seront égaux au double du rectangle compris sous AB, BC, et au carré de AC ; mais le gnomon KLM et les carrés CF, HN forment le carré total ADEB et le carré CF qui sont construits sur AB, BC : donc les carrés de AB et de BC sont égaux au double du rectangle compris sous AB, BC, et au carré de AC.

Donc si une droite est partagée en deux parties d'une manière quelconque, le carré de la droite entière et le carré de l'un de ses segments sont égaux au double du rectangle compris sous la droite entière et ce segment, et au carré de l'autre segment ; ce qu'il fallait démontrer.

PROPOSITION VIII.

THÉORÈME.

Si une droite est partagée en deux parties d'une manière quelconque, le quadruple du rectangle compris sous la droite entière et un de ses segments, avec le quatre de l'autre segment, est égal au carré construit sur la droite entière et le premier segment, considérés comme, ne formant qu'une seule droite.

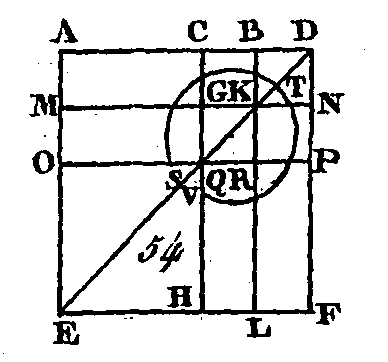
Que la droite AB (fig. 54) soit partagée en deux parties d'une manière quelconque au point C : je dis que le quadruple du rectangle compris sous les droites AB, BC avec le carré de AC, est égal au carré construit sur les droites AB, BC, considérées comme ne formant qu'une seule droite.

Prolongez la droite DB dans la direction de AB ; faites BD égal à CB ; décrivez sur AD le carré AEFD (prop. 46. II), et construisez une double figure.

Puisque la droite GB est égale à la droite BD, et que la droite CB est égale à la droite GR (prop. 34. I) et la droite BD égale aussi à la droite KN, la droite GK sera égale à la droite KN; la droite QR est égale à la droite RP par la même raison. Puisque CB est égal à BD, et GK égal à KN, le rectangle CK sera égal au rectangle BN, et le rectangle GR égal au rectangle KP (prop. 36. I) ; mais le rectangle CK est égal au rectangle RN (prop. 43. I), car ils sont les compléments du parallélogramme CP : donc le rectangle BN est égal au rectangle GR : donc les quatre rectangles BN, KC, GR, RN sont égaux entre eux : donc ils sont le quadruple du rectangle CK. De plus, puisque CB est égal à BD et que BD est égal à BK, c'est-à-dire à CG (34. I), et CB égal à GK, c'est-à-dire à GQ, la droite CG sera égale à la droite GQ; or QR est égal à RP : donc le rectangle AG est égal au rectangle MQ (prop. 36. I), et le rectangle QL égal au rectangle RF ; mais le rectangle MQ est égal au rectangle QL (prop. 43. I), puisqu'ils sont les compléments du parallélogramme ML : donc les rectangles AG, RP sont égaux : donc les quatre rectangles AG, MQ, QL, RF sont égaux entre eux, et sont par conséquent quadruples du rectangle AG. Mais on a démontré que les quatre carrés CK, BN, GR, RN, étaient quadruples du carré CK : donc les huit figures qui composent le gnomon STV sont quadruples du rectangle AK, et puisque le rectangle AK est compris cous les droites AB, BD ; car BK est égal à BD (cor. 4. II), le quadruple du rectangle AK sera compris sous les droites AB, BD ; mais il a été démontré que le gnomon STV est quadruple du rectangle AK ; donc le rectangle qui est compris sous les droites AB, BD est égal au gnomon STV ; donc si nous ajoutons à ces quantités égales le carré OH qui est égal au carré de AC (cor. 4. II), le quadruple du rectangle compris sous les droites AB, BD, et le carré de AC seront égaux au gnomon STV et au carré OH, mais le gnomon STV et le carré OH comprennent tout le carré AEFD qui est décrit sur AD : donc le quadruple du rectangle compris sous les droites AB, BC et le carré de AC est égal au carré construit sur les droites AB, BC considérées comme ne faisant qu'une seule droite.

Donc si une droite est partagée en deux parties égales d'une manière quelconque, le quadruple du rectangle compris sous la droite entière et un de ses segments et le carré de l'autre segment, sont égaux au carré construit sur la droite entière et le premier segment, considérés comme ne formant qu'une seule droite ; ce qu'il fallait démontrer.

PROPOSITION IX.

THÉORÈME.

Si une droite est partagée en deux parties égales et en deux parties inégales, les carrés des segments inégaux sont doubles du carré de la moitié de cette droite et du carré de la droite interceptée entre les points de section.

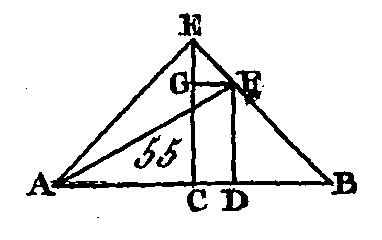
Que la droite AB (fig. 55) soit partagée en deux parties égales au point C et en deux parties inégales au point D : je dis que les carrés de AD, DB sont doubles des carrés de AC, CD.

Du point C conduisez une droite CE qui soit perpendiculaire à la droite AB (prop. 11. I) ; faites la droite EC égale à l'une ou à l'autre des droites AC, CB, et menez les droites EA, EB ; par le point D conduisez la droite DF parallèle à la droite EC (prop. 31. I), et par le point F conduisez la droite FG parallèle à la droite AB, et menez la droite AF.

Puisque la droite AC est égale à la droite CE, l'angle EAC sera égal à l'angle AEC (prop. 5. I) ; et puisque l'angle ACE est droit, les angles AEC, EAC seront égaux à un angle droit (prop. 32. I); mais ces deux angles sont égaux entre eux : donc chacun des angles AEC, EAC est la moitié d'un angle droit. Par la même raison, chacun des angles CEB, EBC est aussi la moitié d'un angle droit : donc l'angle total AEB est droit. Puisque l'angle GEF est la moitié d'un angle droit et que l'angle EGF est droit, car il est égal à l'angle intérieur et opposé ECB (prop. 29. I), l'angle EFG sera la moitié d'un angle droit : donc l'angle GEF est égal à l'angle EFG : donc le côté EG est égal au côté GF (prop. 6. I). De plus, puisque l'angle EBD est la moitié d'un angle droit, et que l'angle FDB est droit, car il est égal à l'angle intérieur et opposé ECB, l'angle BFD sera la moitié d'un angle droit : donc l'angle FBD est égal à l'angle DFB : donc le côté DF est égal au côté DB (prop, 6. I). Puisque la droite AC est égale à la droite CE, le carré de AC sera égal au carré de CE : donc les carrés de AC, CE sont doubles du carré de AC; mais le carré de EA est égal aux carrés de AC, CE (prop. 47. I), puis l'angle. ACE est droit : donc le carré de EA est double du carré de AC. De plus, puisque EG est égal à GF et que le carré de EG est égal au carré de GF, les carrés de EG, GF seront doubles du carré de GF ; mais le carré de EF est égal aux carrés de EG, GF (prop. 47. I) : donc le carré de EF est double du carré de GF; mais la droite GF est égale à la droite CD (prop. 34. I) : donc le carré EF est double du carré de CD ; mais le carré de AE est double du carré de AC : donc les carrés de AE, EF sont doubles des carrés de AC, CD ; or le carré de AF est égal aux carrés de AE, EF (prop. 47. I) puisque l'angle AEF est droit : donc le carré de AF est double des carrés de AC, CD; mais les carrés de AD, DF sont égaux au carré de AF (prop. 47. I) car l'angle ADF est droit : donc les carrés de AD, DF sont doubles des carrés de AC, CD ; or la droite DF est égale à la droite DB : donc les carrés de AD, DB seront doubles des carrés de AC, CD.

Donc si une droite est partagée en deux parties égales et en deux parties inégales, les carrés des deux segments inégaux sont doubles du carré de la moitié de cette droite et du carré de la droite interceptée entre les deux points de section ; ce qu'il fallait démontrer.

PROPOSITION X.

THÉORÈME.

Si une ligne droite est coupée en deux parties égales, et si on lui ajoute directement une droite qui ait la même direction, le carré d'une droite composée de la ligne droite entière et de la droite ajoutée, et le carré de la droite ajoutée, sont doubles du carré de la moitié de cette ligne droite et du carré d'une droite composée de la moitié de cette ligne droite et de la droite ajoutée comme ne faisant qu'une seule droite.

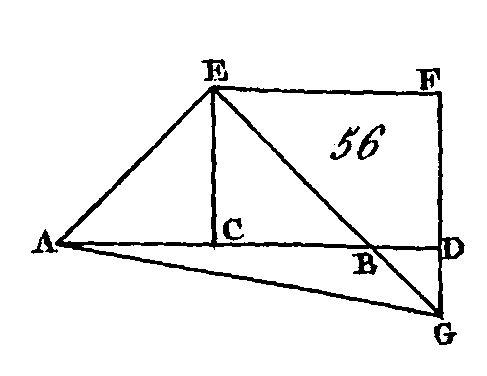
Que la droite AB (fig. 56) soit partagée en deux parties égales au point C, et qu'on lui ajoute directement une droite quelconque BD : je dis que les carrés de AD, DB sont doubles des carrés de AC, CD.

Du point C conduisez la droite CE perpendiculaire sur AB (prop. 11. I) ; faites la droite CE égale à l'une ou à l'autre des droites AC, CB; menez les droites AE, EB; par le point E conduisez la droite EF parallèle à la droite AD, et par le point D conduisez la droite DF parallèle à la droite CE. Puisque la droite EF tombe sur les parallèles EC, FD, les angles CEF, EFD sont égaux à deux droits (prop. 29. I) : donc les angles FEB, EFD sont moindres que deux angles droits ; or deux droites se rencontrent quand elles sont prolongées à l'infini du côté où elles forment deux angles moindres que deux droits (ax. 11) : donc les droites EB, FD, prolongées du côté BD, se rencontreront. Prolongez ces droites, et supposons qu'elles se rencontrent au point G ; menez la droite AG.

Puisque la droite AC est égale à la droite CE, l'angle AEC sera égal à l'angle EAC (prop. 5. I) ; or l'angle ACE est droit : donc chacun des angles EAC, AEC est la moitié d'un angle droit (prop. 32. I). Par la même raison, chacun des angles CEB, EBC est la moitié d'un angle droit : donc l'angle AEB est droit. Puisque l'angle EBC est la moitié d'un angle droit, l'angle DBG est aussi la moitié d'un angle droit (prop. 15. I). Mais l'angle BDG est droit (prop. 29. I), car il est égal à l'angle alterne DCE : donc l'angle DGB est la moitié d'un angle droit : donc l'angle DGB est égal à l'angle DBG : donc le côté BD est égal au côté GD (prop. 6. I). De plus, puisque l'angle EGF est la moitié d'un angle droit, et que l'angle EFD est droit, car il est égal à l'angle opposé ECD (prop. 34. I), l'angle FEG est la moitié d'un angle droit : donc l'angle EGF est égal à l'angle FEG : donc le côté GF est égal au côté EF (prop. 6. I) ; et comme la droite EC est égale à la droite CA, le carré de EC est égal au carré de AG : donc les carrés de EG, GA sont doubles du carré de GA. Or le carré de EA est égal aux carrés de EC, CA (prop. 47. I) donc le carré de EA est double du carré de AC. De plus, puisque la droite GF est égale à la droite EF, le carré de FG est égal au carré de FE : donc les carrés de FG, FE sont doubles du carré de EF; or le carré de EG est égal aux carrés de GF, FE (prop. 47. I) donc le carré de EG est double du carré de EF ; mais la droite EF est égale à la droite CD : donc le carré de EG est double du carré de CD ; mais on a démontré que le carré de EA est double du carré de AC, donc les carrés de AE, EG sont doubles des carrés de AC, CD ; mais le carré de AG est égal aux carrés de AE, EG (prop. 47. I) : donc le carré de AG est double des carrés de AC, CD. Or les carrés de AD, DG sont égaux au carré de AG (prop. 47. I), donc les carrés de AD, DG sont doubles des carrés de AC, CD ; mais la droite, DG est égale à la droite DB : donc les carrés de AD, DB sont doubles des carrés de AC, CD.

Donc si une ligne droite est partagée en deux parties égales et si on lui ajoute directement une droite qui ait la même direction, le carré d'une droite composée de la ligne droite entière et de la droite ajoutée, et le carré de la droite ajoutée, sont doubles du carré de la moitié de la ligne droite et au carré d'une droite composée de la moitié de la ligne droite et de la droite ajoutée comme ne faisant qu'une seule droite; ce qu'il fallait démontrer.

PROPOSITION XI.

PROBLÈME.

Partager une droite donnée de manière que le rectangle compris sous la droite entière et l'un de ses segments, soit égal au carré de l’autre segment.

Soit AB (fig. 57) la droite donnée : il faut partager la droite AB de manière que le rectangle compris sous la droite entière et l'un de ses segments, soit égal au carré de l'autre segment.

Sur la droite AB décrivez le carré ABDG (prop. 46. I), partagez la droite AC en deux parties égales en E (prop. 10. I), et menez la droite BE ; ayant prolongé ensuite la droite GA vers F, faites la droite EF égale à la droite BE (prop. 3. I), décrivez sur AF le carré FH, et prolongez la droite GH vers K : je dis que la droite AB est partagée en H de manière que le rectangle compris sous AB et BH est égal au carré de AH.

 Puisque la droite AC est coupée en deux parties égales en E, si nous lui ajoutons directement la droite AF, le rectangle compris sous les droites CF, FA et le carré de AE, pris ensemble, seront égaux au carré de EF (prop. 6. II); mais la droite EF est égale à la droite EB : donc le rectangle compris sous CF, FA et le carré de AE, pris ensemble, sont égaux au carré de EB; mais les carrés de BA, AE sont égaux au carré de EB (prop. 47. I), car l'angle BAE est droit ; donc le rectangle compris sous CF, FA avec le carré de AE est égal aux carrés de BA, AE. Donc, si on retranche le carré de AE qui est commun, le rectangle compris sous CF, FA sera égal au carré de AB ; mais le rectangle FK est compris sous les droites CF, FA, puisque la droite AF est égale à la droite FG, et le carré de AB est égal au carré AD : donc le rectangle FK est égal au carré AD : donc, si l'on-retranche le rectangle commun AK, le carré FH sera égal au rectangle HD; mais le rectangle HD est compris sous les droites AB, BH, puisque AB est égal à BD et que FH est le carré de AH: donc le rectangle compris sous AB, BH sera égal au carré de AH.

Donc la droite AB est coupée au point H, de manière que le rectangle compris sous AB, BH est égal au carré de AH ; ce qu'il fallait faire.

PROPOSITION XII.

THÉORÈME.

Dans les triangles obtusangles le carré du côté opposé à l'angle obtus est égal aux carrés des deux côtés qui comprennent l'angle obtus, et au double du rectangle compris sous le coté de l'angle obtus qui est prolongé jusqu'à la perpendiculaire abaissée du sommet de l'angle opposé et sous la droite interceptée entre la perpendiculaire et le sommet de l'angle obtus.

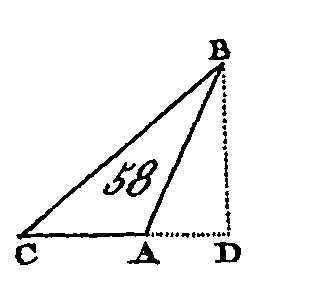
Soit ABC (fig. 58) un triangle obtusangle dont l'angle BAC est obtus; du point B conduisez une perpendiculaire BD sur le côté prolongé CA : je dis que le carré de BC est égal aux carrés de BA, AC, et au double du rectangle compris sous les droites CA, AD.

Puisque la droite CD est coupée d'une manière quelconque au point A, le carré de CD sera égal aux carrés de CA, AD, et au double du rectangle compris sous les droites CA, AD (prop. 4. II) : donc si on ajoute à ces quantités égales le carré de DB, les carrés de CD, DB seront égaux aux carrés de CA, AD, DB, et au double du rectangle compris sous les droites CA, AD ; mais le carré de CB est égal aux carrés de CD, DB (prop. 47. I), car l'angle CDB est droit, et le carré de AB est égal aux carrés de AD, DB : donc le carré de CB est égal aux carrés de CA, AB, et au double du rectangle compris sous les droites CA, AD.

Donc dans les triangles obtus angles le carré du côté opposé à l'angle obtus est égal aux carrés des deux côtés qui comprennent l'angle obtus et au double du rectangle compris sous le côté de l'angle obtus qui est prolongé jusqu'à la perpendiculaire abaissée du sommet de l'angle opposé et sous la droite interceptée entre la perpendiculaire et le sommet de l'angle obtus ; ce qu'il fallait démontrer.

PROPOSITION XIII.

THÉORÈME.

Dans les triangles acutangles, le carré d'un côté opposé à un angle aigu est égal aux carrés des côtés qui comprennent cet angle aigu moins le double du rectangle compris sous le côté de l'angle aigu sur lequel tombe la perpendiculaire abaissée du sommet de l'angle opposé, et sous la droite interceptée entre cet angle aigu.

Soit le triangle acutangle ABC (fig. 59) dont l’angle B est aigu du point A conduisez sur la droite BC la perpendiculaire AD : je dis que le carré de AC égale les carrés de CB, BA moins le double du rectangle compris sous les droites CB, BD.

Puisque la droite CB est coupée; d’une manière quelconque au point D, les carrés de CB, BD seront égaux au double du rectangle compris sous les droites CB, BD, et au carré de DC (prop. 7. II) : donc si nous ajoutons à ces quantités égales le carré de AD, les carrés de CB, BD, DA seront égaux au double du rectangle compris sous les droites CB, BD, et aux carrés de AD, DC ; mais le carré de AB est égal aux carrés de BD, DA (prop. 47. I), car l'angle ADB est droit, et le carré de AC est égal aux carrés de AD, DC : donc les carrés de CB, BA sont égaux au carré de AC et au rectangle compris sous les droites CB, BD : donc le carré de AC égale les carrés de CB, BA, moins le double du rectangle compris sous CB, BD.

Donc dans les triangles acutangles le carré d'un côté opposé à un angle aigu est égal au carré des deux autres côtés qui comprennent l'angle aigu moins le double du rectangle compris sous le côté de l'angle aigu, sur lequel tombe la perpendiculaire abaissée du sommet de l'angle opposé et sous la droite, interceptée entre la perpendiculaire et cet angle aigu.[2]

PROPOSITION XIV.

PROBLÈME.

Construire un carré égal à une figure rectiligne donnée.

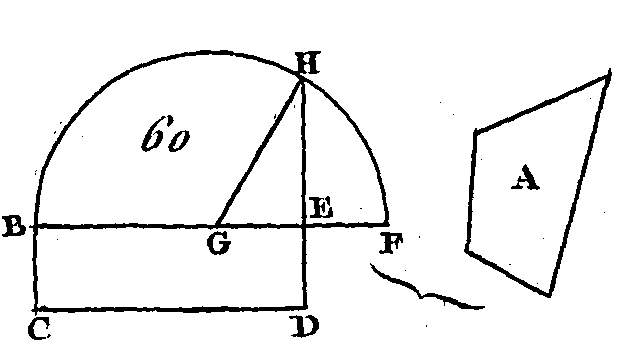
Soit A (fig. 60) la figure rectiligne donnée : il faut construire un carré qui soit égal à cette figure.

Construisez un rectangle BD égal à la figure rectiligne donnée A (prop. 45. I). Si le côté BE était égal au côté ED, on aurait déjà fait ce qu'on proposait, car le carré BD aurait été construit égal à la figure rectiligne A. Si, au contraire, l'un des côtés BE, ED est plus grand que l'autre, et si le côté BE est le plus grand, prolongez-le vers F, et faites, EF égal à ED (prop. 3. I); ayant ensuite partagé la droite FB en deux parties égales au point G, du point G et avec un intervalle égal à l'une ou à l'autre des droites GB, GF, décrivez la demi-circonférence BHF (dem. 3), prolongez DE jusqu'en H, et menez la droite GH.

Puisque la droite BF est partagée en deux parties égales au point G et en deux parties inégales au point E, le rectangle compris sous les droites BE, EF et le carré de EG, seront égaux au carré de GF (prop. 5. II) ; mais la droite GF est égale à la droite GH : donc le rectangle compris sous les droites BE, EF et le carré de EG seront égaux au carré de GH ; mais les carrés de HE, GE sont égaux au carré de GH (prop. 47. I) : donc le rectangle compris sous les droites BE, EF et le carré de GE, pris ensemble, sont égaux aux carrés de HE, GE : donc, si nous retranchons le carré commun de GE, le rectangle compris sous les droites BE, EF sera égal au carré de EH ; mais le rectangle compris sous les droites BE, EF, est le parallélogramme BD, puisque la droite EF est égale à la droite ED : donc le parallélogramme BD est égal au carré de HE; or le parallélogramme BD est égal, par construction, a la figure rectiligne A : donc la figure rectiligne A est égale au carré construit sur la droite EH.

Donc, le carré construit sur la droite EH est égal à la figure rectiligne donnée A ; ce qu'il fallait faire.

FIN DU SECOND LIVRE.