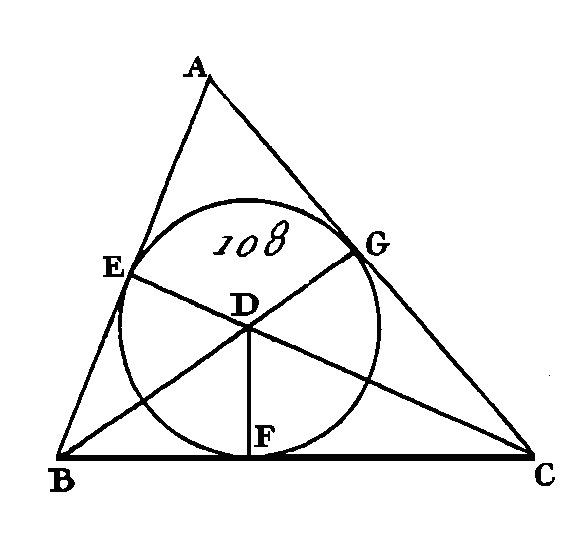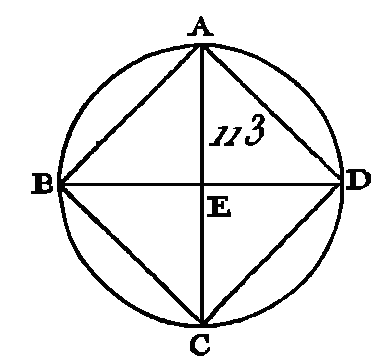INTRODUCTION -GEOMETRIE LIVRE I - LIVRE II - LIVRE III - LIVRE VI

Éléments de Géométrie : livre IV

EUCLIDE

ÉLÉMENTS DE GÉOMÉTRIE

LIVRE IV.

DÉFINITIONS.

1. Une figure rectiligne est dite inscrite dans une figure rectiligne, lorsque chaque angle de la figure inscrite touche chaque côté de celle dans laquelle elle est inscrite.

2. Semblablement une figure est dite circonscrite à une figure, lorsque chaque côte de la figure circonscrite touche chaque angle de la figure autour de laquelle elle est circonscrite.

3. Une figure rectiligne est dite inscrite dans un cercle, lorsque chaque angle de la figure inscrite touche la circonférence de ce cercle.

4. Une figure rectiligne est dite circonscrite à un cercle, lorsque chaque côté de la figure circonscrite touche la circonférence de ce cercle.

5. Semblablement un cercle est dit inscrit dans une figure rectiligne, lorsque la circonférence du cercle touche chaque côté de la figure dans laquelle elle est inscrite.

6. Un cercle est dit circonscrit à une figure rectiligne, lorsque la circonférence du cercle touche chaque angle de la figure autour de laquelle elle est circonscrite.

7. Une droite est dite appliquée dans un cercle, lorsque ses extrémités sont dans la circonférence de ce cercle.

PROPOSITION PREMIÈRE.

PROBLÈME.

Dans un cercle donné, appliquer une droite égale à une droite donnée qui ne soit pas plus grande que le diamètre.

Soit ABC (fig. 105) le cercle donné, et D la droite donnée moins grande que le diamètre de ce cercle : il faut dans le cercle ABC appliquer une droite égale à la droite D.

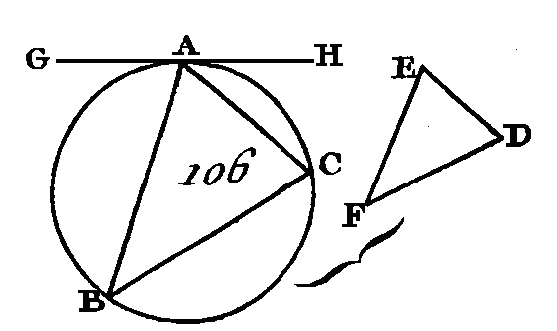
Conduisez le diamètre BC du cercle ABC. Si la droite BC est égale à la droite D, on a déjà fait ce que l'on proposait : car on a appliqué dans le cercle ABC une droite égale à la droite D. Si, au contraire, la droite BC est plus grande que la droite D, faites la droite CE égale à la droite D (prop. 3. I), et du centre C et avec l'intervalle CE décrivez la circonférence AEF (dem. 5.), et conduisez-la droite CA (dem. 1). Puisque le point C est le centre du cercle AEF, la droite CA sera égale à la droite CE; mais la droite D est égale à la droite CE : donc la droite D sera égale à la droite CA.

Donc, dans le cercle donné ABC on a appliqué la droite CA égale à la droite donnée D qui est moindre que son diamètre ; ce qu'il fallait faire.

PROPOSITION II.

PROBLÈME.

Dans un cercle donné, inscrire un triangle qui soit équiangle à un triangle donné.

Soit ABC (fig. 106) le cercle donné et DEF le triangle donné : il faut dans le cercle ABC inscrire un triangle qui soit équiangle au triangle donné DEF.

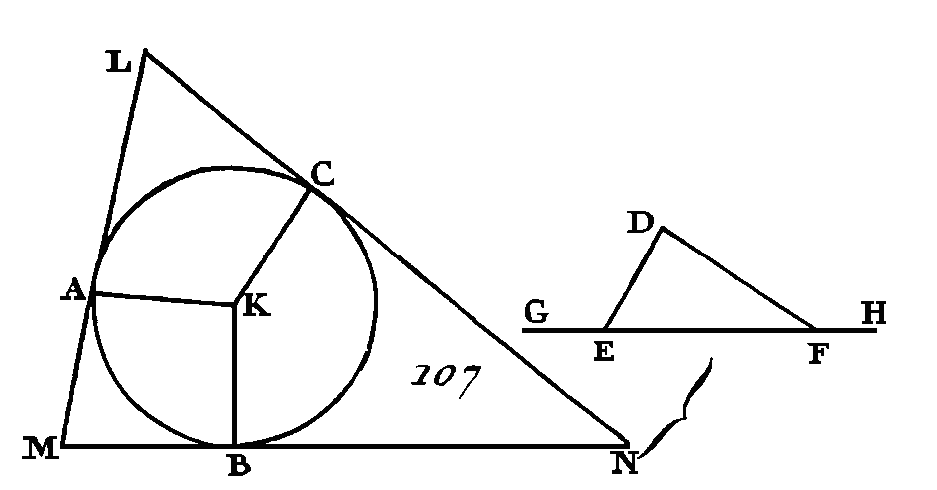
Conduisez la droite GAH de manière qu'elle touche le cercle ABC au point A, et sur la droite AH et au point A faites l'angle HAC égal à l'angle DEF (prop. 23, I). De plus, sur la droite GA et au point A faites l'angle GAB égal à l'angle FDE, et menez la droite BC.

Puisque la droite HAG touche le cercle ABC et que la droite AG a été menée du point de contact, l'angle HAC est égal à celui qui est placé dans le segment alterne du cercle, c'est-à-dire à l'angle ABC (prop. 32. III) ; mais l'angle HAC est égal à l'angle DEF : donc l'angle ABC est égal à l'angle DEF. Par la même raison l'angle ACB est égal à l'angle FDE : donc l'angle restant. BAC sera égal à l'angle restant EFD (prop. 32. I) : donc le triangle ABC est équiangle au triangle DEF, et il est inscrit dans le cercle ABC (déf. 3. IV). Donc dans le cercle donné on a inscrit un triangle équiangle au triangle donné ; ce qu'il fallait faire.

PROPOSITION III.

PROBLÈME.

Autour d'un cercle circonscrire un triangle équiangle à un triangle donné.

Soit ABC (fig. 107) le cercle donné et DEF le triangle donné : il faut autour du cercle ABC circonscrire un triangle équiangle au triangle donné DEF.

Prolongez la droite EF de part et d'autre vers les points H, G (dem. 2), prenez le centre K du cercle ABC (prop. 1. III) ; conduisez d'une manière quelconque la droite KB, faites sur la droite KB et au point K un angle BKA égal à l'angle DEG, et l'angle BKC égal à l'angle DFH (prop. 25. I) ; par les points A, B, C conduisez les droites LAM, MBN, NCL de manière qu'elles soient tangentes au cercle ABC (prop. 17. III). Puisque les droites LM, MN, NL touchent le cercle ABC aux points A, B, C et que les droites KA, KB, KC sont menées du centre K aux points A, B, C, les angles seront droits aux points A, B, C (prop. 18. III); et puisque les quatre angles du quadrilatère AMBK sont égaux à quatre angles droits (prop. 32. I), car ce quadrilatère peut se diviser en deux triangles; mais parmi les angles de ce quadrilatère, les angles KAM, KBM sont droits : donc les angles restants AKB, AMB seront égaux à deux angles droits ; mais les angles DEG, DEF sont égaux à deux droits (prop. 13. I) : donc les angles AKB, AMB sont égaux aux angles DEG, DEF ; mais l'angle DEG est égal à l'angle AKB : donc l'angle restant AMB sera égal à l'angle restant DEF. Nous démontrerons semblablement que l'angle LNM est égal à l'angle DFE : donc l'angle restant MLN est égal à l'angle EDF (prop. 32. I): donc le triangle LMN est équiangle avec le triangle DEF, et il est circonscrit autour du cercle ABC (déf. 4. IV). Donc un triangle équiangle avec un triangle donné a été circonscrit autour du cercle donné ; ce qu'il fallait faire.

PROPOSITION IV.

PROBLÈME.

Inscrire une circonférence de cercle dans un triangle donné.

Soit ABC (fig. 108) le triangle donné : il faut dans le triangle ABC inscrire un cercle.

Partagez en deux parties égales les angles ABC, BCA par les droites BD, CD qui se rencontrent au point D, et du point D conduisez sur les droites AB, BC, CA les perpendiculaires DE, DF, DG (prop, 12. I).

Puisque l'angle ABD est égal à l'angle CBD, car l'angle ABC a été partagé en deux parties égales, et que l'angle droit BED est égal à l'angle droit BFD, les deux triangles EBD, DBF auront deux angles égaux à deux angles et un côté égal à un côté, car BD, qui est opposé à deux angles égaux, est commun : donc ils auront les autres côtés égaux aux autres côtés (prop. 36. I) ; donc le côté DE sera égal au côté DF. Par la même raison le côté DG sera égal au côté DF: donc la circonférence décrite du point D avec un intervalle égal à une des droites DE, DF, DG passera par les autres points et touchera les droites AB, BC, CA, parce que les angles sont droits en E, F, G ; car si cette circonférence coupait ces droites, la perpendiculaire à l'extrémité d'un diamètre tomberait dans le cercle; ce qui est absurde (prop. 16. III). Donc la circonférence décrite du point D avec un intervalle égal à une des droites DE, DF, DG ne coupera point les droites AB, BC, CA : donc elle les touchera, et cette circonférence sera inscrite dans le triangle ABC (déf. 5. IV).

Donc dans le triangle donné ABC on a inscrit la circonférence de cercle EFG ; ce qu'il fallait faire.

PROPOSITION V.

PROBLÈME.

Autour d'un triangle donné décrire une circonférence de cercle.

Soit ABC (fig. 109) le triangle donné : il faut autour du triangle donné ABC décrire une circonférence de cercle.

Partagez les côtés AB, AC en deux parties égales aux points D, E (prop. 10. I), et des points D, E conduisez sur les droites AB, AC les perpendiculaires DF, EF (prop. 11. I) ; ces perpendiculaires se rencontreront ou dans le triangle ABC, ou dans la droite BC, ou hors du triangle ABC.

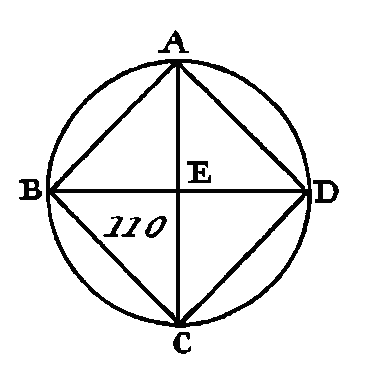
Supposons d'abord que ces perpendiculaires se rencontrent dans le triangle au point F; menez les droites BF, FC, FA; puisque la droite AD est égale à la droite DB, et que la perpendiculaire DF est commune, la base AF sera égale : la base FB (prop. 4. I). Nous démontrerons semblablement que la droite CF est égale à la droite FA : donc la droite BF est égale à la droite FC : donc les trois droites FA, FB, FC sont égales entre elles : donc si du centre F et avec un intervalle égal à une des droites FA, FB, FC on décrit une circonférence, cette circonférence passera par les autres points, et cette circonférence sera décrite autour du triangle ABC (déf. 6. 4); décrivez la circonférence ABC.

Supposons actuellement, que les droites DF, EF se rencontrent dans la droite BC et au point F, comme dans la figure 109* ; menez la droite AF. Nous démontrerons semblablement que le point F est le centre de la circonférence circonscrite au triangle ABC.

Supposons enfin que les droites DF, EF se rencontrent hors du triangle ABC, au point F comme dans la figure 109** ; menez les droites AF, FB, FC. Puisque la droite AD est égale à la droite DB et que la perpendiculaire DF est commune, la base AF sera égale à la base F B (prop. 4. I). Nous démontrerons semblablement que la droite CF est égale à la droite FA : donc la droite BF est égale à la droite FC: donc si du centre F et avec un intervalle égal à une des droites FA, FB, FC on décrit une circonférence, elle passera par les autres points, et cette circonférence sera circonscrite autour du triangle ABC ; décrivez donc la circonférence ABC.

Donc une circonférence de cercle a été circonscrite autour du triangle donné ; ce qu'il fallait faire.

COROLLAIRE.

Il est évident que si le centre du cercle tombe dans le triangle, et si l'angle ABC est compris dans un segment plus grand qu'un demi-cercle, cet angle sera moindre qu'un angle droit. Si le centre du cercle tombe sur la droite BC, si cet angle est compris dans un demi-cercle, cet angle sera droit ; si enfin le centre du cercle tombe hors du triangle ABC, et si cet angle est compris dans un segment plus petit qu'un demi-cercle, cet angle sera plus grand qu'un angle droit : donc si le triangle donné est acutangle, les droites DE, EF se rencontreront dans le triangle ; si ce triangle a un angle droit BAC, les droites se rencontreront dans la droite BC ; si enfin cet angle a un angle obtus, ces droites se rencontreront hors du triangle ABC.

PROPOSITION VI.

PROBLÈME,

Décrire un carré dans un cercle donné.

Soit ABCD (fig. 110) le cercle donné : il faut décrire un carré dans le cercle ABCD.

Conduisez les diamètres AC, BD du cercle ABCD de manière qu'ils soient perpendiculaires l'un sur l'autre (prop. 11. I) ; menez les droites AB, BC, CD, DA.

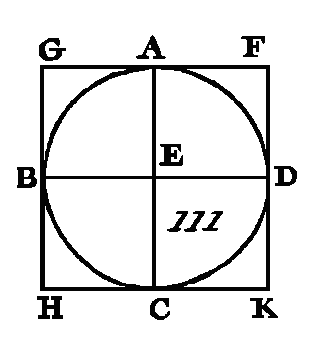
Puisque la droite BE est égale à la droite ED, car le point E est le centre, et que la droite EA est commune et perpendiculaire sur BD, la base AB sera égale à la base AD (prop. 4. I). Par la même raison, chacune des droites BC, CD est égale à chacune des droites BA, AD : donc le quadrilatère ABCD est équilatère. Je dis aussi qu'il est rectangulaire ; car puisque la ligne droite B D est un diamètre du cercle ABCD, la figure DAD sera un demi-cercle : donc l'angle BAD est droit (prop. 31. I); par la même raison chacun des angles ABC, BCD, CDA sera droit aussi : donc le quadrilatère ABCD est rectangulaire ; mais on a démontré qu'il est équilatère : donc ce quadrilatère est un carré, et ce quatre est inscrit dans le cercle ABCD.

Donc on a inscrit le carré ABCD dans le cercle donné ABCD ; ce qu'il fallait faire.

PROPOSITION VII.

PROBLÈME.

Circonscrire un carré à un cercle donné.

Soit ABCD (fig. 111) le cercle donné : il faut circonscrire un carré au cercle ABCD.

Conduisez dans le cercle ABCD les deux diamètres AC, BD de manière qu'ils soient perpendiculaires l'un sur l'autre ; et par les points A, B, C, D conduisez les droites FG, GH, HK, KF de manière qu'elles soient tangentes du cercle ABCD (prop. 17. III).

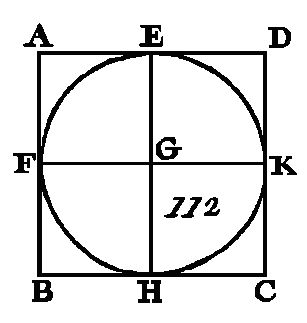
Puisque la droite FG est tangente du cercle ABCD, et que la droite EA a été conduite du centre E au point de contact qui est en A, les angles seront droits en A (prop. 18. III). Par la même raison les angles seront droits en B, C, D. Puisque l'angle AEB est droit et que l'angle EBG est droit aussi, la droite GH sera parallèle à la droite AC (prop. 28. I). Par la même raison la droite AG est parallèle à la droite FK. Nous démontrerons semblablement que l'une et l'autre des droites GF, HK est parallèle à la droite BED : donc les figures GK, GC, AK, FB, BK sont des parallélogrammes : donc la droite GF est égale à la droite HK (prop. 34. I), et la droite GH égale à la droite FK; et puisque la droite AC est égale à la droite BD, que la droite AC est égale à Tune et à l'autre des droites GH, FK, et que la droite BD est égale à l'une et à l'autre des droites GF, HK, les droites GH, FR seront égales aux droites GF, HK : donc le quadrilatère FGHK est équilatère, et je dis qu'il est rectangulaire ; car puisque le quadrilatère GBEA est un parallélogramme, et que l'angle AEB est droit, l'angle AGB sera droit aussi (prop. 34. I). Nous démontrerons semblablement que les angles qui sont placés vers les points H, K, F sont des angles droits : donc le quadrilatère FGHK est rectangle. Mais on a démontré qu'il est équilatère j donc le quadrilatère est un carré, et il est circonscrit autour du cercle ABCD.

Donc on a circonscrit un carré au cercle donné; ce qu'il fallait faire.

PROPOSITION VIII.

PROBLÈME.

Inscrire un cercle dans un carré donné.

Soit ABCD (fig. 112) le carré donné : il faut inscrire un cercle dans le carré ABCD.

Coupez en deux parties égales l'une et l'autre des droites AB, AD aux points F, E (prop. 10. I), et par le point E conduisez la droite EH parallèle à l'une et à l'autre des droites AB, CD (prop. 31. I), et par le point F conduisez aussi la droite FK parallèle à l'une et à l'autre des droites AD, BC : donc chacune des figures AK, KB, AH, HD, AG, GC, BG, GD est un parallélogramme, et leurs côtés opposés sont égaux (prop. 34. ï). Puisque la droite AD est égale à la droite AB, que la droite AE est la moitié de AD et la droite AF la moitié de AB, la droite AE sera égale à la droite AF. Mais les côtés qui leur sont opposés sont égaux : donc la droite F G est égale à la droite GE. Nous démontrerons semblablement que les droites GH, GK sont égales aux droites FG, GE, chacune à chacune : donc les quatre droites. GE, GF, GH, GK sont égales entre elles : donc le cercle décrit du centre G avec un intervalle égal à une des droites GE, GF, GH, GK passera par les autres points, et sera tangent aux droites AB, BC, CD, DA, parce que les angles en E, F, H, K sont droits ; car si la circonférence coupait les droites AB, BC, CD, DA, la perpendiculaire à l'extrémité d'un diamètre entrerait dans le cercle ; ce qui est absurde (prop. 16. III) : donc la circonférence de cercle décrite du centre G avec un intervalle égal à une des droites GE, GF, GH, GK ne coupera point les droites AB, BC, CD, DA: donc elle sera tangente à ces droites, et elle sera inscrite dans le carré ABCD (déf. 5. IV).

Donc on a inscrit une circonférence de cercle dans le carré donné ; ce qu'il fallait faire.

PROPOSITION IX.

PROBLÈME.

Circonscrire un cercle à un carré donné.

Soit ABCD (fig. 113) le carré donné : il faut à ce carré ABCD circonscrire une circonférence de cercle.

Menez les droites AC, BD qui se coupent mutuellement au point E.

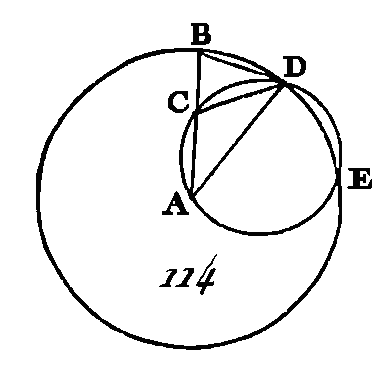
Puisque la droite DA est égale à la droite AB et que la droite A G est commune, les deux droites DA, AC sont égales aux deux droites BA, AC ; mais la base DC est égale à la base BC : donc l'angle DAC est égal à l'angle BAC (prop. 8. I): donc l'angle DAB est coupé en deux parties égales par la droite AC. Nous démontrerons semblablement que chacun des angles ABC BCD, CDA est coupé en deux parties égales par les droites AC, DB : donc puisque l'angle DAB est égal à l'angle ABC, que l'angle EAB est la moitié de l'angle DAB, et l'angle EBA la moitié de l'angle ABC, l'angle EAB sera égal à l'angle EBA : donc le côté EA est égal au côté EB (prop. 6. I). Nous démontrerons semblablement que les droites EC, ED sont égales aux droites EA, EB, chacune à chacune : donc les quatre droites EA, EB, EC, ED sont égales entre elles : donc la circonférence de cercle décrite du centre E avec un intervalle égal à une des droites EA, EB, ED passera par les autres points et elle sera circonscrite au carré ABCD ; circonscrivez le cercle ABCD.

Donc on a circonscrit un cercle à un carré donné ; ce qu'il fallait faire.

PROPOSITION X.

PROBLÈME.

Construire un triangle isocèle qui ait chacun des angles de sa base double du troisième angle.

Soit la droite AB (fig. 114) ; que cette droite soit coupée en un point C de manière que le rectangle compris sous les droites AB, BC soit égal au carré de CA (prop. 11. II) ; du centre A et avec l'intervalle AB décrivez la circonférence BDE (dem. 3); dans le cercle BDE menez la corde BD égale à la droite AC qui est moindre que le diamètre de ce cercle (prop. 1. IV), et ayant conduit les droites DA, DC, circonscrivez la circonférence ACD au triangle ACD (prop. 5. IV).

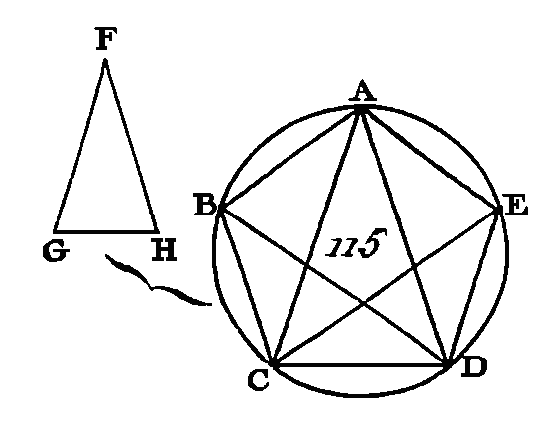
Puisque le rectangle compris sous les droites AB, BC est égal au carré de la droite AC et que la droite AC est égale à la droite BD, le rectangle compris sous les droites AB, BC sera égal au carré de BD : puisque le point B est pris hors du cercle ACD et que du point B on a mené un cercle ACD, les droites BCA, BD, dont l'une coupe le cercle et dont l'autre ne le coupe point, et puisque le rectangle compris sous les droites AB, BC est égal au carré de BD, la droite BD sera tangente au cercle ACD (prop. 37. III). Donc, puisque la droite BD est tangente et que la corde DC a été menée du point de contact D, l'angle BDC sera égal à celui qui est compris dans le segment alterne du cercle, c'est-à-dire à l'angle DAC (prop. 32. III). Mais, puisque l'angle BDC est égal à l'angle DAC, si nous ajoutons un angle commun CDA, l'angle total BDA sera égal aux deux angles CDA, DAC. Mais l'angle extérieur BCD est égal aux deux angles CDA, DAC (prop. 32. I): donc l’angle BDA est égal à l'angle BCD ; mais l'angle BDA est égal à l'angle CBD (prop. 5. I), puisque le côté AD est égal au côté AB ; donc l'angle DBA sera égal à l'angle BCD : donc les trois angles BDA, DBA, BCD sont égaux entre eux ; et puisque l'angle DBC est égal à l'angle BCD, le côté BD sera égal au côté DC (prop. 6. I); mais le côté BD est supposé égal au côté CA : donc le côté AC est égal au côté CD : donc l'angle CDA est égal à l'angle DAC (prop. 5. I) : donc les angles CDA, DAC, pris ensemble, sont double de l'angle DAC ; mais l'angle BCD est égal aux angles CDA, DAC (prop. 32. I) : donc l'angle BCD est double de l'angle DAC ; mais l'angle BCD est égal à chacun des angles BDA, DBA : donc chacun des angles BDA, DBA est double de l'angle DAB.

Donc on a construit un triangle isocèle. ADB, dont chacun des angles de sa base BD est double du troisième angle ; ce qu'il fallait faire.

PROPOSITION XI.

PROBLÈME.

Dans un cercle donné, inscrire un pentagone, équilatéral et équiangle.

Soit ABCDE (fig. 115) le cercle donné : il faut inscrire dans ce cercle un pentagone équilatéral et équiangle

Soit le triangle isocèle FGH, ayant, chacun des angles de sa base G, H double de l’angle E (prop. 10. IV). Inscrivez dans le cercle. ABCDE un triangle ACD équiangle avec le triangle FGH (prop. 2. IV), de manière que l'angle CAD soit égal à l'angle F, et de manière que chacun des angles ACB, CDA soit égal à chacun des angles G, H qui sont placés sur la base GH. Chacun des angles ACD, CDA sera double de l’angle CAD. Partagez chacun des angles ACD, CDA en deux parties égales par les droites CE, DB (prop. 9. I), et menez les droites AB, BC, DE, EA.

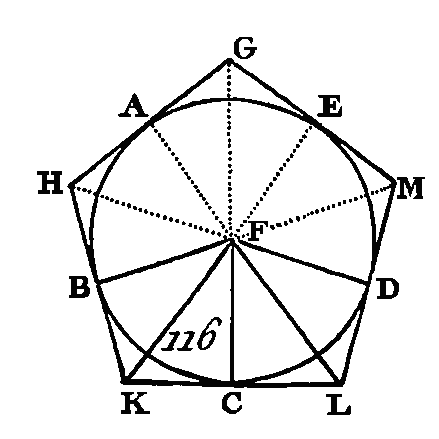
Puisque chacun des angles ACD, CDA est double de l'angle CAD, et que chacun de ces angles est coupé en deux parties égales par les droites CE, DB, les cinq angles DAC, ACE, ECD, CDB, BDA sont égaux entre eux; mais des angles égaux sont appuyés sur des arcs égaux (prop. 26. III) : donc les cinq arcs AB, BC, CD, DE, EA sont égaux; mais des cordes égales sous-tendent des arcs égaux (prop. ag. III) : donc les cinq cordes AB, BC, CD, DE, EA sont égales entre elles : donc le pentagone ABCDE est équilatéral. Je dis qu'il est aussi équiangle ; car puisque l'arc AB est égal à l'arc DE, si l’on ajoute un arc commun BCD, l'arc total ABCD sera égal à l'arc total EDCB. Or l'angle AED est appuyé sur l'arc ABCD et l'angle BAE est appuyé sur l'arc EDCB : donc l'angle BAE est égal à l'angle AED (prop. 27. III) ; par la même raison chacun des angles ABC, BCD, CDE est égal à chacun des angles BAE, AED : donc le pentagone ABCDE est équiangle; mais il a été démontré, qu'il est équilatéral. Donc dans un cercle donné, on a inscrit un pentagone équilatéral et équiangle; ce qu'il fallait faire.

PROPOSITION XII.

PROBLÈME.

Circonscrire à un cercle donné un pentagone équilatéral et équiangle.

Soit ABCDE (fig. 116) le cercle donné: il faut à ce cercle circonscrire un pentagone équilatéral et équiangle.

Supposons que les points A, B, C, D, E soient les sommets des angles d'un pentagone inscrit dans ce cercle (prop. 11. IV), de manière que les arcs AB, BC, CD, DE, EA soient égaux; par les points A, B, C, D, E, conduisez à ce cercle les tangentes GH, HK, KL, LM, MG (prop. 17. III); et ayant pris le centre F du cercle ABCDE, menez les droites FB, FK, FC, FL, FD.

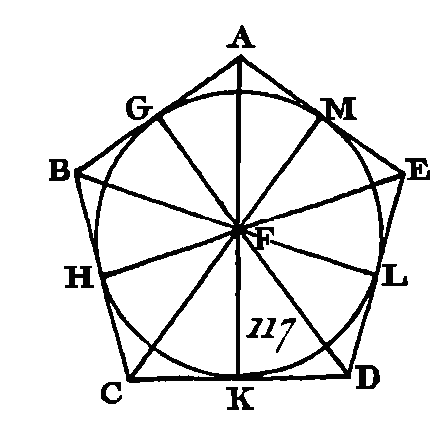
Puisque la droite KL touche le cercle ABCDE au point C, et que la droite FC a été menée du centre F au point de contact C, la droite F C sera perpendiculaire sur KL (prop. 18. III): donc chacun des angles FCK, FCL est droit; chacun des angles FBH, FBK, FDL, FDM est droit par la même raison. Puisque l'angle FCK est droit, le carré de la droite FK est égal aux carrés des droites FC, CK (prop. 47. I).

Le carré de la droite FK est égal aux carrés des droites FB, BK, par la même raison : donc les carrés des droites FC, CK sont égaux aux carrés des droites FB, BK; mais le carré de la droite FC est égal au carré de la droite FB : donc le carré restant de la droite CK sera égal au carré restant de la droite BK : donc la droite CK est égale à la droite BK. Puisque la droite FB est égale à la droite FG et que la droite FK est commune, les deux droites BF, FK sont égales aux deux droites CF, FK ; mais la base BK est égale à la base CK : donc l'angle BFK est égal à l'angle KFC, et l'angle BKF à l'angle FKC (prop. 8. I) : donc l'angle BFC est double de l'angle KFC et l'angle BKC double de l'angle FKC. Par la même raison l'angle CFD est double de l'angle CFL, et l'angle CLD double de l'angle CLF. Puisque l'arc BC est égal à l'arc CD, l'angle BFC sera égal à l'angle CFD (prop. 27. III) ; mais l'angle BFC est double de l'angle KFC, et l'angle DFC double de l'angle LFC : donc l'angle KFC est égal à l'angle CFL : donc les deux triangles FKC, FLC ont deux angles égaux à deux angles, chacun à chacun, et un côté égal à un côté, puisque le côté FC leur est commun : donc ces deux triangles ont leurs autres côtés égaux aux autres côtés, et l'angle restant égal à l'angle restant (prop. 26. I) : donc la droite KC est égale à la droite CL, et l'angle FKC égal à l'angle FLC. La droite KL sera double de la droite KC, puisque la droite KC est égale à la droite CL. Par la même raison la droite HK sera double de la droite BK. De plus, puisqu'on a démontré que la droite BK est égale à la droite KC, que la droite KL est double de la droite KC et la droite HK double de la droite BK, la droite HK sera égale à la droite KL. Nous démontrerons semblablement que chacune des droites GH, GM, ML est égale à l'une ou à l'autre des droites HK, KL : donc le pentagone GHKLM est équilatéral. Je dis aussi qu'il est équiangle ; car puisque l'angle FKC est égal à l'angle FLC, et qu'on a démontré que l'angle HKL est double de l'angle FKC et l'angle KLM double aussi de l'angle FLC, l'angle HKL sera égal à l'angle KLM. Nous démontrerons par une raison semblable que chacun des angles KHG, HGM, GML est égal à l'un ou à l'autre des angles HKL, KLM : donc les cinq angles GHK, HKL, KLM, LMG, MGH sont égaux entre eux : donc le pentagone GHKLM est équiangle. Nous avons démontré qu'il est équilatéral, et il est circonscrit au cercle ABCDE ; ce qu'il fallait faire.

PROPOSITION XIII.

PROBLÈME.

Dans un pentagone équilatéral et équiangle, inscrire un cercle.

Soit ABCDE (fig. 117) le pentagone équilatéral et équiangle donné : il faut inscrire un cercle dans le pentagone ABCDE.

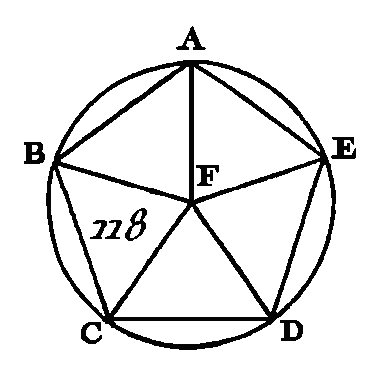
Partagez chacun des angles BCD, CDE en deux parties égales par les droites CF, DF (prop. 9. I) ; et du point F où les deux droites CF, DF se rencontrent, menez les droites FB, FA, FL. Puisque la droite BC est égale à la droite C D et que la droite FC est commune, les deux droites BC, CF sont égales aux deux droites DC, CF ; mais l'angle BCF est égal à l'angle DCF : donc la base BF est égale à la base DF (prop. 4. I) ; le triangle BFC est égal au triangle DCF et les autres angles, qui sous-tendent des côtés égaux dans ces deux triangles sont égaux entre eux (prop. 4. I) : donc l'angle CBF sera égal à l'angle CDF et puisque l'angle CDE est double de l'angle CDF et que l'angle CDE est égal à l'angle ABC et l'angle CDF égal à l'angle CBF, l'angle CBA sera double de l'angle CBF, et par conséquent l'angle ABF sera égal à l'angle FBC : donc l'angle ABC est partagé en deux parties égales par la droite BF. Nous démontrerons semblablement que chacun des angles BAE, AED est partagé en deux parties égales par les droites FA, FE. Actuellement du point F conduisez sur les droites AB, BC, CD, DE, EA les perpendiculaires FG, FH, FK, FL, FM. Puisque l'angle HCF est égal à l'angle KCF et que l'angle droit FHC est égal à l'angle droit FKC, les deux triangles FHC, FKC auront deux angles égaux à deux angles et un côté égal à un côté ; savoir, le côté commun FC qui soutend des angles égaux : donc ces deux triangles auront les autres côtés égaux aux autres côtés (prop. 26. I), et la perpendiculaire FH sera égale à la perpendiculaire FK. On démontrera semblablement que chacune des droites FL, FM, FG est égale à l'une ou à l'autre des droites FH, FK : donc les cinq droites FG, FH, FK, FL, FM sont égales entre elles : donc si du centre F et avec un intervalle égal à une des droites FG, FH, FK, FL, FM on décrit une circonférence de cercle, cette circonférence passera par les autres points et touchera les droites AB, BC, CD, DE, EA, parce que les angles sont droits en G, H, K, L, M ; en effet, si au lieu de les toucher, elle les coupait, la perpendiculaire menée à l'extrémité d'un diamètre entrerait dans le cercle ; ce qui a été démontré absurde (prop. 16. 3) : donc la circonférence décrite du centre F avec un intervalle égal à une des droites FG, FH, FK, FL, FM ne coupera point les droites AB, BC, CD, DE, EA: donc elle les touchera. Décrivez la circonférence GHKLM.

Donc on a inscrit une circonférence de cercle dans un pentagone équilatéral et équiangle ; ce qu'il fallait faire.

PROPOSITION XIV.

PROBLÈME.

Circonscrire une circonférence de cercle à un pentagone équilatéral et équiangle donné.

Soit ABCDE (fig. 118) un pentagone équilatéral et équiangle : il faut à ce pentagone circonscrire une circonférence de cercle.

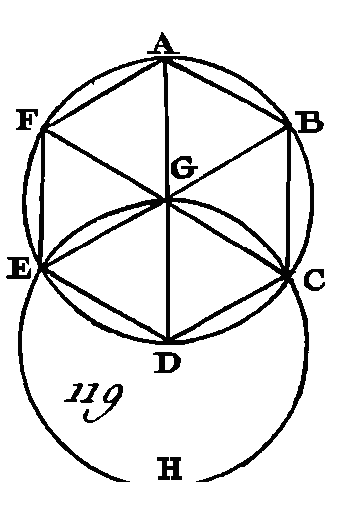
Partagez en deux parties égales chacun des angles BCD, CDE par les droites CF, FD (prop. 9. I), et du point F où ces droites se rencontrent, menez aux points B, A, E les droites FB, FA, FE. Nous démontrerons, comme dans la proposition précédente, que chacun des angles CBA, BAE, AED est coupé en deux parties égales par les droites BF, FA, FE. Puisque l'angle BCD est égal à l'angle CDE, et que l'angle FCD est la moitié de l'angle BCD, et l'angle CDF la moitié de l'angle CDE, l'angle FCD sera égal à l'angle FDC : donc le côté FC est égal au côté FD (prop. 6. I). On démontrera semblablement que chacune des droites FB, FA, FE est égale à chacune des droites FC, FD : donc les cinq droites FA, FB, FC, FD, FE sont égales entre elles : donc la circonférence décrite du point F et avec un intervalle égal à une des droites FA, FB, FC, FD, FE passera par les autres points et sera circonscrite au pentagone équilatéral et équiangle ABCDE. Décrivez la circonférence ABCDE.

Donc une circonférence de cercle a été circonscrite à un pentagone équilatéral et équiangle ; ce qu'il fallait faire.

PROPOSITION XV.

PROBLÈME.

Inscrire dans un cercle donné un hexagone équilatéral et équiangle.

Soit ABCDEF (fig. 119) le cercle donné : il faut dans ce cercle inscrire un hexagone équilatéral et équiangle.

Menez le diamètre AD du cercle ABCDEF, prenez le centre G de, ce cercle, et du centre D avec l'intervalle DG décrivez la circonférence EGCH (dem. 3) ; menez les droites EG, CG, prolongez-les vers les points B, F, et menez les droites AB, BC, CD, DE, EF, FA : je dis que l'hexagone ABCDEF est équilatéral et équiangle.

Puisque le point G est le centre du cercle ABCDEF, la droite GE sera égale à la droite GD. De plus, puisque le point D est le centre du cercle EGCH, la droite DE sera égale à la droite DG ; mais on a démontré que la droite GE est égale à la droite GD : donc la droite GE est égale à la droite ED : donc le triangle EGD est équilatéral : donc ses trois angles EGD, GDE, DEG sont égaux entre eux, puisque dans les triangles isocèles les angles à la base sont égaux entre eux (prop. 5. I) ; mais les trois angles d'un triangle sont égaux à deux droits (prop. 32. I) : donc l'angle EGD est le tiers de deux angles droits. On démontrera semblablement que l'angle DGC est le tiers de deux angles droits ; donc, puisqu'une droite CG tombant sur la droite EB fait les angles de suite EGC, CGB égaux à deux droits (prop. 13. I), l'angle restant CGB sera le tiers de deux angles droits : donc les angles EGD, DGC, CGB sont égaux entre eux; mais les angles BGA, AGF, FGE sont égaux aux angles EGD, DGG, CGB, parce que ces angles sont opposés par le sommet (prop. 15. I): donc les six angles EGD, DGC, CGB, BGA, AGF, FGE sont égaux entre eux; mais des angles égaux s'appuient sur des arcs égaux (prop. 26. III) : donc les six arcs AB, BC, CD, DE, EF, FA sont égaux entre eux ; mais des arcs égaux sont sous-tendus par des cordes égales (prop. 29. III) : donc les six cordes sont égales entre elles : donc l'hexagone ABCDEF est équilatéral. Je dis qu'il est équiangle, car puisque l'arc AF est égal à l'arc ED, si nous leur ajoutons à chacun l'arc ABCD, l'arc total FABCD sera égal à l'arc total EDCBA : donc, puisque l’angle FED s'appuie sur l'arc FABCD et que l'angle AFE s'appuie sur l'arc EDCBA, l'angle AFE est égal à l'angle DEF (prop. 27. III). On démontrera semblablement que les autres angles de l'hexagone ABCDEF sont égaux chacun à l'un ou à l'autre des angles AFE, FED : donc l'hexagone ABCDEF est équiangle. Mais on a démontré qu'il est équilatéral, et il est inscrit dans le cercle ABCDEF.

Donc on a inscrit un hexagone équilatéral et équiangle dans un cercle donné; ce qu'il fallait faire.

Il suit manifestement de là que le côté de l'hexagone est égal au demi-diamètre du cercle.

Si par les points A, B, C, D, E, F nous menons des tangentes au cercle, on circonscrira à ce cercle un hexagone équilatéral et équiangle en suivant la méthode que nous avons donnée pour le pentagone ; c'est aussi de la même manière que nous inscrirons et que nous circonscrirons une circonférence de cercle à un hexagone donné.

PROPOSITION XVI.

PROBLÈME.

Inscrire dans un cercle donné un quindécagone équilatéral et équiangle.

Soit ABCD (fig. 120) le cercle donné : il faut dans ce cercle inscrire un quindécagone équilatéral et équiangle.

Inscrivez dans le cercle ABCD le côté AC d'un triangle équilatéral et le côté AB d'un pentagone équilatéral. Puisque la circonférence entière ABCD doit être partagée en quinze parties égales, l'arc ABC qui est la troisième partie de la circonférence en contiendra cinq, et l'arc AB qui est le cinquième de la circonférence en tiendra trois : donc l'arc restant BC en contiendra deux. Partagez l'arc restant BC en deux parties égales au point E (prop. 30. III), chacun des arcs BE, EC sera la quinzième partie de la circonférence du cercle ABCD : donc si l'on porte une des droites BE, EC sur la circonférence ABCD autant de fois qu'on le pourra (prop. 1. IV), on aura un quindécagone équilatéral et équiangle qui sera inscrit dans cette circonférence; ce qu'il fallait faire.

En suivant la méthode que nous avons donnée pour le pentagone, si par les points de division d'un cercle on conduit des tangentes à ce cercle, on circonscrira à ce cercle un quindécagone équilatéral et équiangle. En suivant la même méthode, nous inscrirons et nous circonscrirons une circonférence de cercle à un quindécagone équilatéral et équiangle donné.

FIN DU QUATRIÈME LIVRE.