|
ALLER A LA TABLE DES MATIÈRES DE HERON
HÉRON D’ALEXANDRIE
LES MÉCANIQUES. ou L’ÉLÉVATEUR DE HÉRON D’ALEXANDRIE,
PUBLIÉES POUR LA PREMIÈRE FOIS SUR LA VERSION ARABE DE QOSTÂ IBN LÛQÂ. ET TRADUITES EN FRANÇAIS par M. LE BARON CARRA DE VAUX LIVRE II INTRODUCTION LIVRE I LIVRE III
Oeuvre numérisée par Marc Szwajcer
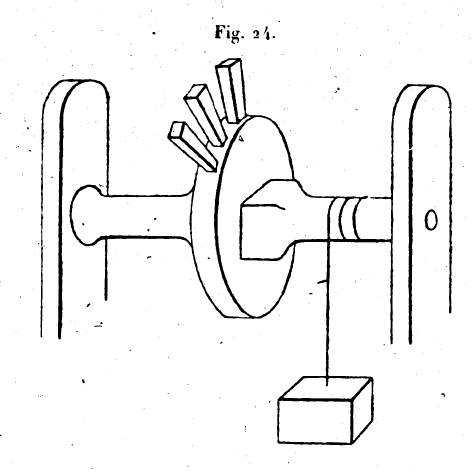
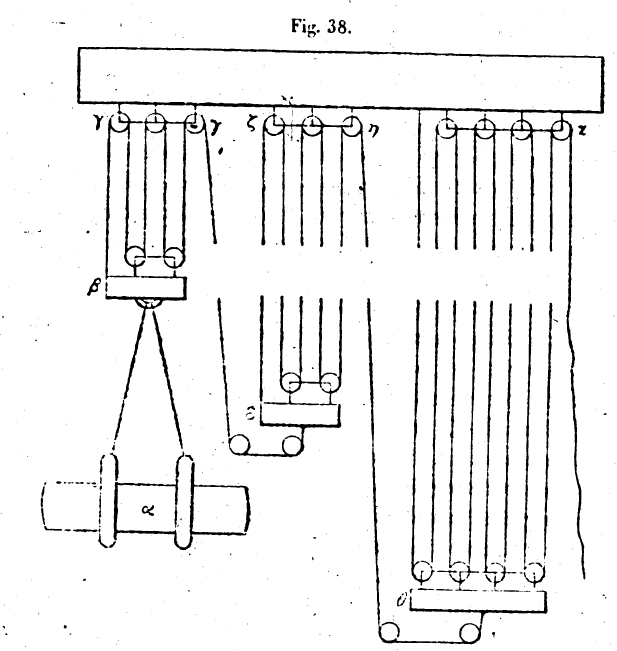
LIVRE II.I. — 1. Les machines simples par lesquelles on meut un poids donné avec une puissance donnée sont au nombre de cinq; il faut indiquer quels sont leurs formes, leurs modes d’emploi et leurs noms. Ces machines sont fondées sur un principe naturel unique, bien pi’el1es soient très différentes en apparence. Voici leurs noms: le treuil, le levier, la poulie, le coin et la vis sans fin. Le treuil se construit de cette façon: on prend une pièce de bois dur équarrie en forme de poutre; on en rabote et on en arrondit les extrémités, et on les garnit d’anneaux de cuivre, faits avec soin destinés à rendre insensibles les aspérités de l’arbre; de la sorte, chacune de ces extrémités étant introduite dans un trou arrondi et revêtu de cuivre ouvert dans une paroi solide et fixe, elle y tourne avec facilité. Le morceau de bois, ainsi travaillé, s’appelle axe. On monte ensuite dans le milieu de l’arbre un tambour percé d’un trou carré de même section que l’arbre; on l’y ajuste bien pour que le tambour et l’arbre montés l’un sur l’autre tournent ensemble. Ce tambour s’appelle peritrochium,[1] ont le sens est,: ce ‘qui entoure. Cette construction achevée, nous séparons sur l’axe, de chaque côté du tambour une partie rabotée, autour de laquelle s’enroulera la corde. Puis nous perçons sur le pourtour extérieur du tambour des trous, aussi nombreux que la commodité le demandera, et mesurés exactement de façon que, lorsqu’on y aura introduit des clous de bois, on puisse faire tourner avec ces clous le tambour et l’arbre.
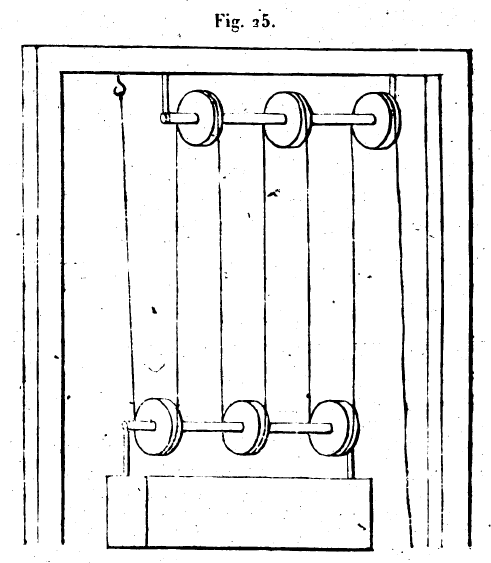
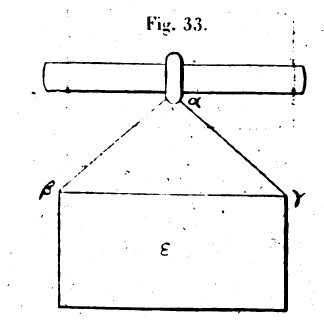
Nous venons d’exposer comment on doit construire le treuil; nous allons expliquer maintenant la manière de s’en servir. Quand vous voulez mouvoir un grand poids avec une puissance moindre que lui, vous attachez la corde à laquelle est lié le poids à la partie de l’arbre qui a été séparée des deux côtés du tambour; vous introduisez ensuite dans les trous que nous avons forés sur le pourtour du tambour des clous de bois, et, en appuyant de haut en bas sur ces clous, vous faites tourner le tambour. Alors le poids est mû avec une faible puissance, et les cordes s’enroulent sur l’arbre, ou du moins leurs tours se superposent si elles ne s’enroulent pas tout du long sur l’arbre même La dimension de cet instrument doit être proportionnée à la grandeur des corps lourds qu’il est destiné à transporter. Le rapport des parties doit être dans la mesure du rapport du poids à mouvoir à la puissance motrice; nous le démontrerons dans la suite. 2. Deuxième machine simple. — La deuxième machine simple est celle que l’on appelle le levier. Peut-être cette machine est-elle la première qui ait été inventée pour mouvoir les corps d’un poids excessif. En effet, lorsque des hommes voulurent mouvoir un corps d’un poids excessif, ce qu’ils eurent à faire tout d’abord pour le mettre en mouvement fut de le transporter au-dessus du sol; et comme ils n’avaient sur lui aucune prise, puisque toutes les parties de sa base reposaient sur la terre, ils durent avoir recours à un artifice; ils creusèrent donc un peu la terre au-dessous du corps lourd; puis, prenant un long morceau de bois, ils en introduisirent l’extrémité dans cette excavation, et ils appuyèrent sur l’autre extrémité; le poids leur sembla plus léger. Ils placèrent sous ce morceau de bois une pierre dont le nom est hypomochlium,[2] ce qui signifie : placé sous le levier; et appuyant de nouveau, ils trouvèrent le poids plus léger encore. Quand cette force fut mise en évidence, on connut qu’il était possible de mouvoir par ce moyen des poids considérables. Ce morceau de bois s’appelle levier, qu’il soit rond ou équarri; et plus on rapproche la pierre placée sous lui du poids à mouvoir, plus le mouvement est facile, comme nous le démontrerons dans la suite. 3. Troisième machine simple. . La troisième machine simple est celle que l’on appelle la moufle. Lorsque nous voulons élever un poids, quel qu’il soit, nous y attachons des cordes, et nous nous proposons de tendre les cordes jusqu’à le soulever; nous avons besoin pour cela il une puissance égale au poids que nous voulons élever. Si, après avoir détaché les cordes du poids, nous lions l’une de leurs extrémités à une poutre fixe; puis que nous introduisions l’autre extrémité sous une poulie affermie sur le milieu du fardeau, et que nous tendions alors les cordes, nous mouvrons le poids plus aisément. Si nous accrochons une autre poulie à la poutre fixe, et que nous y fassions passer l’extrémité de la corde, en la tendant, nous mouvrons le poids avec plus de facilité encore. Si nous attachons encore une poulie au fardeau pour y glisser l’extrémité de la corde, cette aisance que nous avons à mouvoir le poids augmentera. En suivant ce procédé, nous multiplierons les poulies accrochées à la poutre fixe et au poids que nous voulons porter; nous introduirons successivement l’extrémité de la
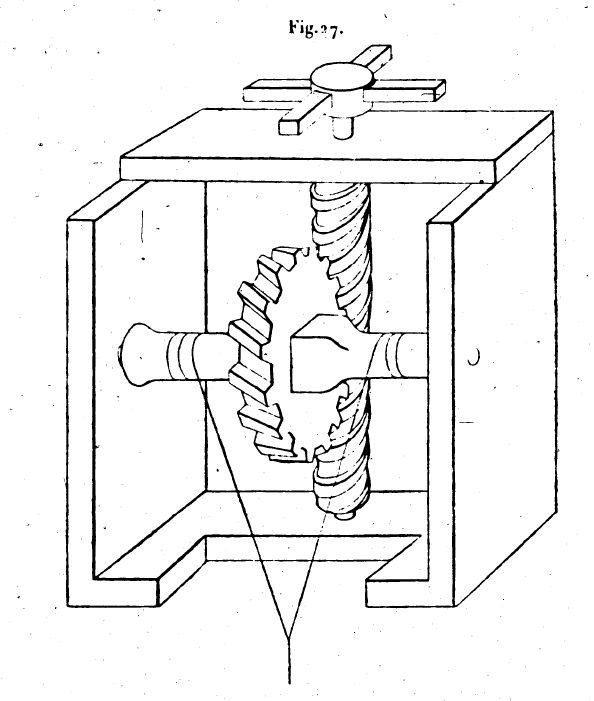
corde dans l’une des poulies fixes et dans l’une de celles qui sont liées au fardeau, et, faisant revenir à nous ce bout de la corde pour la tendre, nous verrons s’accroître la facilité avec laquelle nous élèverons le poids. Plus nous multiplierons les poulies sur lesquelles les cordes passent, plus cette facilité sera grande. Mais il faut que la première extrémité de la corde soit fixe, attachée à la poutre fixe, et que la corde aille de là vers le poids. Les poulies qui sont accrochées au support fixe doivent être affermies au moyen d’une autre pièce de bois, et elles doivent tourner autour d’un même axe qui est appelé manganum;[3] cette pièce d bois est attachée à la poutre fixe par d’autres cordes. Quant aux poulies liées au fardeau, elles sont rangées sur un autre axe égal au premier et attaché au fardeau. Il est nécessaire que les poulies soient montées sur l’axe de telle façon qu’elles ne puissent pas se rapprocher les unes des autres parce que, si elles se touchaient, leur rotation. deviendrait difficile. Nous avons dit que plus les poulies étaient multipliées, plus était grande la facilité avec laquelle on élevait le poids, et que l’extrémité de la corde devait être attachée au support; c’est ce que nous prouverons dans la suite. 4. Quatrième machine simple. — la quatrième machine simple, qui suit les précédentes, est celle qui est appelée le coin. Elle sert dans quelques-unes des préparations des parfumeurs et pour produire l’adhésion de parties disjointes clans certains ouvrages de menuiserie. Ses emplois sont variés; mais, le plus souvent, on s’en sert pour fendre la partie inférieure des pierres que l’on veut détacher, après les avoir au préalable séparées, sur les côtés, de la masse dont on veut les détacher. On ne pourrait, pour cet usage, employer aucune des autres machines, même en le associant toutes; le coin seul peut agir dans ce cas. Il agit par le coup qui l’atteint, quel que soit ce coup, et il ne cesse pas d’agir après le coup donné. Cela, est manifeste; souvent en effet, sans que le coin soit frappé, il fait du bruit et bouge, parce qu’il fend par sa propre force. Plus l’angle du coin est aigu plus il, agit avec facilité, comme nous le montrerons. 5. Cinquième machine simple. -— C’est celle qui est appelée la vis. Les instruments dont nous avons parlé reposent sur des principes très clair et il sont complets en eux-mêmes; c’est ce qu’on constate en maintes circonstances où on les emploie. La vis, au contraire, présente quelque difficulté dans sa construction et dans son usage, qu’elle soit employée seule ou qu’une autre puissance lui soit associée. Elle n’est cependant pas autre chose qu’un coin courbe, qui ne reçoit pas de coups, mais qu’un levier met en mouvement. Ce que nous allons dire rendra cette proposition évidente. Nous définissons ainsi la nature de la ligne tracée sur la vis : supposons que l’une des arêtes d’une figure cylindrique se meuve sur la surface du cylindre, et qu’un point soit mobile sur cette arête à partir de son extrémité; ce point parcourt l’arête entière dans le temps que l’arête met à faire une fois tout le tour de la surface cylindrique et revenir à la position de laquelle die est partie. La courbe que décrit le point, sur la surface du cylindre est un tour de vis; et c’est là ce qu’on appelle la vis. Lorsque nous voulons tracer cette ligne sur la surface du cylindre, nous opérons de cette manière : nous nous donnons sur un plan deux lignes perpendiculaire l’une à l’autre, l’une égale à l’arête du cylindre, l’autre égale à la circonférence du cylindre, c’est-à-dire à la circonférence de sa base; et nous joignons les deux extrémités de ces deux lignes qui comprennent l’angle droit, par une ligne qui soutend l’angle droit. Nous appliquons la ligne égale à l’arête du cylindre sur cette arête, et la ligne égale à la circonférence de la base du cylindre sur cette circonférence. La ligne qui soutend l’angle droit s’enroule sur la surface du cylindre et décrit un tour de vis. Nous pouvons partager l’arête du cylindre en autant de parties égales qu’il nous plait, et tracer dans chacune de ces portions un tour de vis. Il y aura ainsi sur le cylindre de nombreux tours de vis, et le cylindre sera une vis. Le cylindre autour duquel s’enroule une seule fois la corde de l’angle droit s’appelle vis à un tour; j’entends que l’arête du cylindre ne soutend qu’une seule ligne courbe qui part de l’une de ses extrémités et qui aboutit à l’autre. Quand nous voulons nous servir de la vis, nous Creusons, suivant cette ligne enroulée sur le cylindre une rainure qui pénètre assez avant flans l’épaisseur du cylindre pour qu’il soit possible d’y introduire le doigt de bois appelé tylos.[4] La vis s’emploie ensuite de cette manière : on en arrondit et on en polit les extrémités, et on les fait passer dans deux ouvertures rondes pratiquées dans des supports fixes, de façon qu’elles tournent avec facilité. Puis on dresse verticalement et parallèlement au cylindre de la vis une règle de bois appelée kânôn : cette règle porte une rainure à bords parallèles ouverte dans sa surface, du côté où elle regarde la vis. On introduit une extrémité du morceau de bois appelé tylos dans la rainure de la vis et l’autre extrémité dans la rainure de la règle. Quand nous voulons mouvoir un lourd fardeau avec cet instrument, rions prenons l’une des
cordes appelées syzyx,[5] nous en attachons l’un des bouts au fardeau que nous voulons soulever, et l’autre à la pièce de bois appelée tylos. Nous avons percé à une extrémité de la vis de trous en différents sens; nous introduisons dans ces trous des clous de bois, à l’aide desquels nous tournons la vis. Le doigt de bois s’élève en se mouvant dans la rainure creusée dans la vis; en montant il tire la corde, qui entraîne le fardeau qui lui est attaché. Nous pouvons ajuster à l’extrémité de la vis, dans la partie qui est extérieure an support fixe au lieu des clous de bois, un bras équarri et muni d’une poignée; nous tournons alors la vis au moyen de ce bras, et le fardeau s’élève. La rainure hélicoïdale qui se trouve, sur le cylindre est tantôt carrée et tantôt lenticulaire. La rainure carrée est celle dont les parois sont perpendiculaires à la surface du cylindre et qui est limitée à deux lignes; la rainure lenticulaire est celle qui a des parois inclinées et qui est limitée à une seule ligne. Celle-ci s’appelle filet lenticulaire et l’autre s’appelle filet carré. 6. Quand la vis est employée seule, c’est de cette façon qu’elle s’emploie. Mais lorsqu’elle est employée autrement, associée à une autre machine simple, à savoir à celle lui consiste en un arbre portant un tambour, voici ce qu’elle devient. Imaginons que le tambour monté sur l’arbre porte des dents de bois; une vis est placée au contact du tambour elle est perpendiculaire au sol ou parallèle au plan du sol. Les dents de bois engrènent avec la rainure hélicoïdale, et les extrémités de la vis sont dans deux trous arrondis percés dans les supports fixes, comme nous l’avons décrit précédemment. Une portion de l’extrémité de la vis vient à l’extérieur du support fixe, et c’est sur elle que l’on fixe un bras de bois muni d’une poignée, à moins que l’on ne perce dans cette portion extérieure des trous pour y introduire des clous de bois qui serviront à faire tourner la vis.
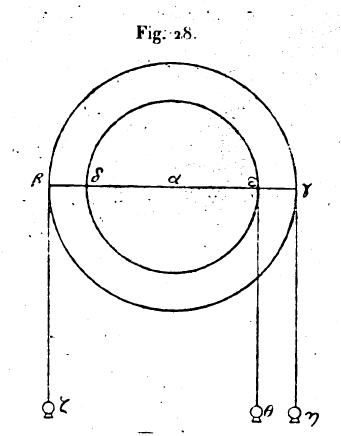
Quand nous voulons élever un fardeau avec cet instrument, nous attachons à l’arbre, des deux côtés du tambour les cordes liées au fardeau; nous tournons la vis avec laquelle nous avons fait engrener les dents de bois du tambour; le tambour tourne ainsi que l’arbre et le poids s’élève II. 7. —Nous avons achevé d’exposer la construction des cinq machines simples dont la description précède, et d’expliquer leur mode d’emploi. Quant à la cause qui fait que chacun de ces instruments meut des poids considérables avec une très faible puissance, nous allons maintenant en parler comme il suit. Supposons deux cercles avant un même centre α ; soient leurs diamètres les deux lignes βγ, δε ; ces deux cercles sont mobiles autour du point a, qui est leur centre commun, et perpendiculaires au plan de l’horizon. Suspendons aux deux points β, γ deux poids égaux, désignés par ζ et η. Il est évident que les cercles ne penchent ni d’un côté ni de l’autre, puisque les deux poids ζ et η sont égaux et les distances βα, αγ égales. Faisons de βγ un fléau de balance mobile autour d’un point de suspension qui est le point α. Si nous transportons en ε le poids qui est appliqué en γ, le poids inclinera ζ vers le bas, et il fera tourner les cercles. Mais si nous augmentons le poids θ, il fera de nouveau équilibre au poids ζ et le rapport du poids θ au poids ζ sera égal au rapport de la distance βα à la distance αε. Ainsi la ligne βε joue le rôle d’un fléau de balance mobile autour d’un point de suspension, qui est le point α.
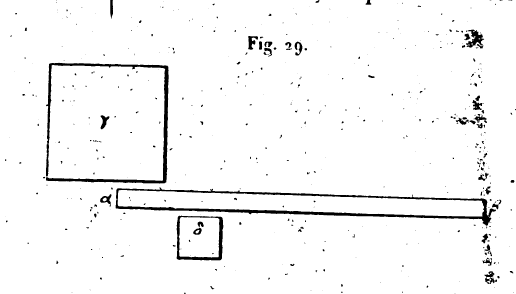
Archimède a déjà donné cette proposition dans son livre sur l’équilibre entre les poids. Il est évident, par là, que nous pouvons mouvoir un corps très lourd avec une faible puissance, lorsque, étant donnés deux cercles concentriques et un grand poids appliqué à un arc quelconque du grand cercle, le rapport de la ligne issue du centre du grand cercle à la ligne issue du centre du petit est plus grand que le rapport du grand poids à la faible puissance qui le meut. La faible puissance l’emporte alors sur le grand poids. 8. Nous allons maintenant appliquer aux cinq machines simples la démonstration que nous venons de faire sur l’exemple du cercle ; après cette analyse, leur exposition aura acquis toute sa clarté. Les anciens la faisaient toujours précéder de ce lemme. Donnons d’abord la démonstration pour l’instrument appelé levier. Le levier meut les poids de deux façons: soit qu’on le place dans une position parallèle au sol, soit que, incliné, il s’élève au-dessus du sol On le met en action en appuyant et abaissant vers la terre l’extrémité qui se trouve élevée au-dessus d’elle
Supposons d’abord le levier parallèle au sol et représenté par la ligne αβ ; soit au point α le poids que le levier doit mouvoir : c’est le poids γ. La puissance motrice est appliquée au point β. La pierre placée sous le levier et sur laquelle il tourne est au point δ. La distance βδ est plus grande que δα. Lorsque nous levons l’extrémité β du levier et que nous portons vers le haut ce bras du levier à partir de la pierre sur laquelle il tourne, le poids qui est en γ se meut dans l’autre sens. Le point β décrit un cercle autour du centre d et le point décrit aussi, autour du même centre, un cercle plus petit que le cercle décrit par le point β. —Si le rapport de βδ à da était égal au rapport entre le poids γ et la puissance appliquée en β, le poids γ ferait équilibre à la puissance β. Si le rapport βδ à δα est plus grand que le rapport du poids à la puissance, il est clair que la puissance l’emporte sur le poids, parce que l’on a là deux cercles concentriques, que le poids est sur un arc du petit cercle, et la puissance motrice, sur un arc du grand. Il est donc évident que la même chose qui se passe pour deux cercles montés sur un même centre a lieu pour le levier. Et le levier qui meut les corps graves opère par la même cause qui agit dans les deux cercles. 9. Imaginons encore un levier représenté par la ligne αβ et mobile sur une pierre, qui est δ. L’un des bouts du levier, marqué α, est engagé sous un fardeau γ, tandis que l’autre bout, marqué β, est élevé au-dessus du sol. Si nous abaissons l’extrémité du levier β dans la direction du sol, nous mettons en mouvement le poids γ.
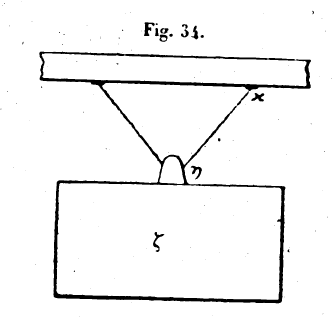
Je dis que le poids n’est pas mû dans ce ras de la même manière qu’il l’était dans le premier, parce que, dans l’opération présente, une partie seulement du poids est mue et une autre partie demeure fixée à terre. Imaginons un plan passant par le point ε, et perpendiculaire sur l’horizon, et soit εζθ la portion du poids qu’il sépare; εζη est une portion équivalente à celle-ci.[6] Si nous concevons que le poids total εηθ soit séparé du fardeau et laissé dans la position dans laquelle il se trouve, il ne penchera ni d’un côté ni de l’autre, ni du côté θ ni du côté η, à cause de l’égalité des poids εθζ et εηζ. Donc la portion εηθ du fardeau n’utilise aucune partie de la puissance ; et le levier meut seulement la section εηκλ du fardeau. Si le levier mouvait tout le poids εθχλ le rapport βδ/δα serait égal au rapport du poids εθκλ à la puissance appliquée en β ; mais il ne le meut pas tout entier, car une partie en est adhérente au plan supposé, et cette partie est la moitié du poids total ;[7] si en effet nous n’imaginions pas ce plan et que nous ajoutions à la puissance motrice une quantité correspondant à la portion du poids qu’il tient équilibre, l’extrémité du levier où agit la puissance serait vers le bas, et le bout a s’élèverait, parce que les puissances agissent sur les poids selon la loi de proportionnalité. Le plan supposé retient donc la moitie du poids; alors, si la puissance appliquée en β fait équilibre au poids, le rapport βδ/δα sera égal au rapport du poids εηκλ à la force b et la quantité de puissance nécessaire pour élever le poids à partir du sol sera moindre que précédemment.[8] Le poids sera dans une position d’équilibre, sans l’intervention d’aucune force, lorsque le plan passant par le point e et perpendiculaire à l’horizon le divisera en deux parties égales. Ce mode d’emploi du levier revient au cercle, mais il est différent du premier. La balance se ramène aussi au cercle, cela est évident puisque le cercle est une sorte de balance. 10. Le treuil n’est pas autre chose que deux cercles concentriques, l’un petit, c’est le cercle de l’arbre, l’autre grand, c’est le cercle du tambour. Il est juste de suspendre le poids à l’axe et la force motrice au tambour, parce que, de cette façon, une faible puissance l’emporte sur un grand poids. Ceux qui nous ont précédé l’ont dit déjà nous ne l’avons répété que pour que notre livre, soit complet, et pour que la composition en soit bien ordonnée. 11. Expliquons maintenant la cause de l’action dans la moufle. Soit un tambour monté autour du point a, et garni d’une corde dite syzyx;[9] βγ est cette corde. Tendons ses deux extrémités en leur attachant un poids d soulevé de terre. Il est évident que la tension des deux brins de corde sous, l’effort du poids est la même, et qu’elle équivaut, pour chacun d’eux, à la moitié du poids d. En effet, si la tension des deux brins n’était pas égale, celui dont la tension est la plus grande tirerait l’autre et l’élèverait.[10]
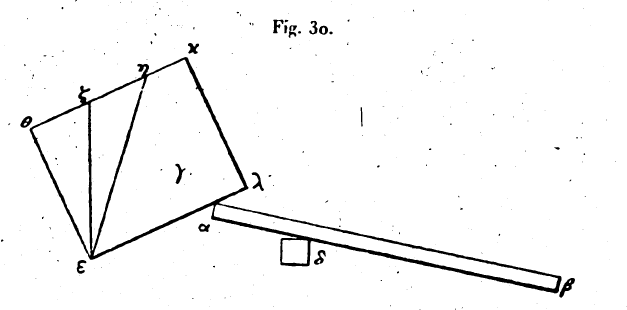
Mais nous ne voyons rien de cela; chacun des deux brins tendus de la corde est en repos. Si donc nous partageons le poids d en deux moitiés, c’est-à-dire en deux parties égales, il est évident que les deux brin tendus de la corde resteront en repos, puisque le poids qui les tend tous deux est le même, et précisément celui qui les tendait d’abord. La moitié du poids fait donc équilibre à un poids qui lui est égal. Les deux parties tendues de la corde sont encore égales, en un autre sens, à savoir que des poids égaux sont suspendus à des bras de levier égaux; la corde tendue, touche la circonférence du tambour en deux points opposés l’un à l’autre et dont les distances au centre sont égales; et les poids sont comme suspendus à ces deux points. De la sorte et dans ce système, un fardeau de grand poids n’est pas équilibré par une faible puissance. C’est pourquoi, parmi les instruments élévateurs composés de poulies, ceux-ci sont dits à traction simple, et l’organe que l’on appelle l’élévateur simple, c’est la corde partagée en deux brins tendus. 12. Parlons maintenant de l’appareil à traction double. C’est celui dans lequel la corde est partagée en trois brins. De même, chaque fois que se répètent l’aller et le retour de la corde, l’instrument est désigné d’après le nombre de ces répétitions diminué d’une unité, afin que son nom rappelle le nombre qui est inférieur à celui-là d’une unité. Imaginons donc que l’extrémité de la corde qui est en d passe dans une poulie, et qu’elle aille
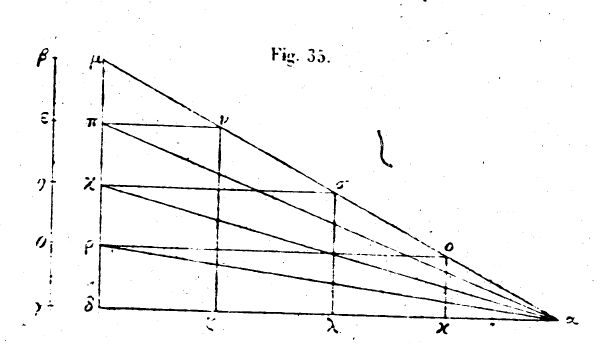
de là s’attacher à un support fixe, voisin de la poulie α au point η. La tension des brins de corde sera égale, pour la cause que nous avons dite; chacun des brins tend le tiers du poids. Si donc on divise le poids ζ en trois parties égales, en sorte que la somme des parties θ, β soit le double de la portion γ, le poids restera en repos et il ne penchera ni dans un sens ni dans l’autre, et le poids suspendu au brin γ fera équilibre au poids double suspendu aux autres brins. Si nous employons, au lieu du segment γ qui est le tiers du poids, une puissance équivalente pour tendre la corde, le poids du segment restant ne l’emportera pas sur elle, bien qu’elle soit moindre que lui. Les effets seront analogues si nous faisons entrer l’extrémité de la corde qui est en η, dans une poulie fixée au point η, et que nous la tirions jusqu’à ce qu’elle vienne s’attacher au poids ζ, au point κ. Chaque brin de corde supportera alors un quart du poids. Et si l’on partage encore le poids suivant cette nouvelle division, de façon que la somme des portions marquées θ, β, γ soit égale à trois fois la portion κ, celle-ci fera équilibre au reste du poids. Le rapport du nombre des brins de cordes tendus par chaque partie du poids à la corde qui le tire est égal au rapport du poids au contrepoids. Il faut donc, pour l’ensemble du fardeau, que le rapport du poids donné à la puissance qui le meut soit comme le rapport du nombre des cordes tendues par chaque segment du poids aux cordes tirées par la puissance motrice. Par exemple, si le poids est de 50 talents et la force motrice de 5 talents, il faudra que les brins tendus qui portent le poids soient dix fois plus nombreux que les brins tendus par la puissance de 5 talents. Ainsi les brins tendus qui portent le poids étant au nombre de dix, le brin auquel s’applique la puissance motrice sera unique. Mais les brins qui portent le poids étant vingt, ceux auxquels s’applique la puissance motrice seront au nombre de deux. A cette condition la puissance fait équilibre au poids. Si nous voulons que la puissance l’emporte sur le poids, ou nous renforcerons la puissance ou nous augmenterons le nombre des brins qui portent le poids. L’exposition de la machine élévatrice à poulies, appelée moufle, est achevée; nous voyons maintenant avec évidence que nous pouvons mouvoir un poids donné avec une puissance donnée. 13. On est conduit, selon la manière d’opérer, à appeler l’appareil où la corde pliée est tendue deux fois
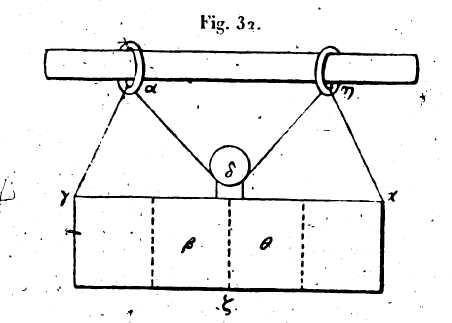
seulement, tantôt à traction simple tantôt à traction double, selon la puissance qui y est appliquée. Imaginons par exemple une poulie au point α, une corde passe sur elle, les deux brins tendus de cette corde viennent aux points β et γ, où ils sont attachés à un poids qui est le poids ε. Si nous partageons ce poids en deux, les deux parties qui seront de chaque côté se feront équilibre, et cette poulie sera dite à traction simple, parce que la puissance, dans ce cas, sera équilibré à un poids égal à elle-même. Imaginons au contraire un autre poids au point ζ, et fixons-y une poulie η ; faisons entrer dans cette poulie une corde, et attachons-en les deux extrémités à un support fixe, en sorte que le poids ζ demeure suspendu.
Chacun des deux brins de la corde sera tendu par la moitié du poids; et si on délie l’un des deux bouts de la corde, celui qui est attaché au point κ, et qu’on continue à maintenir la corde dans la même position, on aura à porter la moitié du poids. Le poids se trouve donc être double de la puissance qui le retient. Par là il est évident qu’il existe dans le support fixe, à une extrémité de la corde tendue, une puissance équivalente à celle qui est appliquée à l’autre extrémité et cette puissance retient aussi le poids. C’est pourquoi cette poulie a été justement appelée à traction double. Ainsi la corde, étant partagée en deux segments tendus, peut être appelée élévatrice simple ou élévatrice double. Il suit évidemment de là qu’il convient d’attacher l’extrémité de la corde à un support fixe et non au poids que l’on se propose d’élever, parce que la puissance inhérente à ce support s’ajoute à la puissance motrice et l’aide à mouvoir le poids. Il est donc clair que, lorsque l’extrémité de la corde unique est attachée au fardeau, le fardeau fait équilibre à une puissance qui lui et égale, au lieu que, l’autre extrémité étant attachée à un support fixe, la puissance fait équilibre à un poids double d’elle-même, et le poids est mû par une puissance moindre que celle qui le mouvait d’abord. 14. Le coin est mû par le coup dans un certain temps, car il n’y a pas de mouvement sans temps; et ce coup agit seulement par un contact qui ne se prolonge pas sur le coin, même pendant un temps très court. Il s’ensuit évidemment qu’après que le choc a cessé, le coin se meut encore; c’est ce que nous apprenons aussi, d’une autre manière, par les sons qui, après le coup, se font entendre pendant quelque temps dans le coin et par les mouvements qui accompagnent le mouvement de son angle. Donc la percussion agit même pendant le temps très court qu’elle persiste sur le coin. Cela est manifeste dans le cas où on lance une pierre ou une flèche, qu’on la lance à la main ou avec un instrument : en effet, après que la pierre a quitté la main, nous la voyons traverser avec force un grand espace, sans que la main la pousse: d’où l’on comprend que le coup ne persiste pas sur le coin pendant un temps appréciable, et que pourtant le coin après le coup, continue à se mouvoir. 15. Je dis que toute percussion même très faible peut mouvoir tout coin. Supposons un coin dont l’angle soit au point a, et dont le sommet soit la ligne δμ. Il est mis en mouvement par une percussion βγ, et soit ad la quantité dont il pénètre.
Il est possible disons-nous, qu’il soit mû par une très faible percussion. Ôtons de la percussion βγ une percussion représentée par βε, moindre que toute percussion donnée; je dis que la percussion βε, prise isolément, enfonce une certaine partie du coin. En effet, puisque la percussion βγ produit un enfoncement αδ, la percussion γε produit un enfoncement moindre que αδ soit αζ. Lorsqu’on ajoute de nouveau la percussion βε, tout l’enfoncement résulte du coup représenté par βγ; donc la percussion βε, considérée en elle-même, produit l’enfoncement δζ. Si nous imaginons la percussion βγ partagée en percussions égales à be, à savoir βε, εη, ηθ, θγ, l’enfoncement αδ se divisera aussi en segments égaux à δζ, qui seront ακ, κλ, λζ, ζδ, chacune des percussions βε, εη, ηθ, θγ produisant respectivement les enfoncements δζ, ζλ, λκ, κα. Menons des lignes parallèles à la ligne δμ qui représente la tête du coin; ce sont les lignes ζν, λσ, κο ; puis des lignes parallèles à la ligne ad et qui sont πν, χσ, ρο; les lignes δρ, ρχ, χπ, πμ sont égales. Si nous joignons les points π, χ, ρ au point α, nous formons quatre triangles dont les sommets sont au point a et dont les bases sont les lignes μπ, πχ, χρ, ρδ et chacun d’eux est enfoncé par une percussion égale à la percussion βε d’une longueur égale à la ligne αδ. C’est donc la même chose de dire que la percussion βε enfonce le coin tout entier de la longueur dc ou ak, ou de dire qu’elle enfonce le coin dont le sommet est δρ de la longueur αδ, parce que, dans le mouvement de tout le coin sous l’effet de cette percussion, la ligne κο se déplace de la longueur ακ, au lieu que, dans le mouvement du coin dont le sommet est δρ, cette ligne δρ, égale à κο, se déplace de la longueur ad. Donc δρ est enfoncé par la percussion βε de la longueur ad.[11] Il résulte évidemment que le rapporte la percussion βε à la percussion totale βγ est le même que le rapport de la portion de coin ayant dr pour sommet au coin entier. De même si l’on compare le temps dans lequel se meut le coin dont le sommet est δρ avec le temps dans lequel se fait l’enfoncement de tout le coin par la percussion βγ, le rapport de ces quantités équivaut encore à celui de la percussion βε à la percussion totale.[12] A un autre point de vue nous ne trouvons pas de différence entre le mouvement produit par la percussion βγ sur le sommet δμ, c’est-à-dire sur tout le coin, et le mouvement produit par chacune des percussions βε, εη, ηθ, θγ. sur chacun des coins dont les sommets sont μπ, πχ, χρ, ρδ parce que les percussions partielles égalent ensemble la percussion totale. Donc la percussion βε enfonce le coin dont le sommet est μπ de la même quantité que la percussion totale enfonce tout le coin, et que chacune des autres percussions enfonce chacun des autres coins. Si le corps chassé est l’un seulement des petits coins, il est enfoncé par une seule percussion de la quantité dont tout le coin enfoncé par l’effet d’une somme de percussions et son mouvement est proportionnel aux percussions, j’entends celles qui sont représentées par βε, εη, ηθ, θγ.[13] C’est pourquoi le rapport entre les temps est comme le rapport entre les percussions, ou comme le rapport entre le sommet du coin total et le sommet d’un des petits coins. Et plus l’angle du petit coin est aigu, plus la quantité de puissance nécessaire pour l’enfoncer est faible par rapport à celle qui fait pénétrer le coin total. 16. Il nous reste à expliquer la cause de l’action dans la vis. Commençons d’abord par exposer la construction des tours de la vis. Loue nous voulons tracer une vis, nous prenons un morceau de bois dur et fort, de telle longueur que nous voulons; la partie dont nous nous proposons de former la vis doit être polie, son épaisseur égale partout, et sa surface cylindrique. Nous partageons ce cylindre en segments égaux, de la hauteur d’un tour de vis. Puis nous nous donnons sur un plan deux lignes droites perpendiculaires entre elles, l’une égale à la circonférence du cylindre, l’autre à la hauteur du tour de vis; et nous joignons les deux extrémités de ces lignes par une droite soutendant l’angle droit. Nous faisons un triangle d’une feuille de laiton, pareil celui que nous venons de tracer et assez mince pour que nous puissions le courber comme nous voulons. Cela fait, posons l’arête égale à la hauteur du tour de vis sur le premier des segments égaux que nous avons délimités sur l’arête du cylindre, et enroulons le triangle de laiton mince sur la pièce de bois cylindrique. L’autre angle aigu du triangle viendra rejoindre l’angle droit de la figure de laiton, puisque la base du triangle est égale à la circonférence du cylindre. Nous collons alors les deux angles, et nous traçons le tour de vis le long du côté qui soutend l’angle droit. Puis, faisant glisser le triangle mince jusqu’au second segment, nous amenons son côté sur la seconde division de l’arête, et nous répétons la première opération pour tracer le second tour de vis qui doit continuer le premier. Nous faisons de même jusqu’à ce que nous ayons tracé l’hélice sur tous les segments de la pièce de bois cylindrique. Lorsque nous emploierons la vis, nous serons obligés de placer à l’entrée de la rainure hélicoïdale le doigt de bois appelé tylos; c’est lui qui transporte le poids; lorsqu’on tourne la vis, cet organe monte et le poids s’élève avec lui. 17. Il ne faut pas se représenter la vis autrement que comme un coin enroulé, le triangle dont l’hypoténuse décrit l’hélice de la vis est en effet une sorte de coin, qui a pour sommet l’arête égale à la hauteur du tour de vis, et pour angle l’angle aigu du triangle, celui auprès duquel on place la pièce appelée tylos. C’est ainsi que la vis se ramène à un coin tortu, enroulé, qui n’entre pas en action par l’effet d’une percussion, mais de sa rotation; on le fait tourner au lieu de le frapper; et le poids parait plus léger. Mais, en rendant le fardeau plus aisément transportable la vis agit au contraire du coin; car le coin agit dans l’intérieur du corps, et le fend, le corps restant dans le même lieu, tandis que la vis, qui est un coin tortu reste elle-même à sa place et tire le poids vers elle. Comme nous avons démontré, pour le coin, que celui dont l’angle est moindre meut le poids avec une puissance plus faible que celle qui est nécessaire à un coin d’angle plus ouvert, de même il importe de dire, à propos la vis, que celle où la distance entre les tours de vis est plus faible, meut le poids avec plus de facilité que celle où cette distance est plus grande; la réduction de cet intervalle correspond en effet à la réduction de l’angle. Donc la vis dans laquelle le pas de l’hélice est plus grand exige pour mouvoir le poids plus de puissance, et celle où ce pas est moindre exige une puissance moindre.
18. Lorsqu’un tambour à dents de bois engrène avec la rainure de la vis, la vis, à chaque tour qu’elle fait, meut une dent; c’est ce que nous allons démontrer de cette manière : imaginons une vis, soit αβ, sur laquelle est tracée une hélice dont les tours successifs sont désignés par α, δ, ζ. Supposons qu’un tambour muni de dents de bois soit monté près de la vis; ηγεθ est ce tambour, et ses dents ηγ, γε, εθ engrènent avec les tours de la vis. Supposons que la dent γε entre exactement dans l’un des tours de vis, et que les autres dents n’entrent pas dans les autres tours de vis; si nous tournons la vis en sorte que le point e soit chassé du côté γ, ε vient en γ, et après un tour de la vis, la dent γε vient à la place de la dent γη, et la dent εθ à la place de la dent γε. Ainsi, dans une rotation complète de la vis, l’intervalle d’une dent est déplacé tout entier. Il faut imaginer la même chose pour les autres dents. Autant donc il y a de dents sur le tambour, autant de rotations doit accomplir la vis, pour que le tambour en accomplisse une seule. 19. Quand la vis tourne, l’organe en bois appelé tylos se meut, d’après ce que nous avons dit plus haut, et soulève le poids en s’élevant. Il est nécessaire, lorsque la vis ne se meut pas, que ce doigt de bois soit maintenu en repos à sa place, quelque force qu’on lui applique, afin que, au moment ou l’on cesse de tourner, le poids ne vienne pas à l’emporter sur la vis; c’est-à-dire que ce doigt, ayant été introduit dans la rainure hélicoïdale et servant d’arrêt ne doit pas glisser hors de cette rainure, car, s’il glissait, tout le poids redescendrait au lieu d’où il a été hissé. Cet organe ne sort pas de la rainure hélicoïdale, lorsque son extrémité est bien ajustée à la rainure et qu’elle y entre comme dans une chaussure. Il faut pour cela que les tours de vis se rapprochent d’être parallèles à la base du cylindre sur lequel la vis est tracée. Quand les tours sont ainsi disposés, ils sont comme des chaussures enserrant l’organe en bois qui tire le poids. Si, au contraire, les tours de vis formés par la rainure hélicoïdale ont une inclinaison très forte, jusqu’à se rapprocher d’être parallèles à l’arête du cylindre, alors, lorsqu’un poids très lourd sera suspendu au doigt de bois, ou qu’une force considérable pèsera sur lui, cet organe réagira contre la rotation imprimée à la vis et il la fera tourner en sens contraire. Par là nous voyons que la vis peut mouvoir l’organe appelé tylos comme elle-même peut être mue par cet organe. Elle le meut lorsque la rainure hélicoïdale est voisine d’un cercle; dans ce cas, la rotation de la vis venant à cesser, le doigt de bois demeure en repos à la même place, maintenant le poids suspendu; au contraire, lorsque la rainure hélicoïdale a une inclinaison très forte, quand cesse la rotation de la vis, l’organe ne demeure pas en repos, mais c’est lui qui meut la vis. En effet si au bout perforé de la vis on fixe une corde, et qu’à l’extrémité de cette corde on attache un poids, la rainure hélicoïdale ayant une forte inclinaison, nous disons que, lorsque nous élevons l’organe appelé tylos, le poids s’élève aussi ; mais quand nous cessons d’élever l’organe, le poids s’arrête et reste suspendu car cet organe s’oppose au mouvement de la vis, quand la rainure est près d’être parallèle à l’arête du cylindre. S’il n’y avait pas sur le cylindre de rainure hélicoïdale, mais qu’on y creusât, suivant l’une de ses arêtes, une rainure à bords parallèles, le doigt de bois opposerait une résistance absolue à la rotation de la vis. Quand au contraire les tours de vis se rapprochent les uns des autres, et qu’on élève le doigt de bois, le fardeau ne redescend pas, à moins que cet organe ne soit tiré par une très grande force; ainsi, le poids étant suspendu au doigt de bois, lorsque les tours de vis sont rapprochés et que nous tournons la vis, le poids s’élève; quand nous cessons de tourner la vis, le poids demeure en repos et reste suspendu. Mais quand les tours de vis sont fortement inclinés, nous ne pouvons mouvoir le poids à moins de faire agir sur la vis une puissance considérable.[14] Nous en avons dit assez sur la nature de la vis et sur son usage. III. 20. Les cinq machines simples qui meuvent le poids se ramènent à des cercles montés sur un seul centre; c’est ce que nous avons démontré sur les diverses figures que nous avons précédemment décrites. Je remarque pourtant qu’elles se ré luisent encore plus directement à la balance qu’aux cercles; on a vu en effet que les principes de la démonstration des cercles ne nous sont, venus que de la balance; on démontre que le rapport du poids suspendu au petit bras de la balance, au poids suspendu au grand bras, est égal au rapport du grand bras au petit.[15] Ces cinq machines simples sont parfois toutes impuissantes à agir, quand on veut, par leur moyen, mouvoir des poids très grands avec des forces légères. Pour les trois premières, nous sommes amenés à en augmenter les dimensions à mesure qu’augmente le poids que nous voulons élever; je parle du treuil, du levier et de la moufle. Pour les deux autres, c’est-à-dire celles qui sont fondées sur le principe de la vis, nous sommes conduits à en diminuer les dimensions à mesure que ce poids augmente. Si par exemple nous voulons mouvoir un poids de 1.000 talents avec une puissance équivalente à 5 talents, et que nous nous servions, pour cette opération, du treuil, il faut que la ligne allant du centre du tambour à sa circonférence soit deux cents fois la ligne allant du centre de l’arbre à sa surface, et même un peu plus que cela. Si nous nous servons du levier, il faut que son grand bras auquel est appliquée la puissance motrice ait avec le petit bras,[16] qui porte le poids ce rapport, et même un rapport un peu supérieur. Mais le travail, avec ces instruments-là est difficile ou presque impossible. En effet, si nous donnons au diamètre de l’arbre une demi-coudée pour qu’il ait la force de supporter le fardeau, nous devons faire le diamètre du tambour de 100 coudées et un peu plus, et cette construction sera difficile. Il en est de même pour le levier et pour la moufle, parce que nous ne pouvons pas partager le levier dans un tel rapport, ni employer un nombre de poulies aussi considérable. Il faut donc user d’artifices pour faire évanouir les difficultés que nous opposent ces trois machines. 21. Nous disons que beaucoup de figures se ramènent au cercle, à savoir les sphères et les cylindres; leur mouvement est une rotation, comme on l’a démontré dans le livre précédent.[17] Nous nous proposons d’ abord de mouvoir un grand poids avec une faible puissance, au moyen du treuil et en levant l’obstacle indiqué. Supposons que le poids que nous voulons mouvoir soit de 1.000 talents, et la puissance motrice de 5 talents. Il faut d’abord amener la puissance à faire équilibre au poids. parce que, cet équilibre une fois réalisé, il nous sera possible d’obtenir que la puissance l’emporte sur le poids, en ajoutant un faible excès au rapport entre les organes de l’instrument. L’arbre autour duquel s’enroule la corde qui porte le poids est en a ; le tambour monté sur l’arbre est au point b. Pour faciliter la construction de l’instrument, faisons le diamètre du tambour égal seulement à cinq fois le diamètre de l’arbre. Il faut alors que la puissance appliquée au tambour, et qui doit faire équilibre à un poids de 1.000 talents, soit de 200 talents; mais la puissance qui nous est donnée n’est que de 200 talents. Il ne nous est donc pas possible de mouvoir, au moyen du tambour b et avec cette puissance, le poids donné. Faisons alors un arbre muni de dents, soit l’arbre γ, qui engrène avec les dents du tambour β, de la sorte, quand l’arbre γ est mis en mouvement, son mouvement se transmet au tambour et à l’arbre donné d’abord; donc quand l’arbre γ se meut, le poids donné est mû aussi. Or cet arbre γ est mû par la puissance qui meut le tambour β, car nous avons démontré que, lorsque deux cercles qui engrènent[18] sont sur des centres distincts, ils sont mus par une même puissance.[19] C’est pourquoi il n’y a pas de différence entre le mouvement du poids par le tambour β et son mouvement par l’arbre γ. Soit encore un tambour fixé sur ce arbre, le tambour δ, et faisons, par exemple, son diamètre égal à cinq fois le diamètre de l’arbre γ. Il faut que la force appliquée au tambour d, et qui doit faire équilibre au poids soit de 40
talents. Supposons qu’un autre arbre, l’arbre e, engrène avec ce tambour; la force motrice en ε sera aussi de 40 talents. Montons un tambour sur l’arbre ε, soit le tambour ζ, et faisons son diamètre égal à huit fois le diamètre de l’arbre ε, puisque la puissance de 40 talents vaut huit fois une puissance de 5 talents. La puissance appliquée au tambour et capable de faire équilibre au poids de 1.000 talents devra alors être de 5 talents. C’est celle qui est donnée. Pour que la puissance l’emporte sur le poids, nous devrons faire le tambour ζ un peu plus grand ou le pignon ε un peu plus petit. Et quand nous aurons fait ainsi, la puissance l’emportera sur le poids. Si nous voulons employer des pignons et des roues de grande dimension dans cette construction, il n’en est pas moins nécessaire d’obtenir le même rapport, parce que, quand nous voulons par la puissance faire équilibre au poids, il faut que l’ensemble des rapports produise l’équilibre; quand nous voulons ensuite que la puissance l’emporte sur le poids, il faut ajouter à ce rapport d’ensemble un excès, au-dessus de la valeur pour laquelle l’équilibre a lieu. Voilà donc la manière de mouvoir au moyen du treuil, le poids donné. Si l’on préfère ne pas se servir de roues dentées, des cordes s’enrouleront sur les tambours et sur les arbres. Nous sommes conduits à la construction que nous avons exposée, par la nécessité que le mouvement du tambour placé en dernier lieu se transmette au premier arbre qui tire le poids. Cette disposition des arbres et des tambours exige des supports fixes, percés de trous dans lesquels passent les extrémités des arbres; et quand on dresse ces supports, on doit les établir sur un sol stable et ferme. 22. Cet instrument et toutes les machines de grande force qui lui ressemblent sont lents, parce que, plus est faible la puissance comparée au poids très lourd qu’elle meut, plus est long le temps que demande le travail. Il y a un même rapport entre les puissances et les temps.[20] Par exemple, lorsqu’une puissance de 200 talents a été appliquée au tambour β, et quelle a mis le poids en mouvement, il faut un tour entier de β pour que le poids se meuve de la longueur de la circonférence de l’arbre α. Si le mouvement est donné à l’aide du tambour δ, il faut que l’arbre γ tourne cinq fois pour que l’arbre fasse un seul tour, puisque le diamètre du tambour est cinq fois celui de l’arbre γ et que cinq tours de γ valent un tour de β. Cette remarque se renouvelle pour la suite des organes du train, soit que nous fassions les arbres égaux entre eux ainsi que les tambours, soit que nous leur donnions des rapports variés, connue ceux que nous avons choisis. Le tambour δ fait mouvoir le tambour γ et les cinq tours que doit effectuer le tambour δ prennent cinq fois le temps d’un seul tour ; 200 talents, d’autre part, valent cinq fois 40 talents. Ainsi le rapport du poids à la force motrice est égal à l’inverse du rapport d’ensemble des arbres et des tambours, quelque nombreux qu’ils soient. Cela achève la démonstration. 23. Il nous faut maintenant mouvoir le poids avec la même puissance au moyen de l’instrument appelé moufle. Soit le poids au point α; marquons β le lieu à partir duquel nous le tirons, et γ ce qui fait face à β, c’est-à-dire, le support fixe vers lequel nous voulons hisser le fardeau. Donnons à l’appareil cinq poulies; et soit encore γ le point où se trouve la première poulie par laquelle le poids est tiré. Il faut que la force appliquée en γ et qui doit faire équilibre à 1.000 talents soit de 200 talents. Mais la force donnée n’est que de 5 talents. Faisons partir de la poulie γ une corde allant à un autre moufle placée en ε, et soit ζ le support fixe qui portent, par exemple, cinq poulies, dont la première tirée soit en η. La force appliquée en devra être une force de 40 talents. Nous conduirons encore la corde qui passe en η vers d’autres poulies placées en θ et correspondant à un support fixe κ; soit aussi κ le point d’application de la puissance. Comme 40 talents valent huit fois 5 talents, cette moufle devra avoir huit poulies. La puissance de appliquée en k et capable de faire équilibre à 1.000 talents sera alors de 5 talents; et pour amener cette puissance à l’emporter sur le poids, il suffira de donner à la moufle plus de huit poulies. La puissance sera alors plus forte que le poids.
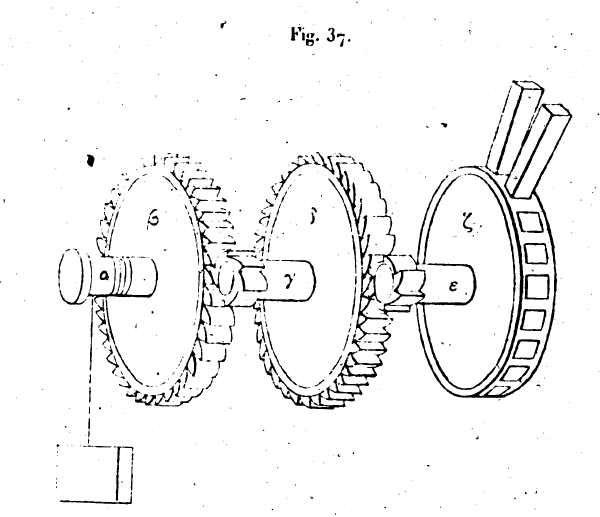
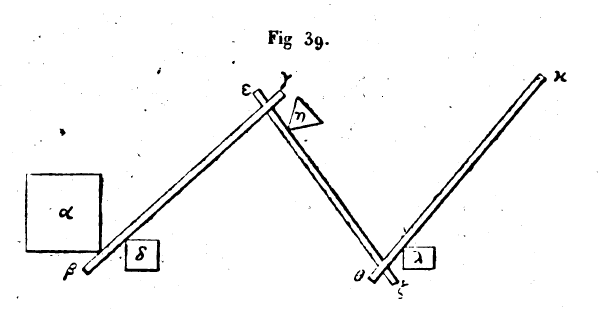
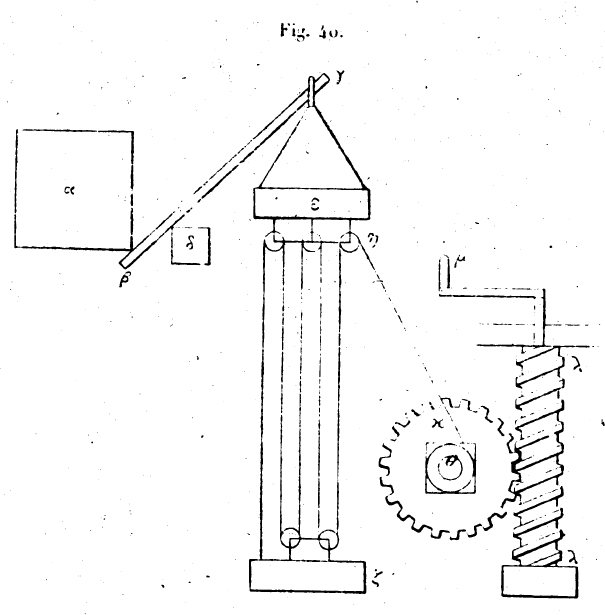
24. Le ralentissement de la vitesse a lieu aussi dans cette machine. Cela est évident. En effet, l’instrument présentant le rapport indiqué dans cet exemple, lorsque la puissance appliquée en γ et qui est de 200 talents, tire le poids de b en γ, elle doit faire glisser les cinq cordes tendues qui passent sur les cinq poulies, de la longueur qui sépare β de γ ; et à son tour la puissance appliquée en h doit faire glisser les cordes cinq fois. Si nous faisons égales les deux distances entre β et γ, entre ε et ζ, une seule des cordes qui occupent l’intervalle y passera pendant que passeront les cinq cordes qui occupent l’intervalle εζ, parce que pour que le poids parcoure la distance qui sépare β de γ, il faut faire glisser cinq cordes de la longueur de l’intervalle βγ. Donc le rapport entre les temps est égal à l’inverse[21] du rapport entre les puissances motrices. Pour limiter le nombre des cordes, il faut rendre la distance εζ égale à cinq fois la distance βγ, et la distance θκ égale à huit fois la distance εζ. De cette façon les mouvements des moufles combinées s’achèveront ensemble.[22] 25. Le poids peut être mû avec le levier de la manière suivante : soit le poids au point a et soit βγ le levier; la pierre placée sous le levier est au point δ. Nous voulons mouvoir le poids avec le levier en partant de sa position parallèle au sol. Soit gd égal à cinq fois δβ. La force appliquée en γ et capable de faire équilibre à 1.000 talents sera de 200 talents. Soit un autre levier εζ ; le sommet e de ce levier est articulé avec l’extrémité γ, de façon que le mouvement de ε se transmette à γ. La pierre servant d’appui au second levier est en η, et l’extrémité ε se meut vers δ. ζη est égal à cinq fois he ; la force appliquée en ζ sera donc de 40 talents. Prenons encore un autre levier θκ ; articulons le point θ sur le point ζ, et donnons-lui un mouvement de sens contraire à celui de ε. La pierre placée sous ce levier est au point λ. Soit κλ égal à huit fois λθ. La puissance appliquée sera donc de 5 talents et elle fera équilibre au poids. Si nous voulons que la puissance l’emporte sur
le poids, il nous suffira de faire κλ plus grand que huit fois λθ. Ou bien si λκ est égal à huit fois λθ, ζη à cinq fois ηε, et si γδ est plus grand que cinq fois δβ, la puissance l’emportera encore sur le poids. 26. Le ralentissement de la vitesse a encore lieu cette fois selon le même rapport. Il n’y a pas en effet de différence entre ces leviers, et les treuils; car ces leviers sont comme des cercles, mobiles autour des centres δ, η, λ qui sont les pierres sur lesquelles ils tournent; les cercles des arbres dans les treuils sont représentés ici par ceux que décrivent les points β, ε, θ et les tambours le sont par les cercles que décrivent les points γ, ζ, κ. Comme nous avons déjà démontré, au sujet des treuils, que le rapport entre les puissances est égal à l’inverse[23] du rapport des temps, la même démonstration s’applique dan le cas présent. 27. Pour le coin et pour la vis, nous ne pouvons pas parler de la même manière, parce que, comme nous l’avons démontré plus haut, ils ne présentent pas les mêmes difficultés; c’est ici le contraire qui arrive : l’effet de la puissance augmente quand les dimensions de deux instrument diminuent. Nous avons dû user, d’artifices à l’égard des appareils dont les dimensions augmentent avec le poids, afin de pouvoir toujours employer des instruments de petites dimensions pour la facilité du travail ; mais, quant à la vis et au coin, il n’est besoin d’aucun artifice pour les rapetisser en vue de rendre le travail plus facile. 28. Le ralentissement de la vitesse a lieu aussi dans ces deux instruments. Cela est évident. Il faut plus de temps pour frapper de nombreux coups que pour en frapper un seul, et pour tourner de nombreux tours de vis que pour en tourner un seul. Nous avons démontré que le rapport entre les angles du coin, est comme l’inverse du rapport entre les percussions motrices. Donc le rapport entre les temps est comme l’inverse[24] du rapport entre les puissances. 29. Dans ce qui précède, nous avons mû le poids donné à l’aide de plusieurs treuils, de plusieurs leviers composés de plusieurs poulies. Mais nous pouvons aussi mouvoir le poids donné par une combinaison de ces diverses machines, en les montant les unes à la suite des autres, excepté le coin, qui, seul, est mû par des percussions. Démontrons maintenant que les quatre machines simples, combinées entre elles, peuvent aussi mouvoir le poids donné. Soit le poids donné au point α; un levier se trouve en βγ ; le point β marque l’extrémité du levier engagée sous le poids; l’extrémité γ est relevée. La pierre sur laquelle se meut le levier est au point δ. Soit γδ égal à cinq fois δβ. La force appliquée en γ devra être de 200 talents pour faire équilibre au poids α. Lions à l’extrémité γ du levier une moufle que nous désignerons par ε ; l’autre partie de la, moufle parallèle à la première et établie sur un support fixe se trouve en ζ. La traction sur cette machine s’exerce au point η si nous donnons 3 poulies à cette moufle, la force de traction devra être de 40 talents. Établissons encore un treuil θκ, dont l’arbre est en θ et le tambour en κ. La corde qui glisse sur les poulies de la moufle vient s’enrouler autour de l’arbre du treuil et le tambour porte des dents perpendiculaires à son plan de rotation ; avec ces dents nous faisons engrener une vis λ munie d’une manivelle marquée m par laquelle on la tourne. Les dents du tambour entrent dans la rainure de la vis. Alors, quand nous tournons la vis, son mouvement de rotation se transmet au tambour κ ; il se transmet en même temps à l’arbre θ ; la corde de la moufle s’enroule sur cet arbre; l’extrémité γ du levier est abaissée et le poids s’élève. Soit le diamètre du tambour κ égal à quatre
fois le diamètre de l’arbre θ ; la puissance appliquée en κ sera de 20 talents. Enfin donnons à la manivelle μ une longueur double du diamètre du cylindre de la vis. La puissance appliquée en μ, qui fera équilibre à 1,000 talents, sera de 5 talents. Si donc nous augmentons d’un excès quelconque la longueur de ce bras de manivelle, la puissance, qui est de 5 talents, l’emportera sur le poids. Le treuil et la vis sont montés tous deux dans un châssis solide en forme de coffre ; les extrémités de l’arbre reposent dans les deux parois verticales de ce support, et l’extrémité inférieure de la vis tourne dans le bas du support fixe, tandis que son extrémité supérieure traverse le couvercle du coffre ; cette extrémité est équarrie et l’on y fixe un tambour dans lequel s’adapte le bras de bois. Ce châssis en forme de coffre doit être installé sur un sol stable, dur de bons fondements d’un solidité parfaite. Alors lorsqu’on tourne la manivelle, le poids s’élève 30. Pour le coin et la vis nous opérons comme il suit. L’angle du coin que nous voulons construire est l’angle αβγ, qui est aigu. Je dis que les coins dont l’angle est plus aigu meuvent le poids avec une percussion plus faible, c’est-à-dire avec une moindre puissance. Mais il arrive, s’ils atteignent une acuité excessive, qu’on ne peut plus les employer. Menons la ligne βδ perpendiculaire sur bg en vue de renforcer le coin, puis une ligne de parallèle à βγ, et du point e, élevons perpendiculairement la ligne εγ. Construisons un coin d’après le tracé ainsi déterminé; αβδε est ce coin. Nous l’introduisons un peu sous le fardeau par son arête bd, son sommet étant αε. Il est évident qu’en frappant le coin αβγ, nous enfonçons αβδε. Pour le prouver, prolongeons les
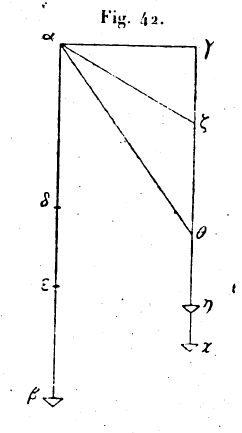
deux lignes αβ, δε, jusqu’à γ ; elles forment un angle égal à l’angle αβγ ; αζε est donc aussi un coin que la même puissance peut mouvoir. Imaginons que son extrémité comprise entre les points βζδ soit engagée sous le fardeau : ce coin se trouvera préparé. Telle est l’explication du coin. Il n’est pas d’ailleurs absolument nécessaire que nous donnions aux coins des angles aigus ; nus avons en effet démontré que toute percussions si faible soit-elle, est capable de mouvoir tout coin, quand elle est fréquemment répétée, et, que l’emploi des angles aigus revient à celui des faibles percussions. On n’est donc jamais obligé de faire usage, de coins à angles très aigus. 31. Il est possible d’appliquer à la vis la même construction. Il faut, pour cela, que nous menions dans l’angle de l’hélice figuré par αβγ, une perpendiculaire αγ sur βγ, égale à l’épaisseur du doigt de bois que nous nous proposons d’introduire dans la rainure hélicoïdale ; nous construirons ensuite un cylindre dont la circonférence aura la longueur de la ligne εζ ; nous tracerons l’hélice à l’aide de ces lignes avec un pas égal à αε ; enfin nous creuserons la rainure hélicoïdale en lui donnant la hauteur αγ. Cette construction nous permettra d’introduire le doigt de bois dans la rainure hélicoïdale. 32. Après avoir démontré, pour chacune de ces machines, que nous pouvons mouvoir un poids donné avec une force donnée, nous devons ajouter que, s’il était possible que tous les organes fussent parfaitement rabotés et lisses, taillés dans une matière homogène et avec des dimensions parfaitement exactes, il serait aussi possible d’employer ces machines aux travaux dont nous avons parlé, en conservant les rapports indiqués. Mais comme les hommes ne peuvent pas polir et égaliser une pièce avec une absolue perfection, on est forcé d’ajouter un de puissance destine à vaincre les frottements des organes; on produit excès en prenant des rapports un peu supérieurs à ceux que nous avons indiqués; on évite ainsi que ces imperfections ne fassent obstacle au mouvement et que l’expérience ne démente ce qui a été démontré. IV. — 33. Il faut nécessairement que ceux qui veulent avoir la connaissance de l’art mécanique sachent quelles causes agissent dans chaque mouvement : c’est ce que nous avons déjà exposé en traitant de l’élévation des corps lourds, par les méthodes des sciences physiques. Nous avons rendu compte de tout ce qui survient dans le fonctionnement des machines que nous avons citées; car il importe que rien ne soit présent sans preuve à ceux qui étudient, et que rien ne soit pour eux l’objet d’un doute : mais que, au contraire, tout problème qui se posera à eux doive trouve dans ce que nous disons sa solution exacte. Nous rappellerons donc divers principes déjà enseignés par les anciens et qui rentrent dans notre sujet. Tout d’abord nous posons que nulle proposition ne peut contredire une autre proposition antérieurement connue. Nos recherches partiront de ce est évident et de ce qui ne peut avoir que des causes évidentes. C’est pourquoi notre étonnement serait grand si nous voyions nos résultats contredire nos prémices et les résultats déjà acquis par nous. Il est manifeste celui qui veut avancer profondément dans la découverte des causes doit partir d’un ou de plusieurs principes physiques, et rapporter à ces principes toute question qui se présente à lui : les questions, en effet, sont complètement élucidées lorsque leur cause est mise au jour et quelle est justement l’une des vérités connues auparavant. Prenons pour principe que le léger est facilement mû et que le lourd l’est difficilement ; et qu’un même poids est mû plus aisément par une plus grande que par une moindre puissance, c’est en effet ce que nous voyons constamment : aussi ces deux propositions sont-elles évidentes. Il faut d’ailleurs savoir que tout ce que nous recherchons contient quelque chose d’obscur et de caché parce qu’on pose pas de problème où la cause soit claire et manifeste. On doit savoir aussi que le principe de toutes les questions qui se soulèvent en mécanique et de l’obscurité qui enveloppe la recherche des causes dans cette science, c’est que nous ne pouvons pas voir les corps graves partagés entre les forces qui les meuvent. Cette répartition devient pourtant sensible dans beaucoup de circonstances et en particulier lorsqu’on cherche à mouvoir ces corps; ainsi le corps qu’un homme seul ne meut pas ou ne meut qu’avec difficulté, est aisément mû par un groupe d’hommes. Si le poids de l’objet mû pesait tout entier sur chaque homme, il n’y aurait pas de différence à ce qu’il fût mû par un seul homme ou par un groupe. Mais nous voyons que le mouvement est plus aisé pour le groupe; donc puisque dans un groupe chacun supporte quelque chose de la totalité du fardeau et que le mouvement est rendu plus facile pour tous, il est évident que le poids se partage entre ceux qui le meuvent. 34. Question 1: Pourquoi le chariot à deux roues porte-t-il les fardeaux plus aisément que le chariot à quatre roues — Parce que, dans le chariot à deux roues le poids peut se partager en deux portions égales des deux côtés de l’axe, au lieu que, dans le chariot à quatre roues il ne le peut pas ; le poids ne se partage pas des deux côtés en deux parties égales ; il porte tout entier devant les deux roues de derrière et derrière les deux roues de devant ; mais cette inégalité dans la répartition du poids fait perdre à la roue sa vitesse ; car une roue ne tourne d’un mouvement rapide que parce que le poids se répartit également entre toutes ses portions. Question 2: Pourquoi les bêtes de somme ont-elles de la peine à tirer les chariots dans le sable —. Parce que plusieurs des rayons des roues sont enfoncés dans le sable et que, quand on tire les roues, le sable qui est devant elles les cale. Une autre difficulté vient de ce que les pieds des bêtes pénètrent dans le sable et qu’elles ont peine à les lever. En, terrain ferme, cela n’arrive pas. Question 3 : Pourquoi un même poids ajouté sur une balance en équilibre ne produit-il pas toujours la même inclinaison, et pourquoi produit-il une inclinaison plus grande quand la balance est moins chargée ? —Si, par exemple, il y a dans les deux plateaux 3 mines et que nous ajoutions dans l’un d’eux une demi-mine, ce plateau penche fortement. Si dans chaque plateau, il y a 10 mines, et que nous placions dans l’un d’eux une demi-mine en plus, l’inclinaison du fléau est dans ce cas très légère. — Parce que, dans ces divers cas le poids est mû par des puissances différentes; les 3 mines sont mues par un poids qui est leur égal, plus 1/6 de poids, tandis que les 10 mines sont mues par un poids égal à elles-mêmes, plus la moitié d’un dixième de ce poids; car la demi-mine est le 1/20 de 10 mines et le 1/6 de 3 ; or le poids que meut la plus grande puissance a un mouvement plus facile. Question 4 : Pourquoi les grands poids tombent-ils, à terre dans un temps moindre que les poids plus légers. — Parce que, de même que le mouvement de des corps est facile quand ils sont mus extérieurement par une puissance plus grande, de même, s’ils sont sollicités intérieurement par une plus grande puissance, ils se meuvent plus aisément. Or la puissance et l’attraction, dans les mouvements physiques, se communiquent en plus grande quantité aux poids lourds qu’aux poids légers. Question 5 : Pourquoi un même poids, lorsqu’il est plat, tombe-t-il terre plus lentement que lorsqu’il et sphérique ? — Ce n’est pas, comme plusieurs le pensent, parce que le corps étendu oppose par sa surface une grande résistance à l’air, au lieu que le corps sphérique, ayant toutes ses parties rentrées les unes dans les autres, n’oppose à l’air qu’une faible résistance; c’est parce que le poids qui tombe à plat est composé de parties nombreuses dont chacune reçoit de la puissance en proportion de son étendue ; donc, dans le mouvement de ce corps chacune de ses parties possède une part de la puissance qui le meut, correspondant à son propre poids, et la puissance n’agit pas sur lui d’une manière homogène. Question 6 : Pourquoi la flèche lancée du milieu de la corde parcourt-elle une longue distance ? — Parce que la tension est alors plus grande : d’où la force d’impulsion plus grande aussi. C’est pourquoi on fait les arcs en corne, pour qu’il soit possible de les ployer; quand ils sont fortement ployés, la corde portant la flèche est très tendue, et elle acquiert une puissance considérable qui jette la flèche à une grande distante. Au contraire, les arcs durs, dont les extrémités ne se prêtent pas à la flexion, envoient la flèche à une distance moindre. Question 7: Pourquoi rompt-on plus vite un bâton quand on l’appuie sur le genou en son milieu? — Parce que, lorsqu’on place le genou en deçà de la moitié, l’une des deux portions du bâton étant plus longue que l’autre, il constitue une sorte de fléau partagé en deux segments inégaux, et la main la plus éloignée du genou l’emporte sur la plus proche ; les mains ne peuvent résister l’une à l’autre que si elles se trouvent ensemble aux extrémités du bâton à des distances égales du point d’appui. Question 8 : Pourquoi un bâton est-il d’autant plus faible qu’il est plus long et d’autant plus flexible qu’il amincit davantage à l’une de ses extrémités — Parce que le bâton long subit l’action de forces multiples réparties entre ses différents segments, et dont la somme l’emporte sur la résistance de la partie fixe par laquelle il est soutenu. Il se produit ici la même chose que dans le cas d’un bâton court au bout duquel on suspend quelque chose qui tend à l’abaisser. L’accroissement de longueur du bâton joue le même rôle que ce poids qui appuie sur le bâton court. Le bâton long supporte de lui-même, du fait de sa longueur, la même action que le bâton court au bout duquel on pend un corps lourd. Question 9 : Pourquoi arrache-t-on les dents avec des pinces et non avec la main ?— Parce que nous pouvons pas saisir la dent avec la main tout entière, mais seulement avec deux doigts; et de même qu’il nous est plus difficile de soulever un poids avec deux doigts qu’avec toute la main, de même aussi il est plus difficile de saisir et d’extraire quelque chose avec deux doigts qu’avec toute la main; dans les deux cas, la puissance est la même ; mais la division des bras de la pince autour du clou qui les relie fait que la main peut vaincre la résistance de la dent, car la main, s’appuie sur le plus grand segment du levier que forment ces bras ; l’écartement des pinces facilite le mouvement de la dent; en effet, la racine de la dent est l’objet sur lequel s’exerce l’action du levier, et si l’écartement des pinces est plus grand que la racine de la dent sur laquelle le levier se meut d’une quantité suffisante, la main l’emporte sur la résistance de la racine. Il n’y a pas de différence entre mouvoir un poids et vaincre une force équivalente à ce poids ; quand nous contractons la main après l’avoir ouverte il en résulte un sentiment d’effort qui n’est pas dû au poids de la main mais à la force avec laquelle les muscles sont liés les une aux autres. Question 10 : Pourquoi, quand on fait tourner des fléaux de balance horizontaux, qu’ils, soient lourds on légers, se meuvent-ils plus vite que lorsqu’on les incline ? — Parce que lorsqu’on les fait tourner, leur poids étant égal de tous les côtés, ils se meuvent autour d’un centre qui est leur point de suspension. Au contraire, quand nous les inclinons, nous élevons un poids, parce que l’inclinaison de l’un des élève l’autre : il y a donc là un mouvement qui n’est pas naturel, je veux dire le mouvement ascendant du poids. Le mouvement naturel est aisé, c’est celui qui tire en bas le poids. Il est plus aisé d’abaisser un poids que de le tirer en haut. Question 11 : Pourquoi le mouvement des poids suspendus est-il facile ? — Parce que la force du poids est déjà presque toute occupée par la force qui le maintient suspendu, et comme il ne lui reste plus une grande puissance, il devient facile de le pousser. C’est ce qui arrive aussi dans la balance; son fléau étant suspendu quand nous le tirons, il se meut facilement. Question 12 : Pourquoi les grosses pierres qui sont sur le bord de la mer sont-elles pour la plupart rondes ? — Parce qu’elles avaient d’abord des angles aigus, et que le mouvement de la mer les ayant heurtées les unes contre les autres, leurs angles se sont brisés à cause de leur faiblesse. Question 13 : Pourquoi, lorsque nous voulons mouvoir un poids suspendu en écartant de lui la main et la plaçant sur le support fixe auquel il est suspendu ou près de ce support, trouvons-nous le mouvement difficile ? — En effet, si nous cherchons à mouvoir le poids à partir du point fixe auquel il est suspendu, nous trouvons que c’est difficile et même tout à fait impossible. Si la main s’éloigne du point fixe, elle meut le poids mais avec peine: le mouvement étant toujours près de s’arrêter complètement. Mais plus la main qui donne le mouvement s’écarte du point fixe, plus le mouvement devient facile. Supposons, par exemple, que le support. stable auquel le poids est suspendu soit a. La corde est la ligne αβ. Menons la ligne αγ perpendiculaire sur la ligne ab, et marquons sur la ligne αβ deux points quelconques que nous désignons par les lettres δ, ε. Tirons alors la corde à partir du point δ, et brisons-la en sorte qu’elle figure la ligne azh, le poids venant en h. Je dis que ν est plus levé que b. Pour le démontrer, prolongeons la ligne ηζ jusqu’en γ; puisque azh est plus grand que γζη, il est clair que le point η est plus haut que le point β. Supposons encore que la corde soit tendue à partir d’un point ε que l’on amène sur la ligne γη, le poids étant dans la même situation, c’est-à-dire se trouvant au bout de la longueur αβ. Comme αε est plus grand que αζ, ε viendra plus bas que α, en θ par exemple. Joignons αθ ; aq sera un segment de αθη. Je dis que le poids suspendu vient plus bas que ν. En effet
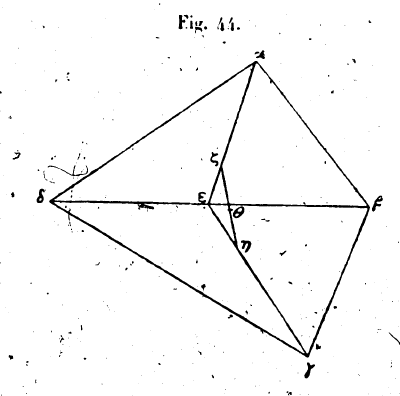
puisque la somme de αζ et de ζθ est plus grande que αθ et que la ligne ηθ est commune, αζ + ζη, c’est-à-dire ab, est plus grand que αθ + θη ; soit la somme αθ + θκ égale à αβ; le poids viendra en κ. Or κ est plus bas que η ; donc, quand nous tirons le poids à partir du point ε, il vient en κ, et quand nous le tirons à partir du point δ, il vient en η. Ainsi on élève davantage le poids en partant du point d qu’en partant du point ε; et pour porter le poids plus haut, il faut une plus grande force que pour le porter moins haut, parce que, pour le porter dans un lieu plus élevé, il faut un temps plus long. Question 14 : Pourquoi les radeaux formés d’un seul plancher vont-ils vite sur l’eau ? — Parce qu’ils n’appuient sur l’eau que par une très petit portion d’eux-mêmes; donc l’eau qui fait obstacle à leur mouvement est aussi en très petite quantité, et le vent vainc facilement la résistance que l’eau oppose à leur mouvement. Question 15 : Pourquoi le gouvernail qui est très petit peut-il guider de grandes barques ? — Parce que lorsqu’un homme étendu à terre est tiré par un autre dans quelque direction que ce soit, son corps se place dans cette direction; ainsi le gouvernail, prenant soit point d’appui sur l’eau, fait tourner toute la barque. Question 16 : Pourquoi les flèches se plantent-elles dans les cottes de maille et les cuirasses, et ne se plantent-elles pas dans de voiles flottantes ?— Parce que, quand l’objet qui porte le coup atteint un corps qui lui cède et ne lui fait pas obstacle à sa marche, il ne produit pas d’effet intense; sa vitesse et sa puissance, si grandes soient-elles, se dispersent au contact d’une substance qui s’écarte devant lui et qui ne lui résiste point. Au contraire, lorsqu’un corps dur en rencontre un autre dur comme lui et le heurte, celui-ci ne lui cède point, mais il lui résiste ; alors le corps choquant ne perd aucune portion de sa force, et le coup qu’il donne est très rude. C’est pour la même cause que ceux qui se jettent de très haut dans l’eau ne se font pas de mal. Question 17 : Pourquoi les liquides, naturellement pesants peuvent-ils être déplacés vite et avec facilité ? Nous voyons par exemple, un homme seul mouvoir en une fois 1.000 qist d’eau, — Parce que l’eau est composée de particules qui se séparent sans peine ; elle n’est pas, comme la pierre et le bois, compacte et difficile à diviser; au contraire, ses parties se séparent aisément ; c’est parce qu’elle n’a pas de consistance par elle-même, mais elle coule vers le bas; il en résulte que si nous en déplaçons une faible quantité, toute la masse s’écoule par l’endroit d’où cette portion est tombée. V. — 35. Nous devons encore démontrer des propositions qui sont utiles pour l’étude de la traction et de la pression exercées sur les corps et qui sont différentes de celles que nous avons rappelées dans le livre précédent. Ce sont d’autres résultats postérieurs à ceux-là; Archimède et d’autres auteurs les ont exposées déjà. Tout d’abord nous dirons comment on trouve le centre de gravité d’un triangle qui a partout même poids et même épaisseur. Soit le triangle αβγ le triangle donné. Divisons la ligne βγ par moitié au point δ, et joignons les points αδ. Si nous faisons tenir le triangle sur la ligne αδ, il ne penchera ni d’un côté, ni de l’autre parce que les deux triangles αβδ, αβγ sont égaux. Divisons aussi par moitié la ligne αγ au point ε et joignons les point βε. Si nous faisons tenir le triangle sur la ligne βε, il ne penchera non plus ni d’un côté ni de l’autre. Ainsi, le triangle étant posé sur chacune des lignes αδ, βε, ses parties se l’ont équilibre, et il n’incline ni d’un côté ni d l’autre. Le point où se coupent ces lignes n’est autre que le centre de gravité de ce triangle. C’est le point ζ. Il faut imaginer que le point ζ est au milieu de l’épaisseur du triangle. Il est évident que, si nous joignons les deux points ad et que nous divisions la ligne ad au point ζ en deux segments dont l’un αζ soit le
double de l’autre ζδ, le point ζ est le centre de gravité; en effet, si nous joignons les points δ, ε, les deux lignes αγ, βγ, ayant été divisées à ces deux points, la ligne αβ sera parallèle à la ligne de. On aura alors αγ/γε = αβ/δε. Or αγ est le double de γε ; donc la ligne ab est double de γε ; donc la ligne est double de de. On a aussi αβ/εδ = αζ/δζ ; donc αζ est le double de ζδ, tout cela à cause de l’égalité des angles des triangles αβζ, δζε. 36. Nous nous proposons de faire la même recherche pour le quadrilatère Soit αγγδ le quadrilatère donné. Joignons βδ et partageons le en deux moitiés au point ε ; puis tirons les lignes αε, εγ, et divisons-les aux points ζ et η de telle façon que αζ soit double de ζε et γη double de ηε. Le centre de gravité du triangle αβδ sera au point ζ et le centre de gravité du triangle bdg au point h. Nous ne trouvons pas de difficultés à nous représenter que tout le poids du triangle abd est concentré au point z que tout le poids du triangle βδγ l’est au point η. La ligne devient une sorte de fléau de balance, aux extrémités duquel sont appliqués ces deux poids; si nous divisons la ligne ζη au point θ de telle sorte θη soit à ζη comme le poids ζ, qui est celui du triangle αβδ, est au poids η, qui est celui du triangle βδγ, le point θ autour duquel ceS poids se trouveront en équilibre sera le centre de gravité de ce quadrilatère.
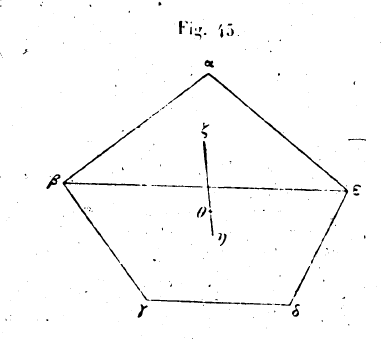
37. Nous nous proposons de faire la même opération pour le pentagone αβγδε. Joignons βε et construisons le centre de gravité un triangle αβε : il tombe au point ζ ; soit le centre de gravité du quadrilatère βγδε au point η. Joignons les points et partageons la ligne ζη en deux segments tels que ηθ soit à θζ comme le
poids du triangle αβε est au poids du quadrilatère δγδε : le point θ sera le centre de gravité de la figure αβγδε. On doit imaginer qu’on ferait de même pour tout polygone. 38. Nous nous proposons, étant donnés un triangle ayant partout même poids et même épaisseur et des supports dans des situations identiques sous les points α, β, γ, de démontrer comment on peut trouver la portion du poids du triangle αβγ qui pèse sur chaque support. Divisons la ligne βγ par moitiés au point δ et joignons les deux points α, δ puis partageons la ligne αδ en deux segments, au point ε, de telle sorte que le segment αε soit double de εδ ; le point ε sera le centre de gravité du triangle dont il faut que nous répartissions le poids total entre les supports. Si nous imaginons que la ligne αδ se tienne horizontalement en équilibre lorsqu’elle est suspendue au point ε, le poids appliqué en d sera double du poids appliqué en a, puisque la ligne αε est
double de εγ. Si, ensuite, nous imaginons que le poids appliqué en d soit réparti entre les deux points β, γ, la ligne βγ se tenant horizontalement en équilibre, en chacun des deux points y sera appliquée la moitié du poids qui est en δ, puisque les deux lignes βδ, δγ sont égales. Or, le poids qui est en δ est double de celui qui est en α.[25] Donc les poids appliqués aux points α, β, γ sont égaux, et les pieds supportent des poids égaux. 39. Soit encore un triangle αβγ, ayant partout même poids et même épaisseur, et reposant sur des supports placés dans des situations identiques. Un poids est posé ou suspendu en un point quelconque de ce triangle, et nous nous proposons de chercher quelle portion de ce poids ε supporte chacun des pieds. Joignons εα et prolongeons cette ligne jusqu’en δ ; partageons le poids appliqué en ε en deux parties telles que si l’on suspend le triangle sur la ligne αδ, il se tienne horizontalement en équilibre. Le poids appliqué en δ sera au poids appliqué en α comme la ligne αε est à εδ. Divisons alors le poids appliqué en δ en telle proportion que si l’on suspend à ce point la ligne βγ, elle reste horizontalement en équilibre. Le poids γ sera au poids β comme βδ est à δγ. Or le poids qui est en δ est connu; on connaîtra donc les deux poids qui s’appliquent en β et en γ : le poids qui porte sur α est d’ailleurs connu. Donc les poids qui pèsent sur les trois supports sont connus. 40. Nous nous proposons, étant donnés un triangle αβγ et des poids appliqués en ses sommets, de trouver dans l’intérieur du triangle point tel que, lorsqu’on suspend le triangle, il reste horizontalement en équilibre. Partageons la ligne αβ au point δ de telle sorte que βδ soit à da comme le poids appliqué en a est au poids appliqué en β. Le centre de gravité de l’ensemble des deux poids est au point δ. Menons la ligne δγ et partageons-la au point ε de façon que le rapport de γε à εδ soit égal celui du poids qui est en δ au poids qui est en γ. Le point ε sera le centre de gravité pour l’ensemble des poids et ce sera le point de suspension cherché.
41. Répétons cette démonstration sur un polygone. Soit le polygone αδγδε; suspendons aux points α, β, γ, δ, ε des poids connus. Partageons la ligne αβ au point ζ de façon que βζ soit à ζα comme le poids α est au poids β. Le point ζ est le centre de gravité des deux poids appliqués en α et en β. Partageons aussi la ligne δε au point η, de façon que δη soit ηε comme le poids e est au poids δ. Le point η est le centre de gravité pour l’ensemble des deux poids appliqués en ε et δ. Joignons alors ζη et divisons cette ligne au point q en telle proportion que la somme de α et de β soit à la somme de δ et de ε comme ηθ est à ηζ. Le point θ sera donc le centre de gravité pour l’ensemble des quatre points αβδε. Joignons enfin les points γθ et divisons la ligne γθ au point κ dans une proportion telle que γκ soit à κθ comme la somme des poids αβδε est au poids γ. Le point κ sera le centre de gravité pour l’ensemble de tous les poids.
FIN DU SECOND LIVRE.
[1] Grec περιτρόχιον. [2] Grec ὑπομόχλιον [3] Grec μάγγανον [4] Grec τύλος [5] Mot douteux. [6] Εζη est … à celle-ci. Nous ajoutons cette phrase. [7] La moitié … ; c’est un rapport pris pour l’exemple [8] Que précédemment. Nous ajoutons ces mots.
[9]
Nous transcrivons l’arabe [10] Le sens de cette phrase est douteux. [11] Le raisonnement et obscur dans la rédaction arabe. [12] La pensée est mal formulée dans le texte. [13] La rédaction arabe est ici défectueuse. [14] La rédaction laisse à désirer dans la dernière partie de ce paragraphe. Le manuscrit donne ici une figure qui reproduit à peu de différence près la figure du paragraphe 3 ou 5 de ce livre et que nous nous abstenons de répéter. [15] Ce préambule est évidemment hors de propos. [16] Nous ajoutons le second terme du rapport, omis dans le texte. [17] Comme dans le paragraphe précédent, ce début est certainement déplacé. [18] Cercles qui engrènent, conjecture, le texte est mangé en cet endroit. [19] Même. Le texte dit faible. [20] Le texte de ce paragraphe a souffert. Nous sommes forcé de traduire un peu librement. [21] L’inverse. Nous ajoutons ce mot. [22] La ligne du manuscrit occupe une demi-feuille; mais elle est presque insignifiante. Le nombre des poulies y est quelconque. [23] L’inverse. Nous ajoutons ce mot. [24] L’inverse. Nous ajoutons ce mot dans cette phrase et dans la précédente. [25] Double de celui qui est en α. Nous ajoutons ces mots. |






 par
le grec σύζυξ.
par
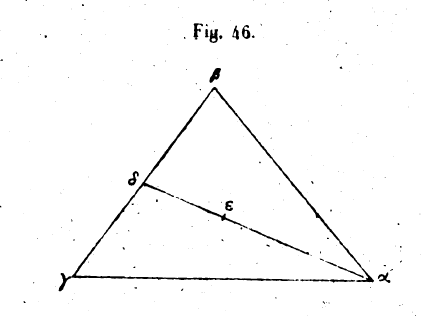
le grec σύζυξ.