|
ALLER A LA TABLE DES MATIÈRES DE HERON
HÉRON D’ALEXANDRIE
LES MÉCANIQUES. ou L’ÉLÉVATEUR DE HÉRON D’ALEXANDRIE,
PUBLIÉES POUR LA PREMIÈRE FOIS SUR LA VERSION ARABE DE QOSTÂ IBN LÛQÂ. ET TRADUITES EN FRANÇAIS par M. LE BARON CARRA DE VAUX LIVRE I INTRODUCTION LIVRE II LIVRE III
Oeuvre numérisée par Marc Szwajcer
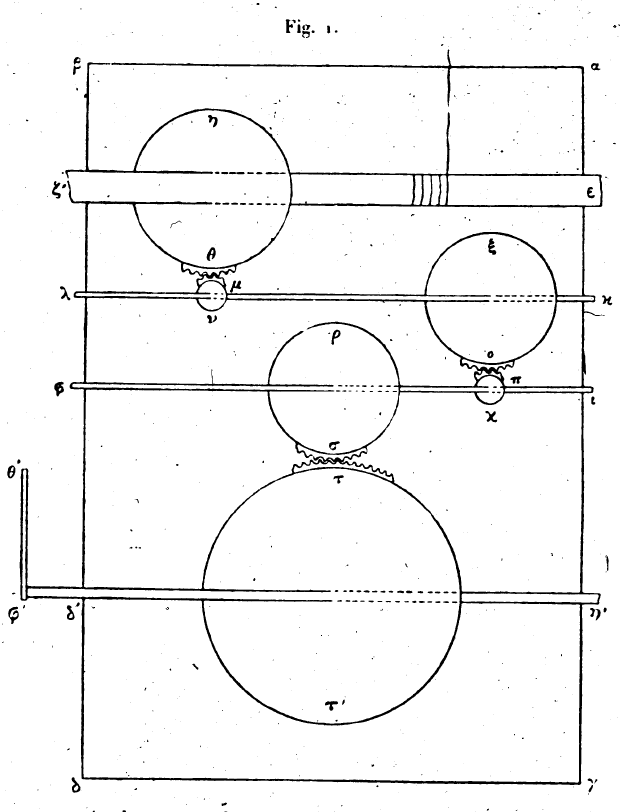
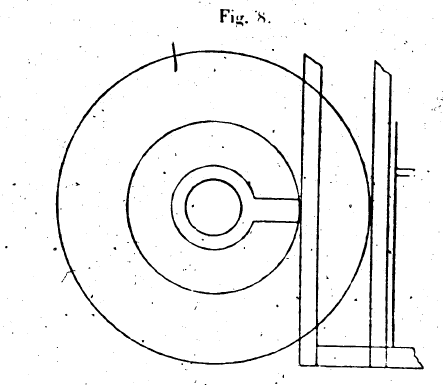
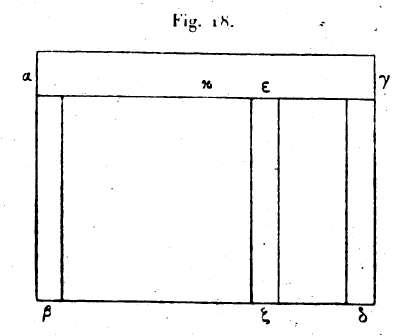
LES MÉCANIQUES ou L’ÉLÉVATEUR DE HÉRON D’ALEXANDRIE, LIVRE Ier.I. — 1. Nous nous proposons de mouvoir un poids donné avec une force donnée au moyen d’un train d’engrenages. Construisons un châssis solide, une sorte de coffre;[1] sur ses parois longues, parallèles entre elles, reposent des axes parallèles et ayant entre eux des distances telles que les roues dentées qu’ils portent engrènent l’une avec l’autre, comme nous le montrerons. Soit αβγδ ce châssis; plaçons-y un axe εζ dont le mouvement soit aisé et sur lequel est fixée un roue dentée, la roue ηθ. Prenons le diamètre de cette roue égal, par exemple, à cinq fois celui de l’axe εζ. Pour déterminer ce que nous nous proposons:, admettons que le poids que nous voulions mouvoir soit de 1.000 talents et la puissance, motrice de 5 talents; ainsi l’homme ou l’enfant qui tourne la manivelle est capable de mouvoir de lui-même, sans le secours d’une machine, un poids de 5 talents. Nous entrons la corde à laquelle est suspendu le poids par un trou ménagé dans la paroi ab,
puis nous enroulons autour de l’axe εζ. Si donc la roue ηθ tourne, la corde s’enroule et le poids est mû. Pour mouvoir la roue ηθ, il faut une puissance de 200 talents, puisque le diamètre de la roue est cinq fois le diamètre de l’axe, selon l’hypothèse. C’est ce qui a été démontré dans l’exposé des cinq machines simples.[2] Mais nous ne disposons pas d’une puissance de 200 talents, et la roue ne peut se mouvoir. Construisons alors un second axe parallèle à l’axe εζ, à savoir: l’axe κλ. Une roue dentée, la roue μν est fixe sur lui; la roue hq est aussi pourvue de dents qui engrènent avec celles de la roue μν. Sur l’axe κλ, fixons une autre roue ξο, d’un diamètre égal à cinq, fois celui de μν. Il faudra, pour élever le poids la roue ξο, 40 talents, le cinquième de 200 talents étant de 40 talents. Faisons encore engrener avec la roue ξο d’une autre roue πχ fixée sur un nouvel axe ιφ, et fixons aussi sur cet axe une seconde roue dont le diamètre soit cinq fois celui de la roue πχ. Soit ρσ cette nouvelle roue. La force qui, appliquée à la roue ρσ, mettra le poids en mouvement, sera de 8 talents; mais la puissante qui nous est donnée n’est que de 5 talents. Montons donc une autre roue dentée ττ ’ dont le diamètre soit double de celui de 1a roue rs. Une puissance de 4 talents devra être appliquée à la roue ττ ’. La force qui nous est donnée étant de 5 talents, il se trouvera une puissance de 1 talent en excès, qui servira à vaincre la résistance que peut présenter le train. Il résulte clairement de ce que nous avons décrit que lorsque le moteur meut la roue ττ ’, l’axe η ’ δ ’ tourne, et que la roue ρσ tourne en même temps qu’elle, elle fait tourner l’axe ιφ. Celui-ci entraîne la roue pc et le mouvement se transmet à la roue ξο ; cette roue fait tourner l’axe κλ qui entraîne la roue μν ; de là le mouvement se transmet encore à la roue ηυ, l’axe εζ tourne, les cordes s’enroulent sur lui et le poids s’élève. C’est ce que nous voulions démontrer. Glose : Il faut prolonger l’axe jusqu’en η ’ δ ’ et lui mener une perpendiculaire égale à la moitié du diamètre de la roue ττ' ou plus grande. Et Dieu est le plus savant ! II. — 2. Ici il y a une lacune dans le grec. Ceci été écrit dans l’hypothèse qu’il doit en être ainsi.[3] Les cercles fixés sur un même axe accomplissent toujours leur mouvement dans un seul sens, qui est celui dans lequel l’axe se meut. Mais les cercles montés sur deux axes et engrenant l’un avec l’autre au moyen de dents se meuvent dans deux sens opposés. L’un tourne à droite, l’autre à gauche. Si les deux cercles qui engrènent sont égaux, l’un accomplit sa rotation à droite dans le même temps que l’autre accomplit la sienne à gauche. Mais s’ils sont inégaux et que l’un d’eux soit plus grand que l’autre, le petit tourne plusieurs fois tandis que l’autre fait un seul tour; et le nombre des tours du petit dépend de sa grandeur. 3. Ce lemme étant posé, faisons tourner deux cercles que nous prenons d’abord égaux entre eux l’un ηεκδ, l’autre ζγθε, de centre a et β, et se touchant au point ε. Ils se meuvent à partir de ce point et dans le même temps, d’une quantité égale à une demi-circonférence. Pendant ce temps, le point ε décrit l’arc εηδ, et il vient en δ, après avoir subi le même déplacement que le point γ. Il y a des points qui se meuvent dans la même direction, d’autres se meuvent dans des directions opposées. Les points semblablement placés dans les deux cercles ont des mouvements de directions contraires; ceux qui sont symétriquement placés ont des mouvements de même direction. Il est d’ailleurs possible que des points qui sont dits se mouvoir dans des directions opposées meuvent dans le même sens; en effet,
supposons que ces points entrent en mouvement à partir d’un même point de départ ε, et imaginons les deux lignes ζαθ, ηβκ perpendiculaires sur la ligne γδ. Le mouvement sur l’arc εζ est opposé à celui qui a lieu sur l’arc εη, car celui-ci s’accomplit vers la droite et celui-là vers la gauche. Les mouvements peuvent aussi s’effectuer dans la même direction, lorsque nous considérons des points pris à des distances égales de ζ et de κ, ou bien encore si nous remarquons que les mouvements vers γδ sur les deux arcs ζγ, ηδ, sont égaux; il convient de faire la même remarque sur les deux arcs γδ, δκ et sur les deux arcs θε, κε. Nous disons encore que les mouvements peuvent avoir lieu dans la même direction que les deux points δ, δ, par exemple, se meuvent dans la même direction En effet le point e se meut sur l’arc εζγ, et le point d sur l’arc γκε; ils se rapprochent ou s’éloignent respectivement des points ζ et κ de quantités égales. Or ce mouvement s’appelle mouvement en sens opposés. C’est pourquoi l’opposition ou l’identité des sens des mouvements sont relatifs; il faut donc distinguer dans chaque mouvement les mouvements, qui s’effectuent dans un même sens et ceux qui s’effectuent en sens opposés.[4] Voilà ce qu’il convient de considérer dans le cas où les cercles sont égaux. Ce qui suit concerne les cercles inégaux. 4. Supposons les deux cercles inégaux. Ils ont leurs centres aux points α et β ; le plus grand est celui qui a son centre en α. Les rapports ne se présentent plus ici sous une forme parfaite comme dans le cas de cercles égaux. Soient deux points qui tournent à partir du point ε, et, pour rendre un exemple faisons le diamètre γε double du diamètre εδ. L’axe εζγ sera alors double de l’arc εηδ comme l’a démontré Archimède; donc, dans le temps que met le point ε à parcourir l’arc εζ, en se mouvant dans la direction de γ, ce même point ε se mouvant en sens inverse parcourt l’arc εηδ ; dans le temps aussi que ce point partant de ζ met à décrire l’arc ζγ, un point partant de δ décrit l’arc δκε et parvient au point ε. Donc le point qui décrit la circonférence εηδκε suit tantôt une direction opposée à celle du point qui décrit l’arc εζγ et tantôt une direction de même sens. De même, pendant le temps que le point γ parcourt l’arc γθε, le point ε parcourt le cercle εηδκε, tantôt allant dans la direction de γ et tantôt dans la direction contraire. Si l’arc d’un des cercles valait trois fois l’arc homologue, ou s’il était avec lui dans un autre rapport quelconque, nous démontrerions encore que les points mobiles vont tantôt dans une même direction, tantôt dans des directions opposées; — et Dieu est notre aide ...
5. Si nous imaginons qu’on place un cercle touchant au point κ celui dont le centre est en β, nous démontrerons de ce troisième cercle tout ce que nous avons dit du premier. En effet, si le premier cercle se meut d’un mouvement contraire à celui du second, et le second d’un mouvement contraire à celui du premier, le mouvement du premier sera semblable à celui du troisième. Si une chose se meut du même mouvement qu’une autre et que celle-ci se meuve d’un mouvement contraire à une troisième chose, la première se mouvra d’un mouvement contraire celui de la troisième. Y a-t-il encore un quatrième cercle, il sera l’objet de la même démonstration. En résumé, ce qui se produit dans le cas de trois cercles se répète dans tout système de cercles en nombre impair, et ce qui se produit dans le cas de deux cercles se répète dans tout système où les cercles sont associés deux à deux. Vous voyez aussi que l’identité ou l’opposition des directions des mouvements n’ont pas lieu seulement dans le cas de deux cercles ou d’un plus grand nombre de cercles, mais aussi dans le cas d’un cercle unique; car un point unique se meut successivement dans une direction et dans la direction opposé. Ce point mobile étant parti d’un point quelconque, se meut dans une même direction jusqu’à ce qu’il ait décrit l’arc du demi-cercle et, quand il décrit l’arc du second demi-cercle, il se meut dans une direction opposée à la première. 6. Les grands cercles, d’autre part, n’ont pas toujours un mouvement plus rapide que les petits cercles; il arrive aussi que les petits cercles se meuvent plus vite que les grands. Quand les deux cercles sont fixés sur un même centre, les grands cercles meuvent plus vite que les petits. Si les cercles sont écartés l’un de l’autre, tout en faisant partie d’un même appareil, c’est-à-dire s’ils ne sont pas fixés sur un même axe, connue cela a lieu dans les chariots qui ont de grandes roues, les petits cercles se meuvent plus vite que les grands, parce que leur déplacement est le même et que dans le même temps tous deux sont entraînés également. Il faut donc que le petit cercle fasse plusieurs tours tandis que le grand n’en fait qu’un: c’est pourquoi le mouvement du petit est plus rapide. 7. Il se peut aussi que les mouvements du grand et du petit cercle aient la même vitesse, même si les cercles sont fixés sur un même centre autour duquel ils se meuvent. Imaginons donc deux cercles fixés sur un même centre, le centre a. Menons une ligne quelconque β β ’ tangente au grand cercle. Joignons les deux points αβ ; la ligne ab sera perpendiculaire sur la ligne β β ’; la ligne β β ’ est parallèle la ligne γ γ ’ et celle-ci touche le petit cercle. Menons encore du point a une ligne parallèle à ces deux là, soit α α ’. Si nous imaginons que le grand cercle roule sur la ligne le petit cercle roulera en glissant sur la ligne γγ ’ ; et si le grand cercle décrit un tour, il est clair que le petit décrira un tour aussi; la position de ces cercles sera alors celle des cercles dont le centre est en α ’, et la position de la ligne αβ celle qu’occupe la ligne
α ’β ’. Ainsi la ligne sera égale à la ligne γγ ’, et cette ligne β β ’ est celle que le grand cercle enveloppe lorsqu’il accomplit un tour, de même que la ligne γγ est celle sur laquelle tourne le petit cercle lorsqu’il accomplit un tour. Donc le mouvement du petit cercle a la même vitesse que celui du grand, puisque la ligne β β ’ est égale à la ligne γγ ’, et que, lorsque des choses se déplacent dans des temps égaux de quantités égales, leurs mouvements sont égaux en vitesse. On pensera peut-être que cette conclusion est absurde parce que la circonférence du grand cercle ne peut pas être égale à celle du petit. Aussi disons-nous que le petit cercle ne tourne pas seulement sur la ligne γγ ’, mais qu’il est en même temps entraîné dans le parcours du grand cercle; et c’est par l’effet de deux mouvements que le petit cercle arrive à se mouvoir avec la même rapidité que le grand. Si, en effet, nous supposions que le grand cercle fût animé d’une rotation et que le petit ne tournât pas, mais qu’il fût fixé au point γ, il n’en parcourrait pas moins la ligne γγ ’ dans le même temps que le centre parcourrait la ligne αα ’ égale aux lignes β β ’ et γγ ’. Il n’est donc pas nécessaire dans ce mouvement que la circonférence du petit cercle accomplisse une rotation, puisque nous voyons le centre, qui ne peut absolument pas tourner, parcourir la distance indiquée par l’effet du mouvement qui entraîne le grand cercle. 8. Un même point animé de deux mouvements d’égale vitesse peut décrire des lignes d’inégale longueur. C’est ce que nous allons démontrer ... Supposons une figure plane, quadrangulaire, aux côtés parallèles et aux angles droits; et soit αβγδ cette ligure; αδ est sa diagonale. Le point a parcourt d’un mouvement régulier la ligne αβ, et la ligne αβ elle-même se transporte d’un mouvement régulier sur les lignes ag, bd, de façon qu’elle reste constamment parallèle à la ligne γδ. Enfin le temps dans lequel le point α vient en α est égal à celui que met la ligne αβ pour venir en γδ. Je dis que; dans le même temps, le point α décrit deux lignes d’inégale longueur. En effet, quand la ligne αβ s’est mue pendant un temps donné; et quelle a pris une position telle que εζ, le point qui s’est mû sur la ligne αβ se trouve, en cet instant sur εζ et le rapport de αγ à αβ, c’est-à-dire à δγ est égal au rapport de la longueur αε à la longueur de la ligne sur laquelle se meut le point comptée depuis e jusqu’au point. Or le rapport αγ / γδ est égal au rapport αε / εη. Donc le point qui se meut sur la ligne αβ est venu en η sur la ligne αδ qui est la diagonale. Ce raisonnement pourrait être répété; il prouve que le point qui parcoure la ligne αβ reste toujours sur la ligne αδ et tandis qu’il la parcourt, il se meut sur chacune des deux lignes αδ et αβ qui sont d’inégale longueur Donc ce point qui se meut d’un mouvement régulier décrit deux lignes inégales. Cependant, comme nous l’avons dit, le mouvement du point sur la ligne αβ est simple, au lieu que son mouvement le long de la diagonale αδ est composé du mouvement de αβ sur les droites αγ, βδ et du mouvement de α sur la droite αβ. Ainsi le point a décrit dans le même temps et d’un mouvement régulier deux lignes inégales; c’est ce que nous voulions démontrer.
III. 1. Parlons maintenant de la machine dont nous augmentons ou dont nous diminuons les figures planes et solides dans un rapport donné afin que nous puissions grandir les figures solides et planes. Par exemple; le trait de la baliste [?], selon un certain rapport. Occupons-nous d’abord des figures planes. Donnons-nous une ligne quelconque de genre connu, nous nous proposons de trouver une autre ligne telle que les deux figures tracées sur les deux lignes semblables soient entre elles dans un rapport égal au rapport donné. Soit donc connu le rapport qui existe entre la ligne donnée et une autre, et supposons qu’entre les deux lignes dont on connaît le rapport, une troisième soit moyenne proportionnelle. Elle sera la ligne cherchée, car lorsque trois lignes forment entre elles une proportion, le rapport de la première à la troisième est égal au rapport de la figure construite sur la première à la figure construite semblablement sur la seconde. 10. Proposons-nous de plus de trouver une autre ligne telle que les figures solides provenant de deux lignes, et tracées semblablement, soient l’une avec l’autre dans un rapport donné. Soit une ligne quelconque ayant avec une autre un rapport donné, et supposons qu’entre ces deux lignes, il y en ait deux autres qui leur soient moyennes proportionnelles. Si cela est, nous avons atteint notre but, car, lorsque quatre lignes s’ordonnent en trois rapports égaux, le rapport de la première à la quatrième est égal au rapport de la figure solide construite sur la première à la figure solide construit semblablement sur la seconde. 11. Comment donc trouverons-nous deux moyennes proportionnelles consécutives entre deux lignes données ? Nous ferons cette démonstration par une méthode qui ne nécessitera pas la considération des solides, et qui nous conduira à la manière d’opérer la plus aisée. Soient αβ, βγ les deux lignes données; l’une est perpendiculaire sur l’autre; ce sont les deux lignes entre lesquelles nous voulons trouver deux moyennes proportionnelles. Achevons le rectangle αβγδ, en menant les deux droites δγ, δα ; joignons βγ, γα ; puis faisons passer par le point β une règle qui coupe les deux droites de, dz, et que nous amènerons par la rotation dans la position où les droites issues du point h et aboutissant aux points d’intersection de la règle avec les lignes γε, αζ sont égales. Soit εβζ cette position, les deux lignes εη, ηζ étant égales. Je dis que les deux droites αζ, γε sont moyennes proportionnelles entre les deux droites αβ, βγ ; αβ sera le premier terme des rapports, αζ le second, γε le troisième et γβ le quatrième. En effet le quadrilatère αβγδ a les côtés parallèles et les angles droits.
Donc les quatre lignes δη, ηα, ηβ, ηγ sont égales. La ligne ηδ étant égale à la ligne ηα et la ligne ηζ étant déjà menée, nous avons : δζ x ζα + αη 2 = ηζ2 et de même δε x εγ + γη2 = ηε2. Or les deux lignes εη, ηζ sont égales ; il en résulte δζ x ζα + αη2 = δε x εγ + γη2. Mais γη2 = αη2; il reste δε x εγ = δζ x ζα ou bien εδ/δζ = ζα/γε on a d’ailleurs : εδ/δζ = αβ/αζ = εγ/γβ. Donc les rapports αζ/γε et γε/βγ sont égaux au rapport αβ/αζ. Ainsi nous avons construit deux moyennes proportionnelles consécutives entre αβ et βγ, à savoir les deux lignes αζ et γε. C’est ce que nous voulions démontrer. 12. Nous savons déjà comment nous pouvons grandir ou diminuer dans un rapport donné les figures régulières, planes ou solides. Il est nécessaire maintenant de trouver un instrument qui nous permette de résoudre le même problème dans le cas des figures irrégulières à deux ou à trois dimensions. Donnons d’abord des notions propres à faciliter notre démonstration, nous la ferons après. On dit que des figures, planes ou solides, régulières ou non, sont semblables et semblablement placées, lorsque dans l’une d’elles on peut tracer une figure rectiligne semblable à celle que l’on trace dans les autres et semblablement placée. Et l’on dit que des figures sont semblables entre elles, lorsque dans l’une d’elles on peut tracer des figures rectilignes, telles qu’il soit possible de décrire, dans les autres, des figures semblables à celles-là. 13. Lorsqu’une ligne se meut autour d’un point quelconque, et que sur cette ligne on donne deux points qui la partagent, à partir du point fixe, selon un rapport donné, ces points, en se mouvant sur cette ligne décrivent des figures semblables. Si elle est mobile dans un plan, les figures décrites sont planes. Si elle est mobile, non dans un plan, mais dans l’espace, les figures décrites sont solides. Ainsi nous concevons que les points, par leur rapprochement mutuel décrivent les surfaces des figures; rien n’empêche en effet d’imaginer cette hypothèse dans l’ordre des représentations sensibles, et elle est plus juste et plus parfaite dans le sens abstrait. A ce point de ne, des figures sont dites semblables, lorsque l’une est décrite dans l’autre et que l’on donne un point tel que les lignes issues de ce point vers les limites linéaires ou superficielles des figures soient coupées par ces limites dans un rapport constant. 14. Après ce préliminaires, démontrons que nous pouvons trouver une figure semblable à toute figure donnée et étant avec elle dans un rapport donné. Nous commencerons notre démonstration par les figures planes. Supposons donc une ligne quelconque, la ligne αβ fixée au point α et mobile dans un plan. Sur elles sont les deux points β et ν, qui parcourent les lignes des figures. Le point β décrit dans le plan une ligne βγδεζ, et le point α, décrit la ligne ηθκλμ. Nous disons que les deux figures βγδεζ et ηθκλμ. sont semblables. En effet, traçons sur βγδεζ une figure rectiligne, c’est le polygone ainsi désigné, et traçons aussi la figure ηθκλμ. Joignons le point a aux points βγδεζ nous obtenons les lignes déjà menées. Joignons aussi ηθκλμ. Puisque les droites αβ, αγ, αδ, αε, ατ sont divisées proportionnellement au points η, θ, κ, λ, μ, selon l’hypothèse, la figure rectiligne βγδεζ est semblable à la figure rectiligne ηθκλμ.
Nous démontrerions de même qu’il est possible de tracer dans la figure ηθκλμ une figure rectiligne semblable à toute figure rectiligne tracée dans la figure βγδεζ donc les figures que décrivent les points sont semblables. 15. Exposons maintenant comment nous traçons, au moyen d’un instrument, une figure semblable à une figure plane donnée, selon un rapport donné. Établissons deux safihas[5] fixées sur un centre commun, dentées, bien assujetties autour d’un même axe, mobiles dans le plan où se trouve la figure à laquelle nous voulons construire une figure semblable. Que les safihas aient entre elles un rapport égal au rapport donné. Contre chacune des safihas se trouve une règle dentée, dont les dents sont placées de façon à engrener avec celles de la safiha.
Ces deux règles sont guidées dans la rainure d’une autre règle, mobile autour de l’axe des safihas, par le moyen d’un manchon. A l’extrémité des deux règles[6] dentées sont des sortes de mires[7] qui se meuvent le long des figures semblables; ces mires doivent glisser sur une ligne droite passant par le centre des safihas, et se mouvoir toujours sur un même rayon autour de ce centre. Nous visons du même coup les trois mires; elles se trouvent ainsi toujours sur une même ligne droite. Il faut placer les mires sur les deux règles dentées à la même distance des règles que la mire centrale des deux safihas, puis on en recourbe l’extrémité de façon qu’elle atteigne le plan dans lequel nous voulons tracer les figures semblables. Si donc on amène l’une des mires sur la ligne qui limite la figure donnée, l’autre mire en sera éloignée d’une distance telle que les distances des deux mires au centre des safihas seront entre elles dans le rapport des diamètres des safihas.[8] La règle qui sert de guide doit être placée un peu de côté pour que la mire qui se déplace sur la ligne donnée puisse parcourir cette ligne. Alors l’autre centre décrit la figure semblable à la première figure; et il la décrit dans le rapport donné parce que les safihas dentées ont entre elles ce rapport. 16. Cette figure semblable à la figure donnée et ayant avec elle un rapport donné, nous l’avons construite dans le lieu où se trouvait la figure donnée, et c’est en ce lieu que nous nous sommes proposé de tracer la figure semblable. Si maintenant nous voulons la construire, non en ce lieu, mais dans un autre, quel qu’il soit, nous agirons de la façon suivante. Soit αβγδεζ la figure semblable à la figure donnée, et supposons que nous
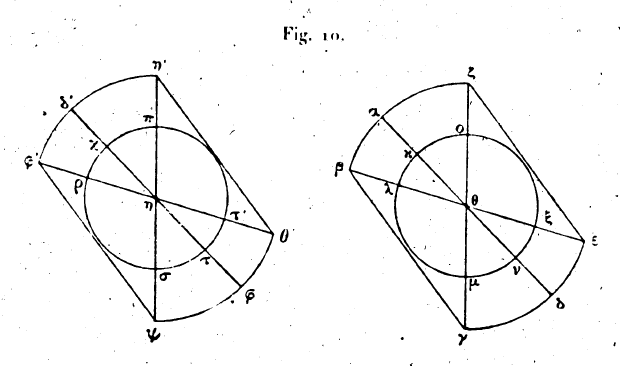
voulions la transporter aux environs du point η. Prenons dans l’intérieur de la figure αβγδεζ un point quelconque, le point θ ; décrivons autour des deux points η, θ comme centres, deux cercles égaux dans le plan; divisons-les en segments égaux deux à deux, aux points κ, λ, μ, ν, ξ, ο ; χ, ρ, σ, τ, τ ’, π. Joignons les premiers au centre θ, et prolongeons ces rayons jusqu’à leur intersection avec la figure. Puis, du point η comptons des longueurs égales à celles de la figure αβγδεζ. Soit !a ligne ακ égale à la ligne χδ', soit λβ égal à ρφ'’, μγ égal à σψ, νδ à τφ, ξε à τ ’θ ’ et οζ à πη ’. Faisons alors passer une courbe par les points η ’ δ ’ φ ’ ψ φ θ ’ et les points trouvés de la même manière. Si les cercles égaux de centres θ et η ont été divisés en un plus grand nombre de secteurs, les points déterminés sont plus voisins les uns des autres et la courbe tracée est plus exacte et plus parfaite. Décrivons donc la courbe η ’ δ ’ φ ’ ψ φ θ ’; elle est égale à la ligne αβγδεζ, et semblablement placée, parce que les figures planes sont égales et semblablement placées lorsqu’elles peuvent être superposées l’une à l’autre. 17. Dans le cas des figures solides, régulières ou non , on doit encore imaginer ce déplacement effectué par un procédé analogue, c’est-à-dire que l’on prendra une sphère tenant lieu de cercle ou construite sur lui , ou toute autre figure; on en prendra une seconde égale et semblablement placée, et l’on marquera sur elles des points homologues ; ceux-ci seront joints à d’autres points situés dans 1e milieu de ces figures; on prolongera ces rayons, et les lignes ainsi menées détermineront une figure solide égale à la figure construite en premier lieu et semblablement placée. 18. Pour construire des figures solides semblables, nous procédons de cette manière: prenons deux tablettes de bois dur, planes et mobiles autour de leur ligne d’intersection, et ayons soin que celle-ci ne se déplace pas dans le mouvement des tablettes; c’est ce qui a lieu quand les centres des tourillons sur lesquels se meuvent les tablettes sont situés sur cette ligne commune. La grandeur des tablettes doit être proportionnelle à celle de la plus grande des deux figures solides semblables. Cela étant (fait et il était utile de l’indiquer), prenons deux outils de fer semblables à la pince que l’on appelle chèlè.[9] Les membres de ces outils qui s’ouvrent sont égaux en longueur; les bouts en sont recourbés et munis d’une pointe. Lorsque deux d’entre eux sont recourbés, il en résulte une figure triangulaire.
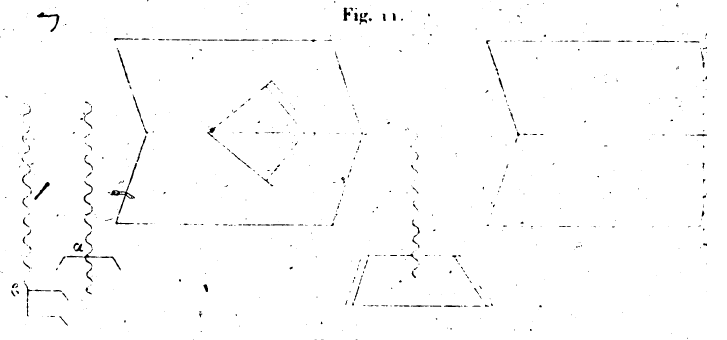
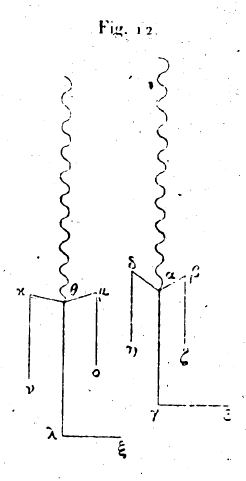
Soit le rapport entre les deux solides exprimé par le rapport de 3 entre les côtés homologues de ces triangles.[10] Représentons l’une des pinces par les lignes αβ, αγ, αδ, les parties recourbées étant γε, βζ, δη. L’autre figure se compose des lignes θκ, θλ, θμ, et les parties recourbées y sont les lignes kn, lx, mo. Les deux triangles semblables sont ηεζ, νξο. Construisons sur la ligne d’intersection des deux tablettes mobiles et sur l’une d’elles une figure égale à celle de la pince de fer et semblablement placée. Menons à partir de l’un des côtés du triangle une ligne Parallèle à la base de ce triangle; elle limitera un autre triangle égal à celui de la pince de fer qui ressemble au chèlè. A chacune des pinces est attachée une verge d’étain, dont l’extrémité est ferrée et solide, afin que lorsqu’on la courbe puis qu’on l’abandonne, elle demeure en repos sans trembler, comme font les deux verges d’étain qui servent à faire les effigies humaines. La forme de cette pince qu’on appelle chèlè ressemble de l’instrument qui est appelé galéagre.[11] Quant aux tablettes dont nous avons parlé, elles se meuvent l’une vers l’autre d’un mouvement tel que, lorsqu’il a cessé, elles demeurent fixes, sans tremblement, comme les écrevisses. Telle est la manière de construire l’instrument ; nous allons parler maintenant de son mode d’emploi.
Quand nous voulons construire une figure solide semblable à une autre figure donnée et étant avec elle dans un rapport donné, nous approchons de la pince triangulaire la surface de la figure solide, de façon que la surface vienne, de chaque côté, en contact avec les pointes. Nous approchons aussi l’autre pince, ressemblant au chèlè, de la figure que nous voulons construire, et, si nous voulons la faire plus grande que la figure correspondante, amenons la plus grande figure contre le plus grand triangle et l’autre contre le triangle restant. Supposons que nous voulions construire la figure semblable dans de la pierre, dans du bois dur ou dans quelque autre matière. Nous marquons sur chaque corps la place des pointes; les points qui sont ainsi déterminés occupant sur les corps des positions semblables, voici comment on délimite les autres parties: pour rendre notre exposition plus claire, supposons que nous voulions, tracer un œil dans l’image d’un homme ou d’un autre animal. Nous plaçons les pointes de la pince sur l’objet connu, c’est-à-dire sur le corps auquel il nous a été proposé de construire une figure semblable ; puis nous courbons l’extrémité de la verge d’étain que possède la pince jusqu’à ce qu’elle atteigne l’œil en question. Nous enlevons ensuite la pince et nous la montons sur le triangle qui a été tracé sur l’une des tablettes; puis nous élevons ou abaissons l’autre tablette, sur laquelle il n’y a rien de tracé, jusqu’à ce qu’elle vienne toucher l’extrémité de la verge. Enlevant alors la pince, nous menons deux lignes joignant le point qu’a marqué la verge d’étain sur la tablette aux extrémités du côté du triangle situé sur la ligne d’intersection des deux tablettes. Nous gardons les tablettes immobiles l’une par rapport à l’autre et nous menons par l’autre point situé sur la ligne d’intersection une parallèle à la base jusqu’à sa rencontre avec la ligne déjà menée. Alors nous prenons l’autre pince, nous montons l’extrémité des dents aiguës et préalablement recourbées sur le triangle situé dans la première tablette et égal au triangle formé par les repères choisis; nous courbons la verge d’étain jusqu’à ce qu’elle atteigne le point déterminé par la ligne parallèle dans l’autre tablette ; enfin, nous enlevons la pince pour la porter sur les points marqués dans la figure non encore employée. Sur quelque point du corps que vienne l’extrémité de la verge, ce point sera celui qui occupera la place de l’œil de l’image, c’est-à-dire une position homologue à celle qu’occupe le point sur lequel a été recourbée la première verge. La verge sera de même recourbée sur les autres parties de la figure. Ainsi nous traçons les points homologues sur la pierre. Ensuite nous construirons la surface délimitée par ces points, car ce sont eux qui forment la figure à la ressemblance de la figure proposée, et dans le rapport de grandeur donné. Quant à la ligne parallèle dont il a été question, on peut la mener dans la seconde tablette avec facilité, après avoir tracé sur la tablette une parallèle quelconque à la ligne d’intersection. Que les figures obtenues par ce procédé soient semblables, cela est évident, parce quelles proviennent des figures correspondantes et semblablement placées, qui ont pour bases les triangles décrits par les extrémités des verges dans chaque corps. Qu’elles aient entre elles un rapport donné, cela est évident aussi, parce que les figures correspondantes au moyen desquelles les corps ont été délimités ont le rapport de 3 entre les côtés homologues : c’est en effet ce que l’on a admis pour les côtés des triangles semblables; donc les solides sont l’un avec l’autre dans le rapport donné.[12] 19. Si nous voulons construire des corps semblables, mais renversés, nous opérerons avec cet instrument en renversant les trois points dans chaque figure, en partant de la position qu’ils occupent dans le cas de similitude; il résultera de la jonction de ces points par des lignes deux triangles égaux aux triangles marqués par les pointes de la pince, j’entends ceux qui sont tracés sur la première tablette. Les deux instruments seront transportés dans des directions opposées, et l’on déterminera ainsi des points consécutifs qui délimiteront les parties du corps où l’on aura opéré. Si nous voulons construire des figures symétriques l’une de l’autre, en sorte que, l’une avançant le pied droit, l’autre avance le gauche d’une quantité semblable à celle dont la première avance le droit, et de même pour les autres membres, nous procéderons ainsi : nous porterons l’instrument vers le point marqué sur la
seconde tablette et dans là direction opposée, de façon qu’il soit symétriquement placé, c’est-à-dire que la perpendiculaire issue du point susdit sur la ligne d’intersection soit distante de la première extrémité, de la distance qui sépare l’autre ligne de l’autre point dans l’autre direction, et qu’elle soit aussi égale à l’autre perpendiculaire; ainsi, soit la ligne d’intersection des deux tablettes la ligne αβ ; soient les extrémités du côté du triangle les points γ, δ et, le point marqué, le point ε. Menons sur la ligne γ une perpendiculaire, tombant en ζ ; prenons la longueur δη égale à la longueur γζ. La ligne ηθ sera égale à la ligne εζ, perpendiculaire sur l’intersection. Donc on ne courbera pas l’extrémité de la verge dans le voisinage du point ε, mais dans le voisinage du point θ. Nous continuerons de même à la porter dans le sens opposé, et nous construirons symétriquement les différentes parties du corps.[13] IV. 20. Beaucoup de personnes se plaçant à des points de vue faux, pensent que les fardeaux placés à terre ne peuvent être mis en mouvement que par une puissance qui leur est équivalente. Nous démontrerons que les poids qui ont une telle position peuvent être mus par une force moindre que toute force donnée; et nous expliquerons pour quelle cause cela ne parait pas évident dans le fait. Imaginons un fardeau posé à terre, dont la surface soit bien égale et unie, et de substance compacte. Le plan sur lequel est ce poids peut être incliné dans les deux sens, c’est-à-dire droite et à gauche. Inclinons-le d’abord à droite. Il est évident que le poids penchera vers la droite, parce qu’il est dans la nature des corps graves de se mouvoir vers le bas, si rien ne les étaye et ne s’oppose à leur mouvement. Si ensuite le côté incliné est rapproché peu à peu du plan horizontal et remis de niveau, le poids sera sensible à ces différences; si le plan s’incline dans un autre sens, c’est-à-dire vers la gauche le poids les descendra encore le long du plan incliné, même si l’inclinaison est fort petite, car il a besoin d’être soutenu par une certaine puissance pour ne pas se mouvoir. Lorsque le plan est replacé de niveau, sans inclinaison dans aucun sens, le poids demeure en repos sans qu’aucune puissance le retienne, jusqu’à ce que le plan soit incliné dans un sens ou dans l’autre; alors le poids penche dans ce sens par l’effet de la pesanteur qui le fait partir d’un côté ou de l’autre; il n’a donc pour entrer en mouvement que la puissance très petite capable de soulever le plan. Donc le poids est mû par toute force, si petite soit-elle. 21. Les eaux qui se trouvent sur un plan non incliné ne coulent pas, mais elles restent immobiles sans pencher d’aucun côté. Si l’on vient à donner au plan la moindre inclinaison, elles s’écoulent toutes le long de la pente, et il ne reste plus sur le plan la moindre particule d’eau, à moins qu’il ne contienne des cavités, au fond desquelles de faibles quantités d’eau se trouvent retenues, comme dans le creux des coupes. L’eau produit ces effets parce que ses parties ne sont pas adhérentes entre elles et qu’elles sont extrêmement divisibles; les corps solides au contraire n’ont point, d’après leur nature, des surfaces lisses, et ils ne peuvent point s’aplanir; aussi arrive-t-il par le fait de l’aspérité de ces corps qu’ils s’étayent les uns les autres, et les uns prennent leur point d’appui sur les autres, comme les dents d’un engrenage. De là naissent des obstacles parce que lorsqu’ils se trouvent en grandes masses et unis les uns aux autres, il faut, pour les manier, réunir une force considérable. L’expérience, qui est la meilleure éducatrice, a appris à placer sous les tortues[14] des pièces de bois de forme cylindrique, qui ne touchent le sol que par une étroite ligne de contact; le frottement en est réduit autant que possible. On emploie aussi des pieux, sur lesquels le fardeau se meut avec facilité, à condition que le poids de l’appareil dépasse celui du fardeau. D’autres personnes affermissent sur le sol des planches rabotées et rendues bien lisses et les enduisent de suif afin d’en adoucir les aspérités. Ils meuvent alors le poids avec une force très faible. Les colonnes, quoique lourdes, lorsqu’elles sont renversées sur le sol de façon à ne le toucher que le long d’une arête, sont mises en mouvement avec facilité. Il en est de même de la sphère; nous en avons déjà parlé. 22. Quand nous voulons élever un poids, nous avons besoin d’une force qui lui soit égale. Imaginons une poulie,[15] élevée et mobile, dressée au-dessus du sol; elle meut d’un mouvement aisé autour d’un axe, monté sur des tourillons; la surface de son pourtour porte une corde, dont une extrémité est attachée au fardeau et dont l’autre extrémité est liée à la puissance qui la tire. Je dis que ce poids est mû par une force qui lui est égale. S’il y a à cette seconde extrémité, non une force, mais un poids égal à celui qui tend le premier brin, il est évident que ces poids égaux n’inclinent l’instrument ni dans un sens ni dans l’autre; le fardeau n’est pas assez fort pour entraîner le poids attaché au second brin, non plus que ce poids pour entraîner le fardeau puisque le poids attaché en second lieu équivaut au fardeau donné d’abord. Lors donc que le poids reçoit un accroissement si faible soit-il, l’autre poids se trouve entraîné en haut. Ainsi la puissance destinée à mouvoir le fardeau, dès qu’elle lui est supérieure, l’emporte sur lui et le met en mouvement, abstraction faite du frottement qui survient dans la rotation de l’instrument et de la rigidité dans les cordes, qui font obstacle au mouvement. 23. Les poids placés sur des plans inclinés tendent naturellement en bas, comme il arrive dans le mouvement de tous les corps. Si cela n’a pas lieu comme nous le disons, on doit penser que la cause signalée plus haut agit.[16] Proposons-nous de tirer vers le haut un poids posé sur un plan incliné. Le sol de ce plan est doux et uni de même que la partie de la surface du poids, qui s’appuie dessus. Nous aurons recours à quelque puissance ou à quelque poids appliqué de l’autre côté, pour faire d’abord équilibre au poids donné, afin qu’un excès de puissance l’emporte sur ce poids et le tire en haut. Pour établir parfaitement notre démonstration, faisons-la pour le cas d’un cylindre placé sur le plan incliné. Comme les cylindres ne touchent pas le sol par une grande surface, il est dans leur nature de rouler en bas. Imaginons donc un plan passant par l’arête qui touche le plan incliné et perpendiculaire sur ce plan. Il est clair que ce plan passe par l’axe du cylindre et qu’il divise ce corps en deux parties égales ; car étant donné un cercle et une tangente, lorsqu’on élève à partir du point de contact une ligne faisant avec la tangente un angle droit, elle va rencontrer le centre du cercle. Par la même arête du cylindre, menons un autre plan perpendiculaire sur l’horizon : il ne se confondra pas avec le premier plan, et il partagera le cylindre en deux portions inégales, dont la plus petite se trouvera vers le haut et la plus grande vers le bas ; la plus grande l’emportera sur la plus petite, puisqu’elle est plus grande et le cylindre roulera. Mais si, considérant le plan mené perpendiculairement à l’horizon, nous imaginons qu’on enlève de la portion la plus grande qu’il détermine dans le cylindre une quantité égale à celle dont elle excède la portion la plus petite, les deux portions se feront équilibre ; leur poids reposera immobile sur l’arête qui touche le sol incliné, et ne tendra ni d’un côté ni de l’autre ni en haut , ni en bas. On a donc besoin d’une puissance équivalente à cette différence pour faire équilibre au poids et, dès qu’on ajoutera à cette puissance le plus léger excès, elle l’emportera sur le poids.[17] V. — 24. On voit bien qu’il faut de toute nécessité que ceux qui apprennent les arts mécaniques sachent ce que c’est que la pesanteur et ce qu’est le centre de gravité, soit dans les corps soit dans les figures non corporelles; bien que la pesanteur et un l’inclinaison[18] ne s’entendent exactement que des corps, cependant personne ne s’opposera à ce que nous disions que dans les figures géométriques, solides et planes, le centre d’inclinaison, le centre de gravité est en tel point. Cette question a été exposée par Archimède avec des développements suffisants. Il faut savoir à ce sujet que Praxidamas (?), qui était un peintre, a donné du centre de gravité une définition physique. Il a dit que centre de gravité ou d’inclinaison est un point tel que, lorsque le poids est suspendu par ce point, il est divisé en deux portions équivalentes. A la suite de cela Archimède et les mécaniciens qui l’ont imité, ont scindé cette définition, et ils ont distingué le point de suspension du centre d’inclinaison; le point de suspension est un point quelconque sur le corps ou sur la figure non corporelle, tel que lorsque l’objet suspendu est suspendu à ce point, ses portions se font équilibre, c’est-à-dire qu’il n’oscille ni ne s’incline. L’équilibre est l’état d’équivalence entre une chose et une autre, comme on le constate dans la balance, lorsqu’elle s’arrête parallèlement au plan de l’horizon ou à quelque autre plan. Archimède dit que les corps graves peuvent rester sans inclinaison autour d’une ligne ou autour d’un point: autour d’une ligne, lorsque, le corps reposant sur deux points de cette ligne, il ne penche d’aucun côté;[19] alors le plan perpendiculaire à l’horizon, même par cette ligne, en quelque endroit qu’on la transporte, demeure perpendiculaire et ne s’incline pas autour d’elle. Quand nous disons que le corps grave penche, nous voulons seulement exprimer son déplacement vers le bas c’est-à-dire son inclinaison dans la direction du sol. Quant à l’équilibre autour d’un point, il a lieu lorsque le corps y étant suspendu, quel que soit le mouvement du point, ses parties s’équivalent entre elles. Lorsqu’un corps grave fait équilibre à un autre corps grave et que tous deux sont suspendus à deux points d’une ligne partagée par moitiés et reposant sur le point de division, cette ligne est parallèle à l’horizon, si le rapport des grandeurs des poids est égal à l’inverse du rapport des distances respectives de leurs points de suspension au point de division de la ligne. Les poids suspendus de cette façon se font équilibre sans inclinaison du fléau; c’est ce qu’Archimède a démontré dans ses livres sur les équilibres des figures où sont employés les leviers. Les choses se passent de même pour les crochets que pour les supports, parce qu’un crochet et un support, c’est une même chose quant à la force. Les supports auxquels sont accrochés les poids sont aussi ceux qui portent les poids. Il peut arriser que ces supports soient en nombre considérable, illimité. Le centre de gravité dans chaque corps est un point unique vers lequel sont tirés les crochets qui tiennent aux supports. Le centre de gravité dans certains corps est extérieur à la substance du corps, c’est ce qui a lieu par exemple dans les arcs et les bracelets. Les lignes selon lesquelles les crochets sont tendus convergent toutes en un point commun. Pour le démontrer, nous imaginons un plan quelconque perpendiculaire sur l’horizon et qui coupe un corps de façon que les sections s’équilibrent. Il apparaît manifestement que ce plan partage le corps en deux parties équivalentes. Il pénètre donc dans le corps; imaginons un autre plan qui coupe aussi le corps dans les mêmes conditions, et qui y pénètre comme y a pénétré le premier, ces deux plans se couperont suivant une droite ; or si l’intersection ne rencontre pas le point de suspension, il en résultera que le corps sera à la fois en équilibre et ne le sera pas. Transportons aux supports cette démonstration. Imaginons un corps en équilibre autour d’un plan vertical, et que ce corps soit aussi en équilibre par rapport à une ligne verticale menée par un certain point de ce plan. Lorsque cette ligne sera menée, elle pénétrera dans le corps ; si elle tombe en dehors du corps, le plan menée par elle tombera aussi en dehors du corps ; mais il est évident que cela est impossible : donc la ligne pénètre dans le corps et le partage en deux parties équivalentes. Imaginons que l’équilibre ait lieu autour d’un autre point distinct du premier ; il arrivera ici ce qui est arrivé d’abord, c’est-à-dire que la ligne issue de ce point pénétrera dans le milieu du corps; mais les deux lignes seront distantes l’une de l’autre; et si par elles on mène deux plans, ils ne se couperont pas. Il sera donc possible de mener par deux lignes deux plans qui ne se coupent pas. Ainsi l’on aboutit à la même conclusion que précédemment : ce qui est proposé est impossible. Par là on sait que les plans se coupent, que les lignes se rencontrent et qu’elles sont dans un même plan. Prolongeons ce plan vers la surface du corps; il décrit une ligne d’intersection : soit un troisième point situé hors de cette ligne. Imaginons que le corps soit en équilibre autour de ce nouveau point et menons de ce point une ligne vers la surface du corps; d’après ce que nous avons dit plus haut, cette ligne prolongée coupe les deux lignes par lesquelles nous avons fait passer les deux plans, et elle les rencontre précisément en leur point d’intersection parce que lorsqu’une ligne rencontre deux lignes qui se coupent et qu’elle n’est pas dans leur plan, elle les l’encontre en leur point (d’intersection. Il serait absurde que ces lignes ne se rencontrassent pas en ce point d’intersection, puisqu’elles sont dans des plans divers. Donc toutes les lignes selon lesquelles les organes de suspension se trouvent tirés se réunissent en un point : c’est celui qu’on nomme le centre d’inclinaison et de gravité. VI. — 25. Il est nécessaire d’expliquer comment on soutient, comment on porte et transporte les corps graves, avec les développements convenables pour une introduction. Archimède a traité cette matière avec un art très sûr dans son livre appelé Livre des Supports ; pour nous, nous établirons ce qu’on a besoin d’en connaître pour d’autres objets, et nous ferons usage de ces résultats, dans ma mesure qui peut convenir aux étudiants. Voici la voie que nous suivrons: Soient des colonnes en nombre quelconque : elles supportent des poutres transversales ou une paroi posées sur elles dans des situations identiques ou diverses, dépassant par l’une de leurs extrémités ou par les deux ensemble, et ces colonnes sont également ou inégalement distancées; nous voulons connaître quelle portion du poids supporte chacune d’elles. Un exemple semblable est offert par ce cas : une longue poutre, partout de même poids est portée par des hommes également espacés sur sa longueur et entre ses extrémités ; elle dépasse par l’une de ses extrémités ou par les deux ensemble. Nous voulons connaître quelle portion de son poids chaque homme supporte. Le problème est le même dans les deux cas. 26. Soit un fardeau homogène et ayant même épaisseur partout posé sur des colonnes; αβ est ce fardeau. Supposons-le placé sur deux colonnes αγ et βδ. Chacune des deux colonnes αγ et βδ supporte la moitié du poids αβ. Supposons encore qu’une autre colonne εζ partage la distance αβ dans une proportion quelconque. Nous voudrions savoir quelle portion du poids supporte chacune des colonnes αγ, εζ et βδ.. Imaginons le poids ab divisé au point e selon une ligne qui prolonge l’axe de la colonne. Il est évident que le segment αε fait porter la moitié son poids sur chacune des deux colonnes αγ et ετ et que chacune des deux
colonnes εζ et βδ supportent la moitié du poids du segment εβ. En effet, il n’y a pas de différence dans le poids que supportent les colonnes, que la poutre reposant sur elles soit continue ou divisée, parce continue ou divisée, la somme de son poids est toujours sur les colonnes. Donc la colonne εζ porte la moitié du poids de εβ et la moitié du poids de αε, c’est-à-dire la moitié du poids total αβ ; la colonne αγ supporte la moitié du poids de αε, et la colonne βδ la moitié du poids de εβ. Si nous divisons la moitié de αβ dans le rapport de la distance αε à la distance εβ, le poids du segment proportionnel à αε est porté par αγ, et le poids du segment proportionnel à εβ l’est par βδ. Plaçons encore une autre colonne ηθ. Il est évident que αγ supporte la moitié de αε, βδ la moitié de ηβ, εζ la moitié de αη, et ηθ la moitié de εβ, c’est ab tout entier, et c’est ce qui repose sur l’ensemble des colonnes. Si les colonnes sont plus nombreuses, le même raisonnement fait connaître quelle portion du poids supporte chacune d’elles. 27. – Cela étant, soient les supports αβ, γδ dans des positions identiques, et supposons qu’il y ait sur eux un corps partout de même grosseur et de même poids; αγ est ce corps. Nous avons déjà dit que chacun des
deux montants αβ, γδ supporte la moitié du poids αγ. Déplaçons maintenant le support γδ et rapprochons-le de αβ, soit εζ sa nouvelle position. Nous voulons savoir encore quelles portions du poids portent αβ et εζ. La distance αε, ou bien est égale à la distance εγ, ou bien elle est plus petite ou plus grande qu’elle. Supposons-la égale. Il est clair que le poids de αε fait équilibre au poids de εγ. Si nous enlevons le support αβ, le fardeau αγ restera stable dans sa position, il est donc évident que le support αβ ne porte rien du poids ; le poids αγ repose sur εζ seul.
Si nous faisons la distance γε plus grande que la distance αε, le poids αγ s’abaisse du côté de γ. Soit enfin la distance εγ plus petite que la distance αε, prenons εη égal à γε ; ηγ sera en équilibre sur εζ seul. Plaçons un montant en ηθ. Si nous imaginons que le poids est coupé au point η, le segment ηγ reposera sur εζ seul, et la moitié de αη pèsera sur chacun des deux montants αβ, ηθ. Lorsque le montant ηθ viendra à manquer, la résistance qu’il représentait sera transportée au point h dans le corps continu. Donc ab supporte la moitié du poids αη, et εζ supporte le reste, c’est-à-dire ηγ et la moitié de αη. Si nous imaginons αγ partagé par moitiés au point κ, κε est la moitié de αη ; lorsque le montant qui était d’abord en e est transporté sous le point κ, il supporte la totalité du poids αγ ; et toutes les fois que ce montant s’écarte du point qui partage le poids en deux parties égales, on voit quelle est la portion du poids que supporte ab ;le reste porte sur l’autre montant. 28. Puisqu’il en est ainsi, imaginons deux supports αβ, εζ dans la même position que plus haut. La partie εγ dépasse, et nous partageons αγ en deux moitiés au point κ. Nous avons déjà démontré que le montant ab
porte le poids de κε, et que le montant εζ porte le reste, du poids de αγ. Supposons qu’il ait un support sous le point γ ; soit γδ ce support. Il est démontré ainsi que le montant αβ porte la moitié du poids de εα et le montant δγ la moitié du poids de εγ, et que le montant εζ porte la moitié du poids de αγ. Avant d’introduire de montant γδ, nous avons montré quelle partie du poids supportent respectivement αβ et εζ. Il apparaît donc clairement que, à la suite de l’introduction du support γδ sous le poids, la portion du poids qui pèse sur le support αβ est plus grande qu’auparavant d’une quantité équivalente à la moitié de εη ou de εγ, au lieu que celle qui pèse sur εζ est moindre qu’auparavant d’une quantité équivalente à εγ. La portion du poids que supporte δγ, d’après cela, est la moitié de εγ, puisque, ce support étant ajouté sous le poids, allège la charge de εζ d’un poids égal à celui de εγ, et rejette sur le montant αβ un poids égal à la moitié de εγ ; car c’est la quantité restante et c’est celle que nous avions déjà obtenue par l’autre procédé. Par là on voit que lorsqu’un poids quelconque repose sur des montants et qu’à ces montants on en ajoute un autre, l’un des premiers montants, celui qui est à l’extrémité du fardeau, supporte une grande portion du poids que celle qu’il supportait avant cette adjonction, au lieu que l’autre montant en supporte une moindre portion qu’auparavant. Et puisque les trois supports αβ, εζ, γδ, étant dressés, le montant αβ porte la moitié de αγ, si le support γδ vient à manquer, il est évident que la portion εγ, qui dépasse joue le rôle de levier; elle enlève une partie du poids qui pesait sur αβ et elle apporte une surcharge de poids au support εζ, sans que d’ailleurs le corps grave change de position. 29. Qu’une force légère ne puisse pas, sans l’intermédiaire de quelque machine, mouvoir un poids très lourd, c’est un fait de toute évidence. Deux hommes meuvent avec facilité un poids qu’un homme seul ne mouvrait pas, même en y mettant toute sa force. Nous voyons bien que le fardeau n’est mis en mouvement qu’après que la force du second homme est venue s’ajouter à celle du premier; mais ce second homme tout seul ne le mouvrait pas. Cela est évident parce que si le premier homme s’arrête et laisse tout le poids au second celui-ci ne meut pas le fardeau. Si l’on partage le fardeau en deux moitiés, le premier homme seul meut sa moitié et laisse l’autre en repos. La moitié que meut cet homme seul était adhérente à l’autre moitié avant que celle-ci en fût détachée. Pour la même raison, lorsque des forces nombreuses mettent en mouvement un certain poids et qu’une seule de ces forces vient à faire défaut, l’ensemble des forces qui restent après que celle-ci a manqué ne peuvent mouvoir ce poids. Si des forces réunies ont commencé à mouvoir le poids après l’addition d’une dernière force donnée, elles le meuvent avec facilité. La même chose se manifeste dans les percussions; lorsque de nombreux coups ont ébranlé la solidité d’un objet, un seul coup frappé en plus le réduit en morceaux. Et ce n’est pas seulement l’effet de l’ensemble des percussions, mais aussi de ce dernier seul. Il y a de cela des exemples sensibles si nous avons un poids et que nous puissions le lever mais après de grands efforts, n’est-il pas évident que notre force se mesure à ce poids ? 30. Soient les supports αβ, γδ, sur lesquels repose un corps ayant partout même poids et même épaisseur. Soit εζ ce corps : il dépasse ces deux supports; nous voulons savoir quelle portion de son poids pèse sur
chacun des deux montants. Nous avons déjà démontré que, lorsque un poids εζ est placé sur des supports γδ et αβ, γδ Supporte du poids une portion plus grande que celle qui est supportée par αβ, d’une quantité équivalente au double de γζ. Et γε étant placé sur γδ, le montant supporte du poids une portion plus grande que celle qui est supportée par γδ d’une quantité équivalente au double de αε. Il est donc clair que gd supporte de plus que αβ une portion du poids équivalente à l’excès du double de γζ sur le double de αε. Si γζ est égal à αε, chacun des deux pieds γδ, αβ supporte du poids une quantité égale, et si l’une de ces longueurs augmente, le pied correspondant supporte un accroissement de charge proportionnel. De ce que nous avons dit plus haut, il résulte avec évidence que, quand des poutres où des parois ayant partout même épaisseur et même poids reposent sur des colonnes ou des supports, espacés inégalement et sans règle nous pouvons savoir sur lequel des ces supports pèse le plus grand poids, et quel est l’excès de charge sur ce support. S’il a sur les piliers des solives ou quelque autre chose, ces mêmes procédés sont applicables. De même encore, lorsque des hommes portent à bras ou sur les épaules une poutre ou une pierre, les uns étant au milieu, les autres au bout, qu’ils soient du même côté du fardeau ou des deux côtés, nous savons clairement quelle portion du poids pèse sur chacun d’eux. 31. Soit un autre corps αβ, égal aussi et de même poids dans toutes ses parties; il repose sur des supports dressés dans des positions identiques αγ, et βδ. Il est clair que, sur chacun des supports, pèse la moitié du poids ab. Suspendons un poids à αβ, au point ε ; si le point ε divise αβ par moitiés, il est évident que chacun des deux pieds supporte une moitié du poids αβ plus une moitié du poids suspendu au point ε ou chargé en ce point. Si le point ε ne divise pas αβ en deux parties égales, divisons le poids suspendu en deux portions
dans le rapport βε/εα ; le poids de la portion proportionnelle à εβ pèsera sur αγ, et celui de la portion proportionnelle à αε pèsera sur βδ. De plus, chacun des deux pieds supporte la moitié de αβ. Suspendons un autre poids au point ζ, et divisons-le dans le rapport αζ/ζβ ; δβ supportera le poids de la partie proportionnelle à αζ, et αγ le poids de la partie proportionnelle à ζβ, et chaque pied supportera de plus la moitié de αβ.[20] On a énoncé un poids proportionnel à ζβ supporté par αγ ; les poids que ce pied supportait avant qu’on en ait suspendu en e et z étaient déjà énoncés; donc tout ce que supportent les deux pieds ag, bd est énuméré et connu. Si l’on continue à suspendre d’autres poids, on saura par la même méthode quel poids pèse sur chacun des deux supports. 32. Beaucoup de gens pensent que lorsque, dans la balance, les poids appliqués à certaines distances du point de suspension se font équilibre les poids sont inversement proportionnels à leurs distances respectives. Mais il ne faut pas énoncer cela sous cette forme négligée nous devons introduire une autre distinction. Supposons que ab soit le fléau d’une balance ayant partout même poids et même épaisseur. Il est suspendu en son milieu, au point γ ; on accroche à des points quelconques, ε et δ, par exemple des cordes ; soient δζ, εη ces cordes et on y suspend deux poids. Le fléau est horizontal— après qu’on a équilibré les poids. Imaginons que les deux cordes passent aux points θκ ; le fléau étant en équilibre, la distance θγ sera à γκ comme le poids η au poids ζ. C’est ce qu’a démontré Archimède dans ses livres sur les leviers. Si nous retranchons du fléau de la balance ce qui avoisine les deux extrémités, c’est-à-dire les parties γα, κβ, le fléau n’est plus en équilibre.[21]
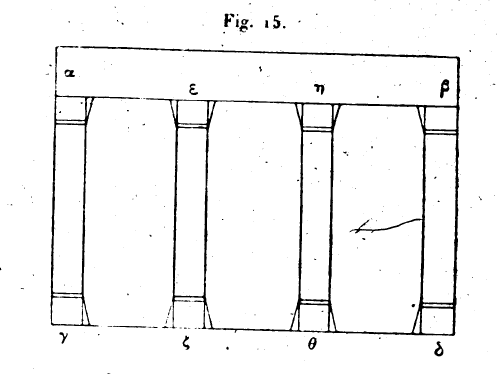
33. Quelques-uns ont pensé à tort que la proportion existant dans l’état d’équilibre n’était plus vraie dans le cas d’un fléau irrégulier.[22] Supposons un fléau de balance n’ayant pas partout même poids ni même épaisseur, et fait de matière quelconque ; il est en équilibre lorsqu’on le suspend au point g ; nous entendons ici par équilibre l’arrêt du fléau dans une position stable, quand bien même il serait incliné dans un sens ou dans un autre. Suspendons ensuite des poids à des points quelconques du fléau ; soient δ et ε ces points; le fléau reprend une position d’équilibre après que les poids ont été suspendus; et Archimède a démontré que, dans ce cas encore, le rapport des poids est égal au rapport inverse des distances respectives. Ce que sont ces distances dans le cas des fléaux irréguliers et inclinés, on l’imagine un faisant tomber une corde du point γ vers le point ζ. Nous menons une ligne que nous imaginons issue du point ζ et qui est la ligne ηζθ; elle doit être établie de façon à
couper la corde à angles droits. Cela étant, et les cordes δη, εθ étant suspendues aux points de, la distance entre la ligne γζ et le point suspendu en ε est marquée par θζ, et l’on aura, au repos du fléau, le rapport de ζη à ζθ, égal au rapport du poids suspendu au point ε, au poids suspendu au point δ. C’est la relation démontrée précédemment.[23] 34. Soit une roue ou une poulie mobile sur un axe de centre a; elle a pour diamètre la ligne βγ parallèle à l’horizon. Aux points β et γ sont accrochées deux cordes βδ et γε, auxquelles sont suspendus des poids égaux. Il est évident que la poulie ne penchera ni dans un sens, ni dans l’autre, parce que les deux poids sont égaux et que les distances à partir du point a sont égales. Soit le poids δ plus grand que le poids appliqué en ε ; il est évident que la poulie penchera du côté β, et le point β descendra avec le poids. Il faut que nous sachions à quelle position s’arrêtera le poids le plus lourd après être descendu. Abaissons donc le point et faisons-le venir au point ζ ; la corde βδ vient en ζη et le poids s’arrête. Il est clair que la corde γε s’enroulera sur la gorge de la poule et qu’elle sera suspendue par le poids à partir du point γ, parce que la partie qui est enroulée n’est pas suspendue; ζη prolongé vient en θ. Puisque les deux poids sont en équilibre, leur rapport est égal à l’inverse[24] du rapport des distances respectives du point de suspension aux cordes. Donc αγ/αθ est égal au rapport du poids η au poids ε. Prenons un rapport αγ/αθ égal au rapport des poids, et menant sur la ligne βγ la perpendiculaire θζ, nous voyons que la poulie s’est inclinée du point β au point ζ et que là elle reste en repos. Nous ferions le même raisonnement pour tout autre poids. Il est donc possible par ce moyen de faire équilibre à un poids quelconque avec un poids plus petit.
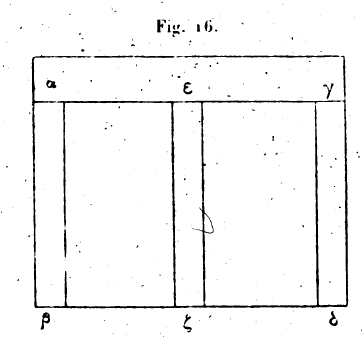
Ce livre suffit comme première introduction aux arts mécaniques. Dans ce qui va suivre, nous parlerons des cinq machines simples avec lesquelles on meut ou l’on tire les corps graves, ainsi que des causes physiques qui les font agir; nous traiterons aussi d’autres choses qui sont de la plus grande utilité dans la question de porter et d’élever les corps graves. FIN DU PREMIER LIVRE.
[1] C’est l’arca ou coffre-fort des Romains; gr. κιβωτός. [2] Ce morceau et déplacé et altéré. Cf. Introduction, et l. II, 21. [3] Cette phrase est obscure. Mais elle laisse entendre que le fragment qui précède a été rapporté en tête d’un manuscrit acéphale. [4] Sous cette rédaction très embarrassée ce paragraphe témoigne d’un effort pour décomposer le mouvement sur les deux cercles dont deux axes dont l’un serait la ligne des cercles et l’autre la perpendiculaire à cette ligne. [5] Safiha = Cercle. [6] Il y a ici une interruption dans le texte arabe, et ce qui suit présente de grandes obscurités. [7] Mires, le texte dit : centres. [8] Ce paragraphe, très peu satisfaisant et accompagné d’une figure très grossière que nous reproduisons ne laisse du moins aucun doute sur le principe de l’instrument qui est si imparfaitement décrit. Soit AC la courbe donnée, O le centre de similitude, je fais tourner le cercle OB jusqu’à ce que la ligne BA rencontre un certain point de la courbe, et je déplace cette ligne dans sa propre direction jusqu’à ce qu’un point de repère fixé sur elle coïncide avec le point de la courbe. La ligne A’B’, tangente au cercle OB’, est venue dans la rotation occuper une position parallèle à celle de AB; je la déplace aussi dans sa propre direction jusqu’à ce que le repère A’, qu’elle porte, vienne sur la droite déterminée par les points O et A. Le repères A et A’ décrivent ainsi des courbes semblables qui sont entre elles dans le rapport des rayons des cercles.
[9]
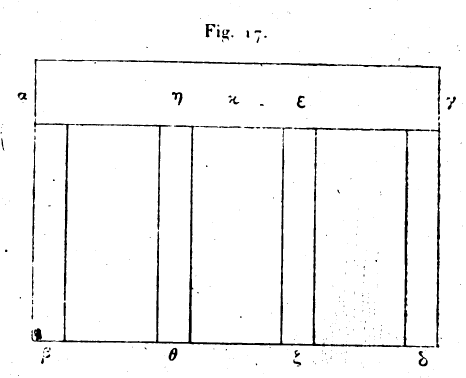
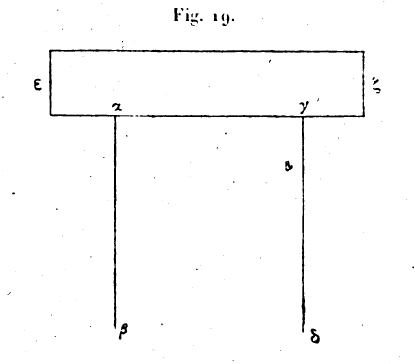
Chèlè: gr. χηλή, pied fourchu, pince, pince de la baliste.
Nous pensons qu’ainsi doit se transcrire l’arabe
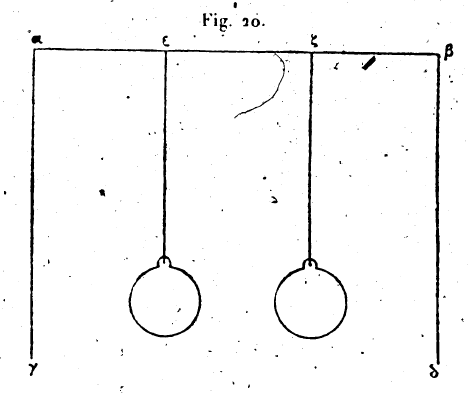
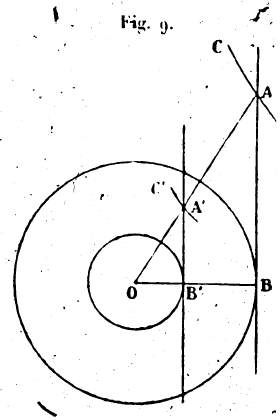
[10] Cette phase est mauvaise. Les lettres indicatrices, dans les phrases qui suivent, demeurent sans emploi dans le reste du morceau. Le texte est défiguré en cet endroit. [11] Galéagre, gr. γαλεάγρα, piège à belette. C’est aussi un organe de la presse. —-- Écrevisse, sorte de pince. Cf. L. III, 7. [12] Toute la description contenue dans ce paragraphe est extrêmement obscure. Les, figures ne le sont pas moins; nous les reproduisons telles qu’elles sont, sans essayer de les restituer. La fig. 12 est une retouche faite en noir sur les détails a et b de la fig. 11. [13] Ce paragraphe 19 n’est pas moins difficile que le précédent.
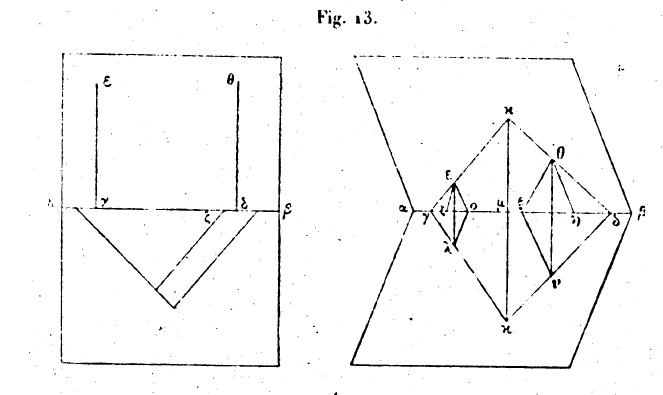
L’altération du texte y est prouvé d’une manière certaine par la présence de deux figures (fig. 13) dont l’une ne correspond pas au texte, et dont l’autre contient des lignes et des lettres dont il n’est pas fait mention. Nous reproduisons ces deux figures. — A la page suivante, p. 17, se trouvent des figures (fig. 14) qui ne se rapportent à aucune partie du texte et que nous recopions aussi. [14] Tortue, gr. χελώνη. Cf. l. III, 1. [15] Poulie. Le terme arabe est douteux. [16] La cause signalée plus haut : le frottement, les aspérités du plan. [17] Équivalente à cette différence : nous précisons le texte. [18] L’inclinaison, sens du gr. ῥοπή. [19] Il ne penche : le texte porte La ligne ne penche. [20] On a énoncé, énuméré et connu. Ce passage est évidemment tronqué, sans pourtant être obscur. [21] Le manuscrit donne trois figures correspondant à cette proposition et à la suivante, toutes trois incomplètes et sans lettres. Le texte aussi paraît avoir souffert. [22] A tort n’est plus vraie dans le cas d’un fléau irrégulier. Ces mots ne sont pas dans le texte où la phrase est incomplète. [23] Notre traduction dans ce paragraphe est plus claire que le texte, qui porte des marques d’altération, sans que la pensée en soit obscurcie. [24] L’inverse. Nous ajoutons ce mot.
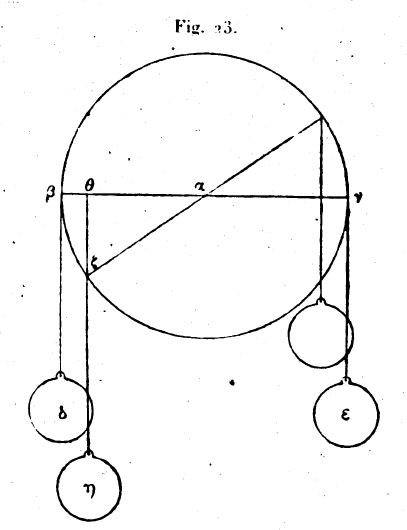
|






 Pince,
le texte dit : pointe.
Pince,
le texte dit : pointe.