RETOUR À L’ENTRÉE DU SITE

ALLER A LA TAΒLE DES MATIERES DE  THÉON DE SMYRNE

 THÉON DE SMYRNE

PHILOSOPHE PLATONICIEN

EXPOSITION DES CONNAISSANCES MATHÉMATIQUES UTILES POUR LA LECTURE DE PLATON

SECONDE PARTIE

MUSIQUE

TROISIÈME PARTIE

ASTRONOMIE

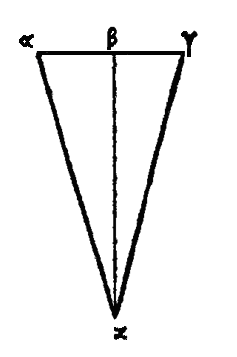
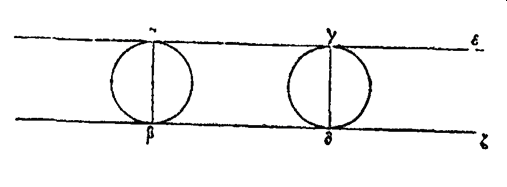
De la forme sphérique de la terre

I. Le monde entier est une sphère et la terre qui est elle-même un sphéroïde est placée au milieu. Que la terre est le centre de l’univers et qu’elle n’en est qu’un point par rapport à la grandeur de l’univers, voilà ce qu’il faut avant tout établir. Un exposé exact de cette doctrine exigerait de trop longues considérations, des écrits trop nombreux; il suffira, pour résumer ce que nous avons à dire, de rappeler les notions sommaires que nous a transmises Adraste.

Nous dirons donc que le monde et la terre sont sphériques, et que celle-ci est au centre du monde et qu’elle n’en est qu’un point; cela résulte de ce que, pour les habitants d’un même lieu, tous les corps célestes se lèvent, se couchent et se lèvent de nouveau aux mêmes points, et qu’ils accomplissent toujours les mêmes révolutions.

La sphéricité du monde est encore démontrée par la raison que, de chaque partie de la terre, notre regard embrasse la moitié du ciel, tandis que l’autre moitié nous la jugeons cachée par la terre, ne pouvant l’apercevoir. D’ailleurs, si nous regardons les points extrêmes du ciel, tous les rayons visuels nous paraissent égaux, et des astres diamétralement opposés décrivent un grand cercle, l’un se couche quand l’autre se lève. Si l’univers, au lieu d’être sphérique, avait la forme d’un cône, d’un cylindre, d’une pyramide ou d’un autre solide, il ne produirait pas cet effet sur la terre : une de ses parties paraîtrait plus grande, une autre plus petite et les distances de la terre au ciel paraîtraient inégales.

II. Et d’abord, la terre est sphéroïdale de l’orient à l’occident; le lever et le coucher des mêmes astres le prouvent bien, ils ont lieu plus tôt pour les habitants des régions orientales, plus tard pour ceux des régions occidentales. Ce qui le montre encore, c’est une même éclipse de lune : elle se produit dans un même espace de temps assez court; pour tous ceux qui peuvent la voir, elle paraîtra à des instants différents : plus on sera vers l’orient, plus vite on la verra et plus tôt on en aura vu une plus grande partie. A cause de la forme arrondie de la terre, le soleil n’en éclaire pas en même temps toute la surface, et l’ombre que la terre projette se déplace d’après un ordre fixe, le phénomène ayant lieu la nuit,

Il est encore évident que la terre est convexe du nord au midi: en effet, pour ceux qui se dirigent vers le midi, à mesure qu’ils avancent, beaucoup d’étoiles, qui sont toujours visibles pour nous, dans leur mouvement autour du pôle, ont un lever et un coucher. De même que d’autres astres, toujours invisibles pour nous, dans leur mouvement autour du pôle qui nous est caché, ont pour eu un lever et un coucher : ainsi, l’étoile dite Canopus[1] est invisible dans les contrées plus septentrionales que Cnide[2] ; mais elle est visible dans les contrées plus méridionales, et elle est toujours de plus en plus élevée à mesure qu’on s’éloigne du nord. Au contraire, quand on va du midi vers le nord, beaucoup d’astres, dont on voyait au midi le lever et le coucher, disparaissent entièrement, tandis que d’autres, situés dans la région des Ourses et qui avaient un lever et un coucher, deviennent toujours visibles et on en voit d’autant plus qu’on avance davantage vers le nord.

Puisque la terre paraît convexe de toutes parts, elle doit être sphérique. D’ailleurs, tout corps pesant se portant naturellement vers le centre, si nous concevions que certaines parties de la terre soient plus éloignées du centre, à cause de leur grandeur, il faudrait nécessairement que les petites parties qui les entourent fussent pressées, repoussées et éloignées du centre, jusqu’à ce que, l’égalité de distance et de pression étant obtenue, tout en équilibre soit constitué en repos, comme deux poutres qui se soutiennent mutuellement ou comme deux athlètes de même force qui se tiennent mutuellement embrassés. Si les différentes parties de la terre sont également éloignées du centre, il faut que sa forme soit sphérique.

En outre, puisque la chute des corps pesants se fait toujours et partout vers le centre, que tout converge vers le même point et qu’enfin chaque corps tombe verticalement, c’est-à-dire qu’il fait avec la surface de la terre des angles toujours égaux, on doit conclure que la surface de la terre est sphérique.

III. La surface de la mer et de toutes les eaux tranquilles est aussi sphérique. On peut le reconnaître de cette manière: si, placé sur le rivage, on observe un objet dont on est séparé par la mer, comme une colline, un arbre, une tour, un vaisseau ou la terre elle-même, puis, si s’abaissant on regarde vers la surface de l’eau, on ne voit plus rien, ou on voit une moindre partie de l’objet, la convexité de la surface de la mer masquant l’objet. Et souvent, pendant une navigation, alors que du pont du navire on ne voit pas encore la terre ou un vaisseau qui s’avance, des matelots grimpés au haut d’un mât c’est-à-dire les aperçoivent, étant plus élevés et comme dominant la convexité de la mer qui faisait obstacle.

On peut démontrer physiquement et mathématiquement que la surface de toute eau tranquille doit être de forme sphérique. L’eau tend, en effet, toujours à couler des parties les plus hautes vers les parties creuses. Or, les parties hautes sont plus éloignées du centre de la terre, les parties creuses le sont moins. La surface de l’eau étant supposée plane, soit αβγ (une ligne droite de) cette surface. Du centre de la terre, tel que le point α, menons à la base la perpendiculaire αβ et menons aux extrémités de cette base les droites κα, κγ.

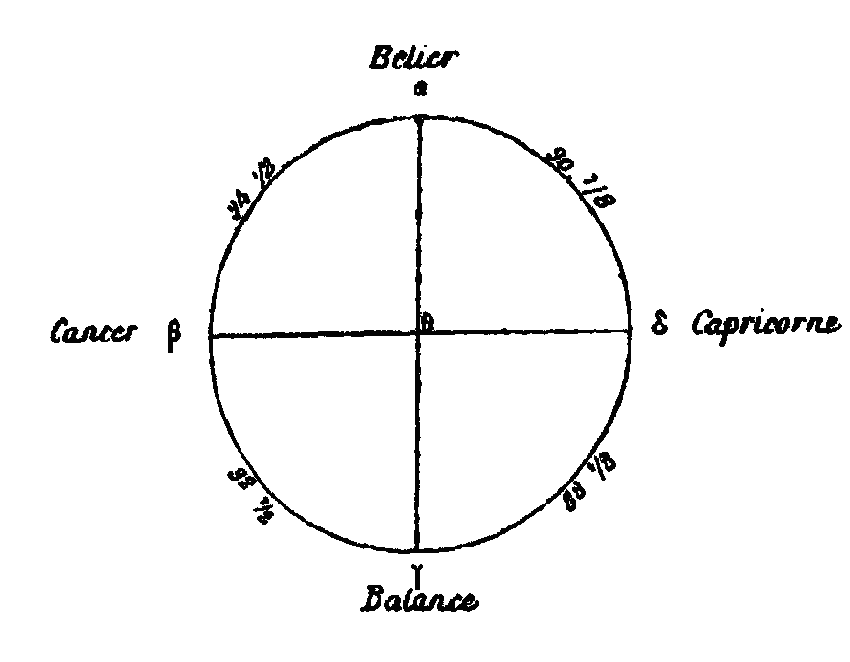
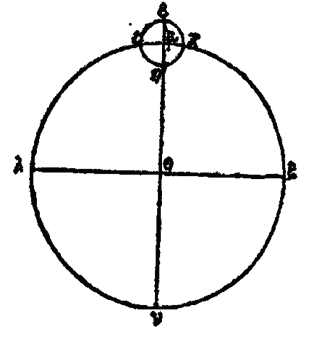
Il est évident que ces deux droites κα, κγ, sont toutes les deux plus grandes que κβ et que les deux points, α, γ, sont plus éloignés du centre que le point β et, par conséquent, plus élevés que l’eau s’écoulera donc des points α, β, vers le point β moins élevé jusqu’à ce que ce dernier point, entouré de nouvelle eau, soit autant éloigné du point κ que α et γ. Pareillement, tous les points de la surface de l’eau seront à la même distance de κ; donc l’eau offre la forme sphérique et la masse entière de l’eau et de la terre est sphérique.

Et qu’on ne dise pas que la hauteur des montagnes ou la profondeur des vallées vient contrarier cette thèse et, prouver que la terre n’est pas une sphère exacte. Ératosthène nous montre, en effet, que le tour de la terre, mesuré suivant la circonférence d’un grand cercle, a une longueur approximative de 252.000 stades, et Archimède nous apprend qu’une circonférence de cercle, développée en ligne droite, vaut trois fois le diamètre et à très peu près le septième de ce diamètre; le diamètre de la terre vaudra donc approximativement 80.182 stades. Trois fois ce nombre, plus un septième de ce nombre, donnent, en effet, 22.000 stades.

Or, et après Ératosthène et Dicéarque, la hauteur verticale des montagnes les plus élevées au-dessus des plaines les plus basses est de 10 stades. Ils ont traduit ce résultat d’observations faites avec la dioptre[3] qui permet de mesurer les hauteurs d’après certains intervalles. La hauteur de la plus grande montagne serait donc à peu près égale à la huit millième partie du diamètre total de la terre. Si nous faisions une sphère d’un pied de diamètre, la largeur d’un doigt étant à peu près égale à 12 diamètres et demi d’un grain de mil, le diamètre de notre sphère égalerait 200 diamètres de grain de mil ou un peu moins, car le pied vaut 16 doigts; le doigt vaut 12 diamètres de grain de mil, et 16 fois 12 font 192. La quarantième partie du diamètre d’un grain de mil est donc supérieure à la huit millième partie d’un pied, car 40 fois 200 font 8000.

Mais nous avons vu que la hauteur de la plus grande montagne est à peu près la huit millième partie du diamètre de la terre, donc le rapport de la quarantième partie du diamètre d’un grain de mil au diamètre d’une sphère d’un pied de diamètre est plus grand que le rapport de la hauteur de la plus grande montagne au diamètre de la terre, Et le rapport de la sphère ayant pour diamètre la quarantième partie de l’épaisseur d’un grain de mil, à la sphère d’un pied de diamètre, est plus grand que le rapport de la sphère de 10 stades de hauteur à la sphère terrestre.

La sphère qui a pour diamètre la quarantième partie du diamètre d’un grain de mil est la 64 000^e partie d’un grain tout entier. La montagne sphérique de 10 stades de diamètre vaut à peu près 24 stades cubes et toute la terre supposée sphérique vaut, en stades cubiques. 270 troisièmes myriades, 250 deuxièmes myriades, 1350 premières myriades, 8297 et la fraction 14/21^e.[4]

En outre on démontre que le rectangle formé par le diamètre d’une sphère et la circonférence d’un grand cercle, développée en ligne droite, égale 4 fois la surface du quart de la sphère, lequel quart égale la surface du cercle. Le carré du diamètre est à la surface du cercle comme 14 est à 11: car la circonférence du cercle égale 3 fois le diamètre plus la septième partie de ce diamètre. Si le diamètre et 7, la circonférence est 22. Le quart de la circonférence est 5 + 1/2. Donc le carré du diamètre étant 49, le cercle avant ce mètre est 38 + 1/2: et si nous doublons pour faire disparaître 1/2, le carré du diamètre étant 98, le cercle ayant ce diamètre sera 77. Or le rapport de ces nombres, exprimé en termes les plus petits et premiers entre eux, est celui de 14 à 11, car la plus grande commune mesure de ces deux nombres est 7 qui et contenue 14 fois dans 98 et 11 fois dans 77. Donc le rapport du cube du diamètre au cylindre circonscrit à la sphère, laquelle est contenue une fois et demi dans le cylindre, d’après Archimède, est aussi égal au rapport de 14 à 11. Ainsi donc quand le cube du diamètre du cercle sera 14, le cylindre circonscrit sera 11 et la sphère 7 + 1/3.

C’est ainsi qu’on trouve les volumes exprimés en nombres de la sphère terrestre et de la plus haute montagne. Une montagne haute de 10 stades, qui serait une sphère, serait beaucoup plus petite par rapport à la terre, que la 64.000^e partie d’un grain de mil, par rapport à une sphère d’un pied de diamètre. Or les montagnes ne sont pas sphériques, et, telles qu’on les voit, elles sont beaucoup plus petites. Mais une telle partie d’un grain de mil, qu’elle soit superposée sur une sphère d’un pied de diamètre, ou qu’elle en soit enlevée et placée dans un creux ne produira aucune différence de forme. Les montagnes les plus élevées ayant 10 stades ont le même rapport avec la terre, elles n’empêcheront donc pas que l’ensemble de la terre et de la mer ne soit réellement une sphère.

Le tour de la terre vaut donc                                            232.000 stades

le diamètre                                                                                     80.182

le carré du diamètre                                                6.429.153.124 st. carrés

le cube                                                          515.502.355.788.568 st. cubiq.

et le quatorzième de ce cube                          36.821.596.812.040 et 4/7,

< Le produit de ce nombre par 22/3 est égal au volume de la terre et vaut, en stades cubiques 270.025.043.508.097 et 14/21.[5] >

IV. La terre est sphérique et placée au centre du monde. Si elle était éloignée de cette position, elle n’aurait point de tout côté la moitié du ciel au-dessus d’elle et l’autre moitié au-dessous. De plus les lignes droites menées de tout point aux extrémités de la sphère céleste ne seraient égales. Que le volume de la terre n’ait aucun rapport sensible avec l’étendue de l’univers, qu’elle n’occupe qu’un point dans cet univers, les pointes des gnomons le montrent en tout lieu de la terre habitée; elles peuvent en effet être prises pour centre de l’orbite solaire, car en changeant de lieu on n’observe aucun changement sensible, Si donc il y a nécessairement un centre pour l’ensemble de toutes les sphères, tous les points de la terre paraissent être ce centre. Il est donc évident que toute la terre n’est qu’un point par rapport à toute la sphère du soleil et à plus forte raison par rapport à la sphère des étoiles. C’est pour cela que la moitié du monde, ou à peu près, apparaît toujours à nos yeux.

Quoique nous puissions dire beaucoup d’autres choses sur la forme de l’univers et de la terre, sur la position centrale de celle-ci, ainsi que sur sa grandeur peu apparente par rapport à l’univers, ce qu’a démontré Adraste de la manière précédente suffira pour l’exposition de ce qui suit. Voici ce qu’il dit ensuite

Des cercles célestes

V. La sphère céleste tournant autour des pôles immobiles et de l’axe qui les joint et au milieu duquel est fixée la terre, tous les astres emportés par cette sphère, et tous les points du ciel, décrivent des cercles parallèles. C’est-à-dire partout équidistants, perpendiculaires à l’axe, et tracés des pôles de l’univers comme centres. On peut compter les cercles décrits par les étoiles, mais les cercles décrits par les autres points sont innombrables. On a donné à quelques-uns de ces cercles des noms particuliers qu’il est utile de connaître pour rendre compte de ce qui se passe au ciel.

Il y en a un au-dessus de nous, autour du pôle toujours apparent et lui-même toujours visible. On l’appelle cercle arctique, à cause des constellations des ourses qu’il traverse. Un autre, du côté opposé, égal au premier, autour du pôle que nous ne voyons jamais, est lui-même toujours invisible pour nous, on l’appelle cercle antarctique. Celui du milieu, qui est un grand cercle, divise toute la sphère en deux parties égales et s’appelle équinoxial, parce que pour les régions correspondantes de la terre il y a égalité entre les jours et les nuits; pour les autres lieux où l’on voit le soleil se lever et se coucher suivant le mouvement général de l’univers, les durées du jour et de la nuit sont égales quand le soleil décrit ce cercle.

Entre le cercle équinoxial et les deux cercles arctiques, il y a d’un côté le tropique d’été situé pour nous en deçà du cercle équinoxial, et de l’autre côté le tropique d’hiver. Le soleil dans sa révolution se rapproche tantôt de l’un tantôt de l’autre, Entre ces deux cercles s’étend en effet obliquement le zodiaque.

VI. Le zodiaque est aussi un grand cercle. Il touche chaque tropique en un point : le tropique d’été en un point du Cancer et l’autre en un point du Capricorne. Il coupe l’équinoxial en deux parties égales et est lui-même divisé également par ce cercle en un point du Bélier et un point du Scorpion. C’est dans sa zone que sont emportés le soleil, la lune et les autres planètes: Phénon qu’on nomme l’astre de Saturne ou, suivant quelques-uns, du soleil, Phaéton l’astre de Jupiter, Pyroïs celui de Mars ou d’Hercule, Lucifer qu’on nomme aussi Vénus, ou encore l’étoile du malin et l’étoile du soir, et près de ces astres Stilbon qu’on nomme aussi Mercure.

VII. On appelle horizon le cercle qui borne notre vue et divise, ainsi qu’on le voit, la terre faisant obstacle, le ciel tout entier en deux parties égales: l’une au-dessus de la terre est l’hémisphère visible, l’autre au-dessous est l’hémisphère invisible. Comme c’est aussi un grand cercle de la sphère, il coupe en deux parties égales les grands cercles tels que l’équinoxial et le zodiaque. Si deux astres sont diamétralement opposés, quand l’un se lève l’autre se couche. L’horizon partage aussi le méridien en deux parties égales,

VIII. Car il y a un autre grand cercle, nommé méridien, qui passe par les deux pôles du monde et que l’on conçoit perpendiculaire à l’horizon. On le nomme méridien par ce que le soleil le coupe au milieu du jour, étant au point le plus élevé de sa course au-dessus de l’horizon. On le nomme quelquefois colure, parce qu’une de ses parties, celle qui est du côté du pôle invisible, est cachée pour nous.

IX. L’équinoxial et le deux tropiques situés de part et d’autre sont des cercles donnés et fixes de grandeur et de position. On dit que des points et des lignes sont donnés de position, quand ils occupent toujours le même lieu: on dit que des surfaces, des lignes, des angles, sont donnés de grandeur, quand on peut trouver des grandeurs égales. Or l’équinoxial et les deux tropiques placés de part et d’autre ont toujours la même position, sont toujours fixes, et on pourrait trouver des cercles égaux : le zodiaque, l’horizon et le méridien étant égaux à l’équinoxial, et le tropique d’été étant égal au tropique d’hiver et réciproquement. C’est pour cela qu’ils sont toujours donnés; il n’est pas en notre pouvoir de les rendre tels ou tels: ils sont naturellement tels; ils sont donnés, nous ne les donnons pas tels.

Quant à ceux qu’il est en notre pouvoir de rendre tels ou tels, ils ne sont pas naturellement donnés. Ceux qui sont naturellement donnés, c’est-à-dire qui sont fixes, et qui existent par eux-mêmes, sont l’équinoxial et les cercles situés de part et d’autre, donnés de grandeur et de position. Le zodiaque est un cercle donné de grandeur et de position par rapport au ciel, mais par rapport à nous, il n’est pas donné de position. Pour nous, en effet, il n’est pas fixe, à cause de son obliquité dans l’univers, qui nous le montre changeant de place.

Le méridien et l’horizon sont aussi donnés de grandeur, car ce sont des grands cercles de la sphère céleste. mais ils changent de position suivant le climat et sont différents dans les différents lieux de la terre. Nous n’avons tous en effet ni le même horizon, ni la même ligne méridienne, ni le même méridien. Quant aux cercles arctique et antarctique qui sont voisins des pôles, ils ne sont donnés ni de grandeur ni de position:[6] suivant la différence des climats plus septentrionaux ou plus méridionaux, on les voit plus grands ou petits. Mais pour la région moyenne de la terre, c’est-à-dire pour la zone qui se trouve sous la ligne équinoxiale et qu’on ne peut habiter à cause de la chaleur, il n’en est pas de même: les deux pôles apparaissent aux extrémités de l’horizon, et on dit quelquefois que la sphère est droite par ce que dans cette région de la terre tous les cercles parallèles sont perpendiculaires à l’horizon.

X. Chacun des autres cercles est un véritable cercle terminé par une seule ligne: mais celui qu’on appelle zodiaque montre une certaine largeur, comme le cylindre d’un tambour: des figures d’animaux sont imaginées sur ce cylindre. On appelle cercle du milieu des signes le grand cercle qui touche les deux tropiques en un point de chacun d’eux, et coupe le cercle équinoxial en deux parties égales. Les deux cercles qui limitent de part et d’autre la largeur du zodiaque sont plus petits que le cercle du milieu.

Des étoiles.

XI. La plupart des astres sont fixes: ils sont emportés ensemble par un mouvement circulaire unique et simple, avec la première sphère qui est la plus grande, comme s’ils lui étaient fixés et s’ils étaient mus par elle. Ils ont toujours la même position relative sur la sphère, conservent entre eux le même ordre et n’éprouvent aucun changement de forme ni de mouvement, de grandeur ni de couleur.

Des planètes.

XII. Le soleil, la lune et les autres astres qu’on nomme errants sont emportés avec l’univers dans le mouvement diurne, d’orient en occident, de même que les étoiles fixes. Mais en dehors de ce mouvement, ils paraissent chaque jour en avoir plusieurs autres. Car, par un mouvement qui leur est propre, ils vont aux signes qui les suivent (dans le mouvement diurne) et non aux signes qui les précèdent entraînés en sens contraire de l’univers, dans une course qu’on appelle mouvement en longitude. De plus, ils ont un mouvement en latitude, du nord au midi et réciproquement, tout en accomplissant leur course en sens contraire du mouvement de l’univers. Les observateurs attentifs les voient emportés du tropique d’été au tropique d’hiver et réciproquement, à travers l’obliquité du zodiaque.

Et dans la largeur du zodiaque, on les voit tantôt plus au nord du cercle du milieu, tantôt plus au midi: les uns s’abaissent plus, les autres moins. En outre ils varient en grandeur, étant tantôt plus éloignés, tantôt plus rapprochés de la terre dans les profondeurs de l’espace. C’est pour cela que la vitesse de leur mouvement à travers les signes paraît inégale : ils ne parcourent pas des espaces égaux dans des temps égaux; ils vont plus vite quand ils paraissent plus grands à cause de leur moins grand éloignement de la terre, ils vont moins vite quand ils paraissent plus petits à cause de leur plus grand éloignement.

La distance parcourue sur le zodiaque, est faible pour le soleil, car elle et à peu près d’une division sur 360. Pour la lune, comme les anciens astronomes l’ont dit, et pour Vénus, elle est pus grande, car elle est de 12 divisions environ. Mercure en parcourt environ 8. Mars et Jupiter environ 5 et Saturne à peu près 3. La lune et le soleil paraissent s’écarter également chacun en latitude du cercle du milieu des signes. Les autres planètes ne s’en écartent pas également, elles sont plus septentrionales dans quelque signe, plus méridionales dans quelque autre.

Quant à la longueur du cercle des point fixes à ce même point, la lune, allant vers les signes suivants et non vers les signes précédents, la parcourt en 2 jours et un tiers, le soleil en une année qui vaut approximativement 365 jours et un quart; Vénus et Mercure vont d’un mouvement inégal, mais peu différent de durée, et pour tout dire ils ont la même vitesse que le soleil, puisqu’on les voit toujours à côté de lui, le suivant tantôt et tantôt le précédant. Mars achève sa course en un peu moins de 2 ans. Jupiter en 12 ans environ et Saturne en un peu moins de 30 ans.

Les conjonctions avec le soleil, les apparitions et les disparitions, qu’on appelle les levers et les couchers, ne sont pas les mêmes pour toute les planètes. La lune, en effet, après sa conjonction avec le soleil, ayant un mouvement plus rapide que lui vers les signes qui suivent apparaît d’abord et se lève le soir, tandis qu’elle disparaît et se couche le matin. Inversement Saturne, Jupiter et Mars qui arrivent moins vite que le soleil aux signes suivants sont précédés et devancés par lui, c’est-à-dire que ces planètes se couchent toujours le soir et se lèvent le matin (après la conjonction).

XIII. Vénus et Mercure qui ont un mouvement égal à celui du soleil, paraissent toujours auprès de lui: tantôt ces deux astres le suivent, tantôt ils le précèdent; tantôt ils paraissent le soir et disparaissent aussi le soir, tantôt ils paraissent à l’aube naissante et disparaissent avec le jour. Tandis que les autres planètes s’éloignent du soleil, de tout intervalle, jusqu’à ce qu’elles lui soient diamétralement opposées, ces deux astres au contraire sont toujours vus auprès de lui. Mercure s’en écarte de 20 degrés environ, c’est-à-dire à peu près de deux tiers de signe, soit vers l’orient, soit vers l’occident: Vénus s’en écarte de 50 degrés environ à l’orient et à l’occident.

XIV. Le lever se fait de plusieurs manières : d’abord proprement et communément, pour le soleil et les autres astres, par leur élévation au-dessus de l’horizon: ensuite pour ceux qui par leur éclat commençant à se distinguer des rayons du soleil, ce qui est encore proprement une manière de se lever. Reste encore le lever appelé lever à la nuit tombante, qui se produit à l’orient après le coucher du soleil, dans la partie du ciel diamétralement opposée. On l’appelle « ἀκρόνυχος » parce qu’il se fait à une extrémité de la nuit, s’est ou commencement. Pareillement le premier coucher est la descente au-dessous de l’horizon. Ensuite il y a le coucher produit par la diffusion de l’éclat de l’astre dans les rayons lumineux alu soleil on l’appelle aussi proprement une disparition. Reste encore le coucher dit coucher de la pointe du jour, quand le soleil se levant, un astre disparaît dans la partie de l’horizon diamétralement opposée.

Parmi les levers et les couchers dépendant du soleil et de ses rayons, c’est-à-dire parmi les phénomènes d’apparition et de disparition, les uns se font le matin, les autres le soir. Le lever de l’astre est au matin, lorsque l’astre précédant les rayons du soleil paraît avant lui à l’orient, comme le lever du Chien. Le lever est au soir, quand l’astre commence à paraître après le coucher lu soleil, comme nous l’avons dit de la lune nouvelle. Pareillement le coucher est au matin quand l’astre, qui les jours précédents se levait avant le soleil, comme la lune, cesse de paraître à son approche; le coucher est au soir, quand le soleil étant tout près d’un astre à l’occident, celui-ci est invisible à cause du rayonnement voisin,

De l’ordre des planètes, et du concert céleste

XV. Relativement à la position et à l’ordre des sphères ou des cercles sur lesquels sont emportées les planètes, voici l’opinion de certains Pythagoriciens. Le cercle de la lune est le plus rapproché de la terre, celui de Mercure est le deuxième au-dessus, puis vient celui de Vénus, celui du soleil est le quatrième, viennent ensuite ceux de Mars et de Jupiter, celui de Saturne est le dernier et le plus rapproché des étoiles. Ils veulent, en effet, que le cercle du soleil tienne le milieu entre les planètes, comme étant le cœur de l’univers et le plus apte à commander. Voici ce que déclare Alexandre d’Étolie:

« Les sphères sont de plus en plus élevées

la lune divine est la plus proche de la Terre; la seconde est Stilbon, astre de Mercure inventeur de la lyre;

vient ensuite Lucifer, astre brillant de la déesse de Cythère;

au-dessus est le soleil traîné des chevaux, et qui occupe le quatrième rang;

Pyroïs, astre du cruel Mars de Thrace, est le cinquième;

Phaéton, astre brillant de Jupiter, est le sixième;

et Phénon, astre de Saturne, près des étoiles, est le septième.

Les sept sphères donnent les sept sens de la lyre et produisent une harmonie, c’est-à-dire une octave, à cause des intervalles qui les séparent deux à deux. »

D’après la doctrine de Pythagore, le monde étant, en effet, harmonieusement ordonné, les corps célestes qui sont distants deux à deux selon les proportions des sons consonants, produisent, par leur mouvement et la vitesse de leur révolution, les sons harmoniques correspondants. C’est pour cela qu’Alexandre s’exprime ainsi dans les vers suivants :

« La terre au centre donne le son grave de l’hypate;

la sphère étoilée donne la nète conjointe;

le soleil placé au milieu des astres errants donne la mèse;

la sphère de cristal donne la quarte par rapport à lui;

Saturne est plus bas d’un demi-ton;

Jupiter s’écarte autant de Saturne que du terrible Mars;

le soleil, joie des mortels, est d’un ton au-dessous;

Vénus diffère d’un trihémiton du soleil éclatant ;

 Mercure renie d’un demi-ton inférieur à Vénus;

vient ensuite la lune qui donne à la nature des teintes si variées ;

enfin, la terre au centre donne la quinte par rapport au soleil

elle a cinq zones, des zones brumeuses à la zone torride, s’accommodant à la chaleur la plus intense, comme au froid le plus glacial.

Le ciel qui comprend six tons, complète l’octave.

Le fils de Jupiter, Mercure, nous représente une Sirène ayant une lyre à sept cordes, image de ce divin monde.[7] »

Dans ces vers, Alexandre a indiqué pour les sphères l’ordre qu’il a voulu, il est évident qu’il a imaginé arbitrairement les intervalles qui les séparent et presque tout le reste. Il dit, en effet, que la lyre à sept cordes, image de l’univers, a été composée par Mercure, et qu’elle donne les consonances de l’octave; puis il établit l’harmonie du monde avec sons qui ne comprennent cependant que six tons.

Il est vrai qu’il attribue à la terre le son de l’hypate, comme étant plus grave que les autres; mais celle-ci étant immobile au centre, ne rend absolument aucun son. Puis, il donne le son de la nète conjointe à la sphère des étoiles et place entre les deux les sept sons des planètes. Il attribue le son de la mèse au soleil. L’hypate ne donne pas avec la mèse la consonance de quinte, mais celle de quarte, et ce n’est pas avec la nète des conjointes qu’elle donne la consonance d’octave, mais avec la nète des disjointes.

Le système n’est pas conforme au genre diatonique, puisque dans ce genre le chant ne comporte ni un intervalle indécomposé de trihémiton, ni deux demi-tons de suite. Il n’est pas non plus chromatique, car dans le genre chromatique la mélodie ne comprend pas le ton indécomposé. Si l’on dit que le système est formé des deux genres, je répondrai qu’il n’est pas mélodieux d’avoir plus de deux demi-tons de suite. Mais tout cela manque de clarté pour ceux qui ne sont pas initiés à la musique.

Eratosthène expose, d’une manière semblable, l’harmonie produite par la révolution des astres, mais il ne leur assigne pas le même ordre. Après la lune qui est au-dessus de la terre, il donne la seconde place au soleil. il dit, en effet, que Mercure, encore jeune, ayant inventé la lyre, monta d’abord au ciel, et qu’en passant près des astres qu’on nomme errants, il s’étonna que l’harmonie produite, par la vitesse de leurs révolutions fût la même que celle de la lyre qu’il avait imaginée…. Dans des vers épiques, cet auteur paraît laisser la terre immobile et veut qu’il y ait huit sons produits par la sphère étoilée et par les sept sphères des planètes qu’il fait tourner autour de la terre; c’est pour cela qu’il fait une lyre à huit cordes, comprenant les consonances de l’octave. Cette explication vaut mieux que celle d’Alexandre.

Les mathématiciens n’établissent ni cet ordre, ni un même ordre parmi les planètes près la lune, ils placent le soleil, quelques-uns mettent au-delà Mercure, puis Vénus, d’autres mettent puis Mercure, ils rangent les autres planètes dans l’ordre que nous avons dit.

Du mythe du Pamphylien dans la « République ».

XVI. Platon, à la fin de la République, voulant exhorter à la justice et à la vertu, raconte une fable dans laquelle, parlant de l’arrangement des corps célestes, il dit qu’un axe traverse le pôle comme une colonne, il ajoute qu’il y a un autre axe du fuseau, avec des boules creuses s’emboîtant les unes dans les autres. Ces boules ne sont autres que les sphères portant les sept planètes; une dernière s sphère, celle des étoiles, enveloppe toutes les autres. Il montre l’ordre de ces sphères, par rapport à la distance de chacun des astres, à leur couleur et à la vitesse de leur mouvement en sens contraire de celui de l’univers. Voici ce qu’il dit :[8]

« Après que chacune de ces âmes eût passé sept jours dans la prairie, il leur avait fallu en partir le huitième se rendre, en quatre jours de marches en un lieu d’où l’on voyait une lumière tendant sur toute la surface du ciel et de la terre, droite comme une colonne, assez semblable à l’arc-en-ciel, mais plus éclatante et plus pure. Il leur avait fallu encore un jour de marche, pour arriver là où l’on voit, au milieu de cette bande lumineuse, les extrémités des attaches fixées au ciel. Cette bande est le lien du ciel et embrasse toute sa circonférence, comme les ceintures des trirèmes (pour empêcher la charpente de se disjoindre). Aux extrémités du lien était tenu le fuseau de la Nécessité. C’est lui qui donne le branle à toutes les révolutions des sphères. La tige et le crochet de ce fuseau étaient de diamant; le fuseau était formé de la même substance et d’autres matières précieuses.

« Voici comment il était fait : il ressemblait pour la forme au fuseau d’ici-bas; mais, d’après la description donnée par le Pamphylien, il faut se le représenter contenant dans sa concavité un autre fuseau plus petit qui en reçoit lui-même un troisième, comme de grands vases ajustés les uns dans les autres, il y en a ainsi un troisième, un quatrième, et quatre autres encore. C’étaient donc en tout huit fuseaux, placés les un dans les autres, dont on voyait d’en haut les bonis circulaires et qui présentaient tous la surface courbe continue d’un seul fuseau autour de la tige passant par le centre du premier. Les bords circulaires de ce fuseau extérieur étaient les plus larges, puis ceux du sixième, du quatrième du huitième, du septième, du cinquième, du troisième et du second allaient en diminuant de largeur selon cet ordre.

« Les bords du plus grand fuseau (sphère des étoiles) étaient de différentes couleurs, le bord du septième (sphère du soleil) était d’une couleur très éclatante, celui du huitième (sphère de la lune) empruntait du septième sa couleur et son éclat. La couleur des cercles du second et du cinquième Saturnne et Mercure était presque la même et ils étaient plus jaunes que les autres; le troisième (Jupiter) avait une couleur très blanche: celle du quatrième Mars était un peu rouge. Enfin, le sixième Vénus occupait le second rang pour l’éclat de sa blancheur.[9] »

« Le fuseau extérieur tout entier faisait sa révolution dans le même sens que l’univers, et, dans l’intérieur, les sept fuseaux concentriques se mouvaient lentement en sens contraire; le mouvement du huitième était le plus rapide, ceux du septième, du sixième et du cinquième étaient moindres et d’une vitesse égale; le quatrième qui a un mouvement rétrograde plus rapide que celui des autres fuseaux et le troisième pour la vitesse, comme il leur parut ; le troisième n’avait que la quatrième vitesse, et le second n’avait que la cinquième. Le fuseau tournait sur les genoux de la Nécessité. Sur chacun de ces cercles émit assise une Sirène qui tournait avec lui et faisait entendre un son toujours le même. De tous ces sons, au nombre de huit, résultait une harmonie parfaite (c’est-à-dire une octave complète). »

Nous expliquons dans les Commentaires de la République cette exposition de Platon. Nous avons aussi construit une Sphère d’après ses explications. Platon dit, en effet, qu’on ferait un travail inutile si on voulait exposer ces phénomènes sans des images qui parlent aux yeux. Il dit que sur les cercles sont assises des Sirènes, c’est ainsi que quelques-uns désignent les planètes elles-mêmes, du mot « σειριάζειν » briller.[10] Du reste, d’après Adraste, les poètes nomment souvent astres brillants « σειρίους » toutes les étoiles. Ainsi, on lit dans Ibyeus : étincelant comme les τείρια qui brillent dans une longue nuit.

D’autres n’appellent particulièrement ainsi que les étoiles brillantes et remarquables. Aratus se sert du verbe σειρᾶν pour indiquer qu’une étoile de la gueule du Chien brille d’un vif éclat,[11] et un poète tragique a dit d’une planète : Quel est donc cet astre brillant, « σείριος » qui passe au dessus de nos têtes?[12] Quelques auteurs prétendent que les astres ne peuvent pas être pris pour des Sirènes, mais que, suivant la doctrine pythagoricienne, des sons et des accords sont produits par leurs révolutions, d’où résulte une harmonie parfaite.

Du mouvement des planètes.

XVII. Pour les planètes, dit Adraste, il y en a qui ont toujours laissées en arrière, tels sont le soleil et la lune qui ne vont jamais vers les signes qui précèdent, mais qu’on voit toujours aller vers ceux qui suivent; aussi ces planètes n’ont-elles jamais de stations ni de rétrogradations. Il en a d’autres qui se meuvent vers les signes précédents et vers les signes suivants, ce sont toutes les autres planètes. C’est pour cela qu’elles paraissent nécessairement tantôt s’arrêter et tantôt rétrograder.

XVIII. Le mouvement contraire est, d’après Adraste, celui d’une planète qui semble toujours aller vers les signes qui suivent à l’orient. Mais, d’après Platon, ce n’est pas une apparence, c’est, en réalité, le mouvement propre d’un astre qui va à l’orient dans les signes suivants, par exemple, du Cancer dans le Lion.

XIX. Le mouvement en avant est le mouvement d’une planète qui semble aller vers les signes précédents à l’occident, par exemple, du Cancer aux Gémeaux.

XX. La station est l’état d’une planète qui semble s’arrêter et rester quelque temps près de quelqu’une des étoiles fixes.

XXI. La rétrogradation est le retour apparent d’une planète de sa station en sens contraire de son premier mouvement. C’est ainsi que cela paraît se produire, mais ce n’est qu’une apparence : la cause est que chaque planète se mouvant au-dessous des étoiles, dans un cercle ou dans une sphère qui lui est propre, nous semble, à cause de la résistance, emportée, relativement à la zone zodiacale qui est au dessus: et, comme l’explique Adraste, ce ne sont là que des hypothèses différentes sur les planètes, hypothèses rendues vraisemblables par l’accord avec les phénomènes.

XXII. Il dit que le monde tel qu’il est, composé des parties si nombreuses et si diverses que nous avons distinguées, se meut d’un mouvement circulaire et propre à sa forme sphérique, et que ce mouvement a été communiqué par un premier moteur; c’est pourquoi ce monde a été arrangé, grâce à une cause supérieure et la meilleure. Le mouvement des planètes a été diversement disposé pour le calcul du temps et leur retour au périgée et à l’apogée, de sorte que ce qui se fait ici-bas suit complètement ce mouvement. C’est, en effet, par les révolutions des astres qui viennent ou s’en vont que sont aussi changées toutes choses ici bas. Le mouvement circulaire des étoiles est simple et unique, il est régulier et uniforme; le mouvement des planètes est, il est vrai, circulaire; mais il ne paraît ni simple et unique, ni uniforme et régulier. Et dans le monde sublunaire autour de nous et jusqu’à nous, tout est changement et mouvement, et comme dit le poète:

Ici-bas on ne voit que l’envie et le meurtre.

Et tous les autres maux.[13]

Il n’y a, en effet, que génération et corruption, accroissement et décroissance, altération en tout genre et changement de lieu. Les planètes, dit Adraste, sont la cause de tous ces phénomènes. On dira que ces choses existent, non comme ce qu’il y a de plus précieux, de divin, d’éternel, de non engendré, d’incorruptible, causé par ce qui est moindre, mortel et périssable, mais bien qu’elles sont ainsi à cause de ce qu’il y a de meilleur, de plus beau, de plus heureux, et que ce qui est ici-bas ne suit que par accident la marche des choses supérieures.

Pour que le mouvement de l’univers qui résulte d’une force active et d’une cause divine, soit circulaire et toujours semblable à lui-même. Il faut que la terre occupe le centre autour duquel se produit le mouvement, et s’il faut qu’elle soit en dessous, il faut aussi que le feu occupe le lien opposé vers l’essence éthérée qui se meut en cercle. Entre les deux éléments ainsi séparés, il faut que les autres, l’eau et l’air, soient en proportion. Cela étant, il faut encore qu’il y ait changement de toutes choses ici-bas, parce que la nature des choses est profondément changeante et qu’elles sont soumises à des forces contraires.

Le changement se fait par le mouvement varié des planètes: en effet, si celles-ci étaient emportées suivant des cercles parallèles par le même mouvement que les étoiles fixes, la disposition de tous les corps étant universellement la même, il n’y aurait ici-bas aucun changement, aucune vicissitude. Or, les solstices et les équinoxes, les mouvements en avant et les retours, en hauteur et en latitude, surtout du soleil et de la lune, mais aussi des autres planètes, amènent les différentes saisons et produisent ici-bas: toutes les transformations, toutes les générations et toutes les altérations. L’aspect varié que présente la révolution des planètes, provient de ce pic, fixées à des cercles propres ou à des sphères propres dont elles suivent le mouvement, elles sont emportées à travers le zodiaque, ainsi que Pythagore l’a compris le premier, par une révolution réglée, simple et égale, mais d’où résulte, par accident, un mouvement apparent varié et inégal.

XXIII. Voici ce que dit Adraste de la position des cercles ou des sphères, position qui rend compte des apparences.

Il est naturel et nécessaire que, comme les étoiles fixes, chacun des autres corps célestes soit emporté uniformément et régulièrement, d’un mouvement simple et qui lui est propre. Je dis que cela sera évident, si, par la pensée, supposant le monde immobile, nous imaginons que les planètes se meuvent au-dessous du zodiaque immobile par hypothèse; leur mouvement alors ne paraîtra plus varié et inégal, mais il paraîtra s’accomplir régulièrement comme nous l’avons montré par la construction de la Sphère de Platon.

Un double mouvement est la cause du mouvement varié apparent dans un sens et dans l’autre: la sphère étoilée est emportée d’orient en occident autour de l’axe qui passe par les potes, et dans le mouvement rapide qui lui est propre. Elle entraîne les planètes et décrit les parallèles que suivent les étoiles; d’un autre côté, les planètes, par un mouvement plus lent qui leur est propre, sont emportées du couchant au levant, dans des temps inégaux, sous le zodiaque oblique aux trois cercles parallèles, le tropique d’hiver, l’équinoxial et le tropique d’été. Ce mouvement s’accomplit autour d’un autre axe, perpendiculaire au zodiaque, et qui s’écarte de l’axe des étoiles de la valeur du côté du pentédécagone régulier.[14] Platon appelle l’axe des planètes tige du fuseau, et même fuseau.

XXIV. Le mouvement est uniforme quand les espaces parcourus en temps égaux sont égaux, sans jamais augmenter ni diminuer de vitesse.

XXV. Le mouvement est régulier, quand le mobile n’a ni station, ni rétrogradation, mais est emporté dans le même sens toujours également. Or, toutes les planètes nous paraissent avoir quelque chose d’inégal certaines même quelque chose de désordonné. Quelle est donc la cause d’une semblable apparence? La principale est que se trouvant sur des sphères ou sur des cercles différents par lesquels elles sont emportées, elles paraissent se mouvoir sur le zodiaque, comme nous l’avons déjà dit.

Du mouvement du soleil

XXVI. Comme conséquences ainsi qu’il a été dit plus haut, les sept planètes, qui ont cependant un mouvement propre simple, décrivent plusieurs cercles différents. Cela deviendra clair pour nous, si nous considérons la plus brûlante et la plus grande de ces planètes, le soleil. Soit αβγδ le zodiaque, θ le centre de ce cercle et de l’univers, qui est en même temps celui de la terre, et soient αγ, βδ deux diamètres perpendiculaires passant par ce point. Soit le point α au commencement du Bélier, β au commencement du Cancer, puis γ au commencement de la Balance et δ au commencement du Capricorne.

Le soleil se trouve en α à l’équinoxe de printemps, en β au solstice d’été, en γ à l’équinoxe d’automne, et en δ au solstice d’hiver; il parcourt irrégulièrement, dans des temps inégaux, les quatre arcs égaux αβ, βγ, γδ, δα. En effet, il va de l’équinoxe du printemps au solstice d’été en 94 jours 1/2, du solstice d’été à l’équinoxe d’automne en 92 jours 1/2, de l’équinoxe d’automne ou solstice d’hiver on 88 jours 1/8, et du solstice d’hiver à l’équinoxe de printemps en 90 jours 1/8, de sorte qu’il parcourt annuellement le cercle entier en 365 jours 1/4 environ; sa plus petite vitesse est en entrant dans les Gémeaux, sa plus grande dans le Sagittaire; dans la Vierge et les Poissons il a une vitesse moyenne

Il est naturel et nécessaire, comme nous l’avons dit, que toutes les créatures divines (les astres) aient un mouvement uniforme et régulier. Il est donc clair que le soleil avant un cours régulier et uniforme, sur un cercle qui lui est propre, paraîtra se mouvoir irrégulièrement pour nous qui le regarderons du point θ sur son cercle αβγδ. Si donc ce cercle avait le même centre que celui de l’univers, c’est-à-dire le point θ, il serait divisé dans les mêmes rapports par les diamètres αγ, βδ nous resterions encore embarrassés en présence de cette égalité des angles au centre et de la similitude des arcs. Il est donc évident que la cause de cette apparence est un mouvement différent qui ne s’effectue pas autour du centre θ. Le point θ sera intérieur à la circonférence, ou il sera sur la circonférence elle-même, ou il sera extérieur. Or il est impossible que la circonférence solaire passe par le point θ, car le soleil rencontrerait la terre dont les habitants auraient les uns toujours le jour, les autres toujours la nuit; il n’y aurait ni lever ni coucher et on ne verrait point le soleil tourner autour de la terre, ce qui est absurde. Il reste donc à supposer le point θ à l’intérieur ou à l’extérieur du cercle solaire. A quelque hypothèse que l’on s’arrête, les apparences seront expliquées, c’est pour cela qu’on peut considérer comme vaines les discussions des mathématiciens qui disent que les planètes ne sont emportées que sur des cercles excentriques, ou sur des épicycles, ou autour du même centre que la sphère étoilée. Nous démontrerons que les planètes décrivent par accident ces trois sortes de cercles, un cercle autour du centre de l’univers, ou un cercle excentrique ou un cercle épicycle. Si nous supposons que le point θ est à l’intérieur du cercle solaire, mais non au centre, on dit que le cercle est excentrique; si le point θ est extérieur, il y a épicycle.

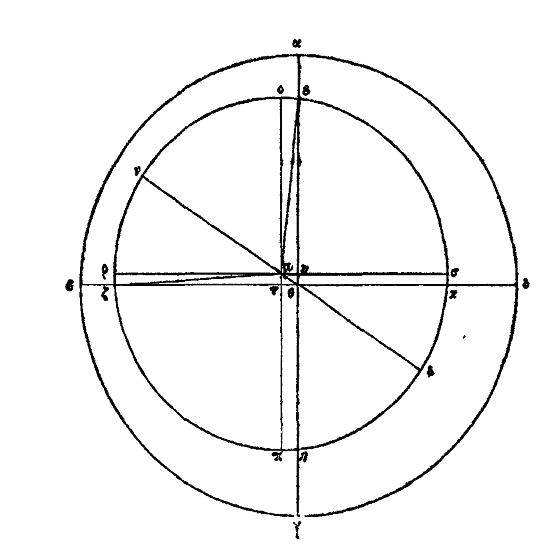
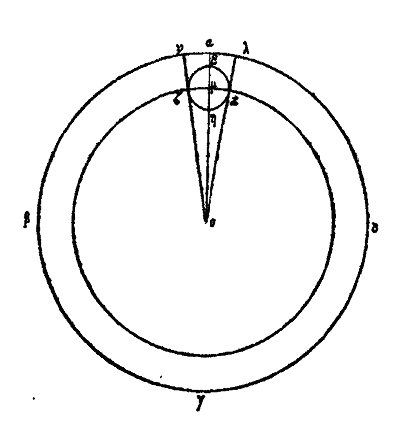
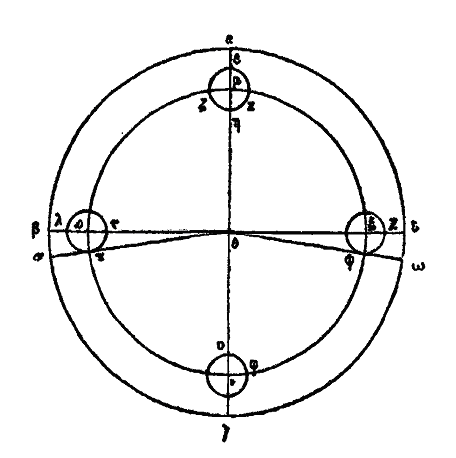
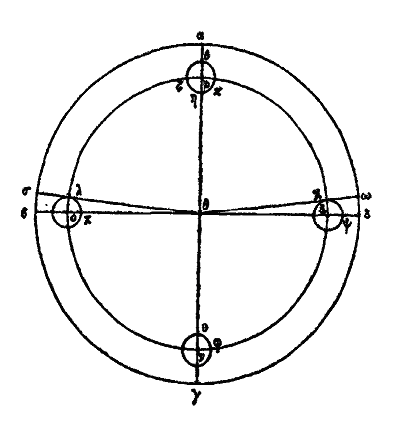
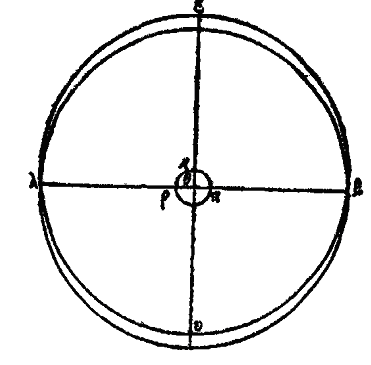
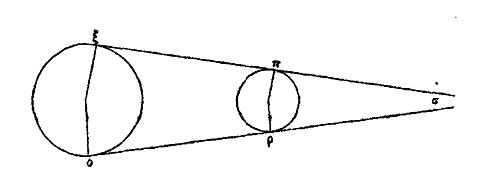
Du cercle excentrique

XXVI bis. Supposons d’abord que le cercle excentrique solaire soit εζηκ, placé de manière à avoir son centre sous l’arc εζ, au point μ par exemple. Supposons encore que le cercle soit divisé en 365 parties et 1/4, que l’arc εζ en contienne 94 1/2, ζη 92 1/2, ηκ 88 1/8 et κε 90 1/8. Il est évident que, lorsque le soleil sera en ε, il nous paraîtra en α, à nous qui le verrons du point θ, suivant une ligne droite. Puis parcourant régulièrement l’arc εζ, qui est la plus grande des quatre divisions de son propre cercle, dans l’espace de 94 jours 1/2, autant de jours qu’il y a de divisions dans l’arc, il parviendra en ζ; là il nous paraîtra en β et il nous semblera avoir parcouru irrégulièrement en un nombre de jours différent (du quart de 365 et 1/4) l’arc αβ qui est le quart du zodiaque.

De même lorsqu’il aura parcouru l’arc ζη, le second de son propre cercle en grandeur, dans l’espace de 92 jours 1/2 qui correspondent au nombre des divisions de l’arc, il se trouvera en η, et il nous paraîtra en γ, il nous semblera qu’il a parcouru irrégulièrement en moins de jours, l’arc βγ, quart du zodiaque, égal au précédent. Pareillement lorsqu’il aura parcouru l’arc ηκ, la plus petite des quatre divisions du cercle, en 88 jours 1/8, nombre égal aux divisions de l’arc, il sera en κ et il nous paraîtra en δ, à nous qui l’observerons du point θ, il nous semblera avoir parcouru l’arc γδ égal aux précédents en un nombre moindre de jours.

Enfin, pour la même raison, lorsqu’il aura parcouru κε en 90 jours 1/8, nombre de jours égal au nombre des divisions de l’arc, et qu’il sera revenu en ε, il nous semblera qu’il a parcouru, en 90 jours 1/8, l’arc δα égal aux autres, et qu’il est revenu en α. C’est pour cela que parcourant uniformément son cercle, il semblera parcourir irrégulièrement le cercle zodiacal. Or si joignant les centres θ, μ, par une ligne droite, nous prolongeons cette ligne de part et d’autre, nous aurons μν = μξ, puisque μ est le centre du cercle εζ. Ainsi donc le soleil en ν sera à sa plus grande distance de la terre et pour nous qui sommes au point θ, il nous paraîtra avoir le minimum de grandeur et de vitesse; ce phénomène paraît se produire vers le 5^e degré 1/2 des Gémeaux.

Arrivé en ξ il sera à sa plus petite distance de la terre et il paraîtra avoir le maximum de grandeur et de vitesse; ce dernier fait semble se produire au 5^e degré 1/2 du Sagittaire. Et avec raison il paraît avoir une grandeur et une vitesse moyenne, quand il occupe les mêmes degrés dans les Poissons et dans la Vierge. C’est ainsi que seront expliquées toutes les apparences.

Le cercle εζηκ est donné de position et de grandeur. Menons, en effet, par le point μ les droites οπ, ρσ respectivement parallèles aux droites αγ, βδ, perpendiculaires entre elles et joignons ζμ, με. Le cercle εζηκ étant divisé en 365 parties et 1/4, il est évident que l’arc εζη en contiendra 187 et l’arc ηκε 178 et 1/4; mais les arcs εο, πη sont égaux, ainsi que les arcs ρζ, σκ; de plus chacun des arcs σπ, πρ, ρο, οσ est représenté par 91 divisions + 1/4 + 1/16.[15] L’angle ομν est donc donné, il est égal à l’angle θμτ. De même l’angle ρμν = υμθ donc le rapport de μτ à μυ c’est-à-dire de μτ à θτ, est donné et le triangle μτθ est donné de forme. Mais le centre θ de l’univers est aussi donné par rapport aux deux points ν et ξ, car l’un de ces points est à la plus grande distance de la terre et l’autre à la plus petite. La ligne droite θμ joint les centres de l’univers et du cercle solaire, Le cercle εζηκ est donc donné de position et de grandeur. On trouve par la considération des distances et des grandeurs que le rapport de la droite θμ à μν est à peu près celui de 1 à 24. Telle est l’hypothèse sur le cercle excentrique, hypothèse qui explique toutes les apparences.

Du cercle épicycle

XXVI ter. Voici maintenant le raisonnement au moyen de l’épicycle. Soit encore le zodiaque «‘8 et le cercle solaire αβγδ qui laisse à l’extérieur le centre θ de l’univers. La sphère étoilée se mouvant du levant β au méridien α, puis du point α au couchant δ, ou le cercle εζηκ sera immobile ou il se mouvra lui-même pendant que le soleil tournera autour de lui. S’il est immobile, il est clair que le soleil ne paraîtra ni se lever ni se coucher; mais il produira toujours le jour pour ceux, qui sont au-dessus de la terre et toujours la nuit pour ceux qui sont au-dessous, par rapport à nous, et, dans une seule révolution (diurne) de l’univers, il paraîtra parcourir tous les signes. Ce qui est contraire aux faits.

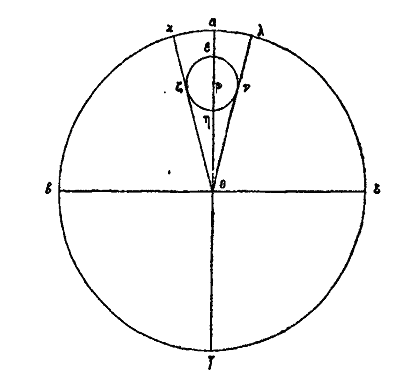
Le cercle se mouvra donc lui-même, et, se mouvant, il se portera dans le même sens que l’univers ou en sens contraire. S’il tourne dans le même sens, c’est avec une vitesse égale, ou plus grande ou plus petite. Supposons qu’il se meuve avec la même vitesse, tirons les droites θζν, θκλ, tangentes au cercle εζ, le soleil paraîtra toujours aller et venir dans l’arc ναλ du zodiaque. En effet, arrivé en ζ il paraîtra en ν ; lorsqu’il sera en ε il paraîtra en α, et transporté en κ il paraîtra en λ. Lorsqu’il aura parcouru l’arc ζεκ, il paraîtra avoir décrit l’arc ναλ vers les signes qui précèdent. Puis lorsqu’il aura parcouru l’arc κηζ, il paraîtra se porter par l’arc λαν vers les signes suivants. Or cela ne se passe pas ainsi, le cercle solaire εζηκ ne se porte donc pas dans le même sens que l’univers avec la même vitesse. Il n’a pas non plus une vitesse plus grande, car alors il paraîtrait devancer les étoiles et parcourir le zodiaque en sens contraire, c’est-à-dire du Bélier aux Poissons et au Verseau. Ce qui n’est pas.

Il est donc évident que le cercle εζηκ se meut dans le même sens que l’univers, avec une vitesse moindre, c’est pour cela qu’il paraît être laissé en arrière et passer dans les signes suivants, de sorte qu’il paraît avoir un mouvement propre, contraire à celui de l’univers, tout étant emporté chaque jour dans le même sens, du levant au couchant. C’est ainsi qu’il paraître passer dans les signes suivants, étant en quelque sorte laissé en arrière.

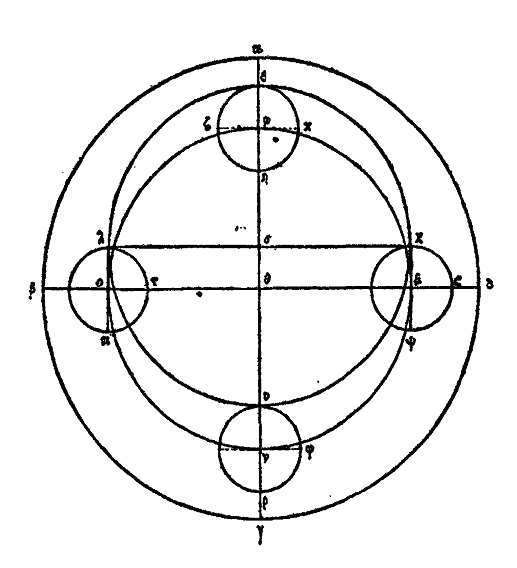
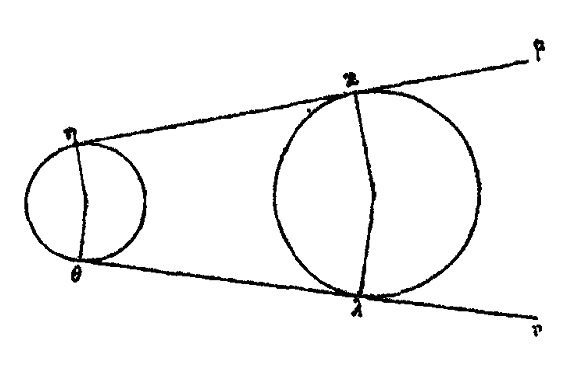
Comment donc ce cercle rendra-t-il compte de ces apparences? Soit μ le centre du cercle solaire. Décrivons le cercle μονξ du centre θ avec le rayon θμ, et supposons que le cercle εζηκ est emporté d’orient en occident en même temps que l’univers et qu’il est laissé en arrière à cause de sa moindre vitesse, ou bien qu’il se meut dans un sens contraire à celui de l’univers, ce qui paraît plus probable à Platon,[16] de sorte que le centre, emporté régulièrement sur le cercle μονξ le parcourt dans l’espace d’un an, et que le soleil, dans ce même laps de temps, achève aussi sa propre révolution, d’un mouvement régulier. En outre, le soleil sera porté sur le cercle εζηκ ou dans le même sens que l’univers ou en sens contraire, c’est-à-dire dans le même sens que son cercle propre, du point κ au point ε et du point ε au point ζ.

Or je dis que le cercle εζηκ étant emporté sur le cercle μονξ, d’un mouvement contraire à celui de l’univers, le soleil se mouvra sur le cercle εζηκ dans le même sens que l’univers et expliquera ainsi les apparences.

Supposons d’abord qu’il soit emporté par un mouvement 5 contraire à celui de l’univers, mais dans le même sens que son cercle, c’est-à-dire de ε en ζ, de ζ en η, de η en κ. Puisque parvenu en ε il sera le plus éloigné de nous, il est clair que α est dans le cinquième degré et demi des Gémeaux, donc γ sera dans le cinquième degré et demi du Sagittaire. Supposons que le point μ centre du cercle solaire, décrive d’un mouvement régulier l’arc μο, quart de la circonférence du cercle μονξ et que le cercle εζηκ soit transporté en λπ, le soleil, emporté régulièrement dans le même sens, décrira l’arc εζ de la circonférence du cercle εζηκ. Il sera donc au point π et il nous apparaîtra en σ, et lorsqu’il aura décrit l’arc εζ, quart de son propre cercle, il paraîtra avoir parcouru l’arc αβσ, plus grand que le quart du zodiaque, et s’être éloigné rapidement du point α.

Le centre ο décrira ensuite l’arc ον, quart de la circonférence, le cercle λπ viendra et φυ, et le soleil aura parcouru l’arc τπ, quart de la circonférence, il sera donc en υ, nous apparaîtra en γ et semblera avoir parcouru l’arc σγ, moindre que le quart du zodiaque et s’être rapproché lentement du point γ. Le point ν ayant parcouru le quart νξ de la circonférence, son cercle sera porté en χψ, et le soleil ayant décrit le quart de la circonférence sera au point ψ, il apparaîtra au point ω et semblera avoir décrit l’arc γω, moindre que le quart de la circonférence, et être venu lentement du point γ.

Enfin le centre ξ, décrivant l’arc ξμ, quart de la circonférence, rétablira le cercle ψχ sur εζηκ, et le soleil lui-même, ayant décrit un arc semblable ψχ, reviendra en ε et apparaîtra en α. Alors aussi il semblera avoir décrit un arc ωδα du zodiaque plus grand que le quart de la circonférence et s’être hâté d’arriver en α. Il est donc évident que dans son mouvement il paraîtra avoir une plus grande vitesse dans les Gémeaux et une moindre dans le Sagittaire. C’est cependant le contraire qu’on observe. Tandis que le cercle solaire est emporté sur la circonférence du cercle concentrique μονξ en sens contraire de l’univers, le soleil ne peut donc pas se mouvoir sur l’épicycle dans le même sens que ce cercle et en sens contraire de l’univers.

Il reste à examiner le cas où l’épicycle ayant un mouvement contraire à celui de l’univers, le soleil se meut sur l’épicycle dans le même sens que les étoiles fixes. C’est ainsi que seront expliquées les apparences. En effet, supposons que le centre de l’épicycle décrive l’arc μο quart de la circonférence du cercle concentrique, et qu’il transporte avec lui l’épicycle en λπ, le soleil aura décrit sur l’épicycle l’arc semblable εκ, il sera donc en λ et il nous apparaîtra en σ, ayant parcouru un arc égal au quart de son propre cercle; mais sur le zodiaque ii semblera avoir parcouru l’arc plus petit ασ, avec une vitesse faible à partir du point α.

Puis le centre ο décrira le quart ον de la circonférence et le soleil décrira l’arc semblable λπ de l’épicycle, alors il sera en υ et paraîtra en γ, semblera avoir parcouru, en augmentant de vitesse vers γ, l’arc du zodiaque σβγ plus grand qu’un quart de circonférence. Que ν soit transporté en ξ, l’arc νξ étant le quart de la circonférence et que le cercle υφ s’applique sur le cercle χψ, le soleil décrivant l’arc υφ semblable aux précédents sera en χ, et paraitra en ω; il semblera avoir parcouru l’arc γδω du zodiaque, plus grand qu’un quart de circonférence, et être passé rapidement de γ en δ.

Le centre parcourant l’arc restant ξμ, l’épicycle χψ reviendra en εζηκ et le soleil, décrivant l’arc semblable χψ qui reste sera rétabli en ε. Il apparaîtra en α et semblera avoir parcouru l’arc ωα, plus petit qu’un quart de circonférence, et s’être lentement approché de α. C’est ainsi que suivant cette hypothèses toutes les apparences s’expliquent, car le soleil paraîtra se mouvoir plus lentement et être plus petit, vers le cinquième degré et demi des Gémeaux et se mouvoir plus rapidement et être plus grand, vers le même degré du Sagittaire. Ce qui est conforme aux apparences. Car il passe du point ε au point κ, tandis que le centre du cercle passe lui-même de μ en ο, ayant un mouvement contraire (à celui de son propre cercle)...

Allant en π, pendant que l’épicycle passe de ο en ν, le soleil, qui va dans le même sens que lui, paraîtra s’avancer sur le zodiaque d’un mouvement en quelque sorte concordant os avec le sien. Pareillement transporté de υ en φ, pendant que l’épicycle passe de ν en ξ, il paraîtra augmenter de vitesse sur le zodiaque, comme s’il devançait son propre cercle. Au contraire, en passant de χ en ψ pendant que l’épicycle passe de ξ en μ, le soleil, transporté en sens contraire du mouvement de son propre cercle, paraîtra accomplir lentement sa marche sur le zodiaque.

On peut trouver la grandeur de l’épicycle et le rapport de la distance des centres au diamètre εη de l’épicycle εζ. Ce rapport inverse du précédent, car il est égal au rapport de 24 à 1, s’obtient par la considération des distances et des grandeurs. La plus grande distance du soleil à la terre est θε, la plus petite est θυ et la différence de ces deux distances est égale au diamètre de l’épicycle. Telle est l’explication au moyen de l’épicycle, le cercle εζκ de la planète se mouvant sur un cercle concentrique qui est μονξ.

Adraste montre ainsi que les phénomènes sont expliqués dans l’une et l’autre hypothèse, celle de l’excentrique et celle de l’épicycle. Hipparque a fait remarquer qu’elle est digne de l’attention du mathématicien, la recherche de l’explication des mêmes phénomènes à l’aide d’hypothèses si différentes, celle des cercles excentriques et celle des cercles concentriques et des épicycles. Adraste a montré que l’hypothèse de l’excentrique est une conséquence de celle de l’épicycle; à dire vrai, l’hypothèse de l’épicycle est aussi une conséquence de celle de l’excentrique.

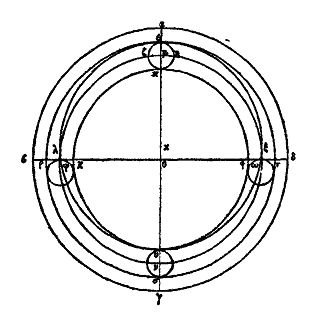
Soit, en effet, αβγδ le zodiaque, θ le centre de l’univers, εζηκ l’épicycle du soleil et μ son centre. Décrivons, du centre θ, avec le rayon θμ, le cercle μονξ ; je dis que le centre parcourant uniformément la circonférence du cercle homocentrique μονξ, d’un mouvement contraire à celui de l’univers et emportant avec lui l’épicycle, il arrivera que le soleil, parcourant dans le même temps l’épicycle εκηζ, d’un mouvement uniforme et dans le même sens que l’univers, décrira aussi l’excentrique égal au concentrique μονξ. Menons, en effet, les diamètres du zodiaque αγ, βδ perpendiculaires entre eux, de manière que le point α soit sur le cinquième degré et demi des Gémeaux et γ sur le même degré du Sagittaire, et des centres ο, ν, ξ, traçons les cercles λπτ, υρφ, χψς, égaux à l’épicycle εζηκ et les diamètres λπ et χψ des cercles λπτ et χψς perpendiculaires au diamètre βδ ; tirons enfin la droite λχ.

Les droites λχ, οξ, sont égales et parallèles entre elles. Les droites λσ et σχ sont donc respectivement égales aux droites οθ et θξ qui sont des rayons du cercle μονξ ; et puisque la droite θσ est égale à ολ, elle sera aussi égale à chacune des droites υν, με. Mais ou a θμ = θν, donc on a aussi υσ = σε, or θσ = υν, et la droite θυ est commune; donc συ =υν. Chacune des deux droites εσ et συ est donc égale au rayon du cercle μονξ; mais on a montré que chacune des droites λσ, σχ est égale au rayon de ce cercle, les quatre droites σε, σλ, συ, σχ, sont donc égales et perpendiculaires entre elles; donc le cercle décrit du centre σ, avec un rayon égal à l’une de ces droites, passera par les points ε, λ, υ, χ, sera égal au cercle μονξ et sera divisé en quatre parties égales par les diamètres ευ, λχ. Décrivons ce cercle et supposons que ce soit ελυχ. Il sera excentrique; le point qui se projette en α, au cinquième degré et demi des Gémeaux, sera le plus éloigné de la terre, et le point qui se projette en γ, au cinquième degré et demi du Sagittaire, en sera le plus rapproché.

Je dis que le soleil, mu, comme on l’a supposé, sur l’épicycle εκηζ, décrira naturellement l’excentrique ελυχ. En effet, que le centre de l’épicycle décrive l’arc μο, quart de la circonférence, le soleil dans le même temps décrira l’arc semblable εκ de l’épicycle, viendra en λ et arrivera de ε en λ ayant parcouru le quart ελ de l’excentrique. Que le centre décrive de nouveau le quart ον de la circonférence, le soleil parcourra l’arc semblable λτ de l’épicycle; il sera donc en υ et décrira a par conséquent l’arc semblable λυ de l’excentrique. Pareillement, pendant que le point ν décrira l’arc νξ, le soleil parcourra l’arc semblable υφ de l’épicycle, il sera donc en χ, ayant décrit par conséquent l’arc semblable υχ de l’excentrique. Enfin, pendant que le point ξ parcourra l’arc εμ le soleil ayant décrit l’arc χς reviendra en ε. Il décrira donc aussi dans le même temps l’arc semblable restant εχ de l’excentrique. Ainsi, en parcourant uniformément tout l’épicycle, pendant que celui-ci est emporté sur le concentrique, le soleil décrit un excentrique; c’est ce qu’il fallait prouver.[17]

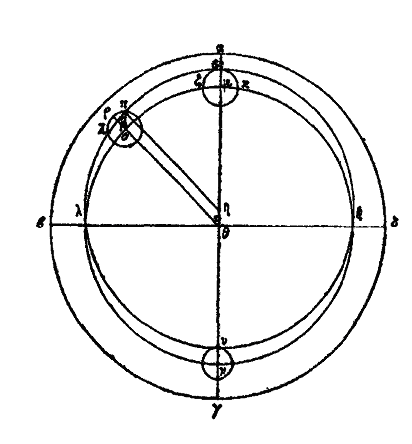
On démontre la même proposition de cette manière. Soit αβγδ le zodiaque[18] et εζκ l’épicycle solaire ayant son centre sur la circonférence du cercle μονξ qui est homocentrique autour du centre θ de l’univers. Soit aussi le point ε, le point le plus éloigné de la terre, au cinquième degré et demi des Gémeaux, je dis que l’épicycle κε, étant emporté sur la circonférence du cercle μονξ d’un mouvement uniforme et contraire à celui de l’univers, et le soleil parcourant dans le même temps l’épicycle εκζ, d’un mouvement uniforme et contraire à l’épicycle, et par conséquent dans le même sens que l’univers, décrira par suite un excentrique égal au concentrique μονξ.

Supposons en effet, que le centre μ ait décrit un arc quelconque μο et que l’épicycle soit arrivé en πρχ, le soleil parti du point ε, c’est-à-dire du point ρ aura décrit dans le même temps l’arc ρπ, semblable à l’arc μο; prenons la droite θη égale au rayon με et tirons les droites ηπ, θρ. Puisque l’arc ρπ est semblable à l’arc ομ, l’angle φ est égal à l’angle τ.[19] Donc la droite πο est parallèle à θη mais elle lui est aussi égale, la droite πη est donc égale et parallèle à la droite οθ. Or la droite θο est égale à la droite ηε. Donc la droite, ηπ est égale à la droite ηε. Donc le cercle décrit du centre η, avec le rayon ηε, passera par π et sera égal au cercle μονξ.

Décrivons le cercle επλυξ (du centre η, avec ηπ = ηε pour rayon); ce cercle sera l’excentrique. Puisque πη est parallèle à ρθ, l’angle φ sera égal à l’angle τ ; c’est-à-dire à πηε, l’arc επ est donc semblable à l’arc πρ (de l’épicycle πρχ). Le soleil partant du point ε décrira par conséquent l’arc επ semblable de l’excentrique. On démontrera de même qu’il en est toujours ainsi; de sorte que le soleil ayant parcouru tout l’épicycle se mouvant lui-même sur un cercle concentrique décrit aussi tout un cercle excentrique. C’est ce qu’il fallait démontrer.

On peut démontrer aussi la proposition inverse. Soit de nouveau αβγδ le zodiaque dont le diamètre est αγ et le centre θ ; soit encore ελυξ le cercle excentrique du soleil, ε le point le plus éloigné du centre de la terre, sous le cinquième degré et demi des Gémeaux, et soit η son centre sur la droite αθ. Décrivons, du centre θ avec le rayon ηε, le cercle μονξ et du centre μ, avec le rayon με, le cercle εζκ. Il est clair que ce sera le même que l’épicycle. Je dis donc que le soleil décrivant uniformément la circonférence ελυξ de l’excentrique, décrira aussi par suite l’épicycle εζκ emporté uniformément dans le même temps sur le concentrique μονξ.

Supposons, en effet, que le soleil ait décrit un arc quelconque επ de l’excentrique. Tirons la droite πη, et sa parallèle θρ. Qu’on prenne ορ égale à θη et qu’on tire πο. Puisque les droites ηπ, θο, sont égales et parallèles, les droites ηθ, πο seront aussi égales et parallèles; mais on a θη = με, donc ορ = οπ, donc le cercle décrit du centre ο avec le rayon ορ passera par le point π et sera le même que l’épicycle εζκ. Décrivons ce cercle πρχ. Α cause du parallélisme des droites (οπ, θη) les angles τ et φ sont égaux; mais dans les cercles à des angles égaux correspondent des arcs semblables, et dans les cercles égaux à des angles égaux correspondent des arcs égaux, que ces angles soient au centre ou sur la circonférence, donc les arcs ρπ, επ, μο sont semblables entre eux, et, de plus, les arcs επ, μο, sont égaux.

Ainsi donc, dans le même temps que le soleil parcourt l’arc επ de l’excentrique, le centre μ de l’épicycle, décrivant l’arc μο, emportera l’épicycle εζκ en πρχ, et le soleil ayant parcouru l’arc επ de l’excentrique en partant du point ε, c’est-à-dire du point ρ, décrira l’arc semblable ρπ de l’épicycle. On peut démontrer qu’il en est ainsi pendant tout le mouvement. Donc, en parcourant tout l’excentrique, le soleil décrit aussi tout l’épicycle. C’est ce qu’il fallait démontrer.

XXVII. Les mêmes démonstrations s’appliquent aux autres planètes. Le soleil paraît faire tous ces mouvements, dans l’une et l’autre hypothèse avec régularité, car les temps des retours à la même longitude, à la même latitude, au même éloignement qui produit l’inégalité qu’on nomme anomalie, sont tellement peu différents les uns des autres, que la plupart des mathématiciens les regardent comme égaux à 365 jours 1/4. Ainsi, quand on considère attentivement le temps du retour en longitude pendant lequel le soleil parcourt le zodiaque, en allant d’un point au même point, d’un solstice au même solstice, ou d’un équinoxe au même équinoxe, c’est à très peu près le temps signalé plus haut, de sorte qu’au bout de quatre ans, le retour à un point de même longitude se fait à la même heure.

Quant au temps de l’anomalie après lequel le soleil au point le plus éloigné de la terre paraît le plus petit et le plus lent dans son mouvement vers les signes suivants, ou après lequel, au point le plus voisin de la terre, il paraît avoir le plus grand diamètre et la plus grande vitesse, il est à peu près de 365 jours 1/2, de sorte qu’au bout de deux ans le soleil paraît revenir à la même distance à la même heure. Enfin, le temps de son retour en latitude, temps après lequel parti du point le plus septentrional ou le plus méridional, il revient au même point, de manière à donner les mêmes longueurs d’ombre des gnomons, il est de 365 jours 1/8, et, par conséquent, on peut dire qu’au bout de huit ans, il sera revenu à la même heure, au même point de latitude.

XXVIII. Pour chacune des autres planètes, les divers temps dont nous avons parlé varient beaucoup, ils sont plus longs pour les uns, plus courts pour les autres. Les durées des retours paraissent d’autant plus variables et plus changeantes dans l’une et l’autre hypothèse que ce n’est pas dans le même laps de temps que chaque planète parcourt son épicycle et l’épicycle son cercle concentrique (au zodiaque): les mouvements sont plus rapides pour les unes, plus lents pour les autres, à raison de l’inégalité des cercles, de l’inégalité des distances au centre de l’univers et des différences d’obliquité par rapport au cercle du milieu des signes c’est-à-dire des différences d’inclinaison et de position.

XXIX. De là vient que, pour toutes les planètes, les stations et les retours, soit vers les signes précédents, soit vers les signes suivants, ne se font pas d’une manière semblable. On observe le phénomène pour cinq planètes, mais d’une manière qui n’est pas absolument semblable. Pour le soleil et la lune, cela ne se fait aucunement; en effet, ces deux astres ne paraissent jamais ni avancer, ni rester stationnaires, ni rétrograder. Comme nous l’avons dit, le soleil paraît emporté sur son propre cercle dans le même temps que l’épicycle sur le concentrique, tandis que l’épicycle de la lune est emporté plus rapidement sur le cercle concentrique au cercle zodiacal, qu’elle ne parcourt elle-même l’épicycle.

XXX. Il est clair qu’il importe peu, pour interpréter les phénomènes, que l’on dise, comme il a été expliqué, que les planètes se meuvent sur des cercles ou que les cercles qui portent ces astres se meuvent autour de leurs propres centres. Je comprends que les cercles concentriques, portant les centres des épicycles, se meuvent autour de leurs propres centres dans un sens contraire à l’univers, et que les épicycles portant les planètes se meuvent aussi autour de leurs centres. Ainsi, je comprends que le cercle μλνξ concentrique se meuve autour de θ, qui est son propre centre et celui de l’univers, dans un sens contraire à l’univers; je comprends, en outre, que le concentrique porte sur sa circonférence le centre μ de l’épicycle εζηκ et que cet épicycle qui porte la planète au point ε, tourne autour du centre μ, dans le même sens que l’univers, s’il s’agit du soleil et de la lune, ou dans un sens contraire, si l’on considère les autres planètes. Ainsi sont expliquées les apparences.

Suivant l’autre interprétation, soit le cercle excentrique ελυξ qui a pour centre le point κ. Considéré par rapport au soleil, ce cercle ελυξ, se mouvant uniformément dans l’espace d’un an, autour du centre κ, et portant le soleil fixé au point ε, rendra compte des phénomènes, si le centre κ se meut par lui-même, non dans un sens contraire à l’univers, mais emporté dans le même sens, et si chaque jour il décrit le cercle κρπ égal au cercle dans l’autre raisonnement.

De la sorte, en effet, le soleil offrira toujours aux mêmes endroits respectifs les plus grandes, les plus petites et les moyennes distances à la terre : les plus grandes, comme il a été dit, au cinquième degré et demi des Gémeaux, les plus petites au même degré du Sagittaire et les moyennes au même degré de la Vierge et des Poissons. En effet, le point de l’excentrique, où est le soleil, vu sous les Gémeaux, dans cette position du cercle, est le plus éloigné de la terre; mais le cercle tournant autour du centre κ, le point ε, transporté où est maintenant le point υ, nous paraîtra dans le Sagittaire à la plus petite distance de la terre. Entre ces deux points extrêmes il se trouvera aux moyennes distances dans la Vierge et les Poissons.

Quant aux autres planètes, c’est en tout lieu du zodiaque qu’elles peuvent être à la plus grande, à la plus petite et à la moyenne distance de la terre et qu’elles peuvent avoir la vitesse minimum, maximum ou moyenne. Du centre θ de l’univers et du rayon θκ, imaginons qu’on décrive le cercle κπρ, puis, que le cercle concentrique et égal à l’épicycle de l’autre hypothèse tourne autour du centre θ de l’univers et qu’il porte avec lui le centre κ de l’excentrique, d’un mouvement contraire à l’univers et dans un temps déterminé, enfin que l’excentrique ελυξ se meuve dans un temps différent autour de son centre κ, portant l’astre fixé sur sa circonférence au point ε ; si on prend les temps propres et particuliers à chaque planète, on rendra compte des phénomènes.

Tout cela nous entraîne trop loin sous prétexte d’accorder les hypothèses et les raisonnements des mathématiciens. Ceux-ci ne considérant que les phénomènes et les mouvements planétaires produits selon le cours des choses, après les avoir observés longtemps dans des lieux favorables, en Babylonie, en Chaldée, en Egypte, recherchaient avec ardeur des principes et des hypothèses qui expliquaient les phénomènes.[20] Ils arrivaient ainsi à confirmer les faits observés et à prédire les phénomènes à venir, les Chaldéens à l’aide de méthodes arithmétiques, les Egyptiens par des méthodes graphiques,[21] tous par des méthodes imparfaites et sans une science suffisante de la nature; car il faut discuter aussi les faits au point de vue physique. Ceux qui ont étudié l’astronomie chez les Grecs ont essayé de le faire en se servant des principes et des observations de ces étrangers. Platon le déclare dans l’Epinomis, comme nous le verrons un peu plus loin, en rapportant ses propres paroles.[22]

XXXI. Aristote, dans son traité Du ciel,[23] parle beaucoup des astres en général et montre qu’ils ne se meuvent ni à travers l’éther tranquille ni avec l’éther, en quelque sorte séparés et indépendants, et qu’ils ne tournent ni ne roulent, mais bien que les nombreuses étoiles fixes sont emportées sur une seule et même sphère, la sphère extérieure et que chaque planète est portée par plusieurs sphères. Il dit encore dans le xi^e livre de la Métaphysique[24] qu’Eudoxe et Callippe mettent les planètes en mouvement à l’aide de certaines sphères. Ce qui concorde, en effet, avec la science naturelle, c’est que les astres ne soient pas emportés de la même manière par certaines courbes circulaires ou hélicoïdales, d’un mouvement contraire à celui de l’univers, et que ces cercles ne roulent pas tous autour de leurs centres, en portant fixés à leurs circonférences les divers astres se mouvant les uns dans le même sens que l’univers, les antres en sens contraire. Comment se pourrait-il, en effet, que de tels corps fussent attachés à des cercles incorporels?

D’après les apparences, des sphères du cinquième corps[25] se meuvent dans les profondeurs du ciel; les unes sont plus élevées les autres moins, les unes sont plus grandes les autres plus petites, les unes sont creuses, les autres pleines sont intérieures aux premières, et les planètes qui y sont fixées, à la manière des étoiles, sont portées d’un mouvement simple, mais de vitesse inégale suivant les lieux. Par un effet qui est la conséquence de tous ces mouvements, elles paraissent se mouvoir diversement et décrire certains cercles excentriques; ou bien, placées sur d’autres cercles, elles paraissent décrire des spirales suivant lesquelles des mathématiciens, trompés par la rétrogradation, pensent qu’elles sont mues.

Comme nous les voyons portées chaque jour par le mouvement de l’univers d’orient en occident et passer par les signes suivants, dans leur course à travers l’obliquité du zodiaque, tantôt plus au nord, tantôt plus au sud, tantôt plus haut, tantôt plus bas, d’où il suit qu’elles paraissent plus ou moins éloignées de la terre, Aristote dit que les anciens les supposaient portées chacune par plusieurs sphères.

Eudoxe dit que le soleil et la lune sont appuyés sur trois sphères : la première est celle des étoiles fixes qui roule autour des pôles de l’univers et entraîne par force avec elle toutes les autres du levant au couchant; la seconde se meut autour de l’axe perpendiculaire au cercle du milieu des signes, c’est par cette sphère que chaque planète paraît exécuter un mouvement en longitude vers les signes suivants; la troisième roule autour de l’axe perpendiculaire au cercle, oblique à celui du milieu des signes. Par cette dernière, chaque astre paraît avoir un mouvement propre en latitude, tantôt à une plus grande distance, tantôt à une plus petite, tantôt plus au nord, tantôt plus au midi, du cercle qui passe par le milieu des signes. Chacune des autres planètes est portée par quatre sphères dont l’une produit le mouvement de la planète en hauteur.

Aristote dit que Callippe ajoutait de nouvelles sphères aux autres planètes, excepté à Saturne et à Jupiter, savoir deux au soleil et à la lune, et une seulement à chacune des autres. Il pense aussi que, si on veut rendre compte des phénomènes, il faut, pour chacune des planètes, d’autres sphères moindres qu’une des sphères qui portent les sphères roulantes. Telle est son opinion ou celle des autres (Eudoxe et Callippe). Si on pensait qu’il est naturel que tout se porte dans le même sens, on voyait cependant les planètes aller en sens contraire; aussi supposait-on que dans les intervalles des sphères déférentes (c’est-à-dire portant les planètes), il y a quelques sphères évidemment solides qui, par leur mouvement propre, font tourner en sens contraire les déférentes en contact, de même que dans des sphères artificielles, des tympans roulant autour de leurs axes peuvent, de leur propre mouvement et à l’aide de dents, faire mouvoir et rouler en sens contraire des corps adjacents et au contact.

XXXII. Il est bien naturel que toutes les sphères se meuvent dans le même sens, entrainées par la sphère extérieure: mais, par un mouvement propre, à cause du rang quelles occupent, de leur place et de leur grandeur, elles se portent les unes plus vite, les autres moins et dans le sens contraire, autour de leurs axes propres obliques à celui de la sphère des étoiles. Ainsi les astres qu’elles portent sont entraînés par le mouvement simple et régulier des étoiles et ce n’est que par un effet, qui est la conséquence du mouvement des sphères, qu’ils paraissent accomplir des mouvements composés, irréguliers et variés; ils décrivent plusieurs cercles, les uns concentriques, les autres excentriques ou épicycles. Pour l’intelligence de ce que nous disons, il faut expliquer en peu de mots la figure qui nous paraît nécessaire pour la construction des sphères.

Soit αβγδ la sphère creuse des étoiles autour du centre θ de l’univers, αε son épaisseur, αγ et βδ deux diamètres (perpendiculaires). Supposons que αγβδ soit un grand cercle et qu’il passe par le milieu des signes; soit, au-dessous de la première, la sphère creuse εροτ, πχυψ, d’une planète, ayant le même centre et pour épaisseur επ. Soit enfin, dans cette épaisseur, la sphère solide εζπη portant un astre errant fixé au point ε. Que toutes soient portées régulièrement dans le même sens par des mouvements simples d’orient en occident; que celle qui produit le mouvement de la planète en latitude tourne seule en sens contraire ou dans le même sens pourvu qu’elle reste en arrière par sa lenteur, car les deux hypothèses rendent compte des phénomènes.

Et maintenant, que la sphère des étoiles tourne autour de l’axe perpendiculaire au plan du cercle équinoxial, et que la sphère creuse de la planète tourne autour de l’axe perpendiculaire au cercle produisant le mouvement en latitude, et oblique à celui qui passe par le milieu des signes. Que la sphère des étoiles tourne très rapidement; que la sphère creuse de la planète tourne plus lentement en sens contraire, de sorte que, dans un temps déterminé, elle ait parcouru dans ce sens contraire toute la sphère des étoiles ou qu’elle le soit laissée en arrière, comme d’autres le veulent, — nous avons dit ailleurs qu’elle est l’opinion la plus vraisemblable; — qu’elle porte la sphère solide soutenant l’astre errant. La sphère solide, tournant régulièrement autour de son axe propre, reviendra au même point, portée dans le même se sens que la sphère étoilée; elle reviendra au même point dans le même temps que la sphère creuse de la planète aura parcouru, en se mouvant en sens contraire, la sphère entière des étoiles ou qu’elle aura été laissée plus ou moins en arrière.

Supposons d’abord qu’elle soit revenue dans le même temps; soit μ le centre de la sphère, décrivons du centre θ, avec le rayon θμ, le cercle μλνξ. Divisons la droite ευ en deux parties égales au point κ, et du centre κ, avec le rayon κε, décrivons le cercle ελυξ, excentrique à l’égard de l’univers. Il est évident que dans le temps que la sphère creuse de la planète, portant la sphère solide, sera laissée en arrière de la sphère des étoiles, le centre μ de la sphère solide parcourra le cercle concentrique μλνξ, paraissant emporté en sens contraire et entraînant cette sphère solide. Il est encore évident que la planète placée au point ε sur la sphère solide décrira (dans le même temps) le cercle εηπζ qui devient l’épicycle du concentrique μλνξ et tourne dans le même sens que l’univers; elle décrira aussi, par conséquent, l’excentrique ελυξ, égal au concentrique, en le parcourant dans un sens contraire à celui de l’univers.

Elle paraîtra donc aux observateurs qui seront en θ, décrire le zodiaque αβγδ, en s’avançant vers les signes suivants en sens contraire du mouvement de l’univers. Elle paraîtra aussi se mouvoir en latitude en raison de l’inclinaison de son plan sur le cercle qui passe par le milieu des signes, les axes de ces sphères étant respectivement perpendiculaires à ces plans. C’est toujours au même lieu qu’elle sera le plus éloignée de la terre et qu’elle paraîtra se mouvoir le plus lentement : c’est au point α du zodiaque, le centre de la sphère solide étant au point μ de la droite αθ, et la planète elle-même étant au point ε. Au point opposé, elle sera toujours le moins éloignée de la terre et paraîtra se mouvoir le plus rapidement : c’est au point γ du zodiaque. La sphère creuse tournant en sens contraire, le centre de la sphère solide sera au point ν de la droite θγ et la planète elle-même sera vue au point γ, c’est-à-dire qu’elle sera au point υ.

Elle aura les distances moyennes et les mouvements moyens en deux endroits : lorsqu’elle sera aux points qui partagent en deux parties égales l’épicycle εζπη et le concentrique μλνξ, tels sont les points ζ et η qui, à cause de la translation des sphères en sens contraire, ou de leur moindre mouvement, sont les mêmes que λ et ξ, lesquels partagent en deux parties égales l’excentrique ελυξ et le concentrique μλνξ et apparaissent dans le zodiaque entre les points α et γ, en β et δ, c’est-à-dire en φ et ω. Tout cela est apparent pour le soleil, puisque les temps de ses retours, autant que nos sens peuvent les percevoir, sont trouvés égaux entre eux, ou à peu près — je parle des durées de ses retours à la même longitude, à la même latitude, au même éloignement, — les points semblables des deux sphères se trouvent toujours, par des mouvements semblables, aux mêmes endroits et paraissent dans les mêmes signes.

Un tel mouvement des planètes et des sphères est naturellement régulier, simple, bien ordonné, mais il est oblique au zodiaque et, à cause de sa lenteur, la planète paraît laissée en arrière par la sphère des fixes; une seule sphère se meut en sens contraire, c’est celle qui porte la sphère solide dite épicycle; cependant le mouvement paraît varié, multiple et inégal. Il se produit vers les signes suivants, ou réellement ou par suite d’un plus lent déplacement: il paraît oblique au zodiaque, et à cause de la rotation de la sphère solide autour de son axe propre, la planète se montre tantôt plus loin et par conséquent plus lente, tantôt plus près et par conséquent animée d’une plus grande vitesse. En un mot le mouvement paraît inégal, il se fait suivant l’épicycle alors qu’il paraît se faire suivant l’excentrique. Il est évidemment conforme à la raison qu’il y ait accord entre les deux hypothèses des mathématiciens sur les mouvements des astres, celle de l’épicycle et celle de l’excentrique: l’une et l’autre s’accordent par accident avec celle qui est conforme à la nature des choses, ce qui faisait l’objet de l’admiration d’Hipparque, surtout pour le soleil, puisque les mouvements de ses sphères s’accomplissent exactement dans des temps égaux entre eux.

Pour les autres planètes il n’y a pas la même exactitude, parce que la sphère solide de la planète ne revient pas dans le même temps à la même position; la sphère creuse reste en arrière de celle des étoiles ou va dans un sens contraire, plus ou moins rapidement; de sorte que leurs mouvements semblables, bien qu’ils s’accomplissent sur des points semblables des sphères, ne se font pas toujours aux mêmes endroits, mais changent sans cesse de place, l’obliquité des sphères ne se produisant pas à la même latitude, et les temps des retours à la même longitude, à la même latitude, au même éloignement étant inégaux et variables, les plus grandes, les plus petites et les moyennes distances, de même que les vitesses variables se produiront dans tous les signes du zodiaque, tantôt sur un point, tantôt sur un autre.

En outre, les mouvements semblables paraissant, comme nous l’avons dit, changer de place, bien qu’ils s’accomplissent sur les mêmes points des sphères, les planètes dans leurs mouvements par accident ne paraissent pas même décrire des cercles, mais des spirales. Il faut donc croire que, pour chaque planète, il y a une sphère propre creuse qui porte dans son épaisseur une sphère solide et que la sphère solide à son tour porte l’astre sur sa surface.

XXXIII. Quant au Soleil, à Vénus et à Mercure, il est possible que chacun de ces astres ait deux sphères propres, que les sphères creuses des trois astres, animées de la même vitesse, parcourent dans le même temps, en sens contraire, la sphère des étoiles fixes et que les sphères solides aient toujours leurs centres sur une même ligne droite, la sphère du soleil étant la plus petite, celle de Mercure étant plus grande et celle de Vénus étant encore plus grande.

Il se peut aussi qu’il n’y ait qu’une seule sphère creuse commune aux trois astres et que les trois sphères solides, dans l’épaisseur de celle-là, n’aient qu’un seul et même centre, la plus petite serait la sphère vraiment solide du soleil, autour de laquelle serait celle de Mercure; viendrait après, entourant les deux autres, celle de Vénus qui remplirait toute l’épaisseur de la sphère creuse commune. C’est pour cela que ces trois astres sont laissés en arrière sur le zodiaque, ou exécutent un mouvement en longitude de sens contraire au mouvement diurne et de même vitesse sans avoir les autres mouvements semblables. Ils paraissent toujours voisins, se dépassant et s’éclipsant mutuellement, Mercure s’éloignant au plus, de part et d’autre du soleil, de vingt degrés au couchant et au levant, et Vénus de cinquante degrés au plus. On comprendra que cette position et cet ordre sont d’autant plus vrais que le soleil essentiellement chaud est le foyer du monde, en tant que monde et animal, et peur ainsi dire le cœur de l’univers, à cause de son mouvement, de son volume et de la course commune des astres qui l’environnent.

Car dans les corps animés, le centre du corps, c’est-à-dire de l’animal, en tant qu’animal, est différent du centre du volume. Par exemple, pour nous qui sommes, comme nous l’avons dit, hommes et animaux, le centre de la créature animée est dans le cœur toujours en mouvement et toujours chaud, et à cause de cela, source de toutes les facultés de l’âme, cause de la vie et de tout mouvement d’un lieu à un autre, source de nos désirs, de notre imagination et de notre intelligence. Le centre de notre volume est différent : il est situé vers l’ombilic.

De même, si l’on juge des choses les plus grandes, les plus dignes et les plus divines, comme des choses les plus petites, fortuites et mortelles, le centre du volume du monde universel sera la terre froide et immobile, mais le centre du monde, en tant que monde et animal, sera dans le soleil qui est en quelque sorte le cœur de l’univers et d’où l’on dit que l’âme du monde prit naissance pour pénétrer et s’étendre jusque dans ses parties extrêmes.

XXXIV. Il est clair que, pour les motifs expliqués, des deux hypothèses, dont chacune est la conséquence de l’autre, celle de l’épicycle paraît la plus commune, la plus généralement admise, la plus conforme à la nature des choses. Car l’épicycle est un grand cercle de la sphère solide, celui que la planète décrit dans son mouvement sur cette sphère, tandis que l’excentrique diffère entièrement du cercle qui est conforme à la nature, et est plutôt décrit par accident. Hipparque, persuadé que le phénomène se produit ainsi, vante l’hypothèse de l’épicycle comme sienne propre et dit qu’il est probable que tous les corps célestes sont uniformément placés par rapport au centre du monde et qu’ils lui sont semblablement unis. Mais lui-même, ne connaissant par suffisamment la science naturelle, n’a pas bien compris quel est le vrai mouvement des astres qui est d’accord avec la nature des choses, ni celui qui est par accident et qui n’est qu’une apparence. Il pose cependant en principe que l’épicycle de chaque planète se meut sur le concentrique et que la planète se meut sur l’épicycle.

Platon paraît préférer aussi l’hypothèse de l’épicycle, il pense que ce ne sont pas des sphères, mais des cercles qui portent les planètes, comme il l’indique à la fin de la République en imaginant des fuseaux emboîtés les uns dans les autres. Il se sert du reste de termes communs: il dit souvent cercles au lieu de sphères, et autour des pôles au lieu de autour de l’axe.

D’après les apparences, dit Aristote, des sphères du cinquième corps (l’éther) se meuvent dans les profondeurs du ciel; les unes sont plus élevées, les autres moins, les unes sont plus grandes, les autres plus petites, les unes sont creuses, les autres pleines sont intérieures aux premières, et les planètes, qui y sont fixées à la manière des étoiles, sont portées d’un mouvement simple, mais de vitesse inégale suivant les lieux. Par un effet qui est la conséquence de tous ces mouvements, elles paraissent se mouvoir diversement et décrire certains cercles excentriques; ou bien, placées sur d’antres cercles, elles paraissent décrire des spirales suivant lesquelles des mathématiciens, trompés par la rétrogradation, pensent qu’elles sont mues.

XXXV. Il faut montrer comment quelques planètes paraissent tantôt avancer, tantôt stationner et tantôt rétrograder; car elles paraissent faire tout cela. Soit le zodiaque αβγδ autour du point θ, centre de l’univers, et εζη l’épicycle de la planète. Du point θ nous observons, tirons les tangentes θζκ, θνλ, l’épicycle, et par le centre μ de l’épicycle, la droite θμεα. Puisque nous voyons en ligne droite, il est clair que l’astre arrivé en ζ nous paraîtra en κ ; puis, lorsqu’il aura parcouru l’arc ζε, il paraîtra avoir décrit l’arc κα vers les signes précédents du zodiaque. De même, lorsqu’il aura parcouru l’arc εν, il paraîtra avoir parcouru en avant l’arc αλ. Lorsqu’ensuite il décrira l’arc νηζ, il paraîtra décrire l’arc λακ, vers les signes suivants du zodiaque. Pendant qu’il s’approchera du point ζ ou qu’il commencera à s’en éloigner, il paraîtra employer plus de temps à se déplacer et stationnera au point κ puis s’étant éloigné du point ζ il avancera de nouveau: ensuite en s’approchant du point ν et en commençant s’en éloigner, il paraîtra de nouveau stationner et enfin rétrograder. Les stations, les rétrogradations et les mouvements en avant et en arrière de chaque planète, se feront tantôt dans un signe, tantôt dans un autre et dans différentes parties des signes, parce que l’épicycle de chacune se déplace toujours vers les signes suivants, que ce mouvement soit réel, ou que l’épicycle soit simplement laissé en arrière.

Des distances moyennes des planètes

XXXVI. Il est utile, pour noire sujet, de savoir qu’elle est la distance moyenne d’une planète, quel que soit le déplacement de l’épicycle ou de l’excentrique. Dans l’hypothèse des épicycles, si nous prenons la distance la plus grande de l’astre à la terre, telle que θε, et puis la plus petite, telle que θν, ainsi que la différence entre la plus grande et la plus petite c’est-à-dire εν, et que nous en prenions le milieu, il est clair que la distance moyenne sera θμ. Si donc du centre θ et de l’intervalle θμ nous décrivons le cercle concentrique μλοξ et que du centre μ avec l’intervalle με, nous tracions l’épicycle εζνη, il est évident que l’astre porté sur l’épicycle sera le plus éloigné de nous au point ε et le moins éloigné au point ν, et à une distance moyenne aux deux points ζ et η d’intersection du concentrique et de l’épicycle, en quelque lieu que soit transporté l’épicycle.

Dans l’hypothèse des excentriques, soit l’excentrique ελυξ dont le centre est κ, soit θ le centre de l’univers, menons la ligne des centres θκ et prolongeons-la de part et d’autre. Si nous décrivons, du centre θ le cercle μλοξ, égal à l’excentrique. Il est clair que c’est le concentrique sur lequel est emporté l’épicycle de l’autre hypothèse, décrit du centre μ avec le rayon με. Lorsque la planète portée par l’excentrique sera en ε, en quelque endroit que cela se produise, elle sera le plus éloignée de nous, elle le sera le moins en υ, les distances moyennes seront aux points λ et ξ d’intersection de l’excentrique et du concentrique, en quelque endroit que tombent ces points par le déplacement de l’excentrique. Il est évident qu’il y a accord dans les deux hypothèses : les plus grandes, les plus petites et les moyennes distances sont les mêmes.

De la conjonction, des occultations et des éclipses

XXXVII. Pour le besoin de notre sujet, il nous reste à parler brièvement des conjonctions et des occultations, disparitions et éclipses. Puisque nous voyons naturellement en ligne droite, que la sphère des étoiles est la plus élevée, et que les sphères planétaires sont placées au-dessous, dans l’ordre que nous avons indiqué, il est clair que la lune étant la planète la plus rapprochée de la terre peut passer devant tous les autres astres qui sont au-dessus d’elle; elle nous cache, en effet, les planètes et plusieurs étoiles, lorsqu’elle est placée en ligne droite enlie notre vue et ces astres, et elle ne peut être cachée par aucun d’eux. Le soleil peut être caché par la lune, et lui-même peut cacher tous les autres astres, la lune exceptée, d’abord en s’approchant et en les noyant dans sa lumière, et ensuite en se plaçant directement entre eux et nous.

Mercure et Vénus cachent les astres qui sont au-dessus d’eux, quand ils sont pareillement placés en ligne droite entre eux et nous; ils paraissent même s’éclipser mutuellement, suivant que l’une des deux planètes est plus élevée le que l’autre, à raison des grandeurs, de l’obliquité et de la position de leurs cercles. Le fait n’est pas d’une observation facile, parce que les deux planètes tournent autour du soleil et que Mercure en particulier, qui n’est qu’un petit astre, voisin du soleil, et vivement illuminé par lui, est rarement apparent. Mars éclipse quelquefois les deux planètes qui lui sont supérieures, et Jupiter peut éclipser Saturne. Chaque planète éclipse d’ailleurs les étoiles au-dessous desquelles elle passe dans sa course.

Des éclipses de soleil et de lune.

XXXVIII. La lune disparaît quand, diamétralement opposée au soleil, elle entre dans l’ombre de la terre. Cela n’arrive pas tous les mois: et le soleil n’est pas éclipsé à toutes les conjonctions de la lune ou néoménie, de même que la lune ne l’est pas à toutes les pleines lunes, parce que leurs cercles sont sensiblement inclinés l’un sur l’autre. Le cercle du soleil paraît emporté, comme nous l’avons dit[26] sous celui qui passe par le milieu des signes sur lequel il est un peu incliné, car il s’en écarte d’un demi-degré de chaque côté; et le cercle de la lune a une obliquité de dix degrés en latitude, comme l’a trouvé Hipparque, ou de douze degrés, comme le pensent la plupart des mathématicien, de sorte qu’elle paraît s’écarter de cinq ou six degrés, au nord ou au sud du cercle qui passe par le milieu des signes.

Si nous supposons prolongés les plans des deux cercles, solaire et lunaire, leur commune intersection sera une ligne droite qui contient les centres des deux cercles. Celle ligne, en quelque façon, sera leur diamètre commun. Les points extrêmes où paraissent se couper les cercles s’appellent les nœuds, l’un ascendant, l’antre descendant ; ils se portent vers les signes suivants du zodiaque. Si la conjonction du soleil et de la lune se fait près des nœuds, les deux astres paraissent voisins l’un de l’autre et la lune cachera à nos veux le soleil qui s’éclipsera d’autant plus que la lune le couvrira davantage. Mais si la conjonction mensuelle ne se fait pas près du nœud, la longitude comptée sur le zodiaque étant la même pour les deux astres, mais la latitude étant différente, les deux astres paraîtront l’un plus au nord, l’autre plus au sud, et le soleil n’étant pas caché ne pourra pas disparaître.

XXXIX. Voici ce qui arrive évidemment pour la lune. Elle s’éclipse, comme nous l’avons dit souvent, lorsqu’elle entre dans l’ombre de la terre; montrons comment il se fait que l’éclipse n’ait pas lieu chaque mois, Les rayons lumineux, se propageant en ligne droite, enveloppent une région obscure: si deux corps sphériques, l’un lumineux et l’autre éclairé par le premier, sont égaux, l’ombre produite est un cylindre indéfini.

Soit, par exemple, αβ le corps lumineux et γδ le corps éclairé, supposons-les tous les deux égaux et sphériques. Les rayons de lumière tels que αγ, βδ dirigés suivant deux génératrices opposées du cylindre tangent aux deux sphères, se propagent en ligne droite; donc les diamètres αβ, γδ étant égaux et perpendiculaires aux tangentes αγε, βδζ, il est clair que ces rayons seront parallèles et que les droites, prolongées indéfiniment, ne se rencontreront pas. Comme cela se produit sur tous les points, il est évident que la sphère y produira une ombre cylindrique indéfinie.

Si, au contraire, le corps lumineux est plus petit, tel que ηθ, et que le corps éclairé soit plus grand, tel que κλ, l’ombre aura la forme d’un cône tronqué indéfini, car le diamètre κλ étant plus grand que le diamètre ηθ, les rayons lumineux κμ et λν prolongés indéfiniment s’éloigneront de plus en plus l’un de l’autre, et il en sera ainsi de tous côtés.

Si le corps lumineux est plus grand, comme b et le corps éclairé plus petit, comme ξο, et que tous les deux soient sphériques, il est clair que l’ombre du corps, c’est-à-dire πρ, aura la forme d’un cône et sera limitée, car les rayons ξπ et ορ prolongés en ligne droite se rencontreront au point σ, puisque le diamètre πρ est plus petit que le diamètre ξο. Ce phénomène se produira de toutes parts.

Par la considération des distances et des diamètres du soleil et de la lune, Hipparque montre que le volume du soleil con tient environ 1880 fois celui de la terre, que le volume de la terre contient plus de 27 fois celui de la lune, et que le soleil est beaucoup plus éloigné que la lune. Il est donc évident que l’ombre de la terre aura la forme d’un cône, qu’elle s’étendra suivant un diamètre commun du soleil et de la terre (c’est-à-dire suivant la droite qui joint leurs centres), et que le diamètre de la lune, même à son maximum, est moindre que la largeur de l’ombre projetée par la terre. Quand le soleil est à un nœud et la lune à l’autre nœud, le soleil, la terre et la lune étant en ligne droite, la lune entre nécessairement dans l’ombre de la terre, et comme elle est plus petite et qu’elle n’a pas d’éclat par elle—même, elle devient invisible, et on dit qu’elle s’éclipse.

Lorsque les centres du soleil, de la terre et de la lune sont exactement placés suivant une ligne diamétrale, c’est-à-dire suivant la même ligne droite, comme nous l’avons dit, la lune pénétrant au milieu de l’ombre, il y a éclipse totale. Lorsque les trois centres ne sont pas tout à fait en ligne droite, il n’y a pas toujours éclipse totale. Mais le plus souvent, au temps des pleines lunes, le soleil et la lune ne passent pas par les nœuds, et la lune sera plus au nord ou plus au midi que l’ombre de la terre. Comme elle n’entre pas dans le cône d’ombre, il ne saurait y avoir éclipse.

Voilà ce que dit Adraste. Dercyllide n’a écrit sur ce sujet avec aucun ordre convenable. Voici cependant ce qu’il indique dans le livre où il traite « Des fuseaux dont il est question dans la République de Platon ».

Des découvertes astronomiques et de leurs auteurs

XL. Eudème dans ses livres « Sur l’astronomie » raconte qu’Œnopide a trouvé le premier l’obliquité du zodiaque et reconnu l’existence de la grande année : d’après lui, Thalès a fait voir que les éclipses de soleil et les retours de cet astre aux solstices n’arrivent pas toujours après le même temps; Anaximandre prétend que la terre est suspendue dans l’espace et se meut autour du centre du monde; Anaximène a montré que la lune reçoit la lumière du soleil et de quelle manière elle s’éclipse. D’autres ont ajouté de nouvelles découvertes à celles-là: que les étoiles se meuvent autour de l’axe immobile qui passe par les pôles, que les planètes se meuvent autour de l’axe perpendiculaire au zodiaque; et que l’axe des étoiles et celui des planètes s’écartent l’un de l’autre, du côté du pentédécagone, et par conséquent d’un angle de 24 degrés.

Des hypothèses de l’astronomie.

XLI. Il dit ensuite : de même qu’en géométrie et en musique, il est impossible, sans faire d’hypothèses, de déduire les conséquences des principes, même en astronomie il convient d’établir d’abord des hypothèses pour pouvoir parler du mouvement des planètes. Avant tout, dit-il, comme tout le monde en convient, il faut arrêter les principes qui doivent servir dans les études mathématiques. Le premier est que la composition du monde est ordonnée et gouvernée par un seul principe et que la réalité se trouve au fond des choses qui existent ou qui paraissent exister, et qu’il ne faut pas dire que le monde est l’infini où notre vue se perd, mais qu’il a ses limites,

Le second principe est que les levers et les couchers des corps divins ne se font pas parce que ces corps s’allument et s’éteignent successivement; si leur état n’était pas éternel, il n’y aurait aucun ordre conservé dans l’univers. Le troisième principe est qu’il y a sept planètes, ni plus ni moins, vérité qui résulte d’une longue observation. Le quatrième est le suivant: puisqu’il n’est pas conforme à la raison que tous les corps soient en mouvement ou qu’ils soient tous au repos, mais puisque les uns sont en mouvement et les autres immobiles, il faut rechercher ce qui est nécessairement au repos dans l’univers et ce qui est en mouvement. Il ajoute qu’il faut croire que la terre, foyer de la maison des dieux, suivant Platon,[27] reste en repos et que les planètes se meuvent avec toute la voûte céleste qui les enveloppe. Ensuite, il repousse avec énergie, comme contraire aux bases de la mathématique, l’opinion de ceux qui veulent que les corps qui paraissent en mouvement soient au repos et que les corps immobiles par nature et par situation soient en mouvement.

Il dit ensuite que les planètes ont un mouvement circulaire, régulier et uniforme, en longitude, en distance et en latitude. Il juge ainsi, bien que nous puissions nous tromper sur ce point. C’est pourquoi il croit que les levers successifs différents dépendent d’un mouvement en longitude et il rejette les raisons faibles et commodes, données par les anciens, d’après lesquelles les planètes seraient laissées en arrière. Mettant de côté tout ce qu’il y a de désordonné et de contraire à la raison dans un tel mouvement, il est juste de croire, dit-il, que les planètes sont emportées lentement par un mouvement contraire celui des étoiles fixes, de sorte que le mouvement intérieur soit produit par le mouvement extérieur.

Il ne pense pas qu’il faille prendre comme causes premières de ces mouvements, des spirales ni des lignes semblables à la course sinueuse d’un cheval. Car ce mouvement est le résultat d’autres mouvements. La cause première du mouvement en spirale est le mouvement qui s’accomplit suivant le cercle oblique du zodiaque. Le mouvement en spirale est en effet, adventice et postérieur, il résulte du double mouvement des planètes. On doit donc regarder comme premier le mouvement suivant le cercle oblique; le mouvement en spirale en est une conséquence, il n’est pas premier.

En outre il ne croit pas que les cercles excentriques soient la cause du mouvement en profondeur. Il pense que tout ce qui se meut dans le ciel est emporté autour d’un centre unique du mouvement et du monde, de sorte que ce n’est que par une conséquence, et non par un mouvement antécédent, comme nous l’avons dit plus haut, que les planètes décrivent des épicycles ou des excentriques dans l’épaisseur des concentriques. Car chaque sphère a une double surface, l’une concave à l’intérieur, l’autre convexe à l’extérieur, dans l’intervalle desquelles les astres se meuvent suivant des épicycles et des concentriques, d’un mouvement qui leur fait décrire, comme conséquence apparente, des excentriques.

Il dit encore que, suivant les apparences, les mouvements des planètes sont irréguliers, mais qu’en principe et en réalité ils sont réguliers: le mouvement est simple et naturel pour tous: il n’y a qu’un très petit nombre de déplacements sur des sphères disposées avec ordre. Il blâme ces philosophes qui, considérant les astres comme inanimés, ajoutèrent aux sphères et à leurs cercles plusieurs autres sphères; ainsi Aristote[28] et parmi les mathématiciens, Ménechme et Callippe ont proposé les sphères déférentes et les spirales. Après avoir établi tout cela, il pense que le ciel se meut avec tous les astres autour de la terre immobile, suivant un très petit nombre de mouvements circulaires, uniformes, harmonieux, concentriques et indépendants. Il montre que, d’après Platon, ces hypothèses rendent compte des apparences.

XLII. Les étoiles se meuvent autour de l’axe immobile qui passe par les pôles, et les planètes autour de l’axe perpendiculaire au cercle zodiacal. Les deux axes s’écartent l’un de l’autre, de la valeur du côté du pentédécagone (et par conséquent d’un angle de 24 degrés). En effet, le zodiaque étant un grand cercle divise le monde en deux parties égales. La circonférence de l’univers étant partagée en 360 degrés, le cercle zodiacal en sépare 180 de chaque coté. L’axe du zodiaque lui étant perpendiculaire divise aussi les 180 degrés en deux parties égales. Or le zodiaque s’étend obliquement du parallèle d’hiver au parallèle d’été, mais on compte 30 degrés du tropique d’été au cercle arctique comme l’enseigne Hipparque, et du cercle arctique au pôle de la sphère des étoiles il y a 16 degrés. En faisant la somme, ou compte donc 66 degrés du tropique d’été au pôle des fixes.

Pour compléter les 90 degrés qui s’étendent jusqu’au pôle de la sphère des planètes, il faut ajouter à cette somme 24 degrés, puisque l’axe des planètes est perpendiculaire au zodiaque. Du pôle de l’axe des planètes au cercle glacial arctique il reste 12 degrés, car tout l’arc de la zone vaut 36 degrés; si on en retranche 24, il reste 12. Il convient d’y ajouter les 30 degrés compris du cercle arctique au tropique d’été, puis les 24 degrés compris du tropique d’été au cercle équinoxial, et encore les 24 degrés compris du cercle équinoxial au tropique d’hiver auquel le zodiaque est tangent. Mais 24 degrés forment la quinzième partie des 360 degrés de la circonférence de l’univers, car 15 fois 24 font 360, nous avons donc raison de dire que les deux axes, celui des étoiles et celui des planètes, s’écartent l’un de l’autre de la valeur du côté du pentédécagone inscrit dans (un grand cercle de) la sphère.

XLIII. Les planètes décrivent des spirales par accident, c’est-à-dire en conséquence de leurs deux mouvements en sens contraire l’un de l’autre. En effet, comme elles sont portées par leur propre mouvement du tropique d’été au tropique d’hiver et réciproquement, en allant lentement, et qu’elles sont rapidement entraînées chaque jour en sens contraire sous la sphère des étoiles, elles ne passent pas en droite ligne d’un parallèle à un autre, mais entraînées autour de la sphère des fixes. En d’autres termes, pour aller sur le zodiaque d’un point à un autre point, leur mouvement ne se fait pas seulement suivant une ligne droite du zodiaque, mais il devient en même temps circulaire autour de la sphère des fixes, de sorte qu’en passant d’un parallèle à un autre elles décrivent des spirales semblables aux vrilles de la vigne; c’est comme si on enroulait une courroie autour d’un cylindre d’un bout à l’autre; telles étaient les lanières enroulées sur les scytales de Laconie et sur lesquelles les éphores écrivaient leurs dépêches.

Les planètes décrivent encore une autre spirale, mais celle-ci non comme si on la traçait sur un cylindre d’un bout à l’autre, mais comme si on la traçait sur une surface plane. Puisque depuis un temps infini, elles passent d’un cercle parallèle à l’autre et de nouveau de celui-ci au premier, et cela sans interruption et sans fin, si nous supposons des lignes droites, disposées en nombre infini, représentant les cercles parallèles et que les planètes se meuvent sur ces parallèles dans le même sens que la sphère des fixes, tantôt vers le tropique d’hiver, tantôt vers le tropique d’été, elles nous paraîtront décrire une hélice sans fin. A cause du mouvement incessant et continu autour de la sphère sur les cercles parallèles, le chemin parcouru sera semblable à celui qui se ferait suivant les lignes droites étendues à l’infini, comme l’indiquent les figures ci-jointes.[29] Les planètes décrivent donc deux spirales par accident, l’une comme autour d’un cylindre, l’autre comme sur une surface plane.

XLIV. Tout cela est très nécessaire et très utile pour la lecture des œuvres de Platon. Or, nous avons dit que nous avions à considérer la musique instrumentale, la musique mathématique et l’harmonie des sphères[30] et que nous rapporterions tout ce qu’il y a nécessairement d’harmonie dans le monde, après ce qui regarde l’astronomie, —car Platon assigne à cette musique des sphères le cinquième rang dans les mathématiques, après l’arithmétique, la géométrie, la stéréométrie et l’astronomie — nous allons donc montrer sommairement ce que Thrasylle expose sur ce sujet, en même temps que notre propre travail antérieur.

Fin de la traduction des Œuvres de Théon de Smyrne

Parvenues jusqu’à nous.

NOTE XVII. — Sur la mesure du volume de la terre (III, iii).

Le passage est altéré et les manuscrits présentent une lacune à la fin. Henri Martin, en essayant de le restituer, a fait une faute de calcul. Le diamètre d de la terre étant égal à 8018g stades, on a

d ² = 64 2915 3124 au lieu de 64 2713 3124.

Le chiffre inexact 7, des centaines de myriades, substitué au chiffre exact 9, a donné à H. Martin des valeurs inexactes pour d ³, pour 1/14 d ³ et pour 22/3 de 1/14 d ³ ou 11/21 d ² qui exprime le volume de la sphère de diamètre d. Il faut

d²= 515 5023 5578 8568 au lieu de 515 3419 9178 8568

1/14 d³ = 36 8215 9684 2040 + 4/7 au lieu de 36 8101 4227 0612

11/21 d³ = 270 0250 4350 8297 + 11/21 au lieu de 269 9410 4331 7821+ 1/3

Ainsi le volume de la terre, évalué en stades cubiques, en supposant le rapport de la circonférence au diamètre égal à 22/7, vaut, d’après la mesure de l’arc de méridien faite par Eratosthène, 270 troisièmes myriades, 250 deuxièmes myriades, 4350 myriades, 8297 monades et 11/21. Non seulement cette fraction est illusoire, mais on peut compter, tout au plus, sur les deux ou trois premiers chiffres du résultat. C’est l’expression de ce volume que nous avons restituée.

NOTE XVIII. — Sur le mythe de Pamphylien dans la République de Platon pp. 616B-617B. (III, xvi).

Il résulte du récit de Platon que, des huit globes concentriques, le premier extérieurement est celui des étoiles fixes, le second est celui qui porte Saturne, le troisième porte Jupiter, le quatrième Mars, le cinquième Mercure, le sixième Vénus, le septième le Soleil et le huitième la lune. La terre est au centre du système.

Les couleurs et les vitesses des fuseaux répondent à celles des astres qu’ils portent, et la largeur inégale des bords colorés répond à l’écart inégal des planètes dans leur course à travers la zone zodiacale et quelquefois au-delà. La sphère des étoiles fixes est en effet, de couleur variée, puisque les étoiles ont des nuances diverses. Le septième cercle, celui du soleil, est très éclatant; le huitième, celui de la lune, lui emprunte son éclat. La nuance un peu jaune du second et du cinquième est bien celle de Saturne et de Mercure. La blancheur du troisième et la rougeur du quatrième caractérisent parfaitement l’aspect de Jupiter et de Mars. Enfin le sixième cercle est donné comme le plus éclatant après le soleil, ce qui est vrai de Vénus. Une vitesse égale est attribuée à Mercure, à Vénus et au soleil : le soleil, dans sa course apparente autour de la terre, entraîne, en effet, Mercure et Vénus.