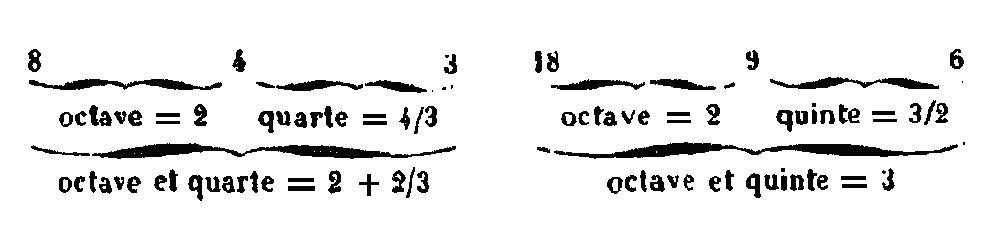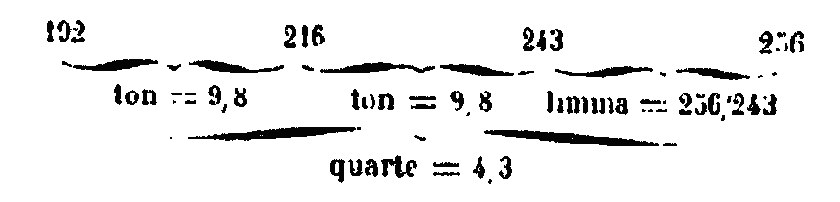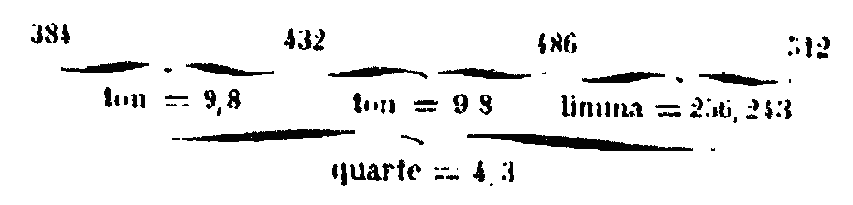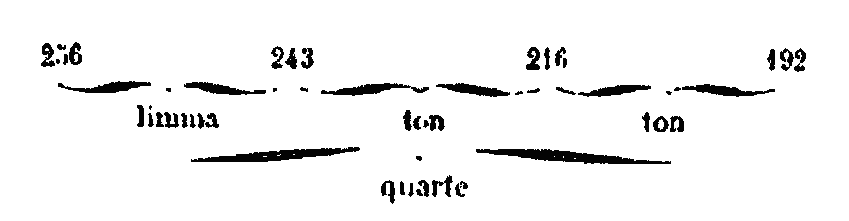RETOUR À L’ENTRÉE DU SITE

ALLER A LA TAΒLE DES MATIERES DE  THÉON DE SMYRNE

 THÉON DE SMYRNE

PHILOSOPHE PLATONICIEN

EXPOSITION DES CONNAISSANCES MATHÉMATIQUES UTILES POUR LA LECTURE DE PLATON

SECONDE PARTIE

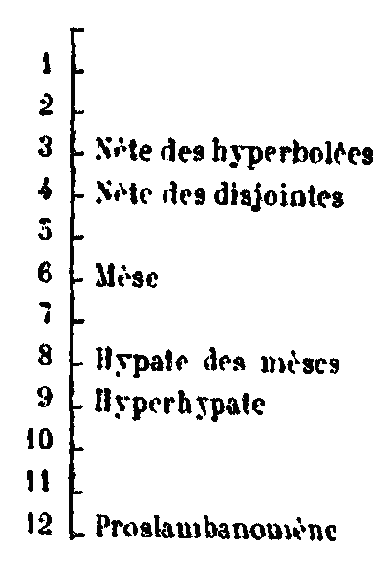
LIVRE CONTENANT LES LOIS NUMÉRIQUES DE LA MUSIQUE,...

INTRODUCTION

I. Puisqu’on dit qu’il y a des nombres consonants, on ne saurait trouver en dehors de l’arithmétique la raison de la consonance, qui a les plus grandes vertus, étant dans l’âme raisonnable la vérité, dans la vie la félicité, dans la nature l’harmonie; et l’harmonie elle-même qui est répandue dans le monde ne s’offrant à ceux qui la cherchent que lorsqu’elle leur est révélée par des nombres. Cette harmonie qui est intelligible se comprend plus facilement quand elle est précédée par l’harmonie sensible. Nous traiterons donc de ces deux harmonies, savoir de celle qui se fait sentir par les instruments, et de l’harmonie intelligible qui consiste dans les nombres.

Et après avoir terminé notre traité sur toutes les mathématiques, nous y ajouterons une dissertation sur l’harmonie du monde, et il ne nous déplaira pas de rapporter ce que nos devanciers ont découvert, non plus que de faire connaître davantage les traditions des Pythagoriciens que nous avons rapportées, sans nous vanter d’en avoir découvert la moindre partie. Désirant donc faire part à ceux qui veulent étudier Platon, de ce qui nous a été transmis par nos prédécesseurs, nous avons jugé nécessaire de composer ce recueil.

Du son et de la voix enharmonique

II. Thrasylle, traitant de l’harmonie sensible des instruments, définit le son une tension de voix enharmonique. Or, le son est dit enharmonique, quand, s’il est aigu, il peut y en avoir un plus aigu encore, et s’il est grave, il peut y en avoir un plus grave encore, en sorte qu’il se trouve intermédiaire. Si donc nous supposons un son qui surpasse toute acuité, il ne saurait être enharmonique, et c’est pour cela que jamais on ne regardera comme un son enharmonique le bruit violent de la foudre dont les blessures sont parfois funestes, comme l’a dit le poète

Et les coups de la foudre ont fait bien des victimes

Sans blessure sanglante.

De même si le son est tellement grave qu’il ne puisse pas y en avoir de plus grave, ce ne sera plus un son, parce qu’il ne sera plus enharmonique. Ce n’est donc ni toute voix, ni toute tension de voix, qu’on appelle son, mais seulement une voix enharmonique, comme celle qui donne la mèse, la nète ou l’hypate.[1]

Des intervalles et de l’harmonie

III. On définit l’intervalle une certaine disposition des sons, les uns par rapport aux autres, telles sont la quarte, la quinte et l’octave. Et on appelle système d’intervalles un certain ensemble, tels que le tétracorde, le pentacorde, l’octacorde.

IV. L’harmonie est la coordination des systèmes, tels sont le lydien, le phrygien, le dorien. Quant aux sons, les uns sont aigus, d’autres sont graves et d’autres moyens. Les sons aigus sont ceux que rendent les nètes, les sons graves ceux que rendent les hypates et les sons moyens ceux que rendent les cordes intermédiaires.

V. Parmi les intervalles, les uns sont consonants, les autres dissonants. Les intervalles consonants sont antiphones, tels que l’octave et la double octave, ou paraphones, tels que la quinte et la quarte. Sont au contraire dissonants les intervalles de sons juxtaposés tels que le ton et le diésis (ou demi-ton). Les intervalles antiphones ou de sons opposés sont consonants, parce que la gravité opposée à l’acuité produit la consonance: et les intervalles paraphones sont consonants, parce que les sons ne sont ni l’unisson ni dissonants, mais qu’il y a un intervalle semblable perceptible. Sont dissonants et non consonants les sons dont l’intervalle est d’un ton ou d’un diésis; car le ton et le diésis sont le principe de la consonance, niais ils ne sont pas la consonance elle-même.

Des consonances.

VI. Adraste le péripatéticien, dans son traité connu De l’harmonie et de la consonance, dit: De même que dans le discours soit écrit, soit parlé, les verbes et les noms en sont les parties les plus importantes ; que les parties essentielles des verbes et des noms sont les syllabes composées de lettres: et que les lettres sont les premiers signes de langages élémentaires, indivisible et les plus courts puisque le discours se compose de lettres et se résout finalement en lettres: de même ce qui fait la partie principale du chant et de toute mélodie, ce sont les systèmes qu’on appelle tétracordes, pentacordes et octacordes, lesquels se composent d’intervalles qui sont eux-mêmes composés de sons. Ces sons étant les éléments premiers et indivisibles dont se compose toute modulation et dans lesquels elle se résout définitivement. Les sons diffèrent les uns des autres par les tensions, les uns étant plus aigus, les autres plus graves. On a défini ces tensions de différentes manières.[2]

Voici, à cet égard, l’opinion qu’on attribue aux Pythagoriciens. Toute modulation et tout son étant une voix, et toute voix étant un bruit, et le bruit étant une percussion de l’air qui n’en est point brisé, il est évident que dans un air immobile il ne saurait y avoir ni bruit, ni voix, ni son. Au contraire, quand l’air est frappé et mis en mouvement, le son se produit: aigu, si le mouvement est rapide; grave, si le mouvement est lent; fort, si le mouvement est violent; faible, si le mouvement est peu sensible. Les vitesses de ces mouvements s’accomplissent suivant certains rapports, ou n’en ont aucun.

De ces vitesses sans rapports, résultent des sons sans rapports et dissonants, auxquels, à proprement parler, ne convient pas le nom de sons et que l’on appellerait plus justement bruit. Au contraire, on doit regarder comme les vrais sons, propres à la modulation, ceux qui ont entre eux certains rapports, soit multiples, soit superpartiels,[3] ou simplement de nombre à nombre. De ces sons, les uns sont seulement concordants, d’autres sont consonants selon les raisons premières et multiples les plus connues, et selon les raisons superpartielles.

Ils font entre eux une consonance, quand un son étant produit par une des cordes d’un instrument, les autres cordes résonnent par l’effet d’une certaine affinité, d’une sorte de sympathie; et aussi, quand deux sons étant produits en même temps, il en résulte un son mixte qui a une douceur et un charme tout particuliers. Parmi les sons successifs concordants, les quatrièmes forment avec les premiers une consonance, savoir celle que pour cette raison nous appelons quarte. Les cinquièmes à la suite donnent la quinte.

Viennent ensuite les huitièmes qui comprennent ces consonances et que nous appelons diapason (octave). En effet, sur la lyre à huit cordes, on trouve que le son qui est le plus grave, et qu’on appelle hypate, s’accorde par opposition avec le dernier et le plus aigu qui est celui de la nète, avec lequel il a la même consonance. Et quand, la musique avant fait des progrès, les instruments ont reçu un plus grand nombre de cordes et ont rendu des sons plus multipliés, un grand nombre de sons, tant aigus que graves, avant ajoutés aux huit anciens on a néanmoins conservé les dénominations des anciennes consonances : quarte, quinte et octave.

Cependant plusieurs autres consonances ont été trouvées à la consonance d’octave, on en a ajouté de plus petites, de plus grandes, ou d’égales, et de la somme des deux résulte une consonance nouvelle, telle qu’octave et quarte, octave et quinte, et double octave ; et si l’on ajoute encore à l’octave quelqu’une des consonances précédentes on obtient la double octave et quarte et ainsi de suite, tant que le son peut être produit et est perceptible à l’oreille. Il y a en effet, une certaine étendue que la voix parcourt en commençant par le son le plus grave pour s’élever au plus aigu et inversement étendue qui est plus grande chez les uns, moins grande chez les autres.

Cette série de modulations n’a pas lieu au hasard, ni sans art et d’après un seul mode, mais d’après certains modes déterminés qu’il faut observer dans les différents genres de mélodie. Car, de même que dans le discours soit parlé, soit écrit, ce n’est pas toute lettre, combinée avec une lettre quelconque, qui produit une syllabe ou un mot; de même, dans la mélodie, ce n’est pas la combinaison de sons quelconque qui produit la voix bien ordonnée, ou qui, à sa place, produit l’intervalle propre la modulation; mais il faut que cette combinaison ait lieu, comme nous venons de le dire, suivant la loi de modes définis.

Du ton et du demi-ton

VII. La partie la plus facile apprécier et la mesure de ce qu’on nomme l’étendue de la voix et de tout son intervalle est appelée ton, de même qu’on appelle coudée la mesure principale de l’espace que parcourent les corps en mouvement. L’intervalle de ton est très facile à distinguer, comme différence des consonances premières les plus connues; car la quinte surpasse la quarte d’un ton.

VIII. Le demi-ton n’est pas ainsi appelé parce que ce serait la moitié d’un ton, comme le pense Aristoxène, de la même manière que la demi-coudée est la moitié de la coudée: mais parce que c’est un intervalle musical moindre que le ton, de la même manière que nous appelons certaine lettre demi-voyelle, non parce qu’elle fait entendre la moitié d’un son, mais parce qu’elle ne fait pas entendre complètement le même son. On démontre, en effet, que le ton, considéré dans la raison sesquioctave (9/8), ne peut pas plus se partager en deux parties égales que tout autre intervalle sesquipartiel, car 9 n’est pas divisible par 2.

Du genre diatonique de la modulation, du genre chromatique et du genre enharmonique

IX. Quand la voix qui est modulée dans les limites de son étendue passe d’un son plus grave à un plus aigu, en produisant l’intervalle d’un demi-ton, qu’ensuite, franchisant l’intervalle d’un ton, elle passe un autre son, et qu’elle continue à moduler, il ne peut y avoir d’autre intervalle, que celui d’un ton, qui produise un autre son agréable et apte à la modulation, et ce son aigu consonant donnera avec le premier la consonance de quarte.

Une modulation de ce genre s’appelle système tétracorde, elle se compose de trois intervalles, savoir d’un demi-ton, d’un ton et d’un autre ton, et de quatre sons, dont les extrêmes, c’est-à-dire le plus grave et le plus aigu, forment une consonance. Cette consonance, que nous avons dit être appelée quarte, se compose donc de deux tons et d’un demi-ton.

Ce genre de modulation s’appelle diatonique, soit parce que d’ordinaire, il s’élève par des tons, soit à cause de la vigueur et de la fermeté qu’il montre.

X. Quand la voix produit un premier son, et que, franchissant un demi-ton, elle s’élève à un son plus aigu, puis passe de là à un troisième, en franchissant encore un demi-ton, et que s’efforçant d’avancer avec modulation, elle en produit encore un autre après celui-ci, elle ne peut observer un autre intervalle qu’un trihémiton incomposé, complément du premier tétracorde, et ne peut produire d’autre son que celui qui limite ce tétracorde en montant vers les sons aigus, et qui avec le plus grave donne la consonance de quarte. Cette modulation se fait donc par un demi-ton, suivi d’un demi-ton et d’un trihémiton incomposé, et ce genre de modulation s’appelle chromatique, parce qu’il s’écarte du premier et qu’il change de couleur, il exprime les affections lamentables et les passions violentes.

XI. Il y a un troisième genre de modulation qu’on appelle enharmonique. C’est celui où partant du son le plus grave la voix module le tétracorde en progressant par un diésis, puis un autre diésis et un double ton.

Du diésis

XII. Les disciples d’Aristoxène appellent diésis mineur le quart de ton ou moitié du demi-ton qu’ils considèrent comme le plus petit intervalle appréciable. Les Pythagoriciens appellent diésis ce qu’on nomme maintenant demi-ton.[4] Aristoxène dit que le genre enharmonique s’appelle ainsi parce qu’il est le meilleur, ce qui lui a fait donner le nom qui convient à tout ce qui est bien ordonné. Cette modulation est très difficile, et comme il le dit lui-même, elle demande as beaucoup d’art et d’étude et ne s’acquiert que par une longue pratique. Le genre diatonique au contraire est simple, noble et plus naturel, c’est pourquoi Platon le préfère.[5]

De la découverte des lois numériques des consonances

XII (bis). C’est Pythagore qui paraît avoir trouvé le premier que les sons consonants ont entre eux des rapports.[6] Les sons qui produisent la quarte ont entre eux le rapport sesquitierce (4/3); ceux qui produisent la quinte ont la raison sesquialtère (3/2); ceux qui produisent l’octave ont entre eux la raison double; ceux qui donnent octave et quarte sont dans le rapport de 8 à 3 qui est polyépimère, car il est égal à 2 + 2/3. Les sons qui donnent octave et quinte sont en raison triple, et ceux qui donnent la double octave sont en raison quadruple. Parmi les autres sons concordant, ceux qui donnent le ton sont dans la raison sesquioctave (9/8), et ceux qui donnent le demi-ton, mais qu’alors on appelait diésis, sont dans le rapport du nombre 256 au nombre 243.[7]

C’est Pythagore, disons-nous, qui paraît avoir découvert ces rapports, par la longueur et la grosseur des cordes, ainsi que par la tension à laquelle il les soumettait en tournant les chevilles, ou par une méthode plus connue, en y suspendant des poids, et dans les instruments à vent par le diamètre de la cavité, par l’intensité plus ou moins grande du souffle, ou par le poids des disques, ou le niveau dans les vases. Quelle que soit la méthode choisie parmi celles que nous venons de citer, on aura la consonance suivant le rapport indiqué, toutes choses égales d’ailleurs.

Pour le moment, contentons-nous de la démonstration qui, dans ce qu’on appelle le canon harmonique, s’obtient par la longueur des cordes : si nous divisons en quatre parties égales une corde tendue sur le canon harmonique, le son produit par la corde entière formera avec celui qui est produit par trois parties de la corde l’accord de quarte, le rapport est sesquitierce ; avec le son produit par deux parties ou la moitié de la corde, il formera l’accord d’octave, le rapport est double; avec le son produit par le quart de la corde, il donnera l’accord de double octave, le rapport est quadruple.

De plus le son produit par trois parties de la corde donnera avec le son produit par la moitié de la corde la consonance de quinte, le rapport est sesquialtère, et, à l’égard du son produit par le quart de la corde, il donnera la consonance d’octave et quinte, le rapport est 3. Si nous divisons la corde en 9 parties égales, le son produit par la corde entière donnera avec le son qui est produit par 8 parties l’intervalle d’un ton, le rapport est sesquioctave.

Le quaternaire 1, 2, 3, 4, renferme toutes les consonances, car il contient celles de quarte, de quinte, d’octave, d’octave et quinte et de double octave, savoir les raisons sesquitierce, sesquialtère, double, triple et quadruple (c’est-à-dire 4/3, 3/2, 2, 3, 4 et ).

Ces consonances, les uns ont voulu les obtenir par des poids, d’autres par des longueurs, d’autres par des mouvements nombrés, d’autres encore par la capacité des vases. On raconte que Lasus d’Hermione et les disciples d’Hippase de Métaponte, ce dernier de la secte de Pythagore, ont observé sur des vases la rapidité et la lenteur des mouvements à l’aide desquels les consonances se calculent en nombres. Prenant plusieurs vases de même capacité et semblables, on a laissé l’un vide et l’on a rempli l’autre à moitié d’un liquide, puis on a frappé chacun d’eux, on a obtenu la consonance d’octave.

Laissant de nouveau un vase vide et remplissant l’autre au quart, on a obtenu, en les frappant, la consonance de quarte; pour l’accord de quinte, on remplissait le tiers d’un vase: le rapport des espaces vides était, pour l’octave celui de 2 à 1, pour la quinte celui de 3 à 2, pour la quarte celui de 4 à 3.

Par la division des cordes, on obtient les mêmes rapports comme nous l’avons vu. Toutefois, on ne se servait pas d’une seule corde, comme dans le canon harmonique, mais de deux cordes à l’unisson également tendues. On interceptait la moitié d’une de ces cordes en pressant le milieu avec le doigt, on obtenait avec la moitié et l’autre corde entière la consonance d’octave; quand on interceptait seulement un tiers, les deux autres tiers et la corde entière donnaient l’accord de quinte, de même pour obtenir la consonance de quarte, on interceptait le quart d’une des deux cordes, en laissant l’autre entière.

On a fait une expérience semblable sur la flûte et on a trouvé les mêmes rapports. Ceux qui ont mesuré les consonances avec des poids, ont suspendu à deux cordes des poids dans les rapports que nous avons dits et qu’on avait obtenus par la longueur des cordes, en déterminant les consonances de ces cordes.

XIII. Le son est le repos de la voix sur une seule intonation, car on dit que le son doit toujours être semblable à lui-même et ne pas admettre la moindre différence ni se composer de différentes tensions de gravité ou d’acuité. Or les voix sont en partie aiguës, en partie graves; c’est pourquoi parmi les sons, l’un, aigu, est rapide, et l’autre, grave, est lent. Si donc on souffle dans deux tuyaux d’une égale grosseur et d’un diamètre égal, percés à la manière d’une flûte, et dont l’un soit deux fois plus long que l’autre, l’air qui s’échappe du tuyau deux fois moins long a une vitesse double et il en résulte la consonance d’octave, le son le plus grave sortant du tuyau le plus long et le son le plus aigu sortant du tuyau le plus court.

La cause en doit être attribuée à la vitesse et à la lenteur du mouvement, et cette cause produit les mêmes consonances dans une seule flûte; à cause de la distance des trous. En effet, si une flûte étant divisée en deux parties égales, on souffle dans la flûte entière, puis jusqu’au trou qui la divise en deux parties, on entendra la consonance d’octave; la flûte étant divisée en trois, et deux tiers étant pris du côté de la languette et un tiers vers l’extrémité, si on souffle dans la flûte entière et dans les deux tiers, on entendra l’accord de quinte. Si elle est divisée en quatre, et que l’on prenne trois parties vers le haut et une vers le bas, en soufflant dans la flûte entière et dans les trois quarts, on aura la consonance de quarte.

L’école d’Eudoxe et celle d’Archytas ont pensé que les rapports des consonances pouvaient être exprimés par des nombres; elles ont reconnu aussi que ces rapports expriment les mouvements, un mouvement rapide correspondant à un son aigu, parce qu’il frappe et pénètre l’air d’une manière plus continue et plus rapide, et un mouvement lent répondant à un son grave, parce qu’il est plus tardif.

Voilà ce que nous avions à dire de la découverte (des lois numériques) des consonances. Revenons maintenant à ce qu’a dit Adraste au sujet de ces instruments qui ont été préparés selon certains rapports dans le but de découvrir les consonances; il dit, en effet, que nous jugeons par l’ouïe la grandeur des intervalles et que les raisons confirment le témoignage des sens. Nous expliquerons bientôt comment les sons qui ont entre eux l’intervalle d’un demi-ton, ainsi que nous l’avons dit, sont dans le rapport de 256 à 243.

De l’addition et de la soustraction des consonances

XIII (bis). Il est évident que les compositions et les divisions des consonances sont entre elles dans le même rapport que les compositions et les divisions des nombres qui mesurent les consonances, comme nous l’avons expliqué. Ainsi l’octave se compose de la quinte et de la quarte et se divise en quinte et quarte. Or la raison de l’octave est double, celle de quarte est sesquitierce (4/3) et celle de la quinte est sesquialtère (3/2). Il est clair que la raison 2 se compose de 4/3 et de 3/2 et se résout dans les mêmes nombres. Ainsi 8 est les 4/3 de 6 et 12 est les 3/2 de 8, or 12 est le double de 6: on a les nombres 6, 8, 12. De même, la raison 2 de 12 à 6 se décompose en deux, le rapport sesquitierce (4/3) de 12 à 9 et le rapport sesquialtère (3/2) de 9 à 6.

Comme la quinte surpasse d’un ton la consonance de quarte, puisqu’elle se compose de trois tons et demi, le ton étant dans le rapport sesquioctave on trouve que le rapport sesquialtère (3/2) surpasse aussi le rapport sesquitierce (4/3) de la raison sesquioctave (9/8): en effet, si de la raison sesquialtère, comme de 9 à 6, on retranche la raison sesquitierce de 8 à 6, le reste est la raison sesquioctave de 9 à 8.[8] Si de même on ajoute à celle-ci la raison sesquitierce de 12 à 9, on complète la raison sesquialtère de 12 à 8.[9]

Comme la consonance d’octave est en raison double et la consonance de quarte en raison sesquitierce (4/3), la somme des deux donne la raison de 8 à 3, car 4 est à 3 dans le rapport sesquitierce et le double de 4 est 8.[10]

La quinte de l’octave est en raison triple, le rapport sesquialtère ajouté à 2 donne, en effet, cette raison, car  rapport de 9 à 6 est sesquialtère et le rapport de 18 à 9 est double, ce qui donne la raison triple pour rapport de 18 à 6.[11]

La double octave est pareillement en raison quadruple, car elle se compose de deux raisons doubles : le double de 6 est 12 et le double de 12 est 24 qui est quadruple de 6 ou plutôt, d’après ce que nous avons dit au commencement, la raison triple ajoutée à la raison sesquitierce donne la raison quadruple. Or la raison d’octave et quinte est 3, celle de quarte est sesquitierce 4/3 et c’est des deux que se compose la double octave. C’est donc justement qu’on voit ici la consonance quadruple, car le triple de 6 est 18 dont les 4/3 sont 21 qui est le quadruple de 6, de même le rapport de 8 à 6 est sesquitierce elle triple de 8 est 24 qui est le quadruple de 6. On peut pousser ces notions aussi loin qu’on voudra, on trouvera toujours les mêmes rapports résultant de la composition des consonances.[12]

Platon a conduit le genre diatonique et l’étendue de ce système jusqu’à la quatrième octave avec une quinte en plus et un ton.[13] Que si quelqu’un objecte, dit Adraste, qu’il ne faut pas pousser si loin le calcul, puisque Aristoxène a limité à la double octave et quinte l’étendue du diagramme qui représente les différents modes, et que les modernes ont le pentédécacorde (lyre à 15 cordes) dont l’étendue la plus considérable ne contient que la double octave [avec un ton de plus], je réponds, poursuit-il, que ces derniers ne considérant que le point de vue pratique, ont réglé les choses de cette manière, parce qu’ils étaient persuadés que ceux qui concourent pour le prix du chant, ne peuvent pousser la voix au-delà de ces limites, et que, d’ailleurs, les auditeurs ne pourraient plus distinguer facilement les sons.

Platon, au contraire, considérant la nature des choses et l’âme qui se compose nécessairement d’harmonie. prolonge le calcul jusqu’aux nombres solides (8 et 27) et joint les termes par deux moyennes, afin de pouvoir embrasser complètement tout ce qui compose le corps solide du monde; et il en étend jusqu’à ce point l’harmonie qui, selon sa nature peut aller à l’infini.

Il dit de plus qu’il est convenable d’attribuer les plus grands nombres aux sons les plus graves, quoique cela ne paraisse pas convenir à certaines tensions, par exemple à la tension qui se fait par la suspension des poids. En effet, de deux cordes égales en longueur et en grosseur, et semblables du reste, celle qui soutiendra le plus grand poids produira le son le plus aigu, à cause de la tension plus grande, car le plus grand poids, produisant une plus forte tension, donne extrinsèquement une plus grande force au son plus aigu par lui-même qui a, d’après cela, une force moindre que le poids suspendu. Au contraire, il est évident qu’un son plus grave, possédant par lui-même une force plus grande que le poids suspendu, se suffit à lui-même pour retenir sa propre harmonie et sa consonance; en sorte que le plus grand nombre doit être attribué à la plus grande force. Cela s’accorde avec le reste, car les longueurs et les grosseurs des cordes, ralentissant le mouvement, les rendent impuissantes et les empêchent de vibrer facilement et de frapper rapidement l’air qui les entoure.

Il est donc évident que les sons les plus graves ont leur force propre selon le nombre le plus grand. On trouve la même chose avec les instruments à vent, car dans ces instruments les sons les plus graves résultent de leur longueur et de la largeur des trous qui font mettre en mouvement une plus grande quantité d’air; ils résultent aussi de la diminution du souffle, comme dans la trompette et dans l’organe vocal où les sons faibles et tempérés ont une force propre plus grande.

La première de toutes les consonances, dit Platon, est la quarte, car c’est par elle qu’on trouve toutes les autres; la quinte n’est séparée de la quarte que par l’intervalle d’un ton.

Du limma

XIV. On peut définir le ton, l’intervalle qui sépare la quinte de la quarte. On trouve que l’octave est la somme de la quarte et de la quinte, car elle se compose de ces deux consonances.

Les anciens prenaient le ton pour premier intervalle de la voix, sans tenir compte du demi-ton et du diésis. Ils ont trouvé que le ton est en raison sesquioctave (9/8). Ils l’ont démontré avec des disques, des vases, des cordes, des tuyaux, des poids suspendus, et de plusieurs autres manières. C’était toujours le rapport de 8 à 9 qui permettait à l’oreille de discerner l’intervalle d’un ton. Le premier intervalle (contenu dans la quarte) est donc le ton; la voix, en franchissant cet intervalle, donne à l’oreille une sensation fixe et bien déterminée. L’oreille peut encore saisir avec précision l’intervalle suivant. Quant à l’intervalle qui vient après et qu’on appelle demi-ton, les uns disent que c’est un demi-ton parfait, les autres disent que c’est un limma (un reste). La consonance de quarte qui est en raison sesquitierce (4/3), n’est donc pas complétée par un ton, c’est-à-dire par un intervalle sesquioctave (9/8).

Tous conviennent que l’intervalle de quarte est supérieur à deux tons et inférieur à trois tons. Aristoxène dit qu’il se compose de deux tons et demi parfaits, tandis que Platon dit que cet intervalle est de deux tons et un reste, et il ajoute que ce reste (limma) n’a pas de nom, mais qu’il est dans le rapport de nombre à nombre, qui est celui de 256 à 243.[14] Tel est le limma, la différence des termes est 13.

Voici la méthode dont on s’est servi pour trouver ce rapport le premier terme ne saurait être 6, puisqu’il n’est pas divisible par 8 et qu’on doit en prendre les 9/8. Il ne saurait non plus être 8, car si les 9/8 de 8 sont 9, on ne saurait prendre ensuite les 9/8 de 9, et il faut prendre les 9/8 des 9/8, puisque la quarte qui est dans le rapport sesquitierce surpasse le double ton. Nous prenons donc le fond sesquioctave, 8 et 9; or, 8 multiplié par lui-même, donne 64 et 9 x 8 donne 72; enfin, 9, multiplié par lui-même, donne 81. Nous avons donc [8, 9,] 64, 72, 81. Si maintenant on multiplie chacun de ces nombre par 3,[15] on a 64 x 3 = 192; 72 x 3 = 216; 81 x 3=243; en sorte que nous avons [8, 9, 61, 72, 81], 192, 216, 243. Après 243, plaçons 192 x 4/3 ou 256 et nous aurons la série des termes suivants

·        le fond sesquioctave 8, 9,

·        les seconds sesquioctaves 64, 72, 81,

·        les troisièmes sesquioctaves 192, 216, 243.

Si on ajoute les 4/3 de 192 ou 26, la consonance de quarte (6/3) sera complétée par deux tons et le limma dont nous avons parlé.

Il y en a quelques-uns qui choisissent pour premier terme le nombre 384, afin de pouvoir en prendre deux fois de suite les 9/8. Ils multiplient le terme 6 par 8, ce qui donne 48, et en multipliant ce nombre de nouveau par 8, ils ont pour produit 384 dont les 4/3 égalent 512. Entre ces deux termes se trouvent deux sesquioctaves; car 384 x 9/8 = 432 et 432 x 9/8 = 486 qui, avec 512, donne le rapport de limma.

Quelques-uns disent que ces nombres ne sont pas pris convenablement, attendu que l’excès du quatrième terme sur le troisième n’est pas 13, nombre que Platon a dit devoir être celui du limma. Mais rien n’empêche que nous ne trouvions dans d’autres nombres le même rapport qui existe entre 256 et 243; car Platon n’a pas pris un nombre déterminé mais seulement la raison du nombre. Or, le rapport qui existe entre 256 et 243 est le même qu’entre 512 et 486, puisque 512 est le double de 256 et 486 le double de 243. Il est manifeste que cet intervalle des nombres 256 et 243, dont la différence est 13, est moindre que le demi-ton, car le ton étant 1 + 1/8, le demi-ton sera la moitié de 1 + 1/8, c’est-à-dire 1 + 1/16. Or, 13/243 est un rapport moindre que 1/18, rapport qui est lui-même moindre que 1/16.[16]

Il n’est d’ailleurs pas possible de partager la raison 1+ 1/8 en deux parties égales, quoique quelques-uns le croient possible, jugeant cette question, non par le raisonnement, mais par l’oreille. Le fond de l’intervalle sesquioctave étant le rapport de 9 à 8,[17] la différence des termes qui est l’unité, n’est assurément pas divisible.

XV. Si quelqu’un demande, au sujet du limma, à quelle consonance il appartient, nous lui dirons qu’il faut le considérer comme appartenant à la quarte; car c’est lui qui fait que la quarte est moindre que deux tons et demi parfaits.

Or, voici comment le ton a été trouvé. La quarte étant dans le rapport 4/3, et la quinte dans le rapport 3/2, on a pris le premier nombre divisible à la fois par 2 et par 3. Ce s nombre est 6 dont les 4/3 égalent 8 et les 3/2 égalent 9. On a 6, 8, 9, et l’excès de l’intervalle 3/2 sur l’intervalle 4/3 est 9/8, car 9 est les 9/8 de 8. On a donné à cette tension le nom de ton.

XVI. Il est manifeste que le ton ne peut être divisé en deux parties égales. Et d’abord, le fond sesquioctave 9/8 a pour différence des termes l’unité qui est indivisible; et puis, cet intervalle étant exprimé en nombres quelconques, la différence des termes ne peut pas toujours se diviser en deux parties égales: ainsi, la différence 27 des termes du rapport de 216 à 243 n’est pas susceptible de la division en deux parties égales, mais en deux nombres qui sont 13 et 14, car l’unité n’est pas divisible. Tantôt nous saisissons le ton par l’opération de l’intelligence, tantôt nous le cherchons dans les nombres et les intervalles, tantôt enfin nous le percevons par l’oreille dans la voix, et nous savons qu’il n’est pas toujours divisible en deux parties égales, soit dans les nombres, ainsi que nous venons de le montrer, soit dans les intervalles sensibles et visibles.

C’est comme dans le canon harmonique : le chevalet qui est sensible a, quoiqu’on fasse, une certaine largeur et ne peut être tellement privé d’épaisseur que, dans le partage du ton, il n’intercepte absolument rien de l’extrémité de la première partie et du commencement de la seconde, de sorte qu’il y aura toujours une certaine partie du ton qui sera absorbée. Dans les partages il y a donc trois choses : les deux divisions et la partie retranchée (par le chevalet). Par l’acte même de la division, une partie de ce qui est divisé se trouve détruite, comme on le voit quand on coupe quelque chose avec une scie. Comme dans certaines choses sensibles, il se perd quelques particules, il en est de même dans toutes les autres choses, quand on fait une section, bien que nos sens ne nous en rendent pas témoignage.

Si, par exemple, avant de diviser une règle en bois, un roseau ou tout autre objet long, vous le mesurez, et qu’ensuite vous le divisiez en plusieurs parties, vous trouverez la longueur de toutes les parties réunies moindre que la longueur de l’objet avant la division, De même, si vous partagez une corde en plusieurs parties et que vous la coupiez, vous trouverez qu’après la section, le développement sera moindre, et si vous voulez tendre de nouveau toutes les parties, vous ne pourrez empêcher en les joignant par les extrémités qu’il ne se perde une partie de la longueur de la corde. Voilà pourquoi deux demi-tons ne seront jamais complets.

Et dans la voix non plus, on ne trouve pas la section du ton en deux parties égaies : car, si après avoir fait entendre un ton suivi d’un autre ton, je produis deux demi-tons, au lieu d’un seul ton, par trois émissions de voix, en montant de deux intervalles, le troisième son est plus aigu que le second et il est d’un ton plus haut que le premier, tandis qu’il ne semble être au-dessus du second que d’un demi-ton; mais ce demi-ton n’est ni égal ni semblable à celui qui se trouve entre le premier son et le second, le plus grave ne pouvant être semblable au plus aigu, et c’est en vain que nous voudrions reproduire deux fois le même son en coupant notre voix, nous donnerons la même résonance, mais il y aura toujours une différence quoique imperceptible à l’oreille.

C’est comme si l’on voulait faire deux piqûres tout à fait semblables, ou pincer également deux fois une corde, il y aura toujours une différence de force en plus ou en moins. Il en sera de même si l’on voulait plonger le doigt deux fois également dans un liquide, ou bien le plongeant dans de l’encre, du miel, de la poix, en retenir la même quantité.

Quant au ton idéal, on conçoit qu’il puisse être divisé en deux parties égales.

XVII. Nous avons à parler maintenant de l’harmonie qui est contenue dans les nombres et à expliquer ce que c’est que le terme qui, dans toute chose, montre la propriété de ce que l’on dit, par exemple, le nombre, la grandeur, la puissance, la masse, la gravité.

En combien de sens se prend le mot λόγος.

XVIII. Le mot λόγος est pris en plusieurs sens par les péripatéticiens ; car on appelle ainsi le langage que les modernes nomment oral et le raisonnement mental sans émission de voix; on appelle encore ainsi le rapport de proportion, et c’est en ce sens qu’on dit qu’il y a rapport de telle chose à telle autre; l’explication des éléments de l’univers; le compte des choses qui honorent ou qui sont honorées, et c’est dans cette acception que nous disons : tenir compte de quelque chose, ou n’en pas tenir compte. On appelle encore λόγος le calcul des banquiers, les discours de Démosthène et de Lysias dans leurs œuvres écrites; la définition des choses, qui en explique l’essence, puisque c’est à cela qu’elle sert; le syllogisme et l’induction; les récits libyques[18] et la fable. On donne aussi le nom de λόγος à l’éloge et au proverbe. C’est encore ainsi qu’on appelle la raison de la forme, la raison séminale et beaucoup d’autres.

Mais, selon Platon, on emploie le mot λόγος en quatre sens : on appelle ainsi la pensée mentale et sans parole, le discours procédant de l’esprit et exprimé par la voix, l’explication des éléments de l’univers et la raison de proportion. C’est de cette raison que nous nous proposons maintenant de parler.

De la raison de proportion

XIX. La raison de proportion de deux termes de même espèce est un certain rapport qu’ils ont entre eux, comme le double, le triple. Il est impossible, dit Adraste, de trouver un rapport entre deux choses qui ne sont pas de même espèce: ainsi on ne peut ni comparer, ni réunir la coudée (mesure de longueur) et la mine (mesure de poids) la chénice (mesure de capacité pour les choses sèches) et la cotyle (mesure de capacité pour les liquides, le blanc et le doux ou le chaud; mais on peut comparer ensemble les choses de même espèce, comme les longueurs avec les longueurs, les surfaces avec les surfaces, les solides avec les solides, les poids avec les poids, les liquides avec les liquides, les choses sèches avec les choses sèches, les nombres avec les nombres, le temps avec le temps, le mouvement avec le mouvement, la voix avec la voix, le suc avec le suc, la couleur avec la couleur, enfin toutes les choses de même espèce.

XX. Nous appelons termes les choses homogènes ou de même espèce, prises pour être comparées ensemble. Quand nous examinons quel rapport existe entre le talent et la mine, nous disons que ce sont des termes de même espèce, parce que l’un et l’autre sont des poids. Il en est de même des autres choses homogènes.

XXI. La proportion est une certaine liaison de rapports, telle que 2 est à 1 comme 8 est à 4.

XXII. Les rapports sont supérieurs, inférieurs ou égaux (à l’unité). Le rapport égal est un et toujours le même, et il l’emporte sur tous les autres, comme étant élémentaire. Tels sont les rapports qui se comparent par la même quantité, comme 1 comparé 1, 2 à 2, 10 à 10, 100 à 100. Parmi les rapports plus grands (que l’unité), les uns sont multiples (c’est-à-dire entiers), d’autres sont sesquipartiels, d’autres sont neutres. Parmi les rapports moindres (que l’unité), les uns sont sous-multiples, d’autres sont sous-sesquipartiels, d’autres sont neutres. Parmi ces raisons, les unes représentent les consonances, d’autres y sont étrangères.

Les raisons multiples qui représentent les consonances sont la raison double, la raison triple, et la raison quadruple. Les raisons sesquipartielles sont la raison sesquialtère (3/2 = 1 + 1/2), et la raison sesquitierce (4/3 = 1 + 1/3). Parmi les neutres, on a la raison sesquioctave (9/8 =1 + 1/8) et le rapport de 256 à 243. Sont opposées à ces raisons la sous-double (1/2) la sous-triple (1/3), la sous-quadruple (1/4, la sous-sesquialtère (2/3), la sous-sesquitierce (3/4), la sous-sesquioctave (8/9) elle rapport de 243 à 256.

La raison double, comme nous l’avons vu plus haut, se trouve dans la consonance d’octave,[19] la raison triple dans la consonance d’octave et quinte, la raison quadruple dans la double octave, la raison sesquialtère (1 + 1/2) dans la quinte, la raison sesquitierce (1 + 1/3) dans la quarte. Quant à la raison sesquioctave (1 + 1/8) c’est un ton et le rapport de 256 à 243 est le limma. Il en est de même des rapports inverses. Parmi les raisons neutres sont la raison sesquioctave (1 + 1/8) et la raison de 256 à 243 qui ne sont pas des consonances et n’y sont pourtant pas étrangères, puisque le ton et le limma sont les principes de la consonance et ont la vertu de la compléter, sans être cependant des consonances.[20]

Il y a en arithmétique des raisons de nombres, non seulement multiples et superpartielles, mais encore des raisons épimères et polyépimères et d’autres raisons que nous expliquerons clairement plus tard. La quarte se compose de deux tons et d’un limma, la quinte de trois tons et d’un limma, l’octave d’une quinte et d’une quarte; mais les rapports de proportion doivent les précéder.

Ainsi, selon les principes de l’arithmétique, comme l’enseigne Adraste, il y a des rapports multiples, d’autres sont sesquipartiels, d’autres épimères, d’autres multi-superpartiels, d’autres polyépimères; d’autres sont neutres, et parmi les rapports plus petits (que l’unité), il y en a de sous-multiples, d’autres sont sous-sesquipartiels; les autres sont inverses des rapports plus grands (que l’unité).

XXIII. Le rapport est multiple quand le plus grand terme contient plusieurs fois le plus petit, c’est-à-dire quand le petit terme mesure exactement le plus grand, sans qu’il reste aucune partie de celui-ci. Le plus grand terme est autant de fois multiple du plus petit que ce dernier le mesure de fois; si par exemple il le mesure deux fois, le rapport est double; s’il le mesure trois fois, le rapport est triple; s’il le mesure quatre fois, le rapport est quadruple; est ainsi de suite. Réciproquement le plus petit terme, comme partie du plus grand; reçoit une dénomination correspondante à la raison multiple: on l’appelle la moitié du terme double, le tiers du terme triple, … et la raison est appelée demie, tiers, et ainsi de suite.

Du rapport superpartiel ou sesquipartiel

XXIV. Le rapport est appelé sesquipartiel quand le plus grand terme contient une fois le plus petit et une partie du plus petit, c’est-à-dire quand le plus grand terme surpasse le plus petit d’une certaine quantité qui en est une partie. Ainsi le nombre 4 est sesquipartiel par rapport à 3, parce qu’il le surpasse d’une unité qui est le tiers de 3. De même 6 surpasse 4 de 2 unités qui sont la moitié de 4.

Chaque rapport sesquipartiel a reçu, d’après le nom de la fraction, une dénomination particulière. Ainsi celui qui surpasse l’unité de la moitié du plus petit terme, comme 3/2 et 6/4, a été appelé sesquialtère, car la plus grande quantité contient la plus petite tout entière plus la moitié de la plus petite. En effet, 3 contient une fois 2, plus l’unité qui est la moitié de 2; 6 contient une fois 4, plus 2 qui est la moitié de 4. Le rapport qui surpasse l’unité du tiers du plus petit terme, comme 4/3, est appelé sesquitierce, celui qui surpasse l’unité d’un quart, comme 3/4 et 10/8, est appelé sesquiquarte, et en continuant de même, on trouve les rapports qu’on nomme sesquiquinte (1 + 1/5), sesquisixte (1 + 1/6),  sesquiseptime (1 + 1/7) qui sont tous sesquipartiels.

Inversement, les rapports des plus petits termes aux plus grands sont appelés sous-sesquipartiels, car de même que le rapport de 3 à 2 est appelé sesquialtère, par analogie le rapport de 2 à 3 est appelé sous-sesquialtère. De même encore le rapport de 3 à 1 est nommé sous-sesquitierce.

Parmi les rapports multiples, le premier et le plus petit est le double, vient ensuite le triple, puis le quadruple, et ainsi de suite indéfiniment en augmentant.

Parmi les rapports sesquipartiels, le premier et le plus grand est le rapport sesquialtère (1 + 1/2), parce que la fraction 1/2 est la première, la plus grande, celle qui se rapproche le plus de l’entier; vient ensuite le rapport sesquitierce (1 + l/3), puis le rapport sesquiquarte (1 + 1/4), et ainsi de suite indéfiniment, en allant toujours en diminuant.

Du rapport épimère

XXV. Le rapport est dit épimère quand le plus grand terme contient une fois le plus petit et en outre plusieurs parties de celui-ci, soit semblables, soit différentes, semblables comme deux tiers, deux cinquièmes, etc. Ainsi le nombre 5 contient 3, plus les deux tiers de 3; le nombre 7 contient 5, plus les deux cinquièmes de 3; le nombre 8 contient 3 et les trois cinquièmes de 5, et ainsi de suite. Les parties sont différentes quand le plus grand terme contient le plus petit, et en outre la moitié et le tiers de celui-ci, comme dans le rapport de 11 à 6, ou la moitié et le quart, comme dans le rapport de 7 à 4, ou encore le tiers et le quart, comme dans le rapport de 19 à 12.[21]

On peut pareillement reconnaître les autres rapports épimères qui surpassent l’unité de deux, de trois ou d’un plus grand nombre de parties, que ces parties soient semblables ou non. Inversement le rapport hypépimère, est celui qu’on obtient en prenant, dans le rapport précédent, la raison du plus petit terme au plus grand.

Du rapport multi-superpartiel et du rapport polyépimère

XXVI. Le rapport est dit multi-superpartiel ou multi-sesquipartiel quand le plus grand terme contient 2 fois ou un plus grand nombre de fois le plus petit et en outre une partie de ce dernier. C’est ainsi que 7 contient 2 fois 3 et en outre un tiers de 3, aussi l’on dit que le rapport de 7 à 3 est bisesquitierce, de même 9 contient 2 fois 4 et en outre le quart de 4, on dit que le rapport de 9 à 4 est bisesquiquarte. De même encore 10 contient 3 fois 3 et en outre le tiers de 3, le rapport est appelé trisesquitierce.

On reconnaîtra de la même manière les autres rapports multi-superpartiels. C’est ce qui arrive toutes les fois que de deux nombres proposés le plus petit ne mesure pas exactement le plus grand, mais que le plus grand donne un reste qui est en même temps une partie du plus petit. Ainsi le rapport de 26 à 8 est multi-superpartiel par ce que 3 fois 8 ne donnent pas complètement 26; en arrivant à 24, au lieu de 26, il y a un reste 2 qui est le quart de 8.

XXVII. Le rapport est appelé polyépimère quand le plus grand terme contient 2 fois, ou plus, le plus petit, et en outre 2 ou plusieurs parties de ce dernier, soit semblables, soit différentes. Ainsi 8 contenant 2 fois 4 et de plus deux tiers de 3, le rapport est dit double avec deux tiers en plus (2 + 2/3); de même le rapport de 11 à 3 est triple avec deux tiers en plus (3 + 2/3); le rapport de 11 à 4 est double, avec une demie et un quart en plus, ou double avec trois quarts en plus (11/4 = 2 + 3/4 = 2 + 1/2 + 1/4).

Il est facile de trouver beaucoup d’autres rapports polyépimères, et cela a lieu toutes les fois que le plus petit nombre ne mesure pas exactement le plus grand, mais qu’il y a un reste formé de plusieurs parties du petit nombre, comme dans le rapport de 14 à 3, car 3 ne mesure pas exactement 14, mais 3 fois 4 font 12, de 14 il reste 2 qui forment deux parties de trois et qu’on nomme deux tiers. Au rapport polyépimère est opposé le rapport hypo-polyépimère (rapport inverse).

XXVIII. La raison de nombre à nombre est celle qui a lieu quand le plus grand n’a avec le plus petit aucun des rapports dont nous avons parlé; comme il sera montré, c’est un rapport de nombre à nombre, réduit à ses plus petits termes, qui mesure le limma; ce rapport est celui de 256 à 243.[22] Il est évident que la raison des plus petits nombres aux plus grands est l’inverse. Elle emprunte son nom aux premiers rapports, comme il a été montré.

Du fond d’un rapport

XXIX. De tous les rapports dont il a été parlé en détail, ceux qui sont exprimés en nombres les plus petits et premiers entre eux sont appelés les premiers ou les fonds de tous les rapports d’espèce semblable (c’est-à-dire égaux). Ainsi le premier et le fond des rapports doubles est le rapport 2 à 1, car après celui-là les rapports doubles sont exprimés en nombres plus grands et composés, comme les rapports de 4 à 2, de 6 à 3, et ainsi de suite indéfiniment.

De même le premier et le fond des rapports triples est le rapport de 3 à 1, les rapports triples exprimés en nombres plus grands et composés vont à l’infini. Il en est de même des autres rapports multiples et des rapports superpartiels, le premier et le fond des rapports sesquialtères est 3/2; pour le rapport sesquitierce c’est 4/3, pour le rapport sesquiquarte c’est 3/2. Il y a une infinité de rapports équivalents exprimés en termes plus grands et composés. On peut faire les mêmes observations sur les autres rapports.

En quoi diffèrent l’intervalle et le rapport.

XXX L’intervalle et le rapport diffèrent en ce que l’intervalle est compris entre des termes homogènes et inégaux, tandis que le rapport lie simplement entre eux des termes homogènes. C’est pourquoi entre des termes égaux il n’y a pas d’intervalle, mais il y a entre eux un rapport qui est celui d’égalité. Entre les termes inégaux, l’intervalle de l’un à l’autre est unique et identique, tandis que le rapport est autre et inverse, d’un terme à l’autre : ainsi de 2 à 1 et de 1 à 2 il n’y a qu’un seul et même intervalle, mais il a deux rapports différents, le rapport de 2 à 1 étant double, tandis que le rapport de 1 à 2 est un demi.

Eratosthène, dans le Platonicien, dit aussi que l’intervalle et le rapport ne sont pas la même chose, parce que le rapport est une certaine liaison de deux grandeurs entre elles et qu’il existe entre des choses différentes ou non, comme quand on dit que le sensible est à l’intelligible dans le même rapport que l’opinion est à la science, ou que l’intelligible diffère du connu par le même rapport que le sensible diffère de l’opinion, tandis que ces choses diffèrent d’un seul intervalle, soit de grandeur, soit de qualité, soit de position, soit de toute autre manière. Par là il est évident que le rapport est autre chose que l’intervalle, car la moitié et le double ne forment pas un même rapport. tandis que l’intervalle est le même.

XXXI. La proportion est une similitude ou identité de plusieurs rapports, c’est-à-dire une similitude des raisons dans plusieurs termes, ce qui a lieu quand le rapport du premier terme au second est égal au rapport du second au troisième ou au rapport de deux autres termes. La première proportion est appelée continue et la seconde discontinue. Il faut trois termes au moins pour une proportion continue, la discontinue suppose au moins quatre termes.

Après la proportion formée de termes égaux, les trois plus petits termes 1, 2, 4, en raison double, forment une proportion continue, car 4 est à comme 2 est à 1; et les nombres 6, 3, 4, 2, forment une proportion discontinue, car 6 est 3 comme 4 est à 2. On observe la même chose avec les autres rapports multiples et la proportion continue est en quelque sorte une proportion à quatre termes, par la répétition du moyen terme. L’explication est la même quand les rapports sont sesquipartiels : ainsi les nombres 9, 6, 1, en rapport sesquialtère (1 + 1/2), forment une proportion continue, et les termes 9, 6, 15, 10, forment une proportion discontinue. On trouverait de même des proportions arec les autres rapports.

Eratosthène dit que le rapport est le principe qui donne naissance à la proportion et qu’il est aussi la première cause de la génération de toutes les choses qui sont disposées avec ordre. Toute proportion se compose, en effet, de rapports et le principe du rapport est l’égalité. Cela est évident dans tous les genres il y a un certain élément propre, ou un principe, dans lequel tous les autres se résolvent, tandis que lui-même ne se résout en aucun d’eux. Or, ce principe est nécessairement indécomposable et indivisible, car tout ce qui peut se décomposer et se diviser est appelé collection et non élément.

Les éléments de la substance sont donc indivisibles selon la substance, ceux de la qualité le sont selon la qualité, ceux de la quantité le sont selon la quantité. Et chaque chose est indivisible et une, selon qu’elle est un élément d’une chose composée ou mixte. Ainsi l’élément de la quantité est l’imité, celui de la grandeur est le point, celui du rapport et de la proportion est l’égalité. Car l’unité ne peut pas se diviser en quantité, ni le point en grandeur, ni l’égalité en rapports multiples. Le nombre naît de l’unité, la ligne du point, le rapport et la proportion de l’égalité: mais ce n’est pas de la même manière, car l’unité multipliée par elle-même n’engendre pas, comme les autres nombres : une fois un est un, tandis que par l’addition le résultat augmente à l’infini.

Quant au point, ce n’est ni par la multiplication, ni par l’addition, qu’il forme la ligne, mais par un mouvement continu, de même que la ligne forme la surface et la surface le solide. Pareillement la raison d’égalité ne s’accroît pas par addition, car si l’on additionne par ordre plusieurs rapports égaux, la raison de la somme donne encore une égalité. Ainsi le point n’est pas une partie de la ligne, ni l’égalité une partie du rapport. Toutefois l’unité fait partie du nombre: car elle reçoit un accroissement par la seule répétition d’elle-même. La cause de ce que nous venons de dire est que l’égalité n’a pas d’intervalle, comme le point n’a pas de grandeur.

Platon semble croire que le lien des mathématiques est unique et qu’il consiste dans la proportion. Il dit, en effet, dans l’Epinomis : il faut que toute figure, toute combinaison de nombres, tout ensemble harmonique, toute révolution astronomique manifeste l’unité de proportion à celui qui apprendra selon la vraie méthode: or, cette unité apparaîtra à quiconque aura bien compris ce que nous enseignons. Il reconnaîtra qu’un seul lien unit naturellement toutes choses.

XXXII. Un nombre moyen diffère du moyen proportionnel.[23] Car un nombre est moyen proportionnel entre deux autres, c’est un terme compris entre eux: mais si un terme est compris entre deux autres, ce n’est pas pour cela un moyen proportionnel entre ces nombres. Il peut arriver, en effet, qu’un nombre compris entre deux extrêmes ne soit pas en proportion avec euχ, comme 2 qui est compris entre 1 et 3, et 2, 3, 4, qui sont compris entre 1 et 10, car on ne peut arriver de 1 à 10 sans passer par 2, 3, 4, et cependant aucun de ces nombres n’est en proportion avec les extrêmes, car le rapport de 1 à 2 n’est pas égal à celui de 2 à 3, et de même le rapport de 1 à 2, 3, ou 4, n’est pas égal à celui de 2, 3, ou 4, à 10. Les moyens proportionnels entre deux nombres sont au contraire compris entre ces nombres : ainsi dans la proportion 1, 2, 4, dont la raison est double, le moyen proportionnel 2 est compris entre 1 et 4.

Des proportions (entre trois nombres).

XXXIII. Thrasylle compte trois proportions principales entre trois nombres: la proportion arithmétique, la proportion géométrique et la proportion harmonique : la proportion arithmétique est celle dont le terme moyen surpasse autant un terme extrême qu’il est surpassé par l’autre, telle est la proportion 1, 3, 5; la proportion géométrique est celle dont le terme moyen contient autant de fois un terme extrême qu’il est contenu dans l’autre, comme 2 fois, 3 fois, telle est la proportion 3, 6, 12: la proportion harmonique entre trois nombres est celle dans laquelle le nombre moyen surpasse un nombre extrême et est surpassé par l’autre, de la même fraction des nombres extrêmes, comme le tiers, le quart, telle est la proportion des nombres 6, 8, 12.

On peut considérer ainsi chacun des rapports : 12 est le double de 6; 18 en est le triple; 2 en est le quadruple: 9 en est les 3/2 et 8 en est les 4/3; 9 est les 9/8 de 8; 12 est les 4/3 de 9, les 3/2 de 8 et le double de 6 : 18 est le double de 9 et 27 est les 3/2 de 18; 8/6 donne la consonance de quarte, 9/6 la consonance de quinte et 12/6 celle d’octave: 18/6 donne octave et quinte, car 12 étant le double de 6 fournit la consonance d’octave et 18 étant les 3/2 de 12 est la consonance de la quinte : on a les nombres relatifs 6, 12, 18;[24] 24/6 donne la consonance de double octave; 9/8 donne le ton et 12/9 la quarte; 12/8 donne la quinte et 18/9 l’octave. La raison 27/18 donne la quinte.

L’octave 12/6 se compose de la quinte 9/6 et de la quarte 12/9, ou encore de la quinte 12/8 et de la quarte 8/6.[25] L’octave 18/9 se compose de la quinte 18/12 et de la quarte 12/9;[26] la raison 24/12 de l’octave se compose de la raison 24/18 de la quarte et de la raison 18/12 de la quinte.[27] Enfin la raison 9/6 qui est une quinte se compose d’un ton 9/8 et d’une quarte 8/6;[28] et la raison 12/8 qui est aussi une quinte se compose d’une quarte 12/9 et d’un ton 9/8.[29]

XXXIV. Le limma est dans le rapport du nombre 2G au nombre 213. Voici comment on trouve ce rapport : on prend deux fois le rapport sesquioctave (on multiple les deux termes tz du premier par 9, les deux termes du second par W) et on triple les résultats, puis on y joint le rapport sesquitierce. Le rapport sesquioctave étant celui de 9 à 8, on forme avec ces deux nombres deux autres rapports sesquioctaves de la manière suivante: 9x9 =81; 9x8= 72; et 8x8= 64; o 81 est les 9/8 de 72 et 72 est les 9/8 de 61. Si nous triplons ces nombres, nous aurons 81 x = 23; 72 x 3 216 et 61 x 3 = 192, Les t,’3 de 192 sont 26. Ce nombre cernpara 213 donne le rapport de limma qui est moindre que 1+1/18.[30]

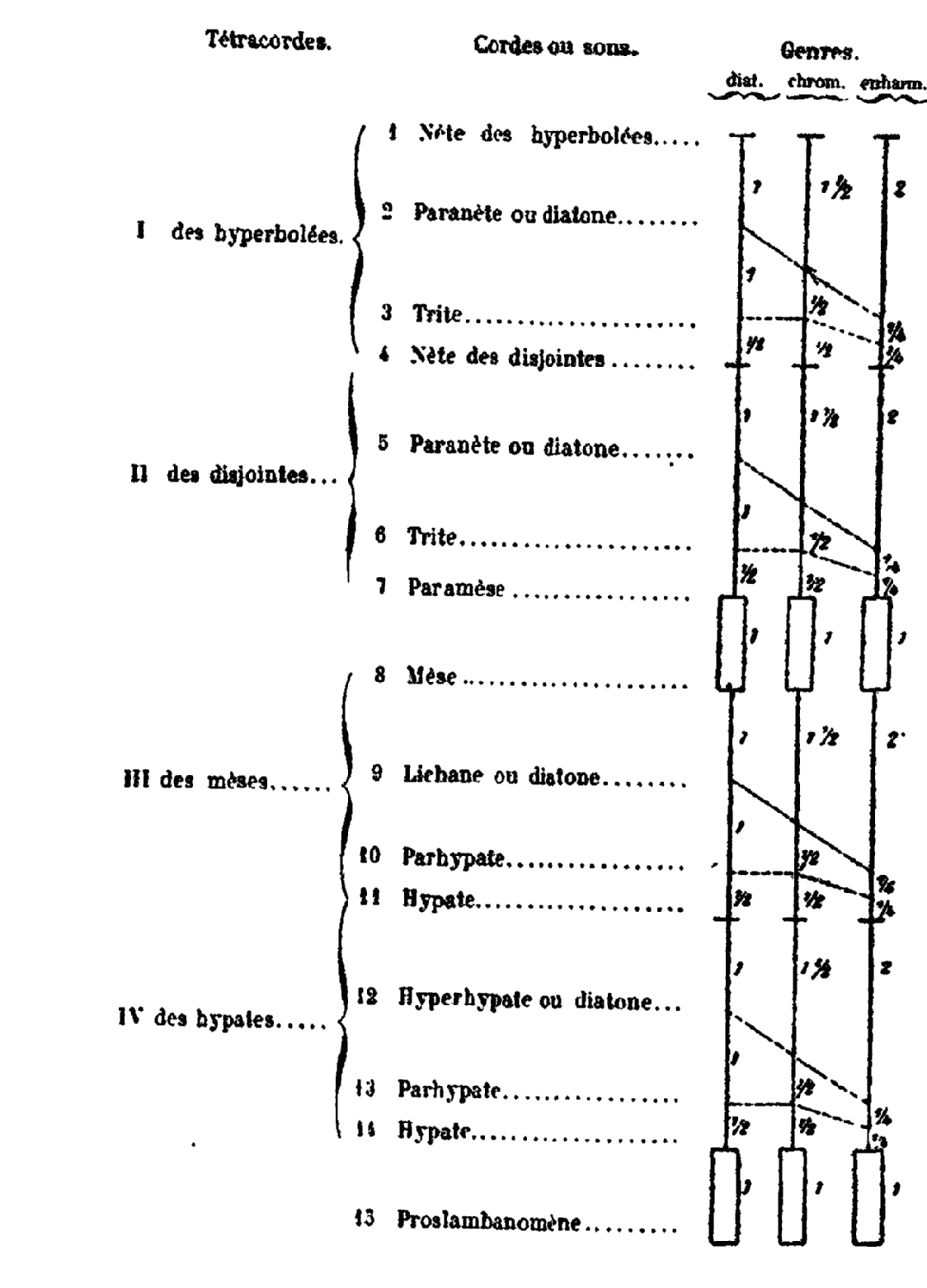
De la division du canon

XXXV. La division du canon se fait suivant le quaternaire de la décade qui se compose des nombres 1, 2, 3, 4 et qui embrasse les raisons sesquitierce, sesquialtère, double, triple et quadruple (c’est-à-dire 4/3, 3/2, 2, 3 et 4.

Voici comment Thrasylle divise ce canon. Prenant la moitié de la corde, il obtient la mèse consonance d’octave qui est en raison double, la tension étant double pour les sons aigus, en sens inverse des mouvements. L’inversion est telle que, quand la longueur totale de la corde est diminuée dans le canon, le ton est augmenté en proportion, et que, quand la longueur est augmentée, le ton décroît d’autant car la demi longueur de la proslambanomène, qui est la mèse par rapport à la corde totale, a une tension double vers l’aigu, et la corde totale qui est double a une tension moitié du côté des sons graves.

La division de la corde en trois donne l’hypate des mèses et la nète des disjointes, la nète des disjointes est la quinte de la mèse, puisque les divisions sont dans le rapport de 2 à 3, et elle est à l’hypate (des mèses) dans le rapport d’octave, puisque les divisions sont comme 1 est à 2. La nète des disjointes donne avec la proslambanomène la consonance d’octave et quinte, car de la proslambanomène à la mèse il y a une octave et les intervalles étant prolongés jusqu’à la nète des disjointes, il y a une quinte de celle-ci à la mèse.

De la mèse à l’hypate (des mèses) il y a une quarte, et de la mèse à la proslambanomène il y a une octave, l’hypate des mèses donnant la quinte par rapport à la proslambanomène. On obtient la même distance d’octave en ajoutant l’intervalle de l’hypate (des mèses) à la mèse, qui est une quarte, à l’intervalle de la mèse à la nète des disjointes qui est une quinte. Les nombres des mouvements (c’est-à-dire des vibrations) varient en sens inverse de la division des longueurs (c’est-à-dire en sens inverse de la longueur de la partie vibrante).

En divisant la corde en quatre, on obtient la diatone des hypates, nommée aussi hyperhypate, et la nète des hyperbolées. La nète des hyperbolées est à la nète des disjointes dans le rapport de quarte, à la mèse dans le rapport d’octave, à l’hypate (des mèses) dans le rapport d’octave et quarte, à l’hyperhypate dans le rapport d’octave et quinte et à la proslambanomène dans le rapport de double octave, en allant vers les tons graves.

L’hyperhypate est à la proslambanomène dans le rapport de quarte, en allant vers les tons graves, et à la mèse dans le rapport de quinte, en allant vers les tons aigus; elle est d’un ton au-dessous de l’hypate (des mèses), et l’intervalle de ton de l’hyperhypate à la dernière corde (la proslambanomène) est égal à l’intervalle de quarte de la nète des disjointes à la nète des hyperbolées; et ici encore le nombre des mouvements est en sens inverse de la grandeur des divisions.

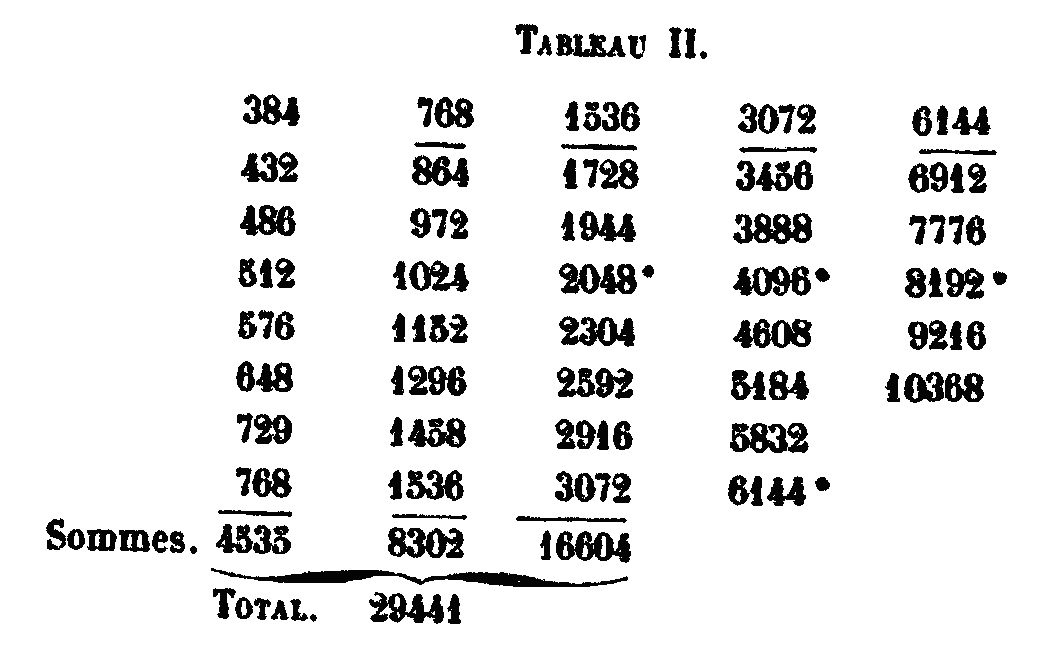
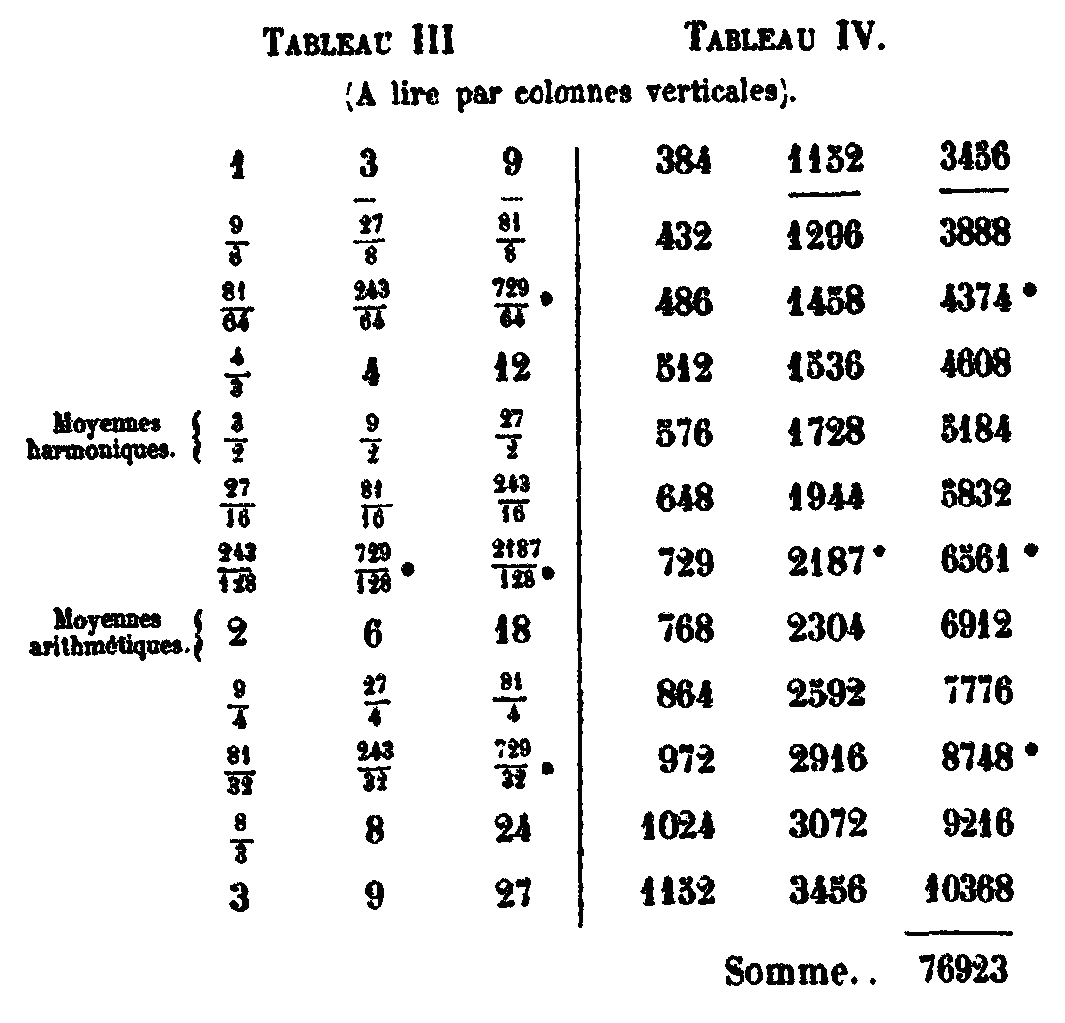
Tout cela sera rendu évident par des nombres, car si on divise la longueur du canon en douze parties convenables, la mèse sera donnée par chaque moitié de la corde totale. L’hypate des mèses sera donnée en supprimant quatre parties au commencement du canon et la nète (les disjointes en prenant quatre parties à l’autre extrémité du canon, de sorte qu’il y aura quatre parties entre elles. L’hyperhypate sera donnée en supprimant trois parties au commencement, elle est distante, d’une division, de l’hypate (des mèses). L’hyperbolée (nète des hyperbolées) s’obtient en prenant trois parties de la corde; elle est distante, d’une division, de la disjointe (nète des disjointes).

Entre l’hyperhypate et la nète des hyperbolées, il y a six divisions, trois au-dessus de la mèse, et trois au-dessous et ainsi le partage est complet. En effet, du commencement du canon à l’hyperhypate on compte trois parties du canon, de là à l’hypate des mèses, une partie, et de celle-ci à la mèse, deux parties. De la mèse à la nète des disjointes, il y a deux parties, de là à l’hyperbolée une partie, enfin de celle-ci à la fin du canon trois parties. Toutes les divisions sont donc au nombre de douze.

La raison de la nète des disjointes à la nète des hyperbolées sera 4/3, c’est le rapport sesquitierce qui donne la consonance de quarte. Le rapport de la mèse à la nète des hyperbolées sera 6/3 = 2 qui est la consonance d’octave. La raison de l’hypate des mèses à la même nète sera 8/3, consonance d’octave et quarte. La raison de l’hyperhypate à la nète sera 9/3 = 3, consonance d’octave et quinte et le rapport de la proslambanomène à la même est 12/3 = 4, consonance de double octave. La raison de la mèse à la nète des disjointes égale 3/2, c’est le rapport sesquialtère, consonance de quinte. L’intervalle de l’hypate (des mèses) à la nète des disjointes égale 8/4 = 2, c’est l’octave. Celui de l’hyperhypate à la même nète égale 9/4, c’est la double quinte (quinte de la quinte). Pour la proslambanomène tout entière, le rapport est 12/4 = 3, consonance d’octave et quinte.

Le rapport de l’hypate des mèses à la mèse est 8/6 = 4/3, c’est la quarte. Celui de l’hyperhypate à la mèse est 9/6 = 3/2, il donne la quinte, celui de la proslambanomène tout entière à la mèse est 12/6 = 2, c’est l’octave. L’hyperhypate est à l’hypate des mèses comme 9 est à 8, c’est la raison d’un ton. Le rapport de la proslambanomène entière à l’hypate des mèses est 12/8 = 3/2 (c’est la quinte). La même corde est à l’hyperhypate comme 12 est à 9, ce rapport égale 4/3, consonance de quarte.

XXXVI. Les nombres de vibrations sont soumis à la proportion inverse, puisqu’on trouve condensés dans le canon le ton dont la raison est sesquioctave (9/8), la consonance de quarte dont la raison est sesquitierce (4/3), et la consonance de quinte dont la raison et sesquialtère (3/2).

La raison 3/2 de la quinte surpasse la raison 4/3 de la quarte, d’un ton qui est égal à 9/8: prenons par exemple le nombre 6 qui est divisible par 2 et par 3, les 4/3 de 6 valent 8, et les 3/2 de 6 valent 9, or 9 est les 9/8 de 8. On a la suite 6, 8, 9, et l’excès de l’intervalle 3/2 sur l’intervalle 4/3 est 9/8. Mais l’intervalle 4/3 de la quarte se compose de deux fois 9/8 et d’un limma, les intervalles doivent donc être remplis par des tons et des limmas. Celle insertion commence à la nète des hyperbolées ; en effet si nous prolongeons celle-ci de la huitième partie de sa longueur, nous aurons la diatone des hyperbolées, qui est plus grave d’un ton.

Si nous prolongeons la diatone de la huitième partie de sa longueur, nous aurons la trite des hyperbolées. qui est plus grave d’un ton que la diatone: le reste de l’intervalle jusqu’à la nète des disjointes sera le limma, complément de la consonance de quarte par rapport à la nète de hyperbolées. Si au contraire nous diminuons d’un neuvième la longueur de la nète des disjointes, nous aurons la chromatique des hyperbolées, qui est d’un ton plus aigu que la nète des disjointes; celle-ci augmente d’un huitième donnera la paranète des disjointes, qu’on appelle aussi diatone et nète des conjointes et qui est plus grave d’un ton que la nète des disjointes.

Que si nous prolongeons la nète des conjointes d’un huitième de sa longueur, nous aurons la trite des disjointes, plus grave d’un ton, et qui est la même que la diatone de conjointes. Et le reste de l’intervalle jusqu’à la paramèse sera le limma. Si nous prolongeons la paramèse d’un huitième, nous aurons la mèse, plus grave d’un ton, et qui complète l’octave. Si nous diminuons la mèse de la nième manière (en retranchant un neuvième de sa longueur), nous aurons la paramèse ou chromatique des conjointes, plus aigu d’un ton que la mèse; en retranchant de celle-ci la neuvième partie, nous aurons la chromatique des disjointes.

La mèse augmentée d’un huitième donnera la diatone des mèses, plus grave d’un ton que la mèse; la diatone des mèses, augmentée d’un huitième, donne la parhypate des mèses, plus grave d’un ton, et de là à l’hypate des mèses il reste un limma pour le complément de la consonance de quarte avec la mèse. Si de l’hypate des mèses on retranche un neuvième, on a la chromatique des mèses, plus aiguë d’un ton, et, si au contraire on l’augmente d’un huitième on a l’hyperhypate, laquelle augmentée d’un huitième donne la parhypate des hypates.

Réciproquement, si l’on divise en 9 parties la longueur de la proslambanomène, et qu’on retranche une de ces parties, à l’inverse de ce que nous avons fait pour les tons aigus, on aura l’hypate des hypates, plus aigu d’un ton que la proslambanomène et terminant le tétracorde des hypates par le rapport de limma quelle a avec la parhypate. C’est ainsi que se complète tout le système immuable du genre diatonique et du genre chromatique.

Quant au système enharmonique, il se déduit du système diatonique en supprimant les diatones que nous faisons entendre deux fois dans chaque octave et en divisant en deux les demi-tons.

Nous trouverons les résultats en nombres en commençant par la nète des hyperbolées que nous supposerons composée de 384 parties, dont on prend successivement les 9/8 et les autres fractions que nous avons indiquées. La proslambanomène en vaudra 10368.[31] Il est superflu d’exposer cela en détail, parce que quiconque aura compris ce qui précède fera facilement le calcul.

Telle est la division du canon donnée par Thrasylle. Quand nous exposerons les éléments de l’astronomie nous montrerons comment tout cela s’applique au système du monde. Revenons maintenant à l’explication des autres moyennes et des nombres moyens, puisque, comme nous l’avons dit, toute moyenne est un nombre moyen, mais que tout nombre moyen n’est pas une moyenne. C’est donc en tant que la moyenne est un nombre moyen, qu’il faut entendre ce qui suit, des moyennes et des nombres moyens.

Du quaternaire et de la décade.

XXXVII. Puisque, comme nous l’avons montré, tous les rapports des consonances se trouvent dans le quaternaire de la décade, c’est de ces nombres que nous avons à parler. La décade constitue en effet le quaternaire, puisque la somme des nombres 1, 2, 3, 4 est 10. Or, ces nombres contiennent la consonance de quarte dans le rapport sesquitierce (4/3), celle de quinte dans le rapport sesquialtère (3/2), celle d’octave dans la raison double, et celle de double octave dans la raison quadruple; et par là est complété le diagramme immuable.

Combien il y a de quaternaire

XXXVIII. L’importance du quaternaire qu’on obtient par addition (c’est-à-dire 1, 2, 3, 4) est grande en musique, parce qu’on y trouve toutes les consonances. Mais ce n’est pas seulement pour cela que tous les Pythagoriciens lui font l’honneur du premier rang : c’est aussi parce qu’il semble renfermer toute la nature de l’univers. C’est pour cette raison que la formule de leur serment était : « J’en jure par celui qui a transmis dans nos âmes le quaternaire, source de la nature éternelle[32] ». Celui qui a transmis, c’est Pythagore, ce qui a été dit de la tétractys paraît venir en effet de ce philosophe.

Le premier quaternaire est celui dont nous venons de parler : il est formé, par addition, des premiers nombres.

Le second est formé, par la multiplication, de nombres pairs et de nombres impairs, à partir de l’unité, de tous ces nombres, l’unité est le premier, parce que, comme nous l’avons dit, elle est le principe de tous les pairs, de tous les impairs et de tous les pairs-impairs, et que son essence est simple. Viennent ensuite trois nombres tant dans la série paire que dans la série impaire. Ils admettent la réunion du pair et de l’impair, parce que tout nombre n’est pas seulement pair où seulement impair. C’est pour cela que dans la multiplication, on prend deux quaternaires, l’un pair, l’autre impair : le pair dans la raison double, le premier des pairs étant 2 qui provient de l’unité doublée: l’impair dans la raison triple, le premier des impairs étant 3 qui provient de l’unité triplée, en sorte que l’unité qui est paire et impaire tout à la fois est commune à l’un et à l’autre. Le second nombre dans les pairs et doubles est 2, dans les impairs et triples, 3. Le troisième dans l’ordre des pairs est 4, dans la série des impairs, 9. Le quatrième parmi les pairs est 8, parmi les impairs, 27.

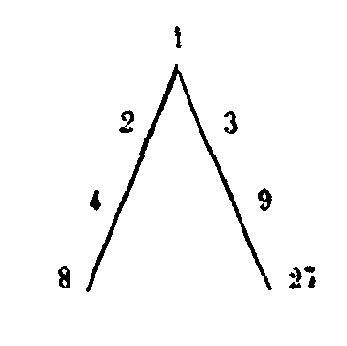
C’est dans ces nombres que se trouvent les raisons des consonances les plus parfaites; le ton y est même compris. Or l’unité contient la raison de principe, de terme et de point. Les seconds 2 et 3 ont la raison latérale, étant incomposés, premiers et mesurés seulement par l’unité, et par conséquent linéaires. Les troisièmes termes, 4 et 9, ont la puissance de la surface carrée, étant également égaux c’est-à-dire des nombres carrés. Les quatrièmes termes, 8 et 27, ont la puissance du solide cubique, étant également égaux également c’est-à-dire des nombres cubiques; en sorte qu’à l’aide des nombres de ce quaternaire, l’accroissement va du terme et du point jusqu’au solide. En effet, après le terme et le point vient le côté, puis la surface et enfin le solide. C’est avec ces nombres que Platon constitue l’âme, dans le Timée. Le dernier de ces sept nombres est égal à la somme de tous les précédents, car on a 1 + 2 + 3 + 4 + 8 + 9 = 27.

Il y a donc deux quaternaires de nombres, l’un qui se fait par addition, l’autre par multiplication; et ces quaternaires renferment les raisons musicales, géométriques et arithmétiques dont se compose l’harmonie de l’univers.

Le troisième quaternaire est celui qui, selon la même proportion, embrasse la nature de toutes les grandeurs: car ce que fait l’unité dans le précédent quaternaire, le point le fait dans celui-ci, et ce que font dans le précédent les nombres 2 et 3 qui ont la puissance latérale (ou linéaire), la ligne, par sa double forme, droite ou circulaire, le fait dans celui-ci, la ligne droite répondant au nombre pair, parce qu’elle a deux termes, et la circulaire à l’impair, parce qu’elle est comprise dans une seule ligne sans terme.

Et ce que sont dans le précédent les nombres 4 et 9 qui ont la puissance de la surface, les deux espèces de surfaces, la surface plane et la surface courbe, le sont dans celui-ci. Enfin ce que sont dans le précédent les nombres 8 et 27 qui ont la puissance du cube, et dont l’un est pair et l’autre impair, le solide le fait dans celui-ci, étant de deux espèces, l’une à surface courbe, comme la sphère et le cylindre, l’autre à surface plane, comme le cube et la pyramide. Le troisième quaternaire est donc celui qui a la propriété de constituer toute grandeur, par le point, la ligne, la surface et le solide.

Le quatrième quaternaire est celui des corps simples, le feu, l’air, l’eau et la terre, et il offre la même proportion que le quaternaire des nombres : car ce qu’est dans celui-ci l’unité, le feu l’est dans celui-là, l’air répond au nombre 2, l’eau au nombre 3, la terre au nombre 4; telle est, en effet, la nature des éléments selon la ténuité ou la densité de leurs parties, en sorte que le feu est à l’air comme 1 est à 2, l’eau comme 1 est à 3, et à la terre comme 1 est à 4. Les autres rapports ont aussi égaux (c’est-à-dire que l’air est à l’eau comme 2 est à 3, et ainsi des autres).

Le cinquième quaternaire est celui des figures des corps simples, car la pyramide est la figure du feu, l’octaèdre la figure de l’air, l’icosaèdre la figure de l’eau, le cube la figure de la terre.

Le sixième est celui des choses engendrées, la semence étant analogue à l’unité et au point supposons l’accroissement en longueur, c’est analogue au nombre 2 et à la ligne: supposons encore l’accroissement en largeur, c’est analogue au nombre 3 et à la surface; supposons enfin l’accroissement en épaisseur, c’est analogue au nombre 4 et au solide.

Le septième quaternaire est celui des sociétés. L’homme en est le principe et pour ainsi dire l’unité. La famille répond au nombre 2, le bourg au nombre 3, la cité au nombre 4; car c’est de ces éléments que se compose la nation.

Tous ces quaternaires sont matériels et sensibles.

Le huitième contient les facultés par lesquelles nous pouvons porter des jugements sur les précédents et qui sont en partie intellectuelles, savoir : la pensée, la science, l’opinion et le sens. Et certes, la pensée doit être assimilée à l’unité dans son essence; la science est comme le nombre 2, parce qu’elle est la science de quelque chose; l’opinion est comme le nombre 3, car elle tient le milieu entre la science et l’ignorance; enfin le sens est comme le nombre 4, car il est quadruple, le tact étant commun à tous, tous les sens agissant par le contact.

Le neuvième quaternaire est celui dont se compose l’animal, corps et âme, l’âme ayant trois parties, la raisonnable, l’irascible, la concupiscible; la quatrième partie est le corps dans lequel l’âme réside.

Le dixième quaternaire est celui des saisons de l’année par la succession desquelles toutes choses prennent naissance, savoir : le printemps, l’été, l’automne, l’hiver.

Le onzième est celui des âges: l’enfance, l’adolescence, la virilité, la vieillesse.

Il y a donc onze quaternaires. Le premier est celui des nombres qui se forment par addition, le second est celui des nombres qui se forment par multiplication; le troisième est celui des grandeurs; le quatrième, celui des corps simples; le cinquième, celui des figures; le sixième, celui des choses engendrées; le septième, celui des sociétés; le huitième, celui des facultés du jugement; le neuvième, celui des parties de l’animal; le dixième, celui des saisons et le onzième, celui des âges. Ils sont proportionnels entre eux : car ce qu’est l’unité dans le premier et le second quaternaire, le point l’est dans le troisième; le feu dans le quatrième; la pyramide, dans le cinquième; la semence, dans le sixième; l’homme, dans le septième: la pensée, dans le huitième et ainsi des autres qui suivent la même proportion.

Ainsi le premier quaternaire est 1, 2, 3, 4. Le second est l’unité, le côté, le carré, le cube. Le troisième est le point, la ligne, la surface, le solide. Le quatrième est le feu, l’air, l’eau, la ferre. Le cinquième est la pyramide, l’octaèdre, l’icosaèdre, le cube. Le sixième est la semence, la longueur, la largeur, la hauteur. Le septième est l’homme, la famille, le bourg, la cité. Le huitième est la pensée, la science, l’opinion, le sens. Le neuvième est la partie raisonnable de l’âme, l’irascible, la concupiscible et le corps. Le dixième est le printemps, l’été, l’automne, l’hiver. Le onzième est l’enfant, l’adolescent, l’homme fait, le vieillard. Et le monde parfait qui résulte de ces quaternaires est arrangé géométriquement, harmoniquement et arithmétiquement, comprenant en puissance toute nature du nombre, toute grondeur et tout corps, soit simple, soit composé. Il est parfait, parce que toutes choses en sont des parties, et que lui-même n’est partie d’aucun autre. C’est pourquoi les Pythagoriciens se servaient du serment dont nous avons rapporté la formule et par lequel toutes choses sont assimilées au nombre.

De la décade.

XXXIX. Les Pythagoriciens n’ont pas été moins sages en ramenant tous tes nombre la décade, puisqu’au delà de dix nous ne comptons aucun nombre : dans l’accroissement nous revenons aux nombres 1, 2, 3, et ainsi de suite. La décade se trouve d’ailleurs dans le quaternaire, puisque la somme des quatre nombres 1, 2, 3. 4 est égale à 10, d’où il suit que les nombres les plus forts, peuvent être considérés comme ayant leur raison dans le quaternaire.

Propriétés des nombres contenus dans la décade.

XL. L’unité est le principe de toutes choses et ce qu’il y a de plus dominant : c’est d’elle que tout émane et elle n’émane de rien. Elle est indivisible et elle est tout en puissance. Elle est immuable et ne sort jamais de sa propre nature par la multiplication (1 x 1 = 1). C’est en elle que demeure tout ce qui est intelligible et ne peut être engendré la nature des idées, Dieu lui-même, l’âme, le beau et le bon, et toute essence intelligible, telle que la beauté elle-même, la justice elle-même, l’égalité elle-même; car nous concevons chacune de ces choses comme étant une et comme existant par elle-même.

XLI. Le premier accroissement, le premier changement de l’unité se fait par le doublement de l’unité qui devient 2, en quoi l’en voit la matière et tout ce qui est sensible, la génération et le mouvement, la multiplication et l’addition, l’union et le rapport d’une chose à une autre.

XLII. Le nombre 2 ajouté à l’unité produit 3 qui est le premier nombre ayant un commencement, un milieu et une fin. C’est pourquoi ce nombre est le premier auquel on puisse appliquer le mot multitude,[33] car des nombres moindres on ne dit pas multitude, mais un ou l’un et l’autre; tandis que de trois, on dit multitude. Nous faisons trois libations pour montrer que nous demandons tout ce qui est bien. Nous appelons trois fois malheureux ceux qui sont au comble de l’infortune, et trois fois heureux ceux qui sont au comble du bonheur.

Le nombre ternaire représente aussi la première nature du plan car il en est comme l’image, la première forme du plan étant le triangle. C’est pour cela qu’il y a trois genres de triangle, l’équilatéral, l’isocèle et le scalène: et qu’il y a aussi trois espèces d’angles, le droit dont la propriété est d’être unique, bien défini et composé de l’égal et du semblable, ce qui fait que tous les angles droits sont égaux entre eux, tenant le milieu entre l’angle aigu et l’angle obtus, plus grands que l’un et plus petits que l’autre. Tous les autres angles sont en nombre infini et indéterminé, car ils sont ou plus grands ou plus petits. Le nombre 3 ajouté à l’unité et à 2 donne 6 qui est le premier nombre parfait, c’est-à-dire égal à la somme de ses parties aliquotes. Ce nombre parfait ajouté au premier nombre carré 4, donne la décade.

XLIII. Le nombre quatre est l’image du solide, et c’est le premier nombre carré parmi les nombres pairs; il complète toutes les consonances, comme nous l’avons montré.[34]

XLIV. Le nombre 5 est la moyenne de (deux nombres dont la somme est) la décade; car si, par l’addition de deux nombres quelconques, on obtient 10, la moyenne de ces nombres sera 5 selon la proportion arithmétique. Ainsi, par exemple, si vous additionnez 9 et 1, 8 et 2, 7 et 3, 6 et 4, la somme sera toujours 10 et la moyenne en proportion arithmétique sera 5, comme le montre le diagramme dans lequel toute addition de deux nombres (opposés) donne 10, la moyenne en proportion arithmétique étant 5 qui surpasse l’un des extrêmes et est surpassé par l’autre, de la même différence.

Ce nombre est aussi le premier qui embrasse les deux espèces de nombres, le pair et l’impair, savoir 2 et 3, car l’unité n’est pas un nombre.

XLV. Le nombre six est un nombre parfait parce qu’il est égal à la somme de ses parties aliquotes, comme on l’a montré. C’est pour cela qu’on l’a appelé mariage, parce que l’œuvre du mariage produit des enfants semblables à leurs parents.[35] La médiété harmonique se constitue d’après ce premier nombre, car, si l’on en prend les quatre tiers 8 et le double 12, on aura la proportion harmonique des nombre 6, 8, 12; 8 surpasse l’un des extrêmes 6 et est surpassé par l’autre extrême 12, de la même fraction des extrêmes, qui est un tiers des extrêmes. Il donne aussi la médiété arithmétique en prenant 9 qui en est les 3/2 et 12 qui en est le double, car 9 surpasse un des extrêmes et est surpassé par l’autre, de la même quantité 3. Enfin, il produit la proportion géométrique quand, étant placé au milieu, on met d’un côté la moitié 3 et de l’autre le double 12, ce qui donne la proportion géométrique des nombres 3, 6, 12 : car alors 6 contient un des extrêmes 3 et est contenu dans l’autre, dans le même rapport 2.

XLVI. Un autre nombre de la décade, le nombre sept, est doué d’une propriété remarquable : c’est le seul qui n’engendre aucun nombre compris dans la décade et qui n’est engendré par aucun d’eux, ce qui a porté les Pythagoriciens à lui donner le nom de Minerve, parce que cette déesse n’a point été engendrée par une mère et n’a point été mère; elle ne provient d’aucune union et n’a été unie personne. Parmi les nombres compris dans la décade, les uns engendrent et sont engendrés, par exemple, 4 multiplié par 2 engendre 8, et il est engendré par 2. D’autres sont engendrés mais n’engendrent pas, comme 6, qui est le produit de 2 par 3, mais qui n’engendre aucun des nombres de la décade; d’autres engendrent mais ne sont point engendrés, comme 3 et qui ne sont engendrés par aucune combinaison de nombres, mais qui engendrent; savoir : 3 produit 9, et, multiplié par 2, produit 6, et 5 multiplié par 2 produit 10.

Sept est le seul nombre qui, multiplié par un autre, n’engendre aucun de ceux qui sont dans la décade, et qui n’est produit par la multiplication d’aucun nombre. Platon, dans le Timée, imitant la nature, constitue l’âme de 7 nombres. Le jour et la nuit, dit Posidonius, ont la nature du pair et de l’impair... Le mois se compose de quatre semaines quatre fois sept jours, dans la première semaine, la lune paraît divisée en deux ; dans la seconde, elle devient pleine: dans la troisième, elle est divisée de nouveau, et, dans la quatrième, elle revient à la rencontre du soleil pour commencer un nouveau mois et croître la semaine suivante.

C’est en sept semaines que le fœtus paraît arriver à sa perfection, comme Empédocle le dit, à mots couverts, dans son Expiations. Quelques-uns pensent que le fœtus mâle met cinq semaines à se perfectionner. C’est aussi dans le septième mois que les fœtus naissent viables. C’est dans le septième mois à partir de leur naissance que les enfants font leurs dents, et c’est à l’âge de sept ans qu’ils perdent leurs premières dents: c’est dans la seconde période de sept ans que la semence et la puberté font leur apparition, et le plus souvent c’est dans la troisième période que la barbe commence à croître. C’est alors aussi que l’homme acquiert sa taille, mais ce n’est que dans la quatrième période qu’il acquiert son embonpoint.

Il faut sept jours pour le diagnostic des maladies, et dans toutes les fièvres périodiques, même dans la fièvre tierce et dans la fièvre quarte, le septième jour est le plus grave. D’une conversion tropicale du soleil à l’autre il y a sept mois, et les planètes sont au nombre de sept. Pareillement, d’un équinoxe à l’autre, on compte sept mois.[36] La tête à sept ouvertures. Il y a sept viscères, le cœur, le poumon, le foie, la rate, les deux reins et l’intestin. Hérophile dit que l’intestin de l’homme a vingt-huit coudées de long, c’est-à-dire quatre fois sept coudées. Enfin, dans la plupart des détroits, le flux et le reflux se font sentir sept fois par jour.[37]

XLVII. Le nombre huit qui est le premier cube se compose de l’unité et du septenaire. Quelques-uns disent qu’il y a huit dieux maîtres de l’univers et c’est aussi ce qu’on voit dans les serments d’Orphée

Par les créateurs des choses à jamais immortelles

le feu et l’eau, la terre et le ciel, la lune

et le soleil, le grand Phanès et la nuit noire.

Et Évandre rapporte qu’en Egypte on trouve sur une colonne une inscription du roi Saturne et de la reine Rhéa : « Le plus ancien de tous, le roi Osiris, aux dieux immortels, à l’esprit, au ciel et à la terre, à la nuit et au jour, au père de tout ce qui est et de tout ce qui sera et à l’Amour, souvenir de la magnificence de l’ordre de sa vie. » Timothée rapporte aussi le proverbe : huit est tout, parce que les sphères du monde qui tournent autour de la terre sont au nombre de huit. Et, comme dit Eratosthène:

« Ces huit sphères s’harmonisent ensemble en faisant leurs révolutions autour de la terre ».

XLVIII. Le nombre neuf est le premier carré parmi les impairs : les deux premiers nombres sont 2 et 3, l’un pair, l’autre impair, qui donnent les deux premiers carrés, et 9.

XLIX. La décade complète la série des nombres, comprenant en elle-même la nature du pair et de l’impair de ce qui est en mouvement et de ce qui est immuable, du bien et du mal. Archytas, dans son livre Sur la Décade, et Philotius, dans son traité De la nature, se sont longuement étendus sur ce sujet.

Des médiétés.

L Revenons maintenant aux proportions et aux médiétés. Il y a plusieurs médiétés : la géométrique, l’arithmétique, l’harmonique, la sous-contraire, la cinquième et la sixième, auxquelles il faut ajouter six autres qui lotir sont sous-contraires. Or, de toutes ces médiétés, Adraste dit que la géométrique est la seule qui soit une vraie proportion et que c’est la première, car toutes les autres en ont besoin, tandis qu’elle-même n’a aucun besoin des autres, comme il le montre ensuite. Il dit que les autres médiétés reçoivent de quelques-uns le nom plus général de proportion.

Parmi les proportions proprement dites, c’est-à-dire géométriques, les unes ont les termes et les rapports rationnels,  comme la proportion 12, 6, 3, dont les termes sont en raison double, ou toute autre proportion numérique: les autres ont des termes inexprimables et irrationnels grandeurs, poids, temps ou autres, en raison double, triple, et en général multiple ou sesquipartielle. Dans la médiété géométrique, le moyen terme, comme nous l’avons dit, est contenu dans un extrême et contient l’autre dans le même rapport (a : b = b : c). Dans la médiété arithmétique, le moyen terme est surpassé par un extrême et surpasse l’autre, du même nombre (a — b = b — c). Enfin, dans la médiété harmonique, le moyen terme est surpassé par un extrême et surpasse l’autre de la même partie des extrêmes.[38]

LI. Adraste montre que la raison d’égalité est la première en ordre, et que c’est l’élément de toutes les raisons dont nous avons parlé précédemment et de toutes les proportions qu’elles donnent. Car c’est d’elle que naissent toutes les autres et c’est en elle qu’elles se résolvent toutes.

Eratosthène dit aussi que toute raison s’accroît ou par un intervalle ou par les termes : or l’égalité a cela de propre qu’elle n’est susceptible d’aucun intervalle, et il est bien évident qu’elle ne peut s’accroître que par les termes. Prenant donc trois grandeurs avec la proportion qui s’y trouve, nous en combinerons les termes et nous montrerons que toutes les mathématiques consistent dans la proportion de certaines quantités et que l’égalité en est le principe et l’élément.

Eratosthène dit qu’il omettra les démonstrations mais Adraste montre clairement que « trois termes quelconques étant donnés en proportion continue, si on en prend trois autres formés de ceux-là, l’un égal au premier, un autre composé du premier et du second, un autre enfin composé du premier, de deux fois le second et du troisième, ces nouveaux termes seront encore en proportion continue[39] ».

De la proportion dont les termes sont égaux, il naît ainsi une proportion en raison double, de la proportion en raison double naît la proportion en raison triple, celle-ci produit la proportion en raison quadruple et ainsi de suite, selon les autres multiples. Soit, par exemple, en trois termes égaux les plus petits possibles, c’est-à-dire en trois unités, la proportion d’égalité (1, 1, 1); si l’on prend trois autres termes de la manière qui a été indiquée, l’un formé du premier seul, l’autre composé du premier et du second, le dernier composé du premier, de deux fois le second et du troisième, on aura les termes 1, 2, 4, qui sont en raison double.

Avec ceux-ci, formons-en de nouveaux par la même méthode, le premier sera égal au premier, le second sera composé du premier et du second, le troisième le sera du premier, de deux fois le second et du troisième, et les termes seront 1, 3, 9, en raison triple. Par la même méthode, on formera avec ces nombres les termes 1, 4, 16, qui sont en raison quadruple, et avec ceux-ci, les termes 1, 5, 25, en raison quintuple, et ainsi à l’infini, en suivant l’ordre des multiples.

1                                   1                      1

1                                   2                      4

1                                   3                      9

1                                   4                      16

1                                   5                      25

1                                   6                      36

1                                   7                      49

1                                   8                      64

1                                   9                      81

1                                   10                    100

Si maintenant on dispose inversement les proportions multiples et qu’on additionne les termes de la même manière, on obtiendra des proportions en raison sesquipartielle: les doubles donneront, en effet le rapport hémiole ou sesquialtère (1 + ½), les triples donneront le rapport épitrite ou sesquitierce (1 + 1/3), les quadruples le rapport sesquiquarte, (1 + 1/4), et ainsi de suite. Soit donnée, par exemple, la proportion en raison double, à trois termes, et soit le plus grand terme placé le premier 4, 2, 1; avec ces termes formons-en de nouveaux selon la méthode indiquée, nous en déduirons 4, 6, 9, qui est une proportion continue dont le rapport est sesquialtère.

Soient de même les trois termes en proportion triple 9, 3, 1: nous en déduirons de la même manière les trois termes proportionnels en raison sesquitierce 9, 12, 16. Avec les quadruples, nous obtiendrons les termes en raison sesquiquarte 16, 20, 25, et ainsi de suite; nous aurons toujours le rapport sesquipartiel (1 + 1/n) correspondant au multiple (n).[40]

4      2          1                                             4          6          9

9      3          1                                             9          12        16

16    4          1                                             16        20        25

36    6          1                                             25        30        36

49    7          1                                             36        42        49

64    8          1                                             49        56        64

81    9          1                                             64        72        81

36    6          1                                             81        90        100

De même, les rapports sesquipartiels (1 + 1/n) nous donnent les rapports épimères ((1 + m/(m+n)) et les rapports multisuperpartiels (a + 1/n); et de nouveau les rapports épimères ((1 + m/(m+n)) nous donnent d’autres rapports épimères et des rapports polyépimères ((a + m/(m+n)).  Nous devons omettre la plupart de ces rapports comme peu nécessaires; il nous faut cependant en considérer quelques-uns. Avec la proportion de raison sesquialtère (1 + 1/2), en commençant par le plus grand terme, on obtient par la méthode indiquée une proportion dont la raison épimère est 1 + 2/3; ainsi la proportion 9, 6, 4 donne par la méthode d’Adraste 9, 15, 25; et, en commençant par le plus petit terme on obtient la proportion dont la raison multisuperpartielle est 2 + 1/2 : on donne 4, 6, 9, on en conclut par la même méthode 4, 10, 25.

Et de la proportion dont le rapport est sesquitierce (1 + 1/3), en commençant par le plus grand terme, on tirera la proportion de raison épimère (1 + 3/4). On a en effet, la proportion 16, 12, 9, qui donne 16, 28, 49, et en commençant par le plus petit terme, on aura la proportion de raison multisuperpartielle 2 + 1/3 dans ces termes 9, 21, 49. Avec la proportion de raison sesquiquarte (1 + 1/4), en commençant par le plus grand terme, on trouvera la proportion de raison épimère 1 + 4/5. La proportion 25, 20, 16, donne, en effet, 25, 45, 81; et, en commençant par le plus petit terme, on en déduira la proportion de raison multisuperpartielle 2 + 1/4. Ainsi, des termes 16, 20, 25, on déduit 16, 36, 81; et on peut continuer ainsi à l’infini, en sorte qu’au moyen de ces proportions, on peut en former d’autres par la même méthode. Nous n’avons pas besoin de développer davantage ce sujet.

LII. De même que toutes ces proportions et toutes leurs raisons se composent de la première raison d’égalité, de même aussi elles se résolvent définitivement en elle. En effet, si une proportion quelconque, à trois termes inégaux, étant donnée, nous soustrayons du moyen terme le plus petit, et du plus grand le plus petit et deux fois le moyen diminué du plus petit, si ensuite nous mettons en ordre les termes ainsi obtenus, nous aurons pour premier terme le même plus petit, puis pour second l’excès du moyen sur le plus petit et enfin pour troisième ce qui est resté du plus grand, la proportion qui résultera de cette décomposition sera celle-là même qui a donné naissance à la nouvelle proposition. Quand on aura répété cette décomposition, on arrivera à la proportion d’égalité qui est la première origine de toutes les proportions et qui elle-même ne peut se résoudre en aucune autre, mais seulement dans la raison d’égalité.

Ératosthène démontre que toutes les figures résultent de quelque proportion, que pour les construire il faut partir de l’égalité et qu’elles se résolvent en égalité. Il n’est pas nécessaire de nous étendre davantage sur ce sujet.

Des Figures

LIII. Nous trouverons les mêmes résultats dans les figures dont la première est le point, qui est un signe sans étendue, sans dimension, étant le terme d’une ligne et tenant la même place que l’unité (dans les nombres). La grandeur qui n’a qu’une dimension et n’est divisible que d’une manière, et la ligne, qui est une longueur sans largeur; la grandeur tendue dans deux sens, est une surface, elle a longueur et largeur; la grandeur ayant trois dimensions, est le solide, qui a longueur, largeur et hauteur. Or, le solide est compris et limité entre des surfaces, la surface est limitée par des lignes et la ligne limitée par des points.

Parmi les lignes, la ligne droite est celle qui est directe et comme tendue, c’est celle qui, entre deux points donnés, est la plus courte de toutes celles qui ont les mêmes extrémités et qui est étendue également entre tous ses points. La ligne courbe est celle qui n’a pas cette propriété. La même différence se retrouve entre le plan et la surface courbe. En effet, la surface est le terme apparent de tout corps solide, suivant deux dimensions. longueur et largeur. Or le plan est une surface droite telle que si une ligne droite la touche en deux points, elle coïncide avec elle dans toute sa longueur. Des lignes droites sont parallèles quand, prolongées à l’infini sur un même plan, elles ne se rencontrent pas et gardent toujours entre elles la même distance.

Les figures planes sont celles dont toutes les lignes sont dans un même plan. Les figures rectilignes sont celles qu’entourent des lignes droites et les figures non rectilignes n’ont pas cette propriété. Parmi les figures planes et rectilignes celles qui sont comprises entre trois cotés sont appelées trilatérales. Celles de quatre côtés sont appelées quadrilatères: on appelle polygones celles qui sont comprises entre un plus grand nombre de lignes droites.

Parmi les quadrilatères, ceux qui ont les côtés opposés parallèles sont appelés parallélogrammes et les parallélogrammes qui ont les angles droits sont appelés rectangles. Les angles sont droits quand une ligne droite en rencontre une autre en formant avec elle deux angles adjacents égaux. Chaque parallélogramme rectangle est dit proprement compris sous les côtés qui forment l’angle droit, et parmi ces rectangles ceux qui ont les quatre côtés égaux sont appelés proprement carrés. Ceux qui ne sont pas dans ce cas sont appelés promèques.[41]

LIV. Parmi les solides, les uns sont compris sous des parallélogrammes plans, au nombre de 6, et sont appelés parallélépipèdes. D’autres sont compris sous des rectangles et sont appelés parallélépipèdes rectangles. De ceux-ci, les uns sont équilatéraux dans tous les sens, c’est-à-dire que la longueur, la largeur et la hauteur sont égales et qu’ils sont compris sous des carrés égaux, ils sont appelés cubes. Ceux qui ont la longueur et la largeur égales, c’est-à-dire les bases carrées, mais dont la hauteur est moindre, sont appelés plinthes ou carreaux. Ceux dont la longueur est égale à la largeur, mais dont la hauteur est plus grande, sont appelés docides ou poutrelles. Enfin, ceux qui ont les trois dimensions inégales, sont appelés parallélépipèdes scalènes.

Propriétés des médiété.

Nous avons maintenant à parler plus en détail des médiétés dont la théorie est indispensable pour comprendre les écrits de Platon. Il y a médiété quand, entre deux termes homogènes inégaux, on prend un autre terme homogène tel que l’excès du premier, qui est en même temps le plus grand, sur ce terme moyen, soit à l’excès de celui-ci sur le plus petit, comme le premier terme est à lui-même ou à l’un des deux autres, ou bien comme le plus petit est à l’un des deux autres.

LV. En particulier, la médiété arithmétique est celle ou le moyen terme surpasse un extrême et est surpassé par l’autre d’un même nombre, comme dans la proportion 3, 2, 1. En effet, le nombre 2 surpasse 1 d’une unité et est aussi surpassé par 3 d’une unité. Ce moyen terme a la propriété d’être la demi-somme des extrêmes; en effet, 3 + 1 = 4 qui est le double du terme moyen 2.

LVI. La médiété géométrique, appelée aussi proprement proportion, est celle dont le moyen terme surpasse un extrême et est surpassé par l’autre dans la raison, multiple ou superpartielle (du premier terme au second on du second au troisième), comme la proportion 1, 2, 4. En effet, 4 est le double de 2, et 2 est le double de l’unité; et de même la différence 2 — 1 est 1, et la différence 4 — 2 est 2. Ces nombres comparés ensemble sont donc en raison double. Cette médiété jouit de la propriété, que le produit des extrêmes est égal au carré du moyen terme ainsi, dans la proportion précédente, le produit des extrêmes est, car 1 x 4 = 4, et le carré de 2 est aussi 4, car 2 x 2 = 4. Donc le produit des extrêmes est égal au carré du moyen terme.[42]

LVII. Il y a proportion harmonique quand, étant donnés trois termes, le premier est au troisième dans le même rapport que l’excès du premier (sur le second) est l’excès du second (sur le troisième). Tels sont les nombres 6, 3, 2: l’extrême 6 est le triple de 2, et l’excès de 6 sur 3 est 3, qui est le triple de l’unité, laquelle est l’excès de 3 sur 2. Cette proportion jouit de la propriété, que le moyen terme surpasse un extrême et est surpassé par l’autre de la même partie des extrêmes. Ainsi, dans la proportion formée des nombres 2, 3, 6, l’extrême 6 surpasse 3 de la moitié de 6, et l’autre extrême 2 est surpassé par 3 de la moitié de 2. De plus, si l’on additionne les termes extrêmes et qu’un multiplie la somme par le terme moyen, on trouve un nombre double du produit des extrêmes. Ainsi 6 + 2 = 8, et 8 multiplié par le moyen terme 3 donne 24; or 6 x 2 = 12 dont le double est 24.[43]

LVIII. On appelle médiété sous-contraire à l’harmonique la médiété dont le troisième terme est au premier comme l’excès du premier (sur le second) est à l’excès du second (sur le troisième) : telle est la médiété formée par les nombres 6, 5, 3, où 6 surpasse 5 d’une unité, et où 5 surpasse 3 de 2 unités, où enfin 3 est moitié de 6, comme l’unité, excès du premier nombre (sur le second), est moitié de 2, excès du second nombre sur le troisième.

LIX. On a la cinquième médiété, quand, étant donnés trois termes, le troisième est au second comme l’excès du premier (sur le second) est à l’excès du second (sur le troisième) : telle est la proportion formée des nombres 5, 4, 2. L’extrême 5 surpasse 4 d’une unité et 4 surpasse l’autre extrême 2 de 2 unités. Or l’extrême 2 est moitié de 4, et l’unité, excès du premier terme (sur le second), est moitié de 2, excès du second (sur le troisième).

LX. On a la sixième médiété, quand, étant donnés trois termes, le second est au premier comme l’excès du premier (sur le second) est à l’excès du second (sur le troisième): telle est la proportion formée des nombres 6, 4, 1. En effet, l’extrême 6 surpasse 4 de 2, et 4 surpasse l’autre extrême 1 de 3, et 1 est à 6 comme 1 est à 1 + l/2. Or 2, excès de 6 sur 4, est à 3, excès de 4 sur 1, dans le même rapport 1 à 1 + 1/2.

Les Pythagoriciens se sont longuement étendus sur ces six médiétés et leurs sous-contraires. Pour nous, qu’il nous suffise d’avoir, selon la méthode de Pythagore, esquissé sommairement ces principes, pour résumer l’exposition des mathématiques.

Comment on trouve les moyens termes des médiétés

LXI. Voici comment on trouve les moyennes. Dans la proportion arithmétique, on ajoute au petit terme la moitié de l’excès du plus grand sur le plus petit, ou bien on additionne les moitiés de chacun des deux nombres donnés, ou enfin on prend la moitié de la somme des deux termes donnés. Soit proposé de trouver le moyen terme, en proportion arithmétique, entre les nombres 12 et 6, on prend l’excès du plus grand 12 sur le plus petit 6, la moitié est 3 qu’on ajoute au plus petit 6, et l’on obtient 9 qui est la moyenne arithmétique entre les nombres 12 et 6, puisqu’elle surpasse l’un et est surpassée par l’autre de 3 unités. De même, si on additionne les extrêmes 12 et 6, la somme est 18, dont la moitié 9 est la moyenne entre les nombres donnés.

Voici maintenant comment on obtient le moyen terme d’une proportion géométrique : on prend la racine carrée du produit des extrêmes. Soient donnés, par exemple, les deux nombres 24 et 6, dont il s’agit de trouver le moyen terme en proportion géométrique. On multiplie les nombres donnés l’un par l’autre, le produit est 144 dont la racine 12 est le moyen terme, car on a 24 : 12 = 12 : 6, en raison double. Si le nombre compris sous les extrêmes est carré, le moyen terme trouvé est rationnel et sa longueur est commensurable avec les extrêmes, se composant d’unités entières. Mais si le nombre compris sous les extrêmes n’est pas un carré parfait, le moyen terme ne sera commensurable qu’en puissance avec les extrêmes.

Le plus souvent on le détermine géométriquement, qu’il soit exprimé en nombre rationnel ou que la raison et les grandeurs soient incommensurables. Voici comment on s’y prend: soient αβ et βγ les deux termes. Plaçons-les en ligne droite et sur la somme αγ, décrivons une demi-circonférence, puis du point β menons à αγ la perpendiculaire βδ, jusqu’à sa rencontre avec la demi-circonférence, je dis que βδ sera la moyenne proportionnelle géométrique entre les droites αβ et βγ. En effet, si l’on joint αδ et δγ on a en δ un angle droit, puisqu’il est inscrit dans une demi-circonférence. Dans le triangle αδγ la hauteur est δβ et les triangles qui sont de part et d’autre sont semblables au triangle total et, par conséquent, semblables entre eux, donc les côtés qui comprennent les angles égaux sont proportionnels et l’on a: αβ : βδ = βδ : βγ; donc βδ est moyenne proportionnelle entre αβ et βγ. C’est ce qu’il fallait démontrer.

Il nous reste à montrer comment on obtient le moyen terme dans la proportion harmonique. Soient donnés deux extrêmes en raison double, comme 12 et 6. On multiplie l’excès du plus grand sur le plus petit, c’est-à-dire 6, par le plus petit 6, puis on divise le produit 36 par la somme des extrêmes, c’est-à-dire par 48, et on ajoute le quotient 2 au plus petit terme 6, on obtient 8 qui sera le moyen terme cherché, car il surpasse un extrême et est surpassé par l’autre de la même fraction des extrêmes, savoir du tiers. La proportion harmonique est donc formée des nombres 12, 8, 6.

Si les extrêmes donnés sont en raison triple, comme let 6, on multiplie par lui-même l’excès du plus grand sur le plus petit, le produit 12 x 12 est 144 dont la moitié égale 72. On divise ce résultat par la somme des extrêmes ou 24, le quotient 3 de la division, ajouté au plus petit terme, donne 9 pour le moyen terme cherché, car il surpasse un extrême et est surpassé par l’autre de la moitié des extrêmes. On a la proportion harmonique des nombres 18, 9, 6.

Pour trouver la moyenne harmonique entre deux termes inégaux quelconques donnés, on peut aussi se servir de la méthode plus générale que nous avons d’abord exposée. Il faut multiplier l’excès par le plus petit extrême et diviser le produit par la somme des extrêmes, puis ajouter le quotient au plus petit terme. Soient donnés, par exemple, les deux termes 12 et 4. En multipliant l’excès de 12 sur 4 c’est-à-dire 8, par le plus petit terme 4, on a pour produit 32. Si maintenant on divise 32 par la somme des extrêmes qui est 16, on a 2 pour quotient. Ce quotient 2, ajouté au plus petit terme 4, donne 6 pour moyenne harmonique entre 12 et 4. En effet, 6 surpasse un extrême et est surpassé par l’autre de la même fraction des extrêmes, soit de la moitié. On a donc la proportion harmonique des nombres 12, 6, 4.[44]

Après cette exposition sommaire, en faveur des lecteurs de Platon, de ce qu’il y a de plus nécessaire et de plus utile dans les parties des sciences mathématiques dont nous avons parlé, il nous reste à faire mention des éléments de l’astronomie.

NOTES

NOTE IX. — Sur l’addition et la soustraction des consonances (II, § xiii bis).

Nommons A, B, C, trois sous tels que l’intervalle de B à A soit, par exemple, une quinte et l’intervalle de C à B une quarte. Soient a, b, c, les nombres correspondants à ces trois sons; c est les 4/3 de b, et b les 3/2 de a, donc c est les 4/3 des 3/2 de a, c’est-à-dire qu’on a: c = 2a. Quoique l’intervalle de C à A soit le produit des deux intervalles qu’il comprend, on dit qu’il est la somme de ces deux intervalles; ainsi l’on dit que l’octave est la somme d’une quinte et d’une quarte, mais le nombre qui mesure l’octave est le produit des deux nombres qui mesurent la quarte et la quinte.

Nommons encore A, B, C, trois sons tels que l’intervalle de B à A soit, par exemple, une quarte et que l’intervalle de C à A soit une quinte. Soient a, b, c, les nombres correspondants à ces sons et x l’intervalle de c à b. On a, d’après la remarque précédente 3/2 = 4/3 x x d’où x = 3/2 : 4/3 = 9/8 = un ton. Quoique l’intervalle de C à B soit le quotient de l’intervalle de C à A par l’intervalle de B à A, on dit qu’il est la différence de ces deux intervalles: ainsi l’on dit que le ton est l’excès de la quinte sur la quarte, mais le nombre qui mesure le ton est le quotient des deux nombres qui mesurent la quinte et la quarte.

NOTE X. — Le diagramme musical de Platon comprend quatre octaves, une quinte et un ton (II, § xiii bis).

Le diagramme musical de Platon comprend, en effet, les sons correspondants aux termes des deux progressions 1, 2, 4, 8, et 1, 3, 9, 27, et s’arrête à 27. Or le premier son de la première octave étant représenté par 1, les premiers sons de la deuxième, de la troisième, de la quatrième et de la cinquième octave sont respectivement représentés par 2, 4, 8, 16. La quinte de cette cinquième octave est exprimée par 16 x 3/2 = 24. Pour ajouter un ton à cette quinte, il faut multiplier 24 par 9/8, le résultat est 27, dernier terme du diagramme de Platon, qui comprend par conséquent quatre octaves plus une quinte et un ton. (Cf. le Timée.)

NOTE XI. — De la valeur du demi-ton (II, § xiv).

La moitié du ton 1 + 1/8 n’est pas 1 + 1/16. Cette moitié x est donnée par l’équation x² = 9/8 d’où x = Racine carrée de 9/8. Mais il faut remarquer que la valeur 1 + 1/16 = 17/16 est très approchée, car si on en fait le carré, on obtient 289/236 qui ne diffère, que de 1/236 du ton 9/8 = (9x32)/(8x32) = 288/256

Le limma est moindre que le demi-ton, parce qu’on a, comme on peut aisément le vérifier,

(256/243)² < 9/8       d’où     256/243 < Racine carrée de 9/8

NOTE XII. — Du système musical parfait formé de deux octaves (II, § xxxv).

L’échelle musicale des anciens Grecs, décrite par Théon, avait l’étendue de la voix humaine. C’était une série descendante de deux octaves. Elle était formée de quatre petits systèmes, composés chacun de quatre sons dont les extrêmes donnaient la quarte, consonance maîtresse de laquelle découlaient les autres (II, xiii bis).

Ces petits systèmes se nommaient tétracordes parce que les sons étaient donnés par la lyre à quatre cordes. Les cordes des instruments et les sons qu’elles rendaient portaient le même nom. Les deux extrêmes de chaque tétracorde étaient invariables ou immobiles; les deux intermédiaires étaient variables ou mobiles, elles recevaient différents degrés de tension constituant trois genres principaux d’harmonie: le diatonique, le chromatique et l’enharmonique.

Le premier tétracorde se nommait tétracorde des supérieures ou des hyperbolées, ὑπερβολαίων.

Le deuxième s’appelait tétracorde disjoint ou des disjointes, διεζευγμένων, parce que sa dernière corde, c’est-à-dire la plus basse, était distincte de la première, ou la plus haute, du tétracorde suivant; elle en différait d’un ton. Les deux premiers tétracordes avaient une corde commune: la plus grave du tétracorde des hyperbolées était en même temps la plus aiguë du tétracorde des disjointes.

Le troisième était le tétracorde moyen ou des mèses, μέσων.

Le quatrième se nommait tétracorde des basses ou des hypates, ὑπατῶν, Ces deux tétracordes avaient une corde commune : la plus grave du tétracorde des mèses était en même temps la plus aiguë du tétracorde des hypates.

Le premier et le second tétracorde ayant une corde commune, ainsi que le troisième et le quatrième, l’ensemble des quatre tétracordes ne rendait que quatorze sons. Pour compléter les deux octaves, on a ajouté au-dessous du son le plus grave du tétracorde des hypates un quinzième son, plus bas d’un ton, qu’on a appelé proslambanomène, προσλαμβανόμενος, sous-entendu φθόγγος, ou προσλαμβανόμενη sous entendu χορδή c’est-à-dire son ajouté ou corde ajoutée.

De même que les tétracordes étaient désignés par des noms relatifs à leur position dans l’échelle musicale, les cordes étaient désignées par des noms relatifs à leur position dans chaque tétracorde.

La plus haute était la nète des hyperbolées, νήτη ὑπερβολαίων.

La seconde était la paranète, παρανήτη, c’est-à-dire voisine de la nète.

La troisième s’appelait trite des hyperbolées, τρίτη.

La quatrième et la cinquième étaient la nète et la paranète des disjointes, νήτη et παρανήτη διεζευγμένων.

La sixième, nommée trite des disjointes, τρίτη, était la troisième du tétracorde disjoint.

La septième et la huitième étalent la paramèse, παραμέση, c’est-à-dire voisine de la mèse, et la mèse, μέση.

La neuvième était la lichane des mèses, λίχανος μέσων.[45]

La dixième et la onzième étaient la parhypate et l’hypate des mèses, παρύπάτη et ὀπάτη.

La douzième était l’hyperhypate, ὑπερρύπατη ou lichane des hypates, λίχανος ὑπάτων.

La treizième et la quatorzième étaient la parhypate des hypates, παροπάτη et l’hypate des hypates, ὑπάτη.

Enfin la quinzième était la proslambanomène.

La seconde corde de chaque tétracorde, c’est-à-dire la paranète des hyperbolées, la paranète des disjointes, la lichane des mèses et l’hyperhypate, étaient appelées aussi, suivant le genre: diatone, chromatique ou enharmonique, des hyperbolées, des disjointes, des mèses ou des hypates.

Voici un tableau de ce système parfait, avec indication des intervalles successifs dans les trois genres, diatonique, chromatique et enharmonique, le demi-ton ou limma étant égal à 256/243.

Système parfait, formé de deux octaves, comprenant les trois genres: diatonique, chromatique, enharmonique.

NOTE XIII. — Diagramme musical de Platon (II, § xxxvi). — Erreur probablement volontaire de Timée de Locres.

Platon pour expliquer, dans le Timée, la formation de l’âme du monde, admet que Dieu divisa d’abord l’essence en sept parties qui sont entre elles comme les termes des deux progressions 1, 2, 4, 8 et 1, 3, 9, 27 dont l’une a pour raison 2 et l’autre pour raison 3.

Il dit ensuite que Dieu inséra, entre les termes successifs de ces deux progressions, deux moyennes dont l’une, que nous appelons moyenne arithmétique, égale leur demi-somme et dont l’autre est telle qu’elle surpasse un extrême et est surpassée par l’autre de la même fraction des extrêmes, c’est-à-dire que x étant la moyenne insérée entre a et b, on a :        x —a : b — x = a : b, d’où

x = 2ab/(a+b) = ab / ((a+b)/2))

de sorte que cette moyenne entre deux nombres s’obtient en divisant le double produit de ces deux nombres par leur somme, ou le produit des deux nombres par leur demi-somme. On l’appelle une moyenne harmonique.

Par cette double insertion on obtient les nombres suivants (à lire par colonnes horizontales):

1                       4/3      3/2      2

2                       8/3      3          4

4                       16/3    6          8

Dans cette progression, le rapport de la moyenne arithmétique à la moyenne harmonique égale 9/8: c’est la valeur du ton.

Platon insère ensuite entre chaque terme de la progression double et la moyenne harmonique qui le suit, ainsi qu’entre la moyenne arithmétique et le terme suivant, deux termes tels que le rapport de chacun d’eux au précédent soit aussi 9/8.

Cette opération effectuée sur la progression 1, 2, 4, 8, et prolongée jusqu’à ce qu’on obtienne le terme 27, donne les résultats contenus dans le tableau suivant:

Pour substituer à ces nombres, généralement fractionnaires, des nombres entiers proportionnels, on peut les réduire au même plus petit dénominateur commun 128 x 3 = 384 et les multiplier tous par ce dénominateur, on obtient alors le tableau suivant:

Si on insère de même une moyenne harmonique et une moyenne arithmétique entre les termes successifs de la progression triple, on obtient les nombres (à lire par colonnes horizontales):

1                       3/2      2          3

3                       9/2      6          9

9                       27/2    18        27

Les Intervalles de 4 à 3, de 3 à 9, et de 9 à 27, étant ceux d’octave et quinte, Proclus[46] admet que Platon a d’abord rempli l’intervalle de 4 à 3, comme ceux de la progression double, et qu’il a ensuite triplé les termes obtenus de 1 à 3, pour avoir ceux de 3 à 9, et triplé les termes de 3 à 9, pour avoir ceux de 9 à 27.

L’opération ainsi effectuée donne des résultats qu’on peut multiplier par 128 x 3=384, plus petit commun multiple des dénominateurs, pour leur substituer des nombres entiers proportionnels. On obtient ainsi les deux tableaux suivants:

Nous faisons suivre d’une étoile les termes de la progression triple (tableaux III et IV) qui ne font pas partie de celle des doubles, et les termes de la progression double (tableaux I et II) qui ne font pas partie de celle des triples.

On lit dans le traité De l’âme du monde et de la nature qui porte le nom de Timée de Locres (ch. 1, à la fin): « Dieu fit l’âme la première, en prenant dans le mélange dont il l’a formée, une partie égale à 384 unité. Ce premier nombre trouvé, il est facile de calculer les termes de la progression double et de la progression triple. Tous ces termes disposés suivant les intervalles de tons et demi-tons, sont au nombre de 36 et donnent une somme totale égale à 114 695; et les divisions de l’âme sont elles-mêmes au nombre de 114 693. Or l’intention évidente de Platon a été de ne pas dépasser 8 dans la progression des doubles et 27 dans la progression des triples. Donc son diagramme contient:

1° 22 termes de la progression double, compris de 1 x 384 à 8 x 384 c’est-à-dire de 384 à 3072 (tableau II qui valent 29 441

2° le terme de la progression triple compris, de 384 à 3072, qui ne fait pas partie de la progression double (voyez tableaux IV et II), c’est 2 187 et enfin

3° 12 termes de la progression triple, compris de 9 x 384 à 27 x 384 c’est-à-dire de 3456 à 10368 (tableau IV), qui valent 76 923

SOMME ………………………………………………………………………108 551

Donc le diagramme de Platon contient (22+ 1 + 12) ou 35 termes différents (et non 36), et la somme de ces 35 termes est 108 551 et non 114 695. La différence 6144 des deux résultats est le terme 16 x 384 de la progression des doubles (tableau II), terme dont il ne faut pas tenir compte, car il dépasse 8 x 384 dans la progression des doubles et ne fait pas partie de la progression triple. Si on le compte, il faut compter aussi les deux termes 4096 et 8192, de La progression double, qui ne font pas partie de la progression triple. d

Il y a donc une erreur dans le traité qui porte le nom de Timée de Locres. Si, suivant les intentions de Platon, on ne dépasse pas, en faisant les insertions, les cubes 8 et 27 dans les progressions respectives 1, 2, 4, 8, et 1, 3, 9, 27, le diagramme musical de Platon comprend 35 termes dont la somme est 108 551, inférieure de 6144, à la somme 114 695 de Timée de Locres.[47]

Sachant en quelle vénération les Pythagoriciens avaient le quaternaire,[48] nous croyons fermement que l’erreur du Pseudo-Timée n’est pas involontaire. Le nombre 35 était certainement doué de perfection, c’était le produit du nombre septenaire par la demi-décade; mais le nombre 3 était encore plus parfait, c’était le produit du premier carré pair par le premier carré impair; et, par conséquent, il était lui-même un carré, c’est-à-dire une harmonie, et puis son côté 6 était un nombre vraiment parfait c’est-à-dire égal à la somme de ses parties aliquotes, car on a 6 == 1 + 2 + 3. Le nombre 36 avait une autre vertu, écoutons Plutarque: «... Ce quaternaire, à savoir 36, célébré par les Pythagoriciens, semble avoir ceci d’admirable qu’il est la somme des quatre premiers nombres pairs et des quatre premiers nombres impairs...

(1 + 3 + 5 + 7) + (2 + 4 + 6 + 8) = 16 + 20 = 36

Alors que les philosophes pythagorisant voulaient trouver partout des quaternaires, Timée, pour compléter le grand quaternaire 36, aura ajouté aux 35 termes du diagramme musical de Platon le terme 6144 correspondant au son 16, octave du son 8 qui est le dernier terme de la progression 1, 2, 4, 8.

Si le Pseudo-Timée n’a pas ajouté aussi au diagramme de Platon les deux termes 4096 et 8192, qui sont l’un la quinte aiguë, l’autre la quarte grave de 6144 et qui, comme 6144, ne font pas partie des termes insérés dans la progression des triples, c’est parce qu’alors le nombre total des termes eût été 38, au lieu de 36,

NOTE XIV. — Pourquoi le nombre six était appelé mariage (II, § xlv).

On l’appelait aussi mariage parce qu’il est le produit du premier nombre pair par le premier nombre impair 3. Les nombres impairs étaient considérés comme mâles et les nombres pairs comme femelles. « Si on les divise l’un et l’aultre en unitez, dit Plutarque (traduction d’Amyot), le pair monstrera un lieu vuide au milieu, là où le non-pair a toujours le milieu remply d’une de ses parties, et pour ceste cause, ils (les Pythagoriciens) ont opinion que le pair ressemble plus à la femelle et le non-pair au masle. » (Questions romaines, CII, p. 288 C.)

NOTE XV. — Sur les euripes (II, § xlvi).

On a donné le nom d’euripes aux courants qui se produisent dans les détroits (εὔ, bien, ῥιπί, mouvement rapide, de ῥίπτω, jeter).

Le plus célèbre était celui de Chalcis, entre l’Eubée et la Béotie, et dont la direction changeait sept fois par jour, suivant la plupart des auteurs anciens : « Il y a des marées particulières en certains lieux, dit Pline, ainsi le flux vient plusieurs fois dans le détroit de Messine, à Tauroménium, et sept fois par jour dans l’Euripe, auprès de l’Eubée. (Hist. naturelle, II, c, p. 443 de la trad. de Littré, édition Nisard.)

Le scholiaste de Stobée attribue avec raison les mouvements alternatifs de l’Euripe de Chalcis à l’effort des vagues pour franchir le détroit. (Voyez Eclogae Physicae, t. II, p. 447, éd. Heeren.)

Les variations du flux des euripes étaient très irrégulières: cette inconstance était liée comme Platon dit dans le Phédon : «... Ni dans les choses, ni dans les raisonnements, il n’y a rien de vrai ni de stable; mais tout est dans un flux et un reflux continuel, comme l’Euripe, et rien ne demeure un moment dans le même état. » (Phédon, XXXIX, p. 90 C.) Lucain dit aussi, dans la Pharsale:

« les flots inconstants de l’Euripe entraînent les vaisseaux de Chalcis vers Aulis si funeste aux nochers :

Euripusque trahit, cursum mutantibus undis,

Chalcidicas puppes ad iniquam classibus Aulim.

(La Pharsale, Chant V, v. 235-236.)

L’idée superstitieuse attachée au nombre sept paraît expliquer l’hypothèse de Théon, hypothèse suivant laquelle les euripes varient sept fois par jour.

NOTE XVI. — Détermination de la moyenne harmonique entre deux nombres donnés (II, § lxi).

a, b, c étant les trois nombres qui donnent la proportion harmonique a — b : b — c = a : c, la première règle de Théon se traduit par la formule b = c + (a - c)c/(a + c) , valeur égale à 2ac /(a + c) ; elle est donc générale quel que soit le rapport de a à c.

La seconde règle se traduit par la formule b = c + (a – c)²/2(a + c); cette valeur n’est égale à 2ac/(a + c) que pour a = c, solution à rejeter, et pour a = 3c. Théon donne en effet la seconde règle pour les nombres en rapport triple, 18 et 6.

L’auteur ayant fait la remarque (II, lvii) que, dans la proportion harmonique, le produit de la somme des nombres extrêmes par la moyenne harmonique est égal au double produit des nombres extrêmes, nous sommes étonné qu’il n’ait pas conclu de cette égalité la valeur de la moyenne harmonique.