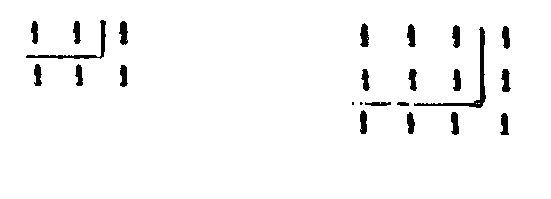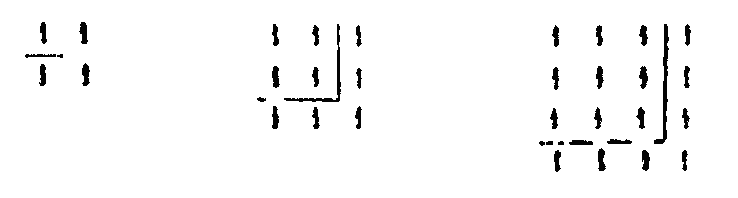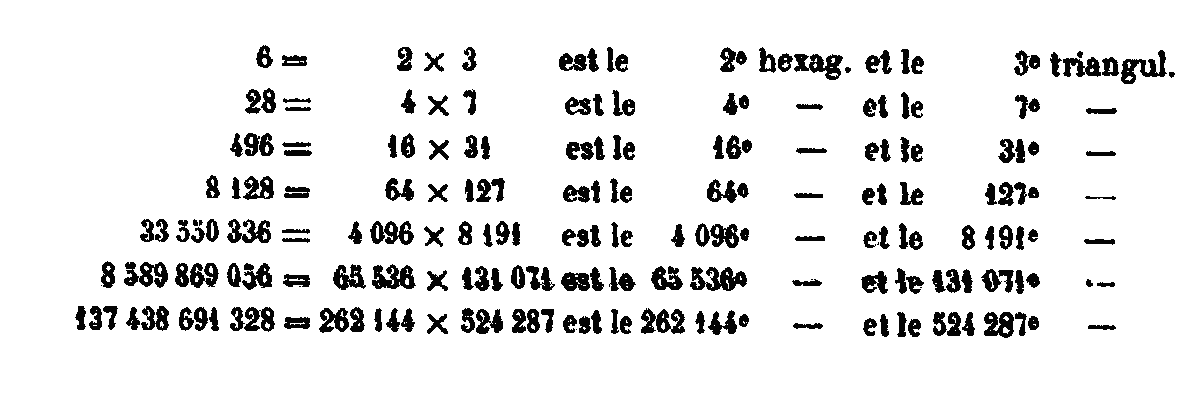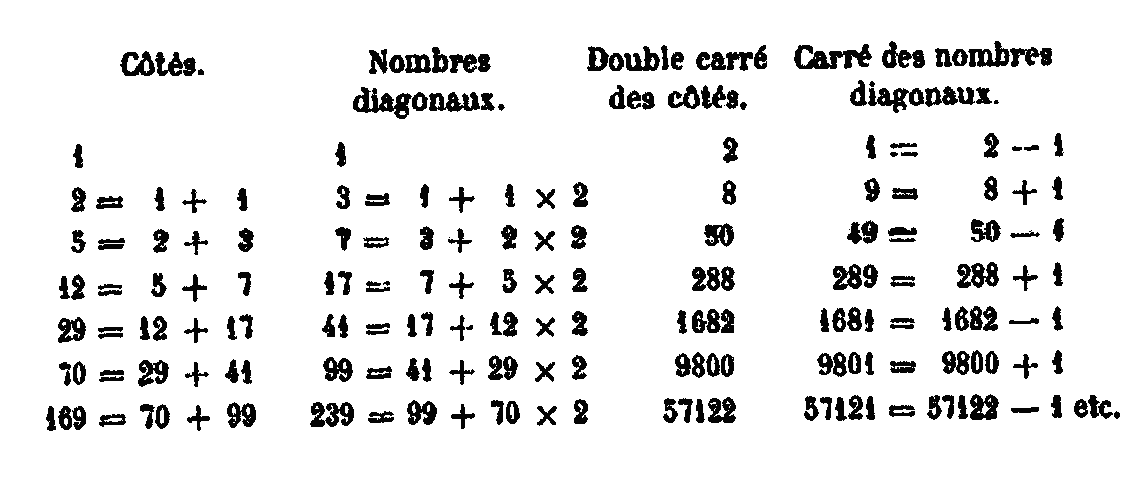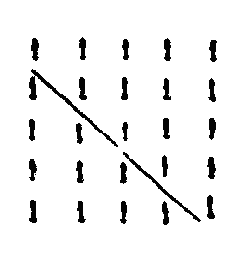RETOUR À L’ENTRÉE DU SITE

ALLER A LA TAΒLE DES MATIERES DE  THÉON DE SMYRNE

 THÉON DE SMYRNE

PHILOSOPHE PLATONICIEN

EXPOSITION

DES CONNAISSANCES MATHÉMATIQUES

UTILES POUR LA LECTURE DE PLATON

PREFACE

Nous n’avons aucune donnée précise sur l’époque à laquelle vécut Théon de Smyrne; mais il est certainement postérieur au musicographe Thrasylle, puisqu’il le cite dans ses écrits et il est probablement antérieur à l’astronome Claude Ptolémée, auteur de l’Almageste qu’il n’eût pas manqué de citer, si Ptolémée l’avait précédé. Il doit donc avoir vécu entre le temps de Tibère près duquel Thrasylle était en faveur à titre d’astrologue, et le temps d’Antonin-le-Pieux sous lequel Ptolémée s’est illustré.

Il vivait donc sans doute au commencement du second siècle de notre ère, c’est-à-dire au temps de Plutarque, et c’est peut-être ce Théon que Plutarque introduit comme interlocuteur dans son livre Du visage qui apparaît sur le disque lunaire, dans les Questions de table, et dans le livre Sur le ελ du temple de Delphes. C’est sans doute encore lui que Théon d’Alexandrie, commentateur de Ptolémée, appelle « Théon l’ancien. »

Théon a composé un abrégé de mathématiques en cinq livres, qui a pour titre : Des connaissances mathématiques utiles pour la lecture de Platon ; exposition abrégée comprenait: I, l’arithmétique; II, la géométrie (plane); III, la stéréométrie (géométrie de l’espace); IV, l’astronomie; et V, la musique.

La musique se composait alors de trois parties: les lois mathématiques des sons, la musique instrumentale, et l’harmonie des sphères célestes. Dans son travail, Théon omet la musique instrumentale qui était considérée comme étrangère aux spéculations philosophiques et il expose la théorie des nombres musicaux immédiatement après l’arithmétique. Il dit: « Puisque les principes numériques de la musique se rattachent à la théorie des nombres abstraits, nous leur donnerons le second rang pour la facilité de notre étude ». Et quelques lignes plus loin il ajoute: « Ainsi, dans notre plan, les lois numériques de la musique viendront immédiatement après l’arithmétique; mais, d’après l’ordre naturel, la cinquième place doit être donnée à cette musique qui consiste dans l’harmonie des mondes. »

L’arithmétique, les lois mathématiques de la musique et l’astronomie sont seules parvenues jusqu’à nous. Il manque les livres sur la géométrie et sur la stéréométrie, ainsi que l’écrit sur l’harmonie du monde céleste que Théon dit expressément avoir composé. Michel Psellus, écrivain byzantin du xi^e siècle a composé un petit traité sur les quatre sciences mathématiques. Cet écrit paraît être pour l’arithmétique, la musique et l’astronomie, un résumé des pages de Théon, mais il est tellement abrégé que nous ne croyons pas qu’on puisse combler en partie la lacune de Théon par les notions trop succinctes de géométrie et de stéréométrie de Michel Psellus.

La première partie de l’ouvrage de Théon traite des nombres pairs et des nombres impairs, des nombres hétéromèques et des nombres promèques, des nombres semblables, des nombres polygones et des nombres pyramidaux, des nombres latéraux et des nombres diagonaux,... Elle ne contient rien sur l’arithmétique pratique des Grecs, que Platon appelait λογιστική (science du calcul), et qu’il distinguait de l’ἀριθμητική (science des propriétés des nombres). Les démonstrations manquent, Théon se borne à de simples vérifications.

La seconde partie comprend 81 paragraphes: les 38 premiers traitent des nombres musicaux: les 3 autres, qui traitent des analogies, des quaternaires et des médiétés, seraient presque tous mieux à leur place dans la première partie.

La troisième partie traite de la forme de la terre, du mouvement des planètes, des éclipses... Elle contient de nombreuses erreurs que le lecteur relèvera facilement.

……………………………………………………………………………………………………

Nous offrons aux lecteurs de Platon et aux rares amis de l’histoire des sciences la première traduction française de ce qui nous reste de l’Exposition de Théon. Si les mathématiques n’ont rien à gagner à la publication de cette traduction, l’histoire des sciences peut y trouver du moins quelques renseignements utiles. Quant à nous, nous avons trouvé dans Théon la confirmation de l’interprétation que nous avons donnée en 1882 des termes énigmatiques du passage de la République de Platon, où il est question du Nombre géométrique, valeur hypothétique de la grande année après laquelle tous les événements humains devaient se reproduire dans le même ordre.

Tout le premier chapitre est rempli de citations de la République, d’Epinomis, des Lois, de Phédon, de Phèdre et de Théétète, dialogues de Platon ou attribués à Platon. C’est plutôt une introduction à tout l’ouvrage de Théon qu’une partie du livre sur l’arithmétique. Les citations étant rarement textuelles, au moins dans leur entier, sont très probablement faites de mémoire. Lorsque la différence des deux textes est trop sensible, nous avons cru devoir conserver en général celui de Théon. L’exception est signalée en note.

Outre les ouvrages de Platon et d’Aristote, ouvrages que Théon paraît avoir sus par cœur, il avait lu les livres d’un grand nombre d’auteurs dont il cite, dans le cours de son Exposition, plusieurs passages qu’on ne trouve guère ailleurs.

Ce qui nous reste de l’Exposition de Théon nous est parvenu en deux parties: la première (arithmétique et musique) se trouve dans le ms. 307 de la bibliothèque Saint Marc à Venise; la seconde (astronomie) dans le ms. 303 de la même bibliothèque.

…. Le premier manuscrit en parchemin est du xi^e ou xii^e siècle; le second en papier de grand format est du xiv^e ou xv^e siècle. Les titres des chapitres de ces manuscrits étant souvent mal choisis ou assez mal placés, nous avons cru devoir en supprimer plusieurs du corps du texte, nous les reportons alors dans les notes des bas de pages. Nous avons conservé les numéros des paragraphes pour la commodité des renvois.

La Bibliothèque nationale de Paris possède plusieurs manuscrits de Théon …………………………

Voici l’indication de quelques autres bibliothèques qui possèdent des manuscrits de Théon:

En Angleterre, à Cambridge, bibliothèque du collège e de la Trinité; à Oxford, bibliothèque Bodléienne.

En Espagne, à l’Escurial.

En Hollande, à Leyde.

En Italie, à Bologne: à Florence, bibliothèque Laurentienne; à Milan, bibliothèque Ambrosienne; à Turin, bibliothèque royale.

Nous avons collationné plusieurs passages de notre texte sur les manuscrits de la Bibliothèque nationale de Paris et sur les manuscrits de quelques bibliothèques d’Italie, pendant une mission dont nous avons été chargé en 1887 en Italie, en Grèce et en Bavière.

Chalcidius, philosophe platonicien du iii^e siècle, a inséré la plus grande partie de l’astronomie de Théon dans un commentaire latin sur le Timée. D’après H. Martin, qui a remarqué le premier cette insertion, Chalcidius n’a presque rien ajouté à l’ouvrage de Théon, qu’il semble donner comme sien. Il a omis ou résumé plusieurs passages importants et il en a mal compris quelques autres. Il n’a rien négligé, dit H. Martin, pour faire disparaître les traces de son larcin : Furti autem sui vestigia sedulo delevit.

Le commentaire de Chalcidius offre quelque avantage pour la correction du texte de Théon, et réciproquement.

Nous avons été très sobre de notes, de commentaires et de rectifications, voulant éviter de faire jouer à une œuvre scientifique, même très imparfaite, un rôle qui parût secondaire.

………………………………………………………………………………………………………..

J. D. Proviseur honoraire,

Dernier Directeur

de l’école professionnelle française de Mulhouse

Paris, 12 août 1892.

PREMIÈRE PARTIE

INTRODUCTION

De l’utilité des mathématiques

I. Tout le monde conviendra assurément qu’il n’est pas possible de comprendre ce que Platon a écrit sur les mathématiques, si l’on ne s’est pas adonné à leur étude. Lui-même a montré en beaucoup d’endroits que cette connaissance n’est pas inutile et sans fruit pour les autres sciences. Celui-là donc doit être estimé très heureux qui, en abordant les écrits de Platon, possède bien toute la géométrie, toute la musique et l’astronomie. Mais ce sont là des connaissances dont l’acquisition n’est ni rapide, ni facile: elle exige, au contraire, un travail assidu dès la première jeunesse. Dans la crainte que ceux qui n’ont pas eu la possibilité de cultiver les mathématiques et qui désirent néanmoins connaître les écrits de Platon ne se voient forcés d’y renoncer, nous donnerons ici un sommaire et un abrégé des connaissances nécessaires et la tradition des théorèmes mathématiques les plus utiles sur l’arithmétique, la musique, la géométrie, la stéréométrie et l’astronomie, sciences sans lesquelles il est impossible d’être parfaitement heureux, comme il le dit, après avoir longuement démontré qu’on ne doit pas négliger les mathématiques.

Eratosthène, dans le livre qui a pour titre le Platonicien, rapporte que les Déliens ayant interrogé l’oracle sur le moyen de se délivrer de la peste, le dieu leur ordonna de construire un autel double de celui qui existait déjà. Ce problème jeta les architectes dans un étrange embarras. Ils se demandaient comment on peut faire un solide double d’un autre. Ils interrogèrent Platon sur la difficulté. Celui-ci leur répondit que le dieu avait ainsi rendu l’oracle, non qu’il eût aucun besoin d’un autel double, mais pour reprocher aux Grecs de négliger l’étude des mathématiques et de faire peu de cas de la géométrie.

Pour entrer dans ces vues d’Apollon Pythien, il s’étendit, dès lors longuement, dans ses entretiens, sur l’utilité des mathématiques. C’est ainsi que dans l’Epinomis, voulant exciter à les étudier, il dit : « Personne, certes, ne saurait être heureux dans l’Etat, s’il les ignore; telle est la voie, telle est l’éducation, telles sont les sciences, faciles ou non à apprendre, qui peuvent conduire à cette fin; on n’a pas le droit de négliger les dieux.... » Plus loin il dit encore que « s’il y en a un seul qui voit tel (mathématicien), c’est celui-là qui sera favorisé de la fortune et au comble de la sagesse et de la félicité ».

Dans la République, voici ce qu’il écrit: « A partir de vingt-cinq ans,[1] ceux qu’on aura choisis obtiendront des distinctions plus honorables et on devra leur présenter dans leur ensemble les sciences que tous, dans l’enfance, ont étudiées isolément, afin qu’ils saisissent sous un point de vue général et les rapports que ces sciences ont entre elles, et la nature de l’être. ». Il prescrit de se livrer d’abord à l’étude de l’arithmétique, puis à celle de la géométrie, en troisième lieu à celle de la stéréométrie, ensuite à celle de l’astronomie qu’il dit être l’étude du solide en mouvement, enfin il exhorte à apprendre en cinquième lieu la musique. Après avoir montré l’utilité des mathématiques, il dit: « Vous êtes amusant, vous qui semblez craindre que je vous impose des études inutiles. Ce n’est pas seulement, du reste, à des esprits médiocres, c’est à tous les hommes qu’il est difficile de se persuader que c’est par ces études, comme avec des instruments, que l’on purifie l’œil de l’âme et qu’on fait briller d’un nouveau feu cet organe qui était obscurci et comme éteint par les ténèbres des autres sciences, organe dont la conservation est plus précieuse que celle de dix mille yeux, puisque c’est par celui-là seul que nous contemplons la vérité ».

Dans le septième livre de la République,[2] parlant de l’arithmétique, ii dit que c’est de toutes les connaissances la plus nécessaire, puisque c’est celle dont ont besoin tous les arts, toutes les conceptions de notre esprit, toutes les sciences et l’art militaire lui-même. « Palamède,[3] dit-il, représente souvent, dans les tragédies, Agamemnon comme un plaisant général; il se vante d’avoir inventé les nombres et d’avoir mis de l’ordre dans le camp et dans la flotte des Grecs devant Ilion et dans tout le reste, tandis qu’auparavant on n’avait fait aucun dénombrement et qu’Agamemnon lui-même semblait ne pas savoir combien il avait de pieds, car il ignorait complètement l’art de compter. L’arithmétique semble donc par sa nature appartenir à tout ce qui élève l’âme à la pure intelligence et l’amène à la contemplation de l’être; mais personne n’en fait usage comme il faut. Les choses qui ne font qu’une seule impression sur nos sens n’invitent point l’entendement à la réflexion : telle est la vue d’un doigt gros ou mince, long ou court, mais celles qui font naître deux sensations opposées ont le pouvoir de réveiller et d’exciter notre entendement, comme lorsque le même objet nous paraît grand ou petit, léger ou lourd, un ou multiple. C’est donc l’unité et le nombre qui ont la vertu de réveiller et d’exciter notre intelligence, puisque ce qui est un nous paraît quelquefois multiple. La science du calcul et l’arithmétique nous conduisent donc à la connaissance de la vérité.[4]

L’art du calcul ne doit donc pas être traité à la manière du vulgaire, mais de façon à conduire les hommes à la contemplation de l’essence des nombres, non en vue du commerce, comme font les marchands et les courtiers, mais pour le bien de l’âme, en lui facilitant les moyens de s’élever de l’ordre des choses qui passent, vers la vérité et l’être.

C’est, en effet, cette étude qui, donnant à notre âme un puissant élan vers la région supérieure, l’oblige à raisonner sur les nombres tels qu’ils sont en eux-mêmes, sans jamais souffrir que la discussion porte sur des unités visibles et tangibles. Il dit encore dans le même livre: « Ceux qui savent calculer s’appliquent avec succès à toutes les sciences, et ceux mêmes qui ont l’esprit plus lent, deviennent par là plus intelligents ». Dans le même livre il assure encore que, dans la guerre même, l’art de calculer est très utile pour les campements, pour la prise de possession des places, pour la concentration et le développement des troupes. Plus loin, faisant l’éloge des mêmes sciences, il dit que la géométrie s’occupe des surfaces, mais que l’astronomie a pour objet le solide en mouvement, qu’en conséquence elle oblige l’âme à regarder en haut et à passer des choses de la terre à la contemplation de celles du ciel. Dans le même écrit, il parle de la musique parce que, pour la contemplation de tout ce qui existe, il faut deux choses, « l’astronomie et l’harmonie qui, selon la doctrine des Pythagoriciens, sont deux sciences sœurs ». Ceux-là donc font un travail inutile qui, cherchant à saisir les nuances diatoniques et à comparer les sons, se contentent de prêter attentivement l’oreille et de s’approcher le plus possible de l’instrument, comme s’ils voulaient surprendre la conversation du voisin. Les uns disent qu’ils entendent un certain son particulier entre deux sons et que l’intervalle est le plus petit qui se puisse apprécier. Les autres doutent de l’existence de ce son. Préférant tous l’autorité de l’oreille à celle de l’esprit, ils cherchent la vérité en pinçant les cordes et en tournant les clefs de leurs instruments. Mais les arithméticiens habiles cherchent par la réflexion quels sont les nombres qui répondent aux consonances et forment l’harmonie, et quels sont ceux qui répondent aux dissonances. Cette étude conduit à la recherche du bien et du beau, toute autre est inutile. Toute méthode, si elle est générale et s’étend à toutes les propriétés communes des choses, en resserrant les liens de leurs affinités mutuelles, portera son fruit selon l’ardeur et le zèle avec lesquels on s’y sera appliqué. Il est impossible, en effet, que les dialecticiens qui y sont habiles ne sachent pas se rendre compte à eux-mêmes, et rendre compte aux autres, de la raison des choses. C’est à quoi personne n’arrivera s’il ne prend ces sciences pour guide, car c’est en raisonnant d’après elles que nous arrivons à la contemplation des choses.

Dans l’Epinomis, Platon revient encore sur l’arithmétique qu’il appelle « un don de Dieu[5] » et il dit que personne ne saurait devenir vertueux sans elle. Passant ensuite à la description du contraire, il dit: « Si on ôtait le nombre à l’humanité, on lui rendrait impossible toute prudence : l’âme de  l’animal destitué de raison serait incapable d’aucune vertu; elle n’aurait même plus son essence. Certes l’animal qui ne sait distinguer ni deux ni trois, qui ne connaît ni le pair ni l’impair, enfin qui ne sait rien du nombre, ne sera jamais en état de rendre raison d’aucune chose, ne la connaissant que par les sens et la mémoire. Privé de la vraie raison, il ne deviendra jamais sage. Passons en revue tout ce qui a rapport aux autres arts, nous verrons qu’il n’en est aucun qui puisse subsister, aucun qui ne périsse, si on ôte la science du nombre. A ne considérer que les arts, on pourrait croire avec quelque raison que cette science n’est nécessaire au genre humain que pour des objets de peu d’importance; ce serait déjà beaucoup. Mais celui qui considérera ce qu’il y a de divin dans l’origine de l’homme et ce qu’il y a de mortel en lui, quel besoin de piété il a envers les dieux, celui-là reconnaîtra en lui le nombre, et nul, fut-il un prophète, ne saura ni ne comprendra jamais de combien de facultés et de force le nombre est pour nous la source. Il est évident, par exemple, que la musique ne peut se passer de mouvements et de sons mesurés par les nombres, et il n’est pas moins évident que le nombre, comme source de tous les biens, ne saurait être la cause d’aucun mal. » Au contraire, celui à qui tout nombre échappe manque en quelque sorte de raison; il est sans ordre, sans beauté, sans grâce et enfin privé de toutes les perfections. Plus loin, il continue ainsi : « Personne ne nous persuadera jamais qu’il y ait pour le genre humain une vertu plus grande et plus auguste que la piété, car c’est par elle que celui qui a pris soin de s’instruire acquiert les autres vertus. Il montre ensuite comment on inspire la piété envers les dieux; puis il dit que c’est par l’astronomie qu’il faut commencer, car, s’il est honteux de commettre le mensonge à l’égard des hommes, il l’est bien plus de le commettre à l’égard des dieux. Or, celui-là est menteur qui se fait des dieux une fausse opinion, l’exprime et n’a pas même étudié la nature des dieux sensibles, c’est-à-dire l’astronomie. « Ignorez-vous, dit-il, que celui-là est nécessairement très sage qui est véritablement astronome, non pas astronome à la manière d’Hésiode, s’occupant à observer le lever et le coucher des astres, mais celui qui scrute les révolutions des sept planètes, de la connaissance desquelles tout le génie de l’homme est à peine capable[6] ». Or celui qui se propose de préparer les esprits des hommes à ces études, lesquelles supposent beaucoup de connaissances préliminaires, doit s’être rendu les sciences mathématiques familières dès son enfance et pendant toute sa jeunesse, et, parmi ces sciences, la meilleure, la principale, est la science des nombres abstraits et séparés de toute matière, celle aussi de la génération et de la vertu du pair et de l’impair, en tant qu’elle contribue à faire connaître la nature des choses. Après cette science, il en est une, dit-il, à laquelle on a donné le nom parfaitement ridicule de géométrie, car elle comprend une assimilation de nombres qui ne sont pas semblables entre eux par nature, assimilation que met en évidence la condition des surfaces. Il fait ensuite mention d’une autre science qu’il appelle stéréométrie : si quelqu’un, dit-il, multipliant trois nombres, rend le produit semblable (à un autre) de dissemblable qu’il était, il fera une œuvre vraiment divine et merveilleuse. Dans les Lois, parlant de l’harmonie musicale, il dit que la plus grande et la plus belle harmonie politique est la sagesse. On ne la possède qu’autant qu’on vit selon la droite raison; quant à celui à qui elle fait défaut, il est le corrupteur de sa propre maison, c’est un citoyen inutile au salut et à la prospérité de l’Etat, puisqu’il vit dans une extrême ignorance[7] ».

Et dans le troisième livre de la République, voulant prouver que le philosophe est seul musicien, il dit : « Par les dieux immortels, nous ne serons jamais musiciens, ni nous ni ceux dont nous devons faire l’éducation comme gardiens, tant que nous ne connaîtrons pas toutes les formes de la tempérance, du courage, de la générosité et de la grandeur et tant que nous n’aurons pas compris tout ce qui, dans le monde, est conforme ou contraire à ces vertus, tant que nous ne saurons pas les reconnaître et en reconnaître les images dans ceux qui les possèdent, sans en négliger une seule, grande ou petite, les regardant comme faisant partie du même art et de la même étude[8] ». Par ces paroles et par celles qui précèdent, il prouve l’utilité de la musique, et il montre que le seul philosophe est réellement musicien, tandis que celui qui est vicieux et méchant est étranger aux Muses. Car, dit-il, la vraie et sincère probité des mœurs, celle vertu qui consiste dans le bon et honnête règlement de notre vie, suit la droite raison, c’est-à-dire l’usage conforme à la raison. Il ajoute que les compagnons de la droite raison sont la décence, la cadence et l’accord, la décence dans le chant, l’accord dans l’harmonie, la cadence dans le rythme. Par contre, l’improbité ou la corruption des mœurs est essentiellement liée à la perversion de la raison, c’est-à-dire à l’usage corrompu de la raison, et ses compagnons sont l’indécence, la confusion et le désaccord dans tout ce qu’on fait, de soi-même ou par imitation, de sorte que celui-là seul est musicien qui a de bonnes mœurs et, comme on le voit par cc qui précède, il est aussi le vrai philosophe, si toutefois, dès les premières années de son adolescence, quand on lui eut appris la musique, il prit des habitudes de décence et d’ordre, car la musique joint un plaisir innocent à l’utilité. Il est impossible, dit Platon, que celui-là devienne musicien parfait, qui n’a pas en tout des habitudes de bonne éducation, qui n’a pas les idées de décence, de noblesse d’âme et de tempérance. Il doit reconnaître que ces idées se retrouvent partout et ne les mépriser ni dans les petites choses ni dans les grandes. Car c’est au philosophe qu’il appartient de connaître les idées, et personne ne connaîtra la modestie, la tempérance et la décence, s’il est lui-même immodeste et intempérant. Mais les choses qui font l’ornement de la vie humaine, le beau, l’harmonieux, l’honnête, tout cela est l’image de cette beauté, de cet accord, de ce bel ordre éternel et qui a une existence véritable, c’est-à-dire que ces choses sensibles sont les caractères et l’expression des choses intelligibles ou des idées.

Les Pythagoriciens dont Platon adopte souvent les sentiments, définissent aussi la musique une union parfaite de choses contraires, l’unité dans la multiplicité, enfin l’accord dans la discordance. Car la musique ne coordonne pas seulement le rythme et la modulation, elle met l’ordre dans tout le système; sa fin est d’unir et de coordonner, et Dieu aussi est l’ordonnateur des choses discordantes, et sa plus grande œuvre est de concilier entre elles, par les lois de la musique et de la médecine, les choses qui sont ennemies les unes des autres. C’est aussi par la musique que l’harmonie des choses et le gouvernement de l’univers se maintiennent; car ce que l’harmonie est dans le monde, la bonne législation l’est dans l’Etat, et la tempérance l’est dans la famille. Elle a, en effet, la puissance de mettre l’ordre et l’union dans la multitude. Or, l’efficacité et l’usage de cette science, dit Platon, se voient dans quatre des choses qui appartiennent à l’humanité : l’esprit, le corps, la famille et l’Etat. En effet, ces quatre choses ont besoin d’être bien ordonnées et constituées.

Voici encore ce que Platon dit des mathématiques dans les livres de la République : « L’homme de bien est celui qui, éprouvé par la peine ou le plaisir, agité par le désir ou par la crainte, conserve toujours, sans jamais les rejeter, les idées droites qu’on lui a données en faisant son éducation. Je vais vous dire à qui il me paraît semblable. Quand nos teinturiers veulent teindre la laine en pourpre, ils commencent par choisir, parmi les laines de diverses couleurs, celle qui est blanche. Ils font ensuite leur préparation, et il ne faut pas peu de soin pour que la laine prenne la fleur de la couleur. C’est ainsi qu’ils opèrent, et grâce à cette méthode, les couleurs s’incorporent à la laine et leur éclat ne peut être enlevé ni à l’aide de lessive, ni autrement. Que si, au contraire, le teinturier ne prend pas ces précautions, on sait ce qui arrive, et comment les laines conservent peu la couleur qui s’efface et disparaît. Il faut opérer de même pour nos facultés[9] ». Nous apprenons aux enfants la musique, la gymnastique, les lettres, la géométrie et l’arithmétique, ne négligeant rien pour qu’ils reçoivent, comme une teinture, les raisons de toutes les vertus que nous leur enseignons; après leur avoir administré préalablement des détersifs, et d’autres préparations, consistant dans ces sciences, qui sont comme autant de médicaments astringents, leurs sentiments resteront indélébiles, leur caractère aura été formé par l’éducation. Cette couleur et cette teinture que nous leur aurons données, ne pourront être effacées par aucune lessive, —je veux dire par la volupté plus dangereuse que toute perversité et que toute habitude, — ni par la douleur, ni par la crainte et la cupidité, plus corrosives que toutes les lessives. Nous pouvons encore comparer la philosophie à l’initiation aux choses vraiment saintes et à la révélation des mystères qui ne sont pas des impostures.[10] Il y a cinq parties dans l’initiation : la première est la purification préalable, car on ne doit pas faire participer aux mystères indistinctement tous ceux qui le désirent, mais il y a des aspirants que la voix du héraut écarte, tels sont ceux qui ont les mains impures, ou dont la parole manque de prudence; et ceux-là mêmes qui ne sont pas repoussés doivent être soumis à certaines purifications. Après cette purification, vient la tradition des choses sacrées (qui est proprement l’initiation). Vient en troisième lieu la cérémonie qu’on appelle la pleine vision (degré supérieur de l’initiation). La quatrième, qui est la fin et le but de la pleine vision, est la ligature de la tête et l’imposition des couronnes, afin que celui qui a reçu les choses sacrées devienne capable d’en transmettre à son tour la tradition à d’autres, soit par la dadouchie (port des flambeaux), soit par l’hiérophantie (interprétation des choses sacrées), soit par quelque autre sacerdoce. Enfin la cinquième, qui est le couronnement de toutes celles qui précèdent, est d’être ami de Dieu et de jouir de la félicité qui consiste à vivre dans un commerce familier avec lui.

C’est absolument de la même manière que se fait la tradition des raisons platoniques. On commence, en effet, dès l’enfance par une certaine purification consistant dans l’étude de théories mathématiques convenables. Selon Empédocle[11] « il faut que celui qui veut puiser dans l’onde pure des cinq fontaines commence par se purifier de ses souillures ». Et Platon dit aussi qu’il faut chercher la purification dans les cinq sciences mathématiques, qui sont l’arithmétique, la géométrie, la stéréométrie, la musique et l’astronomie. La tradition des principes philosophiques, logiques, politiques et naturels répond à l’initiation. Il appelle pleine vision[12] l’occupation de l’esprit aux choses intelligibles, aux existences vraies et aux idées. Enfin il dit que par la ligature et le couronnement de la tête, on doit entendre la faculté qui est donnée à l’adepte, par ceux qui l’ont enseigné, de conduire les autres à la même contemplation. La cinquième est cette félicité consommée dont ils commencent à jouir et qui, selon Platon, « les assimile à Dieu, autant que cela est possible ».

Celui qui voudrait démontrer l’utilité et la nécessité des sciences mathématiques pourrait en dire beaucoup plus tong. Mais de crainte que je ne paraisse m’arrêter plus que de raison louer ces sciences, je vais commencer l’explication des théorèmes nécessaires, non pas de tous ceux qui seraient nécessaires aux lecteurs pour devenir de parfaits arithméticiens, géomètres, musiciens ou astronomes, car ce n’est pas le but que se proposent tous ceux qui veulent lire les écrits de Platon; mais j’expliquerai les théorèmes qui suffisent pour comprendre le sens de ses écrits. En effet, Platon lui-même ne veut pas que l’on continue jusque dans l’extrême vieillesse à tracer des figures géométriques ou à chanter des chansons, choses qui conviennent aux enfants et qui sont destinées à préparer et à purifier leur esprit, pour le rendre capable de comprendre la philosophie. Il suffit que celui qui veut aborder nos écrits, ou les livres de Platon, ait parcouru les premiers éléments de la géométrie, pour qu’il comprenne facilement nos explications. Toutefois ce que nous dirons sera tel, que nous pourrons être compris même de celui qui ignore complètement les mathématiques.

ARITHMÉTIQUE

De l’ordre dans lequel on doit étudier les mathématiques

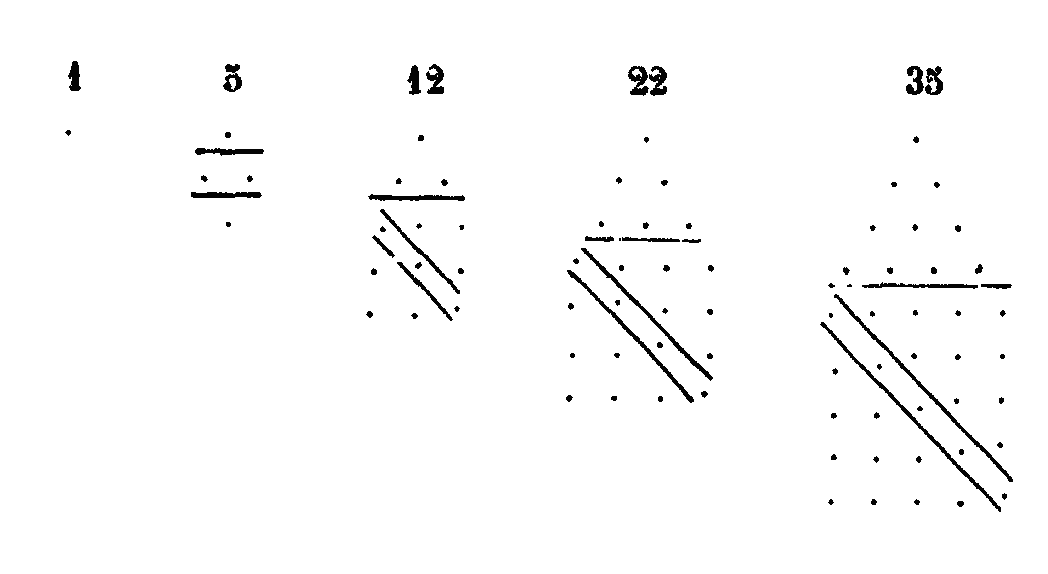
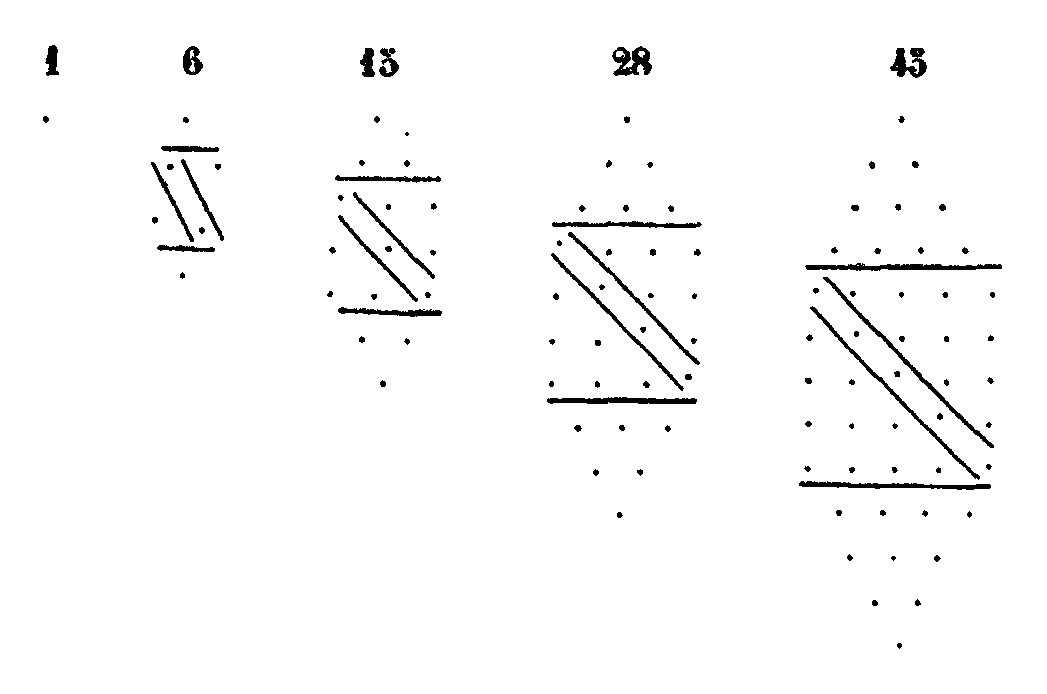
II. Nous allons commencer par les théorèmes arithmétiques auxquels se rattachent de très près les théorèmes musicaux qui se traduisent par des nombres. Nous n’avons nul besoin de musique instrumentale, ainsi que l’explique Platon lui-même, lorsqu’il dit qu’il ne faut pas tourmenter les cordes des instruments, (l’oreille tendue) comme des curieux qui sont aux écoutes. Ce que nous désirons c’est de comprendre l’harmonie et la musique célestes; cette harmonie, nous ne pouvons l’examiner qu’après avoir étudié les lois numériques des sons. Quand Platon dit que la musique occupe le cinquième rang[13] (dans l’élude des mathématiques), il parle de la musique céleste, laquelle résulte du mouvement, de l’ordre et du concert des astres qui cheminent dans l’espace. Mais nous devons donner à la musique mathématique la seconde place (c’est-à-dire la mettre) après l’arithmétique, comme le veut Platon, puisqu’on ne peut rien comprendre à la musique céleste, si l’on ne connaît celle qui a son fondement dans les nombres et dans la raison. Puis donc que les principes numériques de la musique se rattachent à la théorie des nombres abstraits, nous leur donnerons le second rang pour la facilité de notre étude.

Selon l’ordre naturel, la première science serait celle des nombres, qu’on appelle arithmétique. La seconde serait celle qui pour objet les surfaces, et qu’on appelle géométrie. La troisième est celle qui pour objet les solides, et qu’on appelle stéréométrie. La quatrième traite des solides en mouvement, c’est l’astronomie. Quant à cette musique dont l’objet est de considérer les relations mutuelles des mouvements et des intervalles, quelles que soient ces relations, il n’est pas possible de la comprendre avant d’avoir saisi celle qui est basée sur les nombres. Ainsi, dans notre plan, les lois numériques de la musique viendront immédiatement après l’arithmétique mais, d’après l’ordre naturel, la cinquième place doit être donnée à cette musique qui consiste dans l’étude de l’harmonie des mondes. Or, selon la doctrine des Pythagoriciens, les nombres sont pour ainsi dire le principe, la source et la racine de toutes choses.

De l’Un et de la monade

III. Le nombre est une collection de monades, ou une progression de la multitude commençant et revenant à la monade (par l’addition ou la soustraction successive d’une unité). Quant à la monade, c’est la quantité terminante — principe et élément des nombres — qui, une fois débarrassée de la multitude par soustraction, et privée de tout nombre, demeure ferme et fixe: il est impossible de pousser plus loin la division. Si nous divisons en plusieurs parties un corps sensible, ce qui était un devient plusieurs, et si l’on soustrait chacune des parties, il se terminera à un; et si cet un, nous le divisons de nouveau en plusieurs parties, il en sortira la multitude, et en enlevant chacune de ces parties, on reviendra à un, de sorte que ce qui est un, en tant qu’un, est sans parties et indivisible.[14] Tout autre nombre étant divisé est diminué et réduit en parties plus petites que lui, comme 6 en 3 et 3, ou en 4 et 2, ou en 5 et 4. Ce qui est un, dans les choses sensibles, si on le divise, est diminué à la manière des corps, et par le partage qu’on en fait, il est divisé en parties plus petites que lui; mais il augmente comme nombre; car, à la place de ce qui était un, il y a plusieurs. C’est d’après cela que ce qui est un est indivisible. Nulle chose, en effet, ne peut être divisée en parties plus grandes qu’elle-même. Mais ce qui est un, divisé en parties plus grandes que l’entier, se divise à la manière des nombres en parties égales en somme) à l’entier. Par exemple, si un corps, unité sensible, est divisé en six parties, 1, 1, 1, 1, 1, 1, ces parties sont égales à l’unité; mais, si on le divise en 5 et 2, les parties sont plus grandes que l’unité; en effet, 1 et 2, comme nombres, surpassent un. La monade donc, en tant que nombre, est indivisible. Si elle est appelée monade, c’est, ou bien parce qu’elle demeure immuable et ne sort pas des limites de sa nature; en multipliant, en effet, la monade par elle-même, nous aurons toujours la monade : une fois un donne toujours un; et, si nous multiplions la monade jusqu’à l’infini, elle restera toujours monade. Ou bien encore, elle est appelée monade, parce qu’elle est séparée et mise seule en dehors de la multitude des autres nombres. Comme le nombre diffère de ce qui est nombré, de même la monade diffère de ce qui est un. Le nombre, en effet, est une quantité intelligible, comme la quantité 5 et la quantité 10, qui ne sont pas composées de corps sensibles, mais de choses intelligibles. Quant à la quantité nombrable, elle se trouve dans les choses sensibles telles que 5 chevaux, 5 bœufs, 5 hommes. Donc la monade est l’idée d’un un intelligible, lequel un est indivisible. Quant à l’un qui se rencontre dans les choses sensibles, on le dit un en soi, comme un cheval, un homme.[15]

IV. La monade sera donc le principe des nombres; et l’un le principe des choses nombrées. Ce qui est un, en tant que sensible, peut, à ce qu’on assure, être divisé à l’infini, non en tant qu’il est nombre ou principe du nombre, mais en tant qu’il est sensible, en sorte que la monade qui est intelligible, n’admet pas de division, mais que ce qui est un, étant sensible, peut être divisé à l’infini. Les choses nombrées diffèrent encore des nombres, en ce qu’elles sont corporelles, tandis que les nombres sont incorporels. Mais, sans faire cette distinction, « les modernes considèrent la monade et la dyade comme principes des nombres ; quant aux Pythagoriciens, ils font consister les principes des nombres dans les séries des termes successifs par lesquels se conçoivent les pairs et les impairs »; ils disent, par exemple, que le principe de trois dans les choses sensibles est la triade, que le principe de tout ce qui est quatre, parmi les choses sensibles, est la tétrade, et ainsi de même pour tous les autres nombres. Ils prétendent en outre que la monade est le principe de tous ces nombres et que l’un est libre de toute variété, l’un qui se trouve dans les nombres n’étant pas tel ou tel un, c’est-à-dire n’étant pas une certaine quantité et une diversité à l’égard d’un autre un, mais étant l’un considéré en lui-même. Car c’est par là qu’il devient le principe et la mesure des choses qui lui sont soumises, de même que chacune des choses qui existent est dite un, comme étant participante de la première essence et de l’idée de ce qui est un. Archytas et Philolaüs se servent indifféremment des mots un et monade, et ils disent que la monade est l’un. La plupart ajoutent su nom de monade l’épithète « première », comme s’il y avait une monade qui ne fût pas première, et comme si celle qu’ils appellent première était plus universelle, et qu’elle fût la monade et l’un, — car ils l’appellent aussi l’un — et comme si elle était l’essence première et intelligible qui fait que toutes les choses qui sont un, soient telles. C’est en vertu d’une participation à cette essence que toutes choses sont appelées un. C’est pourquoi le nom même un ne dit pas de quelle chose il s’agit, ni quelle en est l’espèce, mais il s’applique à toutes choses. Ainsi, la monade et l’un étant tout à la fois intelligibles et sensibles, ces deux choses ne diffèrent en rien l’une de l’autre. Quelques-uns mettent une autre différence entre l’un et la monade : l’un ne change pas selon la substance, et ce n’est pas lui qui fait que la monade ou les impairs changent selon l’essence. Il ne change pas non plus selon la qualité, car c’est lui-même qui est monade, et non comme les monades qui sont plusieurs. Il ne change pas non plus selon la quantité, car il n’est pas composé, comme les monades auxquelles s’ajoute une autre monade. Il est un et non plusieurs: c’est pour cela qu’on l’appelle lui seul un. Et quoique Platon, dans le Philèbe, se soit servi de l’expression « les unités », il ne les a pas appelées ainsi d’après l’un, mais d’après la monade qui est une participation de l’un. Cet un, qui se distingue de la monade dont il est l’essence, est quelque chose de tout à fait immuable. L’un diffère donc de la monade, en tant qu’il est défini et terme, tandis que les monades sont indéfinies et indéterminées.

Du nombre pair et du nombre impair

V. Une première division partage les nombres en deux espèces: les uns sont appelés pairs, les autres impairs. Les pairs sont les nombres qui peuvent se diviser en deux parties égales, comme deux et quatre, les impairs au contraire sont les nombres qui ne peuvent se diviser qu’en parties inégales, comme cinq et sept. Quelques-uns ont dit que le premier des impairs est l’unité. Car pair est le contraire d’impair, et l’unité est nécessairement paire ou impaire; or elle ne peut pas être paire, puisque, non seulement elle ne se divise pas en parties égales, mais elle ne se divise même pas du tout; donc l’unité est impaire. Que si vous ajoutez un nombre pair à un autre nombre pair, le tout sera pair; or, l’unité, ajoutée à un nombre pair, donne un tout impair: donc, encore une fois, l’unité n’est pas paire, elle est impaire. Cependant, Aristote dit, dans le Pythagoricien,[16] que l’un participe des deux natures. En effet, ajouté à un nombre pair, il donne un nombre impair; mais, ajouté à un nombre impair, il donne un nombre pair, ce qu’il ne pourrait faire s’il ne participait des deux natures. C’est pourquoi on l’appelle pair-impair. Archytas paraît avoir été aussi de ce sentiment. La première idée de l’impair est donc l’unité, comme aussi dans le monde, on attribue la qualité d’impair à ce qui est défini et bien ordonné. Au contraire, la première idée du pair est le binaire indéfini, ce qui fait que, dans le monde aussi, on attribue la qualité de pair à tout ce  qui est indéfini, inconnu et désordonné. C’est pourquoi le binaire est appelé indéfini, parce qu’il n’est pas défini comme l’unité. Quant aux termes qui se suivent par une série continue, en commençant par l’unité, ils augmentent toujours d’une quantité égale, chacun surpassant d’une unité celui qui le précède; mais, à mesure que les termes augmentent, leur rapport mutuel diminue. Soient, par exemple, tes termes 1, 2, 3, 4, 5, 6, la raison du nombre 2 à l’unité est double; celle du nombre 3 au nombre 2 est sesquialtère (1 + 1/2); celle du nombre 4 au nombre 3 est sesquitierce (1 + 1/3); celle du nombre 5 au nombre 4 est sesquiquarte (1 + 1/4); enfin celle du nombre 6 au nombre 5 est sesquiquinte (1 + 1/5). Or le rapport 1 + 1/5 est plus petit que 1 + 1/4; 1 + 1/4 est plus petit que 1 + 1/3; 1 + 1/3 est plus petit que 1 + 1/2; et enfin 1 + 1/2 est plus petit que 2. Et on trouverait que la raison décroît de même pour les autres nombres. On voit aussi que les nombres successifs sont alternativement pairs et impairs.

Du nombre premier ou incomposé

VI. Parmi les nombres, les uns sont dits premiers absolus ou incomposés; d’autres sont premiers entre eux, mais non absolument; d’autres sont absolument composés; d’antres, composés entre eux. Les nombres absolument premiers et incomposés sont ceux qu’aucun nombre ne peut mesurer, si ce n’est l’unité. Tels sont 3, 5 7, 11, 13, 17…. et autres semblables. Ces nombres sont aussi appelés linéaires et euthymétriques, parce que les longueurs et les lignes ne sont considérées que dans une seule dimension. On les appelle aussi impairement-impairs. On leur donne donc cinq dénominations différentes : premiers, incomposés, linéaires, euthymétriques et impairement-impairs. Ce sont les seuls qui ne soient pas divisibles; ainsi aucun des autres nombres, différents de l’unité, ne peut diviser le nombre 3, de sorte que 3 puisse résulter de leur multiplication. En effet, une fois 3 fait 3. De même, une fois 5 fait 5, une fois 7 fait 7, et une fois 11 fait 11. Et c’est pour cela qu’on appelle ces nombres impairement-impairs;[17] car ils sont impairs, et l’unité qui les mesure est également impaire. Aussi les seuls impairs peuvent être premiers ou incomposés. En effet, les nombres pairs ne sont pas premiers et incomposés; ils n’ont pas la seule unité pour mesure, d’autres nombres les mesurent: par exemple, 2 mesure 4, car 2 fois 2 font 4; 2 et 3 mesurent 6, car 2 fois 3 et 3 fois 2 font 6. Tous les autres nombres pairs, à l’exception de 2, sont mesurés de même par des nombres plus grands que l’unité. Le nombre 2 est le seul, parmi les pairs, qui soit dans le même cas que plusieurs impairs, de n’avoir que l’unité pour mesure. En effet une fois 2 est 2. C’est pour cela qu’on a dit que le nombre 2 a la nature du nombre impair, parce qu’il a la même propriété que les impairs. On appelle premiers entre eux, mais non absolument, les nombres qui ont pour commune mesure l’unité, quoique d’autres nombres les mesurent, si on les considère séparément, comme 8 que mesurent 2 et 4, 9 que mesure 3, et 10 que mesurent 2 et 5. Ils ont, en effet, l’unité pour commune mesure, soit entre eux, soit par rapport à leurs facteurs premiers : on a [une fois 3 égale 3] une fois 8 égale 8, une fois 9 égale 9, et une fois 10 égale 10.

Du nombre composé

VII. Les nombres composés sont les nombres mesurés par un nombre moindre qu’eux-mêmes, comme 6 qui est mesuré par 2 et 3. Les nombres composés entre eux sont ceux qui ont une mesure commune comme 8 et 6, qui ont 2 pour commune mesure, car 2 fois 3 font 6 et 2 fois 4 font 8. Tels sont encore 6 et 9 qui ont 3 pour commune mesure, car 3 fois 2 font 6 et 3 fois 3 font 9. Quant à l’unité, elle n’est pas un nombre, mais le principe du nombre; et, quant au nombre 2, il n’est pas indéfini, il est le premier nombre différent de l’unité et, quoique pair, il n’a pas de diviseur plus grand que l’unité. Les nombres composés qui sont le produit de deux nombres sont appelés plans; on les considère comme ayant deux dimensions, longueur et largeur. Ceux qui sont le produit des trois nombres sont appelés solides, comme possédant la troisième dimension. Enfin, on appelle circuit le résultat de la multiplication de nombres les uns par les autres.

Des diverses sortes de nombres pairs.

VIII. Parmi les nombres pairs, les uns sont pairement pairs d’autres impairement-pairs, d’autres enfin pairement-impairs. On reconnait qu’un nombre est pairement-pair quand il réunit ces trois conditions 1° qu’il soit engendré par deux pairs multipliés entre eux; 2° que toutes les parties en soient paires jusqu’à la réduction à l’unité; 3° qu’aucune de ses parties n’ait le même nom qu’un nombre impair. Tels sont 32, 64, 128, et ainsi de suite en procédant par une progression double. En effet, 32 est le produit des nombres 4 et 8 qui sont pairs. Toutes les parties en sont paires, savoir : la moitié 16, le quart 8, le huitième 4, les parties sont de même nom que les nombres pairs, la moitié est considérée comme le nombre binaire, il en est de même du quart, du huitième (qui sont considérés comme les nombres 4, 8). Il en est de même des autres nombres.[18]

IX. On appelle nombres pairement impairs les nombres mesurés par le nombre 2 et par un nombre impair quelconque et qui ont, par conséquent, des moitiés impaires quand on fait la division par 2. Tel est 2 fois 7 ou 14. On les appelle pairement impairs, parce qu’ils ont pour mesure le nombre 2, qui est pair et, en outre, un nombre impair; 2 a l’unité; 6 a le nombre 3; 10 a le nombre 5; 14 a 7. Ces nombres, une fois faite la division par 2, sont partagés en deux parties impaires, et, après la première division, ils n’en admettent plus d’autre en deux parties égales. En effet, la moitié de 6 est 3, mais 3 ne peut se diviser en parties égales, car l’unité (qui reste après la division par 2) est indivisible.[19]

X. Les nombres impairement pairs sont ceux qui résultent de la multiplication de deux nombres quelconques, l’un impair, l’autre pair, lesquels, multipliés l’un par l’autre, sont divisés par le nombre 2 en deux parties paires; mais, si l’on emploie de plus grands diviseurs, les quotients sont tantôt pairs, tantôt impairs. Tels sont les nombres 12 et 20, qui valent respectivement 3 fois 4, et 5 fois 4. Or, en divisant 12 successivement par 2, 3 et 4, on a 12 = 2 x 6 =3 x 4 = 4 x 3. On a de même 20 = 2 x 10 = 4 x 5 = 5 x 4.[20]

Des nombres carrés, hétéromèques, parallélogrammes

XI. Parmi les nombres composés les uns sont également égaux, c’est-à-dire carrés et plans, quand ils résultent de la multiplication de deux nombres égaux (le résultat est également égal ou carré). Tels sont les nombres 4 et 9, car 2 fois 2 font 4 et 3 fois 3 font 9.

XII. Au contraire, les nombres composés sont inégalement inégaux, quand ils résultent de la multiplication de deux nombres inégaux. Tel est 6, car 2 fois 3 font 6.

XIII. Parmi ces nombres, on nomme hétéromèques, ceux qui ont un côté (facteur) plus long que l’autre d’une unité. Or, le nombre qui surpasse le nombre impair d’une unité est pair, donc les hétéromèques ne comprennent que des nombres pairs. En effet, l’unité, principe de tous les nombres, étant impaire et tendant à la production des autres, a fait, en se doublant elle-même, le nombre 2 qui est hétéromèque, C’est pourquoi le nombre 2, étant hétéromèque et surpassant l’unité d’une unité, rend hétéromèques les nombres pairs qui surpassent les impairs d’une unité. Or, les nombres dont il s’agit s’engendrent de deux manières, par la multiplication et par l’addition. Par l’addition, les nombres pairs ajoutés aux nombres pairs qui les précèdent, produisent les nombres hétéromèques. Soient, en effet, les nombres pairs successifs

2, 4, 6, 8, 10, 12, 14, 16, 18.

Par l’addition, on a 2+4=6; 6+6=12; 12+8=20; 20 + 10=30; en sorte que les sommes sont les nombres hétéromèques 6, 12, 20, 30 et ainsi des suivants.[21] Les mêmes nombres hétéromèques sont également obtenus par la multiplication des pairs et des impairs successifs, le premier nombre étant multiplié par le suivant. Soit, en effet,

1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

On a 1 fois 2=2; 2 fois 3=6; 3 fois 4=12; 4 fois 5=20; 5 fois 6=30; et ainsi de suite. Les nombres hétéromèques sont ainsi appelés, parce que c’est l’addition de l’unité à l’un des côtés qui fait la première diversité des côtés.

XIV. Les nombres parallélogrammes sont ceux qui ont un côté plus grand que l’autre de 2 unités, comme 2 fois 4, 4 fois 6, 6 fois 8, 8 fois 10, qui valent 8, 24, 48, 80.

XV. Les nombres engendrés par l’addition des nombres impairs successifs sont carrés. Soit, en effet, la série des impairs 4, 3, 5, 7, 9, 11; 1 et 3 font 4 qui est carré, car il est également égal, 2 fois 2 font 4; 4 et 5 font 9, qui est aussi carré, car 3 fois 3 font 9; 9 et 7 font 16, qui est carré, car 4 fois 4 font 16; 16 et 9 font 25, c’est encore un nombre carré, car il est également égal, 5 fois 5 font 25. On continuerait ainsi à l’infini. Telle est donc la génération des nombres carrés par l’addition, chaque impair étant successivement ajouté au carré obtenu en sommant les impairs précédents à partir de l’unité.[22] La génération a lieu aussi par la multiplication, en multipliant un nombre quelconque par lui-même, comme 2 fois 2 font 4, 3 fois 3 font 9, 4 fois 4 font 16,

XVI. Les carrés consécutifs ont pour moyens, en proportion géométrique, des hétéromèques, c’est-à-dire des nombres dont un côté est plus long que l’autre d’une unité; mais les hétéromèques consécutifs n’ont pas des carrés pour moyens proportionnels.

Ainsi, soient les nombres 1, 2, 3, 4, 5; chacun d’eux multiplié par lui-même donne un carré: 1 x 1=1; 2 x 2=4; 3 x 3=9; 4 x 4=16; 5 x 5=25; aucun des facteurs ne sort de ses propres limites, car le nombre 2 ne fait que se doubler lui-même, 3 ne fait que se tripler... Les carrés successifs sont donc 1, 4, 9, 16, 25. Je dis qu’ils ont pour moyens les hétéromèques. Prenons, en effet, le carrés successifs 1 et 4, le moyen entre eux est le nombre hétéromèque 2 : si nous posons la série 1, 2, 4, le moyen 2 contient l’extrême 1, autant de fois qu’il est contenu dans l’autre extrême 4; 2 est en effet, le double de 1, et 4 le double de 2. Soient encore les carrés 4 et 9, leur moyen est le nombre hétéromèque 6. Si nous mettons en ligne 4, 6, 9, le rapport du moyen 6 au premier extrême est égal au rapport du deuxième extrême à 6, car le rapport de 6 à 4 est sesquialtère (1 + 1/2), comme le rapport de 9 à 6. Il en est de même des carrés suivants.

Les hétéromèques, au contraire, produits de facteurs qui diffèrent d’une unité, ne restent pas dans leurs propres limites et ne comprennent pas les carrés. Ainsi 2 x 3=6; 3 x 4=12; et 4 x 5=20. Or, aucun des (premiers) facteurs ne demeure dans ses propres limites, il change dans la multiplication, le nombre 2 se multipliant par 3, le nombre 3 par 4, et 4 par 5.

De plus, les nombres hétéromèques engendrés ne comprennent pas les nombres carrés. Ainsi 2 et 6 sont des hétéromèques successifs entre lesquels se trouve le carré 4; mais celui-ci n’est pas compris entre eux d’après la proportion géométrique continue, en sorte qu’il ait le même rapport avec les extrêmes. Si nous disposons en ligne 2, 4, 6; 4 aura un rapport différent avec les extrêmes, car le rapport de 4 à 2 est double et celui de 6 à 4 est sesquialtère (1 + 1/2). Or, pour que 4 fut moyen proportionnel, il faudrait que le rapport du premier terme au moyen fût égal au rapport du moyen au troisième terme. Pareillement 9, nombre carré, est compris entre les hétéromèques successifs 6 et 12, mais il n’a pas le même rapport avec les extrêmes, car le rapport de 9 à 6 est sesquialtère (1 + 1/2), tandis que celui de 12 à 9 est sesquitierce (1 + 1/3). Il en est de même des hétéromèques suivants.[23]

Des nombres promèques

XVII. Un nombre promèque est un nombre formé de facteurs inégaux quelconques dont l’un surpasse l’autre, soit d’une unité, soit le deux, soit d’un plus grand nombre. Tel est 24 qui vaut 6 fois 4, et autres nombres semblables. Il y a trois classes de nombres promèques. En effet, tout nombre hétéromèque est en même temps promèque, en tant qu’il a un côté plus grand que l’autre; mais, si tout nombre hétéromèque est par là même promèque, la réciproque n’est pas vraie, car le nombre qui a un côté plus long que l’autre de plus d’une unité, est promèque; mais il n’est pas hétéromèque, puisque celui-ci se définit un nombre dont un côté surpasse l’autre d’une unité, comme 6, puisque 2 x 3 = 6.

Un nombre est encore promèque quand, suivant les multiplications diverses, il a un des côtés tantôt plus long d’une unité, tantôt plus long de plus d’une unité. Tel est 12 qui résulte de 3 x 4 et de 2 x 6, en sorte qu’à raison des côtés 3 et 4, le nombre 12 est hétéromèque, et qu’à raison des côtés 2 et 6, il est promèque. Enfin, un nombre est encore promèque, si, résultant de toute espèce de multiplication, il a un côté plus long que l’autre de plus d’une unité. Tel est 40, qui est le produit de 10 par 4, de 8 par 5 et de 20 par 2. Les nombres de cette espèce ne peuvent être que promèques. Le nombre hétéromèque est celui qui reçoit la première altération après le nombre formé de facteurs égaux, l’addition d’une unité faite à l’un des deux côtés égaux étant la première altération. C’est pourquoi les nombres qui résultent de cette première altération des côtés ont été appelés, avec raison, hétéromèques; mais ceux qui ont un côté plus grand que l’autre d’une quantité supérieure à l’unité ont été appelés promèques, à cause de la plus grande différence de longueur entre les côtés.

XVIII. Les nombres plans sont les nombres produits par la multiplication de deux nombres représentant la longueur et la largeur. Parmi ces nombres, il y en a qui sont triangulaires, d’autres sont quadrangulaires, pentagones et en général polygones.

Des nombres triangulaires, de la manière dont ils s’obtiennent, et des autres nombres polygones

XIX. Les nombres triangulaires s’obtiennent de la manière que nous allons indiquer. Et d’abord les pairs successifs ajoutés les uns aux autres produisent les hétéromèques. Ainsi le premier pair 2 est en même temps hétéromèque, car il vaut 1 x 2. Si maintenant à 2 on ajoute 4, la somme sera 6 qui est encore un hétéromèque, puisqu’il vaut 2 x 3 et il en est de même des suivants à l’infini. Mais, afin que ce que nous venons de dire soit plus clair, nous allons le montrer ainsi.

Supposons que le premier pair 2 soit représenté par les deux unités 1, 1, la figure qu’elles forment est hétéromèque, car elle a 2 en longueur et 1 en largeur. Après le nombre 2 vient le nombre pair 4; si nous ajoutons les quatre unités aux deux premières, en les plaçant autour (à angle droit), nous aurons la figure du nombre hétéromèque 6, car sa longueur est 3 et sa largeur 2. Après le nombre 4 vient le nombre pair 6. Si nous ajoutons les 6 unités aux 6 premières en les plaçant autour (à angle droit), la somme sera 12 et la figure sera hétéromèque, comme ayant 4 en longueur et 3 en largeur, et ainsi de suite à l’infini par l’addition des nombres pairs

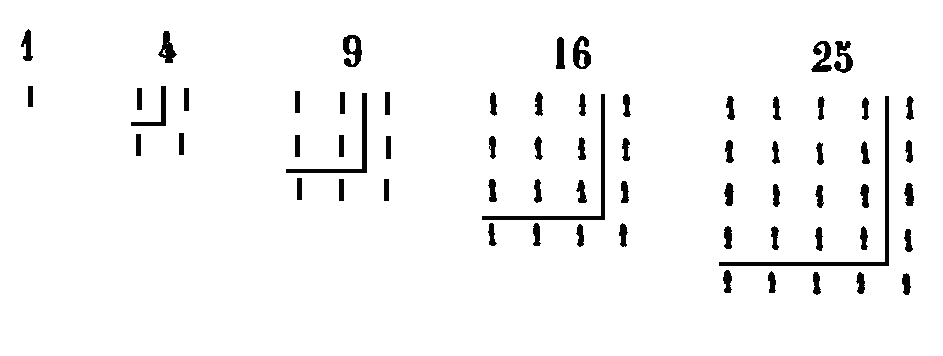
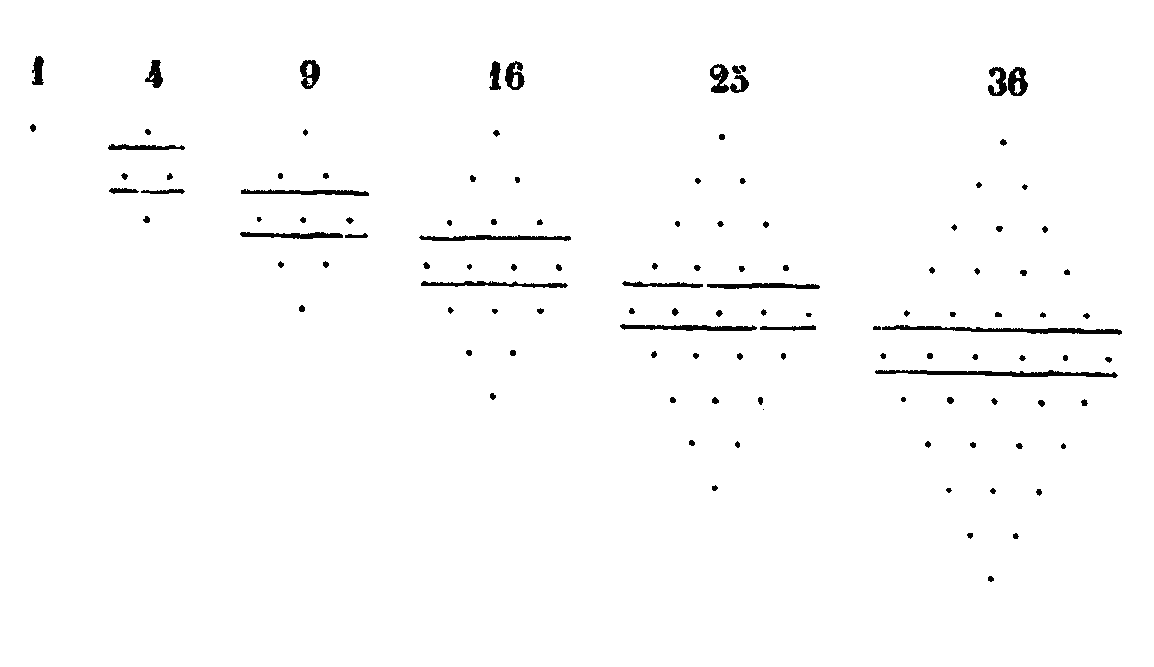
A leur tour, les impairs ajoutés ensemble donnent les nombres carrés. Or, les impairs successifs sont 1, 3, 5, 7, 9, 11. En les additionnant d’une manière continue, on obtient les nombres carrés. Ainsi l’unité est le premier nombre carré, car 1 x 1 = 1. Vient ensuite le nombre impair 3. Si on ajoute ce gnomon à l’unité,[24] on obtient un carré également égal, car il a 2 tant en longueur qu’en largeur. L’impair qui vient suite est 5. Si on ajoute ce gnomon au carré 4, on obtient un nouveau carré 9, qui a 3 en longueur comme en largeur. Vient ensuite l’impair 7 qui, ajouté au carré 9, donne le carré 16, dont la longueur et la largeur valent 4, et ainsi de suite à l’infini.

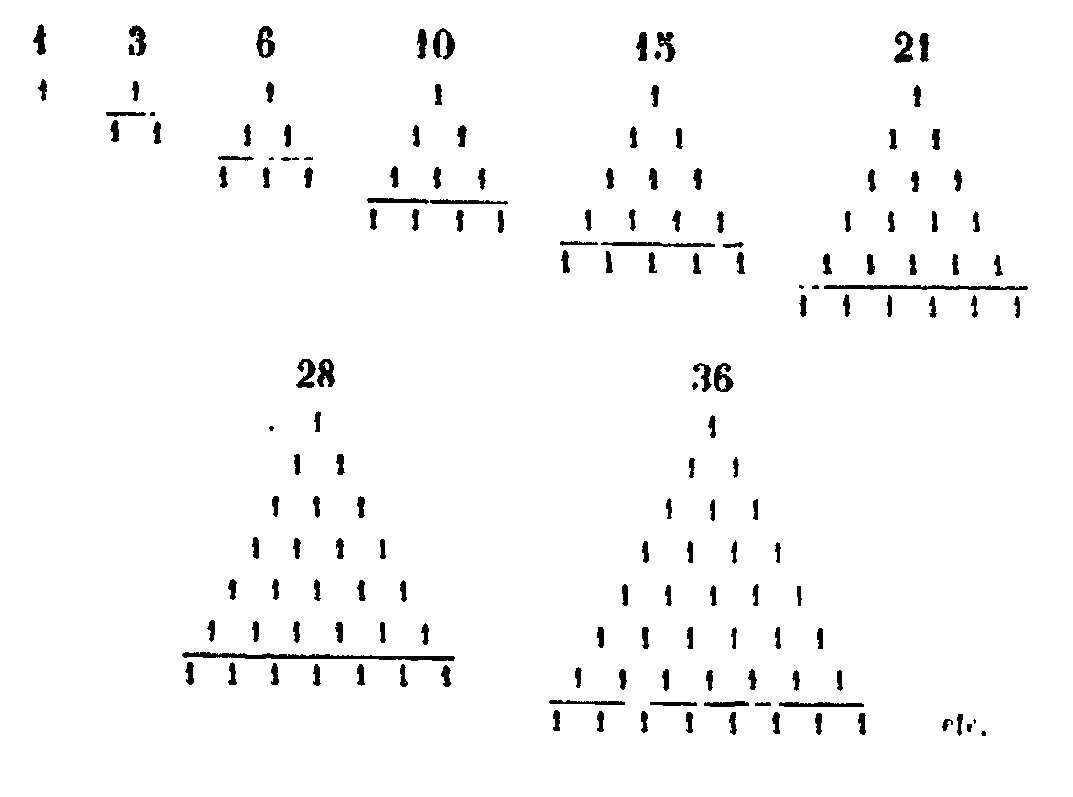
De même, en additionnant non plus seulement les pairs seuls ou les impairs seuls, mais les pairs et les impairs, nous obtiendrons les nombres triangulaires. La suite des pairs et des impairs est 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; c’est en les additionnant que nous formerons les nombres triangulaires. Le premier est l’unité, car si elle n’est pas tel en acte, elle est tout en puissance, étant le principe de tous les nombres. Si on lui ajoute le nombre 2, on a le nombre triangulaire 3. Si à ce nombre on ajoute 3, on obtient 6, et, en ajoutant 4 à celui-ci, on a 10. Si à ce dernier on ajoute 5, la somme est 15. Ajoutez 6, vous aurez 21. Ajoutez 7 à ce dernier, vous a aurez 28 qui, augmenté de 8, deviendra 36. Et celui-ci augmenté de 9 deviendra 45. Ajoutez 10, vous aurez 55. Et ainsi de suite à l’infini. Or, il est évident que ces nombres sont triangulaires, d’après la figure obtenue en ajoutant aux premiers nombres les gnomons successifs.[25] Les nombres triangulaires obtenus par addition seront donc 3, 6, 10, 15, 21, 28, 36, 45, 55…. et ainsi de suite.

XX. Les carrés sont produits, comme nous l’avons dit, par l’addition des impairs successifs, en commençant par l’unité. Ils ont cela de particulier, qu’ils sont alternativement pairs et impairs, tout comme les nombres simples sont alternativement pairs et impairs, c’est ce qu’on peut voir dans la série

1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Si maintenant on dispose les nombres pairs et impairs par ordre, en commençant par l’unité, on verra que les gnomons qui se surpassent de 2 étant additionnés ensemble, forment les carrés, comme nous l’avons montré ci-dessus les impairs en commençant par l’unité, se surpassent en effet de 2 les uns les autres, de même, les nombres qui se surpassent de 3 étant additionnés, toujours en commençant par l’unité, forment les pentagones. Ceux qui se surpassent de donnent les hexagones; en sorte que la raison des gnomons, qui donnent un polygone, est toujours moindre de 2 unités que le nombre des angles de la figure.

Il y a un autre ordre de nombres polygones, donné par les nombres multiples à partir de l’unité. En effet, parmi les nombres multiples à partir de l’unité, comme les doubles, les triples et ainsi de suite, les termes sont carrés de deux en deux, et cubiques de trois en trois. De plus, ceux qui se suivent de 6 en 6 sont à la fois carrés et cubiques; comme cubiques, leurs côtés sont des nombres carrés, et comme carrés, leurs côtés sont des nombres cubiques. Voici comment nous montrons que les nombres multiples, commençant par l’unité, sont carrés de deux en deux, cubiques de trois en trois, et à la fois carrés et cubiques de six en six. Disposons plusieurs nombres en progression double

1, 2, 4, 8, 16, 32, 64, 128, 256.

Le premier double est 2. Vient ensuite 4 qui est carré, puis 8 qui est cubique, puis de nouveau 16 qui est carré. Celui-ci est suivi de 32, après lequel vient 64, tout à la fois carré et cubique. On a ensuite 128 suivi de 256 qui est carré ; et l’on pourrait continuer de même jusqu’à l’infini.

Dans la progression triple on trouvera pareillement les carrés alternes. De même dans la progression quintuple et dans les autres progressions multiples. Si on omet alternativement deux termes, on trouvera que les termes restants sont des cubes; et si on en omet cinq, on trouvera que ceux qui restent sont à la fois carrés et cubiques.[26]

Les carrés ont cette propriété d’être exactement divisibles par 3, ou de le devenir étant diminués d’une unité. Ils sont aussi exactement divisibles par 4, ou le deviennent après la soustraction d’une unité.

Le carré (pair), qui devient divisible par 3 après avoir été diminué d’une unité, est divisible par 4, ce qui est le cas de 4. Le carré, qui devient divisible par 4 après avoir été diminué d’une unité, est divisible par 3, ce qui est le cas de 9.[27] Un carré peut être à la fois divisible par 3 et par 4, comme 36. Enfin, le carré qui n’est divisible ni par 3 ni par 4, comme 25, admet ces deux diviseurs après la soustraction d’une unité.[28]

XXI. Parmi les nombres, les uns également égaux sont carrés, les autres inégalement inégaux sont hétéromèques ou promèques. Et, pour tout dire, les produits de deux facteurs sont plans et ceux de trois facteurs sont solides. On leur donne les noms de nombres plans triangulaires ou carrés, ou de nombres solides, et d’autres noms semblables, non au sens propre. mais par comparaison avec les espaces qu’ils semblent mesurer, Ainsi 4 est appelé nombre carré, parce qu’il mesure un espace carré ; et c’est pour une raison fondée sur une analogie semblable que 6 est appelé hétéromèque.

XXII. Parmi les nombres plans, les carrés sont tous semblables entre eux. Parmi les nombres plans qui ont les côtés inégaux, ceux-là sont semblables, dont les côtés, c’est-à-dire les nombres qui les comprennent, sont entre eux dans le même rapport. Prenons l’hétéromèque 6 dont les côtés, longueur et largeur, sont 3 et 2, et un autre nombre plan 24 dont les côtés, longueur et largeur, sont 6 et 4. La longueur de mn est à la longueur de l’autre comme la largeur de l’un est à la largeur de l’autre, car on a 6 : 3 = 4 : 2. Donc les nombres plans 6 et 24 sont semblables. Tantôt les mêmes nombres représentent des longueurs, quand ils sont pris comme côtés, pour la formation d’autres nombres; tantôt ils représentent des nombres plans, quand on les considère comme produits par la multiplication de deux nombres: tantôt enfin ils représentent des solides, quand ils sont produits par la multiplication de trois nombres.

Tous les cubes sont semblables, ainsi que les autres solides (parallélépipèdes rectangles) qui ont les côtés proportionnels, en sorte qu’il y ait le même rapport entre la longueur de l’un et la longueur de l’autre, la largeur de l’un et la largeur de l’autre, et enfin la hauteur de l’un et la hauteur de l’autre.

XXIII. De tous les nombres plans et polygones, le premier est le nombre triangulaire, comme parmi les figures rectilignes planes la première est le triangle. Nous avons exposé précédemment[29] la génération des triangulaires, et nous avons vu qu’elle consiste à ajouter au nombre 1 la suite naturelle des nombres pairs et des nombres impairs. Or, tous les nombres successifs qui servent à former les triangulaires, les quadrangulaires et les nombres polygones quelconques, sont appelés gnomons; et les côtés d’un triangle quelconque ont toujours autant d’unités qu’on contient le dernier gnomon ajouté. Prenons d’abord l’unité, qui n’est pas un triangle en acte, comme nous l’avons déjà dit, mais en puissance; car étant comme la semence de tous les nombres, l’unité possède aussi la faculté d’engendrer le triangle.

Quand elle s’adjoint le nombre 2, elle donne naissance au triangle dont les trois côtés contiennent autant d’unités qu’en a le gnomon ajouté 2, et tout le triangle contient autant d’unités qu’en contiennent les gnomons ajoutés ensemble. Car la somme du gnomon 1 et du gnomon 2 égale 3, en sorte que tout le triangle se compose de trois unités et qu’il a deux unités à chacun de ses côtés, c’est-à-dire autant d’unité qu’il y a de gnomons ajoutés ensemble.

Le triangle 3 s’adjoint ensuite le gnomon 3, qui surpasse le nombre 2 d’une unité, et le triangle entier devient 6. Ses côtés ont chacun autant d’unités qu’il y a de gnomons ajoutés, et le triangle vaut autant d’unités que les gnomons ajoutés en contiennent, car en ajoutant à l’unité 2 et 3, on a le nombre 6.

Le nombre 6 augmenté du gnomon 4 donne le triangle de 10 unités dont les côtés ont chacun 4 unités. En effet, le gnomon qu’on vient d’ajouter est 4 et tout le triangle se compose des unités des 4 gnomons, savoir 1 + 2 + 3 + 4. Le nombre 10 étant augmenté du gnomon 5 on a le triangle 15 dont 3 chaque côté a 5 unités, étant composé de 5 gnomons, et c’est de la même manière que les gnomons suivants forment les nombres triangulaires correspondants.

XXIV. Quelques nombres sont appelés circulaires, sphériques ou récurrents. Ce sont ceux qui multipliés carrément ou cubiquement, c’est-à-dire selon deux ou selon trois dimensions, reviennent au nombre qui a été leur point de départ. Tel est aussi le cercle qui revient au point où il a commencé, car il consiste en une seule ligne et il commence et se termine au même point. Parmi les solides, la sphère a la même propriété, car elle est décrite par la révolution d’un cercle autour d’un diamètre, le cercle revenant la position d’où il est parti. De même les nombres qui par la multiplication finissent par eux-mêmes, sont appelés circulaires ou sphériques. Ces nombres sont 5 et 6. En effet 5 x 5 = 25 ; 25 x 5 =125; 6 x 6 = 36; et 36 x 6 = 216.

XXV. Ainsi que nous l’avons dit,[30] les nombres carrés s’engendrent par l’addition des impairs, c’est-à-dire de ceux qui, en partant de l’unité, se surpassent de 2 les uns les autres. C’est ainsi que 1+3=4; 4+5=9; 9+7=16; 16+9=25.

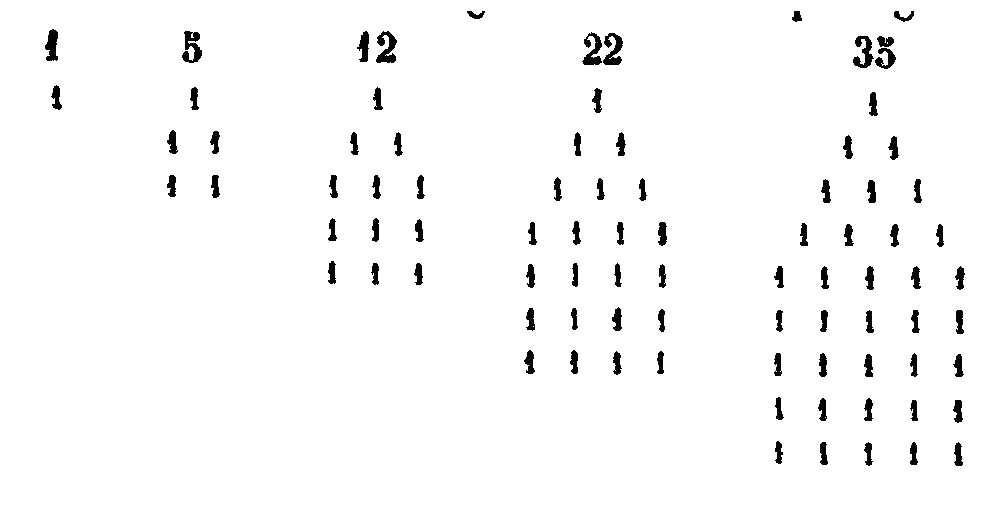
XXVI. — Les nombres pentagones sont ceux qui se forment par l’addition des nombres se surpassant de 3 les uns les autres, à partir de l’unité. Leurs gnomons sont donc 1, 4, 7, 10, 13, 16, 19 …………. et les polygones eux-mêmes sont 1, 5, 12, 22, 35, 51, 70 ………. et ainsi de suite. Voici la figure des nombres pentagones:

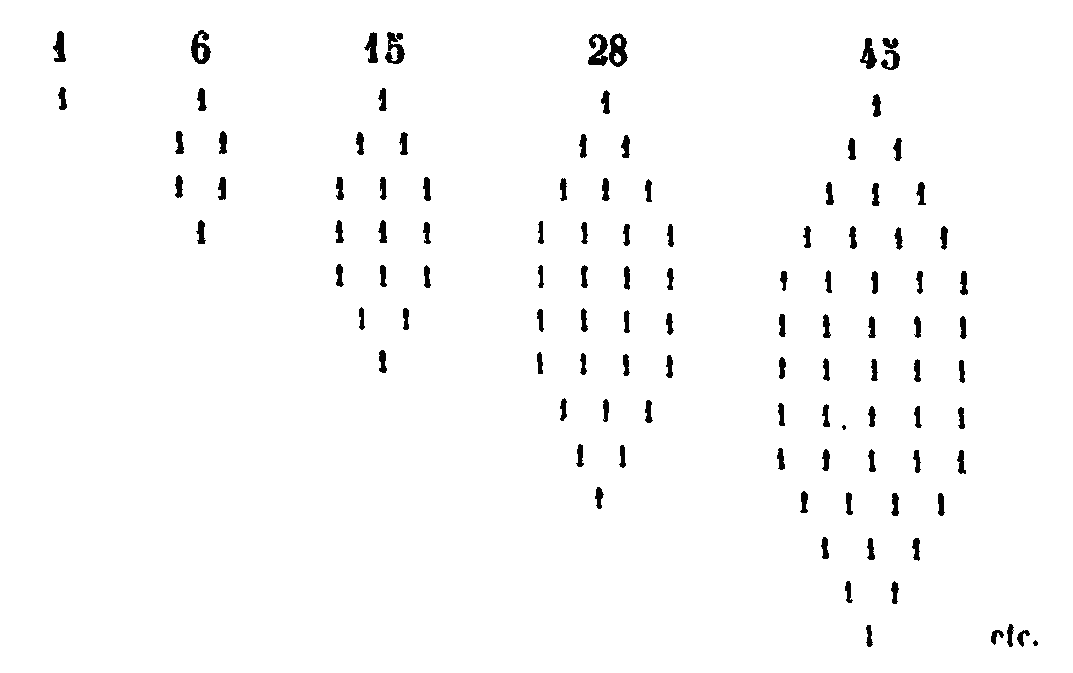
XXVII. Les nombres hexagones sont ceux qui se forment par l’addition de nombres se surpassant de 4 les uns les autres, à partir de l’unité. Les gnomons sont 1, 5, 9, 13, 17, 21, 25 … d’où résultent les hexagones 1, 6, 15, 28, 45, 66, 91 …………

Voici leur figure:

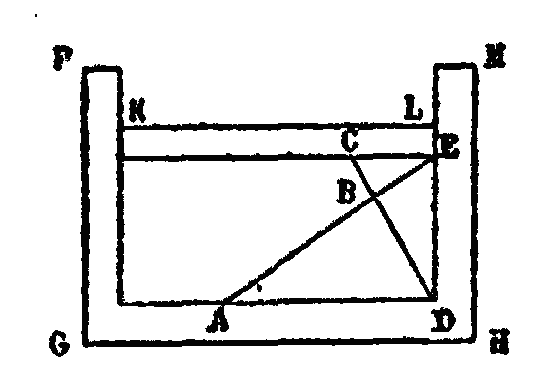
Les autres nombres polygones se composent de la même manière. Les heptagones sont ceux qui se forment par l’addition de nombres se surpassant les uns les autres de 5, à partir de l’unité. Les gnomons sont 1, 6, 11, 16, 21, 26 ……… d’où résultent les heptagones 1, 7, 18, 34, 55, 81………

Les octogones sont pareillement composés de nombres qui se surpassent de 6 partir de l’unité, les ennéagone, de nombres se surpassant de 7, à partir de l’unité, les décagones de nombres se surpassant de 8. Ainsi généralement, dans tous les polygones, en ôtant deux unités du nombre des angles, on aura la quantité dont les nombres servant à former le polygone doivent se surpasser les uns les autres.[31]

XXVIII. La somme de deux triangles successifs donne un carré. Ainsi, 1 et 3 font 4 ; 3 et 6 font 9 ; 6 et 10 font 16; 10 et 15 font 25 ; 15 et 21 font 36; 21 et 28 font 49; 28 et 36 font 64; 36 et 45 font 81. Les nombres triangulaires qui suivent, combinés ensemble, forment aussi des carrés, de même que la réunion de deux triangles linéraires présente la figure d’un quadrangle.[32]

XXIX. Parmi les nombres solides, les uns ont leurs cotés égaux [comme quand on multiplie entre eux trois nombres égaux] les autres ont les côtés inégaux. Parmi ces derniers, les uns ont tous les côtés inégaux; d’autres ont deux côtés égaux et un autre inégal. Parmi ceux qui ont deux côtés égaux, les uns ont le troisième côté plus grand, les autres l’ont plus petit.

Ceux qui ont les côtés égaux étant également égaux également, sont appelés cubes. Ceux au contraire qui ont tous les côtés inégaux, et qui sont inégalement inégaux inégalement, sont appelés bomisques (petits autels). Ceux qui ont deux côtés égaux et le troisième plus petit que les deux autres, étant également égaux déficients, ont été appelés plinthes ou carreaux. Enfin, ceux qui ont deux côtés égaux et le troisième plus grand que les deux autres, étant également égaux excédants, sont appelés docides ou poutrelles.

Des nombres pyramidaux.

XXX. Les nombres pyramidaux sont ceux qui mesurent les pyramides et les pyramides tronquées. Or, une pyramide tronquée est (ce qui reste d’)une pyramide dont la partie supérieure a été enlevée. Quelques-uns ont donné à une telle figure tronquée le nom de trapèze (solide), par analogie avec les trapèzes plans; car on appelle ainsi ce qui reste d’un triangle dont une ligne droite parallèle à la base a retranché la partie supérieure.[33]

Des nombres latéraux et des nombres diagonaux

XXXI. De même que les nombres ont en puissance les rapports des triangulaires, des tétragones, des pentagones et des autres figures, de même nous trouverons que les rapports des nombres latéraux et des nombres diagonaux se manifestent dans les nombres selon des raisons génératrices, car ce sont les nombres qui harmonisent les figures. Donc comme l’unité est le principe de toutes les figures, selon la raison suprême et génératrice, de même aussi le rapport de la diagonale et du côté se trouve dans l’unité.

Supposons par exemple deux unités dont l’une soit la diagonale et l’autre le côté, car il faut que l’unité qui est le principe de tout soit en puissance le côté et la diagonale; ajoutons au côté la diagonale et à la diagonale ajoutons deux côtés, car ce que le côté peut deux fois, la diagonale le peut une fois.[34] Dès lors la diagonale est devenue plus grande et le côté plus petit. Or, pour le premier côté et la première diagonale, le carré de la diagonale unité sera moindre d’une unité que le double carré du côté unité, car les unités sont en égalité, mais un est moindre d’une unité que le double de l’unité. Ajoutons maintenant la diagonale au côté, c’est- à-dire une unité à l’unité, le côté vaudra alors 2 unités; mais, si nous ajoutons deux côtés à la diagonale, c’est-à-dire 2 unités à l’unité, la diagonale vaudra 3 unités; le carré construit sur le côté 2 et 4, et le carré de la diagonale est 9 qui est plus grand d’une unité que le double carré de 2.

De même ajoutons au côté 2 la diagonale 3, le côté deviendra 5. Si à la diagonale 3 nous ajoutons deux côtés, c’est-à-dire 2 fois 2, nous aurons 7 unités. Le carré construit sur le côté est 2, et celui qui est construit sur la diagonale 7 est 49, qui est moindre d’une unité que le double 50 du carré 25. De nouveau, si au côté 5 on ajoute la diagonale 7, on obtient 12 unités; et si à la diagonale 7 on ajoute 2 fois le côté 5, on aura 17 dont le carré 289) est plus grand d’une unité que le double (288) du carré de 12. Et ainsi de suite en continuant l’addition. La proportion alterne : le carré construit sur la diagonale sera tantôt plus petit, tantôt plus grand, d’une unité, que le double carré construit sur le côté, en sorte que ces diagonales et ces côtés seront toujours exprimables.

Inversement les diagonales comparées aux côtés, en puissance, sont tantôt plus grandes d’une unité que les doubles, tantôt plus petites d’une unité. Toutes les diagonales sont donc, par rapport aux carrés des côtés, doubles alternativement par excès et par défaut, la même unité combinée également avec tous, rétablissant l’égalité, en sorte que le double ne pèche ni par excès, ni par défaut; en effet, ce qui manque dans la diagonale précédente se trouve en excès, en puissance, dans la diagonale qui suit.[35]

Les nombres parfaits, des nombres abondants et des nombres déficients

XXII. En outre, parmi les nombres, les uns sont appelés parfaits, d’autres abondants et d’autres déficients. On appelle parfaits ceux qui sont égaux à la somme de leurs parties aliquotes, comme 6. Les parties de 6 sont, en effet, la moitié 3, le tiers 2, et le sixième 1, qui additionnées ensemble donnent 6.

Voici comment sont engendrés les nombres parfaits : si nous disposons les nombres en progression double à partir de l’unité, et que nous les additionnions jusqu’à ce que nous obtenions un nombre premier et non composé, et si nous multiplions cette somme par le dernier terme additionné, le produit sera au nombre parfait.[36] Disposons donc les nombres en progression double 1, 2, 4, 8, 16. Additionnons 1 et 2, la somme est 3; si nous la multiplions par le dernier nombre additionné qui est 2, nous aurons 6 qui est le premier nombre parfait car 1 + 2 + 3 = 6. Si nous additionnons maintenant les trois doubles successifs 1, 2, 4, la somme 7, multipliée par le dernier nombre additionné 4 donne 28, qui est le second nombre parfait. Il a en effet pour parties aliquotes la moitié qui est 14, le quart qui est 7, le septième qui est 4, le quatorzième qui est 2, et le vingt-huitième qui est 1 et l’on a 1+2+4+7+14=28).

Le nombre abondant est le nombre dont les parties aliquotes additionnées ensemble font une somme plus grande que le nombre proposé, Tel est 12, dont la moitié est 6, le tiers 4, le quart 3, le sixième 2 et le douzième 1. Or, toutes ces parties additionnées ensemble donnent la somme 16 plus grande que le nombre proposé 12.

Le nombre déficient est le nombre dont les parties aliquotes additionnées ensemble donnent une somme moindre que le nombre proposé. Tel est 8 dont la moitié est 4, le quart 2 et le huitième 1. Il en est de même du nombre 10 que les Pythagoriciens appellent cependant parfait pour une autre raison dont nous parlerons en son lieu.[37]

On dit aussi que le nombre 3 est parfait, parce qu’il est le premier qui ait un commencement, un milieu et une fin: et il est à la fois ligne et surface, c’est, en effet, un nombre triangulaire équilatéral dont tous les côtés valent deux unités. Enfin le nombre 3 est le premier lien et la puissance du 15 solide, car l’idée de solide repose sur les trois dimensions.

NOTES

NOTE I. — Problème de la duplication du cube. Solution mécanique de Platon (Introduction)

Le problème de la duplication de l’autel, avec la condition que le nouvel autel soit semblable au premier, se ramène à la duplication du cube d’une arête. Hippocrate de Chio trouva que si l’on insère deux moyennes proportionnelles continues x et y entre le côté a d’un cube et le double 2a de ce côté, la première moyenne x est le côté du cube double. On a en effet, par définition

a/x = x/y = y/2a        d’où a³/x³= axy/2axy = ½  et x³=2a³

Platon a résolu le premier le problème des deux moyennes proportionnelles. Il y employa un instrument formé de deux règles XL, GH, dont l’une mobile parallèlement à l’autre fixe, glissait entre les rainures de deux montants FG, MH, fixés perpendiculairement à celle-ci.

Les géomètres anciens ne pouvaient pas disposer des ressources de l’algèbre qu’ils ne connaissaient pas; mais les proportions, qu’ils maniaient avec une très grande habileté, quoiqu’ils n’eussent aucune notation particulière, leur fournissaient des procédés de calcul très simples et très ingénieux. En combinant les proportions par voie de multiplication, de division.., et en simplifiant les rapports de la proportion finale, ils parvenaient à ne conserver qu’une inconnue dans des questions qui en comportaient plusieurs.

Soient a et b les deux droites entre lesquelles on veut insérer deux moyennes proportionnelles, On trace deux droites perpendiculaires AE, CD, sur lesquelles on prend, à partir de leur point de concours. AB=a et BC=b. Puis on applique l’instrument sur la figure de manière que le bord d’une règle passe par le point A. et le bord de l’autre par le point C. On écarte alors, plus ou moins, la règle mobile de la règle fixe, et en même temps on fait tourner l’instrument dans le plan de la figure, jusqu’à ce que les bords des deux règles passant toujours par les points A et C, les prolongements des droites AB et BC passent en même temps par les sommets du rectangle que forme l’instrument.

Les deux triangles ADE, CDE étant rectangles, la hauteur de chacun d’eux est moyenne proportionnelle entre les segments de l’hypoténuse, et l’on a:

AB/BD = BD/BE = BE/BC

Ainsi BD et BE sont deux moyennes proportionnelles entre AB et BC, c’est-à-dire entre a et b.

Cette solution de Platon est mécanique, puisqu’elle exige l’usage d’un instrument, autre que la règle et le compas. Elle nous a été transmise par Eutocios d’Ascalon, géomètre du vi^e siècle dans un commentaire sur le livre II du traité De la sphère et du cylindre par Archimède

NOTE II. — Sur le sophisme: Un, en tant qu’un, est sans parties et indivisible. I, § iii.

Problème d’Achille et de la tortue.

Le raisonnement de Théon est un sophisme. J’ai un objet sensible, dit-il, je le divise en plusieurs parties que je supprime successivement une à une, il viendra un moment ou il ne restera plus qu’un objet sensible. Je divise de nouveau cet un sensible en plusieurs parties que je supprime de même une à une, jusqu’à ce qu’il ne reste plus qu’un objet. En opérant ainsi, j’arrive toujours à un, donc un, en tant qu’un, est sans parties et indivisible:

L’un des plus célèbres sophismes est de Zénon d’Elée, qui vivait au v^e siècle avant notre ère, on le nomme l’Achille. En voici l’énoncé : Achille va dix fois plus vite qu’une tortue qui a un stade d’avance, on demande s’il l’atteindra et à quelle distance.[38]

Zénon prétendait qu’Achille n’atteindrait jamais la tortue, car, disait-il, pendant qu’Achille parcourra la stade qui le sépare de la tortue, celle-ci avancera de 0,1 de stade; pendant qu’Achille parcourra ce dixième, la tortue qui va dix fois moins vite, avancera de 0,01 de stade; pendant qu’Achille parcourra ce centième, la tortue avancera de 0,001 : et ainsi de suite. Donc il s’écoulera un nombre infini d’instants avant la rencontre, et Achille n’atteindra jamais la tortue.

Cela revient à affirmer, dit Aristote, « que jamais le plus lent, quand il est en marche, ne pourra être atteint par le plus rapide, attendu que le poursuivant doit, de toute nécessité, passer d’abord par le point d’où est parti celui qui fuit sa poursuite, et qu’ainsi le plus lent conservera constamment une certaine avance. Leçons de physique, VI, ix, t. II, p. 396 de la trad. de B. Saint-Hilaire.

L’erreur de Zénon est manifeste, car Achille atteint la tortue à une distance de son point de départ, égale à 1 stade et 1/9^e  ou 10/9^e  de stade. En effet, pendant qu’il parcourt ces 10/9^e  de stade, la tortue, qui va dix fois moins vite, en parcourt 1/9^e ; or l’espace parcouru par Achille est alors égal à l’espace parcouru dans le même temps que la tortue, plus à l’espace qui les séparait, donc il y a rencontre.

Zénon ne voit pas que la somme des espaces parcourus pendant le nombre infini des instants successifs du mouvement d’Achille et de la tortue représente une distance finie, et que, dans le cas du mouvement uniforme, le nombre infini de ces instants successifs représente un temps fini. 

NOTE III. — Sur les nombres hétéromèques I, § xvi.

Soient (n — 1) n = n² — n et n (n+ 1) = n² + n deux hétéromèques successifs. Le carré compris entre n² — n et n² + n est n². Or n² est la moyenne arithmétique entre n² — n et n² + n, et la moyenne arithmétique entre deux nombres est plus grande que leur moyenne géométrique; donc, comme Théon le vérifie, le carré compris entre deux hétéromèques successifs n’est pas la moyenne géométrique entre ces deux nombres. Mais la moyenne géométrique entre deux carrés successifs est un hétéromèque; soit, en effet x la moyenne géométrique entre deux carrés successifs n² et (n+1)², on a x² = n² (n +1)², d’où x = n (n+1), nombre hétéromèque. puisque les deux facteurs diffèrent d’une unité.

NOTE IV. — Sur les nombres carrés (I, § xx).

Tout nombre étant un multiple de 6 ou un multiple de 6, plus 1, plus 2, plus 3, plus 4 ou plus 5, est de la forme 6n, 6n ± 1, 6n ± 2, ou 6n ± 3. Donc tout carré est de la forme 36n²,  36n² ± 12n + 1, 36n² ± 24n +4 ou 36n² + 36n + 9.

1° S’il est de la forme 36n² ± 24n + 4, il est divisible par 4, et non par 3, mais la soustraction d’une unité donne le reste 36n² ± 24n + 3 qui est divisible par 3;

2° S’il est de la forme 36n² + 36n + 9, il est divisible par 3, et non par 4, mais la soustraction d’une unité donne le reste 36n² + 36n + 8 qui est divisible par 4;

3° S’il est de la forme 36n², il est à la fois divisible par 3 et par 4, et par conséquent 36n²— 1 ne l’est pas;

4° Enfin, s’il est de la forme 36n² ± 12n + 1, il n’est divisible ni par 3 ni par 4, mais la soustraction d’une unité donne le reste 36n² ± 12n qui est à la fois divisible par 3 et par 4.

NOTE V. — Des nombres polygonaux (I, §§ xix-xxvii).

Nous allons résumer cette théorie des nombres polygones en y ajoutant quelques explications. Soit d la raison d’une progression par différence commençant par l’unité, les premiers termes seront :

1, 1+d, 1+2d, 1+3d, 1 +4d, 1+5d, 1+6d, 1+7d...

Si on fait les sommes successives des termes, à partir de l’unité, on obtient les nombres correspondants :

1, 2 +2d, 3+3d, 4+6d, 5+10d, 6+15d, 7+24d, 8+28d... Les termes de la seconde suite se nomment des nombres polygones, et ceux de la première en sont les gnomons. Si on donne à d, dans les deux suites, les valeurs successives 1, 2, 3, 4, 5, 6,... on obtient les gnomons et les nombres polygones suivants:

En désignant par k le n-ième gnomon et par l  le n-ième nombre polygone, on a k = 1 + (n — 1)d

et l =1+(1+d)+(1+2d)+(1+3d)+(1+4d+(1+5d) + …..+ (1 + (n—1)d) = n +d(1+2+3+4+5…..+ n—1)

d’où l = n + dn(n-1)/2                        [A]

Or n(n — 1)/2, est la somme des (n — 1) premiers nombres à partir de l’unité, est le (n—1)ième nombre triangulaire, on a donc ces deux théorèmes:

1° Le n-ième nombre polygone égale n, plus d fois le (n — 1)ième nombre triangulaire, d étant la raison de la progression des gnomons;

2° Les nombres polygones, de même rang n, forment une progression par différence, dont le premier terme est n, et dont la raison est le (n — 1)ième nombre triangulaire.

Les nombres triangulaires sont ainsi nommés, parce que, si on dispose les uns au-dessous des autres les gnomons à ajouter et décomposés en unités, on a des figures triangulaires.

Les nombres carrés sont ainsi nommés, parce qu’on peut donner la forme carrée aux groupes d’unités dont ces nombres se composent.

On peut aussi obtenir la figure des nombres carrés par la formule l = n + dn(n — 1)/2 qui, pour d=2, devient l = n + n(n — 1).

On écrira sur une ligne les n unités du nombre n, puis on placera, de part et d’autre de cette ligne, les unités dont se compose le (n — 1)ième nombre triangulaire; on obtiendra les figures quadrangulaires suivantes, en remplaçant les unités par des points:

Les nombres pentagones sont donnés par la formule l = n + 3n(n — 1)/2. On obtiendra donc leur représentation en ajoutant à n, trois fois le (n — 1)ième nombre triangulaire; ils peuvent donc être figurés de la manière suivante:

On aura les nombres hexagonaux en ajoutant à n, quatre fois le (n — 1)ième nombre triangulaire; on peut donc leur donner cette forme:

On peut remarquer que la suite naturelle des nombres hexagonaux est égale à la suite des nombres triangulaires de rang impair. On démontre, en effet, que le n-ième nombre hexagone est égal au (2n — 1)ième nombre triangulaire; car, d’après la formule générale [A], donnée plus haut, chacun d’eux égale n(2n — 1).

Une autre remarque à faire, c’est que les nombres parfaits, c’est- à-dire égaux à la somme de leurs parties aliquotes, sont tous hexagones et par conséquent triangulaires.

En effet le n-ième hexagone l = n(2n — 1). Supposons n = 2^k on aura l = 2^k (2^k+1 — 1). C’est la formule qui donne les nombres parfaits quand le facteur 2^k+1 — 1 est premier; donc les nombres parfaits sont hexagones et par conséquent triangulaires. Ainsi

et ainsi des autres.

NOTE VI. — Des nombres pyramidaux (I, xxx).

Le n-ième nombre pyramidal, à base triangulaire, est la somme des n premiers nombres triangulaires. On démontre qu’il est égal à n(n+1)(n+2)/(1 x 2 x 3)

De même, le n-ième nombre pyramidal, à base carrée, est la somme des n premiers nombres carrés. On démontre qu’il est égal à n(n+1)(2n+1)/(1 x 2 x 3)

Le nombre pyramidal tronqué s’obtient en évaluant la pyramide totale et celle qui en a été enlevée, on prend la différence des deux valeurs. Soit une pyramide triangulaire tronquée dont le côté de la base inférieure vaut s et celui de La base supérieure p, le nombre pyramidal tronqué vaudra

[n (n+1)(n+2) — (p-1) p (p+1)] /(1 x 2 x 3)

NOTE VII. — Des nombres latéraux et des nombres diagonaux (I, § xxxi)

Les nombres latéraux et les nombres diagonaux sont définis par leur génération. Théon explique ainsi: il prend d’abord le côté 1 et la diagonale 1, puis il détermine successivement les autres côtés, en ajoutant au côté précédent la diagonale, et il détermine les autres nombres diagonaux en ajoutant à la diagonale précédente deux fois le côté correspondant. On obtient, d’après cette règle, le tableau suivant, complété par l’addition du double carré des côtés, et du carré des nombres diagonaux :

Cette règle de Théon donne, en nombres entiers, la résolution du triangle rectangle isocèle, avec cette condition que la différence entre le carré de l’hypoténuse et le double carré du côté de l’angle droit ne soit que d’une unité, c’est-à-dire qu’elle donne, en nombres entiers, les solutions de l’équation y² — 2x² = ± 1. Supposons que y = a et x = b soient une solution de l’équation, c’est-à-dire qu’on ait a² — 2b² = ± 1, je dis que x = b + a et y = a + 2b en sont aussi une solution. On déduit, en effet, de ces deux dernières relations y² — 2x²  = 2b² — a². Or a² — 2b² = ± 1 par hypothèse, donc y² — 2x² = ± 1. Mais y = x = 1 est une première solution de l’équation y² — 2x² = — 1, on en conclura donc une infinité d’autres solutions, d’après la règle donnée par Théon.

NOTE VIII. — De la perfection du nombre dix (I, § xxxii).

Le nombre 10=1 +2 + 3 + 4; or I était le principe des nombres; 2 représentait la première ligne (la ligne droite qui est définie par deux de ses points); 3 représentait la première surface (le triangle défini par ses trois sommets); et 4 représentait le premier solide (le tétraèdre défini par ses quatre sommets). Donc la décade 1 + 2 + 3+ 4 symbolisait tout ce qui existe.