L'ARENAIRE.
Il
est des personnes, ô roi Gélon, qui pensent que le nombre des grains de sable
est infini. Je ne parle point du sable qui est autour de Syracuse et qui est
répandu dans le reste de la Sicile, mais bien de celui qui se trouve non
seulement dans les régions habitées, mais encore dans les régions inhabitées.
Quelques-uns croient que le nombre des grains de sable n'est pas infini, mais
qu'il est impossible d'assigner un nombre plus grand. Si ceux qui pensent ainsi
se représentaient un volume de sable qui fût égal à celui de la terre, qui
remplît toutes ses cavités, et les abîmes delà mer, et qui s'élevât jusqu'aux
sommets des plus hautes montagnes, il est évident qu'ils seraient bien moins
persuadés qu'il pût exister un nombre qui surpassât celui des grains de sable.
Quant à moi, je vais faire voir par
des démonstrations géométriques auxquelles tu ne pourras refuser ton
assentiment, que parmi les nombres dénommés par nous dans les livres adressés à
Zeuxippe, il en est qui excèdent le nombre des grains d'un volume de sable égal
non seulement à la grandeur de la terre, mais encore à celui de l'univers
entier.
Tu sais que le monde est appelé par la
plupart des astronomes une sphère dont le centre est le même que celui de la
terre et dont le rayon est égal à la droite placée entre le centre de la terre
et celui du soleil. Aristarque de Samos rapporte ces choses en les réfutant,
dans les propositions qu'il a publiées contre les astronomes. D'après ce qui est
dit par Aristarque de Samos, le monde serait beaucoup plus grand que nous
venons de le dire; car il
suppose que les étoiles et le soleil sont immobiles ; que la terre tourne autour
du soleil comme centre; et que la grandeur de la sphère des étoiles fixes dont
le centre est celui du soleil, est telle que la circonférence du cercle qu'il
suppose décrite par la terre est à la distance des étoiles fixes comme le centre
de la sphère est à la surface. Mais il est évident que cela ne saurait être,
parce que le centre de la sphère n'ayant aucune grandeur, il s'ensuit qu'il ne
peut avoir aucun rapport avec la surface de la sphère. Mais à cause que l'on
conçoit la terre comme étant le centre du monde, il faut penser qu'Aristarque a
voulu dire que la terre est à la sphère que nous appelons le monde, comme la
sphère dans laquelle est le cercle qu'il suppose décrit par la terre est à la
sphère des étoiles fixes; car il établit ses démonstrations, en supposant que
les phénomènes se passent ainsi ; et il paraît qu'il suppose que la grandeur de
la sphère dans laquelle il veut que la terre se meuve est égale à la sphère que
nous appelons le monde (α).
Nous disons donc que si l'on avait une
sphère de sable aussi grande que la sphère des étoiles fixes supposée par
Aristarque, on pourrait démontrer que parmi les nombres dénommés dans le
Livre des Principes, il y en aurait qui surpasseraient le nombre de grains
de sable contenus dans cette sphère.
Cela posé, que le contour de la terre
soit à peu près de trois cent myriades de stades (β), mais non plus grand. Car
tu n'ignores point que d'autres ont voulu démontrer que le contour de la terre
est à peu près de trente myriades de stades. Pour moi, allant beaucoup plus
loin, je le suppose dix fois aussi grand, c'est-à-dire que je le suppose à peu
près de trois cent myriades de stades, mais non plus grand. Je suppose ensuite,
d'après la plupart des astronomes dont nous venons de parler, que le
diamètre de la terre est plus grand que celui
de la lune, et que celui du soleil est plus grand que
celui de la terre ; je suppose enfin que le diamètre du soleil est environ
trente fois aussi grand que le diamètre de la lune, mais non plus grand. Car
parmi les astronomes dont nous venons de parler, Eudoxe a affirmé que le
diamètre du soleil était environ neuf fois aussi grand que celui de la lune;
Phidias, fils d'Acupatre, a dit qu'il était environ douze fois aussi grand ; et
enfin Aristarque s'est efforcé de démontrer que le diamètre du soleil était plus
grand que dix-huit fois le diamètre de la lune et plus petit que vingt fois.
Pour moi, allant encore plus loin, afin de démontrer sans réplique ce que je me
suis proposé, je suppose que le diamètre du soleil est à peu près égal à trente
fois le diamètre de la lune, mais non plus grand. Je suppose, outre cela, que le
diamètre du soleil est plus grand que le côté d'un polygone de mille côtés
inscrit dans un grand cercle de la sphère dans laquelle il se meut : je fais
cette supposition, parce qu'Aristarque affirme que le soleil paraît être la sept
cent vingtième partie du cercle qu'on appelle le Zodiaque.
J'ai fait tous mes efforts pour
prendre, avec des instruments, l'angle qui comprend le soleil et qui a son
sommet à l'œil de l'observateur. Cet angle n'est pas facile à prendre, parce
qu'avec l'œil, les mains et les instruments dont on se sert pour cela, on ne
peut pas le mesurer d'une manière bien exacte. Mais il est inutile de parler
davantage de l'imperfection de ces instruments, parce que cela a déjà été fait
plusieurs fois. Au reste, il me suffit, pour démontrer ce que je me suis
proposé, de prendre un angle qui ne soit pas plus grand que celui qui comprend
le soleil et qui a son sommet à l'œil de l'observateur; et ensuite un autre
angle qui ne soit pas plus petit que celui qui comprend le soleil et qui a aussi
son sommet à l'œil de l'observateur.
C'est pourquoi ayant placé une longue
règle sur une surface plane élevée dans un endroit d'où l'on pût voir le soleil
levant; aussitôt après le lever du soleil, je posai perpendiculairement sur
cette règle un petit cylindre. Le soleil étant sur l'horizon et pouvant être
regardé en face (γ), je dirigeai la règle vers le soleil, l'œil étant à
une de ses extrémités, et le cylindre étant placé entre le soleil et l'œil de
manière qu'il cachât entièrement le soleil. J'éloignai le cylindre de l'œil
jusqu'à ce que le soleil commençât à être aperçu le moins possible de part et
d'autre du cylindre, et alors j'arrêtai le cylindre. Si l'œil apercevait le
soleil d'un seul point, et si l'on conduisait de l'extrémité de la règle où
l'œil est placé des droites qui fussent tangentes au cylindre, il est évident
que l'angle compris par ces droites serait plus petit que l'angle qui aurait son
sommet à l'œil et qui embrasserait le soleil ; parce qu'on apercevrait quelque
chose du soleil de part et d'autre du cylindre. Mais à cause que l'œil
n'aperçoit pas les objets par un seul point ; et que la partie de l'œil qui voit
à une certaine grandeur (δ), je pris un cylindre dont le diamètre ne fût pas
plus petit que la largeur de la, partie de l'œil qui voit ; je posai ce cylindre
à l'extrémité de la règle où l'œil était placé, et je conduisis ensuite deux
droites tangentes aux deux cylindres. Il est évident que l'angle compris par ces
tangentes dut se trouver plus petit que l'angle qui embrassait le soleil et qui
avait son sommet à l'œil.
On trouve un cylindre dont le diamètre
ne soit pas plus petit que la largeur de la partie de l'œil qui voit de la
manière suivante : on prend deux cylindres d'un petit diamètre, mais d'un
diamètre égal, dont l'un soit blanc et dont l'autre ne le soit pas ; on les
place devant l'œil, de manière que le cylindre blanc soit le plus éloigné et que
l'autre soit le plus près
possible et touche le visage. Si les diamètres des cylindres sont plus petits
que la largeur de la partie de l'œil qui voit, il est évident que cette partie
de l'œil aperçoit, en embrassant le cylindre qui est près du visage, l'autre
cylindre qui est blanc ; elle le découvre tout entier, si les diamètres des
cylindres sont beaucoup plus petits que la largeur de la partie de l'œil qui
voit ; sinon, elle n'en découvre que quelques parties placées de part et d'autre
de celui qui est près de l'œil. Je disposai donc de cette manière deux cylindres
dont l'épaisseur était telle que l'un cachait l'autre par son épaisseur sans
cacher un endroit plus grand. Il est évident qu'une grandeur égale à l'épaisseur
de ces cylindres n'est pas, en quelque façon, plus petit que la largeur de la
partie de l'œil qui voit.
Pour prendre un angle qui ne fut pas
plus petit que l'angle, qui embrasse le soleil et qui a son sommet à l'œil, je
me conduisis de la manière suivante : Après avoir éloigné de l'œil le cylindre
jusqu'à ce qu'il cachât le soleil tout entier, je menai de l'extrémité de la
règle où l'œil était placé des droites tangentes au cylindre. Il est évident que
l'angle compris par ces droites dut se trouver plus grand que celui qui embrasse
le soleil et qui a son sommet à l'œil.
Ces angles ayant été pris de cette
manière, et les ayant comparés avec un angle droit, le plus grand de ces angles,
qui avait son sommet au point marqué sur la règle, se trouva plus petit que la
cent soixante-quatrième partie d'un angle droit et le plus petit se trouva plus
grand que la deux centième partie de ce même angle. Il est donc évident que
l'angle qui embrasse le soleil et qui a son sommet à l'œil est plus petit que la
cent soixante-quatrième partie d'un angle droit et plus grand que la deux
centième partie de ce même angle.
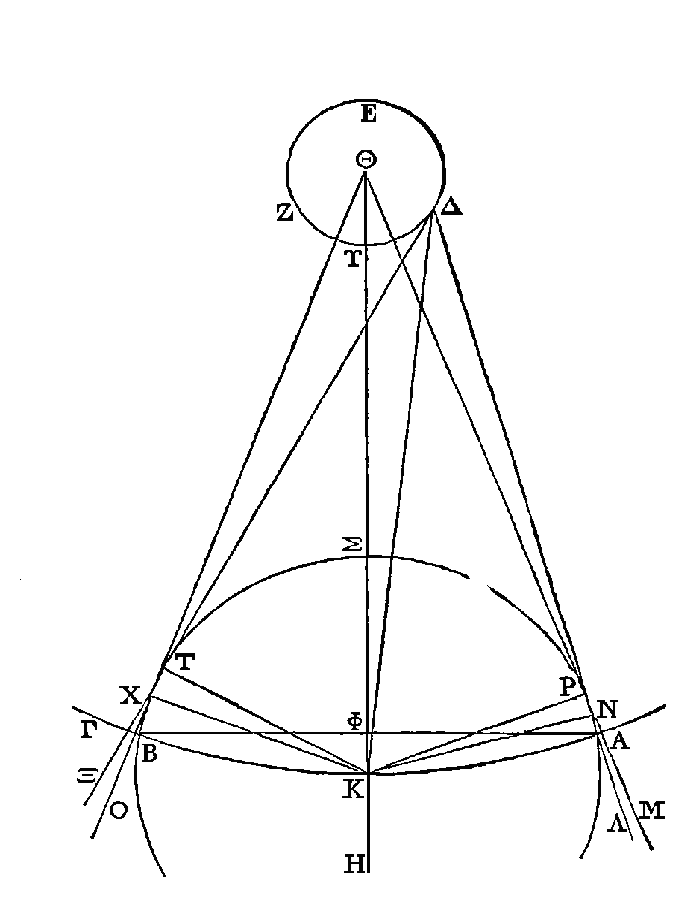
Cela étant ainsi, on démontre que le
diamètre du soleil est
plus grand que le côté d'un polygone de mille côtés inscrit dans un grand cercle
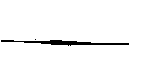
de la sphère du monde. En effet, supposons un plan conduit par le centre de la
terre, par le centre du soleil et par l'œil de l'observateur, le soleil étant
peu élevé au-dessus de
l'horizon. Ce plan coupera la sphère du monde suivant le cercle
ABΓ,
la terre suivant le cercle
AEZ,
et
le soleil suivant le cercle ΣH. Que le point Θ soit le centre de la terre, le
point
K
le
centre du soleil, et le point Δ l'œil de l'observateur. Conduisons des droites
tangentes au cercle ΣH; savoir, du point Δ les droites ΔA, ΔΞ tangentes aux
points N et T, et du point Θ les droites
ΘM,
ΘO tangentes aux points Ρ et Χ. Θue ces droites ΘM, ΘO coupent la circonférence
du cercle ABΓ aux points A,
B.
La droite ΘK sera plus
grande que la droite
ΔK,
parce que l'on suppose le soleil au-dessus de
l'horizon (ε).
Donc l'angle compris par les droites
ΔΛ,
ΔΞ est
plus grand que l'angle compris
par les droites
ΘM, ΘO
(ζ). Mais
l'angle compris par les droites
ΔΛ,
ΔΞ est plus grand que la
200e partie d'un angle droit et plus petit
que la 164e partie de
ce même angle ; parce que cet angle est égal à l'angle qui
embrasse le soleil et qui a son sommet à l'œil. Donc l'angle compris par les
droites ΘM, ΘO est plus
petit que la 164e partie d'un angle droit. Donc la droite
AB
est plus petite que la
corde de la 656e partie de la circonférence du cercle
ABΓ.
Mais la raison du contour du polygone
dont nous venons de parler au rayon du cercle ABΓ est moindre que la raison de
44 à 7 ; parce que la raison du contour d'un polygone quelconque inscrit dans un
cercle au rayon de ce cercle est plus petite que la raison de 44 à 7. Car tu
n'ignores pas que nous avons démontré que le contour d'un cercle quelconque est
plus grand que le triple du diamètre, augmenté d'une certaine partie qui est
plus petite que le 7e de son diamètre, et plus grande que les 10/71e
(de la Mesure du Cercle, prop. 3). Donc la raison de BA à
ΘK est moindre que la raison de 11 à 1148 (η). Donc la droite BA est plus petite
que la 100e partie de
ΘK
(θ). Mais le diamètre du cercle
ΣH est égal à BA; parce que la droite ΦA moitié de BA est égale à
KΡ,
à cause que les droites ΘK, ΘA étant égales, on a abaissé de leurs extrémités
des perpendiculaires opposées au même angle. Il est donc évident que le diamètre
du cercle ΣH est plus petit que la 100e partie de
ΘK.
Mais le diamètre
EΘΥ
est plus petit que le diamètre
du cercle
ΣH, parce
que le cercle AEZ est plus petit que le cercle ΣH; donc la somme des droites
ΘΥ, KΣ
est plus petite que la 100e partie de ΘK. Donc la raison de ΘK à ΥΣ
est moindre que la raison de 100 à 99 (ι). Mais ΘK n'est pas plus petit que ΘΡ,
et ΣΥ est plus petit que ΔT ; donc la raison de ΘΡ à ΔT est moindre que la
raison de 100 à 99. De plus, puisque les côtés
KΡ,
KT
des triangles rectangles
ΘKΡ,
ΔKT
sont égaux, que les
côtés ΘΡ, ΔT sont inégaux et que le côté ΘΡ est le plus grand, la raison de
l'angle compris par les côtés ΔT,
ΔK
à l'angle compris par
les côtés ΘΡ,
ΘK
sera plus grande que la
raison de la droite
ΘK
à la droite ΔK, et moindre que
la raison de ΘΡ à ΔT; car si parmi les côtés de deux triangles rectangles qui
comprennent l'angle droit, les uns sont égaux et les autres inégaux, la raison
du plus grand des angles inégaux compris par les côtés inégaux au plus petit de
ces angles, est plus grande que la raison du plus grand des côtés opposés à
l'angle droit au plus petit de ces côtés, et moindre que la raison du plus
.grand des côtés qui comprennent l'angle droit au plus petit (κ). Donc la
raison de l'angle compris entre les côtés ΔΛ, ΔΞ à l'angle compris entre les
côtés ΘO,
ΘM
est moindre
que la raison de
ΘΡ à ΔT, laquelle est certainement
moindre que la raison de 100 à 99. Donc la raison de l'angle compris par les
côtés
ΔΛ, ΔΞ à
l'angle compris entre ΘM, ΘO est moindre que la raison de 100 à 99. Mais l'angle
compris par les côtés
ΔΛ,
ΔΞ est plus grand que la 200e
partie d'un angle droit; donc l'angle compris par les côtés
ΘM,
ΘO sera plus grand que les 99/2000e d'un angle droit. Donc cet angle
sera plus grand que le 203e d'un angle droit. Donc la droite
BA
est plus grande que la
corde d'un arc de la circonférence du cercle ABΓ divisée en 812 parties. Mais le
diamètre du soleil est égal à la droite
AB ;
il est donc évident que le
diamètre du soleil est plus grand que le côté d'un polygone de mille côtés.
Cela étant posé, on démontre aussi que
le diamètre du monde est plus petit qu'une myriade de fois le diamètre de la
terre, et que le diamètre du monde est plus petit que cent myriades de myriades
de stades. Car puisqu'on a supposé que le diamètre du soleil n'est pas plus
grand que trente fois le diamètre de la lune, et que le diamètre de la terre est
plus grand que le diamètre de la lune, il est évident que le diamètre du soleil
est plus petit que trente fois le diamètre de la terre. De plus, puisqu'on a
démontré que le diamètre du soleil est plus grand que le côté d'un polygone de
mille côtés inscrit dans un grand cercle de la sphère du monde, il est évident
que le contour du polygone de mille côtés dont nous venons de parler est plus
petit que mille fois le diamètre du soleil. Mais le diamètre du
soleil est plus petit que trente fois le diamètre de la terre; donc le contour
de ce polygone est plus petit que trois myriades de fois le diamètre de la
terre. Mais le contour de ce polygone est plus petit que trois myriades de fois
le diamètre de la terre et plus grand que le triple du diamètre du monde, parce
qu'il est démontré que le diamètre d'un cercle quelconque est
plus petit que la troisième partie du contour d'un
polygone quelconque qui est inscrit dans ce cercle, et qui a plus de six côtés
égaux. Donc le diamètre du monde est plus petit qu'une myriade de fois le
diamètre de la terre. Il est donc évident que le diamètre du monde qui est plus
petit qu'une myriade de fois le diamètre de la terre sera plus petit que cent
myriades de myriades de stades. Mais nous avons supposé que le contour de la
terre ne surpasse pas trois cents myriades de stades, et le contour de la terre
est plus grand que le triple de son diamètre, parce que le contour d'un cercle
quelconque est plus grand que le triple de son diamètre; il est donc évident que
le diamètre de la terre est plus petit que cent myriades de stades. Mais le
diamètre du monde est plus petit qu'une myriade de fois le diamètre de la terre
; il est donc évident que le diamètre du monde est plus petit que cent myriades
de myriades de stades.
Voilà ce que nous avons supposé
relativement aux grandeurs et aux distances, et voici ce que nous supposons
relativement aux grains de sable. Soit un volume de sable qui ne soit pas plus
grand qu'une graine de pavot ; que le nombre des grains de sable qu'il renferme
ne surpasse pas une myriade, et que le diamètre de cette graine de pavot ne soit
pas plus petite que la quarantième partie d'un doigt.
Voilà ce que je suppose, et voici ce
que je fis à ce sujet. Je plaçai des graines de pavot en droite ligne sur une
petite règle, de manière qu'elles se touchassent mutuellement ; vingt-cinq de
ces graines occupèrent une longueur plus grande que la largeur d'un doigt. Je
supposai que le diamètre d'une graine de pavot était encore plus petit, et qu'il
n'était que le quarantième de la largeur d'un doigt, afin de ne point éprouver
de contradiction dans ce que je m'étais proposé. Telles sont les suppositions
que nous faisons. Mais je pense qu'il est nécessaire à présent d'exposer les
dénominations de nombres ; si je n'en disais rien dans ce livre, je craindrais
que ceux qui n'auraient pas lu celui que j'ai adressé à Zeuxippe ne tombassent
dans l'erreur.
On a donné des noms aux nombres
jusqu'à une myriade et au-delà d'une myriade, les noms qu'on a donné aux nombres
sont assez connus, puisqu'on ne fait que répéter une myriade jusqu'à dix mille
myriades.
Que les nombres dont nous venons de
parler et qui vont jusqu'à une myriade de myriades soient appelés nombres
premiers, et qu'une myriade de myriades des nombres premiers soit appelée
l'unité des nombres seconds; comptons par ces unités, et par les dizaines, les
centaines, les milles, les myriades de ces mêmes unités, jusqu'à une myriade de
myriades. Qu'une myriade de myriades des nombres seconds soit appelée l'unité
des nombres troisièmes, comptons par ces unités, et par les dizaines, les
centaines, les milles, les myriades de ces mêmes unités, jusqu'à une myriade de
myriades; qu'une myriade de myriades des nombres troisièmes soit appelée l'unité
des nombres quatrièmes; qu'une myriade de myriades de nombres quatrièmes soit
appelée l'unité des nombres cinquièmes, et continuons de donner des noms aux
nombres suivants jusqu'aux myriades de myriades de nombres composés de myriades
de myriades des nombres troisièmes.
Quoique cette grande quantité de
nombres connus soit certainement plus que suffisante, on peut cependant aller
plus loin. En effet, que les nombres dont nous venons de parler soient appelés
les nombres de la première période, et que le dernier nombre de la première
période soit appelé l'unité des nombres premiers de la seconde période. De plus,
qu'une myriade de myriades des nombres premiers de la seconde période soit
appelée l'unité des nombres seconds de la seconde
période; qu'une myriade de
myriades des nombres seconds de la seconde période soit appelée l'unité des
nombres troisièmes de la seconde période, et continuons de donner des noms aux
nombres suivants jusqu'à un nombre de la seconde période qui soit égal aux
myriades de myriades de nombres composés de myriades de myriades. De plus, que
le dernier nombre de la seconde période soit appelé l'unité des nombres premiers
de la troisième période, et continuons de donner des noms aux nombres suivants
jusqu'aux myriades de myriades de la période formée d'une myriade de myriades de
nombres de myriades de myriades (λ).
Les nombres étant ainsi nommés, si des
nombres continuellement proportionnels, à partir de l'unité, sont placés les uns
à la suite des autres, et si le nombre qui est le plus près de l'unité est une
dizaine, les huit-premiers nombres, y compris l'unité, seront ceux qu'on appelle
nombres premiers; les huit suivants seront ceux qu'on appelle seconds et les
autres nombres seront dénommés de la même manière d'après la distance de leur
octade à l'octade des nombres premiers. C'est pourquoi le huitième nombre de la
première octade sera de mille myriades, le premier nombre de la seconde octade,
qui est l'unité des nombres seconds, sera une myriade de myriades, parce qu'il
est décuple de celui qui le précède ; le huitième nombre de la seconde octave
sera de mille myriades des nombres seconds, et enfin le premier nombre de la
troisième octade qui est l'unité des nombres troisièmes sera une myriade de
myriades des nombres seconds, parce qu'il est décuple de celui qui le précède.
Il est donc évident qu'on aura plusieurs octades ainsi qu'on l'a dit.
Il est encore utile de connaître ce
qui suit. Si des nombres sont continuellement proportionnels à partir de
l'unité, et si
deux ternies de cette progression sont multipliés l'un par
l'autre, le produit sera un terme de cette progression éloignée d'autant de
termes du plus grand facteur que le plus petit facteur l’est de l'unité. Ce même
produit sera éloigné de l'unité d'autant de termes moins un que les deux
facteurs le sont ensemble de l'unité (μ).
En effet, soient A, B, Γ, Δ,
E, Z, H, Θ,
I, K, Λ
certains nombres
proportionnels à partir de l'unité; que A soit l'unité. Que le produit de Δ par
Θ soit Χ. Prenons un terme
Λ
de la progression éloignée de Θ
d'autant de termes que Δ l'est de l'unité. Il faut démontrer que Χ est égal à
Λ.
Puisque les nombres A, B, Γ, Δ,
E, Z, H,
Θ,
I, K, Λ
sont proportionnels, et que Δ est autant éloigné de
A
que
Λ
l'est de Θ, le nombre Δ sera au
nombre A comme le nombre
Λ
est au nombre Θ ; mais Δ est
égal au produit de A par Δ ; donc Λ est égal au produit de Θ par Δ (ν) ;
donc
Λ
est
égal à Χ. Il est donc évident que le produit de Δ par Θ est un terme de la
progression, et qu'il est éloigné du plus grand facteur d'autant de termes que
le plus petit l'est de l'unité. De plus il est évident que ce même produit sera
éloigné de l'unité d'autant de termes moins un que les facteurs le sont ensemble
de l'unité. En effet, le nombre des termes A, B, Γ, Δ,
E, Z, H, Θ est égal au nombre des
termes dont Θ est éloigné de l'unité; et le nombre des termes I,
K, Λ est plus petit d'une unité
que le nombre des termes dont Θ est éloigné de l'unité, puisque le nombre de ces
termes avec Θ est égal au nombre des termes dont Θ est éloigné de l'unité.
Ces choses étant en partie supposées
et en partie démontrées, nous allons faire voir ce que nous nous sommes
proposés. En effet, puisque l'on a supposé que le diamètre d'une graine de pavot
n'est pas plus petit que la quarantième partie de la largeur d'un doigt, il est
évident qu'une sphère qui a un diamètre de la
largeur d'un doigt n'est pas
plus grande qu'il ne le faut pour contenir six myriades et quatre mille graines
de pavots. Car cette sphère est égale à soixante-quatre fois une sphère qui a un
diamètre d'un quarantième de doigt; parce qu'il est démontré que les sphères
sont entre elles en raison triplée de leurs diamètres. Mais on a supposé que le
nombre des grains de sable contenus dans une graine de pavot n'était pas de plus
d'une myriade ; il est donc évident que le nombre des grains de sable contenus
dans une sphère ayant un diamètre de la largeur d'un doigt ne surpassera pas une
myriade de fois six myriades et quatre mille. Mais ce nombre renferme six unités
des nombres seconds et quatre mille myriades des nombres premiers; ce nombre est
donc plus petit que dix unités des nombres seconds. Une sphère qui a un diamètre
de cent doigts est égal à cent myriades de fois une sphère qui a un diamètre
d'un doigt, parce que les sphères sont en raison triplée de leurs diamètres (ξ).
Donc si l'on avait une sphère de sable dont le diamètre fût de cent doigts, il
est évident que le nombre des grains de sable serait plus petit que celui qui
résulte du produit de dix unités des nombres seconds par cent myriades. Mais dix
unités des nombres seconds sont, à partir de l'unité, le dixième terme d'une
progression dont les termes sont décuples les uns des autres, et cent myriades
en sont le septième terme, à partir aussi de l'unité. Il est donc évident que le
nombre qui résulte du produit de ces deux nombres est le sixième terme de la
progression à partir de l'unité. Car on a démontré que le produit de deux termes
d'une progression qui commence par un, est distant de l'unité d'autant de termes
moins un que les facteurs ensemble le sont de l'unité. Mais parmi ces seize
termes, les huit premiers conjointement avec l'unité, appartiennent aux nombres
premiers, et les huit autres appartiennent aux nombres seconds,
et le dernier terme est de mille myriades des nombres
seconds. Il est donc évident que le nombre des grains de sable contenus dans une
sphère de cent doigts de diamètre, est plus petit que mille myriades des nombres
seconds.
Une sphère d'un diamètre d'une myriade
de doigts est égal à cent myriades de fois une sphère d'un diamètre de cent
doigts. Donc, si l'on avait une sphère de sable d'un diamètre d'une myriade de
doigts, il est évident que le nombre des grains de sable contenus dans cette
sphère serait plus petit que celui qui résulte du produit de mille myriades de
nombres seconds par cent myriades. Mais mille myriades de nombres seconds sont
le seizième terme de la progression, à partir de l'unité, et cent myriades en
sont le septième terme, à partir aussi de l'unité; il est donc évident que le
nombre qui résulte du produit de ces deux nombres sera le vingt-deuxième terme
de la progression, à partir de l'unité. Mais parmi ces vingt-deux termes, les
huit premiers y compris l'unité appartiennent aux nombres qu'on appelle
premiers, les huit suivants aux nombres qu'on appelle seconds, les six restants
à ceux qu'on appelle troisièmes, et enfin le dernier terme est de dix myriades
des nombres troisièmes. Il est donc évident que le nombre des grains de sable
contenus dans une sphère qui aurait un diamètre de dix mille doigts, ne serait
pas moindre que dix myriades des nombres troisièmes. Mais une sphère qui a un
diamètre d'une stade est plus petite qu'une sphère qui a un diamètre d'une
myriade de doigts. Il est donc évident que le nombre des grains de sable
contenus dans une sphère qui aurait un diamètre d'une stade, serait plus petit
que dix myriades des nombres troisièmes.
Une sphère qui a un diamètre de cent
stades est égal à cent myriades de fois une sphère qui a un diamètre d'une
stade.
Donc si l'on avait une sphère de sable
aussi grande que celle qui a un diamètre de cent stades, il est évident que le
nombre des grains de sable serait plus petit que le nombre qui résulte du
produit d'une myriade de myriades des nombres troisièmes par cent myriades. Mais
dix myriades des nombres troisièmes sont le vingt-deuxième terme de la
progression à partir de l'unité, et cent myriades en sont le septième terme, à
partir aussi de l'unité. Il est donc évident que le produit de ces deux nombres
est le vingt-huitième terme de cette même progression, à partir de l'unité. Mais
parmi ces vingt-huit termes, les huit premiers, y compris l'unité, appartiennent
aux nombres qu'on appelle premiers; les huit suivants, à ceux qu'on appelle
seconds ; les huit suivants, à ceux qu'on appelle troisièmes ; les quatre
restants, à ceux qu'on appelle quatrièmes, et le dernier de ceux-ci est de mille
unités des nombres quatrièmes. Il est donc évident que le nombre des grains de
sable contenus dans une sphère d'un diamètre de cent stades, serait plus petit
que mille unités des nombres quatrièmes.
Une sphère qui a un diamètre de dix
mille stades est égale à cent myriades de fois une sphère qui a un diamètre de
cent stades. Donc si l'on avait .une sphère de sable qui a un diamètre de dix
mille stades, il est évident que le nombre des grains de sable serait plus petit
que celui qui résulte du produit de mille unités des nombres quatrièmes par cent
myriades. Mais mille unités des nombres quatrièmes sont le vingt-huitième terme
de la progression, à partir de l'unité, et cent myriades en sont le
septième, à partir aussi de l'unité. Il est donc évident que le produit sera le
trente-quatrième terme, à partir de l'unité. Mais parmi ces termes, les huit
premiers, y compris l'unité, appartiennent aux nombres qu'on appelle premiers;
les huit suivants, à ceux qu'on appelle seconds ; les huit suivants, à ceux
qu'on appelle troisièmes ; les huit suivants, à ceux qu'on appelle quatrièmes ;
les deux restants, à ceux qu'on appelle cinquièmes ; et le dernier de ceux-ci
est de dix unités de nombres cinquièmes. Il est donc évident que le nombre des
grains de sable contenus dans une sphère ayant un diamètre d'une myriade de
stades, serait plus petit que dix unités des nombres cinquièmes.
Une sphère qui à un diamètre de cent
myriades de stades est égal à cent myriades de fois une sphère ayant un diamètre
d'une myriade de stades. Donc si l'on avait une sphère de sable ayant un
diamètre de cent myriades de stades, il est évident que le nombre des grains de
sable serait plus petit que le produit de dix unités des nombres cinquièmes par
cent myriades. Mais dix unités des nombres cinquièmes sont le trente-quatrième
terme de la progression, à partir de l'unité, et cent myriades sont le septième
terme, à partir aussi de l'unité. Il est donc évident que le produit de ces deux
nombres sera le quarantième terme de la progression, à partir de l'unité. Mais
parmi ces quarante termes, les huit premiers, y compris l'unité, appartiennent
aux nombres qu'on appelle premiers; les huit suivants, à ceux qu'on appelle
seconds; les huit suivants, à ceux qu'on appelle troisièmes ; les huit qui
suivent les nombres troisièmes, à ceux qu'on appelle quatrièmes; les huit qui
suivent les nombres quatrièmes, à ceux qu'on appelle cinquièmes, et le dernier
de ceux-ci est de mille myriades de nombres cinquièmes. Il est donc évident que
le nombre des grains de sable contenus dans une sphère ayant un diamètre de cent
myriades de stades serait plus petit que mille myriades des nombres cinquièmes.
Une sphère qui a un diamètre d'une
myriade de myriades de stades est égale à cent myriades de fois une sphère ayant
un diamètre de cent
myriades de stades. Si donc l'on avait une sphère de sable dont le diamètre fut
d'une myriade de myriades de stades, il est évident que le nombre des grains de
sable serait plus petit que le produit de mille myriades de nombres cinquièmes
par cent myriades. Mais mille myriades des nombres cinquièmes sont le
quarantième terme de la progression, à partir de l'unité, et cent myriades sont
le septième, à partir aussi de l'unité. Il est donc évident que le produit de
ces deux nombres est le quarante-sixième de la progression, à partir de l'unité.
Mais parmi ces quarante-six termes, les huit premiers, y compris l'unité,
appartiennent aux nombres qu'on appelle premiers; les huit suivants, à ceux
qu'on appelle seconds; les huit suivants, à ceux qu'on appelle troisièmes; les
huit qui suivent les nombres troisièmes, à ceux qu'on appelle quatrièmes; les
huit qui viennent après les nombres quatrièmes, à ceux qu'on appelle cinquièmes;
les six restants à ceux qu'on appelle sixièmes, et le dernier de ceux-ci est de
dix myriades des nombres sixièmes. Il est donc évident que le nombre des grains
de sable contenus dans une sphère qui aurait un diamètre de dix mille myriades
de stades, serait plus petit que dix myriades des nombres sixièmes.
Une sphère qui a un diamètre de cent
myriades de myriades de stades est égal à cent myriades de fois une sphère qui a
un diamètre d'une myriade de myriades de stades. Si donc l'on avait une sphère
de sable dont le diamètre fût de cent myriades de myriades, il est évident que
le nombre des grains de sable serait plus petit que le produit de dix myriades
des nombres sixièmes par cent myriades. Mais dix myriades des nombres sixièmes
sont le quarante-sixième terme de la progression, à partir de l'unité, et cent
myriades en sont le septième, à partir aussi de l'unité; il est donc évident que
le produit de ces deux
nombres sera le cinquante-deuxième terme de la progression, à partir de l'unité.
Mais parmi ces cinquante-deux termes, les quarante-huit premiers, y compris
l'unité, appartiennent aux nombres qu'on appelle premiers, seconds, troisièmes,
quatrièmes, cinquièmes et sixièmes, les quatre restants appartiennent aux
nombres septièmes, et le dernier de ceux-ci est de mille unités des nombres
septièmes. Il est donc évident que le nombre des grains de sable contenus dans
une sphère ayant un diamètre de cent myriades de myriades de stades, sera plus
petit que mille unités des nombres septièmes.
Puisque l'on a démontré que le
diamètre du monde n'est pas de cent myriades de myriades, il est évident que le
nombre des grains de sable contenus dans une sphère égale à celle du monde, est
plus petit que mille unités de nombres septièmes. On a donc démontré que le
nombre des grains de sable contenus dans une sphère égale en grandeur à celle
que la plupart des astronomes appellent monde, serait plus petit que mille
unités des nombres septièmes.
Nous allons démontrer à présent que le
nombre des grains de sable contenus dans une sphère aussi grande que la sphère
des étoiles fixes, supposée par Aristarque, est plus petit que mille myriades
des nombres huitièmes. En effet, puisque l'on suppose que la terre est à la
sphère que nous appelons le monde comme la sphère que nous appelons le monde est
à la sphère des étoiles fixes supposée par Aristarque; que les diamètres des
sphères sont proportionnels entre eux et que l'on a démontré que le diamètre dû
monde est plus petit qu'une myriade de fois le diamètre de la terre, il est
évident que le diamètre de la sphère des étoiles fixes est plus petit que dix
mille fois le diamètre du monde. Mais les sphères sont entre elles en raison
triplée de leurs diamètres; il
est donc évident que le nombre des
grains de sable contenus .dans une sphère aussi grande que la sphère des étoiles
fixes, supposée par Aristarque, serait plus petit qu'une myriade de myriades de
myriades de fois la sphère du monde; car il a été démontré que le nombre des
grains de sable qui feraient un volume égal au monde est plus petit que mille
unités de nombres septièmes. Il est donc évident que si l'on formait de sable
une sphère égale à celle qu'Aristarque suppose être celle des étoiles fixes, le
nombre des grains de sable serait plus petit que le produit de mille unités des
nombres septièmes par une myriade de myriades de myriades. Mais mille unités des
nombres septièmes est le cinquante-deuxième terme de la progression à partir de
l'unité, et une myriade de myriades de myriades en est le treizième, à partir
aussi de l'unité; il est donc évident que le produit sera le soixante-quatrième
terme de la progression. Mais ce nombre est le huitième des nombres huitièmes,
c'est-à-dire qu'il est de mille myriades des nombres huitièmes; il est donc
évident que le nombre des grains de sable contenus dans une sphère aussi grande
que celle des étoiles fixes supposée par Aristarque, est plus petit que mille
myriades des nombres huitièmes (ο).
Je pense, ô roi Gélon, que ces choses
ne paraîtront pas très croyables à beaucoup de personnes qui ne sont point
versées dans les sciences mathématiques; mais elles seront démontrées pour ceux
qui ont cultivé ces sciences et qui se sont appliqués à connaître les distances
et les grandeurs de la terre, du soleil, de la lune et du monde entier. C'est
pourquoi j'ai pensé qu'il ne serait pas inconvenant que d'autres les
considérassent de nouveau.
FIN DE L'ARÉNAIRE.
COMMENTAIRE SUR L'ARÉNAIRE.
(α)
Il est évident qu'Aristarque
considère le centre d'une sphère comme étant une surface infiniment petite; et
qu'eu employant cette analogie, il ne se propose de faire entendre autre chose,
sinon que l'orbite de la terre est infiniment petite, par l'apport à la distance
des étoiles au soleil. On aurait tort d'être surpris qu'Aristarque ait connu
cette immense distance des étoiles : de cela seul que la hauteur méridienne des
étoiles est toujours la même pendant une révolution de la terre autour du
soleil, il lui était facile de conclure que, dans la supposition de l'immobilité
des étoiles et du soleil, l'orbite de la terre devait être infiniment petite par
rapport à la distance des étoiles.
(β) Une myriade veut dire dix mille;
un stade était d'environ cent vingt-cinq pas géométriques.
(γ) Archimède prend le soleil à
l'horizon pour que l'œil puisse en soutenir l'éclat sans en être trop incommodé
; car il n'avait pas de moyen pour le dépouiller d'une grande partie de sa
lumière,
(Delambre.)
(δ) La partie de l'œil qui aperçoit
les objets n'est autre chose que la prunelle dont le diamètre varie à chaque
instant, selon que la lumière est plus ou moins vive. De cette manière il
pourrait arriver que le cylindre trouvé d'après la méthode d'Archimède fût, au
moment de l'observation, d'un diamètre plus petit ou plus
grand que celui de la prunelle, et alors l'observation
manquerait d'exactitude.
(ε) Car si le centre du soleil était à
l'horizon, la droite ΔK serait tangente à la terre, et par conséquent
perpendiculaire sur le rayon qui joint les points Δ, Θ; et alors la droite ΘK
serait plus grande que la droite
ΔK.
Mais à mesure que le soleil
s'élève au-dessus de l'horizon, l'angle
ΘΔK
augmente et l'angle AΘK diminue
; donc la droite
ΘK
sera encore plus grande que la
droite ΔK, lorsque le soleil est au-dessus de l'horizon.
(ζ) En effet, les deux triangles
ΔNK, ΘΡK
ayant chacun un angle droit en N et en Ρ ; le côté
KN
étant égal au côté KΡ, et
l’hypoténuse
ΔK
étant plus petite que
l’hypoténuse ΘK, l'angle NΔK sera plus grand que l'angle ΡΘK. Donc le double du
premier sera plus grand que le double du second, c'est-à-dire que l'angle ΛΔΞ
sera plus grand que l'angle MΘO.
(η) La raison du contour du polygone
de 656 côtés inscrit dans le cercle ABΓ à KΘ étant moindre que la raison de 44 à
7, la raison d'un des côtés de ce polygone à KΘ sera moindre que la raison de
44/656e à 7, c'est-à-dire moindre que la raison de 44 à
4592, ou bien de 11 à 1148. Mais
la droite AB est plus petite que je côté d'un polygone de 656 côtés ; donc la
raison de AB à KΘ est moindre que la raison de 11 à 1148.
(θ) Car la raison de
BA
à ΘK est moindre que la raison
de 11 à 1148, c'est-à-dire que BA/ΘK < 11/1148 ou bien en divisant la seconde
fraction par 11,
BA/ΘK < 1/(104+4/11). Donc à plus
forte raison BA/ΘK < 1/100. Donc si
BA
est un, ΘK sera plus grand que
cent. Donc BA est plus petit que le centième de ΘK.
(ι) Car puisque le diamètre du cercle
ΣH est plus petit que la
centième partie de
ΘK, et que ΘΥ +
ΣK
est plus petit que le diamètre
du cercle ΣH, il est évident que ΘΥ +
ΣK
sera plus petit que la centième
partie de ΘK. Donc la droite
ΘK
étant partagée en cent parties
égales, la droite ΥΣ sera plus grande que quatre-vingt-dix-neuf parties de ΘK.
Donc la raison de ΘK à ΥΣ est moindre que la raison de cent à
quatre-vingt-dix-neuf.
(κ) Soient les deux triangles
ABΓ, ΔEZ, ayant des angles droits en B et E. Θue BΓ soit égal à EZ et
AB
plus grand que
ΔE:
je dis que la raison de
l'angle
Δ
à
l'angle
A, qui
est plus petit que l'angle Δ, est plus grande que la raison de AΓ à ΔZ, et que
la raison de l'angle
Δ
à l'angle A est moindre que la
raison de
AB
à
ΔE.
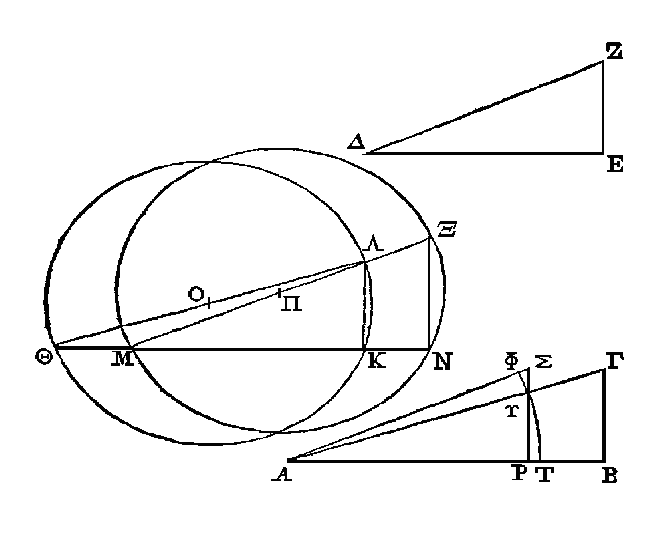
Faisons le triangle
ΘKΛ
égal et semblable au triangle
ABΓ. Prenons MK égal à ΔE, et menons la droite MΛ. Le triangle MKΛ sera égal et
semblable au triangle ΔEZ. Prolongeons MΛ vers Ξ, jusqu'à ce que MΞ
s.oit égal à ΘΛ.
Prolongeons aussi MK vers N, et du point Ξ conduisons la droite ΞN
perpendiculaire sur MN. Le triangle MNΣ sera semblable au triangle MKΛ. Du point
O, milieu de ΘΛ, et avec le rayon OΛ, décrivons une circonférence de cercle :
cette circonférence passera par le point K. Du point Π, milieu de MΞ, et
avec le rayon ΠΞ, décrivons aussi une circonférence de cercle :
cette circonférence passera par
le point N ; et ces deux
circonférences seront égales, puisque leurs diamètres sont égaux.
Puisque les angles ΞMN, ΛΘK ont leurs
sommets à des circonférences égales, ces angles seront entre eux comme les arcs
compris par leurs côtés, c'est-à-dire que l'angle ΞMN sera à l'angle ΛΘK comme
l'arc ΞN est à l'arc ΛK. Mais dans des cercles égaux, la raison des arcs est
plus grande que la raison des cordes ; donc la raison de l'angle ΞMN à l'angle
ΛΘK
est
plus grande que la raison de ΞN à ΛK. Mais ΞN est à ΛK comme MΞ est à MΛ. Donc
la raison de l'angle ΞMN à l'angle ΛΘK est plus grande que la raison de ΘΛ à
MΛ,
c'est-à-dire que la raison de l'angle Δ à l'angle A est plus grande que la
raison de AΓ à ΔZ.
Faisons à présent AΡ égal à
ΔE.
Du
point
Ρ
élevons une perpendiculaire sur
AB
;
faisons ΡΣ égal à EZ, et joignons
AΣ.
Le triangle
AΡΣ
sera égal et semblable au
triangle ΔEZ. Du point A et avec le rayon AΥ décrivons l'arc ΦΥT. L'angle ΦAΥ
sera à l'angle ΥAT comme le secteur
ΦAΥ
est au secteur ΥAT. Mais la
raison du secteur ΦAΥ au secteur ΥAT est moindre que la raison du secteur ΦAΥ au
triangle AΡΥ ; donc la raison de l'angle ΦAΥ à l'angle ΥAT est moindre que la
raison du secteur
ΦAΥ
au triangle AΡΥ, et moindre par
conséquent; que la raison de ΣΥ à ΥΡ. Donc par addition, la raison de l'angle
ΦAΥ à l'angle ΥAT est moindre que la raison de ΣΡ ou de ΓB à
ΥΡ.
Mais
ΓB
est à ΥΡ comme
AB
est à AΠ ; donc la raison de
l'angle
ΦAT
à
l'angle
ΥAT
est
moindre que la raison de AB à AΡ, c'est-à-dire que la raison de l'angle
ZΔE
à l'angle
ΓAB
est moindre que la raison de AB
à ΔE, ξ
(λ)
Le système de numération
imaginé par Archimède est fondé sur les mêmes principes que le nôtre. Au lieu de
nos neuf chiffres significatifs, il se sert des lettres de l'alphabet. Sans
doute Archimède avait un caractère qui lui tenait lieu de notre zéro. Dans son
système, comme dans le nôtre, les unités des caractères dont il se sert forment
une progression géométrique dont la raison est dix. La seule différence consiste
en ce que les unités sont à gauche au
lieu d'être à droite. Voyez le Tableau du système
d'Archimède comparé avec le nôtre.
(μ)
C'est la propriété
fondamentale des logarithmes, et c'est par le moyen de cette propriété
qu'Archimède va exécuter tous ses calculs.
(ν) Puisque
Δ
: A :: Λ : Θ, on aura A x Λ = Θ x Δ. Mais Δ = Δ x A ; donc A x Λ
= Θ x Δ x A; donc Λ = Θ x Δ.
(ξ)
J'ai supposé, d'après
Archimède, que le diamètre d'une graine de pavot était la quarantième partie de
la largeur d'un doigt; qu'une graine de pavot contenait 10,000 grains de sable;
qu'un stade valoir 10,000 doigts, et que le diamètre de la sphère des étoiles
fixes était de 10,000,000,000 stades. J'ai fait les calculs, et j'ai trouvé que
le nombre des grains de sable contenus dans la sphère des étoiles fixes serait
de 64 suivi de 61 zéros. Ainsi Archimède a raison de dire que ce nombre est plus
petit que 100 suivi de 61 zéros, c'est-à-dire plus petit que mille
myriades des nombres huitièmes.
FIN DU COMMENTAIRE SUR L’ARENAIRE
|