ARCHIMÈDE

LEMMES.

PROPOSITION PREMIÈRE.

Si deux cercles aeb, ced se touchent mutuellement en un point ; si leurs diamètres ab, cd sont parallèles, et si l'on joint les deux points b, d et le point de contact e par les droites de, bd; je dis que la ligne bde sera une ligne droite.

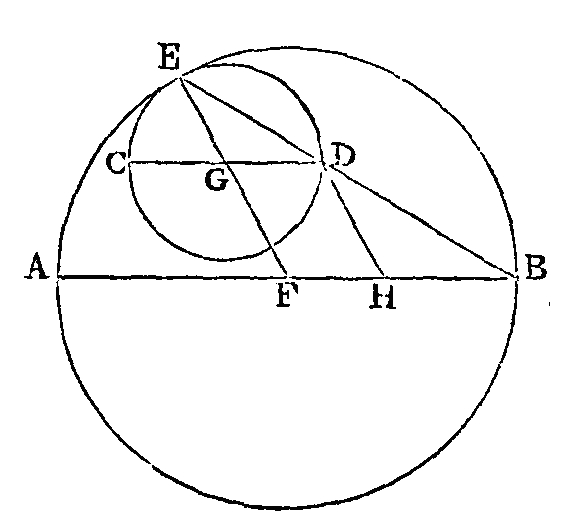
Que les points g, f soient les centres de ces deux cercles. Menons la droite gf et prolongeons-la jusqu'en e (a). Conduisons la droite dh parallèle à gf. Puisque la droite hf est égale à la droite gd et que les droites gd, eg sont égales, il est évident que si des droites égales fb, fe, on retranche les droites égales fh, ge les droites restantes gf ou dh et hb seront égales. Donc les deux angles hdb, hbd seront égaux. Mais les deux angles egd, efb sont égaux et par conséquent les deux angles egd, dhb ; donc les deux angles ged, gde qui sont égaux entre eux seront égaux aux deux angles hdb, hbd. Donc l'angle edg est égal à l'angle dbf. Donc si à ces angles égaux on ajoute l'angle gdb, les deux angles gdb, fbd qui sont égaux à deux droits seront égaux aux deux angles gdb, gde. Donc ces deux derniers angles sont aussi égaux à deux droits. Donc la ligne edb est une ligne droite. Ce qu'il fallait démontrer (b).

PROPOSITION II.

Que cba soit un demi-cercle ; que les droites dc, db soient des tangentes; que la droite be soit perpendiculaire sur ac, et joignons ad. Je dis que bf est égal à fe (a).

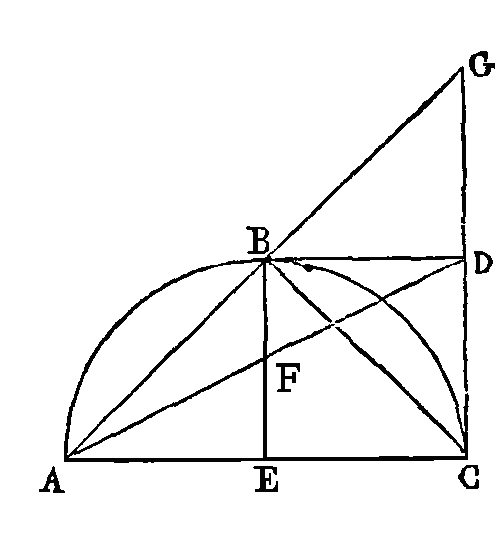
Menons la droite ab, et prolongeons cette droite. Prolongeons aussi la droite cd jusqu'à ce qu'elle rencontre la droite ag au point g, et joignons cb. Puisque l'angle cba est dans le demi-cercle, cet angle sera droit, ainsi que l'angle cbg. Mais la figure dbec est un rectangle. Donc dans le triangle rectangle gbc la droite bd menée du point b, est perpendiculaire sur la base. Mais les droites bd, dc seront égales, puisqu'elles sont deux tangentes au cercle ; donc cd est égal à dg (b), ainsi que nous le démontrons dans les propositions qui regardent les rectangles. Mais dans le triangle rectangle gac, la droite be est parallèle à la base, et du milieu de la base on a conduit la droite da qui coupe cette parallèle au point f ; donc la droite bf sera égale à la droite fe. Ce qu'il fallait démontrer.

PROPOSITION III.

Soit un segment de cercle ca. Que b soit un point quelconque de son arc; que bd soit perpendiculaire sur ac ; et que la droite de soit égale à la droite da, et l'arc bf égal à l'arc ba. Je dis que la droite cf est égale à la droite ce.

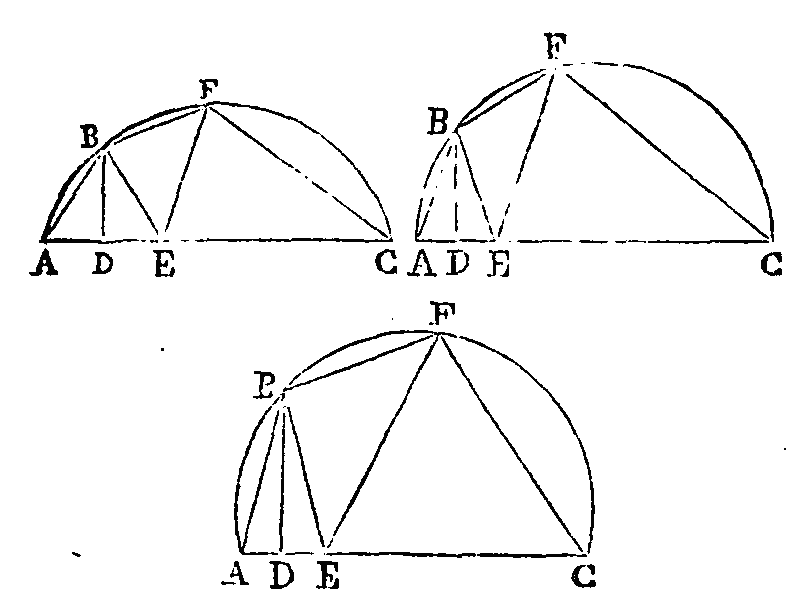
Menons les droites, ab, bf, fe, eb. Puisque l’arc ba est égal à l'arc bf, la corde ab sera égale à la corde bf. Mais la droite ad est égale à ed ; les angles sont droits en d, et la droite db est commune ; donc la droite ab sera égale à be. Donc bf est égal à BE, et l'angle bfe égal à l'angle bef. Mais le quadrilatère cfba est inscrit dans un cercle; donc l'angle cfb conjointement avec l'angle cab qui lui est opposé, ou avec l'angle bea, est égal à deux angles droits. Mais l'angle ceb, conjointement avec l'angle bea est aussi égal à deux angles droits; donc les deux angles cfb, ceb sont égaux. Donc les angles restants cfe, cef sont aussi égaux. Donc la droite ce est égale à la droite cf. Ce qu'il fallait démontrer.

PROPOSITION IV.

Soit un demi-cercle abc. Sur son diamètre ac construisons deux demi-cercles dont l'un soit ad et l'autre dc. Que db soit perpendiculaire sur ac. La figure qui résulte de cette construction, et qui est comprise entre l'arc du demi grand cercle et entre les deux arcs des plus petits demi-cercles se nomme Arbelon. Je dis que l'Arbelon est égal au cercle qui a pour diamètre la perpendiculaire db.

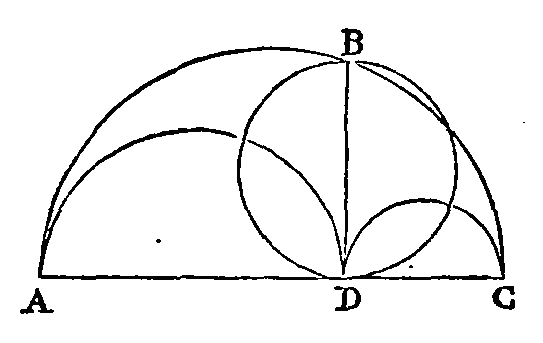
Puisque la droite db est moyenne proportionnelle entre les deux droites da, dc, le rectangle compris sous les droites ad, dc sera égal au carré de db. Ajoutons de part et d'autre le rectangle compris sous ad, dc, et les carrés de ad et de dc. Le double du rectangle compris sous ad, dc, conjointement avec les deux carrés de ad et de dc, c'est-à-dire le carré de ac sera égal au double du carré de db, conjointement avec les deux carrés de ad, dc (a). Mais les cercles sont entre eux comme les carrés de leurs rayons; donc le cercle qui a pour diamètre la droite ac est égal au double du cercle qui a pour diamètre la droite bd, conjointement avec les deux cercles qui ont pour diamètres les droites ad, dc. Donc le demi-cercle, qui a pour diamètre ac, est égal au double du cercle qui a pour diamètre db, conjointement avec les deux demi-cercles qui ont pour diamètres les droites ad, dc. Donc si nous retranchons de part et d'autre les deux demi-cercles ad, dc, la figure comprise entre les trois demi-circonférences des cercles ac, ad, dc, c'est-à-dire l'Arbelon, sera égal au cercle dont le diamètre est db. Ce qu'il fallait démontrer.

PROPOSITION V.

Soit un demi-cercle ab. Que c soit un point quelconque de son diamètre. Construisons sur son diamètre les deux demi-cercles ac, cb ; du point c élevons la droite cd perpendiculaire sur ab ; et de part et d'autre de cette perpendiculaire décrivons deux cercles qui touchent cette perpendiculaire et les arcs des demi-cercles. Je dis que ces deux cercles sont égaux entre eux.

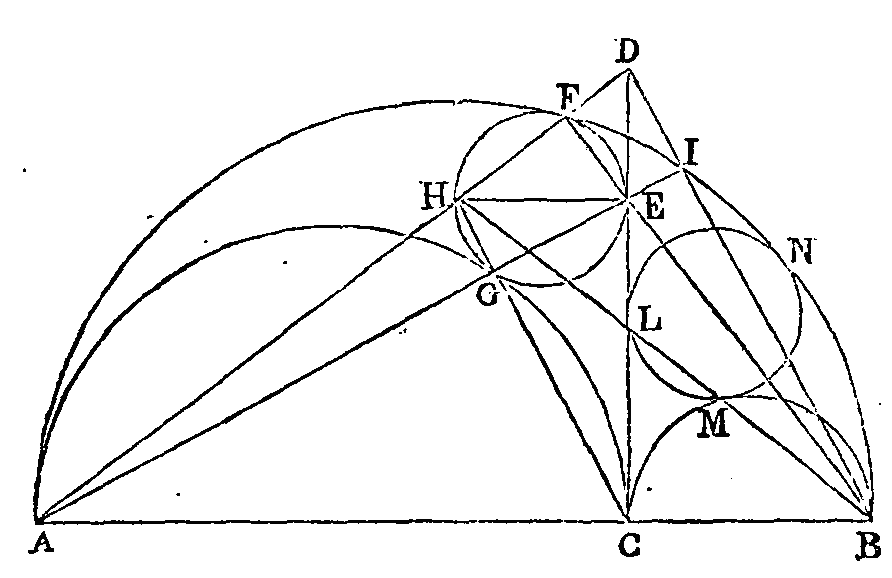
Supposons qu'un de ces cercles touche la perpendiculaire soc en e; qu'il touche la circonférence du demi-cercle ab au point F, et la circonférence du demi-cercle ac au point g. Menons le diamètre he perpendiculaire sur dc. Le diamètre he sera parallèle au diamètre ab, parce que les deux angles hec, ace sont droits. Joignons fh, ha. La ligne af sera une ligne droite, ainsi qu'on l'a démontré dans la première proposition ; et les droites af, ce se rencontreront en un point d, parce que les angles dac, dca pris ensemble sont moindres que deux droits. Joignons aussi fe, eb; la ligne efb sera aussi une ligne droite, ainsi que nous l'avons dit; et cette droite sera perpendiculaire sur ad, parce que l'angle afb est droit à cause qu'il est compris dans le demi-cercle ab. Joignons hg, gc. La ligne hc sera une ligne droite. Joignons eg, ga. La ligne ega sera une ligne droite. Prolongeons cette droite vers i, et joignons bi. La droite bi sera perpendiculaire sur ai. Joignons di. Puisque les lignes ad, ab sont deux droites ; que du point d on a conduit la droite dc perpendiculaire sur ab ; que du point b on a conduit la droite bf perpendiculaire sur da ; que ces deux perpendiculaires se coupent mutuellement au point e, et que de plus la droite ae prolongée jusqu'en i est perpendiculaire sur bi, la ligne bid sera une ligne droite, ainsi que nous l'avons démontré dans nos propositions qui regardent les triangles rectangles (a). Mais les deux angles agc, aib sont droits, les droites bd, cg étant parallèles, et la raison de ad à dh, qui est la même que la raison de ac à he, est encore la même que la raison de ab à bc (b); donc le rectangle compris sous ac, cb est égal au rectangle compris sous ab, he. Nous démontrerons semblablement que dans le cercle lmn, le rectangle compris sous ac, cb est égal au rectangle compris sous ab et sous le diamètre du cercle lmn, et l'on conclura de là que les diamètres des cercles efg, lmn sont égaux. Donc ces deux cercles sont égaux. Ce qu'il fallait démontrer.

PROPOSITION VI.

Soit un demi-cercle abc. Prenons un point d sur son diamètre, de manière que la raison de ad à dc soit la même que la raison de trois à deux; sur ad, dc décrivons deux demi-cercles.

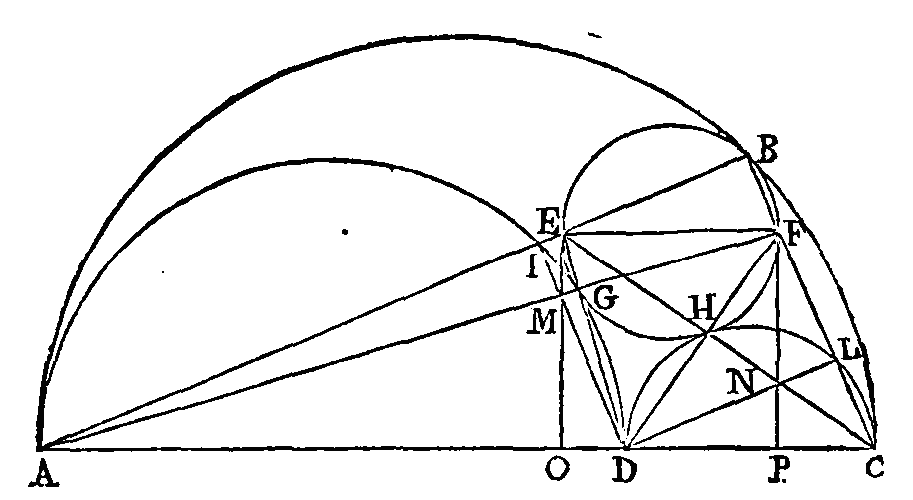
Supposons un cercle ef tangente aux trois autres demi-cercles, et menons dans ce cercle le diamètre ef parallèle au diamètre ac. Il faut trouver la raison du diamètre ac au diamètre ef.

Joignons ae, eb, et cp, fb. Les lignes cfb, aeb seront des lignes droites, ainsi qu'on l'a démontré dans la proposition 1^re. Menons aussi les deux lignes fga, ehc, on démontrera que ces deux lignes seront des droites ainsi que les deux lignes de, df.

Joignons di, dl, ainsi que em, fn, et prolongeons ces dernières droites vers o, p. Puisque dans le triangle aed, la droite ag est perpendiculaire sur ed ; que la droite di est perpendiculaire sur ae, et que les droites ag, di se coupent au point m, la droite emo sera perpendiculaire sur ad (a), ainsi que nous l'avons démontré dans notre exposition des propriétés des triangles, sur laquelle est fondée la démonstration précédente. La droite fp sera semblablement perpendiculaire sur ca. Mais les angles en l, et b sont droits; donc dl sera parallèle à ab, et di parallèle à cb. Donc ad est à dc comme am est à fm, et comme ao est à op. Mais cd est à da comme cn est à ne, et comme cp est à po; et nous avons supposé que ad était à dc comme trois est à deux; donc ao est à op comme trois est à deux. Mais of est à cp comme trois est à deux; donc les trois droites ao, op, pc sont proportionnelles. Donc la droite pc étant quatre, la droite op sera six, la droite ao neuf et la droite ca dix-neuf. Mais po est égal à ef ; donc ac est à ef comme dix-neuf est à six. Donc nous avons trouvé la raison demandée.

Si la raison de ad à dc était différente, si par exemple elle était la même que la raison de quatre à trois ou de cinq à quatre ou tout autre raisonnement, et la manière de procéder ne serait pas différente (b). Ce qu'il fallait trouver.

PROPOSITION VII.

Si un cercle est circonscrit à un carré, et si un autre cercle lui est inscrit, le cercle circonscrit sera double du cercle inscrit.

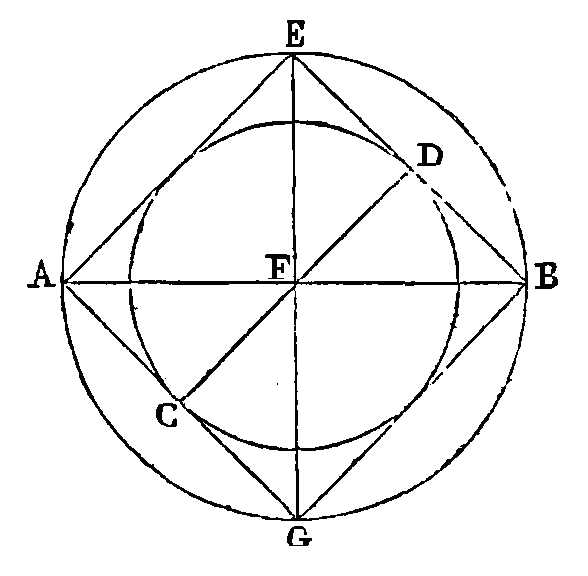
Circonscrivons un cercle ab au carré ab, et inscrivons-lui le cercle cd. Que ab soit la diagonale du carré et le diamètre du cercle circonscrit. Conduisons dans le cercle inscrit le diamètre cd parallèle au côté ae, qui est égal à cd. Puisque le carré de ab est double du carré de ae ou de dc, et que les cercles sont entre eux comme les carrés de leurs diamètres, le cercle ab sera double du cercle cd. Ce qu'il fallait démontrer.

PROPOSITION VIII.

Si une corde ab d'un cercle est plongée, et si l'on fait bc égal au rayon de ce cercle ; si ensuite l'on joint le point c et le centre du cercle qui est le point d, et si l'on prolonge cd jusqu'en e, l'arc ae sera triple, de l'arc bf.

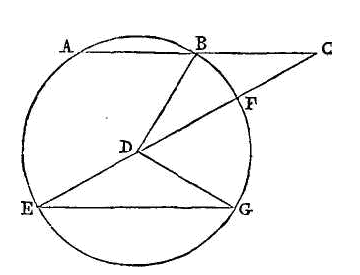
Menons eg parallèle à ab, et joignons db, dg. Puisque l'angle deg est égal à l'angle dge, l'angle gdc sera double de l'angle deg. Mais l'angle bdc est égal à l'angle bcd, et l'angle ceg égal à l'angle ace; donc l'angle gdc sera double de l'angle cdb, et l'angle entier bdg triple de l'angle bdc. Donc l'arc ae qui est égal à bg sera triple de l'arc bf. Ce qu'il fallait démontrer.

PROPOSITION IX.

Si dans un cercle deux droites ab, cd, qui ne passent pas par le centre, se coupent à angles droits, les arcs ad, cb pris ensemble, seront égaux aux deux arcs ac, db pris ensemble.

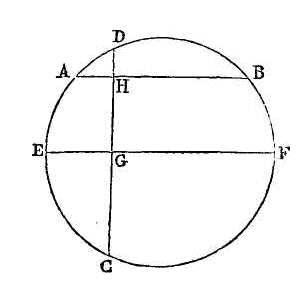
Menons le diamètre ef parallèle à ab ; ce diamètre coupera cd en deux parties égales au point g. Donc l'arc ec sera égal à l'arc éd. Mais l'arc edf est égal à la demi-circonférence, ainsi que l'arc ecf, et l'arc ed est égal à l'arc ea, conjointement avec l’arc ad; donc l'arc cf, conjointement avec les deux arcs ea, ad sera égal à la demi-circonférence. Mais l'arc ea est égal à l'arc bf; donc l'arc cb, conjointement avec l'arc ad est égal à la demi-circonférence. Donc la somme des arcs ec, ea, c'est-à-dire l'arc ac, conjointement avec l'arc db est aussi égal à la demi-circonférence. Ce qu'il fallait démontrer.

PROPOSITION X.

Soient le cercle abc ; la tangente da ; la sécante db, et la tangente dc. Menons la droite ce parallèle à db, et la droite ea qui coupe la droite db en f. Du point f abaissons la perpendiculaire fg sur la droite ce. Je dis que la perpendiculaire fg coupera la droite ec en deux parties égales au point g.

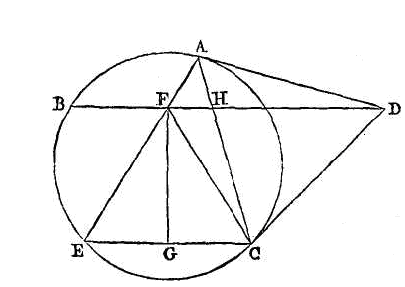
Joignons ac. Puisque la droite da est tangente, et que la droite ac est une corde, l’angle dac sera égal à l'angle du segment alterne abc, c'est-à-dire à l'angle aec. Mais l'angle aec est égal à l'angle afd, parce que les droites ce, bd sont parallèles; donc les angles dac, afd sont égaux. Donc les deux triangles daf, ahd ont les angles afd, had égaux chacun à chacun, mais ils ont de plus un angle commun en d ; donc le rectangle compris sous fd, dh est égal au carré de da, et par conséquent au carré de dg. Donc puisque fd est à dc comme cd est à dh, et que l'angle bdc est commun, les triangles dfc, dch sont semblables. Donc l'angle dfc est égal à l'angle dch, qui est égal à l'angle dah, et celui-ci est égal à l'angle afd. Donc les deux angles afd, cfd sont égaux. Mais l'angle dfc est égal à l'angle fce, et nous avons vu que l'angle dfa est égal à l'angle aec ; donc dans le triangle fec l'angle fcg est égal à l'angle feg. Mais les deux triangles fge, fgc ont de plus chacun un angle droit en g et un côté commun gf ; donc la droite cg est égale à la droite ge. Donc la droite ce est coupée en deux parties égales en g. Ce qu'il fallait démontrer.

PROPOSITION XI.

Si dans un cercle deux cordes ab, cd se coupent mutuellement à angles droits en un point e qui ne soit pas le centre, la somme des carrés des droites ae, be, ec, ed sera égale au carré du diamètre.

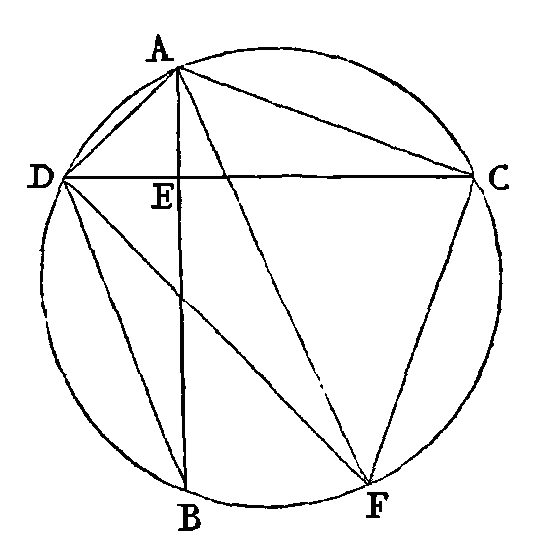
Menons le diamètre af, et les droites ac, ad, cf, db. Puisque l'angle aed est droit, cet angle sera égal à l'angle acf. Mais l'angle adc est égal à l'angle afc; puisqu'ils comprennent le même arc; donc dans les triangles ade, afc, les autres angles caf, dae sont égaux chacun à chacun. Donc les deux arcs cf, db sont égaux, et par conséquent les cordes de ces arcs. Mais la somme des carrés de de et de eb est égale au carré de bd, et par conséquent au carré de cf ; la somme des deux carrés de ae et de ec est égale au carré de ca, et la somme des carrés de cf et de ca est égale au carré du diamètre fa ; donc la somme des carrés de ae, eb, ce, ed est égale au carré du diamètre. Ce qu'il fallait démontrer.

PROPOSITION XII.

Soit un demi-cercle décrit sur AB comme diamètre. Du point C conduisons deux droites tangentes aux points D, E. Menons les droites EA, DB, qui se coupent mutuellement au point F. Joignons CF et prolongeons CF jusqu'en G. Je dis que la droite CG sera perpendiculaire sur AB.

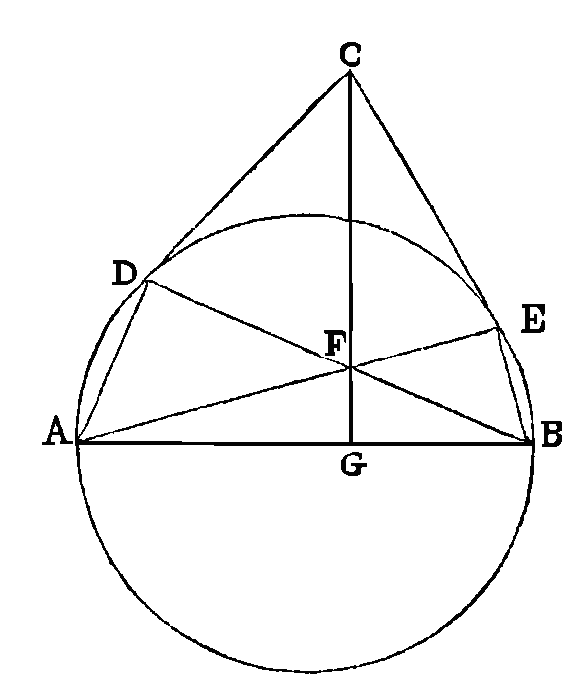
Joignons DA, EB. Puisque l'angle BDA est droit, la somme des deux angles restants DAB, DBA du triangle DAB, sera égale à un droit. Mais l'angle AEB est droit; donc la somme des deux angles DAB, DBA est égale à l'angle AEB. Donc si nous ajoutons de part et d'autre l'angle FBE, la somme des deux angles DAB, ABE sera égale à la somme des angles FBE, FEB, et par conséquent à l'angle extérieur DFE du triangle FBE. Mais la droite CD est tangente au cercle, et DB une corde ; donc l'angle CDB est égal à l'angle DAB. Semblablement l'angle CEF est égal à l'angle EBA. Donc la somme des angles CBF, CDF est égale à l'angle DFE. Mais nous avons démontré dans le livre des quadrilatères que si entre deux droites égales CD, CE qui se rencontrent en un point, on mène deux droites DF, EF qui se coupent mutuellement, et si l'angle DFE compris par ces deux droites est égal à la somme des deux angles CEF, CDF, la droite CF sera égale à chacune des droites CD, CE (a). D'où il suit que CF sera égal à CD. Donc l'angle CFD est égal à l'angle CDF, c'est-à-dire à l'angle DAG. Mais l'angle CFD, conjointement avec l'angle DFG, est égal à deux angles droits; donc l'angle DAG, conjointement avec l'angle DFG est égal à deux droits. Mais la somme des deux angles restants ADF, AGF du quadrilatère est égale à deux droits, et l'angle ADB est droit; donc l'angle AGC est droit. Donc CG est perpendiculaire sur AB. Ce qu'il fallait démontrer.

PROPOSITION XIII.

Que deux droites AB, CD se coupent mutuellement dans un cercle; que AB soit un diamètre; que CD ne soit point un diamètre, et des points A, B conduisons les droites AE, BF perpendiculaires sur CD. Je dis que les droites CF, DE seront égales.

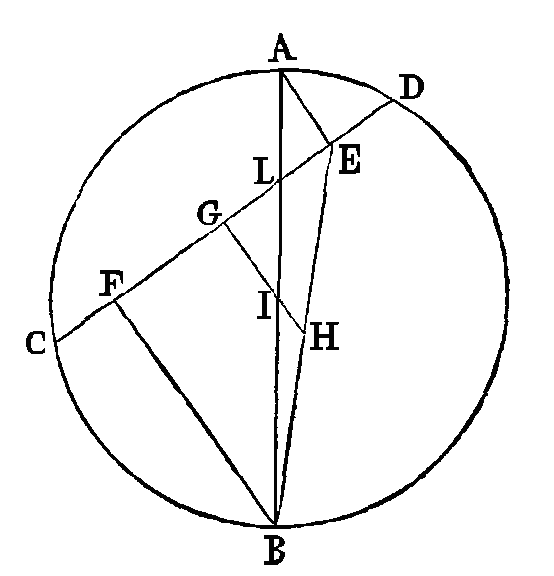
Joignons EB. Du point I, qui est le centre du cercle, conduisons la droite IG perpendiculaire sur CD, et prolongeons-la jusqu'au point H de la droite EB. Puisque la perpendiculaire IG est menée du centre sur CD, cette perpendiculaire partagera la droite CD en deux parties égales en G. Mais les droites IG, AE sont deux perpendiculaires sur CD; donc ces deux perpendiculaires sont parallèles. Mais BI est égal à IA ; donc la droite BH est égale à la droite HE. Donc, à cause de l'égalité de ces deux droites, et à cause que BF est parallèle à HG, la droite FG sera égale à la droite GE. Donc si des droites égales GC, GD, on retranche les droites égales GF, GE, les droites restantes FC, ED seront égales. Ce qu'il fallait démontrer.

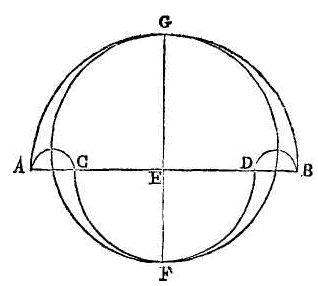
PROPOSITION XIV.

Soit un demi-cercle AB. De son diamètre AB retranchons les parties égales AC, BD. Sur les droites AC, CD, BD décrivons des demi-cercles ; que le point E soit le centre des deux demi-cercles AB, CD. Que la droite EF soit perpendiculaire sur AB, et prolongeons la droite EF vers G. Je dis que le cercle qui a la droite FG pour diamètre est égal à la surface comprise par la demi-circonférence du demi grand cercle, par la demi-circonférence de deux demi-cercles qui sont placés dans le grand demi-cercle, et enfin par la demi-circonférence du demi-cercle qui est hors du demi grand cercle. La figure comprise entre les quatre demi-circonférences des demi-cercles AB, CD, DB, AC s'appelle Salinon.

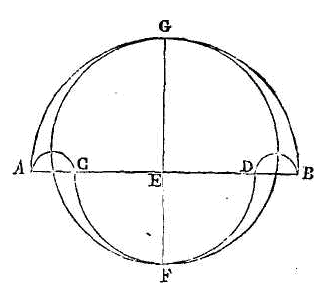
Puisque la droite DC est coupée en deux parties égales au point E, et qu'on lui a ajouté la droite CA, la somme des carrés des droites DA, CA sera double de la somme des carrés des droites DE, EA (a). Mais FG est égal à DA ; donc la somme des carrés des deux droites FG, AC est double de la somme des carrés des deux droites DE, EA. Mais AB est double de AE, et CD double de ED ; donc la somme des carrés des deux droites AB, DC est quadruple de la somme des carrés des deux droites DE, EA, et par conséquent double de la somme des carrés des deux droites GF, AC. Donc la somme des deux cercles qui ont pour diamètres les droites AB, DC sera semblablement double de la somme des cercles qui ont pour diamètres les droites GF, AC. Donc la somme des demi-cercles qui ont pour diamètres les droites AB, CD est égale à la somme des deux cercles qui ont pour diamètres les deux droites GF, AC. Mais le cercle qui a pour diamètre la droite AC est égal à la somme des deux demi-cercles AC, BD; donc si l’on retranche de part et d'autre les deux demi-cercles AC, BD qui sont communs, la figure restante, qui est comprise entre les quatre demi-circonférences des demi-cercles AB, CD, DB, AC, et qu'on appelle Salinon, sera égale au cercle qui a pour diamètre la droite FG. Ce qu'il fallait démontrer.

PROPOSITION XV.

Soit AB un demi cercle; que AC soit le côté du pentagone inscrit, et AD la moitié de l'arc AC. Menons la droite CD, et prolongeons-la jusqu'à ce qu'elle rencontre en E la droite BA prolongée. Menons la droite BD, qui coupe la droite CA en un point F, et du point F abaissons sur AB la perpendiculaire FG. Je dis que la droite EG sera égale au rayon du cercle.

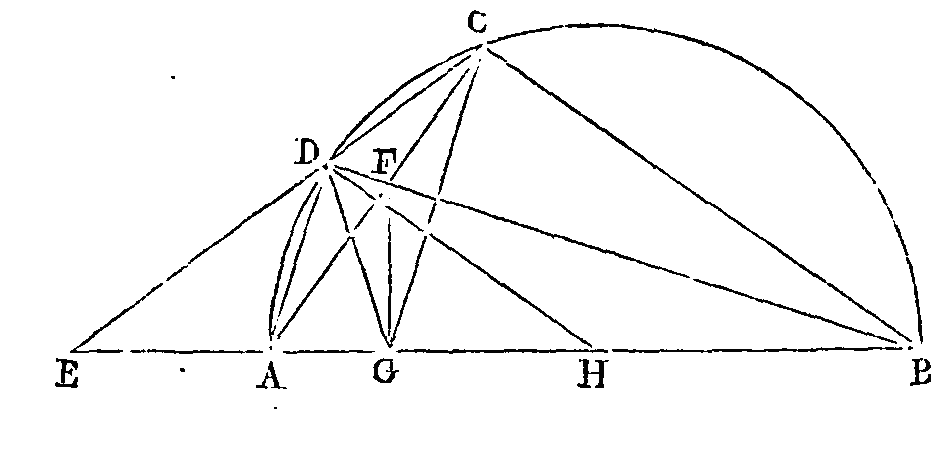
Joignons CB. Que le point H soit le centre du cercle. Joignons HD, DG et AD. Puisque l'angle ABC qui embrasse le côté du pentagone vaut les deux cinquièmes d'un angle droit, chacun des angles CBD, DBA vaudra le cinquième d'un angle droit. Mais l'angle DHA est double de l'angle DBH; donc l'angle DHA vaut les deux cinquièmes d'un droit. Mais les deux triangles GBF, GFB ont chacun un angle égal en B, et chacun un angle droit en G et C ; ils ont de plus un côté commun FB ; donc BC sera égal à BG. Mais les deux triangles CBD, GBD ont les côtés CB, BG égaux entre eux, ainsi que les deux angles FBC, FBG, et ils ont de plus le côté BD commun, donc les deux angles BCD, BGD sont égaux. Mais chacun de ces angles, qui vaut les six cinquièmes d'un angle droit, est égal à l'angle externe DAE du quadrilatère BADC, qui est inscrit dans le cercle (a); donc l'angle restant DAB sera égal à l'angle DGA, et le côté DA égal au côté DG. Mais l'angle DHG vaut les deux cinquièmes d'un angle droit, et l'angle DGH vaut les six cinquièmes d'un angle droit; donc l'angle restant HDG vaut les deux cinquièmes d'un droit Donc DG est égal à GH. Mais l'angle externe ADE du quadrilatère ADCB inscrit dans le cercle est égal à l'angle CBA, qui vaut les deux cinquièmes d'un angle droit et à l'angle GDH, et de plus dans les deux triangles EDA, HDG, les deux angles EDA, HDG, sont égaux ainsi que les deux angles DGH, DAE et les deux côtés DA, DG; donc EA sera égal à HG. Donc si l'on ajoute de part et d'autre AG, la droite EG sera égale à la droite AH. Ce qu'il fallait démontrer.

Il suit de là que la droite DE est égale au rayon du cercle. Car puisque l'angle DAE est égal à DGH, la droite DH sera égale à la droite DE. Je dis de plus que la droite EC est partagée en moyenne et extrême raison en D, et que DE est le plus grand segment. En effet, la droite ED est le côté d'un hexagone, et DC le côté d'un décagone (b). Ce qui est démontré dans les éléments. Ce qu'il fallait démontrer.

FIN DES LEMMES D'ARCHIMÈDE

COMMENTAIRE SUR LE LIVRE DES LEMMES.

PROPOSITION I.

(a) II est évident que le rayon FG prolongé ira au point de contact.

(b) Le manuscrit arabe ne parle que du cas où les circonférences du cercle se touchent intérieurement ; et cependant comme le cas où les cercles se touchent extérieurement est nécessaire dans la suite, je vais le démontrer.

Que les deux cercles ABE, DCE se touchent extérieurement au point E, et que leurs diamètres DC, AB soient parallèles. Joignons DE, EB. Je dis que la ligne DEB est une ligne droite. Joignons les centres de ces cercles par la droite GF ; cette droite passera par le point de contact E. Puisque les droites DC, AB sont parallèles, l'angle DGE sera égal à l'angle EFB ; mais les triangles DGE, EFB sont isolés. Donc les angles GDE, GED sont égaux entre eux et aux angles FEB, FBE. Donc l'angle GED est égal à l'angle FEB. Donc la somme des angles GED, GEB est égale à la somme des angles FEB, BEG. Mais la somme des angles FEB, BEG est égale à deux angles droits ; donc la somme des angles DEG, GEB est aussi égale à deux droits ; donc la ligne DEB est une ligne droite. Ce qu'il fallait démontrer.

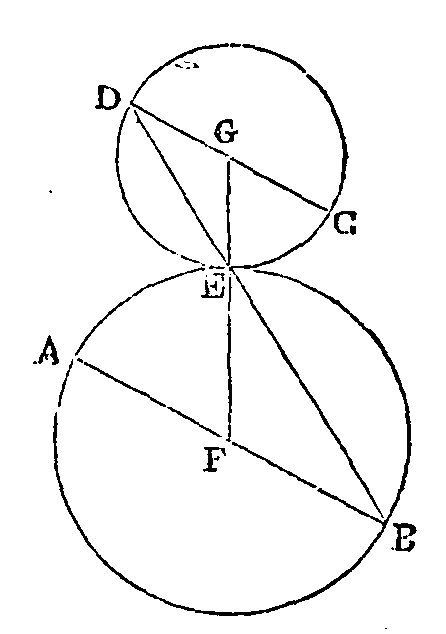
PROPOSITION II.

(a) Cette proposition a deux cas, le premier a lieu lorsque la perpendiculaire BE passe par le centre, et le second lorsque cette perpendiculaire ne passe pas par le centre. La démonstration du manuscrit arabe ne comprend que le premier cas ; la démonstration suivante qui comprend les deux cas est de Torelli.

Que CBA soit un demi-cercle ; que les droites DC, DB soient des tangentes; que BE soit perpendiculaire sur AC ; menons la droite AD qui rencontre la droite BE au point F; je dis que BF sera égal à FE.

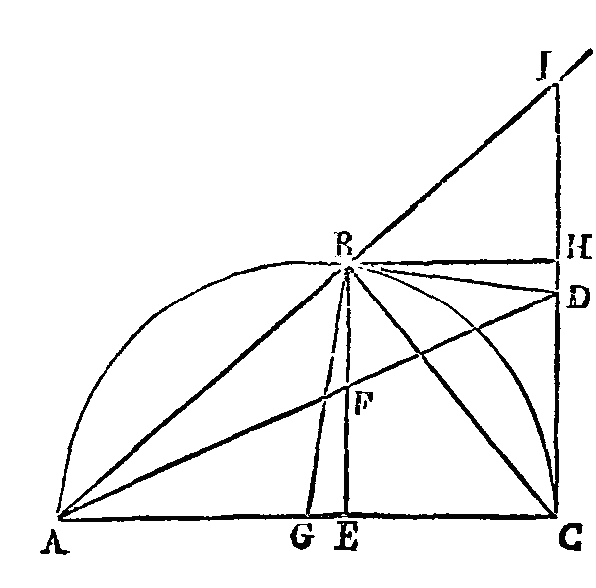
Menons la droite AB, et que cette droite prolongée rencontre CD au point I. Du point G, qui est le centre du demi-cercle CBA, menons GB, et du point B la droite BH parallèle à AC. Puisque l'angle EBH est égal à l'angle GBD, si l'on supprime l'angle commun EBD, l'angle DBH sera égal à l'angle GBE. Mais l'angle IBH est égal à l'angle ABG, puisqu'ils sont chacun égal à l'angle IAC ; donc l'angle IBD, qui est composé des deux angles DBH, IBH est égal à l'angle ABE qui est composé des deux angles GBE, ABG. Mais l'angle BID est égal à l'angle ABE ; donc l'angle IBD est égal à l'angle BID; car les choses qui sont égales à une troisième sont égales entre elles ; donc la droite BD est égale à la droite ID. Mais les droites BD, DC sont égales entre elles ; donc les droites ID, DC seront aussi égales entre elles. Mais les triangles AID, ABF sont semblables, ainsi que les triangles AIC, ABE, et encore les triangles ADC, AFE ; donc ID est à BF comme DC est à FE. Donc par permutation ID est à DC comme BF est à FE. Mais ID est égal à DC 5 donc BF est aussi égal à FE, ce qu'il fallait démontrer.

(b) En effet, l'angle DCB est égal à l'angle DBC, à cause de l'égalité des droites DB, DC. Mais l'angle DBG a pour complément l'angle DBC, et l'angle DGB a pour complément l'angle DCB, c'est-à-dire l'angle DBC ; donc les deux angles DBG, DGB ont le même complément. Donc ils sont égaux. Donc le côté GD est égal au côté DB. Mais le côté DB est égal au côté DC ; donc GD est égal à DC.

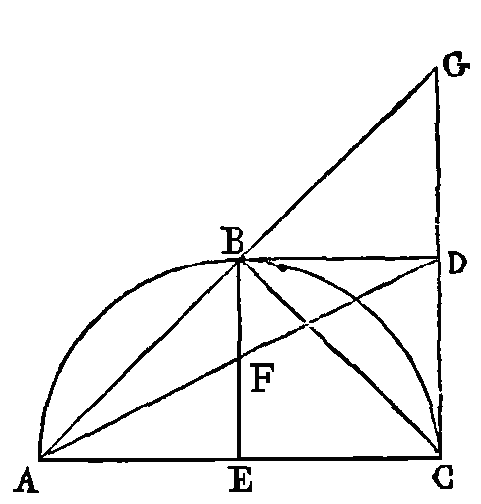
PROPOSITION IV

(a) Puisque AD x DC = BD², si nous ajoutons de part et d'autre AD x DC +AD² + DC², nous avons AD² + 2 AD x DC + DC² = BD² + AD x DC + AD² + DC², c'est-à-dire AC² = 2 x BD² + AD² + DC².

PROPOSITION V.

(a) Soit le triangle ABD ayant un angle aigu en D. Menons les droites AI, BF perpendiculaires sur les côtés BD, AD, et par les points D, E conduisons la droite DC ; je dis que la droite DC est perpendiculaire sur sa droite AB.

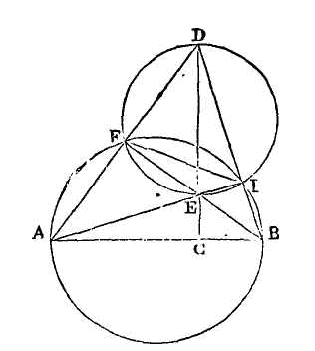
Autour de AB comme diamètre, décrivons une circonférence de cercle ; cette circonférence passera par les points F, I, à cause des angles droits AFB, AIB. Autour de DE, comme diamètre, décrivons aussi une circonférence de cercle, cette circonférence passera aussi par les points F, I, par la même raison.

Joignons FI. L'angle EDI est égal à l'angle IFE, parce que ces deux angles sont compris dans le même segment. Mais l'angle IFB est égal à l'angle BAI par la même raison ; donc les deux angles BAI, BDC sont égaux ; donc les deux triangles BAI, BDC sont semblables, puisqu'ils ont un angle égal de part et d'autre et un angle commun en B. Mais l'angle BIA est droit; donc l'angle BCD est droit aussi ; donc la droite DC est perpendiculaire sur AB.

Il suit évidemment de là que si des trois angles d'un triangle, on mène des perpendiculaires sur les côtés opposés, ces trois perpendiculaires se couperont en un seul et même point.

Supposons à présent que DC soit perpendiculaire sur AB, que BF soit perpendiculaire sur AD, et que AI soit perpendiculaire sur BI ; joignons ID ; je dis que la ligne BID est une ligne droite.

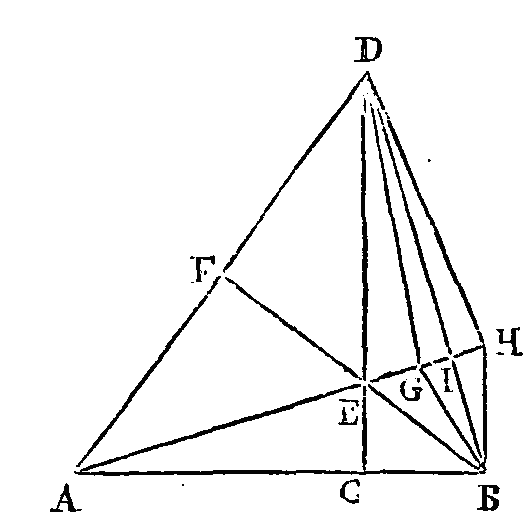
Que cela ne soit point. La droite qui joindra les points B, D passera du côté G ou du côté H. Supposons d'abord qu'elle passe du côté G et qu'elle soit BGD ; l'angle BGA sera droit. Mais l'angle BIA est droit par supposition ; donc l'angle extérieur BGA est égal à l'angle intérieur opposé BIA, ce qui est absurde. Supposons qu'elle passe du côté H et qu'elle soit BHD ; l'angle BHA sera droit. Mais l'angle BIH est droit aussi; donc l'angle extérieur BIA est égal à l'angle intérieur opposé BHA, ce qui est encore absurde. Donc la droite qui joint les points B, D ne passe ni du côté G ni du côté H ; donc elle passe par le point I ; donc la ligne BID est une ligne droite.

(b) Car puisque les droites AC, HE sont parallèles, la droite AD est à DH comme AC est à HE, et que les droites DB, HC sont aussi parallèles, la droite AD est à DH comme AB est à BC ; donc la raison de AD à DH, la raison de AC à HE et la raison de AB à BC sont égales entre elles.

PROPOSITION VI.

(a) Voyez la note (a) de la proposition précédente.

(b) Cette proposition pouvant se démontrer généralement, il était fort inutile de prendre des nombres pour exemple.

PROPOSITION XII.

(a) Soit le quadrilatère ABDC, de manière que AB soit égal à AC, et que l'angle BDC soit égal aux deux angles ABD, ACD pris ensemble. Je dis que AD est égal à AB ou à AC.

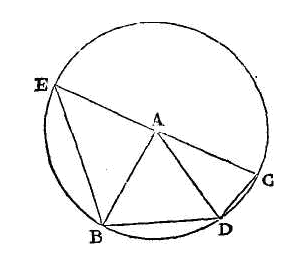
Prolongeons CA jusqu'à ce que son prolongement AE soit égal à AC, et joignons EB. Puisque AE est égal à AB, l'angle AEB est égal à l'angle ABE. Donc l'angle BDC avec l'angle AEB est égal aux trois angles DCA, DBA, ABE pris ensemble, c'est-à-dire aux deux angles DCA, DBE. Mais les quatre angles d'un quadrilatère valent quatre angles droits; donc deux angles opposés du quadrilatère BDCE valent deux angles droits. Donc on peut circonscrire une circonférence de cercle au quadrilatère BDCE. Mais les trois droites AC, AB, AE sont égales ; donc le point A est le centre de la circonférence DCE. Donc AD est égal à AB ou à AC.

PROPOSITION XIV.

(a) En effet, puisque DA est égal à 2 EC + CA, le carré de DA égalera 4EC² + 4 EC x CA + CA² ; et puisque EA est égal à EC + CA, le carré de EA égalera EC² + 2 EC x AC + CA². Donc la somme des carrés des droites DA, CA égalera 4 EC² + 4 EC x CA + CA² + CA², et la somme des carrés des droites DE, EA égalera EC² + EC²+ 2 CD x AC+ CA², c'est-à-dire que la somme des carrés des droites DE, BE égalera 2 EC + 2 EC x CA + CA². D'où il suit que la somme des carrés des droites DA, CA est double de la somme des carrés des droites DE, EA.

PROPOSITION XV.

(a) Car les deux angles BCD, BGD ont chacun pour supplément l'angle BAD.

(b) Euclide, liv. IV, prop. 11.

FIN DU COMMENTAIRE SUR LES LEMMES D'ARCHIMEDE.