ARCHIMÈDE

DES CORPS QUI SONT PORTÉS SUR UN FLUIDE.

LIVRE PREMIER.

HYPOTHÈSE PREMIÈRE.

On suppose que la nature d'un fluide est telle que ses parties étant également placées et continues entre elles, celle qui est moins pressée est chassée par celle qui l’est davantage. Chaque partie du fluide est pressée par le fluide qui est au-dessus suivant la verticale, soit que le fluide descende quelque part, soit qu'il soit chassé d'un lieu dans un autre.

PROPOSITION I

Si une surface est coupée par un plan toujours par le même point, et si la section est une circonférence de cercle, ayant pour centre le point par lequel passe le plan coupant, cette surface sera une surface sphérique.

Qu'une surface soit coupée par un plan mené par le point K, et que la section soit toujours une circonférence de cercle ayant pour centre le point K. Je dis que cette surface est une surface sphérique.

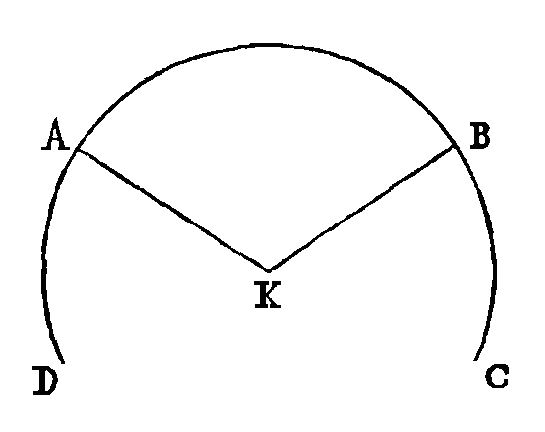
Car si cette surface n'est pas sphérique, les droites menées du point K à cette surface ne seront pas toutes égales. C'est pourquoi, que A, B soient des points dans cette surface, et que les droites AK, KB soient inégales. Par les droites AK, KB conduisons un plan qui fasse, dans cette surface, une section qui soit la ligne DABC. La ligne DABC sera une circonférence de cercle qui aura pour centre le point K ; parce que l'on a supposé que la section de cette surface était un cercle. Donc les droites AK, KB sont égales entre elles. Mais elles sont inégales; ce qui est impossible. Il est donc évident que cette surface est une surface sphérique.

PROPOSITION II.

La surface de tout fluide en repos est sphérique ; et le centre de cette surface sphérique est le même que le centre de la terre.

Supposons un fluide en repos. Que sa surface soit coupée par un plan conduit par le centre de la terre. Que le centre de la terre soit le point K, et que la section de cette surface soit la ligne ABCD. Je dis que la ligne ABCD est un arc de cercle dont le centre est le point K.

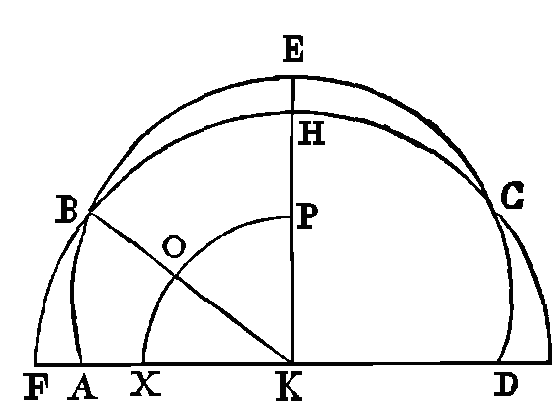
Car si cela n'est pas, les droites menées du point K à la ligne ABCD ne seront pas égales. Prenons une droite BK plus grande que certaines droites menées du point K à la ligne ABCD, mais plus petite que certaines autres; et du centre K, avec un intervalle égal à cette droite, décrivons un arc de cercle. L'arc de ce cercle sera en partie en dehors de la ligne ABCD et en partie en dedans; puisque le rayon de cet arc est plus grand que certaines droites menées du point K à la ligne ABCD, et plus petit que certaines autres. Que FBH soit l'arc de cercle dont nous venons de parler. Ayant joint les points B, K, menons les droites FK, KHE qui fassent des angles égaux avec la droite KB. Du centre K décrivons, dans un plan et dans le fluide, un arc XOP. Les parties du fluide qui sont dans l'arc XOP s'ont également placées et continues entre elles. Mais les parties qui sont dans l'arc XO sont pressées par le fluide qui est contenu dans ABOX, et les parties qui sont dans l'arc OP sont pressées par le fluide qui est contenu dans BEPO. Donc les parties du fluide qui sont dans l'arc XO et dans l'arc OP sont inégalement pressées. Donc celles qui sont moins pressées seront chassées par celles qui le sont davantage (hyp. 1). Donc le fluide ne restera pas en repos. Mais on a supposé qu'il était en repos; il faut donc que la ligne ABCD soit un arc de cercle ayant pour centre le point K. De quelque manière que la surface du fluide soit coupée par un plan conduit par le centre de la terre, nous démontrerons semblablement que la section sera une circonférence de cercle, et que son centre sera le même que celui de la terre. D'où il suit évidemment que la surface d'un fluide en repos est sphérique, et que le centre de cette surface est le même que le centre de la terre; puisque cette surface est telle qu'étant coupée toujours par le même point, sa section est un arc de cercle, ayant pour centre le point par lequel passe le plan coupant.

PROPOSITION III.

Si un corps qui, sous un volume égal, a la même pesanteur qu'un fluide (a), est abandonné dans ce fluide, il s'y plongera jusqu'à ce qu'il n'en reste rien hors de la surface du fluide; mais il ne descendra point plus bas.

Soit un corps de même pesanteur qu'un fluide. Supposons, si cela est possible, que ce corps étant abandonné dans ce fluide, une partie reste au-dessus de sa surface. Que ce fluide soit en repos. Supposons un plan qui, étant conduit par le centre de la terre, coupe le fluide et le corps plongé dans ce fluide, de manière que la section de la surface du fluide soit abcd et que la section de ce corps soit ehtf. Que le centre de la terre soit le point k. Que bhtc soit la partie du corps qui est dans le fluide, et que befc soit la partie qui est en dehors. Supposons une pyramide, qui ait pour base un parallélogramme placé dans la surface du fluide (b), et pour sommet le centre de la terre. Que les sections des faces de la pyramide, par le plan dans lequel est l'arc abcd, soient kl, km. Dans le fluide et au-dessous de ef, th, supposons une autre surface sphérique xop, ayant le point k pour, centre, de manière que xop soit la section de sa surface par le plan de l'arc abcd.

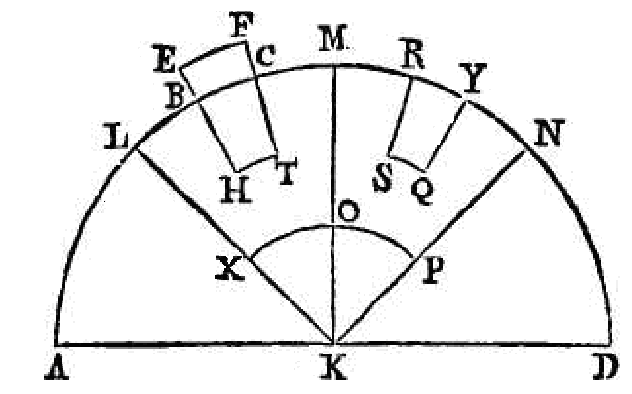
Prenons une autre pyramide égale et semblable à la première ; qu'elle lui soit contiguë et continue, et que les sections de ses plans soient km, kn. Supposons dans le fluide un autre solide rsqy composé du fluide, et égal et semblable à bhtc qui est la partie du corps ehtf plongé dans le fluide. Les parties du fluide qui, dans la première pyramide, sont contenues dans la surface xo et qui dans la seconde pyramide sont contenues dans la surface op, sont également placées et continues entre elles ; mais elles ne sont pas semblablement pressées. Car les parties du fluide contenues dans xo sont pressées par le corps ehtf, et par le fluide placé entre les surfaces xo, lm et entre les faces de la pyramide ; et les parties contenues dans po sont pressées par le solide rsqy et par le fluide placé entre op, pm, et entre les faces de la pyramide. Mais la pesanteur du fluide placé entre mn, op est plus petite que la pesanteur du fluide placé entre lm, xo solide; car le solide rsqy est plus petit que le solide ehtf, puisque rsqy est égal à bhtc, et l'on a supposé que, sous un volume égal, le corps plongé dans le fluide a là même pesanteur que ce fluide. Donc si on retranche les parties égales, les restes seront inégaux. Il est donc évident que la partie du fluide contenue dans la surface op sera chassée par la partie qui est contenue dans la surface xo ; et que le fluide ne restera pas en repos (1). Mais on a supposé qu'il était en repos; donc il ne reste rien du corps plongé dans le fluide, au-dessus de la surface de ce fluide. Cependant ce corps ne descendra point plus bas; car les parties du fluide, étant également placées, le pressent semblablement, puisque ce corps à la même pesanteur que le fluide.

PROPOSITION IV.

Si un corps plus léger qu'un fluide est abandonné dans ce fluide, une partie de ce corps restera au-dessus de la surface de ce fluide.

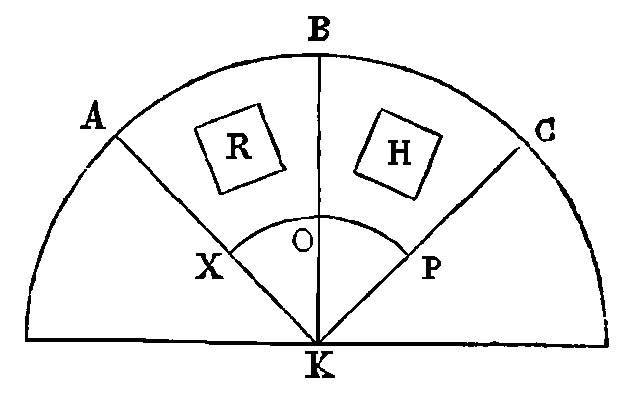
Soit un corps plus léger qu'un fluide ; que ce corps abandonné dans ce fluide soit submergé tout entier, si cela est possible, de manière que nulle partie de ce corps ne soit au-dessus de la surface du fluide. Que le fluide soit en repos. Supposons un plan qui, étant conduit par le centre de la terre, coupe le fluide et le corps plongé dans ce fluide. Que la section de la surface du fluide soit l'arc de cercle abc, et la section du corps, la figure ouest la lettre r. Que le centre de la terre soit k. Supposons, comme auparavant, une certaine pyramide qui comprenne la figure r, et dont le sommet soit le point k. Que les faces de cette pyramide soient coupés par le plan abc, suivant ak, kb; et prenons une autre pyramide qui lui soit égale et semblable, et dont les plans soient coupés par le plan abc, suivant les droites bk, kc. Dans le fluide et au-dessous du corps plongé dans le fluide, imaginons une surface sphérique, ayant pour centre le point k, et que cette surface sphérique soit coupée par le même plan abc suivant xop. Enfin, supposons dans la dernière pyramide un solide h qui soit composé du fluide et qui soit égal au corps r.

Les parties du fluide qui, dans la première pyramide, sont contenues dans la surface xo, et qui, dans la seconde pyramide, sont contenues dans la surface op, sont également placées et continues entre elles, et cependant elles ne sont pas semblablement pressées; car celles qui sont dans la première pyramide sont pressées par le corps r et par le fluide contenu dans cette pyramide en abox, et celles qui sont dans la seconde pyramide sont pressées par le corps h et par le fluide contenu dans cette pyramide en pobc. Mais la pesanteur du corps r est plus petite que la pesanteur du fluide contenu dans h, puisque le corps, sous un égal volume, est supposé plus léger que le fluide. Mais la pesanteur du fluide qui contient le solide r est égal à la pesanteur du fluide qui contient le solide h, puisque les pyramides sont égales. Donc la partie du fluide qui est dans la surface op est pressée davantage. Donc cette partie chassera la partie moins pressée, et le fluide ne restera pas en repos (î). Mais on a supposé que le fluide était en repos, donc le corps ne sera pas entièrement submergé, et une partie de ce corps restera au-dessus de la surface du fluide.

PROPOSITION V.

Si un corps plus léger qu'un fluide est abandonné dans ce fluide, il s'y enfoncera jusqu'à ce qu'un volume de liquide égal au volume de la partie du corps qui est enfoncé ait la même pesanteur que le corps entier.

Faisons la même construction qu'auparavant. Que le fluide soit en repos, et que le corps ehtf soit plus léger que le fluide. Si le fluide est en repos, ses parties, qui sont également placées, seront semblablement pressées. Donc le fluide contenu dans les surfaces xo, op est semblablement pressé. Donc le fluide contenu dans les surfaces xo, op, est pressé par un poids égal.

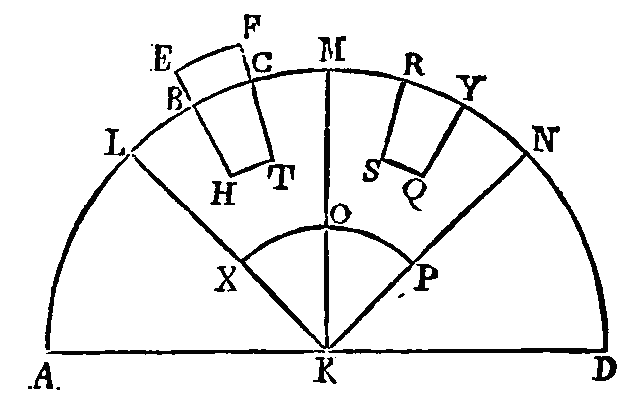
Mais la pesanteur du fluide qui est dans la première pyramide, le corps bhtc excepté, est égale à la pesanteur du fluide qui est placé dans la seconde pyramide, le fluide rsqy excepté. Il est donc évident que la pesanteur du corps ehtf est égale à la pesanteur du fluide rsqy. D'où il suit qu'un volume du fluide égale à la partie du corps qui est enfoncée a la même pesanteur que le corps entier.

PROPOSITION VI

Si un corps plus léger qu'un fluide est enfoncé dans ce fluide, ce corps remontera avec une force d'autant plus grande, qu'un volume égal du fluide sera plus pesant que ce corps.

Que le corps a soit plus léger qu'un fluide; que b soit la pesanteur du corps a, et que bc soit la pesanteur d'une partie du fluide, ayant un volume égal à celui de a. Il faut démontrer que le corps a, étant enfoncé dans le fluide, remontera avec une vitesse d'autant plus grande que la pesanteur c est plus grande.

Prenons une grandeur d dont la pesanteur soit égale à une grandeur composée de l'une et de l'autre grandeur, c'est-à-dire de a et de d sera plus légère que le fluide; car la pesanteur de la grandeur composée de ad est bc. Mais la pesanteur d'une partie du fluide ayant un volume égal à celui de ces deux grandeurs est plus grande que bc, parce que bc est la pesanteur d'une partie du fluide ayant, un volume égal à celui de a. 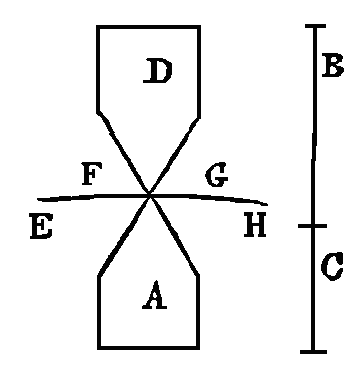Donc si l'on abandonne dans le fluide la grandeur composée de ad, elle s'y enfoncera jusqu'à ce qu'un volume du fluide égal à la partie submergée ait une pesanteur égale à celle de la grandeur entière, ainsi que cela a été démontré (5). Que la surface d'un fluide quelconque soit une portion de la circonférence efgh. Puisqu'un volume d'une partie du fluide égal à celui du corps a a la même pesanteur que les grandeurs a et d, il est évident que la partie submergée est le corps a, et que d tout entier est hors de la surface du fluide. Il est donc évident que le corps a remonte avec une force égale à la force d qui est au-dessus de efgh et qui le presse en bas ; puisque l'une de ces forces n'est point détruite par l'autre. Mais la grandeur d est portée en bas avec une pesanteur égale à c ; car on a supposé que la pesanteur d est égale à c. Donc la proposition est évidente.

PROPOSITION VII.

Si un corps plus pesant qu'un fluide est abandonné dans ce fluide, il sera porté en bas jusqu'à ce qu'il soit au fond; et ce corps sera d'autant plus léger dans ce fluide, que la pesanteur d'une partie du fluide, ayant le même volume que ce corps, sera plus grande.

Il est évident qu'un corps plus pesant qu'un fluide, étant abandonné dans ce fluide, sera porté en bas, jusqu'à ce qu'il soit au fond ; car les parties du fluide qui sont au-dessous sont plus pressées que les parties qui leur sont également adjacentes; puisque l'on a supposé que le corps est plus pesant que le fluide.

L'on démontrera que le corps est plus léger de la manière suivante. Soit un solide a plus pesant que le fluide ; que bc soit la pesanteur du corps a, et que b soit la pesanteur d'une partie du fluide, ayant un volume égal à celui de a. Il faut démontrer que le corps a, plongé dans le fluide, a une pesanteur égale.

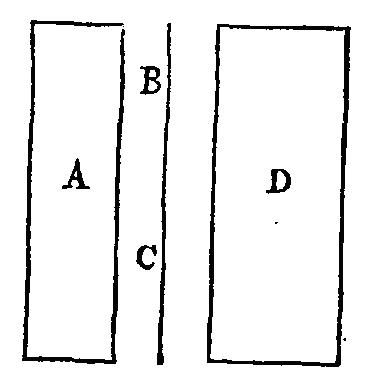
Prenons une autre grandeur d qui soit plus légère que le fluide, et dont la pesanteur soit égale à b ; que se soit la pesanteur d'une portion du fluide, ayant un volume égal à la grandeur d. Les deux grandeurs a, d étant réunies, la grandeur composée de ces deux grandeurs aura la même pesanteur que le fluide. Car la pesanteur de la somme de ces deux grandeurs est égale à la somme des pesanteurs bc et b. Mais la pesanteur d'une portion du fluide, ayant un volume égal à la somme de ces deux grandeurs, est égale à la somme des pesanteurs ; donc ces grandeurs étant abandonnées et plongées dans le fluide, auront la même pesanteur que le fluide, et elles ne seront portées ni en haut ni en bas ; parce que la grandeur a, qui est plus pesante que le fluide, sera portée en bas, et reportée en haut avec la même force par la grandeur d. Mais la grandeur d, plus légère que le fluide, sera portée en haut avec une force égale à la pesanteur c ; car on a démontré qu'un corps plus léger que le fluide est porté en haut avec une force d'autant plus grande, qu'une partie du fluide ayant un volume égal à ce corps, est plus pesante que ce même corps. Mais une portion du fluide qui a un volume égal à d est plus pesant que d de la pesanteur c ; il est donc évident que le corps a est porté en bas avec une pesanteur égale à c. Ce qu'il fallait démontrer.

HYPOTHÈSE II.

Nous supposons que les corps qui, dans un fluide, sont portés en haut, le sont chacun suivant la verticale qui passe par leurs centres de gravité.

PROPOSITION VIII.

Si une grandeur solide qui est plus légère qu'un fluide, et qui a la figure d'un segment sphérique, est abandonnée dans un fluide, de manière que la base du segment ne touche point le fluide, le segment sphérique se placera de manière que l'axe du segment ait une position verticale. Si l’on incline le segment de manière que la base du segment touche le fluide, il ne restera point incliné, s'il est abandonné à lui-même, et son axe reprendra une position verticale.[1]

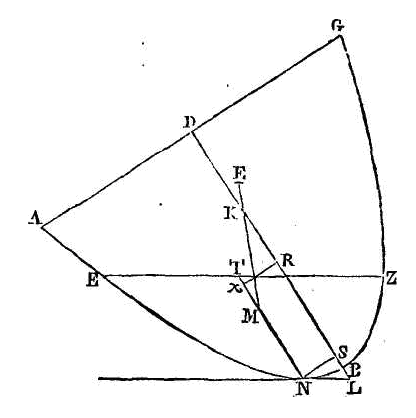
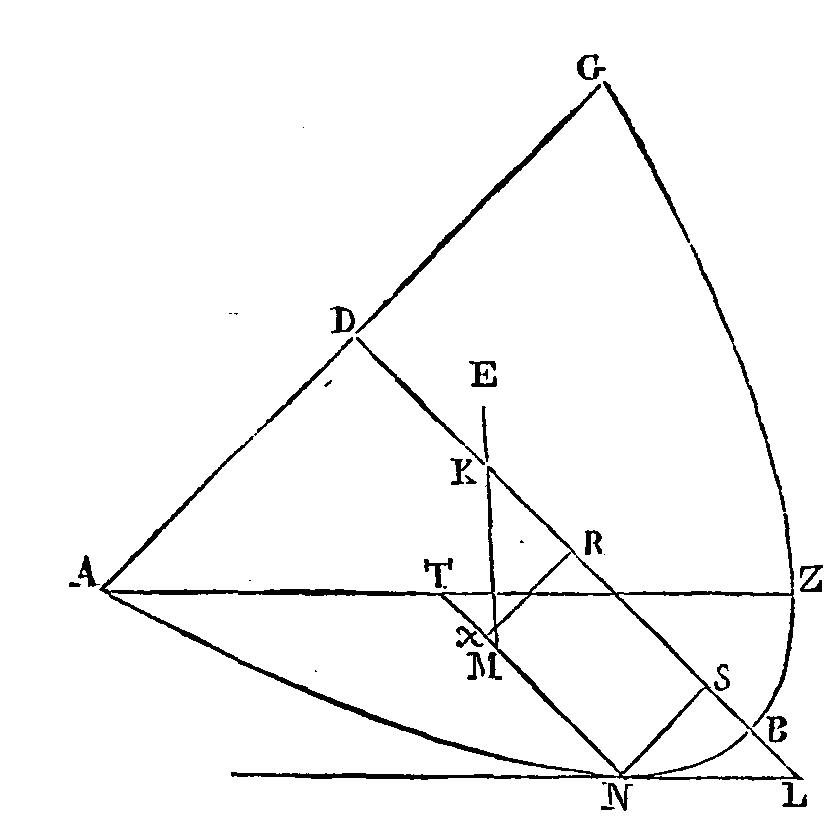
« Supposons qu'une grandeur telle que celle dont nous venons de parler, soit abandonnée dans un fluide. Conduisons un plan par l'axe du segment et par le centre de la terre. Que la section de la surface du fluide soit l'arc abcd ; que la section de la surface du segment soit l'arc efh; que eh soit une droite, et que ft soit l'axe du segment. Que le segment soit incliné de manière que son axe ft n'ait pat une position verticale. Il faut démontrer que le segment ne restera point en repos, et que son axe reprendra une position verticale.

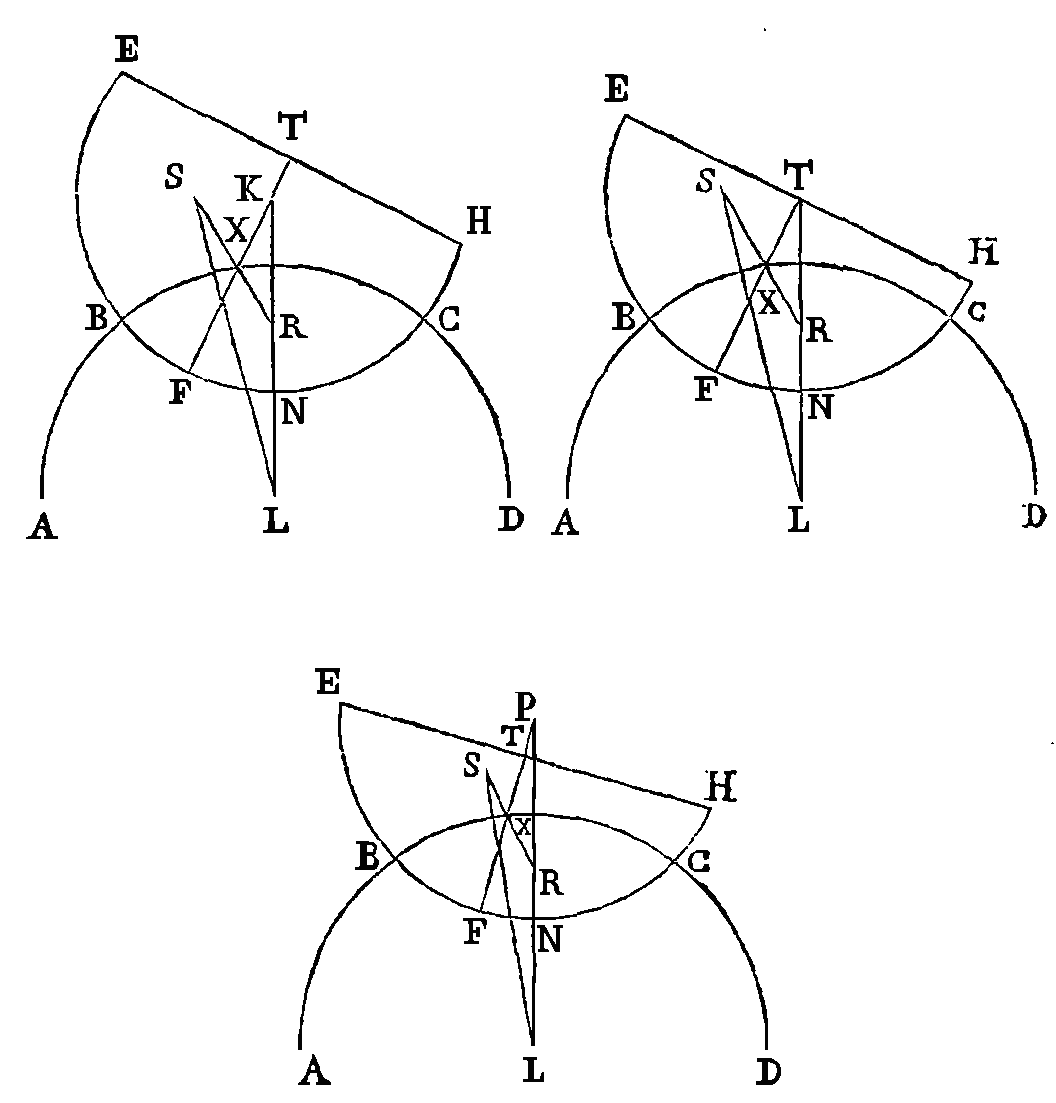
Le centre de la sphère est dans la droite ft. Supposons d'abord que le segment soit plus grand que la moitié de la sphère. Que le point t soit le centre de la sphère, dans la demi-sphère; que dans un segment plus petit le centre soit p, et que dans un segment plus grand le centre soit le point k. Par le point k et par le centre de la terre l, menons la droite kl qui coupe l'arc efh au point n. Puisqu'un segment sphérique quelconque a son axe dans la droite menée du centre perpendiculairement sur sa base, et qu'il a aussi, dans son axe, son centre de gravité, l'axe de la partie submergée qui est composée de deux segments sphériques, sera dans la verticale menée par le point k. D'où il suit que son centre de gravité sera dans la droite nk. Supposons qu'il soit en r. Or le centre de gravité du segment entier est dans la ligne ft entre k et f. Qu'il soit en x. Le centre de gravité du reste du segment qui est hors du fluide sera dans la ligne rx, prolongé vers le point x, jusqu'à ce que son prolongement soit à rx comme la pesanteur de la partie plongée dans le fluide est à la pesanteur de la partie qui est hors du fluide (a). Que le point s soit le centre de gravité de la figure dont nous venons de parler, et par le point s conduisons la verticale ls. La figure qui est hors du fluide sera portée en bas, par sa pesanteur, suivant la droite sl, et la partie submergée sera portée en haut suivant la droite rl (hyp. 2). Donc la figure ne restera pas en repos, puisque les parties qui sont vers e seront portées en bas, et celles qui sont vers h seront portées en haut (hyp. 2), et cela continuera jusqu'à ce que la droite ft ait une position verticale. On démontrera la même chose dans les autres segments sphériques.

PROPOSITION IX.

Si un segment sphérique plus léger qu'un fluide est abandonné dans ce fluide, de manière que la base entière soit dans le fluide, il se placera de manière que l'axe du segment ait une position verticale.

Qu'une grandeur telle que celle dont nous avons parlé, soit abandonnée dans un fluide; et supposons un plan mené par l'axe du segment et par le centre de la terre. Que l'arc abcd soit la section de la surface du fluide ; que l'arc efh soit la section de la surface du segment; que eh soit une ligne droite, et ft l'axe du segment. Supposons, si cela est possible, que ft n'ait pas une position verticale. Il faut démontrer que le segment ne restera point en repos, et que son axe reprendra une position verticale.

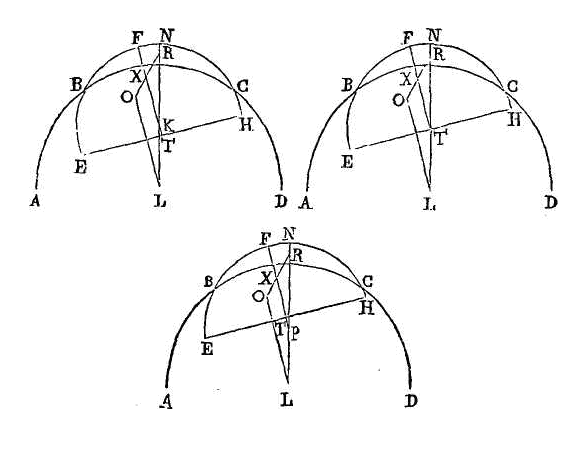
Le centre de gravité du segment sera dans la droite ft. Supposons d'abord que le segment soit plus grand que la moitié de la sphère. Que dans la demi-sphère, le centre soit le point t ; que dans un segment plus petit le centre soit le point p, et que dans un segment plus grand le centre soit le point k. Par le point k et par le centre de la terre l, menons kl. Le segment qui est hors de la surface du fluide a son axe dans la verticale menée par le point k. Il aura, d'après ce qui a été dit plus haut, son centre de gravité dans la droite nk. Que son centre de gravité soit le point r. Or, le centre de gravité du segment entier est dans la droite ft, entre k et f. Qu'il soit au point x. Le centre de gravité du reste du segment, c'est-à-dire de la partie qui est dans le fluide sera, dans la droite rx, prolongée vers le point x, jusqu'à ce que son prolongement soit à xr, comme la pesanteur de la partie du segment qui est hors du fluide est à la pesanteur du segment qui est dans le fluide (a). Que le point o soit le centre de gravité de la partie qui est hors du fluide ; et par le point o menons la verticale lo. La partie du segment qui est hors du fluide sera portée en bas, par sa pesanteur, suivant la droite kl, et la partie qui est dans le fluide sera portée en haut, par sa pesanteur, suivant la droite ol (hyp. 2, liv. i). Donc le segment ne restera pas en repos, puisque les parties qui sont vers h seront portées en bas, et celles qui sont vers e seront portées en haut, et cela continuera jusqu'à ce que ft ait une position verticale.

LIVRE SECOND.

PROPOSITION PREMIÈRE.

Si une grandeur solide quelconque plus légère qu'un fluide est abandonnée dans ce fluide, la pesanteur de cette grandeur sera à la pesanteur d'un volume égal de ce fluide, comme la partie de cette grandeur qui est submergée est à la grandeur entière.

Abandonnons dans un fluide une grandeur solide quelconque fa plus légère que ce fluide. Que a soit la partie submergée, et que f soit la partie qui est hors du fluide. Il faut démontrer que la pesanteur de la grandeur fa est à la pesanteur d'un volume égal de ce fluide comme a est à fa.

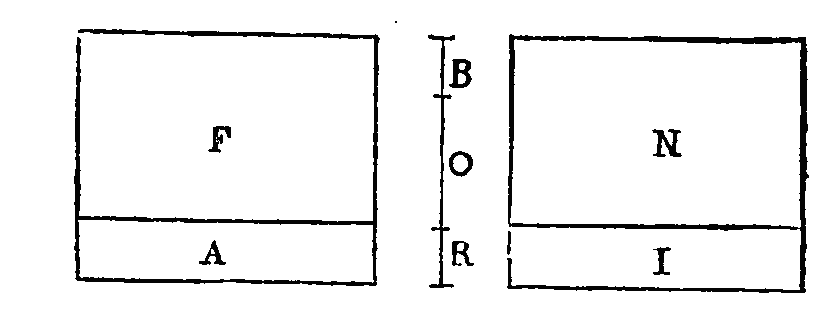
Prenons un volume ni du fluide qui soit égal à la grandeur fa; que n soit égal à f, et i égal à a. Que la pesanteur de fa soit b ; que la pesanteur de ni soit or, et que la pesanteur de i soit r. La pesanteur de fa sera à la pesanteur de ni comme b est à or. Mais puisque la grandeur fa abandonnée dans le fluide est plus légère que le fluide, il est évident qu'un volume du fluide égal à la partie de la grandeur fa qui est submergée, a la même pesanteur que la grandeur fa, ainsi que cela a été démontré plus haut (1, 5). Mais le fluide i dont la pesanteur est r répond à a, et la pesanteur de fa est b ; donc b qui est la pesanteur de la grandeur entière fa, sera égale à la pesanteur du fluide i, c'est-à-dire à r. Puisque la pesanteur de la grandeur fa est à la pesanteur du fluide ni qui lui est correspondant, comme b est à or; que b est égal à r, et que r est à or comme i est à .ni, et comme a est à fa, il s'ensuit que la pesanteur de fa sera à la pesanteur d'un volume égal du fluide comme la grandeur a est à la grandeur fa. Ce qu'il fallait démontrer.

PROPOSITION II.

Lorsqu'un segment droit (a) d'un conoïde parabolique n'a pas son axe plus grand que trois fois la moitié du demi-paramètre (b); si ce segment, quelle que soit sa pesanteur par rapport à celle d'un fluide, est abandonné dans ce fluide, et s'il est posé incliné de manière que sa base ne touche point le fluide, il ne restera point incliné, mais il se placera verticalement. Je dis qu'il est placé verticalement, lorsque sa base est parallèle à la surface du fluide.

Soit un segment droit d'un conoïde tel que celui dont nous venons de parler. Que ce segment soit posé incliné. Il faut démontrer qu'il ne restera point incliné, mais qu'il se placera verticalement.

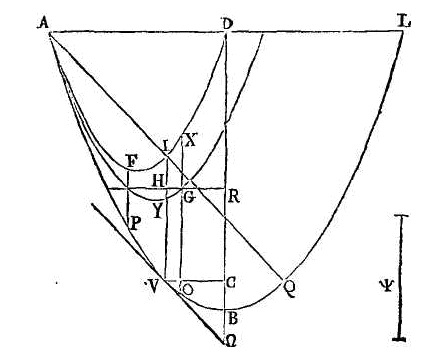
Conduisons par l'axe un plan perpendiculaire sur la surface du fluide (g); que la section du segment soit la parabole apol; que no soit l'axe du segment et le diamètre de la parabole, et que la section de la surface du fluide soit la droite is. Si le segment n'est pas vertical, la droite al ne sera point parallèle à is. Donc la droite no ne formera pas des angles droits avec la droite is.

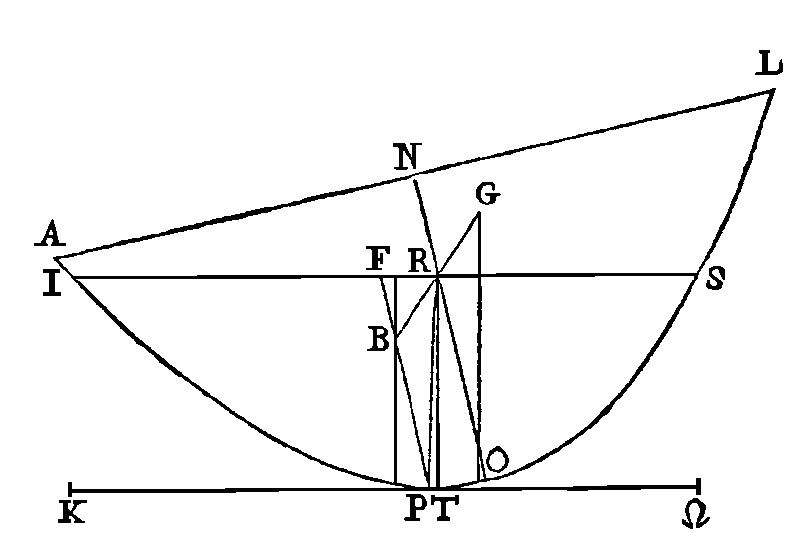
Conduisons une droite kw qui touche la parabole au point p[2] et qui soit parallèle à is. Du point p conduisons jusqu'à is la droite pf parallèle à on. Cette droite sera le diamètre de la parabole ipos, et l'axe de partie du segment qui est submergée. Prenons ensuite les centres de gravité (d); que le point r soit le centre de gravité du segment apol, et que le point B soit le centre de gravité du segment ipos. Conduisons la droite br, et prolongeons-la vers g. Que le point g soit le centre de gravité de la figure restante isla. Puisque la droite no est égale à trois fois la moitié de ro, et que cette droite est plus petite que trois fois la moitié du demi-paramètre, la droite ro sera plus petite que la moitié du paramètre. Donc l'angle rpω sera aigu (e). En effet, puisque la moitié du paramètre est plus grande que ro, la perpendiculaire menée du point r sur kω, c'est-à-dire rt, rencontrera la droite fp hors de la parabole; elle tombera par conséquent entre le point p et le point ω. Donc si par les points b, g, on conduit des parallèles à rt, ces parallèles feront des angles droits avec la surface du fluide, et la partie qui est dans le fluide sera portée en haut, selon la perpendiculaire menée par le point b, parallèlement à rt (liv. 1, hyp. 2); et la partie qui est hors du fluide sera portée en bas, suivant la perpendiculaire menée par le pointe Donc le segment apol ne restera point en repos, puisque ce qui est vers a sera porté en haut et que ce qui est vers l sera porté en bas, jusqu'à ce que no ait une position verticale » (z).

PROPOSITION III.

Lorsqu'un segment droit d'un conoïde parabolique n'a pas son axe plus grand que trois fois la moitié du paramètre, si ce segment, quelle que soit sa pesanteur par rapport à celle d'un fluide, est abandonné dans ce fluide, si sa base est toute entière dans le fluide, et s'il est posé incliné, il ne restera point incliné, mais il se placera de manière que son axe ait une position verticale (a).

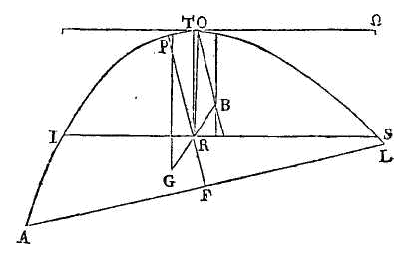
Abandonnons dans un fluide un segment tel que celui dont nous venons de parler. Que sa base soit dans le fluide. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que pf soit l'axe du segment et le diamètre de la parabole; et que la section de la surface du fluide soit la droite is. Si le segment est incliné, son axe n'aura pas une position verticale. Donc la droite pf ne formera pas des angles droits avec la droite is. Conduisons une droite kω parallèle à is et tangente à la parabole apol au point o. Que le point r soit le centre de gravité du segment apol, et le point B le centre de gravité de ipos. Joignons la droite br; prolongeons cette droite, et que le point g soit le centre de gravité de la figure restante isla. On démontrera semblablement que l'angle rok sera aigu, et que la perpendiculaire menée du point r sur kω tombera entre k et ω. Que cette perpendiculaire soit rt. Si des points g, b, on conduit des parallèles à rt, la partie du segment qui est dans le fluide sera portée en haut (liv. i, hyp. 2), suivant la perpendiculaire menée par le point g, et la partie qui est hors du fluide sera portée en bas, suivant la perpendiculaire menée par le point B. Donc le segment apol, ainsi posé dans le fluide ne restera point en repos; puisque ce qui est en a sera porté en haut, et ce qui est en l sera porté en bas, jusqu'à ce que la droite pf ait une position verticale.

PROPOSITION IV.

Lorsqu'un segment droit d'un .conoïde parabolique plus léger qu'un fluide, a son axe plus grand que trois fois la moitié du demi-paramètre; si la raison de la pesanteur de ce segment à la pesanteur d'un volume égal du fluide n'est pas moindre que la raison du carré de l'excès de l'axe sur trois fois la moitié du demi-paramètre au carré de l'axe; si ce segment étant abandonné dans ce fluide, sa base ne touche pas le fluide, et s'il est posé incliné, il ne restera pas incliné, mais il se placera verticalement.

Soit un segment d'un conoïde parabolique tel que celui dont nous venons de parler. Supposons, s'il est possible, que ce segment étant abandonné dans le fluide ne soit pas placé verticalement, mais bien incliné. Conduisons par l'axe un plan qui soit perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que la droite no soit l'axe du segment et le diamètre de la parabole, et que la section de la surface du fluide soit la droite is. Si le segment n'est pas placé verticalement, la droite no ne fera point des angles égaux avec la droite is. Conduisons la droite kw tangente à la parabole en un point p, et parallèle à la droite is, et du point p conduisons la droite pf parallèle à la droite on. Prenons les centres de gravité : que le point r soit le centre de gravité du segment apol, et le point b le centre de gravité du segment qui est dans le fluide. Menons la droite br, prolongeons cette droite vers g, et que le point g soit le centre de gravité de la grandeur solide qui est hors du fluide.

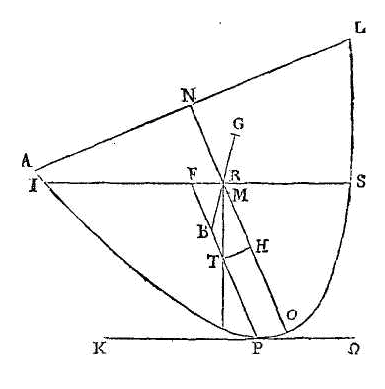
Puisque la droite no est égale à trois fois la moitié de ro, et que no est plus grande que trois fois la moitié du demi-paramètre, il est évident que la droite no est plus grande que le demi-paramètre. Que la droite rh soit égale au demi-paramètre, et que oh soit double de hm. Puisque no est égal à trois fois la moitié de ro, et que mo est aussi égal à trois fois la moitié de ho, la droite restante nm sera égale à trois fois la moitié de rh (a). Donc l'excès de l'axe sur trois fois la moitié du demi-paramètre est d'autant plus grand que la droite mo est plus grande (b). Mais on a supposé que la raison de la pesanteur du segmenta la pesanteur d'un volume égale du fluide, n'est pas moindre que la raison du carré construit sur l'excès de l'axe sur trois fois la moitié du demi-paramètre au carré construit sur l'axe; il est donc évident que la raison de la pesanteur du segment à la pesanteur d'un pareil volume du fluide n'est pas moindre que la raison du carré construit sur mo au carré construit sur no (g). Mais la raison de la pesanteur du segment à la pesanteur d'un volume égal du fluide est la même que la raison de la partie submergée au segment entier, ainsi que cela a été démontré plus haut (2, 1), et la raison de la partie submergée au segment entier est la même que la raison du carré pf au carré de no, parce qu'on a démontré dans le Traité des Conoïdes et des Sphéroïdes, que si un conoïde parabolique est partagé en deux parties par des plans menés d'une manière quelconque, les segments sont entre eux comme les carrés construits sur les axes. Donc la raison du carré de pf au carré de no n'est pas moindre que la raison du carré de mo au carré de no. Donc pf n'est pas plus petit que mo, ni bp plus petit que ho (d). Donc si du point h on conduit une perpendiculaire sur no, elle rencontrera bp, et elle tombera entre b et p (e). Que cette perpendiculaire rencontre la droite bp au point t. Puisque pf est parallèle à l'axe, que ht lui est perpendiculaire, et que rh est égal au demi-paramètre, si la droite menée du point r au point t est prolongée, elle fera des angles droits avec la tangente à la parabole au point p (z). Donc cette droite fera des angles droits avec la droite is, et avec la surface du fluide qui passe par la droite is. Donc si par les points b, g, on conduit des parallèles à rt, ces parallèles feront des angles droits avec la surface du fluide, et la partie du segment qui est dans le fluide sera portée en haut, suivant la droite menée par le point b parallèlement à rt, et la partie qui est hors du fluide sera portée en bas, suivant la droite menée par le point g, jusqu'à ce que le segment droit du conoïde soit placé verticalement.

PROPOSITION V.

Lorsqu'un segment droit d'un conoïde parabolique plus léger qu'un fluide a son axe plus grand que trois fois la moitié du demi-paramètre ; si la raison de la pesanteur du segment à la pesanteur du fluide n'est pas plus grande que la raison de l'excès du carré de l'axe sur le carré de l'excès de l'axe sur trois fois la moitié du demi-paramètre au carré de l'axe; si ce segment étant abandonné dans le fluide, sa base est toute entière dans ce fluide, et s'il est posé incliné, il ne restera point incliné, mais il se placera de manière que son axe ait une position verticale.

Abandonnons dans un fluide un segment tel que celui dont nous venons de parler, et que sa base soit toute entière dans le fluide. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que la droite no soit l'axe du segment et le diamètre de la parabole, et que la section de la surface du fluide soit la droite is. Puisque l'axe n'a point une position verticale, la droite no ne fera pas des angles droits avec la droite is. Conduisons la droite kw tangente à la parabole en un point p et parallèle à is. Par le point p menons la droite pf parallèle à no, et prenons les centres de gravité : que le point r soit le centre de gravité de apol, et le point b le centre de gravité de la partie qui est hors du fluide. Menons la droite br ; prolongeons-la vers le point g, et que ce point soit le centre de gravité de la partie du segment qui est dans le fluide. Prenons rh égal au demi-paramètre ; que oh soit double de hm, et faisons le reste comme nous l'avons dit plus haut.

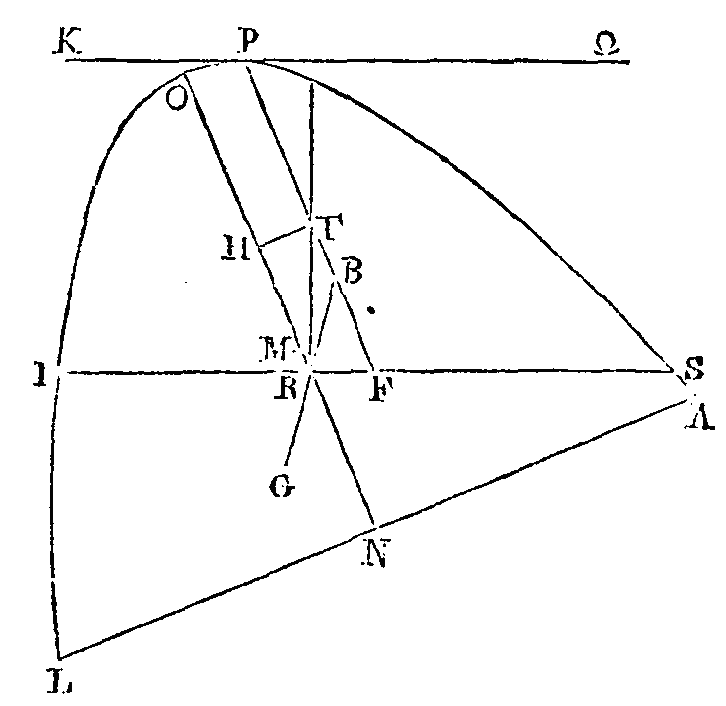
Puisque l’on a supposé que la raison de la pesanteur du segment à la pesanteur du fluide n'est pas plus grande que la raison de l'excès du carré de no sur le carré de mo au carré de no (a), et que l’on a démontré dans la première proposition que la pesanteur du segment est à la pesanteur d'un volume égal du fluide comme la partie du segment qui est submergée est au segment entier, la raison de la partie submergée au segment entier ne sera pas plus grande que la raison dont nous venons de parler. Donc la raison du segment entier à la partie qui est hors du fluide ne sera pas plus grande que la raison du carré de no au carré de mo (b). Mais la raison du segment entier à la partie qui est hors du fluide est la même que la raison du carré de no au carré de pf (g) ; donc la raison du carré de no au carré de pf n'est pas plus grande que la raison du carré de no au carré de mo. D'où il suit que pf n'est pas plus petit que om, ni pb plus petit que oh. Donc la perpendiculaire élevée du point h sur la droite no, rencontrera la droite bp entre les points p et b. Que cette perpendiculaire rencontre bp au point t. Puisque dans la parabole la droite pf est parallèle au diamètre no, que la droite ht est perpendiculaire sur le diamètre, et que la droite rh est égale au demi-paramètre, il est évident que rt prolongée fera des angles droits avec kpω, et par conséquent avec is. Donc rt est perpendiculaire sur la surface du fluide. Donc si par les points b, g, on mène les droites parallèles à rt, ces parallèles seront perpendiculaires sur la surface du fluide. Donc la portion du segment qui est hors du fluide sera portée en bas, suivant la perpendiculaire menée par le point b, et la portion qui est dans le fluide sera portée en haut, suivant la perpendiculaire menée par le point g (liv. i, hyp. 2). Donc le segment apol, ne restera point en repos; mais il se mouvra dans le fluide jusqu'à ce que l'axe no ait une position verticale.

PROPOSITION VI.

Lorsqu'un segment droit d'un conoïde parabolique plus léger qu'un fluide a son axe plus grand que trois fois la moitié du demi-paramètre, mais cependant trop petit pour qu'il soit au demi-paramètre comme quinze est à quatre; si ce segment étant abandonné dans ce fluide, sa base touche la surface du fluide, il ne restera jamais incliné de manière que la base touche la surface du fluide en un seul point.

Soit un segment tel que celui dont nous venons de parler. Abandonnons-le dans le fluide, comme nous l'avons dit, de manière que la base touche le fluide en un seul point. Il faut démontrer que le segment ne gardera point cette position, mais qu'il tournera jusqu'à ce que sa base ne touche en aucune manière la surface du fluide.

Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que la section de la surface du fluide soit la droite as, et que no soit l'axe du segment et le diamètre de la parabole. Coupons no en un point f, de manière que of soit double de fn, et en un point ω, de manière que no soit à fω comme quinze est à quatre. Menons ωk perpendiculaire sur no. La raison de no à fω sera plus grande que la raison de no au demi-paramètre. Que fb soit égal au demi-paramètre. Menons la droite pc parallèle à as et tangente à la parabole apol en un point p, et la droite pi parallèle à no. Que la droite pi coupe d'abord kω au point h.

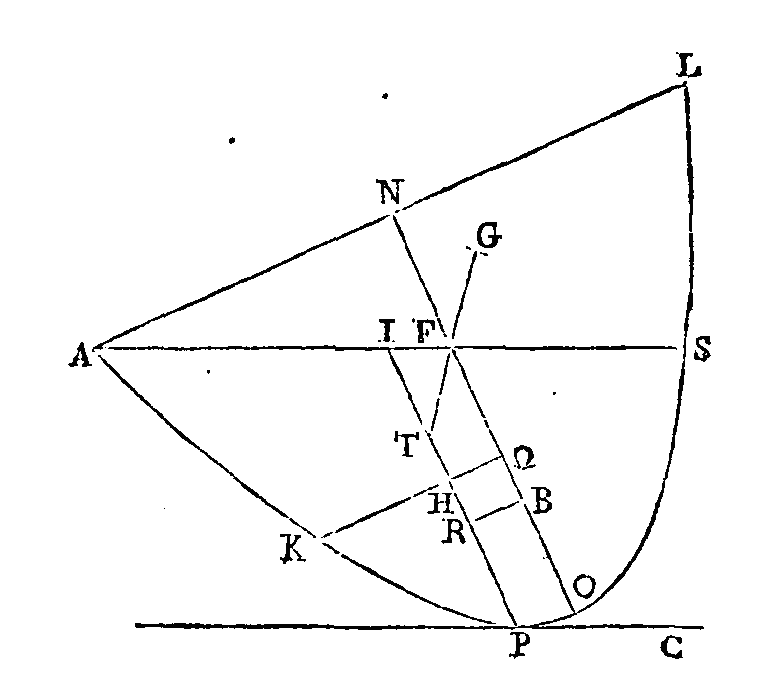
Puisque dans le segment apol qui est compris par une droite et par une parabole, la droite kω est parallèle à al; que la droite pi est parallèle au diamètre; que cette droite est coupée au point h par la droite kω, et que as est parallèle à la tangente au point p, il faut nécessairement que la raison de pi à ph soit la même que la raison de no à ωo, ou qu'elle soit plus grande, car cela a déjà été démontré (a). Mais nω est égala trois fois la moitié de ωo ; donc pi est égal à trois fois la moitié de hp ou plus grand que trois fois la moitié(b); donc ph est double de hi ou plus petit que le double. Que pt soit double de ti; le point t sera le centre de gravité de la partie qui est dans le fluide. Menons la droite tf; prolongeons cette droite; que le point g soit le centre de gravité de la partie qui est hors du fluide, et du point b élevons la droite br perpendiculaire sur no. Puisque pi est parallèle au diamètre no ; que br lui est perpendiculaire, et que fb est égal au demi-paramètre, il est évident que fr prolongé fera des angles égaux avec la tangente à la parabole apol au point p, et par conséquent avec as et avec la surface du fluide. Mais les droites menées par les points t, g parallèlement à fr seront perpendiculaires sur la surface du fluide; donc la partie du segment apol qui est dans le fluide sera portée en haut suivant la perpendiculaire, menée par le point t (liv. i, hyp. 2), et la partie qui est hors du fluide sera portée en bas suivant la perpendiculaire menée par le point g.

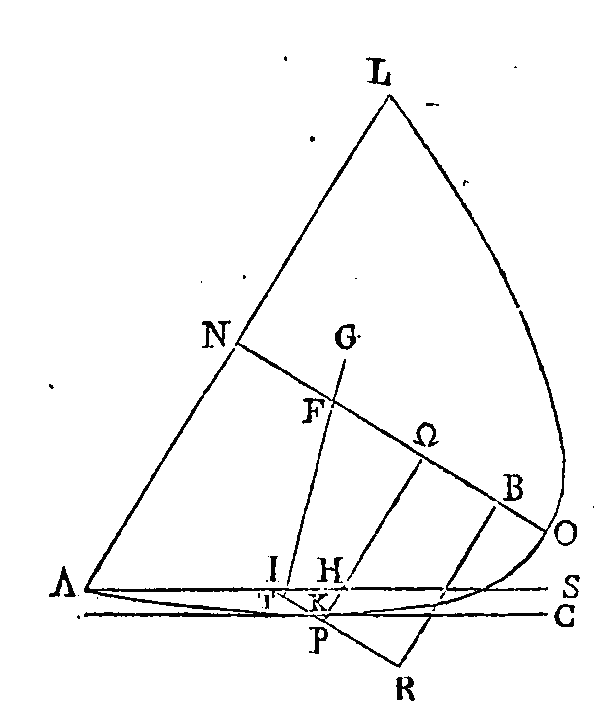
Donc le segment solide apol tournera et sa base ne touchera en aucune manière la surface du fluide. Mais si la droite pi ne coupe pas la droite kω, comme dans la seconde figure, il est évident que le point t, qui est le centre de gravité de la partie submergée tombera entre le point p et le point i, et l’on démontrera le reste d'une manière semblable.

PROPOSITION VII.

Lorsqu'un segment droit d'un conoïde parabolique plus léger qu'un fluide a son axe plus grand que trois fois la moitié du demi-paramètre, mais cependant trop petit pour qu'il soit au demi-paramètre comme quinze est à quatre; si ce segment étant abandonné dans un fluide, sa base entière est dans le fluide, le segment ne restera jamais incliné de manière que sa base touche le fluide; mais sa base sera toute entière dans le fluide et ne touchera sa surface en aucune manière.

Soit un segment tel que celui dont nous venons de parler. Qu'il soit abandonné dans un fluide comme nous l'avons dit, de manière que sa base touche la surface du fluide en un seul point. Il faut démontrer qu'il ne gardera point cette position, mais qu'il tournera jusqu'à ce que sa base ne touche en aucune manière la surface du fluide.

Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que la section de la surface du fluide soit la droite as, et que la droite pf soit l’axe du segment et le diamètre de la parabole. Coupons pf en un point r de manière que rp soit double de rf, et en un point ω, de manière que pf soit à rω comme quinze est à quatre. Menons la droite ωk perpendiculaire sur pf. La droite rω sera plus petite que le demi-paramètre. Prenons une droite rh qui soit égale au demi-paramètre; menons la droite co tangente à la parabole au point o et parallèle à sl, et menons aussi la droite no parallèle à pf. Que cette droite coupe d'abord au point i la droite kω. Nous démontrerons, comme auparavant, que la droite no est ou égale à trois fois la moitié de oi, ou plus grande que deux fois la moitié. Que la droite oi soit plus petite que le double de in; que ob soit double de bn, et faisons les mêmes choses qu'auparavant.

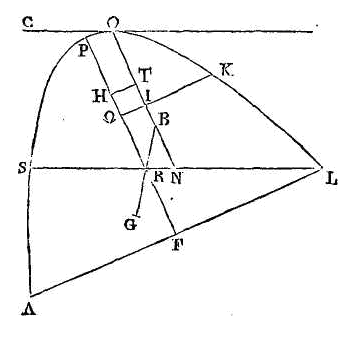
Si l'on mène la droite rt, nous démontrerons semblablement que cette droite sera perpendiculaire sur co et sur la surface du fluide. Donc les droites menées par les points b, g parallèlement à rt, seront perpendiculaires sur la surface du fluide. Donc la partie du segment qui est hors du fluide sera portée en bas suivant la perpendiculaire qui passe par le point b, et la partie qui est dans le fluide sera portée en haut suivant la perpendiculaire qui passe par le point g (liv. 1, hyp. 2). D'où il suit évidemment que le segment tournera jusqu'à ce que sa base ne touche en aucune manière la surface du fluide, parce que sa base touchant le fluide en un point, le segment est porté en bas du côté l. Si la droite no ne coupait point la droite ωk, on n'en démontrerait pas moins les mêmes choses.

PROPOSITION VIII.

Lorsqu'un segment droit d'un conoïde parabolique a son axe plus grand que trois fois la moitié du demi - paramètre, mais cependant trop petit pour qu'il soit au demi-paramètre comme quinze est à quatre; si la raison de la pesanteur du segment à la pesanteur du fluide est moindre que la raison du carré de l'excès de l'axe sur trois fois la moitié du demi-paramètre au carré de l'axe; si ce segment étant abandonné dans le fluide, sa base ne touche point le fluide, il ne se placera point verticalement, et il ne restera point incliné, à moins que l'axe ne fasse avec la surface du fluide un angle égal à celui dont nous parlerons plus bas.

Soit un segment tel que celui dont nous venons de parler. Que bd soit égal à l'axe; que bk soit double de kd; que rk soit égal au demi-paramètre, et que cb soit égal à trois fois la moitié de br. La droite cd sera égale à trois fois la moitié de kr (a). Que la raison du carré de fq au carré de db soit la même que la raison de la pesanteur du segment à la pesanteur du fluide ; et que f soit double de q. Il est évident que la raison de fq à db sera moindre que la raison de cb à bd ; car cb est l'excès de l'axe sur trois fois la moitié du demi-paramètre (b). Donc fq est plus petit que bc, et par conséquent f est plus petit que br. Que RΨ soit égal à f ; conduisons la droite ΨE perpendiculairement sur bd ; que le carré de ΨE soit la moitié du rectangle compris sous KR, ΨB, et joignons be. Il faut démontrer que lorsque le segment est abandonné dans le fluide comme nous Tarons dit, il restera incliné de manière que l'axe fera avec la surface du fluide un angle égal à l’angle EBΨ.

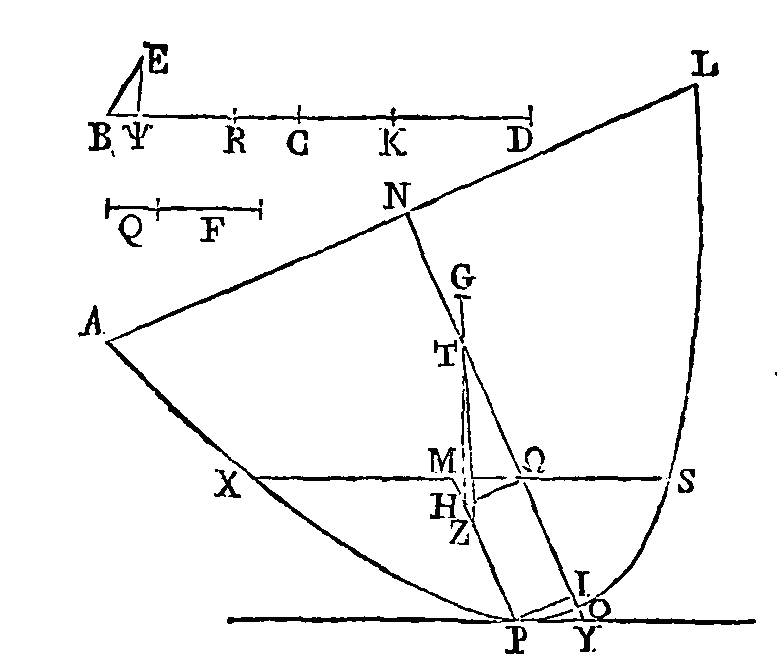
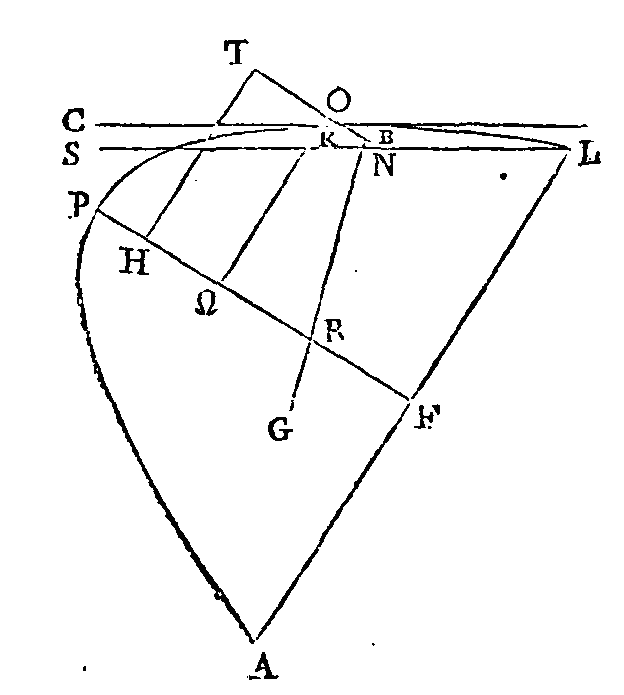
Abandonnons le segment dans le fluide de manière que sa base ne touche point la surface du fluide ; que l’axe ne fasse point avec la surface du fluide un angle égal à l'angle EBΨ, si cela est possible, et supposons qu'il fasse d'abord un angle plus grand. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide ; que la section du segment soit la parabole apol ; que la section de la surface du fluide soit la droite xs, et que no soit l'axe du segment et le diamètre de la parabole. Menons la droite py parallèle à xs et tangente à la parabole apol en un point p ; la droite pm parallèle à no et la droite pi perpendiculaire sur no. Que de plus la droite br soit égale à ΟΩ ; la droite rk égale à TΩ, et que ΩH soit perpendiculaire sur l'axe. Puisqu'on suppose que l'axe du segment fait avec la surface du fluide un angle plus grand que l'angle B, l'angle pyi sera plus grand que l'angle B. Donc la raison da carré de pi au carré de yi est plus grande que la raison du carré de EΨ au carré de ΨB. Mais la raison du carré pi au carré de iy est la même que la raison de kr à iy (g), et la raison du carré de EΨ au carré de ΨB est la même que la raison de la moitié de kr à ΨB (d); donc la raison de kr à iy est plus grande que la raison de la moitié de KR à ΨB. Donc iy est plus petit que le double de ΨB. Mais yi est double de oi, donc oi est plus petit que ΨB, et IΩ plus grand que ΨR. Mais ΨR est égal à f; donc iΩ est plus grand que f. Mais, par supposition, la pesanteur du segment est à la pesanteur du fluide comme le carré de fq est au carré de bd ; la pesanteur du segment est à la pesanteur du fluide comme la partie submergée est au segment entier (2, 1), et la partie submergée est au segment entier comme le carré de pm est au carré de on. Il s'ensuit donc que le carré de pm est au carré de on comme le carré de fq est au carré de bd. Donc fq est égal à pm. Mais on a démontré que ph est plus grand que f ; il est donc évident que pm est plus petit que trois fois la moitié de ph, et par conséquent ph est plus grand que le double de hm. Que pz soit double de zm. Le point t sera le centre de gravité du segment entier, le point z le centre de gravité de la partie qui est dans le fluide, et le centre de gravité de la partie restante sera dans la droite zt prolongée jusqu'en g. On démontrera de la même manière que la droite th est perpendiculaire sur la surface du fluide. Donc la partie du segment qui est plongée dans le fluide sera portée hors du fluide suivant la perpendiculaire menée par le point z sur la surface du fluide (liv. i, hyp. 2); et la partie qui est hors du fluide sera portée dans le fluide suivant la perpendiculaire menée par le point g. Donc le segment ne restera pas incliné, ainsi qu'on l'a supposé, mais il ne se placera pas verticalement, parce que parmi les perpendiculaires menées par les points z, g, celle qui est menée par le point z tombe du côté où est le point l, et celle qui est menée par le point g tombe du côté où est le point a. D'où il suit que le centre de gravité z est porté en haut, et que le centre de gravité g est porté en bas. Donc toutes les parties du segment qui sont vers le point a seront portées en bas, et toutes les parties qui sont vers le point l seront portées en haut.

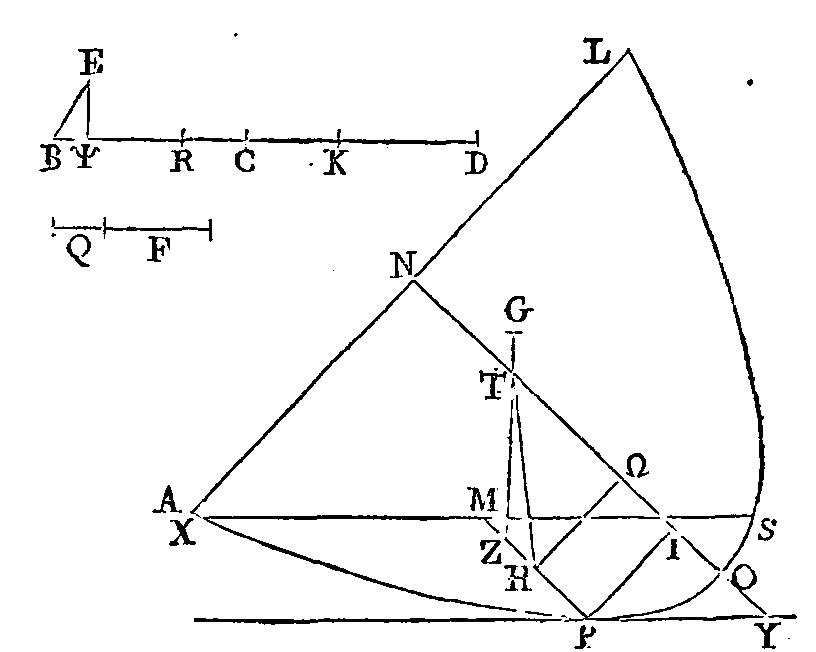
Que l'axe du segment fasse avec la surface du fluide un angle plus petit que l'angle b, le reste étant supposé comme auparavant. La raison, du carré de pi au carré de iy, sera moindre que la raison du carré de EΨ au carré de ΨB. Donc la raison de kr à iy est moindre que la moitié de kr à ΨB. Donc iy est plus grand que le double de ΨB. Mais iy est double de oi; donc oi sera plus grand que ΨB. Mais la droite entière OΩ est égale à rb, et la droite restante ΩI est plus petite que ΨR ; donc la droite ph sera plus petite que f. Donc puisque mp est égal à fq, il est évident que pm sera plus grand que trois fois la moitié de ph, et que ph sera plus petit que hm. Que pz soit double de zm ; le point t sera le centre de gravité du segment entier, et le point z le centre de gravité de la partie qui est dans le fluide. Joignons la droite zt, et cherchons le centre de gravité de la partie qui est hors du fluide dans le prolongement de cette droite. Que le point g soit son centre de gravité. Par les points z, g menons des perpendiculaires sur la surface du fluide, ces perpendiculaires seront parallèles à th. Il suit de là que le segment ne restera point en repos, mais qu'il tournera jusqu'à ce que son axe fasse avec la surface du fluide un angle plus grand que celui qu'il fait actuellement.

Mais on avait supposé auparavant que l'axe faisait un angle plus grand que l'angle b, et alors le segment ne restait point en repos; il est donc évident que le segment restera en repos, si l'axe fait avec la surface du fluide un angle égal à l'angle b ; car de cette manière la droite io sera égale à ΨB; la droite ΩI égale à ΨR, et la droite ph égale à f. Donc la droite mp sera égale à trois fois la moitié de ph, et la droite ph double de hm. Donc puisque le point h est le centre de gravité de la partie qui est dans le fluide, la partie qui est dans le fluide sera portée en haut, et la partie qui est hors du fluide sera portée en bas, suivant la même perpendiculaire. Donc le segment restera en repos, parce qu'une partie n'est point chassée par l'autre.

PROPOSITION IX

Lorsque le segment droit d'un conoïde parabolique a son axe plus grand que trois fois la moitié du demi-paramètre mais trop petit pour que la raison de l'axe au demi-paramètre soit la même que la raison de quinze à quatre; si la raison de la pesanteur du segment à la pesanteur du fluide est plus grande que la raison de l'excès du carré de l'axe sur le carré de l'excès de l'axe sur trois fois la moitié du demi-paramètre au carré de l'axe ; si ce segment étant abandonné dans le fluide, sa base est toute entière dans le fluide, et s'il est posé incliné, il ne tournera point pour se placer verticalement, et il ne restera incliné que lorsque son axe fera avec la surface du fluide un angle égal à celui dont nous avons parlé plus haut.

Soit un segment tel que celui dont nous venons de parler. Supposons db égal à l'axe du segment. Que la droite bk soit double de kd; la droite kr égale au demi-paramètre, et la droite cb égale à trois fois la moitié de br. Que la raison de l’excès du carré de bd sur le carré de fq au carré de bd soit la même que la raison de la pesanteur du segment à la pesanteur du fluide ; et que la droite f soit double de q. Il est évident que la raison de l'excès du carré de bd sur le carré de bc au carré de bd est moindre que la raison de l'excès du carré de bd sur le carré de fq au carré de bd; car bc est l'excès de l'axe sur trois fois la moitié du demi-paramètre. Donc l'excès du carré de bd sur le carré de fq est plus grand que l'excès du carré de bd sur le carré de bc. Donc la droite fq est plus petite que la droite bc, et la droite f plus petite que la droite br. Que RΨ soit égal à f. Menons sur bd la perpendiculaire ΨE dont le carré soit égal à la moitié du rectangle compris sous kr, ΨB. Je dis que si ce segment étant abandonné dans le fluide, sa base est toute entière dans le fluide, il se placera de manière que son axe fera avec la surface du fluide un angle égal à l'angle b.

Abandonnons le segment dans le fluide comme on vient de le dire, et que son axe ne fasse pas un angle égal à l'angle b, mais d'abord un angle plus grand. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que la section de la surface du fluide soit la droite ci, et que la droite no soit l'axe du segment et le diamètre de la parabole. Coupons l'axe aux points Ω, t comme auparavant. Conduisons la droite yp parallèle à ci, et tangente à la parabole en un point p ; la droite mp parallèle à no, et la droite ps perpendiculaire sur l'axe. Puisque l’axe du segment fait avec la surface du fluide un angle plus grand que l'angle b, l'angle syp sera plus grand que l'angle b. Donc la raison du carré de ps au carré de sy est plus grande que la raison du carré de ΨE au carré de ΨB. Donc la raison de kr à sy est plus grande que la raison de la moitié de kr à yb. Donc sy est plus petit que le double de ΨB, et so plus petit que ΨB. Donc SΩ, est plus grand que RΨ, et ph plus grand que f. Donc puisque la raison de la pesanteur du segment à la pesanteur du fluide est la même que la raison de l'excès du carré de bd sur le carré de fq au carré de bd, et que la raison de la pesanteur du segment à la pesanteur du fluide est la même que la raison de la partie submergée au segment entier (2, 1), il s'ensuit que la raison de la partie submergée au segment entier est la même que la raison de l'excès du carré de bd sur le carré de fq au carré de bd. Donc la raison du segment entier à la partie qui est hors du fluide sera la même que la raison du carré de bd au carré de fq (a). Mais la raison du segment entier à la partie qui est hors du fluide est la même que la raison du carré de no au carré de pm ; donc pm sera égal à fq.

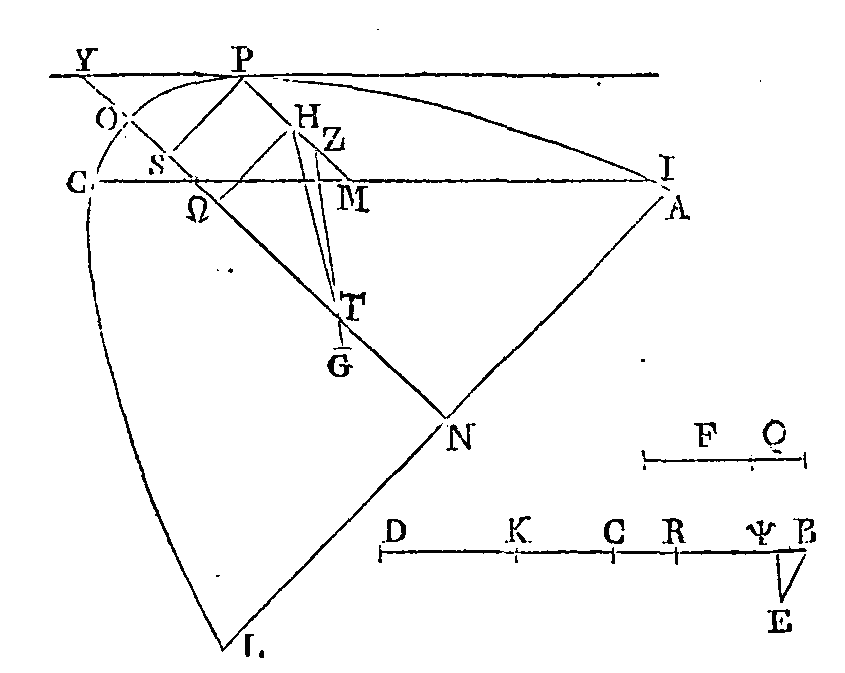
Mais on a démontré que ph est plus grand que F ; donc mh sera plus petit que q, et ph plus grand que le double de hm. Que pz soit double de zm ; joignons la droite zt, et prolongeons cette droite vers g. Le point t sera le centre de gravité du segment entier; le point z le centre de gravité de la partie qui est hors du fluide, et le centre de gravité de la partie restante qui est dans le fluide sera dans le prolongement de la droite zt. Que le point g soit son centre de gravité. Nous démontrerons, comme nous l'avons fait plus haut, que th est perpendiculaire sur la surface du fluide, et que les parallèles à th menées par les points z, g sont aussi perpendiculaires sur la surface du fluide. Donc la partie qui est hors du fluide sera portée en bas suivant la perpendiculaire qui passe par le point z, et la partie qui est dans le fluide sera portée en haut suivant la perpendiculaire qui passe par le point g (liv. 1, hyp. 2). Donc le segment ne restera pas incliné ainsi, mais il ne tournera pas de manière que l'axe devienne perpendiculaire sur la surface du fluide, puisque ce qui est du côté l sera porté en bas, et que ce qui est du côté a sera porté en haut, ce qui est évident d'après ce qui a été démontré. Si l'axe fait avec la surface du fluide un angle plus petit que l'angle b, on démontrera semblablement que le segment ne gardera point cette position, mais qu'il s'inclinera jusqu'à ce que l'axe fasse avec la surface du fluide un angle égal à l'angle b.

PROPOSITION X.

Lorsqu'un segment droit d'un conoïde parabolique plus léger qu'un fluide, et que la raison de son axe à trois fois la moitié du demi-paramètre est plus grande que la raison de quinze à quatre ; si ce segment étant abandonné dans ce fluide, sa base ne touche point le fluide, il sera tantôt vertical et tantôt incliné; il sera quelquefois incliné de manière que sa base touchera la surface du fluide en un seul point, et cela dans deux positions différentes (a) ; quelquefois sa base s'enfoncera davantage dans le fluide, et quelquefois sa base ne touchera en aucune manière la surface du fluide, suivant la raison de la pesanteur du segment à la pesanteur du fluide. Nous allons démontrer séparément chacune de ces propositions.

Soit un segment tel que celui dont nous venons de parler. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol; que bd soit l'axe du segment et le diamètre de la parabole. Coupons bd en un point k, de manière que bk soit double de kd, et en un point c, de manière que bd soit à kc comme quinze est à quatre. Il est évident que kc sera plus grand que le demi-paramètre. Que kr soit égal au demi-paramètre; que ds soit égal à trois fois la moitié de kr. La droite sb sera égale à trois fois la moitié de br (b). Joignons ab; du point c et sur bd élevons la perpendiculaire ce, qui coupe la droite ab au point e; et par le point e conduisons ez parallèle à bd. Partageons ab en deux parties égales au point t, et conduisons th parallèle à bd. Supposons deux paraboles aei, atd décrites l'une autour de ez comme diamètre et l'autre autour de th; que ces deux paraboles soient semblables à la parabole abl (g). La parabole aei passera par le point k (d), et la perpendiculaire élevée du point r. sur bd coupera la parabole aei. Que cette perpendiculaire la coupe aux points y, g; et par les points y, g conduisons les droites pyq, ogn parallèles à bd. Que ces parallèles coupent la parabole atd aux points f, x. Conduisons enfin les droites fΦ, ox qui touchent la parabole apol aux points p, o.

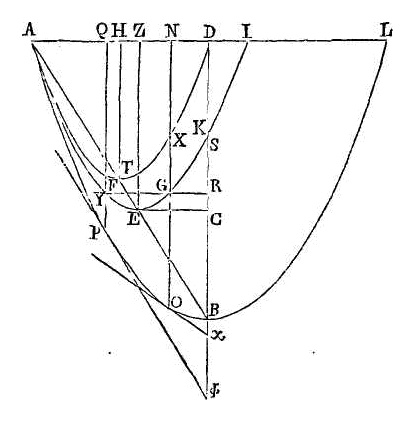
Puisqu'on a trois segments plans apol, aei, atd compris par des droites et par des paraboles; que ces segments sont semblables et inégaux, et qu'ils se touchent sur chacune des bases; que du point n on a élevé la perpendiculaire nxgo, et du point q la perpendiculaire qfyp, la raison de og à gx sera composée de la raison de il à la, et de la raison de ad à di (e). Mais il est à la comme deux est à cinq (z) ; parce que cb est à bd comme six est à quinze, c'est-à-dire comme deux est à cinq, parce que cb est à bd comme eb est à ba, et comme dz est à da, et parce que les droites li, la sont doubles des droites dz, da, et que ad est à di comme cinq est à un (h). Mais la raison composée de la raison de deux à cinq, et de la raison de cinq à un est la même que la raison de deux à un; et deux est double de un. Donc go est double de gx. On démontrera, par le même raisonnement, que py est double de yf. Donc puisque la droite ds est égale à trois fois la moitié de kr, la droite bs sera l'excès de l'axe sur trois fois la moitié du demi-paramètre. Donc lorsque la raison de la pesanteur du segment à la pesanteur du fluide est la même que la raison du carré de bs au carré de bd, ou lorsqu'elle est plus grande, si le segment étant abandonné dans le fluide, sa base ne touche point le fluide, il restera dans une position verticale; car d'après ce qui a été démontré plus haut (2, 4), lorsque le segment a son axe plus grand que trois fois la moitié du demi-paramètre, et lorsque la raison de la pesanteur du segment à la pesanteur du fluide n'est pas moindre que la raison du carré de l'excès de l'axe sur les trois fois la moitié du paramètre au carré de l'axe, si l'on abandonne le segment dans le fluide, comme on l'a dit le segment restera dans une position verticale.

2.

Lorsque la raison de la pesanteur du segment à la pesanteur du fluide est moindre que la raison du carré de sb au carré de bd, mais plus grande que la raison du carré de xo au carré de bd, si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il restera incliné de manière que sa base ne touchera la surface du fluide en aucune manière, et l'axe fera avec la surface du fluide un angle plus grand que l'angle x.

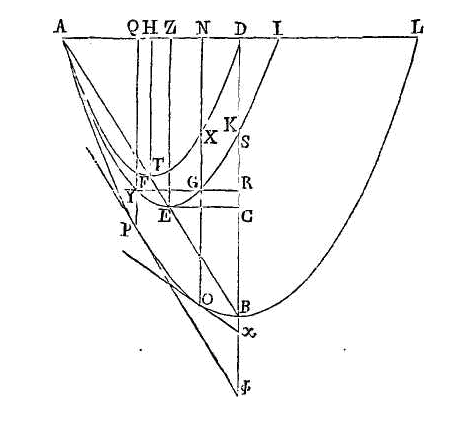
3.

Lorsque la raison de la pesanteur du segment à la pesanteur du fluide est la même que la raison du carré xo au carré de bd, si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il se placera de manière que sa base touchera la surface du fluide en un seul point, son axe faisant avec la surface du fluide un angle égal à l'angle x. Mais lorsque la raison de la pesanteur du segment à la pesanteur du fluide est la même que la raison du carré de pf au carré de bd, si le segment étant abandonné dans le fluide, est incliné sans que la base touche le fluide, il restera incliné de manière que sa base touchant la surface du fluide en un seul point, son axe fera un angle égal à l'angle Φ.

4.

Lorsque la raison de la pesanteur d'un segment à la raison de la pesanteur du fluide est plus grande que la raison du, carré de fp au carré de bd, mais moindre que la raison du carré de xo au carré de bd, si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il se placera de manière que sa base s'enfoncera dans le fluide.

5.

Lorsque la raison de la pesanteur du segment à la pesanteur du fluide est moindre que la raison du carré de fp au carré de bd, si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il restera incliné de manière que son axe fera avec la surface du fluide un angle plus petit que l'angle Φ, sa base ne touchant en aucune manière la surface du fluide. Toutes ces propositions seront démontrées les unes après les autres.

 DÉMONSTRATION DE LA SECONDE PARTIE.

Que la raison de la pesanteur du segment à la pesanteur du fluide soit plus grande que la raison du carré de xo au carré de bd, mais moindre que le carré de l'excès de l’axe sur trois fois la moitié du demi-paramètre au carré de bd, et que la raison du carré de la droite Ψ au carré de bd soit la même que la raison de la pesanteur du segment à la pesanteur du fluide. Il est évident que Ψ sera plus grand que xo et plus petit que l'excès de l'axe sur trois fois la moitié du demi-paramètre. Appliquons entre les paraboles amql, axd une certaine droite mn qui soit égale à Ψ. Que cette droite coupe la troisième parabole au point h, et la droite rg au point v. On démontrera que mh est double de hn, comme on a démontré que go est double de gx (a). Par le point m menons la droite my tangente à la parabole amql au point m, et la droite mc perpendiculaire sur bd. Ayant ensuite mené la droite an, et l'ayant prolongée vers q, les droites an, nq seront égales entre elles (b) ; car puisque dans les paraboles semblables amql, axd on a mené des bases à ces paraboles les droites aq, an qui font des angles égaux avec les bases, la droite qa sera à la droite an comme la est à ad. Donc an est égal à nq, et aq parallèle à my (g). Il faut démontrer que si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il restera incliné de manière que la base ne touchera en aucune manière la surface du fluide, l'axe fait avec la base un angle plus grand que l'angle x.

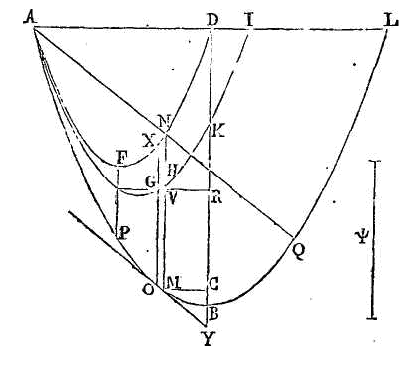
Abandonnons le segment dans le fluide, et qu'il soit placé de manière que sa base touche la surface du fluide en un point. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apol, et la section de la surface du fluide la droite ao. Que la droite bd soit l'axe du segment et le diamètre de la parabole. Coupons bd aux

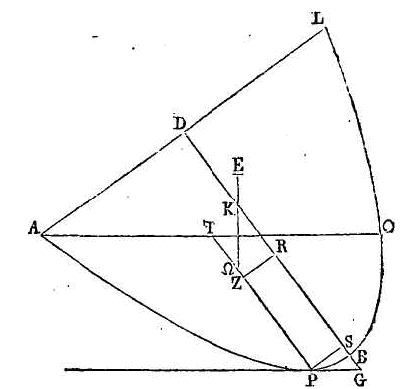
points k, r, comme cela a été dit. Menons la droite va parallèle à ao et tangente à la parabole au point p, et de ce point menons pt parallèle à bd, et ps perpendiculaire sur bd. Puisque la pesanteur du segment est à la pesanteur du fluide comme le carré de Ψ est au carré de bd ; que la pesanteur du segment est à la pesanteur du fluide comme la partie du segment qui est submergée est au segment entier (2, 1), et que la partie submergée est au segment entier comme le carré de tp est au

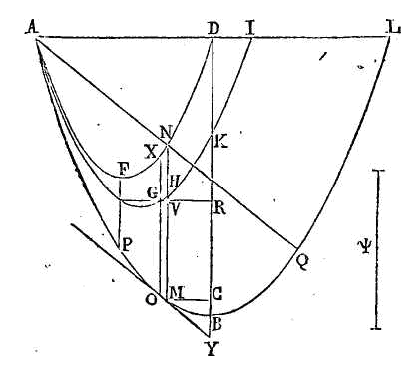
carré de bd(d), la droite Ψ sera égale à tp. Donc les droites mn, pt sont égales entre elles, ainsi que les segments amq, apo. Puisque dans les paraboles égales et semblables apol, amql, on a conduit des extrémités des bases les droites ao, aq, de manière que les segments retranchés font des angles égaux avec les axes, les angles qui sont en y, g seront égaux, ainsi que les droites yb, gb, et les droites bc, bs. Donc les droites cr, sr sont aussi égales entre elles, ainsi que les droites mv, pz, et les droites vn, zt. Donc puisque mv est plus petit que le double de vn, il est évident que pz sera plus petit que le double de zt. Que pΩ soit le double de ΩT. Menons la droite ΩK, et prolongeons-la vers e. Le point k sera le centre de gravité du segment entier, et le point Ω le centre de gravité de la partie qui est dans le fluide, et le centre de gravité de la partie qui est hors du fluide sera dans la droite ke. Que le point e soit son centre de gravité. Mais la droite kz sera perpendiculaire sur la surface du fluide; donc les droites menées par les points e, Ω parallèlement à kz, le sont aussi. Donc le segment ne restera pas en repos, mais il se placera

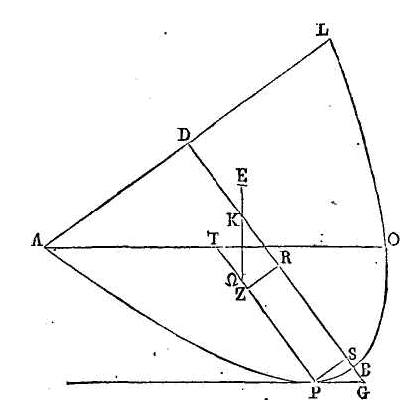
de manière que sa base ne touche en aucune manière la surface du fluide, parce que la base touchant la surface du fluide en un point, le segment est porté en haut du côté du point a. Il est donc évident que le segment se placera de manière que l'axe fera avec la surface du fluide un angle plus grand que l'angle x.

DEMONSTRATION DE LA TROISIEME PARTIE.

Que la pesanteur du segment soit à la pesanteur du fluide comme le carré de xo est au carré de bd. Abandonnons le segment dans le fluide de manière que sa base soit inclinée et ne touche point cependant le fluide. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole apml ; que la section de la surface du fluide la droite im, et que bd soit l’axe du segment et le diamètre de la parabole. Coupons la droite bd, comme auparavant, et menons la droite pn parallèle à im et tangente au point p ; la droite pt parallèle à pb, et la droite ps perpendiculaire sur bd. Il faut démontrer que le segment posé ainsi ne restera pas en repos, mais qu'il s'inclinera jusqu'à ce que la base touche la surface du fluide en un point.

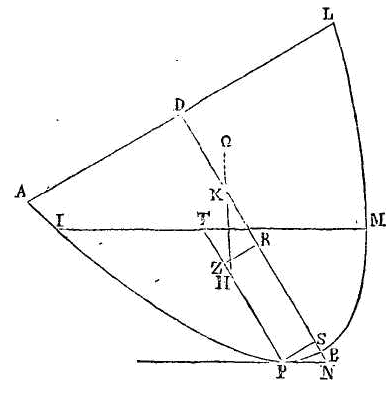
Que la figure soit la même que la précédente. Menons oc perpendiculaire sur bd; joignons la droite ax, et prolongeons-la vers q. La droite ax sera égale à la droite xq. Menons ensuite ox parallèle à aq. Puisqu'on suppose que la pesanteur du segment est à la pesanteur du fluide comme le carré de xo est au carré de bd, comme la partie submergée est au segment entier, c'est-à-dire comme le carré de tp est au carré de bd, la droite tp sera égale à xo, et les segments ipm, aoq seront aussi égaux puisque leurs diamètres sont égaux. De plus, puisque dans les segments égaux et semblables aoql, apml, on a mené les droites aq, im qui séparent des segments égaux, l’une de l'extrémité dé la base et l'autre d'un point qui n'est pas l'extrémité de la base; il est évident que celle qui est menée de l'extrémité de la base fait avec l'axe du segment entier un angle aigu plus petit (a). Mais

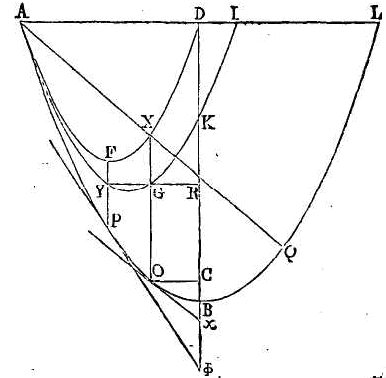
l'angle qui est en x est plus petit que l'angle qui est en n ; donc bc est plus grand que bs, et cr plus petit que sr. Donc og est plus petit que pz, et gx plus grand que zt. Donc pz est plus grand que le double de zt, parce que og est double de gx. Que ph soit double de ht. Menons la droite hk, et prolongeons-la vers Ω. Le point k sera le centre de gravité du segment entier; le point h sera le centre de gravité de la partie qui est dans le fluide, et le centre de gravité de la partie qui est hors du fluide sera dans la droite kΩ. Que le point Ω soit son centre de gravité. On démontrera semblablement que la droite kz et que les parallèles à kz menées par les points h, Ω sont perpendiculaires sur la surface du fluide. Donc le segment ne restera point en repos, mais il s'inclinera jusqu'à ce que sa base touche en un point la surface du fluide, et il restera dans cette position. Car alors dans les segments égaux aoql, apml, on aura conduit des extrémités des bases des droites aq, am qui séparent des segments égaux ; parce que l’on démontrera, comme nous l'avons fait plus haut, que aoq est égal à apm. Donc les angles aigus qui forment les droites aq, am avec les diamètres des segments sont égaux entre eux, parce que les angles x et n sont égaux (b).

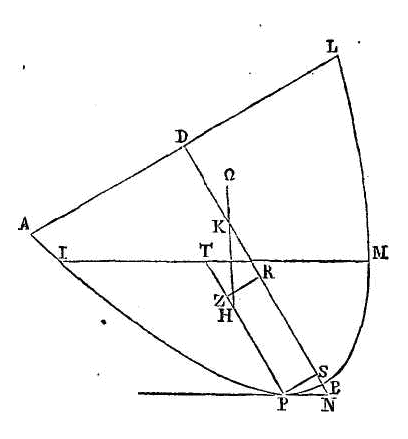
Donc si l’on prolonge la droite hk vers Ω, le point k sera le centre de gravité du segment entier, le point h le centre de gravité de la partie submergée, et le centre de gravité de la partie qui est hors du fluide sera dans la droite hk.

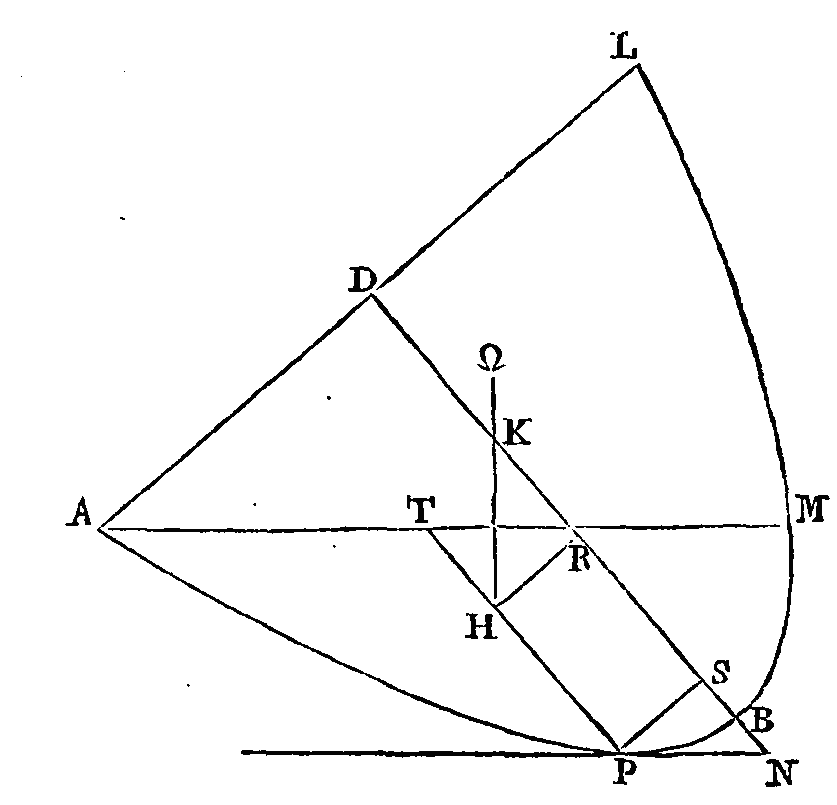
Que son centre de gravité soit le point Ω. Or, la droite hk est perpendiculaire sur la surface du fluide; donc la partie qui est dans le fluide sera portée en haut, et la partie qui est hors du fluide sera portée en bas, suivant les mêmes droites. Donc le segment restera en repos, sa base touchant la surface du fluide en un point, et l'axe fera avec la surface du fluide un angle égal à l'angle x. Si la pesanteur du segment est à la pesanteur du fluide comme le carré de pf est au carré de bd, on démontrera semblablement que si le segment est abandonné dans le fluide de manière que sa base ne touche point le fluide, le segment restera incliné de manière que la base touchera la surface du fluide en un point, et que l'axe fera avec la surface du fluide un angle égal à l'angle Φ.

DEMONSTRATION DE LA QUATRIEME PARTIE.

Que la raison de la pesanteur du segment à la pesanteur du fluide soit plus grande que la raison du carré de fp au carré de bd, mais moindre que la raison du carré de xo au carré de bd, et que la raison de la pesanteur du segment à la pesanteur du fluide soit la même que la raison du carré de Ψ au carré de bd. La droite sera plus grande que fp et plus petite que xo. Appliquons entre les paraboles avql, axd une droite iv qui soit égale à Ψ et parallèle à bd, et qui rencontre la troisième parabole au point y. Nous démontrerons que vy est double de yi, comme on a démontré que og est double de gx. Menons du point v la droite VΩ tangente à la parabole avql au point v. Joignons la droite ai, et prolongeons-la vers q. Nous démontrerons de la même manière que la droite ai est égale à la droite iq, et que la droite aq est parallèle à VΩ. Il faut démontrer que si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, la base du segment s'enfoncera dans le fluide plus qu'il ne le faut pour qu'elle ne touche le fluide qu'en un seul point.

Abandonnons le segment dans le fluide, comme nous l'avons dit, et que d'abord il soit incliné de manière que sa base ne touche le fluide en aucune manière. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole anzg ; que la section de la surface du fluide soit la droite ez, et que l'axe du segment et le diamètre de la parabole soit la droite bd. Coupons bd aux points k, r, comme auparavant. Menons la droite nl parallèle à ez et tangente à la parabole anzg au point n; que la droite nt soit parallèle à bd, et que la droite ns soit perpendiculaire sur bd. Puisque la pesanteur du segment est à la pesanteur du fluide comme le carré de Ψ est au carré de bd, la droite Ψ sera égale à nt, ce que l'on démontrera comme on l'a fait plus haut. Donc nt est égal à vi.

Donc les segments avq, enz sont égaux entre eux. Mais dans les paraboles égales et semblables avql, anzg, l'on a conduit les droites aq, ez, qui séparent des segments égaux, l'une étant conduite de l'extrémité de la base et l'autre étant conduite d'un point qui n'est pas l'extrémité de la base ; donc celle qui est conduite de l'extrémité de la base fera avec le diamètre du segment un angle aigu qui sera plus petit. Mais parmi les angles des triangles nls, VΩC, l'angle en l est plus grand que l'angle en Ω ; donc bs est plus petit que bc, et sr plus grand que cr. Donc nx est plus grand que vh, et xt plus petit que hi. Donc puisque vy est double de yi, il est évident que nx est plus grand que le double de xt. Que mn soit double de mt. Il suit évidemment de ce qui a été dit, que le segment ne restera point en repos, mais qu'il s'inclinera jusqu'à ce que sa base touche la surface du fluide en un point, comme on le voit dans la figure.

Que les autres choses soient les mêmes. Nous démontrerons de nouveau que nt est égal à vi, et que les segments avq, anz sont égaux entre eux. Donc puisque dans les segments égaux et semblables avql, avzg, on a conduit les droites aq, az qui séparent des segments égaux, ces droites feront des angles égaux avec les diamètres des segments. Donc les angles des triangles nls, vΩc, qui sont vers les points l, Ω, sont égaux; donc la droite bs est égale à la droite bc ; la droite sr égale à cr ; la droite nx égale à vh, et la droite xt égale à hi. Mais vy est double de yi; donc nx sera plus grand que le double de xt. Que nm soit double de mt. Il est encore évident que le segment ne restera pas en repos, mais qu'il s'inclinera du côté du point a. Mais on supposait que le segment touchait la surface du fluide en un point; il est donc nécessaire que sa base s'enfonce davantage dans le fluide.

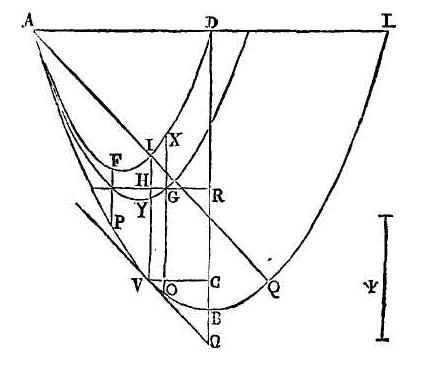
DÉMONSTRATION DE LA CINQUIEME PARTIE.

Qu'enfin la raison de la pesanteur du segment à la pesanteur du fluide soit moindre que la raison du carré de fp au carré de bd, et que la raison de la pesanteur du segment à la pesanteur du fluide soit la même que la raison du carré de Ψ au carré de bd. La droite Ψ sera plus petite que pf. Appliquons de nouveau, entre les paraboles avql, axd, une certaine droite vi qui soit parallèle à bd, et qui coupe la parabole du milieu au point h, et la droite ry au point y. Nous démontrerons que vh est double de hi, comme nous avons démontré que og est double de gx. Menons ensuite la droite VΩ tangente à la parabole avql au point v, et la droite vc perpendiculaire sur bd. Joignons la droite ai, et prolongeons-la vers q. La droite ai sera égale à iq, et la droite aq parallèle à la droite VΩ. Il faut démontrer que si le segment étant abandonné dans le fluide, est incliné sans que sa base touche le fluide, il se placera de manière que son axe fera avec la surface du fluide un angle plus petit que l'angle o, et que sa base ne touchera en aucune manière la surface du fluide.

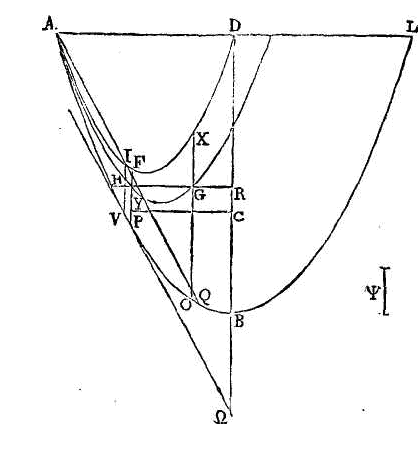
Abandonnons le segment dans le fluide, et qu'il soit placé de manière que sa base touche la surface du fluide en un point. Conduisons par l'axe un plan perpendiculaire sur la surface du fluide. Que la section du segment soit la parabole anzl ; que la section de la surface du fluide soit la droite az, et que bd soit l'axe du segment et le diamètre de la parabole. Coupons bd aux points k, r, comme on l'a dit plus haut; menons la droite nf parallèle à az et tangente à la parabole au point n ; la droite nt parallèle à bd, et la droite ns perpendiculaire sur bd. Puisque la pesanteur du segment est à la pesanteur du fluide comme le carré de Ψ est au carré de bd, et que la partie submergée est au segment entier comme le carré de nt est au carré de bd,

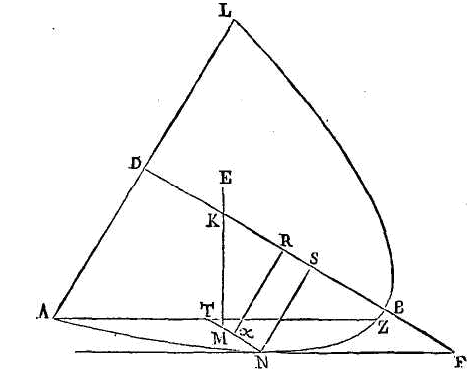
d'après ce qui a été dit, il est évident que nt sera égal à Ψ. Donc les segments anz, avq sont égaux. Mais dans les segments égaux et semblables avql, anzl, on a mené des extrémités des bases les droites aq, az qui séparent des segments égaux ; il est donc évident que ces droites feront des angles égaux avec les diamètres des segments, et que les angles des triangles nfs, VΩC, placés en f, Ω sont égaux, ainsi que les droites sb, cb et les droites sr, cr. Donc les droites Nx, gy sont égales, ainsi que les droites xT, yi. Mais la droite gh est double de hi ; donc la droite Nx sera plus petite que le double de xT. Que nm soit double de nt; menons la droite mk, et prolongeons-la vers e. Le point k sera le centre de gravité du segment entier; le point m le centre de gravité de la partie qui est dans le fluide, et le centre de gravité de la partie qui est hors du fluide sera dans le prolongement de la droite mk. Que le point e soit son centre de gravité. Il suit évidemment de ce qui a été démontré, que le segment ne restera point en repos, mais qu'il s'inclinera de manière que sa base ne touchera la surface du fluide en aucune manière. On démontrera de la manière suivante que le segment se placera de manière que l'axe fasse avec la surface du fluide un angle plus petit que l'angle Φ. En effet, si cela est possible, que l'axe ne fasse pas un angle plus petit que l'angle Φ. Que les autres choses soient disposées comme on le voit dans la figure. Nous démontrerons de la même manière que nt est égal à Ψ, et par conséquent à gi.

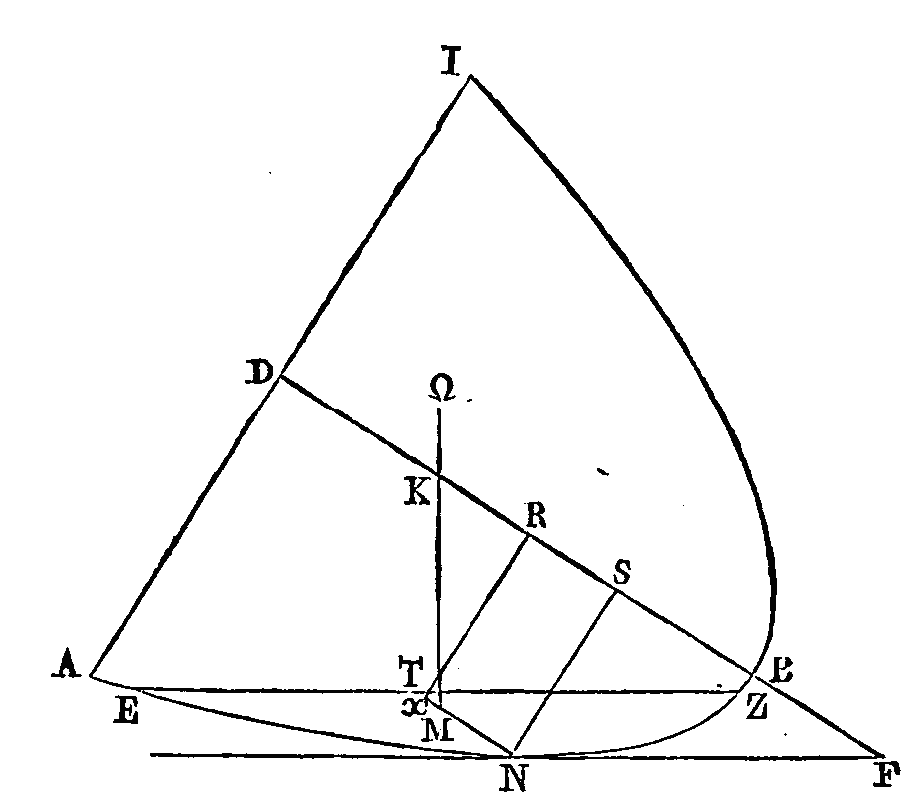
Mais dans les triangles pΦc, nfs, l'angle f n'est pas plus petit que l'angle Φ, donc la droite bs ne sera pas plus grande que bc. Donc la droite sr ne sera pas plus petite que cr, ni la droite Nx plus petite que py. Mais puisque la droite pf est plus grande que nt, et que la droite pf est égale à trois fois la moitié de py, la droite nt sera plus petite que trois fois la moitié de Nx, et par conséquent la droite Nx plus grande que le double de xT. Que la droite nm soit double de mt; menons la droite mk, et prolongeons-la. Il suit évidemment, d'après ce qui a été dit, que le segment ne restera pas en repos, mais qu'il tournera jusqu'à ce que l’axe fasse avec la surface du fluide un angle plus petit que l'angle Φ.

FIN DES CORPS PORTÉS SUR UN FLUIDE

COMMENTAIRE SUR LES DEUX LIVRES

DES CORPS PORTÉS SUR UN FLUIDE.

LIVRE PREMIER.

PROPOSITION III.

(a) C’est-a-dire, si un corps qui a la même pesanteur spécifique qu'un fluide est abandonné dans ce fluide.

(b) Ce parallélogramme n'est point une surface plane, mais bien une portion de la surface de la sphère comprise entre quatre arcs de grands cercles.

PROPOSITION VIII.

(a) Voyez la prop. 8 de l'Equilibre des Plans.

PROPOSITION IX.

(a) Voyez la note (a) de la prop. 8.

LIVRE SECOND.

PROPOSITION II.

(a) Un segment droit d'un conoïde est celui dont l'axe est perpendiculaire sur sa base.

(b) Archimède ne considère ici la parabole que dans le cône rectangle. (Voyez la note (a) de la lettre à Dosithée qui est à la tête du Traité des Conoïdes et des Sphéroïdes.) Cette parabole est telle que son demi-paramètre est égal à la droite placée entre sou sommet et le sommet du cône. Voilà pourquoi le demi-paramètre est appelé par lui la droite jusqu'à l'axe.

En effet, soit le cône droit et rectangle ABEC. Coupons ce cône par l'axe, et que la section soit le triangle ABC. Par le point D conduisons un plan perpendiculaire sur le plan du triangle ABC, et parallèle à AC.

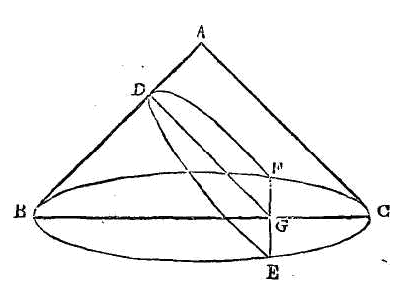
La section EDF sera une parabole. Nommons y, l'ordonnée EG ; x, l'abscisse DG, et p le paramètre. Les triangles semblables BAC, BDG donnent DA : GC :: DB ou DG ou x : BG. Donc DA = (GC * x)/DG. Mais BG = 2x² donc DA = DA = (GC * x)/ 2x²

Mais y²=px, et y² = BG x GC; donc px=BC x GC = 2x² x GC. Donc GC = px/2x². Donc au lieu de l'équation DA = (GC * x)/ 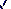2x² nous aurons DA = px²/(2x² * 2x²) = px²/2x² = p/2. Donc DA est égal à la moitié du paramètre.

Il est évident qu'à mesure que le point D s'éloigne du point A, le demi-paramètre et par conséquent le paramètre augmente ; qu'au point A le paramètre est infiniment petit, et qu'à une distance infiniment grande du point A, le paramètre sera infiniment grand. D'où il suit que la section d'un cône rectangle peut donner toutes les paraboles possibles. Donc ce qu'Archimède dit de la parabole qui est la section d'un triangle rectangle, et par conséquent ce qu'il dit aussi d'un segment droit d'un conoïde parabolique convient à toutes sortes de paraboles et à toutes sortes de conoïdes paraboliques.

(g) Dans le premier livre toutes les constructions se faisaient par rapport au centre de la terre ; on y considérait par conséquent la surface d'un fluide en repos comme étant une surface sphérique. Pour plus de simplicité, Archimède considère, dans le second livre, la surface d'un fluide en repos comme étant une surface plane, et par conséquent la section de cette surface par un plan est considérée comme étant une ligne droite.

(d) Frédéric Commandin a démontré le premier dans son Traité du Centre de gravité des Solides (prop. 29), que le centre de gravité d'un conoïde parabolique est un point de l'axe qui le divise, de manière que la partie qui est vers le sommet est double de la partie qui est vers la base ; de cette manière le point R étant le centre de gravité du conoïde parabolique APOL, la droite OR est double de la droite RN; et le point B étant le centre de gravité du conoïde IPOS, la droite PB est double de la droite BF.

D'où il suit que la droite NO est égale à trois fois la moitié de RO, et PF égal à trois fois la moitié de PB.

Archimède regarde comme démontré que le centre de gravité d'un conoïde parabolique est aux deux tiers de son axe à partir du sommet. Cela n'est démontré dans aucun des ouvrages existants d'Archimède, ni dans aucun des ouvrages des géomètres anciens; d'où je conclus que l'ouvrage où cette proposition était démontrée du temps d'Archimède n'est point parvenu jusqu'à nous.

(e) En effet, prolongeons RO jusqu'à ce que KH soit égal au demi-paramètre. Par le point H menons sur HN la perpendiculaire HV; prolongeons FP, et joignons RV. Par le point P menons sur NH la perpendiculaire PX, et par le point P menons sur KΩ la perpendiculaire PY. La droite XY, qui est la sous-normale, sera

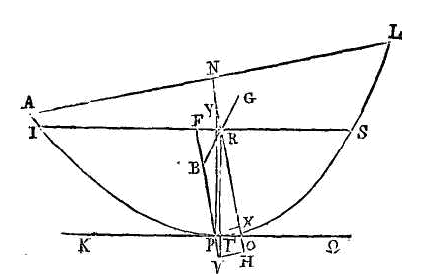
égale à RH, puisque la sous-normale est égale à la moitié du paramètre, la droite PX est égale à VH, et les angles sont droits en X et en H. Donc les deux triangles PXY, VHR sont égaux. Donc les droites PY,VR sont parallèles; mais PY est perpendiculaire sur KΩ; donc RV est aussi perpendiculaire sur KΩ. Donc l'angle RPΩ est aigu; donc la perpendiculaire abaissée du point R sur PΩ passe entre P et SI. Donc la droite RT ne rencontrera la droite FP que hors de la parabole,

(z) D'après la proposition 6 du premier livre, et d'après la seconde hypothèse du même livre, la partie du conoïde qui est dans le fluide est portée en haut suivant la verticale qui passe par le point B avec la même force que la partie qui est hors du fluide est portée en bas, suivant la verticale qui passe par le point G, jusqu'à ce que le conoïde ait une position verticale. En effet, les deux parties du conoïde ayant alors leurs centres de gravité dans l'axe du conoïde qui aura une position verticale, la partie qui est dans le fluide tendra à monter avec la même force que celle qui est hors du fluide tendra à descendre. Donc ces deux forces se détruiront; donc le conoïde restera en repos.

PROPOSITION III.

(a) Il serait inutile d'avertir que le segment est supposé plus léger que le fluide.

PROPOSITION IV.

(a) Puisque NO = 3/2 RO, et MO = 3/2 OH, on aura NO — MO = 3/2 RO — 3/2 OH, ou bien NM = 3\2 (RO — OH) = 3/2 RH.

(b) En effet, lorsque MO augmente, la droite NM diminue, et par conséquent 3\2 RH ; et lorsque 3\2 RH ou RH, c'est-à-dire le demi-paramètre, diminue, l'excès de l’axe sur le demi-paramètre devient plus grand.

(d) Car PF n'étant pas plus petit que MO, la droite BP qui est égale aux deux tiers de BF, ne sera pas plus petite que la droite HO, qui est égale aux deux tiers de MO.

(e) La perpendiculaire HT tombera entre B et P. En effet, menons une tangente à la parabole au point O, cette tangente sera hors de la parabole, et la droite HO sera égale à la droite PT prolongée jusqu'à la tangente. D'où il suit que si la droite BP prolongée jusqu'à la tangente était égale à HO, la perpendiculaire menée par le point H passerait par le point B. Mais la droite BP prolongée jusqu'à la tangente, est plus grande que HO, puisque BP n'est pas plus petit que HO ; donc la perpendiculaire menée par le point H tombe entre B et P.

(z) Pour démontrer que la droite RT prolongée fera des angles droits avec la tangente KΩ, élevons du point P une perpendiculaire PV sur KΩ, et abaissons du point P une perpendiculaire PX sur NO. La sous-normale VX est égale au demi-paramètre RH ; la droite PX est égale à la droite TH, et lès angles sont droits en X et en H. Donc les deux triangles VXP, RHT sont égaux. Donc NP est parallèle à RT. Mais NP est perpendiculaire sur KΩ; donc RT prolongé sera aussi perpendiculaire sur KΩ.

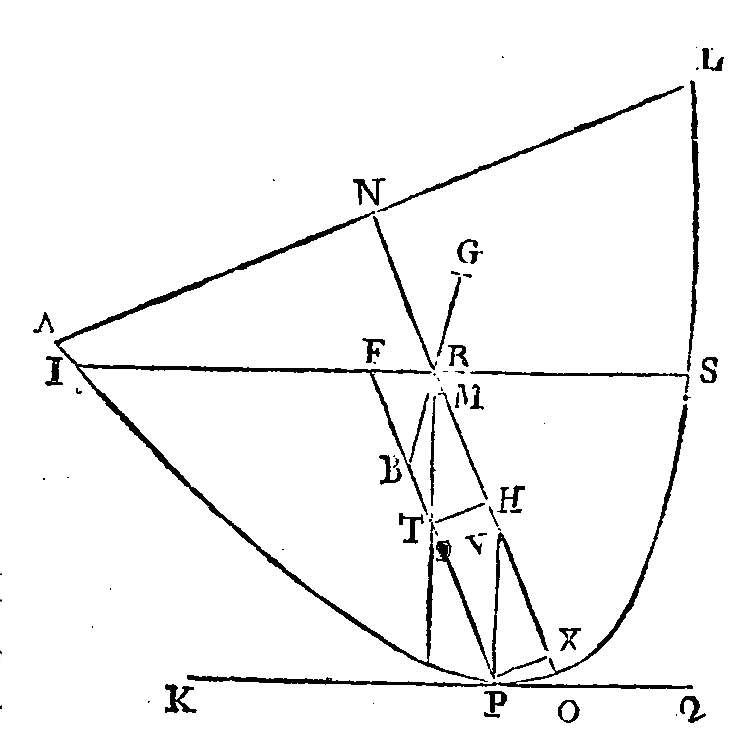
PROPOSITION V.

(a) On a supposé que la raison de la pesanteur du segment à la pesanteur du fluide n'est pas plus grande que la raison de NO² — (NO — 3/2 RH)² à NO². Pour faire voir que la seconde supposition est la même que la première, il suffit de démontrer que MO est égale à NO moins 3\2 HR. En effet, OH = OR — HR. Mais OR = 2/3 ON; donc OH = 2/3 ON — HR. Ce qui donne 3\2 OH = ON — 3\2 HR. .Mais HO/2 = HM ; donc 3\2 OH = OM; donc OM = ON — 3\2 HR.

(b) Puisque la raison de la partie du segment qui est submergée au segment entier, n'est pas plus grande que la raison de NO² — MO² à NO², par inversion, la raison du segment entier à la partie du segment qui est submergée, ne sera pas plus grande que la raison de NO² à NO² — MO². Donc, par soustraction, la raison du segment entier à la partie qui n'est pas submergée, n'est pas plus grande que la raison de NO² à MO².

(g) Prop. 26 des Conoïdes et des Sphéroïdes.

PROPOSITION VI.

(a) La démonstration de cette proposition ne se trouve ni dans Archimède ni dans aucun des Géomètres anciens. La démonstration suivante est de Torelli.

La construction restant la même, que les droites ΩK, CP se rencontrent au point B ; et par le point B menons la droite BV tangente à la parabole.

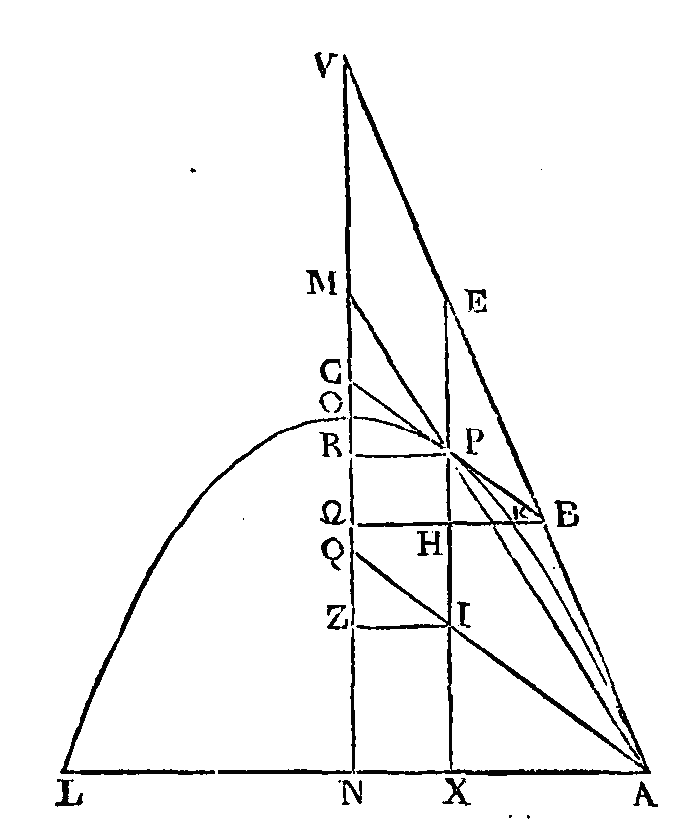
D'abord que la droite BV touche la parabole au point A, et rencontre les diamètres IP, NO aux points E, V. Que les droites BP, AI rencontrent le diamètre NV aux points C, Q. Par les points P, I, menons les droites PB, IZ parallèles à AL, et que ces droites rencontrent NO aux points R, Z. Enfin, menons AP, et que cette droite rencontre NV au point M. La droite IP sera égale à PE, la droite NO à OV et la droite RO à OC. (Prop. 35 et cor. de la prop. 51 du liv. i d'Apoll.) Mais à cause des parallèles EH, VΩ, la droite EP sera à la droite VC comme BP est à BC ; c'est-à-dire, comme BH est à CΩ ; et à cause des droites égales EP, PI, et par construction, la droite VM sera égale à la droite MQ. Mais RZ est égal à IP ou à EP ; donc RZ est à VG comme PH est à CΩ. Mais CV est égal à RN; donc RZ est à RN comme RΩ est à CΩ. Donc, par soustraction, RZ est à ZN comme KΩ est à CR. Mais IP est à CM comme AP est à PM, et AP est à PM comme AX est à XN ou IZ, c'est-à-dire, comme IX ou ZN est à QZ ; donc à cause des droites égales IP, RZ, la droite RZ est à CM comme ZN est à QZ. Donc, par permutation, la droite RZ est à la droite ZN comme CM est à QZ. Mais à cause des droites égales IZ, PR, et à cause des parallèles IZ, PR et IQ, PC, les droites QZ, CR

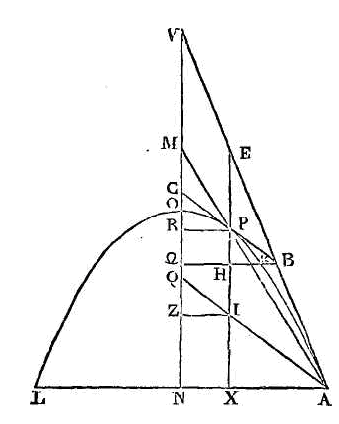
seront égales entre elles. Donc RΩ est à CR comme CM est à CR. Donc les droites CM, RΩ sont égales entre elles. De plus, la droite AV est à BV comme VN est à VΩ, et comme VQ est à VC. Donc si l'on divise les antécédents par deux, la droite VO sera à la droite OΩ comme VM est à VC. Donc, par soustraction, la droite VO est à la droite OΩ comme VM est à MC; c'est-à-dire que NO est à OΩ comme QM est à MC. Donc, par soustraction, la droite NΩ est à la droite OΩ comme QC est à CM. Donc, puisque les droites QC, PC et les droites CM, KΩ, PH sont égales entre elles, la droite NΩ sera à la droite OΩ comme PI est à PH.

En second lieu, que VB touche la parabole en T, et conduisons la droite TR parallèle à AI ou à CB; et que la droite TR rencontre PI en R. Menons TF parallèle à AN ou à ΩK, et que TF rencontre ON au point F. Prolongeons IA, et que son prolongement rencontre la tangente BT au point G. Menons la droite GD parallèle à AN, et que GD rencontre ON. au point D. A cause des parallèles ΩB, DG, FT et PB, IG, RT,

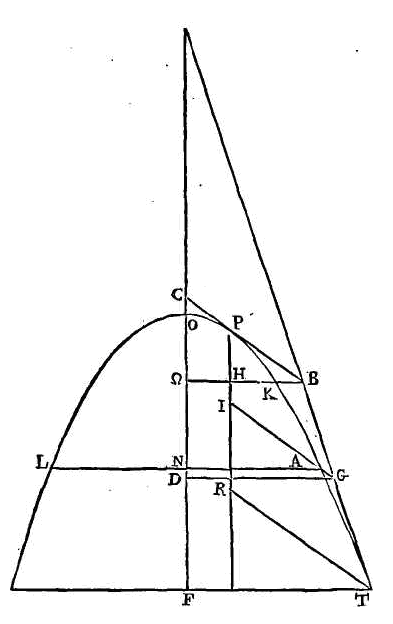
la droite DΩ sera à la droite FΩ comme BG est à BT ; et BG sera à BT comme PI est à PR. Donc DΩ est à FΩ comme PI est à PR. Mais on démontrera comme on l'a fait plus haut que FΩ est à ΩO comme PR est à PH ; donc DΩ est à ΩO comme PI est à PH. Mais la raison de DΩ à ΩO est plus grande que la raison de NΩ à ΩO ; donc la raison de la droite PI à la droite PH est plus grande que la raison de la droite NΩ à la droite ΩO.

(b) Car puisque NO : FΩ :: 15 : 4, la droite FΩ = 4 x NO / 15. Donc NΩ = NF + NΩ = NO/3 + 4 x NO/15 = 9 x NO / 15. Donc OΩ = NO — 9 x NO / 15 = 6 x NO / 15.

Donc NΩ : ΩO :: 9 x NO / 15 : 6 x NO / 15 :: 9 : 6 : 3 : 2.

Donc NΩ est égal à trois fois la moitié de ΩO.

PROPOSITION VIII.

(a) En effet, puisque la droite BK est double de la droite KD, la droite BD sera égale à trois fois la moitié de BK. Mais CB est égal à trois fois la moitié de BR ; donc BD : CB :: 3/2 BK : 3/2 BR : : BK : BR ; donc par permutation BD : BK :: CB : BR. Mais le premier terme est au second comme la différence des antécédents est à la différence des conséquents, c'est-à-dire que BD : BK :: BD — CB : BK — BR :: CD : KR ; et BD : BK :: 3 : 2 ; donc CD : KR :: 3 : 2 ; donc CD = 3/2 KR

(b) Car puisque CD est égal à trois fois la moitié du paramètre, la droite CB sera l'excès de l'axe sur trois fois la moitié du paramètre. Mais par supposition la raison du carré de FQ au carré de DB est la même que la raison de la pesanteur du segment à la pesanteur du fluide; et la raison de la pesanteur du segmenta la pesanteur du fluide est moindre que la raison du carré de CB au carré de BD ; donc la raison du carré de FQ au carré de DB est moindre que la raison du carré de CB au carré de BD ; donc le carré de FQ est plus petit que le carré de CB ; donc la droite FQ est plus petite que la droite CB.

(g) Dans la parabole, le carré de l'ordonnée est égal au rectangle compris sous le paramètre et l'abscisse, ou au rectangle compris sous le demi-paramètre et sa sous-tangente. Donc PI² = KR x IY ; donc PI² : IY² :: KR x IY : IY² :: KR : IY.

(d) Car puisqu'on a supposé que EΨ² = (KR x ΨB)/2, on aura EΨ² : ΨB² :: (KR x ΨB)/2 : ΨB :: KR/2 : ΨB.

PROPOSITION IX.

(a) Puisque la raison de la partie submergée du segment au segment entier est la même que la raison de l'excès du carré de BD sur le carré de FQ au carré de BD, par inversion et par soustraction la raison du segment entier à la partie qui est hors du fluide sera la même que la raison du carré de BD au carré de FQ.

PROPOSITION X.

(a) Parce que lorsqu'un point de la base touche la surface du fluide, la base peut être toute entière hors du fluide, ou toute entière dans le fluide.

(b) En effet, puisque BD est égal à trois fois la moitié de BK, et que DS est aussi égal à trois fois la moitié de KR, on aura BD : DS :: 3/2 BK : 3/2 KR :: BK : KR; ou par permutation BD : BK :: DS : KR ; donc BD : BK :: BD — DS : BK — KR :: SB : BR. Mais BD = 3/2 BK ; donc SB = 3/2 BR

(g) Voyez la note (b) de la lettre à Dosithée, qui est à la tête du Traité des Conoïdes.

(d) Puisque BK = 2KD, on aura BC + CK = (CD — CK) x 2, d'où l'on déduit CK =(2CD — BC)/3. Mais KC : DB :: 4 : 15 ; donc KC = 4DB/15 = (4BC+ 4CD)/15. Donc (2CD — BC)/15 = (4 BC + 4 CD)/15 ou bien 2 CD = 3BC, ce qui donne la proportion suivante CD : BC :: B: 2. Mais CD : CB :: AE : EB :: AZ : ZD ; donc AZ : ZD :: 3 : 2. Mais DB : BK :: 3 : 2 ; donc la parabole AEI passe par le point K. (Traité de la Parabole, propos. 4.)

(e) En effet, que la droite NΨ soit tangente à la parabole ABL, et qu'elle rencontre les droites DB, NO, ZE, HT aux points Ψ, T, V, M, la droite BE sera à la droite EZ comme DA est à AZ. (Apoll. liv. vi, prop. 11.) Donc BD : EZ :: DΨ : ZV. Mais la droite DΨ est double de la droite BD ; donc la droite sera ZV double de la droite EZ. Donc la droite AΨ est tangente à la parabole AEI. On démontrera de la même manière que la droite AΨ est tangente à la parabole ATD.

D'après la proposition 5 du Traité de la Parabole, on a les proportions suivantes, AL : AN :: NG : GO ; IA : AN :: NG : GG, et AD : AN : NG : GX et ces proportions donnent GO = (AN x NG)/ AL ;

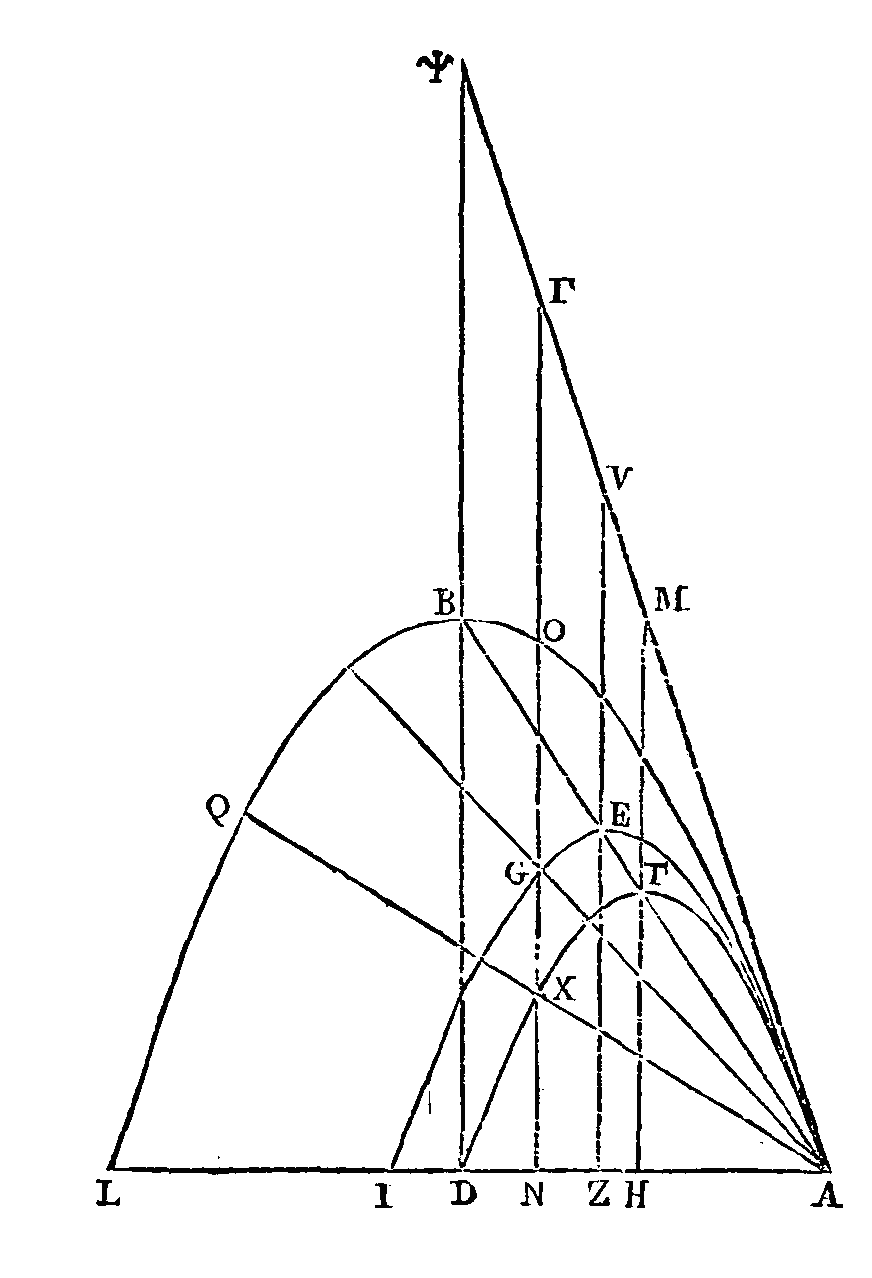
GG = (AN x NG)/ IA, et GX = (AN x NG)/ AD. Mais OG = GG — GO = (AN x NG)/ IA — (AN x NG)/ AL et GX = GX — GG = (AN x NG)/ AD — (AN x NG)/ IA ; donc

OG : GX :: (AN x NG)/ IA — (AN x NG)/ AL : (AN x NG)/ AD — (AN x NG)/ IA :: (I/AI — I/AL) : (I/AD — I/IA) :: (AL — IA)/(IA x AL) : (IA — AD)/(AD x IA) :: IL/AL : ID/AD :: IL x AD : LA x DI ; donc la raison de OG à GX est composée des raisons de IL à LA et de AD à ID.

(z) On a démontré que DC : CB :: 3 : 2 ; donc par addition DC ou ZE : DB :: 3 : 6. Mais à cause des paraboles semblables AEI, ABL, on a ZE : DB :: AI : AL; donc AI : AL :: 3 : 5 ; donc LA — AI : LA :: 5 —-3 : 5; c'est-à-dire IL : LA :: 2 : 5.

(h) On a démontré que AZ : ZD :: 3 : 2 ; donc AZ + DZ : ZD :: 5 : 2 ; c'est-à-dire que AD : ZD :: 5 : 2. Mais LA : LI :: 5 : 2 ; donc LA : LI :: AD : DZ. Mais LA est double de AD ; donc LI est double de DZ ; donc les droites LI, LA sont doubles des droites DZ, DA.

Puisque BD : DC :: 15 : 9 :: 30 : 18 . on aura BD/2 : DC :: BO/2 : 18 ou bien TH : DC :: 15 : 18 :: 5 : 6. Mais à cause de paraboles semblables, TH : BC ou EZ :: AD : AI; donc AD : AI :: 5 : 6 ; donc AD : AI — AD :: 5 : 6 — 5, c'est-à-dire que AD : DI :: 5 : 1.

SECONDE PARTIE DE LA PROPOSITION 10.

(a) Première partie de la prop. 10.

(b) D'après la prop. 5 de la Quadr. de la Parab. (fig. de la note (e) de la prop. 10), on a LN : NA :: NO : OG, et par addition LA : NA :: NG : OG ; donc NA = (LA x OG)/ NG. Mais d'après la même proposition on a encore DA : NA :: NG : XG ; donc NA =(DA x XG)/ NG; donc (LA x OG)/ NG = (DA x XG)/ NG, ou bien LA x OG = DA x XL; donc LA : DA :: XG : OG. Mais LA est double de DA ; donc XG est double de OG ; donc XO = OG. Menons la droite AX et prolongeons-la jusqu'en Q. D'après la prop. 5 du Traité de la Parabole, on a QX : XA :: XO : OG. Mais XO = OG ; donc QX =XA; donc dans la figure de la seconde partie, AN = OQ.

TROISIÈME PARTIE DE LA PROPOSITION 10.

(a) Cela est évident ; car si la droite menée du point M au point I était menée au point A, cette dernière droite ferait avec l'axe un angle aigu plus petit que celui que fait la droite MI avec l'axe. Mais alors le segment retranché serait plus grand que le segment AOQ. Pour que le premier segment devînt égal au second, il fau-droit que la droite menée du point A au point M tournât autour du point A, en s'approchant du point B; donc l'angle aigu formé par l'axe et par la droite menée par le point A, diminuerait encore. D'où je conclus que la droite menée du point A fait avec l'axe un angle aigu plus petit que l'angle que fait avec l'axe la droite menée du point I.

(b) Voyez la seconde partie.

FIN DU COMMENTAIRE SUR LES CORPS PORTES SUR UN FLUIDE.