PLATON

OEUVRES COMPLÈTES

LA RÉPUBLIOUE  

LIVRE VII

514 Maintenant, repris-je, représente-toi de la façon que 514a voici l'état de notre nature relativement à l'instruction et à l'ignorance. Figure-toi des hommes dans une demeure souterraine, en forme de caverne, ayant sur toute sa largeur une entrée ouverte à la lumière; ces hommes sont là depuis leur enfance, les jambes et le cou enchaînés, de sorte qu'ils ne peuvent bouger ni voir ailleurs que 514b devant eux, la chaîne les empêchant de tourner la tête; la lumière leur vient d'un feu allumé sur une hauteur, au loin derrière eux; entre le feu et les prisonniers passe une route élevée : imagine que le long de cette route est construit un petit mur, pareil aux cloisons que les montreurs de marionnettes dressent devant eux, et au-dessus desquelles ils font voir leurs merveilles (455).
Je vois cela, dit-il.
Figure-toi maintenant le long de ce petit mur des hommes portant des objets de toute sorte, qui dépassent le mur, et des statuettes d'hommes et d'animaux, en 515 pierre, en bois, et en toute espèce de matière (456); naturellement, parmi ces porteurs, les uns parlent et les autres se taisent.
Voilà, s'écria-t-il, un étrange tableau et d'étranges prisonniers.
Ils nous ressemblent (457), répondis-je; et d'abord, penses-tu que dans une telle situation ils aient jamais vu autre chose d'eux-mêmes et de leurs voisins que les ombres projetées par le feu sur la paroi de la caverne qui leur fait face?
Et comment? observa-t-il, s'ils sont forcés de rester la tête immobile durant toute leur vie? 515b
Et pour les objets qui défilent, n'en est-il pas de même?
Sans contredit.
Si donc ils pouvaient s'entretenir ensemble ne penses-tu pas qu'ils prendraient pour des objets réels les ombres qu'ils verraient (458)?
Il y a nécessité.
Et si la paroi du fond de la prison avait un écho, chaque fois que l'un des porteurs parlerait, croiraient-ils entendre autre chose que l'ombre qui passerait devant eux?
Non, par Zeus, dit-il.
515c Assurément, repris-je, de tels hommes n'attribueront de réalité qu'aux ombres des objets fabriqués.
C'est de toute nécessité.
Considère maintenant ce qui leur arrivera naturellement si on les délivre de leurs chaînes et qu'on les guérisse de leur ignorance. Qu'on détache l'un de ces prisonniers, qu'on le force à se dresser immédiatement, à tourner le cou, à marcher, à lever les yeux vers la lumière : en faisant tous ces mouvements il souffrira, et l'éblouissement 515d l'empêchera de distinguer ces objets dont tout à l'heure il voyait les ombres. Que crois-tu donc qu'il répondra si quelqu'un lui vient dire qu'il n'a vu jusqu'alors que de vains fantômes, mais qu'à présent, plus près de la réalité et tourné vers des objets plus réels, il voit plus juste? si, enfin, en lui montrant chacune des choses qui passent, on l'oblige, à force de questions, à dire ce que c'est? Ne penses-tu pas qu'il sera embarrassé, et que les ombres qu'il voyait tout à l'heure lui paraîtront plus vraies que les objets qu'on lui montre maintenant?
Beaucoup plus vraies, reconnut-il.
515e Et si on le force à regarder la lumière elle-même, ses yeux n'en seront-ils pas blessés? n'en fuira-t-il pas la vue pour retourner aux choses qu'il peut regarder, et ne croira-t-il pas que ces dernières sont réellement plus distinctes que celles qu'on lui montre?
Assurément.
Et si, repris-je, on l'arrache de sa caverne par force, qu'on lui fasse gravir la montée rude et escarpée, et qu'on ne le lâche pas avant de l'avoir traîné jusqu'à la lumière du soleil, ne souffrira-t-il pas vivement, et ne se plaindra-t-il pas de ces violences? Et lorsqu'il sera parvenu à la 516 lumière pourra-t-il, les yeux tout éblouis par son éclat, distinguer une seule des choses que maintenant nous appelons vraies?
Il ne le pourra pas, répondit-il; du moins dès l'abord.
Il aura, je pense, besoin d'habitude pour voir les objets de la région supérieure. D'abord ce seront les ombres qu'il distinguera le plus facilement, puis les images des hommes et des autres objets qui se reflètent dans les eaux, ensuite les objets eux-mêmes. Après cela, il pourra, affrontant la clarté des astres et de la lune, contempler 516b plus facilement pendant la nuit les corps célestes et le ciel lui-même, que pendant le jour le soleil et sa lumière.
Sans doute.
À la fin, j'imagine, ce sera le soleil - non ses vaines images réfléchies dans les eaux ou en quelque autre endroit - mais le soleil lui-même à sa vraie place, qu'il pourra voir et contempler tel qu'il est.
Nécessairement, dit-il.
Après cela il en viendra à conclure au sujet du soleil, que c'est lui qui fait les saisons et les années, qui gouverne tout dans le monde visible, et qui, d'une certaine manière, 516c est la cause de tout ce qu'il voyait avec ses compagnons dans la caverne (459).
Evidemment, c'est à cette conclusion qu'il arrivera.
Or donc, se souvenant de sa première demeure, de la sagesse que l'on y professe, et de ceux qui y furent ses compagnons de captivité, ne crois-tu pas qu'il se réjouira du changement et plaindra ces derniers?
Si, certes.
Et s'ils se décernaient alors entre eux honneurs et louanges, s'ils avaient des récompenses pour celui qui saisissait de l'oeil le plus vif le passage des ombres, qui se rappelait le mieux celles qui avaient coutume de venir les premières ou les dernières, ou de marcher ensemble, et 516d qui par là était le plus habile à deviner leur apparition (460), penses-tu que notre homme fût jaloux de ces distinctions, et qu'il portât envie à ceux qui, parmi les prisonniers, sont honorés et puissants? Ou bien, comme le héros d'Homère (461), ne préférera-t-il pas mille fois n'être qu'un valet de charrue, au service d'un pauvre laboureur, et souffrir tout au monde plutôt que de revenir à ses anciennes illusions et de vivre comme il vivait? 516e
Je suis de ton avis, dit-il; il préférera tout souffrir plutôt que de vivre de cette façon-là.
Imagine encore que cet homme redescende dans la caverne et aille s'asseoir à son ancienne place : n'aura-t-il pas les yeux aveuglés par les ténèbres en venant brusquement du plein soleil?
Assurément si, dit-il.
Et s'il lui faut entrer de nouveau en compétition, pour juger ces ombres, avec les prisonniers qui n'ont point quitté leurs chaînes, dans le moment où sa vue 517 est encore confuse et avant que ses yeux se soient remis (or l'accoutumance à l'obscurité demandera un temps assez long), n'apprêtera-t-il pas à rire à ses dépens (462), et ne diront-ils pas qu'étant allé là-haut il en est revenu avec la vue ruinée, de sorte que ce n'est même pas la peine d'essayer d'y monter? Et si quelqu'un tente de les délier et de les conduire en haut, et qu'ils le puissent tenir en leurs mains et tuer, ne le tueront-ils pas (463)?
Sans aucun doute, répondit-il.
Maintenant, mon cher Glaucon, repris-je, il faut 517b appliquer point par point cette image à ce que nous avons dit plus haut, comparer le monde que nous découvre la vue au séjour de la prison, et la lumière du feu qui l'éclaire à la puissance du soleil. Quant à la montée dans la région supérieure et à la contemplation de ses objets, si tu la considères comme l'ascension de l'âme vers le lieu intelligible tu ne te tromperas pas sur ma pensée, puisque aussi bien tu désires la connaître. Dieu sait si elle est vraie. Pour moi, telle est mon opinion : dans le monde intelligible l'idée du bien est perçue la dernière et avec 517c peine, mais on ne la peut percevoir sans conclure qu'elle est la cause de tout ce qu'il y a de droit et de beau en toutes choses; qu'elle a, dans le monde visible, engendré la lumière et le souverain de la lumière (464); que, dans le monde intelligible, c'est elle-même qui est souveraine et dispense la vérité et l'intelligence; et qu'il faut la voir pour se conduire avec sagesse dans la vie privée et dans la vie publique.
Je partage ton opinion, dit-il, autant que je le puis.
Eh bien ! partage-la encore sur ce point, et ne t'étonnes pas que ceux qui se sont élevés à ces hauteurs ne veuillent plus s'occuper des affaires humaines, et que leurs âmes 517d aspirent sans cesse à demeurer là-haut. Cela est bien naturel si notre allégorie est exacte.
C'est, en effet, bien naturel, dit-il.
Mais quoi? penses-tu qu'il soit étonnant qu'un homme qui passe des contemplations divines aux misérables choses humaines ait mauvaise grâce et paraisse tout à fait ridicule, lorsque, ayant encore la vue troublée et n'étant pas suffisamment accoutumé aux ténèbres environnantes, il est obligé d'entrer en dispute, devant les tribunaux ou ailleurs, sur des ombres de justice ou sur les images qui projettent ces ombres, et de combattre les interprétations 517e qu'en donnent ceux qui n'ont jamais vu la justice elle-même (465)?
Il n'y a là rien d'étonnant.
En effet, repris-je, un homme sensé se rappellera que 518 les yeux peuvent être troublés de deux manières et par deux causes opposées : par le passage de la lumière à l'obscurité, et par celui de l'obscurité à la lumière; et ayant réfléchi qu'il en est de même pour l'âme, quand il en verra une troublée et embarrassée pour discerner certains objets, il n'en rira pas sottement, mais examinera plutôt si, venant d'une vie plus lumineuse, elle est, faute d'habitude, offusquée par les ténèbres, ou si, passant de l'ignorance à la lumière, elle est éblouie de son trop 518b vif éclat; dans le premier cas il l'estimera heureuse en raison de ce qu'elle éprouve et de la vie qu'elle mène; dans le second, il la plaindra, et s'il voulait rire à ses dépens, ses moqueries seraient moins ridicules que si elles s'adressaient à l'âme qui redescend du séjour de la lumière (466).
C'est parler, dit-il, avec beaucoup de sagesse.
Il nous faut donc, si tout cela est vrai, en conclure ceci ; l'éducation n'est point ce que certains proclament qu'elle 518c est ; car ils prétendent l'introduire dans l'âme, où elle n'est point, comme on donnerait la vue à des yeux aveugles (467).
Ils le prétendent, en effet.
Or, repris-je, le présent discours montre que chacun possède la faculté d'apprendre et l'organe destiné à cet usage, et que, semblable à des yeux qui ne pourraient se tourner qu'avec le corps tout entier des ténèbres vers la lumière, cet organe doit aussi se détourner avec l'âme tout entière de ce qui naît, jusqu'à ce qu'il devienne capable de supporter la vue de l'être et de ce qu'il y a de 518d plus lumineux dans l'être; et cela nous l'appelons le bien, n'est-ce pas?
Oui.
L'éducation est donc l'art qui se propose ce but, la conversion de l'âme, et qui recherche les moyens les plus aisés et les plus efficaces de l'opérer; elle ne consiste pas à donner la vue à l'organe de l'âme, puisqu'il l'a déjà; mais comme il est mal tourné et ne regarde pas où il faudrait, elle s'efforce de l'amener dans la bonne direction.
Il le semble, dit-il.
Maintenant, les autres vertus, appelées vertus de l'âme, paraissent bien se rapprocher de celles du corps - car, en réalité, quand on ne les a pas tout d'abord, on les peut 518e acquérir dans la suite par l'habitude et l'exercice (468); mais la vertu de science appartient très probablement à quelque chose de plus divin (469), qui ne perd jamais sa force, et qui, selon la direction qu'on lui donne, devient 519 utile et avantageux ou inutile et nuisible. N'as-tu pas encore remarqué, au sujet des gens que l'on dit méchants mais habiles, combien perçants sont les yeux de leur misérable petite âme, et avec quelle acuité ils discernent les objets vers lesquels ils se tournent? Leur âme n'a donc pas une vue faible, mais comme elle est contrainte de servir leur malice, plus sa vue est perçante, plus elle fait de mal.
Cette remarque est tout à fait juste, dit-il.
Et cependant, poursuivis-je, si de pareils naturels étaient émondés dès l'enfance, et que l'on coupât les excroissances de la famille du devenir, comparables à des masses de plomb, qui s'y développent par l'effet de la 519b gourmandise, des plaisirs et des appétits de ce genre, et qui tournent la vue de l'âme vers le bas; si, libérés de ce poids, ils étaient tournés vers la vérité, ces mêmes naturels la verraient avec la plus grande netteté, comme ils voient les objets vers lesquels ils sont maintenant tournés.
C'est vraisemblable, reconnut-il.
Mais quoi ! n'est-il pas également vraisemblable, et nécessaire d'après ce que nous avons dit, que ni les gens sans éducation et sans connaissance de la vérité, ni ceux qu'on laisse passer toute leur vie dans l'étude, ne sont 519c propres au gouvernement de la cité, les uns parce qu'ils n'ont aucun but fixe auquel ils puissent rapporter tout ce qu'ils font dans la vie privée ou dans la vie publique, les autres parce qu'ils ne consentiront point à s'en charger, se croyant déjà transportés de leur vivant dans les îles fortunées.
C'est vrai, dit-il.
Il nous incombera donc, à nous fondateurs, d'obliger les meilleurs naturels à se tourner vers cette science que nous avons reconnue tout à l'heure (470) comme la plus sublime, à voir le bien et à faire cette ascension; mais, 519d après qu'ils se seront ainsi élevés et auront suffisamment contemplé le bien, gardons-nous de leur permettre ce qu'on leur permet aujourd'hui.
Quoi donc?
De rester là-haut, répondis-je, de refuser de descendre de nouveau parmi les prisonniers et de partager avec eux travaux et honneurs, quel que soit le cas qu'on en doive faire (471).
Hé quoi ! s'écria-t-il, commettrons-nous à leur égard l'injustice de les forcer à mener une vie misérable, alors qu'ils pourraient jouir d'une condition plus heureuse?
519e Tu oublies encore une fois, mon ami, que la loi ne se préoccupe pas d'assurer un bonheur exceptionnel à une classe de citoyens, mais qu'elle s'efforce de réaliser le bonheur de la cité tout entière, en unissant les citoyens par la persuasion ou la contrainte, et en les amenant à se faire part les uns aux autres des avantages que chaque 520 classe peut apporter à la communauté; et que, si elle forme de tels hommes dans la cité, ce n'est point pour les laisser libres de se tourner du côté qu'il leur plaît, mais pour les faire concourir à fortifier le lien de l'État.
C'est vrai, dit-il, je l'avais oublié.
Au reste, Glaucon, observe que nous ne serons pas coupables d'injustice envers les philosophes qui se seront formés chez nous, mais que nous aurons de justes raisons à leur donner en les forçant à se charger de la conduite et de la garde des autres. Nous leur dirons en effet : 520b « Dans les autres cités, il est naturel que ceux qui sont devenus philosophes ne participent point aux travaux de la vie publique, puisqu'ils se sont formés eux-mêmes, malgré le gouvernement de ces cités; or il est juste que celui qui se forme soi-même et ne doit sa nourriture à personne, ne veuille en payer le prix à qui que ce soit. Mais vous, nous vous avons formés dans l'intérêt de l'État comme dans le vôtre pour être ce que sont les chefs et les rois dans les ruches; nous vous avons donné une éducation meilleure et plus parfaite que celle de ces 520c philosophes-là, et vous avons rendus plus capables d'allier le maniement des affaires à l'étude de la philosophie (472). Il faut donc que vous descendiez, chacun à votre tour, dans la commune demeure, et que vous vous accoutumiez aux ténèbres qui y règnent; lorsque vous vous serez familiarisés avec elles, vous y verrez mille fois mieux que les habitants de ce séjour, et vous connaîtrez la nature de chaque image (473), et de quel objet elle est l'image, parce que vous aurez contemplé en vérité le beau, le juste et le bien. Ainsi le gouvernement de cette cité qui est la vôtre et la nôtre sera une réalité et non pas un vain songe, comme celui des cités actuelles, où les chefs se battent pour des ombres et se disputent l'autorité, 520d qu'ils regardent comme un grand bien (474). Voici là-dessus quelle est la vérité : la cité où ceux qui doivent commander sont les moins empressés à rechercher le pouvoir, est la mieux gouvernée et la moins sujette à la sédition, et celle où les chefs sont dans des dispositions contraires se trouve elle-même dans une situation contraire. »
Parfaitement, dit-il.
Eh bien ! crois-tu que nos élèves résisteront à ces raisons et refuseront de prendre part, à tour de rôle, aux labeurs de l'État, tout en passant d'ailleurs ensemble la majeure partie de leur temps dans la région de la pure lumière?
C'est impossible, répondit-il, car nos prescriptions sont justes et s'adressent à des hommes justes. Mais il est 520e certain que chacun d'eux ne viendra au pouvoir que par nécessité, contrairement à ce que font aujourd'hui les chefs dans tous les États.
Oui, repris-je, il en est ainsi, mon camarade; si tu découvres pour ceux qui doivent commander une condition 521 préférable au pouvoir lui-même, il te sera possible d'avoir un État bien gouverné; car dans cet État seuls commanderont ceux qui sont vraiment riches, non pas d'or, mais de cette richesse dont l'homme a besoin pour être heureux : une vie vertueuse et sage. Par contre, si les mendiants et les gens affamés de biens particuliers viennent aux affaires publiques, persuadés que c'est là qu'il faut en aller prendre, cela ne te sera pas possible; car on se bat alors pour obtenir le pouvoir, et cette guerre domestique et intestine perd et ceux qui s'y livrent et le reste de la cité (475).
Rien de plus vrai, dit-il.
Or, connais-tu une autre condition que celle du vrai 521b philosophe pour inspirer le mépris des charges publiques ?
Non, par Zeus.
D'autre part, il ne faut pas que les amoureux du pouvoir lui fassent la cour, autrement il y aura des luttes entre prétendants rivaux.
Sans doute.
Par conséquent, à qui imposeras-tu la garde de la cité, sinon à ceux qui sont les plus instruits des moyens de bien gouverner un État, et qui ont d'autres honneurs et une condition préférable à celle de l'homme public?
À personne d'autre.
521c Veux-tu donc que nous examinions maintenant de quelle manière se formeront des hommes de ce caractère, et comment on les fera monter vers la lumière, comme certains sont montés, dit-on, de l'Hadès au séjour des dieux (476)?
Comment ne le voudrais-je pas?
Cela ne sera pas, apparemment, un simple tour de palet (477); il s'agira d'opérer la conversion de l'âme d'un jour aussi ténébreux que la nuit vers le jour véritable, c'est-à-dire de l'élever jusqu'à l'être; et c'est ce que nous appellerons la vraie philosophie.
Parfaitement.
Il faut donc examiner quelle est, parmi les sciences, 521d celle qui est propre à produire cet effet.
Sans doute.
Quelle est donc, Glaucon, la science qui attire l'âme de ce qui devient vers ce qui est? Mais, en parlant, ceci me revient à l'esprit : n'avons-nous pas dit que nos philosophes devaient être dans leur jeunesse des athlètes guerriers (478)?
Si, nous l'avons dit.
Il faut donc que la science que nous cherchons, outre ce premier avantage, en ait encore un autre.
Lequel?
Celui de ne pas être inutile à des hommes de guerre.
Assurément il le faut, si la chose est possible.
521e Or, c'est par la gymnastique et la musique que nous les avons précédemment formés (479).
Oui.
Mais la gymnastique a pour objet ce qui devient et ce qui meurt, puisque c'est du développement et du dépérissement du corps qu'elle s'occupe.
Évidemment.
Elle n'est donc pas la science que nous cherchons.
Non.
Serait-ce la musique, telle que nous l'avons décrite 522 plus haut?
Mais, répliqua-t-il, elle n'était, s'il t'en souvient, que la contrepartie de la gymnastique, formant les gardiens par l'habitude, et leur communiquant au moyen de l'harmonie un certain accord - et non la science - et une certaine eurythmie au moyen du rythme; et dans les discours ses caractères étaient semblables, qu'il s'agît de discours fabuleux ou véridiques; mais d'étude qui conduisît au but que tu te proposes maintenant, elle n'en comportait aucune (480).
522b Tu me rappelles très exactement ce que nous avons dit; en vérité, elle n'en comportait aucune. Mais alors, excellent Glaucon, quelle sera cette étude? Car les arts nous sont tous apparus comme mécaniques...
Sans doute. Mais quelle autre étude reste-t-il si nous écartons la musique, la gymnastique et les arts?
Eh bien ! répondis-je, si nous ne trouvons rien à prendre hors delà, prenons quelqu'une de ces études qui s'étendent à tout.
Laquelle?
Par exemple cette étude commune, qui sert à tous les 522c arts, à toutes les opérations de l'esprit et à toutes les sciences, et qui est une des premières auxquelles tout homme doit s'appliquer.
Laquelle? demanda-t-il.
Cette étude vulgaire qui apprend à distinguer un, deux et trois; je veux dire, en un mot, la science des nombres et du calcul; n'est-il pas vrai qu'aucun art, aucune science ne peut s'en passer?
Certes !
Ni, par conséquent, l'art de la guerre?
Il y a grande nécessité.
En vérité, Palamède (481), chaque fois qu'il apparaît 522d dans les tragédies, nous présente Agamemnon sous les traits d'un fort plaisant général. Ne prétend-il pas en effet, que c'est lui, Palamède, qui, après avoir inventé les nombres, disposa l'armée en ordre de bataille devant Ilion, et fit le dénombrement des vaisseaux et de tout le reste, comme si avant lui rien de cela n'eût été dénombré et qu'Agamemnon, apparemment, ne sût pas combien de pieds il avait, puisqu'il ne savait pas compter. Quel générai serait-ce là à ton avis?
Un général singulier, dit-il, si la chose était vraie.
522e Dès lors, repris-je, nous poserons comme nécessaire au guerrier la science du calcul et des nombres.
Elle lui est tout à fait indispensable s'il veut entendre quelque chose à l'ordonnance d'une armée, ou plutôt s'il veut être homme (482).
Maintenant, demandai-je, fais-tu la même remarque que moi au sujet de cette science?
Laquelle?
523 Quelle pourrait bien être une de ces sciences que nous cherchons et qui conduisent naturellement à la pure intelligence; mais personne n'en use comme il faudrait, quoiqu'elle soit parfaitement propre à élever jusqu'à l'être.
Que veux-tu dire?
Je vais t'expliquer ma pensée; ce que je distinguerai comme propre ou non à mener au but dont nous parlons, considère-le avec moi, puis donne ou refuse ton assentiment, afin que nous puissions voir plus clairement si la chose est telle que je l'imagine.
Montre ce dont il s'agit.
Je te montrerai donc, si tu veux bien regarder, que 523b parmi les objets de la sensation les uns n'invitent point l'esprit à l'examen, parce que les sens suffisent à en juger, tandis que les autres l'y invitent instamment, parce que la sensation, à leur sujet, ne donne rien de sain.
Tu parles sans doute des objets vus dans le lointain et des dessins en perspective.
Tu n'as pas du tout compris ce que je veux dire.
De quoi donc veux-tu parler? demanda-t-il.
Par objets ne provoquant point l'examen, répondis-je, j'entends ceux qui ne donnent pas lieu, en même temps, à deux sensations opposées; et je considère ceux qui y 523c donnent lieu comme provoquant l'examen, puisque, qu'on les perçoive de près ou de loin, les sens n'indiquent pas qu'ils soient ceci plutôt que le contraire. Mais tu comprendras plus clairement ce que je veux dire de la manière suivante : voici trois doigts, le pouce, l'index et le majeur (483).
Fort bien, dit-il.
Conçois que je les suppose vus de près; maintenant, fais avec moi cette observation.
Laquelle?
Chacun d'eux nous paraît également un doigt; peu 523d importe à cet égard qu'on le voie au milieu ou à l'extrémité, blanc ou noir, gros ou mince, et ainsi du reste. Dans tous ces cas, l'âme de la plupart des hommes n'est pas obligée de demander à l'entendement ce que c'est qu'un doigt, car la vue ne lui a jamais témoigné en même temps qu'un doigt fût autre chose qu'un doigt.
Certes bon, dit-il.
Il est donc naturel, repris-je, qu'une pareille sensation n'excite ni ne réveille l'entendement. 523e
C'est naturel.
Mais quoi? la vue discerne-t-elle bien la grandeur et la petitesse des doigts, et à cet égard lui est-il indifférent que l'un d'eux soit au milieu ou à l'extrémité? et n'en est-il pas de même pour le toucher à l'égard de l'épaisseur et de la minceur, de la mollesse et de la dureté? et les données des autres sens ne sont-elles pas pareillement défectueuses? N'est-ce pas ainsi que chacun d'eux procède? D'abord le sens préposé à la perception de ce 524 qui est dur a charge de percevoir aussi ce qui est mou, et il rapporte à l'âme que le même objet lui donne une sensation de dureté et de mollesse.
Il en est ainsi.
Or, n'est-il pas inévitable qu'en de tels cas l'âme soit embarrassée et se demande ce que signifie une sensation qui lui présente une même chose comme dure et comme molle? De même dans la sensation de la légèreté et dans celle de la lourdeur (484), que doit-elle entendre par léger et par lourd si l'une lui signale que le lourd est léger, et l'autre que le léger est lourd?
524b En effet, dit-il, ce sont là d'étranges témoignages pour l'âme et qui réclament l'examen.
Il est donc naturel, repris-je, que l'âme appelant alors à son secours le raisonnement et l'intelligence tâche de se rendre compte si chacun de ces témoignages porte sur une chose ou sur deux.
Sans doute.
Et si elle juge que ce sont deux choses, chacune d'elles lui paraît une et distincte de l'autre.
Oui.
Si donc chacune lui paraît une, et l'une et l'autre deux, elle les concevra comme séparées; car si elles n'étaient pas séparées elle ne les concevrait pas comme étant deux 524c mais une.
C'est exact.
La vue a perçu, disons-nous; la grandeur et la petitesse non point séparées, mais confondues ensemble, n'est-ce pas?
Oui.
Et pour éclaircir cette confusion, l'entendement est forcé de voir la grandeur et la petitesse non plus confondues, mais séparées, contrairement à ce que faisait la vue.
C'est vrai.
Or, n'est-ce pas de là que nous vient d'abord la pensée de nous demander ce que peuvent être la grandeur et la petitesse (485)?
Si fait.
Et c'est de la sorte que nous avons défini l'intelligible et le visible.
524d Précisément.
Voilà donc ce que je voulais faire entendre tout à l'heure, quand je disais que certains objets invitent l'âme à la réflexion, et que d'autres ne l'y invitent point, distinguant comme propres à l'y inviter ceux qui donnent lieu simultanément à deux sensations contraires, et ceux qui n'y donnent point lieu comme impropres à éveiller l'intelligence.
Je comprends maintenant, dit-il, et je suis de ton avis. Et le nombre et l'unité, dans quelle classe les ranges-tu? Je ne sais, répondit-il.
Eh bien ! juges-en d'après ce que nous venons de dire. Si l'unité est perçue en elle-même, de façon satisfaisante, par la vue ou par quelque autre sens, elle n'attirera pas 524e notre âme vers l'essence, non plus que le doigt dont nous parlions tout à l'heure; mais si la vue de l'unité offre toujours quelque contradiction, de sorte qu'elle ne paraisse pas plus unité que multiplicité, alors il faudra un juge pour décider; l'âme est forcément embarrassée, et, réveillant en elle l'entendement, elle est contrainte de faire des recherches et de se demander ce que peut être l'unité en soi; c'est ainsi que la perception de l'unité est de celles qui conduisent et tournent l'âme vers la conemplation 525 de l'être.
Certes, dit-il, la vue de l'unité possède ce pouvoir à un très haut degré, car nous voyons la même chose à la fois une et multiple jusqu'à l'infini.
Et s'il en est ainsi de l'unité, poursuivis-je, il en est de même de tout nombre (486)?
Sans doute.
Or, la logistique et l'arithmétique portent tout entières sur le nombre (487)?
Certainement.
Ce sont par conséquent des sciences propres à conduire 525b à la vérité.
Oui, éminemment propres.
Elles sont donc, semble-t-il, de celles que nous cherchons, car l'étude en est nécessaire au guerrier pour ranger une armée, et au philosophe pour sortir de la sphère du devenir et atteindre l'essence, sans quoi il ne serait jamais arithméticien.
C'est vrai dit-il.
Mais notre gardien est à la fois guerrier et philosophe?
Sans doute.
Il conviendrait donc, Glaucon, de prescrire cette étude par une loi, et de persuader à ceux qui doivent remplir 525c les plus hautes fonctions publiques de se livrer à la science du calcul, non pas superficiellement, mais jusqu'à ce qu'ils arrivent, par la pure intelligence, à connaître la nature des nombres; et de cultiver cette science non pas pour la faire servir aux ventes et aux achats, comme les négociants et les marchands (488), mais pour l'appliquer à la guerre, et pour faciliter la conversion de l'âme du monde de la génération vers la vérité et l'essence.
Très bien dit.
Et j'aperçois maintenant, après avoir parlé de la 525d science des nombres, combien elle est belle et utile, sous bien des rapports, à notre dessein, à condition qu'on l'étudie pour connaître et non pour trafiquer.
Qu'admires-tu donc si fort en elle?
Ce pouvoir, dont je viens de parler, de donner à l'âme un vigoureux élan vers la région supérieure, et de l'obliger à raisonner sur les nombres en eux-mêmes, sans jamais souffrir qu'on introduise dans ses raisonnements des nombres visibles et palpables (489). Tu sais en effet ce que 525e font les gens habiles en cette science : si l'on essaie, au cours d'une discussion, de diviser l'unité proprement dite, ils se moquent et n'écoutent pas. Si tu la divises, ils la multiplient d'autant, dans la crainte qu'elle n'apparaisse plus comme une, mais comme un assemblage de parties (490).
C'est très vrai, dit-il.
526 Que crois-tu donc, Glaucon, si quelqu'un leur demandait : « Hommes merveilleux, de quels nombres parlez-vous? Où sont ces unités, telles que vous les supposez, toutes égales entre elles, sans la moindre différence, et qui ne sont pas formées de parties? » que crois-tu qu'ils répondraient?
Ils répondraient, je crois, qu'ils parlent de ces nombres qu'on ne peut saisir que par la pensée, et qu'on ne peut manier d'aucune autre façon.
Tu vois ainsi, mon ami, que cette science a l'air de nous être vraiment indispensable, puisqu'il est évident qu'elle 526b oblige l'âme à se servir de la pure intelligence pour atteindre la vérité en soi.
Oui, elle est remarquablement propre à produire cet effet.
Mais n'as-tu pas observé que les calculateurs-nés sont naturellement prompts à comprendre toutes les sciences, pour ainsi dire, et que les esprits lourds, lorsqu'ils ont été exercés et rompus au calcul, même s'ils n'en retirent aucun autre avantage, y gagnent au moins celui d'acquérir plus de pénétration (491).
C'est incontestable, dit-il.
Au reste, il serait difficile, je pense, de trouver beaucoup 526c de sciences qui coûtent plus à apprendre et à pratiquer que celle-là.
Certes.
Pour toutes ces raisons, il ne faut pas la négliger, mais y former les meilleurs naturels.
Je suis de ton avis.
Voilà donc, repris-je, une première science adoptée; examinons si cette deuxième, qui s'y rattache, nous convient en quelque manière.
Laquelle? demanda-t-il; est-ce de la géométrie que tu veux parler?
D'elle-même, répondis-je.
En tant qu'elle se rapporte aux opérations de la guerre, 526d il est évident qu'elle nous convient; car pour asseoir un camp, prendre des places fortes, resserrer ou étendre une armée, et lui faire exécuter toutes les manoeuvres qui sont d'usage dans les batailles ou dans les marches, le même général se montre autrement supérieur s'il est géomètre que s'il ne l'est pas.
Mais en vérité, répliquai-je, il n'est pas besoin pour cela de beaucoup de géométrie et de calcul. Il faut donc 526e examiner si le fort de cette science et ses parties les plus avancées tendent à notre but, qui est de faire voir plus facilement l'idée du bien. Or y tend, disons-nous, tout ce qui force l'âme à se tourner vers le lieu où réside le plus heureux des êtres, que, de toute façon, elle doit contempler.
Tu as raison.
Par conséquent, si la géométrie oblige à contempler l'essence, elle nous convient; si elle s'arrête au devenir, elle ne nous convient pas (492).
C'est notre opinion.
527 Or, aucun de ceux qui savent un peu de géométrie ne nous contestera que la nature de cette science est directement opposée au langage qu'emploient ceux qui la pratiquent.
Comment? demanda-t-il.
Ce langage, assurément, est fort ridicule et misérable; car c'est en hommes de pratique, ayant en vue les applications, qu'ils parlent de carrer, de construire sur une ligne, d'ajouter, et qu'ils font sonner d'autres mots semblables 527b, alors que cette science tout entière n'a d'autre objet que la connaissance.
C'est parfaitement vrai.
Ne faut-il donc pas convenir encore de ceci?
De quoi?
Qu'elle a pour objet la connaissance de ce qui est toujours et non de ce qui naît et périt.
Il est aisé d'en convenir, dit-il; la géométrie est en effet la connaissance de ce qui est toujours (493).
Par suite, mon noble ami, elle attire l'âme vers la vérité, et développe en elle cet esprit philosophique qui élève vers les choses d'en haut les regards que nous abaissons à tort vers les choses d'ici-bas.
Oui, elle produit cet effet autant qu'il se peut. 527c
Il faut donc, autant qu'il se peut, prescrire aux citoyens de ta Callipolis de ne point négliger la géométrie; elle a d'ailleurs des avantages secondaires qui ne sont pas à mépriser.
Lesquels?
Ceux que tu as mentionnés, répondis-je, et qui concernent la guerre; en outre, pour ce qui est de mieux comprendre les autres sciences, nous savons qu'il y a une différence du tout au tout entre celui qui est versé dans la géométrie et celui qui ne l'est pas.
Oui, par Zeus, du tout au tout.
Voilà donc la seconde science que nous prescrirons aux jeunes gens.
Prescrivons-la, dit-il.
Et maintenant l'astronomie sera-t-elle la troisième 527d science? Que t'en semble?
C'est mon avis; car savoir aisément reconnaître le moment du mois et de l'année où l'on se trouve est chose qui intéresse non seulement l'art du laboureur et l'art du pilote, mais encore, et non moins, celui du général.
Tu m'amuses, dis-je; en effet, tu sembles craindre que le vulgaire ne te reproche de prescrire des études inutiles. Or il importe beaucoup, encore que ce soit difficile, de croire que les études dont nous parlons purifient et ravivent en chacun de nous un organe de l'âme gâté et aveuglé 527e par les autres occupations - organe dont la conservation est mille fois plus précieuse que celle des yeux du corps, puisque c'est par lui seul qu'on aperçoit la vérité. À ceux qui partagent cette opinion tes propos paraîtront extrêmement justes; mais ceux qui n'ont là-dessus aucune lumière trouveront naturellement que ces propos ne signifient rien; car en dehors de l'utilité pratique, ils ne voient dans ces sciences aucun autre avantage digne de mention. Demande-toi donc auquel de ces deux groupes d'auditeurs tu t'adresses; ou bien si ce n'est ni pour les 528 uns ni pour les autres, mais pour toi principalement que tu raisonnes, sans envier pourtant à un autre le profit qu'il peut tirer de tes raisonnements.
C'est le parti que je choisis, répondit-il : de parler, de questionner et de répondre principalement pour moi.
Reviens alors en arrière, dis-je, car tout à l'heure nous n'avons pas pris la science qui suit immédiatement la géométrie (494).
Comment cela? demanda-t-il.
Après les surfaces nous avons pris les solides déjà en mouvement, avant de nous occuper des solides en eux-mêmes 528b; or l'ordre exige qu'après ce qui est élevé à la seconde puissance on passe à ce qui l'est à la troisième, c'est-à-dire aux cubes et aux objets qui ont de la profondeur.
C'est vrai, dit-il; mais il me semble, Socrate, que cette science n'est pas encore découverte.
Aussi bien, repris-je, cela tient à deux causes : d'abord, aucune cité n'honore ces recherches, et comme elles sont difficiles, on y travaille faiblement; ensuite, les chercheurs ont besoin d'un directeur sans lequel leurs efforts seront vains. Or il est difficile d'en trouver un, et le trouverait-on, dans l'état actuel des choses, ceux qui s'occupent de ces 528c recherches ont trop de présomption pour lui obéir. Mais si une cité tout entière coopérait avec ce directeur et honorait cette science, ils obéiraient, et les questions que pose cette dernière, étudiées avec suite et vigueur, seraient élucidées, puisque même à présent, méprisée du vulgaire, tronquée par des chercheurs qui ne se rendent pas compte de son utilité (495), en dépit de tous ces obstacles, et par la seule force du charme qu'elle exerce, elle fait des progrès; aussi n'est-il pas surprenant qu'elle en soit 528d au point où nous la voyons (496).
Certes, dit-il, elle exerce un charme extraordinaire. Mais explique-moi plus clairement ce que tu disais tout à l'heure. Tu mettais d'abord la science des surfaces ou géométrie.
Oui.
Et l'astronomie immédiatement après; puis, tu es revenu sur tes pas.
C'est que, dans ma hâte d'exposer rapidement tout cela, je recule au lieu d'avancer. En effet, après la géométrie, vient la science qui étudie la dimension de profondeur; mais comme elle n'a encore donné lieu qu'à des recherches ridicules, je l'ai laissée pour passer à l'astronomie, c'est-à-dire au mouvement des solides. 528e
C'est exact.
Plaçons donc l'astronomie au quatrième rang, en supposant que la science que nous laissons à présent de côté se constituera quand la cité s'en occupera.
C'est vraisemblable, dit-il. Mais comme tu m'as reproché tout à l'heure de faire un éloge maladroit de l'astronomie, je vais la louer maintenant d'une manière conforme au point de vue sous lequel tu l'envisages. Il est, 529 ce me semble, évident pour tout le monde qu'elle oblige l'âme à regarder en haut et à passer des choses d'ici-bas aux choses du ciel.
Peut-être, répliquai-je, est-ce évident pour tout le monde sauf pour moi; car je n'en juge pas ainsi.
Et comment en juges-tu? demanda-t-il.
De la façon dont la traitent ceux qui prétendent l'ériger en philosophie, elle fait, à mon avis, regarder en bas.
Comment l'entends-tu?
Ma foi ! elle ne manque pas d'audace (497) ta conception de l'étude des choses d'en haut ! Tu as l'air de croire qu'un homme qui regarderait les ornements d'un plafond 529b, la tête penchée en arrière, et y distinguerait quelque chose, userait, ce faisant, de sa raison et non de ses yeux !
Peut-être, après tout, est-ce toi qui en juges bien et moi sottement; mais je ne puis reconnaître d'autre science qui fasse regarder en haut que celle qui a pour objet l'être et l'invisible; et si quelqu'un tente d'étudier une chose sensible en regardant en haut, bouche béante, ou en bas, bouche close, l'affirme qu'il n'apprendra jamais - car la science ne comporte rien de sensible - et que son âme ne regarde pas en haut mais en bas, étudiât-il couché à 529c la renverse sur terre ou flottant sur le dos en mer (498) !
Tu as raison de me reprendre; je n'ai que ce que je mérite. Mais comment disais-tu qu'il fallait réformer l'étude de l'astronomie pour la rendre utile à notre dessein?
Voici, dis-je. On doit considérer les ornements du ciel comme les plus beaux et les plus parfaits des objets de 529d leur ordre, mais, puisqu'ils appartiennent au monde visible, ils sont bien inférieurs aux vrais ornements, aux mouvements selon lesquels la pure vitesse et la pure lenteur, dans le vrai nombre et toutes les vraies figures, se meuvent en relation l'une avec l'autre, et meuvent ce qui est en elles (499); or ces choses sont perçues par l'intelligence et la pensée discursive et non par la vue; ou peut-être crois-tu le contraire?
Nullement.
Il faut donc, poursuivis-je, se servir des ornements du ciel ainsi que de modèles dans l'étude de ces choses invisibles, comme on ferait si l'on trouvait des dessins tracés 529e et exécutés avec une habileté incomparable par Dédale ou par quelque autre artiste ou peintre : en les voyant, un géomètre estimerait que ce sont des chefs-d'oeuvre de fini, mais il trouverait ridicule de les étudier sérieusement dans le propos d'y saisir la vérité sur les rapports des 530 quantités égales, doubles ou autres.
En effet, ce serait ridicule.
Et le véritable astronome, ne crois-tu pas qu'il éprouvera le même sentiment en considérant les mouvements des astres? Il pensera que le ciel et ce qu'il renferme ont été disposés par leur créateur avec toute la beauté qu'on peut mettre en de pareils ouvrages; mais quant aux rapports du jour à la nuit, du jour et de la nuit aux mois, des mois à l'année, et des autres astres au soleil, 530b à la lune et à eux-mêmes, ne trouvera-t-il pas qu'il est absurde de croire que ces rapports soient toujours les mêmes et ne varient jamais - alors qu'ils sont corporels et visibles - et de chercher par tous les moyens à y saisir la vérité (500) ?
C'est mon avis, dit-il, maintenant que je viens de t'entendre.
Donc, repris-je, nous étudierons l'astronomie comme la géométrie, à l'aide de problèmes, et nous laisserons les 530c phénomènes du ciel, si nous voulons saisir vraiment cette science, et rendre utile la partie intelligente de notre âme, d'inutile qu'elle était auparavant.
Certes, dit-il, tu prescris là aux astronomes une tâche maintes fois plus difficile que celle qu'ils font aujourd'hui !
Et je pense, ajoutai-je, que nous prescrirons la même méthode pour les autres sciences, si nous sommes de bons législateurs. Mais pourrais-tu me rappeler encore quelque science qui convienne à notre dessein?
Non, du moins pas sur-le-champ.
Cependant le mouvement ne présente pas qu'une seule forme : il en a plusieurs, ce me semble. Un savant pourrait 530d peut-être les énumérer toutes; mais il en est deux que nous connaissons.
Lesquelles?
Outre celle que nous venons de mentionner, une autre qui lui répond (501).
Quelle?
Il semble, répondis-je, que comme les yeux ont été formés pour l'astronomie, les oreilles l'ont été pour le mouvement harmonique, et que ces sciences sont soeurs, comme l'affirment les Pythagoriciens, et comme nous, Glaucon, nous l'admettons, n'est-ce pas (502)?
Oui.
Comme l'affaire est d'importance, nous prendrons leur 530e opinion sur ce point et sur d'autres encore, s'il y a lieu; mais, dans tous les cas, nous garderons notre principe.
Lequel?
Celui de veiller à ce que nos élèves n'entreprennent point d'étude en ce genre qui resterait imparfaite, et n'aboutirait pas au terme où doivent aboutir toutes nos connaissances, comme nous le disions tantôt au sujet de l'astronomie. Ne sais-tu pas que les musiciens ne traitent pas mieux l'harmonie? S'appliquant à mesurer les accords 531 et les tons perçus par l'oreille, ils font, comme les astronomes, un travail inutile (503).
Et par les dieux! s'écria-t-il, c'est de façon ridicule qu'ils parlent de « fréquences » (504) et tendent l'oreille comme s'ils pourchassaient un son dans le voisinage (505); les uns prétendent qu'entre deux notes ils en perçoivent une intermédiaire, que c'est le plus petit intervalle et qu'il faut le prendre comme mesure (506); les autres soutiennent au contraire qu'il est semblable aux sons précédents; 531b mais les uns et les autres font passer l'oreille avant l'esprit.
Tu parles, dis-je, de ces braves musiciens qui persécutent et torturent les cordes en les tordant sur les chevilles. Je pourrais pousser plus loin la description, et parler des coups d'archet qu'ils leur donnent, des accusations dont ils les chargent, des dénégations et de la jactance des cordes (507); mais je la laisse et je déclare que ce n'est pas d'eux que je veux parler, mais de ceux que nous nous proposions tout à l'heure d'interroger sur l'harmonie; car ils font la même chose que les astronomes 531c : ils cherchent des nombres dans les accords perçus par l'oreille, mais ils ne s'élèvent pas jusqu'aux problèmes, qui consistent à se demander quels sont les nombres harmoniques et ceux qui ne le sont pas, et d'où vient entre eux cette différence.
Tu parles là, dit-il, d'une recherche sublime.
Elle est utile en tout cas pour découvrir le beau et le bien; mais poursuivie dans un autre but, elle est inutile.
Il le semble, approuva-t-il.
Je pense, repris-je, que si l'étude de toutes les sciences 531d que nous venons de parcourir (508) aboutit à la découverte des rapports et de la parenté qu'elles ont entre elles, et montre la nature du lien qui les unit, cette étude nous aidera à atteindre le but que nous nous proposons, et notre peine ne sera point perdue; sinon, nous aurons peiné sans profit.
J'en augure de même; mais tu parles là d'un bien long travail, Socrate.
Veux-tu dire le travail du prélude, ou quel autre? Ne savons-nous que toutes ces études ne sont que le prélude de l'air même qu'il faut apprendre? Car certes, les habiles 531e en ces sciences ne sont pas, à ton avis, des dialecticiens.
Non, par Zeus! dit-il, à l'exception d'un très petit hombre parmi ceux que j'ai rencontrés.
Mais, demandai-je, crois-tu que des gens qui ne sont pas capables de donner ou d'entendre raison puissent jamais connaître ce que nous disons qu'il faut savoir?
Je ne le crois pas non plus, répondit-il.
Eh bien ! Glaucon, repris-je, n'est-ce pas enfin cet air 532 même que la dialectique exécute? Il est intelligible, mais la puissance de la vue l'imite, qui, nous l'avons dit, essaie d'abord de regarder les êtres vivants, puis les astres, et enfin le soleil lui-même. Ainsi lorsqu'un homme essaie, par la dialectique, sans l'aide d'aucun sens, mais au moyen de la raison, d'atteindre à l'essence de chaque chose, et qu'il ne s'arrête point avant d'avoir saisi par la seule intelligence l'essence du bien, il parvient au terme 532b de l'intelligible, comme l'autre, tout à l'heure, parvenait au terme du visible.
Assurément.
Mais quoi? n'est-ce pas là ce que tu appelles la marche dialectique?
Sans doute.
Rappelle-toi, poursuivis-je, l'homme de la caverne : sa délivrance des chaînes, sa conversion des ombres vers les figures artificielles et la clarté qui les projette, sa montée du souterrain vers le soleil, et là, l'impuissance où il est encore de regarder les animaux, les plantes et la lumière du soleil, qui l'oblige à contempler dans les eaux leurs images divines et les ombres des êtres 532c réels, mais non plus les ombres projetées par une lumière qui, comparée avec le soleil, n'est elle-même qu'une image - voilà précisément les effets de l'étude des sciences que nous venons de parcourir : elle élève la partie la plus noble de l'âme jusqu'à la contemplation du plus excellent de tous les êtres, comme tout à l'heure nous venons de voir le plus perçant des organes du corps s'élever à la contemplation de ce qu'il y a de plus lumineux dans le monde matériel et visible.
532d Je l'admets ainsi, dit-il, quoique assurément ce me semble difficile à admettre; mais, d'un autre côté, ce me semble, aussi, difficile à rejeter. Cependant - comme il s'agit de choses dont nous n'avons pas à nous entretenir aujourd'hui seulement, mais sur lesquelles il nous faudra revenir plusieurs fois - supposons qu'il en est comme tu dis, passons à l'air lui-même, et étudions-le de la même façon que le prélude. Dis-nous donc quel est le caractère 532e de la puissance dialectique, en combien d'espèces elle se divise, et quels sont les chemins qu'elle suit (509); car ces chemins conduisent, apparemment, à un point où le voyageur trouve le repos des fatigues de la route et le terme de sa course.
Tu ne serais plus, mon cher Glaucon, capable de me 533 suivre - car, pour moi, la bonne volonté ne me ferait nullement défaut; seulement ce ne serait plus l'image de ce dont nous parlons que tu verrais, mais la réalité elle-même, ou du moins telle qu'elle m'apparaît. Qu'elle soit vraiment telle ou non, ce n'est pas le moment de l'affirmer, mais qu'il existe quelque chose d'approchant, on peut l'assurer n'est-ce pas?
Certes !
Et aussi que la puissance dialectique peut seule le découvrir à un esprit versé dans les sciences que nous venons de parcourir, mais que, par toute autre voie, c'est impossible.
Cela aussi mérite d'être affirmé.
533b Au moins, repris-je, il est un point que personne ne nous contestera (510) : c'est qu'il existe une autre méthode (en dehors de celles que nous venons de parcourir (511) qui essaie de saisir scientifiquement l'essence de chaque chose. La plupart des arts ne s'occupent que des désirs des hommes et de leurs goûts, et sont tout entiers tournés vers la production et la fabrication, ou l'entretien des objets naturels et fabriqués. Quant à ceux qui font exception, et qui, avons-nous dit, saisissent quelque chose 533c de l'essence - la géométrie et les arts qui viennent à sa suite - nous voyons qu'ils ne connaissent l'être qu'en songe, et qu'il leur sera impossible d'en avoir une vision réelle tant qu'ils considéreront les hypothèses dont ils se servent comme intangibles, faute de pouvoir en rendre raison. En effet, quand on prend pour principe une chose que l'on ne connaît pas, et que l'on compose les conclusions et les propositions intermédiaires d'éléments inconnus, le moyen que pareil accord fasse jamais une science?
Il n'en est aucun, répondit-il.
La méthode dialectique est donc la seule qui, rejetant les hypothèses, s'élève jusqu'au principe même pour établir solidement ses conclusions, et qui, vraiment, tire 533d peu à peu l'oeil de l'âme de la fange grossière où il est plongé (512) et l'élève vers la région supérieure, en prenant comme auxiliaires et comme aides pour cette conversion les arts que nous avons énumérés. Nous leur avons donné à plusieurs reprises le nom de sciences pour nous conformer à l'usage; mais ils devraient porter un autre nom, qui impliquerait plus de clarté que celui d'opinion, et plus d'obscurité que celui de science - nous nous sommes servis quelque part, plus haut (513), de celui de connaissance discursive. Mais il ne s'agit pas, ce me semble, de disputer sur les noms quand on a à examiner 533e des questions aussi importantes que celles que nous nous sommes proposées.
Certes non ! dit-il (514).
Il suffira donc, repris-je, comme précédemment, d'appeler science la première division de la connaissance, pensée discursive la seconde, foi la troisième, et imagination 534 la quatrième; de comprendre ces deux dernières sous le nom d'opinion, et les deux premières sous celui d'intelligence, l'opinion ayant pour objet la génération, et l'intelligence l'essence; et d'ajouter que ce qu'est l'essence par rapport à la génération, l'intelligence l'est par rapport à l'opinion, la science par rapport à la foi, et la connaissance discursive par rapport à l'imagination (515). Quant à la correspondance des objets auxquels s'appliquent ces relations, et à la division en deux de chaque sphère, celle de l'opinion et celle de l'intelligible, laissons cela, Glaucon, afin de ne pas nous jeter dans des discussions beaucoup plus longues que celles dont nous sommes sortis.
534b Pour ma part, j'adhère à ce que tu as dit, dans la mesure où je suis capable de te suivre.
Appelles-tu aussi dialecticien celui qui rend raison de l'essence de chaque chose? et celui qui ne le peut faire, ne diras-tu pas qu'il a d'autant moins l'intelligence d'une chose qu'il est plus incapable d'en rendre raison à lui-même et aux autres?
Comment pourrais-je refuser de le dire?
Il en est de même du bien. Qu'un homme ne puisse, en la séparant de toutes les autres, définir l'idée du bien, et, 534c comme dans un combat, se frayer un passage à travers toutes les objections, ayant à coeur de fonder ses preuves non sur l'apparence, mais sur l'essence; qu'il ne puisse avancer à travers tous ces obstacles par la force d'une logique infaillible : ne diras-tu pas d'un tel homme qu'il ne connaît ni le bien en soi, ni aucun autre bien, mais que, s'il saisit quelque fantôme du bien, c'est par l'opinion et non par la science qu'il le saisit, qu'il passe sa vie présente en état de rêve et de somnolence, et qu'avant 534d de s'éveiller ici-bas il ira chez Hadès dormir de son dernier sommeil?
Par Zeus ! je dirai tout cela, et avec force.
Mais si un jour tu devais élever effectivement ces enfants, que tu élèves et que tu formes en imagination, tu ne leur permettrais pas, je pense, s'ils étaient dépourvus de raison, comme les lignes irrationnelles (516), de gouverner la cité et de trancher les plus importantes questions?
Non, en effet, dit-il.
Tu leur prescriras donc de s'appliquer particulièrement à recevoir cette éducation qui doit les rendre capables d'interroger et de répondre de la manière la plus savante possible.
534e Je le leur prescrirai, dit-il, de concert avec toi.
Ainsi, repris-je, tu crois que la dialectique est en quelque sorte le couronnement suprême de nos études, qu'il n'en est point d'autre qu'on soit en droit de placer au-dessus, et qu'enfin nous en avons fini avec les sciences 535 qu'il faut apprendre.
Oui, répondit-il.
Il te reste maintenant à régler quels sont ceux à qui nous ferons part de ces études, et de quelle manière.
Évidemment.
Te rappelles-tu le premier choix que nous avons fait des chefs (517), et quels sont ceux que nous avons élus?
Comment non? dit-il.
Eh bien ! sois assuré qu'il faut choisir des hommes de même nature, c'est-à-dire qu'il faut préférer les plus fermes, les plus courageux, et autant qu'il se peut, les plus beaux. En outre, il faut chercher non seulement 535b des caractères nobles et forts, mais encore des dispositions appropriées à l'éducation que nous voulons leur donner.
Précise quelles sont ces dispositions.
Il leur faut, bienheureux ami, de la pénétration pour les sciences et de la facilité à apprendre; car l'âme se rebute bien plutôt dans les fortes études que dans les exercices gymnastiques : la peine lui est plus sensible parce qu'elle n'est que pour elle seule, et que le corps ne la partage point.
C'est vrai, dit-il.
Il faut donc que l'homme que nous cherchons ait de la mémoire, une constance inébranlable, et l'amour de 535c toute espèce de travail. Autrement crois-tu qu'il consentirait à s'imposer, en plus des travaux du corps, tant d'études et d'exercices?
Il n'y consentira, répondit-il, que s'il est heureusement doué sous tous les rapports.
La faute que l'on commet aujourd'hui, repris-je, et qui est cause du mépris qui retombe sur la philosophie, tient, comme nous l'avons dit précédemment, à ce que l'on s'adonne à cette étude sans en être digne; en effet, il ne faudrait point que l'abordent des talents bâtards, mais seulement des talents authentiques.
Comment l'entends-tu? demanda-t-il.
D'abord, celui qui veut s'y appliquer ne doit pas être 535d boiteux dans son amour pour le travail, c'est-à-dire laborieux pour une moitié de la tâche, et paresseux pour l'autre, ce qui est le cas de l'homme qui aime la gymnastique, la chasse, et se livre avec zèle à tous les travaux corporels, mais n'a par ailleurs aucun goût pour l'étude, la conversation, la recherche, et déteste tout travail de ce genre. Est boiteux aussi celui dont l'amour pour le travail se porte du côté opposé.
Rien n'est plus vrai.
Et de même, par rapport à la vérité, ne regarderons-nous 535e pas comme estropiée l'âme qui, haïssant le mensonge volontaire et ne pouvant le souffrir sans répugnance en elle-même, ni sans indignation chez les autres, admet aisément le mensonge involontaire, et qui, prise en flagrant délit d'ignorance ne s'indigne point contre elle-même, mais se vautre dans cette ignorance comme un pourceau dans la fange (518).
536 Si fait, dit-il.
Et relativement à la tempérance, poursuivis-je, au courage, à la grandeur d'âme et à toutes les parties de la vertu, il ne faut pas mettre moins d'attention à discerner le sujet bâtard du sujet bien né. Faute de savoir les distinguer, les particuliers et les États ne s'aperçoivent pas qu'ils prennent - chaque fois qu'il leur arrive d'avoir recours à des offices de ce genre - ceux-là comme amis, ceux-ci comme chefs, des gens boiteux et bâtards.
Ce n'est que trop ordinaire.
Prenons donc soigneusement nos précautions contre 536b toutes ces erreurs. Si nous n'appliquons à des études et à des exercices de cette importance que des hommes bien conformés de corps et d'âme, la justice elle-même n'aura aucun reproche à nous faire, et nous maintiendrons l'État et la constitution; mais si nous appliquons à ces travaux des sujets indignes, c'est le contraire qui arrivera, et nous couvrirons la philosophie d'un ridicule encore plus grand.
Ce serait vraiment honteux, dit-il.
Sans doute, mais il me semble qu'en ce moment moi aussi je me rends ridicule (519).
En quoi? demanda-t-il.
J'oubliais que nous nous livrons à un simple jeu, et 536c j'ai un peu trop élevé le ton. Mais en parlant, j'ai jeté les yeux sur la philosophie, et, la voyant bafouée d'une manière indigne, je crois que je me suis emporté, presque mis en colère, et que j'ai parlé contre les coupables avec trop de vivacité.
Non, par Zeus ! dit-il, ce n'est pas l'avis de ton auditeur.
Mais c'est celui de l'orateur, répliquai-je. Quoiqu'il en soit, n'oublions pas que, dans notre premier choix, nous avons élu des vieillards, et qu'ici ce ne sera pas possible; car il ne faut pas croire Solon (520) lorsqu'il dit 536d qu'un vieillard peut apprendre beaucoup de choses : il est moins capable d'apprendre que de courir; les grands et les multiples travaux sont l'affaire des jeunes gens.
Nécessairement.
L'arithmétique, la géométrie, et toutes les sciences qui doivent servir de préparation à la dialectique, seront donc enseignées à nos élèves dès l'enfance, mais cet enseignement sera donné sous une forme exempte de contrainte (521).
Pourquoi donc?
Parce que l'homme libre ne doit rien apprendre en 536e esclave; en effet, que les exercices corporels soient pratiqués par contrainte, le corps ne s'en trouve pas plus mal, mais les leçons qu'on fait entrer de force dans l'âme n'y demeurent point.
C'est vrai.
Ainsi donc, excellent homme, n'use pas de violence dans l'éducation des enfants, mais fais en sorte qu'ils 537 s'instruisent en jouant : tu pourras par là mieux discerner les dispositions naturelles de chacun.
Ces propos sont raisonnables.
Te souviens-tu, demandai-je, de ce que nous avons dit plus haut : qu'il fallait conduire les enfants à la guerre sur des chevaux, en spectateurs, et, lorsqu'on le pourrait sans danger, les approcher de la mêlée et leur faire goûter le sang, comme aux jeunes chiens?
Je m'en souviens, répondit-il.
Dans tous ces travaux, repris-je, ces études et ces alarmes, celui qui se montrera constamment le plus agile, tu le mettras dans un groupe à part.
537b A quel âge?
Quand ils quitteront le cours obligatoire d'exercices gymniques; car ce temps d'exercices, qui sera de deux à trois années (522), ne pourra être employé à autre chose, la fatigue et le sommeil étant ennemis de l'étude; d'ailleurs, l'une des épreuves, et non la moindre, consistera à observer comment chacun se comporte dans les exercices gymniques.
Certainement, dit-il.
Après ce temps, ceux que l'on aura choisis parmi les jeunes gens parvenus à leur vingtième année obtiendront des distinctions plus honorables que les autres, et on 537c leur présentera réunies ensemble les sciences qu'ils ont étudiées sans ordre dans leur enfance, afin qu'ils embrassent d'un coup d'oeil les rapports de ces sciences entre elles et à la nature de l'être.
Seule en effet, dit-il, une telle connaissance se fixe solidement dans l'âme où elle entre.
Elle offre aussi un excellent moyen de distinguer l'esprit propre à la dialectique de celui qui ne l'est pas : l'esprit synoptique est dialecticien, les autres ne le sont pas.
Je suis de ton avis.
C'est donc une chose qu'il te faudra examiner, repris-je, 537d et ceux qui, avec les meilleures dispositions en ce sens, seront solides dans les sciences, solides à la guerre, et dans les autres travaux prescrits par la loi, ceux-là, quand ils finiront leur trentième année, tu les tireras du nombre des jeunes gens déjà choisis pour leur accorder de plus grands honneurs, et rechercher, en les éprouvant par la dialectique, quels sont ceux qui, sans l'aide des yeux ni d'aucun autre sens, peuvent s'élever jusqu'à l'être même, par la seule force de la vérité; et c'est là une tâche qui réclame beaucoup d'attention, mon camarade.
Pourquoi? demanda-t-il.
Ne remarques-tu pas, répondis-je, le mal qui atteint 537e la dialectique de nos jours, et les progrès qu'il fait (523)?
Quel mal?
Ceux qui s'y livrent, dis-je, sont pleins de désordre.
C'est bien vrai.
Mais crois-tu qu'il y ait là quelque chose de surprenant, et ne les excuses-tu pas?
Par où sont-ils excusables?
Ils sont dans le cas, expliquai-je, d'un enfant supposé qui, élevé au sein des richesses, dans une nombreuse et 538 noble famille, au milieu d'une foule de flatteurs, s'apercevrait, étant devenu homme, qu'il n'est pas le fils de ceux qui se disent ses parents, sans pouvoir retrouver ses parents véritables. Peux-tu deviner les sentiments qu'il éprouverait à l'égard de ses flatteurs et de ses prétendus parents, avant qu'il eût connaissance de sa supposition, et après qu'il en serait instruit? Ou veux-tu écouter ma prédiction là-dessus?
Je veux bien, dit-il.
Je prévois donc qu'il aura d'abord plus de respect pour son père, sa mère et ses parents supposés que pour 538b ses flatteurs, qu'il les négligera moins s'ils se trouvent dans le besoin, qu'il sera moins disposé à leur manquer en paroles et en actions, qu'il leur désobéira moins, sur l'essentiel, qu'à ses flatteurs, aussi longtemps qu'il ignorera la vérité.
C'est probable, dit-il.
Mais quand il connaîtra la vérité, je prévois que son respect et ses attentions diminueront pour ses parents et augmenteront pour ses flatteurs, qu'il obéira à ces derniers bien mieux qu'auparavant, réglera sa conduite d'après leurs conseils, et vivra ouvertement en leur 538c compagnie, tandis que de son père et de ses parents supposés il ne se souciera nullement, à moins qu'il ne soit d'un très bon naturel.
Tout se passera comme tu dis; mais comment cette comparaison s'applique-t-elle à ceux qui se livrent à la dialectique?
Voici. Nous avons dès l'enfance des maximes sur la justice et l'honnêteté : nous avons été formés par elles comme par des parents; nous leur obéissons et nous les respectons.
En effet.
538d Or il y a, opposées à ces maximes, des pratiques séduisantes qui flattent notre âme et l'attirent à elles, mais ne persuadent pas les hommes tant soit peu sages, lesquels honorent les maximes paternelles et leur obéissent.
C'est vrai.
Eh bien ! qu'on vienne demander à un homme ainsi disposé : qu'est-ce que l'honnête? Quand il aura répondu ce qu'il a appris du législateur, qu'on le réfute à plusieurs reprises et de plusieurs manières, qu'on le réduise à penser 538e que ce qu'il tient pour tel n'est pas plus honnête que déshonnête; qu'on en fasse autant pour le juste, le bon, et tous les principes qu'il honore le plus; après cela, comment, dis-moi, se comportera-t-il à leur égard sous le rapport du respect et de la soumission?
Nécessairement, il ne les respectera ni ne leur obéira plus de la même manière (524).
Mais, repris-je, quand il ne croira plus, comme auparavant, que ces principes soient dignes de respect et apparentés à son âme, sans avoir cependant découvert les 539 vrais principes, se peut-il qu'il en vienne à un autre genre de vie que celui qui le flatte?
Non, cela ne se peut, répondit-il.
On le verra donc, je pense, devenir rebelle aux lois, de soumis qu'il était.
Nécessairement.
Dès lors, il n'y a rien que de naturel dans ee qui arrive aux personnes qui s'appliquent ainsi à la dialectique, et comme je le disais tout à l'heure, elles méritent qu'on leur pardonne.
Et qu'on les plaigne, ajouta-t-il.
Afin de ne pas exposer à cette pitié tes hommes de trente ans, ne faut-il pas prendre toutes les précautions possibles avant de les appliquer à la dialectique?
Si, certes, dit-il.
Or, n'est-ce pas une importante précaution de les empêcher de goûter à la dialectique tant qu'ils sont jeunes? 539b Tu as dû remarquer, je pense, que les adolescents, lorsqu'ils ont une fois goûté à la dialectique, en abusent et en font un jeu, qu'ils s'en servent pour contredire sans cesse, et qu'imitant ceux qui les réfutent, ils réfutent les autres à leur tour, et prennent plaisir, comme de jeunes chiens, à tirailler et à déchirer par le raisonnement tous ceux qui les approchent (525).
Oui, ils y prennent un merveilleux plaisir.
Après avoir maintes fois réfuté les autres, et été maintes fois réfutés eux-mêmes, ils en arrivent vite à ne plus 539c rien croire du tout de ce qu'ils croyaient auparavant; et par là eux-mêmes et la philosophie tout entière se trouvent discrédités dans l'opinion publique.
Rien de plus vrai.
Mais un homme plus âgé ne voudra point tomber dans une pareille manie; il imitera celui qui veut discuter et rechercher la vérité plutôt que celui qui s'amuse et contredit pour le plaisir; il sera lui-même plus mesuré et 539d rendra la profession philosophique plus honorable au lieu de la rabaisser.
C'est exact, dit-il.
Et n'était-ce pas le même esprit de précaution qui nous faisait dire précédemment qu'on ne devait admettre aux exercices de la dialectique que des naturels ordonnés et fermes, et qu'il ne fallait pas, comme aujourd'hui, en laisser approcher le premier venu, qui n'y apporte aucune disposition.
Si, répondit-il.
Donc, l'étude de la dialectique, si l'on s'y livre sans relâche et avec ardeur, à l'exclusion de tout autre travail, comme on faisait pour les exercices du corps, ne demandera guère que le double des années consacrées à ceux-ci.
Veux-tu dire six ou quatre ans? demanda-t-il.
539e Peu importe, dis-je, mets cinq ans. Après quoi tu les feras de nouveau descendre dans la caverne, et tu les obligeras à remplir les emplois militaires et toutes les fonctions propres aux jeunes gens, afin que, pour ce qui est de l'expérience, ils ne soient pas en retard sur les autres. Et tu les éprouveras dans l'exercice de ces fonctions pour voir si, tirés de tous côtés par la tentation, 540 ils restent fermes ou se laissent ébranler.
Et quel temps fixes-tu pour cela?
Quinze ans, répondis-je. Et lorsqu'ils auront atteint l'âge de cinquante ans (526), ceux qui seront sortis sains et saufs de ces épreuves, et se seront distingués en tout et de toute manière, dans leur conduite et dans les sciences, devront être menés au terme, et contraints d'élever la partie brillante de leur âme vers l'être qui dispense la lumière à toutes choses; et quand ils auront contemplé le bien en soi, ils s'en serviront comme d'un modèle 540b pour régler la cité, les particuliers et leur propre personne, chacun à son tour, pendant le reste de leur vie; ils passeront la plus grande partie de leur temps dans l'étude de la philosophie, mais quand leur tour viendra, ils accepteront de peiner aux tâches d'administration et de gouvernement par amour pour la cité, y voyant non pas une noble occupation, mais un devoir indispensable; et ainsi, après avoir formé sans cesse des hommes qui leur ressemblent, pour leur laisser la garde de l'État, ils iront habiter les îles des Bienheureux. La cité leur consacrera des 540c monuments et des sacrifices publics, à titre de démons, si la Pythie le permet, sinon, à titre d'âmes bienheureuses et divines.
Ils sont tout à fait beaux, Socrate, s'écria-t-il, les gouvernants que tu viens de façonner comme un sculpteur !
Et les gouvernantes aussi, Glaucon, ajoutai-je; car ne crois pas que ce que j'ai dit s'applique aux hommes plutôt qu'aux femmes - j'entends à celles qui auront des aptitudes naturelles suffisantes.
Tu as raison, avoua-t-il, si tout doit être égal et commun entre elles et les hommes, comme nous l'avons établi (527).
540d Eh bien ! repris-je, m'accordez-vous maintenant que nos projets concernant l'État et la constitution ne sont pas de simples souhaits; que la réalisation en est difficile, mais possible d'une certaine manière, et non pas autrement qu'il a été dit, à savoir lorsque les vrais philosophes - soit plusieurs soit un seul (528) - devenus les maîtres d'un État, mépriseront les honneurs qu'on recherche aujourd'hui, les considérant comme indignes d'un homme libre et dépourvus de toute valeur, feront au contraire le plus grand cas du devoir et des honneurs qui en sont la récompense et, regardant la justice comme 540e la chose la plus importante et la plus nécessaire, la servant et travaillant à son développement, organiseront leur cité conformément à ses lois?
Comment? demanda-t-il.
Tous ceux, répondis-je, qui dans la cité auront dépassé l'âge de dix ans, ils les relégueront aux champs, et, ayant 541 soustrait les enfants à l'influence des moeurs actuelles, qui sont celles des parents, ils les élèveront selon leurs propres moeurs et leurs propres principes, qui sont ceux que nous avons exposés tout à l'heure. Ne sera-ce pas le moyen le plus rapide et le plus aisé (529) d'établir un État doté de la constitution dont nous avons parlé, de le rendre heureux, et d'assurer les plus grands avantages au peuple chez lequel il se sera formé?
Si, certainement; et il me semble, Socrate, que tu as b bien montré comment il se réalisera, s'il doit un jour se réaliser.
N'en avons-nous pas dit assez sur cet État et sur l'homme qui lui ressemble? Il est en effet facile de voir quel doit être cet homme selon nos principes.
Oui, approuva-t-il, et comme tu dis ce sujet me paraît épuisé (530).

455. À propos de cette image, voy. l'étude d'A. Diès : Guignol à Athènes dans le Bulletin de l'Association Guillaume Budé, 14-15, 1927.
456. Ces objets sont faits de matières diverses comme le monde visible est composé des quatre éléments (Jowett et Campbell).
457. Comparez le tableau que trace Eschyle de la vie des hommes primitifs. (Prométhée enchaîné, v. 447-53, tr. Paul Mazon): « Au début ils voyaient sans voir, ils écoutaient sans entendre, et, pareils aux formes des songes, ils vivaient leur longue existence dans le désordre et la confusion. Ils ignoraient les maisons de briques ensoleillées... ils vivaient sous terre, comme les fourmis agiles, au fond de grottes closes au soleil. » Ils ne sortirent de cet état de barbarie que lorsque Prométhée leur eut enseigné la science des saisons, puis celle des nombres. On voit que pour Platon l'homme sans éducation (ŽpaÛdeutow;) est comparable au primitif.
458. Nous suivons ici le texte de l'édition Burnet : eÞ oïn dial¡gesyai oåoÛ t' eäen pròw Žll®louw, oé taèta ²g» ’n tŒ önta aétoçw nomÛzein ‘per õrÒen; ;
459. Aristote s'était inspiré de ce passage dans le fragment suivant, que nous ne connaissons que par une traduction de Cicéron (De natura Deor. lib. II, 95) : « Praeclere ergo Aristoteles: Si essent, inquit, qui sub terra semper habitavissent bonis et illustribus domiciliis, quae essent ornata signis atque picturis instructaque rebus iis omnibus, quibus abundant ii, qui beati putantur, nec tamen exissent unquam supra terram, accepissent autem fama et auditione esse quoddam numen et vim deorum; deinde aliquo tempore patefactis terrae faucibus, ex illis abditis sedibus evadere in haec loca, quæ nos incolimus, atque exire potuissent : cum repente terram et maria caeIumque vidissent, nubium magnitudinem ventorumque vim cognovissent aspexis­sentque solem ejusque cum magnitudinem pulchritudinemque, tum etiam efficientiam cognovissent, quod is diem efficeret toto caelo luce diffusa; cum autem terras nox opacasset, tum caelum totum cernerent astris distinctum et ornatum lunæque luminum varietatem tum crescentis, tum senescentis, eorumque omnium ortus et occasus atque in omni aeternitate ratos immutabilesque cursus : quæ cum viderent, profecto et esse deos et haec tanta opera deorum esse arbitrarentur. »
460. Platon pense sans doute à ces hommes d'État dont la science purement empirique ne remonte pas des effets aux véritables causes. Cf. liv. V, 473 c et liv. VI, 488 b.
461. Odyssée XI, vers 489, déjà cité au livre III, 386 c.
462. Cf. Phédon, 249 d; Théétète, 174 c - 175 b; Sophiste, 216 d.
463.Dans la bouche de Socrate ces paroles prennent un sens prophétique. N'est-ce pas d'ailleurs le condamné des Onze qui, dans le Phédon, déclare connaître l'art de la mantique, comme les oiseaux d'Apollon? ƒEgÆ d¢ kaÜ aétòw ²goèmai... oé xeÝron ¤keÛnvn (tÇn kæknvn) t¯n mantik¯n ¦xein parŒ toè despñtou....
464. Voy. livre VI, 506 e.
465. Comp. l'admirable portrait du philosophe dans le Théétète, 173-74-75.
466. Dans le Sophiste (254 b) Platon remarque qu'il est également difficile de connaître le vrai philosophe et le sophiste : le premier parce qu'il vit dans une région de lumière aveuglante, le second parce qu'il se réfugie dans une zone d'obscurité impénétrable.
467. Allusion aux sophistes. - La thèse que Platon expose ici découle de sa théorie de la réminiscence. L'âme humaine enferme un élément divin (yeÝñn ti), le noèw, naturellement apte à voir la vérité, comme l'exil à voir la lumière. Or cette aptitude, ou plus exactement cette puissance comme dit Platon, lui vient de ce qu'il a déjà pu contempler la vérité. C'est pourquoi, tourné vers l'être réel, le noèw ne le découvre pas, à proprement parler, mais le qu'une reconnaît. La connaissance (m‹yhsiw) forme du souvenir (Žn‹mnhsiw). Voy. le Ménon 81 a sqq. et le Phédon 72 e- 76 d.
468. Aristote développe la même idée dans l'Éthique à Nicomaque II, 1. 1103 a, 17-31.
469. ² de toè fron°sai (Žret®) i. e. ² frñnhsiw. - On remarquera que la signification de ce mot a sensiblement évolué depuis le livre IV, 433 c, où il servait à désigner une vertu toute pratique: la prudence des chefs.
470. Voy. liv. VI, 505 a.
471. Jowett et Campbell observent que ce bonheur est comparable à celui des saints et des ermites chrétiens qui, transportés eux aussi de leur vivant dans les îles fortunées, ne consentent pas sans répugnance à se mêler des affaires humaines.
472. kaÜ mllon dunatoçw Žmfot¡rvn met¡xein - Žmfot¡rvn : « et publicorum negotiorum et philosophiæ (Stallbaum). »
473. eàdvla - Par ce mot Platon désigne à la fois les objets dont les ombres se projetaient dans la caverne (skeuast‹), et ces ombres elles-mêmes (skiaÛ), c'est-à-dire l'ensemble des choses sensibles (õrat‹ sive dojast‹). - "tta ¤stÜ kaÜ Ïn : « que sont ces images, et de quelles réalités elles sont les images. »
474. Dans les démocraties - et c'est là leur vice capital - le pouvoir est la proie des ambitions les plus vulgaires.
475. Malgré ces luttes intestines les démagogues savent, quand il le faut, se serrer les coudes pour piller l'État, comme le notait déjà le vieil Hérodote : « kakñthtow toÛnun ¤gginom¡nhw ¤w tŒ koinŒ ¦xyea m¢n oék ¤ggÛnetai toÝsi kakoÝsi, filÛai d¢ ÞsxuraÛ: oß gŒr kakoèntew tŒ koinŒ sugkæcantew poieèsi. (Enquête, III, 82). »
476. On peut citer comme exemples Dionysos et Sémélé (voy. Pausanias II, 31, 2), Esculape et Briarée, le géant aux cent bras (Hésiode, Théogonie, 617-721).
477. Allusion au jeu du palet (ôstrakÛnda) décrit par Pollux IX, 111. Les joueurs étant divisés en deux camps par une ligne tracée sur le sol, on jetait en l'air un palet, noir d'un côté, blanc de l'autre, en criant nçj µ ²m¡ra. Suivant que le palet tombait sur l'une ou l'autre de ses faces, les « noirs » partaient à la poursuite des « blancs » ou inversement.
478. Voy. liv. III, 403 e et 416 d.
479. Liv. II, 376 e sqq.
480. On voit par là ce qui distingue les deux cycles d'éducation. Dans le premier on se proposait de développer les dons naturels de l'enfant, de lui faire aimer et pratiquer la vertu avant même de la connaître. Pour parvenir à ce résultat on avait recours à l'habitude. Mais maintenant il s'agit de donner un fondement rationnel aux qualités acquises. Dans ce second cycle on procédera donc suivant une méthode rigoureusement scientifique.
481. Les trois grands tragiques avaient écrit chacun une tragédie sur Palamède. On en trouvera les fragments dans Dindorf: Eschyle 180 sqq.; Sophocle 426 sqq.; Euripide 582 sqq.
482. Cf. Lois 819 d, où Platon déclare que l'ignorance de l'arithmétique lui paraît être le fait, non pas d'un homme, mais d'un pourceau :oék ŽnyrÅpinon ŽllŒ êhnÇn tinÇn eànai mllon yr¡mmatvn.
483. Le meilleur commentaire du passage qui suit se trouve dans le Phédon 101 a sqq, et dans le Théétète 154 c.
484. ² toè koæfou kaÜ ² toè bar¡ow - Ces sensations relèvent de ce que les psychologues modernes appellent le sens de la résistance.
485. En séparant les éléments confondus dans la sensation, et en cherchant à pénétrer leur nature, la nñhsiw s'élève, degré par degré, jusqu'à la conception de la théorie des idées.
486. Tout nombre est en effet « un système de monades, ou la progression d'une quantité à partir de la monade, et sa régression se terminant à la monade : Žriymñw ¤sti sæsthma mon‹dvn, µ propodismòw pl®youw Žpò mon‹dow Žrxñmenow kaÜ Žnapodismòw eÞw mon‹da katal®gvn. » (Theonis Smyrnei expositio rerum mathematicarum ad legendum Platonem utilium, édit. E. Hiller, p. 18). Cf. la définition d'Euclide (VII, 2) : (« (Žriymñw ¤sti) tò sæsthma ¤k mon‹dvn sugkeÛmenon pl°yow. »
487. Les mathématiciens grecs distinguaient l'arithmétique, ou science des nombres, de la logistique, ou art du calcul. On s'est demandé si Platon avait toujours observé cette distinction; mais la comparaison du Gorgias, 451 b, 453 e, du Théétète, 198 a (sur l'arithmétique), avec le Gorgias, 451 c, le Charmide, 166 a, le Politique, 259 e (sur la logistique), ne laisse pas de doute à cet égard (Adam, éd. cit., II, p. 113 n.).
488. Si en effet on l'étudie dans un but purement pratique, on n'en comprendra jamais la haute portée. Les connaissances que l'on pourra ainsi acquérir constitueront un art, mais non pas une véritable science.
489. La même distinction est établie par Aristote entre les nombres mathématiques (mayhmatikoÛ) et les nombres sensibles (aÞsyhtikoÜ µ svmatikoÛ). Voy. Bonitz : Index Arist. s. v. Žriymñw.
490. « Dans l'enseignement de l'arithmétique, l'unité était représentée par une ligne. Si l'élève, par une erreur bien naturelle, attribuait une signification à la longueur de cette ligne, et proposait de la diviser, le maître lui montrait que, dans les questions arithmétiques, il était indifférent que la ligne fût divisée en quatre ou multipliée par quatre, du moment que sa longueur, grande ou petite, devait également représenter l'unité abstraite. L'un ainsi conçu est sans parties. Si on l'imagine divisé, chaque partie est égale au tout. Pareille distinction entre l'arithmétique populaire et l'arithmétique scientifique est clairement établie dans le Philèbe 56 e. » (Jowett et Campbell, éd. cit., III, p. 334.)
491. Cf. Lois, liv. V, 547 a, b.
492. I. PLATON ET LES MATHÉMATIQUES. - Les pages que l'on vient de lire et celles qui suivent attestent l'importance que Platon attribuait aux sciences mathématiques. Pendant son enfance, à Athènes, il en avait probablement appris les éléments sous la direction de maîtres réputés. Après la mort de Socrate, au cours du long voyage qu'il fit en Egypte et en Afrique du Nord, il rencontra l'un des plus célèbres géomètres de l'époque, Théodore de Cyrène, qui l'initia à ses méthodes (voy. Cicéron, De finibus, V, 29; De republ., I, 10, et Diogène Laërce, III, 6). Plus tard, vers 389, visitant la Grande-Grèce, il se lia d'amitié avec Archytas de Tarente et put, tout en prenant connaissance des travaux de ce savant, approfondir les théories arithmétiques des Pythagoriciens. Quand, l'année suivante, il revint dans sa patrie pour y fonder l'Académie, il avait donc reçu une excellente formation mathématique, et n'ignorait sans doute aucune découverte notable de la géométrie contemporaine. On conçoit aisément qu'une science qui venait de lui ouvrir des horizons si nouveaux ait pris de bonne heure une place considérable dans son enseignement. D'ailleurs, Platon nourrissait naturellement un goût très vif pour les mathématiques, et c'est par leur étude qu'il dut s'acheminer vers la dialectique, couronnement suprême de l'édifice du savoir. Cette méthode, qui l'avait conduit à la contemplation de la vérité, il l'indiqua à ses disciples comme la seule qui pût les élever hors des ténèbres du devenir, et ouvrir les yeux de leur âme aux pures lumières de l'être. Que Platon ait considéré l'étude des mathématiques comme absolument indispensable au philosophe, on en trouve la preuve dans maints passages des Dialogues, et le témoignage des anciens est unanime sur ce point. On connaît la célèbre devise qu'il avait fait inscrire sur la porte de son école : « Que nul n'entre sous mon toit s'il n'est géomètre : MhdeÜw Žgevm¡trhtow eÞsÛtv moè t¯n st¡ghn.» (Tzetzès, Chiliades, VIII, 973; Philoponus, In Arist. de anim., p. 117, 26). Ce principe fut rigoureusement appliqué à l'Académie, même après la mort de Platon. Diogène Laërce nous apprend en effet que Xénocrate avait coutume de répondre à quiconque manifestait le désir de suivre ses leçons, sans avoir appris la musique, la géométrie et l'astronomie : « Va-t'en, car tu ne possèdes pas les anses de la philosophie : Poreæou... labŒw gŒr oék ¦xeiw filkosofÛaw (De vit. phil., IV, 10). » « L'admiration de Platon pour les mathématiques, a écrit fort justement G. Milhaud (Philosophes géomètres de la Grèce, p. 158), qui déborde de ses œuvres et qui se dégage de tout ce que la tradition nous a dit de lui, n'a donc rien d'extérieur ni de superficiel. Il les a connues, cultivées avec passion; et quand il demande, dans la République, aux futurs philosophes de s'enfermer longtemps dans l'étude et dans la méditation de ces sciences, c'est qu'il en a subi le charme puissant. » A l'appui de cette assertion on pourrait citer les noms des mathématiciens illustres qui se sont formés à l'Académie : Eudoxe de Cnide, Ménechme, Dinostrate - dont nous parlerons plus loin - Speusippe - premier successeur de Platon à la tête de l'école, qui avait composé un traité sur les Nombres aujourd'hui perdu - Amyclas d'Héraclée, Philippe d'Opunte, et bien d'autres encore; on pourrait enfin noter qu'Euclide, qui devait un demi-siècle plus tard rassembler en un traité méthodique les découvertes géométriques de ses prédécesseurs, est qualifié par Proclus de philosophe platonicien (In Euclidis lib. prim. elem. comm., éd. Friedlein, p. 68). Il est donc permis de conclure que l'Académie a été, dès sa fondation, un centre de recherches et d'études mathématiques extrêmement important. Nous n'avons pas à examiner ici l'influence que ces recherches et ces études ont exercée sur la pensée du philosophe. (Dans la République Socrate précise lui-même la place qu'elles doivent occuper dans l'éducation, et l'on peut voir par là ce qu'a dû être cette influence). Nous n'avons pas non plus à nous demander si Platon a pressenti, comme le laisseraient supposer certains passages du Timée, le rôle merveilleux qui serait un jour dévolu aux mathématiques dans l'étude de la nature. Et aussi bien, eût-il eu cette intuition, il n'en aurait pas moins persisté à regarder la dialectique comme la science suprême, parce qu'indépendante et anhypothétique. Quant à la doctrine des idées-nombres, qu'Aristote prête à Platon dans les livres M et N de sa Métaphysique - et qui ne se peut réclamer, on le sait, d'aucun texte de la collection platonicienne - elle est purement métaphysique. Il serait donc hors de propos de l'examiner dans cette note. Elle a d'ailleurs fait l'objet de savantes études auxquelles nous nous permettons de renvoyer le lecteur. (Voy. notamment : L. Robin, La théorie platonicienne des idées et des nombres d'après Aristote; L. Brunschvicg, Les étapes de la philosophie mathématique, p. 61 sqq.; P. Shorey, De Platonis idearum doctrina; G. Rodier, Etudes de philosophie grecque, p. 37 sqq.).
En résumé, et quelle que soit la réponse que l'on donne à ces questions, ceci reste à retenir : l'intérêt que Platon portait aux mathématiques ne s'est jamais démenti; dans tous ses ouvrages le philosophe parle de ces sciences avec un secret enthousiasme, car, autant que pour l'évidence et la certitude de leurs raisons, il les aimait pour leur beauté, qui préfigure celle des essences éternelles et de leur principe, l'Idée du Bien.

II. LES MATHÉMATIQUES AU TEMPS DE PLATON.
A) ARITHMÉTIQUE. - On sait que l'étude des nombres avait été poussée assez loin, dès le Ve siècle, par l'école pythagoricienne. Au début du IVe siècle, les mathématiciens connaissaient sans doute les propriétés respectives des progressions arithmétique et géométrique, qu'ils considéraient comme résultant, l'une de la proportion additive, l'autre de la proportion multiplicative. Mais il est certain qu'ils ignoraient les rapports de ces deux sortes de progressions, qui devaient, près de vingt siècles plus tard, servir de base à la théorie des logarithmes. Or il semble, d'après un passage du Timée (35 b - 36 c), que Platon ait au moins deviné, sinon parfaitement défini, l'importance de ces rapports. En lisant attentivement tout le passage, a écrit F. Hoefer (Histoire des Mathématiques, p. 141), on peut se convaincre qu'il y est question d'une progression arithmétique servant à nombrer les termes d'une progression géométrique concomitante, qui pouvait commencer par 1, 2, 4... aussi bien que par 1, 3, 9... ou par 1, 10, 100... Platon devait être frappé comme d'un trait de lumière, en voyant qu'il suffisait, par exemple, d'additionner deux termes quelconques (exposants) de la progression arithmétique, pour avoir immédiatement le produit des deux termes correspondants de la progression géométrique, et pour montrer en même temps - ce qui devait être pour lui un objet de non moindre surprise - que les termes extrêmes, également distants les uns des autres, sont égaux aux deux termes moyens, additivement pour la progression arithmétique, multiplicativement pour la progression géométrique : enfin que, lorsque le milieu ou le centre ne se compose que d'un seul terme (ce qui arrive lorsque les termes sont en nombre impair), il faut doubler ce terme dans la progression arithmétique et le multiplier une fois avec lui-même (l'élever au carré) dans la progression géométrique. »
Ces remarques nous permettent d'imaginer quel devait être l'intérêt de l'enseignement oral de Platon, sur lequel la tradition ne nous a malheureusement laissé que des indications bien vagues.
Les irrationnelles. - L'une des plus grandes découvertes mathématiques du Ive siècle est celle de l'existence de quantités irrationnelles. Les Pythagoriciens avaient établi une identification absolue entre le nombre et la grandeur. Ils croyaient que toute grandeur est décomposable en un nombre déterminé de points. Pourtant, ils avaient eux-mêmes démontré l'impossibilité d'exprimer par un nombre entier la longueur de la diagonale du carré. Cette démonstration mérite d'être résumée ici, car, comme le remarque M. Léon Brunschvicg, elle donne une idée claire des ressources logiques de la mathématique grecque : « Si la diagonale est commensurable au côté du carré, le rapport peut-être mis sous la forme d'une fraction irréductible d/c Le théorème de Pythagore d² = 2c² montre immédiatement que d est pair, d'où l'on conclurait, puisque d et c sont premiers entre eux, que c est impair. Mais la parité de d permet d'exprimer le théorème sous la forme suivante
4 (d/2)² = 2 c² ou 2 (d/2)² = c²
ce qui entraînerait la parité de c. Si d et c sont supposés commensurables, il résulte de l'hypothèse que c est à la fois impair et pair. Ainsi se trouve établie à la lumière d'un raisonnement rigoureux l'impossibilité de faire correspondre un nombre déterminé d'unités à la diagonale d'un carré qui a l'unité pour côté. (Brunschvicg, Les Etapes de la philosophie mathématique, p. 47.) Mais les Pythagoriciens considéraient ce cas comme une simple exception. C'est probablement à Théodore de Cyrène et à Eudoxe de Cnide que sont dues les premières découvertes sur les irrationnelles consignées au livre X des Eléments d'Euclide, découvertes qui reposent : 1° sur une définition très générale de la notion de rapport; 2° sur l'étude des propriétés des proportions. Plusieurs passages des Dialogues prouvent que Platon s'était vivement intéressé à ces travaux. Dans le Théétète, par exemple, (147 d) il rappelle les écrits de son maître Théodore qui avait établi l'irrationnalité de  %5, %7, et poursuivi la recherche des racines carrées irrationnelles jusqu'à %17. Dans les Lois (liv. VII, 820 c) il regrette qu'on n'apprenne pas aux jeunes gens à distinguer les grandeurs commensurables entre elles des grandeurs incommensurables, et il souligne l'importance capitale de cette distinction. Enfin, dans le Ménon (82 sqq.), il démontre que le carré double d'un carré donné a pour côté le diamètre (la diagonale) de ce carré, c'est-à-dire une grandeur irrationnelle.
Cette notion d'irrationnalité, qui fut la source de tant de découvertes mathématiques, eut pour premier effet de modifier la théorie pythagoricienne des nombres. A l'idée de série discontinue - qui explique la formation des nombres par addition ou composition, c'est-à-dire d'une manière purement quantitative - on substitua l'idée de série continue - qui introduit dans cette formation quelque chose d'irréductible et de proprement qualitatif. « Le nombre, a pu écrire G. Milhaud (op. cit., p. 352), aura désormais un sens assez élevé pour qu'on n'aperçoive pas de limite à la complication et à l'hétérogénéité des éléments dont il fixe le mode de dépendances ». Ainsi se trouve ouverte la voie qui devait conduire à l'étude des quantités infinitésimales.

B) GÉOMÉTRIE PLANE ET STÉRÉOMÉTRIE. - C'est au cours du Ve siècle, et dans la première moitié du IVe, que furent découvertes la plupart des démonstrations contenues dans les Éléments d'Euclide. À la vérité, ce traité n'était pas le premier du genre. Theudios de Magnésie, Athénée de Cyzique, Hermotime de Colophon, avaient composé des ouvrages semblables que nous ne connaissons que par quelques rares mentions des géomètres alexandrins et de Suidas.
Le problème de l'aire du cercle retint de bonne heure l'attention des mathématiciens. L'un des premiers Hippocrate de Chios, qui florissait vers 440, l'étudia avec méthode, et, ayant reconnu l'impossibilité de carrer directement cette aire (c'est-à-dire de l'exprimer directement par une aire rectiligne), il crut tourner l'obstacle en cherchant d'abord l'aire de la lunule, qu'il carrait, selon Eudème, de la manière suivante (voy. Simplicius : In Arist. Phys. comm., éd. H. Diels, p. 56, sqq.)

Soit un demi-cercle de diamètre AB. Par le centre A menons le rayon DG perpendiculaire au diamètre, et joignons les points AG et GB. Nous aurons ainsi tracé deux des côtés du carré inscriptible dans le cercle. Sur AG comme diamètre construisons maintenant le demi-cercle AEG. Sa surface sera égale à celle du quadrant AGD (puisque l'on a : AB² = 2 AG², et que les cercles sont entre eux comme les carrés de leurs diamètres - Euclide, XII, 2). Mais ce quadrant et le demi-cercle ont un segment commun compris entre la droite AG et l'arc de centre D qu'elle sous-tend. En le retranchant nous ferons apparaître l'égalité des aires respectives de la lunule AEG et du triangle rectangle AGD. Or l'aire de ce dernier est le quart de celle du carré de côté AG. Elle est donc elle-même égale à un carré de côté AG/2. Cela démontré, voici comment Hippocrate procédait à la quadrature du cercle :Soit un demi-cercle de diamètre AB (voy. fig. 2). En prenant ce diamètre comme rayon, traçons le demi-cercle GD dans lequel nous inscrirons une moitié d'hexagone régulier - le trapèze GEZD. Sur les côtés GE, EZ, ZD construisons les demi-cercles GHE, EYZ, ZKD. Chacun d'eux sera égal au demi-cercle AB puisque le côté de l'hexagone régulier inscrit dans une circonférence est égal au rayon de cette dernière. D'autre part les demi-cercles GD et AB sont entre eux comme les carrés de leurs diamètres (voy. supra) : l'aire du premier est donc équivalente à quatre fois l'aire du second, c'est-à-dire à l'aire des quatre demi-cercles AB, GHE, EYZ, ZKD. Mais ces trois derniers ont avec GD des segments de cercle communs. Si l'on en fait abstraction, on voit que l'aire du trapèze GEZA est égale à l'aire des trois lunules GE, EZ, ZD, plus l'aire au demi-cercle AB. Or l'aire des lunules est carrable (voy. supra). En la retranchant du trapèze GEZD, il restera donc une aire carrable elle aussi, qui, doublée, sera équivalente à celle du cercle AB.
La démonstration est ingénieuse, mais radicalement fausse. Comme l'ont bien vu les géomètres de l'antiquité (cf. Eudème cit. par Simplicius, p. 57, et Eutocius, Comm. in dim. circuli, éd. Heiberg, p. 264), elle repose sur un paralogisme : son auteur admet implicitement que toute lunule est carrable, alors que cette proposition ne s'applique, en réalité, qu'à un nombre fort restreint de lunules. Nous n'en conclurons pas néanmoins, avec Montucla et certains érudits plus récents, que le procédé d'Hippocrate est un simple tour de passe-passe géométrique, car ce serait oublier que nous sommes ici en présence d'une pensée qui, à peine consciente de ses ressources, se trouve aux prises avec des difficultés dont elle n'évalue pas exactement l'étendue. D'ailleurs nous savons par Eudème que les recherches du géomètre de Chios ne s'étaient pas bornées à la quadrature de la lunule construite sur le côté d'un carré. II avait étudié d'autres cas se prêtant à une solution analogue (voy. à ce sujet Simplicius, éd. cit., pp. 60-69, et, dans l'Appendix Hlppocratea de cette même édition, p. XXIII, sqq.: H. Usener, De supplendis Hippocratis quas omisit Eudemus constructionibus; P. Tannery, In Simplicii de Antiphonte et Hippocrate excerpta). On trouvera donc assez naturel que le succès de ces diverses tentatives l'ait engagé à généraliser le sens d'une découverte d'où semblaient pouvoir se déduire des conséquences du plus haut intérêt.
Antiphon, contemporain d'Hippocrate de Chios, s'occupa comme lui de la quadrature du cercle. Pour résoudre ce problème, il inscrivait dans une circonférence une série de polygones réguliers, dont il doublait chaque fois le nombre de côtés. Il espérait arriver ainsi à un polygone dont le contour se confondrait avec celui du cercle. Or, comme tout polygone régulier est carrable (cf. Euclide II, 14), il en concluait que le cercle est également carrable. Eudème, qui fit la critique de ce procédé (voy. Simplicius, éd. cit., p. 55), lui reprochait de n'être point géométrique. En effet, dit-il en substance, on démontre en géométrie que toute grandeur est divisible à l'infini (cf. Euclide III, 16). Donc, en réduisant par des dichotomies successives la surface comprise entre le côté du polygone et l'arc qu'il sous-tend, on ne l'épuisera jamais, c'est-à-dire qu'on ne parviendra point à trouver une droite assez petite pour s'appliquer exactement ( ¤farmñsai) à cet arc. Et aussi bien le côté du polygone inscrit coupera toujours la circonférence en deux points. Cette critique était irréfutable aux yeux d'un géomètre grec, et devait d'ailleurs le rester jusqu'à l'invention du calcul infinitésimal, puisque Archimède lui-même, qui sut tirer un merveilleux parti de la méthode d'exhaustion, n'en persista pas moins à lui refuser toute valeur apodictique. Pourtant, bien qu'erronée, la solution d'Antiphon contenait en germe l'une des notions les plus fécondes de la mathématique moderne : la notion de limite des accroissements indéfinis d'une variable.
La solution d'Eudoxe, assez voisine sans doute de celle d'Antiphon, ne nous est point parvenue. Nous savons toutefois que ce géomètre, qui fut aussi l'un des plus grands astronomes de son temps, avait perfectionné la méthode de dichotomie ou d'exhaustion, et s'en était servi pour calculer le volume du cône et de la pyramide (voy. Archimedis opera, éd. Heiberg, tome I, p. 4, et tome III, p. 248).
Hippias d'Elis, le sophiste que Platon met en scène dans les deux dialogues qui portent son nom, s'intéressa tout particulièrement au problème de la trisection des angles. Proclus nous apprend (In Euclidis lib. pr. comm., éd. Friedlein, pp. 272 et 356) qu'il l'avait résolu à l'aide d'une courbe savante, la quadratrice (tetragvnÛzousa). Mais il semble que cette courbe ait été découverte par Dinostrate. D'après ce qu'en dit Pappus (Collectio Mathem., lib. IV, prop. 26, éd. Hultsch, p. 252), on peut la décrire de la façon suivante :

Traçons le quart de cercle AOB (flg. 3), et menons la tangente BG. Supposons maintenant que le rayon OA parcoure d'un mouvement uniforme l'angle AOB jusqu'à ce qu'il atteigne la position OB, et imaginons qu'en même temps, et du même mouvement uniforme, une droite, confondue d'abord avec OA, s'élève, parallèlement à elle-même, jusqu'à la position BG. À chaque instant le rayon et la droite se couperont en un point dont la trajectoire sera la quadratrice.
On voit aisément que par construction, le rapport du quadrant AB au rayon OA = R, est égal au rapport de OA sur OC :
Aussi bien est-ce parce qu'elle permet de définir ce rapport par deux lignes droites que la courbe reçut le nom de quadratrice: on croyait qu'elle pourrait servir à la quadrature du cercle. En langage algébrique moderne on représenterait la quadratrice par l'équation :

Il est clair maintenant que cette courbe permet d'opérer la multisection de l'angle d'une manière très simple; en effet, en divisant OB en n parties, et en menant par les points obtenus des parallèles à OA, on déterminera sur la quadratrice des points M, N, P... qui, joints au centre O, diviseront l'angle AOB en n sections.
La quadratrice de Dinostrate est sans doute la première courbe transcendante qu'aient connue les mathématiciens de l'antiquité, et - il n'est pas inutile de le rappeler - il semble bien qu'elle fut découverte par l'un de ces jeunes philosophes qu'avaient formés les méthodes d'éducation décrites au vile livre de la République.
Un autre disciple de Platon, Ménechme, frère de Dinostrate, se signala lui aussi par d'importantes découvertes en géométrie (voy. Proclus, In Euclidis lib. prim. comm. éd. cit. pp. 67 et 111). Il est, en effet, l'inventeur de la théorie des sections coniques tomaÜ kvnikaÛ ), ou du moins des principes fondamentaux de cette théorie, exposée et développée, comme on sait, par Apollonius de Perge dans un ouvrage célèbre (IIIe siècle av. J.-C.). « Ce sont, dit Eudème (cité par G. Milhaud, pp. 82-83), d'anciennes découvertes dues à la Muse des Pythagoriciens que la parabole des aires, leur hyperbole ou leur ellipse. C'est de là que plus tard on prit ces noms pour les transporter aux sections coniques : tandis que pour ces hommes anciens et divins c'était dans la construction plane des aires sur une droite déterminée qu'apparaissait la signification de ces termes. Si vous prenez la droite tout entière et que vous y terminiez l'aire donnée, on dit que vous faites la parabole de cette aire; si vous lui donnez une longueur qui dépasse la droite, c'est l'hyperbole, ou une longueur qui lui soit inférieure c'est l'ellipse, une partie de la droite restant en dehors de l'aire construite. » En langage moderne, si nous désignons par y² et par j l'aire et la droite données, nous dirons que le problème consiste à déterminer une longueur x satisfaisant à l'une des trois équations:
y² = px (parabole).
y² = px + x² (hyperbole).
y² = px - x² (ellipse).

Telles sont les données qui servirent de point de départ à Ménechme pour caractériser les sections coniques. En coupant un cône par un plan perpendiculaire à l'une de ses génératrices on obtient en effet, suivant que l'angle au sommet est droit, obtus ou aigu, trois figures qui satisfont respectivement aux relations de la parabole, de l'hyperbole et de l'ellipse pythagoriciennes, et auxquelles on peut, par conséquent, donner ces noms (voy. à ce sujet l'excellent exposé de G,, Milhaud, op. cit. p. 166 sqq.), Certains historiens des mathématiques ont douté que Ménechme soit allé bien loin dans l'étude des courbes ainsi définies, et qu'il ait connu leurs plus intéressantes propriétés. On verra plus loin que ce doute est assez peu fondé, et qu'au contraire l'inventeur des sections coniques sut tirer de sa découverte de très belles applications. Remarquons par ailleurs que les nouvelles courbes furent étudiées de bonne heure comme lieux géométriques, c'est-à-dire comme des ensembles de points ayant une propriété par­ticulière, une propriété caractéristique, un sæmptvma, comme dit Proclus, qui contient en lui-même l'essence de la courbe, et donne, avec la définition, toutes les propriétés (Milhaud, op. cit., p. 174) ». C'était déjà, deux mille ans avant Descartes et Fermat, la géométrie analytique qui prenait naissance, sinon dans sa forme, du moins dans son esprit.

La duplication du cube ou problème Délien. - Pour expliquer comment ce problème s'imposa à l'attention des géomètres, les auteurs anciens racontaient deux anecdotes qui nous ont été conservées par Eutocius (voy. la lettre d'Eratosthène à Ptolémée Evergète in Arch. op. tom. III, p. 102 sqq). D'après la première, un poète tragique aurait introduit sur la scène le roi Minos élevant un monument à Glaucus : les architectes donnèrent à ce monument cent pieds en tous sens. Mais le roi l'ayant trouvé peu digne de sa magnificence, ordonna qu'on le fît double. Cette question fut proposée aux géomètres, qu'elle embarrassa beaucoup, jusqu'à ce qu'Hippocrate de Chios leur apprît qu'elle se réduisait à trouver deux moyennes proportionnelles. C'était, dit Ératosthène, tomber dans un embarras non moins grand. Plus tard, les habitants de Délos, à qui l'oracle avait ordonné de doubler l'autel d'Apollon, se trouvèrent en présence du même problème. Ne sachant comment le résoudre, ils envoyèrent des délégués au fondateur de l'Académie pour lui demander conseil.
Sans prétendre établir l'authenticité de ces faits, constatons que le problème de la duplication du cube fut l'objet, dans l'entourage de Platon, de sérieuses et savantes recherches. Depuis Hippocrate, comme on vient de le voir - et comme le confirme Proclus (In Eucl. comm. éd. cit. p. 213) - il se ramenait à trouver deux moyennes proportionnelles entre le côté du cube donné et le double de ce côté. En effet, si l'on a c/x = x/y = y/2c, x répondra à la question, c'est-à-dire sera bien le côté d'un cube double de c²; car, en effectuant le produit des moyens et des extrêmes il vient: x² = cy et 2cx =y²;ce qui donne : y = x²/c , et 2cx = x⁴/c² ou 2 c² = x².
En fait, on ne pouvait manquer d'élargir ces données, et de chercher une méthode pour insérer deux moyennes proportionnelles entre deux quantités quelconques. Sous cette forme nouvelle la question devait avoir pour Platon un intérêt tout particulier, ainsi que l'atteste un passage célèbre du Timée (31 b sq.), où il s'efforce de justifier mathématiquement l'existence des quatre éléments.
Outre la solution que l'on attribue au philosophe, nous résumons ci-dessous celles d'Archytas et de Ménechme, qui nous semblent propres à donner une idée de l'état des mathématiques grecques dans la première partie du IVe siècle.

1° Solution de Platon. - Elle est fondée sur cette remarque que si l'on porte deux valeurs a et b sur deux lignes se coupant à angle droit, les deux moyennes proportionnelles entre ces valeurs, BD et BE (voy. fig. 4), seront, sur le prolongement de AB et de GB, les hauteurs des triangles rectangles AED et EDG. On aura, en effet : BD²= EB x BG; et BE² = AB x BD, ce qui peut s'écrire :

AB/BE = BE/BD = BD/BG

Après avoir pris AB et BG sur deux lignes perpendiculaires, on déterminera les points E et D à l'aide d'un appareil très simple. On prendra une règle fixe munie, à ses extrémités, de deux montants à angle droit. Le long de ces montants on ménagera des rainures dans lesquelles pourront glisser deux clefs adaptées à une règle mobile qui, dans toutes ses positions, devra rester parallèle à la règle fixe. Cela fait, il suffira de disposer l'appareil de telle sorte que A et G étant respectivement en contact avec la règle mobile et la règle fixe, le prolongement de AB tombe en D, et celui de GB en E.
Le caractère essentiellement pratique de ce procédé a inspiré des doutes sérieux sur son attribution à Platon. Et aussi bien, les méthodes d'enseignement préconisées au VIe livre de la République semblent exclure l'emploi de tout appareil matériel, fût-ce à titre pédagogique. D'autre part, Plutarque (Symp., VIII; quaest., II, 1) affirme que Platon aurait blâmé Archytas d'avoir résolu le même problème à l'aide d'une construction mécanique - ce qui est d'ailleurs inexact. Telles sont les graves objections que l'on peut faire à la thèse de l'authenticité. En ce qui concerne la seconde on observera toutefois : 1° que nous ne savons pas sur quelle autorité Plutarque fonde son assertion; 2° que cet écrivain n'était pas précisément un spécialiste des questions géométriques. Il est vrai qu'Eutocius d'Ascalon, qui rapporte la solution attribuée à Platon, vivait au VIe siècle de notre ère : du simple point de vue chronologique son témoignage appelle donc bien des réserves. Mais il faut tenir compte du fait que le commentateur d'Archimède était un mathématicien de profession, et qu'il a eu sans doute en main - ses citations nous le prouvent - les traités géométriques de l'école d'Alexandrie. On rappellera de plus que, d'après la lettre d'Ératosthène dont il a été parlé plus haut, les délégués de Délos vinrent consulter Platon sur un cas particulier et concret. Or les solutions d'Archytas et d'Eudoxe, dit Eratosthène, étaient purement théoriques, et celle de Ménechme d'une application sinon impossible, du moins malaisée sumb¡bhke d¢ psin aétoÝw ŽpodeiktikÇw gegraf¡nai, xeirourg°sai d¢ kaÜ eÞw xreÝan peseÝn m¯ dænasyai pl¯n ¤pÜ braxæ ti toè Men¡xmou kaÜ taèta desxerÇw. - op. cit. p. 106). En l'occurrence, rien n'empêche d'admettre que le philosophe, pour répondre au désir des prêtres d'Apollon, leur ait indiqué un moyen commode de trouver les dimension: de l'autel à construire. C'est là, nous semble-t-il, la seule hypothèse qui puisse justifier l'attribution d'Eutocius.

2° Solution d'Archytas. - Soient a et b (a > b) les deux droites représentant les quantités données. Imaginons un demi-cylindre droit de rayon 2 [voy. fig. 5 et 6 (Outre la figure de l'édition Heiberg (fig. 5) nous donnons une seconde figure en perspective.)], et, sur le plan de coupe de ce demi-cylindre, un demi-cercle de diamètre a = AD. Sur la base du demi-cylindre prenons AB = b, et prolongeons jusqu'à rencontre avec la tangente menée en D. Supposons maintenant que le demi-cercle construit sur AD tourne vers B autour du point A. Il coupera la surface latérale du demi-cylindre suivant une ligne courbe. Or, si nous faisons tourner AP et la tangente PD en sens inverse autour de l'axe AD, ces droites engendreront un cône de révolution dont la surface latérale coupera la courbe en un point K. En joignant le point A aux points K et I (projection de K), nous aurons les deux moyennes proportionnelles cherchées : AK et sa projection AI sur le plan ABD. [Nous calculerions aujourd'hui AI en fonction de l'angle (PAD) du triangle générateur. En effet : AI = AK cos yj.

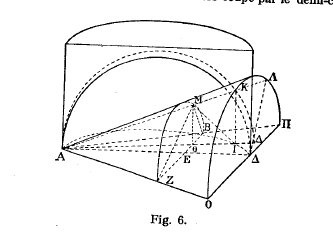
Démonstration. - Supposons que le demi-cercle mobile AD se trouve dans la position DKA. Il est alors coupé par le demi-cerclee ngendré, dans la formation du cône, par la révolution de EB en EZ. Comme ces deux demi-cercles sont perpendiculaires au plan ABD, leur ligne d'intersection est elle-même perpendiculaire à ce plan. Or BMZ est rectangle (comme inscrit dans un demi-cercle), et l'on a :

MY² = BY x YZ.

Mais : BY x YZ = YI x AY (produits des segments de deux cordes se coupant à l'intérieur d'un cercle). Donc : MY² = YI x AY; on en conclut que AMI est droit. Mais l'angle AKD l'est aussi (comme inscrit dans un demi-cercle). On a donc :

AD/AK = AI/AM (01)

D'autre part, la similitude des triangles AKD et AKI (rectangles ayant un angle aigu égal) nous fournit la relation:

AD/AK = AK/AI (02)

En égalant (1) et (2) il vient :

AD/AK = AK/AI = AI/AM

Or AD = a, et AM = AB = b. AK et sa projection AI sont donc bien les moyennes proportionnelles cherchées (Arch. opera, tom. in, pp. 98-102). On notera comme l'un des traits les plus originaux de cette solution l'emploi d'une courbe à double courbure.

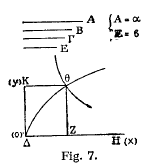
3° Première solution de Ménechme. - Soient a et b deux quantités données entre lesquelles on veut insérer deux moyennes proportionnelles. Traçons deux axes rectangulaires Ox et Oy (voy. fig. 7). Sur l'axe Ox construisons la parabole x = y²/a. Prenant ensuite les axes Ox et Oy comme asymptotes, construisons l'hyperbole : x = ab/y
Ces deux courbes se rencontrent en un point 0, dont les coordonnées (ZY et KY -, ou AZ) seront les moyennes proportionnelles cherchées. En effet, on a par construction :

ZY²= a x DZ;

ce qui peut s'écrire :

a/ZY = ZY/DZ (01)

Et d'autre part : ZY x KY (ou DZ) = ab; ou :

a/ZY = DZ/b (02)

Egalons (1) et (2), il vient :

a/ZY = ZY/DZ = DZ/b (a)

4° Autre solution. - Soient a et b les deux quantités données. Traçons comme précédemment deux axes perpendiculaires Ox et Oy (voy. fig. 8). Sur l'axe Oy construisons la parabole y = x²/b et sur l'axe Ox la parabole x = y²/a. Ces deux courbes se coupent en un point Z dont les coordonnées ZD et ZE sont les moyennes proportionnelles cherchées. En effet, on a par construction :

BD² = BG x BE, ce qui peut s'écrire :

BG/BD = BD/BE = (01) AB = a EG = b

Et d'autre part : BE² = BA X AB, ou :

BD/BE = BE/AB (02)

D'où, en égalant (1) et (2) :

BG/BD = BD/BE = BE/AB -AB

Or : BD = EZ, et BE = ZD. Les coordonnées du point Z sont donc bien les moyennes proportionnelles cherchées (Arch. op., tom. III pp. 92-98). On voit que les valeurs données a et b sont les coefficients d'un système de deux équations dont les inconnues sont les deux moyennes demandées.

LES CINQ SOLIDES RÉGULIERS. - Des cinq solides réguliers inscriptibles dans la sphère, les Pythagoriciens ne connaissaient que le cube, la pyramide et le dodécaèdre. C'est Théétète, semble-t-il, qui découvrit l'octaèdre et l'icosaèdre. Au témoignage de Suidas il avait écrit un traité sur ce sujet, qu'Euclide mit probablement à profit pour la composition du XIIIe livre de ses Éléments.
On sait que dans le Timée (53 c - 55 c) Platon assigne aux quatre corps élémentaires la forme de solides réguliers, qu'il engendre en partant, pour les trois premiers - tétraèdre, octaèdre, icosaèdre - du triangle scalène, et pour le quatrième - cube - du triangle isocèle. Quant au dodécaèdre, qu'il décrit sans le nommer, il déclare que le démiurge s'en servit pour tracer le plan de l'univers (voy. Th.-H. Martin, Etudes sur le Timée, II, p. 242). D'après l'Epinomis (981 c), ce cinquième polyèdre serait la forme de l'éther. Sans chercher à concilier ces deux passages, remarquons que Platon y applique à sa cosmogonie des découvertes récentes, faites en quelque sorte sous ses yeux, et auxquelles il avait peut-être collaboré.

LES MÉTHODES. - Il n'entre point dans notre propos d'étudier ici les procédés employés par les géomètres du IVve siècle. Nous nous contenterons de signaler ce que la science grecque, doit, sous le rapport des méthodes, à l'auteur de la République. 1° En découvrant, et en définissant avec la plus grande rigueur possible le processus de l'analyse, Platon a doté les mathématiques de leur instrument essentiel. Par régression analytique toute question peut être en effet ramenée à des lemmes fondamentaux à partir desquels on procède pour la résoudre. Ainsi, les vérités mathématiques se diviseront en deux grandes classes, l'une comprenant les axiomes, les hypothèses, les postulats et les définitions, l'autre les théorèmes, les problèmes et les porismes. Partant des données contradictoires de l'expérience, le mathématicien, après les avoir dissociées, les recréera logiquement, d'après un certain nombre de principes qu'au préalable il aura posés.
2° Mais il est évident que de tels principes auront un caractère purement hypothétique. En montrant qu'ils ne se peuvent expliquer par eux-mêmes, et qu'ils doivent être rattachés à un principe suprême qui les justifie et les fonde en certitude, Platon a nettement délimité les domaines respectifs de la métaphysique et de la science positive, d'expression plus ou moins mathématique. Sur ce point comme sur bien d'autres, ses vues anticipent des thèses modernes.

Bibliographie. - Outre les ouvrages cités dans la présente note, on peut consulter : C. Bretschneider, Die Geometrte und die Geometer vor Euklides (1870); Allmann, Greek Geometry from Thales to Euclid (1877); P. Tannery, La Géométrie Grecque (1887); Cantor, Vorlesungen über Gesch. d. Math., I (1894); H. Zeuthen, Geschichte d. Math. im Altert. und. Mittelalter (1896. Trad. française de Mascart, 1902); Th. Heath, A History of Greek Mathematics 1, From Thales to Euclid (1921). - Sur Platon : Blass, De Platone Mathematico (1861); Rothlauf, Die Math. z. Platons Zeit u. s. Beziehungen zu ihr (1878); - Sur la méthode platonicienne: L. Brunschvicg, Les Etapes de la Philosophie Mathématique (3e éd. 1929).

(a) Pour mettre en évidence l'intérêt de ces solutions nous les avons interprétées en langage algébrique moderne. Le lecteur pourra toutefois se faire une juste idée des originaux d'après la traduction, que nous donnons ci-après, de la première solution de Ménechme : « Soient A et E les deux lignes données. On demande de trouver entre elles deux moyennes proportionnelles. Supposons le problème résolu, et soient B et G les moyennes cherchées. Prenons une ligne droite, de position donnée, arrêtée en D, et soit DZ égal à G ; menons en Z la perpendiculaire ZY, et soit ZY égal à B. Puisque les trois lignes A, B, G sont proportionnelles, on aura A x G = B². Donc le rectangle formé par la ligne donnée A et par G, i. e. DZ, sera égal au carré de B. i. e. de ZY, et par suite le point Y sera sur la parabole décrite par D. Menons les droites YK et YK, parallèles à DZ et à YZ, comme le rectangle B x G est donné, puisqu'il est égal au rectangle A x E, le rectangle KY x YZ est aussi donné. Le point Y est donc sur l'hyperbole ayant pour asymptotes KD et DZ : il est par conséquent donné ainsi que le point Z.
On procédera à la construction de la manière que voici. Soient A et E les droites données, et une ligne de position déterminée, arrêtée en D ; par ce point à décrivons une parabole d'axe DH et de paramètre A, c'est-à-dire telle que les carrés des perpendiculaires élevées sur DH [nous dirions aujourd'hui les ordonnées] soient égaux aux aires construites sur A, en prenant comme largeurs les segments de DH compris entre ces perpendiculaires et le point D [nous dirions les abscisses]. Soit DY cette parabole, et YZ perpendiculaire à DH. Sur KD et DZ pris comme asymptotes construisons une hyperbole telle que les parallèles menées de cette courbe à KY et YZ forment une aire égale au rectangle A x E. L'hyperbole coupera la parabole en un point Y. Menons les perpendiculaires YK et YZ. Nous aurons : ZY² = A x DZ, ou: A : ZY = YZ. Et par ailleurs A x E = YZ x ZD, ou : A : ZY = ZD x E. Par conséquent : A : ZY = ZY : ZD = ZD : E. Or, si B = YZ, et G = DZ, il vient : A : B = B : G = G : E. Les droites A, B, G, E sont donc bien, comme on le demande, en proportion continue (Arch. op. tome III, p. 92 sqq.).

493. Les notions géométriques sont, en effet, immuables et éternelles ŽkÛnhta kaÜ Žýdia), et de plus, elles nous introduisent à la connaissance des lois de l'univers.
494. L'erreur commise volontairement par Socrate lui permet de souligner, en quelque sorte, l'ordre rigoureux des sciences.
495. Nous adoptons ici la correction de Madvig, et nous lisons:êpò tÇn pollÇn Žtimazñmena kaÜ kolouñmena êpò tÇn zhtoæntvn ktl au lieu de : êpò tÇn de zhtoæntvn.
496. Voy. supra note 492.
497. oék ŽgennÇw moi dokeÝw ktl. - Socrate s'amuse ici de la remarque étourdie de Glaucon. Dans le Timée (91 d), le philosophe raille également ceux qui conçoivent d'une manière aussi audacieuse les choses d'en-haut : « La race des oiseaux, dit-il, pourvus de plumes au lieu de poils, n'est qu'une légère métamorphose de ces hommes sans malice, frivoles, grands parleurs des choses célestes, qui estiment dans leur simplicité qu'on peut emprunter au témoignage de la vue de solides démonstrations. »
498. Ce passage répond, semble-t-il, aux burlesques accusations portées par Aristophane contre Socrate dans les Nuées, v. 171 sqq.
499. D'après Platon « la véritable astronomie, écrit M. Duhem (Le Système du Monde, tome I, pp. 94-95), est celle qui, à l'aide du raisonnement géométrique, découvre les combinaisons cinématiques simples dont le Dhmiourgñw suprême a usé pour produire les entrelacs compliqués des mouvements astronomiques visibles. Ces mouvements composants méritent seuls d'être appelés réels et vrais. » L'astronome platonicien observera les trajectoires des astres, mais sachant que les données de l'expérience sensible ne contiennent qu'une très faible part de vérité - puisqu'elles ne sont que des images ou des reflets - il cherchera à retrouver les trajectoires véritables en passant d'une forme imparfaite, fournie par l'observation, à la forme parfaite la plus proche. C'est du moins ce que semble entendre Socrate quand il dit plus loin (529 d) t» perÜ tòn oéranòn poikilÛ& paradeÛgmasi xrhst¡on. Ainsi compris; ce passage s'accorde avec le témoignage suivant de Simplicius (In Arist. de Caelo, éd. Heiberg p. 488) : « Platon, au dire de Sosigène, proposait ce problème aux astronomes : quels mouvements uniformes et réguliers faut-il supposer pour sauvegarder les données de l'expérience relatives aux déplacements des astres errants : tÛnvn êpoteyeisÇn õmalÇn kaÜ tetagm¡nvn kin®sevn diasvy» tŒ perÜ tŒw kin®seiw tÇn planvm¡nvn fainñmena. »
500. Cf. Timée, 28 a-b et 37 d.
501. Platon est persuadé que l'âme humaine et l'âme de l'univers sont réglées selon les mêmes accords. C'est pourquoi sa propédeutique trouve son couronnement naturel dans les deux sciences de l'Harmonie : l'astronomie et la musique.
502. Sur la théorie pythagoricienne des sons, reprise ici par Platon, voy. Théon de Smyrne, éd. E. Hiller, p. 50 sqq.
503. Platon juge ce travail inutile parce qu'il croit, comme Héraclite, que les harmonies que l'oreille n'entend point sont supérieures à celles qu'elle entend rmonÛh Žfan¯w faner°w kreÛssvn).
504. puknÅmata : ainsi appelées, dit Schneider, « propter sonorum in angusto spatio quasi confertorum frequentiam ».
505. oåon ¤k geÛtonvn fvn¯n yhreuñmenoi. - Sur le sens de cette expression voy. le Thesaurus d'H. Estienne, éd. Hase, s. v. geÛtvn.
506. « Il y avait en Grèce deux écoles rivales enseignant la théorie de la musique : 1° l'école pythagoricienne ou mathématique qui identifiait chaque intervalle avec un rapport; 2° l'école des musiciens (mousikoÛ) qui mesuraient tous les intervalles comme multiples ou fractions du ton. » (Note d'Adam, tome. II, p. 133.).
507. L'image est empruntée au traitement que l'on infligeait aux esclaves coupables d'une faute grave.
508. La classification des sciences qui vient d'être proposée se résume dans le tableau suivant :On remarquera que les sciences sont ici rangées dans leur ordre de complexité croissante. Chaque science, indépendante de celles qui la suivent, doit s'appuyer sur toutes celles qui la précèdent. Ainsi se trouve mise en évidence l'unité organique des disciplines de la di‹noia.
509. Sur la dialectique platonicienne, voy. J. Adam, éd. cit., tome II, pp. 168-79.
510. Nous avons adopté l'interprétation d'Adam. II paraît, en effet, difficile de lier Éw avec Žmfisbht®sei. Il est plus naturel de le faire accorder avec ²mÝn... l¡gousin.
511. Les mots entre parenthèses, nécessaires au sens, ne se trouvent pas dans le texte.
512. Image empruntée à la théologie orphique.
513. Voy. liv. VI, 511 d-e.
514. Nous n'avons pas traduit les mots : Žll' ù ’n mñnon dhloÝ pròw t¯n §jin safeneÛ& l¡gei ¤n cux», qui ne présentent aucun sens satisfaisant, et que nous considérons, avec J. Adam, comme interpolés (voy. éd. cit. tome II, p. 192).
515. Comme le rapport ¤pist®mh pròw pÛstin n'est autre chose, sous une expression différente, que le rapport nñhsiw pròw dñjan, on doit avoir (voy. fig. 1, note 442, liv. VIe) GB/AG = EB/DG = GE/AD
On avait en effet par hypothèse : AD/DG = GE/EB, d'où l'on tire par composition AB+ DG/ DG = GE+EB/EB ou AG/DG = GB/EB et, en permutant les extrêmes; EB/DG = GB/AG Mais l'égalité : AD/DG = GE/EB donne également, par permutation des extrêmes : EB/DG = GE/AD. On a donc bien : GB/AG = EB/DG = GE/AD. L'énoncé de ces rapports prouve que Platon connaissait parfaitement les propriétés de la proportion qu'il établit au VIe livre, 509 d.
516. Socrate joue ici sur le mot logoi qui, dans le langage mathématique, désignait les quantités incommensurables entre elles. A l'époque où fut composée la République, l'étude de ces quantités était, pour ainsi dire, à l'ordre du jour dans le monde savant.
517. Au livre III, 412 b sqq.
518. L'homme qui n'est point animé du désir de s'instruire, qui préfère la paix factice de l'ignorance aux hasards de la recherche et de la découverte, doit être regardé comme un menteur involontaire, puisqu'il est lui-même la dupe du mensonge qu'il nourrit en son âme.
519. Certes, Socrate entend garder un ton de bonne compagnie, mais le regret qu'il exprime ici est évidemment ironique, car qui pourrait le trouver ridicule sinon ces hommes « sérieux et pratiques » qui se moquent d'un passe-temps dont l'enjeu est la vérité?
520. « ghro‹skv d'aÞeÜ pollŒ didaskñmenow : Je vieillis, mais j'apprends toujours beaucoup de choses. » (Solon, frgt 18, Poet. lyr. Gr. éd. Bergk).
521. Il ne faut pas oublier que Platon ne légifère ici que pour une élite qui possède naturellement l'amour de la science et le goût du travail.
522. Comme à Athènes, où les jeunes gens faisaient leur service militaire de dix-huit à vingt ans.
523. Platon se rend parfaitement compte du danger que présente l'étude de la dialectique quand on l'aborde trop tôt et sans avoir reçu une solide formation préalable.
524. Si la connaissance de la vérité est la condition même de la vertu, le scepticisme, comme l'ignorance, ne peut être qu'une source de vices et de désordres.
525. Cf. Philèbe 15 d, et Phédon, 90 c.
526. Héraclide nous apprend que la loi défendait aux Chalcidiens de remplir une magistrature ou une ambassade avant d'avoir atteint l'âge de cinquante ans: « nñmow d¢ ·n Xalkideèsi m¯ rjai mhd¢ presbeèsai neÅteron ¤tÇn pent®konta » (Fr. Hist. Gr. II, p. 222) ». Mais en général de pareilles conditions d'âge étaient rarement imposées dans les États grecs.
527. Au livre V, 451 c. sqq.
528. Le meilleur gouvernement est, en effet, aristocratique ou monarchique. Voy. liv. IV, 445 d.
529. En préconisant cette mesure, ou plus exactement cet expédient, Socrate entend se débarrasser une fois pour toutes d'une question qu'il sait fertile en difficultés.
530. Avec le VII, livre se termine la partie proprement constructive de la République. Platon s'occupera maintenant de prouver l'excellence de la cité qu'il a fondée en imagination, en lui opposant les cités déchues, et en étudiant simultanément les caractères humains qui leur correspondent.

terminé le 28 novembre 2004