CHAPITRE X

ALLER A LA TABLE DES MATIERES DE PTOLEMEE

CLAUDE PTOLÉMÉE.

DE LA COMPOSITION MATHÉMATIQUE

PREMIER LIVRE (seconde partie)

CHAPITRE X.

DE L'ARC COMPRIS ENTRE LES TROPIQUES.

APRES avoir donné les valeurs des droites inscrites dans le cercle, il s'agit d'abord, comme nous l'avons dit, de montrer de combien le cercle oblique, qui entoure le zodiaque par le milieu, est incliné sur l'équateur, c'est-à-dire quel rapport a le grand cercle qui passe par les pôles de ces deux cercles, avec l'arc qui est compris entre ces pôles, et qui est égal à la distance de chacun des points tropiques (solstices) au point qui leur correspond dans l'équateur. 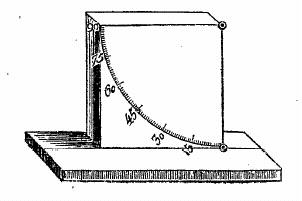Cet arc se mesure par le moyen d'un instrument dont voici la construction qui est bien simple.
Nous ferons un cercle de cuivre de mêmes dimensions dans toute sa grandeur, parfaitement façonné au tour, et dont toutes les surfaces forment entr'elles des angles droits. Nous nous en servirons comme d'un méridien, en le divisant en 360 degrés donnés au grand cercle, et chaque degré, en autant de subdivisions qu'il en pourra recevoir. A ce cercle, nous en adapterons en dedans un autre, mais plus petit, de manière que leurs surfaces soient dans le même plan, et que ce petit cercle puisse tourner sur son centre, dans le grand cercle, du midi vers les ourses, et des ourses vers le midi. Nous fixerons sur deux points diamétralement opposés de l'une des faces latérales de ce petit cercle, deux petits prismes égaux, parallèles entr'eux, et qui regarderont directement le centre des cercles, par celles de leurs faces qui se regarderont l'une l'autre ; et au milieu de leur largeur nous ajouterons deux aiguilles minces qui se prolongeront sur la surface du grand cercle dont elles parcourront les divisions. Quand on a disposé cet instrument pour les usages auxquels on l'emploie, en l'affermissant sur une petite colonne de dimensions convenables, on pose en plein air la base de la colonne sur un pavé bien horizontal, en prenant garde que le plan des cercles soit perpendiculaire sur le plan de l'horizon, et parallèle à celui du méridien, La première de ces conditions s'obtiendra par le moyen d'un fil à plomb tombant du point le plus élevé du cercle, et amené, par le moyen des calles qu'on mettra sous le pied du support, à marquer le point diamétralement opposé en bas. La seconde condition sera remplie au moyen d'une ligne méridienne tracée bien visiblement sur le plan, sous le support, et en faisant mouvoir l'instrument de côté, jusqu'à ce que l'on voie le plan des cercles parallèle à cette ligne. L'instrument étant ainsi placé, nous avons observé le soleil allant vers les ourses, puis vers le midi, en faisant tourner, dans les instants de midi, le cercle intérieur, jusqu'à ce que le prisme inférieur fût couvert par l'ombre du prisme supérieur. Les extrémités des aiguilles marquaient, de chaque côté, en haut et en bas, de combien de divisions de la circonférence, le centre du soleil était éloigné du point vertical, sur le méridien.
Nous avons fait cette observation d'une manière encore plus commode, en nous servant, au lieu des cercles, d'un parallélépipède quadrangulaire de pierre ou de bois, bien dressé, et dont une des faces soit bien unie et bien applanie. Sur cette face, prenant pour centre un de ses angles, nous décrivons un quart de cercle, et nous tirons, du centre à l'arc, les lignes qui comprennent l'angle droit du quart de cercle. Nous partageons cet arc en 90 degrés et en leurs subdivisions ; ensuite, après avoir fixé sur une des droites, qui doit être perpendiculaire sur le plan de l'horizon, et du côté du midi, deux petits cylindres droits parfaitement égaux, et façonnés l'un comme l'autre au tour, l'un, juste sur le centre, et l'autre à l'extrémité inférieure de cette droite, nous plaçons cette même face du parallélépipède sur la ligne méridienne tracée dans le plan qui est dessous, ensorte que cette face soit parallèle au plan du méridien et à la ligne du fil à plomb qui passe par les petits cylindres, et perpendiculaire sur le plan de l'horizon. Cette ligne se détermine au moyen de petites calles qui mettent l'instrument dans une situation parfaitement verticale. Nous observions ainsi, à midi, l'ombre du petit cylindre du centre, en mettant sur l'endroit où elle tombait dans l'arc gradué, quelque chose qui nous le fit mieux distinguer ; et, marquant le milieu de cette ombre, nous prenions la division de l'arc du quart de cercle coïncidente à ce milieu , parce qu'elle nous donnait sur le méridien l'écart (la déclinaison) du soleil en latitude.

Par ces observations, et surtout par celles que nous avons faites avec soin dans les temps des conversions (solstices) en plusieurs périodes (années), nous avons reconnu, par la marque qui, à compter du point vertical, tombait toujours sur les mêmes divisions du méridien, et les donnait généralement égales, tant dans les solstices d'été, que dans les solstices d'hiver, que l'arc du méridien, compris entre la limite la plus boréale et la limite la plus australe, qui est l'arc d'entre les tropiques, vaut constamment 47 degrés et plus que les deux tiers, mais moins que les trois quarts d'un degré : quantité qui est la même qu'Eratosthène avait trouvée, et dont Hipparque s'est servi. Car l'arc du méridien entre les tropiques contient ainsi 11 des parties dont le méridien en contiendrait 83.
Il est aisé, par une conséquence de cette observation, de connaître les climats (latitudes) des lieux d'où l'on observe, en prenant le point qui tient le milieu entre les deux limites, car ce point est dans l'équateur ; et l'arc. compris entre ce point et le point vertical, car cet arc est égal à la hauteur du pôle sur l'horizon.

CHAPITRE XI.

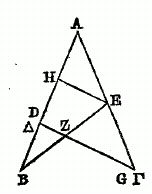
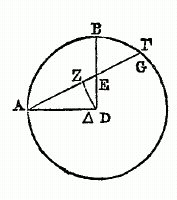
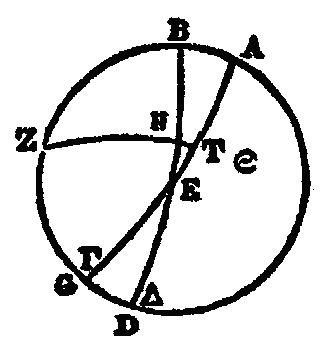
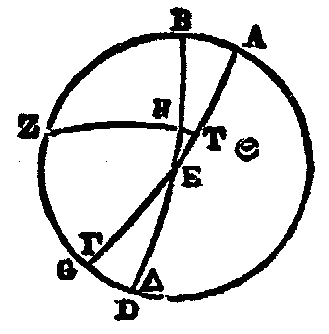
PRÉLIMINAIRES POUR LES DÉMONSTRATIONS SPHÉRIQUES.

L'ORDRE des matières demandant que, conséquemment à ce qui précède, nous donnions les valeurs respectives des arcs des grands cercles qui passent par les pôles de l'équateur, lesquels arcs sont compris entre l'équateur et le cercle qui ceint le zodiaque par le milieu de sa largeur, nous exposerons d'abord des lemmes courts et utiles, par le moyen desquels nous rendrons aussi simples et aussi abrégées qu'il est possible, la plupart des démonstrations des problèmes sphériques.

Si à deux droites AB et AG, on en mène deux autres BE et GD, qui s'entre coupent au point Z , je dis que la raison de GA à AE est composée de la raison de GD à ZD, et de celle de ZB à BE. Car soit menée par le point E une droite EH parallèle à la droite GD , puisque ces deux droites GD et EH sont parallèles, la raison de
GA à EA est la même que celle de GD à EH. Prenant auxiliairement ZD, la raison de GD sera composée de la raison de GD à DZ et de celle de DZ à EH. Ainsi, la raison de GA à AE est composée de celle de GD à DZ et de celle de DZ à EH. Or, !a raison de DZ à EH est la même que celle de ZB à BE, à cause de EH et ZD , parallèles aussi. Donc la raison de GA à AE est composée de celle de GD à DZ et de celle de ZB à BE. C'est ce que j'avois à démontrer.

On démontre de même par décomposition (diérèse), que la raison de GE à EA est composée de celle de GZ à DZ et de celle de DB à BA, en menant une droite par le point A parallèlement à BE, et prolongeant GDH jusqu'à cette droite. Car, puisque AH est parallèle à EZ, GZ est à ZR comme GE est à EA. Prenant la droite ZD auxiliaire, la raison de GZ à ZR est composée de celle de GZ à ZD, et de celle de DZ à ZR. Mais la raison de DZ à ZR est la même que celle de DB à BA, à cause des droites BA, ZR menées à travers les parallèles AH, BZ. Donc la raison de GZ à ZR est composée de celle de GZ à ZD , et de-celle de DB à BA. Mais la raison de GE à EA est la même que celle de GZ à ZR ; donc la raison de GE à EA est composée de celle de GZ à DZ , et de celle de DB à BA : ce que nous voulions aussi démontrer.

Soit encore le cercle ABG dont le centre est D ; et soient pris sur sa circonférence trois points A, B, G, tels que les arcs AB , BG, soient chacun plus petits que la demi-circonférence, (ce qui doit s'entendre également des autres arcs que nous prendrons dans la suite.) Joignez AG et DEB ; je dis que, comme la droite qui soutend le double de l'arc AB, est à celle qui soutend le double de l'arc BG, de même la droite AE est à la droite EG. Car soient abaissées les perpendiculaires AZ et GH des points A et G sur DB ; puisque AZ est parallèle à GH, et que la droite AEG est menée au travers de ces parallèles, AE est à EG comme AZ est à GH. Mais il y a le même rapport entre AZ et GH, qu'entre la soutendante du double de l'arc AB et la soutendante du double de l'arc BG. Car chacune de ces perpendiculaires est la moitié de celle de ces soutendantes à laquelle elle appartient. Donc le rapport de AE à EG est le même que celui de la soutendante de l'arc double de AB à la soutendante de l'arc double de BG. Ce qu'il fallait démontrer.

Il suit de là, que l'arc entier AG, et le rapport de la soutendante du double de AB à la soutendante du double de BG, étant donnés, chacun des arcs AB et BG sera par là même aussi donné. En effet, dans cette figure , soient joints les points A , D, par la droite AD, et du centre D abaissez la perpendiculaire DZ sur AEG ; il est évident que, l'arc AG étant donné, l'angle ADZ qui mesure la moitié de cet arc sera donné, et que tout le triangle ADZ est ainsi donné. Mais la droite entière AG étant donnée, et AE étant à GE, par la supposition, comme la soutendante du double de l'arc AB est à la soutendante du double de l'arc BG, il en résulte que AE sera donnée ; ainsi que sa portion ZE ; et par conséquent, la droite DZ étant donnée, l'angle sous EDF du triangle rectangle EDZ sera donné, et aussi l'angle entier ADB. Ainsi donc, l'arc AB sera donné, de même que l'autre arc BG. C'est ce qu'il s'agissait de démontrer.

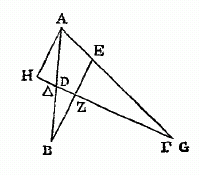
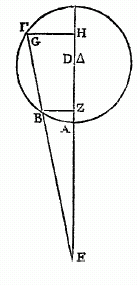
Soit encore le cercle ABG décrit autour du centre D ; et, soient pris sur sa circonférence, trois points A, B , G, tels que chacun des arcs AB, AG, soient plus petits que la demi-circonférence (ce qu'il faut entendre également des arcs qui seront pris ainsi dans la suite). Soient menées les droites DA, GB, prolongées et se réunissant en E ; je dis que, comme la soutendante du double de l'arc GA est à la soutendante du double de l'arc AB, de même la droite GE est à la droite BE : car, conformément au premier lemme, si de B et de G nous abaissons les perpendiculaires BZ et CH sur DA, on verra, à cause du parallélisme de ces deux perpendiculaires, que GE est à EB comme GH à BZ, c'est-à-dire, comme la corde du double de l'arc GA est à la corde du double de l'arc AB : ce qui était à démontrer.

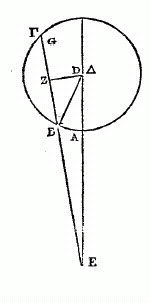
Il suit de là que, quand l'arc GB serait seul donné, avec le rapport de la corde du double de GA à celle du double de AB, on trouverait bientôt l'arc AB. Car, dans une pareille figure, si l'on mène la droite DB, et qu'on abaisse la perpendiculaire DZ sur BG, l'angle sous BDZ qui soutend la moitié de l'arc BG, sera donné, ainsi que tout le triangle rectangle BDZ. Mais le rapport de EG à EB étant donné, la droite GB sera aussi donnée, ainsi que la droite EB, et par là aussi toute la droite EBZ. Donc» puisque la droite DZ est donnée, l'angle sous EDZ de ce triangle rectangle même (EDZ) sera donnée et par conséquent aussi l'autre angle, celui qui est nous EDB; donc l'arc AB sera donné (c).

Cela posé, soient décrits sur la surface d'une sphère, des arcs de grands cercles, de manière que les deux arcs BE et GD, mêmes aux deux arcs AB et AG, s'entrecoupent au point Z, et. que chacun soit moindre que la demi-circonférence, (ce qui doit se supposer pour toutes ces constructions); je dis que le rapport de la sous-tendante du double de l’arc GE à la sous-tendante du double (d) de l'arc EA est composé du rapport de la sous-tendante du double de l'arc GZ à la sous-tendante du double de l'arc ZD et du rapport de la sous-tendante du double de l'arc DB à la sous-tendante du double de l'arc BA.

Car soit H le centre de la sphère, et soient menées de ce point sur B, Z, E, intersections des cercles, les droites HB, HZ et HE. Joignez AD, par une droite qui se prolonge jusqu'à ce qu'elle rencontre HB prolongée aussi en T. Menez DG et AG qui couperont HZ en K et HE en L : les trois points T, K, L, seront sur une seule et même ligne droite, parce qu'ils sont tout à la fois sur deux-plans, l'un sur celui du triangle AGD, l'autre sur celui du cercle BZE. La droite qui les joint, fait que les deux droites TL et GD, menées aux deux TA et GA, se coupent l’une l'autre au point K. Par conséquent, la raison de GL à LA est composée de celle de GK à KD et de celle de DT à TA. Mais comme GL est à LA, de même la sous-tendante de l'arc double de GE est à la sous-tendante de l'arc double de EA. Et comme GK est à KD, de même la sous-tendante du double de l'arc GZ est à celle du double de l'arc DZ. De plus, comme DT est à TA, de même la sous-tendante .du double de l'arc DB est à celle du double de l'arc BA. Donc la raison de la corde du double de l'arc GE à la corde du double de l'arc EA, est composée de la raison delà corde du double de l'arc GZ à la corde du double de l’arc ZD, et de la raison de la corde du double de l'arc DB à la corde du double de l'arc BA.

On démontre aussi, par de semblables raisons et par le moyen de pareilles droites, construites de même sur une surface plane, que la raison de la corde du double de l’arc GA à la corde du double de .l'arc EA, est composée de la raison de la corde du double de l'arc GD à la corde du double de l'arc DZ, et de la raison de la corde du double de l'arc ZB à la corde du double de l'arc BE. Ce qu'il fallait démontrer.

CHAPITRE XII.

DES ARCS COMRIS ENTRE L'EQUATEUR ET LE CERCLE OBLIQUE (ECLIPTIQUE).

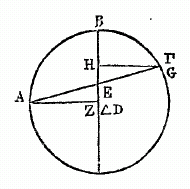
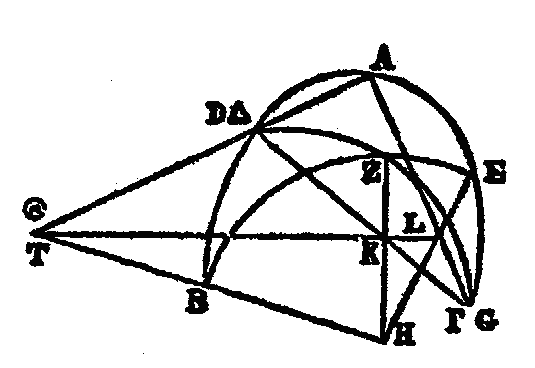
Le théorème précédent nous conduit à démontrer d'abord, de la manière suivante, les valeurs des arcs proposés ci-dessus. Soit le grand cercle ABGD passant par les pôles de l’équateur et du cercle oblique qui ceint le zodiaque ; soit AEG la demi-circonférence de l'équateur; soit BED celle de l'oblique; soit le point E leur intersection à l'équinoxe du printemps, en sorte que B soit le point tropique (solstice) d'hiver, et D celui d'été; et soit, sur l'arc ABG, le point Z pris pour pôle de l'équateur AEG. Prenez sur l'oblique tin arc EH de 30 des degrés dont 360 font la circonférence du grand cercle; par les points Z, B, décrivez l'arc ZHT d'un grand cercle, et soit proposé de trouver HT. (Soit dit ici une fois pour toutes les démonstrations semblables, afin de ne pas le répéter en chacune, que quand nous disons, des valeurs des arcs ou des droites, qu'elles sont d'un certain nombre de degrés ou parties, nous entendons pour les arcs, que ces degrés sont de ceux dont le grand cercle en contient 360 à sa circonférence; et pour les droites, que leurs parties sont de celles dont le diamètre du cercle en contient 120).

Puisque dans cette construction de grands cercles, aux deux arcs AZ et AE sont menés les arcs ZT, EB, qui s'entrecoupent au point B, la raison de la sous-tendante du double de l'arc ZA à la sous-tendante du double de l'arc AB, est composée de la raison de la sous-tendante du double de l'arc TZ à celle du double de l'arc TH, et de la raison de la sous-tendante du double de l’arc HE à celle du double de l'arc EB. Or le double de l'arc ZA est de 180 degrés, et la droite qui le soutend, est de 120 parties; le double de l'arc AB, suivant le rapport conforme au nôtre, de 83 à 11, est de 47° 42' 40", et sa sous-tendante vaut 48^p 31' 55"; en outre, le double de l'arc HE est de 6o°, et sa sous-tendante vaut 60^p; le double de l'arc EB est de 180°, et sa sous-tendante vaut 120^p; donc (a), si de la raison de 120^p à 48^p 31' 55", nous retranchons celle de 60 à 120, restera la raison de la sous-tendante du double de l'arc ZT à la sous-tendante du double de l'arc TH, laquelle raison est celle de 120^p à 24^p 15' 57". Or le double de l'arc ZT est de 180°, et la droite qui le soutend, a 120^p ; donc la sous-tendante du double de l'arc TH a 24^p 15' 57" de ces mêmes parties du diamètre : par conséquent, le double de faire TH contient 23° 19' 59", et l'arc TH lui-même est de 11° 40', à très peu près (ou 11° 39’ 49’’ 5).

(b) Supposons maintenant l'arc EH de 60 degrés, et tout le reste de même que ci-dessus; le double de l'arc EH est de 120°, et la sous-tendante de ce double are, de 103^p 55' 23". Si nous retranchons encore de la raison de 120 à 48^p 31' 65" celle de 103^p 55' 23" à 120, il en résultera la raison de la sous-tendante du double de ZT à celle du double de TH, c'est-à-dire, celle de 120 à 42^p 1' 48". Or la corde du double de l’arc ZT est de 120^p; donc la corde de double de l’arc TH sera de 42^p 1' 48", et par conséquent le double de l’arc TH est de 41^p 0' 18", et l'arc TH est de 20^p 30' 9". C’est ce que noua voulions démontrer,

En calculant de même les valeurs de tous les arcs en particulier, nous dresserons une table des 90 degrés du quart de cercle» où se trouveront les quantités que nous venons de démontrer. Nous donnons ici cette table toute construite.

CHAPITRE XIII.

DES ASCENSIONS DANS LA SPHÈRE DROITE.

Après ces démonstrations, viennent naturellement celles des valeurs des arcs de l'équateur, que déterminent les cercles qui passent par ses pôles et par des points donnes du cercle oblique. Nous saurons ainsi (a) en combien de temps équinoxiaux, les segments du cercle oblique traverseront le méridien en tous lieux, et l'horizon dans la sphère droite ; car ce n'est que dans cette position de la sphère, que l'horizon passe par les pôles de l’équateur.

Soit donc donné, dans la figure précédente, l’arc EH de l'oblique, d'abord de 30°, et qu'il s'agisse de trouver l'arc ET de l'équateur. Suivant ce qui précède, la raison de la sous-tendante du double de l'arc ZB à celle du double de l'arc BA est composée de la raison de la sous-tendante du double de l’arc ZH à celle du double de l'arc HT, et de la raison de la sous-tendante du double de l'arc TE à celle du double de l'arc EA. Mais le double de l’arc ZB est de 132^p 17' 10", et sa sous-tendante est de 109^p 44' 53"; le double de l'arc AB est de 47^p 42' 40", et sa corde est de 48^p 31' 55". En outre, le double de l'arc ZH est de 156° 40' 1", et sa corde est de 117^p 31' 15". Le double de l’arc HT est de 23^p 19' 59"; et sa corde est de 24^p 15' 57". Si donc, de la raison 109^p 44' 53" à 48^p 31' 55" (b), nous ôtons celle de 117^p 31' 15" à 24^p 15' 57", restera la raison de la corde du double de l'arc TE à cette du double de l'arc EA, raison qui est celle de 54^p 52' 26" à 117" 31' 15" égale à la raison de 56^p 1' 25" à 120^p. Or le double de l'are EA est de 180°, et sa corde est de 120^p; donc la corde du double de l’arc TE est de 56^p 1' 25". Par conséquent le double de l’arc TE sera de 55° 40' à très peu près, et TE de 27° 50'.

Supposons maintenant l'arc EH de 60^p, de sorte que tout le reste demeurant comme ci-dessus, le double de l’arc ZH devienne de 138° 59' 42" et sa sous-tendante de 112^p 23' 56". Le double de l'arc HT de 41° 0' 18" et sa sous-tendante de 42^p 1' 48". Si donc (c), de la raison de 109^p 44' 53" à 48^p 31' 55", nous ôtons la raison de 112^p 23' 56" à 42^p 1' 48", restera la raison de la sous-tendante du double de TE à celle du double de la sous-tendante de EA, laquelle raison est celle de 95^p 2' 40" à 112^p 23' 56", la même que la raison de 101^p 28' 20" à 120^p. Or la sous-tendante du double de l’arc EA est de 120^p, par conséquent celle du double de l'arc TE vaudra ces 101^p 28' 20". Mais le double de l’arc TE est de 115° 28' à très peu près, donc l'arc TE est de 57° 44'.

Il est donc démontra que la première dodécatémorie de l'oblique, depuis le point de l’équinoxe, passe au méridien dans le même temps que les 27° 50' de l'équateur, «t que la seconde répond de même à 29° 54'. Car on a démontré que les deux ensemble passent avec les 57° 44' de l'équateur. Donc la troisième dodécatémorie correspondra aux mêmes temps que le reste du quart de l'équateur, c'est-à-dire aux 32^t 16' restants. En effet, tout le quart de l'oblique emploie à traverser le méridien, le même temps que le quart de l'équateur, puisque l'un et l'autre sont compris entre les mêmes cercles qui passent par les pelés de l'équateur.

Nous avons calculé, en suivant cette méthode, les arcs de l'équateur qui passent au méridien avec les arcs du cercle oblique, de dix en dix degrés, attendu que les arcs plus petits croissent sensiblement par des différences presqu'égales entre elles. Nous donnerons ces arcs, pour qu'on puisse voir du premier coup d’œil combien de temps chacun emploiera à traverser le méridien partout comme nous avons dit, et l'horizon dans la sphère droite, en commençant, par la dizaine qui répond au point de l’équinoxe.

Or la première met 9 temps 10'; la seconde, 9^t 15'; la troisième, 9^t 25': en sorte qu'ensemble elles font pour le premier douzième (dodécatémorie) de l'oblique, la somme de 27 temps 50'. La quatrième dizaine est de 9^t 40'; la cinquième, de 9^t 58', la sixième, de 10^t 16'; ce qui donne pour les temps qui répondent au second douzième, 29^t 54'. La septième a 10^t 34'; la huitième, 10^t 47', et la neuvième, 10^t 55', faisant ensemble 32 temps 16' pour le troisième douzième qui se termine aux points tropiques. Ainsi le total est de 90 temps pour le quart du cercle.

Il est évident par ce que nous venons de dire, que tout se passe dans le même ordre pour les autres quarts de la circonférence, tout étant disposé de la même manière en chacun d'eux. Nous supposons toujours que la sphère est droite, c'est-à-dire que l’équateur n'est pas incliné sur l'horizon.

fin du premier livre de la composition

mathemathique de cl. ptolémée