Ptolémée, de la composition mathématique (traduction)

ALLER A LA TABLE DES MATIERES DE PTOLEMEE

PREMIER LIVRE

DE LA COMPOSITION MATHÉMATIQUE

DE CLAUDE PTOLÉMÉE.

AVANT-PROPOS.

C'EST avec raison, ce me semble, mon cher Syrus, que, dans la saine philosophie, la théorie a été distinguée de la pratique. Car s'il est arrivé que la pratique soit précédée de la théorie ; on ne trouvera pas entre l'une et l'autre une moins grande différence, non seulement en ce qu'il peut se rencontrer quelques-unes des vertus morales en plusieurs personnes qui n'ont rien appris, tandis que sans instruction il est impossible de rien savoir ; mais encore en ce que la théorie et la pratique tirent leur plus grande perfection, celle-ci, d'un exercice constant et assidu dans les mêmes travaux, l'autre de ses progrès dans la découverte des règles à suivre. Voilà pourquoi nous avons jugé convenable de conformer tellement nos opérations aux principes, que nous ne perdions jamais de vue, pas même dans les moindres choses, ce qui peut contribuer à la beauté de l'ordre et de la méthode ; et d'employer la plus grande partie de nos méditations à la recherche de ces principes si beaux et si nombreux, de ceux surtout qui composent la science mathématique.

En effet, Aristote divise très bien les sciences spéculatives en trois principaux genres, celui de la physique, celui des mathématiques, et celui des choses divines. Car tout ce qui existe, consistant dans la matière, la forme et le mouvement, quoiqu'aucune de ces trois choses ne puisse être vue, mais seulement conçue séparée des autres, dans son sujet, si l'on cherche particulièrement la cause première du mouvement primitif de l'univers, on trouvera que c'est Dieu invisible et immuable ; et sa forme, genre qui est l'objet de la science des choses divines, ne doit être cherchée qu'au-dessus du monde matériel, parce que nous n'en connaissons que l'action seule, absolument distincte de tout ce qui tombe sous nos sens. Mais la forme qui embrasse la qualité matérielle et toujours variable, comme la blancheur, la chaleur, la douceur, la mollesse, et autres de ce genre, s'appellera physique, la substance en étant comprise généralement parmi celles qui sont corruptibles et sublunaires. Quant à la forme expresse de la qualité, dans les espèces et les mouvements trajectoires, la figure la quantité, la grandeur, le lieu, le temps et autres choses semblables, comme ce genre, est l'objet de nos recherches : elle constitue la science mathématique qui tient, pour ainsi dire, le milieu entre les deux autres ; non seulement parce qu'elle peut s'acquérir et par le moyen des sens, et sans le secours des sens ; mais encore parce qu'elle embrasse tous les êtres, sans exception, tant ceux qui sont sujets à la mort, que ceux qui en sont exempts ; les premiers, dans les mutations de formes, qui en sont inséparables, les autres, qui sont éternels et d'une nature éthérée, dans leur invariabilité constante. On voit par là que, de ces spéculations, il y en a deux dont les objets sont moins palpables qu'ils ne sont sentis intimement. Telles sont, celle qui traite des choses divines, attendu qu'elles sont invisibles autant qu'incompréhensibles ; et,celle qui s'occupe des choses naturelles, parce que l'instabilité de leur matière empêche de les bien connaître :

en sorte qu'il n'y a nulle espérance que jamais les philosophes s'accordent dans ces sciences. Les mathématiques seules donnent à ceux qui s'y appliquent avec méthode, une connaissance solide et exempte de doute, les démonstrations y procédant par les voies certaines de calcul et de mesure. Nous avons résolu d'en faire aussi le sujet de nos méditations et de nos travaux, et nous avons choisi de préférence la science des mouvements célestes, comme la seule dont l'objet soit immuable et éternel, et la seule qui soit susceptible de ce degré d'évidence, de certitude et d'ordre qui la met à l'abri de toute variation ; ce qui est le caractère de la science. Elle ne contribuera pas moins que les deux autres, à nous instruire de ce qu'elles sont. Car elle nous ouvrira la voie aux choses divines par la connaissance que nous donnera de la force éternelle et distinguée de toute autre, le rapport qu'elle seule peut découvrir entre les substances éternelles et impassibles ; et celles qui sont sensibles, mobiles et mouvantes, par les incidents, l'ordre et la disposition de leurs mouvements. Elle ne servira pas peu dans l'étude de la physique, en ce que ce qui est propre à la substance matérielle, se connaît par sa maniée d'obéir aux impulsions du mouvement ; par exemple, ce qui est corruptible, par le mouvement en ligne droite ; ce qui est incorruptible, par le circulaire ; la pesanteur et la légèreté, ou l'activité et la susceptibilité d'action, par le mouvement tendant au centre ou s'éloignant du centre. Elle contribuera même - plus que toute autre chose - à nous rendre meilleurs, en nous rendant plus attentifs à ce qu'il y a de bon et de beau dans les actions morales. Car la conformité que trouvent entre les choses divines et le bel ordre de ces propositions, ceux qui les étudient, les rend amoureux de cette beauté divine, et les accoutume à la prendre pour modèle de leur conduite, par une sorte d'influence qui lui assimile les facultés de l'âme.

Et nous aussi, instruits par les travaux de ceux qui avant nous se sont appliqués à cette science, nous nous efforçons d'augmenter ce goût pour les vérités éternelles ; et, en nous proposant de rassembler ce qu'il sera possible de recueillir encore des découvertes qui ont été faites en ce genre, avec celles qui ont déjà été publiées, nous entreprendrons de les présenter avec la brièveté dont cette matière est susceptible, et d'une manière facile à saisir par ceux qui déjà y sont initiés. Enfin, pour atteindre le but de cet ouvrage, nous exposerons dans un ordre convenable, tout ce qui pourra servir à la théorie des corps célestes ; et, pour abréger, nous nous contenterons de rapporter ce qui a été suffisamment expliqué par les anciens, et nous perfectionnerons de tout notre pouvoir ce qui n'est pas exactement conçu, ni assez bien démontré.

CHAPITRE I.

DE L'ORDRE DES THÉORÈMES.

NOUS commencerons cet ouvrage par considérer d'abord la relation de la terre. en général avec tout le ciel ; ensuite, entrant dans les détails, nous parlerons premièrement de la situation du cercle oblique et de la position des lieux de cette partie de la terre que nous habitons, ainsi que des différences qui existent entre les uns et les autres, par les diverses inclinaisons de leurs horizons respectifs ; car ces préliminaires faciliteront les recherches qui suivront. En second lieu, nous considérerons le mouvement du soleil, celui de la lune et toutes leurs circonstances. Car, sans cette connaissance préalable, il serait impossible d'appuyer sur une méthode certaine, la théorie des étoiles. Puis, continuant sur ce plan, pour terminer par les étoiles, nous exposerons d'abord la sphère de celles qu'on appelle fixes ; ensuite viendront les cinq astres qu'on nomme planètes. Nous entreprendrons d'expliquer chacune de ces choses, en posant pour principes et pour bases de ce que nous voulons trouver, ce qui est évident, réel et certain, tant dans les phénomènes, que dans les observations anciennes et modernes, et en déduisant de ces conceptions leurs conséquences démontrées par des procédés accompagnés de figures linéaires.

Avant tout, il faut admettre généralement que le ciel est de forme sphérique, et qu'il se meut à la manière d'une sphère ; que la terre, par sa figure, prise dans la totalité de ses parties, est sensiblement un sphéroïde. Qu'elle est au milieu de tout le ciel, comme dans un centre ; et que, par sa grandeur et sa distance relativement à la sphère des étoiles fixes, elle n'est qu'un point sans mouvement et sans, déplacement. Nous allons parcourir brièvement chacune de ces assertions, pour les rendre plus présentes à l'esprit.

CHAPITRE II.

LE CIEL SE MEUT SPHÉRIQUEMENT.

L'OBSERVATION a sans doute suffi aux anciens pour leur donner les premières idées sur ces objets. Ils voient, en effet, le soleil, la lune et les étoiles transportés d'orient en occident, dans des cercles toujours parallèles entr'eux, commencer par se lever d'en bas, comme de terre ; et, parvenus peu à peu en haut, redescendre d'une manière semblable, s'abaisser et finir par disparaître comme tombant sur terre ; et, après quelque temps de disparition, se montrer de nouveau, comme se levant d'un autre point, et se couchant de même, en observant exactement les vicissitudes réglées qui ramènent généralement et les mêmes temps et les mêmes lieux des levers et des couchers.

La révolution circulaire des étoiles toujours visibles, contribua le plus à l'idée de sphéricité dont on eut bientôt acquis la certitude, en voyant, surtout, que cette révolution se fait en tournant autour d'un centre unique et le même pour toutes. Ce point fut nécessairement pris pour le pôle de la sphère céleste ; car les étoiles qui en sont les plus voisines, parcourent de plus petits cercles, et les autres qui en sont plus éloignées, décrivent des cercles plus grands, à proportion de leur éloignement, jusqu'à la distance où commencent les étoiles qui disparaissent ; parmi celles-ci, on voyait les plus proches des étoiles toujours visibles demeurer moins de temps dans leur disparition, et celles qui en sont plus éloignées rester d'autant plus longtemps cachées, que leur distance est plus grande. Cela seul a suffi d'abord pour faire naître cette idée que les observations suivantes ont confirmée ; toutes les apparences se trouvant absolument contraires à toute autre opinion.

Car, supposons que le mouvement des astres se fasse en ligne droite et sans fin, comme quelques-uns l'ont cru ; quel sera le moyen que l'on imaginera pour expliquer comment il se fait que ces astres reparaissent tous les jours aux lieux où ils ont paru commencer à se mouvoir ? Comment pourraient-ils y retourner s'ils allaient à l'infini, et toujours dans une même direction ? Ou bien, s'ils revenaient sur leurs pas, comment le feraient ils, sans être aperçus ? Ou comment ne disparaitraient-ils pas en diminuant insensiblement de grandeur ? Ne nous paraissent-ils pas, au contraire, plus grands, à l'instant où ils vont disparaître, et ne sont-ils pas couverts peu-à-peu et comme coupés par la surface de la terre ? Il serait absurde de soutenir que les astres s'allument en sortant de la terre, et qu'ils s'éteignent ensuite, en y rentrant Car, si l'on accordait qu'un si bel ordre, tant dans les grandeurs et les quantités, que, dans les distances, les lieux et les temps, se maintient par hasard, tel que nous le voyons constamment ; si l'on admettait qu'une partie de la terre a la vertu d'allumer, et une autre celle d'éteindre ; et surtout que la même partie allume pour certaines nations et éteint pour d'autres, et que les mêmes astres sont allumés ou éteints pour les unes, mais pas encore pour les autres ; si, dis-je, on accordait des choses aussi ridicules ; qu'aurions nous à dire quant aux étoiles toujours visibles qui ne se lèvent et ne se couchent jamais ? ou, pour quelle raison, les astres qui s'allument et s'éteignent ne se lèvent et ne se couchent-ils pas pour tous les lieux, tandis que ceux qui n'éprouvent pas les mêmes alternatives, sont toujours partout au-dessus de la terre ? Car, il ne peut se faire que les mêmes étoiles s'allument et s'éteignent pour certains lieux, et non pour les autres. Il est bien reconnu cependant que les mêmes étoiles se lèvent et se couchent pour certaines parties de la terre, et nullement pour d'autres.

En un mot, quelqu'autre figure que la sphérique qu'on suppose au mouvement des corps célestes, il faut que les distances de la terre au ciel et à ses parties, en quelque lieu qu' elle soit, et de quelque manière qu'elle soit située, soient inégales. Dès lors, les grandeurs et les distances des astres entre eux ne paraîtraient pas les mêmes aux mêmes personnes en chaque révolution, puisqu' elles seraient tantôt dans un plus grand éloignement, tantôt dans un moindre ; c'est pourtant ce qui ne se voit point. Car si les astres nous paraissent plus grands quand ils sont dans l'horizon ; ce n'est pas qu'ils soient moins éloignés de nous, mais c'est à cause de la vapeur humide qui environne la terre entre nos yeux et les astres, comme les choses plongées dans l'eau nous y paraissent d'autant plus grandes, qu'elles y sont plus profondément enfoncées.

Une autre raison qui milite en faveur de l'idée de sphéricité ; c'est que les instruments construits pour indiquer les heures, ne pourraient pas être justes, dans toute autre hypothèse que la nôtre seule ; c'est aussi que la révolution des corps célestes se faisant rapidement et sans obstacle, la figure la plus favorable le cercle, et, dans les solides, la sphère ; c'est qu'enfin, de toutes les figures différentes, mais isopérimètres, les plus grandes sont celles qui ont le plus d'angles. Ainsi, le cercle est le plus grand des plans ; la sphère, le plus grand des solides ; et le ciel, le plus grand des corps.
Ce n'est pas tout : des raisons physiques viennent encore à l'appui de cette opinion. De tous les corps, l'air est celui dont les parties sont les plus subtiles et les plus semblables. Or, les surfaces des corps composés de parties semblables, ont aussi leurs parties semblables ; et les seules surfaces dont les parties soient semblables, sont la circulaire parmi les plans et la sphérique parmi les solides ; donc, puisque l'air n'est pas plan, mais solide, il s'ensuit qu'il ne peut être que sphérique. Et, pareillement, la nature a composé tous les corps terrestres et corruptibles de figures rondes, mais dont les parties ne sont point semblables, et les corps divins et aériens de molécules sphériques et semblables. Or, si les étoiles étaient planes et comme des disques ; elles ne paraîtraient pas à ceux qui les regardent en même temps de différents lieux de la terre, avoir la figure ronde. Il est donc à présumer que l'atmosphère où elles sont plongées, étant partout de nature semblable, est par conséquent de forme sphéroïdale ; et que, par une suite de ce que ses parties sont semblables entr'elles, elle se meut circulairement et uniformément.

CHAPITRE III.

LA TERRE EST SENSIBLEMENT DE FORME SPHÉRIQUE DANS L'ENSEMBLE DE TOUTES SES PARTIES.

POUR concevoir que la terre est sensiblement de forme sphérique, il suffit d'observer que le soleil, la lune et les autres astres ne se lèvent et ne se couchent pas pour tous les habitants de la terre à la fois, mais d'abord pour ceux qui sont à l'orient, ensuite pour ceux qui sont à l'occident. Car nous trouvons que les phénomènes des éclipses, particulièrement de la lune, qui arrivent toujours dans le même temps absolu, pour tous les hommes, ne sont pourtant pas vues aux mêmes heures, relativement à celle de midi, c'est-à-dire, aux heures également éloignées du milieu du jour, mais que, partout, ces heures sont plus avancées pour les observateurs orientaux, et moins pour ceux qui sont plus à l'occident. Or, la différence entre les nombres des heures où les uns et les autres voient ces éclipses, étant proportionnelle aux distances de leurs lieux respectifs, on en conclura que la surface de la terre est certainement sphérique, et que de l'uniformité de sa courbure prise en totalité, il résulte que chacune de ses parties fait obstacle aux parties suivantes, et en borne la vue d'une manière semblable pour toutes. Il en serait tout autrement, si la terre avait une autre figure, comme on peut s'en convaincre par les réflexions suivantes.

Si la surface terrestre était concave, les habitants de ses parties occidentales seraient les premiers qui verraient les astres se lever ; si elle était plane, tous ses habitants ensemble et à la fois les verraient se lever et se coucher ; si elle était composée de triangles, de quadrilatères ou de polygones de quelqu'autre figure, tous les habitants d'une même face plane verraient les phénomènes dans le même temps, chose qui toutefois ne paraît pas avoir lieu. Il est certain aussi, que la terre n'est pas un cylindre dont la surface regarde le levant et le couchant, et dont les bases soient tournées vers les pôles du monde, conjecture qu'on pourrait juger plus vraisemblable ; car, si cela était, les habitants de la surface convexe ne verraient pas perpétuellement de certaines étoiles ; mais ou elles se lèveraient et se coucheraient entièrement, ou les mêmes à égale distance les unes d'un pôle, les autres de l'autre, seraient toujours invisibles pour tous. Cependant plus nous avançons vers les ourses, plus nous découvrons d'étoiles qui ne se couchent jamais, tandis que les australes disparaissent à nos yeux dans la même proportion. En sorte qu'il est encore évident, qu'ici, par un effet de la courbure uniforme de la terre, chaque partie fait obstacle aux parties latérales suivantes, de la même manière ; ce qui prouve que la terre a dans tous les sens une courbure sphérique. Enfin, sur mer si, de quelque point que ce soit, et dans toute direction quelconque, nous voguons vers des montagnes, ou d'autres lieux élevés, nous voyons ces objets comme sortir de la mer où ils étaient auparavant cachés par la courbure de la surface de l'eau.

CHAPITRE IV.

LA TERRE OCCUPE LE CENTRE DU CIEL.

DE la question de la figure de la terre, si l'on passe à celle de sa situation, on reconnaîtra que ce qui paraît arriver autour d'elle, ne peut paraître ainsi, qu'en la supposant au milieu du ciel comme au centre d'une sphère. En effet, si cela n'était pas, il faudrait, ou qu'elle fût hors de l'axe à égale distance de chaque pôle ; ou que, si elle était dans l'axe, elle fût plus proche de l'un des pôles, ou enfin, qu'elle ne fût ni dans l'axe, ni à égale distance de l'un ou de l'autre pôle.
Ce qui prouve que la première de ces trois, suppositions n'est pas vraie, c'est que, si la terre était placée de l'un ou de l'autre côté de l'axe, en sorte que certains points de la surface terrestre fussent au-dessus ou au-dessous de cet axe, ces points n'auraient jamais d'équinoxes, s'ils avaient la sphère droite, parce qu'alors
l'horizon couperait toujours le ciel en deux parties inégales, l'une au-dessus et l'autre au-dessous de la terre. Dans la sphère oblique, ou il n'y auroit pas d'équinoxes, ou bien ils n'arriveraient pas au milieu du passage d'un tropique à l'autre, ces distances étant nécessairement inégales, dans cette hypothèse. Car ce ne serait, plus le cercle équinoxial, le plus grand des cercles parallèles décrits par la révolution autour des pôles, qui serait coupé en deux parties égales par l'horizon, mais un des cercles qui lui sont parallèles, soit boréaux, soit méridionaux. Cependant, tout le monde convient unanimement que ces distances sont égales pour tous les lieux, en ce que les accroissements des jours comparés à celui de l'équinoxe, jusqu'au plus long dans les conversions (points tropiques, solstices) d'été, sont égaux à leurs diminutions jusqu'au plus court dans les points tropiques d'hiver. Si la terre était plus avancée vers l'orient ou vers l'occident, les grandeurs et les distances des astres dans l'horizon ne paraîtraient, à aucun point de la surface, ni les mêmes, ni égales, le soir et le matin ; et le temps, depuis le lever de ces astres jusqu'à leur arrivée au méridien, ne serait pas pour ces points égal à celui que ces mêmes astres emploieraient à aller du méridien à leur coucher. Cependant il n'est personne qui ne voie combien cela est contraire à l'expérience journalière.

Quant à la seconde hypothèse, qui place la terre dans l'axe du monde, mais plus avancée vers un pôle que vers l'autre, on pourrait lui objecter que, dans ce cas, le plan de l'horizon couperait en chaque climat le ciel en deux parties inégales, l'une au-dessus, et l'autre au-dessous de la terre, en raison de l'excentricité. Il couperait le ciel en deux parties égales, dans la sphère droite seulement. Mais dans la sphère oblique, où le pôle le plus proche est toujours visible, la partie du ciel supérieure à la terre serait plus petite, et l'inférieure plus grande en raison de la plus grande obliquité de la sphère. En sorte que le grand cercle qui passe par le milieu des animaux (signes), serait coupé en deux parties inégales par l'horizon. Toutefois, cela ne se voit nulle part : partout, six de ses douze divisions égales (dodécatémories) paraissent toujours au-dessus de la terre, les six autres étant invisibles ; et quand ces six dernières paraissent au-dessus, les six autres sont invisibles à leur tour. Ce qui prouve que les divisions du zodiaque sont coupées en deux moitiés par l'horizon, en ce que les mêmes demi-cercles sont entièrement, tantôt supérieurs, tantôt inférieurs à la terre.

Et, généralement, si la terre n'était pas située dans le cercle équinoxial, mais qu'elle fût plus avancée vers l'un ou l'autre pôle, soit boréal, soit austral, il arriverait que, même sensiblement, les ombres projetées de l'orient par les gnomons, ne feraient plus, dans les équinoxes une même ligne droite avec leurs correspondantes venant de l'occident, sur des plans parallèles à l'horizon. Cependant on voit constamment le contraire, preuve évidente que la troisième supposition est inadmissible, puisque les raisons qui montrent l'absurdité des deux premières, se rencontrent également dans celle-ci pour la combattre et la détruire.
En un mot, si la terre n'occupait pas le centre du monde, l'ordre que nous voyons s'observer dans les accroissements et décroissements des jours et des nuits, serait troublé et confondu. Outre que les éclipses de lune ne pourraient pas se faire pour toutes les parties du ciel, dans l'opposition diamétrale au soleil; parce que souvent la terre ne serait pas interposée entre les points où ces astres sont diamétralement opposés, mais dans des distances moindres que le demi-cercle.

CHAPITRE V.

LA TERRE EST COMME UN POINT A L'ÉGARD DES ESPACES CÉLESTES.

LES grandeurs et les distances des astres, observées de quelque point que ce soit de la terre, paraissant toujours égales et semblables en tous les lieux d'où on les voit dans les mêmes instants, et les observations des mêmes étoiles, faites en différents climats, ne présentant aucune différence, il est clair qu'elle n'est sensiblement que, comme un point relativement à l'espace qui s'étend jusqu'à la sphère des étoiles appelées fixes. Ajoutons encore, que les gnomons, et les centres des sphères armillaires, placés en quelqu'endroit que ce soit de la terre, donnent les apparences et les circonvolutions des ombres avec autant de précision et de conformité aux phénomènes en question que si ces instruments étaient placés au centre même de la terre.
Enfin une marque évidente que cela est ainsi, c'est que tous les plans qui passent par nos yeux, et que nous appelons horizons, coupent toujours la sphère céleste en deux parties égales : ce qui ne pourrait pas se faire, si la grandeur de la terre avait une proportion sensible avec la distance du ciel ; car alors il n'y aurait que le plan passant par le centre de la terre, qui pût partager la sphère céleste en deux moitiés. Mais par quelqu'autrepoint de la surface de la terre qu'on fît passer des plans horizontaux, ils feraient toujours en-dessous des segments plus grands qu'en dessus.

CHAPITRE VI.

LA TERRE NE FAIT AUCUN MOUVEMENT DE TRANSLATION.

PAR des preuves semblables aux précédentes, on démontrera que la terre ne peut être transportée obliquement, ni sortir absolument du centre. Car, si cela était on verrait arriver tout ce qui aurait lieu, si elle occupait un autre point que celui du milieu. Il me paraît, d'après cela, superflu de chercher les causes de la tendance vers le centre ; une fois qu'il est évident par les phénomènes mêmes, que la terre occupe le milieu du monde et que tous les corps pesants se portent vers elle ; et cela sera aisé à comprendre, si l'on considère que la terre ayant été démontrée, de forme sphérique, et, suivant ce que nous avons dit, placée au milieu de l'univers, les tendances et les chutes des corps graves, je dis celles qui leur sont propres, se font toujours et partout perpendiculairement au plan mené sans inclinaison par le point d'incidence où il est tangent. Il est clair qu'ils se rencontreraient tous au centre, s'ils n'étaient pas arrêtés par la surface, puisque la droite menée jusqu'au centre est perpendiculaire sur le plan qui touche la sphère au point d'intersection dans le contact même.

Ceux qui regardent comme un paradoxe qu'une masse comme la terre ne soit appuyée sur rien, ni emportée par aucun mouvement, me paraissent raisonner d'après les préjugés qu'ils prennent de ce qu'ils voient arriver aux petits corps autour d'eux, et non d'après ce qui est propre à l'universalité du monde, et c'est ce qui cause leur erreur. Ils seraient loin d'y tomber s'ils savaient que la terre, toute grosse qu'elle est, n'est pourtant qu' un point, comparativement au ciel, qui l'environne. Ils trouveraient qu'il est possible que la terre, étant un infiniment petit relativement à l'univers, soit maîtrisée de toutes parts et maintenue fixe par les efforts qu'exerce sur elle également et suivant des directions semblables, l'univers qui est infiniment plus grand qu'elle, et composé de parties semblables. Il n'y à ni dessus ni dessous dans le monde ; car on n'en peut concevoir dans une sphère. Quant aux corps qu'il renferme, par une suite de leur natures, il arrive que ceux qui sont légers et subtils sont comme poussés par un vent vers le dehors et vers la circonférence, et ils nous paraissent aller en haut, parce que c'est ainsi que nous appellons l'espace qui est au-dessus de nos têtes jusqu'à la surface qui nous enveloppe. Il arrive au contraire que les corps pesants et composés de parties épaisses se dirigent vers le milieu comme vers un centre, et nous paraissent tomber en bas, parce que c'est de ce nom que nous appelions ce qui est au-dessous de nos pieds dans la direction du centre de la terre.
Mais on doit croire qu'ils s'arrêteraient autour de ce milieu, par l'effet opposé de leurs chocs et de leurs efforts. On conçoit donc que la masse entière de la terre, qui est si considérable en comparaison des corps qui tombent sur elle puisse les recevoir dans leur chute, sans que ni leurs poids ni leurs vitesses lui communiquent le moindre mouvement. Mais si la terre avait un mouvement qui lui fût commun avec tous les autres corps graves, elle les précéderait bientôt par l'effet de sa masse, et laisserait sans autre appui que l'air, les animaux et les autres corps graves, et serait bientôt portée hors du ciel même. Toutes ces conséquences sont du dernier ridicule, même à imaginer.
Il y a des gens qui, tout en se rendant à ces raisons, parce qu'il n'y a rien a y opposer, prétendent que rien n'empêche de supposer, par exemple, que le ciel étant immobile, la terre tourne autour de son axe ; d'occident en orient ; en faisant cette révolution une fois par jour à très peu près ; ou que, si l'un et l'autre tournent, c'est autour du même axe, comme nous avons dit, et d'une manière conforme aux rapports que nous observons entr'eux.

Il est vrai que, quant aux astres eux-mêmes, et en ne considérant que les phénomènes, rien n'empêche peut-être que, pour plus de simplicité, cela ne soit ainsi ; mais ces gens-là ne sentent pas combien, sous le rapport de ce qui se passe autour de nous et dans l'air, leur opinion est ridicule. Car, si nous leur accordions que les choses les plus légères et composées de parties les plus subtiles ne se meuvent point, ce qui serait contre nature, ou ne se meuvent pas autrement que les corps de nature contraire, tandis que ceux qui sorti dans l'air, se meuvent si visiblement avec plus de vitesse que ceux qui sont plus terrestres ; si nous leur accordions que les choses les plus compactes et les plus pesantes ont un mouvement propre, rapide et constant, tandis qu'il est pourtant vrai qu'elles n'obéissent qu'avec peine aux impulsions qui leur sont données ; ils seraient obligés d'avouer que la terre, par sa révolution, aurait un mouvement plus rapide qu'aucun de ceux, qui ont lieu autour d'elle, puisqu'elle ferait un si grand circuit en si peu de temps. Les corps qui ne seraient pas appuyés sur elle, paraîtraient donc toujours avoir un mouvement contraire au sien ; et, ni les nuées, ni aucun des corps lancés, ou des animaux qui volent, ne paraîtraient aller vers l'orient ; car, la terre les précéderait toujours dans cette direction ; et anticiperait sur eux par par son mouvement vers l'orient, en sorte qu'ils paraîtraient tous, elle seule exceptée, reculer, en arrière vers l'occident.

S'ils disaient que l'atmosphère est emportée par la terre avec la même vitesse que celle-ci, dans sa révolution, il n'en serait pas moins vrai que les corps qui y sont contenus, n'auraient pas la même vitesse. Ou s'ils en étaient entraînés comme ne faisant qu'un corps avec l'air, on n'en verrait aucun précéder ni suivre ; mais tous paraîtraient stationnaires ; et, soit qu'ils volassent ou qu'ils fussent lancés, aucun n'avancerait ou ne s'écarterait jamais ; c'est pourtant ce que nous voyons arriver, comme si le mouvement de la terre ne devait leur causer ni retard ni accélération.

CHAPITRE VII.

IL Y A DANS LE CIEL DEUX PREMIERS MOUVEMENTS DIFFÉRENTS.

CES hypothèses qu'il nous suffira d'avoir exposées sommairement, étaient un préliminaire indispensable pour les détails où nous allons entrer, et nous serviront pour les conséquences que nous en tirerons. Elles seront d'ailleurs confirmées par leur accord avec les phénomènes qui seront démontrés dans la suite. Il faut pourtant encore poser en principe que le ciel a deux mouvements différents, l'un par lequel tout, est emporté d'orient en occident dans des cercles parallèles entr'eux, décrits semblablement et avec une vitesse égale autour des pôles de la sphère qui fait cette révolution uniformément. Le plus grand de ces cercles est celui qu'on appelle cercle équinoxial (équateur), parce qu'il est le seul qui, soit coupé en deux moitiés par l'horizon qui est un autre grand cercle de la sphère, et parce qu'il rend sensiblement pour toute la terre le jour égal à la nuit, quand le soleil le parcourt. L'autre mouvement est celui en vertu duquel les sphères des astres font de certaines révolutions en un sens contraire à la direction du premier mouvement, autour d'autres pôles que, ceux de cette première révolution. Nous supposons que cela s'exécute ainsi, parce que d'abord nous voyons, chaque jour, tout ce qui est au ciel, sans exception, se lever, parvenir au méridien et se coucher en suivant des routes sensiblement conformes et parallèles au cercle équinoxial ; en quoi consiste proprement le premier mouvement. On découvrit ensuite, en observant plus assidûment, que, si les distances réciproques des étoiles et leurs autres circonstances, telles que l'identité de leurs lieux dans le premier orbe, ne varient jamais, il n'en est pas de même du soleil, de la lune et des planètes. Car nous voyons ces astres-ci faire des mouvements divers et inégaux entr'eux, mais tous contraires au mouvement du monde, et tous vers l'orient et vers celles d'entre les étoiles fixes qui arrivent plus tard au méridien, en gardant toujours leurs mêmes distances réciproques, et tournant comme entraînées par la même sphère.

Si ce mouvement contraire des planètes se faisait dans des cercles parallèles à l'équateur, c'est-à-dire autour des pôles du premier mouvement, il suffirait d'imaginer pour toutes un seul mouvement qui seroit une conséquence du premier. Il paraîtrait vraisemblable que la différence entre les révolutions des planètes et celle des étoiles vint d'un simple retard, d'un moindre degré de vitesse, et, non pas d'un mouvement réellement contraire. Mais en même temps qu'elles s'avancent vers l'orient, les planètes s'approchent aussi de l'un ou de l'autre pôle, d'une quantité qui n'est pas la même en tout temps ni pour toutes, en sorte que ces variations paraîtraient être causées par autant d'impulsions particulières. Au reste,si cette marche paraît inégale quand on la rapporte à l'équateur et à ses pôles, elle devient uniforme et régulière quand on la rapporte au cercle oblique, qui, par là, paraît être proprement le cercle commun des planètes. Dans la réalité pourtant, il n'est le cercle que du soleil qui le décrit par son mouvement annuel, mais on peut dire qu'il est aussi celui de la lune et des autres planètes qui ne s'en écartent jamais ni au hasard ni sans règle, mais circulent dans des plans dont les inclinaisons sur le cercle oblique déterminent pour chacune d'une manière uniforme les écarts on déclinaisons de part et d'autre (de l'équateur). Or ce cercle oblique étant un grand cercle de la sphère, comme cela se voit par les déclinaisons égales du soleil, alternativement plus boréal et plus austral que l'équateur; et les planètes faisant leurs révolutions le long de ce seul et même cercle, comme nous l'avons dit, il fallait nécessairement admettre ce second mouvement, différent du mouvement général du monde, en ce qu'il se fait autour des pôles de ce cercle oblique, et en sens contraire à ce premier mouvement. Maintenant, si nous concevons un grand cercle qui passe, par les pôles des deux premiers, c'est-à-dire par les pôles de l'équateur et du cercle incliné sur lui, il les coupera en deux également et à angles droits, ce qui marquera quatre points sur ce cercle oblique. Les deux points déterminés par l'équateur seront diamétralement opposés, et s'appelleront équinoxiaux : l'un qui est le passage du midi vers les ourses, s'appelle l'équinoxe du printemps ; le point opposé est l'équinoxe d'automne. Les deux points déterminés par le cercle qui passe par les pôles des deux autres, sont de même opposés diamétralement, et s'appellent tropiques. Celui qui est au midi de l'équateur, est le tropique d'hiver ; celui qui est vers les ourses, est le tropique d'été.

On concevra donc le seul et premier mouvement, celui qui embrasse tous les autres, comme circonscrit et limité par le grand cercle (le colure des solstices), qui passe par les pôles des deux cercles, emporté et emportant avec lui d'orient en occident dans ce mouvement autour des poles de l'équateur, tout le reste qui marche comme à la suite du cercle qu'on appelle méridien, lequel ne diffère du colure, qu'en ce que tout méridien ne passe pas par les pôles du cercle oblique ; et on appelle ce cercle, méridien, parce qu'on le conçoit toujours perpendiculaire à l'horizon, et que cette position partageant par moitié l'hémisphère supérieur et inférieur, contient les milieux des temps que durent les nychthémères. Le second mouvement, qui se compose de plusieurs autres, est embrassé par le premier et embrasse les sphères de toutes les planètes ; il est emporté par le premier, comme nous avons dit, et en même temps il entraîne les planètes en sens contraire autour des pôles du cercle oblique. Ces pôles portés eux-mêmes sur le cercle qui opère la première révolution, c'est-à-dire sur le cercle (colure) qui passé par les pôles de l'oblique et de l'équateur, tournent avec lui, comme cela doit être ; et, dans la seconde révolution qui se fait en sens contraire de la première, les pôles du grand cercle oblique ; selon lequel se fait cette révolution, conservent toujours la même position relativement à l'équateur.

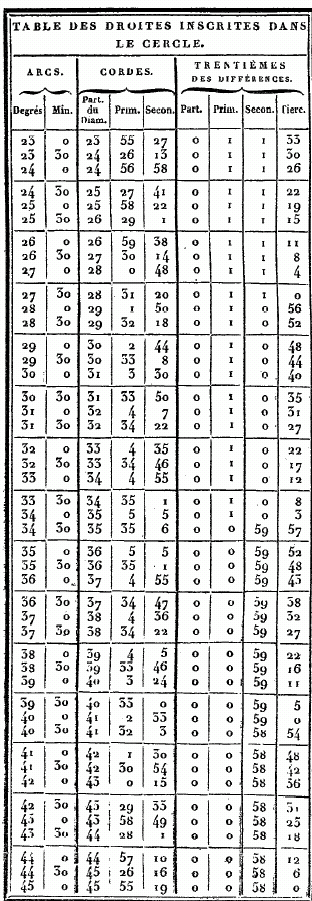
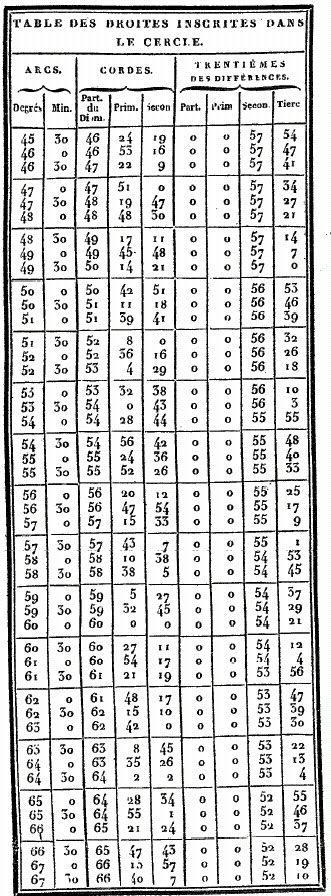
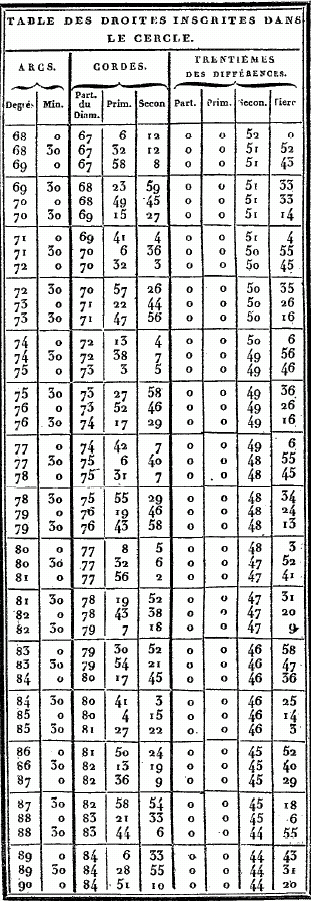
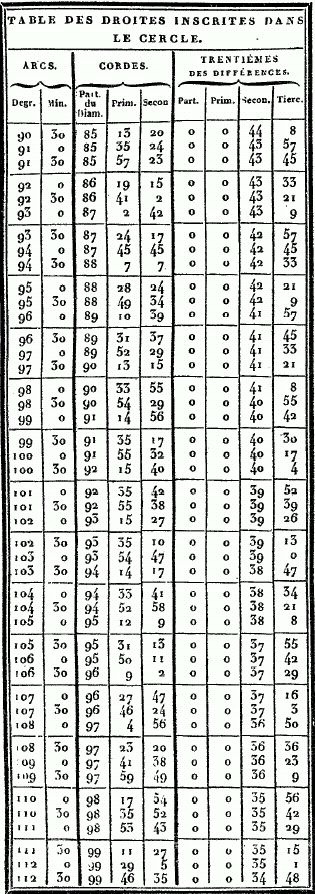
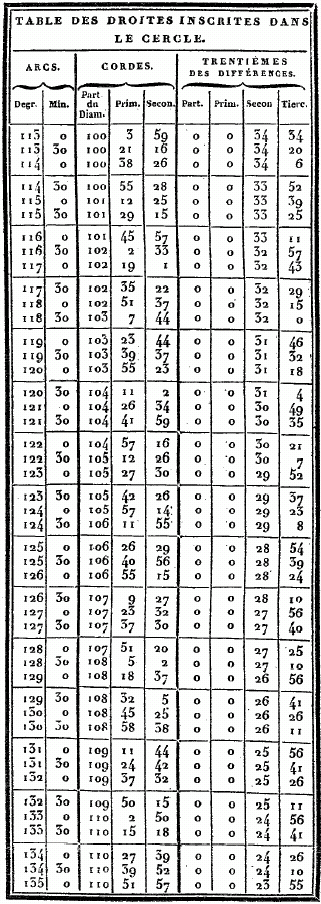
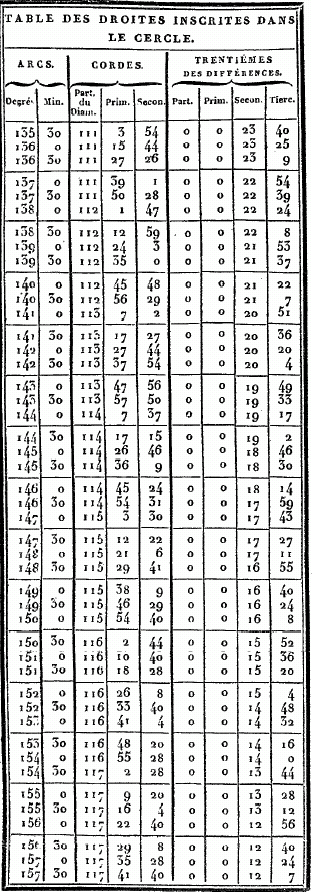
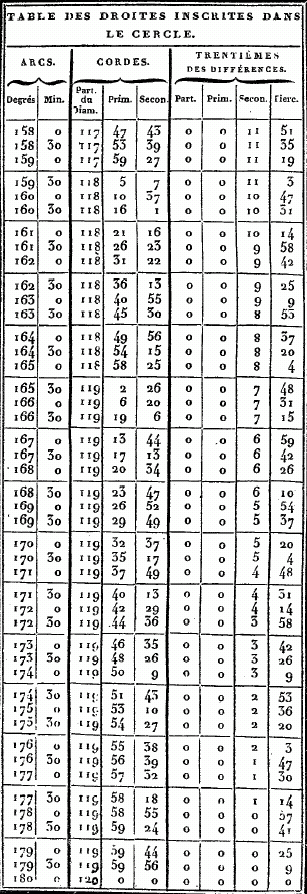
CHAPITRE VIII.

DES NOTIONS PARTICULIÈRES.

TELLE est l'exposition sommaire des principes généraux par lesquels il convenait de commencer ce Traité. Nous allons entier dans le détail des connaissances particulières. La première est, à, notre avis, celle qui donne la valeur de l'arc (du grand cercle qui passe par les pôles de l'équinoxial et de l'oblique) compris entre ces pôles. Nous croyons nécessaire de dire auparavant par quelle méthode on mesure les droites, inscrites dans le cercle, et nous accompagnerons nos démonstrations, de figures qui les rendront plus palpables.

CHAPITRE IX.

ÉVALUATION DES DROITES INSCRITES DANS LE CERCLE.

POUR la facilité de la pratique, nous allons maintenant construire une table des valeurs de ces droites, en partageant la circonférence en 360 degrés. Tous les arcs de notre table iront en croissant d'un demi-degré, constamment, et nous donnerons pour chacun de ces arcs la valeur, de la soutendante, en supposant le diamètre partagé en 120 parties. On verra par l'usage, que ce nombre était le plus commode qu'on pût choisir. Nous montrerons d'abord comment, au moyen d'un nombre, le plus petit possible, de théorèmes, qui sont toujours les mêmes, on se fait une méthode générale et prompte pour obtenir ces valeurs. Nous ne nous bornerons pas à la table où l'on pourrait prendre, ces valeurs sans en connaître la théorie, mais nous faciliterons les moyens de les éprouver et de les vérifier, en donnant les méthodes de construction. Nous emploierons en général la numération sexagésimale, pour éviter l'embarras des fractions ; et, dans les multiplications et les divisions, nous prendrons toujours les résultats les plus approchés, de manière que ce que nous négligerons ne les empèchera d'être sensiblement justes.

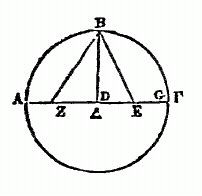
Soit d'abord le demi-cercle ABG décrit sur le diamètre ADG autour du centre D, et soit élevé, à angles droits, de D, sur AG , le rayon DB ; soit DG coupée en son milieu au point E ; joignez EB, et prenez EZ égale à EB ; enfin, joignez ZB ; je dis que ZD est le côté d'un décagone, et BZ celui d'un pentagone. En effet, puisqu'on a cette droite DG coupée en deux moitiés en E, et qu'on l'a prolongée par la droite DZ ; le rectangle compris sous GZ et ZD, plus le carré de ED, est égal au carré de EZ, c'est-à-dire au carré de EB, puisque EB est égale à ZE. Mais les carrés de ED et de DB sont égaux au carré de EB ; donc le rectangle construit sur GZ et ZD, plus le carré de ED ,font une somme égale à celle des carrés de ED et de DB ; donc, retranchant le carré de DE commun de part et d'autre, le reste, qui est le rectangle sur GZ et DZ, est égal au carré de DB, ou au carré de GD ; donc GZ est coupée en moyenne et extrême raison au point D. Or, puisque le côté de l'hexagone et celui du décagone inscrits dans le même cercle se trouvent sur une même droite en la coupant en moyenne et extrême raison, et que la droite ou rayon GD est le côté de l'hexagone, il s'ensuit que ZD est le côté du décagone. Pareillement, puisque le carré du côté du pentagone est égal à la somme des carrés des côtés du décagone et de l'hexagone inscrits dans le même cercle, et que le carré de l'hypoténuse FEZ est égal au carré de BD qui est le côté de l'hexagone, et au carré de DZ qui est le côté du décagone, il s'ensuit que BZ est égal au côté du pentagone.

Faisant donc, comme je l'ai dit, le diamètre du cercle de 120 parties, DE qui est la moitié du rayon, sera de 30, et son carré sera de 900. Le rayon BD est de 60, et son carré est de 3600 ; mais le carré de EB, c'est-à-dire celui de EZ, est de 4500 : par conséquent, la longueur de cette ligne EZ est de 67^P, 4', 55", à très peu près, et DZ est de 37^P, 4', 55" ; donc le côté du décagone qui soutend un arc, de 36 des degrés dont la circonférence en contient 360, est de 37^P, 4', 55" des parties dont le diamètre en contiént 120^P. De plus, puisque la ligne DZ est de 37^P, 4', 55", son carré est de. 1375^P, 4', 15" ; mais le carré de DB est de 3600 des mêmes parties, et la somme de ces deux carrés est égale au carré de BZ qui est par conséquent de 4975^P, 4', 15" ; donc la ligne BZ est de 70^P, 32', 3",environ : ainsi le côté du pentagone qui soutend 72 des degrés dont la circonférence en contient 360, contient 70^P, 32', 3", des parties dont le diamètre en contient 120^P. Or il est évident que le côté de l'hexagone qui soutend 60 degrés, et qui est égal au rayon, est de 60 parties. De même, le carré du côté du quadrilatère qui soutend 90 degrés de la circonférence, est égal au double carré du rayon ; et le carré du côté du triangle qui soutend 120 de ces mêmes degrés, est égal au triple carré du rayon. Mais le carré du rayon est de 3600 parties : on en conclura le carré du côté de ce quadrilatère, de 7200 ; et celui du côté de ce même triangle, de 10800 parties. Par conséquent, la droite qui soutend 90 degrés de la circonférence, sera en longueur à peu près de 84^P 51' 10" des parties dont le diamètre en contient 120 ; et celle qui soutend 120 degrés sera de 103^P 55' 23" de ces mêmes parties du diamètre.

Ces droites se prendront ainsi facilement par elles-mêmes, et il est aisé de voir par là que, au moyen des droites données, on aura bientôt celles qui soutendent le reste de la demi-circonférence, attendu que la somme de leurs carrés est égale au carré du diamètre. Par exemple la droite qui soutend 36 degrés de la circonférence, ayant été démontrée de 37^P 4' 55" des parties du diamètre, et son carré de 1375^P 4' 15", tandis que le carré du diamètre est de 14400, le carré de la droite qui soutend le reste 144^d de la demi-circonférence, sera donc de 13024^P 55' 45" ; et la longueur de cette droite sera de 114^P 7' 37", à peu près, et de même pour les autres. Nous montrerons dans la suite comment les autres soutendantes se déduisent de celles-ci, quand nous aurons exposé un lemme qui en facilitera la pratique.

Soit un quadrilatère quelconque inscrit dans le cercle ABGD ; soient menées les diagonales AG, BD : il s'agit de prouver que le rectangle, construit sur AG et BD, est égal aux deux rectangles des côtés opposés AB GD, et AD BG. Soit fait l'angle ABE égal à l'angle DBG ; si nous ajoutons à chacun l'angle commun EBD, l'angle ABD égalera l'angle EBG. Mais BDA est égal à BGE ; car ces deux angles sont inscrits et appuyés sur le même arc ; donc le triangle ABD est équiangle au triangle BGE. On a donc l'analogie : BG est à GE, comme BD est à DA : par conséquent, le produit de BG multiplié par AD est égal à celui de BD multiplié par GE. Maintenant puisque l'angle ABE est égal à l'angle DBG, et que l'angle BAE est égal à l'angle BDG, le triangle ABE est équiangle au triangle BGD ; on a donc l'analogie : BD est à DG, comme BA est à AE, donc le rectangle BA DG est égal au rectangle BD AE. Or il a été prouvé que le rectangle BG AD est égal au rectangle BD GE ; par conséquent le rectangle entier AG BD, est égal aux deux rectangles AB DG, et AD BG. Ce qu'il fallait démontrer.

Cela posé, soit décrit un demi-cercle ABGD sur le diamètre AD ; soient menées du point A les deux droites AB, AG, données de grandeur chacune en parties du diamètre donné de 120 parties, et joignez BG ; je dis que cette ligne est aussi donnée : car soient menées les droites BD GD ; elles sont aussi données, parcequ'elles sont soutendantes du reste de la demi-circonférence. Mais le quadrilatère ABGD étant inscrit dans le cercle, il s'ensuit que la somme des rectangles AB GD et AD BG est égale au rectangle AG BD. Or le rectangle construit sur AG et BD est donné, ainsi que le rectangle sur AB et GD, donc AD BG est aussi donné ; mais AD est le diamètre, donc la droite BG se trouve par là donnée. Ainsi nous voyons clairement que si deux arcs sont donnés avec leurs soutendantes, la droite qui soutend la différence de ces deux arcs sera aussi donnée ; et il est évident que, par le moyen de ce théorème, nous inscrirons beaucoup d'autres droites qui soutendent les différences des deux arcs dont les soutendantes seront données, et que par conséquent, nous trouverons facilement celle qui soutend 12 parties de la circonférence, puisque nous avons celle de 60 et celle de 72 degrés.

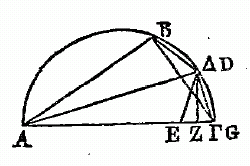
Soit encore proposé, étant donnée une droite inscrite dans un cercle, de trouver la soutendante de la moitié de l'arc soutendu par cette droite. Pour cela, soit le demi-cercle ABG décrit sur le diamètre AG ; soit donnée la droite GB, et soit l'arc GB coupé par moitié, au point D. Soient menées les droites AB, AD, BD, DG, et du point D soit abaissée la perpendiculaire DZ sur AG je dis que ZG est la moitié de la différence entre AB et AG ; car, soit prise AE égale à AB, et joignons la droite DE ; puisque AB est égale à AE, et que AD est commune, les deux côtés AB, AD, sont égaux aux deux AE, AD, chacun à chacun, et l'angle BAD est égal à l'aigle EAD ; la base BD est donc égale à la base DE. Mais BD est égale à DG ; donc DG est égale à DE. Le triangle DEG étant donc isocèle, soit abaissée du sommet la perpeiïdiculaire DZ sur la base, EZ est égale à ZG ; or EG entière est la différence des droites AB, AG ; donc ZG est la moitié de cette différence. Ainsi, puisque la droite, qui soutend l'arc BG étant donnée. AB qui soutend le reste de la demi circonférence est aussi donnée, ZG moitié de là différence entre AG et AB, sera aussi par là même donnée, mais puisque, dans le triangle rectangle AGD, étant menée la perpendiculaire DZ, le triangle rectangle ADG devient équiangle au triangle DGZ, et que GD est à GZ comme AG est à GD, il s'ensuit que le rectangle AG GZ est égal au carré fait sur GD ; donc la droite GD qui soutend la moitié de rare BG, sera donnée de longueur.
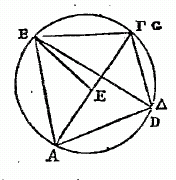
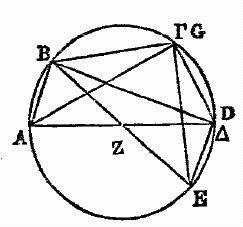
Ce théorème servira à faire trouver la plupart des autres soutendantes en prenant les moitiés des arcs donnés. Par exemple, au moyen de la droite qui soutend l'arc de 12 degrés, on trouvera celles des arcs de 6^d, de 3^d, de 1 1/2^d et de 1/2 1/4 d'un seul degré. Or nous trouvons par le calcul, que la soutendante de 1 1/2^d contienta très peu près 1^P 34' 15", des parties dont le diamètre en contient 120, et que celle de 1/2 1/4 en contient 0^P 47' 8".

Soit encore le cercle A B G D autour du diamètre AD, et du centre Z. Soient pris depuis le point A les deux arcs donnés consécutifs AB, BG, et joignons leurs soutendantes données AB, BG : je dis que, si nous joignons les points A et G par la droite AG, cette droite sera aussi donnée. Car, soit mené de B en E, le diamètre BZE, et soient tirées les droites BD, DG, GE, DE, il est clair qu'à cause de la droite BG, GE sera donnée ; et qu'à cause de AB, BD sera aussi donnée, ainsi que DE. Or, d'après ce que nous avons démontré, le quadrilatère BGDE étant inscrit au cercle, et les diagonales BD, GE y étant menées, le rectangle de ces diagonales est égal à la somme des rectangles faits sur les côtés opposés du quadrilatère. Ainsi, puisque le rectangle BD GE étant donné, celui qui est construit sur BG et DE, est aussi donné, il s'ensuit que le rectangle BE GD est aussi donné. Or le diamètre BE est donné ; donc l'autre côté GD sera donné, et on en conclura aisément la valeur de GA, qui soutend le reste de la demi-circonférence. Par conséquent, si deux arcs sont donnés, ainsi que leurs soutendantes, on trouvera par ce théorême la droite qui soutend la somme de ces deux arcs.

Il est évident que, si nous ajoutons à toutes les soutendantes (cordes) prises précédemment, celle de 1 1/2 degré, et que nous prenions les soutendantes de ces sommes, nous inscrirons aisément toutes celles qui, rendues doubles, pourront être divisées juste par 3 . Il ne restera d'omises encore que celles qui seront dans les intervalles des accroissements par 1 1/2, deux en chaque ; attendu que nous inscrivons par demi -degrés. C'est pourquoi, quand nous aurons trouvé la corde d'un demi-degré, cette corde combinée, par addition et par soustraction, avec les cordes données quii embrassent ces intervalles, nous servira à compléter toutes les autres intermédiaires. Mais parce que la soutendante de l'arc de 1 1/2 étant donnée, celle qui soutend le tiers de cet arc n'est pas pour cela donnée par les lignes; car, si elle l'était, nous aurions par cela même la corde dé 1/2^d ; nous chercherons d'abord la corde de 1^d, par le moyen de celle de 1 1/2 degré et de celle de 1/2 1/4, à l'aide d'un lemme qui, quoiqu'il ne puisse pas donner la juste valeur d'une droite inscrite dans le cercle, donne au moins les plus petites avec assez de précision, pour qu'il n'y ait pas de différence sensible d'avec celles que l'on déterminerait rigoureusement. Je dis donc que, si l'on mène dans le cercle deux droites inégales, la plus grande sera à la plus petite, en moindre raison que l'arc décrit sur la plus grande, à l'arc soutendu par la plus petite.

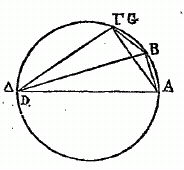
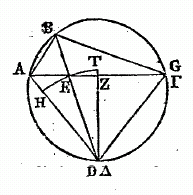
En effet, soit le cercle ABGD, et soient menées dans ce cercle deux droites inégales dont la plus grande est BG et la plus petite AB ; je dis que la droite BG est à BA, en moindre raison que l'arc BG à l'arc AB. Soit, en effet, l'angle ABG coupé en deux angles égaux par la droite BD et soient menées les droites AEG,AD et GD l'angle ABG étant coupé en deux également par la droite BED, la droite GD est égale à la droite AD, et GE est plus grand que EA. Abaissez une perpendiculaire DZ du point D sur la droite AEG ; puisque AD est plus grande que ED et ED plus grande que DZ, le cercle décrit du centre D et de l'intervalle DE, coupe AD, et passe au-delà de DZ. Soit donc décrit l'arc HET, et prolongez DZ en T ; puisque le secteur DET est plus grand que le triangle DEZ, et que le triangle DEA est plus grand que le secteur DEH, il s'ensuit que le triangle DEZ est en moindre raison, relativement au triangle DEA, que le secteur DET, relativement au secteur DEH. Mais comme le triangle DEZ est au triangle DEA, ainsi la droite EZ est à la droite EA ; et comme le secteur DET est au secteur DEH, ainsi l'angle ZDE est à l'angle EDA : donc la droite ZE est à la droite EA, en moindre raison que l'angle ZDE à l'angle EDA. Et, par conséquent, par addition (componendo), la droite ZA est à da droite EA, en moindre raison que l'angle ZDA à l'angle ADE ; doublant les premiers termes de ces raisons, la droite GA est à la droite AE, en moindre raison que l'angle GDA à l'angle EDA ; et, par soustraction (dividendo), la droite GE est à la droite EA, en moindre raison que l'angle GDE à rangle EDA. Mais comme GE est à EA, ainsi GB est à BA, et comme l'angle GBD est à l'angle BDA, ainsi l'arc GB est à l'arc BA : concluons, que la droite GB est à la droite BA, en moindre raison que l'arc GB à l'arc BA.

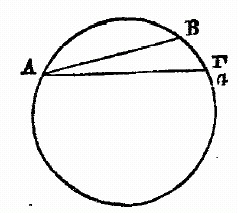
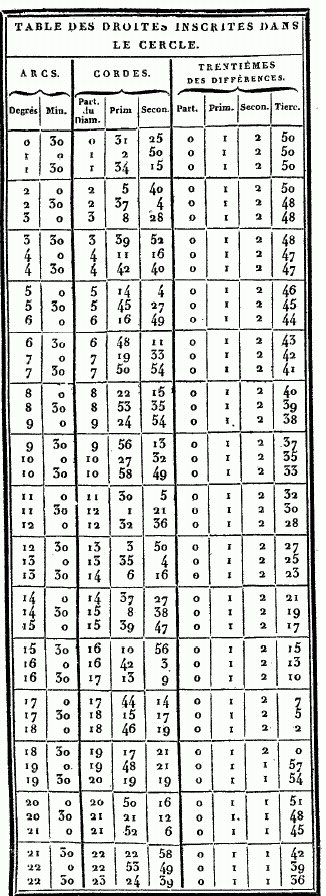
Cela posé, soit le cercle ABG ; menez-y deux droites AB et AG, en supposant AB soutendante de 1/2 1/4 et AG soutendante d'un degré. Puisque la droite AG est en moindre raison relativement à la droite BA, que l'arc AG à l'arc AB, et que l'arc AG vaut l'arc AB plus un tiers de cet arc AB , la droite GA est plus grande que la droite AB, de moins d'un tiers de AB. Mais on a démontré que cette droite AB vaut O^P 47' 8" des parties dont il y en a 120 dans le diamètre, donc la droite GA a moins que 1^P 2' 50"de ces mêmes parties ; car cette dernière quantité est à peu près les 4/3 de 0^P 47' 8".

Soient encore, dans la même figure, la droite AB soutendante de l'arc d'un degré, et AG de l'arc d'un degré et demi. Puisque l'arc AG est à l'arc AB comme 1 1/2^P. est à 1^P ; il s'ensuit que la droite AG est à la droite AB en moindre raison que 1 1/2 à 1. Mais nous avons prouvé que la soutendante AG de 1 1/2, vaut 1^P 34' 15" des parties dont 120 font le diamètre ; donc la droite AB est plus grande que 1^P 2' 50" de ces mêmes parties : car 1 1/2 est à 1 comme 1, 34', 15" sont à I, 2', 50 ". Ainsi donc, puisqu'il est démontré que la droite qui soutend 1^d , est plus grande et plus petite que la quantité I^P, 2', 50", nous la prendrons de 1^P, 2', 50", à peu près, des parties dont 120 font la longueur du diamètre. Et, par suite de ce que nous venons de démontrer, et de ce que la soutendante de 1/2 se trouve de 0^d, 31' 25", approximativement, les autres intervalles seront remplis comme nous l'avons dit. Par exemple, pour le premier, il est prouvé que la soutendante de 2^d se trouve par la somme de celles de 1/2 et de 1 1/2, et celle de 2 1/2 par la différence de celle de 2, qui est donnée, a celle de 3 ; et ainsi des autres.

Telle est, à mon avis, la manière la plus facile de trouver toutes les droites inscrites dans le cercle. Mais, comme je l'ai dit, afin d'avoir sous la main les valeurs toutes prêtes de ces droites pour tous les cas où l'on en a besoin , nous placerons, ci-dessous, des tables de 45 lignes chacune, disposées en trois colonnes, dont la première contiendra les grandeurs des arcs croissant successivement par demi-degrés ; la seconde donnera leurs soutendantes évaluées en parties dont le diamètre en contient 120 ; et la troisième offrira le trentième des accroissements de ces soutendantes pour chaque demi-degré ; de sorte, qu'ayant ainsi l'augmentation moyenne, pour un soixantième, sensiblement égale à l'augmentation juste, nous pourrons calculer promptement les parties proportionnelles qui conviendront à chacune des soutendantes des arcs intermédiaires à ceux qui sont marqués dans ces tables, de demi en demi-degrés. Il est aisé de voir que, si l'on était dans le doute de quelque faute de copie, pour quelqu'une de ces soutendantes, on pourroit en faire aisément la vérification ou la correction à l'aide des théorèmes précédents, soit par celui qui donne la soutendante de l'arc double, soit par celui qui donne celle de la somme ou de la différence, soit enfin par celui qui donne la soutendante du supplément au demi-cercle. Voici maintenant ces tables toutes dressées.