GAUDENCE

INTRODUCTION HARMONIQUE

AVANT-PROPOS.

� Je chante pour les savants; fermez la porte (sur vous), profanes.[1] Tel pourrait �tre � bon droit le d�but de quiconque se dispose � discourir sur l'harmonique. Ces sortes de discours concernent les sons, les intervalles et les syst�mes, les tons et les m�taboles, enfin la m�lop�e dans tous les genres de chant[2] celui qui voudra entendre discourir sur ces mati�res devra exercer d'avance son oreille � une exacte perception par une pratique exp�rimentale, de fa�on � reconna�tre, parmi les intervalles, le consonant et le dissonant, afin que, en s'appliquant, par un raisonnement suivi, � saisir les propri�t�s des sons, il puisse acqu�rir une science compl�te, gr�ce � l'appoint de l'exp�rience et du raisonnement. Quant � celui qui viendrait �couter ces le�ons sans �tre capable de bien percevoir un son m�lodique ou dont l'oreille n'aurait pas �t� exerc�e, qu'il s'en aille en �fermant la porte� sur ses oreilles[3] ; car, m�me �tant pr�sent, ses oreilles seront bouch�es, vu qu'il ne serait pas pr�par� � conna�tre par la perception les mati�res trait�es. Pour notre part, nous nous adressons d�s le commencement aux personnes qui, par l'exercice, ont acquis une pratique rigoureuse.

I. Sur la Voix.

Le lieu de la voix,[4] c'est l'intervalle qui va du grave � l'aigu et inversement; c'est dans ce lieu que se produit tout mouvement de la voix, soit parl�e, soit discontinue,[5] soit surtendue, soit rel�ch�e.[6]

Les sons employ�s dans la voix parl�e, qui nous sert � converser entre nous, parcourent ce lieu, contigus les uns aux autres, soumis � une sorte de flux qui les porte vers l'aigu ou en sens contraire, mais sans qu'ils s'arr�tent sur une tension donn�e[7] ; tandis que la voix appel�e �discontinue� ne sera en aucune fa�on contigu� � elle-m�me[8] et n'�prouvera rien qui ressemble � un flux, mais espac�e dans ses propres parties et franchissant, sans qu'on s'en aper�oive, un certain intervalle, elle semble s'arr�ter sur les limites des lieux qu'elle franchit, et rend manifeste sa propre tension.[9] Voil� pourquoi elle a re�u, ajuste titre, la qualification de � discontinue �, par opposition � la voix � parl�e �.

A la voix discontinue se rattachent particuli�rement le (chant) m�lodique et le non m�lodique. Quand elle emploie des intervalles rationnels[10] et qu'elle n'est ni en d�faut ni en exc�s � cet �gard, (le chant) est m�lodique; si le chant est en d�faut ou en exc�s, si peu que ce soit, par rapport aux intervalles d�termin�s,[11] il est non m�lodique. On constate en outre une certaine opposition entre le m�lodique et le non m�lodique.[12]

Quand le mouvement de la voix, d'un degr� plus grave, la fait passer � un degr� plus aigu, il y a ce qu'on appelle � surtension � ; dans le cas inverse on dit qu'il y a et il y a en effet rel�chement.[13] La surtension engendre l'acuit� et le rel�chement la gravit�; mais la gravit� diff�re du rel�chement et l'acuit� de la surtension, non seulement comme la cause diff�re de l'effet qu'elle produit, mais de plus en ce que, lorsque la surtension a pris fin et cesse d'exister, l'acuit� na�t et existe. Il en est de m�me de la gravit� par rapport au rel�chement; car un r�sultat commun se produit par l'une comme par l'autre : la tension. En effet, l'acuit� comme la gravit� comportent visiblement (toutes deux) une certaine tension.[14]

II. Sur le Son.

Le son est la chute de la voix sur une seule tension. La tension est le repos et la station de la voix. Lors donc que la voix semble stationner sur une tension unique, nous disons que la voix �met[15] un son capable de prendre rang dans un chant.

Le son poss�de une couleur, un lieu, un temps.[16] Le temps (du son) consiste en ce que nous chantons des sons plus lents en plus de temps et des chants plus courts[17] en moins de temps, de sorte que, dans ce sens, le rythme a �videmment lui aussi un lieu ; seulement les chants doivent �tre rythm�s d'apr�s le temps (la dur�e) des sons. Le lieu du son consiste en ce que nous �mettons tels sons plus graves, tels autres plus aigus; car ceux qui sont manifestement �mis dans le m�me lieu, nous les appelons � homophones �; et ceux qui sont plus aigus ou plus graves (les uns que les autres), nous disons qu'ils sont situ�s dans des lieux diff�rents. La couleur est ce en quoi peuvent diff�rer entre eux des sons qu'on voit situ�s dans le m�me lieu et de la m�me dur�e, comme cela arrive dans la voix pour la nature du chant parl� et dans des cas semblables.[18]

III. Sur l'Intervalle.

L'intervalle est ce qui est compris entre deux sons. Il est �vident que les sons diff�rent n�cessairement entre eux par la tension; car, s'ils avaient la m�me tension, il n'y aurait pas du tout d'intervalle, attendu que la voix para�trait demeurer dans le m�me lieu (sur le m�me degr�). Ainsi donc la diff�rence entre un son plus aigu et un son plus grave, comme celle entre un son plus grave et un son plus aigu, constitue ce qu'on appelle un intervalle. Le ton en est un. D'ailleurs le ton est tant�t une grandeur d'intervalle, tant�t une vari�t� de syst�me[19] ; car le mot ton a cette double acception. Lorsque le ton est un intervalle, il se divise en demi-tons et en di�sis[20] et il forme d'autres intervalles qui exc�dent sa propre �tendue, comme par exemple des trih�mitons,[21] des ditons[22] et d'autres semblables; mais lorsque ce mot sert � d�signer une vari�t� de syst�me, il indique la quantit� de tension de tout le syst�me (donn�).[23]

IV. Sur les Syst�mes.[24]

Parmi les intervalles,[25] les uns sont m�lodiques, les autres non m�lodiques. Parmi les m�lodiques,[26] les uns sont consonants, les autres inconsonants,[27] les uns majeurs, les autres mineurs, les uns premiers et incompos�s,[28] les autres ni premiers ni incompos�s. Quant � reconna�tre les intervalles m�lodiques, ceux qui sont consonants et ceux qui ne le sont pas, 5. c'est le propre de l'oreille ; car la diff�rence qui distingue les sons consonants et les dissonants, les sons m�lodiques et les non m�lodiques r�side principalement dans la diff�rence de la r�sonance. Au surplus on ne dira que peu de chose � ce sujet dans le pr�sent trait�.

Les intervalles sont incompos�s lorsque, entre les sons qui les comprennent, on ne peut chanter un seul son m�lodique par rapport � ceux du m�me genre dans lequel l'intervalle incompos� est consid�r�. Les intervalles compos�s sont ceux entre lesquels on chante un ou plusieurs sons. Ces intervalles sont les m�mes que les syst�mes[29] car, en somme, le syst�me, c'est l'intervalle form� de plus d'un intervalle; or les intervalles premiers et incompos�s, dans chaque genre, sont les communes mesures de tous les autres intervalles et syst�mes compris dans ce m�me genre.

V. Sur les Genres.

Le genre est une division et disposition d'une certaine nature affect�e au t�tracorde. Les genres sont au nombre de trois, le diatonique, le chromatique, l'enharmonique, mais les esp�ces ou nuances des genres sont en plus grand nombre. Dans le genre enharmonique, l'intervalle premier et incompos� est le quart du ton; on l'appelle di�sis enharmonique. Dans le chromatique, c'est le tiers du ton; on l'appelle di�sis chromatique minime. Dans le diatonique, notamment dans celui qu'on nomme synton,[30] c'est le demi-ton qui est l'intervalle premier et incompos�.

On chante le diatonique synton (en allant du grave) � l'aigu, par demi-ton, ton et ton, et (de l'aigu) au grave, naturellement dans l'ordre inverse. Le chromatique se chante, lui aussi,[31] sous plusieurs formes. Une de ses formes, que nous prendrons pour exemple, proc�de (du grave) � l'aigu par demi-ton, demi-ton et trih�miton; � (de l'aigu) au grave, dans l'ordre inverse. Dans le genre enharmonique, le chant proc�de par quart de ton, quart de ton et diton.

VI

En voil� assez pour le moment sur le genre. Revenant sur nos pas, nous allons parler actuellement du nombre, de l'ordre et des intervalles des sons, en ce qui concerne le genre diatonique; car c'est le seul des trois genres qui soit chant� g�n�ralement aujourd'hui, et l'emploi des deux autres est bien pr�s de dispara�tre.

Diagramme des trois genres pour un seul t�tracorde.[32]

Les anciens ont donn� au son le plus grave de tous, celui dont ils firent le point de d�part de l'harmonie[33] (du grave) � l'aigu, le nom de � proslambanom�ne[34] �; et ce son, ils ne le consid�rent pas comme �tant toujours le plus grave par nature, mais comme l'�tant par position.[35] En effet, dans chacun des tropes le proslambanom�ne n'�tait pas toujours le m�me son, mais, au contraire, toujours un son diff�rent, . comme on le montrera un peu plus loin.

Apr�s le proslambanom�ne, on pla�a l'hypate des hypates, toujours distante du son pr�c�dent de l'intervalle toni� (d'un ton) dans les divers genres de l'harmonie. A la suite on pla�a la parhypate des hypates, d'un demi-ton plus aigu� que l'hypate; puis la lichanos des hypates, �loign�e d'un ton, � l'aigu, de la parhypate, et nomm�e aussi diatonique des hypates, dans le genre diatonique. Apr�s cette note prit rang l'hypate des moyennes, pareillement �loign�e d'un ton de la lichanos ou diatonique; et par cette note fut compl�t� le t�tracorde des hypates, commen�ant par l'hypate des hypates et finissant sur l'hypate des moyennes.

Avec cette m�me note, on fit commencer � son tour le t�tracorde des moyennes, de telle fa�on que le son commun aux deux t�tracordes f�t l'hypate des moyennes, note la plus aigu� du premier t�tracorde, celui des hypates, et la plus grave du second, celui des moyennes. Apr�s cette note, vient la parhypate des moyennes, d'un demi-ton plus aigu� que l'hypate (des moyennes), et, apr�s cette parhypate, la lichanos des moyennes ou diatonique des moyennes, pareillement d'un ton plus aigu� que la parhypate (des moyennes).

Vient ensuite la m�se, �loign�e d'un ton aussi de la lichanos des moyennes, et avec celle-ci fut compl�t� le second syst�me de t�tracorde, celui des moyennes.

��..[36]

De cette m�se, � son tour, on fit le point de d�part, tant�t du t�tracorde contigu, appel� pour cette raison t�tracorde conjoint,[37] tant�t du t�tracorde des disjointes, lequel ne partit 8. plus de la m�se, mais de la note appel�e param�se, qui, toujours, c'est-�-dire dans tous les genres de la m�lodie, est �loign�e d'un ton de la m�se.

Les anciens form�rent donc deux syst�mes parfaits, qu'ils nomm�rent, l'un syst�me en conjonction, l'autre syst�me en disjonction.

Lorsqu'ils form�rent le syst�me en conjonction, ils plac�rent imm�diatement apr�s la m�se, la trite des n�tes conjointes,[38] �loign�e d'un demi-ton de la m�se, et, imm�diatement apr�s la trite, la paran�te des n�tes conjointes, plus aigu� d'un ton que la trite; et, � leur suite,[39] la n�te des n�tes conjointes, plus aigu� d'un ton que la paran�te. On a nomm� le t�tracorde ainsi form� �t�tracorde des n�tes conjointes�, �des n�tes s � cause de sa position extr�me (v�aTov) et parce qu'il est la limite de la progression vers l'aigu; �des conjointes� parce qu'il n'est pas s�par� (du t�tracorde) des moyennes, mais qu'il est contigu � ce t�tracorde qui le pr�c�de, moyennant un son commun, la m�se. On a nomm� � trite[40] � la note voisine de la m�se parce qu'elle arrive troisi�me � partir de la fin, � paran�te� celle qui vient � sa suite, et �n�te� la derni�re, comme �tant la limite du mouvement vers l'aigu, ainsi que nous l'avons dit.

��...[41]

Maintenant, lorsqu'on forma le syst�me en disjonction, imm�diatement apr�s la m�se, on pla�a la param�se, toujours et dans tous les genres distante d'un ton de la m�se, comme c'�tait le cas, on l'a vu, (de l'intervalle) du proslambanom�ne � l'hypate des hypates. Cet intervalle re�ut le nom de ton de la disjonction.[42] Avec la param�se on fit commencer le t�tracorde des n�tes disjointes; et, de m�me (que pour le t�tracorde pr�c�dent), on pla�a la trite un demi-ton � l'aigu de la param�se, (puis la paran�te, d'un ton plus aigu�[43]), et, � la suite, plus aigu� d'un ton, la n�te des n�tes disjointes, de laquelle on fit � son tour le commencement du t�tracorde des n�tes hyperbol�ennes, comme �tant aussi le terme et la corde la plus aigu� du t�tracorde des n�tes disjointes et le commencement, en m�me temps que la note la plus grave, du t�tracorde des n�tes hyperbol�ennes.

��.[44]

A la suite de cette note, on pla�a la trite des n�tes hyperbol�ennes, plus aigu� qu'elle d'un demi-ton. Puis, � la suite, on pla�a la paran�te, �loign�e d'un ton de la trite; puis, � l'aigu, la n�te des n�tes hyperbol�ennes, �loign�e d'un ton de la pr�c�dente, et devenue la limite du second syst�me, appel� (syst�me) en disjonction.

��.[45]

VII

Dans le petit syst�me (dit) syst�me en conjonction, il y a trois t�tracordes conjoints les uns aux autres moyennant deux sons, la m�se et l'hypate des moyennes. Le proslambanom�ne est en dehors.

Les valeurs[46] des sons (dans ce syst�me) sont au nombre de onze, savoir :

Proslambanom�ne ;

Hypate des hypates;

Parhypate des hypates;

Lichanos des hypates ;

Hypate des moyennes;

Parhypate des moyennes;

Lichanos des moyennes;

M�se;

Trite des n�tes conjointes;

Paran�te des n�tes conjointes;

N�te des n�tes conjointes.

Dans le grand syst�me, appel� syst�me en disjonction, les t�tracordes sont au nombre de quatre, savoir : t�tracordes des hypates et des moyennes, plus deux t�tracordes des n�tes. Parmi ces t�tracordes, ceux des hypates et des moyennes sont conjoints l'un � l'autre moyennant un son commun, l'hypate des moyennes, et ils sont mis en disjonction avec les autres par le ton qui va de la m�se � la param�se. Les deux autres t�tracordes sont n�cessairement en disjonction avec les (deux) premiers moyennant le m�me ton; mais ils sont en conjonction l'un avec l'autre moyennant un son commun, la n�te des disjointes, et, semblablement,[47] le proslambanom�ne est situ� en dehors de ces t�tracordes.

Les valeurs des sons (dans le grand syst�me) sont au nombre de quinze :

Proslambanom�ne ;

Hypate des hypates;

Parhypate des hypates;

Lichanos des hypates ;

Hypate des moyennes;

Parhypate des moyennes ;

Lichanos des moyennes ;

M�se;

Param�se ;

Trite des n�tes disjointes;

Paran�te des n�tes disjointes;

N�te des n�tes disjointes;

Trite des n�tes hyperbol�ennes;

Paran�te des n�tes hyperbol�ennes ;

N�te des n�tes hyperbol�ennes.

Ainsi donc la r�union des deux syst�mes porte le total des valeurs de sons au nombre de vingt-six, d'entre lesquelles huit sont communes aux deux syst�mes jusqu'� la m�se inclusivement.[48] Par cons�quent, les valeurs se rapportent en tout � dix-huit sons avec lesquels s'ex�cute un chant quelconque par la voix, sur la fl�te et sur la cithare, en un mot toute sorte de m�lodie. Au surplus, les explications qui pr�c�dent seront rendues encore plus claires par le diagramme ci-dessous, dans lequel sont r�unis les deux syst�mes conjoint et disjoint.[49]

��..[50]

Cette combinaison et classification des sons s'applique au genre diatonique, mais ces d�nominations subsistent[51] dans tous les genres, sauf que, pour les sons mobiles, dans le cas d'un changement de genre, on ajoute en chacun d'eux une qualification propre � la d�nomination commune, telle que parhypate � enharmonique[52] �, lichanos � chromatique �, lichanos � diatonique �. Ce qu'on vient de dire sera plus �vident par la suite.

VIII

Parmi les sons m�lodiques, les uns sont homophones, les autres consonants, (d'autres dissonants[53]), d'autres encore paraphones.

Les sons homophones sont ceux qui ne diff�rent entre eux ni par la gravit� ni par l'acuit�.

Les sons consonants sont tels que' lorsqu'ils sont �mis simultan�ment, soit sur des instruments � cordes, soit sur des instruments � vent, le chant d'un son plus aigu par rapport � un son plus grave ou d'un son plus grave par rapport � un son plus aigu est toujours le m�me,[54] comme s'il se produisait pour l'oreille l'illusion d'une fusion et d'une sorte d'unification dans l'�mission des deux sons; c'est alors que nous disons qu'ils sont consonants.

Les sons dissonants sont tels que lorsqu'ils sont �mis simultan�ment sur des instruments � cordes ou sur des instruments � vent, aucune partie du chant, dans son rapport du grave � l'aigu ou de l'aigu au grave, ne para�t �tre la m�me; ou encore, tels que, lorsqu'ils sont �mis simultan�ment, il ne se manifeste aucune fusion entre eux.

Les sons paraphones sont interm�diaires entre le consonant et le dissonant; mais quand on les fait entendre sur un instrument,[55] ils donnent la sensation du consonant[56] ; tel est l'effet produit avec un intervalle de trois tons, celui (par exemple) de la parhypate des moyennes � la param�se,[57] et avec un intervalle de deux tons (tel que) celui de la diatonique des moyennes � la param�se.

IX

Les consonances, dans le syst�me parfait, sont au nombre de six. La premi�re est la quarte (diatessaron); la seconde, la quinte (diapente), laquelle surpasse la quarte de l'intervalle d'un ton. De l� vient que quelques-uns ont d�fini l'intervalle toni� �la diff�rence en grandeur des deux premiers consonants[58] �. La troisi�me consonance se compose des deux pr�c�dentes; c'est l'octave (diapason[59]). En effet la quinte ajout�e � la quarte rend les sons extr�mes consonants entre eux.[60] Ce mode de consonance est appel� octave (diapason). La quatri�me consonance est la r�union de l'octave et de la quarte[61] ; la cinqui�me, la r�union de l'octave et de la quinte; la sixi�me, la double octave (disdiapason).

On peut concevoir d'autres consonances en combinant celles-l� entre elles; mais les instruments ne pourraient en supporter la tension (l'intonation). On a donc �gard � la puissance des instruments et de la voix humaine, qui nous servent � n'�tablir en tout que six consonances.[62]

La consonance de quarte, dans un genre quelconque de la m�lodie, comprend ainsi 4 sons, 3 intervalles, 2 tons �, 5 demi-tons. Semblablement, la consonance de quinte comprend, dans tous les genres, 5 sons, 4 intervalles, 3 tons �, 7 demi-tons. La consonance d'octave comprend 8 sons, 7 intervalles, 6 tons, 12 demi-tons. La quarte redoubl�e (diapason et diatessaron) comprend 11 sons, 10 intervalles, 8 tons �, 17 demi-tons. La quinte redoubl�e (diapason et diapente) comprend 12 sons, 11 intervalles, 9 tons �, 19 demi-tons.

La double octave comprend 15 sons, 14 intervalles, 12 tons, 24 demi-tons.

��.[63]

X

On a trouv� dans certains nombres les rapports des consonances et l'on a calcul� exactement, par toute sorte de proc�d�s, que le rapport de la quarte[64] est sesquitiers, celui de 24 � 1 8 ; le rapport de la quinte, sesquialt�re, celui de 24 � 16 ; le rapport de l'octave, double comme celui de 24 � 12 ; le rapport de la quarte redoubl�e diplasi�pidim�re (8/3),[65] celui de 24 � 9, et, � son tour, le rapport de la quinte redoubl�e, triple, celui de 24 � 8; le rapport de la double octave, quadruple, celui de 24 � 6.

��.[66]

XI

Quant � la d�couverte de ces rapports, on raconte que Pythagore en saisit le principe par hasard un jour qu'il passait devant une forge. Il constata que la percussion des marteaux sur l'enclume donnait des sons, les uns dissonants, les autres consonants. Aussit�t qu'il fut entr� (dans la forge), il recherchait la cause de la dissonance[67] et de la consonance produite par les coups de marteau, et voici celle qu'il d�couvre en voyant que les marteaux[68] �taient de poids diff�rents, et que les rapports des grandeurs constat�s dans les poids �taient la cause de la dissonance et de la consonance des sons produits. En effet, il trouve que les (marteaux) qui ont entre eux, dans leurs poids, un rapport sesquitiers, donnent un son consonant � la quarte; quant � ceux qui ont entre eux un poids en rapport sesquialt�re, il reconna�t que leur percussion produit la consonance de quinte; consid�rant ceux qui ont entre eux un poids double (2/1), il s'aper�oit qu'ils donnent des sons accord�s � l'octave[69] dans les intonations.

Partant de l� pour �tablir un principe de corr�lation entre les consonants et les nombres, il porte son investigation sur un autre mode (d'exp�rience). Attachant (� un clou[70]) deux cordes �gales et semblables et de fabrication identique, il suspend � l'une d'elles un poids de 3 parties et � l'autre un poids de 4 parties, et en les frappant toutes deux, il trouve (deux sons) consonnant suivant la consonance dite diatexsaron (quarte). Puis suspendant � l'une et � l'autre des poids sesquialt�res (entre eux), il trouve qu'elles consonnent entre elles suivant la consonance de diapente (quinte); suspendant des poids doubles (l'un de l'autre), il obtint le diapason (octave)[71] et en produisant le rapport triple, il reconnut (la consonance) de diapason et diapente (quinte redoubl�e), et ainsi de suite pour les autres.

Mais il ne se contenta pas de faire cette seule exp�rience : il en v�rifia la m�thode par un autre proc�d�. Tendant une corde sur une r�gle, il divisa celle-ci en douze parties. Alors, frappant d'abord la corde enti�re, puis la moiti� de sa longueur, soit six parties, il trouva que la corde totale sonnait l'octave avec la demi-corde, r�sultat que, par les autres pro.5. c�d�s, il avait reconnu donner le rapport double. Ensuite, frappant la corde enti�re, puis les trois quarts de cette corde, il vit que la consonance produite �tait la quarte. La percussion de la corde totale et de ses deux tiers lui fait trouver la consonance de quinte, et ainsi des autres. Puis apr�s avoir v�rifi� ces faits de beaucoup d'autres mani�res, il trouve que les m�mes rapports de consonance r�sident dans les nombres pr�cit�s.[72]

XII

Il r�sulte de ce qui pr�c�de que l'intervalle toni� (d'un ton) est dans le rapport sesquioctave (9/8). En effet, si le ton est l'intervalle dont la consonance de quarte diff�re de la quinte,[73] on devra �tablir que la quarte correspond aux nombres 6 et 8, la quinte aux nombres 6 et 9[74] ; or, l'exc�s du rapport sesquialt�re sur le sesquitiers est dans le rapport de 8 � 9. De plus, l'exc�s de la quinte sur la quarte est d'un ton; par cons�quent le ton est dans le rapport de 8 � 9.

XIII

L'intervalle appel� demi-ton n'est pas exactement la moiti� d'un ton. On l'appelle commun�ment demi-ton, mais c'est � proprement parler un limma,[75] et il est dans le rapport de 243 � a56. Il faut donc consid�rer, d'abord que le soi-disant demi-ton est dans le rapport de 243 � a 56, puis, que le rapport de 243 � 256 comprend un intervalle moindre que le demi-ton.[76] En effet, soit donn�e une valeur de son repr�sent�e par le nombre 64, et rapproch� de ce son[77] un son qui -ml. 16. en est distant d'un ton, c'est-�-dire repr�sent� par le nombre 72, et (supposons) qu'on en rapproche un troisi�me, �loign� d'un ton du deuxi�me, c'est-�-dire not� 81 ; le quatri�me son, destin� � compl�ter le t�tracorde, consonant n�cessairement � la quarte avec le premier, sera dans le rapport sesquitiers avec 64 ; ce son sera donc repr�sent� par 85 ⅓, et le rapport[78] le sera en nombres entiers, par (la fraction) 256/243, et tous (les sons) qui, en nombres sup�rieurs, apr�s deux sesquioctaves, compl�teront le reste du t�tracorde, le compl�teront � leur tour suivant ce rapport, c'est-�-dire suivant le rapport de 243 � 256.[79]

��.[80]

XIV

Cela consid�r�, il faut avancer de nouveau que ce rapport est inf�rieur � un demi-ton. Le rapport 256/243 est plus petit que le rapport sesqui dix-septi�me (18/17). Le produit de deux rapports sesqui dix-septi�mes l'un par l'autre ne compl�te pas le sesquioctave; de sorte que, d'une part le rapport sesqui dix-septi�me est moindre que la moiti� du sesquioctave,[81] et d'autre part le rapport de 256 � 243, qui est moindre que le sesqui dix-septi�me, serait � bien plus forte raison moindre que la moiti� du sesquioctave. Donc le soi-disant demi-ton est moindre que le demi-ton proprement dit. Voil� pourquoi on l'a nomm� limma et qu'il est dans le rapport de 256 � 243.[82]

Quant � l'intervalle qui manque au limma pour compl�ter le ton, il s'appelle apotome, mais commun�ment demi-ton aussi, de sorte qu'il y aura un demi-ton majeur et un demi-ton mineur.[83] Le genre diatonique emploie le mineur, mais le chromatique, l'un et l'autre.[84]

XV

Cela �tabli, exposons le diagramme diatonique des sons avec les nombres correspondant � chaque son (en attribuant le plus grand nombre au son le plus grave[85]) dans ce m�me diagramme. Dans un autre, c'est le plus petit nombre qui correspondra au proslambanom�ne.

��.[86]

Donc, dans le premier diagramme, le proslambanom�ne �tant plac� sous le nombre 2304,[87] l'hypate des hypates, �loign�e du proslambanom�ne suivant le rapport de 9 � 8, est plac�e sous le nombre 2048.[88] La parhypate des hypates, �loign�e d'un demi-ton de l'hypate, intervalle appel� proprement limma, suivant le rapport de 256 � 243, est plac�e naturellement sous le nombre 1944.[89] Les autres intervalles sont �tablis semblablement selon qu'il s'agit de rapports de tons ou de demi-tons.[90]

Dans le second diagramme, le proslambanom�ne �tant plac� sous le nombre 648, l'hypate des hypates est plac�e cons�cutivement sous le nombre 729.[91] La parhypate est plac�e sous le nombre 768 et tous les autres (intervalles) progressent cons�cutivement par tons et demi-tons d'une fa�on semblable � la progression des premiers, sauf que les nombres proc�dent (ici) des plus petits aux plus grands.[92]

XVI

J'exposerai � la suite le diagramme du genre chromatique synton, portant les sons avec les nombres qui leur correspondent. On y verra clairement que le genre chromatique emploie les deux sortes de demi-ton, le mineur et le majeur, c'est-�-dire le limma et l'apotome.[93] Le proslambanom�ne commence avec le nombre le plus fort, savoir : 20736. Vient ensuite l'hypate.[94]

��.[95]

XVII

Parmi les dix-huit sons, les uns sont stables et les autres mobiles. Les sons stables sont :

Le proslambanom�ne;

L'hypate des hypates;

L'hypate des moyennes;

La m�se;

La n�te des n�tes conjointes ;

La param�se;

La n�te des n�tes disjointes;

(La n�te des n�tes hyperbol�ennes[96]).

Les sons mobiles sont :

Les parhypates;

Les lichanos ;

Les trites;

Les paran�tes.

(Ils sont mobiles) en ce que dans les modifications[97] de genres, ils modifient leur propre tension. Voil� pourquoi on ajoute au nom commun[98] un nom particulier emprunt� � celui de chaque genre. C'est ainsi que l'on dit, par exemple : � lichanos des moyennes enharmonique, lichanos des moyennes chromatique, lichanos des moyennes diatonique. � II en est de m�me pour la d�nomination des paran�tes, des parhypates et des trites.

XVIII

Je reviendrai encore sur les syst�mes.

Les formes ou esp�ces des t�tracordes sont au nombre de trois. Elles se produisent lorsque, �tant conserv�s l'�tendue d'un t�tracorde et le nombre de ses intervalles, il n'y a que son ordonnance et sa composition qui �prouvent une alt�ration. La premi�re esp�ce est celle qui va de l'hypate des hypates � l'hypate des moyennes; dans cette esp�ce le demi-ton est le premier intervalle au grave.

La seconde va de la parhypate des hypates � la parhypate des moyennes; le demi-ton y occupe le troisi�me rang � l'aigu. La troisi�me va de la lichanos � (l'autre) lichanos; le demi-ton y est plac� au milieu. Les autres (combinaisons[99]) sont semblables � celles-ci.

Les formes ou esp�ces de la quinte sont au nombre de quatre. La premi�re esp�ce est celle qui va de l'hypate des moyennes � la param�se; le demi-ton s'y trouve au premier rang au grave.

La deuxi�me esp�ce va de la parhypate des moyennes � la trite des disjointes; le demi-ton s'y trouve au dernier rang � l'aigu.

La troisi�me esp�ce va de la lichanos des moyennes � la paran�te des disjointes; le demi-ton y occupe le second rang � partir de la fin.

La quatri�me esp�ce va de la m�se � la n�te des disjointes; le demi-ton y occupe le dernier rang � partir du commencement.

��..[100]

XIX

Les formes ou esp�ces du diapason octacorde (quarte) sont en tout au nombre de douze, par cette raison que la quarte a trois formes et la quinte quatre, comme on vient de le montrer, et que l'octave est form�e de leur r�union; mais les formes ou esp�ces m�lodiques et consonantes sont au nombre de sept. Nous en donnerons la raison plus tard.[101]

La premi�re esp�ce est celle qui va de l'hypate des hypates � la param�se; elle se compose de la premi�re esp�ce de la quarte et de la premi�re de la quinte.

La deuxi�me va de la parhypate des hypates � la trite des disjointes; elle se compose de la deuxi�me esp�ce de la quarte et de la deuxi�me de la quinte.

La troisi�me esp�ce va de la lichanos des hypates � la paran�se des disjointes; elle se compose de la troisi�me esp�ce de la quarte et de la troisi�me de la quinte.

��..[102]

La quatri�me esp�ce va de l'hypate des moyennes � la n�te des disjointes; elle se compose de la premi�re esp�ce de la quinte et de la premi�re de la quarte.

La cinqui�me esp�ce va de la parhypate des moyennes � la trite des hyperbol�ennes; elle se compose de la deuxi�me esp�ce de la quinte et de la deuxi�me de la quarte.

La sixi�me esp�ce va de la lichanos des moyennes � la paran�te des hyperbol�ennes ; elle se compose de la troisi�me esp�ce de la quinte et de la troisi�me de la quarte.

La septi�me esp�ce va de la m�se � la n�te des hyperbol�ennes, ou du proslambanom�ne � la m�se; elle se compose de la quatri�me esp�ce de la quinte et de la premi�re de la quarte, ou, inversement, de la troisi�me de la quarte et de la quatri�me de la quinte.

La premi�re esp�ce de l'octave s'appelle mixolydienne;

La deuxi�me, lydienne;

La troisi�me, phrygienne ;

La quatri�me, dorienne;

La cinqui�me, hypolydienne ;

La sixi�me, hypophrygienne;

Quant � la septi�me, elle a �t� appel�e commune, locrienne, et hypodorienne.[103]

��...[104]

XX

Les anciens ont eu recours, pour d�signer les dix-huit sons, � des d�nominations (particuli�res[105]) et � des lettres appel�es signes musicaux, dont c'est le moment de parler. L'�tablissement des signes musicaux a eu pour but la notation des sons, afin que l'on n'e�t pas � �crire le nom de chacun d'eux, mais que l'on p�t distinguer et noter tel ou tel son par un signe unique. Et comme les sons changent (de valeur) suivant leurs divers degr�s de tension et ne restent pas absolument � la m�me place, il a fallu, par suite, non pas un seul signe pour chaque son, mais des signes vari�s, de fa�on � pouvoir noter les diff�rences de tension; car, dans chaque trope ou ton, tous les sons sans exception deviennent diff�rents par la tension.[106] Par exemple, tant�t nous posons le proslambanom�ne, son le plus grave par nature, ce qui est le cas dans le trope hypodorien, et la m�se, son antiphone (son octave), et nous d�nommons les autres sons d'apr�s leur rapport avec ceux-ci; tant�t, donnant � la m�se elle-m�me, actuellement antiphone du proslambanom�ne, le rang de proslambanom�ne, et pla�ant ensuite la m�se, antiphone de celle-ci, et les autres sons en rapport avec ces derniers,[107] nous employons ainsi le syst�me tout-entier.

Souvent aussi, prenant un des sons compris entre le proslambanom�ne et la m�se,[108] comme son initial d'un syst�me, nous l'employons comme proslambanom�ne et nous rapportons � ce son l'intonation de tout le syst�me.[109] Or, dans chaque syst�me, lorsqu'il y a plusieurs syst�mes avant (le syst�me donn�), le rapport qui existe entre la m�se (de l'un) et la m�se (de l'autre) ou entre proslambanom�ne (et proslambanom�ne[110]) existe aussi entre une note homonyme et son homonyme, comme aussi entre syst�me et syst�me. On a donc eu besoin, non pas d'un signe unique pour chacun des sons, mais de plusieurs, en aussi grand nombre qu'il y a de demi-tons dont peut progresser chacun des sons. Quant au nombre des demi-tons dont peut �tre �lev�[111] chacun des sons, il n'est pas facile � d�terminer, car cette d�termination est subordonn�e � la facture des divers instruments et � la puissance de la voix humaine.[112]

Comment il se fait qu'un son �lev� progressivement est not� par autant de signes diff�rents, on le comprendra facilement � l'inspection des diagrammes contenus dans les (introductions[113]) musicales.

XXI

Maintenant, il faut voir seulement[114] de quelle fa�on est �tabli le classement des signes par demi-tons. Soit donn�e telle valeur de son comme �tant la plus grave et (en m�me temps) la premi�re perceptible � l'oreille.[115] Les anciens l'ont not�e au moyen d'un demi-phi couch� [116] et l'ont pos�e comme signe initial. Or il est �vident que cette valeur m�me est assign�e au proslambanom�ne, et non pas � un autre son. En effet, si elle l'�tait � quelque autre, o� placerait-on le proslambanom�ne, puisque le demi-phi est le signe de la valeur la plus grave? Soit donn� � la suite un son plus aigu � son tour d'un demi-ton. Les anciens l'ont not� du signe tau T, et il est clair que le classement de ce son convient au seul proslambanom�ne.[117] En effet, s'il est rapport� � l'hypate ou � quelque autre son, o� placera-t-on par suite le proslambanom�ne, lui qui doit �tre plus grave d'un ton que l'hypate des hypates, puisqu'on n'a laiss� qu'une seule place au demi-ton dans le grave[118] ? Soit donn� maintenant un son plus aigu d'un demi-ton que le son not� tau, son que les anciens ont not� au moyen du double sigma 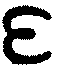. Ce son peut �tre lui aussi le proslambanom�ne d'un syst�me,[119] mais il peut �tre en outre une hypate des hypates,[120] car il est distant d'un ton du son initial le plus grave.

Ainsi donc, en notant toujours d'apr�s la m�me m�thode le son plus aigu d'un demi-ton (que le pr�c�dent), ils (les anciens) ont poursuivi la progression jusqu'� la trenti�me rang�e de demi-tons,[121] et ils exprim�rent au moyen des m�mes signes les notes comprises dans la suite de cette progression des sons par demi-ton, en y ajoutant des accents aigus � partir de la dix-neuvi�me rang�e qui a pour signes

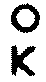
Ils plac�rent un double signe dans chaque rang�e : le signe sup�rieur sert � noter les paroles, et le signe inf�rieur, le jeu instrumental.

Ils plac�rent aussi[122] les signes appel�s homotones[123] qu'il est loisible d'employer indiff�remment � la place des autres; et (en effet) il n'importera aucunement d'employer pour la notation un quelconque des signes quand il y en a plusieurs qui sont homotones.[124] Mais les signes homotones pr�sentent encore un autre avantage : c'est que les di�sis sont not�s au moyen de ces signes, plac�s cons�cutivement, dans les genres enharmonique et chromatique.[125] On s'est expliqu� � leur sujet dans les Introductions.

XXII

Exposons maintenant, en un tableau, les signes (se succ�dant) par demi-tons avec leurs homotones, en pla�ant les homotones respectivement dans la m�me colonne, et les sons plus aigus d'un demi-ton � la suite.

��...[126]

La premi�re rang�e de notes, qui indique parmi les sons la valeur la plus grave,[127] a pour signes le demi-phi couch� et le demi-phi (couch�) retourn� .

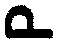La deuxi�me rang�e, plus aigu� d'un demi-ton que le premier son, a pour signes l�upsilon couch�, retourn� et l�upsilon couch�, 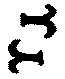.[128] Les signes homotones, c'est-�-dire notant parmi les sons la m�me valeur, sont le tau couch�, retourn� et le tau droit, .

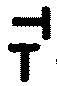La troisi�me rang�e, d'un demi-ton plus aigu� que la seconde, suivant le rapport des rang�es successives, a pour signes le double sigma retourn� et le double sigma, .

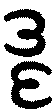La quatri�me rang�e a (pour signes) le rho (renvers�[129]) et (le double sigma couch�) 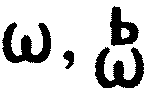; et leurs homotones sont dans la premi�re rang�e[130] le pi renvers� et le double sigma retourn�, .

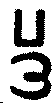La cinqui�me rang�e, qui est semblablement plus aigu� d'un demi-ton que la quatri�me, � car toutes les rang�es cons�cutives sont distantes entre elles d'un demi-ton, � a pour signes un omicron portant une barre � sa partie inf�rieure et un �ta, .

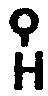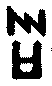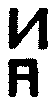La sixi�me rang�e a (pour signes) un double xi renvers� et un double pi renvers�, . Leurs homotones sont l�antinu et le double pi, .[131] (Manquent les neuf rang�es suivantes.)

*****************************

Viennent ensuite (chap. xxiii de l'�dition G. de Jan) dans les manuscrits de Gaudence et dans l'�dition de Meibom, les tableaux, pour le genre diatonique, des tropes hypolydien, hyperlydien, �olien et hypo�olien, ce dernier interrompu apr�s l�hypate des moyennes. Nous jugeons inutile de reproduire ces tableaux, qui ne diff�rent de ceux d'Alypius que par des variantes sans importance, et dont l'attribution � Gaudence nous para�t d'autant plus douteuse que notre auteur, un peu plus haut (p. 22, Meibom au d�but), semble renvoyer le lecteur aux trait�s th�oriques contenant ces sortes de tableaux plut�t qu'� son propre ouvrage. � Voir l'Avertissement.

(suite)

[1] �Αείδω (alias ἀείξω) ξυνετοῖσι θύρας δ' ἐπιθεσθε, βέβηλοι, Cp. Orphica, p. 448, G. Hermann, p. 144, Abel :

Φθέξομαι οἷς θέμις ἐστὶ * θύρας δ' ἐπιθεσθε, βέβηλοι

πάντες ὁμοῦ (alias ὁμῶς).

Ce fragment orphique a �t� cit� souvent par les �crivains pa�ens et chr�tiens avec ou sans la variante βεβήλοις πᾶσιν ὁμοῦ. Les divers manuscrits de Cl�ment d�Alexandrie donnent l�une et l�autre. Au surplus, voici une note int�ressante et assez compl�te sur la question, tir�e de l��dition b�n�dictine de Justin, martyr (1762), p. 18 : Grotius (De Veritate, 1. 1) legit βεβήλοις. Fronto Ducaeus in notis ad Tatianum [p. 34] eodem modo legendum censet. Plerique codices Tatiani βεβήλοις. Sic etiam habent Clemens Alexandrinus, in Cohortat., p. 48, et Theodoretus, serm. I, De curandia Graec. affect., p. 478 et 483. Lectionem Clementis [βεβήλοις] tuentur Hoeschel et Polter vin doctissimi. Sed tamen retinendum esse βεβήλοι patet ex Aristobulo qui apud Eusebium, Praepar. evang., l. XIII, hunc versum addit a Justino omissum:

φεύγοντες δικαίων θεσμοὺς θείοιο τεθέντος

πᾶσι νόμου.

� Ex his postremis verbis ortum est illud πάντες ὅμως quod apud Justinum et Clementem legitur, vel πᾶσιν ὁμῶς, quod in nonnullis Clementis codicibus manu scriptis exstare testatur Hoeschelius. Iidem versus occurrunt iterum in libris De Monarchia [Justini]. Legunt βεβήλοι Porphyrius apud Eusebium Praepar. evang. III, 7, Cyrillus I, Julianus, p. 26. � �Voir ci-dessous la note 3. � Annotation de C. de Jan : �Justinus (vel potius Apollinarius Laodicensis) in Cohortatione ad Graecos, c. 15, haec verba citat �, etc.

[2] Cette classification des parties de l'harmonique ou de la science des sons se rencontre pour la premi�re fois chez Aristox�ne (El�ments harmoniques), puis chez Cl�onide ou le pseudo-Euclide (Introduction harmonique).

[3] Cp. Platon, Banquet, p. 218 b : Οἱ δ'οἰκέται καὶ εἴ τις ἄλλος ἐστὶ βέβηλός τε καὶ ἄγροικος, πύλας πάνυ μεγάλας τοῖς ὡσὶν ἐπίθεσθε. Scholie : 'Εντεῦθεν παρώδησε Καλλίμαχος ἐν ὕμνῳ Δήμητρος καλάτου τὸ � θύρας δ' ἐπιθεσθε, βέθηλοι �.

[4] Il ne faut pas confondre le lieu de la voix ou son �tendue, avec le lieu d'un son, c'est-�-dire le degr� qu'il occupe dans l'�chelle m�lodique. (Cp. le chapitre II.)

[5] Cp. Aristox�ne, El�ments harmoniques, p. 8. Meibom.

[6] Autrement dit, soit �lev�e, soit abaiss�e.

[7] Tension (τάσις), c'est ce que nous appelons degr� d'intonation, par analogie avec la tension des cordes sonores.

[8] Ne produira pas de sons contigus entre eux.

[9] Nous supprimons les mots ἐν τοῖς πέρασι... qui paraissent �tre une glose marginale destin�e � expliquer les mots ἐν τοῖς ὅροις et introduite abusivement dans le texte.

[10] Ῥητοῖς χρώμενον διαστέμασι. Nous dirions en langage moderne � des intervalles justes �.

[11] D�termin�s par la constitution des �chelles m�lodiques.

[12] L'auteur semble vouloir faire entendre que le m�lodique et le non m�lodique sont le contraire l'un de l'autre, mais qu'ils ne diff�rent pas entre eux comme le chant non m�lodique, par exemple, diff�re de la voix parl�e.

[13] Par analogie avec la surtension et le rel�chement d'une corde sonore.

[14] Cp. Aristox�ne, El. harm., p. 9 et suiv.

[15] On voit que nous corrigeons εἶναι en ἱέναι. On trouve dans Platon ἱέναι φωνήν (Lois, X, p. 890 D).

[16] Un temps (χρόνον), une dur�e.

[17] Nous lisons comme Meibom βραχυτέρους au lieu de βραδυτέρους, et plus loin μέλη au lieu de μέρη.

[18] Note de Meibom : �Exempli causa, parhypate enarmonii generis et chromatici in eodem loco esse videntur; revera tamen non sunt. Differant itaque colore, etc. Vide Euclidem, p. 10, vers. 17.� Il n'y a aucun rapport entre la χρόα dont parle Gaudence et celle du pseudo-Euclide. Celui-ci �num�re les nuances des genres diatonique et chromatique, tandis que Gaudence, � notre avis, entend par χρόα la couleur de la voix dans le sens o� Aristote mentionne les voix λευκήν, μελαίναν, φαίαν, σουφήν (Topiques, 15); ἀμαυράν (pseudo-Aristote, De audibilibus, p. 802). Aristote qualifie la voix blanche εὐήκοον. Cp. Sextus Empiricus, Adversus Mathematicos, VI, p. 133 E, qui parle des voix φαιά, μέλαινα et λευκή.

[19] Le ton n'est pas une vari�t� de syst�me quelconque, mais tant�t une des formes de l'heptacorde ou de l'octacorde, tant�t une �chelle de transposition. Ce double sens, attribu� au mot τόνος, a jet� un grand trouble, m�me chez lc9 anciens, dans l'histoire de la musique grecque.

[20] Di�sis (δίεσις), division (du ton en quarts de ton, en tiers de ton, etc.).

[21] Trih�miton, intervalle de tierce mineure.

[22] Diton, intervalle de tierce majeure.

[23] C'est-�-dire le rang occup� par une s�rie r�guli�re de dix-huit sons dans l'�chelle g�n�rale des sons m�lodiques, laquelle comprend trois octaves, plus l'intervalle d'un ton.

[24] Meibom estime que ce titre doit �tre supprim�; que la suite est la continuation du chapitre pr�c�dent, et que celui qui concerne les syst�mes a �t� perdu. Sans aller aussi loin que Meibom, nous inclinons � croire qu'il vaudrait mieux intituler la section pr�c�dente � sur les intervalles et les syst�mes �. Le passage d'Aristox�ne relatif aux intervalles et aux syst�mes (El. harm., p. 16-17) autorise cette mani�re de voir. La d�finition du syst�me dans le texte de Gaudence et la phrase qui la suit est pour nous une preuve qu'il ne manque rien.

[25] Nous lisons comme Meibom διαστημάτων au lieu de συστημάτων, qu'un copiste trop intelligent aura cru devoir adopter sur la foi du titre de ce chapitre.

[26] (Parmi les m�lodiques.) Lu ἐμμελῶν au lieu de μελῶν, correction de Meibom confirm�e par le Marcianus V (Jan), par le manuscrit de Paris 2456 et par celui de l'Escurial φ, II, 5.

[27] 'Ασύμφωνα. Nous disons plut�t � dissonants �.

[28] L'intervalle � premier ou incompos� � est, comme on va le voir, celui qui- pour parler notre langue musicale, s�pare deux degr�s conjoints.

[29] Il y a cependant une diff�rence essentielle entre l'intervalle compos� et le syst�me. Tous deux comprennent a la v�rit� plusieurs intervalles; seulement, dans le syst�me, on consid�re les divers sons qu'il renferme, tandis que dans l'intervalle compos� l'on n'a �gard qu'aux deux sons extr�mes. L'intervalle incompos� est form� par ce que nous appelons deux degr�s conjoints.

[30] Σύντονος, tendu, aigu, dur. Les intervalles du t�tracorde dans ce genre sont obtenus par les cordes mobiles les plus aigu�s.

[31] Il semble, d'apr�s les mots καὶ αὐτό, que les deux vari�t�s du genre diatonique (voir Aristox�ne, El. harm., p. 51) auraient d� �tre mentionn�es en t�te de ce paragraphe.

[32] Le tableau annonc� par ce titre manque dans les manuscrits dont quelques-uns, notamment le Vaticanus 191, le ms. de l'Escurial φ, II, 5 (n� 199 du catalogue Miller) et le Parisinus 2456, lui ont r�serv� un espace blanc, mais la planche II, dans notre �dition d'Aristox�ne (El. harm.), conform�e au texte de cet auteur (p. 25 Meibom), peut en donner une id�e exacte.

[33] Dans la terminologie musicale des anciens Grecs, le mot ἁρμονία signifie suivant le cas : 1� l'�chelle m�lodique totale, comme dans ce passage; 2� l'�chelle de sept ou de huit sons, compos�e de deux t�tracordes. soit conjoints, soit disjoints; 3� le genre enharmonique.

[34] Προσλαμβανόμενος (φθόγγος), son ajout� (au grave du t�tracorde le plus grave).

[35] Un son grave par nature (φύσει) l'est absolument, tandis qu'un son grave par position (θέσει) est grave par rapport aux sons qui, dans une �chelle m�lodique donn�e, sont plus aigus que lui. Tel son peut encore �tre envisag� sous le rapport de sa puissance, ou valeur (δυνάμει), c'est-�-dire quant � la fonction qu'il occupe dans une �chelle m�lodique donn�e. Pour que la fonction d'une note soit d�termin�e, il faut que cette note re�oive, outre son nom particulier, celui du t�tracorde, du genre et du ton ou trope dans lesquels elle est plac�e.

[36] Place pour un tableau dans les manuscrits. � Voir � la fin de ce trait� le tableau n� 1.

[37] T�tracorde conjoint. On dit ordinairement τετράχορδον συνημμένων, t�tracorde des (cordes) conjointes.

[38] Dans tout ce passage, les mots συνημμένων, διεζευγμένων et ὑπερβολαίων sont constamment suivis du mot νητῶν (lire νήτων), lequel, suivant Meibom, serait une interpolation d�nu�e de sens, due � quelque savant m�diocre (Sciolus). Ce mot peut fort bien �tre de Gaudence lui-m�me. La premi�re hypate donne son nom au t�tracorde des hypates (ὑπάτων), la m�se � celui des moyennes (μέσων). Semblablement les n�tes ont pu, � l'origine, pr�ter leur nom aux t�tracordes o� elles ont une place et qui seraient diff�renci�s chacun par la particularit� qui le distingue, savoir t�tracordes des conjointes, des disjointes, des hyperbol�ennes. Toutefois il faut reconna�tre que le mot en question n'appara�t d'une mani�re constante chez aucun autre musicographe. Nous ne le retrouvons que dans un tableau dress� par Porphyre ( Commentaire sur les Harmoniques de Ptol�m�e, II, vii, p. 352, Wallis), tel que le donne le manuscrit de Paris 2456, mais appliqu� seulement aux trois derni�res notes, en montant, du t�tracorde des hyperbol�ennes, et dans l'Anonyme de Bellermann, � 83 (t�tracorde des conjointes), d'apr�s le manuscrit de Naples 262.

[39] Les manuscrits de Meibom portent ταύτης qu'il corrige en ταύτῃ. Les manuscrits de C. de Jan et le 2456 donnent ταύταις, mais ταύτῃ vaudrait mieux.

[40] Τρίτη, troisi�me (en descendant).

[41] Voir notre tableau n� 2.

[42] On dit aussi τόνος διαζευγτικός, ton disjonctif.

[43] Nous abr�geons l'addition de C. de Jan : εἶτα παρανήτην τῶν διεζευγμένων νητῶν τόνῃ τρίτης ὀξυτέραν.

[44] Voir notre tableau n� 3.

[45] Voir notre tableau n� 4.

[46] Δυνάμεις.

[47] Semblablement, c'est-�-dire comme dans le petit syst�me.

[48] Le petit syst�me comprend 11 sons, le grand syst�me 15, total 26. Les 8 sons communs aux deux syst�mes sont le proslambanom�ne et les 7 sons compris dans les t�tracordes des hypates et des moyennes.

[49] Le tableau annonc� ici manque dans tous les manuscrits de Gaudence. Il devait �tre l'�quivalent de celui que contient notre traduction d'Aristox�ne (planche I, 1^�re ligne, genre diatonique).

[50] Voir notre tableau n� 5.

[51] L'addition de Meibom : sont <les m�mes>, est inutile.

[52] Note de Meibom : �Musicorum nemo ita unquam locutus. Lege : λιχανὸς ἐναρμόνιος. Meibom a peut-�tre raison, ma�s la le�on du texte n'a rien d'invraisemblable , attendu que la parhypate enharmonique occupe dans l'�chelle m�lodique un rang qui lui est absolument propre. Wallis (Opera mathematica, t. III, Appendix de veterum harmonica ad hodiernam comparata, p. 155) propose ici une addition : οἷον παρυπάτη ἐναρμόνιος < καὶ παρυπάτη χρωματικὴ, καὶ παρυπάτη διάτονος, καὶ λιχανὸς ἐναρμόνιος > καὶ λιχ. χρωμ. καὶ λιχ. διάτονος. Cette addition n'est pas n�cessaire. Gaudence veut simplement citer quelques exemples � l'appui de son assertion.

[53] Bonne addition de Meibom.

[54] En d'autres termes, deux sons consonants, tout en diff�rant entre eux par le degr� d'intonation, donnent par leur �mission simultan�e la sensation d'un seul et m�me son.

[55] Meibom a lu κράσει au lieu de κρούσει donn� par la vulgate; κρούσει a �t� maintenu � bon droit par C. de Jan. Gaudence, un peu plus haut, n'a parl� que des sons entendus simultan�ment sur des instruments. D'ailleurs l'expression ἐν κράσει, dans le sens de ἐὰν κραθῶσι, serait d'un hell�nisme douteux.

[56] Cette d�finition des sons paraphones diff�re totalement de celle des intervalles paraphones qu'on lit dans Th�on de Smyrne : �Parmi les intervalles, des uns sont consonants, les autres dissonants. Les intervalles consonants sont antiphones, tels que l'octave et la double octave, � ou paraphones, tels que la quinte et la quarte. (Exposition des connaissances math�matiques utiles pour la lecture de Platon, trad. par Jean Dupuis; Paris, 1892, p. 83.) Manuel Bryenne (Harmoniques, I, 5) a copi� le passage de Th�on, et Michel Psellus (Synopsis musica) s'en est inspir�.

[57] Dans le genre diatonique.

[58] Tels sont Aristox�ne, El. harm., p. 21, Euclide, Division du canon, p. 34.

[59] Les mots ἡ διὰ πασῶν pourraient fort bien �tre une glose marginale ins�r�e dans le texte. Le raisonnement qui les suit se rapporte directement � la proposition qui les pr�c�de. Voir dans l'�d. C. de Jan la scholie du ms. de Naples.

[60] En d'autres termes, le son le plus grave d'une quarte sonne l'octave avec le son le plus aigu de la quinte cons�cutive.

[61] Gaudence, ici comme ailleurs, se montre aristox�nien. Les pythagoriciens n'admettaient pas la quarte redoubl�e ou compos�e (onzi�me), par la raison qu'elle est repr�sent�e au moyen d'une fraction non super-particuli�re, mais super-partiente (8/3). Voir notre traduction d'Euclide, Division du canon, p. 44, note 1. Mais plus loin (chap. xiii) il traitera du demi-ton en pythagoricien.

[62] Le manuscrit du Vatican et celui de Naples ajoutent ici : ἐξ ὧν que C. de Jan corrige en ἒξ νόμον. Notre traduction a b�n�fici� de cette correction.

[63] Voir notre tableau n� 6.

[64] C'est-�-dire le rapport de tension, sur un monocorde, entre deux sons accord�s � la quarte.

[65] Διπλασιεπιδίμοιρος λόγος. Th�on de Smyrne (ouvr. cit�, p. 79, Hiller) cite ce rapport comme exemple de λόγος πολλαπλασιεπιμερής.

[66] Voir notre tableau n� 7.

[67] Ici et plus bas nous lisons διαφωνίας au lieu de διαφορᾶς. C. de Jan conserve le mot du texte.

[68] Τὰς σφύρας. � Voir la note suivante.

[69] Le r�cit de cette d�couverte se lit en outre chez Nicomaque, Manuel d'harmonique, p. 10; Jamblique, De Vita pythagorica, I, 6; Macrobe, In Somnium Scipionis; Bo�ce, Institution musicale, I, 10; enfin dans le cinqui�me fragment du texte grec dit de l'Hagiopolite, publi� par A.-J.-H. Vincent, texte qui donne σφαίρας au lieu de σφύρας. Vincent a conclu de cette variante (Notices, etc., p. a66) que l'exp�rience, mal comprise par tous les autres historiens, a �t� faite sur des sph�res (σφαῖραι) ou des vases de forme plus ou moins sph�rique et non sur des marteaux (σφύραι) avec lesquels on les travaillait. � Cp. notre traduction de Nicomaque, p. 19, note 4.

[70] Nous suppl�ons ἀπὸ πασσάλου, d'apr�s ce texte de Nicomaque (op. cit., p. 11): ἀπὸ ἐνὸς πασσάλου . . . ἀπαρτήσας τέσσαρας χορδάς κ. τ. λ.

[71] Le membre de phrase relatif � l'octave manquait dans les manuscrits de Meibom. C. de Jan l'a r�tabli dans son �dition. Il avait �t� restitu� par J. Franz (De musicis graecis, 1840, p. 9), d'apr�s le manuscrit 191 du Vatican, et nous l'avions retrouv� � l'Escurial (ms. φ, II, 5), � Paris (Bibl. nat., n� 2456) et en partie � Florence (ms. Riccardi, n� 41). Cette lacune provient d'un hom�ot�leuton : κρούσας εὑρίσκει συμφωνούσας < αι'τὰς ἀλλήλαις κατὰ τὴν διὰ πέντε συνμφωνίαν * διπλασίονα δὲ ἐπειδὴ τὰ βάρη καθῆψε, διὰ πασῶν εὗρε συμφονούσας > τὰς χορδάς * τριπλάσιον δὲ κ. τ. λ.

[72] En d'autres termes, les rapports num�riques obtenus dans les diverses exp�riences restent les m�mes pour chaque consonance donn�e.

[73] D�finition commune aux aristox�niens et aux pythagoriciens.

[74] L'argumentation de l'auteur suppose la r�solution des nombres 6 et 8 en rapport sesquitiers (4/3) et des nombres 6 et 9 en rapport sesquialt�re (3/2)

[75] Limma, λεῖμμα, reste d'une soustraction

[76] C'est-�-dire moindre que le rapport correspondant au demi-ton.

[77] Dans le sens de l'aigu au grave.

[78] Le rapport du quatri�me son avec le troisi�me, c'est-�-dire le rapport de l'intervalle compl�mentaire du t�tracorde avec le rapport du soi-disant demi-ton. Il nous semble inutile d'ajouter ici, comme le fait C. de Jan (apr�s πε καὶ τρίτου) : καὶ ὁ τέταρτος ἄρα φθόγος < πρὸς τὸν τρίτον λόγον ἕξει τῶν πε γ' πρὸς τὰ πα > ὅπερ ἐστὶν κ. τ. λ.

[79] Le rapport du quatri�me son du t�tracorde (diatonique) avec le troisi�me est repr�sent� par 85 ⅓ : 81. En multipliant ces deux nombres par le d�nominateur 3 (afin de convertir le nombre fractionnaire en fraction simple), on obtient en effet la fraction 256/243.

[80] Voir notre tableau n� 8.

[81] 18�/17� = 324/289 < (9/8)/2

[82] Note de C. de Jan : 17/18 = 192/203, 243/256 = 192/ 202

[83] Pour les pythagoriciens, le limma est le demi-ton mineur et l'apotome est le demi-ton majeur.

[84] On verra dans notre tableau n� 10 comment se r�partissent les demi-tons majeur et mineur dans le genre chromatique.

[85] Addition de Meibom. C. de Jan suspecte l'authenticit� de la phrase suivante. � Meibom propose une autre lecture de tout le passage : ἀριθμῶν] ἐν μὲν τῷ πρώτῳ διαγγράματι τοῦ μείζονος ἀριθμῶν * ἐν δὲ δευτέρῳ, τοῦ ἐλάσσονος πρὸς τῷ προσλαμβανομένῳ τιθεμένου. Nous conjecturons cette autre r�daction : ἀριθμῶν] < τοῦ μείζονος > ἐν τοῦτῳ τῷ διαγγράματι, ἐν ἄλλῳ δὲ τοῦ ἐλάσσονος πρὸς τῷ προσλαμβανομένῳ τιθεμένου. Cp. l'�d. C. de Jan.

[86] Voir ces deux diagrammes dans notre tableau n� 9, A et B.

[87] En choisissant le nombre 2304, Gaudence a obtenu des multiples de 9 et de 8 en nombre suffisant pour les quatorze intervalles compris dans le syst�me disjoint.

[88] 9 / 8 = 2304 / 2048.

[89] 256/243 = 2048/1944. Les manuscrits donnent 1764. Correction de Meibom.

[90] Nous avons reproduit ce premier diagramme sur les donn�es de Meibom, en nous conformant plus exactement que lui � la disposition suivie par Gaudence.

Dans le genre diatonique de Gaudence le petit intervalle d'un t�tracorde est un demi-ton mineur ou limma dont le rapport (256/243) est obtenu en divisant la quarte (4/3) par le diton (9�/8� = 81/64) soit 256/243. On sait qu'en acoustique, pour soustraire une petite fraction d'une plus grande, on divise la deuxi�me par la premi�re, et que pour additionner deux rapports on les multiplie l'un par l'autre.

[91] 8/9 = 648/729. Dans ce second diagramme, Gaudence renverse les rapports �tablis dans le premier. Richter (De musica arte Graecorum, Munster, 1856, p. 12-21) a cru trouver dans ce passage de notre auteur un argument de plus � l'appui de sa th�orie, d'apr�s laquelle le diagramme aurait �t� dispos� dans les deux sens, de telle sorte que le proslambanom�ne aurait �t� pour les instruments le son le plus grave, et pour la voix le son le plus aigu. C'est une erreur fondamentale, d�j� commise par Drieberg (Aufschl�sse �ber die Musik der Griechen, p. 6 et suiv. ; � voir aussi les pages 21, 76 et 128 de son W�rterbuch der griech. Musik). Gaudence se borne � dire que les rapports des sons qui composent le diagramme peuvent �tre not�s par deux progressions inverses, l'une dans laquelle c'est le nombre minimum qui est affect� � la note la plus aigu�, l'autre o� c'est le nombre maximum. Il n'�tablit aucun rapport entre chaque son et le nombre de vibrations de la corde qui le produit. Les anciens, pour �valuer les degr�s d'intonation des sons, ne consid�raient pas ce nombre, mais simplement la longueur de cordes tendues �galement ou le degr� de tension de cordes de longueur identique. En r�sum�, dans le premier diagramme, Gaudence nous parait avoir voulu exposer la progression d�croissante, du grave � l'aigu, des portions d'un monocorde frapp�es isol�ment, et, dans le deuxi�me, la progression croissante des poids suspendus � une corde.

[92] Dans ce deuxi�me diagramme, restitu� par Meibom d'apr�s l'explication de Gaudence et transform� ici, comme le premier, dans le sens de cette explication, Meibom a figur� les fractions des deux diagrammes par 9/8 et 256/243 au lieu de 8/9 et 243/256. Il n'a pas vu, semble-t-il, que les fractions doivent �tre renvers�es dans le second. Richter (op. cit., p. 19) est tomb� dans la m�me m�prise. Meibom aurait pu dire qu'il avait trouv� les �l�ments de sa restitution dans les manuscrits de l'Anonyme publi� par Bellermann (� 96 de son �dition), p. 40 de la traduction de Vincent, o�, pour le dire en passant, les nombres sont r�duits de moiti�.

[93] Dans chaque t�tracorde du genre chromatique synton, le demi-ton grave est un limma, ou demi-ton mineur, et le demi-ton aigu, une apotome ou demi-ton majeur.

[94] Vient ensuite l'hypate. Le texte grec dit : 'Εξῆς ἡ πάτω. Vatic. 191 : 'Εξῆς ἡ 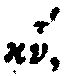, alt�ration probable de 'Ε, ἡ 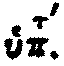Correction de Meibom : 'Εξῆς ἡ ὑπάτη. Les notes de Meibom sur Euclide, p. 68, contiennent une restitution des calculs relatifs � ce diagramme. Nous les reproduisons (tableau n� 10), apr�s v�rification comme les pr�c�dente, et avec quelques modifications.

Nous avons expliqu� plus haut (note 2 de la page 75) comment le limma est repr�sent� par la fraction 256/243. L'apotome, qui forme un ton complet avec le limma, est, en cons�quence, repr�sent�e par la formule

(9/8) / (256/243), Soit (9/8 x 243/256) = 2187/2048

[95] Voir notre tableau n� 10.

[96] Restitu� par les manuscrits de C. de Jan, par le 2456 de Paris, par celui de l'Escurial et conjecturalement dans les notes de Meibom (moins le mot νητῶν qu'il n'admet pas comme authentique).

[97] Meibom corrige μεταβολαῖς en διαφοραῖς, correction au moins inutile. Il nous semble que l'auteur a rapproch� avec intention μεταβολαῖς et μεταβάλλουσιν. Il est vrai que l'expression διαφοραὶ γενῶν se rencontre chez d'autres musicographes.

[98] C'est-�-dire au nom (du son) commun aux divers genres.

[99] C'est-�-dire celles des autres t�tracordes.

[100] Voir notre tableau n� 11.

[101] Cette explication ne se retrouve ni dans Gaudence, ni chez aucun autre musicographe. Bryenne dit seulement (Harmoniques, p. 385, Wallis) qu'il y a sept esp�ces d'octaves, sautant, ajoute-t-il, que d'intervalles incompos�s�.

Meibom, dans ses notes sur Euclide (p. 58), critique vivement notre auteur (ineptit, dit-il) d'avoir limit� � douze le nombre des esp�ces d'octaves, et il porte ce nombre � vingt et un. Il ne s'est pas aper�u que Gaudence parle exclusivement des esp�ces � m�lodiques et consonantes �, c'est-�-dire des combinaisons dans lesquelles figurent distinctement les formes ou esp�ces des deux consonances de quarte et de quinte. Le tableau ci-dessous va faire voir que le nombre 12 doit �tre maintenu.

1. 1^re esp�ce de la quarte et 1^re esp�ce de la quinte (1^er ton).

2. 1^re esp�ce de la quarte et 2^e esp�ce de la quinte.

3. 1^re esp�ce de la quarte et 3^e esp�ce de la quinte.

4. 1^re esp�ce de la quarte et 4^e esp�ce de la quinte.

5. 2^e esp�ce de la quarte et 1^re esp�ce de la quinte.

6. 2^e esp�ce de la quarte et 2^e esp�ce de la quinte (2^e ton).

7. 2^e esp�ce de la quarte et 3^e esp�ce de la quinte.

8. 2^e esp�ce de la quarte et 4^e esp�ce de la quinte.

9. 3^e esp�ce de la quarte et 1^re esp�ce de la quinte.

10. 3^e esp�ce de la quarte et 2^e esp�ce de la quinte.

11. 3^e esp�ce de la quarte et 3^e esp�ce de la quinte (3^e ton).

12. 3^e esp�ce de la quarte et 4^e esp�ce de la quinte (7^e ton).

Gaudence ne consid�re pas � part les interversions de ces combinaisons. La 1^�re, la 6^e et la 11^e, interverties, engendrent respectivement les 4^e, 5^e et 6^e tons. � Sur les vingt et une combinaisons que propose Meibom, il n'y a que les sept tons qui remplissent la double condition �nonc�e par Gaudence. Les autres contiennent soit un demi-ton entre deux tons, soit une s�rie de quatre ou de cinq tons cons�cutifs, ce qui les emp�che de correspondre � des esp�ces distinctes de quarte ou de quinte.

[102] Voir notre tableau n� 12.

[103] Nous r�sumons ci-dessous le contenu du chapitre xix en ajoutant aux donn�es de Gaudence (voir nos tableaux nos 12 et 13) la concordance des notes antiques et des notes modernes. Au lieu de 1^�re esp�ce de quarte, etc., nous �crirons, pour abr�ger, 1^�re quarte, etc. � Les notes modernes, prises dans l'�chelle naturelle et correspondant par cons�quent � celles du trope hypolydien, ne repr�sentent que les sons du genre diatonique synton. La note en italique est commune aux deux groupes constitutifs de l'octave.

1^�re esp�ce d'octave : 1^�re quarte et 1^�re quinte. Hypate des hypates� param�se. 1^er ton ou ton mixolydien. �. 1. 1 : �. 1. 1. 1. (si, ut, r�, mi, fa sol, la, si.)

2� : 2^e quarte et 2^e quinte. Parhypate des hypates � trite des disjointes. 3^e ton ou ton lydien, 1. 1. � : 1. 1. 1. �. (ut, r�, mi, fa, sol, la si ut.)

3� : 3^e quarte et 3^e quinte. Lichanos des hypates � paran�te des disjointes. 3^e ton, ou ton phrygien. 1. �. 1 : 1. 1. �. 1. (r�, mi, fa, sol, la, si, ut, r�.)

4� : 1^�re quinte et 1^�re quarte. Hypate des moyennes � n�te des disjointes. 4^e ton ou ton dorien. �. 1. 1. 1 : �. 1. 1. (mi, fa, sol, la, si, ut, r�, mi.)

5� : 2^e quinte et 2^e quarte. Parhypate des moyennes � trite des hyperbol�ennes. 5^e ton, ou ton hypolydien. 1. 1. 1. � : 1. 1. �. (fa, sol, la, si, ut, r�, mi, fa.)

6� : 3^e quinte et 3^e quarte. Lichanos des moyennes � paran�te des hyperbol�ennes. 6^e ton, ou ton hypophrygien. 1. 1. �. 1. : 1. �. 1. (sol, la, si, ut, r�, mi, fa, sol.)

7� : 4^e quinte et 1^�re quarte ou 3^e quarte et 4^e quinte. M�se � n�te des hyperbol�ennes ou proslambanom�ne � m�se. 7^e ton, ou ton hypodorien, appel� aussi locrien et commun. 1. �. 1. 1 : 1. 1. (la, si, ut, r�, mi, fa, sol, la), ou, � l'octave aigu� : 1. �. 1 : 1. 1. (la, si, ut, r�, mi, fa, sol, la.)

En pr�sentant la double combinaison de la 7^e esp�ce d'octave, Gaudence nous donne � croire qu'il n'attache pas d'importance � la position relative des t�tracorde et pentacorde dont la r�union forme l'octacorde.

[104] Voir notre tableau n� 13.

[105] C. de Jan proscrit le mot ὀνόμασι et hasarde la proposition de le remplacer par σχήμασι, en renvoyant � Bacchius, � 97.

[106] Tous les tropes �tant �chelonn�s par demi-tons, le proslambanom�ne, et chacun des autres sons d'un trope donn�, monte d'un demi-ton au-dessus de la note correspondante du trope qui le pr�c�de imm�diatement.

[107] C'est ce qui a lieu lorsqu'on passe du trope hypodorien � l'hyperphrygien. La m�se hypodorienne devient le proslambanom�ne hyperphrygien.

[108] Nous avions song� � corriger μέσης en ὑπάτης. La correction faite par C. de Jan (τῶν au lieu de τὸν) a pour effet de rendre μέσης plus vraisemblable.

[109] Les manuscrits de Meibom omettent les mots προσλαμβανομένῳ τε αὐτῷ χρώμετα καὶ, et donnent εἰς ἀρχὴν au lieu de τὴν τάσιν.

[110] Addition de Meibom.

[111] Litt�ralement : �tre augment� progressivement.

[112] La voix humaine se divisait en r�gions hypato�de, m�so�de, n�to�de et hyperbolo�de, d�nominations auxquelles correspondent respectivement les anciennes d�nominations de bassus, tenor, contra, superus, en italien : basso, tenore, alto, soprano (A.-J.-H. Vincent, Notices, etc., p. 120). Aristide Quintilien (De musica, p. 24) dit que le ton (ou trope) dorien se chante tout entier (avec la voix). Pour les instruments, l'Anonyme de Bellermann, � 23 (trad. Vincent, Notices, p. 13) indique de la mani�re suivante la r�partition des diff�rents tropes entre les instruments � vent et � cordes.

Hydraule ou orgue : tropes hypophrygien, hypolydien, phrygien, lydien, hyper�astien , hyperlydien.

Cithare : tropes hypolydien, iastien, lydien, hyper�astien.

Fl�te : tropes hypophrygien, hypo�olien, hypolydien, �astien, phrygien, lydien, hyper�astien.

Musique de danse (instruments de percussion ?) : hypodorien, hypophrygien , hypolydien, dorien, phrygien, lydien, hyperdorien.

[113] Nous ajoutons εἰσαγωγαῖς avec Meibom et C. de Jan.

[114] Fr. Bellermann a donn� une traduction allemande des chapitres xxi et un dans son ouvrage intitul� Die Tonleitern, etc., p. 57-59. Voir aussi sa page 75. � � Seulement�, c'est-�-dire sans entrer dans les explications pour lesquelles l'auteur renvoie aux � Introductions �.

[115] En tant que son m�lodique.

[116] Dans les tableaux d'Alypius ce signe est figur� ainsi : . Le manuscrit 2456 de Paris donne le signe . Il s'agit du signe instrumental, � en juger par la forme assign�e aux signes suivants.

[117] Le proslambanom�ne du trope hypo�astien.

[118] Ajoutons : et que les tropes sont �chelonn�s par demi-tons.

[119] Le trope en question est l'hypophrygien.

[120] L'hypate des hypates du trope hypodorien.

[121] Note de Bellermann intercal�e dans la traduction de ce passage : � Also, wie die Uebersicht der Noten auf Blatt 3 der Beilagen zeigt, bis zu b oder ais, d. i. und . � Par le rapprochement de ces deux signes, Bellermann semble faire allusion au 30^e degr� de l'�chelle g�n�rale de demi-tons, situ� d'une part dans le lydien et d'autre part dans le mixolydien, tandis que, selon nous, Gaudence n'a en vue que le 30^e degr� de cette �chelle, situ� dans le trope dorien. En effet le double signe , situ� au 19^e degr�, n'appara�t avec l'accent que dans le trope iastien, qui suit imm�diatement le dorien.

[122] Dans les tableaux des sons, dans le diagramme. Cp. Aristide Quintilien, p. 26, Mb.

[123] Homotones, servant � noter des sons de m�me hauteur.

[124] Note intercalaire de Bellermann : � Dies ist nur insofern richtig, als das Gesetz, nach dem die auf einerlei chromatische Stufe stehenden Noten gebraucht werden, nicht immer den akustischen Unterschieden, die sie eigentlich ausdr�cken, entspricht. �

[125] Note intercalaire de Bellermann : �Nur dann, wie sich pag. 51 zeigte, wann der tiefste Tetrachordonton ein ursprungliche Note ist (note naturelle); ist er eine Apotomeerh�hung (note di�s�e), so werden die chromatischen und enharmonischen Intervalle nicht durch Benutzung dieser gleich hohen Noten ausgedr�ckt. �

[126] Voir notre tableau n� 14.

[127] En d'autres termes, la note la plus grave de la premi�re rang�e.

[128] Meibom, qui avait γάμμα au lieu de υ dans son manuscrit, reconna�t avec raison que le gamma n'a rien � faire ici; seulement, pour trancher la difficult�, il supprime tout ce qui concerne ce signe. Bellermann a devin� la vraie solution, confirm�e par les manuscrits de C. de Jan : �Es leuchtet ein, dass dies ein Irrthum ist, und hier von den Noten die Rede sein m�sste, deren Gestalt zur Verwechslung mit (ou plut�t ) kann verf�hrt haben. � Un copiste aura confondu la lettre Y avec le gamma et introduit le nom de cette derni�re lettre � la place de la premi�re. Cp. Aristide Quintilien, p. 15, 27 et 28, o� les signes propos�s par Bellermann occupent pr�cis�ment le deuxi�me rang. Du reste ces signes ne se rencontrent dans aucune des pi�ces musicales qui nous sont parvenues jusqu'ici.

[129] Le mot ἀπεστραμμένον (que nous corrigeons en ἀνεστραμμένον), omis chez Meibom, retrouv� par Bellermann dans le manuscrit de Leipzig et par nous dans le manuscrit 2456, de Paris, figure aussi dans ceux de Jan. � Meibom a lu ω comme les manuscrits. Nous restituons le double sigma couch� dont l'om�ga, ω, est une alt�ration facilement explicable par la pal�ographie.

[130] Le texte dit : � dans la quatri�me rang�e �, ce qui nous semble n'offrir aucun sens. Nous corrigeons en . La confusion du δ avec l'α est fr�quente dans les manuscrits. (Cp. Bast, Commentatio palaeographica, p. 155, 703, etc.)

D'autre part, les deux doubles signes homotones sont intervertis dans les tableaux d'Alypius. qui donnent pour note initiale du quatri�me trope (l'hypo�olien) le pi renvers� et le double sigma retourn�, et pour quatri�me son dans l'�chelle par demi-tons du premier trope (l'hypodorien), le rho renvers� et le double sigma couch�.

[131] Ici encore le texte pr�sente une interversion par rapport aux tableaux d'Alypius. Gaudence mentionne comme note initiale de la sixi�me rang�e (trope dorien) ce qui est dans ces tableaux la troisi�me note du troisi�me trope (hypophrygien) et comme �tant sa note homotone la note initiale du sixi�me trope d'Alypius.

[132] Si la corde totale, divis�e en 24 parties, donne par exemple le son UT, la portion de cette corde comprenant 18 de ces parties, consid�r�e isol�ment au moyen d�un curseur, donnera le son aigu FA et ainsi des autres portions.

[133] � = (64 / 85 ⅓) = 243 /256, , intervalle moindre qu�un demi-ton.

INTRODUCTION HARMONIQUE (partie I - partie II)

Oeuvre num�ris�e par Marc Szwajcer