PROCLUS

HYPOTYPOSES

HYPOTYPOSES

DE

PROCLUS DIADOCHUS

PHILOSOPHE PLATONICIEN.

OU REPRÉSENTATIONS DES HYPOTHÈSES ASTRONOMIQUES.

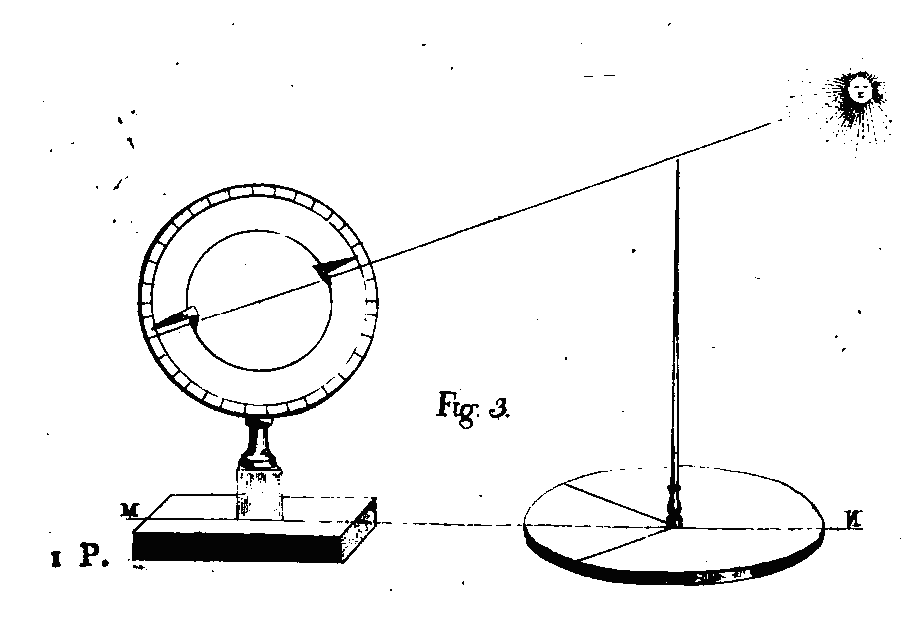
O mon ami! le grand Platon estimait vraiment sage celui qui s'élevant au-dessus de ses sens, et transporté en idée au-delà de la sphère mobile, y verrait dans leur juste proportion, le ralentissement et l'accélération même des astres. Mais tu penses que, de la terre où nous sommes, nous pouvons, étant témoins de ce grand spectacle, reconnaître les révolutions célestes, en tirer des observations de faits utiles pour l'astronomie, et y voir réalisées les hypothèses que les Aristarque, les Hipparque, les Ptolémée, et d'autres ont coutume de proposer d'après ces phénomènes pour les expliquer. Car tu voudrais savoir par quels procédés on les rend intelligibles, ne voulant, autant que tu le pourras, rien ignorer de ce qui a été découvert par les anciens dans la théorie de l'univers. Pendant que je demeurais avec vous autres en Lydie, je te promis qu'aussitôt que nous en aurions le loisir, je t'expliquerais tout cela à ma manière, et puisque nous voilà aujourd'hui arrivés à Athènes, et qu'une divinité bienfaisante nous a délivrés de tout embarras, je vais te tenir ma promesse, et te démontrer les mouvements des corps célestes, tant ceux des étoiles, que ceux des planètes, en t'exposant, comme le veut Platon, les méthodes dont la vérité est reconnue de ceux qui aiment à contempler le ciel, ne voulant pas moi-même m’épargner la peine d'entrer dans ces détails. Mais je n’y entrerai que sobrement, et je me persuade que ce que je te dirai, suffira pour te faire bien comprendre ces hypothèses, sur lesquelles ils établissent toute leur théorie. Pour moi, je crois qu’il ne faut pas d'abord tant s'étendre sur les phénomènes. Dans leur incertitude, ils ont tourné leurs recherches vers la cause de chacun, en supposant directement que les mouvements des corps célestes devaient être circulaires et réglés, bien que ce mouvement circulaire ne soit pas le même pour tous, ni sans mélange de quelque autre, mais cependant toujours assujetti à des lois constantes. Car un mouvement toujours le même dans la même raison, et dans un ordre toujours semblable à lui-même, convient à ceux des corps que nous apercevons, qui sont les plus divins, surtout à ceux que l’on suppose se mouvoir avec une certaine intelligence, qui affecte toujours l'ordre dans ceux en qui elle réside. Persuadés de ce principe qui ne peut jamais tromper, et mécontents de l'apparence de désordre qui règne dans le ciel, ils ont cherché à établir des hypothèses ou suppositions qui substituassent des révolutions périodiques, circulaires et soumises à des calculs particuliers pour chacun des astres, à des mouvements vagues et indéterminés. Pour que tu voies d'après quelles difficultés, imaginant des hypothèses qui rendissent raison des mouvements de ces corps qui leur paraissaient si dignes d'une nature divine, ils en composèrent la doctrine des lois auxquelles obéissent les corps célestes, je vais essayer de te développer les particularités propres à chacun d'eux.[1]

La première chose qui les empêchait d'admettre les mouvements, tels qu'ils paraissent, c'était la variation de vitesse, tantôt plus grande, tantôt moindre, dans les planètes, le soleil et la lune, et l'irrégularité avec laquelle ils parcourent en temps inégaux les quarts de cercle qui sont égaux entre eux.

Ensuite, la lune et les autres planètes allant tantôt vers le nord, tantôt vers le midi à différents lieux du ciel, tandis que le soleil ne faisait ses conversions qu'en un seul point de chaque côté, il fallut que, remarquant le plus grand éloignement, ils vissent jusqu'à quel point au-delà ou en deçà des tropiques les planètes s'écartent.

Ce qui excita aussi leur curiosité, ce fut non seulement le mouvement irrégulier des planètes en longitude et en latitude, mais encore ses augmentations et ses diminutions, avec des stations entre elles. Car ces astres paraissent tantôt se mouvoir vers l'orient, tantôt portés vers les points opposés, et tantôt demeurer à la même place; et ce qu'il y a de plus incroyable, c'est qu'en allant toujours, ils sont arrêtés, et qu'en marchant vers les mêmes points, ils se fixent Tout cela parut digne de recherche aux personnes curieuses des choses célestes, d'autant plus qu'on ne voyait ni le soleil ni lu lune produire ces effets, mais seulement les planètes, et on voulut en savoir la cause.

Les diverses distances de ces cinq planètes au soleil, soit diamétralement opposées à cet astre, ou plus couvent formant avec lui des triangles, des carrés et des hexagones, comme on dit que le font Mars, Jupiter et Saturne ; d'autres circulant autour du soleil, tantôt l'atteignant et tantôt atteints par cet astre, comme Vénus, et Mercure qui ne s'écartent jamais de lui de la quantité d'un côté d'hexagone, mais Vénus s'éloignant plus du soleil que Mercure. On a aussi cru devoir chercher la cause de ces différences, et pourquoi chacun de ces deux astres ne fait pas deux fois de suite sa phase occidentale ou orientale, mais étant en conjonction avec le soleil, paraît oriental, et étant occidental atteint encore le soleil, et ainsi toujours, quoique cela paroisse faux, comme on l'a dit dans le livre des phases singulières.

Ils paraissent d'ailleurs tantôt plus grande, tantôt plus petits, comme tombant dans un abîme profond, et tantôt plus près, tantôt plus loin de nous. Car Mars paraît quelquefois ne pas être éloigné du soleil, ni Vénus de Mercure; et on ne les distingue que par leurs différentes couleurs, et même on aperçoit quelque différence à la lune dans les éclipses totales de soleil, étant quelquefois tellement située relativement au soleil, qu'elle le cache tout entier à notre vue ; et quelquefois cependant an milieu du temps où les centres de ces deux astres et notre vue sont dans une seule et même ligne droite, on voit le bord extérieur du soleil, ce qui est une preuve que la lune est tantôt plus proche et tantôt plus éloignée de nous. Car sa grandeur qui est toujours la même, ne couvre un aussi grand espace apparent à notre vue, quand elle est plus éloignée de nous, que lorsqu'elle est à une moindre distance de la terre.

En outre, ces mêmes astres sont tantôt visibles dans leur plus grande proximité du soleil, tantôt invisibles dans leur plus grande digression. Car supposons Vénus répondant à la même longitude que le soleil, et faisant son lever après lui le matin, étant à plusieurs degrés de distance de lui, nous ne la voyons pas parce qu'elle lui est inférieure. Ce qui a paru si digne d'attention, à ceux qui observent les astres, qu'on en a écrit des livres qui traitent des choses singulières de Vénus.

Je dis que le septième article est l’ordre des planètes, à l'égard les unes des autres. Or, ce qui prouve assez que la lune est la plus voisine de la terre, c'est sa révolution en longitude, qui est la plus courte de toutes, et son passage au-dessous du soleil et de toutes les autres planètes. Car nous avons déjà dit qu'elle est intérieure à Vénus, Mercure, Mars, Jupiter et Saturne, de manière que dans une ligne où ces trois seraient placés, dans le prolongement du diamètre du soleil, Saturne occuperait le point le plus haut, Mars le point le plus bas, et Jupiter le milieu, et par là se démontrent les vitesses de leurs mouvements, le plus élevé faisant sa révolution dans le temps le plus long, et le plus bas dans le temps le plus court ; mais Vénus et Mercure, quoiqu'ayant un mouvement égal à celui du soleil, paraissant tantôt précéder, et tantôt suivre, l'un par rapport à l'autre, d'où il paraît impossible d'assigner leurs places relatives entre eux quant au centre de la terre et du monde.

Les points du zodiaque ne restant pas à leur même place, sont transportés de sorte que les points des solstices, tels que les donne le calcul, ne répondent plus aux solstices visibles ; mais on voit le soleil aller vers les points austraux avant que d'avoir atteint son ancienne limite boréale, et passer aux points boréaux avant que d'avoir atteint le point austral d'où, autrefois il retournait, ce qui se voit par le calcul qui montre qu'il en est de même pour tous les autres points du cercle ; les observations prouvant que le soleil parvient toujours à des points de conversion qui précédent ceux de ses conversions passées. C'est ce que nous voyons en effet, en chaque année, où le soleil parvient à son plus haut point vers le nord avant d'avoir atteint son ancien point tropique, et se lever comme l'ayant déjà passé.

Ajoutons à cela que les étoiles fixes, ainsi nommées parce qu'elles ne changent pas de place, attiraient aussi leur attention, car les observations montraient que, par rapport au pôle du monde, elles décrivent des cercles dont les circonférences en étaient plus ou moins éloignées, comme si leurs mouvements se faisaient autour de quelque autre pôle que celui de l'univers, c'est pourquoi il faut chercher comment elles se meuvent, si elles ont un autre mouvement que le circulaire, quelle est la durée de leur révolution, où est ce pôle, et quel il est.

Je dis en dixième lieu, que de ceux qui voient ces merveilles, il n'y a que peu d'hommes qui ne les observent pas de leurs yeux seulement, mais qui aiment à les examiner avec soin. Je parle des éclipses de soleil et de la lune. A considérer leurs rapports mutuels, tant en grandeurs, qu'en durées des périodes de leurs retours, leurs inclinaisons, et les mouvements des lieux écliptiques; car c'est une chose étonnante, que les éclipses ne se fassent pas toutes au même lieu, et ne reviennent pourtant pas irrégulièrement et sans ordre, en quelque endroit qu'elles arrivent, mais toujours en des points écliptiques du zodiaque de plus en plus occidentaux.

Tous ces phénomènes me paraissent avoir excité les anciens, qui portaient leurs regards vers le ciel, au lieu de les fixer sur la terre, à en chercher les causes en s'élevant à leur théorie, et nous invitent nous-mêmes, dans l'admiration que nous partageons avec eux pour ce grand spectacle, à ne pas les voir avec indifférence, ni à en entendre parler sans y prêter attention. Car à dire vrai, c'est par quelque inspiration divine que nous nous sentons poussés à entrer dans cet examen, et à nous y étendre d'autant plus que nous apercevons dans ces hypothèses mêmes, beaucoup de choses qui ne s'accordent pas avec l'expérience; outre d'ailleurs que les astronomes n'ont pas employé les mêmes, et que ceux qui les ont employées n'eut n'ont pas tiré les mêmes résultats.

L'histoire nous apprenant que, pour pouvoir expliquer les inclinaisons pythagoriciennes, les excentriques et les épicycles ont été inventés comme un moyen suffisant et le plus simple de tous, et qu’il faut, d’après le conseil de Pythagore, chercher à les approfondir et démontrer par les propositions les plus courtes et les plus simples, que ce qu’on aura trouvé mieux que toute autre méthode aux corps célestes. Nous exposerons, en suivant ces principes, les conséquences qui en dérivent et qui sont confirmées par les phénomènes ; et nous essaierons d'expliquer la méthode de Ptolémée, sans le suivre actuellement. Car il l’expose par des problèmes astronomiques qu'elle résout en allant du plus simple au plus composé. Nous, au contraire, nous démontrerons d'abord ces hypothèses par lesquelles ils expliquaient les inégalités apparentes des mouvements célestes que quelques-uns regardaient comme très régulières. Car ils pensaient généralement comme nous le croyons aussi d’après eux, que les corps célestes obéissent à un mouvement régulier avec plus de facilité, n'étant point sujets à la destruction, que les corps matériels terrestres qui ne peuvent avoir qu’un mouvement irrégulier par l'effet de l'augmentation et de la diminution qu’il reçoit.

Admettons d'abord que les mouvements des astres errants ou planètes ne s'exécutent pas dans un seul cercle, ni autour des pôles de l'univers. Car ces astres ne décrivent pas des cercles parallèles à l’équateur, et tous ces cercles n’ont pas le même pôle et ne sont pas parallèles, mais les planètes les parcourent obliquement à ce cercle et aux autres parallèles qu'elles coupent dans leurs écarts en latitude. C’est pour cela qu'elles ne décrivent pas leurs orbites autour du même pole que celui de l’univers, ni toutes autour d un même pôle, qui n’est pas celui du monde. Car elles n’ont pas toutes une même limite ni boréale ni australe, mais elles s’écartent plus ou moins de chaque coté. Chacune décrit son orbite oblique aux parallèles, laquelle passe par les limites propres à chacune. Et puisque leurs pôles sont différents, il faut nécessairement que les cercles qui passent par ces pôles soient plus ou moins inclinés, ainsi que ces pôles eux-mêmes en plus ou moins grande distance à l'équateur, en proportion de cette distance ; mais ce qu'ils ont de commun, c'est que le pôle de chaque orbite oblique est autant distant du pôle des parallèles à l'équateur, que sa limite boréale la plus grande est distante du plus grand parallèle (l’équateur). Car si tu conçois la limite boréale de la plus grande orbite oblique, et que tu décrives un grand cercle par cette limite et par le pôle des parallèles à l'équateur, ce grand cercle sera perpendiculaire sur l'équateur, parce qu'il passe par les pôles de celui-ci. Prends sur ce grand cercle un quadrant, depuis le pôle qui est au nord du point que nous avons dit être la limite boréale de la lune, ce quadrant sera égal, comme tu vois, à celui qui est compris sur ce grand cercle entre le pôle de l'équateur et cet équateur. Et retranchant la portion commune à ces deux quadrants, tu trouveras l'arc compris entre les deux pôles égal à celui qui est entre la limite boréale de la lune et l'équateur. Il en est de même pour le soleil. Car il est également démontré que si on décrit un méridien passant par le pôle du monde et le point tropique d'été, l'arc de ce méridien qui sera compris entre le pôle du zodiaque et le pôle de l'univers, sera égal à l’arc compris entre l'équateur et le point tropique d'été par lequel passent le zodiaque, le cercle tropique d'été, et les quadrants pris vers le nord sur le point tropique d'été. Car il est évident que la distance du zodiaque à son pôle est toujours un quart de cercle, parce que le méridien qui coupe à angles droits le tropique qui est un des cercles parallèles, est décrit passant par le pôle, et coupe à angles droits le zodiaque qui touche le tropique au point de conversion commun à ces deux cercles, comme Théodose l'a démontré dans le second livre des sphériques. De même pour les autres planètes dont nous parlerons, prenant les limites boréales des cercles obliques qu'elles décrivent, et traçant des méridiens qui passent par ces limites et par le pôle des parallèles à l'équateur, ainsi que par les limites boréales des parallèles, les quarts de cercles de ces méridiens, pris depuis ces limites du même côté que le pôle du tropique d'été, nous feront trouver les pôles de chacune, qui seront à même distance chacun du pôle des parallèles à l'équateur, que l'orbite elle-même est éloignée de l'équateur qui est le plus grand des parallèles. Tu sais déjà que les limites boréales étant différentes les unes des autres, à cause de l'inclinaison plus ou moins grande des orbites obliques, les pôles de celles-ci seront plus ou moins distants du pôle des cercles parallèles à l'équateur. Fais donc maintenant attention à ce qui te reste à savoir. Car je vais passer à la théorie générale des hypothèses, et te dire ce qui a obligé nos prédécesseurs à les établir.

Sachons d'abord que les mouvements des astres errants ou planètes, n'est pas circulaire, et ne s'exécute pas autour des pôles de l'univers; car ces astres ne décrivent pas des cercles parallèles à l'équateur. Le soleil ainsi que la lune et les autres planètes paraissant faire leurs mouvements en sens contraire à celui de l'univers, il faut nécessairement que les astres les exécutent dans des cercles qui aient pour centre celui de l'univers, ou dans des cercles excentriques. Or, la terre étant fixe au centre de l'univers, comment ces astres sont-ils tantôt plus proches, tantôt plus éloignés de la terre, si ce n'est parce qu'ils se meuvent dans des cercles excentriques, à moins que leurs mouvements ne soient pas uniformes? supposition qui répugne à la nature des corps célestes. La cause de leur inégalité apparente de mouvement ne doit donc pas être attribuée à des vitesses irrégulières, mais à leurs orbites qui les rapprochent et les éloignent alternativement de la terre immobile au centre du monde.

(F. 1) Imaginons le cercle ΑB, dont le centre soit en Γ ; et un autre cercle EΖ non concentrique au premier, et dont le centre soit en Δ. Menons par ces centres une droite ΑEΖB, dans laquelle seront les centres Γ, Δ. Il est évident que l'astre qui parcourt le cercle EΖ, paraîtra aux personnes qui sont sur la terre en Γ, apogée ou dans sa plus grande distance à la terre, quand il sera en Ζ, et périgée ou dans sa moindre distance à la terre, quand il sera en Ζ ; car Ζ est moins éloigné de Γ, que ne l'est E, parce que le centre du cercle EΖ est sur la droite EΓ, et non sur la droite ΓΖ. Αinsi donc, que Γ soit plus élevé ou plus bas, rien n'empêchera, par rapport à la terre, que l'astre ne paroisse apogée et périgée. Or, le point Γ gardant toujours la même place, l'astre s'approchera de Γ, ou s'en éloignera pour les habitants de la terre en Γ.

Telle est la première hypothèse ou supposition qu'établissent les astronomes, qui veulent expliquer l'uniformité du mouvement des astres qui décrivent des cercles : c'est que les astres ne se meuvent pas dans des cercles concentriques au monde, de sorte qu'en parcourant d'un mouvement uniforme ces mêmes cercles, ils paraissent parcourir d'un mouvement inégal les segments du zodiaque. Car dans deux cercles, non concentriques, les droites menées du centre du cercle intérieur, au cercle extérieur, ne font pas sur la circonférence des segments semblables à ceux qu'elles font sur.la circonférence extérieure.

En effet, soient encore les cercles non concentriques ΑΒ dont le centre est Γ, et EΖ dont le centre est Δ ; et soient menées du centre Δ, les droites ΔΘ, ΔH, ΔΛ, ΔK, qui coupent des portions égales entre elles sur la circonférence intérieure, je dis que ΘH n'est pas égal à ΛK. Car si ces segments étaient égaux, en joignant ΓΘ, ΓH, ΓΛ, ΓK, les angles en Γ opposés à ces arcs seraient égaux ; car Γ est le centre du cercle ΑB. Donc, comme l'angle ΘΔH est à l'angle ΘΓH, ainsi serait l'angle ΛΔK à l'angle ΛΓK, ce qui est impossible, car l'angle ΛΓK est plus grand que l'angle ΛΔK, et l'angle ΘΓK est plus petit que l'angle ΘΛH; donc les portions ΘH, ΛK, ne sont pas égales entre elles. Quand donc l'astre parcourant le cercle EΖ, décrira des portions égaler de circonférence déterminées par des droites menées du centre Δ au cercle EΖ, il ne paraîtra pas décrire de portions égales sur la circonférence du cercle ΑB, mais parcourir l'arc ΘH moindre que l'arc ΛK. Donc dans un temps égal, il paraît se mouvoir moins rapidement, quand il parcourt les portions apogées de la circonférence; et plus vite, quand il en décrit lés portions périgées. Car E est apogée, et Ζ périgée.

Cela est évident, et il suit de ce que l'astre parcourt des portions inégales du cercle ΑΒ en temps égaux, qu'il paraîtra réciproquement y décrire des portions égales de la circonférence en temps inégaux. Enfin, il parcourra uniformément son cercle EΖ, et il y décrira des portions égales de circonférence en temps égaux, car c'est le mouvement uniforme qui paraîtra inégal sur le cercle ΑB, en faisant sur celui-ci des arcs inégaux en temps égaux, et en parcourant les portions apogées en plus de temps, les périgées en moins, et les moyennes en temps moyens, dans les distances moyennes. Ainsi, en faisant un cercle concentrique à l'univers, il faut admettre un excentrique circulant sur le concentrique, sur la circonférence duquel soit son centre qui la parcourt, et l'astre circulant sur l'excentrique, en parcourant successivement les portions tantôt les plus proches du centre du concentrique, tantôt celles qui en sont les plus éloignées, en même temps que ce cercle se meut uniformément sur la circonférence du concentrique, et l'astre uniformément aussi sur le cercle excentrique, en sorte que pour le centre du concentrique, le mouvement dans les segments du cercle extérieur paraît irrégulier et inégal.

(F. 2) Concevons deux cercles concentriques ΑB, EΖ, décrits autour du centre Γ, et un petit cercle HΘ qui parcourt EΖ sur lequel est son centre, tandis crue l'astre parcourt uniformément ce petit cercle; il est évident que quand il sera en H, il sera à sa plus grande distance du centre Γ, et en Θ à la moindre, et que dans les positions également éloignées de ces points, il sera dans ses distances moyennes à ce centre. Si donc nous prenons les deux droites ΓK menées du centre au cercle ΑB, (ou bien les deux ΓΛ) qui coupent des portions égales sur la circonférence HΘ, ces droites ne couperont pas des portions égales sur-la circonférence ΑB, mais la plus petite sera HN la plus, éloignée du centre Γ, et la plus grande, la plus proche ; cela n'a pas besoin d'autre démonstration. Par conséquent, l'excentrique HΘ parcourant le concentrique ΑΒ uniformément et l'astre décrivant des portions égales sur l'excentrique HΘ, le mouvement sur ΑΒ paraîtra inégal en temps égaux, aux personnes qui le regarderont du centre Γ.

En admettant ces deux sortes d'excentriques, ce ne peut être qu'à deux conditions : ou le centre de l'univers est en dedans de l'excentrique sur lequel l'astre est porté, ou il n'y est pas contenu, ou il le touche. Ce dernier cas est impossible, car jamais nous ne voyons les astres toucher la terre. Ainsi, l'excentrique ne pouvant être conçu que dans le cas de, l'une ou de l’autre des deux premières conditions, on peut expliquer comment le mouvement des excentriques étant égal, il paraît cependant inégal. Nommons proprement excentrique, le cercle qui renferme le centre de l'univers, comme dans la première figure; et épicycle, cercle qui se meut autour d'un autre cercle sur lequel est son centre, soit qu'il parcoure cet autre, soit que cet autre se transporte en tournant autour de son propre centre. Les astronomes ont dû admettre ces deux hypothèses qui peuvent expliquer cette inégalité, à cause du besoin que nos yeux en ont pour s'en rendre raison. L'excentrique suffit seul pour expliquer les apparences que le soleil présente, ainsi que l’épicycle porté sur le concentrique seul. Mais pour les autres astres, il faut employer les deux hypothèses, c'est ce qu'on appelle l’excentrico-épicycle, où l’on suppose l’épicycle en mouvement sur l'excentrique ; et cela devient sensible par la comparaison du mouvement simple du soleil, à celui de la lune qui est plus composé, en ce qu’il faut appliquer à celui-ci les deux hypothèses tout ensemble. Et ce mouvement de la lune est cependant encore plus simple que celui des autres astres. Car nous trouverons que ceux-ci ont encore besoin d'une autre hypothèse, la sphère des fixes, ayant un mouvement qu’on dit être d un degré en cent ans, hypothèse qui n'est pas nécessaire pour expliquer Ce qui développera à mesure que nous avancerons. Maintenant après avoir montré les hypothèses communes de l'anomalie apparente, nous allons passer à l'examen de chacune en particulier, en commençant par celle du soleil, comme la plus simple de toutes.

Nous voyons le soleil faire sa révolution dans un cercle oblique aux parallèles, et passer successivement au midi et au nord de l'équateur, en décrivant toujours le même cercle qu'on nomme le mitoyen du zodiaque. Cette dénomination vient de ce que les autres astres passant au-dessus et en dedans de ce cercle, font leurs retours d'un côté ou de l’autre, tandis que le soleil au contraire parcourt toujours le même cercle qui tient le milieu entre les autres cercles obliques décrits par les autres astres qui s'en écartent en dedans et en dehors, après l'avoir traversé, par l'effet de la variété apparente de leurs mouvements différents du sien.

Tout cela se conçoit sensiblement. Ainsi la première chose que nous ayons à faire, est de fixer les termes, l'un boréal, l'autre austral, de l'orbite solaire, et de savoir à quelle distance ils sont chacun, du plus grand des cercles parallèles, afin de pouvoir en conclure la distance des pôles du cercle oblique, et de ceux des parallèles ; car cette distance est la même, comme je l'ai déjà dit, que celle de leurs limites au plus grand parallèle : pour avoir les limites tant boréale qu'australe, prends l'instrument que je vais décrire de manière à t'en faire connaître l'usage.

(F. 3) Prépare un de cercle de cuivre, de modique grandeur, et telle qu'elle ne le rende ni difficile à mouvoir, ni peu susceptible d'être bien divisé par trop de petitesse. Mais qu'il soit assez bien proportionné, pour que son diamètre soit au moins d'une demi-coudée, et que le rayon étant de 60 parties égales, la largeur de sa circonférence soit de 4 de ces parties, et l'épaisseur de 2 ½. Et pour montrer ce que j'entends par l'épaisseur et la largeur, que ce soit un cercle dont le limbe ne soit pas arrondi, mais tellement façonné au tour, que sa face extérieure se termine à angles droits à celles des côtés, l'intérieure de même, et les quatre faces perpendiculaires étant entre elles, l'intérieure et l'extérieure seront, l'une inférieure, l'autre supérieure, et parallèles. Ce cercle étant ainsi fabriqué, j'appelle profondeur la distance de la surface concave à la surface convexe de son limbe, c'est la largeur des plans qui sont entre ces deux surfaces. Et j'appelle épaisseur de ce limbe, la distance entre ces deux plans. Il est clair d'après cela, qu'il faut que la droite menée du centre à la surface extérieure, étant de 60 parties égales, la droite menée de ce centre à la surface intérieure, soit de 56, et la portion comprise entre la surface concave et la surface convexe, de 4 des parties dont la droite menée à la surface concave en a 56, et dont la droite menée à la surface convexe en a 60, et la perpendiculaire d'un de ces deux plans à l'autre, mesurant l'épaisseur, sera 2 ½ de ces mêmes parties.

Après avoir ainsi préparé ce cercle, lions le diviserons en 360 portions égales sur chacun des plans auxquels nous avons donné le nom de profondeur, et en autant de moindres portions qu'il sera possible, de telle sorte que chacune des portions soit subdivisée en 60, afin que nous l'ayons non seulement divisé en parties, mais encore chacune d'elle en minutes, car c'est par cette division que nous parviendrons à une plus grande justesse dans nos opérations. En effet, la distance au plus grand des parallèles ne se termine pas précisément à une des 360 divisions, elle aboutît à des minutes. Or il est clair que la division en minutes ne doit pas être marquée sur la largeur entière du limbe, mais seulement la division en 360 portions ; et la subdivision en minutes, sur la moitié de cette largeur, par des traits plus grands pour les portions ou degrés, plus petits pour les minutes. Le cercle ainsi divisé nous servira de méridien sur lequel nous chercherons à prendre l'intervalle de la limite boréale et de la limite australe de l'obliquité de l'orbite solaire.

Après ce cercle, nous en façonnerons un autre au tour, assez grand pour pouvoir s'adapter exactement par sa circonférence convexe à la circonférence concave du méridien, colure, et y tourner, sans en quitter la face intérieure ; ce méridien ayant un limbe large de 4 des parties dont le rayon en a 60 comme nous l’avons dit, le limbe de second cercle en aura 2 ½. Il est clair qu'ayant tous deux la même épaisseur, il ne s'écarte pas du méridien, mais est toujours dans le plan du cercle extérieur, lorsqu'on le fait aller vers le nord et vers le midi, en dedans du cercle extérieur. Nous ajouterons au cercle intérieur deux pinnules perpendiculaires sur son plan, opposées l'une à l'autre, l'une du coté de l'orient, l'autre du côté de l'occident, car l'épaisseur du méridien ne fait sensiblement rien. Les pinnules doivent être des parallélogrammes faits d'une plaque mince de cuivre avec un trou au milieu, dans la rencontre des diagonales tracées sur chacune, d'où s'élèveront des triangles rectangles perpendiculaires à ces parallélogrammes, tels que leurs bases soient la moitié du plus petit côté des pinnules, et diamétralement opposées, sur le cercle intérieur, de façon que les parallélogrammes soient; perpendiculaires a la face latérale de ce cercle, dont le limbe sera surpassé par ces triangles, qui aboutiront par leurs extrémités au limbe du cercle extérieur ou colure. Ainsi, quand le cercle intérieur sera mis en mouvement dans le cercle extérieur qui demeurera immobile, les extrémités des triangles, parcourant les divisions de l'extérieur, les montrera à l’œil qui regardera par les trous des pinnules perpendiculaires sur le plan du cercle, et tournées diamétralement l'une vers l'autre.

Pour adapter ces deux cercles l'un à l'autre, prenez deux fiches que vous fixerez en deux points opposés de l'intérieur du grand cercle, et qui s'étendront jusqu'à embrasser la largeur du plus petit, de manière à le tenir ferme, et à ne pas le laisser s'écarter de la circonférence concave du plus grand, ni à l'empêcher d'y couler. Quand ils seront placés l'un dans l'autre, par, le bord extérieur du petit, inséré dans le bord intérieur du grand implanté sur une petite colonne quadrangulaire de huit de hauteur_> dans une rainure de sa face supérieure, à angles droits, de même forme que le cercle extérieur qui y sera reçu. Ce pied sera posé perpendiculairement à l’horizon sur la méridienne, qui coupera en deux parallélogrammes égaux, la base carrée. Le plus grand cercle qui renferme le cercle intérieur, demeurant ferme sur le pied, le cercle intérieur qui sera mis en mouvement dans la concavité du cercle extérieur, laisse voir sans obstacle au travers des parallélogrammes perpendiculaires, et marque en même temps, par les triangles qui avancent sur le limbe du cercle extérieur, les degrés de celui-ci auxquels aboutiront les sommets de ces triangles. Quant au parallélisme à l'horizon, on le prend par le moyen de quelques cales posées de côté et d'autre au-dessous d'une planche sur laquelle portera le pied du soutien, de manière qu'elle ne penche d'aucun côté. Ce que l'on reconnaîtra en y versant de l'eau qui restera à la même place sans couler vers quelque part qui serait plus basse. Car le poids de toute matière pesante l'entraîne toujours vers les parties inférieures. Ensuite voici comment on aura la ligne méridienne:

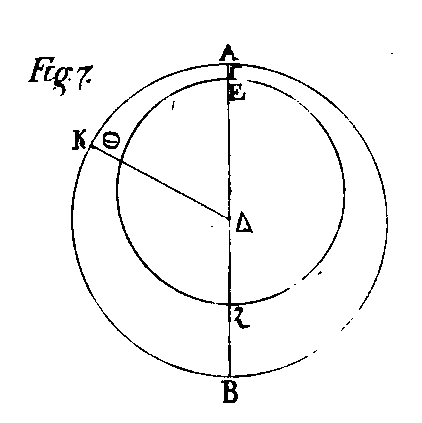
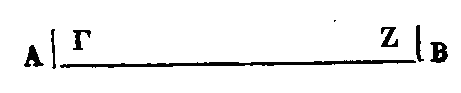
Après avoir planté un gnomon vertical sur la base carrée, et décrit un cercle autour du pied de ce gnomon, comme autour d'un centre, on observe avant midi, le moment où l'ombre du gnomon atteint la circonférence de ce cercle, pour marquer exactement le point où elle tombe, et ensuite après midi l'autre point où l'ombre aboutit, quand elle atteint encore la circonférence, et joignant par l'application d'une règle ces deux points, on coupe la droite tracée de l'un avant midi, à l'autre après, en deux parties égales, puis appliquant la règle sur le point du milieu et sur le centre du cercle, la droite tracée le long de cette règle, jusqu'à la circonférence, sera la ligne méridienne dans tous ses points; parce qu'à midi toutes les ombres qui tombent du gnomon se confondent avec eux.

Après quoi, on pose le soutien sur cette ligne, dans la direction de la méridienne, et quand la concavité entière du cercle intérieur sera ombragée, au moment où elle le sera, vous serez certain qu'il est midi, et que le soleil est alors dans le plan du méridien. Ensuite, faisant mouvoir le cercle intérieur, jusqu'à ce que le rayon du soleil passe par les ouvertures des deux pinnules, quand vous l'y apercevrez vous remarquerez sur quel degré tombe l'extrémité du triangle le plus austral, et vous marquerez ce degré. En opérant ainsi, quand le soleil sera parvenu à l'extrémité du sagittaire, ainsi qu'à la fin des gémeaux, le nombre des degrés marqués par les pointes des triangles, d'un de ces points à l'autre sur le cercle méridien, sera en latitude la grandeur de l'écart du soleil, d'un point tropique à l'autre, et la moitié de cet écart nous donnera la quantité dont chaque cercle tropique est distant du plus grand de tous les cercles parallèles (de l'équateur.)

Voilà ce que nous nous proposions. Il s'ensuit que l’arc entre le pôle des parallèles, et le pôle du cercle oblique mitoyen du zodiaque, est connu. Et ce segment se trouve, par le moyen de cet instrument, être de 23 degrés 51 minutes 20 secondes. C'est à très peu près l’arc mesuré par le côté du pentédécagone inscrit dans le grand cercle. Telle est la mesure en latitude, de cette inclinaison. Car en doublant ces degrés et ces fractions primes et secondes de degrés, nous aurons la quantité de degrés et fractions, dont les points tropiques de l'orbite solaire, sont distants sur le méridien ou colure. Or, comme nous l'avons déjà dit, le soleil et les planètes ayant été démontrés, quoique se mouvant uniformément, ne pas parcourir des cercles concentriques au mouvement général de l'univers, il est évident qu'il faut regarder le soleil comme excentrique, successivement plus et moins éloigné de la terre, et paraissant avoir différentes vitesses, tantôt plus grande, tantôt moindre.

(F. 4) Soit le cercle excentrique ΑBΓΔ autour du centre E, et notre œil non en E, mais en Ζ, de façon que Ζ étant le centre de l'univers _s le point où est notre œil soit censé ne pas différer de ce centre, d'après ce qui a été dit : savoir, que la terre n'est proportionnellement qu'un centre et un point, relativement à l'univers; ce qui est évident, comme nous l'avons dit, par cela seul que nous ne voyons au-dessus de la terre que les moitiés du zodiaque et des autres grande cercles, tels que l'équateur, le méridien, le cercle lactée, et autres pareils, comme si notre œil était an centre de la terre et non à la surface. Ainsi donc le point Ζ étant le centre du monde, faisons passer par les deux centres la droite ΑEΖ, et imaginons le soleil parcourant d'un mouvement uniforme l'arc ΑΒ depuis l'apogée Α ; et menons du centre E la droite EB qui tourne avec le soleil, de Α en B. Menez la droite ΖB de l'œil Ζ au soleil B. Il est évident que si nous regardons sur l'excentrique l’arc ΑΒ sous l'angle ΑΖB, le soleil nous paraîtra avoir parcouru cet arc mesuré par cet angle ; or il l’a parcouru, non en allant autour du centre Ζ, mais autour du centre E. Son mouvement angulaire est donc celui qui est désigné sur la circonférence de l'excentrique, par l'arc que déterminent les côtés de l'angle ΑEB dont le sommet est au centre de cet excentrique. Si l'angle ΑΖB était égal à ΑEB, il serait indifférent de voir du centre E ou du point Ζ, le mouvement du soleil. Mais l'angle en E est plus grand que l'angle en Ζ, car si le mouvement angulaire était donné par le triangle EBΖ, il nous paraîtrait moindre; puisque l'optique nous apprend que les grandeurs des angles à l’œil, paraissent diminuer par l'éloignement de l’œil. De même, supposant que le soleil se meut de Α en Θ, joignant EΘ, ΖΘ, le mouvement angulaire uniforme se verra en E, plus grand que celui qui paraîtra se faire autour du point Ζ.

Menant encore la droite BE en Δ, supposons que le soleil a parcouru l'arc ΓΔ depuis le point Γ. Si nous observions du point E, il nous paraîtrait s'être avancé d'un arc égal à l’arc ΑB. Car ces deux arcs sous-tendent deux angles égaux qui ont leurs sommets au centre E ; mais puisque nous voyons du point Ζ l'arc ΓΔ, joignons ΖΔ, alors l'arc ΓΔ nous paraîtra égal a celui qui soutend l'angle ΓΖΔ plus grand que l’angle ΓEΔ, de sorte que le soleil paraîtra avoir parcouru un espace plus grand que le vrai, après le périgée Γ, comme un espace moindre que le vrai après l'apogée Α. Or, la différence est pour B l'angle B du triangle BEΖ, et en Δ l'angle Δ du triangle ΔEΖ. Donc après l'apogée, il faut la retrancher du mouvement moyen pour trouver l’apparent ; et après le périgée, il faut l’y ajouter. Par conséquent, il faut d'abord trouver le mouvement uniforme ou moyen du soleil, et ensuite chercher l’apparent, soit par addition ou par soustraction. C'est ainsi que, dans l'hypothèse de l'excentrique, nous trouverons toujours la différence entre le mouvement apparent et le mouvement uniforme du soleil. Montrons actuellement qu'on l'obtient également dans l'autre hypothèse.

(F. 5) Soit le cercle ΑBΓΔ concentrique au monde, autour du centre E où est notre œil, que le soleil ne parcoure pas ce cercle, car il ne paraîtrait pas parcourir, d'un mouvement irrégulier, des espaces tantôt plus grands, tantôt plus petits, en temps égaux; mais qu'il se meuve sur un autre cercle dont le centre sera toujours sur la circonférence du cercle ΑBΓΔ, et soit ΖHΘK, cet autre cercle, auquel on mènera la droite EΖ, de sorte que Ζ sera le point apogée. Maintenant, que cet épicycle aille de Α en B, transporté par l'extrémité Α de la droite EΑ, pendant que le soleil sur cet épicycle va de l'apogée Ζ vers H, dans le même sens. Il est évident que pendant le mouvement de l'épicycle sur l'arc ΑB, le mouvement de l'épicycle, de Α en B, sera uniforme, mais que le mouvement apparent est celui du soleil joint à celui de l'épicycle _y qui sont, en joignant la droite HE, compris dans l'angle ΑEH, de telle sorte que le mouvement apparent est plus grand que le mouvement uniforme.

Actuellement, pendant que l'épicycle avance ainsi, supposons que le soleil ne marche pas dans le même sens, mais qu'il s'avance de Ζ en K. Il est clair que, dans cette supposition, le mouvement uniforme se faisant de Α en B, le mouvement apparent serait celui qui est déterminé par l'angle ΑEK, moindre que le mouvement angulaire uniforme ou moyen, c'est ce qui a été démontré dans l'hypothèse de l'excentrique. Or, dans celle-ci, le mouvement angulaire depuis l'apogée montrait toujours le mouvement moyen plus grand que l'apparent ; mais dans l'hypothèse de l'épicycle, le moyen est moindre, si le soleil se transporte dans le même sens que l'épicycle; et plus grand, comme dans l'excentrique, si le soleil va en sens contraire du mouvement de l'épicycle.

Or, comme cet effet est commun aux deux hypothèses, il s'ensuit que dans celle de l'épicycle il faut admettre que l'épicycle marche suivant l’ordre des signes, tandis que l'astre va de la même vitesse en sens contraire sur l'épicycle, afin que les mouvements égaux se rencontrent à la fin toujours avec les mouvements Inégaux; c'est-à-dire, de manière que si l'épicycle a parcouru deux minutes, par exemple, ou trois, le soleil en parcoure autant sur l'épicycle ; et que le soleil et l'épicycle se rétablissent en même temps et aux mêmes points d'où ils sont partis, l'épicycle sur le cercle ΑBΓΔ qui le porte, et le soleil sur l'épicycle ΖΘ.

(F. 6) Pour réunir les deux hypothèses, l'apogée étant toujours à même distance de notre œil, ainsi que le périgée à la sienne, concevons l'excentrique ΑΒ autour du centre Γ, et notre œil en Δ, ΑE égale à ΔΓ; et autour du centre Δ le cercle EΖ, avec l'épicycle ΑΘ, sur la circonférence duquel l'apogée est Α, et le périgée Θ. Cela posé, il est clair que le soleil parcourant l'excentrique, ou l'épicycle, sera apogée en Α, et périgée en B, au point diamétralement opposé ; de sorte que l'apogée Α de l'épicycle est l'apogée Α de l'excentrique, et le périgée au lieu de Θ, sera B de l'excentrique, car alors le soleil sera en B qui était le périgée de l'épicycle ΑΘ.

Ajoutons pour plus ample intelligence des hypothèses, qu'il n'y a aucune différence relativement à l’apogée et au périgée et qu’il résulte de tout ceci, que la droite comprise entre les deux centres est nécessairement égale à celle qui est menée du centre de l'épicycle à sa circonférence; car il faut dans les deux hypothèses, que la distance de notre œil à l'apogée, soit toujours la même, il faut chercher quel rapport il y a entre la ligne intermédiaire des centres Γ, Δ, et le rayon de l'excentrique. Car ce sera le même que celui du rayon de l'épicycle au rayon du cercle concentrique au cercle mitoyen du zodiaque. Car les rayons de l'excentrique et du concentrique sont égaux, savoir, ΑΓ et EΔ, pour que l'apogée soit le même, comme je l'ai dit. On a cherché et trouvé ce rapport par des méthodes graphiques : ce n'est pas ici le lieu de les exposer, car nous ne nous proposons rien-autre chose actuellement que de t'expliquer les hypothèses à l'aide desquelles on tâche de démontrer les causes des phénomènes.

Or on prouve que l'intervalle des centres Γ, Δ, est la 24^e partie du rayon de l'excentrique, de telle manière que le rayon du cercle concentrique au mitoyen du zodiaque est au contraire égal à vingt-quatre fois le rayon de l'épicycle.

Cela bien conçu, il reste à voir où est l'apogée, et où est le périgée du soleil. Je veux dire à quels degrés du zodiaque ils répondent, et si chacun arrive toujours au même point, ou bien s'ils s'en écartent, comme les autres astres. Pour cette recherche, il faut d'abord bien concevoir ce que c'est que la révolution du soleil, c'est-à-dire, trouver en combien de temps le soleil revient d'un point à ce même point juste. Or il faut comparer ce retour, non à une fixe, car les étoiles vont ensemble vers les points suivants du ciel; c'est pourquoi si on les prenait pour termes de leur comparaison, comme par exemple, l'étoile du cœur du lion, il faudrait non seulement prendre la révolution du soleil, mais encore y faire entrer le mouvement de l'étoile en un an.

Or, comme cette étoile s'avance d'un centième de degré vers l'orient, pendant cet espace de temps, il s'ensuit, disent les astronomes, qu'il faut rapporter aux points tropiques solsticiaux et aux points équinoxiaux, les retours de révolutions du soleil et des autres planètes, parce que ces points sont immobiles. Car c'est ce qu'affirment ces astronomes, quoique d'autres, prétendent que les points tropiques ont un mouvement, non circulaire, mais varient de quelques degrés.

Comparant ainsi, à ces points comme immobiles, le cours du soleil, ils trouvent que la durée de sa révolution prise d'un certain point jusqu'au même point, comme d'un solstice au même solstice, ou d'un équinoxe au même équinoxe, est de 365 ¼ jours moins un trois-centième, en toute rigueur,

L'année égyptienne ne tient pas compte du quart de jour. C'est pourquoi les Égyptiens n'ajoutent pas au bout de quatre ans, un jour aux cinq de plus que les trente de chaque, mois, pour faire six jours. Et ce quart accumulé fait parcourir aux mois toutes les saisons. Quant à ceux qui règlent l'année sur les observations susdites, non seulement ils font chaque quatrième année de 366 jours, mais encore, ils suppriment ce jour, tous les 300 ans, à cause du trois-centième de jour qui est de moins sur chaque année ; et prenant pour la durée de l'année solaire, le temps que donnent ces observations, ils trouvent le mouvement moyen de chaque jour, en divisant le nombre de degrés du zodiaque, par la longueur de.ee temps. Or, le nombre des jours de l’année étant de 365 jours et 15 minutes du jour, à cause du quart, elle ne se termine pas à ces 15 minutes, mais à 12 secondes de moins, à cause du trois-centième. Car si nous divisons le jour en parties proportionnelles à celles du degré, nous aurons 60 minutes du jour, dont 15 seront le quart de ce jour; ou bien soixante fois soixante secondes qui font 60 minutes, et la 300^e partie des 3.600 secondes est 12". Ainsi, le quart du jour divisé en parties proportionnelles à celles du degré aura 15' de jour, d'où ôtant les 12", restent 14' 48". Si l’on divise maintenant par cette quantité le nombre 360 degrés d'une révolution, on trouve que le mouvement moyen n'est pas tout à fait d'un degré par jour, mais de 59', 8", 17'", 13^iv, 12^v, 32^vi; ils ne poussent la subdivision des soixantièmes que jusque là, parce que les septimes ne diffèrent pas sensiblement des sixtes.

Prenant ensuite la 24^e partie de ce mouvement moyen de chaque jour, ils ont le mouvement, horaire; et le multipliant par 30, le produit est le mouvement moyen pour chaque mois. Ayant ainsi le mouvement moyen annuel, mensuel, journalier et horaire, et revenant aux observations (car tout ce qu'ils ont écrit, consiste en observations ou en calculs, et d'après les observations, en démonstrations graphiques, ou en hypothèses), ils trouvent que le temps employé à parcourir le quart de cercle du bélier au cancer, est plus long que pour celui de la balance au capricorne, et que dans les deux quarts restants, il met moins de temps à passer du capricorne au bélier, et plus du cancer à la balance. Puis, ils ont déterminé dans lequel des quatre quadrants il reste le plus longtemps, et dans lequel il demeure le moins; et poussant cette recherche jusqu'à la dernière rigueur, ils démontrent ou par des observations, ou par des méthodes géométriques, que l'apogée de l'orbite solaire est en cinq degrés 30 minutes des gémeaux, et le périgée au même nombre de degrés et minutes du sagittaire. Et comme ou l'a dit d'abord, ayant vu que les plus grands et les moindres mouvements du soleil se faisaient toujours dans les mêmes lieux seulement de cet astre, ils ont dit que son apogée et son périgée étaient immobiles et n'avaient jamais lieu dans les autres points du zodiaque.

(F. 7) Ces points une fois trouvés, on pourra se faire une représentation figurée du mouvement du soleil. Car tracez sur une planche de cuivre, si ce n'est de bois, un zodiaque ΑB, divisé en ses douze parties, chaque partie en 60 minutes, celles-ci en secondes, et en autant de moindres portions encore qu'il sera possible d'y marquer de lignes de divisions, tant en minutes, qu'en secondes et au-dessous. Et prenant le point de l'apogée et celui du périgée, savoir, 5 degrés 30 minutes des gémeaux, et autant du sagittaire, faites y passer un diamètre, sur lequel vous marquerez un point depuis le centre, à la distance d'une des 30 parties égales du rayon. Prenant 24 fois cette distance, son extrémité sera un point par lequel vous décrirez du centre un cercle EΖ intérieur au cercle mitoyen du zodiaque : ce sera l'orbite solaire. Prenant ensuite dans les éphémérides le lieu où est alors le soleil, puis ayant divisé aussi l'excentrique en degrés et minutes et soixantièmes inférieures, autant que vous le pourrez, placez-y le soleil au point que les éphémérides vous auront donné. Et ayant le mouvement moyen du soleil pour chaque jour, marquez-le sur l'excentrique, et menez au point où il tombe, une droite tirée du centre du cercle mitoyen du zodiaque. Puis; prolongeant jusqu'à la règle placée dans le cercle mitoyen du zodiaque, vous y aurez l'époque, c'est-à-dire, le lieu apparent : comme si sur les cercles décrits vous supposiez le soleil en Θ, joignant ΔΘ, prolongeant jusqu'au cercle mitoyen, vous trouverez le point K, et comptant depuis Γ, les degrés et portions de degrés depuis Α, vous avez le lieu du soleil, en cette époque, c'est-à-dire en ce point. Car le cercle mitoyen du zodiaque est partagé en douze portions égales, puis celles-ci en degrés, en soixantièmes primes de degré, en soixantièmes secondes de chaque prime, et ainsi de suite autant que cette division peut se subdiviser. Vous marquerez en noir les points où les lignes aboutissent, de façon à pouvoir les effacer ensuite, pour y faire passer d'autres lignes, et décrire seulement les deux cercles avec leurs divisions et la quantité de leur excentricité. L'hypothèse des excentriques est la plus simple. Mais on démontre aussi que l'hypothèse de l'épicycle satisfait également, et parvient au même résultat que celle de l'excentrique, et qu'en supposant un épicycle, l'excentrique même se trouve décrit par l'astre. Voici quelle est cette démonstration, telle qu'elle a été donnée par Hilarion d’Antioche.

(F. 8) Soit le cercle ΑBΓΔ concentrique au mitoyen du zodiaque, et les lignes ΑΓ, ΔB, perpendiculaires l'une sur l'autre, décrit autour des centres Α, B, Γ, Δ, des épicycles égaux. Soit aussi l'astre à l'apogée E, et l'épicycle sur la même droite que l'apogée. Que l'astre parcoure sur l'épicycle, et le centre de l'épicycle sur le concentrique, dans le même temps, chacun un quart de cercle. Dès lors, au même instant que l'épicycle sera parvenu en B, et l'astre en K, après avoir parcouru le quart de cercle EK, ce quart de cercle a été décrit par l'astre, et en parcourant des quarts de cercles, l'épicycle sera en Γ, en même tempe que l'astre en N, après avoir décrit KN, et le demi-cercle EKN sera parcouru. Continuant toujours à se mouvoir de même, l'épicycle sera en Δ, et l'astre en Σ sur l'épicycle qui décrira ainsi l'arc NΣ, et continuant toujours de se mouvoir sur le dernier quart de cercle, il reviendra en Α, et l'astre en E, après avoir décrit l'arc ΣE. Or il est clair que la ligne décrite par l'astre en mouvement; est une circonférence de cercle, car toutes les lignes tracées sur une sphère sont circulaires, EKNΣ est donc un cercle. Maintenant, je dis que ce cercle excentrique est égal au concentrique ΑBΓΔ. Joignez les droites KB, ΣΔ, tracez les diamètres IBΑ, ΖΔΘ de l'épicycle, menez IΖ et ΛΘ qui coupent ΑΓ aux points Φ, X. Puisque KN, NΣ sont des quarts de cercle, et que les angles aux centres B, Δ, sont droits, les diamètres IBΛ, ΖΔΘ sont parallèles. Or ils sont égaux ; et les droites qui joignent des droites égales et parallèles, sont aussi égales et parallèles, donc IΦΖ, BΟΔ, ΛXΘ sont parallèles. Et puisque KΟ, ΟΣ, sont des cotés de parallélogrammes, ΔΟ, IΦ, ΟΔ, ΦΖ sont aussi égales. Or BΟ est égale à ΟΔ, car ce sont des rayons du concentrique, par conséquent IΦ est égale à ΦΖ. En outre, puisque IB est égale a ΦΟ, et IB à EΑ, car l’une et l'autre sont des rayons de l'épicycle, il s'ensuit que EΑ est égale à ΦΟ. Soit ΑΦ une droite commune, EΦ est donc égale à ΑΟ. Et puisque ΑΟ est on rayon du concentrique, il s'ensuit que chacune des droites IΦ et ΦΖ est égale à EΦ; donc ces trois droites sont égales, donc Φ est le centre du cercle EKNΣ, et le centre du concentrique est Ο, en sorte que le cercle EKNΣ est excentrique et égal au concentrique, et que la distance ΟΦ de leurs centres est égale au rayon EΑ de l'épicycle, et que l'excentrique a été décrit par le mouvement de l'astre sur l'épicycle.

Démontrons actuellement que l'astre décrit l'épicycle dans le même temps sur le cercle concentrique au cercle mitoyen du zodiaque, «n allant d'occident en orient.

(F. 9) Soit l'excentrique EKΛ, et son centre Φ, Θ le centre du concentrique, le diamètre EΑΦΘΓ, et que l'astre ait parcouru un arc EK sur l'excentrique. Menons du centre Φ de l'excentrique le rayon ΦK en K, tirons ainsi du centre Θ de concentrique une droite ΘΖ parallèle à ΦK, et soit ΘΖ égale à ΘE, et ΦK égale et parallèle à ΘB, les rayons ΘB et ΦK étant égaux et parallèles, les droites BK et ΦΘ qui les joignent seront par là même égales et parallèles entre elles. Et puisque les droites EΦ et ΘΑ sont égales, ôtons-en la portion commune ΦΑ, les portions restantes ΦΘ, ΑE, seront égales, en sorte que ΖB sera égale à ΘΦ. Mais BK est aussi égale à ΘΦ, donc BΖ sera égale à BK. Donc le cercle décrit du centre B, et du rayon BΖ passera en K, et le cercle KΛΖ sera égal à celui qui serait décrit du centre Α et du rayon ΑE. Et puisque KΘ est en parallélogramme, et que les angles opposés sont égaux à chacun des angles opposés externes, il s'ensuit que les angles ΖBK, KΦE et BΘΑ sont égaux et centraux, de sorte que les arcs EK, ΑB, sur lesquels ils sont appuyés, sont semblables, ainsi que l'arc ΖK de l'épicycle. Par conséquent, au même instant que le soleil paraît en K, section commune de l'épicycle et de l'excentrique, es pendant que l'épicycle parcourt l’arc BK de l'excentrique, le soleil paraîtra avoir parcouru l'arc ΖK de l'épicycle, comme si l'épicycle avait transporté son centre de Α en B.

Nonobstant cette démonstration de l’hypothèse suivant laquelle le soleil, en marchant uniformément, paraît aller irrégulièrement, les tables montrent qu'il y a certaines différences entre le mouvement uniforme et le mouvement apparent, et elles enseignent les cas où il faut retrancher de mouvement égal pour trouver le mouvement apparent, quand le mouvement moyen est plus grand que celui-ci, et de combien il l'est, et les cas où il faut ajouter la différence des mouvements à celui qui est le moindre des deux. En faisant cette opération qu'on appelle prostaphérèse, on trouve le soleil là où il paraît. Or il a été démontré que la plus grande différence entre le mouvement uniforme et le mouvement apparent, dans l'hypothèse de l'excentrique, a lieu quand la droite menée de notre œil au soleil apparent, est perpendiculaire ou tombe à angles droits sur le diamètre qui passe par les centres des deux cercles; mais que dans l'hypothèse de l'épicycle, c'est quand la droite menée de notre œil au soleil touche l'épicycle, et pendant le trajet depuis l'apogée jusqu'au périgée, dans l'excentrique et l'épicycle, ainsi que quand il se fait du périgée à l'apogée dans l'une et l'autre hypothèse, avec cette différence, que l'équation est additive dans le trajet depuis le périgée, parce qu'alors le mouvement uniforme est moindre; mais soustractive dans le trajet depuis l'apogée, parce qu'il est démontré qu'alors le mouvement uniforme devient plus grand que le mouvement apparent. Après avoir exposé l'hypothèse, qui explique les mouvements du soleil, nous passerons à la lune qui demande des méthodes plus compliquées, et nous l'en démontrerons l'hypothèse comme suite de ce que nous avons dit du soleil.

Il faut d'abord admettre pour la lune une orbite oblique, et trouver la quantité de son écart du cercle mitoyen du zodiaque en latitude, comme nous avons trouvé celui de ce cercle mitoyen relativement à l'équateur. On trouve, en regardant par l'instrument qui a été décrit, que la lune s'écarte du cercle mitoyen du zodiaque, de cinq degrés et demi tant en latitude boréale qu'en latitude australe. Si donc nous supposons un grand cercle passant par ces deux points, ce cercle aura le même centre que le zodiaque, et on verra la lune se mouvoir sur ce cercle incliné au mitoyen du zodiaque, vers le pôle, étant tantôt plus boréale que l’équateur et tantôt plus australe. Supposons aussi que ce cercle oblique se meuve non suivant la succession des signes, comme la lune, mais d'orient en occident, en coupant le cercle mitoyen du zodiaque, non dans les même points constamment, car il serait impossible, si les nœuds demeuraient toujours les mêmes, que l'orbite lunaire allât à l'occident, vers lequel il est toujours attiré en coupant le cercle mitoyen du zodiaque en des points toujours plus occidentaux. Comme si tu imaginais deux anneaux, l'un immobile, et l'autre mobile qui glisserait par sa surface concave sur la surface convexe du premier. Telle soit donc l'orbite inclinée dans laquelle se font les éclipses, quand la conjonction et la pleine lune arrivent dans ses nœuds ou intersections avec le cercle mitoyen du zodiaque, ces nœuds se nomment pour cette raison écliptiques. Alors les luminaires y sont dans une même ligne droite avec le centre du cercle mitoyen du zodiaque et notre œil. Car il n'y a pas d'autre point commun à ces deux cercles, et il faut leur concours pour former les éclipses, car l'un est l'orbite de la lune, et l'autre est l'orbe du soleil, et leur rencontre est indispensable pour que chacun de ces deux astres soit éclipsé l'un ou l'autre. Cela est évident. Il est clair aussi que par le mouvement de cette orbite inclinée, il arrivera chaque année des éclipses, et que les points où elles se feront, seront toujours de plus en plus à l'occident. Or le mouvement journalier de ce cercle, et par conséquent de ces points est, dit-on, de trois minutes environ. Cette orbite étant donc inclinée au cercle mitoyen du zodiaque, imagine un cercle excentrique dans le même plan, et si tu veux l'excentricité de cet excentrique, pose-la de 40° 41' des 10° 19' de celle des deux excentriques, et conçois-le se mouvant vers l'occident comme celui dans le plan duquel il est, et je dis qu'il se meut non autour de son propre centre, mais autour du centre de cet oblique, car ce centre-ci est celui du cercle mitoyen du zodiaque, son mouvement journalier étant de 11° 9'; et sur cet excentrique ainsi en mouvement, imagine l'épicycle ayant son centre sur la circonférence de cet excentrique, et transporté vers l'orient autour du centre du zodiaque, comme il a été dit ci-dessus. Son mouvement journalier, par les périodes de retour de la lune, a été dit de 13° 14'. Mais parce que le cercle oblique, dans le plan duquel sont l'excentrique et l'épicycle, étant transporté vers l'occident, porte l’épicycle et l'excentrique de 3' en sens contraire à celui dans lequel il se meut lui-même, il se fait que le mouvement journalier de l'épicycle devient de 13° 11' par la soustraction de la quantité dont il est diminué par celui du cercle oblique de la lune suivant une direction opposée. Supposons maintenant dans le plan de l'oblique, l'excentrique transporté dans le même sens que l'oblique, et autour du même centre, et l’épicycle se mouvant sur l'excentrique vers l'orient, et ayant sur la circonférence de l'excentrique son centre par lequel il parcourt cette circonférence, et enfin, concevons la lune allant sur cet épicycle en sens contraire, c'est-à-dire, vers l'occident. Tu sauras ensuite les causes de ces suppositions compliquées, après que j'aurai décrit graphiquement tous ces cercles.

(F. 10) Soit ΑΒ le cercle mitoyen du zodiaque parcouru par le soleil autour du centre E, et ΓΔ le cercle oblique sur lequel la lune va en latitude, concentrique, et dont le centre est par conséquent aussi le point E, et dans le plan de cet oblique, l'excentrique ΖΘ, sur lequel est l'épicycle HK. Que ΓΔ se meuve vers l'occident, autour du centre Α, et ΖΘ autour du même centre, mais l'épicycle HK vers l'orient, et la lune sur HK, vers l'occident, car tout ce supposé s'accordera avec les apparences, et tous ces mouvements étant uniformes, l'apparence fera voir des irrégularités dans le mouvement de la lune. Ces hypothèses étant bien conçues, il faut encore savoir les bien appliquer.

Puisque la lune se voit dans son mouvement en latitude sortir du cercle mitoyen du zodiaque, il a fallu nécessairement admettre que l'orbite lunaire est inclinée sur l'orbite solaire, et comme on a vu que les éclipses ne se faisaient pas dans le même lieu de ces cercles en chaque année, ni en des points situés plus à l'orient, comme d'abord dans le bélier, ensuite dans le taureau, puis dans les gémeaux, mais tout au contraire, on a admis qu'il faut que l'orbite inclinée de la lune transporte ses nœuds vers l'occident. Car une éclipse doit toujours se faire en des points communs des deux orbites. En voyant que la lune avait tantôt le plus grand mouvement, tantôt le moindre, on pensa nécessairement qu'elle était successivement plus apogée et plus périgée. C'est pourquoi on attribua ce mouvement de la lune à un épicycle, comme on l'avait fait pour le soleil. Quand on eut remarqué que dans l'apogée le mouvement uniforme était plus grand que le mouvement apparent de la lune sur l'épicycle, On supposa qu'elle allait en sens contraire de celui de l'épicycle. C'est ce qui a été démontré dans l'hypothèse pour le soleil; mais quand on vit que dans des points pareils de l’épicycle, la lune ne produisait pas les mêmes différences du mouvement uniforme, d'avec le mouvement apparent, ce qui peut se faire, comme nous le démontrerons, par un excentrique qui porte l'épicycle, mais non dans le cas du concentrique, on fut forcé d'introduire le mouvement par l'excentrique, en posant pour cela sur l'excentrique l'épicycle sur lequel on dit que la lune est portée. Or, voici comment on démontre que dans le cas du concentrique, les mouvements produisent en des points pareils, des différences égales, et dans la supposition de l'excentrique, des différences inégales.

(F. 11) Soit autour du centre E, le cercle ΑΓ concentrique au cercle mitoyen du zodiaque, et l'épicycle ΖHΘ autour du centre Α, ainsi que cet épicycle autour du centre Γ. Soit aussi la lune en deux points pareils H de chaque côté, en sorte qu'elle y soit également éloignée de l'apogée Ζ, et tracez les droites EH, HΑ en haut, et pareillement EH, ΓH en bas. Puisque ΖH est la même droite en l'une et en l'autre position de l'épicycle, l'angle ΖΑH est égal à l'angle ΖΓH, et les angles de suite sont égaux. L'angle EΑH est donc égal à l'angle EΓH. Mais les droites EΑ, EΓ sont égales, ainsi que les droites ΑH, ΓH, donc les angles ΑEH, ΓEH sont égaux, et l'angle ΑHE est égal à ΓHE. Or ces angles étaient les différences entre le mouvement uniforme et le mouvement apparent.

(F. 12) Dans cette figure, ne supposons plus un cercle concentrique, mais un cercle excentrique ΑM décrit autour du centre N et supposant les mêmes points pareils Ζ, H, Ζ, Ο, dans l'épicycle ΑH, MΟ, joignons-les par les droites ΑH, MΟ. Les arcs ΖH, ΓΟ sont donc égaux, puisque le point H est pareil au point Ο, et les droites ΑH, MΟ sont égales ; et puisque la droite EΑ est plus grande que la droite EM, faisons EM égale à ΑΠ, et joignons HΠ. Puisque dans les triangles ΠΑH, EMΟ, les côtés HΑ et ΑΠ sont égaux aux côtés MΟ, EM, et embrassent des angles égaux, les bases étant égales, l'angle ΑΠH est égal à l'angle MEΟ, mais l'angle ΑΠH étant plus grand que l'angle ΑEH, il s'ensuit que l'angle MEΟ est plus grand que l'angle ΑEH de l'excentrique. Si vous menez la droite HE, l'excentrique étant le cercle sur lequel l'épicycle se meut, les mouvements de la lune aux points Π, Ο de l’épicycle font les différences des mouvements uniformes d'avec les mouvements apparents. Or puisqu'on voit par les observations et les calculs, que les différences entre les angles égaux et les angles apparents, c'est-à-dire, entre les mouvements uniformes et les apparents de la lune, allant en sens contraire sur l'épicycle, sont inégales, on est forcé de supposer que ce n'est pas sur un cercle concentrique que l'épicycle est porté, mais sar un cercle excentrique tel que ΑM. Comme il est évident que l'épicycle doit se mouvoir sur un excentrique, et l'excentrique autour de son propre centre, de sorte que son point actuellement apogée deviendra périgée, il est clair que ces points changent de place; car si le mouvement du cercle se faisait autour du centre tel que E du plan oblique, ce mouvement serait contre nature, puisqu'il ne s'opérerait pas autour de son propre centre. Pour que tout cela s'effectue bien, il est nécessaire de supposer, dans le plan du cercle oblique, un cercle qui loi soit concentrique, et dans celui-ci un cercle excentrique qui le touche au point apogée, et qui se meuve comme le plan oblique vers l'occident, que ce concentrique emporte avec lui par son mouvement autour de son centre propre l'excentrique ; et qu'il transporte de place en place l'apogée où est le point de contact. Soit donc dans le plan du cercle obliqué, un concentrique, et dans celui-ci un excentrique qui le touche et qui est emporté par lui, et sur l'excentrique soit un épicycle transporté vers l'orient par l'excentrique, et autour de lui, enfin sur l'épicycle, la lune qui se meut vers l'occident, par les causes que nous avons dites.

(F. 13) Décrirons maintenant le plan oblique ΑB, et dans ce plan le concentrique ΓΔ, puis l'excentrique qui le touche en Γ, enfin l'épicycle ayant son centre Ζ sur cet excentrique, et la lune sous forme de ménisque en ce point. Que le plan oblique ΑΒ glisse sur le cercle mitoyen du zodiaque par les nœuds d'environ 3 minutes par jour. Que le centre de l’épicycle avance par lui-même dans le plan oblique non de 13° 14' mais de 13° 11' seulement, à cause de la soustraction des 3 minutes dont l’excentrique est emporté par le concentrique à l'oblique vers l’occident de l'oblique, de 11° 9' dans le même plan, en y ajoutant les 3' du mouvement de l'oblique, l'excentrique se trouvera emporté par le cercle concentrique à l'oblique, de 11° 12' par jour. Or si le centre de l'épicycle se meut de 13° 11' par la soustraction des 3', et l'apogée de l'excentrique de 11° 12' vers les points opposés, on en conclura que le centre de l'épicycle s’éloigne chaque jour de l'apogée en tournant en sens contraire, de 24° 23' ; et comme le mouvement journalier et uniforme du soleil, est comme nous l'avons déjà vu de 59' 8" 17"', etc., jusqu'aux sixtes, comme nous l'avons dit, et celui de la lune tel qu'il a été démontré; si on ôte du mouvement journalier de la lune, le mouvement journalier moyen du soleil, il est évident que le reste sera la quantité dont ces deux luminaires seront distants l'un de l'autre. Cette distance est de 12° 11' 50", dont le double est 24° 23', dont le centre de l’épicycle s'éloigne chaque jour de l'apogée de l'excentrique. Ainsi la quantité dont le centre de l'épicycle s'éloigne chaque jour, de l'apogée de l'excentrique, en tournant en sens contraire, est double de la distance journalière des luminaires. D'où il faut nécessairement conclure qu'en chaque mois l'épicycle est deux fois dans l'apogée, et deux fois dans le périgée. Car si pendant toute la durée d'un mois, les luminaires, s'écartent l'un de l'autre des 360 degrés de la circonférence du cercle, il s'ensuit que la lune est deux fois en rencontre avec le soleil, puisque autant il retranche du mouvement mensuel de la lune, en allant lui-même dans le même sens qu'elle, autant elle ajoute par le surplus de mouvement de son orbe sur celui du soleil.

Pendant le mois entier la distance des luminaires est de 360°, les distances étant doublées, et le centre de l’épicycle s’éloignant du double de ces distances loin de l'apogée de l'excentrique, il s'ensuit qu'ils s'éloignent l’un de l’autre deux fois de 360 degrés en un mois. Mais si l'épicycle parcourt ainsi deux fois l'excentrique, pour faire deux fois 360 degrés, il est évident que la conjonction arrivant dans l'apogée de l'excentrique, quand l'épicycle est dans la moitié du mois, ayant parcouru l'excentrique entier, il sera dans l'apogée à l’opposition, et parcourant l'excentrique entier encore dans l'autre moitié du mois, la conjonction se fera dans l'apogée encore. Si cela est effectivement, il est vrai aussi que le périgée sera toujours dans les dichotomies, (quartiers) après avoir parcouru la moitié du cerclé dans la première dichotomie, et ensuite la seconde après la pleine lune. Mais une preuve que toute pleine lune ou opposition arrive nécessairement dans l'apogée de l'excentrique, quand l'épicycle y a son centre, c'est qu'alors la lune est dans son moindre mouvement. Cas il est clair que ce mouvement étant le plus lent se fait alors le plus loin de la terre, comme le mouvement le plus rapide est le plus périgée, et celui-ci se fait dans les dichotomies. Tout cela serait impossible, si l'excentrique étant immobile, l'épicycle seul circulait. Car la lune portée sur l'épicycle se trouve passer deux fois en chaque mois par le zodiaque en parcourant son cercle. Et puisque l'excentrique tourne en sens contraire emporté par le cercle concentrique au plan oblique, les phénomènes s’accordent en vertu de la révolution de l’excentrique vers l'occident, et de la révolution contraire de la lune vers l'orient. Car pendant que l'épicycle parcourt une fois l'excentrique, la lune se trouvera parcourir la moitié du cercle mitoyen du zodiaque ; car l'excentrique en tournant en sens contraire, porte alors la lune et la situe de façon que quand l'épicycle parcourt l'excentrique entier, elle paraît avoir parcouru la moitié du cercle mitoyen du zodiaque, à cause de la soustraction opérée par la révolution contraire des mouvements de l'épicycle relativement au cercle mitoyen du zodiaque, c'est ce qui est évident par les raisonnements et les calculs faits sur les mouvements journaliers du nœud, d'où il faut conclure que le mouvement de la lune se fait selon toute apparence naturellement vers l'occident, mais que par accident il paraît se faire vers l'orient. Cela est nécessairement vrai dans l'hypothèse de l’épicycle, pour le soleil, porté en effet dans l'hypothèse de l'excentrique sur ce cercle vers l'orient. Mais pour la lune, les deux hypothèses paraissant nécessaires, il n'est pas nécessaire absolument de dire que la lune se meut par elle-même vers l'orient.

A cette exposition des hypothèses, j'ajouterai les conséquences démontrées qui s'en déduisent. Et d'abord je te dirai que la lune est assujettie à des parallaxes, quelles sont ces parallaxes, et comment on les mesure, non seulement celles du soleil, mais encore celles de la lune. On les mesure par un instrument très utile que son usage a fait nommer l'instrument des parallaxes.[2] Il serait curieux d'en donner la construction et l'usage, mais Ptolémée l’a si bien décrit, qu'il serait superflu de répéter ici ce qu'il en a dit. Ces règles parallactiques ont pour but, comme leur nom l'annonce assez, de montrer la différence entre les lieux vrais et les lieux apparents de la lune. Cette différence se termine par une droite menée du centre de la terre à la lune, et par une autre droite que nous y tirons de la surface où nous sommes quand nous regardons la lune. Ces deux lignes aboutissent à des points différents, parce que la terre n'est pas comme un point central relativement à la sphère ou orbite de la lune, comme par rapport à la sphère des fixes. Car en donnant à la terre une certaine grandeur assez considérable relativement à cette orbite, il faut nécessairement que la droite menée du centre de la terre, à la lune, ne soit pas la même que celle qu'on y mène de la surface de la terre, quoique nous voyons que, relativement à la sphère des fixes, la terre n'est que comme un point central. Quelques-uns, tels qu'Aristarque de Samos, ont déjà supposé un rapport de grandeur entre la terre et la lune. C'est pourquoi il compare les différentes proportions de distances et de grandeur, de la terre, du soleil, et de la lune. Et ceux, qui ont examiné cette question de plus près, ont reconnu par la parallaxe, que non seulement la terre n'est pas comme un point à l'égard de l'orbite de la lune, mais encore qu'elle a relativement à cette orbite une grandeur considérable. Car la parallaxe est la différence entre les lieux.de la lune, tels qu'ils paraîtraient si elle était vue du centre de la terre_r et tels qu'ils paraissent étant vus de la surface terrestre, comme nous l'avons déjà dit. Ceux qui sont venus ensuite ont trouvé, dans les parallaxes de la lune, la preuve que la terre n'est pas un simple point par rapport à la lune, vu que cet astre est proche de nous. Et quant au soleil, il a paru à ceux qui ont mesuré par les gnomons, que la terre est en même rapport à l'orbite solaire, qu'à la sphère fixe. C'est la supposition de ceux qui ont tracé les premiers analemmes, tel que fut Diodore, mais ceux qui observent les périodes solaires croient reconnaître, entre la terre et la sphère du soleil, une certaine proportion de grandeur, et il paraît qu'Hipparque est l'auteur de cette opinion ; en sorte que cette question n'est plus indécise, vu que la terre n'est comme un point que relativement à la sphère des fixes, et même aux astres supérieurs au soleil. Mais tu verras bientôt ce que c'est que la parallaxe, en décrivant un cercle autour d'un autre qui représentera la terre, et en menant deux droites, l'une du centre du cercle intérieur, et l'autre d'un autre point, jusqu'à l'horizon, comme je vais le dire :

(F. 14). Soit le grand cercle ΑΒ représentant un méridien, soit ΓΔ un méridien céleste relativement auquel la terre n'a pas une grandeur sensible, et soit un troisième cercle HΘ décrit entre les deux autres, et passant par un point au-dessus de la terre et par le centre de la lune, ce centre est porté sur HΘ. Mais les lieux de la lune sont vus sur ΓΔ et sont différents pour les personnes qui les voient du centre de ΑB, et pour celles qui lès voient de la circonférence de ce cercle, a moins que la lune ne soit verticale pour les unes et les autres Car alors il n'y a qu'une seule ligne droite ΖΑHΓ qui passe par le centre de la lune et des observateurs qui la voient. Mais si elle n'est pas verticale, comme quand elle est en quelque point Θ, il y aura parallaxe, par l’intersection des droites ΖΘ et ΑΘ en Θ, et par leur prolongement en Δ et en E. Car la lune étant en Δ sur la droite qui passe par son centre, elle paraîtra être en E à l'œil qui est en Λ ; et il se fera en Θ une parallaxe (changement) de lieu de la lune par rapport au centre de la terre, en celui où elle paraît étant vue de la surface terrestre. Et comme le cercle ΓΔ est un méridien, il est vertical à l'horizon qu'il coupe à angles droits, en passant par les pôles de l'horizon. C'est pour cela qu'on a nommé parallactique l'instrument qui a été fabriqué pour mesurer les parallaxes dans le méridien: C'est ce que tu verras clairement par la construction de l’instrument et par son usage, en menant du méridien une ligne, comme j'ai déjà, dit qu'il faut la tracer. Par le moyen de cet instrument, et des calculs que l'on fait d'après les observations, on dresse une table des différences de la lune vraie et de la lune apparente; on appelle vraie celle qui est rapportée an centre de la terre, et apparente quand on la rapporte à la surface terrestre. Différences qui n'existent pas pour la sphère fixe. Car le demi-cercle se voit de la surface comme du centre de la terre, les points de l'hémisphère céleste paraissant à tous ceux de la surface terrestre, comme si tous ceux-ci ensemble n'en étaient qu'un seul. Or cet instrument nous a montré que le plus grand écart de la lune en latitude est de cinq degrés à très peu près, en prenant sa distance au point vertical.

Selon Archimède, dans son Arénaire, le diamètre de la terre est égal à 30 fois le diamètre de la lune ; et Aristarque faisait le diamètre Terre = 1/720^e du zodiaque, et disait que la terre tourne autour du soleil dans le zodiaque, sous les étoiles fixes, et que le zodiaque est au grand cercle de la sphère des fixes, comme la terre est à l'univers. Selon Ptolémée, p. 243, l. v. vol. 1, le diamètre entier de la lune sous-tend un arc de 31 minutes 20"; et p. 347, l. v., c. 16, il dit que le diamètre de la lune étant 1, celui de la terre est 3 2/5 environ, et celui du soleil 18 4/5. Il dit, p. 346, que le rayon de la terre étant 1, sa distance moyenne au soleil est de 1210.

Car (F. 24) le point vertical étant Α, et l'équateur Γ, il est évident que la distance de Α à Γ est égale à la hauteur du lieu terrestre où est placé l'instrument. Prenant donc Δ pour le point solsticial où se termine la plus grande obliquité du cercle mitoyen du zodiaque, on connaîtra le reste ΑΔ. Si on prend la quantité dont la lune s'écarte le moins de Α, comme en B, le reste BΔ sera connu, et on trouve par là de combien est le plus grand écart de la lune en latitude, sur le demi cercle vertical. Or il est évident que la lune nous paraîtra toujours dans notre climat, éloignée du point vertical, dans sa plus grande latitude, et au terme boréal de son orbite inclinée, car c'est ce qui a lieu par exemple pour ceux qui sont à une latitude de 28° 51', leur point vertical est élevé de la même quantité au-dessus de l'équateur. Si donc on en retranche les 23° 51' de l'obliquité du cercle mitoyen du zodiaque, restent 5 degrés dont la lune s'écarte de ce cercle pour ceux dont le climat est à la latitude que je viens de dire, et non seulement pour eux, mais encore pour tout autre climat, tant celui dont le point vertical est atteint par la lune, parvenue à sa plus grande latitude, que pour ceux dont la latitude est d'un nombre moindre de degrés et minutes. C est ce que tu comprendras aisément et que tu as même déjà bien compris, à ce qu’il me semble.

Après avoir expliqué ce que c'est que la parallaxe, et ce qui la cause, savoir : la grandeur sensible de la terre relativement à l'orbite lunaire, et cette parallaxe se faisant en deux directions, en longitude et en latitude : j appelle en latitude le transport vers le nord et vers le sud ; et en longitude le transport vers l'orient et vers l'occident, de la lune vraie en lune apparente. On démontre par les calculs des parallaxes de la lune, la différence de ces parallaxes, comme tu le verras dans le cinquième livre de la composition mathématique (de l'Almageste), d'où il suit que la terre a une certaine proportion de grandeur, et n'est pas comme une centre ni un point comparativement à la sphère du soleil.[3] Par les calculs des parallaxes on calcule les distances du soleil et de la lune à la terre, ainsi que les grandeurs de ces trois corps. Les plus anciens astronomes, dit Ptolémée, entreprirent de déterminer les rapports des diamètres du soleil, et de la lune, soit en prenant, par des instruments propres à mesurer le temps, L'espace de temps que le diamètre de chacun de ces deux astres emploie à monter au dessus de l'horizon, soit en se servant pour cela d'instrument à eau, nommés hydromètres; et Hipparque, par le moyen de la dioptre qu'il construisit en une règle de quatre coudées, en forme de gouttière portant des pinnules perpendiculaires, par lesquelles il considérait les grandeurs des diamètres des luminaires, et les observait avec plus de précision ; Ptolémée l’imita. Admettons donc les observations des anciens, et la construction, de l'instrument d'Hipparque.

Et d'abord nous disons qu'on mesure le temps par l'écoulement uniforme de l'eau, comme le mécanicien Héron l’a enseigné dans ses livres sur les horoscopes hydrauliques. Car on prépare un vase qui a une ouverture, comme celle d’une clepsydre, par laquelle l'eau peut s'écouler uniformément, comme on la fait toujours écouler dans ce genre d'instruments. Celui-ci est fabriqué de façon, qu'au moment où le soleil lance son premier rayon au dessus de l'horizon, on commence à faire couler l'eau. On garde à part l'eau qui s'est écoulée pendant le temps que le disque du soleil met à monter sur l'horizon; ensuite on lui compare l'eau conservée dans un autre vase et qui a continué à couler sans interruption, et uniformément pendant le nycthémère entier jusqu’au lever suivant du soleil pour mesurer de combien la quantité de celle-ci l'emporte sur l'autre qui a été prise pendant le lever du disque entier. Ils disent que ces deux quantités sont proportionnelles aux temps, et que l'eau est à l'eau, comme le temps est au temps. Et ils ont conclu que par là on peut mesurer le disque du soleil par son diamètre, comme n'y ayant aucune différence entre l’arc du soleil soutenu par ce diamètre, et l'hypoténuse', c'est-à-dire, la droite prise pour ce diamètre. D'autres prenant quelqu'un des horoscopes ordinaires, ou instruments a mesurer les heures, tel que le scaphé ou toute autre machine gnomonique, ou quelque fontaine artificielle, mesuraient de même la durée du lever du disque du soleil, et en marquaient la différence d'avec la durée du jour équinoxial, en comparant ces deux durées par leur instrument; ou bien prenant l’espace de temps par un instrument a le mesurer au moyen de l'eau, ils disaient que le rapport des temps équinoxiaux, à la quantité ainsi prise, était le même que le rapport de la circonférence du cercle au diamètre du soleil.

Tout cela, dit Ptolémée, est très peu raisonnable, parce qu'il arrive souvent que le trou se bouche par quelque accident, mais surtout parce que l'eau qui sort pendant an nycthémère n'est pas nécessairement en proportion avec celle qui sort pendant le lever du soleil, vu qu'ordinairement les quantités prises tombent en portions incommensurables; et qu'il n'est pas exact de prendre la droite et l'arc qu'elle soutend, comme étant une même chose. Enfin, ce qu'on cherche, quoiqu'il faille le trouver seulement dans les équinoxes, ne fait pas que nécessairement le même point équinoxial, soit tel qu'il ne rende pas le jour inégal à la nuit. Car, en d'autres saisons que celles des équinoxes, il arrive de fréquents changements dans les temps. D'ailleurs il est impossible de trouver monde, et autre la révolution du nycthémère. En outre, les grandeurs paraissant amplifiées dans les horizons, on ne pourra pas juger avec précision, à cause des différences des grandeurs, sous lesquelles les astres paraissent en différents lieux par l'effet de la différence de l'état de l'atmosphère, pour chacun d'eux. Ils ont pourtant mesuré ainsi le diamètre de la lune, dans le temps de l'équinoxe, parce qu'alors qu'elle est pleine, elle est nécessairement opposée diamétralement au soleil, qui marche aussi dans le point équinoxial. Ils comparèrent l'eau qui sortait pendant le lever du soleil à celle qui sortait pendant le lever de la lune, et ils ne conclurent l'excédent ou l'égalité dans l'un et dans l'autre. Mais cela est ridicule. Car il est impossible de voir à la fois les levers des deux luminaires au moment de l'équinoxe, et il faut de toute nécessité qu'alors la lune paraisse se lever plus tard que le soleil au-dessus de l'horizon, parce qu'elle se meut plus vite que lui vers les points orientaux du ciel, ce qui fait qu'elle est en arrière du lever apparent qui se porte vers les points occidentaux. C'est ce qui a déterminé Ptolémée à chercher par la dioptre d'Hipparque, ce qui est ici en question.

Il prépara une règle susceptible d'être placée sur tous ses côtés, et non moindre que de quatre coudées de longueur. Il en partagea toute la longueur, par une ligne mitoyenne, dans laquelle il pratiqua un canal en forme de hache-où il posa perpendiculairement un prisme régulier, dont il fît entrer la base dans la concavité du canal, de manière qu'elle put en parcourir aisément toute la longueur, le prisme demeurant toujours perpendiculaire sur cette face de la règle. Il inséra de même un autre prisme perpendiculaire mais fixe sur cette règle, pour y être toujours l'oculaire dans l'usage de l'instrument. Il perça ce dernier prisme d'un trou vers le milieu de sa· largeur, mais un peu plus vers la base, c'est-à-dire, du côté de la règle. Il fit à l'autre prisme, que j'ai dit devoir parcourir la règle, deux trous, l'un à la même hauteur que celui du prisme immobile, et dans la même ligne droite, l'autre vers l'extrémité supérieure du prisme mobile et dans le plan des deux autres trous. Soit la règle ΑB, dont la partie Α soit proche de l'œil, et où l'on a implanté le prisme oculaire ΑΦ, et l'autre prisme BΖ qui peut parcourir toute la longueur de la règle. Celui-ci a deux trous placés en ligne verticale, l'un près de la base dans la direction ΑB, l'autre vers Ζ à la partie supérieure de ce prisme mobile ; telle est la forme de cet instrument (vu de profil) :

Voici maintenant comment il faut s'en servir et le placer. Posez la règle dans la direction du levant ou du couchant, quand le soleil· est dans l'horizon céleste parallèle a l'horizon terrestre, si l'air est serein et qu'il n'y ait aucun obstacle qui empoche de viser à l'horizon, l'observateur qui a l'œil au prisme immobile, pousse le prisme mobile vers la partie de la règle qui est exposée au soleil, en l'avançant et le reculant, jusqu'à ce que par les trous Γ, B, des deux prismes, il puisse voir le bord inférieur du soleil, et par les trous ΓΖ le bord supérieur. Car en les visant ainsi, on aura l'angle ΖΓB qui mesure le diamètre apparent du soleil, c'est-à-dire, proportionnellement à la distance du prisme mobile à l'immobile. Cela étant fait, dit Ptolémée, marquons le lieu où nous aurons vu le diamètre du soleil. Et faisant la même chose sur la lune, nous trouverons par les différences de ses diamètres apparents dans ses diverses distances, quand elle paraîtra sous-tendre un arc égal au diamètre du soleil. C'est ce qui a lieu quand le prisme mobile est à une même distance de l'immobile sur la règle, pour la lune que pour le soleil, ce qu'on reconnaît bientôt par la comparaison de l'une et de l'autre. Le diamètre du soleil se trouve toujours le même, et ne paraît pas varier de grandeur, vu par la dioptre, soit dans l'apogée, soit dans le périgée de cet astre. Mais le diamètre de la lune paraît plus on moins grand, dans ses diverses distances. Son diamètre apparent ne paraît égal à celui du soleil qu'alors que la lune étant pleine est dans les points apogées de son orbite, et tout à la fois en conjonction arec le soleil, comme cela arrive dans les éclipsée de soleil. Si cela est effectivement vrai, il n'y a aucune vérité dans ce qu'a dit le péripatéticien Sosigène, dans ce qu'il a écrit sur les révolutions des corps célestes : « Que le soleil dans les éclipses périgées se voit non pas dépasser en entier, mais des bords seulement de son disque, la circonférence de la lune, et éclairer sans empêchement. » Car si on admet cette assertion, ou le soleil montrera différentes grandeurs apparentes, de son diamètre, ou le diamètre apparent de la lune dans les points apogées paraîtra, étant vu par la dioptre, différer de celui du soleil.

Après avoir pris les diamètres apparents, on calcule par eux et par les éclipses, !e rapport réduit à son expression la plus simple, des hémisphères de ces astres embrassés par les rayons visuels qui partent de nos yeux, et on obtient ce rapport par plusieurs méthodes. Par exemple: le diamètre de la lune étant 1, et celui de le terre 3 2/5, celui du soleil sera 18 4/5. Le diamètre de la terre est donc de 2/5 plus grand que le triple du diamètre de la lune, et celui du soleil plus grand de 18 4/5. Les cubes de ces nombres, font voir que celui du diamètre de la lune est 1, celui du diamètre ou axe de la tette 39° 18', et celui du diamètre du soleil 6.644 fois celui de la lune, de sorte que les corps sphériques de ces astres sont dans les mêmes rapports entre eux. Car si tu conçois des sphères autour des diamètres égaux aux côtés de ces cubes, elles seront en raison triplée des diamètres ; or les cube des côtés respectifs sont en raison triplée, donc les sphères seront entre elles en raison triplée de leurs diamètres respectifs. Par conséquent le globe du soleil est soixante-dix fois cent fois plus gros que celui de la terre.

Ce qui vient d'être dit sert aussi à trouver leurs distances. Car le rayon de la terre étant 1, la plus grande distance de la lune dans les syzygies est 64° 10', celle du soleil 1.210; et celle du centre de la terre au sommet du cône d'ombre, 268. D'où il est clair que la lune est de beaucoup surpassée par ce cône dans lequel elle tombe quand elle éprouve des éclipses.

Voilà ce que Ptolémée démontre graphiquement. Mais Aristarque dit que la distance du soleil à la terre est plus de 18 fois, mais moins de 30 fois la distance de la lune à la terre, et que ce rapport est celui du diamètre du soleil au diamètre de la lune, en se fondant sur les hypothèses qu'il a posées d'après les dichotomies de la lune. Il ajoute que le diamètre du soleil est à celui de la terre en raison plus grande que celle de 19 à 3, c'est-à-dire, plus grande que six fois et un tiers de fois, mais moindre que sept fois et un sixième de fois, fondé sur l'hypothèse qui fait la largeur de l'ombre égale à deux lunes. Il est donc évident que ce qu'Aristarque a dit indéfiniment des diamètres du soleil et de la lune comparée, a été déterminé par Ptolémée à quatre cinquièmes de plus que 18, en démontrant que le nombre 19 est trop fort d'un cinquième seulement d'unité, dont il s'en faut que le diamètre de la lune soit à celui du soleil dans le rapport de 1 à 19. En voilà assez sur l'hypothèse de la lune.

Ptolémée continue par l'exposition des hypothèses sur les cinq planètes. D'autres astronomes les traitent chacune à part ; mais ce grand homme croit devoir démontrer auparavant le mouvement de la sphère des fixes, d'un degré en cent ans vers l’orient. Ce mouvement le plus incroyable de tous s’exécute autour des pôles du zodiaque. Il conclut des observations qu'il a comparées, que la distance des étoiles à l'équateur devient pour les unes plus petite, pour les autres plus grande. Et il trouve par ses démonstrations, que le mouvement de cette sphère en longitude, autour des pôles du zodiaque est d’un degré en cent ans, comme je l'ai déjà dit. Mais voyant par les observations, des différences dans les distances des étoiles l'équateur, il décida que chaque distance à l'écliptique est invariable; mais les inégalités dans les distances à l’équateur se montrant fort nombreuses dans les différences d'éloignement de chaque étoile fixe par les changements de déclinaison, Ptolémée n'en prend que deux: L’une pour une étoile plus boréale que l'équateur, et qui va du point tropique d'hiver vers l'orient ; en sorte que depuis le bélier jusqu’au cancer les derniers des arcs de cercles, compris entre elle et l'équateur, sont plus grands que les premiers. L'autre, pour une étoile plus australe que l'équateur, laquelle allant toujours vers l'orient, fait, depuis le solstice d'été, les derniers des arcs de cercles qui sont compris entre elle et l'équateur, de la balance au capricorne, plus grande que les premiers. Ptolémée en a conclu que les étoiles s'éloignent toujours de plus en plus de l'équateur, depuis le bélier jusqu'au cancer, dans l’hémisphère boréal et de la balance jusqu'au capricorne dans l'hémisphère austral. Et il suit des anciens calculs, que les étoiles avancent en longitude, d'un degré par siècle. Pour le prouver, il compare trois observations anciennes au moyen desquelles il démontre par le contact des étoiles avec la lune, leurs positions en longitude et en latitude. Et d'abord il compare l'observation de la pléiade par Timocharis avec celle de la même étoile par Agrippa ; et il trouve que dans les 375 années écoulées entre ces deux observations, la distance de cette étoile au cercle mitoyen du zodiaque, est toujours demeurée de 3° 2/3 en latitude boréale, mais qu'en longitude, elle était du temps de Timocharis, sur 29° 1/2 à l'orient du point équinoxial du printemps: et du temps d'Agrippa sur 33 ¼; la différence 3° 45' de ces deux lieux est proportionnelle aux 375 années, ci-dessus énoncées, d'intervalle entre ces deux observations.

Secondement, comparant encore celle de Timocharis à celle où il a trouvé la latitude australe de l'étoile, la même de 2 degrés, mais sa longitude augmentée d'environ un septième de degré en douze années d'intervalle de ces deux observations, il les compare à une autre observation du géomètre Ménélas, et il trouve dans celle-ci celte même étoile encore à une latitude australe de 2 degrés, mais de 3° 55' plus avancée en longitude vers l'orient, qu'elle n'était dans la première observation de Timocharis faite 391 ans auparavant; et de 3° 45' plus orientale que dans la seconde observation faite 379 ans avant celle de Ménélas. En sorte qu'ici encore on trouve la même proposition entre le nombre des années et celui des degrés.

Ptolémée rapporte une troisième observation de Timocharis, faite sur Antarès dans le front du scorpion, comparée à celle de Ménélas. Il y trouve pareillement cette étoile a la même distance de 1° 1/3 environ de latitude boréale, mais sa position en longitude qui était de 32 degrés à l'orient de l’équinoxe d'automne, du temps de Timocharis, fut observée de 35° 55' par Ménélas: et les 3° 55' de différence pour les 391 ans d'intervalle entre ces deux observations, sont proportionnels à la précession séculaire de 1 degré très peu près. Ptolémée pense qu'il faut admettre ce mouvement général des fixes, d'un degré par siècle, pour sauver les apparences, c’est-à-dire pour rendre raison des phénomènes. Et les hypothèses exposées ici te prouveront la nécessité de ce mouvement pour pouvoir tout expliquer.

Ensuite, examinant quel est le rang des cinq planètes, Ptolémée pense qu'il est plus probable qu'absolument certain qu'elles sont disposées de manière que, celles qui embrassent le soleil dans leur cours en s’éloignant de lui à toute distance, sont au-dessus de lui, mais que celles qu'il embrasse sont au-dessous, sans pouvoir en donner de preuve suffisante. Car l’on entreprend de démontrer que Mercure et Vénus ne sont pas inférieurs au soleil, parce que jamais ils ne passent devant lui, comme la lune le fait, c'est une mauvaise raison, selon Ptolémée, attendu que ce n'est parce qu'ils ne sont pas inférieurs au soleil, qu’ils ne sont jamais en conjonction avec lui, mais c'est parce qu'ils ne sont pas dans le même plan que lui, quand ils sont dans leur conjonction inférieure, comme nous le voyons démontré par les hypothèses de ces astres. Car dans le treizième livre de la syntaxe ou composition mathématique, dans lequel il traite principalement des preuves de leur latitude relativement au cercle mitoyen du zodiaque, dessous du soleil, se trouvent toujours sur leurs épicycles respectifs, soit dans les apogées, dans les périgées, ou, quel que soit le lieu qu'ils occupent, ils sont nécessairement hors du cercle mitoyen du zodiaque. Car ils sont dans les nœuds de l'orbite du soleil et de 1’excentrique sur la circonférence duquel sont portés les épicycles de ces astres qui sont dans les apogées ou dans les périgées, et ces apogées et périgées sont inclinés sur le cercle mitoyen du zodiaque, de toute la quantité de l'écart ou inclinaison, des épicycles sur ce cercle. C'est pourquoi eux et le soleil ne sont pas dans un seul plan, et c'est la raison pour laquelle les épicycles ne se trouvent jamais passer devant lui dans les apogées ni dans les périgées de ces astres, pendant leurs révolutions rapportées au soleil, mais ils suivent toujours la position de l'excentrique qui a été démontré être incliné au cercle mitoyen du zodiaque.

C'est pourquoi étant en chacune des conjonctions dans des plans inclinés à l'orbite solaire ils évitent la rencontre du soleil. Tout cela, quoique maintenant énoncé sans une grande précision, te deviendra plus clair par un exposé plus exact des hypothèses. Mais puisque nous trouvons dans ce que nous avons dit du soleil et de la lune, leurs distances par le moyen de l'instrument appelé parallactique, ainsi que les proportions de leurs distances à la terre, il est bon de savoir qu'on ne peut pas observer par cet instrument les distances de Mercure et de Vénus. Car le principe de l'observation des luminaires est qu'elle doit se faire au moment où ils sont dans le méridien. Mais il est impossible d'apercevoir ces deux planètes, quand elles sont, dans le méridien, à cause de l'éclat du soleil qui éclaire alors l'hémisphère supérieur de la terre, pendant les passages de ces deux astres au méridien. Ainsi, il n'y a aucun moyen de prendre les différences des distancée pour ces astres de la même manière que pour la lune par cet instrument. Nous dirons dans la suite, s'il plaît à Dieu, comment on peut démontrer par les hypothèses le rang qu'elles occupent. Maintenant, après avoir fait mention de l'impossibilité de déterminer les distances de ces deux planètes que l'on dit avoir.une course égale à celle du soleil, passons, aux hypothèses qui servent à expliquer les causes des phénomènes, en ce qu’on dit qu'elles les démontrent analogues aux qualités invariables propres aux corps célestes, comme ayant tous des mouvements uniformes, l'irrégularité, comme nous l’avons dit souvent, dans la complication des différents mouvements n'étant qu'apparente et non réelle. Et nous commencerons par examiner l'hypothèse qui traite de Mercure comme différant le plus de toutes les autres.

Admettons d'abord que pour ces astres, ainsi que pour la lune, on appelle mouvement en longitude celui du centre de l'épicycle sur la circonférence de l'excentrique, et mouvement d'anomalie, le mouvement contraire de l'astre sur son épicycle. C'est pourquoi on dit période de longitude, pour signifier le retour de l'épicycle aux points mêmes d'on il est parti, comme à l'apogée ou au périgée ; et période d'anomalie, pour dire le parcours entier de l'épicycle par l'astre. Ayant donc égard en même temps à ces deux mouvements simultanés, on cherche en combien d'années chacun de ces astres a fait un certain nombre de retours d'anomalie ; et en combien, un nombre de retours en longitude. Et par ces deux sortes de nombres, on trouve les moyens mouvements en longitude, qui· sont ceux des épicycles _: sur les circonférences des excentriques·; et les mouvements moyens d'anomalie qui sont les mouvements journaliers, mensuels et horaires de ces astres eux-mêmes sur les circonférences de leurs épicycles respectifs, somme pour le soleil et la lune.

Ajoutez à cela, que l'anomalie paraissant double pour les planètes, l'une appartenant au mouvement rapporté au zodiaque et aux parties du zodiaque, car les planètes paraissent courir les unes plus vite et les autres plus lentement, comme nous l'avons montré en parlant du soleil ; l'autre anomalie étant celle de la position relativement an soleil·, car leurs digressions loin de lui ne sont pas égales en temps égaux ; cette double anomalie nous étant connue aussi dans la lune, et les hypothèses étant au nombre de deux, l’une qui suppose l'excentrique et que nous avons dit être la plus simple, l’autre qui suppose l'épicycle parcourant un cercle concentrique, les astronomes préfèrent comme par nécessité l'hypothèse de l'excentrique pour l'anomalie qui a rapport aux parties du zodiaque, parce que les planètes dans les apogées et les périgées paraissent a nous autres qui sommée placés au centre de ce cercle, se mouvoir irrégulièrement par rapport aux parties de ce même cercle. Et pour l'anomalie considérée relativement aux digressions et élongations, ils choisissent l'hypothèse de l'épicycle, comme pour expliquer les mouvements de la lune, nous attribuons à l'épicycle ses différentes périodes de configurations relatives au soleil.

Il faut maintenant combiner les deux hypothèses pour expliquer la double anomalie de ces astre, et prendre à part chacune de ces cinq planètes qui se meuvent sur leurs épicycles propres, en même temps que nous n'oublierons pas le mouvement simultané de l'épicycle sur l'excentrique qui le porte, il faut aussi pour ces cinq astres faire deux excentriques, l'un mobile et l’autre immobile, égaux l'un à l'autre, au-dessus de l'un desquels, de celui qui paraît toujours sans mouvement, seront toujours les centres des épicycles, et autour du centre de l’autre qui est le mobile, le centre des épicycles exécutera, comme on le dira, son mouvement incliné en suivant la série des signes d'occident en orient ce qui a été dit jusqu'à présent fera suffisamment connaître les raisons pour lesquelles les épicycles ne se meuvent pas selon les excentriques immobiles. Après ces préliminaires, nous allons exposer l'hypothèse des mouvements de Mercure.

(F. 15) Concevons, comme pour la lune, un plan incliné au cercle mitoyen du zodiaque, d'une quantité d'obliquité mesurée sur le cercle qui passe par les pôles, égale à la distance boréale ou australe en latitude dont Mercure s'écarte du cercle mitoyen du zodiaque ; et que tout ce plan étant celui dans lequel les excentriques sont conçus décrits, se meuve autour du centre du cercle mitoyen du zodiaque suivant l’ordre des signes, en transportant avec lui les apogées et les périgées des excentriques, conséquemment à ce qui a été enserré de la sphère des fixes, d'un degré par siècle. Dans ce plan incliné avançant ainsi d'un degré en cent ans vers l'orient, supposons un cercle excentrique ΑΒ autour du centre Δ, et soit E le centre du cercle mitoyen du zodiaque, dans lequel centre est notre œil ; la droite ΑΒ passant par les deux centres Δ, E, et par l'apogée et le périgée, et ΔΖ au-dessus de Δ comme vers l'apogée, égale à ΔE, et encore ΖH égale à chacune des droites ΔE, ΔΖ ; et autour du point H comme centre, un autre cercle excentrique ΘK égal au cercle ΑB, et dont le rayon soit égal au rayon ΔΑ ; et l'épicycle ΛM ayant son centre toujours sur l'excentrique ΘK, et transporté uniformément et circulairement par la droite MΛ vers les points orientaux, d'un mouvement égal à celui qu'on trouve être le mouvement uniforme de l'épicycle, le diamètre ΛM gardant toujours à l'égard de chacun de ces cercles la même position, et faisant circuler l'astre autour du point Δ, et la droite ΔΛ aboutissant toujours aux mêmes points ΛM sur l'épicycle, et non successivement à d'autres points, comme dans la lune, à cause de la déclivité de l'épicycle, dont le centre soit toujours sur la circonférence de l'excentrique ΘK. Que cet excentrique ΘK, sur lequel est porté le centre de l'épicycle, tourne en sens contraire de cet épicycle, c'est-à-dire, vers les points occidentaux, d'une vitesse égale à celle de ce même épicycle, en sorte que si celui-ci tourne de deux minutes d'espace, en une heure d'occident en orient, celui-là tourne de deux minutes aussi d'espace dans le même temps, tellement que leur distance soit toujours double dans leur mouvement, et que chacun faisant une révolution dans une année relativement aux points du zodiaque, ils en fassent deux relativement l'un à l'autre, parce que leur distance devient double de celle de chacun deux aux points du zodiaque. Enfin, que l'astre se meuve sur l'épicycle, quoiqu'emporté dans le même sens que lui vers les points orientaux ; mais que l'autre excentrique ΑΒ demeure en repos ayant toujours les apogées et les périgées dans les mêmes points du zodiaque, comme nous avons dit que le cercle excentrique du soleil tient toujours l'apogée dans le 5^e degré 30 minutes des gémeaux, et le périgée dans le même degré et demi du sagittaire, que néanmoins l'excentrique ΘK tourne autour du centre Ζ, et non autour de son centre H, en sorte que la droite ΖHΘ qui le fait tourner autour du point Ζ, décrive un petit cercle ou roulette, qui n'excède pas le point Δ, centre de l’excentrique immobile ΑB.

Pour mettre plus de clarté dans l'exposition de cette hypothèse, souvenons-nous que pour le soleil et la lune, nous avons dit que leurs épicycles tournaient d'occident en orient, mais ces astres au contraire, d'orient en occident sur les circonférences de leurs épicycles respectifs, et que par cette raison, ils s'accordaient avec les apparences, vu qu'ils se trouvaient avoir leurs mouvements les plus lents dans les apogées, et les plus rapides dans les périgées. Car, ainsi le soleil dans les gémeaux parcourt un même espace plus lentement en plus de temps, et dans le sagittaire un espace plus rapidement en moins de temps. Et la lune paraît de même se mouvoir le plus vite dans les périgées et le plus lentement dans les apogées, en se transportant suivant la direction d'occident en orient. C'est ce qui est ici posé pour principe. Or je dis que l'astre, s'il se transportait en sens contraire à l’épicycle, ne s'accorderait pas avec les apparences. C'est pourquoi il est nécessaire que tous les deux se meuvent également vers l’orient, savoir l'astre sur l'épicycle, et l'épicycle sur l'excentrique. Car Mercure, de même que les quatre autres planètes paraissent se rapprocher le plus des mouvements moyens et exacts, depuis les apogées, et le moins depuis les périgées. C'est pour cela qu'on dit que la planète et l'épicycle tournent dans le même sens vers l'orient. Car cette supposition sauve toutes les apparences. Or, puisque les épicycles ainsi transportés font les angles de chaque côté de l'apogée égaux, il n'était pas possible de les supposer faire ce transport uniquement sur les excentriques tournants ; sinon ce qui a été dit n'aurait pas lieu. Car les angles faits de part et d'autre des apogées et des périgées à distances égales et en temps égaux, ne peuvent être égaux que dans la supposition des excentriques immobiles, et non si on les suppose mobiles, comme les savants qui ont traité de ces objets, l'ont prouvé par des figures géométriques et par des démonstrations. Ainsi donc puisqu'on voyait par les observations, que non seulement les apogées et les périgées se faisaient toujours en un seul lieu, toujours le même relativement au cercle mitoyen du zodiaque, mais encore de chaque côté, en des lieux différents, il fallait supposer non un seul excentrique avec un épicycle tournant autour de lui, mais un autre cercle excentrique et mobile sur lequel est porté le centre de l'épicycle. Et il sera démontré que les astres font leur plus grande anomalie, non seulement dans l'apogée et dans le périgée de l'excentrique immobile, mais encore en d'autres lieux, et cela est visible dans Mercure, de la manière que je vais dire.

La droite qui passe par les deux centres, l'un du zodiaque, et l'autre qui est dans le diamètre de l'excentrique immobile, aboutit au bélier et à la balance, en sorte que l'apogée est dans l'excentrique, au bélier même, et le périgée à la balance. Mais par d'autres observations plus exactes on a reconnu que l'astre fait ses plus grandes digressions dans les gémeaux et le verseau, et qu'il est plus apogée dans ces signes que dans celui du bélier, et qu'il sera plus périgée, tantôt dans les gémeaux, tantôt dans le verseau. Car s'il est immobile, il faudra absolument un troisième excentrique. S'il n'y en a qu'un, il n'y aura qu'un apogée et un périgée. Cet excentrique tournera donc afin que l'épicycle paraisse avoir chacun de ses points changeant de place, et que l'astre, en circulant sur lui, paroisse apogée de chaque côté du bélier. Mais puisqu'avec deux excentriques, il a fallu que l'épicycle tournât autour de l'un et de l'autre, et relativement à l'un et à l'autre, afin d'être dans les apogées de l'excentrique immobile, et de paraître porté en d'autres apogées par le mouvement de l'excentrique mobile, c'est ce qui l'a fait supposer transporté autour du centre de l'excentrique immobile, mais ayant toujours son centre sur l'excentrique mobile, par la droite qui va du centre de l'immobile à son centre (de lui épicycle), et qui fait toujours circuler et pencher cet épicycle autour de ce centre d'excentrique, comme tu vois dans la figure ci-jointe. Mais l'observation ayant montré que Mercure ne s'écarte pas du soleil, à la distance des planètes supérieures à cet astre, l'épicycle de Mercure est supposé plus grand que celui du soleil, afin que l'un et l'autre de ces deux astres allant avec la même vitesse, la planète Mercure arrivée aux points de l'épicycle circonférence de l'excentrique, paroisse se lever avant le soleil, ou se coucher après lui, en parcourant de plus grands

(F. 16) Car soient les deux excentriques immobiles, ΑΒ celui du soleil, et ΓΔ celui de Mercure, Ζ le centre du cercle mitoyen au zodiaque, et la droite ΖΘ qui traverse les deux épicycles. L’épicycle KΛ étant le plus grand, si quand le soleil est en M ou en N de son épicycle, Mercure est dans les points de contact (de son épicycle et de l'excentrique du soleil), cette planète est alors aperçue dans sa plus grande distance, comme par exemple en K, ou en Λ. Mais comme on a trouvé, par quelques observations, la distance de l’apogée dans la droite qui passe par le 10^e degré du bélier, et le 10^e de la balance ; et que par d'autres observations plus anciennes, on l'avait trouvé dans le 6^e, en calculant d'après l'intervalle des temps de ces observations, on a conclu que l’apogée et le périgée ont un mouvement qui leur fait parcourir un degré en cent ans ; et que par l'effet de ce mouvement, ils font avancer pareillement le plan entier d'occident en orient.

Telles sont les raisons qui ont fait imaginer ces hypothèses. Après avoir ainsi enseigné à expliquer ce qui appartient à Mercure, en passant aux autres planètes, on trouve que la position du centre de leur excentrique est différente de ce qu'elle est pour Mercure. Car supposant tout le reste égal, comme le plan oblique; le mouvement séculaire des apogées et des périgées, d'un degré; l'un des excentriques immobiles, et l'autre en mouvement ; et l'épicycle transporté par la droite qui le fait tourner autour du centre de l'excentrique immobile, tout cela étant commun, on voit la différence des hypothèses dans la manière dont on place le second excentrique. Car on ne prend pas son centre, comme, on l’a fait pour Mercure, au-dessus de Δ pour les quatre autres planètes, mais coupant ΔE en deux parties égales en Ζ, on décrit autour de Δ l'excentrique mobile KΘ et sur cet excentrique, l'épicycle autour de son centre Θ, transporté autour de Δ par la droite ΛΘM, d'un mouvement toujours le même, comme il a été dit auparavant, tant de l'épicycle, que de l'astre vers les signes suivants, tandis que le plan oblique fait tourner les apogées et les périgées dans le même sens, comme on l'a dit, l'autre excentrique tourné en sens contraire de celui de l'épicycle, c'est-à-dire, vers les signes précédents, afin qu'il s'effectue des prostaphérèses par l'effet des mouvements contraires de ces excentriques. (F. 17)

Telles sont les conditions communes des hypothèses établies pour toutes les planètes. Nous allons parler de celles qui leur sont particulières par rapport à l’excentrique. Nous disons donc, qu'on prend pour Mercure, comme pour le soleil et la lune, la raison d'excentricité _r proportionnellement à la plus grande distance au soleil, de sorte que le rayon de l'excentrique étant de 60 parties, l'intervalle des centres en a 3, et le rayon de l'épicycle 21° 30’.

Après avoir démontré ces quantités pour Mercure, comme tu les as vues dans le neuvième livre de la composition mathématique de Ptolémée, on démontre de la même manière que la planète de Vénus fait sur son excentrique et son épicycle, le même mouvement que Mercure, un de ses excentriques demeurant toujours immobile, et l'autre tournant dans le même sens que celui où ses apogées et ses périgée» sont transportés, et son épicycle circulant aussi avec la même vitesse que celui au soleil. C'est pourquoi on les appelle isodromes. Mais l'épicycle de Vénus est plus grand que celui de Mercure, c'est pour cela que Vénus s'écarte du soleil à une plus grande distance, quand elle est dans les nœuds de l'épicycle et de l'excentrique, à cause de la grandeur de son épicycle. L'excentrique, autour du centre duquel l'épicycle est transporté par la droite prolongée depuis le centre de cet excentrique jusqu'au centre de l'épicycle, demeure immobile, l'épicycle ΛM dont le centre est Θ, se mouvant sur le rayon vecteur ΔMΘΛ, l'apogée de l'excentrique immobile a été observé, dit-on, dans le capricorne, et son périgée dans le scorpion. Mais l'autre excentrique qui tourne autour d'un autre centre, qui est le point du milieu entre les deux centres du zodiaque et de l'excentrique immobile, fait circuler l'épicycle, et on démontre par les figures géométriques et par les calculs faits d'après l'observation que des 60 parties du rayon de l'excentrique, il y en a 1 ¼ de part et d’autre entre les centres, et que le rayon de l'épicycle en a 43^P 10'.

Telles étant les hypothèses pour Vénus, on, démontre de même pour les trois autres planètes, qui s'éloignent du soleil à toute distance, leurs proportions d'excentricité, tant par les positions où elles sont en conjonction avec le soleil, que par leurs apparitions acronyques, dans lesquelles chacune des trois se voit sur une droite menée de l'œil au centre de l'épicycle, comme si la planète ne circulait pas sur un épicycle, mais sur un excentrique seulement.

Dans Mars, en effet, ou trouve par le calcul que des 60 parties du rayon de son excentrique, la droite qui joint les deux centres E, Δ, du zodiaque et du cercle autour duquel circule le centre de l'épicycle, en a 12 et le rayon de son épicycle 39 ½.

Pour Jupiter, de même, le rayon de son excentrique étant de 60 parties, la distance des centres en a 20, j'entends du centre E du zodiaque, et du centre Δ de l'excentrique autour duquel l'épicycle est transporté par un mouvement uniforme, ainsi chaque moitié de cet intervalle en a 5 ½, et le rayon de l’épicycle 11 ½.

Pour Saturne, on trouve par les mêmes procédés, que des 60 parties du rayon de son excentrique, l'intervalle des deux centres est de 6° 50'; d'où il est évident que chaque moitié qui est la distance du centre de l'autre excentrique, est de 3^P 25', et le rayon de l’épicycle selon lequel Saturne circule est de 6^P 30'.

C’est par ces méthodes, que l'on trouve pour chacune de ces trois planètes, les différences entre leurs mouvements nommés moyens, et les quantités à y ajouter ou à en retrancher pour rendre tels qu'ils paraissent, savoir: uniforme, le mouvement de l’épicycle autour de l'excentrique, comme parcourant des espaces égaux de l'excentrique en temps égaux; mais inégal, celui de l'astre sur l’épicycle, relativement à notre œil. Car par ce dernier mouvement les angles paraissent différer des angles égaux, comme nous l'avons dit auparavant pour le soleil. C'est ce que montrent les exposés des tables de mouvements. Or, puisque les cinq planètes ont cela de commun, qu'elles paraissent tantôt précéder, tantôt s'arrêter, comme nous l'avons dit au commencement de ce livre, au contraire de ceux qui se sont auparavant appliqués à l'étude du ciel, nous jugeons qu'il démontrer la cause, en vertu de l’hypothèse ou supposition de laquelle le soleil et la lune ne paraissent jamais stationnaires ni rétrogrades, tandis que chaque planète montre ces apparences. Nous disons donc que les épicycles tournant uniformément sur l'excentrique et le concentrique, et ces astres sar les épicycles d'un mouvement inégal, si le mouvement de l’épicycle est plus grand que celui de l'astre sur l’épicycle, duquel, en paraissant dans les périgées aller en sens contraire, il retranche la marche vers les points conséquente de l'épicycle, il n'y aura aucune apparence de mouvement vers les points antécédents du monde, parce que la quantité additive dont l'épicycle avance vers les points conséquente, est plus grande que la quantité soustractive dont l'astre avance vers les points antécédents. Si au contraire le mouvement soustractif de l'astre est plus grand que le mouvement additif de l’épicycle, alors l'astre paraîtra marcher vers les points antécédents. Mais quand la différence de ces deux mouvements sera nulle ou presque nulle, l'astre paraîtra stationnaire. Cet énoncé deviendra clair par la démonstration suivante :

(F. 18) Soit l'épicycle ΓΔ en mouvement autour du cercle concentrique ou excentrique ΑB, vers les points Δ suivants ou conséquents, et que l'astre aille sur cet épicycle dans le même sens. Il est évident qu'en parcourant l'arc ΓΔ cet astre ajoute au mouvement de l'épicycle vers Δ. Mais en parcourant l'arc périgée que j'appelle ΔΓ, cet arc devient soustractif, comme se portant en sens contraire à celui selon lequel il a parcouru l’arc apogée de l'épicycle, alors il paraît aller vers les points antécédents Γ.

Le mouvement de l'épicycle, qui se fait toujours vers les points conséquents, suivants, orientaux, étant plus grand, l'arc soustractif est invisible à nos yeux, et paraît s'ajouter à la marche de l'astre ; mais le mouvement soustractif de l'astre dans les points périgées de l'épicycle étant plus grand, l'astre ne semble plus aller vers les points suivants, par la raison d'un moindre mouvement, il paraît au contraire aller toujours alors vers les points antécédents. Mais quand les différences des arcs soustractifs et des arcs additifs sont à leur minimum, l'astre paraît stationnaire à ceux qui le regardent. Il suffit de représenter graphiquement les points où se fait tout ce qui est supposé, pour voir que la planète paraît stationnaire pour la raison qui vient d'être exprimée. C'est la manière dont l'explique Apollonius de Perge, la même dont s'est servi Ptolémée dans le douzième livre de sa composition mathématique, et qui suppose également que l'épicycle est porté sur un concentrique.

Si nous menons depuis noire œil une droite qui réponde au rayon visuel, et qui coupe l'épicycle en un point tel que la moitié de la portion de cette droite dans l'épicycle, soit à sa portion depuis notre œil jusqu'au périgée, en même raison que la vitesse de l'épicycle à la vitesse de l'astre, le point par lequel cette droite passe dans l'arc périgée, marque l'intervalle des rétrogradations et des directions, en sorte que l'astre paraisse stationnaire en Γ.

(F. 19.) Car soit décrit le cercle ΑΔBΓ autour du centre, et son diamètre ΑB, qui, prolongé, aboutisse au point Ζ où l'œil est supposé être. Prenez dans l'arc périgée de ce cercle un point T, tel que la droite ΖT traversant le cercle, la moitié de TΓ, c'est-à-dire, TH, soit à ΖT qui est la droite menée de nos yeux jusqu'à l'arc périgée, vu de notre œil, en même raison que la vitesse déterminée de l'épicycle, à la vitesse déterminée de l'astre. Car on mesure les espaces parcourus, et car eux on détermine les vitesses, que nous disons être distinguées les unes des autres au moyen du calcul et des prostaphéreses, (quantités à ajouter ou à retrancher) et l'on prouve que la planète arrivée en T, paraît s'arrêter, quoique devant aller vers l'occident; et qu'elle fait sa première station, et décrit l'arc d'antécédence TB. La moitié du temps qu'elle y emploie se terminant en B. Si donc on prend de chaque côté de B un arc égal à BT, on aura l’arc BΘ pour la seconde moitié terminé au point Θ, après laquelle l'astre paraît continuer suivant la série des signes.

On prouve ainsi, par une construction graphique, que cela est possible _t au moyen de la droite TΖ menée au point Γ, dans le rapport donné ; et que par cette droite seule on peut expliquer les apparences des stations, pour lesquelles on a dressé des tables de ce qui précède, où l'on a mis les intervalles des plus grands et des moindres mouvements, ainsi que ces mouvements même ; et on y voit pour chaque planète, le temps qu'elle emploie à rétrograder, car ce temps n'est pas le même pour toutes. Et c'est la cause pour laquelle les planètes paraissent tantôt plus, tantôt moins de temps aller en arrière ; et pour laquelle Mercure et Vénus apparaissent plus ou moins longtemps à l'orient en avançant vers l'occident, comme aussi dans leurs apparitions du soir, cette cause lait que leurs mouvements paraissent ou moyens ou les plus grands que ces astres puissent avoir ; et c'est pour la même cause encore qu'on les voit sous le soleil se mouvoir plus ou moins vite. Nous avons décrit brièvement ces objets traités plus au long par plusieurs auteurs.

Mais après avoir parlé des rétrogradations et des stations, il conviendrait de parler aussi du mouvement des cinq planètes en latitude, et de leur position sur leurs épicycles. Ptolémée l’a fait d'une manière très satisfaisante dans le treizième livre de sa composition. L'excentrique de toutes les planètes leur paraît incliné au cercle mitoyen du zodiaque, en sorte qu'un des demi-cercles est plus boréal, et l'autre plus austral que l'écliptique, et que l'épicycle même n'est pas dans un même plan que l'excentrique sur la circonférence duquel son centre est porté, mais qu'il est incliné sur l'excentrique qu'il ne fait que toucher.

Quant aux trois autres planètes, Saturne, Jupiter et Mars, on dit d'après les observations, que quand elles parcourent le segment apogée de l'excentrique, elles paraissent toujours plus boréales que le cercle mitoyen du zodiaque, et surtout quand elles sont dans les périgées de leurs épicycles respectifs, de manière que si les épicycles étant dans une situation, telle que celle des apogées, ces astres paraissent se porter davantage vers le cercle mitoyen du zodiaque, et dans les périgées au contraire s'en éloigner. Mais quand elles passent dans le segment périgée, alors elles paraissent plus australes que le cercle mitoyen du zodiaque. Et l’on en conclut que les segments boréaux des excentriques sont plus proches du cercle mitoyen du zodiaque, que les segments austraux ; et que des deux diamètres des épicycles, dont l'un passe par les points apogée et périgée, et dont l'autre est perpendiculaire au premier, celui-ci est penché vers le cercle mitoyen du zodiaque, par l'effet de l'inclinaison qui l'approche du centre du zodiaque, tandis que le diamètre perpendiculaire est tangent à la circonférence par le seul centre de l'épicycle. Dans Vénus et Mercure, l'excentrique étant incliné sur le cercle mitoyen du zodiaque, et l'épicycle sur l'excentrique, on dit qu'on a observé une différence d'avec les trois autres planètes, savoir, que dans ces deux, les limites boréales ne sont pas précisément dans les apogées des excentriques, mais que dans ces trois, les limites boréales sont piste dans les apogées de ces cercles, quoiqu'il y ait pour Saturne une distance de 50^p, moindre pour Jupiter où elle n'est que de 20, et la plus petite pour Mars. On a aussi reconnu dans Vénus et Mercure, que l'excentrique a un mouvement sur le plan du zodiaque, proportionnel an mouvement de l'épicycle sur l'excentrique, en sorte que quand l'épicycle arrive aux nœuds on l'excentrique coupe le cercle mitoyen du zodiaque, l'excentrique et le zodiaque sont comme appliqués l'un sur l’autre dans un seul plan. Mais l'épicycle passant dans l'autre demi-cercle, l'excentrique se transporte aussi en d'autres parties du zodiaque; que dans Vénus, le premier demi-cercle, qui contient l'apogée, devient austral, et l’autre demi-cercle où est le périgée devient boréal, et que l'épicycle, en faisant tourner le périgée, paraît de part et d'autre dans les apogées et les périgées, au nord du cercle mitoyen du zodiaque. Mais que dans Mercure, au contraire, la position de l'apogée est dans la limite australe, et que le transport du demi-cercle boréal se fait vers le sud, en sorte que l'épicycle parcourant les périgées paraît plus austral. Tout ce qui vient d'être énoncé, ainsi que ce qu'ont dît sur cette matière ceux qui en ont traité, va te devenir clair par les figures suivantes :

(F. 20) Soit le cercle concentrique ΑBΓΔ dans le plan du cercle mitoyen du zodiaque, et l'excentrique EBΖΔ incliné sur lui, leur intersection commune BΔ passant par le centre H du cercle mitoyen du zodiaque; et soit Θ le centre de l'excentrique. Soit, dans le plan ΑBΓΔ, menée de H, la droite HΑ perpendiculaire à BΔ, et dans le plan de l'excentrique la perpendiculaire à la même section BΔ. L'inclinaison de ces deux droites est donc l'angle ΑHE des deux plans du cercle mitoyen du zodiaque et de l'excentrique, dans lesquels elles sont tracées. Le point E est la limite boréale de l'excentrique, et le point Ζ est sa limite australe. Décrivons autour du centre E un épicycle incliné à l'excentrique, prolongeons le plan qui passe par EKΛ, et qui fait, par son prolongement, la section KΛ dans l'épicycle, laquelle forme avec la droite EH l'inclinaison de l'épicycle sur l'excentrique.

Concevons l'apogée de l'épicycle en K, et le périgée en Λ. Il est clair qu'ainsi l'angle HEΛ est l'inclinaison de cet épicycle sur l'excentrique, le périgée Λ étant vers l'ourse (boréal.) Soit dans le plan de l'excentrique, MN perpendiculaire à KΛ, et conservant sensiblement son parallélisme, à l'égard du plan de l'excentrique. L'épicycle étant arrivé en B, qui est le nœud descendant de l'astre sortant de son trajet boréal, l'épicycle en ce point, place son diamètre qui passe par l'apogée et le périgée, en une seule ligne droite avec la section commune BΔ, mais la droite MN est à angles droits sur cette section commune, et toujours dans le plan du cercle mitoyen du zodiaque. C’est pourquoi il est évident que l'épicycle est dans le plan du cercle mitoyen du zodiaque, et qu'ainsi chacune des trois planètes paraît toujours dans le plan du zodiaque, en quelque point qu'elles soient de leurs orbites. L'épicycle étant dans la limite australe Ζ, son inclinaison sur l'excentrique, est mesurée par l'angle HΖΛ égal à l'angle HEΛ, et le périgée Λ austral, la droite MN dans le plan de l'excentrique est perpendiculaire sur KΛ, et tangente au point Ζ du cercle. Continuant d'avancer vers l'autre nœud qui est l'ascendant Δ, d'où il remonte dans l'hémisphère boréal, que la ligne KΛ qui passe par les apogées et les périgées, fasse une seule ligue droite avec la section commune des cercles, de sorte qu'elle se confonde avec la BΔ; mais que la ligne MN et le plan où elle est tracée, soient dans un même plan que le cercle mitoyen du zodiaque, en sorte que, encore où est l'épicycle, là paraît l'astre comme étant dans le cercle mitoyen du zodiaque. Mais quant aux trois planètes, l'inclinaison de leur excentrique respectif demeure constante, telle qu'est celle que mesure l'angle EHΑ. Mais on dit que dans Vénus et Mercure, cette inclinaison change à mesure que l'épicycle avance ; savoir : celui de Vénus dans l'hémisphère boréal, celui de Mercure dans l'hémisphère austral; je veux dire, que quand l'épicycle est dans le nœud ascendant, le cercle excentrique tel que EΖ est dans le plan du cercle mitoyen du zodiaque tel que ΑB, non que le point E y soit confondu avec le point Α, car s'il l'était, il ne serait pas excentrique, mais parce que ces deux cercles s'entrecoupent dans un seul plan. Et il est clair que leurs sphères ayant de la profondeur, on conçoit à différentes hauteurs les points E, Α, Ζ, Γ, par lesquels passe une seule ligne droite.

Mais quand l'épicycle est dans le nœud ascendant Δ, il fait, comme on l’a dit, une seule ligne de la droite KΛ avec la commune section des cercles, tandis qu'il est lui-même dans le plan du cercle mitoyen du zodiaque. Mais quand l'épicycle monte de Δ en E limite boréale de l'excentrique, en augmentant rapidement son inclinaison sur lui, alors l'excentrique s'élève dans l'hémisphère plus boréal que le cercle mitoyen du zodiaque, de la quantité dont E avance vers les ourses depuis le point Δ de la droite qui est la commune section, et alors son plus grand écart est l'arc de Α en E du cercle qui passe par les pôles du zodiaque. Alors aussi, la plus grande inclinaison de l'épicycle sur l'excentrique est l'angle EHΛ. C’est ce qui arrive, quand l'épicycle est au point le plus apogée. Mais quand après son départ de ce point, il a gagné le nœud descendant B, l'excentrique rejoint le cercle mitoyen du zodiaque sous l'angle EHΛ, en même temps que le point E revient sur la droite de commune section, en suivant toujours la même proportion, de sorte qu'en B les trois cercles sont réunis dans un seul plan ; savoir : l'excentrique, le cercle mitoyen du zodiaque, et l'épicycle, en gardant leur position relative, comme trois cercles décrits se coupant dans un seul plan, en sorte que l'écart de ces cercles entre eux diminue en même raison que leur inclinaison.

Mais quand l'astre de Vénus après avoir passé le nœud descendant, commencera à parcourir le segment périgée BΖΔ de l'excentrique, en allant de B en Ζ, ce segment écarté du cercle mitoyen du zodiaque, ne s'écarte plus comme auparavant vers le demi-cercle austral, mais vers le boréal du cercle mitoyen du zodiaque, en sorte que le point Ζ est plus boréal que le point Γ dans le cercle qui passe par les pôles du cercle mitoyen du zodiaque, ce qui rétablit l'écart · proportionnel des plans. Et l'avance de Ζ vers le nord, augmente l'inclinaison de l'épicycle sur l'excentrique, jusqu'à ce que, au périgée Ζ, il soit dans son plus grand écart de Γ sur l'arc du cercle, ou colure, qui passe par les pôles (de l'écliptique), l'angle HΖΑ, qui est le plus grand de cet écart; étant égal à l'angle EHΔ. De là, l'épicycle parcourant le segment ΖΔ, l'inclinaison de l'épicycle sur l'excentrique se met dans le plan ΔΑB du cercle mitoyen du zodiaque, et le segment austral BΖΔ de l'excentrique devient plus boréal que l'austral BΓΔ du concentrique. Car on dit qu'on a vu, par les observations, que cette planète, dans sa limite la plus boréale, paraît plus boréale que le segment boréal du cercle mitoyen du zodiaque; mais que quand elle est à sa limite la plus australe, elle ne paraît jamais plus australe que le segment austral du cercle mitoyen du zodiaque, mais qu'au contraire, elle est toujours plus boréale que la demi-circonférence de ce cercle la plus proche de cette planète, soit que celle-ci soit dans l'hémisphère boréal, ou dans l'hémisphère austral. C'est pourquoi il a été nécessaire de supposer cette contrariété de marche des segments de l'excentrique, pour expliquer les apparences, et pour montrer que l'astre sur l'épicycle, parcourant l'excentrique, paraît toujours plus boréal que l'orbite solaire, de quelque côté qu'il soit de cette orbite.

On suppose le contraire pour Mercure. L'excentrique parcourant son segment apogée depuis le nœud ascendant, le point E devient plus borla! que Α, jusqu'à ce qu'il fasse le plus grand angle d'inclinaison de l’épi cycle sur l'excentrique. Αlors le point E, limite boréale, à sa plus grande distance du point tropique Α, est vu plus austral que celui-ci sur le cercle (ou colure) qui passe par les pôles, et nécessairement la planète en ce point E paraît plus australe que le soleil dans le point tropique d'été. Ensuite, les plans se rapprochent par la diminution de leur inclinaison, jusqu'au nœud descendant, où les plans se confondent en un seul. L'astre partant de là, les plans de l'excentrique et du cercle mitoyen du zodiaque recommencent à s'écarter, de manière que l'astre arrivé en Ζ paraît toujours plus austral que le segment austral du cercle mitoyen du zodiaque, c'est ce que montrent les observations en conséquence desquelles on a établi ces hypothèses. Ainsi donc chacun des segments de l'excentrique de Mercure, tant l'apogée que le périgée, est réputé être toujours plus austral que le segment ΑΖΓ de l'orbite solaire, et doit être l'un et l'autre dans un seul plan par rapport à elle quand l'astre est dans les nœuds. Il faut donc y admettre une pareille rencontre des segments de l'un et de l'autre cercle, et ensuite un pareil écart, chose que n'exigent pas les excentriques des trois planètes, Saturne, Jupiter et Mars. Car ils sont immobiles ; et chacun de ces trois astres, quand il parcourt le segment apogée, est plus boréal que le demi-cercle boréal de son excentrique, relativement au cercle mitoyen du zodiaque, et plus austral que le demi-cercle austral, comme nous avons dit pour la lune.

Telles sont les différences dans les mouvements des cinq planètes en latitude, et leurs causes. Ajoutons que l'on dit que les limites boréales, comme E, des excentriques, sont aussi les plus apogées, en sorte que leur plus grand écart répond à leur plus grande latitude; et aussi, que les autres limites se trouvent dans les périgées, tellement que le point Ζ qui est la limite de l'écart en latitude, est aussi le moindre écart de l'astre relativement au centre du cercle mitoyen du zodiaque. Mais dans les trois autres planètes, il en est tout autrement pour les points les plus apogées, et pour les points les plus périgées, comme nous l'avons montré pour le soleil. Car le point le plus apogée est pour l'une dans 5 ½ degrés et quelques minutes des gémeaux, tandis que la limite boréale est au premier degré du cancer, auquel degré est le point tropique. Ainsi l'excentrique a sa limite boréale en un point, et son apogée en un autre point, en sorte que la plus grande distance en profondeur, n'est pas la même que celle en latitude, et je dis que cela a lieu pour Saturne. Car Ptolémée rapporte qu'il a observé sa limite boréale dans le 3^e degré de la balance, à très peu près, et son apogée en 20° 10' du scorpion, à la distance de 46 degrés 50' l'un de l'autre; dans Jupiter, l'apogée en 11° 9' de la Vierge, et la limite boréale en 1° de la balance ; et dans Mars, la limite boréale à la fin du cancer près de l'apogée.

C'est ainsi que nous exposons, après les avoir rassemblées de toutes parts, les hypothèses qui ont été imaginées pour expliquer les phénomènes célestes. Et à cet exposé, afin que tu les comprennes plus aisément, je joindrai les moyens dont on se sert ordinairement pour trouver ce que l'on cherche.

Ptolémée ayant donné dans le cinquième livre de sa composition mathématique, la description d'un instrument utile pour les observations de la lune, c'est-à-dire, de celui qu'on nomme astrolabe pour les sept orbites, je vais t'en exposer la fabrique et l'usage, le mieux qu'il me sera possible. Le météoroscope diffère de l'astrolabe en ce que par celui-ci on peut observer tout ce qu'on peut observer par l'autre, et plusieurs autres objets utiles dans l'astronomie, par le grand nombre de cercles dont l'astrolabe est composé. Car il consiste dans neuf cercles, et il suffit pour toutes les observations ; voici maintenant comment on le construit:[4]

On commence par préparer deux cercles de diamètres égaux, et à limbes quadrangulaires. De deux des quatre faces de ces limbes, l'une est convexe en dehors, l'autre est concave en dedans, toutes deux parallèles et séparées par la profondeur qui est leur intervalle, comme je l'ai dit plus haut. On enclave les deux cercles l'un dans l'autre de manière qu'ils restent perpendiculaires l’un sur l'autre, à quoi on parvient si les arcs compris entre les points correspondants de ces cercles sont égaux. Et voici la manière de les enclaver : après avoir fait une entaille dans la face intérieure et concave de l'un, jusqu'à moitié de la profondeur ou largeur de cette face, et de même dans la face extérieure ou convexe de l'autre, ces entailles étant égales dans l’un et l'autre, de manière qu'en s'emboitant par ces entailles entrées l'une dans l'autre, les deux cercles se mordent mutuellement jusqu'aux deux surfaces extérieure et intérieure de leurs limbes, les extrémités de ces entailles diamétralement opposées n'excéderont pas les bords et les deux cercles rendus ainsi perpendiculaires l'un à l'autre, serviront l'un de colure passant parles pôles du zodiaque, l'autre de cercle mitoyen du zodiaque ; et leurs intersections dans les entailles représenteront, l'une le premier degré au cancer, l'autre celui du capricorne, car c'est au commencement des signes, que le colure des solstices coupe le cercle mitoyen (écliptique.) Après quoi on masque, sur le cercle colure, à la distance d’un quart de cercle loin de l’enclave, le pôle de l'autre cercle, c'est-à-dire du mitoyen du zodiaque. On insère dans ce point un petit cylindre qui déborde en dehors et en dedans, et qui sert à faire tourner, sur ce point et sur celui qui lui répond diamétralement où l’on a fait également entrer un pareil cylindre, deux autres cercles ajoutés aux deux premiers, et attachée sur ces cylindres. L'un de ces cercles ajoutés est extérieur et contient dans sa concavité la surface convexe du colure, l'autre est intérieur et est contenu par sa convexité dans la surface concave des deux premiers cercles taxes entre les deux ajoutés. Après avoir construit celte machine, on divise ainsi en 360 parties égales l’anneau ou cercle qui représente le mitoyen du zodiaque : on écrit sur douze divisions égales de la surface convexe les noms des douze signes. On subdivise ensuite sur les faces latérales du limbe, chacune des douze parties qui répond à un des douze signes, en cinq portions égales, et depuis le milieu de chaque face latérale jusqu'à la concave, on ajoute les divisions de degré en degré. Quand à l'anneau le plus intérieur, on divise ses faces latérales de cinq en cinq degrés, et chacun de ces espaces en ses degrés depuis le milieu de la face jusqu'à sa circonférence concave et intérieure. On insère dans le bord concave de l'anneau le plus intérieur un plus petit anneau dont le limbe soit aussi épais, mais moins large· que celui du cercle dans l’intérieur duquel il est adapté, afin qu'il puisse y glisser sans en sortir, quand on le fait aller et venir dans la concavité de ce cercle intérieur. On implante sur ce petit anneau deux prismes égaux ou visières diamétralement parallèles, et regardant le centre de l'instrument, avec un trou dans chacune diamétralement opposé l'un à l'autre, afin de pouvoir viser au travers. Nous avons dit comment il faut ajuster toutes ces pièces ensemble. Cet instrument est ainsi composé de cinq cercles en anneaux dont le plus intérieur est le plus petit de tous. Au-dessus est celui qui est gradué sur la largeur de son limbe. Par-dessus sont le cercle mitoyen du zodiaque, et l'extérieur qui passe par les pôles de ce dernier. On y ajoute les deux cercles dont nous avons parlé au commencement de ce traité, par lesquels on trouve les mouvements boréaux et austraux du soleil, en portant sur la circonférence convexe du cercle extérieur, le côté du pentédécagone, depuis le point où il est attaché par le pôle au colure,[5] dans l’arc compris entre le pôle du zodiaque et la section du cancer.

Et à l'extrémité de ce côté, on implante perpendiculairement un cylindre avec un autre point diamétralement opposé, chacun d'une hauteur égale à la largeur du limbe du cercle extérieur. Après quoi nous disposons tellement ces deux cercles relativement aux cinq autres susdits, qu'en prenant par le moyen de ceux-ci les hauteurs du soleil et de la lune, suivant leurs mouvements en latitude, le plus extérieur de tous ces cercles tourne sur les pôles de l'équateur, tandis que les deux par lesquels on prend les astres, tournent sur les pôles du zodiaque en longitude.

Telle est la construction de cet instrument. Voici maintenant comment on s'en sert : après l'avoir établi sur un plan parallèle à l'horizon, par le moyen d'un soutien dans la direction de la méridienne, si nous voulons prendre le lieu du soleil, nous faisons tourner le cercle ou colure qui passe par les pôles, et qui est le quatrième au-dessous du plus extérieur, jusqu'à ce que le cercle qui représente le zodiaque tournant avec lui, soit exactement ombragé sur sa surface concave. Car il est évident qu'alors le zodiaque de l'instrument sera dans le même plan que le zodiaque céleste. En le tenant dans cette situation, nous ferons aller le cercle extérieur jusqu'à ce qu'il soit lui-même ombragé sur sa surface concave aussitôt que cela est, c'est-à-dire, quand l'ombre des demi-circonférences qui regardent le soleil, par leur convexité, tombe sur la concavité des demi-circonférences opposées, nous disons que le degré qui répond au soleil sur le zodiaque, dont la surface supérieure est divisée comme je l'ai dit, est le lieu du soleil. Connaissant ainsi le point qu'il occupe dans le ciel, nous trouverons également le lieu de la lune quand elle sera au-dessus de l'horizon, en tournant vers elle le cercle intérieur, et le petit cercle, jusqu'à ce nous l'apercevions par un de nos yeux, au travers des pinnules de ce petit cercle. Car il sera plus aisé de trouver ainsi son lieu en longitude, par le degré auquel elle répond dans le zodiaque, et sa latitude boréale ou australe, par le degré du cercle intérieur perpendiculaire au cercle mitoyen du zodiaque. Car autant se trouvera grande la distance de ce degré à la section commune du cercle colure et du zodiaque, autant sera grande la distance de la lune au cercle mitoyen du zodiaque, de part ou d'autre de ce cercle. Après avoir pris ainsi, après le jour, le lieu de la lune, par le moyen de celui du soleil pris pendant le jour, on peut aussi, le lieu de la lune en quelque nuit que ce soit, étant connu par le secours de la table des éphémérides, avoir par son moyen le lieu des étoiles, en transportant le cercle mobile vers l'étoile brillante qu'on veut observer. Car on prendra la distance de cette étoile à la lune, comme on a pris la distance de la lune au soleil. Si la lune n'est pas au-dessus de l'horizon, en calculant par les tables à quel point du zodiaque la lune répondrait si elle paraissait, et en regardant l'étoile par les pinnules, on voit la distance de cette étoile à ce point, et par conséquent à la lune. C'est ainsi que Ptolémée, dans le septième livre de sa composition mathématique, a trouvé que l'étoile du cœur du lion était, de son temps, sur le 2^e ½ degré de ce signe, après avoir été observée par Hipparque au 30^e du cancer. Il prit, pour faire cette comparaison, pendant la nuit, la distance de la lune au lieu du soleil, pris pendant le jour, en tenant compte du chemin que la lune avait fait dans l'intervalle des observations des deux astres, je parle du mouvement diurne pendant le jour où la lune fut observée, et du mouvement nocturne pendant la nuit de l'observation du cœur du lion. Ayant ainsi trouvé la distance du lieu de la lune au lieu de l'étoile observée, il calcula la distance de celui-ci au cercle mitoyen du zodiaque, à l'aide de la distance du lieu de la lune à ce cercle.

Tels sont la construction et l'usage de l'astrolabe. Tu feras bien de te procurer cet instrument pour les observations surtout de la lune, et pour celles qu'on ne peut faire sur les étoiles, que par le moyen de la lune, comme Ptolémée l'a très bien écrit. Nous avons dit, dans le préambule, quelles avaient été les causes qui avoient poussé les hommes curieux de ce genre de connaissance à les étudier. Nous allons exposer les réponses à toutes les difficultés faites sur les suppositions, en admettant les unes et en examinant les autres.

La première difficulté consiste dans le mouvement, tantôt accéléré, tantôt retardé de sept astres mobiles. Car il paraissait étonnant d'y voir tout à la fois de la régularité et de l'irrégularité, et l'on dit que les excentriques et les épicycles réfutent cette objection, parce que le mouvement qui y est régulier paraît se faire irrégulièrement, par l'effet de la position de ces cercles qui ne sont pas concentriques au cercle mitoyen du zodiaque, tandis que c'est de ce centre même que noue voyous ces mouvements. Deuxièmement, les transports boréaux et austraux de la lune et des autres planètes, et différents pour chacune, tandis que le soleil continue toujours sans aller d'un coté ni de l'autre. La cause de ces mouvements est que les limites boréales ne sont pas les mêmes, et ne répondent pas aux mêmes points du cercle mitoyen du zodiaque, mais sont différentes pour chacun de ces astres, tandis que les limites boréales de la lune changent de place, ce qui fait qu'elle paraît tantôt les passer, tantôt les précéder. Troisièmement les anticipations et les retards qui se remarquent dans les cinq planètes seules. J'ai déjà expliqué la cause de ces apparences qui consiste en ce que le mouvement de l'astre sur l'épicycle, étant plus rapide que celui de l'épicycle, sur l'excentrique, fait que ces astres sur ces cercles, devenant périgées, paraissent mouvements soustractifs, parce que leur plus grande vitesse les porte vers les points précédents ou occidentaux, tandis que le mouvement des cercles se fait vers les points suivants ou orientaux ; car le mouvement de tout cercle, dans l'un ou l'autre des demi-cercles, est contraire à celui qui se fait dans le reste du cercle. Si donc au mouvement de l'astre, en sens contraire _y tu ajoutes la vitesse plus grande du cercle, tu auras la raison de l'apparence de la rétrogradation. Cela n'a lieu que pour les cinq planètes, parce qu'elles seules, dit-on, vont plus vite sur leurs épicycles, que ces épicycles. Quatrièmement, les différentes digressions de ces planètes, à toute distance dans les unes, et non dans les autres, et dans celles-ci plus ou moins. On en attribue la couse aux épicycles, ceux de Mercure et de Vénus, se mouvant avec la même vitesse que le soleil, et non ceux des autres planètes, et étant plus grands que celui du soleil, et celui de Vénus plus grand que celui de Mercure. C'est pourquoi ces astres ne s'écartent pas a toute distance à cause de la vitesse égale de leurs épicycles, et étant toujours supérieurs au soleil, et devenant invisibles à cause de la grandeur excédente de leurs épicycles, sur lesquels ils peuvent paraître dans leurs écarts de part et d'autre, parce que leur épicycle est plus grand, les apparitions du matin et du soir, de Vénus et de Mercure se faisant alternativement sur leurs épicycles. Car c'est par le mouvement soustractif que ces deux planètes font leurs apparitions du matin et par l’additif celles du soir. Ptolémée a dit, dans le treizième livre de sa composition mathématique, que les apparitions singulières de Mercure, au soir, manquent après celles du matin, vers le commencement du scorpion, et qu'au contraire celles qui devaient se faire le matin ne se faisaient point vers le commencement, du taureau, il en assigne les causes dans la différence des nombres de l'apparition de Mercure en ces signes d'avec la fin de l'apparition, de sorte qu'avant d'avoir fait son apparition, il termine sa digression, et revient sur ses pas par cette raison. C’est ainsi qu’il démontre qu’au commencement du taureau, par le résultat du calcul, l'astre ne peut être vu qu'à 22° 16' de distance du soleil, mais que la fin de sa digression ne se fait qu’à 12° 13' de distance, donc il ne paraît pas à 22° 16' de distance, c'est qu'il revient sur ses pas quand il a terminé sa digression qui n’excède pas 22° 13’ de distance au soleil, avant que de pouvoir devenir visible le matin, et il s'ensuit que son apparition du matin manque dans les premiers degrés du taureau. Voilà comment on tâche de rendre raison de ces apparences singulières.[6]

Cinquièmement, la grandeur des astres paraissant tantôt plus, tantôt moins forte, attribuée aux mouvements de leurs excentriques et de leurs épicycles qui les portent tantôt plus près, tantôt plus loin de la terre, et les rendent invisibles aux yeux des spectateurs. C’est ce qui fait paraître le soleil plus grand à l'horizon, l'atmosphère y étant plus dense et plus humide, fait aussi bien voir les différences de l'apogée et du périgée dans les astres vus par les observations.

Sixièmement, les apparitions de ces astres dans leur proximité du soleil, et leurs disparitions leur éloignement de cet astre en différents lieux, attribuées à leurs différentes latitudes. Tu le verras par les inclinaisons des cercles qu’ils décrivent relativement au mitoyen du zodiaque, car rien ne s'y oppose, Vénus répondant aux mêmes degrés que le soleil quand elle le rencontre. Mais parce que son orbite est plus boréale que l’orbite solaire, on la voit se lever avant lui, quand elle parcourt la portion boréale de son orbite, et c est ce qui fait attribuer à ses écarts en latitude, les singulières apparitions dont Ptolémée a fait mention telles que au commencement de son lever matutinal qui se fait seulement deux jours après le coucher du soir ; et dans la Vierge, 16 jours après. Tu as tout cela démontré géométriquement dans les apparitions singulières.

Septièmement, l'ordre et le rang des astres mobiles. Nous en avons déjà parlé. Quelques-uns croient l'avoir trouvé par le moyen des périgées et des apogées. L'apogée de la lune étant plus proche de la terre que le périgée de Mercure ; l'apogée de celui-ci plus que le périgée de Vénus, et l'apogée de Vénus plus que le périgée du soleil ; et ils placent ces astres d'après ces apparences. Car prenant comme démontrée la plus grande distance de la lune à la terre, égale à 64,10 rayons terrestres; et la plus petite du soleil, égale à 1.160, la différence d'avec 6.410, est 1.096 à peu près. En supposant d'abord qu'il n'existe pas de vide dans l'univers, mais que tous les intervalles sont remplis par des sphères mitoyennes, les philosophes croient devoir examiner les rapports des apogées et des périgées de Mercure et de Vénus, pour savoir s'ils peuvent satisfaire à ces nombres. Or, ils trouvent quel intervalle démontré depuis l'apogée de l'épicycle jusqu'au centre du zodiaque, est à celui depuis le périgée jusqu'au même centre, dans le rayon de 91^r 30' à 33' 4'. Et en disant : comme 33^r 4' sont à 91^r 30', ainsi 64 ^r 10' qui est la plus grande distance de la lune, sont à un quatrième terme, qu'on trouve être de 177^r 33' h peu près, qui sont la plus grande distance de Mercure. Or comme l'espace de 77 ^r 33' à 1160', périgée du soleil, était considérable, ils veulent, pour qu'il n'y ait pas de vide, y insérer une autre sphère, et que ce soit celle de Vénus, parce qu'on a observé que Vénus est inférieur à Mars, comme Mercure circule sous l'orbite de Vénus. Prenant donc le rapport de la distance périgée de celle-ci à sa distance apogée au centre du zodiaque, de 15^r 35' à 104^r 25'; et la distance apogée 177 ^r 33' de Mercure à un quatrième terme, ils trouvent 1150 qui est presque le périgée 1160 du soleil. Et c'est ainsi qu'en démontrant les distances apogées et périgées, on liera les termes extrêmes par des termes moyens.

L'article huitième est ce que nous avons dit des points tropiques (solsticiaux), savoir que le soleil, avant que de les avoir atteints, paraître tourner vers les points opposés, comme si vraiment ils étaient mobiles. En les supposant immobiles, on montre que la cause du passage du soleil sur les pointe opposés avant qu'il soit arrivé aux limites sur le cercle mitoyen du zodiaque, vient de l'excentricité du cercle qu'il parcourt, laquelle ne met pas la limite boréale sur la même droite que le point le plus boréal du zodiaque dans la sphère fixe, mais un peu avant, à cause de l'élévation de l'excentrique à l'apogée dans le 5^e degré des gémeaux. Le calcul ne le montrant pas encore dans la limite boréale du zodiaque de la sphère fixe, l'œil le voit se diriger déjà vers la limite australe, parce qu'il a dévié sur son orbite propre excentrique, de la limite boréal.

Il est bon aussi de savoir pour quelle raison le soleil ne se lève pas constamment au même point dans les équinoxes, mais plus vers l'ourse dans l'équinoxe du bélier, et plus vers le pôle austral dans l’équinoxe de la balance : et pourquoi aussi il ne se lève pas aux mêmes points dans les conversions (solstices), mais en des points plus austraux dans le cancer, et plus boréaux dans le capricorne. La seule cause de tout cela, c'est que l'orbite solaire s'approche plus de la terre que le zodiaque de l’univers, et que ni l’apogée, ni le périgée, n’étant ni dans les points équinoxiaux, ni dans les points tropiques ; mais vers le 5^e degré des gémeaux, comme je l'ai dit plusieurs fois, le point équinoxial du printemps est plus proche de ce degré, que le point équinoxial d'automne, d’où il est évident que le soleil est plus éloigné de la terre dans le point équinoxial du printemps, et plus proche dans celui d'automne. C'est pourquoi sur les astrolabes plans, il paraît plus élevé sur les lignes de midi, le jour de l'équinoxe du printemps, et plus bas le jour de l'équinoxe d'automne. Le soleil fait aussi les ombres des gnomons plus longues dans l’équinoxe du printemps, et plus courtes dans celui d'automne, parce qu'il darde à rayons du cercle qu'il parcourt, et sur lequel il est le plus éloigné de la terre dans l'équinoxe du printemps, et à une plus grande proximité dans l’équinoxe d automne. Or les rayons dardés d’un point plus élevé proviennent des ombres plus courtes; et d'un point plus bas, de plus longues. Enfin, nous saurons pourquoi la différence du périgée à l'apogée produit les variations apparentes en latitude dans les le levers, si en admettant une parallaxe dans le soleil, nous croyons que la terre n'est pas comme un point central relativement à l’orbite lunaire, comme Hipparque et Ptolémée le soutiennent.

(F. 21) Soit dans la sphère fixe, le zodiaque ΑB, et ΑΒ le diamètre de l'équateur, et sur ce diamètre les points Ζ où est le soleil à l'équinoxe du printemps, et H on il est à l'équinoxe d'automne. Car l'un et l'autre sont toujours dans le plan de l'équateur et dans celui de l'orbite solaire, c'est-à-dire, dans la commune section de ces deux plans. L'un sera plus élevé, et l’autre bas à cause de la différence produite par l'apogée et le périgée. L'arc ΓΔ étant donc dans le plan du cercle mitoyen du zodiaque, ainsi que les points Γ boréal et Δ austral, supposons notre œil au point E de la surface terrestre. Ζ sera vu suivant la droite EΖ au dessus de l'horizon, et H suivant la droite EH. Ζ paraîtra donc se lever plus au nord que H, car les points Γ sont supposés boréaux, et les points Δ sont austraux, attendu que la droite EΖ étant plus boréale que l'horizon, et la droite EK plus australe, Ζ paraîtra se lever an point Θ, et H au point K. Cela prouvé, il est évident que le soleil dans l'un et dans l'autre équinoxe ne paraîtra se lever en un seul point, que sur l'équateur, parce qu'il n'y a qu'une seule droite EΖ sur laquelle sont les points Ζ et H, dans la direction desquels l'œil voit le soleil se lever dans les deux équinoxes. Et les gnomons jettent alors des ombres de différentes grandeurs, vu que le soleil n'y est pas à la même distance des points équinoxiaux, à cause qu'il y est plus ou moins apogée. Il est seulement à remarquer que la différence apparente est plus grande dans les levers des équinoxes, qu'elle ne devrait être d'après la parallaxe déterminée du soleil, qui n'est jamais même de trois minutes soixantièmes, cette différence faisant la latitude de près de trois degrés au-dessus de l'horizon, comme tout le monde le voit en observant. Enfin, en admettant nos hypothèses, on verra aussi qu'il est dans l'ordre que ces astres paraissent aller en sens contraires, avant d'atteindre les solstices.

(F. 22) Soit dans la sphère fixe, le cercle ΑΒ mitoyen du zodiaque, et ΓΔ l'orbite excentrique du soleil. Si ΓΔ était concentrique à ΑB, les points K et Ζ seraient l’un boréal, l’autre austral. Pour qu’il devienne excentrique, supposons le plus avancé vers le point E qui est le 5^e degré des gémeaux, le point Γ écarté de la droite ΑB, et l'autre point Δ tombant au-dessous de ΑB. Quand le soleil est arrivé en Γ, il n'est pas encore dans le point tropique ou solstice Α du cercle ΑB, c’est pourquoi il paraît aller vers le sud dans son orbite propre car sa limite boréale est alors en Γ. Et quand il est en Δ, il n’est pas encore arrivé au point tropique du cercle ΑB. Mais dès qu'il est arrivé dans le point tropique le plus austral de son orbite propre, il en part pour continuer sa route en allant vers le point plus boréal E de cette orbite, et il paraît se lever suivant la position de l'excentrique, et non suivant celle du zodiaque de la sphère fixe. C'est pourquoi, dans les astrolabes, il paraît à son plus haut point avant d'être arrivé en Ζ qui est sur la même droite que B, et plus bas que H qui est sur la même droite que Α. Et les ombres des gnomons, avant le point tropique d'été seront plus longues, parce qu'elles viennent d'un point plus bas que ΑB, et avant le point tropique d'hiver plus courtes, comme venant d'un point plus haut. Car ce n'est pas de la sphère fixe ni de sou zodiaque y que le soleil lance ses rayons, mais de son cercle excentrique propre, la limite boréale étant au-dessus, et l’australe au-dessous de la droite qui passe par les deux points tropiques (ou solstices). Ce phénomène a donné lieu a bien des recherches de la part des hommes qui de nos jours se sont appliqués à l'étudier.

Neuvièmement, le mouvement de la sphère des fixes, dont nous avons déjà parlé, comme non admis. Ceux qui le rejettent, disent qu'en l'admettant il est impossible d'expliquer les circonstances mêmes des hypothèses établies pour les cinq planètes; car dans cette opinion on fait mouvoir la sphère des fixes vers l'orient. Mais les phénomènes prouvent qu'il ne faut pas ajouter foi à ce mouvement. Sinon, comment les ourses seraient-elles toujours visibles pendant et depuis tant d'années, quand même elles n'avanceraient que d'un degré par siècle autour des pôles du cercle mitoyen du zodiaque qui ne sont pas ceux du monde. Car il faudrait qu'en obéissant à ce mouvement, elles ne fussent jamais au-dessous de l'horizon, mais qu'elles disparussent à ses parties, comme le prouvent les hommes éclairés en ces matières, qui s'accordent tous à faire mouvoir la sphère des fixes autour du pôle du monde par un mouvement qui la fait tourner vers l'occident.

Le dixième et dernier article que nous avons traité, est celui des éclipses, des conjonctions, des inclinaisons, et autres objets semblables, dont nous connaissons actuellement les causes par le moyen des hypothèses. Car nous savons où arriveront les éclipses, et pourquoi eues n'arrivent pas constamment dans le même point, et où se font les inclinaisons. Car celles-là sont la suite des mouvements des épicycles ; et celles-ci, des lieux des nœuds que nous avons dit changer de place, par l'effet du transport de l'orbite inclinée de la lune, dont l'intersection avec le cercle mitoyen du zodiaque change perpétuellement de place. J'ai exposé cette théorie en traitant de la lune.

Telle est l'hypotypose, représentation des hypothèses ou suppositions astronomiques. Et en terminant ce traité, j'ajouterai à ce que j'y ai dit, que les astronomes (Proclus ne dit pas les aristotéliciens, c'est Valla qui les fourre de son chef dans son latin) qui ont présupposé que les mouvements des corps célestes étaient uniformes, ignoraient que leur essence est l'irrégularité et la variation. Sinon, pourquoi admettrions-nous les excentriques et les épicycles? il faut donc les concevoir comme, simplement fictifs et idéaux, ou comme attachés à des sphères. Car puisqu'ils ne doivent être que des conceptions, ils ne voient pas qu'ils transportent les propriétés matérielles à des conceptions mathématiques, en tirant de la nature de la matière, les causes des mouvements naturels. J'ajouterai encore que ces mouvements seraient impossibles. Car ce n'est pas parce qu'ils se meuvent idéalement, suivant nous, que les astres portés sur ces cercles se meuvent réellement; ce n'est donc que pour les expliquer, qu'on a bien fait de nous enseigner cette belle construction d'hypothèses. Car comment rendre raison autrement pour chaque planète, du repos et du mouvement alternatifs de l'excentrique dans l'un, ou de l'épicycle dans une autre, de sa rétrogradation et de sa direction ? Comment trouver les causes, mais les véritables, de leurs positions dans des plans ou différents ou les mêmes ? autrement, on n'en donnerait pas des raisons qui satisfissent l'esprit. On peut prendre d'autres routes pour expliquer ces effets sans hypothèses, comme dans les autres sciences ; mais on essaie d’étendre, suivant les circonstances, ces hypothèses par lesquelles on doit les expliquer, en disant que tout ce qui peut se faire, n'est pas toujours visible ; en outre, ces hypothèses comme étant les plus simples sont les seules qui conviennent à des corps divins, et on les a imaginées pour trouver le mode des mouvements des astres, qui se meuvent réellement comme on l'a vu afin de montrer l'harmonie qui règne entre eux.