
NICOLAS ARTABASDOS surnommÉ ὁ Ῥαβδᾶς
DEUX LETTRES ARITHMÉTIQUES
traduction française de P. TANNERY.
Œuvre numérisée par Marc Szwajcer

DEUX LETTRES ARITHMÉTIQUES
publiées par P. Tannery
Nicolas Artabasdos surnommé ὁ ‘Ραβδᾶς fut un mathématicien byzantin né à Smyrne et vivant à Constantinople au milieu du XIVe siècle. On connaît de lui deux lettres arithmétiques reproduites ci-dessous qui nous fournissent toutes les deux littéralement le prologue des Arithmetica de Diophante.
— La première lettre, adressée à un certain George Khatzyce, traite des quatre opérations et du calcul approximatif des racines carrées mais elle est plus connue pour le morceau expliquant comment les anciens figuraient sur les doigts les nombres de 1 à 9999.
— La seconde lettre, adressée à un certain Théodore Tzavoukhe de Clazomène, traite aussi des quatre opérations et donne une méthode plus précise de l’approximation des racines carrées ainsi qu’une méthode pour le comput pascal. Elle fut écrite en l’an 1341 (6849 dans le texte).
Outre ces lettres Rhabdas a aussi rédigé pour son fils Paul un petit traité de grammaire et une réédition du traité de Planude sur le Calcul hindou.
Sans exagérer l'intérêt que présentent les écrits arithmétiques d'Artavasde, il est certain qu'ils méritaient d'être publiés dès longtemps; il suffit pour s’en convaincre de passer en revue ce qu'ils renferment de plus saillant, en dehors de la figuration des nombres sur les doigts.[2]
Tout d'abord, pour la numération écrite, nous voyons exposé un mode de notation spéciale des myriades, mode qui, à la vérité, ne paraît pas remonter à une époque très ancienne, mais qu'on doit regarder comme courant dans les manuscrits à partir du xiie siècle , sans qu'il ait jamais été suffisamment détaillé. Ce mode consiste à surmonter chaque lettre numérale désignant des myriades d'autant de trémas superposés que l'ordre de la myriade contient d'unités.
Si Camerarius a indiqué cette notation, il n'a pas marqué ses sources; d'autre part, Montfaucon ne la reconnaît que pour les myriades simples et pense que le tréma ne doit affecter que la dernière lettre à gauche du groupe de la myriade, ce qui est contre l'usage du manuscrit 2428.
Pour le calcul approché d'une racine carrée incommensurable, Rhabdas donne une méthode toute particulière dont l'emploi dans l'antiquité n'a pu être constaté. Cette méthode, assez importante au point de vue théorique, se retrouve déjà généralisée dans Barlaam, mais elle doit être plus ancienne, et Rhabdas ne l'a pas empruntée à son contemporain. En tout pas, c'est la seule que donne un texte grec pour l'expression de la racine carrée approchée avec des fractions ordinaires.
Pour la multiplication et la division des nombres fractionnaires exprimés avec des suites de quantièmes, Rhabdas donne des exemples, où il procède en réduisant au dénominateur commun; c'est, dit-il, une méthode généralement inconnue; il n'est pas douteux cependant qu'ici encore, il ne reproduise la tradition antérieure à Geminus.
Il nous donne ensuite une méthode de comput pascal, qu'il présente comme étant de son invention; il est à remarquer que, sauf un très léger perfectionnement, cette méthode est la même que celle qu'Isaac Argyre s'attribue dans son traité publié par le P. Petau.[3]
L'exposition de la règle de trois, que Rhabdas appelle ϖολιτικὸς λογαριασμός, est un morceau unique en grec; d'un autre côté, pour en expliquer les applications, il donne quelques détails intéressants sur la métrologie de son temps.
Enfin, si les dix-huit problèmes inédits qui terminent la lettre à Tzavoukhe n'offrent guère d'intérêt au point de vue mathématique, ils n'en représentent pas moins, par la forme en historiettes de leurs énoncés, ainsi que par le mode synthétique de leurs solutions sans raisonnement, ce que devaient être les problèmes de même ordre dans les logistiques anciennes.
Rhabdas nous a donc conservé l'antique tradition aussi bien qu'on pouvait l'attendre d'un auteur aussi récent; je devais me demander s'il n'avait pas subi quelque influence de l'arithmétique hindoue-arabe ; l'examen le plus attentif ne m'a fait reconnaître rien de semblable, ou, pour mieux dire, cette influence n'est accusée que par une lacune regrettable : pour les opérations de multiplication et de division avec des nombres de plusieurs figures, au lieu d'exposer la véritable méthode grecque il renvoie au traité sur le Calcul hindou, preuve qu'à cette époque, la commodité des chiffres modernes les avait déjà fait adopter pour les calculs tant soit peu compliqués.
J'ai cherché, dans la traduction, à être aussi fidèle que possible; toute recherche d'élégance eût donné la plus fausse idée du style de Rhabdas. Toutefois une traduction d'un ouvrage mathématique laisse nécessairement à désirer pour la fidélité; car, avant tout, elle doit être claire et par suite en conformité suffisante avec les habitudes du langage mathématique moderne; elle ne peut donc donner qu'une idée plus ou moins approchée des procédés de calcul et de la forme des connaissances théoriques de l'auteur traduit.
IMPROVISÉE A BYZANCE DE CONSTANTIN, PAR
ARITHMÉTICIEN ET GÉOMÈTRE,
SUR LA DEMANDE DU TRÈS HONORÉ MAÎTRE DES REQUÊTES, Me GEORGE LE KHATZYCE, TRÈS FACILE POUR CEUX QUI VEULENT L'ÉTUDIER, ET QUE VOICI.
1. L'éclaircissement des questions sur les nombres, très honoré maître des requêtes, est, comme je le vois, chose qu'il te tient à cœur de connaître; j'ai donc essayé d'en traiter méthodiquement, en commençant par les fondements sur lesquels il repose, l'exposé de la nature et de la puissance des nombres. Ce sujet peut paraître difficile, quand il n'est pas encore familier, car l'esprit des commençants est prompt à se décourager; cependant tu parviendras vite à le saisir, grâce à ta bonne volonté et à mon enseignement, car, avec un maître, on apprend rapidement ce que l'on désire savoir. Tu ne l'ignores pas et tu sais du reste que tout nombre est composé d'une certaine quotité d'unités; il est donc clair que sa valeur peut aller à l'infini. Mais les nombres se trouvant ainsi différents, pour aborder leur étude, voici comment il faut procéder au début; je le dis et pour toi et pour quiconque veut s'initier à la science des nombres.
2. En premier lieu, il faut savoir quelles sont les lettres qu'on y emploie, et quel nombre désigne chacune d'elles; puis comment on doit prendre les nombres sur les deux mains ; après cela apprendre les parépomènes et enfin s'attaquer, pour ainsi dire, au corps même du sujet.
1. Les lettres qui désignent la quotité et la mesure de chacun des nombres sont les suivantes :
α β γ δ ε Ϛ ζ η θ
ι κ λ µ ν ξ ο π
ϟρ σ τ υ φ χ ψ ω Ϡ
α signifie un, β deux, γ trois, δ quatre, ε cinq, l’épisème Ϛ six, ζ sept, η huit, θ neuf; ce sont ce que nous appelons les nombres monadiques.
2. Maintenant ι signifie dix, κ vingt, λ trente, µ quarante, ν cinquante, ξ soixante, ο soixante-dix, π quatre-vingts, et le signe sans nom ϟ quatre-vingt-dix; ce sont là les nombres que nous appelons décadiques.
3. Enfin ρ vaut cent, σ deux cents, τ trois cents, υ quatre cents, φ cinq cents, χ six cents, ψ sept cents, ω (méga) huit cents, et ce qu'on appelle le caractère Ϡ, neuf cents ; ce sont les nombres que nous nommons hécatontadiques.
4. Les mêmes lettres, avec un trait au-dessous, signifient autant de milliers qu'elles signifieraient d'unités sans le trait; avec deux points au-dessus, autant de myriades.
5. Ainsi /α, avec le trait qui le touche et qui descend en obliquant à gauche, signifie un mille, /β deux mille, /γ trois, et de même les lettres suivantes avec le même trait signifient autant de mille qu'elles signifieraient d'unités sans le trait; nous avons ainsi, jusqu'à /θ, les nombres dits chiliontadiques.
6. En mettant, comme je l'ai dit, deux points au-dessus, α signifie une myriade, β deux myriades, γ trois, et ainsi de suite; nous commençons de la sorte une nouvelle série, un autre ordre de nombres, et nous avons les nombres monadiques de myriades simples jusqu'à θ, décadiques jusqu'à ϟ, hécatontadiques jusqu'à Ϡ. Et si, avec le trait, les points sont superposés, les lettres désignent autant de milliers de myriades qu'elles désigneraient de milliers sans les points.
7. Si, au-dessus des points, on en met d'autres, la quotité représentée par la lettre se trouve multipliée par une myriade; c'est ce que nous appelons les myriades doubles ou myriades de myriades; en continuant de même à ajouter des points, nous avons les myriades dites triples et quadruples; avec d'autres points encore, on continuera suivant la même progression et ainsi de suite jusqu'à ce que l'infinitude nous arrête.
1. Voici comment on marque les nombres sur les mains; la gauche sert toujours pour les unités et les dizaines, la droite pour les centaines et les mille; au delà, il faut se servir de caractères, car les mains ne peuvent plus suffire à représenter les nombres.
2. En fermant le premier doigt, le petit, appelé myope, et en étendant les quatre autres et les tenant droits, tu as à la main gauche une unité, à droite un mille.
3. En fermant, avec le même doigt, aussi le second qui le suit, et qu'on appelle paramèse et épibate, les trois autres restant ouverts, comme je l'ai dit, tu as à ta gauche deux, à ta droite deux mille.
4. En fermant le troisième, le sphacèle ou doigt du milieu, avec les deux premiers, et en laissant étendus les deux autres, l'index et le pouce, tu as à gauche 3, à droite 3.000.
5. En fermant seulement le doigt du milieu et le paramèse, c'est-à-dire le second et le troisième, et en laissant ouverts les autres, le pouce, l'index et le myope, tu as à gauche 4, à droite 4.000.
6. En fermant seulement le troisième ou doigt du milieu, et en étendant les quatre autres, tu as 5, à droite 5.000.
7. En fermant seulement l’épibate ou second doigt, les autres étant ouverts, tu as à gauche 6, à droite 6.000. (cf. Macrobe Sat. VII, 13, 10).
8. Maintenant, en tendant le myope ou premier doigt, de façon à toucher la paume, et en tenant droit les autres, tu as 7 et 7.000.
9. En tendant en outre de même le second ou paramèse, et en l'inclinant jusqu'à le rapprocher au plus près du creux de la main, et en laissant droits, comme j'ai dit, les trois autres, le troisième, le quatrième et le cinquième, tu figures à gauche 8, à droite 8.000.
10. En donnant au troisième doigt la même position qu'aux deux premiers, tu as à gauche 9, à droite 9.000.
11. Maintenant, en ouvrant le pouce sans le dresser, mais en le dirigeant un peu de côté, et en pliant un peu l'index jusqu'à ce qu'il touche la première jointure du pouce, de façon à figurer la lettre σ, les trois autres doigts ayant leur ouverture naturelle et n'étant pas séparés les uns des autres, mais réunis, tu marques à gauche 10, à droite 100.
12. En étendant en ligne droite et debout le quatrième doigt ou index de façon à figurer la lettre I, les trois premiers restant unis, mais un peu inclinés et formant un angle avec la paume, enfin le pouce dépassant ces derniers et touchant l'index, tu marques 20 et 200.
13. L'index et le pouce étendus et inclinés de façon à se toucher par leurs extrémités, tandis que les trois autres doigts sont unis et étendus suivant leur position naturelle, signifient 30 et 300.
14. Les quatre premiers doigts étendus directement, tandis que le pouce figure la lettre Γ en dépassant l'index du côté extérieur, signifient à gauche 40, à droite 400.
15. Les quatre premiers doigts étant de même ouverts directement et réunis, tandis que le pouce figure la lettre Γ du côté intérieur sur la base de l'index, signifient 50 et 500.
16. En partant de la même figure et en pliant en cercle l'index autour du pouce de façon à lui faire toucher la phalange intermédiaire entre la première et la seconde jointure, tandis que l'extrémité de l'index va toucher la base du pouce, on marque 60 et 600.
17. Les trois premiers doigts étant ouverts de la façon que nous avons indiquée à plusieurs reprises, le pouce appliqué contre l'index, et ce dernier embrassant en hélice l'extrémité du pouce, signifient 70 et 700.
18. Les trois premiers réunis et inclinés en angle du côté de la paume, le pouce dépassant le doigt du milieu ou troisième, touchant la troisième phalange (celle contre la racine) de ce doigt, et appliqué sur la paume, tandis que l'index, disposé au-dessus du pouce et plié autour de la première jointure de ce dernier, touche de son extrémité la base du pouce, on signifie 80 et 800.
19. Enfin, si l'on ferme le poing, le pouce restant droit, puis qu'on étende les trois premiers doigts en laissant l'index dans la position que lui a donnée la fermeture du poing, on figure à gauche 90, à droite 900.
1. Les parépomènes sont au nombre de six : 1° exposition des lettres; 2° addition; 3° soustraction; 4° multiplication; 5° division; 6° invention de la racine carrée.
2. J'ai déjà parlé de l'exposition des lettres; je vais aborder le reste.
3. L'addition est l'union de deux ou trois nombres dans la quotité d'un seul nombre, comme 1 et 2, 3; 3 et 3, 6; 6 et 4, 10; 10 et 5, 15; 15 et 6, 21; 21 et 7, 28; 28 et 8, 36; 36 et 9, 45. Car ainsi 2 additionnés avec l'unité forment le nombre 3; de même 3 avec 3 font 6; 6 avec 4, 10, etc.
4. La soustraction est le retranchement d'un nombre plus petit ôté d'un plus grand; car le nombre à soustraire doit toujours être plus petit que celui dont on le soustrait. Soit par exemple 9 à retrancher de 45, il restera 36; 8 de 36, il reste 28; 7 de 28, reste 21 ; et de même pour les autres.
5. La soustraction, comme l'addition, te sera facile avec la table qui suit, et que nous a enseignée le très sage Palamède; de même la multiplication.
6. Un nombre est dit multiplier un nombre quand on ajoute à lui-même le multiplicande autant de fois qu'il y a d'unités dans le multiplicateur, et qu'on forme ainsi un nouveau nombre : ainsi par exemple 4 fois 4, 16; 5 fois 8, 40.
7. Il faut savoir que, si le nombre est multiplié par lui-même, le nombre produit est carré équilatéral.
8. Quand un nombre multiplie le nombre qui lui est inférieur ou supérieur d'une unité, le nombre produit est appelé hétéromèque.
9. Quand un nombre est multiplié par lui-même, et que le produit est à son tour multiplié par ce même nombre, le produit final est un cube.
10. Voilà ce qui concerne la multiplication.
Il y a division lorsque, divisant un nombre par un autre, nous considérons ce qui revient à chaque unité du diviseur : ainsi, quand, divisant 12 par 3, nous considérons ce qui revient à chacune des unités de 3; or il revient 4 unités, puisque 3 fois 4, 12.·
11. On peut aussi diviser un plus petit nombre par un plus grand; alors on considère quelle fraction de l'unité revient à chaque unité du plus grand nombre : ainsi, quand, divisant 4 par 16, nous considérons quelle fraction de l'unité revient à chaque unité de 16 ; or il revient ¼ , puisque 4 fois 4 = 16; car, quand on divise le plus petit nombre par le plus grand, il faut diviser l'unité en autant de parties qu'il revient d'unités à chaque unité du plus petit, alors que l'on divise le plus grand par le plus petit; chacune des parties de l'unité ainsi divisée est ce qui revient à chaque unité du plus grand.
12. En général, pour les divisions, il faut savoir que toute division se fait, soit d'un nombre plus grand par un plus petit, soit d'un plus petit par un plus grand, soit d'un égal par son égal. Dans chaque cas, celui qui divise doit savoir ce que chaque nombre doit avoir par unité et quel est le rapport du dividende au diviseur ; pour un plus grand nombre divisé par un plus petit, c'est comme on l’a montré pour 12 et 3 ; pour un plus petit par un plus grand, comme pour 4 et 16; pour des nombres égaux, je pense que c'est clair et familier même pour ceux dont l'esprit n'est pas encore développé; car si l'on divise 3 par 3 ou 5 par 5, il est absolument clair qu'il revient une unité à chaque unité.
13. Voilà pour la division.
La racine d'un carré exact est, pour ainsi dire, évidente pour tous ; car le nombre qui, multiplié par lui-même, fait le nombre carré, en est la racine; quant à celle du carré non exact, voici comment on la trouve par le procédé le plus grossier.
14. Prends le carré exact le plus voisin du carré non exact; il restera en tout cas un certain nombre d'unités entre ce carré exact et le non exact ; trouve la racine du carré exact et double-la, puis divise les unités qui forment le reste, comme on l'a dit, par le nombre double de la racine, et donne-leur ce nombre pour dénominateur; ajoute enfin cette fraction à la racine du carré exact, et sache que tu as ainsi celle du non exact.
15. Soit par exemple à trouver la racine carrée de 11; nous trouvons 9 comme le carré exact qui s'en rapproche le plus; la racine en est 3, car 3 fois 3, 9. Je retranche donc 9 de 11, il reste 2. Je double la racine de 9, c'est-à-dire 3, j'ai 6, et je dénomme les 2 unités du reste d'après 6, deux sixièmes. On trouve ainsi pour la racine de 11, 3 unités et deux sixièmes d'unité; ces deux sixièmes d'unité font un tiers.
16. Voilà l'exposition la plus simple pour la racine carrée ; quant à celle qui est plus minutieuse, comme elle n'est pas facile à saisir, même avec un maître, j'ai réservé d'en parler ailleurs.
1. Il est très important de traiter de l'ordre et de la progression des nombres. Il y a neuf ordres de nombres qui imitent l'ennéade des intelligences supramondaines, et de même que celles-ci sont illuminées par la première et éternelle lumière, de même les nombres, engendrés de l'unité, obtiennent leur puissance suivant leur ordre, les premiers en premier lieu, les derniers en dernier lieu. Nous disons que tous sont engendrés de l'unité; en effet, celle-ci n'est pas nombre, mais génératrice des nombres ; c'est comme la source, la racine, le point de départ de toute pluralité, en cela elle est comme l'image de la divinité ; quand on nous demande ce qu'est un nombre, nous répondons : une réunion d'unités ou une sommation de l'unité.
2. Le premier de tous les ordres[4] est celui des nombres monadiques, le second celui des décadiques, le troisième des hécatontadiques, le quatrième des chiliontadiques, le cinquième des myriades monadiques, le sixième des myriades décadiques, le septième des myriades hécatontadiques, le huitième des myriades chiliontadiques, le neuvième des myriades myriontadiques. Au delà il n'y a plus d'ordre pour les nombres.
3. Observe comment progresse la proportion de ces ordres : en ajoutant une unité à neuf unités, tu fais une décade; en ajoutant à neuf décades une décade, tu feras de même une centaine, et ainsi de suite pour les autres ordres; car pour l'ordre et l'appellation de chaque nombre, tu prends la base dans un seul ordre, celui des nombres monadiques.
4. Ainsi par exemple, si tu veux trouver la base de 10 et de 100 dans les nombres monadiques, tu prends l'unité qui est la première de tous les monadiques, de même que 10 et 100 sont respectivement les premiers dans leur classe ; de même la base de 20 et de 200 est 2; de 30 et de 300, c'est 3; de 40 et 400, c'est 4; de 50 et 500, c'est 5 ; de 60 et 600, c'est 6; de 70 et 700, c'est 7; de 80 et 800, c'est 8 ; de 90 et 900, c'est 9 : de même pour les autres ordres.
5. Pour rendre plus clair par un exemple ce que je veux dire, soit à répondre quel nombre font 30 fois 90 ; il n'est pas facile de le trouver sans être instruit. Tu prends pour chacun des deux nombres le paronyme et de même rang dans les monadiques, et du petit nombre bien connu, tu trouveras le grand; car l'inconnu s'apprend du connu, aussi facilement que le contraire s'apprend par le contraire. Ainsi pour 30, on prendra 3, au lieu de 90, 9, puisque ce sont là les correspondants ; en les combinant par multiplication, on a deux décades et sept unités, c'est-à-dire 27; par conséquent 3 décades multipliées par 9 décades feront 27 centaines, c'est-à-dire 2.700. En effet les nombres décadiques multipliés par les nombres décadiques font des nombres hécatontadiques et chiliontadiques et encore des nombres mixtes de ces deux ordres, comme cela sera éclairci plus loin.
6. Apprends donc, pour répondre à de telles questions, cette règle générale pour la multiplication de tout nombre; bien moins connue et bien plus remarquable que les précédentes, elle en forme pour ainsi dire le sceau empreint par des raisons canoniques, scientifiques et philosophiques. Voici cette règle.
7. Tout nombre monadique multiplié par son semblable donne, comme produit, tantôt un nombre monadique simple, tantôt un décadique simple, tantôt enfin un mixte des deux espèces : on peut le voir exactement sur 3 et 3, 5 et 6, 8 et 8; car 3 par 3 fait 9 qui est un nombre monadique simple ; 5 par 6 fait 30, également simple, mais décadique; enfin 8 par 8 fait 64; voilà le mixte, 60 étant décadique, 4 monadique.
8. De même pour les autres ordres de nombres : tantôt le produit est un nombre simple du même ordre que ces nombres, tantôt c'est un nombre simple de l'ordre supérieur, tantôt enfin, et c'est le plus souvent, c'est un mixte des deux ordres.
9. Ainsi un nombre monadique multiplié par un décadique fait un décadique simple, ou un hécatontadique, ou un mixte de ces deux ordres, comme on peut le voir sur 3 et 20, 5 et 20, 7 et 70 : car 3 par 20 fait 60, simple décadique; 5 par 20 fait 100, simple kécatontadique; enfin 7 par 70 fait 490, mixte de décadique et d'hécatontadique. Or, 3, 5, 7 sont des nombres monadiques, 20, 70 des décadiques, comme nous l'avons dit dans ce qui précède, et ce sont là les nombres dont la multiplication a produit les nombres précités.
10. Avec un hécatontadique, on aura un hécatontadique simple, ou un chiliontadique, ou encore un mixte de ces deux ordres; on peut le reconnaître nettement sur 3 et 300, sur 5 et 200, sur 4 et 900.
11. Avec un chiliontadique, on aura un chiliontadique simple, ou un myriontadique monadique, ou encore un mixte de ces deux ordres, comme on peut le reconnaître clairement sur 4 et 2.000, 5 et 6.000, 8 et 8.000.
12. De même pour les ordres suivants, d'après la même loi, tant qu'on voudra aller.
13. Un nombre décadique multiplié par un décadique fait un hécatontadique simple, ou un chiliontadique simple, ou de même un mixte de ces deux ordres ; on peut voir ce que je viens de dire sur 20 et 20, 40 et 50, 70 et 80, dont les produits sont 400, 2.000, 5.600; tu as là les trois espèces.
14. Avec un hécatontadique, il fait un hécatontadique simple, un myriontadique monadique, ou un mixte de ces deux ordres.
15. Avec un chiliontadique, il fait un myriontadique monadique simple, ou un myriontadique décadique, ou de même un mixte de ces deux ordres.
16. Un nombre hécatontadique, multiplié avec un hécatontadique, fait un myriontadique monadique simple ou un décadique, ou encore un mixte des deux ordres, comme on peut le reconnaître sur 100 et 100, 500 et 800, 400 et 900; car de 100 et 100 vient une myriade, de 500 et 800, 40 myriades, de 400 et 900, 36 myriades.
17. Avec un chiliontadique, il fait un myriontadique décadique simple, ou un hécatontadique, ou un mixte des deux, comme on peut l'apprendre sûrement sur 300 et 3,000 (90 myriades), 40 et 5.000 (200 myriades), 600 et 8.000 (480 myriades).
18. Un nombre chiliontadique, multiplié avec un chiliontadique, fait, comme produit, des myriades hécatontadiques simples, ou des chiliontadiques, ou des mixtes de ces deux ordres; on peut le reconnaître clairement sur 2,000 et 2,000, 4.000 et 5.000, 6.000 et 6.000; car 2.000 par 2.000 fait 400 myriades, 4.000 par 5.000, 2.000 myriades, et 6.000 par 6.000, 3.600 myriades. Pour les autres ordres, la même méthode s'applique toujours en suivant la même progression. Ce que j'ai dit est d'ailleurs bien suffisant, je crois, pour être compris de toute personne intelligente.
[J'ai jugé inutile de reproduire in extenso les Tables de calcul données par Rhabdas comme étant une invention de Palamède. Ce que j'en ai donné me paraît suffisant pour se rendre compte de la disposition.
Une première série concerne l'addition et la soustraction, et se subdivise en 36 tableaux, un pour chacune des lettres numérales depuis ᾱ jusqu'à /θ. Chacun de ces tableaux comporte trois colonnes : dans la première, à gauche, la lettre à laquelle se rapporte le tableau se trouve répétée neuf fois; dans la colonne le plus à droite, sont inscrites dans l'ordre décroissant les neuf lettres du même ordre; enfin, dans la colonne intermédiaire, les sommes des nombres se correspondant dans les colonnes extrêmes.
On a donc ainsi en tout 324 combinaisons pour l'addition ou pour la soustraction.
Dans la série des tables pour la multiplication, les nombres sont de même disposés sur trois colonnes; mais ici les deux premières à gauche représentent les facteurs, la dernière, celle de droite, donne le produit. D'autre part, le facteur le plus petit doit toujours être cherché dans la colonne de gauche, et le plus grand dans la colonne intermédiaire, où d'ailleurs les valeurs vont en croissant.
Ainsi ᾱ
se trouve successivement combiné avec les 37 lettres de
α à
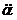 ,
,
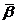 avec
les 36 à partir de
avec
les 36 à partir de 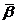 ,
,
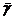 avec
les 35 à partir de
avec
les 35 à partir de 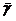 ,
et ainsi de suite, ce qui pour les multiplications pour les nombres
de la décade (de 1 à 9) donne 297 combinaisons jusqu'à la myriade.
,
et ainsi de suite, ce qui pour les multiplications pour les nombres
de la décade (de 1 à 9) donne 297 combinaisons jusqu'à la myriade.
Pour les neuf lettres à partir de la
décade, de
ῑ à
![]() , combinées
d'après les mêmes principes avec les lettres de
ῑ
à
, combinées
d'après les mêmes principes avec les lettres de
ῑ
à 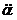 ,
on a de même 216 combinaisons.
,
on a de même 216 combinaisons.
Pour les lettres à partir de la
centaine, de 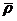 à
à
 ,
on a 135 combinaisons.
,
on a 135 combinaisons.
Enfin à partir de mille, de /α
à 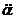 ,
55 combinaisons.
,
55 combinaisons.
En tout, pour la multiplication, 703 combinaisons.
En résumé, ces tables sont analogues, mutatis mutandis, à celles que l'on emploie actuellement dans les écoles primaires de France, où l'usage de la table à double entrée, dite de Pythagore, a été abandonné; mais le grand nombre des lettres numérales grecques les complique naturellement.
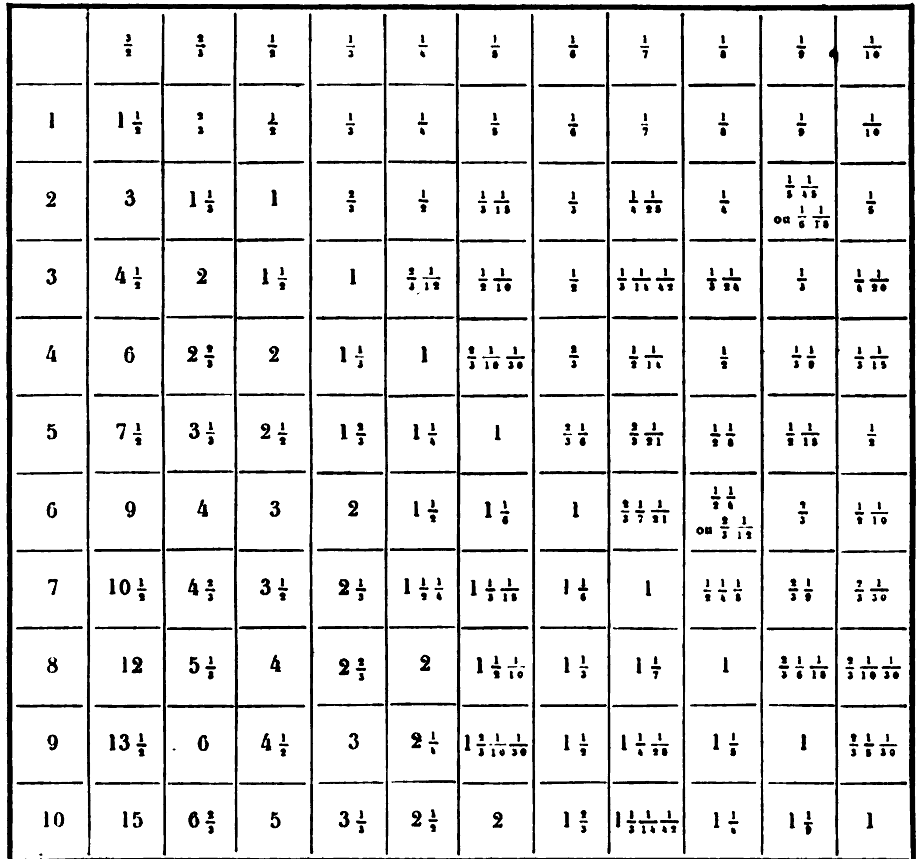
Les tables qui suivent celles de la multiplication et qui sont relatives à la division, manquent dans le manuscrit A. Elles donnent les quotients décomposés en suites de quantièmes, quand il y a lieu, des 10 premiers nombres par les nombres de 2 à 10; de plus, et en première ligne, les deux tiers et leurs inverses (produits par 3/2), mais seulement pour les trois premiers nombres. Des calculs de vérification sont donnés enfin pour un certain nombre de résultats.
J'ai réuni les données de ces tableaux dans celui ci-dessous, où le nombre inscrit dans chaque case est le produit du nombre entier, de 1 à 10, en tête de la même ligne horizontale, par la fraction inscrite en tête de la même colonne verticale.]
Ainsi se font les multiplications simples ; quant aux doubles, triples et au delà, elles se font par une méthode que tu apprendras de la façon la plus claire en étudiant avec soin le discours Sur la multiplication dans le Grand calcul hindou. On procède comme suit : d'abord double avec simple, puis double avec double, puis avec triple et ainsi de suite; en second lieu triple avec simple, puis avec double, puis avec triple et ainsi de suite; de même successivement pour quadruple, quintuple, etc.
La division se fait d'abord en 2, puis en 3, puis en 4, en 5 et ainsi de suite ; on nomme division simple celle qui se fait par un nombre monadique seul; division double, celle par un nombre monadique et décadique; triple, par un nombre monadique, décadique et hécatontadique; quadruple, par un nombre monadique, décadique, hécatontadique et chiliontadique; et ainsi de suite. Nous n'avons parlé ici que des divisions simples; pour toutes les autres, nous les apprendrons exactement dans le discours Sur la division du Calcul hindou.
Les parties de l'unité sont : la première, l'hyphémiole qu'on appelle dimoiron (deux tiers) ; la seconde, le dyoston que nous nommons hémisu (moitié), puis le tiers, le quart, le cinquième, le sixième, le septième, etc.
A MON TRÈS CHER AMI DE COEUR,
THÉODORE TSAVOUKHE DE CLAZOMÈNE,
ÉCRIT CECI DE BYZANCE.
1. L'éclaircissement des questions sur les nombres, illustre et cher Tsavoukhe, est, comme je le sais, chose qu'il te tient à cœur de connaître; j'ai donc essayé d'en traiter méthodiquement, en commençant par les fondements sur lesquels elle repose, l'exposé de la nature et de la puissance des nombres. Ce sujet peut paraître difficile pour les ignorants, puisqu'il ne leur est pas encore familier, car l'esprit des commençants est prompt à se décourager; cependant, toi qui connais déjà les nombres, tu parviendras vite à le saisir, grâce à ta bonne volonté et à mon enseignement, car avec un maître, on apprend rapidement ce que l'on désire savoir.
2. L'objet à traiter comprend ce qui sert à trouver tout nombre, qu'il s'agisse d'un calcul de la vie civile, ou d'un calcul mathématique, c'est-à-dire de l'une des quatre grandes sciences, j'entends : l'arithmétique, la géométrie, l'astronomie, la musique, enfin de tout ce qu'emploie dans ses problèmes le plus grand des arithméticiens, Diophante. Il y aurait six chapitres, à savoir : le premier, l'exposition des signes, éclaircissant la quotité et la valeur de chacun des nombres; le second, l'addition ou la réunion en commun de plusieurs nombres en la quotité d'un seul; le troisième, la soustraction ou retranchement, lorsque de certains nombres nous en retranchons d'autres ou égaux ou inférieurs; le quatrième, la multiplication, quand un nombre quelconque est multiplié par lui-même ou par quelque 'autre ; le cinquième, la division, quand un nombre plus grand est divisé par un plus petit, ou un plus petit par un plus grand; enfin le sixième, l'invention de la racine d'un nombre carré. Mais comme je sais que tu connais parfaitement l'exposition des signes, ce qu'on appelle vulgairement l'alphabet, et aussi bien l'addition, la soustraction et, dans le cas simple et facile, la multiplication et la division, je crois inutile de t'enseigner ces questions; j'aborde donc immédiatement les cas plus variés et plus savants que tu ignores.
3. Par exemple, quelqu'un a demandé à un autre quel nombre fait 3 ⅓ 1/14 1/42 multiplié par lui-même ; l'interrogé n'a pu le trouver facilement, parce qu'il ne connaissait pas de méthode commode; je vais m'empresser de t'en montrer une très remarquable et qui est, à ce que je crois, généralement ignorée; la voici : réduis au dernier quantième les fractions les plus fortes, c'est-à-dire réduis en 42mes, ⅓ et 1/14; il vient en 42mes : pour ⅓, 14; pour 1/14, 3; pour 1/42, 1 ; ce qui fait en tout 18 42mes. Mais comme 18 42mes font 3 7mes, pour plus de commodité et de clarté, je laisse les 42mes et prends les 7mes; je réduis donc aussi les 3 unités en 7mes, ce qui, avec les 3 7mes, fait en tout 24 7mes. Je multiplie donc ces 24 par eux-mêmes et il vient 576 7mes de 7mes; je multiplie de même le 1/7 par lui-même, il vient 4; je divise donc 576 par 49 et il vient 11 unités et 37 49mes, qui, en quantièmes de l'unité, font ⅔ 1/12 1/196· Ainsi 3 ⅓ 1/14 1/42 multiplié par lui-même, fait 11 ⅔ 1/12 1/196.
4. De même, quelqu'un a demandé à un autre quel nombre fait 5 ⅔ 1/5 1/33 1/110 1/330 par 8 ⅔ ¼ 1/156 je suis encore le même procédé, je réduis les fractions les plus fortes de chaque nombre au dernier et plus faible quantième ; puisque, avec 5, le plus faible quantième est 1/330, je réduis les autres fractions en 330mes; j'ai de ces quantièmes : pour 1/330, 1 ; pour 1/110, 3; pour 1/33, 10; pour 1/5, 66; pour ⅔, 220, ce qui fait en tout 300. J'examine si je puis transformer en une quotité de quantièmes plus forts, et je trouve que cela fait 10 11mes, car 30 330mes font un 11me, en sorte qu'il est clair que 300 font 10 11mes.
Je réduis de même les plus fortes fractions qui sont avec 8 au dernier quantième qui les suit, c'est-à-dire au 156me. J'ai : pour 1/156, 1; pour ¼, 39; pour ⅔, 104, ce qui fait en tout 144. J'examine encore si je puis ramener cette quotité à une autre moindre et je trouve que 144 156mesfont 12 13mes.
J'ai donc trouvé que je dois multiplier 5 et 10 11mes par 8 et 12 13mes; je réduis maintenant les nombres aux quantièmes trouvés, 5 en 11mes ce qui fait avec les 10 11mes, 65 11mes; de même 8 en 13mes, ce qui, avec les 12, fait 116 13mes.
Maintenant je multiplie les 65 11mes par les 116 13mes, il vient 7.540 11mes de 13mes ou 143mes; je divise donc 7.540 par 143, et je trouve par la division 52 unités et 104 143mes qui, en quantièmes de l'unité, font ⅔ 1/18 1/429 <1/429> 1/2374. J'ai donc trouvé, comme produit de 5 ⅔ 1/5 1/33 1/110 1/330 par 8 ⅔ ¼ 1/156, le nombre 52 ⅔ 1/18 1/429 <1/429> 1/2374.
5. C'est là ce qu'on appelle les produits plans; le premier est carré, le second hétéromèque; je vais maintenant te montrer comment on fait un produit cube, c'est-à-dire un nombre solide. [Lorsqu'un nombre est multiplié par lui-même, puis le premier nombre par le produit, le résultat final est appelé nombre solide.] Comme par exemple :
Une pierre carrée a été trouvée de 5 spithames 1/5 de largeur, 7 spithames 1/7 de longueur, de 9 spithames 1/6 1/18 de hauteur. Je multiplierai la largeur par la longueur, puis le produit par la hauteur, et le nombre que donne cette multiplication, je dis que c'est le solide de la pierre. Si l'on avait trouvé les nombres sans les fractions y ajoutées, l'opération serait facile, mais par suite de ces fractions et quantièmes, elle devient plus complexe; il nous faut donc un procédé qui nous la rende commode à effectuer. Voici comment je ferai : je réduis chaque nombre au quantième y ajouté, savoir 5 en 5mes à cause du 1/5; il vient en tout, avec le 5me, 26 5mes; de même 7 en 7mes à cause du 1/7, il vient, encore avec le 7me, en tout 50 7mes; enfin 9 en 9mes, puisque 1/6 + 1/18 font 2 9mes; j'aurai en tout, avec les 2 9mes, 83 9mes. Maintenant je multiplie les nombres trouvés, les 26 5mes de largeur par les 50 7 mes de longueur; il vient 1.300; je multiplie à leur tour ces 1.300 par les 83 9mes de la hauteur, il vient 107.900. Maintenant, je multiplie entre eux les nombres homonymes des quantièmes, c'est-à-dire 5 par 7, il vient 35, et 35 par 9, il vient 315. Je divise donc par ce nombre les 107.900 et je trouve 342 ½ unités et 12 ½ 315mes qui font en quantièmes de l'unité 1/28 1/252 ; nous dirons donc que le solide de la pierre en spithames carrées est de 342 ½ 1/28 1/252.
6. Voilà pour la multiplication des nombres accompagnés de fractions et de quantièmes; en ce qui concerne la division, voici ce que je dirai. Quand la division doit se faire par un nombre accompagné de fractions et de quantièmes, je réduis ce nombre aux quantièmes y ajoutés, en observant toutefois, comme pour la multiplication, de prendre le plus faible de ces quantièmes; je réduis également aux mêmes quantièmes les nombre à diviser, après quoi je divise le plus grand par le moindre, et le nombre que me donne cette division, je dis que c'est celui qui, du plus grand, revient au moindre.
Par exemple, je veux diviser 10 par 3 ⅓ 1/14 1/42; je réduis ce dernier nombre au dernier et plus faible quantième, c'est-à-dire au 42me, et je dis : 3 fois 42, 126; ⅓ de 42, 14; 1/14 de 42, 3; 1/42 de 42, 1; le tout ensemble, c'est-à-dire 1 +3 + 14+126 fait 144 42mes. J'examine maintenant si je peux les ramener à un quantième plus fort pour abréger, c'est-à-dire avoir un nombre plus faible que 42; je trouve 7; en effet 144 42mes font 24 7mes; car 1/7 de 42 fait 6, et 6 fois 24, 144, le nombre précédemment trouvé.
Puisque nous avons ramené la division à être faite par des 7mes, je réduis également le nombre à diviser, c'est-à-dire 10, non pas en 42mes mais bien en 7mes, et je dis : 7 fois 10, 70. Je divise donc 70 par 24, et je dis qu'il revient du plus grand nombre au moindre (c'est-à-dire à 3,3 7mes) 3 unités moins 2 24mes ou 1/12, ce qui fait 2 unités ⅔ ¼. Ainsi le nombre 10, divisé par 3,3 7mes, donne, revenant à chaque unité du diviseur 3 unités moins 1/12 comme je l'ai dit.
Qu'il en soit bien ainsi et non autrement, multiplie le nombre trouvé par le diviseur, c'est-à-dire 2 ⅔ ¼ par 24, tu retrouveras 70 7mes, qui font le nombre divisé, c'est-à-dire 10.
Ou autrement : réduis 3 ⅓ 1/14 1/42 en 42mes, il vient 144 42mes; de même 2 ⅔ ¼ en 42mes, il vient de ce côté 122 ½ 42mes. A cause de ½, je double 122 ½, il vient 245 non plus 42mes, mais 84mes; il faut donc que je double aussi les 144 42mes il vient 288 84mes. Je multiplie maintenant les 245 84mes par les 288, également 84mes; le produit est 70.560 84mes de 84mes ou 7.056mes, car 84 multiplié par lui-même fait 7.056. Je divise donc 70.060 par 7.056 et je retrouve 10 unités; en effet 10 multiplié par 7.056 fait 70.560. On trouve ainsi la démonstration vraie de tous points ; tu peux donc te servir de la même méthode pour les cas semblables, et tu ne t'écarteras pas du résultat à atteindre.
7. Voilà pour la division par des nombres accompagnés de fractions et de quantièmes ; il me reste à parler de l'invention de la racine carrée pour les nombres qui ne sont pas vrais carrés; voici comment elle se fait.
La racine d'un carré exact est, pour ainsi dire, évidente pour tous; car le nombre qui, multiplié par lui-même, fait le carré, en est la racine; quant à celle du carré non exact, voici comment on la trouve.
Je retranche du nombre proposé le carré qui en est le plus voisin, puis je double la racine de ce dernier et je divise les unités, qui restent du carré non exact après le retranchement du carré exact, par le double de la racine de ce dernier; les fractions ou quantièmes que donne cette division, je les ajoute à la racine trouvée pour le carré exact, et je dis que j'ai ainsi la racine du carré non exact.
8. Par exemple, soit à trouver la racine de 10; je fais comme suit : puisque le nombre carré le plus voisin du proposé est 9, dont la racine est 3, je prends cette racine de ce carré, ou 3, et je la double; il vient 6. Puisque d'autre part le nombre 10 surpasse le carré 9 d'une unité, je prends l'excès du nombre 10, c'est-à-dire l'unité, que je divise par 6; cette division me donne comme partie de l'unité 1/6, que j'ajoute à la racine du carré exact ou du nombre 9, c'est-à-dire à 3 ; il vient 3 1/6; d'après cela, nous disons que la racine de 10 est 3 1/6, toutefois à une certaine différence près; car 3 1/6, multiplié par lui-même, donne le nombre 10 1/36. Mais la règle a été donnée pour une approximation grossière; si nous voulons trouver avec plus de minutie et d'exactitude la racine de 10, voilà comment nous ferons :
9. Nous prenons la racine trouvée suivant le procédé plus grossier, c'est-à-dire pour 10, 3 1/6, et, à cause du 1/6, nous la réduisons en 6mes; il vient 19 6mes. Nous réduisons de même les 10 unités en 6mes; il vient 60 6mes. Puis je divise 60 par 19, et il vient de cette division 3,3 19mes. Or il faut savoir que 3 1/6 multiplié par 3,3 19mes, fait le nombre 10, sans aucune différence soit en plus, soit en moins. Voici comment se fait cette multiplication : puisque 3 1/6, réduits en 6mes, font 19 6mes, que de même 3,3 19mes, réduits en 19mes, font 60 19mes, nous multiplierons les 19 6mes par les 60 19mes, il vient, en 6mes de 19mes ou en 114mes, 140. Nous divisons donc ce nombre par 114, et nous avons exactement 10, car 10 fois 114 font 1.140.
Mais ce résultat s'obtient en multipliant la racine un peu trop forte par une autre racine plus faible. Pour trouver la racine du nombre 10 d'une façon tout à fait approchée, voici comment nous ferons : nous ajoutons les deux racines, et nous en formons un seul total, dont ensuite nous prenons la moitié; cette division par moitié nous donne un nombre que nous disons être la racine de 10, exacte avec la plus grande approximation.
Ainsi pour 10, nous avons trouvé comme racine suivant le premier procédé 3 1/6, suivant le second 3,3 19mes. Ajoutant ces eux racines, il vient 6,37 114mes, dont la moitié est 3,18 ½ 114mes. Comme ½ se trouve ajouté au numérateur de cette fraction, à cause de ce ½, nous la réduirons en 228mes, et nous dirons que racine de 10 est 3,37 228mes. La multiplication s'en fait comme suit : 3 fois 3, 9[5]; 3 fois 37/228, 111/228; encore les mêmes 37/228 par 3 unités, 111/228; enfin 37/228 multipliés par 37/228 donnent 1.369 228 mes de 28mes, ce qui fait 6/228, et 1/228 de 228me. Ces 6/228, ajoutés aux 222/228 déjà trouvés, font 228/228 ou 1 unité, laquelle, unie aux 9 unités, donne le nombre 10, avec 1/228 de 228me ou 1/51984, ce qui, par rapport au 1/36 en excès dans la première détermination de la racine est beaucoup plus petit, et à très peu près insensible.
10. Soit encore, pour nous exercer davantage, à trouver, avec la plus grande minutie les racines de 3 et de 24. D'abord on recherche quel est le carré le plus voisin; c'est 4 dont la racine est 2. Le double de celle-ci est 4· Puisque le nombre 3 est inférieur d'une unité au carré 4, divise cette unité en défaut par 4, il vient ¼; retranche ce ¼ de la racine de 4, c'est-à-dire de 2, il reste 1 ½ ¼. C'est là la racine du nombre 3, à savoir 1 ½ ¼ multipliée par elle-même, elle donne 3 unités et ¼ de quart, c'est-à-dire 1/16 d'unité.
Nous avons trouvé la racine suivant le procédé grossier; mais il faut la trouver suivant la méthode plus minutieuse ; fais donc comme suit : réduis 1 ½ ¼ en quarts, il vient 7/4; de même les 3 unités en quarts, il vient 12/4 ; divise maintenant 12 par 7; le quotient est 1 ½ 1/7 1/14. Si donc tu multiplies 1 ¾ par 1 10/14, tu trouveras seulement 3 sans différence aucune, soit en plus, soit en moins. Quant à la racine exacte, on l'obtiendra comme suit :
Ajoute les nombres des deux racines trouvées, c'est-à-dire 1 ½ ¼ et 1 ½ 1/7 1/14 ; il vient 3 unités et 13/28, dont la moitié sera 1 ½ et 6 ½ 28mes. À cause du ½ je double ce dernier numérateur, et il vient 13,non plus 28mes, mais bien 56mes. Ainsi en tout 1 41/56; c'est là la racine exacte de 3. Quant au produit de 1 41/56 par lui-même, il s'obtient comme suit : une fois 1, 1; une fois 41/56, 41/56 ; encore une fois les mêmes 41, encore 41, en tout 82/56; enfin 41/56 par lui-même, 1681/56 de 56me, c'est-à-dire 30/56 et 1/56 de 56me. Or 30 et 82 font 112/56, c'est-à-dire 2 unités : ajoutant à 1, on a donc 3 et 1/56 de 56me, ou bien 1/3136 d'unité.
11. Le même procédé nous servira pour la racine de 24. Puisque le nombre carré le plus voisin est 25 (car 16 est loin), je prends la racine de 25, qui est 5; je la double, il vient 10. Comme d'ailleurs le nombre 24 est inférieur d'une unité à 25, je divise par 10, il vient 1/10; je retranche ce 1/10 de la racine de 25, c'est-à-dire de 5, il reste 4 et 9/10 ; c'est là la racine grossière de 24, à savoir 5 unités moins 1/10 ; son produit par elle-même donne 24 unités et 1/10 de 10me ou 1/100. Mais, comme il nous faut trouver la racine exacte de 24, je réduis les 4 unités en 10mes, et il vient avec les 9/10, 49/10; de même les 24 unités en 10mes, il vient 240/10 que je divise par les 49 ; le quotient donne 4 unités et 44/49 qui, multipliés par 4 9/10 font rigoureusement le nombre 24. Pour obtenir la racine exacte demandée, j'ajoute les nombres des deux racines, il vient 8 et 881/490, dont je prends la moitié, qui est 4 et 440 ½ 490mes. A cause du ½, je double et j'ai comme fraction 881/980. Le produit s'obtient comme suit : 4 fois 4, 16; 4 fois les 881/980, 3.524; encore les mêmes par 4, 3.524, ensemble 7048/980 ; enfin les 881/980 par eux-mêmes, 776, 161 qui, divisés par 980, donnent 792/980 et 1/980 de 980me. Ajoutant aux 7.048, il vient 7.840 qui, divisés par 980, font 8 unités ; 8 et 16 font 24. Ainsi nous avons trouvé pour la racine la plus exacte de 24 4 unités et 881/980, et pour son produit par elle-même, 24, et comme quantième de quantième, 1/980 de 980me, c'est-à-dire, comme quantième de l'unité, 1/960400.
12. Voilà pour la racine carrée; quant à l'indiction, au cycle du soleil, à celui de la lune, à la base de cette dernière, au calcul de son jour, aux temps de ses phases, enfin à la Pâque juive et à la chrétienne, je passe tout cela, que tu connais bien, qui est facile et généralement familier; mais je vais te communiquer de préférence une mienne invention relative à la connaissance de notre Pâque. Comme je disputais avec un Juif sur notre foi, il mit en avant en sa faveur que sans la Pâque de la Loi nous ne pouvons trouver la nôtre; je travaillai donc cette question et trouvai une méthode remarquable en ce qu'elle trouve notre pieuse et sainte Pâque en dehors de celle de la Loi; d'ailleurs au lieu de procéder à rebours, en trouvant la sainte Pâque au moyen de celle de la Loi, puis après ce calcul, le Carnaval et le Jeûne de l'Eté, en ordre inverse, notre méthode trouve, suivant l'ordre du temps, d'abord le Carnaval, puis la Pâque, enfin le Jeûne des saints Apôtre en été. Voici cette méthode :
Prends la base actuelle de la lune telle qu'elle est, à l’exception de deux, à savoir 28 et 29 (car je mets celle-ci complètement en dehors à cause de leur égalité avec le nombre jours de février). J'ajoute au nombre de la base, à partir du 1er janvier et en suivant, autant de jours qu'il faut pour compléter 50 jours; si le mois de janvier ne suffit pas, je prends les jours manquant sur février jusqu'à ce que j'arrive à 50. Puis je cherche quel est le dernier jour de ces 50, par rapport à la semaine; l'ayant trouvé par la méthode de l’invention du jour, s'il me reste un, je dis que c'est le dimanche du Prodigue, si deux, le second jour de la semaine du Carnaval, si trois, le troisième jour de la même semaine, et ainsi de suite jusqu'au samedi. Il est clair que le dimanche suivant de la même semaine est celui du Carnaval ; à partir de cette date, je compte 56 jours, et là où s'arrête ce compte, soit en mars, soit en avril, je dis que tombe la sainte Pâque. A partir du jour de la Pâque, je compte maintenant combien il y a de jours jusqu'au 3 mai, et autant je trouve pour ce nombre de jours, autant je dis que sont les jours du Jeûne des saints Apôtres.
13. Pour rendre ceci plus clair, par exemple, supposons que nous ayons à trouver, pour la présente année 6849, le Carnaval, Pâques et le Jeûne de l'été. Puisque pour cette année le cycle de la lune est 9 et sa base 12, je prends ce nombre 12 et j'y ajoute tous les jours du mois de janvier ; il vient 43 et, pour arriver à 50, il me manque 7 jours que je prends sur février; ainsi le 50me jour tombe sur le 7 février et j'ai à chercher par la méthode de l'invention du jour quel jour de la semaine est cette date; je le trouve comme suit :
Le cycle solaire est 17 ; j'y ajoute les quarts qui lui reviennent pour le bissexte, ce qui me fait 4, en tout 21 ; j'ajoute aussi les épactes des quatre mois écoulés depuis le commencement d'octobre jusqu'à février, soit 11 ; il vient 32. J'ajoute enfin les 7 jours de février, et il vient en tout 39, dont je retranche 5 semaines ; il reste 4 jours : je dis donc que le jour en question est le quatrième de la semaine de Carnaval, et que le dimanche suivant, c'est-à-dire, le 11 février, est le Carnaval.
Je veux maintenant trouver la Pâque : je retranche 3 du 11 de février, il reste 8, et je dis que Pâques tombe le 8 avril. En effet lorsque le Carnaval tombe en février, Pâques est en avril; lorsque le Carnaval tombe en janvier, Pâques est en mars. Ou bien autrement : je compte à partir du dimanche de Carnaval les jours suivants jusqu'à ce que j'arrive à 56 ; le jour ainsi obtenu, je dis que c'est celui de Pâques; ainsi le Carnaval a été trouvé le 11 février; il reste sur ce mois 17 jours; j'y ajoute les 31 de mars, il vient 48 ; il me manque, pour atteindre 50, 8 jours que je prends sur avril, et je trouve aussi par cette méthode Pâques au 8 avril.
Je compte maintenant les jours suivants en avril et jusqu'au 3 mai, et je trouve 25 jours ; je dis donc que la durée du Jeûne des saints Apôtres en été est de 25 jours.
Voilà pour ce sujet.
14. Comme d'ailleurs je te sais désireux d'être instruit des calculs qui servent dans la vie civile, ainsi que d'un certain nombre de problèmes arithmétiques indispensables et attrayants, pour que rien d'utile ne t'échappe sur ces questions, j'obéis à la loi de l'amitié et je vais t'expliquer clairement tout ce qui répond à ton désir; prête-moi donc l'attention de ton intelligence.
Toutes les recherches pour calcul de la vie civile se rangent sous trois chapitres et aboutissent par trois sortes de comptes :
En effet, ou bien le deuxième compte multiplie le troisième, et le produit divisé par le premier donne l'achèvement du compte ;
Ou bien le premier multiplie le deuxième, et le produit est divisé par le troisième, ce qui termine le compte;
Ou bien le premier multiplie le deuxième, et le quatrième multiplie le cinquième; ce dernier produit est à son tour multiplié par le troisième, et le nouveau produit est rapporté et comparé au produit du premier par le second, c'est-à-dire divisé par ce dernier produit.
Les deux premiers procédés sont simples et faciles à comprendre; le troisième est plus complexe. Pour les problèmes, il n'y a pas de méthode simple ni uniforme, mais une très diversifiée et affectant de nombreuses formes; il faut donc exposer chaque cas en suivant un ordre régulier et au moyen d'exemples, afin que ce que nous dirons soit éclairci par ces exemples. Mais il convient d'abord de parler des calculs en usage dans la vie civile, comme étant plus simples; puis nous passerons aux problèmes divers.
15. Il faut d'abord s'exercer au premier compte. Soit trois termes numériques, 4, 6, 8; je dis : si 4 devient 6, combien doit devenir 8? Quiconque, ayant un peu d'intelligence, entendra cette question, répondra 12 ; car le rapport est le même de 6 à 4 que de 12 à 8. Mais cela n'arrive pas sans raison; on peut le réduire à une certaine méthode. Si, en effet, le deuxième compte multiplie le troisième, c'est-à-dire 6 multiplie 8, il vient 48 unités; si je les divise par 4, je trouve sans conteste 12 comme quotient, puisque le quart de 48 est 12 unités. Qu'il en soit évidemment ainsi et non autrement, cela résulte de la preuve; car si tu multiplies 12 par 4, tu retrouveras 48, et rien de plus.
Il faut aussi considérer le même problème en le renversant : soit les trois valeurs prises par les mêmes nombres, 12, 8, 6. Voyons si le présent compte donnera bien l'inverse du rapport hémiole, c'est-à-dire l’hyphémiole. Voici comment il faut chercher et dire : si 12 devient 8, combien doit devenir 6? Tout homme sensé répondra immédiatement 4; car le rapport est le même de 12 à 8 que de 6 à 4. Seulement nous considérons ici le rapport hyphémiole, tandis que dans les questions précédentes c'était le rapport hémiole. Mais si tu veux appliquer encore le procédé donné, tu trouveras identiquement le même résultat; car la certitude n'engendre pas l'erreur, pas plus que la lumière n'engendre l'obscurité. Procédons donc suivant la méthode, multipliant, comme nous l'avons dit, le deuxième et troisième compte, c'est-à-dire 8 et 6; le produit est 48. Si tu le divises par le premier nombre, 12, tu trouveras exactement 4, et non moins; car le 1/12 de 48 est 4 et non plus. Si tu veux encore une preuve plus complète, tu retrouveras identiquement le môme résultat; car 4 fois 12 font toujours 48.
16. Pour le troisième compte, il convient de le montrer comme suit sur un exemple : 7 volailles en 5 jours ont mangé 2 aspres de noix; 3 volailles en 2 jours, que mangeront-elles? Je réponds ⅓ d'aspre et 1/105. Pour le montrer démonstrativement suivant la règle donnée, multiplions le premier compte par le deuxième, c'est-à-dire 7 par 5, il vient 35; multiplions de même le quatrième compte par le cinquième, c'est-à-dire 3 par 2 il vient 6. Multiplions encore ce dernier nombre par le troisième compte, c'est-à-dire 2 aspres, il vient 2 fois 6, 12. Je regarde maintenant quelle fraction de 35 est ce nombre, je trouve ⅓ 1/105; car 11 ⅔ en font ⅓, et ⅓ en fait 1/105. Il est donc démontré que les 3 volailles en 2 jours doivent manger ⅓ et 1/105 (d'aspre de noix).
17. Que ces mêmes méthodes s'appliquent à tous les autres calculs, cela va devenir clair par ce que je vais dire maintenant. Tout besoin civil, tout acte de commerce, qui se présente dans notre vie et consiste à vendre, donner ou recevoir, se détermine suivant une de ces trois espèces de mensurations, le poids, le médimne ou la mesure, et la quotité s'exprime suivant une de ces trois mensurations en myriades, milliers, centaines, dizaines, unités ou davantage. S'il s'agit d'une substance métallique, comme l'or, l'argent, le cuivre, le fer, l'étain, le plomb, nous nous servons du poids ou de la balance; si la matière a une très grande valeur, comme les pierres précieuses, les perles, le musc, l'ambre, nous employons, avec le poids, les yeux, l'appréciation, le toucher, l'odorat. Pour les fruits de la terre, les substances sèches, comme le blé, l'orge et les autres sortes de légumes, se mesurent au modios ; les liquides, comme le vin, l'huile, le miel, etc., avec une mesure imperméable faite d'argile ou de cuivre; quant à ce qui sert pour vêtir nos corps, c'est-à-dire les tissus de lin, de coton, de soie, de laine d'Italie, et autres, nous employons la spithame ou la coudée ou l'orgyie; pour tout enfin, la vraie et pure connaissance reconnaît une seule et même méthode, quoique par ignorance et incapacité le vulgaire croie qu'il y a là des procédés variés et différents. Accorde donc ton attention à mon discours qui va remonter à la plus petite des mesures.
18. Le statère, que l'on appelle d'habitude exagion, se divise en 24 carats, et chaque carat en 4 grains de blé ; en sorte qu'à l’exagion il y a 96 grains. Une livre contient 12 onces, et 72 exagia, en sorte qu'il revient à chaque once 6 exagia. D'après ce rapport, pour 10 livres, pour 100, pour 1.000, tu trouveras les onces et les exagia, et tout aussi bien encore les carats et les grains.
Si donc tu as besoin de faire un calcul quelconque, quelles que soient les matières, espèces, mesures, sur lesquelles porte la demande, il faut te rappeler les méthodes données, et t'en servir pour résoudre la question. Tu es assez; intelligent et instruit d'avance pour que cela te suffise; mais de peur que ce que j'ai dit ne paraisse difficile à quelque lecteur de cet écrit, s'il est ignorant et inexpert, j'essayerai autant que possible de le rendre, pour lui, plus clair et plus saisissable en employant des exemples. Voici donc ce que je dirai :
19. L’exagion d'or, ou, comme nous l'appelons ordinairement, l’hyperpyre ou nomisma, ou bien quelque autre des objets dénombrés, a été vendu en compte à tant d'argyries, et tu veux savoir combien de carats du nomisma reviennent à chaque argyrie; compte les argyries donnés, soit 2, soit 3, soit plus, soit moins, et multiplie par le nombre de carats à l’exagion; divise le produit par le nombre des argyries au cours; le résultat de la division sera ce qui revient aux argyries donnés par toi.
Soit, par exemple, l'hyperpyre vendu à 13 argyries; nous voulons savoir combien il revient de carats pour 3 argyries. D'après la méthode donnée., nous multiplierons les 3 argyries par les 24 carats du nomisma, il vient comme produit le nombre 72, que je divise par 13. Je puis retrancher 5 fois le diviseur et il reste 7, que je divise à son tour par 13, ce qui me donne en fractions de 13, pour 6 ½, ½, et pour le ½ qui me reste, 1/26. Je dis donc qu'il revient aux 3 argyries, sur les 24 carats du nomisma, 5 carats ½ et 1/26 de carat, c'est-à-dire à peu près ⅔ d'aspre.
20. Si inversement tu veux savoir au contraire combien d’argyries reviennent à tant de carats donnés, la méthode inverse s'appliquera ; c'est-à-dire tu multiplieras les carats donnés par le nombre des argyries au cours, et tu diviseras le produit par le nombre des carats ; autant de fois tu retrancheras le nombre des carats, autant d’argyries reviendront aux carats donnés. Pour compléter notre explication et nous exercer sur un exemple, nous retournons ainsi la question et nous disons :
Si 24 carats, c'est-à-dire un nomisma, se donnent pour 13 argyries, pour 4 carats, combien faudra-t-il d’argyries ? Je multiplie le deuxième compte par le troisième et je divise par le premier, c'est-à-dire je multiplie les 4 carats par les 13 argyries et j'obtiens ainsi le nombre 52, que je divise par 24; j'en retranche 2 fois 24, et il me reste 4, qui, rapporté à 24, s'en trouvera 1/6. Il faut donc, pour les 4 carats, 2 argyries et 1/6 d'argyrie.
21. Ainsi procède la méthode, quand le nombre diviseur n'est pas suivi d'un quantième, soit ½, soit ⅔, ⅓, ¼, 1/5, 1/6 ou quelque autre, mais qu'au contraire le nombre se trouve sauf (entier). Mais si le nombre diviseur est accompagné d'un quantième, le procédé doit être complété par un autre, comme pour le cours actuel, de 12 ½· argyries au nomisma. Si quelqu'un veut chercher combien de carats valent 3 argyries, il a à multiplier ici les 3 argyries par les 24 carats du nomisma, et diviser le produit par les 12 ½ argyries. Mais à cause du ½, cela présente quelque difficulté. Que faut-il donc faire? A cause du ½, je double les 12 ½ argyries et il me vient 25; de même, si j'avais eu ⅔ ou ⅓, j'aurais triplé; si ¼, quadruplé; si 1/5, quintuplé, et ainsi de suite suivant le nombre dénominateur du quantième. Puisque d'autre part 3 argyries par 24 carats font 72, je double aussi ce produit et j'ai 144, que je divise par 25; je dis donc : 5 fois 25, 125; il reste 19, et j'examine quelle fraction de 25 cela fait; je trouve que 16 ⅔ font ⅔ de 25, 2 1/12 font 1/12 de 25, et le ¼ qui reste, 1/100; car en retranchant 1/12 de ⅓, il reste 7. Je dis donc avec confiance à celui qui pose la question que, si le cours des argyries au nomisma est de 12 ½, il faut, pour 3 argyries 5 carats et ⅔, 1/12, 1/100 de carat.
Cette méthode suffit pour tous les autres calculs; mais pour éclaircir encore davantage la question et rendre plus net encore ce que nous disons, nous allons la considérer pour la livre; après quoi nous nous arrêterons.
22. Si l'on te demande, quand la livre se vend tant d'hyperpyres, ce qui revient à tant d'onces ou à tant d'exagia, multiplie les onces ou les exagia donnés par les nomismata, et le produit, si ce sont des onces, divise-le par les 12 onces à la livre, et déclare qu'il revient autant de nomismata aux onces données ; si ce sont des exagia, divise par les 72 exagia à la livre, et réponds qu'il revient autant de nomismata aux exagia. Si le nombre n'est pas assez grand pour que l'on en retranche entièrement 72, divise le produit par 3, et pour chaque triade retranchée, compte un carat; car certainement tu n'ignoreras pas comment cela se fait, en examinant exactement la chose, que 3 est 1/24 de 72; il convient donc de compter un carat par triade.
23. Si la question est inverse, c'est-à-dire, si l'on demande combien d'onces ou combien d'exagia reviennent à 1, 2 ou 3 nomismata, la multiplication doit aussi se faire inversement, comme on l'a montré pour l’exagion; c'est-à-dire que tu multiplieras les nomismata posés par les 12 onces ou les 72 exagia à la livre, et que tu diviseras le produit par la quotité de nomismata au cours : autant de fois tu retrancheras celle-ci, autant d'onces ou d'exagia tu diras qu'il revient aux nomismata posés.
Pour rendre plus clair et plus évident sur un exemple ce que nous disons, soit la livre vendue à 15 nomismata, on demande combien il faut pour 3 onces. D'après la proportion numérique, un homme intelligent peut répondre aussitôt que, si les 12 onces ont été vendues 15 nomismata, puisque les 3 onces sont ¼ de 12, il faut, pour 3 onces, ¼ des 15 hyperpyres, c'est-à-dire 4 hyperpyres moins ¼. Pour les inexperts, ils pourront répondre en procédant suivant la méthode que j'ai donnée : je multiplie les 3 onces par les 15 nomismata, il vient 45 que je divise par 12; je retranche donc, de 45, 3 fois 12; il reste 9 qui par rapport à 12, est ½ ¼ ou bien ⅓ 1/15.
24. Si l'on fait la question inverse, à savoir combien d'onces reviennent à 3 nomismata, je dis encore, d'après la proportion numérique : puisque 3 nomismata font 1/5 de 15, il revient à 3 nomismata, 1/5 de la livre, c'est-à-dire 2 onces ⅓ 1/15, soit au lieu d'⅓ 1/15, 2 exagia ⅓ 1/15 d'exagion. D'ailleurs ⅓ 1/15 d’exagion font 9 carats ½ 1/10 de carat.
Nous trouvons aussi le même résultat par la méthode : nous multiplions les 3 nomismata par les 12 onces à la livre, nous disons donc que 3 fois 12 font 36, et nous divisons par les 15 nomismata. Je retranche, de 36, 2 fois 15; reste 6 qui, par rapport à 15, fait ⅓ 1/15. Je dis donc qu'il revient aux 3 nomismata, 2 onces ⅓ 1/15.
Pour tous les autres calculs d'affaires de la vie civile, les mêmes méthodes s'appliquent; en voilà donc assez, mon cher ami, de dit sur les calculs de la vie civile.
25. Il y a une autre question dont le calcul se présente pour le monnayage impérial, qui, à ce qu'il me semble, est très digne d'étude et cependant, je crois, généralement mal connue ; elle se ramène à la méthode générale, mais elle échappe ordinairement à cause de sa particularité. La voici :
Quelqu'un a de l'or, soit un compte de 50 exagia; chaque exagion contient 15 grains d'or pur; il a aussi d'autre or, en quantité indéterminée, pour lequel chaque exagion contient 21 grains d'or pur. Il veut faire un alliage des deux de façon à obtenir l’exagion à 18 grains. Combien doit-il prendre du second or pour obtenir une quotité de 50 exagia à 18 grains? Je réponds 7 exagia 1/7. Voici la méthode :
Puisque l'or à monnayer surpasse l'or connu des 50 exagia de 3 carats comme titre, je multiplie par ces 3 les 50 exagia, et j'ai 150 que je divise par le titre en carats de l'or non connu, c'est-à-dire par 21; je dis 7 fois 21, 147; reste 3 qui, par rapport à 21, fait 1/7. Il faut donc ajouter aux 50 exagia, 7 exagia 1/7, de façon à ramener chaque exagion à 18 carats. Tu as là le procédé qui n'échappera pas à ton intelligence.
26. Il est désormais temps de te donner les méthodes pour les problèmes plus élevés et plus dignes d'attention, afin que les voyant au lieu de nous voir, tu renouvelles l'amour de ma tendresse pour toi. Voici quels sont ces problèmes :
I. Quelqu'un dit à un autre : Le 1/5 et le 1/6 des argyries que j'ai, font 21 ; dis-moi combien ai-je en tout d’argyries ? Le second, à l'esprit subtil et exercé dans les questions de ce genre, lui répond brièvement : Tu as en tout 57 3/11; car le 1/5 en est 11 argyries 5/11, et le 1/6 en est 9 6/11, ce qui, en ajoutant, fait 21.
Voici le procédé pour trouver la réponse : multiplie les nombres dénominateurs des quantièmes, c'est-à-dire 5 et 6, cela fait 30; multiplie par 21, il vient 630. Maintenant ajoute 5 et 6, il vient 11 ; divise 630 par 11 ; il vient comme quotient 57 3/11, ce que l'interrogé a répondu au questionneur.
27. II. Le même dit encore au même : J'ai pris, dans le trésor de quelqu'un, le ¼ et le 1/5 de ce qu'il contenait; il a fait le compte du reste, et trouvé 12; je voudrais savoir combien il y avait en tout. La réponse fut : 21 9/11.
Voici la méthode : multiplie les nombres dénominateurs des quantièmes, c'est-à-dire 4 et 5, ce qui fait 20; multiplie ces 20 par le nombre du reste dans le trésor, soit 12; le produit est 240. Ajoute maintenant les nombres dénominateurs des quantièmes, 4 et 5, il vient 9; retranche-les de 20, reste 11; divise donc 240 par 11; le quotient donne 21 9/11. Si de ce nombre on retranche son ¼, et son 1/5, qui font 9 9/11, il reste 12. Ainsi celui qui a répondu que la somme du trésor était 21 9/11, ne s'est pas trompé, mais a bien dit la vérité.
28. III. Le même encore a dit à un autre : En comptant avec les argyries que j'avais, ¼ et 1/5 de leur nombre, j'ai trouvé 30; je voudrais savoir combien je possédais, en dehors de ce ¼ et de ce 1/5. On lui a répondu : 20 20/29.
Voici comment on le trouve : multiplie encore les nombres dénominateurs des quantièmes, soit 4 et 5, il vient 20; ajoute aussi 4 et 5, ce qui fait 9; ajoute à 20, il vient 29. Maintenant multiplie 9 par 30, il vient 270; divise par 29, la division donne 9 9/29. Retranche de 30, il reste 20 20/29. C'est le nombre d’argyries que possédait le questionneur, avant d'en ajouter le ¼ et le 1/5.
29. IV. Un autre a dit à un autre : J'ai fait une affaire et acheté 3 livres ⅓ en tout; puis j'ai revendu, puis racheté 3 livres 1/5 que j'ai emportées; j'ai trouvé que j'avais gagné 10 nomismata. Je veux savoir combien de nomismata étaient engagés dans l'affaire. L'autre répondit : 240 nomismata.
Voici la méthode : vois d'où provient ⅓ et 1/5, tu trouveras bien que c'est de 15. Multiplie donc 3 ⅓ par 15, il vient 50; de même, multiplie 3 1/5 par 15, il vient 48. Multiplie par les 10 nomismata, cela fait 480. Or il a vendu 50 et acheté 48, le gain a donc été la différence 2; divise par conséquent 480 par 2; la division donne 240, car 2 fois 200 font 400, et 2 fois 40, 80. Ainsi il est clair que le nombre des nomismata dans l'affaire était de 240.
30. V. Un autre dit à quelqu'un. : Si tu me donnes 6 des assaries que tu as, et que je les mette avec ce que j'ai, j'aurai le double de toi. Le second lui répondit : Non pas, mais donne-m'en 6 des tiennes, j'aurai autant que toi. Je demande combien avait l'un et combien l'autre.
Solution. L'un avait 42 et l'autre 30.
Voici comment on le trouve : quintuple et septuple le nombre demandé par chacune des deux personnes; le nombre résultant de la multiplication par 5 sera celui que possède l'un, le nombre résultant de la multiplication par 7 sera celui de l'autre. Pour le démontrer : chacun d'eux a demandé 6 à l'autre; dis donc : 5 fois 6, 30, c'est le nombre de l'un; maintenant 7 fois 6, 42. L'un a donc 30, l'autre 42; si donc tu retranches 6 de 30, et que tu les donnes à celui qui a 42, ce dernier aura 48, et il restera 24 à l'autre; or 48 est exactement le double de 24. Si maintenant tu retranches 6 de 42, et que tu les donnes à celui qui a 30, ce dernier aura désormais 36 et il restera à l'autre 36; tous deux auront donc le même nombre.
31. VI. Quelqu'un a donné à son serviteur 100 nomismata, et lui a prescrit de les échanger en totalité contre des argyries qui se donnent à raison de 7 et de 9 pour le nomisma. Mais il veut avoir autant d'argyries au cours de 7 qu'au cours de 9; il veut que le nombre en soit rigoureusement égal de part et d'autre, sans différence en plus ou en moins. Il faut savoir combien de nomismata sont dépensés pour les argyries au cours de 7, combien pour ceux au cours de 9.
Solution. Pour le cours de 7, il faut 56 nomismata ¼, valant 393 argyries ½ ¼; pour le cours de 9, 43 nomismata ½ ¼ valant également 393 argyries ½ ¼. Si en effet tu multiplies 7 argyries par les 56 ¼ nomismata, tu trouveras exactement 393 ½ ¼; de même, si tu multiplies les 9 argyries par les 43 ½ ¼ nomismata, tu trouveras la même quantité.
Voici la méthode : multiplie les 7 argyries et les 9, ce qui fait 63; puis ajoute-les; 7 plus 9 font 16. Maintenant multiplie les 100 nominasta par 63, il vient 6.300; divise par 16, la division donne 393 ½ ¼. Or tu veux connaître combien on a à changer de nomismata au cours de 7, combien au cours de 9; divise donc 393 ½ ¼ par les 7 argyries et par les 9, tu trouveras immédiatement, pour les nomismata au cours de 7, 56 ¼, pour ceux au cours de 9, 43 ½ ¼.
32. VII. Une autre personne a prescrit à son serviteur de lui faire une citerne de mêmes dimensions dans tous les sens, en profondeur, en largeur, en longueur, soit de 10 coudées, pou 1.000 nomismata. Le serviteur, par oubli et inattention, a fait la citerne ayant 5 coudées dans les trois sens; il faut savoir combien il faut lui donner sur les 1,000 nomismata, car un grand différend s'est élevé entre lui et son maître, l'un réclamant le ¼ du prix total, l'autre ne voulant lui donner que le ⅛. Lequel des deux a raison?
Solution. Je pense que c'est celui qui ne veut donner que le ⅛.
Considère la méthode, comment on doit procéder selon la justice : l'un a dit de faire à 10 coudées, l'autre a fait à 5. Fais donc les cubes de 10 et de 5 et regarde quelle fraction du plus grand cube est celui qui vient du plus petit nombre. La fraction que tu trouveras ainsi est celle qu'il convient de donner des γ,000 nomismata. Voici la démonstration : 10 fois 10, 100, et encore 10 fois 100, 1,000, car c'est là ce qu'on appelle faire le cube, puisqu'on a ainsi un nombre solide qui se trouve de dimensions égales dans tous les sens. Fais de même pour 5 et dis : 5 fois 5, 25, et encore 5 fois 25, 125. Maintenant examine quelle fraction de 1.000 est 125; tu trouveras que c'est ⅛·; car 8 fois 125, 1.000 et rien de plus. Ainsi c'est le ⅛ de 1.000 nomismata que doit recevoir celui qui fait la citerne à 5 coudées et non à 10; le maître a donc raisonné convenablement et régulièrement.
33. VIII. Deux marchands amis vont ensemble au marché; quand ils y sont arrivés, ils rencontrent un homme qui a à vendre une pierre d'émeraude, et lui demandent de leur dire exactement quel prix il veut au juste de cette émeraude. Il leur répond : 10.000 pièces d'or. Aussitôt, ils ouvrent leurs bourses et comptent très exactement ce qu'ils ont, chacun pour voir s'il peut payer la pierre; trouvant l'un et l'autre qu'ils ne peuvent la solder entièrement, ils sont fâchés, et le premier dit à son compagnon : Prête-moi le ·1/5 de l'or que tu as, et le mettant avec le mien, j'achèterai l'émeraude. L'autre répond : Non pas; prête-moi, toi, le f de ton or, et, avec le mien, je payerai l'émeraude. Je désire savoir combien de pièces d'or a le premier et combien le second.
Solution. Le premier, celui qui demande 1/5, a 8.235 pièces d'or 10/34; le second, celui qui demande 1/7, a 8.823 18/34. Si donc tu prends 1/5 de ce nombre, soit 1.764 24/34, et que tu l'ajoutes aux 8.235 10/34 du premier, tu trouveras exactement 10.000. De même, si tu prends 1/7 du premier, c'est-à-dire 1.176 16/34, et que tu l'ajoutes aux 8.823 18/34 du second, tu trouveras de même 10.000, rien de plus ni de moins.
Cette solution est très ingénieuse et réclame une grande subtilité; voici comment on l'obtient : Prends les nombres dénominateurs des quantièmes et multiplie-les l'un par l'autre; c'est-à-dire prends pour 1/5, 5, et pour 1/7, 7; dis : 5 fois 7, 35. Retranche de 35 une unité, reste 34; ce sera le diviseur. Maintenant fais la multiplication comme suit : retranche une unité du dénominateur de 1/5, soit de 5, reste 4; multiplie ce nombre par le dénominateur de 1/7, soit 7; il vient 28; multiplie ces 28 par le prix de la pierre, soit les 10.000 pièces d'or, il vient 280.000; prends-en le 1/34 qui est 8.235 10/34; tu as ainsi la quantité d'or que possède le premier marchand. Passe maintenant au second : retranche une unité de 7, reste 6; multiplie par 5, il vient 30; multiplie par le prix de la pierre, il vient 300.00, dont le 1/34 est 8.823 18/34. Si maintenant tu prends de ces deux nombres, le 1/5 de l'un, le 1/7 de l'autre, et que tu ajoutes ces fractions aux nombres possédés par les deux marchands, tu trouveras exactement 10.000 comme je l'ai montré plus haut; ainsi l'un a 8.235 pièces d'or et 10/34, l'autre 8.823 18/34, et la démonstration est vraie.
34. IX. Un autre marchand a de la nacre d'Inde d'une grande valeur qu'il veut vendre; il va dans différentes villes pour l'écouler; d'abord à Alexandrie, il vend ⅛ et 1/9· de tout ce qu'il a; mais ne pouvant y vendre le reste, il vient à Éphèse, où, de la nacre qui lui restait, il écoule 1/6 et 1/7; de là à Smyrne, où il vend ⅓ et ¼ du reste; enfin il s'embarque pour la reine des villes, Constantinople, où il vend encore ¼ et 1/5 de ce qui lui reste. En dernier lieu il trouve que dans sa cassette, il a encore 1 ½ livre. Quelqu'un, qui lui a entendu dire tout cela, veut savoir combien le marchand avait de nacre au commencement.
Solution. 12 livres ⅓ 1/14 [1/204 1/87725 1/701800 1/63372540 1/1247650800] (lisez 1/203 1/736890), quantièmes que, pour plus de commodité et moins de confusion, je dénommerai comme fractions d'après le nombre primitif qui les engendre, à savoir 7188/17545. Mais l'invention de ce nombre n'est pas aussi facile que la réponse; elle est très pénible et fastidieuse; je l'exposerai pourtant avec la grâce de Dieu. Voici comment on procède :
Puisqu'en dernier lieu, il est resté 1 ½ livre de nacre, après retranchement de ¼ et de 1/5, il faut chercher un nombre tel qu'en ôtant son ¼ et son 1/5, il reste 1 ½. Voici comme on le trouve : puisque l'on a dit ¼ et 1/5 à retrancher, prends les nombres dénominateurs 4 et 5 et multiplie-les entre eux, il vient 20; ajoute maintenant 4 et 5, ce qui fait 9, que tu retranches de 20, reste 11. Multiplie donc la 1 ½· livre qui reste au marchand par 20, et divise le produit par 11; le nombre trouvé par la division sera celui dont, en retranchant son ¼ et son 1/5, il restera 1 ½. Nous disons donc : 20 fois 1 ½, 30; dont 1/11 est 2 8/11· C'est là le nombre cherché, tel que, si l'on en retranche son ¼ et son 1/5, il reste 1 ½. En effet, regarde : ¼ de 2 8/11 est 7 ½ 11mes; de même 1/5 est 6/11; ajoutant, on a 13 ½ 11mes; mais les 2 unités réduites en 11mes avec les 8/11 font 30/11; en retranchant 13 ½ 11mes, reste 16 ½ 11mes ou 1 ½ ; car 11 vaut 1, et 5 ½ vaut ½ de 11. Ainsi la démonstration est vraie.
Maintenant passons au second compte : on dit avoir retranché ⅓ et ¼, or, pour le dernier compte, on a trouvé 2 8/11; cherche donc un nombre tel, qu'en en retranchant son ⅓ et son ¼, il reste 2 8/11. Procède donc exactement de la même façon, d'après la méthode exposée : prends les nombres dénominateurs des quantièmes, c'est-à-dire pour ⅓, 3, pour ¼, 4, et dis : 3 fois 4, 12; puis 3 et 4, 7; retranche 7 de 12, reste 5. Multiplie par 12 les 2 8/11, il vient 32 8/11; divise par 5, il vient 6 6/11,. De ce nombre je puis retrancher son ⅓ et son ¼, et il me restera 2 8/11·. En effet, ⅓ de 6 6/11 est 2 2/11; ¼ en est 1 7/11· Si donc de 6 6/11· je retranche 3 9/11 il reste 2 8/11.
Tu as ainsi, avec la démonstration, le second compte de 6 6/11; fais encore un pas et passe au troisième compte à partir de la fin, lequel est le second à partir du commencement. Cherche encore de quel nombre tu peux retrancher son 1/6 et son 1/7, en sorte qu'il reste 6 6/11. Procède toujours de la même manière et dis : 6 fois 7, 42; puis 6 et 7, 13; 13 ôté de 42, reste 29; 6 6/11 multipliés par 42 font 252 252/11; divise par 29, la division donne 9 153/319.
Considère comment elle se fait : je divise les 252 unités par 29 et je trouve 8 unités, avec un reste de 20 unités; mais, comme j'ai en outre 252/11, je réduis ces 20 en 11mes, ce qui fait 220/11; les ajoutant aux 252, il vient 472 que je divise par 11, d'où vient 42 10/11. J'en retranche 1 fois 29, reste 13 10/11. J'ai encore à diviser 13 10/11 par 29 ; à cause des 10/11, je réduis les 13 unités en 11mes, et j'ai 143/11; j'y ajoute les 10/11, ce qui me donne 153/11. Les divisant par 29, il revient, à chaque unité de 29, 5/11 et il me reste 8/11. Je dis donc qu'il revient à chaque unité de 29 sur ce reste, 8/11, de 1/29 ou bien 8/319 ; car 1/319 est 1/11 de 1/29. Pour ramener les fractions à un même dénominateur, je réduis en 29mes les 5/11 qui sont revenus à chaque unité de 29; il vient 145 11mes de 29mes ou bien 319mes, que j'ajoute aux 8, ce qui fait 153. Il revient donc, comme on l'a dit, aux 29, 9 unités et 153/319.
C'est là donc le nombre cherché dont je puis retrancher son 1/6 et son 1/7, en sorte qu'il reste 6 6/11; examine comment cela se fait : 1/6 de 9 est 1 et il reste 3 unités qui font ½ de 6, mais, comme j'ai encore 153/319, je réduis aussi ces 3 en 319mes afin que l'on puisse trouver le résultat plus facilement : il vient 957 ; y ajoutant 153, j'ai 1.110, dont 1/6 est 185/319. C'est là le 1/6 des 9 et 153 fractions, à savoir 1 et 185 fractions. De même j'en prends le 1/7, et j'ai pour 9, 1, reste 2, que je réduis en 319mes, ce qui fait 638; ajoutant les 153 fractions, j'ai en tout 791, dont 1/7 est 113 fractions ; ainsi 1/7 de 9 unités et 153 fractions est trouvé de 1 unité et 113 fractions ; ajoutant ce 1/6 et ce 1/7, il vient 2 unités et en fractions 298/319; les retranchant de 9 et 153 fractions, il reste 6 et en fractions 174/319, ce qui fait 6/11 ; car 6 fois 29 font 174. Ainsi j'ai bien sans aucun doute le nombre cherché.
Passe enfin au quatrième compte, lequel est le dernier à partir de la fin, et le premier à partir du commencement. Examine de quel nombre tu peux retrancher son ⅛ et son 1/9, en sorte que le reste soit de 9 unités et en fractions 153/319. Procède encore selon la méthode donnée : prends donc les nombres dénominateurs des quantièmes, à savoir 8 et 9, et dis comme tu l’as appris au commencement : 8 fois 9, 72; et maintenant 8 et 9, 17; de 72 ôte 17, reste 55. Maintenant multiplie par 72 le nombre 9 153/319; il vient 648 unités et en fractions 11016/319. Divisant par 55, le quotient est, d'une part, 11 unités 43/55, qui, à cause des 11016/319, étant aussi réduits en 319mes, donnent 13.717; en les ajoutant avec les précédents, il vient 24.733 qui, divisés par 55, donnent 449/319 et en plus 38 55mes de 319mes, c'est-à-dire 17.545mes. Des 449 319mes nous en retranchons 319, c'est-à-dire une unité à ajouter aux 11 précédentes, ce qui donnera 12. Il nous restera 130/319, que je réduis en 55mes, à cause des 39/17545; il vient 7.150, qui ajoutés aux 38, donnent 7.188. Le nombre cherché est donc trouvé de 12 unités et 7188/17545; si j'en retranche le ⅛ et le 1/9, il restera 9 153/319 comme tu le trouveras en calculant exactement.
35. X. J'ai donné 7 pièces d'or à mon serviteur, et lui ai prescrit de me prendre du samit de deux couleurs, vert et bleu, autant de chacune des deux couleurs. Mais le prix n'est pas le même pour l'une et pour l'autre : le bleu vaut 1 ½ hyperpyre la coudée, le vert 2 ½ ; je veux savoir ce qu'il faut payer pour chacune de ces deux couleurs et combien il faut en prendre. Je dis qu'il faut prendre de chaque couleur 1 coudée ½ ¼, et payer pour le bleu 2 nomismata ½ ⅛, pour le vert 4 ⅓ 1/24 ou bien ¼ ⅛, ce qui en tout donne bien 7.
Voici comment on procède : ajoute 1 ½ hyperpyre et les 2 ½, ce qui fait 4· Divise 7 par 4; le ¼ en est 1 ½ ¼. Maintenant multiplie le 1 ½ du prix du bleu par 7, puis divise par 4; la division donne 2 nomismata, ½ ⅛ ou 15 carats. Multiplie de même les 2 ½ du prix du vert par 7 et divise par 4 ; la division donne 4 nomismata, ⅓ 1/24 ou 9 carats. Il faut donc prendre de chaque couleur 1 coudée ½ ¼ et payer pour le bleu 2 nomismata 15 carats, pour le vert 4 nomismata 9 carats.
36. XI. Un marchand ayant une certaine somme de nomismata l’a mise dans une affaire, et étant allé à une foire, a doublé son avoir; mais les exacteurs le prennent et lui font payer 15 nomismata. Il remet ce qui lui reste dans le commerce, va dans une autre foire et double encore ce qu'il a; mais les exacteurs le prennent encore et lui font de nouveau payer 15 nomismata. Il recommence encore avec ce qui lui reste, va dans une troisième foire, double encore son avoir, mais toujours repris par les exacteurs et payant encore 15 nomismata, il n'a plus rien. Je veux savoir combien le marchand avait au commencement.
Solution. 13 ⅛·; le double en est 26 ¼ ; ôte 15, reste 11 ¼ ; double, il vient 22 ½, ôte encore 15, reste 7 ½; double encore une fois, il vient 15 sans plus; si on retranche encore 15, il ne reste donc rien.
Voici comment on trouve ce nombre : puisqu'il a dit qu'il doublait, et que la duplication vient de 2, qui dénomme le quantième duoston, que nous appelons d'habitude moitié, si le marchand avait été dans deux foires seulement, il faudrait retrancher le ¼ de 15, et dire que le reste était son avoir primitif; s'il va dans trois foires, il faut retrancher le ⅛ de 15 dans quatre, le 1/16 du nombre de nomismata qu'il perd chaque fois, quel que soit ce nombre. On obtient ainsi le nombre cherché, et ainsi de suite, suivant la même règle.
S'il avait dit autrement, que doublant trois fois son avoir, et payant à chaque foire un nombre donné, il aurait gardé, en fin de compte, soit 12 nomismata, retranche du nombre à payer son ⅛, prends aussi le ⅛ du nombre laissé, et ajoute-le au reste du nombre payé.
Que veux-je dire? par exemple, le marchand a dit qu'étant allé à trois foires, il a chaque fois doublé son avoir, mais payé dans chaque foire 8 nomismata aux exacteurs, et qu'enfin il lui est resté 12 nomismata. Prends-moi, d'après la méthode donnée, les deux nombres 8 et 12; retranche de 8 son ⅛, reste 7; ajoute le ⅛ de 12, soit 1 ½, il vient 8 ½.
Maintenant double ce nombre et retranche une fois 8, il restera 9. Double encore 9, ce qui fait 18, retranche une seconde fois 8, reste 10; double encore 10, ce qui fait 20, et retranche 8 une troisième fois, reste 12; c'est bien le nombre que le marchand a dit lui être resté. Ainsi il avait primitivement 8 nomismata ½ ; en doublant trois fois son avoir, et en payant trois fois 8 nomismata, il lui est resté 12 nomismata, ce que nous avons reconnu par la preuve.
37. XII. Quelqu'un a trois cruches contenant différents liquides : dans l'une, il a en poids 5 livres de miel, dans la seconde, 7 livres de garum, dans la troisième, 9 livres de vinaigre; en sorte que le poids total est 21 livres; il lui arrive de verser le tout dans un même bassin, d'où, ayant mélangé les trois liquides, il veut les verser dans trois vases égaux dont chacun contiendra donc 7 livres du mélange; je demande ce que chaque vase reçoit de chacun des liquides.
Réponse : 1 livre ⅔ de miel, 2 livres ⅓ de garum, 3 livres de vinaigre, ce qui fait en tout 7 livres.
Voici comment on le trouve : ajoute ensemble les nombres des trois liquides, à savoir : 5, 7 et 9, soit 21; multiplie maintenant les 5 livres de miel d'une cruche par les 7 du mélange mis dans chaque vase, il vient 35. Divise par 21 ; le 1/21 en est 1 ⅔. De même, multiplie les 7 livres du garum par les 7 livres du mélange, il vient 49, dont le 1/21 est 2 ⅓. Enfin multiplie les 7 livres du mélange et les 9 livres du vinaigre, il vient 63, dont le 1/21 est 3. Chaque vase a donc reçu de chaque liquide ces quantités, à savoir : 1 livre ⅔ de miel, 2 livres ⅓ de garum, 3 livres de vinaigre, ce qui fait en tout 7. Qu'il en est bien ainsi et non autrement, triple chacune de ces quantités et tu retrouveras celles de chacun des liquides donnés primitivement.
38. XIII. Quelqu'un a dit que, partant d'une ville avec son bâtiment, il a devancé son compagnon, naviguant avec lui, d'un certain nombre de stades qu'il ne donne pas; l'autre fait voile 24 jours après, fait par jour avec son bâtiment 380 stades et atteint le premier au bout de 85 jours. Je veux savoir combien de stades a fait par jour celui qui a fait voile le premier.
Solution. 296 stades ⅓ moins 1/327.
Voici comme on le trouve : multiplie les 85 jours par 380 stades, il vient 32.300; ajoute les 24 jours aux 85, il vient 109; divise 32.300 par 109, la division donne 296 ⅓ moins 1/327. C'est le nombre de stades fait par celui qui a fait voile le premier.
39. XIV.[6] Quelqu'un dit à un autre : Donne-moi de ce que tu as 1 assarion, et prends 4 de ceux que j'ai; nous aurons autant. Le second lui répond : Non pas; mais donne-moi 4 des tiens, et prends 1 des miens; nous aurons la même somme. Je veux savoir combien a le premier, et combien le second.
Réponse. Le premier a 11, le second 5.
Voici comme on le trouve : multiplie par lui-même le nombre donné, quel qu'il soit, puis prend la moitié du produit, et de cette moitié, retranche le moindre nombre, soit 1, soit 2, soit 3; le reste sera ce qu'a l'une des deux personnes; ajoute à cette moitié le moindre nombre, la somme sera ce qu'a l'autre.
Pour éclaircir ce que je dis par un examen plus complet, multiplie 4 par lui-même, il vient 16; la moitié en est 8. Puisque, d'autre part, chacun a proposé 1, retranche-le de 4, il reste 3; ajoute ce nombre à 8, ce qui fait n; le premier a donc ii. Maintenant retranche de même 3 de 8, reste 5; c'est ce qu'a le second. Si donc de n on prend 4, il reste 7, si l'on y ajoute 1, il vient 8; de même si de 5 on retranche 1, il reste 4; si l'on y ajoute 4, il vient 8, et le problème est résolu.
Pour s'exercer davantage, on peut prendre une seconde question : Quelqu'un a demandé à un autre de lui donner 3 et de recevoir 6, en sorte qu'ils aient la même somme; l'autre demande au premier de lui donner 6 et de recevoir 3 et de se trouver ainsi égaux. Je demande combien a l'un et combien a l'autre.
Réponse. L'un a 21, l'autre 15; ce qui se calcule comme suit d'après la méthode donnée : 6 fois 6, 36; la moitié en est 18; retranche maintenant de 6 les 3 proposés, reste 3; ajoute-le et retranche-le de la moitié de 36, soit 18; il vient d'un côté 21, de l'autre 15. Si donc de 15 tu retranches 3, et que tu ajoutes 6, tu auras 18; de même si de 21, tu retranches 6 et que tu ajoutes 3, tu auras encore 18. Ainsi tu as trouvé les deux ayant le même nombre après avoir donné et reçu, en sorte que la méthode est vraie pour tout nombre.
40. XV. Quelqu'un dit à un autre : Il y avait dans ma bourse en argyries ce qu'il y avait dedans; étant allé à une foire, j'en ai dépensé le ⅓ ; puis dans une autre, encore le ¼ du tout; dans une troisième, le 1/5 du tout, et enfin dans une quatrième, j'ai déboursé le 1/6 du tout; après quoi, ouvrant ma bourse, j'y ai trouvé en tout 36 argyries; je demande combien j'en avais primitivement.
Réponse. 720.
Voici comme on le trouve : regarde de quel nombre tu peux retrancher son ⅓, son ¼, son 1/5, son 1/6, à savoir du même nombre; tu diras bien que c'est de 60; car le ⅓ en est 20, le ¼ 15, le 1/5 12, le 1/6 10, ce qui fait en tout 57 ; les retranchant de 60, reste 3. Mais nous cherchions 36; que faut-il donc faire? Je multiplie 36 par 60, il vient 2.160; je divise par les 3 unités du reste, la division me donne 720. Si donc de 720 je retranche son ⅓, son ¼, son 1/5, son 1/6, il ne restera que 36; car le ⅓ de 720 est 240; le ¼, 180; le 1/5, 144; le 1/6, 120, ce qui fait en tout 684, lesquels, retranchés de 720, laissent 36 comme reste.
41. XVI. Quelqu'un ayant formé le vœu de vivre encore le ⅓ et le 1/5 des années qu'il avait déjà vécu, a été exaucé et a vécu en tout 138 ans; je demande quel âge il avait lors de son vœu.
Solution. 90.
Voici comment on le trouve : multiplie les nombres dénominateurs des quantièmes, c'est-à-dire 3 par 5, il vient 15; ajoute maintenant 3 et 5, ce qui fait 8 ; ajoute à 15, il vient 23. Multiplie 138 par 15, ce qui fait 2.070; prends-en le 1/23, qui est 90; il avait donc 90 ans lors de son vœu; car le ⅓ en est 30, le 1/5 18, en tout 48, qui ajoutés à 90, donnent 138.
42. XVII. Quelqu'un avait des moutons autant qu'il en avait; rencontrant des loups, il a perdu ⅓ de son troupeau; s'étant sauvé d'eux, il en rencontre d'autres et perd ¼ de ce qui lui reste; s'étant sauvé une seconde fois et en ayant encore rencontré, il a perdu cette fois le 1/5, et rentré chez lui, n'a plus que 24 moutons. Il faut savoir combien il en avait d'abord.
Réponse. 60.
Voici la méthode : puisqu'en dernier lieu il lui reste 24 moutons, en ayant perdu le 1/5, il en a perdu 6 à cette fois; 24 et 6 font 30; cette autre fois, il avait perdu ¼, soit 10, ce qui avec 30 fait 40. Comme ici il a perdu ⅓, c'était 20 ; or 20 et 40 font 60; il avait donc en tout 60 moutons.
43. XVIII. Trois hommes ont mis dans une bourse 10 hyperpyres, à savoir : l'un 2, l'autre 3, le troisième 5. Ayant fait une affaire avec cette somme, des 10 ils ont fait 4°· Je demande combien revient à chacun des 4o nomismata. Réponse. A l'un 8, à l'autre 12, au troisième 20.
Voici la méthode : ajoute 2 et 3 et 5, ce qui fait 10; multiplie maintenant 40 par 2, il vient 80; divise par 10, le quotient est 8 (car 10 fois 8, 80), donne-le à celui qui a mis 2. Multiplie 40 par 3, il vient 120; divise par 10, et donne le quotient 12 a celui qui a mis 3. Enfin multiplie 5 par 4<>, il vient 200; divise par 10, et donne le quotient 20 à celui qui a mis 5. Ces parts, 20, 12 et 8, ajoutées font 40.
Pour les autres problèmes semblables, l'emploi de la même méthode te donnera sûrement la réponse.
[1] La majeure partie du texte reproduit P. Tannery.
[2] Je crois inutile de rappeler ici les témoignages bien connus d'auteurs anciens qui établissent l'antiquité de ce mode de figuration chez les Grecs et chez les Romains. On peut consulter spécialement à ce sujet l'ouvrage de M. Gow, A short history of greek mathematics (Cambridge, 1884). Mais je ne vois pas qu'on ait encore relevé une preuve décisive de l'emploi de cette figuration pour des calculs offrant une certaine complication. On peut trouver cette preuve dans les Dionysiaques de Nonnos, qui nous montre les astrologues s'en servant. Ainsi ( VI, 58-63 ), Astraios est consulté par Déméter sur l'avenir de sa fille. Astraios calcule, d'après la date et l'heure de la naissance de Perséphone, la position qu'avaient à ce moment les planètes par rapport aux douze signes et la situation qu'avait le zodiaque par rapport à l'horizon. Il placera ensuite une sphère artificielle dans la disposition calculée et considérera les aspects. Il s'agit là de calculs passablement longs. Nonnos attribue à Cadmos la connaissance du même procédé de calcul; c'est l'antique tradition sur l'origine phénicienne de l'arithmétique (IV, 278-279).
[3] Uranologion (1630).
[4] Faut-il lire πασών τάξις ou corriger πάντων?
[5] Jusqu'à présent j'ai adopté pour la notation des fractions le mode qui 'a paru se rapprocher autant que possible de celui de Rhabdas et permettre : se rendre compte exactement de sa façon de traiter ces expressions, désormais, les calculs devenant plus complexes, je suivrai le mode ordinaire, ce qui entraîne des inexactitudes forcées pour la traduction.
[6] J'ai traduit latéralement ce problème qui est posé et traité d'une façon absurde. Les deux conditions qui doivent servir à déterminer les deux inconnues étant identiques, le problème est en réalité indéterminé.
Soit a le plus grand nombre, donné par le premier des deux individus à l'autre, b le plus petit, donné par le second au premier, soit x ce que possède le premier, y ce que possède le second, on a la seule condition
x — a -+- b = y + a — b. D'où x — y = 2 (a — b).
Rhabdas donne x = a²/2 + a — b, et y = a²/2 — (a — b),
d'où l'autre condition x + y= a².
Il m'a paru impossible de restituer le problème sous une forme qui le rende mathématiquement explicable.