RETOUR À L'ENTRÉE DU SITE

EXTRAITS DES MANUSCRITS

Relatifs

A LA GÉOMÉTRIE PRATIQUE DES GRECS.

1° TRAITÉ DE LA DIOPTRE, PAR HÉRON D'ALEXANDRIE

(LE SEUL DES FRAGMENTS CONNUS DE CET AUTEUR, QUI SOIT ENCORE INÉDIT):

2° FRAGMENTS DE PAPPUS;

3° GÉODÉSIE ATTRIBUÉE À UN HÉRON DE BYZANCE;

4° FRAGMENTS DE JULES L’AFRICAIN, ETC.

TEXTES RESTITUÉS, TRADUITS EN FRANÇAIS, ANNOTÉS ET PUBLIÉS POUR LA PREMIERE FOIS

PAR A. J. H. VINCENT,

DE L'ACADÉMIE DES INSCRIPTIONS ET BELLES-LETTRES.

PRÉFACE.

Héron d'Alexandrie, surnommé l'Ancien par les uns, par d'autres le Mécanicien, était disciple du mécanicien Ctésibius. Ce dernier vivait à Alexandrie sous Ptolémée Evergète II, c'est-à-dire sous Ptolémée VII, dit Physcon, dans la seconde moitié du II^e siècle avant notre ère, suivant le témoignage d'Aristoclès cité par Athénée le Sophiste. Les motifs que des critiques modernes avaient allégués pour placer Ctésibius sous Ptolémée II Philadelphe ont été solidement réfutés par Schweighaeuser, par Venturi, par M. Bœckh, et tout récemment par M. Th. Henri Martin, suivant qui la vie du disciple de Ctésibius s'est prolongée très probablement jusque vers le milieu du I^er siècle avant J. C. Plusieurs traités qui lui sont attribués font partie de la collection des Mathematici veteres ; mais le traité dont il s'agit ici, Περὶ διόπτρας n'a jamais été publié ; seulement Venturi en a donné, au commencement de ce siècle, en italien, une sorte de traduction, d'Alexandrie, accompagnée d'assez bons commentaires historiques et scientifiques. Les Grecs nommaient διόπτρα tout instrument au travers duquel on visait: par exemple, la dioptre d'Hipparque, qui servait à mesurer le diamètre apparent du soleil et de la lune'(voir Ptolémée et Proclus). La dioptre d'Héron avait un autre but : elle consistait principalement en un niveau d'eau, mobile sur un trépied; mais ce niveau pouvait être enlevé, et remplacé, soit par une simple alidade mobile horizontalement et verticalement, soit par un plateau circulaire divisé en degrés, et pouvant se fixer, à volonté, dans un plan oblique quelconque. A certains égards donc, la dioptre d'Héron peut être comparée à nos théodolites.[1] Venturi n'a pas compris que l'instrument d'Héron se composait de pièces mobiles, d'où la forme fabuleuse qu'il a été conduit à lui attribuer.

Quant à l'ouvrage même, voici le sommaire des matières et des questions qui s'y trouvent traitées. L'auteur commence par faire la critique des dioptres employées avant lui; puis il cherche à faire sentir les avantages de la sienne (§§ ι et ii). Il en donne la description, ainsi que celle des signaux employés au nivellement (§§ iii-iv); ensuite de quoi il explique le moyen de résoudre, avec son appareil, les problèmes suivants :

1. — Déterminer la différence de niveau de deux points donnés (§ vi). La méthode de l'auteur ne diffère pas de la pratique moderne.

2. — Mener une ligne droite entre deux points tels, que de l'un on ne puisse apercevoir ΐautre (§ vii).

L'auteur procède par une sorte de tâtonnement, en construisant une ligne brisée à angles droits successifs, à peu près comme les arpenteurs romains.

3. — Mesurer la distance, réduite à L’HORIZON, comprise entre le point où l’on est et un point éloigné (§ viii).

L'auteur emploie ici, pour désigner une distance réduite à l'horizon ou cultellée, l'expression πρὸς διαβήτην, que Venturi n'a pas comprise, la traduisant constamment par les mots alla pertica, et entendant désigner ainsi l'emploi d'une sorte de compas.

4. — Mesurer la largeur d'une rivière (§ ix).

Opération identique à celle que les arpenteurs romains nomment varatio.

5. — Mesurer la distance horizontale de deux points éloignés (§ x).

6. — Etant donnée une droite, mener une perpendiculaire à l'une de ses extrémités, sans approcher de la droite ni de l'extrémité (§ xi).

7. — Mesurer la hauteur d'un point inaccessible (§ xii).

8. — Mesurer la différence des hauteurs de deux points inaccessibles (§xiii).

9. — Mesurer leur distance.

10. — Déterminer la position de la droite qui les joint, c'est-à-dire lui mener une parallèle.

11. — Comme application : Déterminer la hauteur d'une montagne.

12. — Déterminer la profondeur d'un fossé (§ xiv).

13. — Percer une montagne suivant une ligne droite qui joigne deux points donnés sur ses flancs (§ xv).

Méthode analogue à celle du deuxième problème.

14. — Creuser, dans une montagne, des puits qui tombent perpendiculairement sur une excavation (§ xvi).

15. — Une galerie souterraine quelconque étant donnée, déterminer, sur le sol au-dessus, un point tel, qu'en y creusant un puits vertical, il aboutisse à un point donné de la galerie (§ xvii).

Au moyen d'une sorte de triangulation double effectuée au cordeau.

16. — Tracer le contour d'un rivage suivant un arc de cercle ou une courbe donnée quelconque (§ xviii).

On mène, par un certain point, des rayons visuels qui rasent les bords d'un plateau horizontal semblable au contour demandé, et placé semblablement par rapport au point proposé.

17. — Relever un terrain suivant un segment de sphère de forme donnée (§ xix).

Méthode analogue à la précédente.

18. — Incliner un terrain suivant une pente déterminée (§ xx).

19. — Fixer, au moyen de la dioptre, sur une certaine droite horizontale menée à partir de nous, un point qui soit éloigné de nous d'une distance donnée (§ xxi).

Au moyen de deux triangles semblables opposés.

20. — D'un point éloigné de nous, prendre, avec la dioptre, une distance égale à une distance donnée, sans approcher de ce point, et sans avoir la droite sur laquelle il faut prendre cette distance (§ xxii).

Au moyen de triangles semblables (quelconques), en employant seulement les rapports des côtés.

21. — Mesurer an champ au moyen de la dioptre (§§ xxiii et xxiv). Par la décomposition en rectangles, trapèzes et triangles. — Plusieurs méthodes.

22. — Les bornes d'un champ ayant disparu, à l'exception de deux ou trois, retrouver, au moyen du plan (dessin), supposé donné, les limites perdues (§ xxv).

A peu près comme les arpenteurs romains.

23. — Partager un terrain en portions données, au moyen de droites menées par un même point (§ xxvi).

24. — Mesurer un champ sans entrer dedans (§ xxvii).

25. — Diviser un trapèze ou un triangle donné, suivant un rapport donné, par une parallèle à la base (§§ xxviii et xxix).

26. — Trouver l'aire d'un triangle en fonction de ses trois côtés (§ xxx). La plus ancienne et la plus élégante des démonstrations de cette célèbre formule.

27. — Etant donnée une fontaine, déterminer son produit (§ xxxi).

28. — Déterminer la distance angulaire de deux astres (§ xxxii). Au moyen du plateau divisé dont il a été question.

29. — Critique de ΐastérisque, c'est-à-dire vraisemblablement de la groma des Romains (§ xxxiii).

30. — Description et usage de l’odomètre (§ xxxiv).

31. — Mesure du sillage d'un navire (§ xxxv).

32. — Déterminer la distance de deux lieux situés sous des climats différents (§ xxxvi).

Par les heures de l'observation d'une même éclipse, faite dans les deux lieux, dont les latitudes sont supposées données. Les heures employées sont les heures temporaires.

33. — Mouvoir un poids donné avec une puissance donnée, au moyen d'un système de roues dentées (§ xxxvii et dernier).

Principe des vitesses virtuelles assez bien indiqué, pour le cas de deux forces, puissance et résistance.

On peut juger, par cet exposé sommaire, que l'ouvrage d'Héron n'augmentera pas de beaucoup nos richesses scientifiques. Est-ce à dire, pour cela, qu'il soit dépourvu de tout intérêt? Tant s'en faut; et l'on peut même dire que, sous le rapport historique, il remplit une véritable lacune. En effet, entre la géométrie élémentaire des Grecs, représentée par Euclide, et la géométrie supérieure, sur laquelle nous possédons d'admirables ouvrages, ceux d'Apollonius de Perge, par exemple, il est une troisième branche de la science, intermédiaire, en quelque sorte, entre les deux autres, et dont, jusqu'à présent, l'histoire est à peine connue : c'est la géométrie pratique, ou géodésie,[2] que l'on peut considérer comme personnifiée sous le nom d'Héron. Or l'ouvrage sur la dioptre est un véritable traité de géométrie pratique, auquel peuvent servir de complément les opuscules et fragments métrologiques que nous connaissons déjà sous le même nom d'Héron, bien que l'on ait coutume de les attribuer à des auteurs différents. En effet, c'est une opinion générale accréditée, qu'outre le maître de Proclus, dont l'existence nous est attestée par Marinus, il y a eu deux autres mathématiciens du nom d'Héron, l'un antérieur à Proclus, Héron d'Alexandrie, distingué par la qualification d'Héron l'Ancien; l'autre, postérieur, dit Héron de Byzance, ou Héron le Jeune. Il serait, je pense, hors de propos de traiter ici, au sujet de la dioptre, cette question de l'existence réelle des divers Héron; question qui se trouve, d'ailleurs, je le pense, maintenant épuisée dans l'excellent travail que M. Th. Henri Martin a publié[3] sous les auspices de l'Académie des inscriptions et belles-lettres. Je ne puis cependant me dispenser d'en dire deux mots.

On s'accorde généralement à reconnaître Héron l'Ancien comme auteur des traités publiés par Thévenot dans le recueil dit des Mathematici veteres, savoir :

De constructione et mensura Manubalistœ; Belopœeca; Spiritalia; De automatoram fabrica.

D'un autre côté, on attribue vulgairement à Héron le Jeune un traité De machinis bellicis (πολιορκητικά dans le manuscrit), et un autre De geodœsia, dont, jusqu'à ce jour, on ne connaissait que des traductions latines, publiées conjointement, en 1572, par Barocci, qui, de son chef, y donne à l'auteur le titre de mécanicien; plus, un recueil ayant pour titre Ονόματα γεωμετρικά, dont une partie seulement a été éditée, une première fois par Dasypodius (en 1670), et une seconde fois (en 1826) par Cf. F. Hasenbalg; plus enfin, une multitude de fragments inédits sur les mesures de surface, de volume et de capacité.[4]

Quant à la provenance véritable de ces fragments, il est incontestable qu'un grand nombre d'entre eux portent l'empreinte de mains et d'époques différentes; mais il ne l'est pas moins qu'en général ils décèlent une origine commune, comme Bœckh lui-même (Metrologische untersuchungen, p. 9) paraît le reconnaître; et cette origine est certainement beaucoup plus ancienne qu'on ne le suppose.

Suivant moi, il a dû exister, sous le nom d'Héron,[5] et cela dès une époque très élevée, une vaste composition qui, servant de texte pour l'enseignement des écoles, s'est transmise, de siècle en siècle, en subissant des modifications successives, des additions, des mutilations, des interpolations. Les professeurs enseignaient Héron comme nous avons vu enseigner Euclide, c'est-à-dire chacun à sa manière, s'accordant sur le fond, mais variant à l'infini dans les détails; c'est ainsi que nous avons eu l'Euclide de Clavius, l'Euclide de Taquet, celui d'Henrion, celui d'Ozanam, et cent autres. De même donc chaque professeur rédigeait à sa manière et dictait son Héron. Dès lors, que nous trouvions Héron cité dans un ouvrage qui porte son nom, il n'y a rien là d'étonnant : c'est, je le répète, identiquement ce qui s'est pratiqué à l'égard d'Euclide dans tout le moyen âge, lorsque l'enseignement de la géométrie appliquée eut fait place, dans les écoles, à celui de la géométrie purement abstraite ; et c'est ce qui se pratique encore aujourd'hui. .Au lieu de dire Héron le Jeune, il fallait dire le nouvel Héron, comme nous disons le nouveau Barème.

Au surplus, quoi qu'il en soit de ce point de controverse, ce qui nous importe à nous, c'est l'âge du Traité de la dioptre; or, à cet égard, nous pouvons affirmer que, s'il y a eu plusieurs Héron, notre traité appartient au plus ancien; et c'est ce qu'il nous suffit de savoir. Cette certitude nous paraît résulter des preuves données par Venturi et complétées par M. H. Martin. En effet, 1° ce traité est intitulé, dans les manuscrits, Ηερωνος Αλεξανδρέως περὶ διόπτρας. Or il n'y a qu'un Héron d'Alexandrie célèbre par ses ouvrages scientifiques, et c'est le disciple de Ctésibius. — 2° L'opuscule analysé par Pappus, sous le titre de βαροῦλκος, d'Héron le Mécanicien, c'est-à-dire d'Héron l'Ancien, est identique avec le chapitre xxxvii du traité Περὶ διόπτρας, où, sans doute, Héron l'Ancien avait inséré ce problème; de même que, suivant le témoignage de Pappus, il répétait, dans ses Μεχανικὰ et dans ses Βελοποιητικὰ, une même solution du problème de la ligne moyenne proportionnelle entre deux lignes données. 3° Le Byzantin du X^e siècle, auteur d'une petite Géodésie que nous publions dans ces extraits, ne paraît connaître qu'un seul mathématicien ancien du nom d'Héron, et c'est celui qu'il désigne lui-même comme disciple de Ctésibius. Or il déclare emprunter à Héron un procédé pour le jaugeage des sources : la description de ce procédé se trouve textuellement dans le traité Περὶ διόπτρας. — 4° Dans un autre passage, il dit avoir mis à profit les œuvres d'Archimède et d'Héron. Or on trouve dans sa Géodésie d'autres emprunts faits au traité Περὶ διόπτρας. — 5° Dans une petite Catoptrique imprimée à Venise, en 1518, sous le nom de Ptolémée, mais qui est un extrait d'une Catoptrique d'Héron l'Ancien, comme Venturi et M. Martin l'ont démontré, l'auteur dit avoir écrit un traité sur la dioptre. — 6° Le préambule et tout le reste du traité Περὶ διόπτρας s'accordent parfaitement avec les autres œuvres d'Héron l'Ancien pour les connaissances théoriques, pour l'esprit pratique, pour la composition et pour le style. —7° Dans l'avant-dernier des problèmes énumérés plus haut, problème où il s'agit d'évaluer la distance de deux lieux de longitudes différentes par la différence des heures d'observation d'une même éclipse de lune, l'auteur prend pour exemple la distance d'Alexandrie à Rome, et suppose que celui qui doit résoudre le problème habite Alexandrie. D'où M. Martin conclut que l'auteur était Alexandrin, et qu'il vivait à une époque où Alexandrie avait plus de relations avec Rome qu'avec Athènes ou Byzance, c'est-à-dire avant l'an 395 de notre ère, date de la séparation de l'empire d'Orient et de l'empire d'Occident, et depuis l'an 81 avant notre ère, date de l'avènement de Ptolémée X, premier roi d'Egypte qui ait tenu sa couronne des Romains. Or nous avons vu que la vie d'Héron l'Ancien doit s'être prolongée au delà de cette dernière époque.

A ces raisons nous pouvons en ajouter deux autres, tirées aussi de l'avant-dernier problème. En effet, 8° l'auteur emploie dans ce problème des heures temporaires, c'est-à-dire des heures variables avec les saisons et les climats, dont douze heures de nuit, comprises entre le coucher du soleil et son lever, et douze heures de jour, comprises du lever au coucher. Or cette manière de mesurer le temps est une nouvelle preuve de l'ancienneté de l'ouvrage; car déjà Claude Ptolémée (au II^e siècle de notre ère) emploie constamment les heures équinoxiales. — 9° Dans ce même problème, Héron adopte, pour la mesure de la circonférence du globe terrestre en stades, l'évaluation d'Eratosthène, c'est-à-dire 252.000 stades. Or cette évaluation a été constamment suivie par Hipparque, bien que Pline lui attribue une correction prétendue, qui, en ajoutant 25.000 stades, aurait encore aggravé l'erreur. Cette même évaluation a été contredite par Posidonius, qui a proposé d'abord 240.000 stades, c'est-à-dire encore trop, et ensuite 180.000 stades, c'est-à-dire trop peu. Mais l'évaluation d'Eratosthène a continué d'être généralement reçue jusqu'aux premières années du II^e siècle de notre ère; elle est admise à ce titre par Théon de Smyrne, dans son Astronomie, où cependant il prouve qu'il connaissait bien les travaux d'Hipparque et de Posidonius. Au contraire, Ptolémée, ayant adopté, à l'exemple de Marinus, la seconde évaluation de Posidonius, a réussi à la faire accepter et à faire abandonner généralement celle d'Eratosthène. Ainsi le traité Περὶ διόπτρας peut fort bien avoir été écrit à Alexandrie dans la première moitié du I^er siècle avant notre ère, c'est-à-dire du vivant de Posidonius, mais non à l'époque de Claude Ptolémée, c'est-à-dire après le deuxième tiers du II^e siècle de notre ère.

Ainsi tout s'accorde à nous faire reconnaître, dans le traité Περὶ διόπτρας, un précieux reste de la géométrie des Egyptiens, et une œuvre authentique d’Héron d'Alexandrie, élève de Ctésibius, et surnommé l'Ancien depuis l'époque où l'on crut en avoir découvert un nouveau.

Ce qui précède suffira, sans doute, pour faire comprendre que, si j'ai réuni au Traité de la dioptre d'Héron d'Alexandrie la Géodésie inscrite sous le nom d'Héron le Jeune, ce n'est point la similitude des noms, similitude vraie ou supposée, qui a pu m'y conduire, mais bien l'analogie des sujets.

En effet, pour ce dernier point d'abord, un rapide coup d'œil jeté sur l'ouvrage suffit pour le faire ressortir avec évidence. L'auteur de la Géodésie commence (§ i[6]), comme Héron d'Alexandrie, auquel il emprunte souvent jusqu’à ses propres expressions, par exposer l'utilité et la nécessité de la dioptre; et, si le préambule n'était suivi d'une lacune dans le manuscrit, il n'est pas douteux que nous trouverions, à la même place, la description de l'instrument : cette description est indiquée dans le texte, et devait y être suivie de quelques détails sur les unités et fractions d'unité des mesures dont l'auteur fait usage.

A la suite se trouvait un premier problème dont la rédaction est également perdue ; mais son objet se trouve indiqué plus loin ; il avait pour but de

Mesurer une ligne droite qui joint deux points dont un seulement est accessible.

C'est le problème résolu par Héron d'Alexandrie, dans son chapitre viii.

L'énoncé du problème suivant manque pareillement; mais on voit, par la solution, conservée presque en entier, que son objet est de

Mesurer la hauteur d'un point ou d'un édifice éloigné, et dont on ne peut approcher (§ ii).

C'est l'objet du chapitre xii d'Héron d'Alexandrie, et la première proposition de Barocci.

L'auteur résout ensuite les problèmes suivants :

Etant donnés deux points éloignés et visibles, trouver leur distance réduite à l'horizon, sans approcher d'aucun des deux, et, de plus, Déterminer la position de la droite qui les joint (§§ iii-v).

C'est l'objet du chapitre x d'Héron d'Alexandrie, et des propositions 2^e, 3^e et 4^e de Barocci.

Mesurer les surfaces planes comprises entre des lignes droites ou courbes (§ vi).

C'est la cinquième proposition de Barocci. Dans les chapitres xxiii et xxiv, Héron d'Alexandrie résout le même problème sous ce titre : Mesurer un champ au moyen de la dioptre.

La proposition 6^e de Barocci (§ vii) n'est qu'une application spéciale à la mesure du cercle.

La proposition 7^e (§ viii) est une extension des précédentes : il y est question de la mesure des volumes.

La proposition 8^e (§ ix) est une application particulière de la précédente à la mesure de la capacité d'une citerne.

La proposition 9^e (§ x) reproduit presque identiquement, non-seulement par l'objet, mais par la rédaction, le chapitre xxxi d'Héron d'Alexandrie, où il est question de déterminer le produit d'une fontaine.

Enfin, la proposition 10^e et dernière (§ xi) a pour but principal, comme le chapitre xxxii d'Héron d'Alexandrie, de

Déterminer la distance angulaire de deux astres.

Mais l'auteur moderne y ajoute des développements d'une assez grande importance, comme on le verra plus tard.

La similitude, l'identité même des objets traités dans les deux ouvrages, est donc complète.

Maintenant, pour ce qui est des noms des auteurs, M. H. Martin a démontré, il est vrai, d'une manière inattaquable, et la personnalité de l'auteur de la Géodésie, et l'originalité de son ouvrage; il a prouvé (ses raisons seront exposées en leur lieu) que cet auteur vivait à Constantinople dans la première moitié du X^e siècle. Mais, quant à affirmer qu'il se nommait Héron, c'est ce que M. H. Martin lui-même n'ose point faire, bien qu'il y incline fortement. Quant à moi, malgré la probabilité plus ou moins grande que chacun peut attribuer à cette hypothèse, dont on pourrait, en définitive, se contenter sans grand inconvénient, j'avouerai que les arguments dont on peut l'appuyer ne me frappent que médiocrement. Les manuscrits aujourd'hui subsistant de cet ouvrage sont inscrits, cela est vrai, sous le nom d'Héron ; mais supposons, pour un instant, que l'auteur ait omis, ce qui n'est nullement impossible, de signer sa rédaction autographe, soit par humilité chrétienne (car il était chrétien), soit par tout autre motif; supposons, ce qui est plus probable, que son nom se soit trouvé d'Alexandrie effacé ou perdu, comme le sont les premiers chapitres de la Géodésie: ne suffisait-il pas que l'objet de l'ouvrage fût le même que celui du Traité de la dioptre, dont il présente, jusqu'à un certain point, une sorte de commentaire et d'application? Ne suffisait-il point qu'Héron y fût invoqué comme en ayant fourni le thème, pour que, dans l'impossibilité de le désigner positivement, on n'ait trouvé rien de mieux, rien autre chose à faire, que de le rapporter à Héron, dont il continuait la doctrine, et d'y appliquer le nom de ce géomètre, non pas comme désignation de l'auteur, mais comme personnification de la doctrine? C'est une induction que je crois fort légitime, et Letronne va beaucoup plus loin que moi en ce genre,[7] lorsque, trouvant, dans un manuscrit sur les mesures, plusieurs titres où est mentionné le nom d'Héron, il conclut, de cela même, que l'ouvrage est tout simplement une compilation rédigée d'après les écrits d'Héron d'Alexandrie.

Au surplus, on conviendra volontiers, avec M. H. Martin, que cette question de nom est bien secondaire; et, comme le dit ce judicieux critique, peu importe ici que l'auteur s'appelle ou ne s'appelle pas Héron : c'est une opinion que l'on peut admettre ou rejeter, sans grave inconvénient de part ni d'autre.

Mais une chose sur laquelle il ne peut y avoir incertitude, c'est, comme je l'ai dit, la personnalité de l'auteur. A cet égard, M. H. Martin a produit des preuves d'autant plus remarquables, qu'il les a puisées, avant de connaître le texte même de l'ouvrage, dans une traduction remplie d'erreurs. Le savant philologue n'en a pas moins reconnu, au travers des contre-sens du traducteur, l'ouvrage d'un Byzantin du X^e siècle; il y a constaté, notamment dans la dernière proposition, des détails topographiques et astronomiques qui ne peuvent s'appliquer, du moins sans s'écarter des plus grandes probabilités, qu'à la latitude de Constantinople, et à l'époque de Constantin Porphyrogénète; enfin il est parvenu à restituer, sans autre secours que l'informe traduction de Barocci, plusieurs passages du texte original ainsi méconnu et défiguré. Quant à moi, ayant, en quelque sorte, assisté à l'exécution de ce chef-d'œuvre de sagacité, je croirais manquer à a· Alexandrie un impérieux devoir, si j'omettais d'en rendre ici témoignage, avant de profiter des résultats qu'il m'a fournis, et que j'ai adoptés pour mon édition, reconnaissant que je n'avais rien à faire de mieux.

Toute la partie de cette publication qui est relative à Héron de Byzance ou à l'opuscule qui porte son nom, est donc autant l'ouvrage de M. H. Martin que le mien, même pour ce qui est relatif au texte; car, j'avais à peine parcouru ce texte, qui venait de m'arriver d'Oxford par l'obligeante entremise de M. E. Miller, que, l'ayant transmis, dans son état entièrement brut, à M. Martin, qui en désirait une prompte communication, je le reçus de nouveau, quelques jours après, entièrement corrigé, restitué et annoté de sa main; de façon que je n'y trouvai presque plus rien à faire que de le traduire, travail devenu très facile, grâce à celui de mon bénévole collaborateur.

Telles sont les observations générales que j'avais à présenter sur le second ouvrage. Je m'abstiendrai d'entrer dans plus de détails, vu l'impossibilité de le faire sans répéter une partie de ce qu'a si bien dit M. H. Martin dans son savant mémoire. Je préfère y renvoyer le lecteur, qui trouvera là tous les détails biographiques que l'on peut désirer sur le sujet.

Je signalerai, en finissant, deux pièces que j'ai cru devoir ajouter pour l'éclaircissement de mes deux auteurs, savoir : un chapitre de Pappus (viii, 10), qui reproduit, en le commentant, le chapitre où Héron d'Alexandrie décrit le barulcus (machine à lever les fardeaux, au moyen d'une roue dentée), et un chapitre de Jules l'Africain (xxi^e des Cestes) sur la mesure des distances et des hauteurs. Ce chapitre se trouve, il est vrai, dans la collection des Mathematici veteres de Thevenot, mais tellement défiguré, comme tout le reste du texte du même auteur, que c'est presque encore une édition princeps que j'en donne.

On trouvera de plus ici, à la suite de chaque proposition, les notes de Venturi presque en totalité; quelques notes extraites de l'ouvrage de M. H. Martin; enfin, quelques antres que j'ai ajoutées aux précédentes. Quant à celles de Barocci, elles ne valaient vraiment pas la peine d'être reproduites. Je n'ai pas négligé de signaler, à l'occasion, les variantes qui pouvaient présenter quelque valeur ou quelque intérêt.

Je ne terminerai point cette introduction sans adresser à mon savant confrère M. Chasles, de l'Académie des Sciences, les remerciements que je lui dois à plus, d'un titre, d'abord pour l'obligeance qu'il a eue de mettre à mon entière disposition le rare ouvrage de Venturi, ensuite pour les encouragements éclairés qu'il a bien voulu donner à mon travail, et sans lesquels je ne l'eusse peut-être point entrepris.

POST-SCRIPTUM.

Il n'existe que trois copies du Traité de la dioptre : l'une fait partie du manuscrit grec n° 24-30 (in-fol. papier) de la Bibliothèque impériale de Paris (fol. 79-118); un second exemplaire appartient à la bibliothèque du séminaire protestant de Strasbourg; il est cou-tenu dans le manuscrit coté G. m. 6 (également in-fol. papier), dont il occupe les folios 81-130. Enfin, une troisième copie se trouve à la bibliothèque de Vienne; mais celle-ci est incomplète et tronquée de près d'un tiers du texte.[8]

Le manuscrit de Paris était le seul que je pusse avoir à ma disposition lorsque j'entrepris mon travail. Au moment de mettre sous presse, et seulement alors, je pus consulter le manuscrit de Strasbourg, qui était depuis un an entre les mains du savant professeur de Weimar, M. Sauppe. Cette circonstance nous annonce vraisemblablement une édition qui précédera peut-être la mienne, et, sans aucun doute, la surpassera.

Quoi qu'il en soit, je n'ai pas perdu un instant pour collationner mes feuilles, déjà presque toutes composées, avec le nouveau texte dont j'obtenais communication. J'ai bientôt reconnu que ce dernier avait servi de type au manuscrit de Paris, et que celui-ci n'en offrait qu'une simple copie, mais très fautive. Dès lors, la plupart des innombrables corrections que je m'étais cru, avec raison, autorisé à faire pour rectifier le sens et épurer le texte, s'étant trouvées confirmées par le manuscrit de Strasbourg, j'ai pris le parti de ne mentionner en général, au bas des pages, que les leçons fournies par ce dernier manuscrit, quand elles différaient des miennes, et de supprimer celles qui ne se trouvaient que dans le manuscrit de Paris, presque toutes étant évidemment des erreurs de copie; j'en ai cependant conservé quelques-unes, en très petit nombre, dignes peut-être de quelque attention, en les distinguant par la lettre P.

J'adresse des remercîments bien sincères à M. Jung, le savant bibliothécaire de la ville et du séminaire protestant de Strasbourg, pour les démarches qu'il s'est empressé de faire à l'effet de rappeler le précieux volume; et, de plus, je ne dois pas négliger de déclarer, pour rendre hommage à la vérité, que M. Sauppe a mis, de son côté, toute la promptitude désirable à renvoyer le manuscrit dès qu'il a pu savoir que j'en avais besoin ; et je lui en fais aussi mes remercîments.

Mais, avant tout, je me fais un plaisir autant qu'un devoir de signaler ici un bonheur inattendu dont mon édition tirera un profit inappréciable : c'est que mon excellent et illustre confrère M. Hase veut bien dérober à ses importants travaux le temps nécessaire pour revoir toutes mes épreuves; c'est là une garantie sur laquelle j'étais loin de pouvoir compter pour cette publication, et je m'empresse d'en témoigner ma reconnaissance à l'éminent helléniste à qui je suis déjà redevable de plusieurs corrections importantes.

Le manuscrit de Strasbourg est d'une belle écriture du xvi^e siècle ; celui de Paris est d'une écriture postérieure, très mauvaise et très négligée. Tous deux contiennent les traités suivants d'Héron : Πνευματικὰ,Βελοποιητικὰ, Περὶ διόπτρας, Τινὰ κλάσματα, et Περὶ αὐτοματοποιητικῆς. Dans le manuscrit de Strasbourg on trouve de plus divers autres traités, soit d'Héron lui-même, soit d'Athénée, de Biton, d'Euclide, qui ne sont pas dans celui de Paris; lequel, de son côté, contient en plus les Harmoniques de Manuel Bryenne, écrits d'une autre main, et reliés postérieurement avec les opuscules d'Héron déjà mentionnés. Au commencement de ce traité d'harmonique on lit la note suivante : « Haec mathematica manuscripta quae nullibi impressa estant mini Matthiae Perneggero reliquit Abraham Unverjagt Schemnicensis Pannoniae Argentina abiens; anno 1600. »

Cette circonstance paraît appuyer l'origine que j'ai attribuée plus haut au manuscrit de Paris.

A. J. H. Vincent.

EXTRAIT DE

PAPPUS[9]

De la même théorie[10] dépend cette question de Mouvoir un poids donné avec une force donnée : c'est là, dit-on, une des inventions mécaniques d'Archimède, à propos de laquelle on lui attribue ce mot : « Donnez-moi un point d'appui et je mouvrai la terre. » Héron d'Alexandrie, dans le livre intitulé Barulcum, expose avec une clarté parfaite un mécanisme propre à produire un semblable effet, en partant pour cela d'une proposition fondamentale qu'il a démontrée dans ses Mécaniques, là où il traite en outre des cinq puissances,[11] c'est-à-dire du coin, du levier, de la vis, de la moufle et du treuil,[12] puissances sur chacune desquelles il démontre comment on peut mouvoir un poids donné avec une force donnée. Quant au Barulcum, c'est au moyen de la juxtaposition d'une suite de roues dentées qu'il résout le problème, en supposant que le diamètre de chaque roue est à celui de son pignon comme 5 est à 1, le poids à mouvoir étant, d'ailleurs, de 1000 talents, et la force motrice de 5 talents. Que l'on nous permette d'adopter, pour notre propre démonstration, le rapport de 2 à 1, de supposer le poids à mouvoir de 160 talents au lieu de 1000, et la force motrice de 4 talents au lieu de 5 ; c'est-à-dire que nous supposons la puissance motrice de l'homme égale à 4 talents lorsqu'il l'exerce par lui-même sans aucune machine.

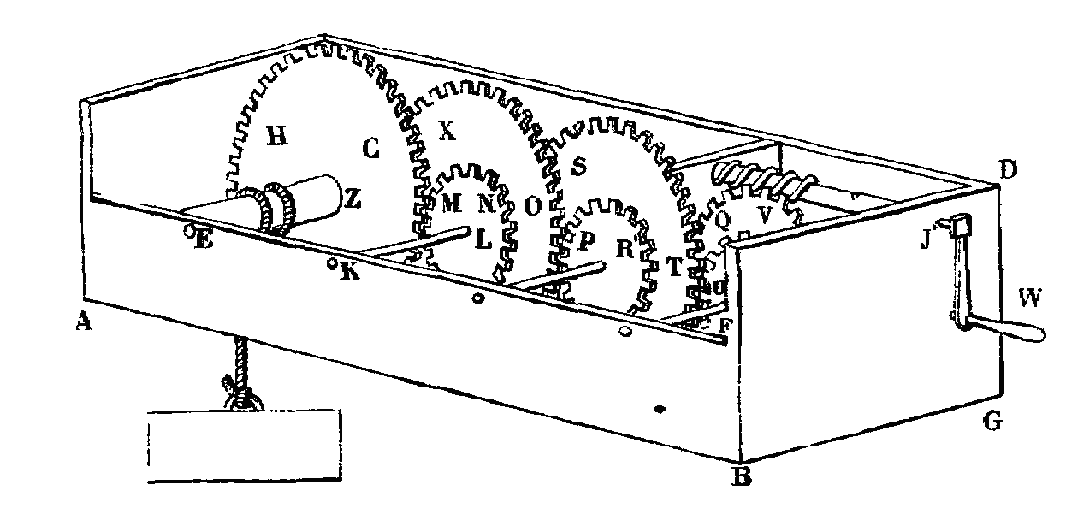
Soit donc ABGD le châssis dont parle Héron [d’Alexandrie]. Dans ses faces parallèles les plus étendues soit engagé un axe EZ qui puisse de y pivoter librement. A cet axe soit fixée la roue dentée CH, dont les dents fassent saillie dans la direction des rayons, et dont le diamètre soit double de celui de la diagonale du tenon suivant lequel l'axe s'engage dans la roue : car il faut dire qu'il est équarri dans son milieu sur une longueur égale à l'épaisseur de la roue dans laquelle il est exactement engagé, tandis qu'il est, d'une manière quelconque, arrondi en cylindre, ou simplement dénudé de son écorce, de chaque côté de cette roue. Supposons des cordes (ce que l'on nomme l'armature) attachées au poids à mouvoir, pénétrant dans le châssis par un trou, ou mieux par une large ouverture pratiquée dans la paroi AB, et venant s'enrouler autour du cylindre EZ de chaque côté de la roue CH : si alors on fait tourner cette roue, à son tour elle fera prendre au cylindre EZ, auquel elle est fixée, un mouvement de rotation autour de pivots d'airain fixés à ses extrémités, et s'engageant dans des crapaudines aussi d'airain et pratiquées dans les parois du châssis ABGD : de cette manière, les cordes enroulées autour du cylindre emporteront le poids du fardeau. Mais, pour faire mouvoir la roue CH, il faudra y appliquer une force de plus de 80 talents, puisque son diamètre est double de celui du cylindre : car c'est là une proposition démontrée par Héron dans ses Mécaniques, là où il a également résolu beaucoup de problèmes utiles et importants pour les usages de la vie.

Puis donc que nous n'avons point à notre disposition cette force de 80 talents, mais seulement une force de 4 talents, soit un autre axe KL, établi comme le premier EZ, parallèlement à celui-ci, auquel sera fixée une autre roue dentée MN, dont les dents puissent engrener avec celles de la roue CH, condition qui sera remplie si le diamètre de la roue CH est au diamètre de MN comme le nombre des dents de CH est au nombre des dents de MN. (Comment obtenir ce résultat, c'est ce que l'on verra plus loin.) La roue MN est donc déterminée. Soit maintenant une autre roue XO également fixée au même axe KL, et dont le diamètre soit double de celui de la roue MN. Cela posé, si l'on veut mouvoir le poids donné au moyen de la roue XO, il faudra employer une force de 40 talents, puisque 80 talents sont le double de 40 talents.

Soit appliquée derechef contre la roue dentée XO, une autre roue dentée PR fixée à un autre axe, et à ce même axe soit fixée une seconde roue ST, ayant de même un diamètre double de celui de la roue PR, mais de façon que ses dents ne puissent s'embarrasser dans celles de la roue MN. La force capable de mouvoir le poids donné au moyen de la roue ST serait donc équivalente à un poids de 20 talents; mais, encore une fois, la force donnée n'est que de 4 talents.

Il faudra donc de nouveau appliquer contre la roue dentée ST une autre roue dentée FU; et, sur le même axe que FU, fixer une seconde roue dentée QV, dont le diamètre soit à celui de FU dans le rapport de 2 à 1. Ainsi la force capable de mouvoir le poids donné en agissant sur la roue QV sera de 10 talents.

Derechef, soit appliquée contre la roue QV une autre roue dentée W&, et sur l'axe de celle-ci soit fixée une roue dentée à dents obliques A"B", dont le diamètre soit à celui de W& dans le rapport des ι ο talents aux 4 talents de la force donnée.

Tout cela étant ainsi disposé, si nous imaginons que le châssis ABGD soit solidement fixé dans une position élevée, le poids donné suspendu après l'axe EZ, et la force motrice des 4 talents pressant sur la roue A"B", aucune de ces deux forces ne pourra l'emporter sur l'autre, quelles que soient la facilité des mouvements de rotation et la perfection que l'on veuille supposer aux engrenages; c'est-à-dire que la puissance des 4 talents d'un côté, et le poids des 160 talents de l'autre, se feront parfaitement équilibre comme dans une balance ordinaire. Mais, si nous ajoutons un petit poids de l'un ou de l'autre des deux côtés, la machine penchera et sera entraînée du côté où l'addition aura été faite. Si, par exemple, nous ajoutons seulement un excès de poids d'une mine à la force des 4 talents, le poids des 160 talents sera enlevé.

Or, au lieu d'effectuer cette addition, établissons, en contact avec la roue A"B", une vis YA' dont le filet engrène avec les dents courbes de cette roue YA'. La manière d'obtenir ce résultat a été expliquée par Héron dans ses Mécaniques, livre déjà cité; et nous-même l'expliquerons plus en détail dans ce qui suivra. Supposons donc que la vis puisse tourner librement dans des trous bien ronds où s'engagent ses pivots; que l'un de ceux-ci fasse saillie hors du châssis, au travers de la paroi BD; et qu'alors, équarri à son extrémité, il reçoive la manivelle JW. Cela étant, si l'on prend cette manivelle et que l'on fasse tourner la vis, on fera en même temps tourner la roue A"B", ainsi que la roue W& qui s'y trouve fixée. Par suite, la roue QV, qui de Pappus, est appliquée contre celle-ci, tournera également, ainsi que la roue UF qui fait corps avec QV; puis ST qui est appliquée contre UF, ainsi que PR qui fait corps avec ST; puis XO qui est appliquée contre PR, ainsi que MN qui fait corps avec XO; puis CH qui est appliquée contre MN, ainsi que EZ qui fait corps avec CH; et alors, l'armature enroulée autour de EZ, en partant du fardeau, enlèvera celui-ci. Quant à dire que le poids doit se mouvoir, c'est ce qui résulte évidemment de l'addition de force provenant de l'emploi de la manivelle, dont l'extrémité décrit un cercle plus grand que la base de la vis. Or il a été démontré, d'une part dans le livre d'Archimède Sur les balances, (Περὶ ζυγῶν), de l'autre dans les Mécaniques de Philon et d'Héron, que Les plus grandes circonférences l'emportent en puissance sur les plus petites, lorsqu'elles sont toutes décrites autour d'un même centre.

Tels sont les principaux points qui, dans la question présente, regardent la théorie mécanique; quant aux appareils, il y en a de plusieurs espèces et de plusieurs sortes à considérer . . . .