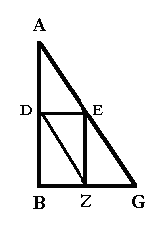RETOUR À L'ENTRÉE DU SITE

EXTRAIT DES

CESTES

DE

JULES L'AFRICAIN.

(Mathematici veteres, p. 296.)

On sait combien le texte de cet auteur a été maltraité par les copistes. C'est au point, comme je l'ai déjà rappelé ailleurs (Notices et extraits des manuscrits, etc. t. XVI, 11^e partie, p. 344), que l'éditeur des Gestes, Thévenot (Math. vet. Paris, 1693), n'a pas osé (Fabricius, Bibl. gr. édit. de Harles, t. IV, p. ai) en essayer une traduction latine. J'ai corrigé ce texte, comme les fragments que j'en ai déjà donnés (lieu cité), d'après les leçons de Boivin, de Meursius, de Lamy, et pour le surplus (j'en demande pardon au lecteur), ex ingenio. Voici le texte restitué, avec la traduction. Je placerai dans les notes, au bas des pages, les leçons du texte imprimé et celles des manuscrits qui pourraient offrir quelque intérêt.

I. Déterminer la largeur d'un fleuve ou la hauteur d'une muraille. (Ch. xxi.)

Pour peu que l'on ait des connaissances de quelque étendue, on doit, je pense, savoir appliquer les éléments d'Euclide; et il n'est pas difficile de résoudre, au moyen du premier livre, le problème qui consiste, soit à Mesurer la largeur d'un fleuve dont les ennemis occupent la rive opposée, afin de pouvoir préparer les matériaux nécessaires pour y jeter un pont, soit à Prendre de loin les hauteurs d'une muraille, afin de disposer, avant d'en approcher, des machines de guerre d'une grandeur convenable. Or, pour faire mieux comprendre notre démonstration, nous la ferons précéder de ce théorème :

II. Si, dans un triangle rectangle, on partage en deux parties égales l'un des côtés de l'angle droit, puis que, par ce point, on élève une perpendiculaire, puis que, par le point de rencontre de cette perpendiculaire avec l'hypoténuse, on mène une parallèle au premier côté: tous les côtés se trouveront partagés en deux parties égales.

En effet, soit le triangle ABG, rectangle en B. Soit AB partagé en deux parties égales au point D. Menons-lui la perpendiculaire DE, et par le point Ε menons à AB la parallèle EZ.

Je dis que les côtés AG et BG se trouvent partagés en deux parties égales, savoir, AG en E, et BG en Z. En effet, joignons DZ. Puisque AD = DB et que DB = EZ, on a aussi AD égal et en même temps parallèle à EZ. Maintenant, les droites qui joignent les extrémités correspondantes de deux droites égales et parallèles sont aussi égales et parallèles. Or, dans le parallélogramme GEDZ, on a DE égal et parallèle à ZG [à cause des triangles égaux ADE, EZG]; donc DZ = EG; mais déjà DZ = AE [à cause des triangles égaux ADE, DBZ] ; donc EG= AE. De même, à cause des parallélogrammes DBEZ, GEDZ, DE égale séparément chacune des droites BZ, ZG, auxquelles il est opposé : donc BZ = ZG.

La démonstration s'applique à tout autre triangle.

III. C'est par suite de cette proposition que l'on peut

Mesurer à distance la largeur d'un fleuve.

Soit A un point de la rive opposée, du côté des ennemis; EE la rive de notre côté, où l'on doit placer la dioptre. Plantons la dioptre [munie de l'équerre] sur notre terrain, en un point I situé de telle manière, que sa distance à la rive la plus proche soit plus grande que la largeur du fleuve, ce qu'il est très facile d'obtenir; et visons deux points [ou deux objets situés dans la direction des branches de l'équerre, c'est-à-dire] à angle droit: l'un sur la rive opposée, tel qu'une pierre, un buisson, ou toute autre chose facile à distinguer, et soit A ce point; l'autre de notre côté, sur l'autre branche de l'équerre, et soit U ce second point. Cela posé, transportant la dioptre en U, je vise le point A, ce qui forme un triangle rectangle. Je partage le côté IU en deux parties égales au point K; et par ce point je mène à IA une parallèle KC, et du point C à IU une parallèle CR. Alors, dans le triangle rectangle AIU, on a le côté IU partagé en deux parties égales au point K, puis KC parallèle à AI, puis enfin parallèle à IU : donc AI est partagé en deux parties égales au point R. Or il est facile de mesurer la distance IR: on connaîtra donc la distance RA ; retranchons RF, le reste sera la largeur du fleuve.

IV. Si l'on trouve trop compliquée une opération qui exige l'emploi d'un si grand espace pris sur notre terrain, et si l'on pense que, par suite, l'œil doit se troubler et les objets se confondre, nous pouvons, sans quitter la rive du fleuve qui est de notre côté, déterminer facilement sa largeur par le procédé suivant :

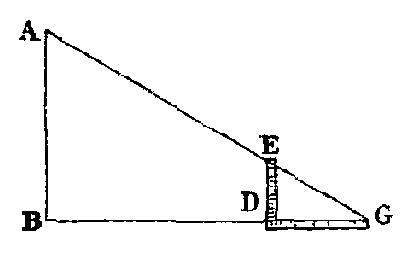
Soit pris de nouveau un point A sur la rive qui nous est opposée, et un point B sur la rive située de notre côté, de manière que AB soit perpendiculaire à la droite BG menée le long du rivage. Prenons un point D sur cette droite BG; et couchons en ce point [perpendiculairement à BG] une règle divisée DE, à l'extrémité Ε de laquelle soit élevé un signal E, de telle façon que, la règle étant appliquée exactement sur la surface du sol, le signal [E] se trouve correspondre bien d'aplomb sur son extrémité. Enfin, transportons l'instrument perpendiculairement [à DE et] le long de BG, jusqu'à ce que d'un point [G] pris sur cette dernière droite, on puisse apercevoir à la fois les trois points G, E, A. On aura alors la proportion BG : GD : : AB : ED.

Mais on connaît BG et GD et par conséquent leur rapport, et par suite le rapport de AB à ED. De plus, ED est connu : donc AB est aussi connu.

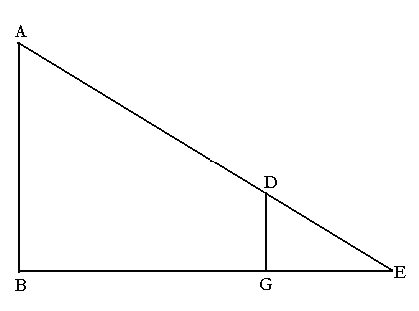
V. On peut, au moyen de la même figure redressée, Prendre la hauteur d'une muraille.

Soit A le sommet de la fortification, B sa base; soit BG une droite menée de la muraille vers nous, hors de la portée du trait. On suspend la dioptre après un bâton auquel on donne le nom de lanterne, et que l'on dresse au point G : soit GD ce bâton. Ayant disposé la dioptre, je vise la crête de la muraille, c'est-à-dire le point A. Puis, passant de l'autre côté [de l'instrument], je prends, sur la même droite, un point Ε formant le triangle EAB dans lequel GD sera parallèle à AB. Alors j'ai EG : GD : : EB : BA. Or le rapport de EG à GD est donné, puisque chacune de ces lignes est donnée : on connaît donc aussi le rapport EB : BA. En outre, EB est donné comme on l'a vu à l'article de la Largeur du fleuve : on connaît donc enfin la hauteur BA, ce qu'il fallait trouver.