RETOUR À L'ENTRÉE DU SITE

ΑΝΩΝΥΜΟΥ ΗΤΟΙ ΗΡΩΝΟΣ ΤΟΥ ΒΥΖΑΝΤΙΟΥ

ΓΕΩΔΑΙΣΙΑ.

Bibl. Bodl. Barocc. ms. 169, fol. 132 v°.

HÉRON DE BYZANCE.

DE LA GÉODÉSIE.

§ I.

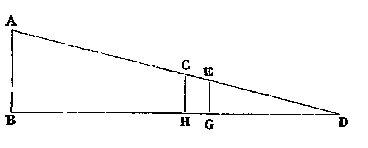
Il est impossible à ceux qui se disposent à assiéger une place de mesurer directement, soit les hauteurs des murailles, soit les distances mutuelles des points éloignés, soit les largeurs des rivières; mais il est facile à ceux qui sont exercés à la construction des figures et à l'usage pratique de la dioptre, de parvenir à déterminer les dimensions des hélépoles qu'il faut appliquer contre les murailles, des ponts volants qu'il faut jeter entre des bateaux pour traverser un fleuve, de façon qu'une armée puisse passer en ordre et sans danger, comme sur le pont le plus solide ou sur un escalier. Or on a vu bien souvent des ingénieurs, séduits par une fausse vraisemblance ou des illusions d'optique, construire et faire approcher des machines trop grandes ou trop petites (comme on l'a vu dans l'ouvrage[1] précédent), et être ainsi la cause du massacre des premiers rangs, que ces machines n'avaient fait que livrer aux mains des ennemis. C'est pourquoi nous avons entrepris d'exposer méthodiquement les avantages de l'emploi de la dioptre et ses usages dans une foule de circonstances de la vie, en choisissant pour cela, chez les auteurs les plus habiles qui nous ont précédé, quelques-uns des résultats les plus élémentaires, que nous éclaircirons au moyen de représentations géométriques fort simples, en appliquant nos démonstrations à quelques figures. On pourra de la sorte, tout en se tenant hors de la portée du trait des ennemis, évaluer exactement, et sans crainte d'erreur, les hauteurs, les grandeurs et les distances. Or cette étude n'est pas seulement d'une grande ressource pour ceux qui sont curieux de s'instruire dans l'art de la guerre; mais on verra de quelle utilité elle peut être pour la conduite des eaux, pour la construction des murailles, pour le tracé des ports, et combien elle facilite la pratique de la géodésie et la théorie des mouvements célestes. Quant à nous, notre devoir est, ici, en évitant les longueurs et les redites, de rejeter ce qui, dans les écrits des anciens, manque de clarté et de lucidité, pour tâcher de nous approprier leurs idées, rendre faciles à saisir d'un coup d'œil les démonstrations mathématiques trop diffuses, ramener à une simplicité convenable et aisément accessible les théories abstraites et trop ambitieuses, enfin rendre la science en quelque sorte palpable pour les hommes d'un esprit pénétrant comme pour ceux qui peut-être étudient par pure récréation, et, en particulier, pour tous ceux qui, dune façon ou d'une autre, s'occupent de la géométrie.

Ici, comme nous l'avons dit dans la Préface, le manuscrit présente une lacune où devait se trouver la description de la dioptre employée par l’auteur. On voit, du reste, par les usages auxquels il l'emploie dans la suite du Traité, que son instrument, comme celui d'Héron l'Ancien, devait présenter un plateau circulaire mobile sur son centre, de manière à pouvoir prendre toutes les positions possibles; que, sur ce plateau, était appliquée une règle ou alidade mobile dans son plan et autour de son centre, munie, à ses deux extrémités, de deux petits godets (ἀγγεῖα [2]: ce sont les ὑέλινα κυλίνδρια d'Héron l'Ancien) faisant l'office de nos pinnules, et dont chacun était percé, à sa partie inférieure, d'une ouverture ou fente (ὀπή) par laquelle était dirigé le rayon visuel. La mobilité du plateau s'obtient au moyen des mêmes pièces nommées τόρμος et χοινικίς (cette dernière expression reçoit ici le synonyme de στρύραξ, et sa circonférence est également divisée en degrés et minutes[3] marqués par un index (μοιρογνωμόνιον).

L'auteur mentionne aussi l'emploi a'wajakn vertical (κάμαζ) portant une mire (διόπτρα ou λυχνία) fixée par un clou (τύλος: c'est peut-être un style, στύλος, comme porte le manuscrit); cette mire joue ici le même rôle que l'ἀσπιδίσκη d'Héron d'Alexandrie ; on la trouvera mentionnée également par Jutes l'Africain. Quant au niveau d'eau, il est permis d'induire des problèmes i^er et ix^e qu'il y en avait un dans la dioptre de l'auteur comme dans celle d'Héron d'Alexandrie.

C'est encore ici le lieu, pour mettre plus de clarté dans ce qui suivra d'entrer dans le détail de la découverte de M. H. Martin[4] sur la localité à laquelle l'auteur emprunte ses exemples dans les problèmes suivants :

Le lieu de la scène, dit-il, est évidemment un hippodrome; « or l'on sait qu'en général, dans les hippodromes antiques, les portes grillées (θύραι, ὕσπληγγες, ostia, carceres) par où partent les chars, étaient à l'un des bouts de l'hippodrome, et que ce bout était terminé en rectangle, tandis que l'autre bout était terminé en hémicycle. Le mur dont il s'agit, dans le premier problème, de mesurer la hauteur au-dessus du seuil des portes, doit donc appartenir au bout rectangulaire de l'hippodrome. Or, dans l'hippodrome de Constantinople, les portes grillées par où partaient les chars étaient surmontées d'une tour, et, sur cette tour, se trouvait un quadrige (τέθριππον) apporté de Chio, et placé là sous Théodore le Jeune. Ce quadrige, décrit d'une manière reconnaissable par Nicétas Choniate, n'est autre que les fameux chevaux de Venise, qui, lors de la prise de Constantinople par les croisés, furent transportés de la tour de l'hippodrome de Constantinople sur le palais de Saint Marc de Venise, et qu'on a pu voir à Paris sous le règne de Napoléon I^er. »

Ce n'est pas tout : « Transportons-nous pour un instant, dit M. H. Martin, au circus maximus de l'ancienne Rome. Dans ce long rectangle, terminé en hémicycle à l'un de ses deux bouts, il y avait, à quelque distance de chacune des deux extrémités, une borne, ou plutôt un groupe de trois bornes, que les chars devaient tourner. Entre ces deux groupes de bornes, dans les deux tiers environ de la longueur de l'arène et à peu près suivant la ligne médiane, s'étendait un long piédestal, duquel s'élevait une rangée de statues, d'obélisques et d'autres petits monuments : c'était ce qu'on nommait l'épine dorsale du cirque (spina) ; c'était un alignement mené entre les deux groupes de bornes (intermetium). Les gradins occupés par les spectateurs étaient séparés de l'arène par une balustrade grillée (cancelli), et, de plus, par un fossé plein d'eau qu'on nommait euripe. Sous Néron, ce fossé fut supprimé. Plus tard, on donna le nom d'euripe à l’intermetium ou spina; c'est-à-dire à la longue file de monuments qui allait d'une borne à l'autre, et autour de laquelle les chars devaient tourner sept fois, etc., etc.

Or on retrouve, dans le deuxième problème, les homes (νύσσαι) et les portes grillées (κάγκελλοι) dont il vient d'être question. « Ces portes, par où partaient les chars, étaient au nombre de 12 [dans l'hippodrome de Constantinople] de même que dans le circus maximus de Rome; et de même aussi, entre la sixième porte et la septième, il y avait une large porte d'entrée.[5] »

Dans le troisième problème, il est fait mention de la partie courbe de l'hippodrome (σφενδόνη τοῦ ἱππικοῦ), et de sa base nommée πέλμα.

Dans le quatrième problème, on retrouve l'euripe (εὔριπος), les balustrades (στήθη,[6] pectoralia), l’escalier qui conduit aux gradins (ἡ τῶν βαθυίδων ἀναβάθρα).

Enfin le troisième problème fait allusion à un point nommé l’écueil (ἄπλους [7]), par une métaphore tirée de la navigation : ce lieu n'est pas navigable, c'est-à-dire que les chars, obligés de doubler la borne, ne doivent jamais passer en deçà, entre elle et le bout de la spina; c'est par une métaphore analogue que celle-ci se nomme euripe.

Il faut dire encore que, vers le bout rectangulaire de l'hippodrome de Constantinople, se trouvait une haute tour, ou une espèce de colonne, où était placé le siège impérial (βασιλικὸν κάθισμα), d'où l'empereur avec sa cour regardait les courses. Il y arrivait, du palais impérial même, par un escalier tournant nommé κοχλίας, et par une estrade (πούλπιτα) qui devait passer pardessus les gradins.

Il y avait encore, de chaque côté de l'euripe, dans une position peu différente de celle du siège impérial, des constructions nommées παρασκεναί, probablement parce que c'était là que les coureurs se préparaient à la course. Les παρασκεναί étaient peut-être des tentes mobiles; mais le siège impérial était un obstacle que les chars devaient éviter.

En résumé, M. H. Martin conclut des quatre premiers problèmes, que l'auteur prend dans l'hippodrome de Constantinople tous ses exemples de mesures de distances, et que, par conséquent, il écrivait pour les habitants de Constantinople, qui avaient chaque jour sous les yeux l’euripe, le siège impérial, le quadrige, et les autres objets dont il parlait.[8] »

Les problèmes 8 et 10 fourniront de nouvelles confirmations de ce résultat. Ce dernier notamment a fourni de plus à M. H. Martin le moyen de déterminer l'époque de l'auteur, comme nous le verrons.

Nous allons maintenant donner ce qui reste du premier problème, avant lequel nous rappellerons qu'il en existait un autre, entièrement perdu aujourd'hui, ayant pour objet, comme celui du § viii d'Héron d'Alexandrie, de Mesurer, à l'aide de la dioptre, la distance horizontale de deux points dont un seul est accessible;

Et, comme application, de Mesurer la largeur d'un fleuve.

Quant au problème suivant, celui dont une partie seulement a été conservée, il a un but analogue à celui du § xii d'Héron d'Alexandrie (traité de la Dioptre); el nous supposons que l'on peut rétablir ici l'énoncé d'après cet auteur.

Il faut admettre que l'opérateur, se trouvant entre les points G, H, a commencé par déterminer les distances des points D et B, au moyen des hauteurs GE, HC, et de la base GH, dont il a les mesures directes.

§ II.

(D'un point élevé que l'on aperçoit, abaisser une perpendiculaire sur le plan horizontal dans lequel on se trouve, sans approcher du point;

Ou simplement (voyez Jules l'Africain)[9] :

Prendre de loin la hauteur d'une muraille.)

…… et la base GD. Il en est de même du rapport de AB à BD. Et ensuite, comme BD est à chacune des droites DG, DH, de même AB est à chacune des hauteurs GH, EG. Quant au pieu ou jalon vertical que l'on plante quelquefois devant l'instrument pour déterminer de plus grandes hauteurs et régler la conduite des eaux [c'est-à-dire pour exécuter un grand nivellement], il doit porter une mire (que l'on nomme aussi lanterne) fixée par un clou au point G. Ayant alors mesuré les bases DG, DH, des petits triangles, bases qui sont sur notre terrain, et en ayant déterminé les longueurs; connaissant d'ailleurs GE et HC, qui sont les hauteurs de la dioptre et du pieu, si je trouve une base décuple de la hauteur, j'en conclus que la ligne entière DB est aussi décuple de AB. Mais je puis déterminer aussi la ligne entière BD, comme on l’a vu à l’article la détermination des longueurs et des largeurs,[10] et, si je la trouve de 120 orgyes, AB en vaudra 12; et telle sera la hauteur du mur, depuis le seuil de la porte, marqué B, jusqu'au sommet de la tour, en un point marqué A sur quelque partie du quadrige. Quant aux parties et fractions, nous en avons assez disserté pour ceux qui en sont curieux, dans les méthodes arithmétiques exposées plus haut.

Relativement aux unités de mesure employées par l'auteur, M. H. Martin observe que les principales mesures itinéraires usitées à Constantinople, au x^e siècle, présentaient des rapports entièrement semblables à ceux des mesures alexandrines correspondantes depuis la conquête romaine jusqu'au iv^e siècle, et différents de ceux des mêmes mesures alexandrines depuis le iv^e siècle, mais que les valeurs absolues de ces mesures avaient pour base le pied romain. « Non seulement les mesures inférieures à l'orgye, dit-il en s'appuyant sur un passage inédit de Constantin Porphyrogénète, mais l'orgye elle-même et les mesures supérieures, étaient alors romaines. Ainsi l'orgye était de 6 pieds, le stade de 600 pieds, le mille de 4500 pieds: mais ces pieds étaient romains au lieu d'être philétériens, c'est-à-dire égyptiens.... Il y avait alors à Constantinople deux coudées, l'une légale, de 2 pieds, et l'autre vulgaire, d'un pied ½ ; c'étaient aussi des pieds romains. »

§ III.[11]

Nous montrerons encore comment, Étant donnés deux points éloignés mais visibles, on peut déterminer leur distance réduite à l'horizon, sans approcher d'aman des deux.

Soient A, B, les deux points donnés, vus au travers des grilles,[12] l'un A à la troisième, l'autre B à la neuvième. Ayant donc établi la dioptre sur la borne d'en haut,[13] près du point G, et ayant placé le plateau de manière que son plan passe par les deux points donnés, je mène deux droites par les pinnules de la règle, savoir la droite GA dans la direction de la troisième grille, l'autre GB dans la direction de la neuvième. Puis je mesure l'une[14] d'elles au moyen de l'instrument, c'est-à-dire par le procédé qui a été enseigné précédemment.[15] L'ayant trouvée, je suppose, de 80 orgyes, je la divise comme je voudrai : soit sa dixième partie, de 8 orgyes, terminée au point D près de la borne. Je transporte la dioptre en ce point; je mène, au moyen de la règle, la droite DE partageant de même la droite GB à sa dixième partie au point E. La droite DE sera aussi la dixième partie de la distance AB. En effet, comme AG est à GD, de même BG est à GE, et de même aussi AB est à DE. Et, en outre, comme DE est à EG, de même AB est à BG, Ayant alors mesuré DE qui est près de nous, et l'ayant trouvée de 4 orgyes, j'en conclus que AB, qui en est décuple, est de 40 orgyes. En résumé, la distance cherchée, c'est-à-dire la distance comprise entre les points A, B, contient 40 orgyes.

§ IV.[16]

Il y a encore un autre moyen de Déterminer la distance de deux points donnés, par la figure ci-jointe.

Imaginons par hypothèse les points A et B situés dans la largeur de l'arène, points que l'on aperçoit, le premier, sur la gauche de l'extrémité courbe de l'hippodrome, et le second, sur la droite. Je place la dioptre près du lieu nommé l’écueil,[17] un peu en deçà de la borne supérieure située à l'opposé, par exemple au point G, de manière que rien ne fasse obstacle aux rayons visuels pour parcourir librement l'espace qui aboutit aux points donnés. Alors, ayant placé le plateau de l'instrument de manière que son plan passe par la corde qui sert de base à l'extrémité courbe de l'hippodrome, je mène deux droites au moyen de la règle, la droite GA vers l'extrémité gauche, et la droite GB vers l'extrémité droite. Ayant alors mesuré l'une[18] comme il a été dit,[19] et l'ayant trouvée, par exemple, de 126 orgyes, je passe à l'autre extrémité de la règle. Puis, tout restant fixe dans la dioptre, je regarde un peu au-dessus du plateau,[20] et je prends, sur le prolongement de BG par exemple, la 18^e partie de sa longueur, soit 7 orgyes,[21] à gauche de l'écueil, au point D; je fixe de la même manière, vers la droite, le point E sur le prolongement de AG; puis je joins DE. Dès lors, puisque EG est la 18^e partie de GA, et DG la 18^e partie de GB, de même aussi la distance DE est la 18^e partie de AB. De même en effet que, dans les deux triangles opposés par le sommet ici représentés, les petits côtés sont aux grands, de même la base du petit triangle est à la base du grand. Ayant donc mesuré la base du petit triangle, qui est située de notre côté, et l'ayant trouvée par exemple de 2 ½ orgyes, j'ai de quoi connaître AB, qui est égale à 18 fois ce nombre; et je trouve en conséquence la distance des points A et B situés aux extrémités de la base de l'hippodrome,[22] c'est-à-dire la corde qui sous-tend la partie courbe; et cette distance est égale à 45 orgyes.[23]

§ V.[24]

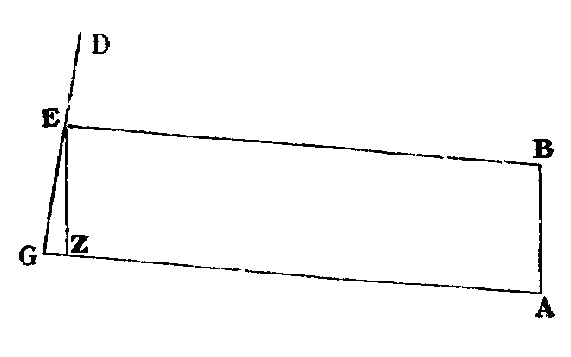
Il est encore possible, non seulement de prendre la distance de deux points donnés, mais de Trouver la position de la droite qui joint les deux points donnés, sans approcher d'aucun d'eux.

Soient A, B, les deux points donnés, l'un A situé dans l'un des sept segments de l'euripe, à la base des balustrades,[25] l'autre B situé au pied du siège impérial, soit au pied de l'un des deux pavillons situés de chaque côté, où se tiennent les coureurs qui se préparent aux concours gymniques. Ayant donc placé la dioptre près de la borne d'en bas, sur le chemin que l'on suit pour tourner cette borne, à l'opposé de B,[26] c'est-à-dire au point G, je regarde par la règle, jusqu'à ce que j'aperçoive en ligne droite, de l'extrémité, ledit point A. Alors, passant à gauche de la dioptre, auprès de la borne, je regarde un peu au-dessus du plateau, et je mène la droite GD en face de l'escalier qui conduit aux gradins,[27] par exemple vers la base des premières balustrades, en dirigeant cette droite sur le point D, perpendiculairement à GA, après lui avoir fait faire, au point G, l'angle droit AGD. Ensuite, je transporte la dioptre le long de GD, jusqu'à ce que j'aperçoive le point B en ligne droite [et perpendiculairement à GD]. Soit, à cet effet, la dioptre établie au point E : la droite BE est donc perpendiculaire à GD, et parallèle à AG. Mais je puis alors mesurer les distances du point G au point A, et du point E au point B, comme je l'ai souvent fait par le moyen des triangles.[28] Si je trouve de cette manière GA égale à EB, j'en conclurai que GE est égale à AB; mais, si l'une est plus grande que l'autre, je retranche la différence de la plus grande, et je joins le point ainsi déterminé à l'extrémité de la plus petite. Par exemple, si je trouve la largeur GE égale à 12 orgyes, GA à 90, et EB à 81, je retranche, du point G au point Z, les 9 orgyes d'excès, et je joins le point Z à l'extrémité E de la plus petite ligne, par la droite ZE égale et parallèle à AB. Dans le cas, en effet, où AG serait égale à BE, la distance AB serait de 12 orgyes comme la distance GE; mais, puisque GA a été trouvé de g orgyes plus grande que BE, ce sont 9 orgyes que ZE enlève à AG, en sous-tendant d'ailleurs un angle droit en G; et, puisque la base GE a 12 orgyes, il s'ensuit que ZE en a 15, comme étant égale en puissance aux deux côtés de l'angle droit.[29] Donc la distance de A à B aura ce même nombre de 15 orgyes. Ainsi l'on a trouvé, non seulement la grandeur de la distance des points A, B, mais encore la position de la droite qui joint ces deux points, comme l'indique la figure tracée ci-devant.

§ VI.[30]

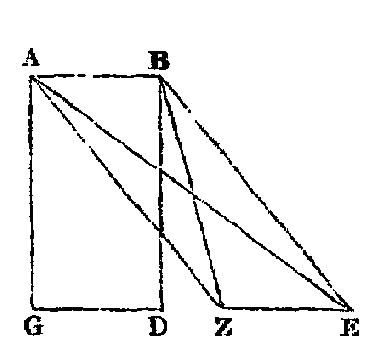
C'est donc ainsi que nous saurons mesurer les lignes droites; voyons maintenant comment on s'y prend pour Mesurer les surfaces planes comprises entre des lignes droites ou courbes.

D'abord pour les carrés et autres rectangles, il faut multiplier la longueur par la largeur, ou réciproquement; et le nombre plan qui en résultera représentera la surface de la figure, c'est-à-dire l'aire comprise entre les quatre côtés, comme on peut le faire voir sur ladite figure. En effet, si AG est de 90 orgyes, et GD de 12, le produit de ces deux nombres donnera 1.080 pour l'aire du rectangle. Ce serait la même chose pour un carré. Une méthode à peu près semblable est applicable à la mesure des rhombes, qui proviennent de la déformation du carré, et des rhomboïdes, qui proviennent de celle des rectangles. Les uns et les autres sont déterminés par les côtés et une diagonale, de telle façon que le rhombe est composé de deux triangles isocèles, et le rhomboïde de deux triangles acutangles ou obtusangles, comme on le voit encore par la même figure, que l'on peut considérer comme provenant de la déformation d'un rectangle qui s'est changé en un rhomboïde compris entre les côtés ZE, AB : il est décomposé en deux triangles acutangles par la diagonale ZB, et en deux triangles obtusangles par la diagonale AE. Quant aux aires des triangles, on les mesure par la moitié de celles des quadrilatères construits sur les triangles [avec la même base et la même hauteur]. En effet, tout quadrilatère se partage, au moyen d'une diagonale, en deux triangles; tout pentagone se partage en trois triangles, tout hexagone en quatre; et de même pour la division des autres figures. Ainsi, lorsque le quadrilatère vaudra 1.000, le triangle vaudra 500. Quant à ce que tout triangle susceptible d'être conçu par l'esprit, ou de tomber sous les sens, a ses trois angles égaux à deux droits, on peut ici le conclure de ce que tout quadrilatère a ses angles égaux à quatre droits,[31] et que l'on peut, au moyen d'une diagonale, le partager en deux triangles ayant six angles, tantôt droits, tantôt aigus ou obtus, en plus ou en moins; et, puisque les six angles de tout quadrilatère forment une somme égale à quatre droits, il s'ensuit donc bien que chacun des deux triangles qui composent le quadrilatère a ses angles égaux à deux droits; et il en est de même de tout triangle qui peut tomber sous les sens ou que l'imagination peut concevoir. Relativement à la mesure des figures nommées trapèzes et trapézoïdes (ainsi classées d'après l'égalité de leurs angles), ainsi que des autres figures classées ou non classées, Archimède et Héron en ont donné, dans leurs traités généraux, des démonstrations complètes. Pour nous, n'ayant pour but que d'encourager ceux qui commencent l'étude des mathématiques, nous avons fait un choix de propositions sur l'art du mesurage, en y ajoutant la ressource des exemples pour mieux fixer l'attention, nous conformant en cela au proverbe qui dit que C’est en faisant des cruches que l'on apprend l'art du potier.[32]

§ VII.

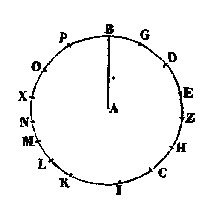
Nous trouverons le diamètre du cercle, et sa circonférence, et son aire, au moyen de la dioptre, en nous établissant à son centre, et sans approcher de sa circonférence.

Pour cela, soit A le centre du cercle; j'établis la dioptre en ce point. Puis, ayant placé le plateau qui en fait partie dans un plan parallèle à la circonférence que l'on doit décrire avec la dioptre, après avoir pris un point en ligne droite par les pinnules de la règle, je conduis circulairement, à partir de ce point, le plateau avec sa règle, autour de l'axe du tube, ou autour du pied de la dioptre quelle que soit sa forme, jusqu'à ce que le mouvement circulaire ramène le plateau dans sa première position. Or, dans ce mouvement, on apercevra nécessairement, sur la circonférence du cercle décrit, certains objets apparents, pierres, buissons, etc., tels que les points, B, G, D, E, Z, H, C, I, K, L, M, N, X, O, P. Ayant donc marqué ces points sur la circonférence du cercle, je mesure la distance entre le point A et le point B, c'est-à-dire entre le centre et la circonférence, comme nous l'avons expliqué dans la mesure des longueurs et largeurs;[33] ayant ainsi trouvé, je suppose, cette distance égale à 105 orgyes, j'ai le diamètre entier du cercle, égal à 210, comme étant double du rayon. Et, comme la circonférence vaut 3 fois le diamètre, plus un septième, cela fait évidemment 660, qui est égal à 3 fois 210, plus un septième de ce dernier nombre.[34] Mais, puisque le produit de la circonférence par le quart du diamètre donne la surface du cercle, suivant ce que dit Archimède, que « Tout cercle est équivalent à un triangle rectangle dans lequel l'un des côtés de l'angle droit serait le rayon et dont la base serait la circonférence, il s'ensuit que le produit du diamètre par la circonférence vaut quatre fois la surface, d'où il résulte que les 210 orgyes du diamètre, multipliées par les 165 du quart de la circonférence,[35] donnent 34.650 pour l'aire du cercle. En effet, 200 multipliés par 100 font 20.000,[36] par 60 font 12.000, et par 5 font 1.000; puis, en second lieu, 10 par 100 font 1.000, par 60 font 600, et par 5 font 50. De sorte qu'en définitive, on a trouvé 105 pour rayon, 210 pour diamètre, et 660 pour la circonférence; puis, la surface ou l'aire entière, résultant de la multiplication de la circonférence par le quart du diamètre, égale à 34.650.

Nous pouvons encore, d'une manière plus facile et sans le secours de la dioptre, connaître le diamètre d'un cercle, son périmètre, et son aire, au moyen d'une simple corde donnée de longueur. Soit donc la corde donnée de 35 orgyes, ou de toute autre longueur. Supposons-la munie, à l'une de ses extrémités, d'un anneau de fer et d'un clou que l'on puisse ficher en terre pour servir de centre, de manière que l'autre extrémité de la corde toujours tendue puisse être conduite circulairement jusqu'à ce qu'elle soit revenue au point de départ. Ainsi, dans la description du cercle, on peut considérer ce cordeau sous trois points de vue,[37] à son commencement, dans son milieu, et à son extrémité : à son commencement on a le centre, représenté par le clou autour duquel tourne le bout du cordeau par le moyen de l'anneau; à son milieu on a des points qui décrivent l'aire du cercle, tandis qu'enfin le bout.de la corde décrit la circonférence dont tous les points B, G, D, E, Z, H, C, sont situés à égale distance du centre. Le cercle se trouvant donc ainsi déterminé, son diamètre sera de 70 orgyes, comme étant double du rayon; sa circonférence, étant égale à 3 fois le diamètre plus un septième, sera de 220;[38] et son aire, égale au produit de la circonférence par le quart du diamètre, vaudra 3.850. En effet, les 70 du diamètre, multipliés par les 50 du quart de la circonférence, donnent 3.500, et par les 5 restant, donnent 35o [ce qui fait en tout 3.850]. En résumé, le cordeau donné étant de 35 orgyes, le diamètre du cercle décrit est de 70 orgyes, la circonférence de 220, et l'aire engendrée, de 3.850.

§ VIII.

Quant aux figures solides, ce n'est pas seulement suivant deux dimensions que l'on doit les considérer, comme les figures planes, mais suivant trois. En effet, tous les corps ont trois dimensions, la longueur, la largeur, et l'épaisseur, que l'on nomme aussi profondeur ou hauteur. Ainsi, pour calculer les figures solides, il faut prendre le nombre plan résultant du produit de la longueur par la largeur, et le multiplier par la troisième dimension, qui est la hauteur.

Commençons par la mesure de la figure cubique, puisque c'est celle dont toutes les dimensions sont égales. En effet, le cube est une figure solide comprise entre 6 carrés égaux; il a 12 arêtes, 8 angles droits, et 6 faces planes, ne formant que 3 dimensions toutes égales entre elles; ce qui fait que les Pythagoriciens, voulant démontrer sur cette figure les rapports harmoniques et divins de la consonance, donnent au cube le nom d’Harmonie. Quant à sa solidité, voici comment on la trouve. Supposons que la hase du cube ait 28 unités de longueur : elle en aura autant de largeur, et sa hauteur sera également de 28 unités. Multipliant les 28 unités de la longueur par les 28 de la largeur, nous aurons 784 pour l'aire de cette base. Multipliant ensuite ce produit par les 28 unités de la hauteur, les 21.952[39] obtenues nous feront voir que telle est la solidité du cube. Maintenant, si nous imaginons un cylindre de même hauteur, inscrit au cube, et comprenant dans son intérieur une sphère dont le grand cercle touche la surface du cylindre, nous verrons d'abord que la hase du cube est à celle du cylindre comme 14 est à 11[40] (pour exprimer ce rapport dans les moindres termes et en nombres premiers entre eux). Ce même rapport sera celui des 6 faces du cube comparées à la surface du cylindre avec ses deux bases, ou des 4 faces latérales du cube comparées à la même surface sans les deux bases; et enfin le rapport des solidités sera encore le même. Ensuite la surface du cylindre sans les bases sera équivalente à celle de la sphère; et, si l'on compte les hases, la surface du cylindre sera une fois et demie celle de la sphère; et il en sera de même des solidités.     »

[Pour démontrer tout cela, nous remarquerons que] la base du cylindre se mesure par le produit du diamètre et du quart de la circonférence, comme on l'a expliqué plus haut ; or, puisque le diamètre a été donné égal à 28, la circonférence sera de 88, égal à trois fois 28 plus le 7^e de ce nombre;[41] maintenant, le quart de ce nombre est 22 ; et 28, multipliés par 22, donne 616[42] pour l'aire de la base du cylindre; et quant à celle du cube, nous l'avons trouvée de 784, nombre qui est au précédent (en nombres premiers entre eux et aussi petits que possible) comme 14 est à 11. En effet, 784 contient 616 et son quart 154, et, en outre, son 44^e qui est 14.[43]

Ce même rapport sera celui des 4 faces latérales du cube par rapport à la surface courbe du cylindre, et celui des 6 faces du cube par rapport à la surface totale du cylindre en y comprenant les bases, et enfin celui des solidités. En effet, les quatre côtés de la base du cube, multipliés par les 28 de la hauteur, donnent 3.136;[44] et les 88 du périmètre de la base du cylindre, multipliés par les 28 de la hauteur, donnent 2.464,[45] qui sont au nombre précédent dans le même rapport de 11 à 14.[46]

Il en est de même des 6 faces du cube, égales à 4.704, par , rapport à la surface totale du cylindre avec ses bases inférieure et supérieure, faisant 3696.[47]

De même, nous avons vu que le volume du cube s'obtient en multipliant les 784 unités de la base par les 28 de sa hauteur, ce qui donne 21.952;[48] or le volume du cylindre s'obtient en multipliant les 616 de sa base par la même hauteur égale à 28, ce qui fait 17.248,[49] nombre qui est au précédent dans le même rapport que 11 à 14,[50] lequel représente ainsi celui du cylindre au cube circonscrit.

Quant à démontrer que le cylindre contient une fois et demie la sphère inscrite, nous y parviendrons par le procédé suivant : nous savons déjà que la surface du cylindre, en y comprenant les plans des bases, est de 3.696, et son volume de 17.248; on montrera aussi maintenant que la surface de la sphère, résultant de la multiplication des 88 unités de la circonférence de son grand cercle par les 28 de son axe, est de 2.464. et que son volume, égal aux 616 unités de la surface de son grand cercle pris pour base, multipliées par les 2/3 de son axe, c'est-à-dire par 18 2/3, est, en conséquence, de 11.498 2/3;[51] de sorte que les surfaces sont entre elles, et que les volumes sont entre eux, dans le rapport de 3 à 2, comme il a été dit; et, par suite, que la sphère est les 2/3 du cylindre circonscrit de même hauteur qu'elle.[52] En effet, toute surface sphérique est quadruple de celle de son grand cercle; et elle résulte du périmètre de celui-ci multiplié par l'axe : car 2.464 est quadruple de 616, et égal à 28 fois 88.

(Maintenant,[53] toute sphère est quadruple du cône qui aurait pour base son grand cercle et pour hauteur le rayon. Car le périmètre de la base du cône, ou 88, multiplié par la moitié de l'axe pris pour hauteur, c'est-à-dire par les 14 du rayon, fait 1.232;[54] et les 616 de la surface, multipliés par le même nombre 14, moitié de l'axe, font 8.624.[55] De sorte que l'hémisphère, considéré, soit sous le rapport de la surface, soit sous celui du volume, est double du cône, et la surface entière en est quadruple.)

Maintenant, le cône est une figure solide comprise entre un cercle pris pour base et un point situé au-dessus. Or, suivant Euclide,[56] lorsque, dans un triangle rectangle, l'un des côtés de l'angle droit restant fixe, le triangle tourne tout à l'entour jusqu'à ce qu'il revienne à sa première position, la figure solide engendrée porte le nom de cône. D'ailleurs, quand la droite qui reste fixe est égale à celle qui se meut en faisant un angle droit avec la première, le cône est rectangle; il est obtusangle, si cette première droite est plus petite, acutangle, si elle est plus grande. — L'axe[57] du cône est la droite qui reste fixe; sa base[58] est le cercle décrit par celle qui tourne. — Or on trouve que tout cylindre est triple du cône qui a même base et même hauteur que lui; et, puisque la surface du cylindre est de 2.464 et son volume de 17.248, tandis que (la surface[59] du cône, calculée d'après le même périmètre égal à 88 et le tiers de l'axe égal à 9 1/3 , donne 821 1/3;[60] puisque, d'ailleurs,) les 616 de la surface de la base, multipliés par le tiers du même axe, donnent 5.749 1/3 pour le volume,[61] il s'ensuit que ces deux figures sont dans le rapport triple,[62] ou qu'enfin le cône est le tiers du cylindre [de même base et] de même hauteur.

On trouve aussi que tout prisme parallélépipède est triple d'une pyramide de même base et-de même hauteur.

Le centre de gravité du cylindre est au milieu de sa hauteur, et il en sera de même du prisme. Quant au centre de gravité du cône, il est situé sur son axe, en un point tel, que sa distance au sommet est triple de sa distance à la base ; et il faut bien qu'il en soit de même de la pyramide.

Quant à la pyramide,[63] c'est une « figure solide comprise entre plusieurs plans menés du plan de la base à un point [supérieur], ou comprise entre une base triangulaire, ou quadrangulaire, ou polygonale quelconque, et un point situé au-dessus. — Enfin, le prisme[64] est une figure solide comprise entre plusieurs plans, dont deux, situés à l'opposé l'un de l'autre, sont égaux, semblables et parallèles, et dont les autres sont des parallélogrammes.

§ IX.

Soit maintenant, pour expliquer la mesure des solides, une construction parallélogramme de dimensions inégales, ou un réservoir de même forme, comme la citerne d'Aétius. Mais ce sera plus facile sur celle d'Aspar,[65] à cause de l'égalité des dimensions de la base, la figure étant celle d'une plinthe : car on nomme ainsi une figure solide comprise entre 6 plans, dont la base a sa longueur et sa largeur égales entre elles, mais dont la hauteur est moindre. En effet, si la hauteur était la même, on aurait un cube, et si elle était plus grande, la figure prendrait la forme d'une solive : car on nomme ainsi la figure dans laquelle la hauteur est plus grande que la longueur et la largeur de la base. Supposons donc la longueur de la base de la citerne d'Aspar égale à 70 orgyes, de même que sa largeur, et soit sa hauteur de 12 orgyes. Ainsi, je veux savoir de combien d'orgyes est la capacité de la citerne, et combien elle peut contenir de pots d'eau. Multipliant les 70 de longueur par les 70 de largeur, j'ai 4.900 orgyes carrées pour la surface de la base; je multiplie ce nombre par les 12 de hauteur, et j'obtiens 58.800;[66] et, comme des dimensions quadruples donnent une surface 16 fois plus grande et un volume 64 fois plus grand; que, d'ailleurs, l'orgye étant de 96 doigts et la coudée de 24, il s'ensuit que l'orgye est quadruple de la coudée quant à la longueur : de tout cela il résulte que la longueur de la base est de 280 coudées, et, par suite, la surface de cette base de 78.400 coudées carrées : car 16 multiplié par 4.900 produit ce même nombre de 78.400. Par suite, la solidité est de 3.763.200, comme le donne 64 multiplié par 58.800.[67] Derechef, puisque des nombres 6 fois plus grands comme longueurs, donnent 36 fois plus pour les surfaces, et 216 fois plus pour les volumes; comme, d'ailleurs, le pied contenant 16 doigts est 6 fois moindre que l'orgye, il s'ensuit que la longueur exprimée en pieds est de 420, la surface de 176.400, et le volume total de 12.700.800 pieds cubes.[68] En effet, 36 multiplié par 4.900 fait 176.400, et 216 multiplié par 58.800 fait 12.700.800.[69] Maintenant, le pied cube, suivant ce qu'établissent les mécaniciens, contient un nombre de doigts cubes égal au cube de la longueur 16, ou 4096. De plus, 16 doigts (lisez 17?) comprennent à peu près 4 onces italiques de liquide, et 51 1/5[70] doigts [c'est-à-dire 3 fois plus], 12 onces ou une livre. 256 doigts feront donc 5 livres ou autant de pots, et 4.096 en donneront 80. Ainsi le pied cube de liquide donne 80 pots ou 80 livres italiques. Autant donc la citerne jauge de pieds cubes, autant elle peut contenir de [fois 80] mesures de liquide.[71] Nous opérerons de la même manière pour évaluer la quantité de l'eau contenue, quelque portion de la profondeur que marque la surface.

Si la figure était cylindrique, il faudrait chercher la surface du cercle de hase, comme nous l'avons dit, et multiplier par la hauteur le nombre de pieds obtenus. Le résultat représentera le poids du liquide contenu, s'il s'agit d'un réservoir. S'il est question de substances solides entassées sous une semblable forme, séparément du faîte ou comble qui peut la surmonter, que ce soit d'ailleurs du blé, de l'orge, des légumes, ou toute autre denrée, que la chose s'évalue en médimnes, en modius, en chœnix, ou en toute autre mesure de moindre valeur, volume ou poids, on en fait de même la supputation en examinant comment le pied cube se compose.

§ X.[72]

Nous pourrons encore connaître, d'après Héron, quel est le produit d'une source.

Mais il faut d'abord savoir que la quantité de l'écoulement n'est pas toujours la même. En effet, dans les temps de pluie, il augmente par la raison que l'eau, surabondant aux sommets des montagnes, jaillit avec plus de force, tandis qu’il cesse dans les temps de sécheresse; mais les fontaines de bonne nature[73] sont peu susceptibles de diminuer dans leur produit, il faut donc, après avoir entièrement circonscrit l'eau de la source de manière qu'elle ne puisse fuir d'aucun côté, fabriquer une conduite en plomb de forme quadrilatère, en ayant soin de lui donner un volume plus grand que celui du courant aux époques de sa plus grande abondance; puis l'adapter à la fontaine de telle façon, que l'eau de celle-ci soit forcée d'y entrer tout entière. Pour cela, il est nécessaire de placer cette conduite au-dessous de la source même, afin qu'elle reçoive toute la veine liquide; et la dioptre[74] nous fournit pour cela le moyen de déterminer le point convenable. La quantité du courant deviendra alors évidente, par sa hauteur à l'embouchure de la conduite. Soit 3 doigts cette hauteur, et 6 doigts la largeur de l'embouchure. Puisque 3 fois 6 font 18, nous voyons que la section de la veine a pour mesure 18 doigts.

Mais on doit bien comprendre qu'il ne suffit pas, pour connaître complètement le produit cherché de la source, de déterminer la section de la veine. Il faut avoir, en outre, sa vitesse : car, plus l'écoulement est rapide, plus la fontaine fournira d'eau; et plus il est lent, moins il y aura de produit. C'est pourquoi, après avoir creusé un réservoir sous le courant, il faut examiner, au moyen d'un cadran solaire, combien il y entre d'eau en une heure, et de là déduire la quantité d'eau fournie en un jour; et, de cette manière, on n'a pas besoin de mesurer la section de la veine : la mesure seule du temps suffira pour nous rendre évident le produit de la source. En effet, chaque journée complète, composée du jour et de la nuit, comprenant 360 temps équinoxiaux qui font en tout 24 heures équinoxiales, chacune de celles-ci comprendra 15 temps, tandis que l'heure temporaire en comprendra tantôt plus tantôt moins, suivant la saison. Mais, comme d'un autre côté l'écoulement est plus abondant pendant l'hiver et qu'il l'est moins pendant l'été, si nous observons, abstraction faite de la saison, combien il passe d'eau dans le bassin pendant une heure temporaire, soit par exemple 20 muids, en multipliant par 24, ce qui donnera ici 480, nous aurons le produit moyen de la fontaine pendant un jour quelconque de l'année.

§ XI.[75]

Après avoir passé en revue, dans ce qui précède, les divers usages que la dioptre peut avoir sur la surface du globe, tels que nous les avons annoncés, nous sommes tout prêts, établis sur cette même surface, à effectuer, grâce à l'emploi du même instrument, l'observation des phénomènes célestes, appréciant par son moyen les grandeurs du soleil et de la lune, évaluant les distances mutuelles des astres, soit des étoiles fixes entre elles, ou des planètes entre elles, ou des fixes par rapport aux planètes. Nous pourrons en effet obtenir les grandeurs cherchées au moyen de la division du plateau en 360 degrés, et des divisions intermédiaires plus petites. Lors donc que nous voudrons évaluer en degrés la distance comprise entre deux astres, nous inclinerons la partie du plateau qui est de notre côté, en portant en haut la partie opposée, jusqu'à ce que nous apercevions dans le même plan les deux astres à la fois. Alors, tout restant fixe dans la dioptre, nous ferons tourner la règle qui est sur le plateau, jusqu'à ce que nous apercevions l'un des astres au travers des deux pinnules. Puis, après avoir noté le degré et la minute marqués par l’index, nous ferons de nouveau tourner la règle jusqu'à ce que nous apercevions le second astre au travers des pinnules, ayant également soin de noter le degré marqué par l’index. Calculant alors le nombre des degrés compris entre les deux points indiqués, nous connaîtrons la distance des deux astres.

Il faut prendre garde que, quand on observe un astre en un certain lieu du zodiaque, pour avoir sa longitude par exemple, en la rapportant aux astres antérieurs, c'est-à-dire en allant du levant au couchant, c'est vers la droite qu'il faut conduire la règle ; mais, si l'on veut rapporter la longitude aux astres postérieurs, c'est-à-dire eu allant du couchant au levant ou au méridien, c'est vers la gauche qu'il faut marcher. Or on appelle signes antérieurs ceux qui vont du Bélier aux Poissons, des Poissons au Verseau, [au Capricorne,] au Sagittaire, et ainsi de suite. Au contraire, on nomme postérieurs les signes qui vont du Bélier au Taureau, aux Gémeaux, au Cancer, et ainsi des autres.

De plus, si c'est en longitude et suivant le zodiaque que nous cherchons une distance, il ne faut pas placer la dioptre au hasard, mais l'établir parallèlement à l'équateur (a); et, si c’est la différence en latitude que nous cherchons, comme du nord au midi, il faut placer l'instrument dans le plan du méridien. Ces lignes ont été gravées par nous-même dans la salle verte du magnifique observatoire du midi du palais impérial Bucoléon (b). Nous avons indiqué leur construction dans notre Méthode pour tracer les cadrans solaires.

Lors donc que nous voudrons fixer clairement, sur le cercle horizontal qui sert de base à l'hémisphère-supérieur de la terre, les points où se lève, où se couche le soleil, soit aux tropiques ou aux équinoxes, soit aux points intermédiaires qui limitent les divers signes du zodiaque, nous commencerons par établir la dioptre à l'équateur, et nous y appliquerons la règle; puis, visant au travers des pinnules vers l'orient et vers l'occident, nous marquerons sur notre horizon les points ainsi déterminés; ce sont ceux qui fixent les époques des équinoxes de printemps et d'automne, époque où le soleil, en y parvenant, entre ainsi dans le signe du Bélier ou dans celui de la Balance. Alors, le plateau étant supposé placé parallèlement à l'horizon, si nous comptons 32° vers le nord (c) en partant des deux points désignés, et que nous y dirigions la règle, nous aurons les points où le soleil se lève et se couche à l'époque du solstice d'été: car c'est à partir de là que le soleil commence à rétrograder, en entrant alors dans le signe du Cancer dont le point initial détermine le tropique d'été. Quant aux levers et couchers qui correspondent aux époques intermédiaires de mois en mois, nous en fixerons le lieu en mesurant 16 et 28 degrés (d) à partir des points équinoxiaux. Revenant alors à ces mêmes points, nous compterons les mêmes nombres respectifs de degrés en allant vers le midi; puis, y dirigeant la règle, nous déterminerons ainsi le lever et le coucher qui correspondent au solstice d'hiver, et ceux des époques intermédiaires de mois en mois. Ces points sont aussi, pris deux à deux à 180° de distance mutuelle sur le cercle horizontal, ceux où les signes diamétralement opposés se lèvent et se couchent : c'est-à-dire, par exemple, que, quand le Cancer se lève, le Capricorne se couche; quand le Verseau se couche, le Lion se lève; et ainsi de suite.

J'ai voulu voir de combien de degrés, en comptant dans le sens des signes antérieurs du zodiaque, l'étoile dite la Brillante des Hyades, nommée aussi Lampauras [ou Aldébaran] (e), était distante de l'étoile nommée Régulus ou Cœur du Lion. Ayant donc visé du côté de l'Orient vers deux heures de la nuit, puis ayant pris la position de Régulus dès qu'il apparut, je notai le degré correspondant tel que l'index de la règle le déterminait sur le plateau. Puis, ayant fait tourner la règle du côté des signes antérieurs, je visai également l'étoile Lampauras dans le signe du Taureau, et je notai de la même manière le degré correspondant. Alors, ayant mesuré sur le plateau le nombre de degrés compris entre les deux points, j'ai trouvé 80 à peu près : c'est la distance qui sépare les deux astres. En effet, en tenant compte du mouvement propre qui s'est effectué depuis les temps de Ptolémée, Régulus est maintenant à 10° ½ dans le signe du Lion, et la Brillante des Hyades est à 20° 2/3 dans le signe du Taureau. Ajoutant ensemble 10° ½ du Lion dans le sens des signes antérieurs, 30° pour chacun des deux signes du Cancer et des Gémeaux, et enfin 9° 1/3 de degré compris dans le Taureau, cela fait également 80. Ce serait la même chose, si l'on comptait dans le sens des signes postérieurs en allant du Taureau au Lion.

Une autre fois, vers minuit, j'ai observé, dans le sens des signes rétrogrades, la distance qui sépare le Cœur du Lion de l'étoile Arcturus, nommée aussi le Bouvier, qui se trouve dans le signe de la Balance, à 31 degrés au nord de l'équateur (f) ; et j'ai trouvé 54° environ : telle est la distance qui sépare Arcturus de Régulus, dans le sens des signes rétrogrades. Et en effet, Arcturus, en tenant compte du mouvement propre, occupe aujourd'hui le 5^e degré de la Balance ; or nous avons 19° ½ pour le Lion, 30 pour la Vierge et 5 pour la Balance; c'est bien à peu près ce que j'avais compté sur le plateau.

On s'y prendrait de la même manière pour toutes les étoiles fixes de première et de deuxième grandeur, ainsi que pour les cinq planètes. Quant à la lune, il faut observer ses distances, non seulement par rapport aux planètes et aux étoiles fixes remarquables, soit qu'elles exercent une influence semblable ou contraire à la sienne, mais encore par rapport aux systèmes nommés nébuleux, tels que la Crèche, la Chevelure, ou les étoiles nommées Pléiades, qui se trouvent a la bifurcation du Taureau, ou à celles qui, placées au milieu des Cornes, sont nommées Hyades à cause de leur ressemblance avec la lettre Y, les mêmes qui produisent les pluies et les orages. Il faut surtout observer la lune, soit aux époques des sept phases (g) qu'elle peut présenter par rapport au soleil, soit seulement lorsqu'elle en approche, soit quand certains astres forment avec elle quelque portion de figure régulière ou entrent en conjonction avec le soleil. Ceux donc qui, possédant l'art de la dioptre, sauront observer les phénomènes et juger par des règles sûres et faciles de l'état du ciel à chaque instant, pourront, non seulement reconnaître les distances des astres, mais encore la constitution et les variations de l'atmosphère, ses dispositions favorables ou défavorables; et ils seront habiles à pronostiquer chaque année les circonstances présagées par le cours des astres.

(a) Outre que l'auteur, dans ce passage, devrait dire écliptique au lieu de zodiaqu, et enseigner à fixer le plateau de la dioptre dans le plan de l'écliptique, il est évident qu'il a mis les mots ἰσημερινης et μεσημβρινῆς à la place l'un de l'autre, d'où la nécessité de la double correction que nous avons faite an texte et suivie dans la traduction.

Mais il y a ici des erreurs plus graves : « Il est bien vrai (dit M. H. Martin[76]) que la dioptre, mise dans le plan du méridien, peut servir à trouver les différences d'ascension droite des étoiles, par les différences des temps de leurs culminations, mais on trouve ainsi des différences d'ascension droite et non de longitude; et on ne les trouve pas par le seul procédé que notre auteur indique, c'est-à-dire par la mesure directe des distances angulaires des étoiles. » Quant aux étoiles situées dans le plan du méridien, en mesurant leurs distances angulaires, on obtient leurs différences de déclinaison; mais on n'obtient immédiatement les différences de latitude que pour les étoiles situées sur le colure des solstices. De même, en mettant la dioptre dans le plan de l'équateur, et en mesurant les distances angulaires des étoiles dans ce plan, on trouverait leurs différences d'ascension droite, mais non leurs différences de longitude. Ainsi notre auteur paraît avoir confondu, de même que les anciens astrologues,[77] les ascensions droites avec les ascensions obliques, et avoir confondu aussi les déclinaisons avec les latitudes. »

(b) « Le palais nommé ὁ βουκολέων, ou bien τὸ τοῦ βουκολέοντος παλάτιον, bâti par Théodose le Jeune, était une dépendance du grand palais impérial de Constantinople, situé près de l'hippodrome. Il y avait aussi près de là un quartier et un port qui portaient le même nom : ce nom était primitivement celui du lieu où ce quartier, ce port et ce palais, avaient été construits. Le nom de Bucoléon, dans ce passage, suffirait seul pour indiquer qu'il s'agit de la capitale de l'empire byzantin. » (Note extraite du Mémoire de M. H. Martin, p. 309.) Peut-être, au lieu de rendre le mot παρακυπτήριον par observatoire, faudrait-il mettre simplement donjon, balcon, c'est-à-dire généralement lieu élevé d'où l'on peut observer et découvrir ce qui se passe aux alentours, sans être spécialement destiné à des observations astronomiques. Quant au mot κοσμντάριον, il est rendu par architrave dans le lexique de la basse grécité de du Cange; mais l'architrave est peu propre à recevoir le tracé des lignes méridienne et équinoxiale : passe pour un plafond, un parquet. C'est donc à peu près à l'aventure que j'ai rendu le mot grec par celui de salle. Au reste, en voyant le mot πρασινῶν, qu'il faut peut-être écrire Πρασίνων, il est difficile de ne pas songer à la Faction verte du cirque : peut-être s'agit-il ici du lieu où elle s'assemblait.

(c) Pour savoir à quelle latitude convient cette amplitude ortive, il faut d'abord fixer l'époque de l'auteur. Or on verra plus loin qu'il mentionne des longitudes d'étoiles qu'évidemment il n'a pas observées lui-même, et qu'il n'a pu que déduire du catalogue de Ptolémée, en ajoutant un degré par siècle pour la variation du point équinoxial, parce que telle est la valeur que Ptolémée attribuait à cet élément. Les nombres qu'il donne pour ces longitudes, ainsi interprétés comme ils doivent l'être, prouvent que l'auteur, au lieu de vivre au commencement du vii^e siècle, comme Letronne prétend l'établir dans ses Recherches sur le système métrique égyptien, vivait en réalité au x^e (huit siècles après Ptolémée), et vraisemblablement entre les années 933 et 943 de notre ère, ainsi que M. H. Martin l'établit dans son Mémoire (p. 275). Cela posé, en prenant pour données les 32° d'amplitude ortive du point solsticial, et 23° 34' pour l'obliquité de l'écliptique, telle qu'elle devait être à l'époque de l'auteur,[78] il faut résoudre un triangle sphérique rectangle dont l'hypoténuse est un arc de grand cercle égal au complément des 23° 34' de l'obliquité de l'écliptique, et dont les côtés de l'angle droit sont : 1° un arc de l'horizon égal au complément des 32° de l'amplitude ortive du point solsticial, et 2° la hauteur du pôle, égale à la latitude cherchée. On trouve ainsi pour cette latitude:[79] 41° 1' 12" {H. Martin 11"). Or la latitude de Constantinople est de 41° 1' 27".La différence [15"] (H. Martin 16") est, comme on le voit, à peine appréciable. Et de plus, si l'on veut connaître au juste l'amplitude ortive des points solsticiaux à Constantinople, pour l'époque de la rédaction de la Géodésie, il n'y a qu'à renverser le calcul:[80] et l'on trouvera ainsi 32° 0' 9" (différence 9"). « Ce qui étonne au premier abord, dit M. H. Martin (p. 3i3), c'est que l'auteur ait pu approcher autant de l'exactitude; mais le fait s'explique : il a donné un nombre rond, et ce nombre rond s'est trouvé exact à 9" près. »

Barocci, en plaçant le lieu de l'observation à 35° de latitude,[81] a encore commis ici une erreur qu'il est facile de reconnaître a priori. En effet, l'amplitude ortive des points solsticiaux croît avec la latitude, depuis l'équateur terrestre, où elle est égale à l'obliquité de l'écliptique, jusqu'au cercle polaire, où elle est de 90°. Ptolémée calcule que pour le parallèle de 36° passant par Rhodes, cette amplitude doit être de 30°. Le parallèle où cette amplitude est de 32° est donc au nord de Rhodes, et non au midi, comme Barocci le prétend. »

(Cf. H. Martin : Recherches, etc. p. 311.)

(d) Pour calculer ces deux amplitudes ortives, il faut[82] chercher d'abord les déclinaisons correspondantes du soleil. Puisque l'auteur n'établit ici aucune distinction entre les quatre quarts de l'année, c'est qu'il néglige l'anomalie du mouvement apparent du soleil dans l'écliptique : nous pouvons faire comme lui, sans qu'il en résulte une erreur sensible sur les déclinaisons du soleil. Prenons donc 30° et 60° comme valeurs approximatives des distances en longitude du soleil au point équinoxial, un mois et deux mois avant ou après l'équinoxe, et prenons toujours 23° 34' pour l'obliquité de l'écliptique. Pour trouver les déclinaisons correspondantes, il faut résoudre un triangle sphérique rectangle, dont on fera l'hypoténuse a d'abord de 30° et ensuite de 60°, et dont un angle sera de 23° 34', valeur de l'obliquité de l'écliptique en 938. Le côté opposé à cet angle est la déclinaison cherchée, qu'on trouve de 11° 31' 53" (H. Martin 54") à un mois et de 20° 15' 30" (H. Martin 29") à deux mois de l'équinoxe.[83] Maintenant, pour trouver l'amplitude ortive du soleil dans ces deux positions [à Constantinople, vers l'an 938], il faut procéder comme ci-dessus pour l'amplitude ortive du soleil aux solstices, à cette seule différence près, que la déclinaison du soleil doit ici remplacer l'obliquité de l'écliptique.[84] » On trouve ainsi 15° 21' 57" au lieu de 16°, et 27° 19' 10" au lieu de 28°. L'erreur est de 38' 3" sur l'une de ces deux amplitudes « ortives, et de 40' 50" sur l'autre. Ainsi 15° et 27° auraient été des nombres ronds plus approximatifs que 16° et 28°; mais, pour que l'auteur ait dû préférer les deux nombres ronds qu'il a donnés, il suffit qu'il se soit trompé de 9' dans une de ces observations et de 11' dans l'autre. Sur l'ensemble des trois amplitudes ortives exprimées en nombres ronds, l'erreur moyenne n'est que de 26' 15" en plus. On ne pouvait guère attendre plus d'exactitude de la part d'un observateur byzantin du x^e siècle. C'est donc bien à Constantinople que ces trois valeurs approximatives conviennent. »

(Cf. H. Martin -.Recherches, etc. p. 314.)

(e) Régulus est presque sur l'écliptique; mais Aldébaran est à 5° 30', et Arcturus à 30° 57' de ce cercle. La dioptre que, de son propre aveu, l'auteur employait, était insuffisante pour lui permettre d'apprécier les longitudes de ces étoiles, et ne pouvait lui en donner immédiatement que les distances angulaires. « L'auteur aurait pu, dit M. H. Martin (p. 317), avec sa dioptre fixée dans le plan du méridien, et en s'aidant d'une horloge hydraulique, prendre successivement l'ascension droite et la déclinaison de chacune d'elles, puis en conclure par le calcul trigonométrique la longitude de chacune et par conséquent leurs différences de longitude. Mais il a eu tort de se vanter, comme il le fait expressément, d'avoir observé directement ces différences avec la dioptre[85]…. Il a pris dans le Catalogue de Ptolémée les longitudes inexactes de ces étoiles, et il en a conclu les longitudes de ces mêmes étoiles pour son temps, en comptant faussement un degré seulement par siècle pour la précession des équinoxes;[86] d'où il résulte que les longitudes assignées par lui à ces trois étoiles, pour son époque, sont celles qu'elles avaient un peu plus de trois siècles auparavant. Quant aux différences de longitude de ces trois mêmes étoiles, le Catalogue de Ptolémée les lui donnait immédiatement : c'est là qu'il a pris ces différences, et ce n'est pas avec une dioptre qu'il aurait pu les observer, comme il prétend l'avoir fait. »

(H. Martin, Recherches, etc. p. 318.)

(f) « Où l’auteur a-t-il pris cette déclinaison d'Arcturus, qui était vraie du temps d'Hipparque, mais qui ne l'était déjà plus du temps de Ptolémée? évidemment …. dans le passage où Ptolémée[87] cite cette observation d'Hipparque. Notre auteur ignore donc ou bien oublie que la précession, qui change les longitudes des étoiles sans changer leurs latitudes, « change leurs déclinaisons : cette erreur ne doit pas nous surprendre de sa part, puisque nous avons vu (note a) qu'il confondait les déclinaisons avec les latitudes. La déclinaison d'Arcturus était d'environ 31° du temps d'Hipparque, parce que cette étoile, dont la latitude est de 30° 57', était alors à 175° 8' environ de longitude. Mais, vers l'an 938, époque où notre auteur écrivait sa Géodésie, la longitude de cette même étoile était de 189° 27' 45"; sa latitude était à peu près[88] de 30° 57', comme maintenant. L'obliquité de l'écliptique était alors de 23° 34'. D'après ces données, il est aisé de calculer « la déclinaison d'Arcturus... Pour cela, il faut résoudre un triangle sphérique dans lequel deux côtés et l'angle compris sont donnés, savoir: un côté qui est la distance du pôle de l'écliptique à celui de l'équateur, ou 23° 34' ; un côté égal au complément de la latitude de l'étoile, ou 59° 3', et l'angle compris, égal à la longitude de l'étoile diminuée de 90°, ou 99° 27' 45". Le 3^e côté, opposé à l'angle connu, est de 65° 28' 45"; et son complément ou la déclinaison d'Arcturus, de 24° 31' 15" seulement... L'erreur de l'auteur est donc de près de 6° ½ sur la déclinaison d'Arcturus telle qu'elle devait être de son temps. Ce n'est donc pas au ciel avec sa dioptre, c’est chez Hipparque, cité par Ptolémée, qu'il a pu voir Arcturus à 31° au nord de l'équateur, quand cette étoile n'était plus qu'à 24° 31' 15" au nord de ce cercle. »

(H. Martin, Recherches, etc. p. 318 et 319.)

(g) Un passage des Θεολογούμενα τῆς ἀριθμητικῆς nous apprend ce qu'il faut entendre par les 7 phases de la lune. Après avoir dit que chacune des 4 phases principales étant de 7 jours, leur ensemble complète le mois lunaire, qui est de 8 jours, l'auteur ajoute qu'à ces 4 phases principales il faut ajouter les 7 formes figuratives (σχηματικαὶ μορφαί), qui sont les suivantes : μηνοειδὴς, διχότομος, ἀμφίκυρτος, πανδέληνος, puis une seconde fois ἀμφίκυρτος, διχότομος, μηνοειδὴς: c'est ce qu'on peut rendre en français par les mots : croissant (deux phases), quartier (premier et dernier), biconvexe (deux phases), pleine lune. Ces sept formes figuratives sont les 7 phases de l'auteur byzantin.

(Cf. Θεολογ. p. 45, éd. d'Ast.)

Quant aux aspects que les astres peuvent présenter entre eux (σχηματισμοί), il faut entendre par là les positions dans lesquelles ils comprennent entre eux des distances angulaires sous-multiples de la circonférence, de telle sorte que les distances rectilignes qui sous-tendent les arcs du grand cercle de la sphère céleste mesurés par ces distances angulaires soient les côtés de quelque polygone régulier inscrit à la sphère, c'est-à-dire à son grand cercle. Sous ce rapport, outre la conjonction et l'opposition, on distingue principalement: l'aspect trine ou trigone, dans lequel les astres sont distants de 120°, l'aspect quadratique ou tétragone qui a lieu dans les quadratures, où ils sont distants de 90°, l'aspect sextile ou hexagone, où ils sont distants de 60°, et l'aspect octogone ou correspondant aux octants, c'est-à-dire à 45°, huitième de la circonférence; encore celui-ci n'est-il mentionné que rarement.

(Voyez Ptolémée, Harmon. III, xiv, p. 149 de Wallis; et Proclus, Paraphr. in Ptolem. Tetrabibl. I, xvi.)

Ces dénominations sont employées bien plus par les astrologues que par les astronomes; et l'on peut juger, par ce dernier passage de la Géodésie, dans quel but notre auteur observait les astres, si vraiment cela lui arrivait quelquefois. — H.V.