NOTE ADDITIONNELLE

TRADUCTION DES TROIS CANONS HARMONIQUES DE FLORENCE

Il sera d’un grand intérêt de comparer avec le traité d’Euclide sur la Division du Canon le document musicologique publié par un jeune philologue, élève de

G. Studemund, M. Adolphe Stamm, de Nassau,[1] d’après un manuscrit de Florence (Plut. LVI, 1, bombyc. du xiii^e siècle). Cette publication, thèse doctorale soutenue à l’Université de Strasbourg, comprend : 1° une copie textuelle du manuscrit, que l’éditeur a trouvé dans un état déplorable; 2° la reconstitution du texte dans laquelle il déclare avoir été secondé par G. Studemund, Fr. Hultsch et par Ch. de Jan ; 3° une traduction latine et une traduction allemande; enfin, 4° une explication critique et exégétique du texte grec et de la matière traitée.

Le temps et l’espace me manquent pour discuter certains points. Je me propose d’y revenir ailleurs. Il est donc entendu que, à moins d’observation spéciale, la traduction qui va suivre est conforme au texte et au sens adoptés par l’éditeur des Tres canones harmonici.

(PREMIÈRE DIVISION DU CANON.)

1. On décrit ici le canon qui contient toute la série (des sons), le proslambanomène étant classé, en particulier, comme point de départ de toutes les régions.

2. Ce canon est partagé en vingt-huit régions égales entre elles. En conséquence

3. L’HYPATE des hypates occupe la région notée 24 1/3(3).

4. La parhypate des hypates 20 1/4

5. La chromatique des hypates 18 26/27

6. La diatonique des hypates 18

7. L’HYPATE des moyennes 16

8. La parhypate des moyennes. 15 9/48

9. La chromatique des moyennes 14 12/54

10. La diatonique des moyennes 13 1/2

11. La MÈSE 12

12. La PARAMÈSE 40 2/3.

13. La trite des disjointes 10 1/8

14. La chromatique des disjointes 9 13/27

15. La NÈTE des conjointes[2] 9

16. La NÈTE des disjointes 8

17. La trite des hyperboléennes 7 19/32

18. Le chromatique des hyperboléennes. 7 1/9

19. La diatonique des hyperboléennes 6 9/12

20. La NETE des hyperboléennes 6

21. Maintenant, comme les sons disposés ainsi, d'après les nombres des intervalles, font correspondre, sur tout le canon, les mesures à ces nombres, ils font même temps progresser l'étendue du son intermédiaire et divisent ln longueur totale (du canon) d'après la puissance (ou fonction du son).

22. Ainsi la mène divise le canon par moitié, comprenant douze régions.

23. Je multiplie cette quantité par elle-même et j'obtiens 144.

24. Je multiplie entre eux les nombres correspondant aux sons premier et extrême, soit le proslambanomène et la mèse, qui comprennent, l'un vingt-quatre régions, l'autre six; produit, 144.

25. De même (je multiplie) l'hypate des hypates et la diatonique des hyperboléennes, 21 1/3 et 6 9/12; produit, 144.

26. La parhypate des hypates et la chromatique des hyperboléennes 20 1/4 et 7 1/9; produit, 144.

27. La chromatique des hypates et la trite des hyperboléennes, 18 26/27 et 7 19/32; produit, 114.

28. La diatonique des hypates et la nète des disjointes, 18 et 8; produit, 144.

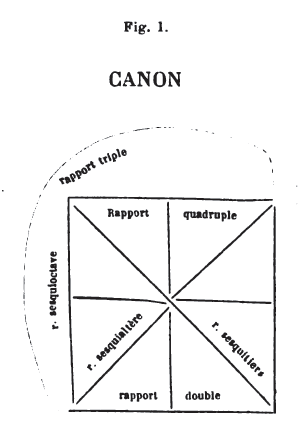
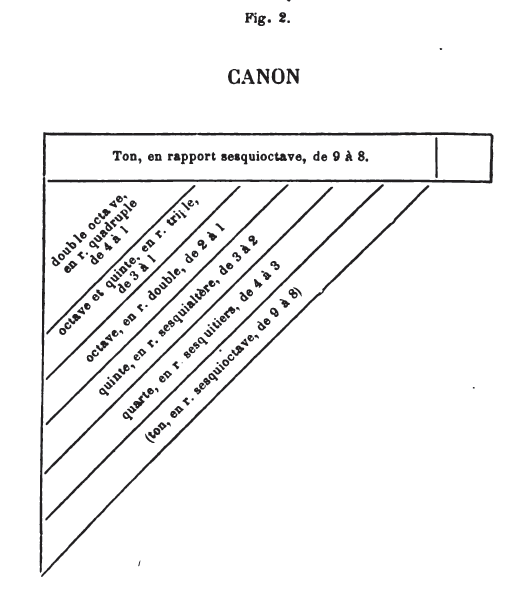
29. L'hypate des moyennes et la diatonique des disjointes, 16 et 9; produit, 144.
30. La parhypate des moyennes et la chromatique des disjointes, 159/48 et 913/27; produit, 144.

31. Chromatique des moyennes et trite des disjointes, 14 12/54 et 10 1/8; produit, 144.

32. La diatonique des moyennes et la paramèse 13 1/2 et 10 2/3; produit, 144.

 (SECONDE DIVISION DU CANON.)

Division du canon, suivant les Pythagoriciens.

1. Prenons, d’après les rapports précités, les sans de la musique, en divisant le canon suivant la consonance musicale.

2. Or, la démonstration se fait (ainsi). Le canon tendu [3] dans sa totalité, si l’on prend la moitié du son produit [4] appelé proslambanomène, le reste du canon aura la consonance d’octave et le son de la mèse.

3. Or, la mèse (corde moyenne) doit sa dénomination, non pas au son produit, mais à la section (du monocorde en deux parties égales).

4. Seconde consonance. J’ai divisé le canon total en quatre parties et j’ai fait abstraction du quart. Frappant le reste, on aura la diatonique des hypates et la consonance de quarte, qui est en rapport sesquitiers.

5. Ensuite partageant le son [5] précité en trois parties et faisant abstraction d’une de ces parties du côté du proslambanomène, tu trouveras l’hypate des moyennes, qui est en rapport sesquialtère, particulier à la consonance de quinte. (Manquent les autres déterminations — Cf. ci-dessus, Euclide, § 26, 1^re figure).

6. Et c’est ainsi que s’est formée la série des sons obtenus par consonance, au moyen de la division du canon pythagorique, tel qu’on l’employait sur l’instrument monocorde.

7. Le rapport et le diagramme sont placés ci-dessous. (1^re figure.)

(TROISIÈME DIVISION DU CANON).

1. Pythagore tendait une corde, puis, la divisant en neuf parties, suivant la notation de certains points, il frappait le son lui-même en particulier [6] ,et trouva ainsi le proslambanomène.

Ensuite faisant abstraction de la neuvième partie, il frappa la corde sur huit parties et reconnut que cette corde sonnait l’hypate des hypates, laquelle note comportait un intervalle de ton (par rapport à la corde totale); et il conçut le ton comme étant dans le rapport sesquioctave ou rapport de 9 à 8.

3. Puis il divisa la corde en quatre parties et, faisant abstraction de la première partie, il frappa la corde sur la longueur des trois autres et reconnut qu’elle donnait la consonance de quarte, laquelle se composait de deux tons et demi (selon les Pythagoriciens, de deux tons et d’un limma). Il reconnut aussi que la corde sonnait la diatonique des hypates en rapport sesquitiers, soit de 4 à 3.

4. Puis il divisa la corde entière en trois parties et, faisant abstraction de la première partie, il frappa la corde sur la longueur des deux autres, et reconnut que celte corde sonnait l’hypate des moyennes, prise en rapport sesquialtère, soit de 3 à 2, c’est-à-dire suivant la consonance de quinte.

5. Puis il divisa la corde (entière) en deux parties et, faisant abstraction d’une des deux moitiés, il frappa la corde sur la longueur de l’autre et reconnut que cette corde sonnait l’octave, ce qui conduit à la mèse, prise en rapport double, soit de 2 à 1.

6. Puis il divisa la corde (entière) en trois parties et, faisant abstraction de deux de ces parties, il frappa cette corde sur la longueur de la troisième, et reconnut que la consonance obtenue était celle d’octave et quinte (quinte redoublée), considérée dans le rapport triple, soit de 3 à 1, ce qui conduit à la nète des disjointes.

7. Puis, divisant la corde en quatre parties et faisant abstraction de trois de ces parties, il frappa cette corde sur la longueur de la quatrième, et reconnut qu’elle donnait la consonance de double octave, considéré dans le rapport quadruple ou de 4 à 4, ce qui conduit à la nète des hyperboléennes.

8. Par cette série d’opérations et la réunion [7] des nombres successifs disposés en proportion, il réalisa la division du canon, ainsi que le montrera plus clairement et le fera mieux comprendre le tableau ci-après, 2^e figure.)