[1] Anecdota Grœca, vol. IV, p. 413-429. L'ouvrage d'Engelmann (Bibliotheca scriptorum classicorum) n'a pas relevé ce texte de Domninus a son rang alphabétique. Haenel, dans son Catalogue des manuscrits, ne mentionne pas ceux qui renferment cet auteur. Pb. Labbe (biblioth. nova mss., p. 117) l'appelle Domnius sive Domnenus.

[2] Voici la traduction des passages les plus importants de cet article (on suit le texte de l'édition Bernhardy) : « Domninus, philosophe, syrien de naissance, de Laodicée et <selon d'autres> de Larissa, en Syrie, disciple de Syrianus et condisciple de Proclus, à ce que rapporte Damascius. Il était versé dans les mathématiques, mais plus superficiel dans les autres branches de la philosophie. Aussi altéra-t-il un grand nombre d'opinions de Platon par les siennes propres, mais, une fois qu'il se fut rendu coupable de cette altération, il en fut suffisamment puni par Proclus, qui écrivit contre lui tout un traité « ayant pour objet, comme dit le titre, de rétablir dans leur pureté les opinions de Platon. » Dans la vie privée, il n'avait rien non plus de supérieur ni de nature à le faire paraître un véritable philosophe……. On rapporte que, lorsqu'il était déjà avancé en âge, Asclépiodote, plus jeune que lui, alla le voir et trouva en lui un homme qui avait quelque chose de hautain et de raide, faisant peu de cas de ceux avec qui il se rencontrait, lorsque c'étaient des profanes (des gens sans connaissances philosophiques !) ou des étrangers, mais surtout des gens trop fiers de la supériorité qu'ils s'attribuaient sur les autres. Asclépiodote ajoutait que lui-même avait été durement traité par lui; qu'en effet il n'avait pas voulu se rendre à l'opinion de Domninus à propos d'un théorème d'arithmétique, ni même (comme il arrive quand on est jeune) lut faire la moindre concession, mais qu'il s'était mis à réfuter les arguments de Domninus d'un ton tellement assuré que celui-ci ne l'avait plus admis dans sa société. » (Suidas, ». v. Δομνῖνος)

[3] Heliodori Larissœi capita opticorum ex bibliotheca F. Lindenbrogii in librario Heringiano, gr. lat. 1610, in-4°. — Damiani philosophi Heliodori Larissœi de opticis libri II, nunc primum (sic) editi et animadversionibus illustrali ab Erasmio Bartholino Casparis filio. Hypsiclis anaphoricus sive de ascensionibus, gr. lat. Paris, Cramoisy, 1657, in-4°. — Traduction latine, dès 1573, publiée à Florence avec les Optica d'Euclide, par Ignatius Dantes.

[4] Domninus est encore mentionné par Marinus (Vita Procli, chap. 26), comme ayant commenté les oracles orphiques. Le Violarium d'Eudocie reproduit les premiers mots de Suidas.

[5] M. O. Riemann a pris la peine de travailler à son tour sur ce texte et sur notre traduction, qui a gagné à ce nouvel examen. Nous accueillons avec empressement la plupart de ses corrections et toutes ses remarques, même lorsqu'elles proposent d'autres solutions que les nôtres. Les lecteurs apprécieront.
 

DOMNINUS DE LARISSE.

MANUEL POUR INTRODUIRE

DANS L'ÉTUDE DE L'ARITHMÉTIQUE

PAR LE PHILOSOPHE DOMNINUS DE LARISSE

 

 

Méthode pour ôter d'un rapport un rapport qui y est contenu.[1]

 

[1] Lorsqu'on nous demande d'ôter d'un rapport un rapport qui y est contenu, ce n'est évidemment autre chose que de décomposer le rapport d'où l'on doit ôter l'autre en ses éléments, savoir le rapport qu'on enlève et le rapport qui reste après lui. En effet, le rapport d'où l'on enlève l'autre se compose du rapport enlevé et de ce qui reste après celui-ci; car nous ôtons le plus petit du plus grand.

[2] Comment donc se fera cette décomposition? N'est-il pas évident que ce sera par un procédé inverse de celui qu'on suivrait pour la composition?[2]

[3] Or, un rapport donné est dit se composer de plusieurs rapports quand les quantités de ces rapports, multipliées entre elles, reproduisent le rapport donné. En effet, si, entre les deux termes d'un rapport, on place un autre terme, le rapport du premier terme au second,[3] multiplié par le rapport du second au troisième, donne le rapport des extrêmes, quel que soit le moyen.

[4] (Fig. 1). Par exemple, soient 2 et 8, dont le moyen sera le nombre 4. Comme 2 est avec 4 dans le rapport de moitié, et 4 avec 8 de même, je multiplie la moitié par la moitié, j'obtiens le quart, et je trouve qu'en effet 2 est le quart de 8.[4]

 

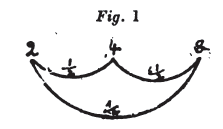
[5] Que si, au lieu de 4, je pose 40 pour terme moyen,[5] le rapport de 2 à 8 se composera encore et du rapport de 2 à 40 et du rapport de 40 à 8 ; car 2 est la 20^e partie de 40 ; mais 40 est le quintuple de 8, et je trouve ici encore que 2 est le quart de 8, car 1/20 multiplié par 5 donne ¼.

[6] Il s'agit donc d'ôter de la quantité qui exprime le grand rapport la quantité du petit. Or, cela se fera de deux manières : ou bien l'on ramènera l'un des termes du petit à être égal au terme correspondant du grand[6] et l'on fera entrer dans l'expression du grand rapport le petit rapport (ainsi modifié); ou bien l'on ramènera l'un des termes du grand à être égal au terme correspondant du petit, et on exprimera le grand rapport de telle sorte qu'il se trouve contenir le petit rapport (tel que celui-ci a été donné). Dans l'un et l'autre cas, le résultat pourra être obtenu de deux façons : car, chacun des deux rapports ayant un antécédent et un conséquent, si l'on fait entrer dans l'expression du grand rapport le petit rapport modifié, on se servira, pour enlever le petit rapport, tantôt de l'antécédent, tantôt du conséquent[7] du grand rapport duquel on enlève l'autre; si au contraire c'est le grand dont on ramène un des termes à être égal au terme correspondant du petit, ce sera encore soit de l'antécédent, soit du conséquent du petit rapport qu'on se servira pour enlever le petit.

[7] Et d'abord, soit à faire entrer dans l'expression du grand rapport le petit rapport (modifié), en se servant, pour enlever le petit rapport, de l'antécédent du grand.

[8] Soient, comme grand rapport, le rapport de 12 à 8, comme petit rapport, le rapport de 6 à 4, qu'il s'agit d'ôter du rapport de 12 à 3.

[9] Je dis donc : comme 6 est à 4, de même 12 est à un autre nombre. Le résultat s'obtiendra par la méthode exposée dans les Eléments,[8] suivant laquelle, trois nombres étant donnés, nous trouvons aussi le quatrième proportionnel.

[10] Je multiplie ainsi le second nombre par le troisième et je divise par le premier. Or, le premier, dans notre exemple, est 6, le second 4 et le troisième 12.

[11] Je dis donc : 4 fois 12 ; je divise le produit 48 par 6, et j'ai 8, avec lequel 12 a le même rapport que 6 avec 4.

[12] (Fig. 2.) Le rapport de 12 à 3 a donc été décomposé en deux rapports : celui de 12 à 8 et celui de 8 à 3.

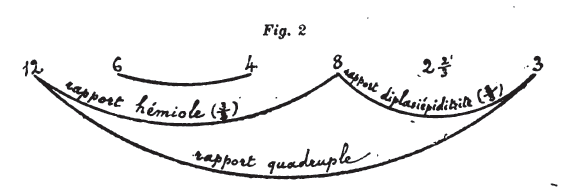
Si l'on ôte celui de 12 à 8 ou, ce qui est dire la même chose, celui de 6 à 4 (car l'un et l'autre est hémiole), il reste celui de 8 à 3, qui est diplasiépiditrite.

<Ce résultat est bien celui qu'on doit avoir> : car[9] les 2 2/3 dont se compose le diplasiépiditrite, multipliés par 1 ½ dont se compose l’hémiole, font 4; en effet, deux fois 1 ½ font 3, et les 2/3 de 1 ½ sont 1.

[13] C'est donc avec raison qu'on a décomposé le rapport de 12 à 3, qui est celui de 4 à 1, en deux rapports : l’hémiole et le diplasiépiditrite; car les deux proportions exprimées par ces deux derniers rapports se résolvent dans le premier.

[14] Si, d'autre part, nous ôtons le petit rapport au moyen du conséquent du grand rapport, nous dirons : comme 6 est à 4, de même un autre nombre est à 3, ou. en renversant les termes, pour avoir comme antécédent un nombre déterminé : comme 4 est à 6, de même 3 est à un autre nombre.

[15] (Fig. 3, 4, 5.) Nous aurons donc encore : 6 multiplié par 3 donne 18; 18 divisé par 4 donne 4 ½. Puis donc qu'il est vrai que, comme 4 est à 6, de même 3 est à 4 ½ inversement aussi, comme 6 est à 4, de même 4 ½ sera à 3; car chacun de ces deux rapports est hémiole. Le rapport de 12 à 3 a donc ici encore été décomposé en deux rapports : celui de 12 à 4 ½ et celui de 4 ½ à 3. Si l'on ôte le rapport de 4 ½ à 3, c'est à-dire celui de 6 a 4, il reste celui de 12 à 4 ½, par l'antécédent, lequel rapport est diplasiépiditrite.

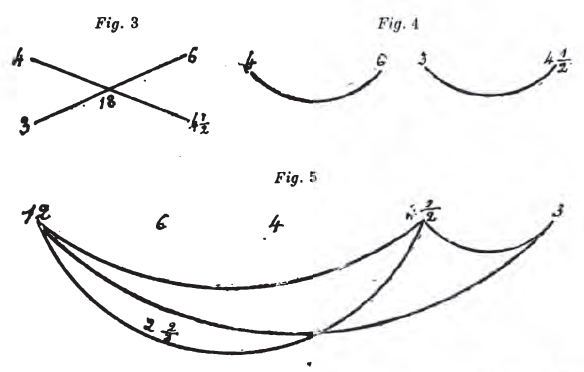
[16] (Fig. 6, 7.) Soit maintenant à ramener l'un des termes du grand rapport au terme correspondant du petit, en se servant, pour ôter le petit rapport, de l'antécédent (du petit rapport). Je dirai : comme 12 est à 3, de même 6 est à un autre nombre. Or, 6 fois 3 font 18; 18 divisé par 12 donne 1 ½. Si je prends[10] ce nombre

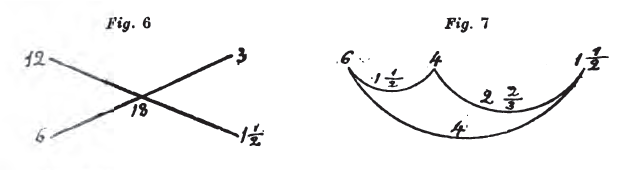
pour conséquent de 4, j'établis un rapport qui équivaut à celui de 6 à 1 ½ ou, ce qui est dire la même chose, à celui de 12 à 3. Après avoir ôté le rapport de 6 à 4, il restera celui de 4 à 1 ½ qui est encore diplasiépiditrite.

[17] Si enfin il s'agit d'ôter le petit rapport en se servant du conséquent du petit, je dirai : comme 3 est à 12, de même 4 est à un autre nombre. 12 fois 4 font 48; 48 divisé par 3 donne 16. Je prends 16 pour antécédent de 6[11] et je dis : 4 est à 16 dans le même rapport que 3 à 12.

[18] Inversement donc, comme 12 est à 3, de même 16 est à 4. Si maintenant l'on ôte du rapport de 16 à 4 ou, ce qui est dire la même chose, de celui de 12 à 3 le rapport de 6 à 4, il restera celui de 16 à 6, qui est encore diplasiépiditrite.

[19] Voilà donc comment il faut opérer en général. Si toutefois nous trouvons dans le grand rapport et dans le petit un terme commun, soit comme conséquent, soit comme antécédent, l'opération nous sera plus facile; car les termes qui restent, si l'on fait abstraction des termes semblables, comprendront précisément le rapport restant.[12]

[20] Par exemple, soit à enlever,[13] du rapport de 12 à 3, celui de 12 à 4; je n'aurai, pour adapter le petit rapport au grand, qu'à écrire 12 en face de 12 et je prendrai pour moyen 4; puis, après avoir ôté le rapport de 12 à 4, il restera le rapport de 4 à 3, qui est épitrite. Or[14] l’épitrite, multiplié par le triple, donne en effet le quadruple.

[21] Toutefois, ici comme plus haut, on peut aussi ramener l'un des termes du grand rapport au terme correspondant du petit ou l'un des termes du petit au terme correspondant du grand, en se servant, pour enlever le petit rapport, tantôt de l'antécédent, tantôt du conséquent de l'un ou de l'autre rapport.[15]

[22] On dit qu'un rapport donné se compose de plusieurs rapports quand les quantités de ces rapports, multipliées entre elles, reproduisent le rapport donné,

[23] Il est évident que si d'un rapport donné on ôte un autre rapport donné, cette opération donnera aussi le rapport qui reste de leur ensemble.[16] En effet, puisque nous connaissons d'une part la quantité du rapport dont un enlève l'autre et d'autre part celle du rapport enlevé, nous connaîtrons aussi la quantité du rapport, restant, laquelle, multipliée par la quantité du rapport qui a été ôté, forme celle du rapport composé.

 

 Ch. E. Ruelle.

 

 

NOTE SUR LE TEXTE PRÉCÉDENT

 

La question traitée ici est celle de la différence des rapports comme on l'entend en acoustique,[17] ce qui revient à une division de fractions.

L'auteur ne sait pas diviser en multipliant par la fraction diviseur renversée, et voici comment il tourne la difficulté.

Il part de cette définition : un rapport donné se compose d'autres rapports quand ceux-ci, multipliés entre eux, reproduisent le rapport donné.

Il pose ensuite un lemme qui revient à ceci : soit le rapport A/B et une quantité C. On a

A/B = A/C x C/B quel que soit C.

Cela dit, il prend un exemple, 12/3 dont il faut retrancher 6/4. Il indique quatre solutions, savoir :

1° Le rapport à retrancher est ramené au même antécédent que 12/3

12/3 = 12/C x C/3

Il détermine le moyen C par une quatrième proportionnnelle 6 : 4 :: 12 : C = 8 d'où

12/3 = 12/8 x 8/3

et, en retranchant 12/8 = 6/4 il reste 8/3, par le conséquent du grand rapport.

2° Le rapport à retrancher est ramené au même conséquent que 12/3

12/3 = C/3 x 12/C

Il détermine le moyen C par la proportion 6 : 4 :: C : 3

Mais il préfère avoir C à la fin; alors il renverse la proportion et il dit 4 : 6 :: 3 : C = 4 ½

d’où 12/3 = (4 ½)/3 x 12/(4 ½)

en en retranchant (4 ½)/3 = 6/4 il reste 12/(4 ½) = 8/3 par l'antécédent du grand rapport.

3° Le rapport dont on retranche est ramené au même antécédent que 6/4

12/3 = 6/C = 6/4 x 4/C

Il détermine le moyen C par une quatrième proportionnelle 12 : 3 :: 6 : C = 1 ½ d'où

12/3 = 6/(1 ½) = 6/4 x 4/(1 ½)

et, en retranchant 6/4 il reste 4/(1 ½) = 8/3 par le conséquent du petit rapport.

4° Le rapport dont on retranche est ramené au même conséquent que 6/4

12/3 = C/4 = C/6 x 6/4

Il détermine le moyen par la proportion 3 : 12 :: 4 : C = 16 d'où

12/3 = 16/4 =16/6 x 6/4

et, en retranchant 6/4 il reste 16/6 = 8/3 par l'antécédent du petit rapport.[18]

Puis l'auteur signale une simplification dans le cas où soit les antécédents, soit les conséquents des rapports donnés sont égaux, et il prend comme exemple 12/3 d'où à retrancher 12/4

Dans la décomposition 12/3 = 12/C x C/3

le moyen C est donné immédiatement, sans qu'on ait à chercher une quatrième proportionnelle

12/3 = 12/4 x 4/3

J. DUMONTIER.