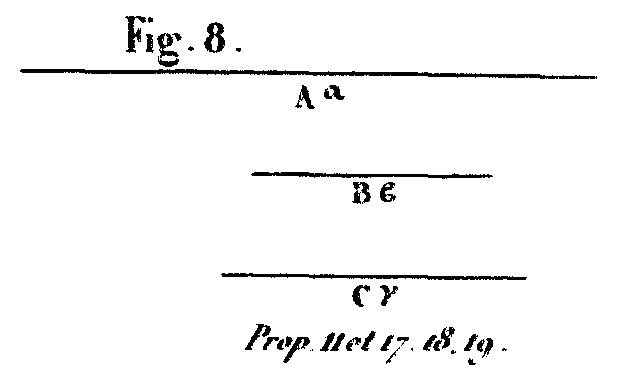RETOUR À L’ENTRÉE DU SITE

ALLER A LA TABLE DES MATIÈRES D'ARISTARQUE DE SAMOSE

TRAITÉ

D’ARISTARQUE

DE SAMOS,

SUR LES GRANDEURS ET LES DISTANCES

DU SOLEIL ET DE LA LUNE;

ET

FRAGMENT DE HÉRON DE BIZANCE

SUR LES MESURES.

TRADUITS DU GREC, POUR LA PREMIERE FOIS

AVEC DES COMMENTAIRES ET DES OBSERVATIONS,

Par M. le Comte de FORTIA D’URBAN,

MEMBRE DE PLUSIEURS ACADEMIES ET SOCIETES LITTERAIRES.

PARIS,

FIRMIN DIDOT PÈRE ET FILS, LIBRAIRES,

RUE JACOB N° 24.

DE L’IMPRIMERIE DE FIRMIN DIDOT.

M DCCC XXIII.

TRADUCTION

DE L’OUVRAGE

D’ARISTARQUE

DE SAMOS,

Sur les grandeurs et les distances

DU SOLEIL ET DE LA LUNE.

HYPOTHÈSES D’ARISTARQUE.

1. La lune reçoit sa lumière du soleil.

2. La terre peut être considérée comme un point, et comme le centre de l’orbite de la lune.

3. Lorsque la lune nous paraît dichotome (coupée en deux portions égales), elle offre à nos regards son grand cercle, qui détermine la partie éclairée et la partie obscure de cet astre.

4. Lorsque la lune nous paraît dichotome, sa distance du soleil est moindre du quart de la circonférence; de la trentième partie de ce quart.

5. La largeur de l’ombre est de deux lunes.

6. L’arc sous-tendu dans le ciel par la lune est la quinzième partie d’un signe.

En admettant ces six hypothèses, il en résulte que la distance du soleil à la terre est plus grande que dix-huit fois la distance de la lune, mais qu’elle est moindre que vingt fois cette distance; et que le diamètre du soleil est en même rapport avec le diamètre de la lune: ce qui se prouve par la position de la lune vers sa dichotomie. Mais la proportion du diamètre du soleil à celui de la lune est plus grande que celle de 19 à 3, et plus petite que celle de 43 à 6. On le démontre parle rapport des distances, par la position autour de l’ombre, et parce que l’arc sous-tendu par la lune est la quinzième partie d’un signe.

PROPOSITION I.

Deux sphères égales peuvent toujours être comprises par un cylindre; inégales par un cône dont ‘le sommet se trouvera du côté de la plus petite sphère; et la ligne droite, tirée par le centre de ces sphères, est perpendiculaire à chacun des deux cercles dans lesquels la surface du cylindre ou du cône touche les sphères.

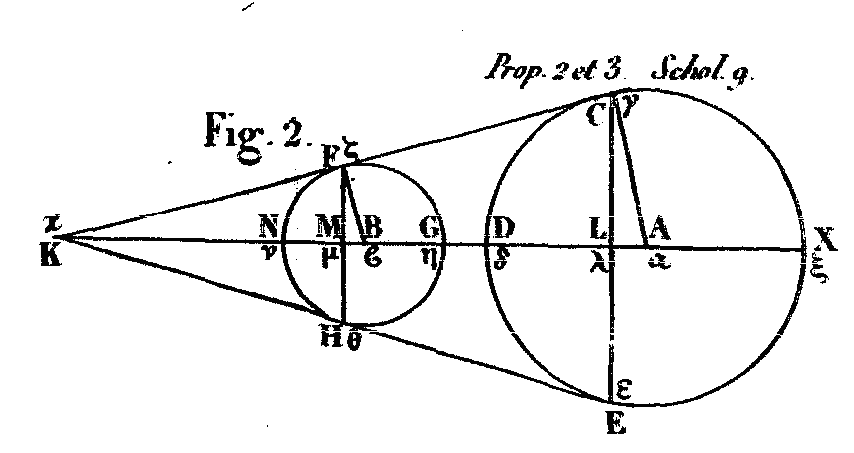
Soient d’abord deux sphères égales (fig. 1), dont les centres soient A et B, et soit prolongée la ligne AB qui joint ces centres (jusqu’à ce qu’elle rencontre la surface de chaque sphère aux points (K, L); par cette ligne AB, soit tracé un plan qui coupe les sphères de manière à ce que les deux sections soient deux grands cercles; que ces deux cercles soient CDE, FGH, et que, par les points A et B, on mène à la ligne AB les deux diamètres perpendiculaires CAE, FBH; enfin, soit tirée la ligne CF. Puisque les rayons AC et BF sont égaux et parallèles, les lignes CF et AB seront aussi égales et parallèles, et ABFC sera un parallélogramme où les angles formés sur la ligne CF seront droits (Euclide, liv. i, propos. 34). Donc la droite CF touchera les cercles CDEK, FGHL (Euclide, liv. 3, propos. 16). Or, si AB restant immobile, le parallélogramme AF et les demi-cercles KCD, GFL font une révolution autour de cette ligne AB, jusqu’à ce qu’ils soient retournés au lieu duquel ils ont commencé à se mouvoir, les demi-cercles KCD, GFL décriront dans ce mouvement deux sphères, et le parallélogramme un cylindre (Euclide, liv. i, défin. 21), qui aura pour base les cercles décrits par les diamètres CE, FH; et ces cercles seront perpendiculaires sur cette ligne AB, puisque, dans tout leur mouvement circulaire, les lignes CE, FH resteront perpendiculaires sur cette même ligne AB. Il est clair aussi que la surface du cylindre sera tangente à celle des deux sphères, puisque CF, dans tout son mouvement circulaire, sera tangente aux demi-cercles KCD, GFL.

PROPOSITION II.

Soient à présent (fig. 2) deux sphères inégales dont les centres soient A et B; et soit la plus grande celle dont le centre est A: je dis que ces sphères seront comprises dans un même cône qui aura son sommet du côté de la plus petite sphère.

Soit tirée la ligne AB qui joindra les deux centres, et que par cette ligne on trace un plan qui formera dans les sphères deux sections, lesquelles seront deux cercles; que ces cercles soient CDE, FGH ; certainement le cercle CDE sera plus grand que le cercle FGH. Le rayon tiré du centre du cercle CDE sera conséquemment plus grand que celui tracé du centre du cercle FGH. Ainsi l’on pourra trouver un point tel que K, qui sera choisi de sorte que le rayon du cercle CDE soit à celui du cercle FGH, comme AK est à BK. Que ce point soit déterminé, et qu’il soit K. Que l’on mène par ce point K la ligne FK tangente au cercle FGH, et que l’on tire le rayon BF; qu’ensuite par le centre A on mène AC parallèle à BF, et que l’on tire la ligne CF. Puisque AK : DK :: AD : BN, et que AD est égal à.AC, et BN à BF, on aura AK : BK :: AC : BF, et AC sera parallèle à BF. La ligne CFK est donc une seule ligne droite. Mais l’angle BFK est droit (Euclid., liv. 3, propos. 18); donc l’angle ACK le sera aussi (Euclid., liv. 3, propos. 17). J’abaisse CL et FM perpendiculaires sur AB Si donc KX demeurant immobile, les demi-cercles DCX, GFN, et les triangles CLK, FKM font une révolution complète autour de cette ligne KX, jusqu’à ce qu’ils se retrouvent au même lieu où leur mouvement a commencé, les demi-cercles DCX, GFN auront décrit des sphères, et les triangles CLK, FKM des cônes (Euclide, liv. ii, défin. 18), dont les bases seront les cercles qui auront pour diamètres CE, FH. Ces cercles seront perpendiculaires sur l’axe KL, et les points L et M seront leurs centres. Quant au cône, il touchera les surfaces des sphères, puisque la ligne CFK, dans tout son mouvement circulaire, touchera les demi-cercles DCX, GFN.

PROPOSITION IIL

Si une sphère est éclairée par une sphère plus grande, sa partie éclairée sera plus grande que sa moitié.

Soit en effet (fig. 2) la sphère dont le centre est B, éclairée par une sphère plus grande dont le centre est A; puisque les deux sphères inégales peuvent être comprises par un même cône ayant son sommet du côté de la plus petite (prop. II), soit construit un cône qui les comprenne, et soit mené un plan quelconque par l’axe; il aura pour sections dans les sphères deux cercles, et dans le cône un triangle. Que ces sections soient pour les sphères les cercles CDE, FGH, et pour le cône le triangle CEK; il est clair que la portion de sphère qui a été décrite par la portion de cercle dont la circonférence est FGH, et qui a pour base le cercle décrit autour du diamètre par la ligne FH, sera la partie éclairée par la portion de sphère qu’a décrite la portion de cercle dont la circonférence est CDE, et qui a pour base le cercle décrit autour du diamètre par la ligne CE, cercle qui est perpendiculaire sur l’axe AB: cas l’arc de cercle FGH est éclairé par l’arc de cercle CDE, puisque les rayons[1] Q) qui joignent leurs extrémités sont CF, EH, et le centre de la sphère B est dans le segment de cercle FGH; c’est pourquoi la partie éclairée de la sphère est plus grande que la moitié de cette sphère.

PROPOSITION III.

Dans la lune, le plus petit cercle possible sépare la partie obscure de la partie éclairée, lorsque le cône, qui comprend le soleil et la lune, a son sommet à notre vue.

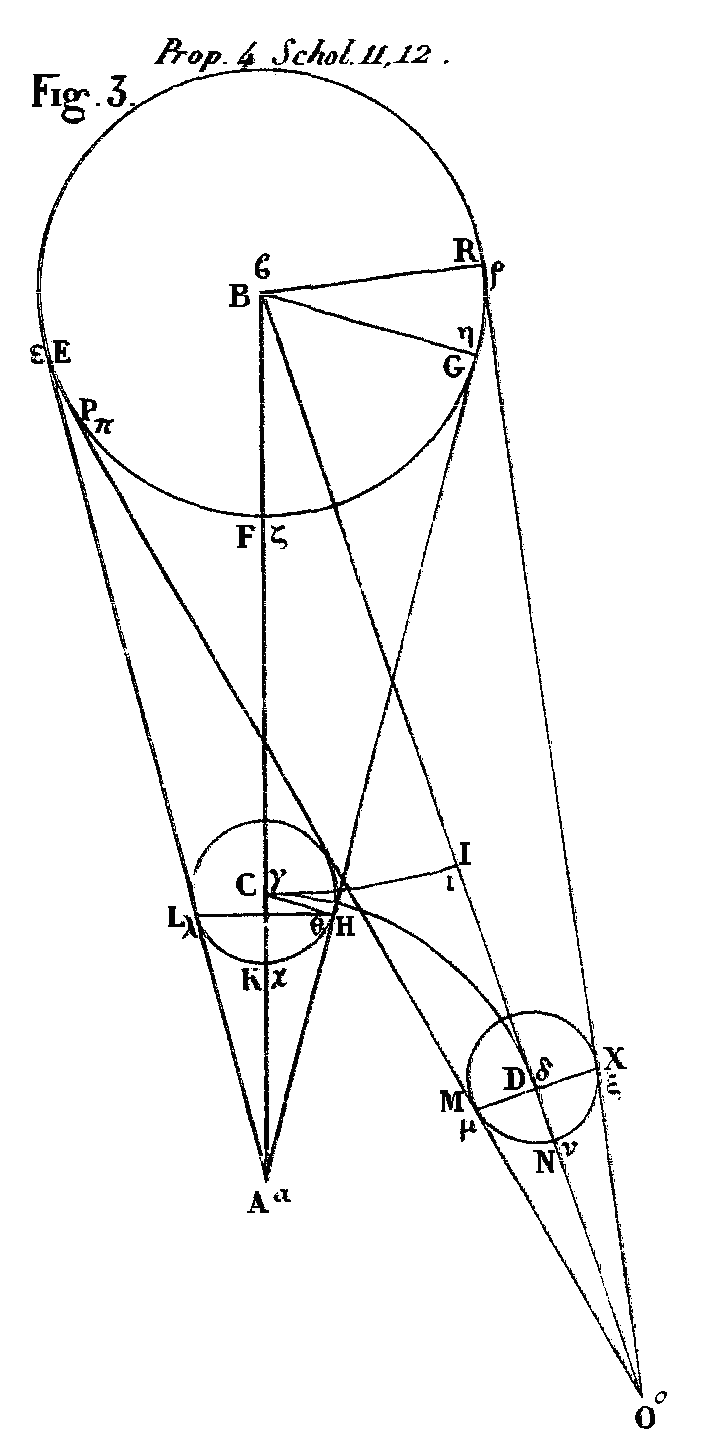
Soit en effet (fig. 3) notre vue au point A, et B le centre du soleil; soit C le centre de la lune, lorsque le cône qui comprend le soleil et la lune, a son sommet à notre vue; soit D ce même centre, lorsque le sommet du cône se trouve dans un autre lieu. Il est clair que les points A, C, B se trouveront sur une même ligne droite AB. Par cette ligne AB et le centre D, je trace un plan qui aura pour section, dans les deux sphères, deux cercles, et, dans les deux cônes, deux triangles; que cette section, dans l’orbite où se meut le cercle de la lune, soit aussi un cercle tel que CD, il est certain que A sera le centre de ce cercle, puisque c’est une de nos hypothèses (savoir la seconde). Que la section faite dans la sphère du soleil, soit le cercle EFR; et HKL dans celle de la lune, lorsque le cône qui comprend le soleil et la lune a son sommet dans notre œil; quand il ne l’a pas, que cette section soit MNX. Que cette section fasse enfin dans les cônes les droites AE, AG, OP, OR; et les axes AB, BO. On aura donc cette proportion: comme le rayon[2] du cercle EFG est à celui du cercle HKL, ainsi celui du cercle EFG est à celui du cercle MNX; mais le rayon du cercle EFG est à celui du cercle HKL comme AB est à AC;[3] et le rayon du cercle EFG est à celui du cercle MNX, comme BO est à DO: donc AB est à AC comme BO est à DO. Dividendo, je trouve BC : AC :: BD : DO. Permutando, il vient BC : BD :: AC : DO. Or BC est plus petit que BD, puisque A est le centre du cercle CD; donc AC est moindre que DO, et le cercle HKL est égal au cercle MNX. Le lemme[4] prouve que HL est plus petit que MX. C’est pourquoi le cercle décrit autour du diamètre HL, qui est perpendiculaire sur la ligne AB, est moindre que le cercle décrit sur le diamètre MX qui est perpendiculaire sur BO. Mais le cercle dont le diamètre est HL, étant perpendiculaire sur AB, est celui qui détermine dans la lune la partie obscure et la partie éclairée, lorsque le cône qui comprend le soleil et la lune a son sommet dans notre œil; et le cercle construit sur le diamètre MX, étant perpendiculaire sur BO, détermine dans la lune la partie obscure et la partie éclairée, lorsque le cône qui comprend le soleil et la lune a son sommet hors de notre œil. Ainsi le cercle qui détermine dans la lune la partie obscure et la partie éclairée, est moindre lorsque le cône qui comprend le soleil et la lune a son sommet dans notre œil.

PROPOSITION V.

Le cercle, qui détermine dans la lune la partie obscure et la partie éclairée, ne diffère pas d’un grand cercle de la lune, quant à l’apparence.

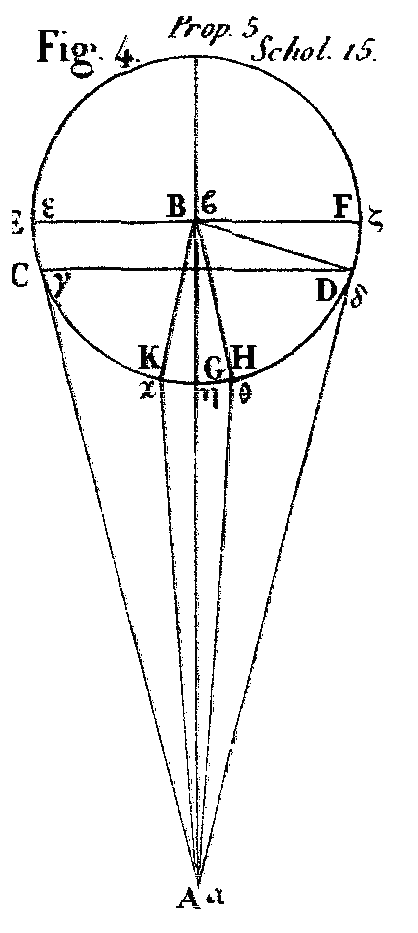
Soit en effet (fig. 4) notre œil placé au point A, et soit B le centre de la lune. Que l’on tire la ligne AB, et que l’on mène par cette ligne AB un plan qui aura pour section un grand cercle de la sphère de la lune; que ce cercle soit ECGDF, et que les sections dans le cône (qui a son sommet à notre œil, et qui comprend la lune,) soient les lignes droites AC, AD, CD: le cercle qui sera formé par la révolution de CD, prise pour diamètre perpendiculairement sur la ligne AB sera celui qui déterminera la partie obscure et la partie éclairée de la lune. Je dis qu’il ne diffère pas d’un grand cercle de la lune, quant à l’apparence. En effet, soit mené par le centre B le diamètre EF parallèlement à CD, et que DF soit partagé en deux parties égales dont ne sera portée des deux côtés du point G et en H; enfin que l’on tire les lignes BK, AK, AH, BD. Puis donc que nous avons supposé (hypothèse 6) que la lune avait pour sous-tendante la quinzième partie d’un signe, l’angle CAD consistera dans la quinzième partie d’un signe. Or, la quinzième partie d’un signe cent quatre-vingtième de tout le zodiaque; CAD sera donc la cent quatre-vingtième partie de quatre angles droits, ou la quarante-cinquième partie d’un angle droit. BAD n’en est que la moitié ; ainsi cet angle BAD est d’un degré. L’angle ADB étant droit, l’angle BAD aura, avec la moitié d’un angle droit, une proportion plus grande que celle de BD à AD. C’est pourquoi BD est moindre que la quarante-cinquième partie de AD; ainsi BG sera beaucoup moindre que la quarante-cinquième partie de AB. Dividendo sera moindre que la quarante-quatrième partie de AG. Donc aussi BH est beaucoup moindre que la quarante-quatrième partie de AH: or BH est à AH dans une plus grande proportion que l’angle BAH à l’angle ABH; ainsi l’angle BAH est plus petit que la quarante-quatrième partie de l’angle ABH. L’angle HAK est double de l’angle BAH, et l’angle HBK est double de l’angle ABH; ainsi l’angle HAK est moindre que la quarante-quatrième partie de l’angle HBK. Mais l’angle HBK est égal à l’angle DBF, c’est-à-dire à l’angle BDC ou à l’angle BAD; ainsi l’angle HAK sera moindre que la quarante-quatrième partie de l’angle BAD: or j’ai prouvé que l’angle BAD est d’un degré. Ainsi l’angle HAK sera moindre que la trois mille neuf cent soixantième partie d’un angle droit. Or, une grandeur vue sous un angle aussi petit, est insensible à notre vue. J’ai dit que l’arc HK était égal à l’arc DF; ainsi, et à plus forte raison, l’arc DF est insensible à notre vue. En effet, si l’on tire une ligne AF, l’angle DAF sera moindre que l’angle HAK: c’est pourquoi le point D paraîtra le même que le point F; par une raison semblable, C paraîtra le même que E, et conséquemment CD, quant à l’apparence, ne diffère point de EF; ainsi le cercle qui détermine dans la lune la partie obscure et la partie éclairée, ne diffère point, quant à l’apparence, d’un grand cercle de la lune.

PROPOSITION VI.

Lorsque la lune nous paraît éclairée à moitié ou dichotome, le grand cercle, qui est posé contre celui qui détermine dans la lune la partie éclairée et la partie obscure, est tourné vers notre œil; c’est-à-dire que le grand cade posé contre celui qui distingue la partie éclairée de la partie obscure et notre œil, sont dans le même plan.

En effet, lorsque la lune n’est éclairée qu’à moitié, le cercle qui distingue la partie éclairée de cet astre de sa partie obscure, se trouve évidemment vers notre œil, et le cercle qui touche celui-là n’en diffère point. Ainsi, lorsque la lune nous paraît dans sa dichotomie, le grand cercle placé auprès de celui qui distingue la partie éclairée de la partie obscure, est tourné vers notre œil.

PROPOSITION VII.

La lune a sa marche au-dessous du soleil; et lorsqu’elle est dichotome, sa distance du soleil est moindre d’un quart de cercle.

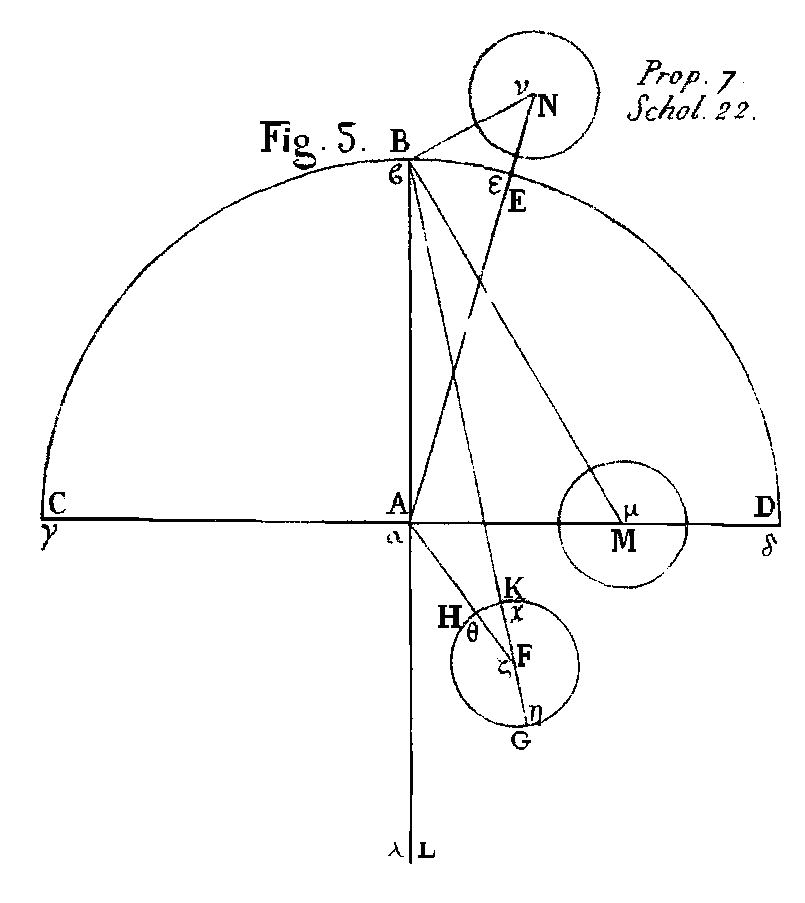
Soit en effet notre œil au point A (fig. 5), et B le centre du soleil; que ces deux points soient joints par une ligne AB, prolongée jusqu’en L, et que l’on fasse passer un plan par cette ligne et par le centre de la lune; ce plan tracera un grand cercle pour section dans la sphère que forme le centre du soleil. Que ce cercle soit CBD; du point A sur la ligne AB j’élève le diamètre perpendiculaire CAD. L’arc BD sera certainement le quart du cercle. Je dis que la lune a sa marche au-dessous du soleil, et que, dans sa dichotomie, sa distance du soleil est moindre d’un quart de cercle, c’est-à-dire que son centre est placé entre les lignes AB, AD et l’arc BED.

Supposons que cela ne soit point. Soit P le centre de la lune entre les lignes AD et AL, et soit tirée BF. Cette ligne BF sera conséquemment l’axe du cône qui comprendra le soleil et la lune, et elle sera perpendiculaire sur le grand cercle de la lune qui y distingue la partie éclairée de la partie obscure. Soit donc ce grand cercle placé auprès de celui qui distingue dans la lune la partie éclairée de la partie obscure GHK. Puisque, dans la dichotomie de la lune, notre œil et le grand cercle placé auprès de celui qui distingue dans la lune la partie éclairée de la partie obscure, sont dans un même plan, soit tirée AF. Cette ligne AF sera certainement dans le plan du cercle GHK, et BE sera perpendiculaire au cercle GHK, comme à AF. Mais l’angle BAF est aussi obtus, ce qui ne se peut pas. Le point F ne peut donc se trouver dans l’angle DAL

Je dis qu’il ne peut non plus se trouver sur la ligne AD. Si en effet cela se pouvait, que ce soit au point M, et que l’on tire la ligne BM; que M soit le centre du grand cercle placé auprès de celui qui distingue la partie éclairée de la partie obscure. On trouver de la même manière que l’angle AMB est perpendiculaire sur le grand cercle; mais BAM doit aussi être perpendiculaire, ce qui ne se peut. Donc le centre de la lune ne peut être sur la ligne AD dans le tems de la dichotomie Il sera conséquemment entre les lignes AB et AD.

Je dis de plus qu’il est dans l’intérieur du quart de cercle BED. Car si cela pouvait être autrement, supposons que ce soit au point N, et que l’on y fasse la même construction; nous prouverons que l’angle ANB est droit. AB (qui est l’hypoténuse du triangle) sera donc plus grand que AN (qui en est le côté). Mais AN est égal à AE. Donc AE sera plus grand que AN, ce qui ne peut être. Le centre de la lune pendant sa dichotomie ne peut donc être au-delà de l’arc BED. On prouvera de même qu’il ne peut être sur l’arc BED. Il sera donc dans l’intérieur du quart de cercle.

De là il résulte que la lune a sa marche au-dessous du soleil, et que, dans sa dichotomie, sa distance du soleil est moindre d’un quart de cercle.

PROPOSITION VIII.

La distance à laquelle le soleil se trouve de la terre est plus grande dix-huit fois, mais moindre de vingt fois que celle à laquelle la lune se trouve de la terre.

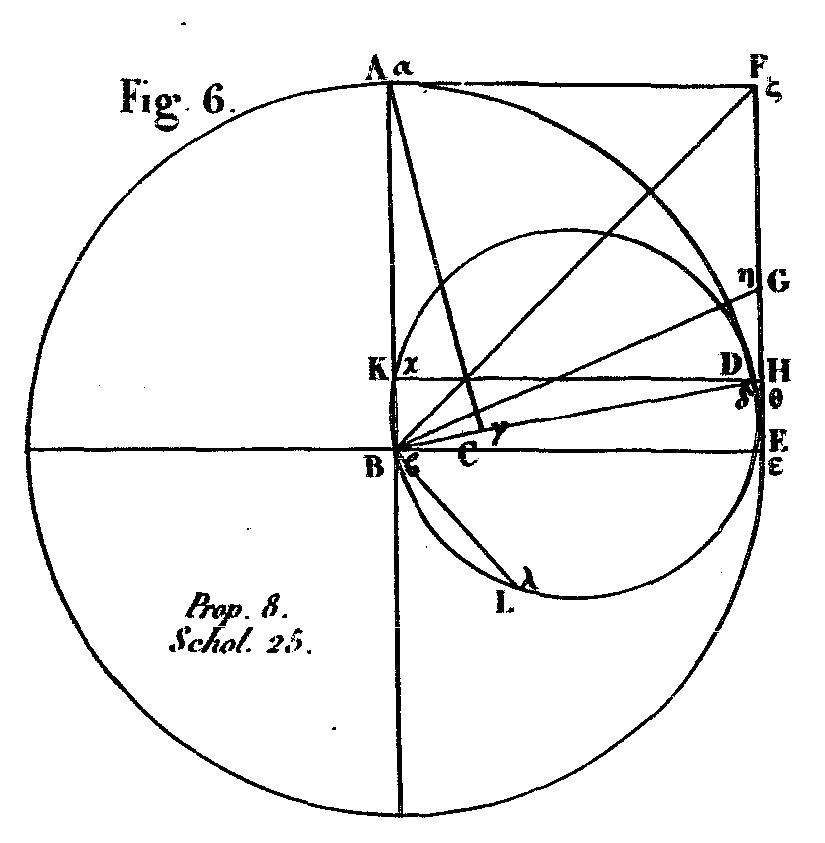
Soit en effet (fig. 6) A le centre du soleil, et B le centre de la terre; que la ligne AB, qui joint ces deux centres, .soit prolongée; que le centre de la lune, dans sa dichotomie, soit C. Par AB et C, je fais passer un plan dont la section avec la sphère, dans laquelle se meut le centre du soleil, sera un grand cercle ADE. Soient tirées les lignes AC, BC, et soit prolongée BC jusqu’en D. Puisque le point C est le centre de la lune dans sa dichotomie, l’angle ACB sera droit. Du centre B je tire sur AB la perpendiculaire BE. L’arc DE sera conséquemment la trentième partie de l’arc ADE. En effet, l’une de nos hypothèses (la quatrième) est que la lune, dans sa dichotomie, est éloignée du soleil d’un quart de la circonférence, moins la trentième partie de ce quart; donc l’angle CBE est aussi la trentième partie d’un angle droit. Soit achevé le parallélogramme AE, et soit tirée la diagonale BF ; l’angle EBF sera la moitié d’un angle droit; que cet angle EBF soit coupé en deux parties égales par la ligne BG; l’angle EBG sera conséquemment le quart d’un angle droit. Mais l’angle DBE est la trentième partie d’un angle droit; donc la proportion de l’angle EBG à l’angle DBE est celle des nombres 15 et 2. En effet, si l’angle droit est divisé en 60 parties, l’angle EBG en aura 15, et l’angle DBE 2; et puisque le rapport de EG à EH est plus grand que celui de l’angle EBG à l’angle DBE, celui de EG à EH sera plus grand que celui de 15 à 2. Or BE est égale à EF, et l’angle en E est droit; ainsi le carré construit sur BF est le double du carré construit sur BE. Mais on a cette proportion: comme le carré construit sur BF est au carré construit sur BE, ainsi le carré construit sur FG est au carré construit sur EG. Ainsi le carré construit sur FG sera double de celui construit sur EG. Or 49 est moindre que le double de 25. Ainsi, le carré construit sur FG a, avec le carré construit sur EG, un rapport plus grand que celui de 49 à 25; et conséquemment le côté FG a, avec le côté EG, un rapport plus grand que celui de 7 à 5. Componendo, on aura EF est à EG dans un rapport plus grand que celui de 12 à 5 ou de 36 à 15. Mais on a prouvé que EG est à EH dans un rapport plus grand que celui de 15 à 2, donc l’antécédent de cette proportion étant égal au conséquent de l’autre, on en conclura que EF : EH dans un rapport plus grand que celui de 36 à 2 ou de 18 à 1. Ainsi EF est plus de 18 fois plus grande que EH. Or EF est égale à BE; donc BE est aussi plus de 18 fois plus grande que EH. A plus forte raison BH sera-t-elle plus de 18 fois plus grande que EH. Mais, à cause de la similitude des triangles, comme BH est à EH, ainsi AB est à BC. AB est donc aussi plus de 18 fois plus grande que BC. Or AB est la distance du soleil à la terre, et BC est celle de la lune à la terre: donc la distance du soleil à la terre est plus de 18 fois plus grande que celle de la lune à la terre.

Il reste à prouver qu’elle est moins de 20 fois plus grande. Pour y réussir, par le point D, je mène DK parallèle à BE, et autour du triangle BDK, je construis le cercle BKDL. BD sera le diamètre de ce cercle, puisque l’angle en K est droit. Je porte le rayon de ce cercle au point L, en sorte que BL sera le côté de l’hexagone. Puis donc que l’angle DBE est la trentième partie d’un angle droit, BDK sera de même la trentième partie d’un angle droit. Ainsi l’arc BK sera la soixantième partie de la circonférence entière. Or BL est la sixième partie de cette même circonférence; ainsi l’arc BL sera décuple de l’arc BK. Mais l’arc BL a, avec l’arc BK, un rapport plus grand que la ligne droite BL avec.la ligne droite BK. Ainsi la droite BL est moins de 10 fois plus grande que la droite BK. Or le diamètre BD est double du rayon BL; ainsi BD est moins de 20 fois plus grande que BK. Mais on a la proportion BD est à BK, comme AB est à BC. Ainsi AB est moins de 20 fois plus grande que BC. Or AB est la distance du soleil à la terre, et BC est celle de la lune à la terre: donc la distance du soleil à la terre est moins de 20 fois plus grande que celle de la lune à la terre. On se souvient qu’il a été démontré que cette première distance est plus de 18 fois plus grande que la seconde.

PROPOSITION IX.

Lorsque le soleil est entièrement éclipsé, un même cône, ayant son sommet à notre œil, comprend le soleil et la lune.

En effet, lorsque le soleil est entièrement éclipsé; c’est à cause de l’opposition de la lune. Le soleil tombe donc dans le cône comprenant la lune qui a son sommet à notre œil. Car, ou le soleil est renfermé dans ce cône, ou il l’excède, ou il est dépassé par lui. S’il l’excède, il ne sera pas éclipsé en entier, et la partie excédante restera en vue; s’il est dépassé par lui, l’éclipse continuera jusqu’à ce que la partie qui le dépasse dans le cône ait été parcourue. Mais il est éclipsé tout entier, et lorsqu’il a été éclipsé un instant, il cesse aussitôt de l’être. Donc il ne dépasse point le cône, et n’est pas dépassé par lui. Il est conséquemment exactement compris et renfermé dans le cône qui comprend la lune et qui a son sommet à notre œil.

PROPOSITION X.

Le diamètre du soleil est plus de 18 fois et moins de 20 fois plus grand que celui de la lune.

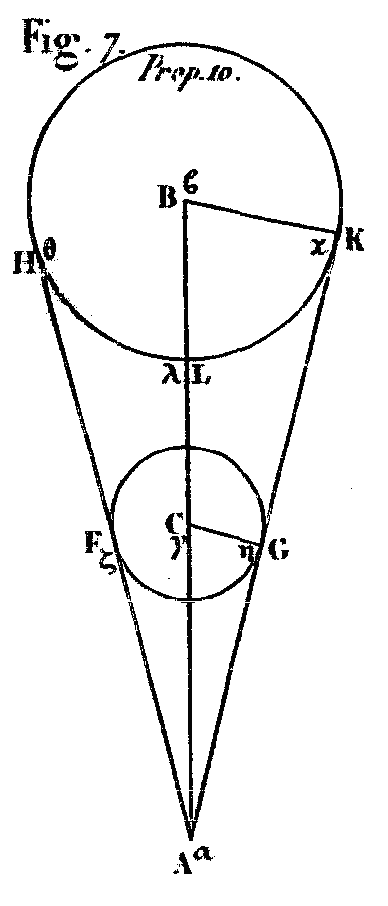
Soit (fig. 7) notre œil placé en A, B le centre du soleil, et C le centre de la lune, lorsque le cône comprenant le soleil et la lune a son sommet dans notre œil, c’est-à-dire lorsque les points A, C, B se trouvent sur une même ligne droite. Soit mené par ACB un plan, qui aura pour sections dans les sphères de grands cercles, et dans le cône des lignes droites. Qu’il fasse ainsi dans les sphères les grands cercles FG, HLK, et dans le cône les lignes droites AFH, AGK. Soient de plus tirés les rayons CG, BK, aux points de contact. On aura AB est à AC comme BK est à CG. Mais on a prouvé (Propos. VIII), que AR est plus de 18 fois et moins de 20 fois plus grand que AC. Donc BK est de même plus de 18 fois et moins de 20 fois plus grand que CG.

PROPOSITION XI.

Le soleil est à la lune en plus grande proportion que 5832 à 1, et en moindre que 8000 à 1.

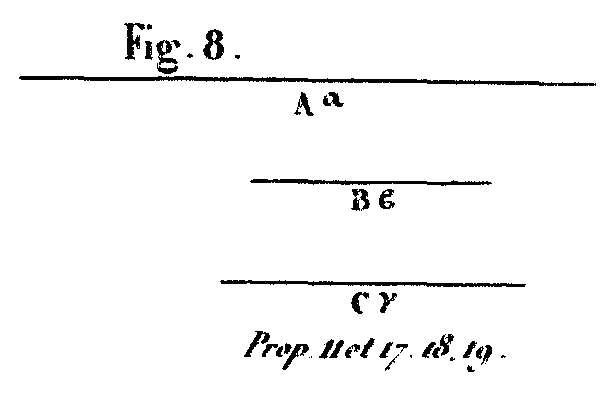
Soit en effet (fig. 8) le diamètre du soleil A, et celui de la lune B. Le rapport de A à B sera donc plus grand que celui de 18 à 1, et moindre que celui de 20 à 1. Or, comme le cube construit sur A est au cube construit sur B, en raison triplée de celle de A à B, et que la sphère produite autour du diamètre A est à la sphère produite autour du diamètre B, aussi en raison triple de A à B, on aura cette proportion: la sphère autour du diamètre A est à celle autour du diamètre B, comme le cube de A est à celui de B. Mais le cube de A est au cube de B en plus grande proportion que celle de 5832 à 1, et moindre que celle de 8000 à 1, puisque le rapport de A à B est plus grand que celui de 18 à 1, et moindre que celui de 20 à 1. Donc le soleil est en plus grand rapport avec la lune que celui de 5832 à 1, et moindre que celui de 8000 à 1.

PROPOSITION XII.

Le diamètre de la lune contient moins de deux quarante-cinquièmes parties de la distance du centre de la lune à notre œil, et il est plus grand que la trentième partie de cette distance.

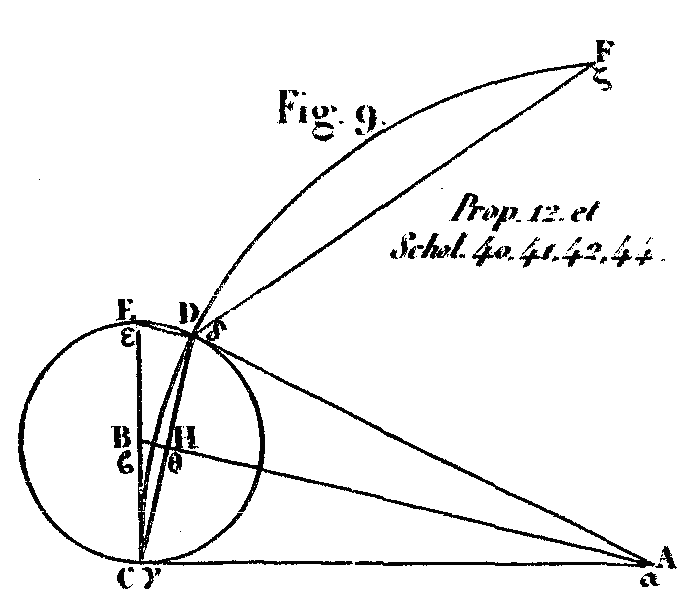
Soit en effet (fig. 9) notre œil au point A, et le centre de la lune au point B, quand le cône qui comprend le soleil et la lune a son sommet à notre œil. Je dis que l’énoncé de cette proposition est vrai. Car soient joints les points A et B par une ligne AB, et soit mené par cette ligne AB un plan qui ait pour section dans la sphère un cercle, et dans le cône des lignes droites. Qu’il fasse donc dans la sphère le cercle CED, et dans le cône les droites AC, AD, et que l’on tire BC qui soit prolongé jusqu’en E. Il est prouvé, par ce qui a été démontré (Propos. V) que l’angle BAC est la quarante-cinquième partie de la moitié d’un angle droit; et, par la même raison, BC est moindre que la quarante cinquième partie de AC. Ainsi BC est beaucoup moindre que la quarante-cinquième partie de AB. Or CE est le double de BC; donc CE est moindre que deux quarante-cinquièmes parties de AB. CE est le diamètre de la lune, et AB la distance à laquelle la lune se trouve de notre œil. Donc le diamètre de la lune, est moindre que deux quarante-cinquièmes parties de la distance de la lune à notre œil.

Je dis à présent que CE est plus grand que la trentième partie de cette même ligne AB. En effet soient tirées les lignes CD, DE, et que du centre A, avec le rayon AC, on décrive le cercle CDF; que l’on porte ensuite sur la circonférence une ligne DF égale à ce rayon AC. Puis donc que l’angle droit CDE est égal à l’angle droit ACB, et que l’angle BAC est égal à BCH, l’angle restant CED est égal à l’angle restant CBH. Ainsi le triangle CDE est semblable au triangle ABC. On aura donc AB est à AC comme CE est à CD; et, en changeant les termes, AB est à CE, comme AC est à CD ou comme DF est à CD. De plus, comme l’angle CAD est la quarante cinquième partie d’un angle droit, l’arc CD sera cent quatre-vingtième partie de la circonférence entière; DF est la sixième partie de cette même circonférence. Ainsi l’arc CD sera la trentième partie de l’arc DF. Or, cet arc CD, moindre que l’arc DF, a avec cet arc DF un rapport moindre que la ligne droite CD avec la ligne droite DF. Ainsi la ligne droite CD est plus grande que la trentième partie de la ligne droite DF. Or DF est égal à AC. Donc CD est plus grande que la trentième partie de cette ligne AC; et, à plus forte raison, CE est plus grande que la trentième partie de AB. D’un autre côté, j’ai démontré en premier lieu que CE était plus petite que deux quarante-cinquièmes parties de AB.

PROPOSITION XIII.

Le diamètre du cercle qui distingue dans la lune la partie obscure de la partie éclairée, est plus petit que le diamètre de la lune, et a cependant avec lui un rapport plus grand que celui du nombre 89 au nombre 90.

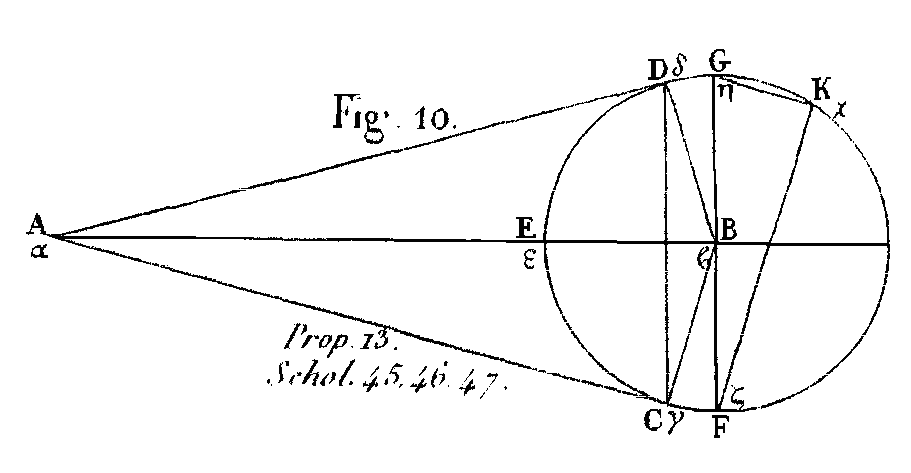
Soit en effet notre œil au point A (fig. 10); que le centre de la lune soit B lorsque le cône qui comprend le soleil et la lune a sou sommet à notre œil; que l’on mène la ligne AB, et que, par cette ligne AB, on fasse passer un plan qui ait pour section dans la sphère de la lune le cercle DEC, et dans le cône les lignes droites AD, AG, CD : CD sera conséquemment le diamètre du cercle qui, dans la lune, distingue la partie obscure de la partie éclairée. Je dis que CD est à la vérité moindre que le diamètre de la lune, mais qu’il a avec lui un rapport plus grand que celui de 89 à 90. Que CD soit plus petit que le diamètre de la lune, c’est ce qui est évident; j’ajoute qu’il a avec lui un rapport plus grand que celui de 89 à 90. Pour le prouver, je mène par le point B le diamètre FG parallèle à CD, et je tire BC. Il résulte des propositions précédentes, que l’angle CAD est la quarante-cinquième partie d’un angle droit, et que l’angle BAC est la quatre-vingt-dixième; mais l’angle BAC est égal à l’angle CBF; donc l’angle CBF est aussi la quatre-vingt dixième partie d’un angle droit, c’est-à-dire la quatre-vingt dixième partie de l’angle EBF; et conséquemment l’arc CF est la quatre-vingt-dixième partie de l’arc ECF; c’est pourquoi l’arc CE est à l’arc ECF, dans le rapport de 89 à 90. Or l’arc CED est double de CE, et FEG est double de ECF; donc l’arc CED est à l’arc FEG dans le rapport de 89 à 90. Mais la ligne droite CD est à la droite FG dans un rapport plus grand que celui de l’arc CED à l’arc FEG; ainsi la ligne CD est au diamètre FG dans un rapport plus grand que celui de 89 à 90.

PROPOSITION XIV.

Une ligne droite qui est contenue dans l’ombre de la terre, sous-tendant l’arc d’un cercle dans lequel se meuvent les extrémités du diamètre qui distingue dans la lune la partie obscure et la partie éclairée, est moindre que le double du diamètre de la lune, et a un plus grand rapport avec ce diamètre, que 88 à 45. Cette même ligne est moindre que la neuvième partie du diamètre du soleil; et elle a avec ce diamètre un plus grand rapport que celui de 22 à 225 ; enfin elle a avec la ligne tirée du centre du soleil perpendiculairement sur l’axe, et terminée aux côtés du cône, un rapport plus grand que celui de 979 à 10125.

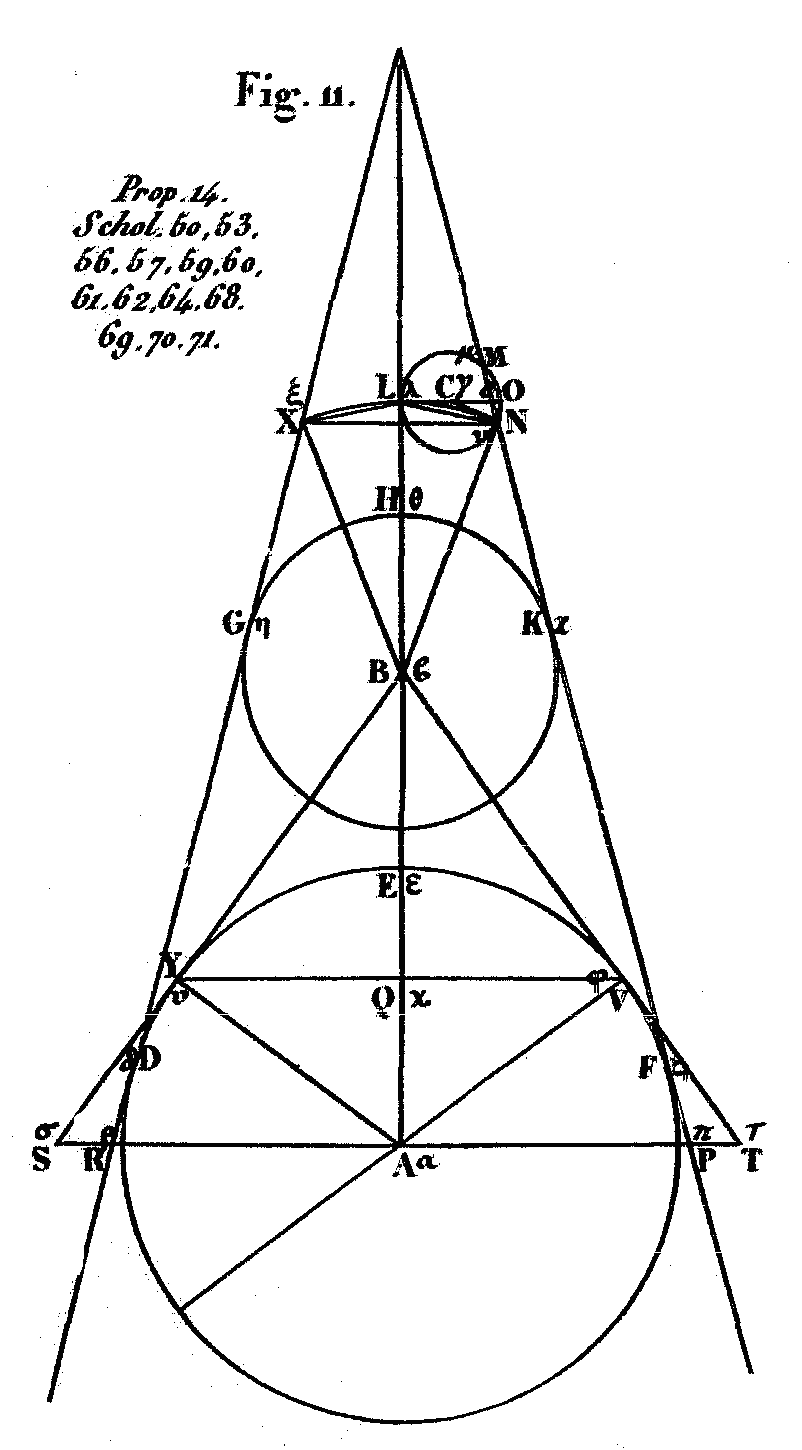
Pour démontrer cette proposition, soit A (fig. 11)[5] le centre du soleil, B celui de la terre, et C celui de la lune au moment où l’éclipse est parfaite, lorsque la lune est tombée toute entière dans l’ombre de la terre; et par les points A, B, C, soit mené un plan qui aura pour sections dans les sphères des cercles, et dans le cône qui comprend le soleil et la terre, des lignes droites. Qu’il produise dans les sphères les grands cercles DEF, GHK, LMN; dans l’ombre de la terre, un cercle dans lequel se meuvent les extrémités du diamètre qui distingue dans la lune la partie éclairée de la partie obscure, NLX; et, dan le cône, les lignes droites DGX, FKN; enfin que l’axe soit ABL. Il est certainement évident que l’arc ABL est tangent au cercle LMN, puisque l’ombre de la terre est de deux lunes; il l’est aussi que l’arc NLX est partagé en deux parties égales par l’arc ABL. J’ai supposé qu’en cet instant la lune commence à tomber toute entière dans l’ombre de la terre. Soient à présent tirées les lignes NX, LN, EN, LX; donc LN est le diamètre du cercle qui distingue dabs la lune la partie éclairée de la partie obscure; et BN est tangente au cercle LNOM, puisque notre œil est en B, et que LN est le diamètre du cercle qui distingue dans la lune la partie éclairée de la partie obscure; puis donc que LX et LN sont égales, leur somme sera double de l’une d’entre elles, LN: c’est pourquoi NX est moindre que le double de cette ligne LN. Que l’on tire les lignes CL, CN, et que CL soit prolongée jusqu’en O: à plus forte raison, NX sera moindre que le double de cette ligne LO; et puisque CL est perpendiculaire à BL, elle sera parallèle à NX. L’angle LXN es; donc égal à l’angle CLN; conséquemment encore LN est égal à LX, et CL à CN. C’est pourquoi le triangle LNX est semblable au triangle CLN. On aura donc la proportion: NX est à LN comme LN est à CL; mais LN est à CL dans une plus grande proportion que 89 à 45; c’est-à-dire le carré construit sur NX est au carré construit sur LN dans une plus grande proportion que 7921 à 2025, et cette même ligne NX sera à LO dans une proportion plus grande que 7921 à 4050. Or 7921 est à 4050 dans une proportion plus grande que 88 à 45; c’est-à-dire que NX est à LO en plus grand rapport que 88 à 45; ou la ligne droite sous-tendant un arc du cercle dans lequel se meuvent les extrémités du diamètre qui détermine la partie éclairée et la partie obscure de la lune, et qui est comprise dans l’ombre de la terre, est plus petite que le double du diamètre de la lune; mais elle a avec ce diamètre un rapport plus grand que celui de 88 à 45.

La même construction étant faite, soit tirée du point A sur AB le diamètre perpendiculaire PAR. Je dis que NX est plus petite que la neuvième partie du diamètre du soleil; mais qu’elle a avec ce diamètre un rapport plus grand que celui de 22 à 225, et avec PR un rapport plus grand que celui de 979 à 10125. En effet, puisqu’il a été prouvé que NX était plus petite que le double du diamètre de la lune, et que le diamètre de la lune était plus petit que la dix-huitième partie du diamètre du soleil, il est clair que NX sera plus petite que la neuvième partie du diamètre du soleil; d’un autre côté, NX a, avec le diamètre de la lune, un rapport plus grand que celui de 88 à 45, et le diamètre de la lune a, avec le diamètre du soleil, un rapport plus grand que celui de 45 à 900. En effet, le diamètre de la lune est au diamètre du soleil dans un rapport plus grand que celui de 1 à 20; et, en multipliant ces deux nombres par 45, on trouvera les deux nombres que je viens de donner. Le rapport de NX au diamètre du soleil sera donc plus grand que celui de 88 à 900, ou de 22 à 225.

Soient à présent menées du point B des tangentes BYS, BVT qui touchent le cercle DEF, et soient tirées les lignes VY, AY. On aura donc cette proportion: comme le diamètre du cercle qui distingue la partie éclairée de la lune de sa partie obscure, est au diamètre de la lune; ainsi VY est au diamètre du soleil. Cette proportion dérive nécessairement de ce qu’un même cône, ayant son sommet à notre œil, comprend le soleil et la lune. Or, le diamètre du cercle qui distingue dans la lune la partie éclairée de la partie obscure, a, avec le diamètre de la lune, un rapport plus grand que celui de 89 à 90. Ainsi VY a, avec le diamètre du soleil, un rapport plus grand que celui de 89 à 90. Par la même raison, QY aura avec AV un rapport plus grand que celui de 89 à 90. Or, QY est à AY comme AY est à AS, puisque AS et QY sont parallèles; donc. AY est à AS dans une proportion plus grande que celle de 89 à 90; à plus forte raison AY est à AR dans un rapport plus grand que celui de 89 à 90. Il en est de même de leurs doubles.

Ainsi le diamètre du soleil est à PR dans un rapport plus grand que celui de 89 à 90; or, on a prouvé que NX est au diamètre du soleil dans un rapport plus grand que celui de 22 à 225; en unissant ces deux proportions, on conclura que NX est à PR dans un plus grand rapport que le produit des nombres 22 et 89 à celui des nombres 90 et 225; c’est-à-dire, que 1958 à 20250, ou leurs moitiés qui sont 979 et 10125.

PROPOSITION XV.

Si l’on tire une ligne droite du centre de la terre au centre de la lune, cette ligne sera avec la ligne droite prise sur l’axe; entre celle qui sous-tend l’arc du cercle contenu dans l’ombre de la terre et je centre de la lune, en plus grande proportion que 675 à 1.

OBSERVATION DE LA FIGURE.

La figure 12 qui me servira pour démontrer cette proposition, est la figure 24 de Wallis. On observera que, dans les figures des deux manuscrits, le point s, z, est le centre de l’arc NLX ou nlx ce qui n’est ni exact, ni conforme à Wallis. De plus la lune, dans ces deux manuscrits, est plus grande que la terre, ou du moins presque égale à la terre, ce qui n’est pas plus exact. Mais, comme la petitesse de la lune met quelque confusion dans la figure, on retrouvera ce même astre plus grand dans la figure 12 bis, où les mêmes lettres sont employées, mais placées plus distinctement.

Soit donc (fig. 12) la même figure que ci-dessus, et que la lune y soit placée de manière que son centre y soit sur l’axe du cône qui comprend le soleil et la terre,[6] soit au centre C; soit de plus MOP un grand cercle de la sphère de la lune, se trouvant dans le même plan, et soit tirée la ligne MO; MO sera donc le diamètre du cercle qui distingue dans la lune la partie obscure de la partie éclairée; soient donc tirées les lignes BM, BO, LX, BX, CM. Il est clair que les lignes droites BM, BO touchent le cercle MOP, puisque MO est le diamètre du cercle qui distingue dans la lune la partie obscure de la partie éclairée: et puisque LX est égal à MO, l’une et l’autre de ces deux lignes étant le diamètre du cercle qui distingue la partie obscure de la partie éclairée; il est clair que l’arc LMX est égal à l’arc MLO, et conséquemment l’arc MX à l’arc LO. Mais LO est égal à LM; donc MX est aussi égal à LM. Or la ligne BX est de même égale à BL, puisque le point B est le centre, de la terre, et que la terre peut être considérée centime un point et un centre, relativement à l’orbite[7] de la lune; de plus MOP est dans le même plan; c’est pourquoi BM est perpendiculaire sur LX, et CM est perpendiculaire sur BM. Ainsi CM est parallèle à LX. Mais SX est aussi parallèle à MR, et conséquemment le triangle LSX est semblable au triangle CRM: ainsi SX est à MR comme LS est à CR; mais SX est moins que double de MR, et conséquemment NX est moins que double de MO; donc aussi LS est moins que double de CR, et RS est beaucoup moins que double de CR; d’où il suit que CS est moins que triple de CR. On aura donc: CR est à CS en plus grand rapport que 1 à 3;. et puisque BC est à CM comme CM est à CR, et que BC est à CM en plus grande proportion que 45 à 1, CM sera à CR en plus grande proportion que 45 à 1; or CR est à CS en plus grande proportion que 1 à 3; conséquemment le rapport de CM à CS sera plus grand que celui de 45 à 3, c’est-à-dire de 15 à 1; or on a prouvé que le rapport de BC à CM est plus grand que celui de 45 à 1; donc enfin, par la comparaison de ces deux rapports, on conclura que BC est à CS dans un rapport plus grand que celui de 675 à 1.

PROPOSITION XVI.

Le diamètre du soleil est au diamètre de la terre en plus grande proportion que 19 à 3, et en moindre que 43 à 6.

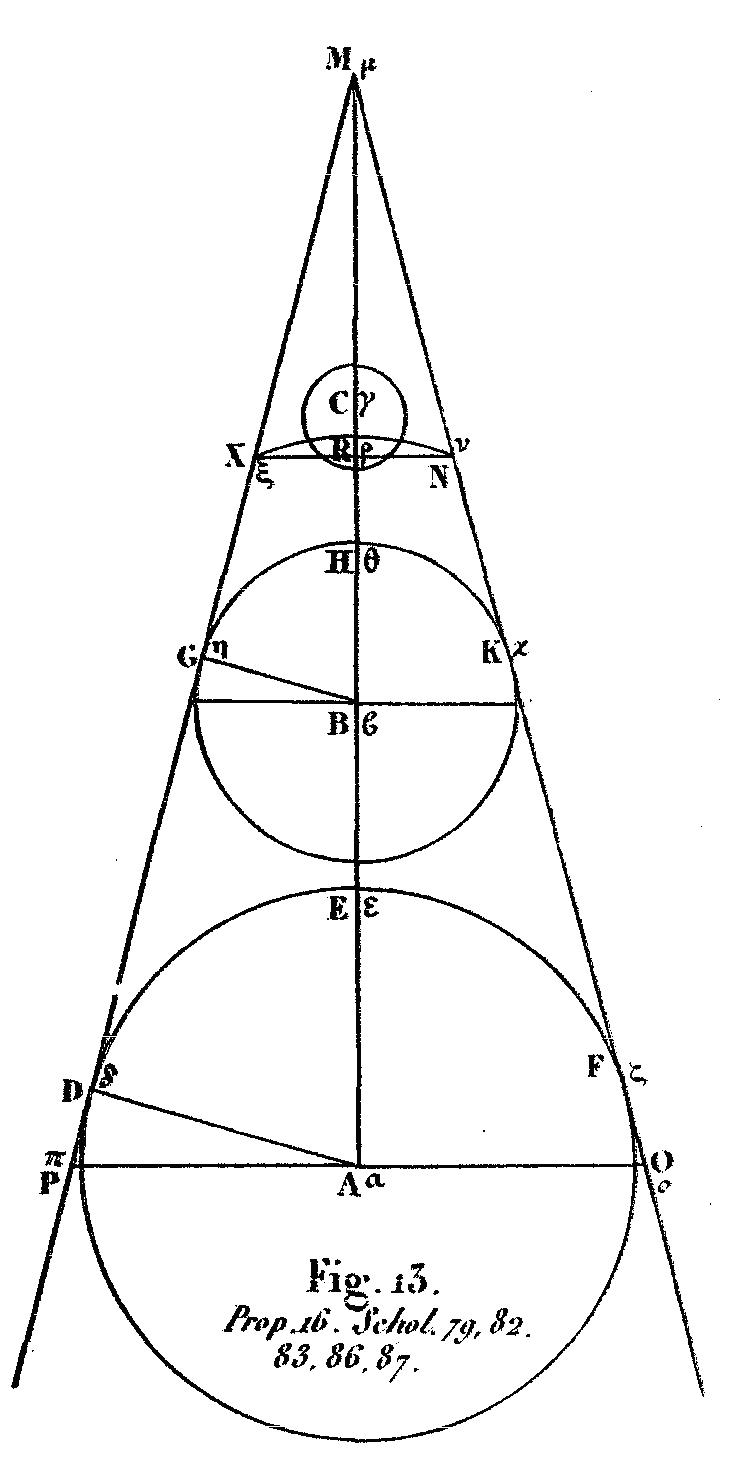
En effet, soit (fig. 13)[8] le centre du soleil en A, celui de la terre en B, et C le centre de la lune au moment où l’éclipse est parfaite; c’est-à-dire où les points A, B, C sont eu ligne droite. Soit aussi mené par l’axe un plan qui ait pour section dans le soleil le cercle DEF, dans la terre le cercle GHK, et dans l’ombre l’arc de cercle NX; enfin dans le cône les lignes droites DM, FM; soit tirée la corde NX, et par le point A, soit menée sur AM la perpendiculaire OAP. Puisque NX est moindre que la neuvième partie du diamètre du soleil, et qu’à plus forte raison le rapport de OP à NX sera plus grand que celui de 9 à 1, le rapport de AM à MR sera conséquemment plus grand que celui de 9 à 1; et convertendo, AM est à AR en moindre rapport que celui de 9 à 8. D’un autre côté, puisque AB est au-delà de 18 fois plus grande que BC, à plus forte raison elle sera plus grande que BR. AB sera, donc à BR dans une proportion plus grande que celle de 18 à 1; et convertendo, BR sera à AB dans une proportion moindre que celle de 1 à 18. Componendo, AR est à AB dans une proportion moindre que celle de 1 à 18. Or, on a prouvé que AM est à AR dans un rapport moindre que celui de 9 à 8; donc le rapport de AM à AB sera moindre que celui de 171 à 144, et que 19 à 16; car les parties semblables ont les mêmes rapports que leurs multiples. C’est pourquoi, convertendo, AM est à BM dans une proportion plus grande que celle de 19 à 3. Or, AM est à BM comme le diamètre du cercle DEF est au diamètre du cercle GHK. Ainsi le diamètre du soleil est au diamètre de la terre dans une plus grande proportion que 19 à 3.

Je dis, en outre, que le rapport de ces deux diamètres est moindre que celui de 43 à 6. En effet, puisque BC est à CE dans une proportion plus grande que celle de 675 à 1, on aura, convertendo, BC est à BR dans une proportion moindre que celle de 675 à 674. Mais AB est à BC dans une proportion moindre que celle de 20 à 1 en comparant les deux termes égaux, on en conclura que AB est à BR dans un rapport moindre que celui de 13500 à 674; c’est-à- dire que 6750 à 337. Convertendo et componendo, il résulte que AR est à AB dans un rapport plus grand que celui de 7087 à 6750. En effet, puisque NX est à OP dans une proportion plus grande que celle de 979 à 10125, on aura, convertendo, OP est à NX dans une proportion moindre que celle de 10125 à 979. Or, OP est à NX comme AM est à MR. Ainsi AM est à MR dans un rapport moindre que celui de 10125 à 979. On aura conséquemment, convertendo, AM est à AR en plus rand rapport que 10125 à 9146. Mais on a aussi AR est à AB en plus grand rapport que 7087 à 6750. En comparant ces deux rapports, il viendra AM est à AR en plus grand rapport que le produit des nombres 10125 et 7087 au produit des nombres 9146 et 6750; c’est-à-dire que 71755875 à 61735500. Or, 71755875 est à 61735500 en plus grand rapport que 43 à 37; donc AM est à BM en plus grand rapport que 43 à 37; ainsi, convertendo, AM est à BM en moindre rapport que 43 à 6. Mais AM est à BM comme le diamètre du soleil est au diamètre de la terre; par conséquent, le diamètre du soleil est au diamètre de la terre en moindre rapport que 43 à 6. Or, il a été prouvé que ce même rapport était plus grand que celui de 19 à 3.

PROPOSITION XVII.

Le soleil est à la terre en proportion plus grande que celle de 6859 à 27, et moindre que celle de 79507 à 216.

Soit en effet (fig. 8) A le diamètre du soleil, B celui de la terre; ou a démontré que la sphère du soleil est à la sphère de la terre, comme le cube du diamètre du soleil est au cube du diamètre de la terre; il en est de même de la lune: ainsi le cube de A est au cube de B, comme le soleil est à la terre. Or, le cube de A est au cube de B en plus grande proportion que 6859 à 27, et en moindre que 79507 à 216; car A est à B en plus grande proportion que 19 à 3, et moindre que 43 à 6; c’est pourquoi le soleil est à la terre en plus grande proportion que 6859 à 27, et moindre que 79507 à 216.

PROPOSITION XVIII.

Le diamètre de la terre est au diamètre de la lune en plus grand rapport que celui de 108 à 43, moindre que celui de 60 à 19.

Soit (fig. 8) A le diamètre du soleil, B celui de la lune, C celui de la terre. Puisque A est à C en moindre rapport que 43 à 6, on aura, convertendo: C est à A en plus grand rapport que 6 à 43; or, le rapport de A à B est plus grand que celui de 18 à 1. Donc, par la comparaison des rapports, C est à B en plus grand rapport que 108 à 43. D’un autre côté, puisque A est à C en plus grand rapport que 19 à 3; on aura, convertendo, C est à A en moindre rapport que 3 à 19; or, A est à B en moindre rapport que 20 à 1; ainsi, en comparant les rapports égaux, C est à B en proportion moindre que 60 à 19.

PROPOSITION XIX.

La terre est à la lune eu proportion plus grande que celle de 1259712 à 79507; et moindre que celle de 216000 à 6859.

Soit en effet (fig. 8) A le diamètre de la terre, et B celui de la lune. Puisque A est à B en plus grande proportion que celle de 108 à 43, et moindre que celle de 60 à 1 le cube construit sur A est au cube construit sur B en proportion plus grande que celle de 1259712 à 79507, et moindre que celle de 216000 à 6859. Mais le cube de A est au cube de B comme la terre est à la lune; ainsi le rapport de la terre à la lune est plus grand que celui de 1259712 à 79507, et moindre que celui de 216000 à 6859.