RETOUR À L’ENTRÉE DU SITE

TABLE DES MATIÈRES DE JEAN PEDIASMOS

    

 

 

JEAN PEDIASIMOS

 

          

MENUES OBSERVATIONS SUR DIVERS POINTS QUI ONT BESOIN D'ETRE ECLAIRCIS PAR L'ARITHMÉTIQUE ; ENTRE AUTRES SUR LA RAISON QUI A FAIT DESIGNER LES CONSONANCES MUSICALES, LA QUARTE, LA QUINTE, ETC., PAR DES DENOMINATIONS NUMERALES.       
   

       Oeuvre numérisée par Marc Szwajcer

 

 

 

 

 

 

 

JEAN PEDIASIMOS

 

Extrait de Louis Mayeul Chaudon, Dictionnaire universel, historique, critique, et bibliographique, 1810.

Jean, surnommé Pediasimos à cause de son égalité d’âme et Galenos pour la sérénité de son esprit, diacre et gardien des archives (chartophilax) de la première Justiniane et de toute la Bulgarie dans le 14^e siècle, a composé des Scolies sur Hésiode et sur le Syrinx de Théocrite. Sa Géométrie, son Abrégé d’un ouvrage du mathématicien Héron, son Allégorie anagogique sur les quatre premiers vers du 4^e livre de l’Iliade, sa courte Dissertation sur trois espèces d’allégories des Fables poétiques, ses Mémoires de physique, de morale et de théologie, existent manuscrits à la bibliothèque impériale de Vienne. Ses Scolies sur Eléomèdes encore inédites se trouvent dans plusieurs bibliothèques ainsi qu’un livre sur les noces. Enfin nous avons un écrit de Jean Pediasimos sur la duplication du cube et un autre sur le I^er livre des Analytiques d’Aristote. Luc Holstenius transcrivit à Paris sur un manuscrit de la bibliothèque aujourd’hui impériale des vers ïambes de cet auteur sur la bonne et la méchante femme ; il les publia avec d’autres anciens ouvrages à Rome en 1638 in 12. Thomas Gale les réimprima dans la 1^ère édition de ses Opuscula mythologica et J. A. Fabricius les a insérés dans le 15^e vol de la Bibliothèque grecque. On en peut lire une traduction en vers par M Fortia.

Polygraphe curieux et érudit, il a écrit sur presque tous les sujets.

 

 

 

MENUES OBSERVATIONS

SUR DIVERS POINTS QUI ONT BESOIN D'ETRE ECLAIRCIS PAR L'ARITHMÉTIQUE ; ENTRE AUTRES SUR LA RAISON QUI A FAIT DESIGNER LES CONSONANCES MUSICALES, LA QUARTE, LA QUINTE, ETC., PAR DES DENOMINATIONS NUMERALES ;

PAR LE SAVANT PHILOSOPHE ET DIACRE

MAÎTRE JEAN PÉDIASIMOS.

 

Le son musical est une émission de voix sur un certain ton, ou, plus exactement, une émission mélodieuse de la voix sur un degré d'intonation déterminé ; car on ne peut appeler son, ni le fracas du tonnerre, ni un murmure qui serait, pour ainsi dire, imperceptible. Ensuite, il faut que l'intonation soit bien une ; car, lorsqu'on frappe successivement deux fois la même corde, ou simultanément deux cordes différentes, il n'en résulte pas un son unique, mais bien deux sons distincts, produits, dans le premier cas, par une corde unique, et, dans le second, par deux cordes. Il faut faire attention que cela s'applique au son de la flûte comme à celui de tout autre instrument, tout aussi bien qu'à la voix naturelle.

L'intonation simultanée[1] de deux sons forme ce que l'on nomme en général un intervalle, et, en particulier, c'est tantôt un diésis, tantôt un demi-ton, tantôt un ton. Le diésis est tantôt la moitié du demi-ton, tantôt le tiers [du ton], suivant la doctrine d'Aristoxène.[2] Le diésis tiers de ton ne se chante que dans le genre enharmonique ; le demi-ton se chante surtout dans le genre chromatique ; et le ton dans le genre diatonique. Il y a deux sortes de demi-ton, un plus petit que l’on nomme limma, et un plus grand que l’on nomme apotome ; et la différence du plus grand demi-ton au plus petit, c'est-à-dire l'excès du premier sur le second, se nomme comma.

Ainsi, pour parler plus clairement, le son est…, ou bien l'on est convenu d'appeler son, le ton d'une corde. L'intervalle est la résonnance simultanée de deux cordes mises ensemble ; et le premier intervalle qu'il est possible de chanter et de rendre sensible à l'oreille se nomme diésis, de dieimi, qui signifie passer, s'introduire, parce qu'il est comme la porte d'entrée et l’ouverture du chant. Le premier intervalle appréciable après celui-là, en allant en augmentant,[3] s'appelle demi-ton ; celui-ci est plus connu, et on l'a d'abord établi dans le rapport du nombre 256 au nombre 243, rapport qui est un peu moindre que celui de 17 à 16.[4] Mais pour quelle raison le rapport de 17 à 16 n'est-il pas exactement la valeur du demi-ton, c'est-à-dire de la moitié du rapport de 9 à 8 ? Parce que, répond-on, quand on partage une quantité continue en deux parties égales, aucune des deux n'est exactement la moitié du tout ; et c'est ce que l'on voit clairement dans le sciage des bois : car, si l'entier est de dix coudées, et qu'on le scie par le milieu, aucune des deux parties ne sera exactement de cinq coudées, puisque, dans les dix coudées, il faut comprendre le trait de la scie.[5] Si donc le chant, si le son d'une corde, est un tout continu, il est impossible que le rapport de 9 à 8, partagé en deux parties égales, donne exactement le rapport de 17 à 16, comme on l'entend lorsqu'on donne à ce dernier la qualification de demi-ton. Quant à la manière de découvrir la valeur du limma, c'est ce que l'on verra par la suite ; et ce sera en même temps une autre manière d'obtenir celle du demi-ton.

Pour le ton, nous allons dire comment on a trouvé qu'il était dans le rapport de 9 à 8. Mais auparavant il faut savoir que, dans l'arithmétique, la première fraction à considérer après l’entier est la moitié, après quoi vient le tiers, puis le quart, et ainsi de suite ; car entier vient de un, demi vient de deux, attendu que de simul, ensemble, on a fait sémi, et que le mot ensemble désigne en premier lieu le nombre deux. Ainsi, de même que nous disons un, deux, trois, quatre, et ainsi de suite, de même aussi nous disons entier, demi, tiers, quart, et ainsi de suite. Mais, dans l'harmonique, comme la progression des sons a lieu du plus faible au plus fort, le premier nombre à considérer est le tiers, ou mieux encore le huitième, fraction d'où dépend, conformément à ce que l'on a dit, l'évaluation du ton ; et ensuite viennent le tiers, puis la moitié, et ainsi de suite. Mais du tiers dérive le rapport de 4 à 3, et de la moitié celui de 3 à 2 ; donc, dans l'harmonique, le premier rapport à considérer est, en fait d'intervalle, celui de 9 à 8 ; et, en fait de système, celui de 4 à 3, que l'on nomme aussi quarte (or un système est une réunion de plusieurs intervalles) ; puis après le rapport de 4 à 3, celui de 3 à 2, que l'on nomme aussi quinte.

Mais pourquoi le rapport de 4 à 3 s'appelle-t-il quarte, et pourquoi celui de 3 à 2 s'appelle-t-ii quinte ? c'est ce que l'on va voir. Commençons, pour cela, par prendre deux cordes d'égale épaisseur ; et, soit au moyen de poids, soit au moyen de chevalets, donnons à l'une une tension représentée par 3, et à l'autre une tension représentée par 4 ; puis frappons ces deux cordes : nous aurons bien le rapport épitrite, puisque le rapport ainsi nommé n'est autre que le rapport de 4 à 3, et que ce dernier est bien aussi celui de la corde dont la tension est 4 à la corde dont la tension est 3. Ensuite prenons une troisième corde, et donnons-lui une tension encore plus forte et justement assez élevée pour être à la première dans le rapport de 3 à 2 : cela fait, nous trouverons que la tension de cette dernière est à celle de la seconde corde dans le rapport sesquioctave.

Nous pouvons, en employant des nombres, rendre évident ce que nous venons de dire. En effet, soient les trois nombres six, huit, et neuf. 8 est d'abord à 6 dans le rapport épitrite. Je cherche un troisième nombre un peu plus grand, qui soit à 6 dans le rapport hémiole, c'est-à-dire de 3 à 2 : ce nombre est 9, comme il est facile de le vérifier ; or l'excès de 9 sur 8 ne peut donner que le rapport sesquioctave. Ce rapport est donc aussi la valeur du ton : en effet c'est le même que l'excès du rapport hémiole sur le rapport épitrite, puisque, quand on retranche[6] le rapport épitrite du rapport hémiole, il reste le rapport de 9 à 8. Ainsi, soit une grandeur a hémiole d'une autre grandeur b [c'est-à-dire que a : b : : 3 : 2], et une troisième grandeur c, épitrite de la même b [c'est-à-dire que c : b : : 4 : 3] : je dis que a est à c dans le rapport de 9 à 8. En effet, puisque a est hémiole de b, il s'ensuit que a contient b plus sa moitié, et que par conséquent 8 fois a valent 12 fois b. Mais 12 fois b valent 9 fois c ; donc 8 fois a valent 9 fois c : c'est-à-dire que a est égal à c plus son huitième. Donc a est à c dans le rapport de 9 à 8.[7]

Ce même principe, que la différence du rapport hémiole au rapport épitrite est le rapport sesquioctave, peut encore se vérifier sur des lignes.

Mais il faut maintenant parler du rapport épitrite considéré dans l'harmonique, et dire pour quelle raison on l’a nommé quarte ; de même, comment le rapport hémiole a été nommé quinte ; et, de même, pourquoi le rapport double a été nommé, en musique, octave ou diapason. Pour cela, il faut savoir que le système nommé quarte se compose de deux tous et un demi-ton, c'est-à-dire de quatre sons. Je cherche donc un nombre à la suite duquel je puisse établir deux intervalles consécutifs d'un ton, et placer un quatrième nombre, qui, étant au premier dans le rapport épitrite, soit, de plus, à une distance de demi-ton du troisième. Or nous avons vu, dans cette introduction arithmétique,[8] que la première puissance[9] de 2 ne peut donner lieu qu'à un seul rapport hémiole, que la seconde ne peut en produire que 2, etc., et que, de même, les puissances successives de 3 et des nombres suivants ne peuvent comporter (en nombres entiers) plus de rapports superpartiels de l'espèce correspondante, que l'on n'a multiplié de facteurs égaux pour former la puissance[10] ; il faudra donc employer la seconde puissance de 8 pour que l'on puisse prendre deux fois le rapport sesquioctave. Or la seconde puissance de 8 est 64 ; mais ce nombre n'est pas divisible par 3 ; afin de pouvoir obtenir un quatrième et dernier nombre qui soit au premier dans le rapport épitrite, je triple 64, de sorte que le résultat ait son huitième et son tiers exacts. J'obtiens ainsi 192, nombre dont le huitième est 24, et le tiers 64. Et, de même que la première puissance de 8, qui est 8 lui-même (soit que l'on prenne ce nombre une fois, deux fois, trois fois, etc., jusqu'à 7 fois), n'admettra jamais qu'un seul rapport sesquioctave, de même la seconde puissance de 8, ou 64, prise une fois, 2 fois, 3 fois, autant de fois que l'on voudra jusqu'à 7, ne produira jamais que deux rapports sesquioctaves. Or le nombre qui est à 192 dans le rapport sesquioctave est 216, et le nombre qui est à celui-ci dans le même rapport est 243 : car le huitième de 192 est 24, et 216 contient 192 tout entier, plus ce huitième 24 ; et, de même, le huitième de 216 est 27, et 243 contient 216 tout entier, plus ce huitième 27. Ainsi donc, après avoir établi à la suite du premier nombre deux rapports sesquioctaves, conformément à la question, je cherche un quatrième nombre qui soit au premier, comme il a été dit, dans le rapport épitrite. Ce nombre est 256 : car le tiers de 192 est 64, et 256 contient 192 tout entier, plus ce tiers 64. Par suite, l'excès du quatrième nombre 256 sur le troisième 243 est la valeur du demi-ton ; car nous avons dit que la quarte se composait de deux tous et un demi-ton, en conservant d'ailleurs le rapport épitrite. Ainsi donc je commence par placer l'un contre l'autre, et de suite, deux rapports sesquioctaves ; j'établis les extrêmes dans le rapport épitrite ; et aussitôt je vois apparaître, comme par enchantement, l'intervalle de demi-ton ; et en effet c'est bien là l'intervalle que présentera, si on les compare, les deux cordes ou les deux sons, intervalle mesuré par le rapport de 256 à 243, qui est approximativement, comme nous l'avons dit, celui de 17 à 16.

Maintenant, nous dirons que le système de quarte a été ainsi nommé, par la raison qu'il est composé de deux tons et un demi-ton, c'est-à-dire de quatre termes ou sons, composition qui, le mettant en quelque sorte à l'unisson des divers éléments dont l'âme est formée, est ainsi la cause des justes proportions de son harmonie. Une figure va rendre sensible ce crue nous disons.

 

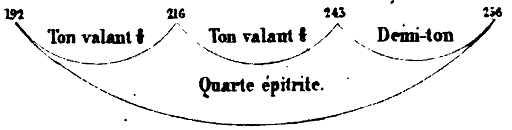
Telle est donc la quarte, le plus simple de tous les systèmes, bien que, l'intervalle étant le résultat d'une combinaison de deux sons, il semble que le système le plus simple dût être formé de trois sons ; or le tiers, d'où résulte le rapport épitrite, n'est pas la plus petite des parties, puisqu'il y en a d'autres plus petites, savoir :1e quart, le cinquième, et ainsi de suite jusqu'au huitième, d'où résulte le rapport sesquioctave, qui produit le ton. Mais il n'était pas possible que le système le plus simple fût le résultat de moins de quatre sons, ni d'un rapport plus petit que le rapport épitrite : car, en considérant deux tous seulement, et par conséquent trois sons, le troisième, comparé au premier, ne donne aucun des rapports superpartiels dont on a déjà parlé. En effet, soit 64 le nombre affecté au premier son ; le premier intervalle de ton pris à la suite du premier son nous donnera 72, et le second, pris de même à la suite du précédent, nous donnera 81, nombre qui n'a avec 64 aucun rapport superpartiel. Ce ne pourrait être, en effet, que le rapport sesquiquarte, puisque deux huitièmes font un quart, et que, par hypothèse, le système dont il s'agit est formé de deux tous, dont chacun est représenté par le rapport sesquioctave. Mais il est impossible que le rapport sesquiquarte soit celui de 81 à 64, puisqu'on ajoutant à 64 son quart, qui est 16, on obtient seulement 80. Or cela provient de ce que, comme on l'a dit, le chant est une grandeur continue, et que, par suite, les petites fractions dans lesquelles on le réduit ne peuvent jamais reproduire l'entier.[11] Dans l'arithmétique, en effet, un quart partagé se change en deux huitièmes, et un huitième en deux seizièmes ; mais, dans la musique, à cause de la nature continue de l'intervalle, le ton ne peut se partager en deux demi-tons, ni deux rapports sesquioctaves produire le rapport sesquiquarte (5 :4) ; et, après une semblable réduction en petites parties, soit dans la géométrie, soit dans l'astronomie par la même raison, on ne parvient jamais, par la multiplication, à un entier complet, mais seulement à quelque chose qui en diffère extrêmement peu : car une quantité, continue, partagée et divisée à l'infini, ne reproduira jamais un entier égal à ses parties. Vu donc qu'il n'était pas possible, avec trois sons seulement, de former un système, on a juxtaposé un quatrième son, en ajoutant une quantité suffisante pour que le nouveau son fût au troisième à peu près dans le rapport de 17 à 16 (ce, qui fait le demi-ton), et, au premier, dans le rapport épitrite ; et c'est ainsi que le premier et le plus simple des systèmes en musique est l'intervalle de quarte : car tel est le nom qu'on lui a donné.

Vient ensuite la quinte, qui n'est autre chose que la quarte augmentée d'un ton ; et c'est en conséquence qu'on l'a nommée quinte ; or voici comment elle est engendrée. Je cherche une puissance de 8, telle que je puisse la multiplier successivement 3 fois par le rapport de 9 à 8 qui représente le ton : cette puissance est la troisième, égale à 512. En effet, la première puissance est 8 ; la seconde, 8 fois 8, ou 64 ; la troisième, 8 fois 64, ou 512 ; or ce nombre, multiplié par le rapport sesquioctave, donne 576 ; celui-ci, multiplié de même, donne 648 ; et enfin celui-ci de même, 729, Ensuite, comme 729 n'est pas à 512 dans le rapport hémiole, je prends à la suite un cinquième nombre qui soit à 512 dans ce rapport, et, de plus, soit à une distance de demi-ton de 729 (distance qui, comme nous l'avons dit, n'est pas exactement la moitié du ton) ; et j'obtiens ainsi le nombre 768. Puis donc que la quinte, comparée à la quarte, n'est autre chose que celle-ci augmentée d'un ton, et que conséquemment elle se réalise en cinq cordes, c'est pour cette raison qu'on l'a nommée quinte. On peut encore, au moyen d'une figure, rendre tout cela plus clair.

Le diapason est composé de 8 cordes,[12] et c'est pourquoi on le nomme diapason ; car l'instrument le plus simple est un instrument à 8 cordes, et celui qui a un plus grand nombre de cordes comprend l'octocorde dans sa composition. C'est donc parce que le rapport double se trouve dans la totalité des cordes de cet instrument qu'on l'a nommé diapason. Or cette consonance se compose de cinq tous et deux demi-tons ; et on l'obtient comme il suit. Je cherche la cinquième puissance de 8, afin de pouvoir placer à la suite 5 rapports sesquioctaves, et j'obtiens 32768. En effet, la première puissance est 8, la deuxième 64, la troisième 512, la quatrième 4096, et la cinquième ledit nombre 32768. Or le nombre qui est à celui-ci dans le rapport sesquioctave, ou qui en est distant d'un ton, est 36864 ; puis le nombre qui est à ce dernier dans le même rapport est 41472 ; après celui-ci vient de même 46656 ; puis, après celui-ci, 52488 ; puis enfin, après ce dernier, 59049. Ensuite, multipliant par la valeur du demi-ton, on a 62208 ; puis, multipliant encore de même,[13] on a enfin 65536, qui est au nombre primitif 32768 dans le rapport double, Suit le tableau du tout.

D'autres expliquent autrement le diapason. Ils disent que la lyre ayant huit cordes (car toute mélodie se réduit essentiellement à 8 sons), on trouve en elle ces trois consonances, savoir : la quarte, la quinte, et le diapason ou l’octave. Or on peut donner une explication plus concluante et plus vraie que la précédente, en disant que le nom de diapason a été appliqué au système en question, par la raison qu'il est la réunion des deux autres systèmes, savoir la quarte et la quinte. Car nous avons dit que la quarte présente le rapport épi tri te, et la quinte le rapport bémiole ; or le rapport épitrite multiplié par le rapport hémiole donne le rapport double, comme aussi le rapport hémiole multiplié par le rapport épitrite. C'est ce qui arrive, par exemple, pour les nombres 2, 3, 4, dont les deux premiers présentent le rapport hémiole, les deux derniers le rapport épitrite, et les deux extrêmes le rapport double. Et l'on trouve constamment la même chose sur d'autres nombres pris comme on voudra.

Ainsi donc la réunion des deux systèmes de la quarte et de la quinte engendre le diapason, nom qui vient, sans aucun doute, de ce que, dans l'instrument, les cordes des deux systèmes indiqués, savoir, la quarte et la quinte, c'est-à-dire encore les rapports épitrite et hémiole, se trouvent mis en évidence ; et toute la musique est renfermée dans ces deux rapports qui sont les premiers en rang ; tous les autres ne viennent qu'à leur suite. Au reste, aucune des deux fractions ne doit passer avant l'autre, ni la moitié qui donne lieu au rapport hémiole, ni le tiers qui donne lieu au rapport épitrite, à moins pourtant que l'on ne croie devoir placer la moitié la première, à cause de son rang naturel. Mais si, en musique, on a mis au premier rang le tiers, fraction qui engendre le rapport épitrite et l'intervalle de quarte, il ne faut pas s'en étonner : car nous avons averti, en commençant, que c'était en allant du petit au grand que se classaient les intervalles mélodiques. Et quant à certains autres rapports qui contribuent également à la constitution de l'harmonie, comme le rapport de 9 à 8, le rapport de 2 à 1, ceux de 8 à 3, de 3 à 1, de 4 à 1, il faut observer que ces nouveaux rapports ne s'écartent pas des deux principaux dont nous avons parlé, mais qu'ils dérivent toujours, soit de la différence ou de l'excès mutuel de ces deux-ci, soit de leur mélange [par voie de multiplication]. Ainsi la différence du rapport hémiole au rapport épitrite, ou l'excès du premier sur le second, donne le rapport de 9 à 8 ; et leur réunion produit le rapport double, ou le rapport de 2 à 1. Ensuite, la réunion du rapport épitrite et du rapport double produit le rapport de 8 à 3 ; le rapport hémiole avec le rapport double donnent le rapport triple ; enfin, le rapport double avec lui-même donné le rapport quadruple, nommé aussi double-diapason ou double-octave.

Les figures suivantes vont rendre cela très clair.

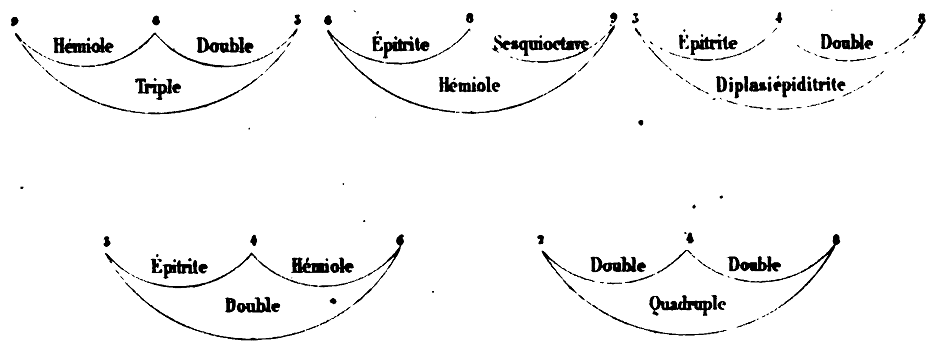
Il est donc démontré que les rapports les plus élémentaires et les premiers de l'harmonie sont ces deux-là, la quarte et la quinte ; que c'est en eux que repose, comme sur ses fondements, toute la mélodie musicale ; et qu'enfin c'est de leur réunion que résulte tout naturellement l'octave nommée aussi diapason. Aussi n'est-ce pas en ajoutant simplement un ton à la quinte que l'on obtient l'octave, de même qu'en ajoutant un ton à la quarte on avait produit la quinte ; non : il faut ajouter deux tous et un demi-ton, puisque l'octave se compose de 5 tons et 2 demi-tons : d'où il résulte bien clairement que l'octave est la réunion des deux intervalles. Et en effet la quarte se compose de 2 tons et 1 demi-ton, et la quinte de 3 tons et 1 demi-ton ; total 5 tons et 2 demi-tons, qui, comme nous l'avons dit, composent l'octave ; ce qui fait que, pour en calculer la valeur, nous avons dû dépasser le nombre 4096, qui n'est que la quatrième puissance de 8. Aussi sommes-nous partis du nombre 32768, comme pouvant donner lieu à cinq rapports successifs de 9 à 8, nécessaires pour reproduire l'octave.

Après l'octave vient la consonance d'octave et quarte (quarte redoublée), dont on a trouvé le rapport égal à celui de 8 à 3 ; or voici comment on l'obtient. Je prends une puissance de 8 qui puisse me donner sept rapports successifs de 9 à 8 : car il y en a 2 dans la quarte et 5 dans l'octave ; il y en aura donc 7 dans leur réunion : Or la 7^e puissance de 8 est 2097162 ; mais, comme ce nombre n'a pas son tiers exact, et que le nombre final doit être au premier dans le rapport de 8 à 3, je multiplie par 3, et il vient 6291456. Le nombre qui est avec celui-ci dans le rapport de 9 à 8 est 7077888 ; nous avons dans le même rapport avec ce dernier le nombre 7962624, puis avec celui-ci le nombre 8967952 [puis le nombre 10077696], puis le nombre 11337408, puis 12754584, puis enfin [14348907. Maintenant, la multiplication par le rapport de 256 à 243 donne 15116544 ; puis une seconde multiplication par le même rapport, 15925248 ; puis une troisième multiplication,[14] ] 16777216. Or ce nombre est au nombre primitif, 6291456, dans le rapport de 8 à 3, puisqu'il contient deux fois ce dernier, et deux fois son tiers en sus ; et quant au nombre 14348907, il le dépasse de 3 demi-tons, c’est-à-dire simplement de trois intervalles moindres qu'un ton chacun : car, que ces intervalles soient plus petits ou plus grands que la moitié véritable du ton, cela ne fait rien ; si on les appelle demi-tons, c'est seulement parce qu'il leur manque quelque chose pour valoir un ton.