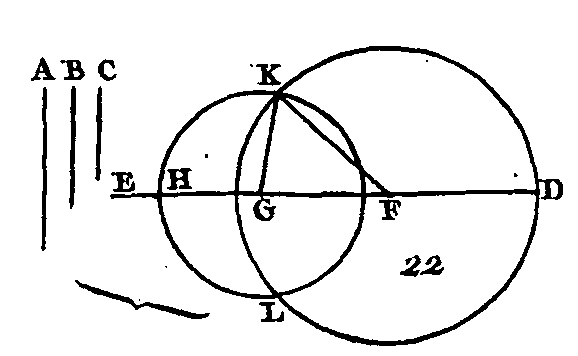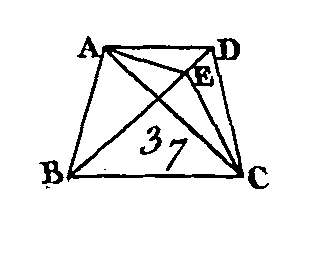INTRODUCTION - GÉOMÉTRIE LIVRE II

ÉLÉMENS

DE

GÉOMÉTRIE

D'EUCLIDE.

LIVRE PREMIER.

DÉFINITIONS.

1. Le point est ce qui n'a aucune partie.

2. La ligne est une longueur sans largeur.

3. Les extrémités d'une ligne sont des points.

4. La ligne droite est celle qui est également placée entre ses points.[1]

5. Une superficie est ce qui a longueur et largeur seulement.

6. Les extrémités d'une superficie sont des lignes.

7. Une superficie plane est celle qui est également placée entre ses lignes droites.

8. Un angle plan est l'inclinaison mutuelle de deux lignes qui se louchent dans un plan et qui ne sont point placées dans la même direction.

9. Lorsque des lignes droites comprennent un angle, l'angle s'appelle rectiligne.

10. Lorsqu'une droite tombant sur une droite fait les angles de suite égaux entre eux, chacun des angles égaux est droit. La droite tombante est dite perpendiculaire sur celle sur laquelle elle tombe.

11. L'angle obtus est celui qui est plus grand que l'angle droit.

12. L'angle aigu est celui qui est plus petit que l'angle droit.

13. On appelle terme ou limite ce qui est l'extrémité de quelque chose.

14. On appelle figure ce qui est compris entre une ou plusieurs limites.

15. Le cercle est une figure plane comprise dans une seule ligne qu'on appelle circonférence ; toutes les droites menées à la circonférence d'un seul point de ceux qui sont placés dans la figure, sont égales entre elles.

16. Ce point se nomme le centre du cercle.

17. Le diamètre du cercle est une droite menée par le centre et terminée de part et d'autre par la circonférence du cercle ; le diamètre partage le cercle en deux parties égales.

18. Un demi-cercle est une figure comprise entre le diamètre et la portion de la circonférence qui est sous-tendue par le diamètre.

19. Un segment de cercle est une portion du cercle comprise entre une droite et la circonférence du cercle.

20. Les figures rectilignes sont celles qui sont terminées par des droites.

21. On appelle trilatères ou triangles les figures terminées par trois droites.

22. Quadrilatères, celles qui sont terminées par quatre.

23. Multilatères, celles qui sont terminées par plus de quatre droites.

24. Parmi les figures trilatères, celle qui est terminée par trois côtés égaux se nomme triangle équilatéral.

25 Celle qui a seulement deux côtés égaux se nomme triangle isocèle.

26. Celle dont tous les côtés sont inégaux se nomme triangle scalène.

27. Parmi les figures trilatères, celle qui a un angle droit se nomme triangle rectangle.

28, Celle qui a un angle obtus se nomme triangle amblygone ou triangle obtusangle.

29. Celle qui a ses trois angles aigus, triangle oxygone ou triangle acutangle.

30. Parmi les figures quadrilatères, celle qui a ses côtés égaux et ses angles droits, se nomme carré.

31. Celle qui a ses angles droits, mais qui n'a pas ses côtés égaux, se nomme carré oblong ou rectangle.

32. Celle qui a ses côtés égaux, mais qui n'a pas ses angles droits, se, nomme rhombe.

33. Celle dont les côtés et les angles opposés sont égaux, mais dont tous les côtés ne sont pas égaux et dont les angles ne sont pas droits, se nomme rhomboïde.

34. Les autres quadrilatères, ceux-là exceptés, se nomment trapèzes.[2]

35. Enfin, les parallèles sont des droites qui, étant placées sur un même plan, et qui étant prolongées de part et d'autre à l'infini, ne se rencontrent nulle part.

DEMANDES.[3]

1. Conduire une droite d'un point quelconque à un point quelconque.

2. Prolonger continuellement, selon sa di rection, une droite finie.

3. D'un point quelconque et avec un inter valle quelconque décrire une circonférence de cercle.

Notions communes ou axiomes.

1. Les quantités qui sont égales aune même quantité sont égales entre elles.

2. Si à des quantités égales on ajoute des quantités égales, les tous seront égaux.

3. Si de quantités égales on retranche des quantités égales, les restes seront égaux.

4. Si à des quantités inégales on ajoute des quantités égales, les tous seront inégaux.

5. Si de quantités inégales on retranche des quantités égales, les restes seront inégaux.

6. Les quantités qui sont doubles d'une même quantité sont égales entre elles.

7. Les quantités qui sont les moitiés d'une même quantité sont égales entre elles.

8. Les choses qui se conviennent mutuellement sont égales entre elles.

9. Le tout est plus grand que sa partie.

10. Tous les angles droits sont égaux.[4]

11. Si une droite tombant sur deux droites fait les angles intérieurs du même côté plus petits que deux droits, les deux droites prolongées à l'infini se rencontreront du côté où les angles sont plus petits que deux droits.

12. Deux droites ne renferment point un espace.

PROPOSITION PREMIÈRE.

PROBLÈME.

Sur une droite donnée et finie, construire un triangle équilatéral.

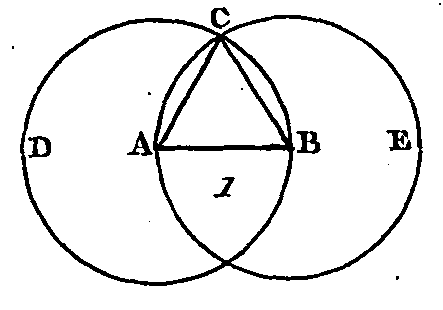
Soit AB (fig. 1) la droite donnée et finie : il faut construire sur la droite AB un triangle équilatéral.

Du centre A et avec un intervalle AB, décrivez la circonférence BCD (dem. 3); ensuite du centre B et avec l'intervalle BA décrivez la circonférence ACE, et du point C, où les circonférences se coupent mutuellement, conduisez aux points A, B, les droites CA, CB (dem. 1).

Car puisque le point A est le centre du cercle CDB, la droite AC sera égale à la droite AB (déf. 15); de plus, puisque le point B est le centre du cercle CAE, la droite BC sera égale à la droite BA; mais il a été démontré que la droite CA était égale à la droite AB : donc chacune des droites CA, CB est égale à la droite AB ; or les quantités qui sont égales à une même quantité sont égales entre elles ; donc la droite CA est égale à la droite CB : donc les trois droites CA, AB, BC sont égales entre elles.

Donc le triangle ABC (déf. 24) est équilatéral, et de plus il est construit sur la ligne donnée et finie AB; ce qu'il fallait faire.

PROPOSITION II.

PROBLÈME.

D'un point donné conduire une droite égale à une droite donnée.

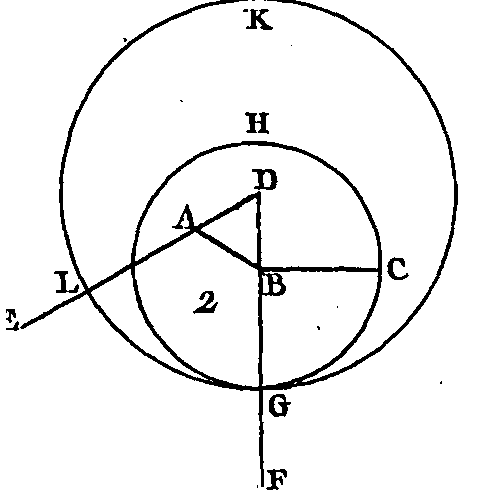
Soit A (fig. 2) le point donné et BC la droite donnée : il faut conduire du point A une droite égale à la droite BC.

Conduisez du point A au point B la droite AB (dem. 1) ; sur cette droite construisez le triangle équilatéral DAB (prop. 1), et prolongez les droites AE, BF dans la direction des côtés DA, DB ; du centre B et avec l'intervalle BC, décrivez la circonférence CGH (dem. 5); et du centre D et avec l'intervalle DG décrivez ensuite la circonférence GKL.

En effet, puisque le point B est le centre du cercle CGH, la droite BG sera égale à la droite BG (déf. 15) ; de plus, puisque le point D est le centre du cercle GKL, la droite DL sera égale à la droite DG ; mais la droite DA est égale à la droite DB : donc la droite AL sera égale à la droite BG (axiome 3) ; mais il a été démontré que la droite BC est égale à la droite BG : donc les droites AL, BC sont égales chacune à la droite BG. Mais les quantités qui sont égales à une même quantité sont égales entre elles : donc la droite AL est égale à la droite BC.

Donc du point donné B on a conduit une droite AL égale à la ligne donnée BC; ce qu'il fallait faire.

PROPOSITION III.

PROBLÈME.

Deux droites inégales étant données, retrancher de la plus grande une droite égale à la plus petite.

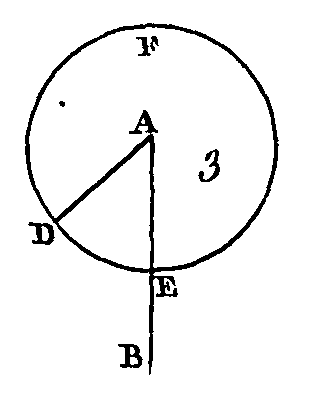
Soient AB et C (fig. 3) les deux droites inégales données dont la plus grande soit AB : il faut de la plus grande AB retrancher une droite qui soit égale à la plus petite C.

Du point A conduisez une droite AD égale à la droite C (prop. 2), et du centre A et avec un intervalle AD décrivez la circonférence DEF (dem. 3).

Puisque le point A est le centre du cercle DEF, la droite AE sera égale à la droite AD ; mais la droite C est égale à la droite AD : donc les deux droites AE, C sont égales chacune à la droite AD : donc la droite AE est égale à la droite C.

Donc les deux droites inégales AB, C ayant été données, il a été retranché de la plus grande AB une droite AE égale à la plus petite C ; ce qu'il fallait faire.

PROPOSITION IV.

THÉORÈME.

Si deux côtés d'un triangle sont égaux à deux côtés d'un autre triangle chacun à chacun, et si l’angle compris entre les côtés égaux est égal dans les deux triangles, la base de l'un sera égale à la base de l'autre; ces deux triangles seront égaux, et les autres angles compris entre les côtés égaux de ces deux triangles seront aussi égaux entre eux.

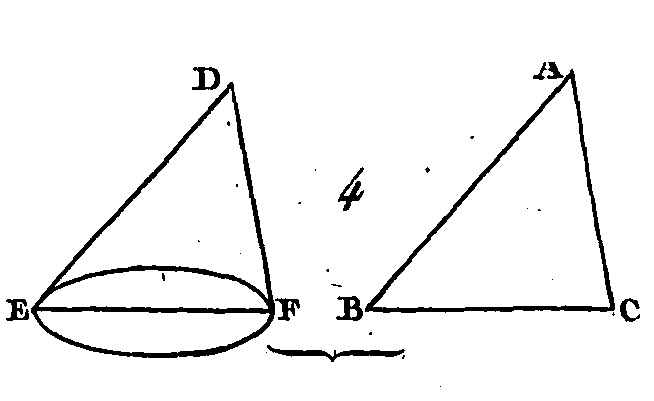
Soient les deux triangles ABC, DEF (fig. 4) dont les deux côtés AB, AC sont égaux aux deux côtés DE, DF chacun à chacun, savoir, le côté AB égal au côté DE, et le côté AC au côté DF ; que l'angle BAC soit aussi égal à l'angle EDF : je dis que la base BC est égale à la base EF, que le triangle ABC est égal au triangle DEF, et que les autres angles compris entre les côtés égaux de ces deux triangles sont aussi égaux chacun à chacun; l'angle ABC égal à l'angle DEF, et l'angle ACB égal à l'angle DFE.

Car si le triangle ABC est appliqué sur le triangle DEF, le point A étant posé sur le point D, la droite AB sur la droite DE, le point B tombera sur le point E, parce que la droite AB est égale à la droite DE ; mais la droite AB s'appliquant exactement sur la droite DE, la droite AG s'appliquera de même exactement sur la droite DF, parce que l'angle BAC est égal à l'angle EDF ; le point C tombera sur le point F, parce que la ligne AC est égale à la ligne DF ; mais le point B tombe sur le point E : donc la base BC est égale à la base EF, car si le point B tombant sur le point E, et le point C sur le point F, la base BG ne s'applique pas exactement sur la base EF, il faut nécessairement que deux lignes droites comprennent un espace, ce qui est impossible (axiome 12) ; donc la base BC s'appliquera exactement sur la base EF, et lui sera égale ; donc aussi le triangle entier ABC s'appliquera exactement sur le triangle entier DEF et lui sera égale. Par conséquent les autres angles de l'un des triangles s'appliqueront exactement sur les autres angles de l'autre triangle et seront par conséquent égaux aussi entre eux ; c'est-à-dire l'angle ABC sera égal l'angle DEF, et l'angle ACB égal à l'angle DFE.

Donc si deux côtés d'un triangle sont égaux à deux côtés d'un autre triangle chacun à chacun, et si l’angle compris entre les côtés égaux est égal dans les deux triangles, la base de l'un sera égale à la base de l'autre ; ces deux triangles seront égaux, et les autres angles compris entre les côtés égaux des deux triangles seront aussi égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION V.

THÉORÈME.

Dans les triangles isocèles les angles placés sur la base sont égaux entre eux et les côtés égaux étant prolongés, les angles placés au-dessous de la base seront aussi égaux entre eux.

Soit le triangle isocèle ABC (fig. 5) dont le côté AB est égal au côté AC; prolongez les droites AB, AC, vers D et vers E (dem. 2) : je dis que l'angle ABC est égal à l'angle ACB et que l'angle CBD est encore égal à l'angle BCE.

Car prenons sur la droite BD un point quelconque F, et de la droite AE retranchons la droite AG égale à la droite AF, qui est plus petite que la droite AE (prop. 3), et conduisons les droites FC et GB.

Puisque la droite AF est égale à la droite AG et la droite AB à la droite AC, les deux droites FA, CA seront égales aux deux droites GA, BA chacune à chacune ; mais ces droites comprennent l'angle commun FAG: donc (prop. 4) la base FC sera égale à la base GB ; le triangle AFG sera égal au triangle AGB et les autres angles compris entre les côtés égaux de ces deux triangles seront aussi égaux entre eux, c'est-à-dire, l'angle ACF égal à l'angle ABG, et l'angle AFC à l'angle AGB ; mais comme la droite AF est égale à la droite AG et la droite AB à la droite AC, la droite BF égalera la droite CG (axiome 5), mais il a été démontré que la droite FC est égale à la droite GB : donc les deux droites BF, FC sont égales aux droites CG, GB chacune à chacune; mais l'angle BFC est égal à l'angle CGB et la droite BC est la base commune de ces deux triangles : donc le triangle BFC sera égal au triangle CGB et les autres angles compris entre les côtés égaux de ces deux triangles seront aussi égaux chacun à chacun (prop. 4) donc l'angle FBC est égal à l'angle GCB, et l'angle BCF égal aussi à l'angle CBG. Mais comme il a été démontré que l'angle total ABG était égal à l'angle total ACF et que l'angle CBG était aussi égal à l'angle BCF, l'angle restant ABC (axiome 3) et l'angle restant ACB placés sur la base seront égaux. Il a été démontré aussi que les angles FBC et GCB placés au-dessous de la base étaient aussi égaux.

Donc dans les triangles isocèles les angles placés sur la base sont égaux entre eux, et les côtés égaux étant prolongés, les angles placés au-dessous de la base seront aussi égaux entre eux; ce qu'il fallait démontrer.

PROPOSITION VI.

THÉORÈME.

Si deux angles d'un triangle sont égaux entre eux, les côtés opposés à ces angles égaux seront aussi égaux entre eux.

Soit le triangle ABC (fig. 6) ayant l'angle ABC égal à l'angle ACB : je dis que le côté AC est égal au côté AB.

Car si le côté AC n'est pas égal au côté AB, l'un d'eux sera plus grand que l'autre. Soit AB le plus grand ; retranchez de AB qui est le plus grand côté (prop. 3) la droite DB égal au plus petit côté AC, et menez la droite DC.

Puisque la droite DB est égale à la droite AC, et que la droite BG est le côté commun, les deux droites DB, BC sont, égales aux deux droites AC, CB chacune à chacune ; mais l'angle DBC est égal à l'angle ACB : donc la base DC est égale à la base AB et le triangle ABC égal au triangle DCB ; c'est-à-dire que le plus grand est égal au plus petit : ce qui est absurde. Donc la droite AB n'est pas plus grande que la droite AG, donc elle lui est égale.

Donc si deux angles d'un triangle sont égaux entre eux, les côtés opposés aux angles égaux seront aussi égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION VII.

THÉORÈME.

Ayant conduit par les extrémités d'une droite deux droites qui se rencontrent, il est impossible de mener des mêmes extrémités deux autres droites qui leur soient égales chacune à chacune, si le point où se rencontrent les deux dernières droites est placé du même côté et s’il n'est pas le même que celui où se rencontrent les deux premières.

Supposons qu'il soit possible de conduire par les extrémités A, B de la droite AB (fig. 7), deux droites AD, DB égales chacune à chacune à deux autres droites AC, CB conduites aussi par les mêmes extrémités A, B et se rencontrant au point C qui est placé du même côté et qui n'est pas le même que celui où se rencontrent les deux droites AD, DB, de manière que les deux droites CA, DA partant de la même extrémité A soient égales entre elles, et que les deux droites CB, DB partant de la même extrémité B soient aussi égales entre elles ; conduisez la droite CD.

Puis donc que la droite AC est égale à la droite AD, l'angle ACD est égal à l'angle ADG (prop. 5) ; d'où il suit que l’angle ADC est plus grand que l'angle DCB, et que l'angle CDB est beaucoup plus grand que DCB; de plus puisque la droite CB est égale à la droite DB, l'angle CDB sera égal à l'angle DCB; mais il a été démontré qu'il est beaucoup plus grand, ce qui est impossible.

Donc ayant conduit par les extrémités d'une droite deux droites qui se rencontrent, il est impossible de conduire par les mêmes extrémités deux autres droites qui leur soient égales chacune à chacune, lorsque le point où se rencontrent ces deux dernières droites est placé du même côté et qu’il n'est pas le même que celui où se rencontrent les deux premières ; ce qu'il fallait démontrer.

PROPOSITION VIII.

THÉORÈME.

Si deux côtés d'un triangle sont égaux à deux côtés d'un autre triangle, chacun à chacun, et si la base de l'un est égale à la base de l'autre, l’angle compris entre les côtés égaux est égal dans les deux triangles.

Soient les deux triangles ABC, DEF (fig. 8) ayant les deux côtés AB, AC égaux aux côtés DE, DF, chacun à chacun, c'est-à-dire le côté AB égal au côté DE, et le côté, AG égal au côté DF ; que la base BC soit aussi égale à la base EF; je dis que l'angle BAC est égal à l'angle EDF.

Car si le triangle ABC est appliqué sur le triangle DEF, le point B sur le point E, et la droite BC sur la droite EF, le point C tombera sur le point F, parce que la droite BC est égale à la droite EF. La droite BC s'appliquant exactement sur la droite EF, les droites BA, AC s'appliqueront exactement sur les droites DE, DF : car si la base BC s'appliquant exactement sur la base EF, les côtés BA, AC ne s'appliquaient pas exactement sur les côtés DE, DF, et prenaient une autre position comme EG, GF, il serait possible, après avoir conduit par les extrémités d'une droite deux droites qui se rencontrent, de mener par les mêmes extrémités deux autres droites qui leur seraient égales chacune à chacune, lors même que le point où se rencontraient les deux dernières serait placé du même côté et ne serait pas le même que celui où se rencontrent les deux premières ; mais cela est impossible (prop. 7) : donc la base BC s'appliquant exactement sur la base EF, il est impossible que les côtés AB, AC ne s'appliquent pas exactement sur les côtés ED, DF : donc ils s'appliquent exactement les uns sur les autres : donc l'angle BAC s'applique exactement sur l'angle EDF : donc il lui est égal.

Si donc deux côtés d'un triangle sont égaux à deux côtés d'un autre triangle, chacun à chacun, et si la base de l'un est égale à la base de l'autre, l’angle compris entre les côtés égaux est égal dans les deux triangles ; ce qu'il fallait démontrer.

PROPOSITION IX.

PROBLÈME.

Partager un angle rectiligne donné en deux parties égales.

Soit BAC (fig. 9) l'angle rectiligne donné: il faut le partager en deux parties égales.

Prenez sur la droite AB un point quelconque D, retranchez de la droite AC la droite AE égale à la droite AD (prop. 3), conduisez la droite DE, sur la droite DE construisez le triangle équilatéral DEF (prop. 1), et conduisez la droite AF : je dis que l’angle BAC est partagé en deux parties égales par la droite AF.

Puisque la droite AD est égale à la droite AE et que la droite AF est commune, les deux droites DA, AF seront égales aux deux droites EA, AF, chacune à chacune ; mais la base DF est égale à la base EF : donc l'angle DAF est égal à l'angle EAF (prop. 8) : donc l'angle rectiligne donné BAC est partagé en deux parties égales par la ligne AF ; ce qu'il fallait faire.

PROPOSITION X.

PROBLÈME.

Partager une droite donnée et finie en deux parties égales.

Soit AB (fig. 10) la droite donnée et finie : il faut partager cette droite AB en deux parties égales.

Construisez sur cette ligne un triangle équilatéral ABC (prop. 1), et partagez l'angle ACB en deux parties égales (prop. 9) ; je dis que la droite AB est partagée en deux parties égales au point D.

Car puisque la droite AC est égale à la droite CB, et que la droite CD est commune, les deux droites AC, CD sont égales aux deux droites BC, CD, chacune à chacune ; mais l'angle ACD est égal à l'angle BCD : donc la base AD est égale à la base BD (prop. 4).

Donc la droite donnée et finie AB est partagée en deux parties égales au point D ; ce qu'il fallait faire.

PROPOSITION XI.

PROBLÈME.

Sur une droite donnée et d'un point donné dans cette ligne, conduire une droite qui fasse deux angles droits avec la droite donnée.

Soit AB (fig. 11) la droite donnée et C le point donné dans cette droite : il faut par le, point C conduire sur la droite AB une droite qui fasse deux angles droits.

Prenez dans la ligne AC un point quelconque D, faites CE égale à CD (prop. 3), construisez sur la droite DE un triangle équilatéral FDE (prop. 1), et menez la droite FG : je dis que la droite CF, conduite par le point C, sur la droite donnée AB, fait deux angles droits avec elle.

Car puisque la droite CD est égale à la droite CE et que la droite FC est commune, les deux droites DC, CF sont égales aux deux droites EC, CF, chacune à chacune; mais la base DF est égale à la base EF : donc l'angle DCF est égal à l'angle ECF (prop. 8). Or ces deux angles sont de suite ; mais quand une droite fait avec une autre les angles de suite égaux entre eux, chacun des angles égaux est droit (déf. 10) : donc chacun des angles DCF, FCE est droit.

Donc la droite FC, conduite par le point G sur la droite AB, fait deux angles droits avec la droite AB ; ce qu'il fallait faire.

PROPOSITION XII.

PROBLÈME.

Sur une droite donnée et indéfinie et d'un point placé hors d'elle, mener une perpendiculaire.

Soit AB (fig. 12) la droite donnée et indéfinie, et C le point donné placé hors de cette droite : il faut sur cette droite donnée et indéfinie AB, conduire du point donné C, pris hors de cette droite, une droite perpendiculaire.

Prenez de l'autre côté de la droite AB un point quelconque D, et du centre C et avec un intervalle CD décrivez une circonférence EFG (dem. 3), partagez la droite EG en deux parties égales au point H (prop. 10), et conduisez les droites CG, CH, CE : je dis que sur la droite indéfinie AB et du point donné C placé hors de cette droite on a mené une perpendiculaire CH.

Car puisque la droite GH est égale à la droite HE, et que la droite CH est commune, les deux droites GH, HC sont égales aux deux droites EH, HC, chacune à chacune ; mais la base CG est aussi égale à la base CE (déf. 15) : donc l'angle GHG est égal à l'angle EHC (prop. 8). Or ces deux angles sont de suite ; mais lorsqu'une droite tombant sur une droite fait avec elle les angles de suite égaux entre eux, chacun de ces angles est droit, et la droite tombante est dite perpendiculaire à celle sur laquelle elle tombe.

Donc on a conduit une perpendiculaire CH sur la droite indéfinie AB, du point donné C, qui est placé hors de cette droite ; ce qu'il fallait faire.

PROPOSITION XIII.

THÉORÈME.

Si une droite placée sur une autre droite fait des angles, elle fera avec elle ou deux angles droits ou deux angles égaux à deux angles droits.

Qu'une droite quelconque AB (fig. 13) placée sur une droite DC fasse les angles CBA, ABD : je dis que les angles CBA, ABD ou seront droits ou égaux à deux droits.

Car si l'angle CBA est égal à l'angle ABD, ces deux angles seront droits (déf. 10). Si le contraire arrive, du point B conduisez la droite BE de manière qu'elle fasse deux angles droits avec la droite DC (prop. 11). Puisque l'angle CBE est égal aux deux angles CBA, ABE, si on ajoute un angle commun EBD, les angles CBE, EBD seront égaux aux trois angles CBA, ABE, EBD. De plus, comme l'angle DBA est égal aux deux angles DBE, EBA, si on ajoute un angle commun ABC, les angles DBA, ABC seront égaux aux trois angles DBE, EBA, ABC ; or il a été démontré que les angles CBE, EBD sont aussi égaux à ces trois angles : donc puisque les choses qui sont égales à une même chose sont égales entre elles, les angles CBE, EBD seront égaux aux angles DBA, ABC; mais les angles CBE, EBD sont deux angles droits ; donc les angles DBA, ABC sont égaux à deux angles droits.

Donc si une droite placée sur une autre droite forme des angles, elle fera ou deux angles droits ou deux angles égaux à deux droits; ce qu'il fallait démontrer.

PROPOSITION XIV.

THÉORÈME.

Si dans un point quelconque d'une ligne droite, deux droites placées de différents côtés font avec elle deux angles de suite égaux à deux droits, ces deux droites seront dans la même direction, c'est-à-dire qu'elles ne formeront qu'une seule et même droite.

Que dans un point B (fig. 14) de la ligne droite ÀB les deux droites BC, BD placées de différents côtés fassent avec elle les angles de suite ABC, ABD égaux à deux droits : je dis que la droite BD est dans la direction de la droite CB.

Car si la droite BD n'est point dans la direction de la droite BC, supposons que la droite BE soit dans la direction de la droite BC (dem. 2).

Puis donc que la droite AB est placée sur la droite CBE, les angles ABC, ABE seront égaux à deux droits (prop. 13) ; mais les angles ABC, ABD sont égaux à deux droits par supposition : donc les angles CBA, ABE sont égaux, aux angles CBA, ABD. Otez l'angle commun ABC, l'angle restant ABE sera égal à l'angle restant ABD, c'est-à-dire que le plus petit sera égal au plus, grand ; ce qui est impossible. La droite BE n'est donc pas dans la direction de la droite BC. Nous démontrerons de la même manière qu'il n'y en a point d'autre qui soit dans la direction de BC, si ce n'est BD. Donc la droite CB est dans la direction BD.

Donc si dans un point quelconque d'une ligne droite, deux droites placées de différents côtés font avec elle deux angles de suite égaux à deux droits, ces deux droits seront dans la même direction ; ce qu'il fallait démontrer.

PROPOSITION XV.

THÉORÈME.

Si deux droites se coupent mutuellement, elles font les angles au sommet égaux entre eux.

Que les deux droites AB, CD (fig. 15) se coupent mutuellement au point E : je dis que l'angle AEC est égal à l'angle DEB, et l'angle CEB égal à l'angle AED,

Car puisque la droite AE est placée sur la droite CD, faisant les deux angles CEA, AED, les angles CEA, AED sont égaux à deux droits (prop. 15). De plus, puisque la droite DE est placée sur la droite AB ; faisant les deux angles AED, DEB, les angles AED, DEB sont égaux à deux droits (prop. 13). Mais il a été démontré que les angles CEA, AED sont égaux à deux droits : donc les angles CE A, AED sont égaux aux angles AED, DEB. Retranchez l'angle commun AED, l'angle restant CEA égalera l'angle restant BED. On démontrera de la même manière que les angles CEB, DEA sont égaux entre eux.

Donc si deux droites se coupent mutuellement, elles feront les angles au sommet égaux entre eux ; ce qu'il fallait démontrer.

COROLLAIRE.

De là il suit manifestement que quel que soit le nombre des lignes qui se coupent en un point, les angles au point de section sont égaux à quatre angles droits.

PROPOSITION XVI.

THÉORÈME.

Ayant prolongé un côté d'un triangle quelconque, l'angle extérieur est plus grand que chacun des angles intérieurs et opposés.

Soit le triangle ABC (fig. 16), prolongez le côté BC jusqu'en D : je dis que l'angle extérieur ACD est plus grand que chacun des angles intérieurs et opposés CBA, BAC.

Partagez la droite AC en deux parties égales en E (prop. 10) ; et après avoir conduit la droite BE, prolongez-la vers le point F, faites la droite EF égale à la droite BE (prop. 3), conduisez la droite FG et prolongez AC jusqu'en G.

Puisque la droite AE est égale à la droite EC et la droite BE égale aussi à la droite EF, les deux droites AE, EB seront égales aux deux droites CE, EF ; chacune à chacune ; l'angle AEB est égal à l'angle FEC (prop. 15), puisqu'ils sont opposés au sommet ; donc la base AB est égale à la base FC (prop. 4) ; le triangle ABE est égal au triangle FEC, et les angles opposés à des côtés égaux sont égaux chacun à chacun : donc l'angle BAE est égal à l'angle ECF (ax. 9) ; mais l'angle ECD est plus grand que l'angle ECF : donc l'angle ACD est plus grand que l’angle BAE. Si on partage le côté BC en deux parties égales, on démontrera de la même manière que l'angle BCG, c'est-si-dire l'angle ACD (prop. 15), est plus grand que l'angle ABC.

Donc, ayant prolongé un côté d'un triangle quelconque, l'angle extérieur est plus grand que chacun des angles intérieurs et opposés ; ce qu'il fallait démontrer.

PROPOSITION XVII.

THÉORÈME.

Deux angles d'un triangle quelconque, de quelque manière qu'ils soient pris, sont moindres que deux droits.

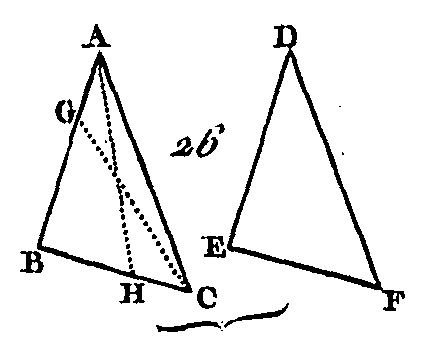
Soit le triangle ABC (fig. 17) : je dis que deux angles du triangle ABC, de quelque manière qu'ils soient pris, sont moindres que deux droits. Prolongez la droite BC jusqu'en D (dem. 2). L'angle extérieur ACD du triangle ABC est plus grand que l'angle intérieur et opposé ABC (prop. 16). Donc si nous ajoutons un angle commun ACB, les angles ACD, ACB seront plus grands que les angles ABC, BCA; mais les angles ACD, ACB sont égaux à deux droits. (prop. 13) : donc les angles ABC, BCA sont moindres que deux droits. On démontrera de la même manière que les angles BAC, ACB sont aussi moindres que deux droits; on démontrera encore la même chose par rapport aux angles CAB, ABC.

Donc deux angles d'un triangle quelconque, de quelque manière qu'ils soient pris, sont moindres que deux angles droits, ce qu'il fallait démontrer.

PROPOSITION XVIII.

THÉORÈME.

Dans tout triangle, un plus grand côté est opposé à un plus grand angle.

Soit le triangle ABC (fig. 18) ayant le côté AC plus grand que le côté AB : je dis que l'angle ABC est plus grand que l'angle BCA.

Puisque le côté AC est plus grand que le côté AB, faites la droite AD égale au côté AB (prop. 3), et conduisez la ligne BD.

L'angle ADB, qui est un angle extérieur du triangle BDC, est plus grand que l'angle intérieur et opposé DCB (prop. 16); mais l'angle ADB est égal à l'angle ABD (prop. 5), parce que le côté AB est égal au côté AD : donc l'angle ABD est plus grand que l’angle ACB : donc l'angle ABC est beaucoup plus grand que l'angle ACB.

Donc dans un triangle quelconque, un plus grand côté est opposé à un plus grand angle, ce qu'il fallait démontrer.

PROPOSITION XIX.

THÉORÈME.

Dans tout triangle, un plus grand angle est opposé à un plus grand coté.

Soit le triangle ABC (fig. 19) ayant l'angle ABC plus grand que l'angle BCA : je dis que le côté AC est plus grand que le côté AB.

Car s'il n'est pas plus grand, le côté AC est égal au côté AB, ou bien il est plus petit. Or le côté AC n'est pas égal au côté AB, car alors l'angle ABC serait égal à l'angle ACB (prop. 5) ; or l'angle ABC n'est point égal à l'angle ACB : donc le côté AC ne sera pas égal au côté AB. Le côté AC n'est pas plus petit que le côté AB, car alors l'angle ABC serait plus petit que l'angle ACB (prop. 18); or l'angle ABC n'est pas plus petit que l'angle ACB ; donc le côté AC ne sera pas plus petit que le côté AB. Mais il a été démontré qu'il ne lui est pas égal : donc le côté AC est plus grand que le côté AB.

Donc dans un triangle quelconque, un plus grand angle est opposé à un plus grand côté ; ce qu'il fallait démontrer.

PROPOSITION XX.

THÉORÈME.

Deux cotés d'un triangle quelconque, de quelque manière qu'ils soient pris sont plus grands que le côté restant.

Car soit le triangle ABC (fig. 20) : je dis que deux côtés du triangle ABC, de quelque manière qu'ils soient pris, sont plus grands que le côté restant ; c'est-à-dire que les côtés BA, AC sont plus grands que le côté BC ; les côtés AB, BC plus grands que le côté AC, et les côtés BC, CA plus grands que le côté AB.

Prolongez le côté AB vers le point D, faites la droite DA égale à la droite CA (prop. 3), et conduisez la droite DC.

Puisque la droite DA est égale à la droite AC, l'angle ADC sera égal à l'angle ACD (prop. 5) ; mais l'angle BCD est plus grand que l'angle ACD (ax. 9) ; donc l'angle BCD est plus grand que l’angle ADC : donc, puisque dans le triangle DCB, l'angle BCD est plus grand que l'angle BDC, et qu'un plus grand côté est opposé à un plus grand angle (prop. 19), le côté DB sera plus grand que le côté BC ; mais la droite DB est égale aux côtés AB, AC; donc les côtés AB, AC sont plus grands que le côté BC. Nous démontrerons de la même manière que les côtés AB, BC sont plus grands que le côté CA, et les côtés BC, CA plus grands que le côté AB.

Donc deux côtés d'un triangle quelconque, de quelque manière qu'ils soient pris, sont plus grands que le côté restant ; ce qu'il fallait démontrer.

PROPOSITION XXI.

THÉORÈME.

Si des extrémités d'un côté d'un triangle on mène deux droites qui se rencontrent dans ce triangle, ces deux droites seront plus courtes que les deux autres cotés du triangle, mais elles comprendront un angle plus grand.

Des extrémités B, C (fig. 21) du côté BC, menez en dedans du triangle ABC les deux droites BD, DC : je dis que les droites BD, DC seront plus petites que les deux autres côtés BA, AC du triangle ABC, et qu’elles comprendront un angle BDC plus grand que l'angle BAC.

Prolongez la droite BD jusqu'au point E.

Puisque deux côtés d'un triangle quelconque sont plus grands que le côté restant (prop. 20), les deux côtés AB, AE du triangle ABE sont plus grands que le côté BE. Donc si nous ajoutons une droite commune EC, les côtés BA, AG seront plus grands que les droites BE, EG. De plus, puisque les deux côtés CE, ED du triangle CED sont plus grands que le côté CD, si nous ajoutons une droite commune DB, les droites CE, EB seront plus grandes que les droites CD, DB ; mais on a démontré que les côtés BA, AC sont plus grands que les droites BE, EC : donc les côtés BA, AC sont beaucoup plus grands que les côtés BD, DC.

Mais comme un angle extérieur d'un triangle quelconque est plus grand qu'un des angles intérieurs et opposés (prop. 16), l'angle BDC, qui est un angle extérieur du triangle CDE, est plus grand que l'angle CED. Par la même raison l'angle CEB, qui est un angle extérieur du triangle ABE, est plus grand que l'angle BAC ; mais il a été démontré que l'angle BDG est plus grand que l'angle CEB : donc l'angle BDC est beaucoup plus grand que l'angle BAC.

Donc si des extrémités d'un côté d'un triangle quelconque on mène deux droites qui se rencontrent dans ce triangle, ces deux droites seront plus petites que les deux autres côtés du triangle, et elles comprendront un plus grand angle ; ce qu'il fallait démontrer.

PROPOSITION XXII.

PROBLÈME.

Avec trois droites égales à trois droites données construire un triangle ; il faut que deux de ces trois droites, de quelque manière qu'elles soient prises, soient plus grandes que la troisième.

Soient données les trois droites A, B, C (fig. 22), dont deux, de quelque manière qu'on les prenne, soient plus grandes que la troisième ; c'est-à-dire les droites A, B plus grandes que la droite C, les droites A et C plus grandes que B, et enfin les droites B et C plus grandes que A : il faut avec trois droites égales aux droites A, B, C construire un triangle.

Supposons la droite DE terminée en D et indéfinie vers E ; faites la droite DF égale à la droite A (prop. 3), la droite FG égale à la droite B et la droite GH égale à la droite C ; ensuite du centre F et avec l'intervalle FD, décrivez la circonférence DKL (dem. 5), du centre G avec l'intervalle GH décrivez la circonférence KLH, et conduisez les droites KF, KG : je dis que le triangle KFG est construit avec trois droites égales aux droites A, B, C.

Car puisque le point F est le centre du cercle DKL, la droite FK est égale à la droite FD (déf. 15) ; mais la droite FD est égale à la droite A : donc la droite KF égale la droite A. De plus, puisque le point G est le centre du cercle LKH, la droite GH est égale à la droite GR; mais la droite GH est égale à la droite C : donc la droite KG égale la droite C ; or la droite KG est égale à la droite B : donc les trois droites KF, FG, GK égalent les trois droites A, B, C. Donc le triangle KFG a été construit avec trois droites KF, FG, GK qui sont égales aux trois droites données A, B, C ; ce qu'il fallait faire.

PROPOSITION XXIII.

PROBLÈME.

Sur une droite donnée et à un point donné dans cette droite, construire un angle égal à un angle donné.

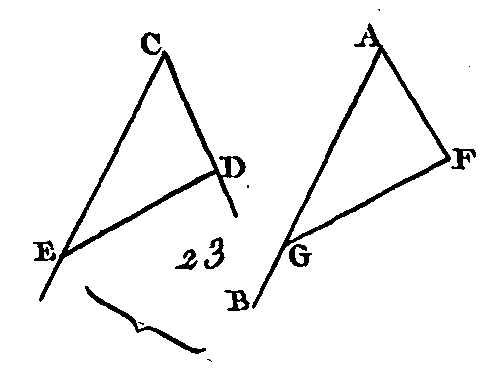
Soit AB (fig. 23) la droite donnée et A le point donné dans cette droite; que DCE soit l'angle donné : il faut sur la droite donnée AB et au point donné A construire un angle rectiligne égal à l'angle rectiligne donné DCE.

Soient pris dans Tune et l'autre ligne CD, CE deux points quelconque D, E ; conduisez la droite DE, et avec trois droites égales aux droites CD, DE, CE, construisez le triangle AFG (prop. 22), de manière que la droite CD soit égale à la droite AF, la droite CE égale à la droite AG, et la droite DE égale à la droite FG.

Puisque les deux droites DC, CE sont égales aux deux droites FA, AG, chacune à chacune, et que la base DE est égale à la base FG, l'angle DCE sera égal à l'angle FAG (prop. 8).

Donc l'angle rectiligne FAG a été construit égal à l'angle rectiligne DCE sur la droite donnée AB, et au point donné A dans cette droite.

PROPOSITION XXIV.

THÉOREME.

Si deux triangles ont deux côtés égaux à deux côtés, chacun à chacun, et si l'un des angles compris entre ces côtés égaux est plus grand que l'autre, la base de l'un de ces triangles sera aussi plus grande que la base de l'autre.

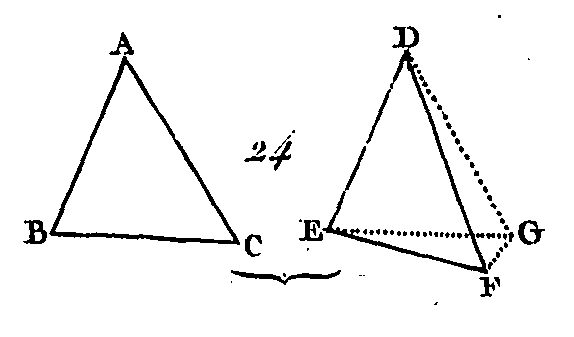
Soient les deux triangles ABC, DEF (fig. 24) dont les deux côtés AB, AC sont égaux aux deux côtés. DE, DF, chacun à chacun, c'est-à-dire le côté AB égal au côté DE et le côté AG au côté DF ; que l'angle BAC soit plus grand que l'angle EDF : je dis que la basé BC est plus grande que la base EF.

Car puisque l'angle BAC est plus grand que l'angle EDF, construisez sur la droite DE et au point D un angle EDG égal à l'angle BAC (prop. 25) ; faites la droite DG égale à l'une ou à l'autre des droites AC, DF (prop. 3), et conduisez les droites GE, FG.

Puisque la droite AB est égale à la droite DE, et la droite AC égale à la droite DG, les deux droites BA, AC seront égales aux deux droites ED, DG, chacune à chacune ; mais l'angle BAC est égal par construction à l'angle EDG: donc la base BC sera égale à la base EG (prop. 4). De plus, puisque la droite DG est égale à la droite DF, et l'angle DFG sera égal à l'angle DGF (prop. 5), donc l'angle DFG sera plus grand que l'angle EGF : donc l'angle EFG sera beaucoup plus grand que l'angle EGF ; mais puisque l'angle EFG du triangle EFG est plus grand que l'angle EGF, et qu'un angle plus grand est opposé à un côté plus grand (prop. 19), le côté EG est plus grand que le côté EF; mais le côté EG est égal au côté BC par construction : donc le côté BC est plus grand que le côté EF.

Donc si deux triangles ont deux côtés égaux à deux côtés, chacun à chacun, et si l'un des angles compris entre ces côtés égaux est plus grand que l'autre, la base de l'un de ces triangles sera plus grande que la base de l'autre.

PROPOSITION XXV.

THÉORÈME.

Si deux triangles ont deux côtés égaux chacun à chacun, et si la base de l'un est plus grande que la base de l'autre, ils auront aussi les angles compris entre les côtés égaux plus grands l'un que l'autre.

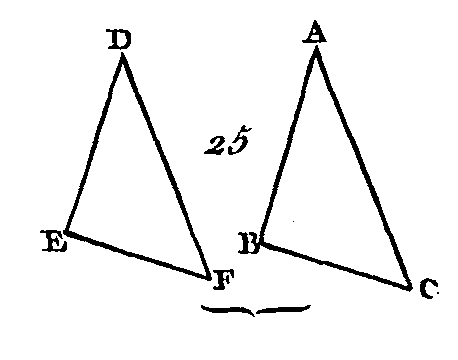
Soient ABC, DEF (fig. 25) deux triangles qui aient les deux côtés AB, AC égaux aux deux côtés DE, DF, chacun à chacun, c'est-à-dire le côté AB égal au côté DE, et le côté AC égal au côté DF; que la base BC soit plus grande que la base EF : je dis que l'angle BAC est plus grand que EDF.

Car si l'angle BAC n'est pas plus grand que l'angle EDF, il lui est égal, ou il est plus petit ; or l'angle BAC n'est pas égal à l'angle EDF, car alors la base B C serait égale à la base EF (prop. 4) ; niais elle ne lui est pas égale ; donc l'angle BAC n'est pas égal à l'angle EDF. L'angle BAC n'est pas plus petit que l'angle EDF, car s'il était plus petit, la base BC serait plus petite que la base EF (prop. 24) ; or elle n’est pas plus petite : donc l'angle BAC n'est pas plus petit que l'angle EDF. Mais il a été démontré qu'il ne lui est pas égal : donc l'angle BAC est plus grand que l'angle EDF.

Donc si deux triangles ont deux côtés égaux, chacun à chacun, et si la base de l'un est plus grande que la base de l'autre, ils auront aussi les angles compris entre les côtés égaux plus grands l'un que l'autre ; ce qu'il fallait démontrer.

PROPOSITION XXVI.

THÉORÈME.

Si deux triangles ont deux angles égaux, chacun à chacun, s'ils ont de plus un coté égal à un côté, ou celui qui est adjacent aux angles égaux ou celui qui est opposé à un des angles égaux, ils auront les autres côtés égaux, chacun à chacun, et le troisième angle de l'un sera encore égal au troisième angle de l’autre.

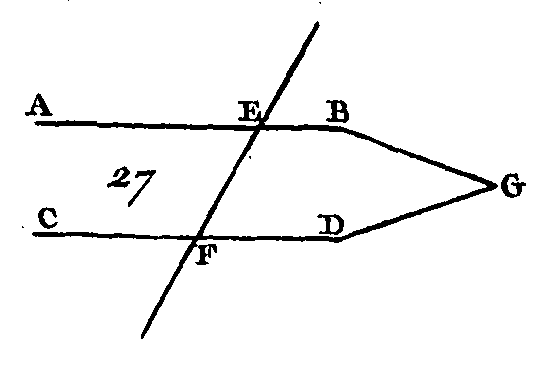
Soient ABC, DEF (fig. 26) deux triangles qui aient les deux angles ABC, BCA égaux aux deux angles DEF, EFD, chacun à chacun, c'est-à-dire l'angle ABC égal à l'angle DEF et l'angle BCA égal à l'angle EFD ; que ces deux triangles aient aussi un côté égal à un côté, et d'abord celui qui est adjacent aux angles égaux, c'est-à-dire le côté BC égal au côté EF : je dis qu'ils auront les autres côtés égaux aux autres côtés, chacun à chacun, c'est-à-dire le côté AB égal au côté DE, et le côté AC égal au côté DF; je dis de plus que l'angle BAC sera encore égal à l'angle EDF.

Car si le côté AB n'est pas égal au côté DE, l'un de ces côtés sera plus grand que l'autre. Soit AB le plus grand côté ; faites la droite GB égale au côté DE (prop. 3), et conduisez la droite GC.

Puisque le côté BG est égal au côté DE, et le côté BC égal au côté EF, les deux côtés BG, BC sont égaux aux deux côtés DE, EF, chacun à chacun ; mais l'angle GBC est égal à l'angle DEF : donc la base GC est égale à la base DF (prop. 4); le triangle GCB est égal au triangle DEF, et les autres angles qui sont opposés à des côtés égaux sont aussi égaux entre eux : donc l'angle GCB est égal à l'angle DFE ; mais l'angle DFE est supposé égal à l'angle BCA : donc l'angle BCG est égal à l'angle BCA, c'est-à-dire que le plus petit est égal au plus grand, ce qui est impossible : donc les côtés AB et DE ne sont pas inégaux : donc ils sont égaux ; ruais le côté BG est égal au côté EF : donc les deux côtés AB, BC sont égaux aux deux côtés DE, EF, chacun à chacun; mais l'angle ABC est égal à l'angle DEF : donc la base AC est égale à la base DF (prop. 4), et le troisième angle BAC est égal au troisième angle EDF.

Supposons à présent que les côtés qui sont opposés aux angles égaux soient égaux, c'est-à-dire le côté AB égal au côté DE : je dis que les autres côtés de l'un de ces triangles sont encore égaux aux autres côtés de l'autre triangle; c'est-à-dire que le côté AC sera égal au côté DF, le côté BC égal au côté EF, et le troisième BAC égal aussi au troisième angle EDF.

Car si le côté BC n'est pas égal au côté EF, l'un de ces côtés sera plus grand que l'autre. Supposons s'il est possible que BC soit le plus grand ; faites BH égal au côté EF (prop. 3), et conduisez la droite AH.

Puisque le côté BH est égal au côté EF et le côté AB égal au côté DE, les deux côtés AB, BH seront égaux aux deux côtés DE, EF, chacun à chacun ; mais ces côtés comprennent des angles égaux : donc la base AH est égale à la base DF (prop. 4) 5 le triangle ABH est égal au triangle DEF, et les autres angles qui sont opposés à des côtés égaux seront aussi égaux, chacun à chacun : donc l'angle BHA est égal à l'angle EFD; mais par supposition l'angle EFD est égal à l'angle BGA : donc l'angle BHA est égal à l'angle BCA, c'est-à-dire que l'angle extérieur BHA du triangle ACH est égal à l'angle BCA intérieur et opposé ; ce qui est impossible (prop. 16) : donc les côtés BG et EF ne sont pas inégaux : donc ils sont égaux. Mais le côté AB est égal au côté DE : donc les deux côtés AB, BC sont égaux aux deux côtés DE, EF, chacun à chacun ; mais ces côtés comprennent des angles égaux : donc la base AC est égale à la base DF (prop. 4) ; le triangle ABC est égal au triangle DEF, et le troisième angle BAC égal aussi à un troisième angle EDF.

Donc si deux triangles ont deux angles égaux, chacun à chacun, et un côté quelconque égal à un côté, ou celui qui est adjacent aux angles égaux, ou celui qui est opposé à un des angles égaux, les autres côtés sont égaux aux autres côtés, chacun à chacun, et ces deux triangles auront un troisième angle égal à un troisième angle ; ce qu'il fallait démontrer.

PROPOSITION XXVII.

THÉORÈME.

Si une droite tombant sur deux autres droites fait les angles alternes égaux entre eux, ces deux droites seront parallèles.

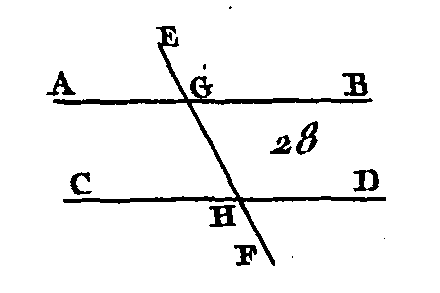
Que la droite EF (fig. 27) tombant sur les deux droites AB, CD fasse les angles alternes AEF, EFD égaux entre eux : je dis que la droite AB est parallèle à la droite CD.

Car si elle ne lui est pas parallèle, les droites AB, CD étant prolongées se rencontreront ou du côté BD ou du côté AC. Prolongez ces droites, et supposons qu'elles se rencontrent du côté BD au point G.

L'angle AEF, qui est hors du triangle EGF, est plus grand que l'angle intérieur et opposé EFG (prop. 16) ; mais par supposition il lui est égal, ce qui est impossible : donc les droites AB, CD prolongées du côté BD ne se rencontreront point. On démontrerait de la même manière qu'elles ne se rencontreront pas non plus du côté AC ; or les droites qui ne se rencontrent d'aucun côté sont parallèles (déf. 25) : donc la droite AB est parallèle à la droite CD.

Donc si une droite tombant sur deux autres droites fait les angles alternes égaux entre eux, ces deux droites seront parallèles ; ce qu'il fallait démontrer.

PROPOSITION XXVIII.

THÉORÈME.

Si une droite tombant sur deux autres droites fait un angle extérieur égal à un angle intérieur opposé et placé du même côté, ou bien si elle fait les angles intérieurs et placés du même côté égaux à deux droits, ces deux droites seront parallèles.

Que la droite EF (fig. 28) tombant sur les deux droites AB, CD fasse l'angle extérieur EGB égal à l'angle intérieur opposé et placé du même côté GHD, ou bien les angles intérieurs et placés du même côté BGH, GHD égaux à deux droits : je dis que la droite AB est parallèle à la droite CD.

Car puisque l'angle EGB est égal à l'angle GHD, et que l'angle EGB est égal à l'angle AGH (prop. 15), l'angle AGH sera égal à l'angle GHD; mais ces angles sont alternes: donc la droite AB est parallèle à la droite CD (prop. 27).

De plus, puisque les angles BGH, GHD sont égaux à deux droits, et que les angles AGH, BGH sont encore égaux à deux droits (prop. 13), les angles AGH, BGH seront égaux aux angles BGH, GHD. Donc si nous retranchons l'angle commun BGH, l'angle restant AGH sera égal à l'angle restant GHD; mais ces deux angles sont alternes : donc la droite AB est parallèle à la droite CD (prop. 27).

Donc si une droite tombant sur deux autres droites fait un angle extérieur égal à un angle intérieur opposé et placé du même côté, ou si elle fait les angles intérieurs et placés du même côté égaux à deux droits, ces droites seront parallèles ; ce qu'il fallait démontrer.

PROPOSITION XXIX.

THÉORÈME.

Si une droite tombe sur deux parallèles, les angles alternes sont égaux entre eux, l'angle extérieur est égal à l'angle intérieur opposé et placé du même côté, et les angles intérieurs placés du même côté sont égaux à deux droits.

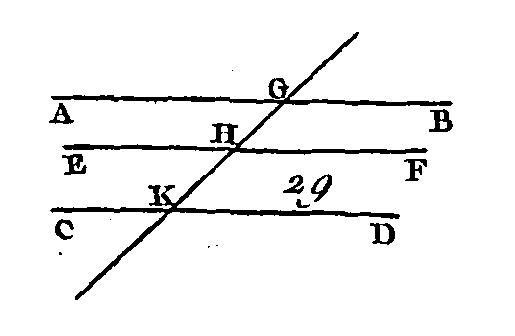
Si la droite EF (fig. 28) tombe sur les parallèles AB, CD, je dis que les angles alternes AGH, GHD seront égaux entre eux, l'angle extérieur EGB sera égal à l'angle intérieur opposé et placé du même côté GHD, et les angles intérieurs et placés du même côté BGH, GHD seront égaux à deux droits.

Car si l'angle AGH n'est pas égal à l'angle GHD, l'un de ces angles sera plus grand. Que l'angle AGH soit le plus grand; puisque l'angle AGH est plus grand que l'angle GHD, si on leur ajoute un angle commun BGH, les angles AGH, BGH seront plus grands que les angles BGH, GHD ; mais les angles AGH, BGH sont égaux à deux droits (prop. 13) : donc les angles BGH, GHD sont moindres que deux droits ; mais deux droites étant prolongées à l'infini du côté où les angles intérieurs sont plus petits que deux droits se rencontrent entre elles (ax. 11) : donc les droites AB, CD prolongées à l'infini se rencontreront ; mais elles ne se rencontreront pas puisqu'elles sont parallèles : donc les angles AGH, GHD né sont point inégaux, donc ils sont égaux. Mais l'angle AGH est égal à l'angle EGB (prop. 15) : donc l'angle EGB sera égal à l'angle GHD. Donc si nous ajoutons un angle commun BGH, les angles EGB, BGH seront égaux aux angles BGH, GHD ; mais les angles EGB, BGH sont égaux à deux droits (prop. 13) : donc les angles BGH, GHD sont égaux à deux droits.

Donc si une droite tombe sur deux parallèles, les angles alternes sont égaux entre eux, l'angle, extérieur est égal à l'angle intérieur opposé et placé du même côté, et les angles intérieurs placés du même côté sont égaux à deux droits ; ce qu'il fallait démontrer.

PROPOSITION XXX.

THÉORÈME.

Les droites qui sont parallèles à une même droite sont parallèles entre elles.

Que chacune des droites AB, CD (fig. 29) soit parallèle à la droite EF : je dis que la droite AB est parallèle à la droite CD.

Conduisez sur ces droites la droite GK.

Puisque la droite GK tombe sur les parallèles AB, EF, l'angle AGH est égal à l'angle GHF (prop. 27). De plus puisque la droite GK tombe sur les parallèles EF, CD, l'angle GHF est égal à l'angle GKD (prop. 28). Or il a été démontré que l’angle AGK est égal à l'angle GHF : donc l'angle AGK est égal à l'angle GKD; mais ces angles sont alternes : donc la droite AB est parallèle à la droite CD (prop. 29).

Donc les droites qui sont parallèles à une même droite sont parallèles entre elles ; ce qu'il fallait démontrer.

PROPOSITION XXXI.

PROBLÈME.

Par un point donné conduire une droite parallèle à une droite donnée.

Soit A (fig. 30) le point donné et BC la droite donnée : il faut par le point A conduire une droite parallèle à la droite BC.

Prenez sur la droite BC un point quelconque t), et menez AD ; construisez sur la droite DA et en tin point A un angle DAE égal à l'angle ADC, et prolongez la droite AF dans la direction de EA.

Puisque la droite AD tombant sur les deux droites BC, EF fait les angles alternés EAD, ADC égaux entre eux, la droite BC sera parallèle à la droite EF (prop. 27).

Donc par le point donné A, la droite EAF a été menée parallèle à la droite donnée BC, ce qu'il fallait faire.

PROPOSITION XXXII.

THÉORÈME,

Ayant prolongé un côté d'un triangle quelconque, l'angle extérieur est égal aux deux angles intérieurs et opposés, et les trois angles intérieurs du triangle sont égaux à deux droits.

Soit le triangle ABC (fig. 31) ; prolongez le côté BC vers D : je dis que l’angle extérieur ACD est égal aux deux angles intérieurs et opposés CAB, ABC, et que les trois angles intérieurs ABC, BCA, CAB sont égaux à deux droits.

Menez par le point C la droite CE parallèle à la droite AB (prop. 21),

Puisque la droite CE est parallèle à la droite AB et que la droite AC tombe sur ces deux droites, les angles alternes BAC, ACE sont égaux entre eux (prop. 29). De plus, puisque la droite AB est parallèle à la droite CE et que la droite BD tombe sur ces deux droites, l'angle extérieur ECD est égal à l'angle intérieur et opposé ABC. Or il a été démontré que l'angle ACE est égal à l'angle BAC : donc l'angle extérieur total ACD est égal aux deux angles extérieurs et opposés BAC, ABC.

Donc si on ajoute un angle commun ACB, les angles ACD, ACB seront égaux aux trois angles ACB, BCA, CAB; mais les angles ACD, ACB sont égaux à deux droits (prop. 13) : donc les angles ACB, CBA, CAB sont égaux à deux droits.

Donc, ayant prolongé un côté de tout triangle, l'angle extérieur est égal aux deux angles intérieurs et opposés, et les trois angles intérieurs du triangle sont égaux à deux droits; ce qu'il fallait démontrer.

PROPOSITION XXXIII.

THÉORÈME.

Les droites qui joignent des mêmes côtés des droites égales et parallèles sont elles-mêmes égales et parallèles.

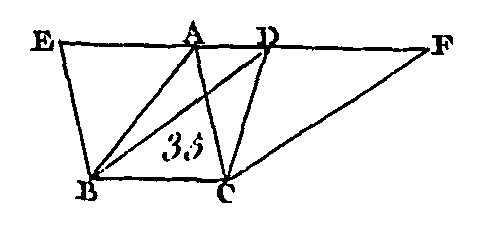
Soient AB, CD (fig. 32) deux droites égales et parallèles ; joignez-les des mêmes côtés par les droites AC, BD : je dis que les droites AC, BD sont aussi égales et parallèles.

Menez la droite BC.

Puisque la droite AB est parallèle à la droite CD et que la droite BC tombe sur ces deux droites, les angles alternes ABC, BCD sont égaux (prop. 29). De plus, puisque la droite AB est égale à la droite CD et que la droite BC est commune aux deux triangles BCA, BDC, les deux droites AB, BC sont égales aux deux droites CD, BC; mais l'angle ABC est égal à l'angle BCD : donc la base AC est égale à la base BD, le triangle ABC est égal au triangle BCD, et les autres angles qui sont opposés à des côtés égaux sont égaux, chacun à chacun : donc l'angle ACB est égal à l'angle CBD. Donc puisque la ligne droite BC tombant sur deux droites AC, BD fait les angles alternes égaux entre eux, la droite AC est parallèle à la droite BD et lui est égale (prop. 27).

Donc les droites qui joignent des mêmes côtés deux droites égales et parallèles, sont elles-mêmes égales et parallèles ; ce qu'il fallait démontrer.

PROPOSITION XXXIV.

THÉORÈME.

Les côtés et les angles opposés des parallélogrammes sont égaux, et la diagonale les partage en deux parties égales.

Soit ACDB (fig. 32) un parallélogramme et BC sa diagonale : je dis que les côtés et les angles opposés du parallélogramme ACDB sont égaux, et que sa diagonale BC le partage en deux parties égales.

Car puisque la droite AB est parallèle à la droite CD et que la droite BC tombe sur ces deux droites, les angles alternes ABC, BCD seront égaux entre eux (prop. 29). De plus, puisque la droite AC est parallèle à la droite BD et que la droite BC tombe sur ces deux droites, les angles alternes ACB, CBD sont égaux entre eux ; donc les deux triangles ABC, CBD ont deux angles ABC, BCA égaux aux deux angles BCD, CBD, chacun à chacun, ils ont de plus un côté commun BC adjacent à des angles égaux: donc ils auront les autres côtés égaux aux autres côtés, chacun à chacun (prop. 26), et le troisième angle égal au troisième angle : donc le côté AB est égal au côté CD, et l'angle BAC égal à l'angle BDC. Puisque l’angle ABC est égal à l'angle BCD, et l'angle CBD égal à l'angle ACB, l'angle total ABD sera égal à l'angle total ACD: Mais il a été démontré que l'angle BAC est égal à l’angle BDC.

Donc les côtés et les angles opposés des parallélogrammes sont égaux entre eux.

Je dis de plus que la diagonale partage les parallélogrammes en deux parties égales. Car puisque la droite AB est égale à la droite CD et que la droite BC est commune aux deux triangles, les deux droites AB, BC seront égales aux droites DC, CB, chacune à chacune ; mais l'angle ABC est égal à l'angle BCD : donc la base AC est égale à la base BC (prop. 4), et le triangle ABC égal au triangle BCD.

Donc la diagonale BC partage le parallélogramme ACDB en deux parties égales ; ce qu'il fallait démontrer.

PROPOSITION XXXV.

THÉORÈME.

Les parallélogrammes qui sont construits sur la même base et entre les mêmes parallèles sont égaux entre eux.

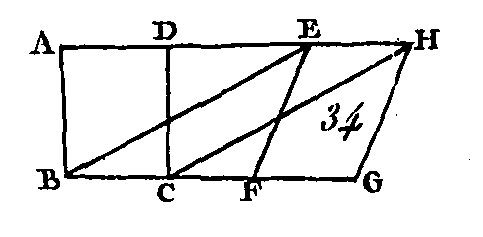
Soient les parallélogrammes ABCD, EBCF (fig. 33) construits sur la même base BC et entre les mêmes parallèles AF, BC : je dis que le parallélogramme ABCD est égal au parallélogramme EBCF.

Car puisque ABCD est un parallélogramme, la droite AD est égale à la droite B C (prop. 34), et par la même raison la droite EF est aussi égale à la droite B C : donc la droite AD est égale à la droite EF : donc, si on ajoute une droite commune DE, la droite totale AE sera égaler la droite totale DF (axiome 2) ; mais la droite AB est égale à la droite DC : donc les deux droites EA, AB sont égales aux deux droites FD, DC, chacune à chacune ; mais l'angle extérieur F'DC est égal à l'angle intérieur EAB (prop. 29) : donc la base EB est égale à la base FC (prop. 4), et le triangle EAB égal au triangle FDC ; donc si l’on retranche la partie commune DGE, le trapèze restant ABGD sera égal au trapèze restant EGCF. Donc si on leur ajoute le triangle commun GBC, le parallélogramme total ABCD sera égal au parallélogramme total EBCF.

Donc les parallélogrammes construits sur les mêmes bases et entre les mêmes parallèles sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXXVI.

THÉORÈME.

Les parallélogrammes construits sur des bases égales et entre les mêmes parallèles sont égaux entre eux.

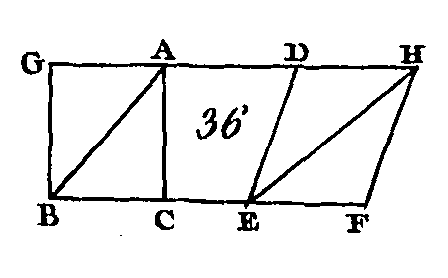
Soient les parallélogrammes ABCD, EFGH (fig. 34) construits sur des bases égales BC, FG et entre les mêmes parallèles AH, BG : je dis que le parallélogramme ABCD est égal au parallélogramme EFGH.

Conduisez les droites BE, CH.

Puisque la droite BC est égale à la droite FG et la droite FG égale à la droite EH, la droite BC sera égale à la droite EH ; mais les droites BC, EH sont parallèles et joignent les droites BE, CH ; or les droites qui joignent des mêmes côtés deux droites égales et parallèles, sont égales et parallèles (prop. 33) : donc les droites EB, CH sont égales, et parallèles : donc EBCH est un parallélogramme, et ce parallélogramme est égal au parallélogramme ABCD (prop. 35) ; car il a la même base BC que lui, et il est construit entre les mêmes parallèles. Par la même raison le parallélogramme EFGH est égal au parallélogramme EBCH ; donc le parallélogramme ABCD est égal au parallélogramme EFGH.

Donc les parallélogrammes construits sur des bases égales et entre les mêmes parallèles, sont égaux ; ce qu'il fallait démontrer.

PROPOSITION XXXVII.

THÉORÈME.

Les triangles construits sur la même base et entre les mêmes parallèles sont égaux.

Soient les triangles ABC, DEC (fig. 35) construits sur la même base BC et entre les mêmes parallèles AD, BC, je dis que le triangle ABC est égal au triangle DBC,

Prolongez de part et d'autre la droite AD vers les points E, F, et par le point B conduisez une droite BE parallèle à la droite CA (prop. 31), et par le point C conduisez aussi une droite CF parallèle à BD.

Les figures EBCA, DBCF sont des parallélogrammes, et le parallélogramme EBCA est égal au parallélogramme DBCF (prop. 35) ; car ils sont construits l'un et l'autre sur la même base et entre les mêmes parallèles ; mais le triangle ABC est la moitié du parallélogramme EBCA; car la diagonale AB le partage en deux parties égales; le triangle DBC est la moitié du parallélogramme DBCF, car la diagonale DC la partage en deux parties égales (prop. 34) ; mais, les moitiés des quantités égales sont égales; entre elles ; donc le triangle ABC est égal au triangle DBC.

Donc les triangles construits sur la même base et entre les mêmes parallèles sont égaux entre eux; ce qu'il fallait démontrer.

PROPOSITION XXXVIII.

THÉORÈME.

Les triangles construits sur des bases égales et entre les mêmes parallèles sont égaux entre eux.

Soient les triangles ABC, DEF (fig. 36) construits sur des bases égales BC, EF et entre les mêmes parallèles BF, AD : je dis que le triangle ABC est égal au triangle DEF.

Car prolongez de part et d'autre la droite AD vers les points G, H; par le point B conduisez la droite BG parallèle à la droite CA (prop. 31), et par le point F conduisez aussi la droite FH parallèle à la droite DE.

Les figures GBCA, DEFH sont des parallélogrammes ; mais les parallélogrammes GBCA, DEFH sont égaux entre eux (prop. 36), car ils sont construits sur des bases égales et entre les mêmes parallèles. Or le triangle ABC est la moitié du parallélogramme GBCA, car la diagonale AB le partage en deux parties égales (prop. 34); le triangle EFD est la moitié du parallélogramme DEFH, car la diagonale DF le partage en deux parties égales ; mais les moitiés des quantités égales sont égales entre elles : donc le triangle ABC est égale au triangle DEF.

Donc les triangles construits sur des bases égales et entre les mêmes parallèles sont égaux entre eux ; ce qu'il fallait démontrer.

PROPOSITION XXXIX.

THÉORÈME.

Les triangles égaux qui sont construits sur la même base et qui sont placés du même côté sont compris entre les mêmes parallèles.

Soient les deux triangles égaux ABC, DBC (fig. 37) construits sur la même base BC et placés du même côté : je dis que ces deux triangles sont compris entre les mêmes parallèles.

Conduisez la droite AD : je dis que la droite AD est parallèle à la droite BC.

Car si la droite AD n'est pas parallèle à la droite BC, conduisez par le point A une droite AE parallèle à la droite BC (prop. 31); conduisez ensuite la droite EC.

Le triangle ABC est égal au triangle EBC (prop. 37), car ces deux triangles sont construits sur la même base BC, et compris entre les mêmes parallèles BC, AE. Mais par hypothèse le triangle ABC est égal au triangle DBC: donc le triangle EBC est égal au triangle DBC, c'est à-dire que le plus grand est égal au plus petit, ce qui ne peut se faire : donc la droite AE n'est point parallèle à la droite BC. Nous démontrerons de même que toute autre droite, excepté AD, ne peut être parallèle à BG : donc la droite AD est parallèle à la droite BC.

Donc les triangles égaux qui sont construits sur la même base et qui sont placés du même côté sont compris entre les mêmes parallèles ; ce qu'il fallait démontrer.

PROPOSITION XL.

THÉORÈME.

Les triangles égaux qui sont construits sur des bases égales et qui sont placés du même côté sont compris entre les mêmes parallèles.

Soient les triangles égaux ABC, CDE (fig. 38) construits sur des bases égales. BC, CE et placés du même côté : je dis qu'ils sont compris; entre les mêmes parallèles. Conduisez la droite AD: je dis que la droite AD est parallèle à la droite BE.

Car si la droite AD n'est pas parallèle à la droite BE, conduisez par le point A la droite AF parallèle à la droite BC, et conduisez ensuite la droite FE.

Le triangle ABC est égal au triangle FCE (prop. 38) ; car ces deux triangles sont construits sur des bases égales et compris entre les mêmes parallèles BE, AF ; mais le triangle ABC est égal au triangle DCE : donc le triangle DCE est égal au triangle FCE, c'est-à-dire que le plus grand est égal au plus petit, ce qui ne peut être : donc la droite AF n'est point parallèle à la droite BE. Nous démontrerons de la même manière que toute autre droite, excepté AD, ne peut être parallèle à BF : donc la droite AD est parallèle à la droite BE.

Donc les triangles égaux qui sont construits sur des bases égales et qui sont placés du même côté sont compris entre les mêmes parallèles ; ce qu'il fallait démontrer.

PROPOSITION XLI.

THÉORÈME.

Si un parallélogramme et un triangle ont la même: base et sont compris entre les mêmes parallèles, le parallélogramme est double du triangle.

En effet, que le parallélogramme ABCD et le triangle EBC (fig. 39) aient la même base et soient compris l'un et l'autre entre les mêmes parallèles BC, AE ; je dis que le parallélogramme ABCD est double du triangle BEC.

Conduisez la droite AC. Le triangle ABC est égal au triangle EBC (prop. 37), car ces deux triangles, sont construits sur la même base BC et compris entre les mêmes parallèles BC, AE ; mais le parallélogramme ABCD est double du triangle ABC, car la diagonale AC partage ce parallélogramme en deux parties égales (prop. 34) : donc le parallélogramme ABCD est aussi double du triangle EBC.

Donc si un parallélogramme et un triangle ont la même base et sont compris entre les mêmes parallèles, le parallélogramme sera double du triangle ; ce qu'il fallait démontrer.

PROPOSITION XLII.

PROBLÈME.

Construire dans un angle donné, un parallélogramme égal à un triangle donné.

Soit ABC (fig. 40) le triangle donné et D l'angle donné : il faut construire un parallélogramme qui soit égal au triangle ABC dans un angle égal à l'angle donné D.

Partagez la droite BC en deux parties égales au point E et conduisez la droite AE ; sur la droite EC et au point E construisez un angle CEF égal à l'angle D (prop. 23), par le point A conduisez une droite AG parallèle à la droite EC (prop. 31), et par le point C conduisez aussi une droite CG parallèle à la droite FE : la figure FECG sera un parallélogramme.

Puisque la droite BE est égale à la droite EC, le triangle ABE sera égal au triangle AEG (prop. 38), car ces deux triangles sont construits sur des bases égales BE, EC, et compris entre les mêmes parallèles BC, AG : donc le triangle ABC est double du triangle AEC ; mais le parallélogramme FECG est double du triangle AEC, car ils ont la même base et ils sont compris entre les mêmes parallèles : donc le parallélogramme FECG est égal au triangle ABC (ax. 6), et il a un angle égal à l'angle D.

Donc le parallélogramme FECG a été construit égal au triangle ABC dans un angle CEF égal à l'angle donné D ; ce qu'il fallait faire.

PROPOSITION XLIII.

THÉORÈME.

Dans tout parallélogramme, les compléments des parallélogrammes qui sont autour de la diagonale sont égaux entre eux.

Soit le parallélogramme ABCD (fig. 41) dont AC est la diagonale autour de laquelle sont les parallélogrammes EH, FG, et les parallélogrammes BK, KD qu'on appelle compléments : je dis que le complément BK est égal au complément KD.

Car puisque la figure ABCD est un parallélogramme dont la droite AC est la diagonale, le triangle ABC est égal au triangle ADC (prop. 34). De plus, puisque la figure EKHA est un parallélogramme dont la droite AK est la diagonale, le triangle AEK est égal au triangle AHK; le triangle KFG est égal au triangle EGC, par la même raison : donc puisque le triangle AEK est égal au triangle AHK, et que le triangle KFC est aussi égal au triangle KGC, le triangle AEK, réuni avec le triangle KGC, est égal au triangle AHK réuni avec le triangle KFC; mais le triangle total ABC est égal au triangle total ADC : donc les restes BK, KD, qu'on appelle compléments, sont égaux entre eux (axiome 3).

Donc dans tout parallélogramme, les compléments des parallélogrammes qui sont autour de la diagonale sont égaux entre eux; ce qu'il fallait démontrer.

PROPOSITION XLIV.

PROBLÈME.

Sur une droite donnée et dans un angle donné, construire un parallélogramme qui soit égal à un triangle donné.

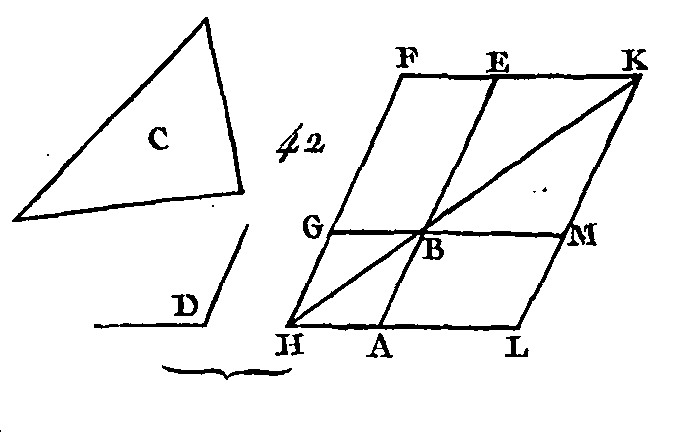
Soient donnés la droite AB (fig. 42), le triangle C et l'angle D : il faut sur la droite AB et dans un angle égal à l'angle D, construire un parallélogramme égal au triangle donné C.

Construisez un parallélogramme BEFG égal au triangle C ; dans un angle EBG égal à l'angle D (prop. 42); placez la droite BE dans la direction de la droite AB; prolongez la droite FG vers H ; et par le point A conduisez la droite AH parallèle à la droite BG ou à la droite EF (prop. 31), et menez la droite GB. Puisque la droite HF tombe sur les parallèles AH, EF, les angles AHF, HFE sont égaux à deux angles droits (prop. 29) : donc les angles BHG, GFE sont moindres que deux angles droits; mais les droites qui sont prolongées à l'infini du coté où les angles intérieurs sont moindres que deux angles droits se rencontrent (ax. 11) : donc les droites HB, FE se rencontreront étant prolongées ; que ces deux droites soient pro longées (dem. 2), et supposons qu'elles se rencontrent en K; par le point K conduisez la droite KL parallèle à la droite EA ou à la droite FH (prop. 31), et prolongez les droites AH, GB vers les points L, M.

La figure HLKF est un parallélogramme dont HK est la diagonale ; autour de la diagonale, HK sont les parallélogrammes AG, ME, et les parallélogrammes LB, BF, qu'on nomme compléments: donc le parallélogramme LB est égal au parallélogramme BF (prop. 43); mais le parallélogramme BF est égal au triangle C ; donc le parallélogramme LB sera égal au triangle C ; et puisque l'angle GBE est égal à l'angle ABM (prop. 15) et que l'angle GBE est égal à l'angle D, l’angle ABM sera égal à l'angle D.

Donc sur la droite donnée AB et dans un angle ABM égal à l'angle D, le parallélogramme LB a été construit égal au triangle donné C ; ce qu'il fallait faire.

PROPOSITION XLV.

PROBLÈME.

Construire, dans un angle donné, un parallélogramme qui soit égal à une figure rectiligne donnée.

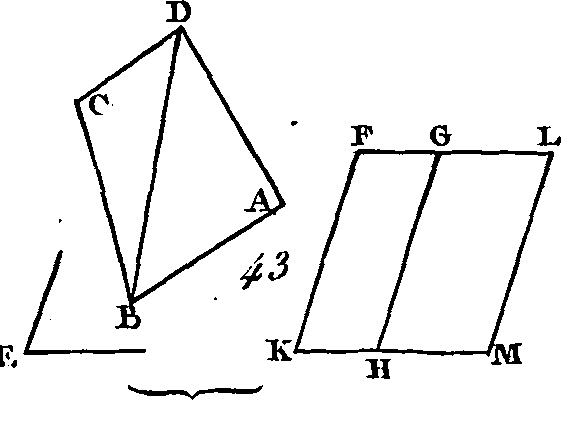
Soit ABCD (fig. 43) la figure rectiligne donnée et E l'angle donné : il faut, dans un angle égal à l'angle E, construire un parallélogramme qui soit égal à la figure ABCD.

Conduisez la droite DB, et construisez dans l'angle HKF égal à l'angle E, un parallélogramme FH qui soit égal au triangle ADB, et sur la droite GH construisez ensuite dans l’angle GHM égal à l'angle E, un parallélogramme GM qui soit égal au triangle DBC.

Puisque l'angle E est égal à chacun des angles HKF, GHM, l'angle GHM sera égal, à l'angle HKF : donc si nous leur ajoutons l'angle commun KHG, les angles FKH, KHG seront égaux aux angles KHG, GHM. Mais les angles FKH, KHG sont égaux à deux angles droits (prop. 29) : donc les angles KHG, GHM seront égaux à deux angles droits. Mais puisque les deux droites KH, HM, placées de différents côtés, font sur la droite GH et au point H de cette droite, deux angles de suite égaux à deux droits, la droite KH est dans la direction de la droite HM (prop. 14) ; et puisque la droite HG tombe sur les parallèles KM, PG, les angles alternes MHG, HGF sont égaux (prop. 29) ; donc si nous leur ajoutons l'angle commun HGL, les angles MHG, HGL seront égaux aux angles HGF, HGL. Mais les angles MHG, HGL sont égaux à deux angles droits (prop. 29) ; donc les angles HGF, HGL seront aussi égaux à deux angles droits ; donc la droite FG est dans la direction de la droite GL; et puisque la droite KF est égale et parallèle à la droite HG, et que la droite HG est aussi égale et parallèle à la droite ML, la droite KF sera égale et parallèle à la droite ML (ax. 1 et prop. 30). Mais ces deux droites sont jointes ensemble par les droites RM, FL : donc les droites KM, FL sont égales et parallèles (prop. 33) : donc la figure KFLM est un parallélogramme ; mais comme le triangle ABD est égal au parallélogramme HF, et que le triangle ABC est égal au parallélogramme GM, la figure totale ABCD sera égale au parallélogramme total KFLM.

Donc le parallélogramme KFLM a été construit égal à la figure rectiligne ABCD, dans l’angle FKM égal à l’angle donné E ; ce qu'il fallait faire.

PROPOSITION XLVI.

PROBLÈME.

Décrire un carré sur une droite donnée.

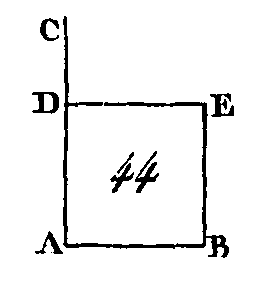
Soit AB (fig. 44) la droite donnée : il faut décrire un carré sur cette droite.

Du point A, donné dans la droite AB, conduisez une droite AC perpendiculaire sur la droite AB (prop. 11) ; faites la droite AD égale à la droite AB (prop. 31); par le point D conduisez la droite DE parallèle à la droite AB (prop. 31), et par le point B conduisez aussi une droite BE parallèle à la droite AD.

La figure ADEB est un, parallélogramme : donc la droite AB est égale à la droite DE, et la droite AD égale à la droite BE; mais la droite AB est égale à la droite AD : donc les quatre droites BA, AD, DE, EB sont égales entre elles : donc le parallélogramme ADEB, est équilatéral. Je dis de plus, qu'il est rectangle, car puisque la droite AD tombe sur les parallèles AB, DE, les angles BAD, ADE sont égaux à deux droits (prop. 29) ; mais l'angle BAD est droit par construction; donc l'angle ADE est droit aussi. Mais les côtés et angles opposés des parallélogrammes sont égaux (prop. 34) ; donc chacun des angles opposés ABE, BED est droit, et par conséquent le parallélogramme ADEB est rectangle ; mais nous avons démontré qu'il était équilatéral.

Donc le parallélogramme ADEB est un carré décrit sur la droite AB ; ce qu'il fallait faire.

PROPOSITION XLVII.

THÉORÈME.

Dans les triangles rectangles, le carré décrit sur le côté opposé à l'angle droit est égal aux carrés construits sur les côtés oui comprennent l'angle droit.

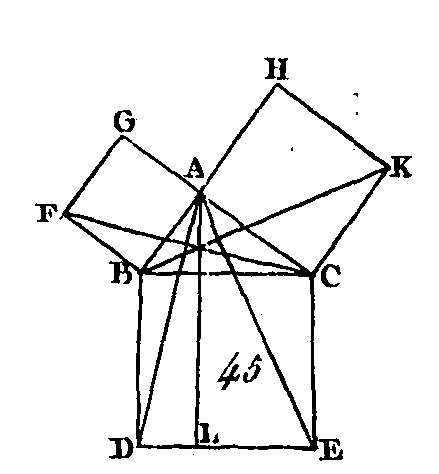
Soit ABC (fig. 45) un triangle rectangle dont l'angle droit est BAC : je dis que le carré construit sur le coté BC est égal aux carrés construits sur les côtés BA, AC.

Construisez le carré BDEC sur le côté BC; construisez aussi les deux carrés GB, HC sur les côtés BA, AC, et par le point A conduisez une droite AL parallèle à l'une ou à l'autre des droites BD, CE, conduisez ensuite les droites

Puisque chacun des angles BAC, BAG est droit et que les deux droites AC, AG, placées de part et d'autre de la droite BA, font au point A, avec la droite AB, deux angles de suite égaux à deux angles droits, la droite CA est dans la direction de la droite AG : la droite AB est dans la direction de la droite AH, par la même raison; et puisque l'angle DBC est égal à l'angle FBA (axiome 10), étant droits l'un et l'autre, si nous leur ajoutons un angle commun ABC, l'angle total DBA sera égal à l'angle total FBC ; mais les deux droites DB, BA étant égales aux deux droites CB, BF, chacune à chacune, et l'angle DBA égal à l'angle FBC, la base AD sera égale à la base FC, et le triangle ABD égal au triangle FBC (prop. 4). Or le parallélogramme BL est double du triangle ABD (prop. 41) car ils ont la même base BD et sont compris entre les mêmes parallèles BD, AL. Le carré GB est aussi double du triangle FBC, car ils ont la même base FB et sont compris entre les mêmes parallèles FB, GC, mais les quantités qui sont doubles de quantités égales sont égales entre elles : donc le parallélogramme BL est égal au carré GB.

Ayant conduit les droites AE, BK, nous démontrerons de la même manière que le parallélogramme CL est égal au carré HC : donc le carré total BDEC est égal aux deux carrés GB, HC ; mais le carré BDEC est construit sur le côté BC, et les carrés GB, HC sont construits sur les côtés BA, AC : donc le carré BE, construit sur le côté BC, est égal aux carrés construits sur les côtés BA, AC.

Donc dans les triangles rectangles, le carré construit sur le côté opposé à l'angle droit est égal aux deux carrés construits sur les côtés qui comprennent l'angle droit ; ce qu'il fallait démontrer.

PROPOSITION XLVIII.

THÉORÈME.

Si le carré qui est construit sur un des côtés d'un triangle est égal aux carrés construits sur les autres côtés du triangle, l'angle compris entre ces deux derniers côtés est droit.

Que le carré construit sur un côté BC (fig. 46) d'un triangle ABC, soit égal aux carrés construits sur les deux autres côtés BA, AC : je dis que l'angle BAC est droit.

Conduisez du point A une droite AD perpendiculaire sur la droite AC (prop. 11) ; faites la droite AD égale à la droite BA, et conduisez la droite DC.

Car puisque la droite DA est égale à la droite AB, le carré construit sur DA sera égal au carré construit sur AB. Donc si nous ajoutons un carré commun, celui qui est construit sur AC, les carrés construits sur DA, AC seront égaux aux carrés construits sur BA, AC. Mais le carré construit sur DC est égal aux carrés construits sur DA, AC (prop. 47) car l'angle DAC est droit. Or le carré construit sur BG est supposé égal aux carrés construits sur BA, AC : donc le carré construit sur DC est égal à celui qui est construit sur BC : donc le côté DC est égal au côté CB ; et comme le côté AD est égal au côté AB et que le côté AC est commun, les deux côtés AD, AC sont égaux aux deux côtés BA, BC, chacun à chacun; mais la base DC est égale à la base CB ; donc l'angle DAC est égal à l'angle BAC (prop. 8) ; mais l'angle DAC est droit : donc l'angle BAC est droit aussi.

Donc si le carré construit sur un côté d'un triangle est égal aux carrés construits sur les deux autres côtés, l'angle compris par ces deux derniers côtés sera droit ; ce qu'il fallait démontrer.

FIN DU PREMIER LIVRE.